Design of Container Ship Main Engine Waste Heat Recovery Supercritical CO2 Cycles, Optimum Cycle Selection through Thermo-Economic Optimization with Genetic Algorithm and Its Exergo-Economic and Exergo-Environmental Analysis
Abstract
1. Introduction
- The design and implementation of three novel supercritical cycles (a simple cycle, a split cycle, and a cascade cycle) are conducted in order to harness waste heat from a container ship main two-stroke diesel engine.
- An integrated thermodynamic, heat transfer, and economic analysis for all the newly designed cycles is performed.
- An optimization procedure is adopted using a genetic algorithm to select the optimal bottoming cycle from the three possible designs in terms of the minimum EPC.
- Exergo-economic and exergo-environmental analyses are carried out for the optimum cycle in order to assess its exergy cost rates and its key exergo-environmental indicators. These combined analyses were performed for the first time for a specially designed, optimized marine energy system.
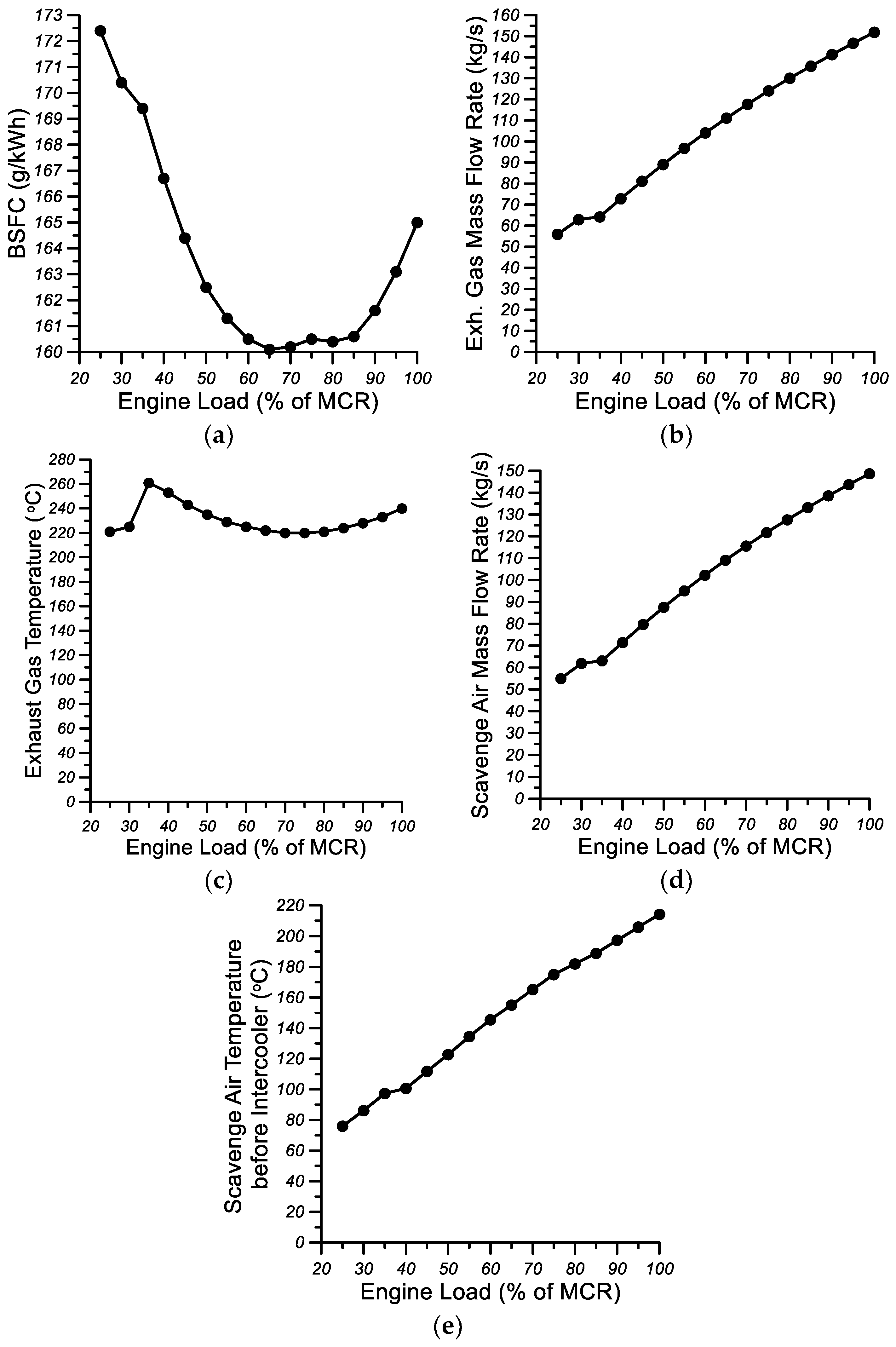
2. Description of the Examined Container Ship Main Diesel Engine
3. Brief Description of the Properties of CO2 as Working Medium
4. Description of Supercritical CO2 Cycles
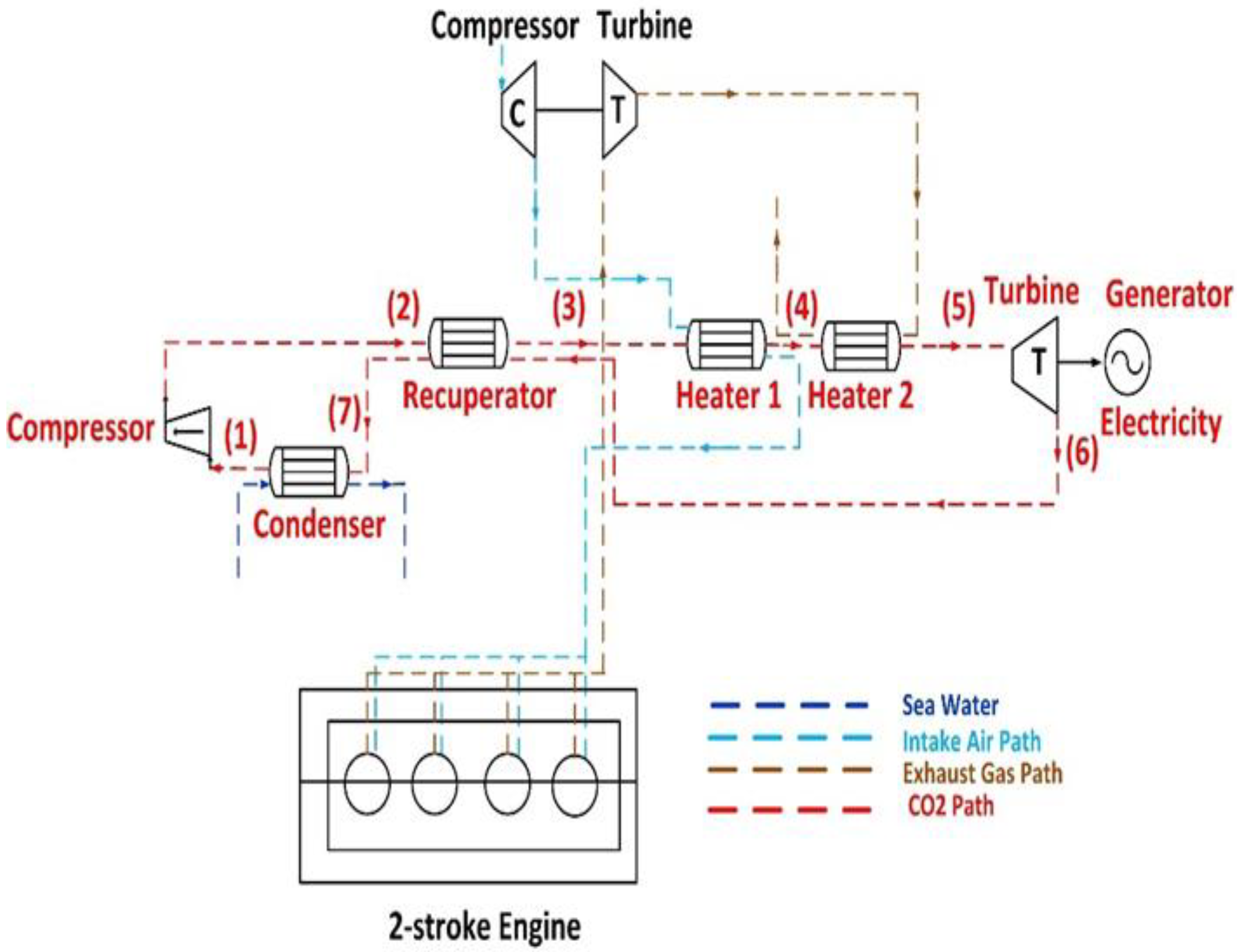
4.1. Description of a Simple Supercritical CO2 Cycle
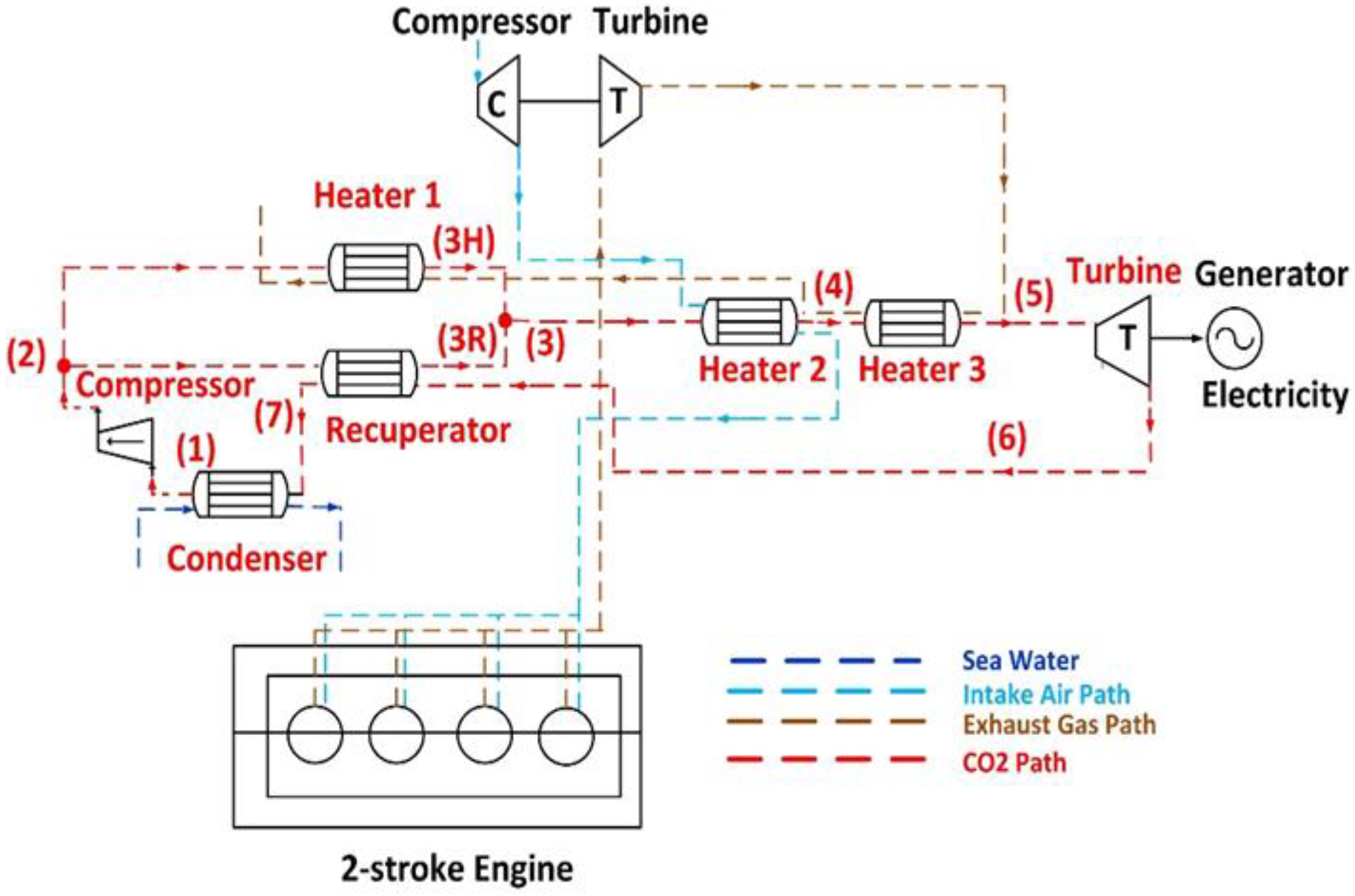
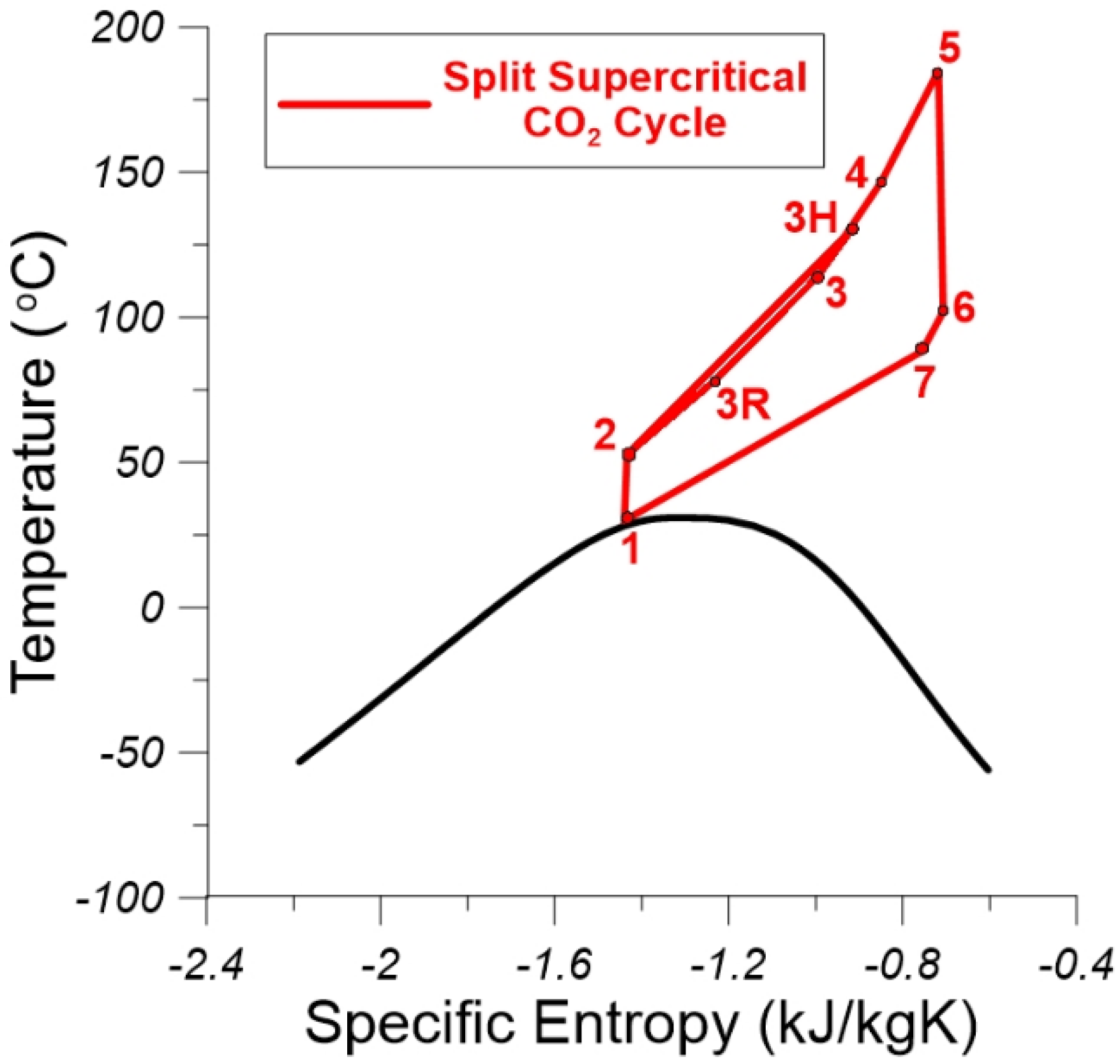
4.2. Description of the Split Supercritical CO2 Cycle
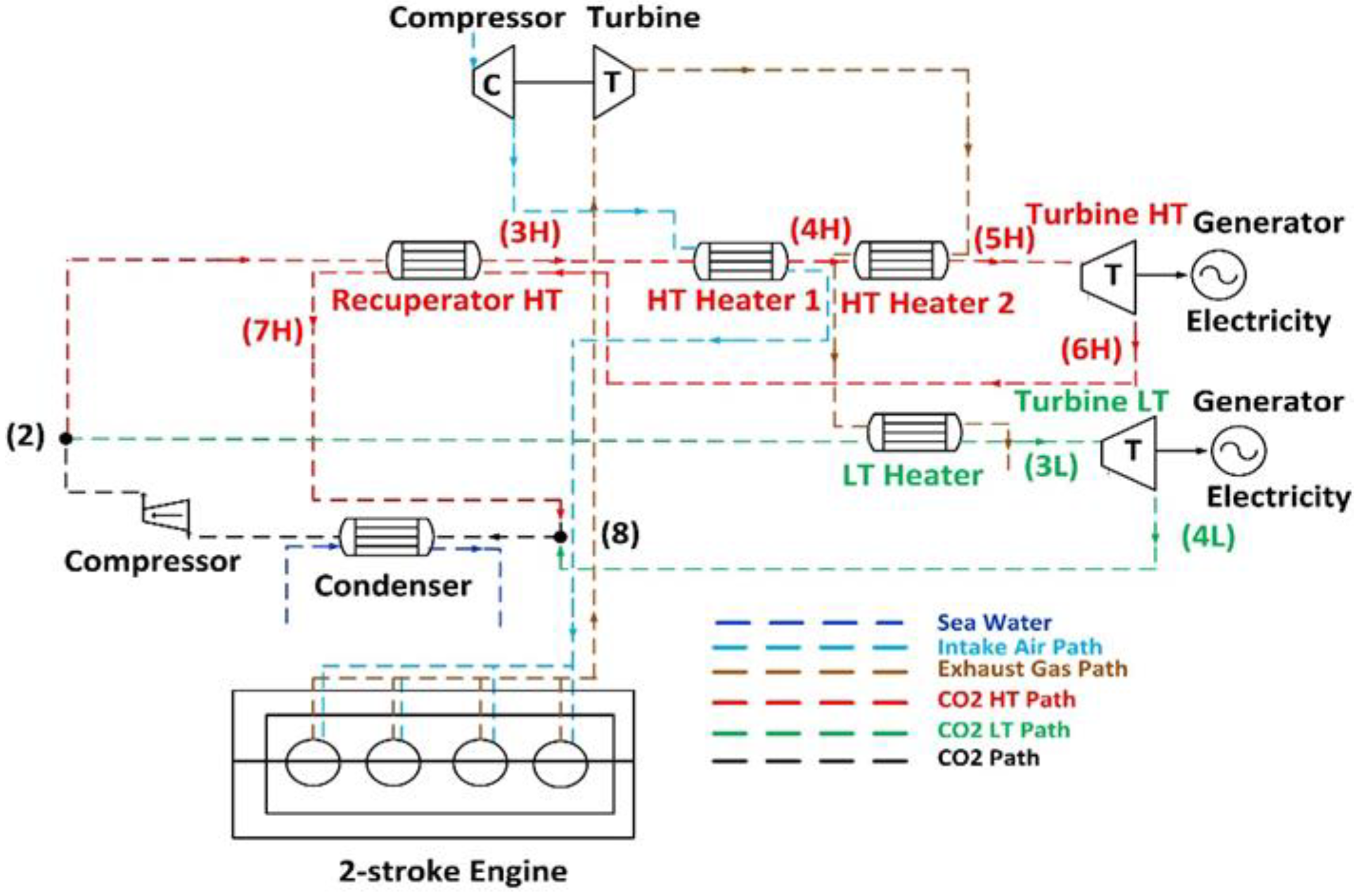
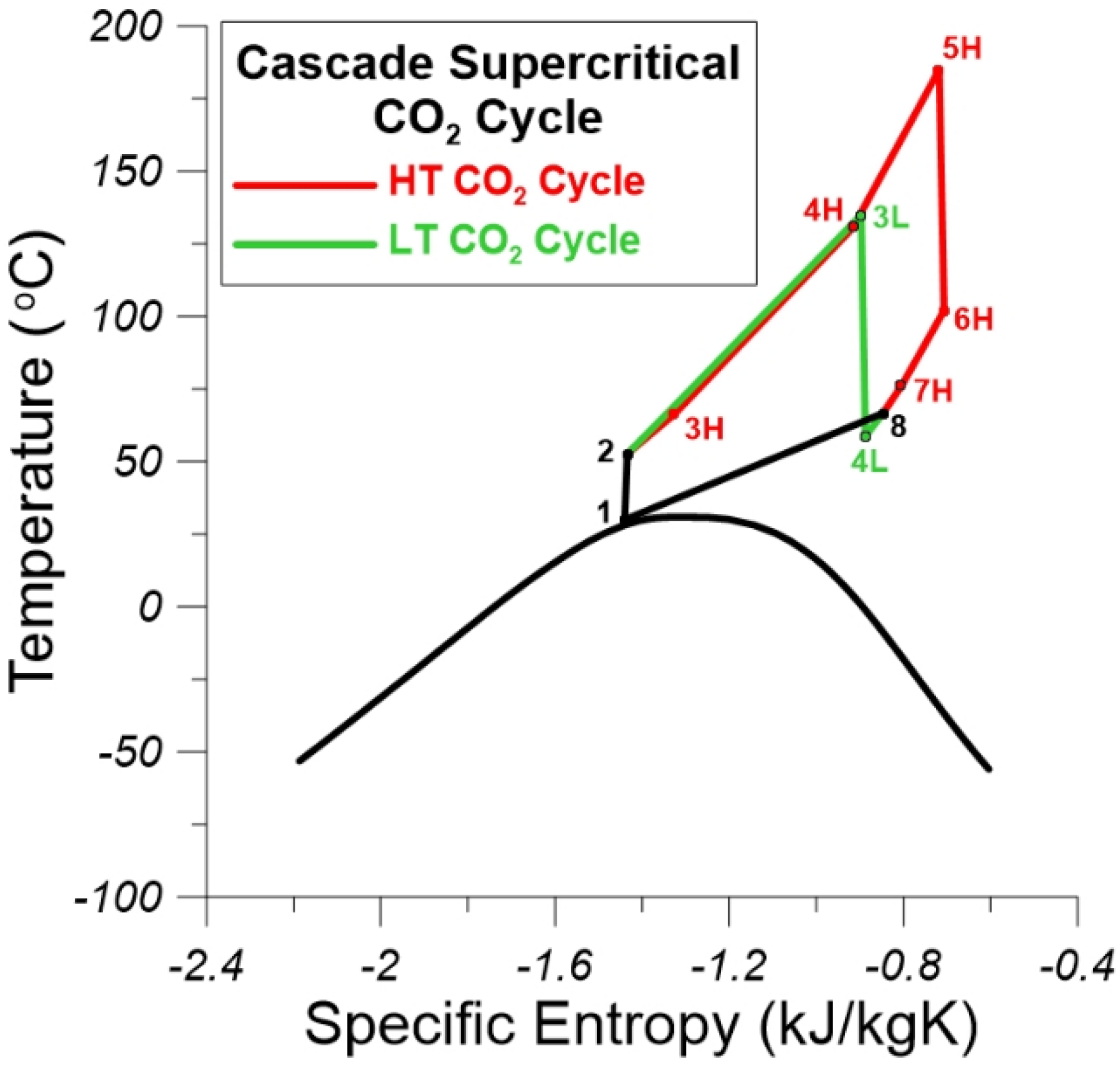
4.3. Description of the Cascade Supercritical CO2 Cycle
5. Energy and Exergy Analysis of the Three Examined Supercritical CO2 Cycles
5.1. Thermodynamic Processes of the Simple Supercritical CO2 Cycle
- Processes 1 and 2: The isentropic efficiency of the compressor and the mechanical power consumption are calculated as follows:
- Processes 2, 3, 6, and 7: The transferred specific heat in the recuperator from the ‘hot’ CO2 stream to the ‘cold’ CO2 stream may be calculated using the following equation:
- Processes 3 and 4: The transferred heat rate from the intake air after the turbocharger to the CO2 stream in Heater 1 may be calculated using the following equation:
- Processes 4 and 5: The transferred heat rate from the exhaust gas to the CO2 stream in Heater 2 may be calculated using the following equation:
- Processes 5 and 6: The isentropic efficiency of the turbine and the calculation of the produced power are depicted as follows:
- Processes 7 and 1: The rejected heat rate from the ‘hot’ CO2 stream to the sea water in the condenser may be calculated using the following equation:
5.2. Thermodynamic Processes of the Split Supercritical Cycle
- Processes 1 and 2: The isentropic efficiency of the compressor and the mechanical power consumption may be calculated in the same way as in the simple cycle.
- State 2: At this state, the stream is divided in two streams:
- Processes 2, 3R, 6, and 7: The transferred heat in the recuperator from the ‘hot’ CO2 stream to the ‘cold’ CO2 stream may be calculated using the following equation:
- Processes 2 and 3H: A part of the heat from the exhaust gas is recovered in Heater 1; this may be calculated using the following equation:
- State 3: Both streams are mixed at this state as follows:
- Processes 3 and 4: The transferred heat from the intake air after the turbocharger to the CO2 stream in Heater 2 may be calculated using the following equation:
- Processes 4 and 5: The remaining heat from the exhaust gas is recovered in the heater 3 and may be calculated as follows:
- Processes 5 and 6: The isentropic efficiency of the turbine and the produced power may be calculated in the same way as in the simple cycle.
- Processes 7 and 1: The rejected heat from the ‘hot’ CO2 stream to the sea water in the condenser may be calculated in the same way as in the simple cycle.
5.3. Thermodynamic Processes of the Cascade Supercritical Cycle
- Processes 1 and 2: The isentropic efficiency of the compressor and the mechanical power consumption are calculated in the same way as in the Split and the Cascade cycle.
- State 2: At this state, the main cycle is divided into two cycles, i.e., the High Temperature (HT) with mass flow:and the Low Temperature (LT) with mass flow:
- High Temperature Stream:
- ○
- Processes 2, 3H, 6H, and 7H: The transferred heat in the recuperator from the ‘hot’ HT CO2 stream to the ‘cold’ HT CO2 stream may be calculated using the following equation:
- ○
- Processes 3H and 4H: The transferred heat from the intake air after the turbocharger to the HT CO2 stream in HT Heater 1 may be calculated using the following equation:
- ○
- Processes 4H and 5H: A part of the heat from the exhaust gas is recovered in HT Heater 2, as may be calculated using the following equation:
- ○
- Processes 5H and 6H: The isentropic efficiency of the HT turbine and the produced power in the HT cycle are depicted as follows:
- Low Temperature Stream:
- ○
- Processes 2 and 3L: The remaining heat from the exhaust gas is recovered in the LT Heater and may be calculated as follows:
- ○
- Processes 3L and 4L: The isentropic efficiency of the LT turbine and the produced power in the LT cycle are depicted as follows:
- State 8: At this state, the HT and LT streams are mixed as follows:
- Processes 8 and 1: The rejected heat from the ‘hot’ CO2 stream to the sea water in the condenser may be calculated using the following relation:
5.4. Exergy Analysis
5.5. Model Assumptions
- Each of the proposed installations operates under steady state conditions.
- Pressure drops in the pipelines are negligible.
- The isentropic efficiency of each compressor and turbine is assumed to be 0.9.
- The effectiveness (ε) of each heat exchanger has been assumed to be 0.9.
- At dead state, and are set at 27 °C and 1 bar.
- The lowest limit of the outlet temperature of the exhaust gas is 150 °C, i.e., 30 °C higher than the dew point of the exhaust gas [21].
6. Heat Transfer Analysis and Dimensioning of Heat Exchangers
- The fouling resistance of internal CO2 stream rin in all plate heat exchangers is set at 0.0002, as proposed by Cao [22].
- The fouling resistance of external intake air flow rout is set at 0.0002 [22].
- The fouling resistance of the external exhaust gas flow rout is set at 0.002 [22].
- The fouling resistance of the external seawater flow rout is set at 0.00009 [22].
7. Economic Analysis
8. Optimization of the Supercritical Cycles with a Genetic Algorithm
- the pressure ratio in the compressor (phigh/plow).
- the pinch point temperature difference (PPTD) in the heat exchanger of the intake air
- the pinch point temperature difference (PPTD) in the heat exchanger of the exhaust gas, where it exits at an intermediate temperature (only in the split and cascade cycles)
- the pinch point temperature difference (PPTD) in the heat exchanger of the exhaust gas, where it exits at its final temperature
- the pinch point temperature difference (PPTD) in the recuperator
- the intermediate temperature of the exhaust gas (only in the split and cascade cycles)
- the final temperature of the exhaust gas
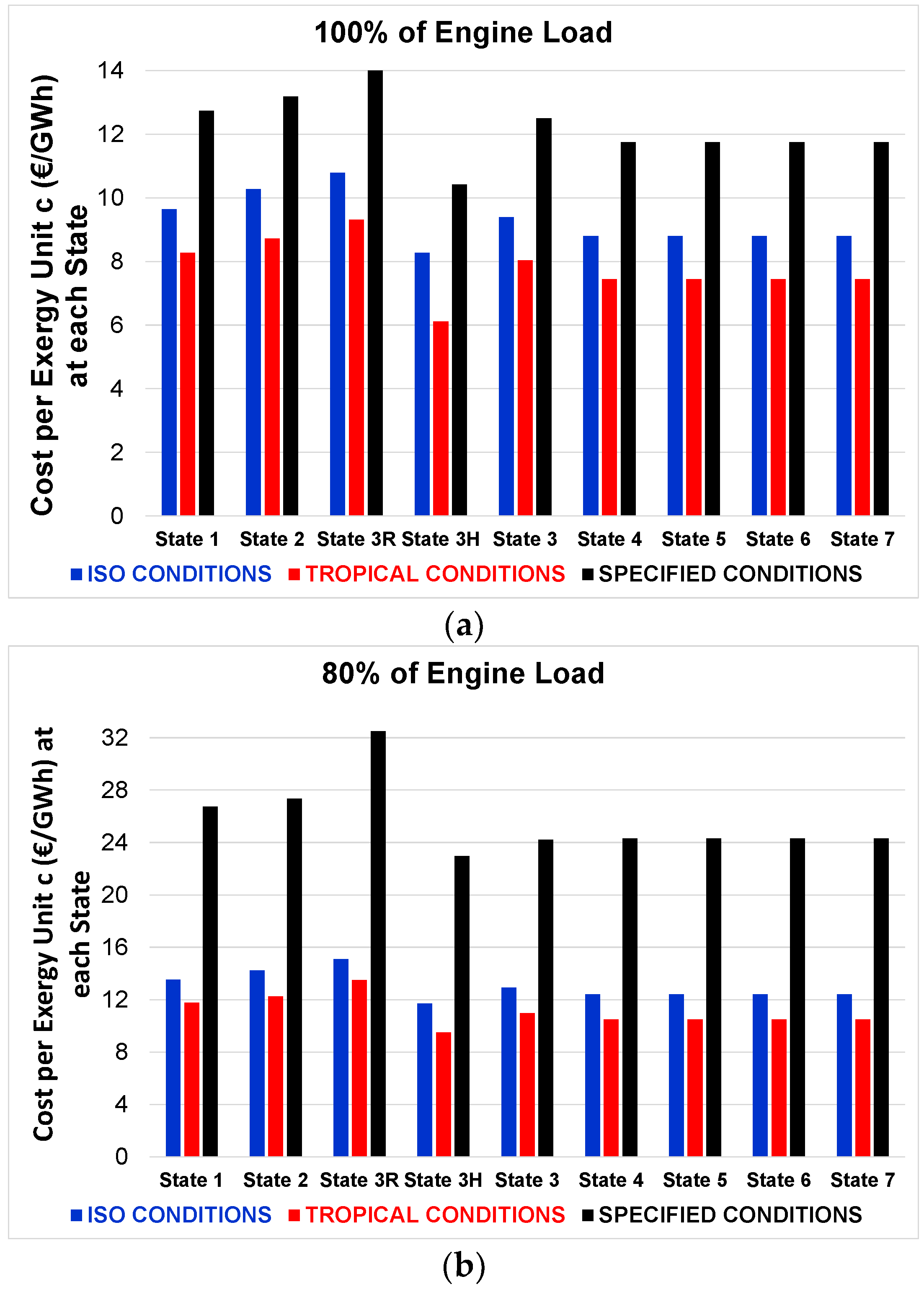
9. Exergo-Economic Analysis
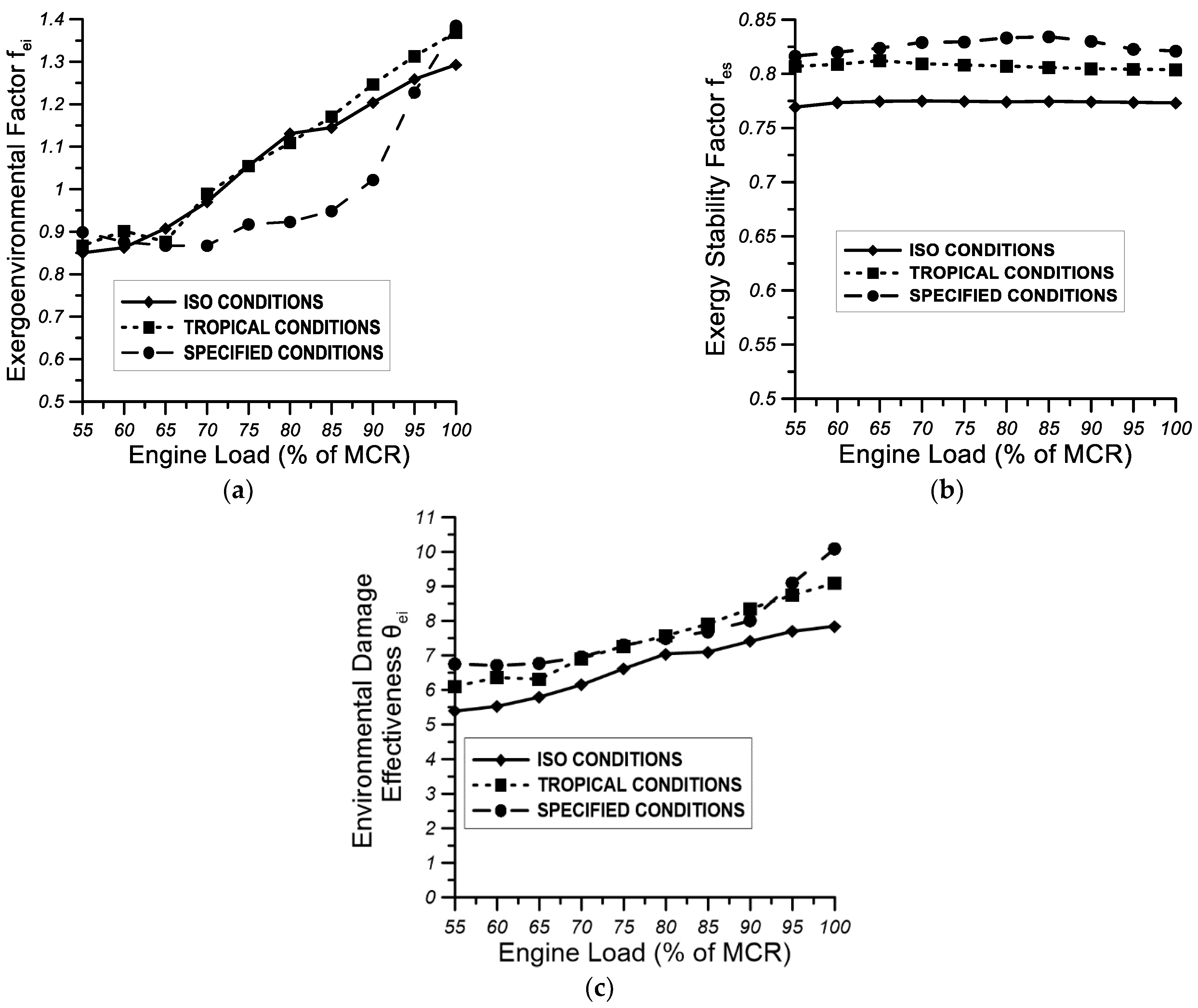
10. Exergo-Environmental Analysis
11. Results and Discussion
11.1. Multi-Optimization in the Simple Cycle
- Pressure Ratio (phigh/plow): 1.5–3.5
- PPTD in the heat exchanger of the intake air: 10–30 °C
- PPTD in the heat exchanger of the exhaust gas: 10–30 °C
- PPTD in the recuperator: 10–30 °C
- Outlet temperature of the exhaust gas:160–190 °C
11.2. Multi-Optimization in the Split Cycle
- Pressure Ratio (phigh/plow): 2–4
- PPTD in the heat exchanger of the intake air: 10–30 °C
- PPTD in the intermediate heat exchanger of the exhaust gas: 10–30 °C
- PPTD in the recuperator: 10–30 °C
- PPTD in the final heat exchanger of the exhaust gas: 10–30 °C
- Intermediate temperature of the exhaust gas: 190–205 °C
- Outlet temperature of the exhaust gas: 150–180 °C
11.3. Multi-Optimization in the Cascade Cycle
- Pressure Ratio (phigh/plow): 1.5–3
- PPTD in the heat exchanger of the intake air: 10–30 °C
- PPTD in the intermediate heat exchanger of the exhaust gas: 10–30 °C
- PPTD in the final heat exchanger of the exhaust gas: 10–30 °C
- Intermediate temperature of the exhaust gas: 190–210 °C
- Outlet temperature of the exhaust gas: 150–180 °C
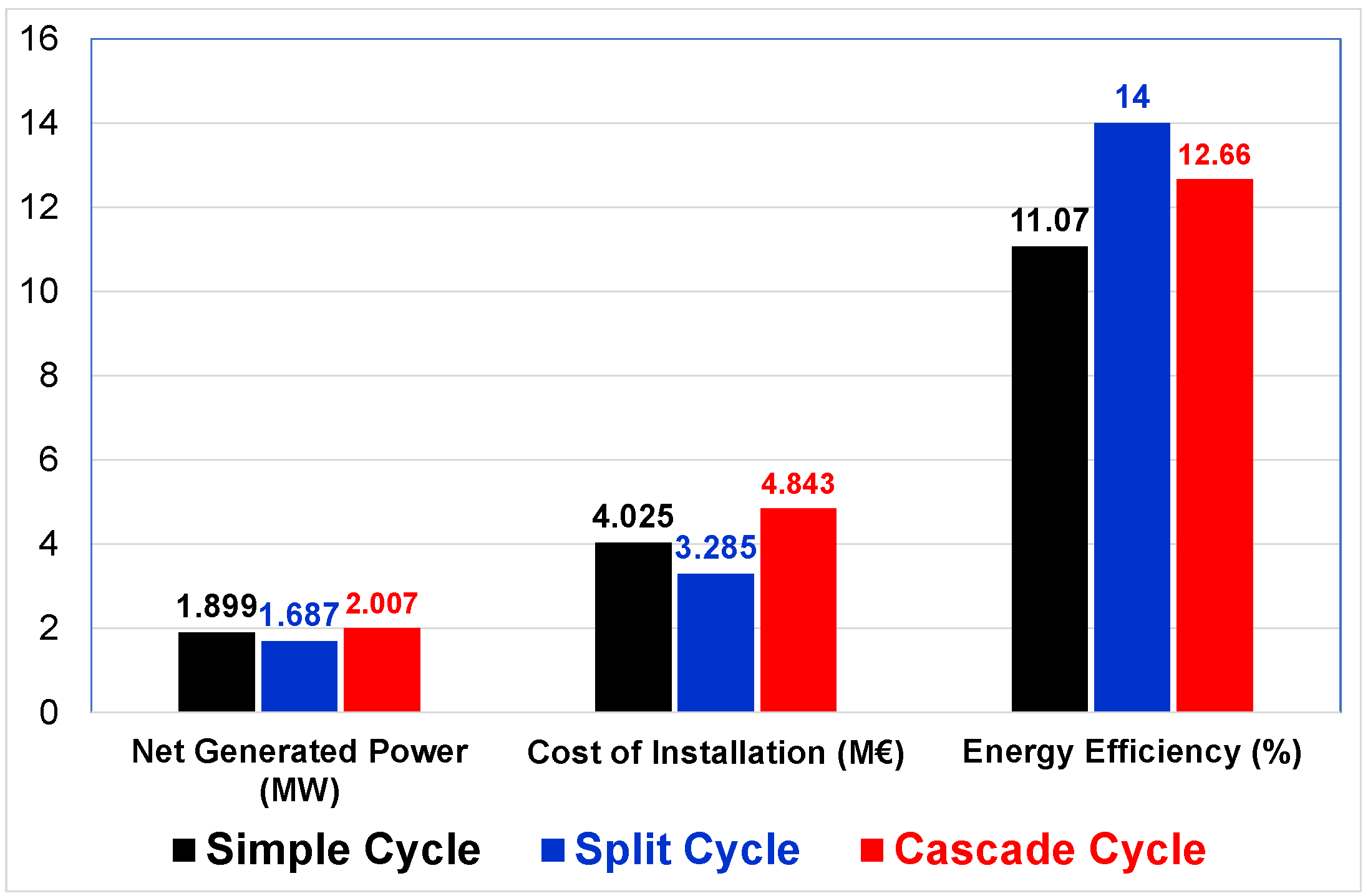
11.4. Comparative Results from the Multi-Optimization of the Supercritical Cycles
11.5. Results from the Exergo-Economic Analysis
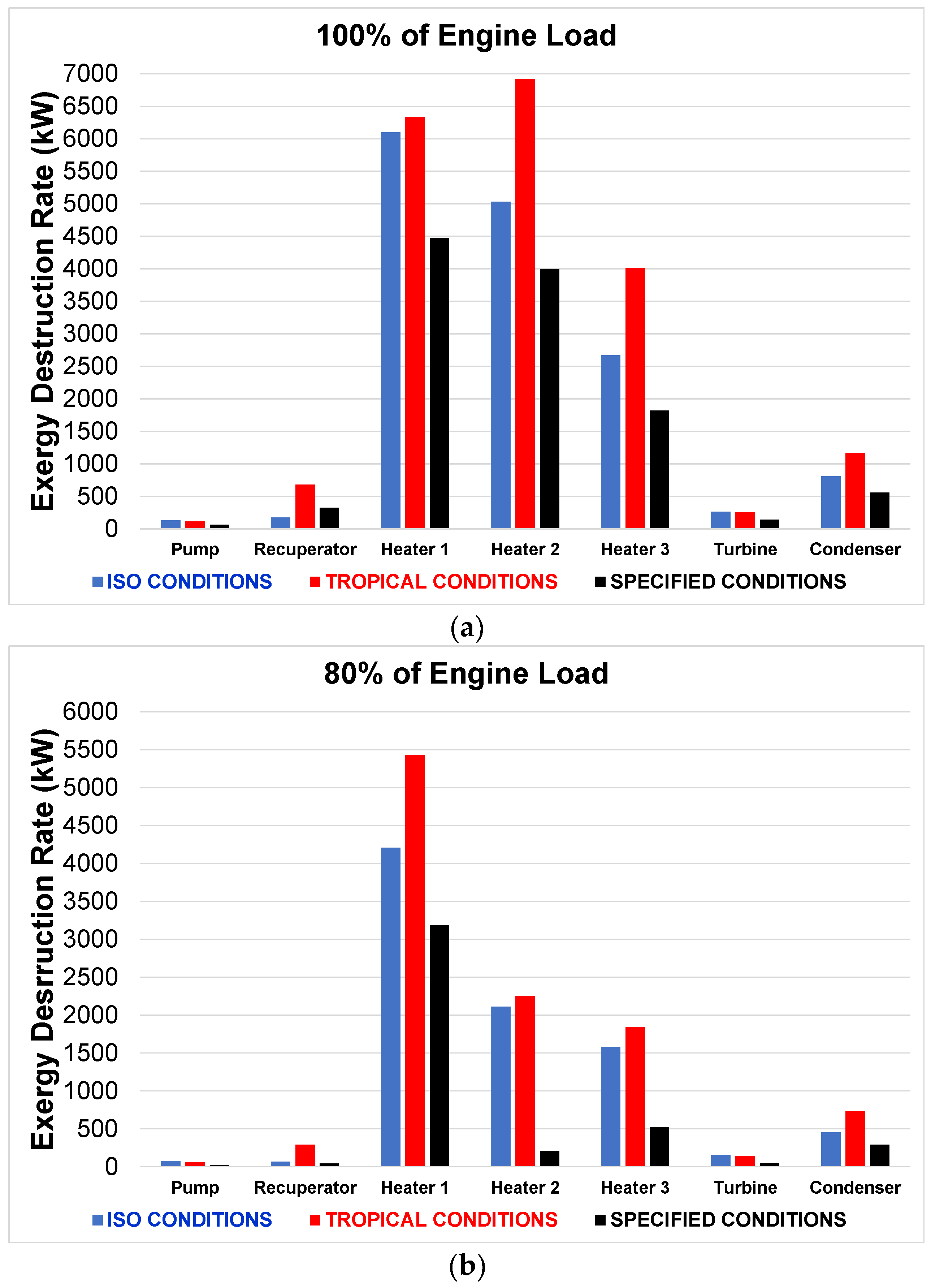
11.6. Parametric Analysis of the Split Supercritical Cycle
- the ISO condition, where the air and seawater temperature are both 25 °C
- the specified condition, where the air and seawater temperature are both 10 °C
- the tropical condition, where the air temperature is 45 °C and the seawater temperature is 36 °C
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | Area (m2) |
| AHX | Heat exchanger area (m2) |
| B1,HX | Constant that is based on the heat exchanger type |
| B2,HX | Constant that is based on the heat exchanger type |
| b | channel spacing (m) |
| C1,HX | Constant that depend on the type of heat exchanger |
| CHX0 | Bare module cost of the heat exchanger |
| C1,C | Constant that is based on the compressor |
| C2,HX | Constant that depend on the type of heat exchanger |
| C2,C | Constant that is based on the compressor |
| C3,HX | Constant that depend on the type of heat exchanger |
| C3,C | Constant that is based on the compressor |
| CEXP | Capital cost of the expander |
| CEXP0 | Bare module cost of the expander |
| CHX | Capital cost of the heat exchanger |
| CHX | Capital cost of the heat exchanger |
| CC | Capital cost of the compressor |
| CC0 | Bare module cost of the compressor |
| cp | heat capacity (J/kgK) |
| cost balance rate | |
| c | cost per exergy unit |
| Dh | Hydraulic port diameter (m) |
| fei | exergoenvironmental factor |
| fk | Maintenance and insurance cost factor |
| FM,HX | Material factor of heat exchanger |
| FBM | Material factor of the compressor |
| FMP | Additional expander factor |
| FP,HX | Pressure factor of heat exchanger |
| FP,C | Pressure factor of the compressor |
| FS | Construction overhead cost factor |
| h | Convective heat transfer coefficient (W/m2 K) |
| h | Specific enthalpy (J/kg) |
| hfull_load | Full load operation hours |
| hin | Convective heat transfer coefficient of the heat exchanger internal flow (W/m2 K) |
| i | Interest rate |
| E | exergy |
| K1,EXP | Constant that is based on the type of the expander |
| K1,HX | Constant that is based on the heat exchanger type |
| K1,C | Constant that is based on the compressor |
| K2,EXP | Constant that is based on the type of the expander |
| K2,HX | Constant that is based on the heat exchanger type |
| K2,C | Constant that is based on the compressor |
| K3,EXP | Constant that is based on the type of the expander |
| K3,HX | Constant that is based on the heat exchanger type |
| K3,C | Constant that is based on the compressor |
| k | Thermal conductivity (W/m K) |
| l | Length (m) |
| LTpl | Plant lifetime |
| m | Mass (kg) |
| Mass flow rate (kg/s) | |
| n | Efficiency |
| N | Number |
| p | Pressure (MPa) |
| phigh | high pressure of the cycle |
| plow | low pressure of the cycle |
| Power output of turbine | |
| Power consumption of compressor | |
| Net power produced | |
| q | Specific heat (J/kg) |
| Q | Heat (J) |
| Heat transfer rate (W) | |
| rin | Fouling resistance of the heat exchanger internal flow (m2 K/W) |
| rout | Fouling resistance of the heat exchanger external flow (m2 K/W) |
| s | Specific entropy (J/kgK) |
| T | Temperature (°C) |
| T0 | Reference temperature of exergy destruction rate (K) |
| U | heat transfer coefficient (W/m2Κ) |
| w | Channel width (m) |
| x | percentage of mass flow rate |
| Greek | |
| β | Rib effect coefficient or chevron angle |
| δ | Fin height (m) |
| ΔT | temperature difference (K) |
| ε | Convection factor or effectiveness of the heat exchanger |
| ε | Heat exchanger effectiveness |
| λ | Thermal conductivity (W/m K) |
| μ | Dynamic viscosity () |
| θei | environmental damage effectiveness factor |
| Subscripts | |
| 0 | Reference |
| is | isentropic |
| recup | recuperator |
| heater1 | heat exchanger of exhaust gas |
| heater2 | heat exchanger of scavenge air |
| heater3 | heat exchanger of exhaust gas |
| air | scavenge air |
| gas | exhaust gas |
| gas,in | exhaust gas inlet |
| gas,out | exhaust gas outlet |
| air,in | scavenge air inlet |
| air,out | scavenge air outlet |
| cond | condenser |
| ex | exergetic |
| water | sea water |
| water,in | sea water inlet |
| water,out | sea water outlet |
| gas,mid | exhaust gas intermediate outlet |
| T | turbine |
| C | compressor |
| D | destruction |
| cond | condenser |
| H | high |
| L | low |
| R | recuperator |
| th | thermal |
| in | input |
| ph | physical |
| max | maximum |
| min | minimum |
| plate | plate heat exchanger |
| tot | total |
| exergy,in | exergy input |
| exergy,out | exergy output |
| w | produced power |
| Dimensionless numbers | |
| Nu | Nusselt number |
| Pr | Prandtl number |
| Re | Reynolds number |
| Abbreviations | |
| bsfc | Brake specific fuel consumption |
| CEPCI | Chemical engineering plant cost index |
| CO2 | Carbon dioxide |
| CRF | Capital recovery factor |
| EPC | Electricity production cost |
| HT | High temperature |
| HX | Heat exchanger |
| LNG | Liquefied natural gas |
| LT | Low Temperature |
| MCT | Module cost technique |
| TIC | Total investment cost |
| TEU | twenty-foot equivalent unit |
| MCR | maximum continuous rating |
| LMTD | Logarithmic mean temperature difference |
References
- UNCTAD. Review of Maritime Transport 2021; United Nations: New York, NY, USA, 2022. [Google Scholar]
- Smith, T.W.P.; Jalkanen, J.P.; Anderson, B.A.; Corbett, J.J.; Faber, J.; Hanayama, S.; O’Keeffe, E.; Parker, S.; Johansson, L.; Aldous, L.; et al. Third IMO Greenhouse Gas Study 2014; The International Maritime Organization: London, UK, 2015. [Google Scholar]
- Joung, T.-H.; Kang, S.-G.; Lee, J.-K.; Ahn, J. The IMO initial strategy for reducing greenhouse gas (GHG) emissions, and its follow-up actions towards 2050. J. Int. Marit. Saf. Environ. Aff. Shipp. 2020, 4, 1–7. [Google Scholar] [CrossRef]
- Jouhara, H.; Khordehgah, N.; Almahmoud, S.; Delpech, B.; Chauhan, A.; Tassou, S.A. Waste heat recovery technologies and applications. Therm. Sci. Eng. Prog. 2018, 6, 268–289. [Google Scholar] [CrossRef]
- Liu, L.; Yang, Q.; Cui, G. Supercritical Carbon Dioxide(s-CO2) power cycle for waste heat recovery: A review from thermodynamic perspective. Processes 2020, 8, 1461. [Google Scholar] [CrossRef]
- Liu, P.; Shu, G.; Tian, H. Carbon dioxide as working fluids in transcritical Rankine cycle for diesel engine multiple waste heat recovery in comparison to hydrocarbons. J. Therm. Sci. 2019, 28, 494–504. [Google Scholar] [CrossRef]
- Wang, X.; Yang, Y.; Zheng, Y.; Dai, Y. Exergy and exergoeconomic analyses of a supercritical CO2 cycle for a cogeneration application. Energy 2017, 119, 971–982. [Google Scholar] [CrossRef]
- Pan, P.; Yuan, C.; Sun, Y.; Yan, X.; Lu, M.; Bucknall, R. Thermo-economic analysis and multi-objective optimization of S-CO2 Brayton cycle waste heat recovery system for an ocean-going 9000 TEU container ship. Energy Convers. Manag. 2020, 221, 113077. [Google Scholar] [CrossRef]
- Su, R.; Yu, Z.; Xia, L.; Sun, J. Performance analysis and multi-objective optimization of an integrated gas turbine/supercritical CO2 recompression/transcritical CO2 cogeneration system using liquefied natural gas cold energy. Energy Convers. Manag. 2020, 220, 113136. [Google Scholar] [CrossRef]
- Xia, W.; Huo, Y.; Song, Y.; Han, J.; Dai, Y. Off-design analysis of a CO2 Rankine cycle for the recovery of LNG cold energy with ambient air as heat source. Energy Convers. Manag. 2019, 183, 116–125. [Google Scholar] [CrossRef]
- Kim, Y.M.; Sohn, J.L.; Yoon, E.S. Supercritical CO2 Rankine cycles for waste heat recovery from gas turbine. Energy 2017, 118, 893–905. [Google Scholar] [CrossRef]
- Belman-Flores, J.M.; Rangel-Hernández, V.H.; Pérez-García, V.; Zaleta-Aguilar, A.; Fang, Q.; Méndez-Méndez, D. An advanced exergoeconomic comparison of CO2-based transcritical refrigeration cycles. Energies 2020, 13, 6454. [Google Scholar] [CrossRef]
- Marques, A.D.S.; Carvalho, M.; Ochoa, Á.A.V.; Souza, R.J.; dos Santos, C.A.C. Exergoeconomic assessment of a compact electricity-cooling cogeneration unit. Energies 2020, 13, 5417. [Google Scholar] [CrossRef]
- Valencia Ochoa, G.; Piero Rojas, J.; Duarte Forero, J. Advance exergo-economic analysis of a waste heat recovery system using ORC for a bottoming natural gas engine. Energies 2020, 13, 267. [Google Scholar] [CrossRef]
- Nami, H.; Mahmoudi, S.M.S.; Nemati, A. Exergy, economic and environmental impact assessment and optimization of a novel cogeneration system including a gas turbine, a supercritical CO2 and an Organic Rankine Cycle (GT-HRSG/SCO2). Appl. Therm. Eng. 2017, 110, 1315–1330. [Google Scholar] [CrossRef]
- CEAS Engine Calculations–MAN Energy Solutions. Available online: https://marine.man-es.com/two-stroke/ceas (accessed on 10 December 2021).
- Choi, B.C.; Kim, Y.M. Thermodynamic analysis of a dual loop heat recovery system with trilateral cycle applied to exhaust gases of internal combustion engine for propulsion of the 6800 TEU container ship. Energy 2013, 58, 404–416. [Google Scholar] [CrossRef]
- Hossain, M.J.; Chowdhury, J.I.; Balta-Ozkan, N.; Asfand, F.; Saadon, S.; Imran, M. Design optimization of supercritical carbon dioxide (s-CO2) cycles for waste heat recovery from marine engines. J. Energy Resour. Technol. 2021, 143, 120901. [Google Scholar] [CrossRef]
- Zahedi, E.; Woerz, C.; Reichardt, G.; Umlauf, G.; Liewald, M.; Barz, J.; Weber, R.; Graf, T. Lubricant-free deep drawing using CO2 and N2 as volatile media injected through laser-drilled microholes. MATEC Web Conf. 2018, 190, 14007. [Google Scholar] [CrossRef][Green Version]
- Wang, X.; Dai, Y. Exergoeconomic analysis of utilizing the transcritical CO2 cycle and the ORC for a recompression supercritical CO2 cycle waste heat recovery: A Comparative study. Appl. Energy 2016, 170, 193–207. [Google Scholar] [CrossRef]
- Liu, P.; Shu, G.; Tian, H. How to approach optimal practical organic Rankine cycle (OP-ORC) by configuration modification for diesel engine waste heat recovery. Energy 2019, 174, 543–552. [Google Scholar] [CrossRef]
- Cao, E. Heat Transfer in Process Engineering; McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- Yang, F.; Cho, H.; Zhang, H.; Zhang, J. Thermoeconomic Multi-objective optimization of a dual loop organic Rankine cycle (ORC) for CNG engine waste heat recovery. Appl. Energy 2017, 205, 1100–1118. [Google Scholar] [CrossRef]
- García-Cascales, J.R.; Vera-García, F.; Corberán-Salvador, J.M.; Gonzálvez-Maciá, J. Assessment of boiling and condensation heat transfer correlations in the modelling of plate heat exchangers. Int. J. Refrig. 2007, 30, 1029–1041. [Google Scholar] [CrossRef]
- Turton, R. Analysis, Synthesis, and Design of Chemical Processes, 5th ed.; Prentice Hall: Boston, MA, USA, 2018. [Google Scholar]
- Lee, S.H.; Lim, D.-H.; Park, K. Optimization and economic analysis for small-scale movable LNG liquefaction process with leakage considerations. Appl. Sci. 2020, 10, 5391. [Google Scholar] [CrossRef]
- Yang, M.-H.; Yeh, R.-H. Thermodynamic and economic performances optimization of an organic Rankine cycle system utilizing exhaust gas of a large marine diesel engine. Appl. Energy 2015, 149, 1–12. [Google Scholar] [CrossRef]
- Yan, Y.-Y.; Lin, T.-F. Evaporation heat transfer and pressure drop of refrigerant R-134a in a plate heat exchanger. J. Heat Transfer 1999, 121, 118–127. [Google Scholar] [CrossRef]
- Nafey, A.S.; Sharaf, M.A. Combined solar organic Rankine cycle with reverse osmosis desalination process: Energy, exergy, and cost evaluations. Renew. Energy 2010, 35, 2571–2580. [Google Scholar] [CrossRef]
- Thanganadar, D.; Asfand, F.; Patchigolla, K. Thermal performance and economic analysis of supercritical carbon dioxide cycles in combined cycle power plant. Appl. Energy 2019, 255, 113836. [Google Scholar] [CrossRef]
- Ghaebi, H.; Parikhani, T.; Rostamzadeh, H.; Farhang, B. Thermodynamic and thermoeconomic analysis and optimization of a novel combined cooling and power (CCP) cycle by integrating of ejector refrigeration and Kalina cycles. Energy 2017, 139, 262–276. [Google Scholar] [CrossRef]
- Yang, X.-S. Nature-Inspired Optimization Algorithms, 1st ed.; Elsevier Inc.: San Diego, CA, USA, 2020. [Google Scholar]
- Bejan, A.; Tsatsaronis, G.; Moran, M.J. Thermal Design and Optimization; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Mohammed, R.H.; Ibrahim, M.M.; Abu-Heiba, A. Exergoeconomic and multi-objective optimization analyses of an organic Rankine cycle integrated with multi-effect desalination for electricity, cooling, heating power, and freshwater production. Energy Convers. Manag. 2021, 231, 113826. [Google Scholar] [CrossRef]
- Shamoushaki, M.; Aliehyaei, M.; Taghizadeh-Hesary, F. Energy, exergy, exergoeconomic, and exergoenvironmental assessment of flash-binary geothermal combined cooling, heating, and power cycle. Energies 2021, 14, 4464. [Google Scholar] [CrossRef]
- Yilmaz, C.; Kanoglu, M.; Abusoglu, A. Exergetic cost evaluation of hydrogen production powered by combined flash-binary geothermal power plant. Int. J. Hydrogen Energy 2015, 40, 14021–14030. [Google Scholar] [CrossRef]
- Zare, V.; Mahmoudi, S.M.S.; Yari, M. On the exergoeconomic assessment of employing Kalina cycle for GT-MHR waste heat utilization. Energy Convers. Manag. 2015, 90, 364–374. [Google Scholar] [CrossRef]
- Ratlamwala, T.A.H.; Dincer, I.; Reddy, B.V. Exergetic and environmental impact assessment of an integrated system for utilization of excess power from thermal power plant. In Causes, Impacts and Solutions to Global Warming; Dincer, I., Colpan, C.O., Kadioglu, F., Eds.; Springer: New York, NY, USA, 2013; pp. 803–824. [Google Scholar] [CrossRef]
- Midilli, A.; Dincer, I. Development of some exergetic parameters for PEM fuel cells for measuring environmental impact and sustainability. Int. J. Hydrogen Energy 2009, 34, 3858–3872. [Google Scholar] [CrossRef]
- Abbaspour, H.; Ehyaei, M.A.; Ahmadi, A.; Panahi, M.; Abdalisousan, A.; Mirzohosseini, A. Energy, exergy, economic, exergoenvironmental and environmental (5e) analyses of the cogeneration plant to produce electrical power and urea. Energy Convers. Manag. 2021, 235, 113951. [Google Scholar] [CrossRef]
- Engineering Equation Solver (EES). F-Chart Software; F-Chart Software: Madison, WI, USA, 2022; Available online: https://www.fchartsoftware.com/ees/ (accessed on 1 June 2022).






| Properties | CO2 |
|---|---|
| Critical Temperature (K) | 304.13 |
| Critical Pressure (MPa) | 7.37 |
| Critical Density (kg/m3) | 467.6 |
| Constant | Value |
|---|---|
| 1.70 | |
| B1,HX | 0.96 |
| B2,HX | 1.21 |
| FM,HX | 2.40 |
| K1,HX | 4.66 |
| K2,HX | −0.1557 |
| K3,HX | 0.1547 |
| C1,HX | 0 |
| C2,HX | 0 |
| C2,HX | 0 |
| Constant | Value |
|---|---|
| 1.70 | |
| FBM | 1.20 |
| K1,C | 2.2897 |
| K2,C | 1.3604 |
| K3,C | −0.1027 |
| C1,C | 0 |
| C2,C | 0 |
| C3,C | 0 |
| Constant | Value |
|---|---|
| 3.5 | |
| 1.70 | |
| K1,EXP | 2.2659 |
| K2,EXP | 1.4398 |
| K3,EXP | −0.1776 |
| Component | Exergetic Cost Rate Balance Equation | Additional Equation |
|---|---|---|
| Compressor | ||
| Recuperator | ||
| Heater 1 | ||
| Heater 2 | ||
| Heater 3 | ||
| Turbine | ||
| Condenser |
| Component | Exergy Destruction Rate |
|---|---|
| Compressor | |
| Recuperator | |
| Heater 1 | |
| Heater 2 | |
| Heater 3 | |
| Turbine | |
| Condenser |
| Parameters | Simple Cycle |
|---|---|
| Phigh/plow | 2.184 |
| ) | 11.6 |
| ) | 16 |
| ) | 10 |
| ) | 5 |
| ) | 164.5 |
| (kg/s) | 71.02 |
| (kW) | 1.899 |
| (kW) | 1.688 |
| (kW) | 8.850 |
| (kW) | 8.305 |
| (%) | 11.07 |
| (€) | 497,802 |
| (€) | 569,981 |
| (€) | 575,062 |
| (€) | 1,119,000 |
| (€) | 844,054 |
| (€) | 419,924 |
| (€) | 4,025,823 |
| EPC (€/kWh) | 0.05637 |
| Parameters | Simple Cycle |
|---|---|
| phigh/plow | 2.679 |
| ) | 15.95 |
| ) | 10 |
| ) | 10 |
| ) | 13.16 |
| ) | 5 |
| ) | 202 |
| ) | 156.5 |
| (kg/s) | 42.88 |
| x | 0.346 |
| (kW) | 1.687 |
| (kW) | 759.8 |
| (kW) | 6.284 |
| (kW) | 2.925 |
| (kW) | 2.843 |
| (%) | 14 |
| (€) | 335,098 |
| (€) | 391,797 |
| (€) | 388,694 |
| (€) | 380,298 |
| (€) | 662,022 |
| (€) | 714,459 |
| (€) | 413,017 |
| (€) | 3,285,385 |
| EPC (€/kWh) | 0.0518 |
| Parameters | Simple Cycle |
|---|---|
| phigh/plow | 2.486 |
| ) | 10 |
| ) | 10 |
| ) | 10 |
| ) | 15.04 |
| ) | 5 |
| ) | 199.9 |
| ) | 150 |
| (kg/s) | 64.57 |
| (kg/s) | 31.64 |
| (kg/s) | 32.93 |
| (kW) | 2.007 |
| (kW) | 1.059 |
| (kW) | 5.383 |
| (kW) | 2.709 |
| (kW) | 6.716 |
| (%) | 12.66 |
| (€) | 443,939 |
| (€) | 517,033 |
| (€) | 559,643 |
| (€) | 530,759 |
| (€) | 1,081,000 |
| (€) | 950,281 |
| (€) | 388,610 |
| (€) | 372,182 |
| (€) | 4,843,447 |
| EPC (€/kWh) | 0.06417 |
| State | Fluid | Pressure (Bar) | T (°C) | Enthalpy (kJ/kg) | Entropy (kJ/kg K) | Exergy (MW) | Costs | |
|---|---|---|---|---|---|---|---|---|
| 1 | 75 | 30 | −215.1 | −1.44 | 9.342 | 455.4 | 13.54 | |
| 2 | 200.93 | 54.64 | −195.7 | −1.434 | 10.100 | 517.7 | 14.24 | |
| 3R | 200.93 | 74.82 | −144.5 | −1.282 | 3.587 | 195.1 | 15.12 | |
| 3H | 200.93 | 144.1 | 6.079 | −0.8846 | 7.637 | 322.1 | 11.72 | |
| 3 | 200.93 | 116 | −46.13 | −1.014 | 11.119 | 517.2 | 12.92 | |
| 4 | 200.93 | 149.6 | 15.39 | −0.8625 | 11.804 | 527.5 | 12.41 | |
| 5 | 200.93 | 188.8 | 75.02 | −0.7274 | 12.624 | 564.2 | 12.41 | |
| 6 | 75 | 99.51 | 16.25 | −0.7155 | 9.949 | 444.7 | 12.41 | |
| 7 | 75 | 84.82 | −3.465 | −0.7694 | 9.798 | 437.9 | 12.41 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vallis, A.G.; Zannis, T.C.; Hristoforou, E.V.; Yfantis, E.A.; Pariotis, E.G.; Hountalas, D.T.; Katsanis, J.S. Design of Container Ship Main Engine Waste Heat Recovery Supercritical CO2 Cycles, Optimum Cycle Selection through Thermo-Economic Optimization with Genetic Algorithm and Its Exergo-Economic and Exergo-Environmental Analysis. Energies 2022, 15, 5398. https://doi.org/10.3390/en15155398
Vallis AG, Zannis TC, Hristoforou EV, Yfantis EA, Pariotis EG, Hountalas DT, Katsanis JS. Design of Container Ship Main Engine Waste Heat Recovery Supercritical CO2 Cycles, Optimum Cycle Selection through Thermo-Economic Optimization with Genetic Algorithm and Its Exergo-Economic and Exergo-Environmental Analysis. Energies. 2022; 15(15):5398. https://doi.org/10.3390/en15155398
Chicago/Turabian StyleVallis, Athanasios G., Theodoros C. Zannis, Evangelos V. Hristoforou, Elias A. Yfantis, Efthimios G. Pariotis, Dimitrios T. Hountalas, and John S. Katsanis. 2022. "Design of Container Ship Main Engine Waste Heat Recovery Supercritical CO2 Cycles, Optimum Cycle Selection through Thermo-Economic Optimization with Genetic Algorithm and Its Exergo-Economic and Exergo-Environmental Analysis" Energies 15, no. 15: 5398. https://doi.org/10.3390/en15155398
APA StyleVallis, A. G., Zannis, T. C., Hristoforou, E. V., Yfantis, E. A., Pariotis, E. G., Hountalas, D. T., & Katsanis, J. S. (2022). Design of Container Ship Main Engine Waste Heat Recovery Supercritical CO2 Cycles, Optimum Cycle Selection through Thermo-Economic Optimization with Genetic Algorithm and Its Exergo-Economic and Exergo-Environmental Analysis. Energies, 15(15), 5398. https://doi.org/10.3390/en15155398









