Event-Triggered Security Consensus for Multi-Agent Systems with Markov Switching Topologies under DoS Attacks

Abstract

This paper studies secure consensus control for multi-agent systems subject to denial-of-service (DoS) attacks. The DoS attacks cause changes in topologies, which will destroy the channels of communication and result in network paralysis. Unlike the existing publications with Markov switching, this paper mainly studies the topological structure changes of the subsystem models after DoS attacks. To ensure the consensus of systems, this paper designs an event triggered to reduce the use of the controller and decrease the influence of channel breaks off caused by DoS attacks. On this basis, different Lyapunov functions are established in each period of attack. Then, stochastic and Lyapunov stable theory is used to form the consensus criteria. Moreover, Zeno behavior is excluded by theoretical analysis. Finally, the simulation experiment proves the effectiveness of the proposed protocol.

1. Introduction

In recent years, multi-agent systems have attracted increasing attention from researchers because they are widely applied to UAV (Unmanned Aerial Vehicle) formation control [1], robot cooperative control [2], smart grid power allocation [3], and so on. One of the instrumental research directions for multi-agent systems is to design coordinated strategies, which describe the micro-communication among agents. There are many methods of study for multi-agent systems consensus, such as impulsive control [4], event-triggered control [5], model predictive control [6], integral sliding-mode control [7], model-free optimal control [8], and so on. However, the collaborative process is highly dependent on the channel.

In fact, due to the simple structure of agents, it is impossible to load complex protection protocols when communicating. Thus, multi-agent systems are easy to attack via DoS attacks [9,10], deception attacks [11], replay attacks [12], etc. Among these attacks, the DoS attacks do great damage to coordinations in multi-agent systems because they break off the channels and prevent information exchange between agents. Therefore, secure consensus for multi-agent systems under attacks has obtained more interest from investigators.

In [13], the authors used the random disturbance information and, considering the packet loss caused by DoS attacks, designed an observer to reconstruct the state of agents. The coupling probability constraint is transformed into the coupling deterministic constraint to resist the DoS attacks. In [14], a secure strategy was proposed to ensure the acceptable operation of multi-agent systems in the environment of DoS attacks. In [15], for attackers attacking different channels, a distributed controller was designed, and the authors considered the state feedback and observer controller so that consensus could still be reached in the environment of DoS attacks. For multi-agent systems in the presence of DoS attacks, the above paper [13,14,15,16] used different control strategies can achieve the goal of multi-agent consensus control. However, when systems are subject to attack, communication resources are restricted. To deal with it, in [17,18,19,20,21] event-triggered strategies were proposed to reduce the use of the controller and decrease the influence of channel break off caused by DoS attacks. In [17], researchers used the distributed sliding mode control method to study the control problem of a nonlinear second-order multi-agent system. In [19], the event-triggered distributed state estimation problem for linear multi-agent systems under DoS attacks was studied. In [20], a distributed event-triggered condition was designed to keep the whole system consistent in the case of multiple communication channel outages caused by irregular DoS attacks.

The above works assume the DoS attacks only destroy the local channels or the global channels when attacked. In fact, the topology of multi-agent systems tends to change because communications are interrupted. To cope with this problem, a switched system model was introduced in reference [22] to deal with changes caused by DoS attacks, and the quantitative relation between consensus performance and attack parameters was established. In [23], the secure consensus problem of multi-agent systems under DoS attacks on the communication topology was studied. The switched systems are usually composed of some subsystem models. The Markovian process has been proved to be effective for describing switching rules caused by the sudden change from the outer environment, topology switching and man-made intervention. In order to describe the process of topology random switching in multi-agent systems, paper [24,25] used the Markov process to establish a topological switching model. In the process of topology switching at present, the transition rates of model changes of different subsystems were given partially or even completely [26,27].

Nevertheless, there are a few works that consider the impact of each possible topology governed by the Markovian process. In fact, DoS attacks may cause the original possible topology to change, and cannot be ignored. Wang et al. [28] considered the impact of the attacks on the topology, but the controller was based on a continuous-time design, and did not consider the DoS attack energy-limited analysis. Moreover, due to the existence of external interference factors, the transition rates of each subsystem model switching are generally not accurate. In this case, the transition rates are deemed to be partly unknown or fully unknown. Meanwhile, DoS attacks cause changes to the possible topologies in the next switched period.

Motivated by the discussions above, we focus on the problem of leader-following multi-agent systems. This paper adopts an event-triggered strategy to control the consensus of multi-agent systems affected by DoS attacks during Markovian switching topologies. The main innovation points of this paper are as follows.

(1)

Different from the topology switching process in reference [20], this paper uses the Markov process to establish the topological switching process. We study the consensus of the topology in the random switching process under the DoS attack. Compared with reference [20], this paper also needs to analyze the random process, so the theoretical analysis process is more complex.

(2)

In order to describe the issue of energy-limited DoS attack, the DoS attack suffered by the multi-agent systems is further analyzed and the upper limit of DoS attack intensity is given, which will be more in line with practical application scenarios.

(3)

Because of the influence of the DoS attacks, the channels between agents will be interrupted. After each attack, the controller of the system will be updated after the communication recovery. Therefore, with the premise of ensuring the secure consensus of the multi-agent systems, an event-triggered control is designed based on stochastic process analysis, a recursive method, and an inequality method to reduce the use of the controller.

The structure of this paper is as follows: Section 2 introduces some preliminary knowledge, algebraic graph theory, the Markovian switching process, and control objectives. In Section 3, a security control scheme based on event triggering is proposed. In Section 4, the stability analysis is carried out. Section 5 gives a numerical example and Section 6 gives a conclusion.

2. Preliminaries

2.1. Notations

In this paper, The notations $\mathbb{R}$ and N denote the sets of real and natural numbers, respectively. The notations $\mathbb{R}$ and ${\mathbb{R}}^{n\times n}$ denote the n-dimensional vector space and $n\times n$ matrix space, respectively. The notation $I_N$ represents an $N\times N$-dimensional matrix in which each element is 1. The notations $\left|\right|·\left|\right|$ and ⊗ represent the Euclidean norm and the Kronecker product, respectively. The notation $C^T$ is the transpose of a matrix C. Moreover, $S=\left\{1,2,\dots ,s\right\}$ represents that the switching signal set is driven by a Markov chain. For two sets, $D_1$ and $D_2$, $D_1\backslash D_2$ denotes the set of elements belonging to $D_1$, but not those belonging to $D_2$.

2.2. Graph Theory

We consider an undirected graph $\mathcal{G}=(\mathcal{V},\mathcal{E}\left(t\right),A)$, where $\mathcal{V}=\left\{v_1,v_2,\cdots ,v_N\right\}$ represents the vertex set of follower agent nodes and $\mathcal{E}\left(t\right)$ represents the set of edges in the graph. The notation ${\mathcal{E}}_{i,j}$ represents the node pair $(v_i,v_j)$, where the node $v_j$ can receive the information sent by the node $v_i$. The neighbor agent node set of the agent node $v_i$ is defined as $N_i=\left\{j\in \mathcal{V}|\left(v_i,v_j\right)\in \mathcal{E}\left(t\right)\right\}$. The notation $\mathcal{A}=\left[a_{ij}\right]\in {\mathbb{R}}^{n\times n}$ is the adjacency matrix of a directed graph. In the matrix $\mathcal{A}$, when ${\mathcal{E}}_{i,j}i\in \mathcal{E}\left(t\right)$, there is $a_{ij}>0$ the weight of the edge ${\mathcal{E}}_{i,j}$; otherwise $a_{ij}=0$. The Laplacian matrix of the figure $\mathcal{G}$ is $L_{ij}=-a_{ij}$ or $L=\mathcal{D}-\mathcal{A}$, where $\mathcal{D}=diag\left\{d_1\left(m\right),\cdots d_n\left(m\right)\right\}$ represents a degree matrix, the notation m is a subsystem mode of multi-agent system in the Markov switching topology process. The adjacency matrix of leader and follower is $\mathcal{B}=diag\left\{b_1\left(m\right),b_2\left(m\right),b_3\left(m\right)\cdots b_n\left(m\right)\right\}$. If the node $v_0$ can send information to the node $v_i$, then $b_i>0$; otherwise, $b_i=0$.

2.3. Markovian Switching Process

The Markovian switching topology is defined as $\overline{\mathcal{G}}\left(r\left(t\right)\right)=\left\{\mathcal{V},\mathcal{E}\left(r\left(t\right)\right),\mathcal{A}\left(r\left(t\right)\right)\right\}$, where $\overline{\mathcal{G}}\left(r\left(t\right)\right)\in \left\{\overline{\mathcal{G}}\left(1\right),\overline{\mathcal{G}}\left(2\right),\overline{\mathcal{G}}\left(3\right),···,\overline{\mathcal{G}}\left(s\right)\right\}$. The notation $r\left(t\right)$ represents the Markovian jump process. For different switching topology sets $\overline{\mathcal{G}}\left(m\right)\left(m\in S\right)$, its adjacency matrix is $\mathcal{A}\left(m\right)$ and its Laplacian matrix is $L\left(m\right)$, as defined in the Graph theory. In the Markovian process, the transition probabilities of different subsystems are determined by the following equation:

$$\mathbb{P}\left\{r(t+\Delta t)=n\left|r\right(t)=m\right\}=\left\{\begin{array}{c}{\pi }_{mn}\left(h\right)h+o\left(h\right),m\ne n\hfill \\ 1+{\pi }_{mn}\left(h\right)h+o\left(h\right),otherwise\hfill \end{array}\right.$$

where $\underset{h\to 0}{lim}\frac{o\left(h\right)}{h}=0$, $o\left(h\right)$ is the little o notation and ${\pi }_{mn}\left(h\right)$ represents the transfer rate between different elements m to elements n in the set S from time t to time $t+h$ and ${\pi }_{mn}\left(h\right)>0$. Apart from this, the transition rates matrix composed of the transfer rates of different elements is expressed as follows, and the set of transition rates is defined as S.

$$\prod =\left(\begin{array}{ccccc}{\pi }_{11}\left(h\right)& {\pi }_{12}\left(h\right)& {\pi }_{13}\left(h\right)& \dots & {\pi }_{1s}\left(h\right)\\ {\pi }_{21}\left(h\right)& {\pi }_{22}\left(h\right)& {\pi }_{23}\left(h\right)& \dots & {\pi }_{2s}\left(h\right)\\ {\pi }_{31}\left(h\right)& {\pi }_{32}\left(h\right)& {\pi }_{33}\left(h\right)& \dots & {\pi }_{3s}\left(h\right)\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ {\pi }_{s1}\left(h\right)& {\pi }_{s2}\left(h\right)& {\pi }_{s3}\left(h\right)& \dots & {\pi }_{ss}\left(h\right)\end{array}\right)$$

2.4. DoS Attack Model

DoS attack is a common cyber attack, which can directly attack the network communication channels. In this paper, we consider that the communication channels between agents are attacked, resulting in communication interruption between two adjacent agents, leaving them unable to transmit information. Without generality, the DoS attack is an energy-limited attack and a random discontinuous attack. Moreover, the DoS attacks are irregular, so intervals that systems suffer from are uncertain, and the whole attack process is random. Therefore, this increases the difficulty of establishing the consensus convergence criteria for this modeled multi-agent system.

Throughout this paper, the DoS attacks can be divided into two phases: one is the system suffered by DoS attacks, while the other is not. In this paper, ${\left\{{\widehat{t}}_k\right\}}_{k\in N}$ is defined as the attack time sequence of the DoS attacks, which means the kth DoS attack time and ${\Delta }_k$ is the duration of the kth DoS attack. This time is not fixed and there is no distribution law. For the entire multi-agent systems that suffered every DoS attack, this paper defines ${\Omega }_k=[{\widehat{t}}_k,{\widehat{T}}_k)$ to represent the attack interval of the kth DoS attack, where ${\widehat{T}}_k={\widehat{t}}_k+{\Delta }_k$ represents the end of the kth DoS attack. ${\Psi }_k=[{\widehat{T}}_k,{\widehat{t}}_{k+1})$ is defined as the period from the end of the kth attack to the beginning of the $k+1$th attack without DoS attack, as shown in Figure 1.

Assumption 1

([21]). DoS attacks are assumed to have limited energy.

When the channel between agents is attacked, the total length of time ${\Xi }_0\left(t_0,t\right)$ that agents cannot communicate is:

$$\begin{array}{c}\hfill {\Xi }_0\left(t_0,t\right)=\cup {\Omega }_k\cap \left[t_0,t\right].\end{array}$$

The system is not attacked, and the normal communication interval ${\Xi }_1\left(t_0,t\right)$ between agents is defined as:

$$\begin{array}{c}\hfill {\Xi }_1\left(t_0,t\right)=\cup {\Psi }_k\cap \left[t_0,t\right]=\left[t_0,t\right]\backslash {\Xi }_0\left(t_0,t\right).\end{array}$$

Definition 1

([29]). $N_k(t_0,t)$ represents the number of attacks on the entire multi-agent systems in $(t_0,t)$, so the corresponding attack frequency $\Gamma \left(t_0,t\right)$ is defined as:

$$\begin{array}{c}\hfill \Gamma \left(t_0,t\right)=\frac{N_k(t_0,t)}{t-t_0}.\end{array}$$

Definition 2

([30]). The attack length rate is the total attack time ${\Xi }_0(t_0,t)$ to the total system operation time $(t_0,t)$ so the corresponding length rate ς is defined as:

$$\begin{array}{c}\hfill \varsigma =\frac{{\Xi }_0(t_0,t)}{t-t_0}.\end{array}$$

3. Problem Formulation

The multi-agent systems considered in this paper include a leader agent and N follower agents. The dynamic model for the i-follower agent in the system is defined as

$${\dot{x}}_i\left(t\right)=\mathrm{A}{x}_i\left(t\right)+B{u}_i\left(t\right),i=1,2,3,4\dots ,N,$$

(1)

where $x_i\left(t\right)\in {\mathbb{R}}^n$ represents the state value of the i follower agent and $u_i\left(t\right)\in {\mathbb{R}}^n$ stands for the control input of the i follower agent. The notations $\mathrm{A}$ and $\mathrm{B}$ are the constant matrices with approximate dimensions, respectively. Assume that the pair (A, B) is stabilizable. The leader agent is defined as $x_0$ and its dynamic model is defined as:

$$\dot{x_0}\left(t\right)=\mathrm{A}{x}_0\left(t\right).$$

(2)

For multi-agent systems with Markovian switching topology under DoS attacks, to reduce the consumption of communication resources between agents and maintain the good consensus effect of multi-agent systems, a distributed event-triggered control is used for consensus control. The controller is designed as

$$u_i\left(t\right)=K_{\left(r\left(t\right)\right)}{y}_i\left(t_k^i\right),t\in \left[t_k^i,t_{k+1}^i\right),$$

(3)

where $t_k^i\left(k=1,2,3,\dots ,k\right)$ represents the triggering time sequence. The event trigger time is defined as $t_{k+1}^i=inf\left\{t>t_k^i|f_i\left(t\right)\ge 0\right\},$ where $f_i\left(t\right)$ is the event trigger function. At the triggering instants, the agent i can sample the information of its neighbors to update its control protocol $u_i\left(t\right)$. The notation $K_{\left(r\left(t\right)\right)}$ denotes the feedback control gain, $y_i\left(t\right)={\displaystyle \sum _{j=1}^N}{a_{ij}}_{\left(r\left(t\right)\right)}\left(x_j\left(t\right)-x_i\left(t\right)\right)+{b_{0i}}_{\left(r\left(t\right)\right)}\left(x_0\left(t\right)-x_i\left(t\right)\right)$. The notation ${a_{ij}}_{\left(r\left(t\right)\right)}$ represents the coupling weight value between agent i and j. If the two agents can establish communication exchange information, ${a_{ij}}_{\left(r\left(t\right)\right)}>0$; otherwise, ${a_{ij}}_{\left(r\left(t\right)\right)}=0$. The notation ${b_{0i}}_{\left(r\left(t\right)\right)}$ represents the coupling weight value between the agent i and the leader. If they can communicate, then ${b_{0i}}_{\left(r\left(t\right)\right)}>0$, otherwise, ${b_{0i}}_{\left(r\left(t\right)\right)}=0$.

For DoS attacks, the above assumption 1 indicates that the attacks are energy-limited, and do not always attack the channel, and they are intermittent. When the attacks work, the communication channel between the agents will be interrupted. Then, the agents cannot communicate normally. Moreover, the topology of the multi-agent systems will change. When the attacks stop, the channel will recover. In other words, only within attack time ${\Omega }_k=[{\widehat{t}}_k,{\widehat{t}}_k+{\Delta }_k)$ will the topology of the subsystems change.

Remark 1.

In ${\Omega }_k=[{\widehat{t}}_k,{\widehat{t}}_k+{\Delta }_k)$, the communication channel of the agent is attacked, then the communication channel is interrupted, which means the information of the agent i and their neighbor, which cannot change adjacent to the agent, will not be collected. The worst case scenario is that the channels of agent i are all interrupted, in which case the agent i will not communicate with all of its neighbors, now $u_i\left(t\right)=0$.

Through the above discussion, the control protocol is designed as

$$\begin{array}{c}\hfill u_i\left(t\right)=\left\{\begin{array}{c}{K}_{\left(r\left(t\right)\right)}{y}_i\left(t_k^i\right),t\in \left[{\widehat{t}}_{k-1}+{\Delta }_{k-1},{\widehat{t}}_k\right)\\ 0,t\in [{\widehat{t}}_k,{\widehat{t}}_k+{\Delta }_k),\end{array}\right.\end{array}$$

(4)

When the DoS attacks disappear, the communication channel will recover and information can be transmitted among agents again. If the event trigger condition is satisfied, the control protocol will work.

In the case of limited system communication resources, the adoption of this protocol can not only reduce the consumption of a large number of communication resources between agents, but can also maintain the consensus of the entire system. The measurement error function for the agent i is defined as

$$e_i\left(t\right)=y_i\left(t_k^i\right)-y_i\left(t\right),t\in \left[t_k^i,t_{k+1}^i\right).$$

(5)

The state error of multi-agent systems is ${\delta }_i\left(t\right)=x_i\left(t\right)-x_0\left(t\right)$. In the communication area ${\Psi }_k$, we can get the equation:

$${\dot{\delta }}_i\left(t\right)=A{\delta }_i\left(t\right)+B{K}_{\left(r\right(t\left)\right)}\left(y_i\left(t\right)+e_i\left(t\right)\right),i=1,2\dots N,$$

(6)

According to the notation $\delta \left(t\right)={\left[{{\delta }_1}^T\left(t\right),{{\delta }_2}^T\left(t\right),{{\delta }_3}^T\left(t\right),\cdots ,{{\delta }_N}^T\left(t\right)\right]}^T$, using Kronecker, we can get:

$$\dot{\delta }\left(t\right)=\left(I_N\otimes A-H_{\left(r\right(t\left)\right)}\otimes B{K}_{\left(r\right(t\left)\right)}\right)\delta \left(t\right)+\left(I_N\otimes B{K}_{\left(r\right(t\left)\right)}\right)e\left(t\right),$$

(7)

when the system is affected by an attack, the following is available:

$$\dot{\delta }\left(t\right)=\left(I_N\otimes A\right)\delta \left(t\right),$$

(8)

where $H_{\left(r\left(t\right)\right)}=L_{\left(r\left(t\right)\right)}+{\mathcal{B}}_{\left(r\left(t\right)\right)}$, $\delta \left(0\right)={\left[{{\delta }_1}^T\left(0\right),{{\delta }_2}^T\left(0\right),{{\delta }_3}^T\left(0\right),\cdots ,{{\delta }_N}^T\left(0\right)\right]}^T.$

Definition 3.

Under uncertain random switching topologies and DoS attacks, if the following inequalities are satisfied, the multi-agent systems based on Markovian switching can achieve mean-square consensus.

$$\begin{array}{c}\hfill \mathbb{E}\left\{{∥{\delta }_i\left(t\right)∥}^2\right\}\le \omega \mathbb{E}\left\{{∥{\delta }_i\left(0\right)∥}^2\right\}{e}^{-\sigma t},\forall t\ge 0,\end{array}$$

(9)

where $\omega >0,\sigma >0$ represent two positive constants, respectively.

Lemma 1.

(Schur Complement) linear matrix inequality

$$\begin{array}{c}\hfill D=\left[\begin{array}{cc}{D}_{11}& D_{12}\\ D_{21}& D_{22}\end{array}\right]<0,\end{array}$$

(10)

equal to one of the following conditions holding:

$\left(i\right)$

$D_{11}<0$, $D_{22}-D_{12}^T{D}_{11}^{-1}{D}_{12}<0$,

$\left(ii\right)$

$D_{22}<0$, $D_{11}-D_{12}{D}_{22}^{-1}{D}_{12}^T<0$.

4. Results

In this section, we provide sufficient conditions for secure consensus with Markov switching topologies under DoS attacks.

4.1. Stability Analysis

Theorem 1.

The secure consensus of leader-following multi-agent systems can be achieved under the following triggering condition.

$$f_i\left(t\right)=\left|\right|e_i\left(t\right)\left|\right|-\beta \left|\right|y_i\left(t\right)\left|\right|,$$

(11)

where $\beta =\frac{{\theta }_i\widehat{\beta }}{2∥Q_{r}B{B}^T{Q}_r∥\left(2\left|N_i\right|+b_{0i\left(r\right)}\right)},$$\widehat{\beta }>0,0<\theta <1$. Given the constants ${\alpha }_1>0,{\alpha }_2>0$, if there are matrices $Q>0$,$Q_r>0$ with appropriate dimensions, $r=1,2,3\dots s$ makes the following matrix inequalities hold:

$$\begin{array}{c}\hfill A^T{Q}_r+Q_{r}A-2{\lambda }_{*}\otimes Q_{r}B{B}^T{Q}_r+\widehat{\beta }{I}_N<0,\end{array}$$

(12)

$$\begin{array}{c}\hfill \left[\begin{array}{cc}{Q}^{-1}{A}^T-{\alpha }_2{Q}^{-1}& Q^{-1}\\ \ast & -QA\end{array}\right]<0,\end{array}$$

(13)

$$\begin{array}{c}\hfill \Gamma \left(t_0,t\right)\le \frac{{\eta }^{*}}{ln\gamma },\end{array}$$

(14)

$$\begin{array}{c}\hfill \varsigma \le \frac{{\alpha }_1-{\eta }^{*}}{{\alpha }_1+{\alpha }_2},\end{array}$$

(15)

where ${\eta }^{*}\in \left(0,{\alpha }_1\right),\gamma >0$, ${\lambda }_{*}={min}_{r\in S}\left({\lambda }_{min}\left(H_{r\left(t\right)}\right)\right)$. The definition of $\Gamma \left(t_0,t\right),\varsigma$ has been given in Definitions 2 and 3, respectively.

Proof of Theorem 1. 

Firstly, the following Lyapunov function is constructed:

$$\begin{array}{c}\hfill V(\delta \left(t\right),r\left(t\right),t)=\left\{\begin{array}{c}{\delta }^T\left(t\right)(I_N\otimes Q_r)\delta \left(t\right),t\in [{\widehat{t}}_{k-1}+{\Delta }_{k-1},{\widehat{t}}_k),\\ {\delta }^T\left(t\right)(I_N\otimes Q)\delta \left(t\right),t\in [{\widehat{t}}_k,{\widehat{t}}_k+{\Delta }_k).\end{array}\right.\end{array}$$

(16)

For the agent in the normal communication region $[{\widehat{t}}_{k-1}+{\Delta }_{k-1},{\widehat{t}}_k)$ and each $r\left(t\right)=r\in S$, the infinitesimal operator ℑ of the Lyapunov function is defined as:

$$\begin{array}{c}\hfill \Im V\left(\delta \left(t\right),r\left(t\right),t\right)=\underset{\Delta \to 0^{+}}{lim}\frac{1}{\Delta }\left\{\mathbb{E}\left\{V\left(\delta \left(t+\Delta t\right),r(t+\Delta t),t+\Delta t\right)\right\}-V\left(\delta \left(t\right),r\left(t\right),t\right)\right\}.\end{array}$$

(17)

Using full probability formulas and conditional expectations:

$$\begin{array}{c}\hfill \Im V\left(\delta \left(t\right),r,t\right)=\sum _{n=1}^s{\pi }_{rq}\left(h\right){\delta }^T\left(t\right)\left(I_N\otimes Q_q\right)\delta \left(t\right)+2{\delta }^T\left(t\right)\left(I_N\otimes Q_r\right)\dot{\delta }\left(t\right).\end{array}$$

(18)

Similar to the calculation of Markov process in [31], we can get

$$\begin{array}{c}\hfill \sum _{n=1}^s{\pi }_{rq}\left(h\right){\delta }^T\left(t\right)(I_N\otimes Q_q)\delta \left(t\right)=0,\end{array}$$

(19)

where $Q_q,q\in S$. Taking the expected values on both sides of Equation (18) above, the following equation can be obtained:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \Im \left(\delta \right(t),r,t)& ={\delta }^T\left(t\right)\left(I_N\otimes \left(A^T{Q}_r+Q_{r}A\right)-\left.2H_r\otimes Q_{r}B{B}^T{Q}_r\right)\delta \left(t\right)\right.\hfill \\ & +2{\delta }^T\left(t\right)\left(I_N\otimes Q_{r}B{B}^T{Q}_r\right)e\left(t\right)\hfill \\ & \le {\widehat{\delta }}^T\left(t\right)\left(I_N\otimes \left(A^T{Q}_r+Q_{r}A\right)-2{\lambda }_{min}\left(H_r\right)\otimes Q_{r}B{B}^T{Q}_r\right)\widehat{\delta }\left(t\right)\hfill \\ & +2{\widehat{\delta }}^T\left(t\right)\left(I_N\otimes Q_{r}B{B}^T{Q}_r\right)\widehat{e}\left(t\right)\hfill \\ & \le \sum _{i=1}^N{\widehat{\delta }}_i^T\left(t\right)\left[\left(A^T{Q}_r+Q_{r}A\right)-2{\lambda }_{min}\left(H_r\right)\otimes Q_{r}B{B}^T{Q}_r\right]{\widehat{\delta }}_i\left(t\right)\hfill \\ & +2\sum _{i=1}^N{\widehat{\delta }}_i^T\left(t\right)Q_{r}B{B}^T{Q}_r{\widehat{e}}_i\left(t\right).\hfill \end{array}\end{array}$$

(20)

For the derivation of the above process, the same treatment method is adopted as in paper [21]. We adopt an orthogonal matrix W, such that $\widehat{\delta }\left(t\right)=\left(W\otimes I_n\right)\delta \left(t\right)$ and $\widehat{e}\left(t\right)=\left(W\otimes I_n\right)e\left(t\right)$, where $W^{T}W=I_N$. Obviously, $W^{T}HW=diag\left\{{\lambda }_{min}\left(H\right),\dots ,{\lambda }_{max}\left(H\right)\right\}$, where ${\sum }_{i=1}^N{\widehat{\delta }}^T\left(t\right)\widehat{\delta }\left(t\right)={\sum }_{i=1}^N{\delta }^T\left(t\right)\delta \left(t\right)$. The minimum eigenvalue of $H_{r\left(t\right)}$ is ${\lambda }_{*}={min}_{r\in S}\left({\lambda }_{min}\left(H_{r\left(t\right)}\right)\right)$ in the whole Markov process. From Equation (12), we can get

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \Im (\delta \left(t\right),r,t)\le -\widehat{\beta }\sum _{i=1}^N{∥{\delta }_i\left(t\right)∥}^2+2\sum _{i=1}^N∥{\delta }_i\left(t\right)∥∥Q_{r}B{B}^T{Q}_r∥∥e_i\left(t\right)∥.\end{array}\end{array}$$

(21)

Notice that, according to the event trigger condition, one has

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill ∥e_i\left(t\right)∥& \le \beta ∥y_i\left(t\right)∥\hfill \\ & =\beta ∥\sum _{j=1}^N{a}_{ij\left(r\right)}\left(x_j\left(t\right)-x_i\left(t\right)\right)+b_{0j\left(r\right)}\left(x_0\left(t\right)-x_i\left(t\right)\right)∥\hfill \\ & \le \beta ∥\sum _{j=1}^N{a}_{ij\left(r\right)}\left(x_j\left(t\right)-x_i\left(t\right)\right)∥+\beta ∥b_{0j\left(r\right)}\left(x_0\left(t\right)-x_i\left(t\right)\right)∥\hfill \\ & \le \beta ∥\sum _{j=1}^N{a}_{ij\left(r\right)}\left({\delta }_j\left(t\right)-{\delta }_i\left(t\right)\right)∥+\beta ∥b_{0j\left(r\right)}{\delta }_i\left(t\right)∥\hfill \\ & \le 2\beta \left|N_i\right|\sum _{j\in N_i}∥{\delta }_i\left(t\right)∥+\beta ∥b_{0j\left(r\right)}{\delta }_i\left(t\right)∥\hfill \\ & =∥{\delta }_i\left(t\right)∥\beta \left(2\sum _{j\in N_i}\left|N_i\right|+b_{0j\left(r\right)}\right).\hfill \end{array}\end{array}$$

(22)

Substituting (22) into (21), it yields

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \Im \left(\delta \right(t),r,t)& \le -\widehat{\beta }\sum _{i=1}^N{∥{\delta }_i\left(t\right)∥}^2+2\sum _{i=1}^N∥{\delta }_i\left(t\right)∥∥Q_{r}B{B}^T{Q}_r∥∥e_i\left(t\right)∥\hfill \\ & \le -\widehat{\beta }\sum _{i=1}^N{∥{\delta }_i\left(t\right)∥}^2+∥Q_{r}B{B}^T{Q}_r∥2\beta \sum _{i=1}^N\left({∥{\delta }_i\left(t\right)∥}^2\left(2\sum _{j\in N_i}\left|N_i\right|+b_{0i\left(r\right)}\right)\right)\hfill \\ & \le -\widehat{\beta }\left(1-{\theta }_i\right)\sum _{i=1}^N{∥{\delta }_i\left(t\right)∥}^2\hfill \\ & \le -{\alpha }_{r}V(\delta \left(t\right),r\left(t\right),t),\hfill \end{array}\end{array}$$

(23)

where ${\alpha }_r=\frac{\widehat{\beta }\left(1-\theta \right)}{{\lambda }_{min}\left(Q_r\right)}$, $\theta \in (0,1)$. The notation $\left|N_i\right|$ is the cardinality of the set $N_i$. It is obvious that $\dot{V}(\delta \left(t\right),r\left(t\right),t)<0$ and $V\left(\delta \right(t),r(t),t)>0$ in the area ${\Psi }_k$. For the Markov process, combined with Equation (25), the following equation can be derived.

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathbb{E}\{\Im V(\delta \left(t\right),r,t)\}\le -{\alpha }_1\mathbb{E}\left\{V(\delta \left(t\right),r\left(t\right),t)\right\},t\in \left[{\widehat{t}}_{k-1}+{\Delta }_{k-1},{\widehat{t}}_k\right).\end{array}\end{array}$$

(24)

The same analysis method is used to analyze the DoS attacks process. In the ${\Omega }_k$ region, due to the attacks on the communication channels between agents, the information transmission between agents cannot be carried out, so some topological structures will change at this time. Therefore, the following equation can be obtained:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \Im V\left(\delta \left(t\right),r,t\right)=2{\delta }^T\left(t\right)\{(I_N\otimes Q)\{I_N\otimes A\}\delta \left(t\right)\\ \hfill \le {\delta }^T\left(t\right)\{I_N\otimes (QA+A^{T}Q)\delta \left(t\right).\end{array}\end{array}$$

(25)

According to Equation (13), the following formula will hold:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathbb{E}\{\Im V(\delta \left(t\right),r,t)\}\le {\alpha }_2\mathbb{E}\left\{V(\delta \left(t\right),r\left(t\right),t)\right\},t\in [{\widehat{t}}_k,{\widehat{t}}_k+{\Delta }_k).\end{array}\end{array}$$

(26)

According to Comparison Lemma, the whole process can be summarized as follows.

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathbb{E}\left\{V\left(\delta \left(t\right),r,t\right)\right\}\le \left\{\begin{array}{c}{e}^{-{\alpha }_1(t-{\widehat{T}}_{k-1})}\mathbb{E}\left\{V_a\left(\delta \left(t\right),r\left(t\right),t\right)\right\},t\in [{\widehat{t}}_{k-1}+{\Delta }_{k-1},{\widehat{t}}_k)\\ e^{{\alpha }_2(t-{\widehat{t}}_k)}\mathbb{E}\left\{V_b\left(\delta \left(t\right),r\left(t\right),t\right)\right\},t\in [{\widehat{t}}_k,{\widehat{t}}_k+{\Delta }_k).\end{array}\right.\end{array}\end{array}$$

(27)

Here, we define $\mathbb{E}\left\{V\left(t\right)\right\}=\mathbb{E}\left\{V\left(\delta \left(t\right),r\left(t\right),t\right)\right\}$ to continue the analysis. In $[{\widehat{t}}_{k-1}+{\Delta }_{k-1},{\widehat{t}}_k)$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathbb{E}\left\{V\left(t\right)\right\}& \le e^{-{\alpha }_1(t-{\widehat{t}}_{k-1}-{\Delta }_{k-1})}\mathbb{E}\left\{V_a\left({\widehat{t}}_{k-1}+{\Delta }_{k-1}\right)\right\}\hfill \\ & \le \gamma e^{-{\alpha }_1(t-{\widehat{t}}_{k-1}-{\Delta }_{k-1})}\mathbb{E}\left\{V_b\left({\widehat{t}}_{k-1}^{-}+{\Delta }_{k-1}^{-}\right)\right\}\hfill \\ & \le \cdots \hfill \\ & \le {\gamma }^k{e}^{-{\alpha }_1\left|{\Xi }_1\left(t_0,t\right)\right|}{e}^{{\alpha }_2\left|{\Xi }_0\left(t_0,t\right)\right|}\mathbb{E}\left\{V_a\left(t_0\right)\right\}.\hfill \end{array}\end{array}$$

(28)

If $t\in [{\widehat{t}}_k,{\widehat{t}}_k+{\Delta }_k)$, then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathbb{E}\left\{V\left(t\right)\right\}& \le e^{{\alpha }_2(t-{\widehat{t}}_k)}\mathbb{E}\left\{V_b\left({\widehat{t}}_k\right)\right\}\hfill \\ & \le \gamma e^{\alpha 2(t-{\widehat{t}}_k)}\mathbb{E}\left\{V_a\left({\widehat{t}}_k^{-}\right)\right\}\hfill \\ & \le \cdots \hfill \\ & \le {\gamma }^{k+1}{e}^{-{\alpha }_1\left|{\Xi }_1\left(t_0,t\right)\right|}{e}^{{\alpha }_2\left|{\Xi }_0\left(t_0,t\right)\right|}\mathbb{E}\left\{V_a\left(t_0\right)\right\},\hfill \end{array}\end{array}$$

(29)

where $\gamma =max\left\{\frac{{\lambda }_{max}\left(Q_{r\left(t\right)}\right)}{{\lambda }_{min}\left(Q\right)},\frac{{\lambda }_{max}\left(Q\right)}{{\lambda }_{min}\left(Q_{r\left(t\right)}\right)}\right\}$. According to Definition 2, we can get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathbb{E}\left\{V\left(t\right)\right\}& \le {\gamma }^{N_k\left(t_0,t\right)}{e}^{-{\alpha }_1\left|{\Xi }_1\left(t_0,t\right)\right|}{e}^{{\alpha }_2\left|{\Xi }_0\left(t_0,t\right)\right|}\mathbb{E}\left\{V\left(t_0\right)\right\}\hfill \\ & ={\gamma }^{N_k\left(t_0,t\right)}{e}^{-{\alpha }_1\left(t-t_0-\left|{\Xi }_0\left(t_0,t\right)\right|\right)}{e}^{{\alpha }_2\left|{\Xi }_0\left(t_0,t\right)\right|}\mathbb{E}\left\{V\left(t_0\right)\right\}\hfill \\ & =e^{N_k\left(t_0,t\right)ln\gamma }{e}^{-{\alpha }_1\left(t-t_0\right)+\left|{\Xi }_0\left(t_0,t\right)\right|\left({\alpha }_1+{\alpha }_2\right)}\mathbb{E}\left\{V\left(t_0\right)\right\}\hfill \\ & =e^{N_k\left(t_0,t\right)ln\gamma }{e}^{-{\alpha }_1\left(t-t_0\right)+\left({\alpha }_1+{\alpha }_2\right)\left[\varsigma \left(t-t_0\right)\right]}\mathbb{E}\left\{V\left(t_0\right)\right\}\hfill \\ & =e^{N_k\left(t_0,t\right)ln\gamma }{e}^{\left(\left({\alpha }_1+{\alpha }_2\right)\varsigma -{\alpha }_1\right)\left(t-t_0\right)}\mathbb{E}\left\{V\left(t_0\right)\right\}.\hfill \end{array}\end{array}$$

(30)

Based on Equations (14) and (15), Equation (30) can be written as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathbb{E}\left\{V\left(t\right)\right\}& \le e^{{\eta }^{*}\left(t-t_0\right)}{e}^{\left(\left({\alpha }_1+{\alpha }_2\right)\varsigma -{\alpha }_1\right)\left(t-t_0\right)}\mathbb{E}\left\{V\left(t_0\right)\right\}\hfill \\ & =e^{\left(\left({\alpha }_1+{\alpha }_2\right)\varsigma -{\alpha }_1+{\eta }^{*}\right)\left(t-t_0\right)}\mathbb{E}\left\{V\left(t_0\right)\right\}\hfill \\ & \le e^{-{\eta }_1\left(t-t_0\right)}\mathbb{E}\left\{V\left(t_0\right)\right\},\hfill \end{array}\end{array}$$

(31)

where ${\eta }_1={\alpha }_1-\left({\alpha }_1+{\alpha }_2\right)\varsigma -{\eta }^{*}>0$ and ${\eta }^{*}\in \left(0,{\alpha }_1\right)$. In conclusion, we can get $\mathbb{E}{∥\delta \left(t\right)∥}^2\le \mathbb{E}\left\{V\left(0\right)\right\}$. This means that the multi-agent systems secure consensus under mean-square consensus is proved. This completes the proof. □

Remark 2.

Since each DoS attack occurs in a random discontinuity when the entire system is running, it is necessary to use the induction method to analyze the whole process. If the stability condition of the entire system in the DoS attacks environment is to be obtained, this is similar to most previous literature processing, such as [21].

4.2. Elimination of Zeno’s Behavior

Next, we will show that in the context of this article, the Zeno behavior does not exist. If the Zeno behavior does not exist, then the minimum event interval between the two adjacent event trigger times will be greater than zero, as expressed in the formula: ${\widehat{T}}_a=inf\{t_k^i-t_{k-1}^i\}>0$.

Proof . 

Firstly, region ${\Xi }_1\left(t_0,t\right)$ is analyzed. The proved method is similar to [21,31]. When $t\in \left[{\widehat{t}}_k+{\Delta }_k,{\widehat{t}}_{k+1}\right)$ the derivation of the measurement error function $e_i\left(t\right)$ of the formula is: When $t\in [{\widehat{t}}_k+{\Delta }_k,{\widehat{t}}_{k+1})$, the derivation of the measurement error function $e_i\left(t\right)$ of the formula is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{d}{dt}\left(∥e_i\left(t\right)∥\right)& \le ∥\sum _{j\in N_i}^N{a_{ij}}_{\left(r\left(t\right)\right)}\left({\dot{x}}_i\left(t\right)-{\dot{x}}_j\left(t\right)\right)+{b_{0i}}_{\left(r\left(t\right)\right)}\left({\dot{x}}_i\left(t\right)-{\dot{x}}_0\left(t\right)\right)∥\hfill \\ & \le ∥A\sum _{j\in N_i}{a_{ij}}_{\left(r\left(t\right)\right)}\left(x_i\left(t\right)-x_j\left(t\right)\right)+B\sum _{j\in N_i}{a_{ij}}_{\left(r\left(t\right)\right)}\left(u_i\left(t\right)-u_j\left(t\right)\right)\hfill \\ & +{b_{0i}}_{\left(r\left(t\right)\right)}\left(A{x}_i\left(t\right)+B{u}_i\left(t\right)-A{x}_0\left(t\right)\right)∥\hfill \\ & \le ∥A\sum _{j\in N_i}{a_{ij}}_{\left(r\left(t\right)\right)}\left(x_i\left(t\right)-x_j\left(t\right)\right)+B\sum _{j\in N_i}{a_{ij}}_{\left(r\left(t\right)\right)}\left(u_i\left(t\right)-u_j\left(t\right)\right)\hfill \\ & +{b_{0i}}_{\left(r\left(t\right)\right)}\left(A{x}_i\left(t\right)-A{x}_0\left(t\right)+B{u}_i\left(t\right)\right)∥\hfill \\ & \le ∥A\left(y_i\left(t_k^i\right)-e_i\left(t\right)\right)+B\sum _{j\in N_i}{a_{ij}}_{\left(r\left(t\right)\right)}\left(u_i\left(t\right)-u_j\left(t\right)\right)\hfill \\ & +B{b_{0i}}_{\left(r\left(t\right)\right)}{u}_i\left(t\right)∥\hfill \\ & \le ∥A∥∥e_i\left(t\right)∥+∥A{y}_i\left(t_k^i\right)+B\sum _{j\in N_i}{a_{ij}}_{\left(r\left(t\right)\right)}\left(u_i\left(t\right)-u_j\left(t\right)\right)+B{b_{0i}}_{\left(r\left(t\right)\right)}{u}_i\left(t\right)∥\hfill \\ & \le ∥A∥∥e_i\left(t\right)∥+{\mathrm{Z}}_i\left(t_k^i\right),\hfill \end{array}\end{array}$$

(32)

where ${\mathrm{Z}}_i\left(t_k^i\right)={∥A{y}_i\left(t_k^i\right)+B{\displaystyle \sum _{j\in N_i}}{a_{ij}}_{\left(r\left(t\right)\right)}\left(u_i\left(t\right)-u_j\left(t\right)\right)+B{b_{0i}}_{\left(r\left(t\right)\right)}{u}_i\left(t\right)∥}_{max}$ let ${\Gamma }_i=∥e_i\left(t\right)∥$. The Equation (22) can be rewritten as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \frac{d}{dt}\left(∥e_i\left(t\right)∥\right)=∥A∥{\Gamma }_i+{\mathrm{Z}}_i\left(t_k^i\right).\end{array}\end{array}$$

(33)

In the $t_{k+1}^i=inf\left\{t>t_k^i|f_i\left(t\right)\ge 0\right\},$ the sufficient condition for the triggering condition is considered as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\Gamma }_i=& ∥e_i\left(t\right)∥\hfill \\ & \le \frac{\beta }{1+\beta }{y}_i\left(t_k^i\right)\hfill \end{array}\end{array}$$

(34)

when the event is triggered, considering $y_i\left(t_k^i\right)>0$ condition. Then, by adopting similar method in [32], there is a link ${\phi }_i\left(t_k^i\right)\ge y_i\left(t_k^i\right)>0.$ So ${\Gamma }_i\le \frac{\beta }{1+\beta }{\phi }_i\left(t_k^i\right).$ If ${\widehat{T}}_a=t_{k+1}^i-t_k^i$, we will get:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\widehat{T}}_a=t_{k+1}^i-t_k^i\ge {\mathrm{T}}_i\ge \frac{\frac{\beta }{1+\beta }{\phi }_i\left(t_k^i\right)}{∥A∥\frac{\beta }{1+\beta }{\phi }_i\left(t_k^i\right)+{\mathrm{Z}}_i\left(t_k^i\right)}.\end{array}\end{array}$$

(35)

This set is non-empty and $T_a=inf\{t_{k+1}^i-t_k^i\}>0$, so in the normal communication region, the Zeno behavior will not occur. When the system is in DoS attack range ${\Xi }_0\left(t_0,t\right)$, it can be seen that the event trigger function will not be triggered. At this time, the Zeno behavior can be excluded. □

Remark 3.

Compared with the existing literature, this article has the following advantages: (i) It considers more complex communication topology, and therefore will be more general than Yang et al. [20], Xu et al. [21]; (ii) it clears the upper limit of DoS attacks, which will be more suitable for the application scenarios in real life compared with the research contents of Yang et al. [20], Wang et al. and other literature; (iii) it saves system control resources. Compared with the research work of Wang et al. [28], unnecessary waste of communication resources can be avoided and control efficiency can be improved.

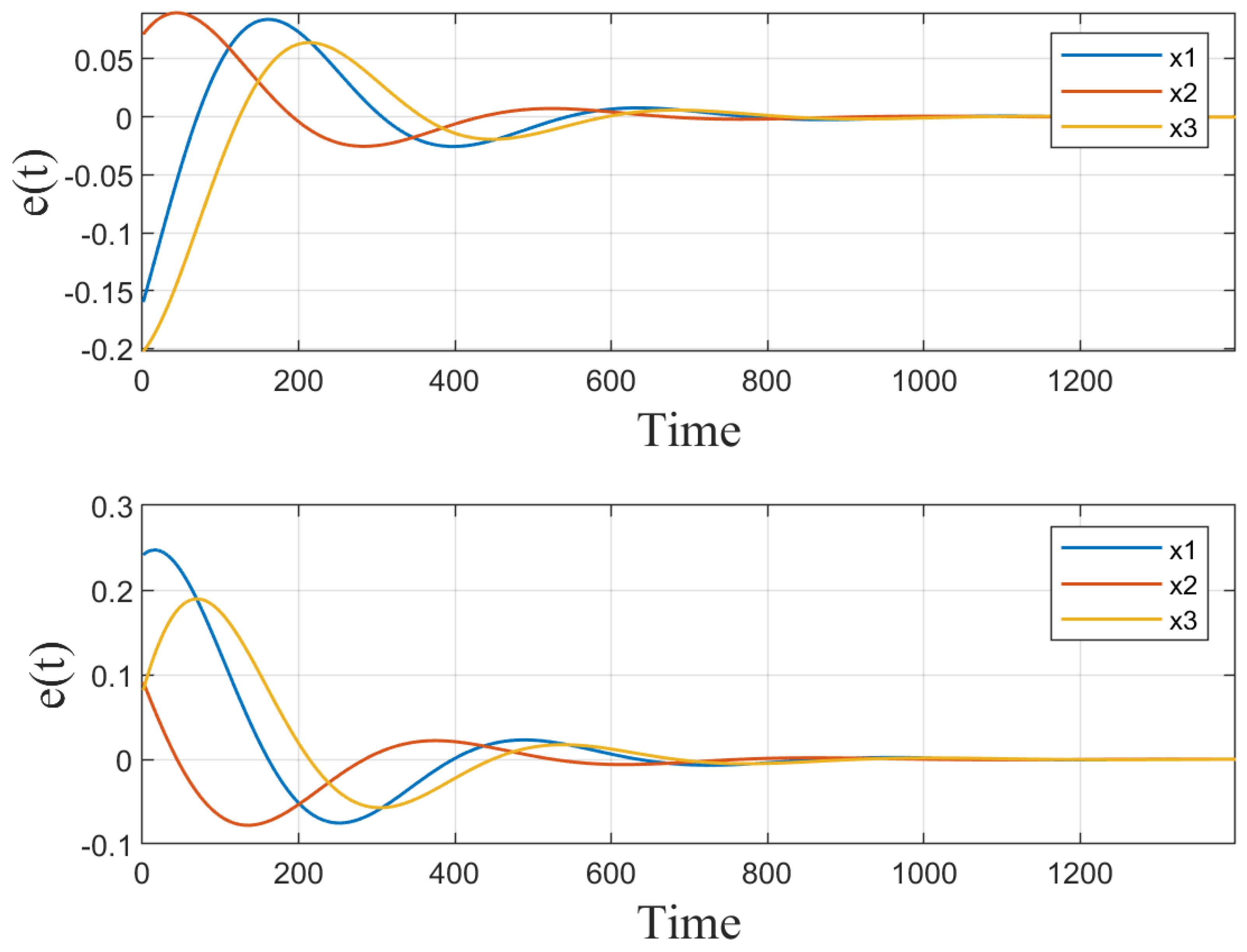
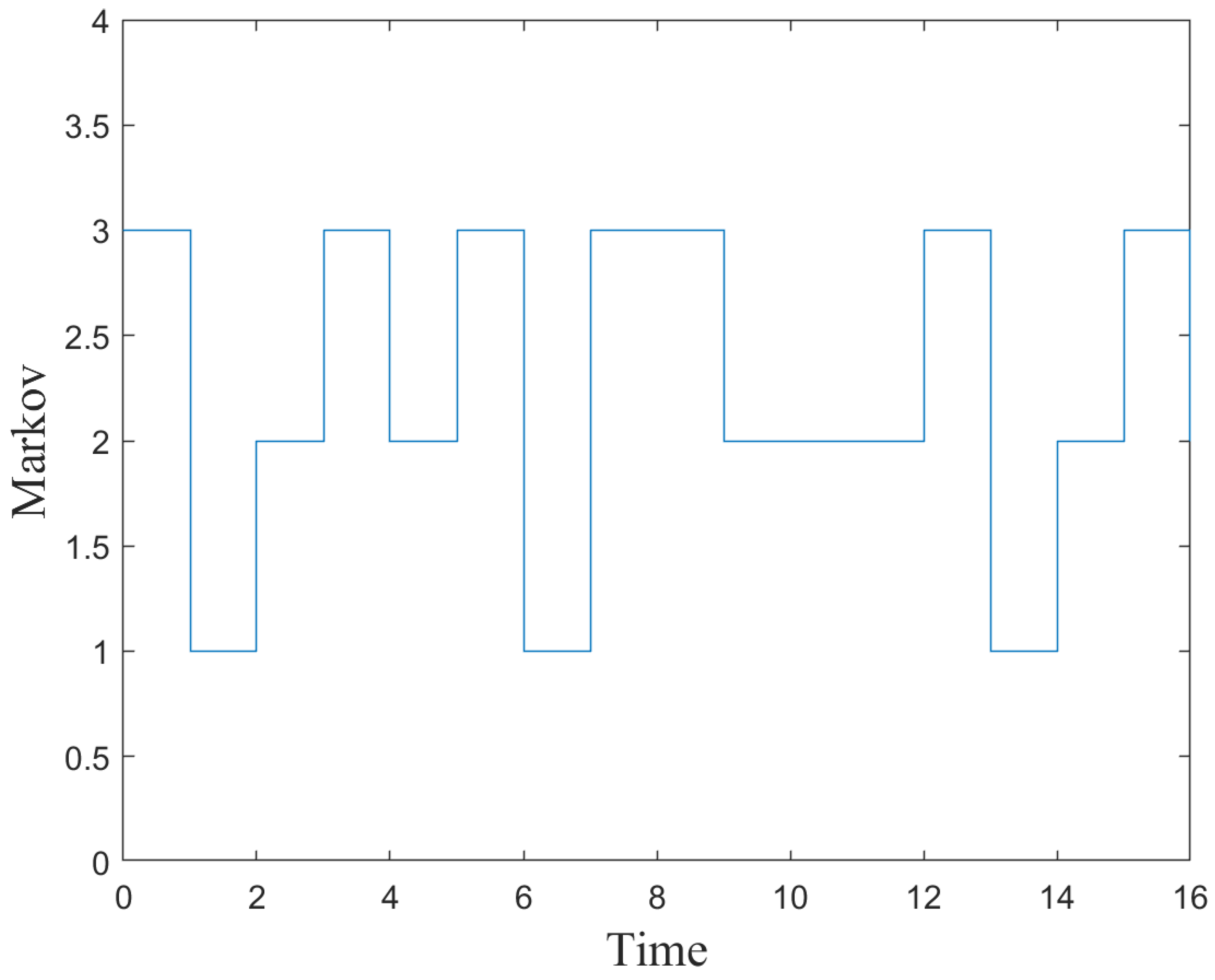
5. Numerical Simulations

This section will give a simulation experiment to verify the effectiveness of the algorithm. Figure 2 is leader–follower system (1) and (2) as a system with one leader and three followers, where $A=\left[\begin{array}{cc}0& -1\\ 2& 1\end{array}\right]$, $B=\left[\begin{array}{cc}1& 0\\ 0& 2\end{array}\right]$. The topological structure corresponding to the DoS attacks is shown in Figure 3. The corresponding H matrices are given as follows:

$$\begin{array}{c}\hfill H\left(1\right)=\left[\begin{array}{ccc}3& -1& -1\\ -1& 3& -1\\ -1& -1& 3\end{array}\right],H\left(2\right)=\left[\begin{array}{ccc}2& -1& 0\\ -1& 3& -1\\ 0& -1& 2\end{array}\right],H\left(3\right)=\left[\begin{array}{ccc}1& 0& 0\\ 0& 2& -1\\ 0& -1& 2\end{array}\right].\end{array}$$

Let $\widehat{\beta }=0.15$, $\theta =0.9$. The feedback gain matrix for different topologies $K\left(1\right)$, $K\left(2\right)$ and $K\left(3\right)$ are

$$\begin{array}{c}\hfill K\left(1\right)=\left[\begin{array}{cc}-0.8538& 0.0402\\ 0.0804& -0.6214\end{array}\right],K\left(2\right)=\left[\begin{array}{cc}-0.7538& -0.0401\\ 0.0802& -0.5814\end{array}\right],K\left(3\right)=\left[\begin{array}{cc}-0.6339& -0.0401\\ 0.0802& -0.5620\end{array}\right].\end{array}$$

The transmission probability matrix is chosen to be ${\pi }_{rq}=\left[\begin{array}{ccc}-1& 0.5& 0.5\\ 0.2& -1& 0.8\\ 0.7& 0.3& -1\end{array}\right]$. Suppose that the initial distribution of the Markov process obeys an invariant distribution ${\overline{\pi }}_1=0.5,$ ${\overline{\pi }}_2=0.3$ and ${\overline{\pi }}_3=0.2$. Choose ${\lambda }_{min}\left(Q\right)=0.8557,{\lambda }_{max}\left(Q\right)=2.0728,{\lambda }_{min}\left(Q_{r\left(t\right)}\right)=0.2765,$ ${\lambda }_{max}\left(Q_{r\left(t\right)}\right)=0.8568,$ $\gamma =7.4966,$ ${\alpha }_1=0.0151,{\alpha }_2=1.46$, ${\eta }^{*}=0.015$. Figure 4 shows the state error value of the agent. It is not difficult to see from Figure 5 that it exhibits the triggering instants for three agents. Figure 6 depicts the time period during which DoS emerges in multi-agent systems, and Figure 7 is the Markovian jump process, respectively.

6. Conclusions

In this paper, we mainly studied the secure consensus control of the multi-agent systems with Markovian switching systems under DoS attack. We used an event-trigger strategy to control the consensus of the leader–follower system. Unlike fixed topology, the topology was controlled by the Markov switching process. Moreover, we considered that DoS attacks cause changes in communication topologies, which lead to network paralysis. We used the stochastic technique, induction, Lyapunov functional protocol, and other related knowledge to design the mean square consensus condition to ensure that the system could reach a stable state. Finally, we used a simulation experiment to prove the validity of the proposed model. Further research works will consider the problem of communication delay in the topology switching process under DoS attacks.