Author Contributions
Conceptualization, V.K., A.M.-D., C.D., J.-Y.L. and D.D.; methodology, V.K., A.M.-D., C.D., J.-Y.L. and D.D.; formal analysis, V.K., A.M.-D., C.D., J.-Y.L. and D.D.; investigation, V.K., A.M.-D., C.D., J.-Y.L. and D.D.; writing—original draft preparation, V.K. and D.D.; supervision, A.M.-D., C.D., J.-Y.L. and D.D.; writing—review and editing, V.K., A.M.-D., C.D., J.-Y.L. and D.D.; All authors have read and agreed to the published version of the manuscript.
Figure 1.
Schema diagram of the test bed.
Figure 1.
Schema diagram of the test bed.
Figure 2.
Pictures of the experimental test bench.
Figure 2.
Pictures of the experimental test bench.
Figure 3.
Logarithmic distribution of points on the I–V curve.
Figure 3.
Logarithmic distribution of points on the I–V curve.
Figure 4.
Acquisition time.
Figure 4.
Acquisition time.
Figure 5.
Main circuit of the I–V tracer.
Figure 5.
Main circuit of the I–V tracer.
Figure 6.
The 205 I–V characteristics in the healthy case measured on 2 September 2019.
Figure 6.
The 205 I–V characteristics in the healthy case measured on 2 September 2019.
Figure 7.
Over-illumination effect (circled in red) on the PV panel.
Figure 7.
Over-illumination effect (circled in red) on the PV panel.
Figure 8.
128 I–V curves after withdrawing the abnormal ones.
Figure 8.
128 I–V curves after withdrawing the abnormal ones.
Figure 9.
Single-diode model PV cell equivalent circuit.
Figure 9.
Single-diode model PV cell equivalent circuit.
Figure 10.
Single-diode model for a PV module with Ns cells in series.
Figure 10.
Single-diode model for a PV module with Ns cells in series.
Figure 11.
Methodology for parameters extraction.
Figure 11.
Methodology for parameters extraction.
Figure 12.
Evolution of the photocurrent with Gpoa for Tpv = 56 °C.
Figure 12.
Evolution of the photocurrent with Gpoa for Tpv = 56 °C.
Figure 13.
Evolution of the photocurrent (Iph) with Tpv for 750 W/m2 ≤ Gpoa ≤ 780 W/m2.
Figure 13.
Evolution of the photocurrent (Iph) with Tpv for 750 W/m2 ≤ Gpoa ≤ 780 W/m2.
Figure 14.
Evolution of the diode saturation current (I0).
Figure 14.
Evolution of the diode saturation current (I0).
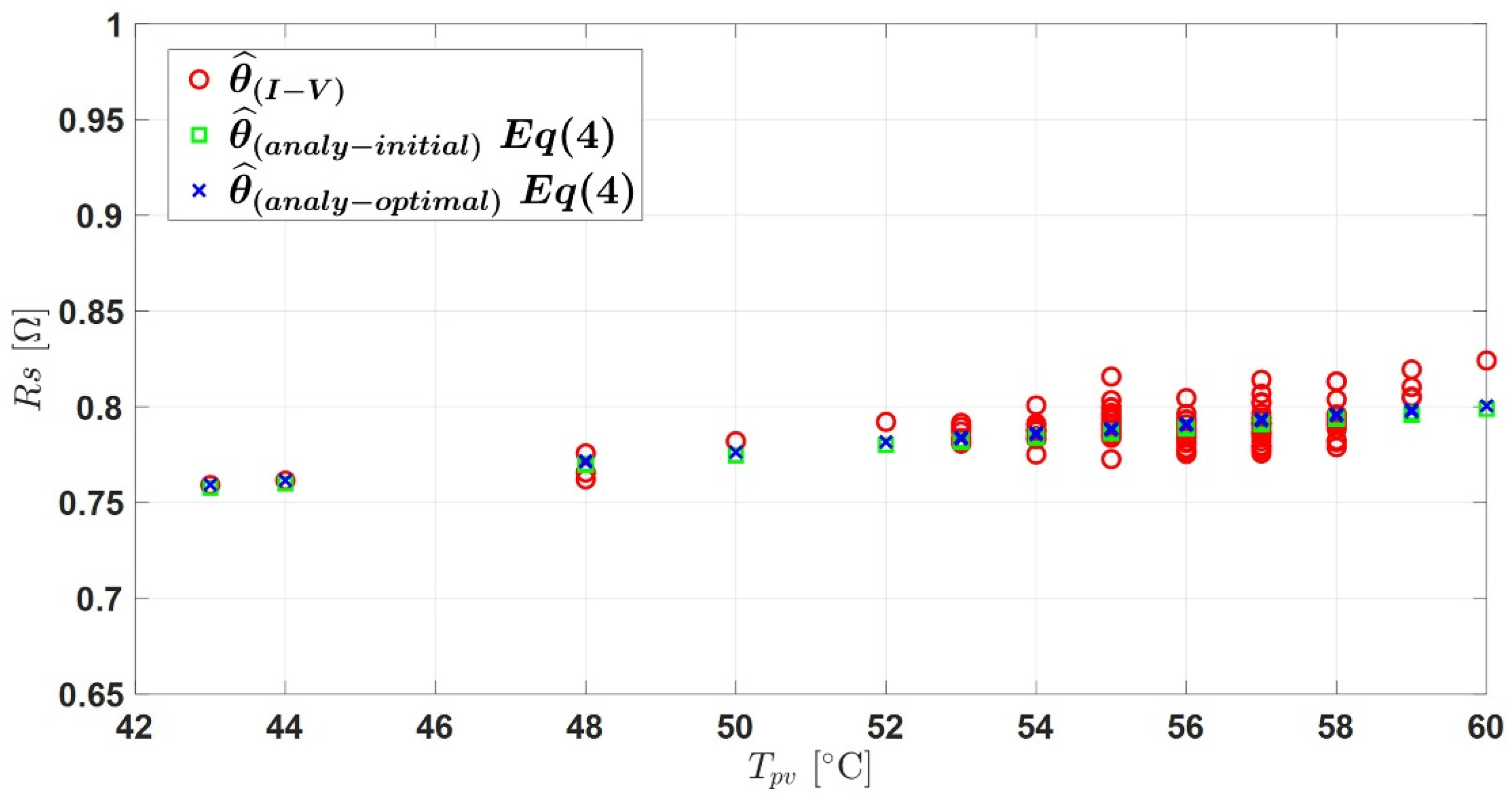
Figure 15.
Evolution of Rs for constant Tpv.
Figure 15.
Evolution of Rs for constant Tpv.
Figure 16.
Evolution of Rs for constant Gpoa.
Figure 16.
Evolution of Rs for constant Gpoa.
Figure 17.
Evolution of Rsh for constant Tpv.
Figure 17.
Evolution of Rsh for constant Tpv.
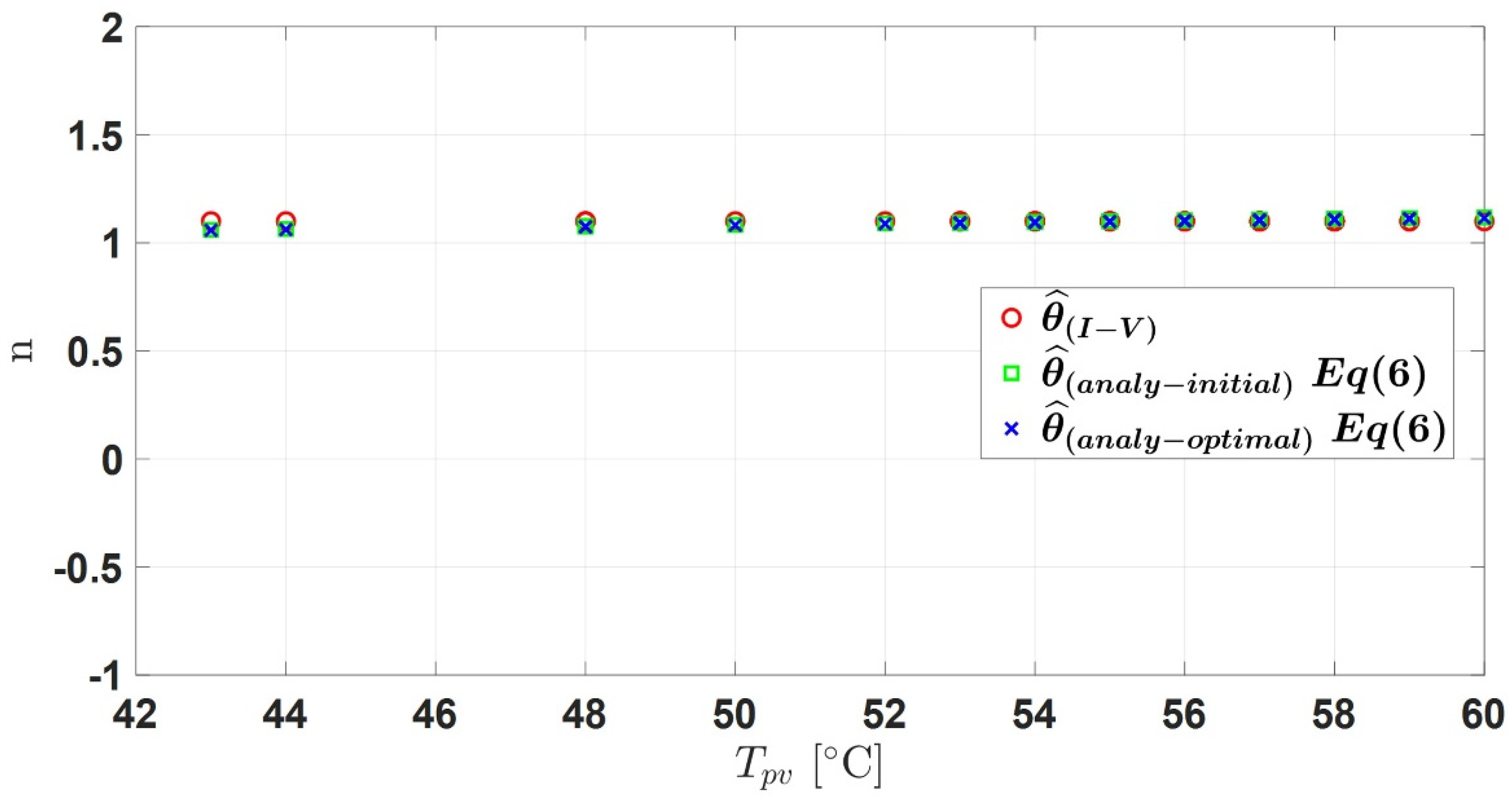
Figure 18.
Evolution of the diode ideality factor (n).
Figure 18.
Evolution of the diode ideality factor (n).
Figure 19.
Estimation of the SDM parameters.
Figure 19.
Estimation of the SDM parameters.
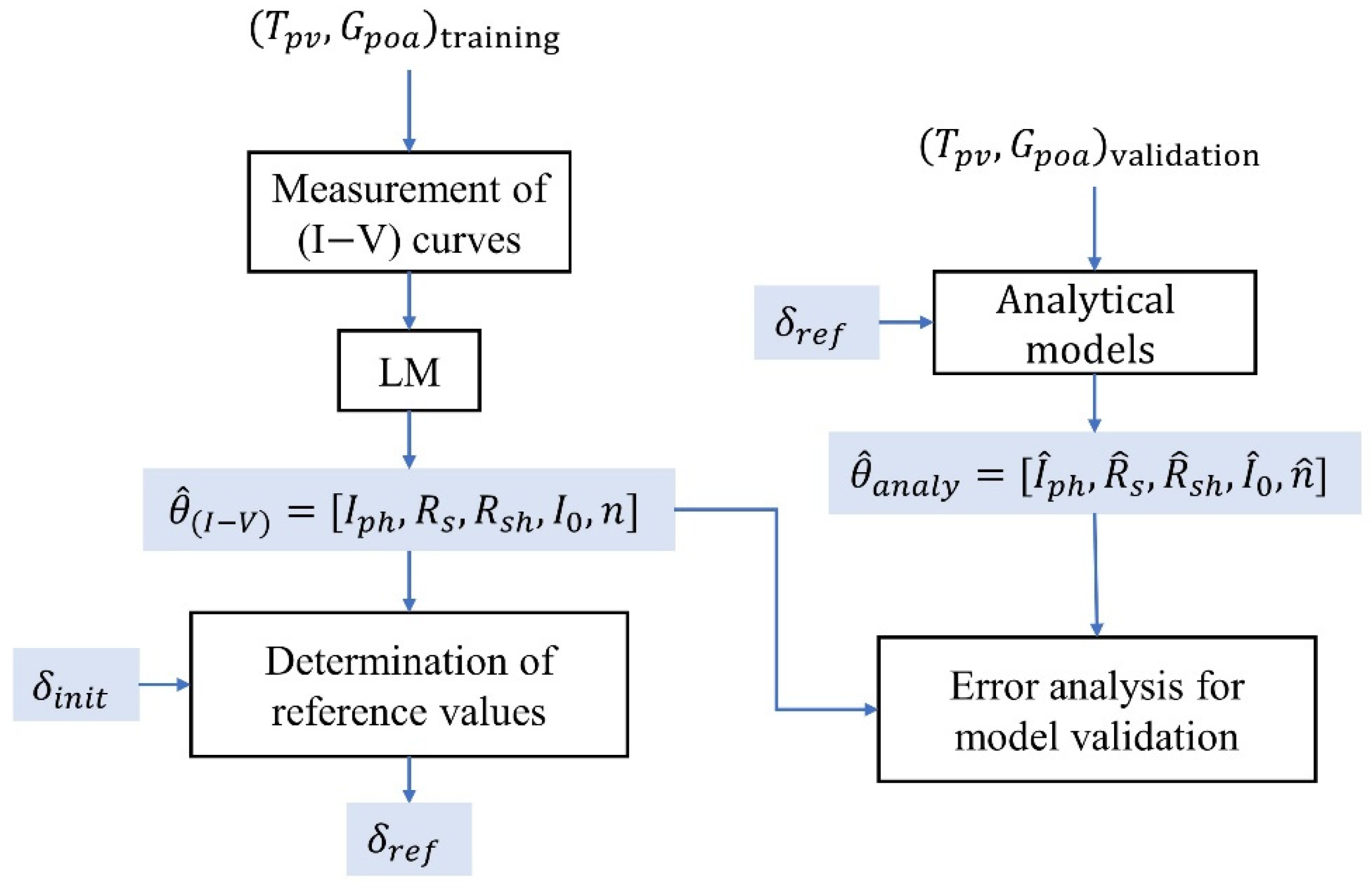
Figure 20.
Flowchart to validate the hybrid PV model.
Figure 20.
Flowchart to validate the hybrid PV model.
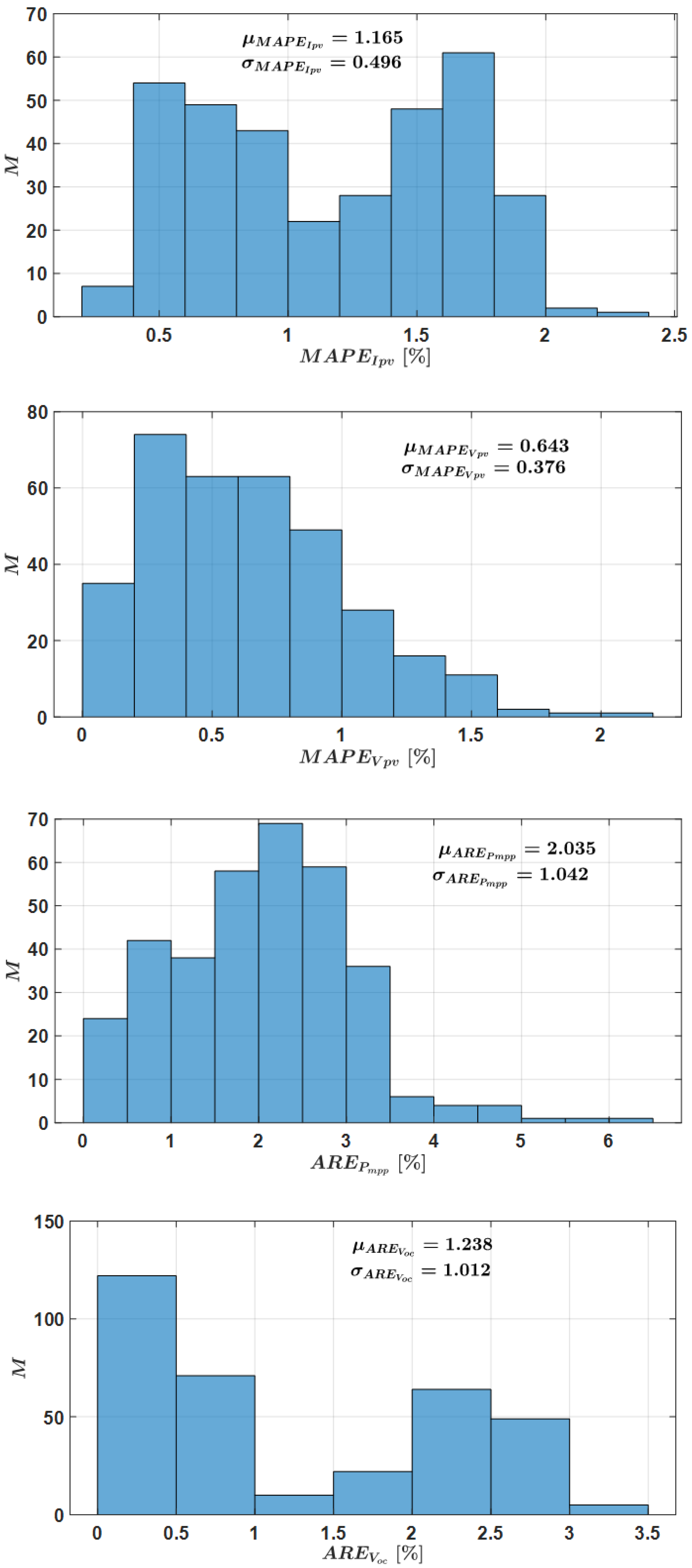
Figure 21.
Histograms of the errors.
Figure 21.
Histograms of the errors.
Figure 22.
Flowchart of the FDD: (a) M1; (b) M2.
Figure 22.
Flowchart of the FDD: (a) M1; (b) M2.
Figure 23.
Histograms of Rs resistances.
Figure 23.
Histograms of Rs resistances.
Figure 24.
Histograms of the residuals for Rs.
Figure 24.
Histograms of the residuals for Rs.
Figure 25.
Effect of series resistance degradation on the other parameters of the SDM.
Figure 25.
Effect of series resistance degradation on the other parameters of the SDM.
Figure 26.
Effect of series resistance Rs faults on the I–V curve characteristics. (a): Fault effect on PV module’s current; (b): Fault effect on PV module’s voltage; (c): Fault effect on maximum power; (d): Fault effect on open-circuit voltage; (e): Fault effect on short-circuit current.
Figure 26.
Effect of series resistance Rs faults on the I–V curve characteristics. (a): Fault effect on PV module’s current; (b): Fault effect on PV module’s voltage; (c): Fault effect on maximum power; (d): Fault effect on open-circuit voltage; (e): Fault effect on short-circuit current.
Figure 27.
FDD in the case of Rsh degradation. (a): Measured and estimated shunt resistance values; (b): Residuals.
Figure 27.
FDD in the case of Rsh degradation. (a): Measured and estimated shunt resistance values; (b): Residuals.
Figure 28.
Effect of Rsh degradation on the other parameters of the SDM.
Figure 28.
Effect of Rsh degradation on the other parameters of the SDM.
Figure 29.
Effect of shunt resistance fault Rsh on the I–V curve characteristics. (a): Fault effect on PV module’s current; (b): Fault effect on PV module’s voltage; (c): Fault effect on maximum power; (d): Fault effect on open-circuit voltage; (e): Fault effect on short-circuit current.
Figure 29.
Effect of shunt resistance fault Rsh on the I–V curve characteristics. (a): Fault effect on PV module’s current; (b): Fault effect on PV module’s voltage; (c): Fault effect on maximum power; (d): Fault effect on open-circuit voltage; (e): Fault effect on short-circuit current.
Table 1.
Parameters under standard test conditions (STC), Gpoa = 1000 W/m2 and Tpv = 25 °C.
Table 1.
Parameters under standard test conditions (STC), Gpoa = 1000 W/m2 and Tpv = 25 °C.
| Electrical Performance under Standard Test Conditions (STC) |
|---|
| 87 W (+10%/−5%) |
| 17.4 V |
| 5.02 A |
| 21.7 V |
| 5.34 A |
| | /°C |
| | /°C |
Table 2.
Comparison with market I–V tracers.
Table 2.
Comparison with market I–V tracers.
| Type | Duration of
Measurement | Cost | Resolution | Acquisition Method | Application |
|---|
| Proposed I–V tracer | 182 ms | 35 € | 26 points | Auto and Cont | Module |
| Chauvin–Arnoux FTV 2000 IV tracer [21] | - | 3650 € | 500 points | Manual | Module |
| HT-Instruments I–V 500 W tracer [22] | - | 4300 € | 128 points | Manual and Auto | Module/String/Array |
| CHROMA Electronic load Model 63600 series [23] | to 40 ms | >4000 € | 1–4096 points | Manual and Auto | Module/String/Array |
| EKO MP 11 IV checker [24] | 5 s | - | 400 points | Manuel and Auto | Module |
| HUAWEI Smart I–V tracer Diagnosis [25] | 1 s | - | 128 points | Manual and Auto | Module/String/Array |
| SOLMETRIC PV analyzer I–V tracer [26] | 0.05–2 s | 5468–11,038 € | 100 to 500 points | Manuel and Auto | Module/String |
Table 3.
Data used for the training stage.
Table 3.
Data used for the training stage.
| No | Data Acquisition | Weather | Number of I–V Curves
|
|---|
| 1 | 2 September 2021 | Sunny | 94 |
| 2 | 8 September 2021 | Sunny | 86 |
| 3 | 10 September 2021 | Partly cloudy | 29 |
| 4 | 14 September 2021 | Partly cloudy | 45 |
| 5 | 15 September 2021 | Partly cloudy | 42 |
| 6 | 19 September 2021 | Partly cloudy | 44 |
| 7 | 20 September 2021 | Partly cloudy | 27 |
| 8 | 23 September 2021 | Partly cloudy | 58 |
| 9 | 24 September 2021 | Sunny | 63 |
Table 4.
Extracted reference values for constant Tpv for the photocurrent model.
Table 4.
Extracted reference values for constant Tpv for the photocurrent model.
| | | [%/°C] |
|---|
| Initial value (STC) | 5.34 | 0.038 |
| Optimized value | 5.817 | 0.061 |
| 6.01% |
Table 5.
Extracted reference values for constant Gpoa for the photocurrent model.
Table 5.
Extracted reference values for constant Gpoa for the photocurrent model.
| | | [%/°C] |
|---|
| Initial value (STC) | 5.817 | 0.061 |
| Optimized value | 5.799 | 0.061 |
| 1.49 % |
Table 6.
Extracted reference values.
Table 6.
Extracted reference values.
| | | [%/°C] |
|---|
| Initial value (STC) | 21.7 | −0.37 |
| Optimized value | 20.68 | −0.519 |
| 7.34% |
Table 7.
Extracted reference values for constant Tpv for the series resistance model.
Table 7.
Extracted reference values for constant Tpv for the series resistance model.
| | | |
|---|
| Initial value (STC) | 0.8 | 0.217 |
| Optimized value | 0.708 | 0.0359 |
| 0.88% |
Table 8.
Extracted reference values for constant Gpoa.
Table 8.
Extracted reference values for constant Gpoa.
| | | |
|---|
| Initial value | 0.708 | 0.0359 |
| Optimized value | 0.709 | 0.0359 |
| 0.92% |
Table 9.
Extracted reference value Rsh_ref.
Table 9.
Extracted reference value Rsh_ref.
| | |
|---|
| Initial value | 80 |
| Optimized value | 49.85 |
| 7.4% |
Table 10.
Extracted reference value nref.
Table 10.
Extracted reference value nref.
| | |
|---|
| Initial value | 1 |
| Optimized value | 1.01 |
| 0.58% |
Table 11.
Summary of the eight reference values extracted from the analytical models.
Table 11.
Summary of the eight reference values extracted from the analytical models.
| The Single Diode of PV Model with Five Electrical Parameters and Eight Reference Values |
|---|
|
|---|
| Parameters of the SDM | Analytical Models | The Eight Reference Values |
|---|
|
[%/°C]
|
|
[%/°C]
|
| |
| |
|---|
| | 5.79 | 0.061 | - | - | - | - | - | - |
| | - | - | 20.68 | −0.519 | - | - | - | - |
| | - | - | - | - | 0.709 | 0.0359 | - | - |
| | - | - | - | - | - | - | 49.85 | - |
| | - | - | - | - | - | - | - | 1 |
Table 12.
Data used for the validation step.
Table 12.
Data used for the validation step.
| No | Data Acquisition | Weather | Number of I–V Curves
|
|---|
| 1 | 3 September 2021 | Partly cloudy | 100 |
| 2 | 9 September 2021 | Partly cloudy | 21 |
| 3 | 12 September 2021 | Partly cloudy | 9 |
| 4 | 13 September 2021 | Partly cloudy | 42 |
| 5 | 22 September 2021 | Partly cloudy | 12 |
| 6 | 8 October 2021 | Partly cloudy | 44 |
| 7 | 9 October 2021 | Partly cloudy | 71 |
| 8 | 10 October 2021 | Partly cloudy | 56 |
| 9 | 11 October 2021 | Partly cloudy | 47 |
| 10 | 15 October 2021 | Partly cloudy | 27 |
Table 13.
Data for the validation of the hybrid PV model.
Table 13.
Data for the validation of the hybrid PV model.
| No | Data Acquisition | Weather | Number of I–V Curves
|
|---|
| 1 | 3 September 2021 | Partly cloudy | 100 |
| 2 | 9 September 2021 | Partly cloudy | 21 |
| 3 | 13 September 2021 | Partly cloudy | 42 |
| 4 | 22 September 2021 | Partly cloudy | 12 |
| 5 | 8 October 2021 | Partly cloudy | 44 |
| 6 | 9 October 2021 | Partly cloudy | 71 |
| 7 | 10 October 2021 | Partly cloudy | 56 |
| 8 | 11 October 2021 | Partly cloudy | 47 |
Table 14.
Data acquisition in case of Rs degradation.
Table 14.
Data acquisition in case of Rs degradation.
| No | Data Acquisition | Weather | Number of I–V Curves
| Fault Level |
|---|
| 1 | 12 April 2021 | Partly cloudy | 38 | |
| 2 | 17 April 2021 | Partly cloudy | 16 | |
| 3 | 18 April 2021 | Partly cloudy | 56 | |
| 4 | 19 April 2021 | Partly cloudy | 34 | |
| 5 | 26 April2021 | Partly cloudy | 61 | |
| 6 | 27 April 2021 | Partly cloudy | 61 | |
| 7 | 20 April 2021 | Partly cloudy | 104 | |
Table 15.
Accuracy of fault level estimation in case of Rs degradation.
Table 15.
Accuracy of fault level estimation in case of Rs degradation.
| Fault Level | | | |
|---|
| (Ω) | 0.22 | 0.33 | 0.39 |
| (Ω) | 0.205 | 0.326 | 0.439 |
| Relative error on Rs % | 1.57 | 0.37 | 4.35 |
Table 16.
Effect of the Rs on the I–V curve characteristics.
Table 16.
Effect of the Rs on the I–V curve characteristics.
| Fault Level | | | |
|---|
| 1.4 | 1.84 | 1.99 |
| 3.15 | 4.06 | 4.48 |
| 3.6 | 4.64 | 5.1 |
| 0.13 | 0.21 | 0.32 |
| 0.01 | 0.032 | 0.067 |
Table 17.
Data acquisition for Rsh degradation.
Table 17.
Data acquisition for Rsh degradation.
| No | Data Acquisition | Weather | Number of I–V Curves
| |
|---|
| 1 | 13 April 2021 | Partly cloudy | 82 | |
| 2 | 5 April 2021 | Partly cloudy | 61 | |
| 3 | 3 April 2021 | Partly cloudy | 39 | |
Table 18.
Three levels of severity for Rsh degradation.
Table 18.
Three levels of severity for Rsh degradation.
| Fault Level |
|
| | |
|---|
| 1 | | 57.89 | 29.46 | 28.42 |
| 2 | | 65.81 | 28.41 | |
| 3 | | 63.8 | 24.20 | |
Table 19.
Fault effect on the I–V curve characteristics.
Table 19.
Fault effect on the I–V curve characteristics.
| Fault Level | | | |
|---|
| 1.11 | 1.98 | 2.64 |
| 0.19 | 0.31 | 0.66 |
| 1.48 | 2.44 | 3.39 |
| 0.45 | 0.51 | 0.57 |
| 0.14 | 0.46 | 0.61 |
Table 20.
Summary of FDD performance.
Table 20.
Summary of FDD performance.
| FDD Method | Fault Types |
|---|
| |
|---|
| M1 | | No effect | | No effect |
| High | | No effect |
| No effect | | High |
| No effect | | No effect |
| No effect | | No effect |
| M2 | | Low | | Low |
| Low | | Low |
| High | | High |
| Low | | Low |
| Low | | Low |