Abstract
This study empirically examines the effect of economic development on carbon emissions and revisits the environmental Kuznets curve in Suzhou, China. The study made use of the Gross Domestic Product Per Capita (GDPPC) of Suzhou, China as an indicator of economic development as it depicts the entire developmental ecosystem that indicates the level of production activities and total energy consumption. Bearing this in mind, the authors postulate that economic development directly increases carbon emissions through industrial and domestic consumptions. For this purpose, linear and non-linear approaches to cointegration are applied. The study finds the existence of an inverted U-shape relationship between economic development and carbon emission in the long run. Trade openness and industrial share are positively contributing to increasing carbon emissions. Energy use shows a positive sign but an insignificant association with carbon emissions. The study concludes that carbon emissions in Suzhou should be further decreased followed by policy recommendations.
1. Introduction
Issues related to climate change have attracted much attention worldwide and have become an increasingly pressing problem facing society [1,2]. Global warming is one of the most serious current events, which has affected human beings socially, politically, and economically in recent decades [3,4]. Reports from the Intergovernmental Panel on Climate Change (IPCC) and other studies show that carbon dioxide (CO2) emissions are the most important contributor [5,6] to global warming. Human activities have greatly exacerbated the process of climate warming and caused many adverse effects on the natural ecological environment on the earth’s surface.
Enduring economic growth and its environmental consequences present a growing concern in the energy-led economic growth paradigm. Numerous empirical studies have been conducted to measure the environmental impacts of energy-led economic activities, whose findings remain disputed. Grossman & Krueger [7] argue that the first phase of economic growth is detrimental to the environment. Still, it later becomes conducive to the quality of the environment when growth surpasses a certain point, known as the Environmental Kuznets Curve (EKC) hypothesis.
According to [3], the growth rate of global primary energy consumption in 2018 reached (2.8%) the highest since 2010. Statistics portrayed that China, the United States of America, and India contribute more than 2/3 of the global energy consumption growth [4]. With the increase in consumption of energy products, carbon emissions from global energy recorded an increase of 1.7% in 2018 to reach a momentous high of 33.1 Gt of equivalent carbon dioxide emissions (GtCO2E) [5], adding 600 million tons of CO2E, equivalent to an increase in the emissions of 400 million vehicles [6]. It is a crystal that, carbon dioxide is the foremost root of global warming. Global warming has brought great repercussions to the natural environment, food, water supply, health, and even social security. Therefore, reducing the quantity of emission of carbon dioxide is a crucial task for all countries in dealing with climate change.
Numerous studies have been conducted to scrutinize the validity of EKC in the context of different countries, regions, and the world as a whole. Some demonstrate that economic growth and environmental quality follow a linear, U- or inverted U-shaped, or even N-shaped relationship. Lau, et al. [8] proposes three different factors or channels determining whether economic growth and environmental quality should follow a linear, U- or inverted U-shaped relationship. The three factors include the scale (volume) of production, composition or means of production, and uses of technology for production.
Suzhou is a city in Jiangsu Province that is located in the Yangtze River Delta with the highest record of economic development in China. Jiangsu is the key province of China’s economic development and the first manufacturing base in China. Among the cities in Jiangsu Province, in 2019 the GDP of Suzhou exceeded 1.9 trillion yuan, ranking among the top 10 in China and the first in Jiangsu Province [9,10,11,12,13]. The GDP of Suzhou not only exceeded the GDP of some provinces in China, but also the GDP of many European countries, such as Portugal, Romania, Finland, and Ukraine. The permanent population of Suzhou is likened to Portugal; however, the GDP of Suzhou far exceeds that of Portugal which is currently a developed country. Emphasizing that the economic benefits produced by this city in China have surpassed that of some developed countries in the world within 2019. The GDP per capita of Suzhou was 179,174.35 yuan in 2019. The performance of Suzhou City has ascribed the name “China’s strongest prefecture-level city” due to its fast-economic development which is unparalleled and amazing throughout the world. Suzhou contributed 19.3% of the total economic volume of Jiangsu Province, and its total energy consumption accounted for only 22.7%. This suggests a strong correlation between energy carbon emission and economic development levels in Suzhou. So, the study aims to examine the nexus between economic growth and carbon emissions empirically by revisiting the environmental Kuznets curve by using the data from Suzhou, a city in Jiangsu Province in China. For this purpose, we apply both specifications of the Autoregressive Distributive Lag (ARDL) model namely linear and non-linear or asymmetric ARDL together with bounds testing approach of cointegration. Our paper is different from previous studies in terms of methodology and context. For instance, our paper is different from Sohag, et al. [9] as they examined the scale, technique, and composition effects of the environmental Kuznets curve by using panel data. This is the first comparative study that compares the findings of linear ARDL and Asymmetric ARDL to examine the nexus between environmental Kuznets curve and economic development along with other control variables as per our information by using time series data. The prior studies used carbon emissions per capita as a proxy of energy efficiency whereas we compiled our energy carbon emissions (CoE) variable by taking the sum of energy emissions multiplied by oxidation rate multiplied by energy consumption [10]. This provides a compressive index for carbon emissions and distinguishes our study from prior studies. The study also examines the measures adopted to reduce carbon emissions in Suzhou.
2. Literature Review
Many empirical studies have examined the linkage between the scale of production (measured in GDP) and environmental quality (carbon emissions). These studies provide evidence that carbon emissions increase due to the increasing scale of production (indexed by GDP growth) while keeping the composition of input and technology constant. For instance, [11] documents that carbon emissions and economic growth are monotonically associated with Bahrain, Egypt, Iran, Kuwait, Oman, Qatar, Saudi Arabia, Syria, and Tunisia. Likewise, a linear relationship between per capita GDP and carbon emissions has been identified for middle-income countries [12] and the particular country cases of Kuwait [13], Saudi Arabia [14], Iran [15], Malaysia [16], and Brazil [17]. However, the linear relationship between growth and carbon emissions explains merely the upward portion of the EKC diagram where economic growth spurs carbon emissions.
Nevertheless, many prior studies observe an inverted U-shaped relationship between carbon emissions and economic growth by confirming the EKC hypothesis for the world in General [18], 19 European countries [19], EU members [20], 17 African countries [21], Malaysia [12,22] and the UK [23]. Conversely, many studies contradict the existence of the EKC hypothesis, demonstrating a U-shaped relationship implying that higher GDP growth accelerates carbon emissions at a greater rate (often for countries overlapping with those considered in the studies cited above). It includes OECD countries [24], Asia, Africa, and Central America [25], Spain [26], and Malaysia [27]. Several studies by Ahmed et al. [28] document that the use of renewable energy can augment economic growth by reducing economic externalities.
In addition, [29] provide evidence of a U-shaped relationship between growth and carbon emissions for OECD member countries. Another strand of literature establishes a bi-directional relation or reverses causal relationship. For instance, [22,30] identify that economic growth and carbon emissions follow a bidirectional association in OECD countries. Conversely, an empirical investigation by [19] surprisingly observes no causal relationship between carbon emissions and income level in the context of Turkey. Despite a large volume of studies, little is known on whether EKC theory holds in the context of OECD countries by contextualizing the three channels of scale, composition, and technology factors. Concerning the composite effects, EKC argues that with an unchanging volume of economic activities and technology, carbon emissions increase or decrease depending on the changing composition of production factors or economic growth paradigm. For instance, ref. [31] demonstrate that an increased contribution of the agriculture sector to GDP helps reduce carbon emissions in low-income countries due to the adaption of non-energy-intensive cultivation processes. In addition, the transformation of the economy from industrial to service orientation leads to diminished carbon emissions in the middle- and lower-middle-income countries. Nevertheless, the higher growth of a service economy positively influences emissions levels in OECD and high-income countries due to energy-led sophisticated technologies [32].
With the impact of economic factors on carbon emissions, the innovation of solar energy technology negatively affects CO2E. By using yearly time series data for the period 1970–2012, Salahuddin, Alam, Ozturk and Sohag [13] examined the influences associated with the income of people, energy consumption, and population growth on CO2 emissions for Indonesia, India, Brazil, and China. Using the ARDL bounds assessment method their outcomes expressed that CO2 emissions significantly escalated with a rise in revenue and energy consumption in all four countries. Likewise, a practical survey from the testing of the environmental Kuznets curve (EKC) hypothesis infers that in the cases of Brazil, China, and Indonesia, CO2 emissions will decrease over time when income increases. Al Mamun, et al. [33] used the newly developed dynamic ARDL simulation process to study the impact of energy consumption and economic growth on environmental degradation in Pakistan and proposed the use of renewable alternative energy to reduce environmental degradation. Shan, et al. [34] also analyzed the nexus of CO2 emissions, economic growth, and energy consumption by decoupling greenhouse gas emissions of CO2 and economic growth over the period 1970–2015. Their study applied different estimation techniques such as the ARDL model, FMOLS, DOLS, and impulse response and variance decomposition. The result supports the Environmental Kuznets Curve (EKC) hypothesis which specified that China’s EKC turning point confirms some inconsistencies when compared to other turning points attained from different studies.
In addition, prior literature argues that an augmented service economy enhances carbon emissions compared to other sectors, although this is heavily conditioned by the massive carbon footprint of transportation, which is part of the service sector [35]. Apart from the growth philosophy, carbon emissions are linked with whether the economy is labor- or capital-intensive. According to the neoclassical growth model, labor and capital substitute each other; thus, higher share capital is linked with higher energy use and higher carbon emissions. In addition, Lau, Choong and Ng [8] argue that institutional quality plays a vital role in reducing carbon emissions in developing and developed countries [36]. Finally, technological advancement and green technology used in the production process play a particular role in defining the intensity of carbon emissions that is generally intensifying in this century due to government regulations and legislation and rising energy prices. We argue that emissions per unit of output would increase or decrease depending on the quality of technological infrastructure when other factors remain constant. Empirical studies demonstrate that the development of technology diminishes the intensity of carbon emissions by improving energy efficiency [12,37,38]. A study highlight that non-carbon content and better technology support decreasing carbon emissions without damaging economic growth Al Mamun, Sohag, Samargandi, & Yasmeen [39]. Al Mamun, Sohag, Shahbaz, Hammoudeh [40] profoundly argues that the shape of the relationship between carbon emissions and economic growth depends on the scale or volume of production, composition, or means of production, and type of technology used in the production process.
Suzhou Zhangjiagang Ecological Environment Bureau, together with Zhangjiagang Branch of the People’s Bank of China and Zhangjiagang Rural Commercial Bank, successfully issued the first 3 million yuan carbon emission quota pledge loan ‘carbon credit’ business in Suzhou. During the 13th Five-Year Plan period, the economic indicators and energy output rate of Suzhou Industrial Park showed positive growth, the carbon emission intensity (carbon dioxide emissions per unit GDP) showed a steady downward trend, and the total carbon emission was relatively decoupled from economic growth.
In summary, by considering all the literature studies conducted by different scholars above, it is found that their main focus was geared toward the economic growth model and did not consider the impact of carbon emission on economic growth by using either carbon emission per capita as dependent variable or Sulphur dioxide omissions per capita as a measure of environmental Kuznets curve. Our study uses a more comprehensive measure for carbon efficiency emissions by constructing a unique index for energy carbon emissions (CoE). This study compares the findings from ARDL and non-linear ARDL to examine the nexus between carbon emissions and economic growth. Based on China’s current status ascribed as the second largest manufacturing country in the world, and taking Suzhou as a reference point for this study, this paper adopts a scientific quantitative analysis model, collects and analyze statistical data, and empirically studies the dialectical connection between economic development and energy carbon emissions, and also provide valuable information for developing countries and regions.
3. Methodology
3.1. Establishment of the Empirical Model
In many academic works on the relationship between technological evolution, economic development, and emissions of greenhouse gas, the earlier quantitative study paradigm began with Kaya identity proposed by Japanese scholar Kaya based on factorization in 1989 [25]. Since then, it gradually leaned towards the vector autoregressive (VAR) model. Most recent literature suggested using linear and non-linear approaches to examine the impact of CO2E on GDP per capita. That is why we use linear and non-linear approaches to examine the empirical relationship between these variables as suggested by unit root analysis. Our empirical model is based on the following production function:
where K = Capital and L = effective labor. Carbon emissions are the outcome of economic activities and its function is as follows:
where ν denotes the carbon emissions efficiency discharged from the production process, particularly from the burning carbon energy. Higher usage of fossil fuel in the production process emits more carbon emissions from coal, oil, gas, etc. However, the use of renewable and clean energy can reduce carbon emissions.
The output (Y) is the function of labor and capital. The concentration of greenhouse gases in the atmosphere is augmenting as a consequence of human activities, hence it can be considered as a core factor in explaining the carbon emissions function. The model is extended as follows:
where and indicates the coefficient of environment Kuznets curve. indicates the coefficient of labor. shows the coefficient of trade openness. > 0 is the coefficient of energy use. > 0 denotes the coefficient of industrial production.
3.2. Variable Selection and Data Sources
The dependent variable of the study is energy carbon emissions (CO2E). The independent variable of the study includes GDP per capita, energy use, industrial share as a percent of GDP. Trade openness and labor are used as control variables of the study. We also included the GDP per capita square variable to capture the monotonic impact of growth in per capita towards carbon emissions. The data has collected from Chinese annual yearbooks from 1998 to 2019. The collected data has been converted into quarters to avoid a degree of freedom issue (1998q1–2019q4). The data has been converted into quarters by using Eviews 12 software.
3.3. Standard Autograssive Distributed Lag Bounds Testing Approach to Cointegration
This approach to cointegration was developed by Pesaran, et al. [41]. This approach has an advantage over Watson [42] granger causality test and Johansen [36] cointegration test. ARDL bounds testing approach can provide both short-run and long-run dynamics. This estimation technique checks the existence of dynamic interactions and cointegration relationships among variables by providing critical leverage during the estimation process. This estimation technique is suitable for finite and small data sizes. This estimation technique uses the OLS method to examine the cointegration relation after selecting suitable lag order of the variables. This estimation technique considers the mix order of integration for instance I(0) or I(1) or mutual but not applicable in case when variables have an I(2) order of integration.
We followed Frimpong Magnus and Oteng-Abayie [43] and Al Mamun, Sohag, Samargandi and Yasmeen [33] and the equation for ARDL is as follows:
where are long-run multipliers, is the drift and are white noise errors.
After estimation of the above equation, we applied the ordinary least squares test to check the existence of no-cointegration among variables. The null hypothesis of no co-integration is against the alternate hypothesis . This estimation technique checks the stability of the model by providing results for the cumulative sum of recursive residuals (CUSUM) and the cumulative sum of squares of recursive residuals (CUSUMSQ).
Furthermore, we applied the normalization test on Y by Co2E (Co2E|LGDPPC, LGDPPC2, LL, LIPGDP, LEU, LTO). We get two asymptotic critical values of bounds test of cointegration when the independent variables are I(d) where 0_d_1. A lower value assumes the regressors are I (0), and an upper value assumes regressors have purely I (1). If the F-statistics is above the upper critical value, the null hypothesis of no long-run relationship can be rejected irrespective of the orders of integration for the time series. Conversely, if the test statistic falls below the lower critical value the null hypothesis cannot be rejected. Lastly, if the statistic falls between the lower and upper critical values, the result is inconclusive. The approximate critical values for the F-test were obtained from Pesaran, Shin and Smith [41]. After establishing the long-run relationship, we estimated the conditional ARDL (p1, q1, q2, q3, q4) as follows:
where all variables are as defined previously. This includes the selection of the order of integration ARDL (p1, q1, q2, q3, q4) model in the seven variables using Akaike information criteria (AIC). Lastly, we obtain the short-run dynamic parameters by estimating an error correction model associated with the long-run estimates. The equation for the short-run dynamic or error correction model of ARDL is as follows:
Here, and are the short-run dynamic coefficients of the model’s convergence to equilibrium and is the speed of adjustment.
3.4. Asymmetric ARDL Model
Asymmetric ARDL is a popular econometric framework that is used to examine the non-linear relationship among variables. We applied Sohag, et al. [44] non-linear ARDL (NARDL) framework that incorporates an error correction mechanism. This framework consists of some distinct features for instance parameters are estimated by OLS through incorporating persistent and stationary variables in a coherent pattern. Therefore, the precise asymmetric long run ARDL model is constructed as follows:
where indicates is a scalar I (1) variable and is decomposed as where and are partial sum processes of positive and negative changes in . where and are partial sum processes of positive and negative changes in We hypothesize a single known threshold value of zero by following Shin, et al. [45] to ensure that the framework demonstrates a clear economic interpretation.
The asymmetric ARDL(p,q) in the level framework can be written as follows:
where is a k − 1 vector of multiple regressors defined such as , is the autoregressive parameter and is an iid process with zero mean and constant zero . Throughout this paper, we will consider is decomposed as and around a threshold of zero, thereby distinguishing between positive and negative changes in the rate of growth of .
The associated error correction form of non-linear ARDL is as follows:
where for j = 1,..., and are the asymmetric long run parameters. By specifying a marginal reduced data generating process of the form .
and expressing conditionally on such that
where is not correlated with by construction. By subtracting (10) from (8) and rearranging it, we obtained this conditional non-linear ECM as follows:
where and for j = 1, …, q − 1.
The existence of a stable long-run relationship is generally examined by using two tests named tBDM-statistic and FPSS. Najarzadeh, et al. [46] proposed tBDM-statistic where null hypothesis as H0: p = 0 against alternative hypothesis H1: p < 0. Whereas Pesaran, Shin and Smith [46] proposed FPSS statistic tests joint null hypothesis as H0: p = θ+ = θ+ = 0. Pesaran, Shin and Smith [41] bounds testing framework offer a mean to get a valid inference of the presence of both stationary and non-stationary variables. Shin, Yu and Greenwood-Nimmo [45] view this characteristic is highly desirable in the presence of partial sum decompositions and may show complex interdependences. Empirically, Shin, Yu and Greenwood-Nimmo [45] proposed the counting of the regressors in xt before decomposition and choosing the suitable critical values those from tabulated in Pesaran and Shin [47] to endorse conservatism.
Equation (6) represents the general form, considering both long-run and short-run asymmetries. The Wald joint significance can be applied to examine the null hypothesis of long-run symmetry π+= π−. In addition, restrictions of short-run symmetry are considered in two different ways: π+= π− for all I = 0, …, q − 1 or = . However, both forms can be evaluated by applying the standard Wald test. Furthermore, we also examined the symmetry of the impact of multipliers (i.e., H0 = π+ = π−).
Shin, Yu and Greenwood-Nimmo [45] state that the effect of asymmetric dynamic multiplier on Yt is related with unit changes in and and is measured recursively from the parameters of the asymmetric ARDL in level (Equation (6)).
4. Empirical Analysis
In the first point of estimation, we draw the quadratic figure whereby X-axis represents the GDP per capita and Y-axis represents the energy carbon emissions level (CO2). The quadric fit is made by regressing the dependent variable (CO2 emissions) on independent variables (GDP Per capita and GDP per capita square). Figure 1 depicts clearly that the energy carbon emissions increase with an increase in GDP per capita. After GDP per capita reaches a certain level, it starts to diminish with further economic growth.
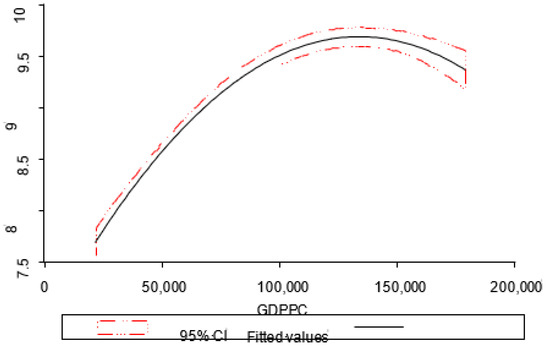
Figure 1.
Relationship between GDP per capita and Carbon emissions (Co2E).
4.1. Unit Root Test
The basic assumption of the traditional econometric model enshrines that data should be stable, but in reality, the trend of many economic variables is not stable. If the data are directly analyzed by regression, it is easy to lead to the problem of “spurious regression” in the results of quantitative regression, and even affect the final judgment [14,27]. Moreover, when two non-stationary time series are regressed, even if higher coefficients are obtained, the analysis results are meaningless and unconvincing. Therefore, before model analysis, it is usually necessary to test the unit root of variables to investigate their stationarity [14,28,29]. Numerous methods of testing unit root exist, but the most well-known unit root testing methods adopted by many scholars are the Augmented Dickey-Fuller test (ADF test), Phillips Perron test (PP test), the DF test, to mention but a few. Here we apply the ADF unit root test to check whether variables are stationary or not. The calculation results are displayed in Table 1.

Table 1.
ADF Unit root test results.
According to the results in Table 1, the variable , LIPGDP, LTO are stationary at level. Whereas , , LEU, and LL are stationary at first difference. Through the unit root testing, the variables are seen to be mixed order of integration, which suggests applying standard ARDL (Auto-regressive Distributed Lag) Bounds Testing approach to cointegration and Non-Linear approach to cointegration namely Auto Regressive Distributed Lag Model (NARDL).
Table 2 shows the values of calculated F-statistics by predicting there is a probability of having cointegrated relations among variables included in the model. We also present the normalization method presented by Pesaran, Shin and Smith [41]. This method considers each variable as the dependent variable in the ARDL-OLS framework. The results depict that Co2E (Co2E|LGDPPC, LGDPPC2, LL, LIPGDP, LEU, LTO) = 5.85; for LGDPPC (LGDPPC|Co2E, LGDPPC2, LL, LIPGDP, LEU, LTO) = 18.04; for LGDPPC2 (LGDPPC2|Co2E, LGDPPC, LL, LIPGDP, LEU, LTO) = 6.84; for LIPGDP (LIPGDP|Co2E, LGDPPC, LGDPPC2, LL, LEU, LTO) = 5.78; for LL (LL|Co2E, LGDPPC, LGDPPC2, LIPGDP, LEU, LTO) = 4.61 and for LEU (LEU|Co2E, LGDPPC, LGDPPC2, LIPGDP, LL, LTO) = 19.96. The finding shows that calculated f-statistics are higher than the critical values at 10%, 5%, and 1% level of significance of upper bounds of the bounds test. Therefore, we conclude that a cointegration relationship exists among variables included in the model when the regressions are normalized on Co2E, LGDPPC, LGDPPC2, LIPGDP, LL, and LEU. These findings are robust from the endogeneity issue as followed by [41] who used to take lag orders to solve this endogeneity problem.

Table 2.
Normalization Results from Bounds Test.
4.2. Empirical Findings from Standard ARDL Model
Table 3 shows the results of the long-run coefficient from the standard ARDL model. The lagged dependent variable is negative and significant which indicates that carbon emissions are being affected by its lag year values. Per capital GDP has a positive and significant relationship with carbon emissions whereas the square of per capita GDP has an inverse and significant relationship towards carbon emissions. This shows the existence of the environmental Kuznets curve in Suzhou, China. An increase in GDP per capita indicates the level of economic development and by increasing the level of economic development, there can be seen an increase in carbon emissions. But after some time, while taking the square of GDP per capita shows a negative relationship with carbon emissions, validates the fact that as GDP per capita grows over time, it will reduce carbon emissions. Labor has a negative but insignificant relationship with carbon emissions. Trade openness and industrial share to GDP have a positive and significant relationship towards carbon emissions. This finding also validates the fact that an increase in trade openness and increase in industrial share in GDP produces more carbon emissions. Energy use has a positive but insignificant relationship with carbon emissions. The increase in energy use generates more carbon emissions but here insignificant relationship does not show the clear picture of energy use towards carbon emissions Suzhou, China.

Table 3.
Long Run coefficients from standard ARDL model.
Table 3 also presents the results of short-run coefficients obtained from the standard ARDL model. The results of short-run coefficients validate the findings of long-run coefficients. GDP per capita, trade openness, energy use has a positive and significant relationship with carbon emissions. This shows that in the short run, these indicators enhance carbon emissions. GDP per capita square and labor have an inverse relationship with carbon emissions during the short run. Energy use has a positive and significant relationship with carbon emissions in the long run. Table 3 also enlist the error correction term that is negative and significant. Error correction term shows the speed of adjustment towards equilibrium, where the value is 48 percent, which means it will take around two and half years to reach equilibrium. Table 4 also includes some diagnostic tests which show that the model is free from serial correlation, heteroscedasticity. The diagnostic tests also indicate that data is normally distributed, and the model is correctly specified. Moreover, the values of t-statistics for the significant results are greater than 1.96 [48].

Table 4.
Results of the impact of carbon emissions on Economic Development.
Figure 2 and Figure 3 show the graph of CUSUM and CUSUMSQ within the critical boundaries at a 5% level of significance. Red and green lines show the reference boundary lines for the cumulative recursive estimates while the blue line shows the trend of coefficients included in the model. These graphs show the stability of long-run coefficients and short-run coefficients included in the error correction framework.
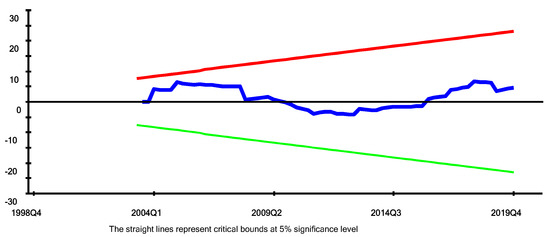
Figure 2.
Plot of Cumulative Sum of Recursive Residuals. Source: Author’s Calculation.
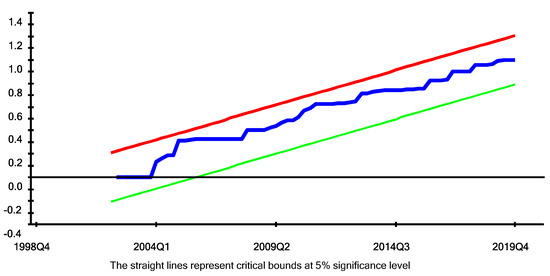
Figure 3.
Plot of Cumulative Sum of Squares Recursive residuals. Source: Author’s Calculation.
4.3. Empirical Findings from Asymmetric ARDL Model
Table 4 indicates the results from asymmetric ARDL both for the long run and short run. The values of FPSS and TBDM depict that the null hypothesis of no cointegration is rejected under the assumption of short-run and long-run asymmetry in the model. The estimates obtained by using the standard ARDL framework also fail to detect asymmetric long-run relationships among variables included in the model. Table 4 shows that the short run and long run asymmetry has been detected by the NARDL estimator efficiently. Furthermore, Table 4 indicates that the long run coefficients of GDPPC+ are 8.48 and GDPPC− is −0.29 respectively. Statistically, when there is a one percent increase in GDP per capita, the increase in carbon emissions will be 8.48%, whereas a decline in GDP per capita decreases carbon emissions by −0.29 percent during the long run. It indicates that the increase in GDP per capita will lead to generating more carbon emissions as compared to the reduction in GDP per capita will reduce carbon emission.
The findings in Table 4 also show that an increase in industrial share increases carbon emissions in the long run. However, labor, trade openness, and energy use do not have any impact on carbon emissions in long run. The quality of these NARDL findings are based on robust assumption, the improved and unrestricted assumptions of NARDL as compared to standard ARDL. The asymmetric test shows that trade openness, energy use, and industrial share to GDP asymmetrically adjusts during the short run but not in the long run. The rest of the regressor follows symmetric adjustment.
The diagnostic test of the NARDL approach shows that model does not contain any normality problem, heteroscedastic, or functional form. The value of adjusted R-Square 0.71 clearly indicates that the model is a good fit. Moreover, the stability test (Figure 4) confirms the stable impact of GDP per capita on carbon emissions as the parameter falls within the critical boundary.
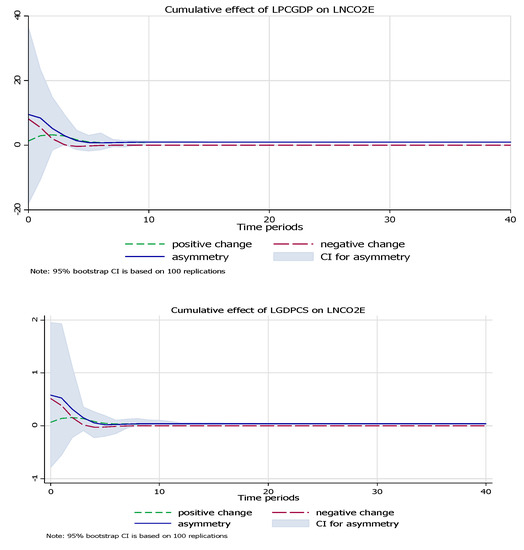
Figure 4.
Stability test of coefficient in NARDL.
5. Conclusions and Countermeasures
This study revisits Environmental Kuznets Curve in Relation to Economic Development and Energy Carbon Emission Efficiency by using data from Suzhou, China. We applied linear ARDL and non-linear ARDL estimation techniques to examine this relationship. Our results indicate that GDP per capita (GDPPC) has a positive and significant impact on carbon emissions both in the short and long run under linear and non-linear assumptions. Also, the square of GDP per capita indicated that, at the initial stages of development, as GDPPC grows, carbon emissions increase, but there comes a point when with an increase in GDPPC, carbon emissions starts declining (Figure 1). The findings of linear ARDL indicate that trade openness and industrial share to GDP positively and significantly increase carbon emissions in long run and all variables included in the model have a significant impact on carbon emissions. The findings from asymmetric ARDL show that GDP per capita, GDP per capita square, and industrial share to GDP have a positive impact on carbon emissions in the long run. The asymmetric findings indicate that only GDP per capita has a long-run asymmetric relationship with carbon emissions. However, trade openness, energy use, and industrial share have a short-run asymmetric relationship with carbon emissions. The rest of the variables have a symmetric relationship with carbon emissions. Asymmetric ARDL permits us to incorporate the possibility of asymmetric effects of positive and negative changes in independent variables on the dependent variable (Table 4) whereas the possible impact on independent variables remains the same in linear ARDL (Table 4). NARDL provides a graph of cumulative dynamic multipliers used to trace out the adjustment patterns following the positive and negative shocks to independent variables (Figure 4). Furthermore, the NARDL model permits any asymmetric switching from short run to long run or vice versa. If we compare findings from both techniques, we can conclude that findings from linear ARDL show all variables increase carbon emissions in the model except labor and energy use. Whereas the findings from asymmetric ARDL indicate that only GDP per capita, GDP per capita square, and industrial share positively influence carbon emission during the long run. In summary, we can conclude that energy conservation and carbon emission reduction will not affect the speed and scale of economic growth, and it is therefore predicted that in the future low-carbon or carbon-free environment and development goals would be achieved. Eventually, implementing green and low-carbon emission measures would be the fulcrum of high-quality economic development. Specifically, there is a need to implement relevant supporting policies to promote the sustainable development of a low-carbon economy by building a high-end efficient and green low-carbon industrial guidance policy system, improving the fiscal and financial support policy system for low-carbon development, and implementing ecological civilization initiatives under the government-led assessment policy system.
Author Contributions
The conception, design, analysis, and material preparation of this study were performed by M.W., M.L., N.E. and H.X.; data collection was performed by H.S.u.d.K., A.H. and M.W.; N.E. edited the final draft of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This study is financed by the National Natural Science Foundation of China Grant no. 7167031130, 71774071 as well as Key Research Base of Universities in Jiangsu Province for Philosophy and Social Science “Research Center for Green Development and Environmental Governance”. Naila Erum acknowledges this paper is supported by the RUDN University Strategic Academic Leadership Program.
Data Availability Statement
The datasets generated for this study were obtained from the China Statistical Yearbook. The analyzed data are available and would be submitted upon request.
Acknowledgments
The all authors of the manuscript do acknowledge the immense support granted by the National Natural Science Foundation of China and the RUDN University Strategic Academic Leadership Program. The authors acknowledge their financial supporters: National Natural Science Foundation of China (72174076 and 71974081).
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Fan, J.-L.; Wang, Q.; Yu, S.; Hou, Y.-B.; Wei, Y.-M. The evolution of CO2 emissions in international trade for major economies: A perspective from the global supply chain. Mitig. Adapt. Strateg. Glob. Chang. 2017, 22, 1229–1248. [Google Scholar] [CrossRef]
- Nicholson-Cole, S.A. Representing climate change futures: A critique on the use of images for visual communication. Comput. Environ. Urban Syst. 2005, 29, 255–273. [Google Scholar] [CrossRef]
- Ang, J.B. CO2 emissions, research and technology transfer in China. Ecol. Econ. 2009, 68, 2658–2665. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Vecchi, G.A.; Reichler, T. Correction to “Expansion of the Hadley cell under global warming”. Geophys. Res. Lett. 2007, 34, L14808. [Google Scholar] [CrossRef]
- Houghton, J.T.; Ding, Y.; Griggs, D.J.; Noguer, M.; van der Linden, P.J.; Dai, X.; Maskell, K.; Johnson, C. Climate Change 2001: The Scientific Basis; The Press Syndicate of the University of Cambridge: Cambridge, UK, 2001. [Google Scholar]
- Kind, V. Pedagogical content knowledge in science education: Perspectives and potential for progress. Stud. Sci. Educ. 2009, 45, 169–204. [Google Scholar] [CrossRef] [Green Version]
- Grossman, G.M.; Krueger, A.B. Economic growth and the environment. Q. J. Econ. 1995, 110, 353–377. [Google Scholar] [CrossRef] [Green Version]
- Lau, L.-S.; Choong, C.-K.; Ng, C.-F. Role of institutional quality on environmental Kuznets curve: A comparative study in developed and developing countries. In Advances in Pacific Basin Business, Economics and Finance; Emerald Publishing Limited: Bentley, UK, 2018. [Google Scholar]
- Sohag, K.; Kalugina, O.; Samargandi, N. Re-visiting environmental Kuznets curve: Role of scale, composite, and technology factors in OECD countries. Environ. Sci. Pollut. Res. 2019, 26, 27726–27737. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Burnett, J.W.; Fletcher, J.J. Spatial analysis of China province level CO2 emission intensity. Renew. Sustain. Energy Rev. 2014, 33, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Omri, A. CO2 emissions, energy consumption and economic growth nexus in MENA countries: Evidence from simultaneous equations models. Energy Econ. 2013, 40, 657–664. [Google Scholar] [CrossRef] [Green Version]
- Sohag, K.; Al Mamun, M.; Uddin, G.S.; Ahmed, A.M. Sectoral output, energy use, and CO2 emission in middle-income countries. Environ. Sci. Pollut. Res. 2017, 24, 9754–9764. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salahuddin, M.; Alam, K.; Ozturk, I.; Sohag, K. The effects of electricity consumption, economic growth, financial development and foreign direct investment on CO2 emissions in Kuwait. Renew. Sustain. Energy Rev. 2018, 81, 2002–2010. [Google Scholar] [CrossRef] [Green Version]
- Samargandi, N. Sector value addition, technology and CO2 emissions in Saudi Arabia. Renew. Sustain. Energy Rev. 2017, 78, 868–877. [Google Scholar] [CrossRef]
- Lotfalipour, M.R.; Falahi, M.A.; Ashena, M. Economic growth, CO2 emissions, and fossil fuels consumption in Iran. Energy 2010, 35, 5115–5120. [Google Scholar] [CrossRef]
- Ang, J.B. Financial development, liberalization and technological deepening. Eur. Econ. Rev. 2011, 55, 688–701. [Google Scholar] [CrossRef]
- Pao, H.-T.; Tsai, C.-M. Modeling and forecasting the CO2 emissions, energy consumption, and economic growth in Brazil. Energy 2011, 36, 2450–2458. [Google Scholar] [CrossRef]
- Caviglia-Harris, J.L.; Chambers, D.; Kahn, J.R. Taking the “U” out of Kuznets: A comprehensive analysis of the EKC and environmental degradation. Ecol. Econ. 2009, 68, 1149–1159. [Google Scholar] [CrossRef]
- Ozturk, I.; Acaravci, A. CO2 emissions, energy consumption and economic growth in Turkey. Renew. Sustain. Energy Rev. 2010, 14, 3220–3225. [Google Scholar] [CrossRef]
- Ahmed, A.; Uddin, G.S.; Sohag, K. Biomass energy, technological progress and the environmental Kuznets curve: Evidence from selected European countries. Biomass Bioenergy 2016, 90, 202–208. [Google Scholar] [CrossRef]
- Sarkodie, S.A.; Adams, S. Renewable energy, nuclear energy, and environmental pollution: Accounting for political institutional quality in South Africa. Sci. Total Environ. 2018, 643, 1590–1601. [Google Scholar] [CrossRef]
- Saboori, B.; Sapri, M.; bin Baba, M. Economic growth, energy consumption and CO2 emissions in OECD (Organization for Economic Co-operation and Development)’s transport sector: A fully modified bi-directional relationship approach. Energy 2014, 66, 150–161. [Google Scholar] [CrossRef]
- Sephton, P.; Mann, J. Compelling evidence of an environmental Kuznets curve in the United Kingdom. Environ. Resour. Econ. 2016, 64, 301–315. [Google Scholar] [CrossRef]
- Ekins, P. The Kuznets curve for the environment and economic growth: Examining the evidence. Environ. Plan. A 1997, 29, 805–830. [Google Scholar] [CrossRef] [Green Version]
- Dietz, S.; Adger, W.N. Economic growth, biodiversity loss and conservation effort. J. Environ. Manag. 2003, 68, 23–35. [Google Scholar] [CrossRef]
- Roca, J.; Padilla, E.; Farré, M.; Galletto, V. Economic growth and atmospheric pollution in Spain: Discussing the environmental Kuznets curve hypothesis. Ecol. Econ. 2001, 39, 85–99. [Google Scholar] [CrossRef] [Green Version]
- Begum, R.A.; Sohag, K.; Abdullah, S.M.S.; Jaafar, M. CO2 emissions, energy consumption, economic and population growth in Malaysia. Renew. Sustain. Energy Rev. 2015, 41, 594–601. [Google Scholar] [CrossRef]
- Ahmed, S.; Alam, K.; Sohag, K.; Gow, J.; Rashid, A.; Akter, M. Renewable and non-renewable energy use and its relationship with economic growth in Myanmar. Environ. Sci. Pollut. Res. 2019, 26, 22812–22825. [Google Scholar] [CrossRef]
- Bella, G.; Massidda, C.; Mattana, P. The relationship among CO2 emissions, electricity power consumption and GDP in OECD countries. J. Policy Model. 2014, 36, 970–985. [Google Scholar] [CrossRef]
- Li, M.; Sun, H.; Agyeman, F.O.; Heydari, M.; Jameel, A.; Salah ud din Khan, H. Analysis of Potential Factors Influencing China’s Regional Sustainable Economic Growth. Appl. Sci. 2021, 11, 10832. [Google Scholar] [CrossRef]
- Alam, M.M.; Murad, M.W.; Noman, A.H.M.; Ozturk, I. Relationships among carbon emissions, economic growth, energy consumption and population growth: Testing Environmental Kuznets Curve hypothesis for Brazil, China, India and Indonesia. Ecol. Indic. 2016, 70, 466–479. [Google Scholar] [CrossRef]
- Alkhathlan, K.; Javid, M. Energy consumption, carbon emissions and economic growth in Saudi Arabia: An aggregate and disaggregate analysis. Energy Policy 2013, 62, 1525–1532. [Google Scholar] [CrossRef]
- Al Mamun, M.; Sohag, K.; Samargandi, N.; Yasmeen, F. Does remittance fuel labour productivity in Bangladesh? The application of an asymmetric non-linear ARDL approach. Appl. Econ. 2016, 48, 4861–4877. [Google Scholar] [CrossRef]
- Shan, Y.; Guan, D.; Liu, J.; Mi, Z.; Liu, Z.; Liu, J.; Schroeder, H.; Cai, B.; Chen, Y.; Shao, S. Methodology and applications of city level CO2 emission accounts in China. J. Clean. Prod. 2017, 161, 1215–1225. [Google Scholar] [CrossRef] [Green Version]
- Alcántara, V.; Padilla, E. Input–output subsystems and pollution: An application to the service sector and CO2 emissions in Spain. Ecol. Econ. 2009, 68, 905–914. [Google Scholar] [CrossRef]
- Johansen, S. Estimation and hypothesis testing of cointegration vectors in Gaussian vector autoregressive models. Econom. J. Econom. Soc. 1991, 1551–1580. [Google Scholar] [CrossRef]
- Wang, K.-M. Modelling the nonlinear relationship between CO2 emissions from oil and economic growth. Econ. Model. 2012, 29, 1537–1547. [Google Scholar] [CrossRef]
- Wu, L.; Kaneko, S.; Matsuoka, S. Driving forces behind the stagnancy of China’s energy-related CO2 emissions from 1996 to 1999: The relative importance of structural change, intensity change and scale change. Energy Policy 2005, 33, 319–335. [Google Scholar] [CrossRef]
- Al Mamun, M.; Sohag, K.; Shahbaz, M.; Hammoudeh, S. Financial markets, innovations and cleaner energy production in OECD countries. Energy Econ. 2018, 72, 236–254. [Google Scholar] [CrossRef] [Green Version]
- Wagner, M. The carbon Kuznets curve: A cloudy picture emitted by bad econometrics? Resour. Energy Econ. 2008, 30, 388–408. [Google Scholar] [CrossRef] [Green Version]
- Pesaran, M.H.; Shin, Y.; Smith, R.J. Bounds testing approaches to the analysis of level relationships. J. Appl. Econom. 2001, 16, 289–326. [Google Scholar] [CrossRef]
- Watson, M.W. Vector autoregressions and cointegration. Handb. Econom. 1994, 4, 2843–2915. [Google Scholar]
- Frimpong Magnus, J.; Oteng-Abayie, E.F. Bounds testing approach: An examination of foreign direct investment, trade, and growth relationships. Am. J. Appl. Sci. 2006. Available online: https://ssrn.com/abstract=927169 (accessed on 10 October 2021).
- Sohag, K.; Taşkın, F.D.; Malik, M.N. Green economic growth, cleaner energy and militarization: Evidence from Turkey. Resour. Policy 2019, 63, 101407. [Google Scholar] [CrossRef]
- Shin, Y.; Yu, B.; Greenwood-Nimmo, M. Modelling asymmetric cointegration and dynamic multipliers in a nonlinear ARDL framework. In Festschrift in Honor of Peter Schmidt; Springer: Berlin/Heidelberg, Germany, 2014; pp. 281–314. [Google Scholar]
- Najarzadeh, R.; Reed, M.; Tasan, M. Relationship between savings and economic growth. The case for Iran. J. Int. Bus. Econ. 2014, 2, 107–124. [Google Scholar] [CrossRef] [Green Version]
- Pesaran, M.H.; Shin, Y. An Autoregressive Distributed Lag Modelling Approach to Cointegration Analysis. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.153.3246&rep=rep1&type=pdf (accessed on 30 June 2021).
- Duffy, F.H.; Bartels, P.H.; Burchfiel, J.L. Significance probability mapping an aid in the topographic analysis of brain electrical activity. Electroencephalogr. Clin. Neurophysiol. 1981, 51, 455–462. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).