Modeling and Monitoring Erosion of the Leading Edge of Wind Turbine Blades
Abstract
:1. Introduction
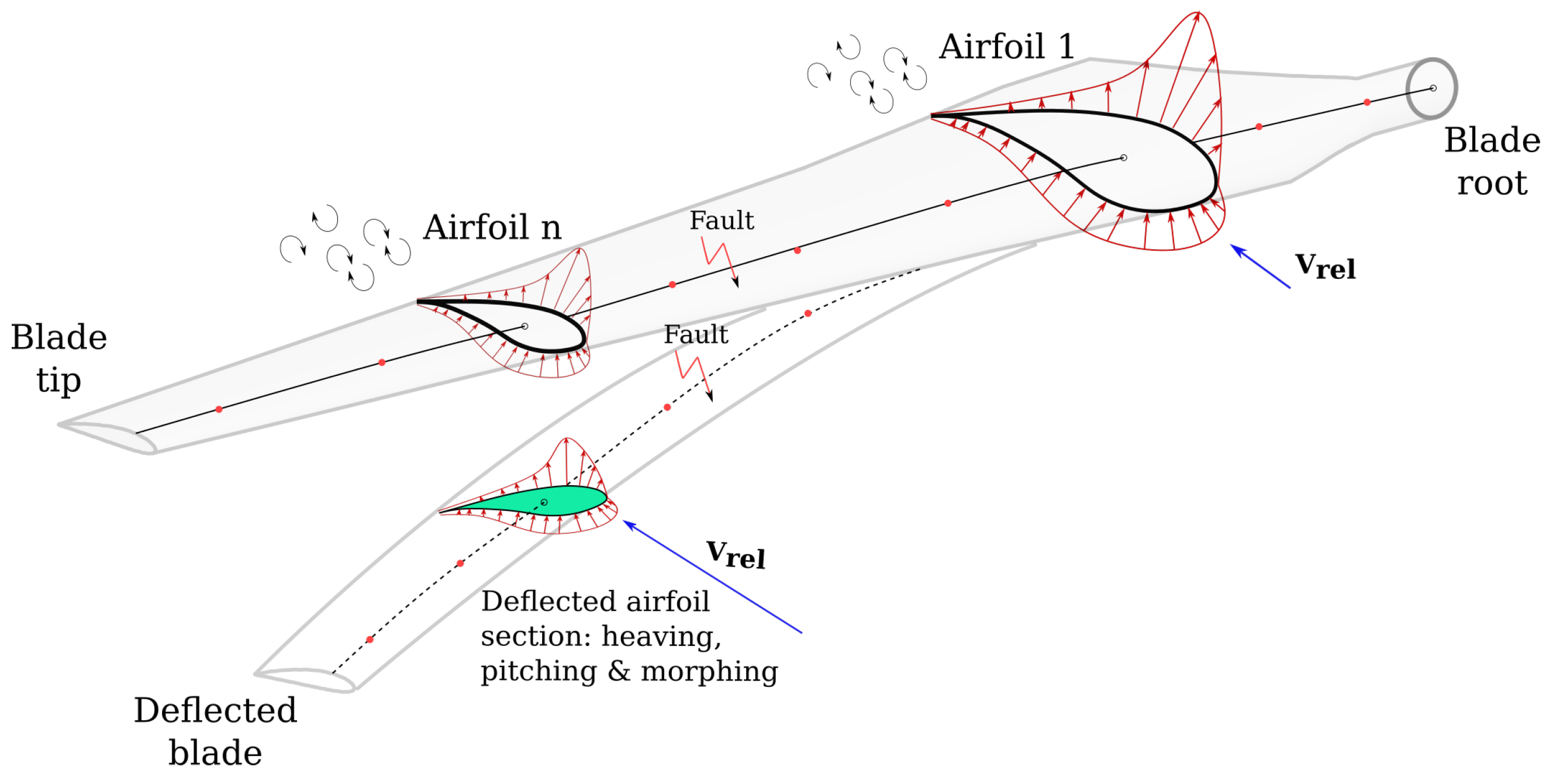
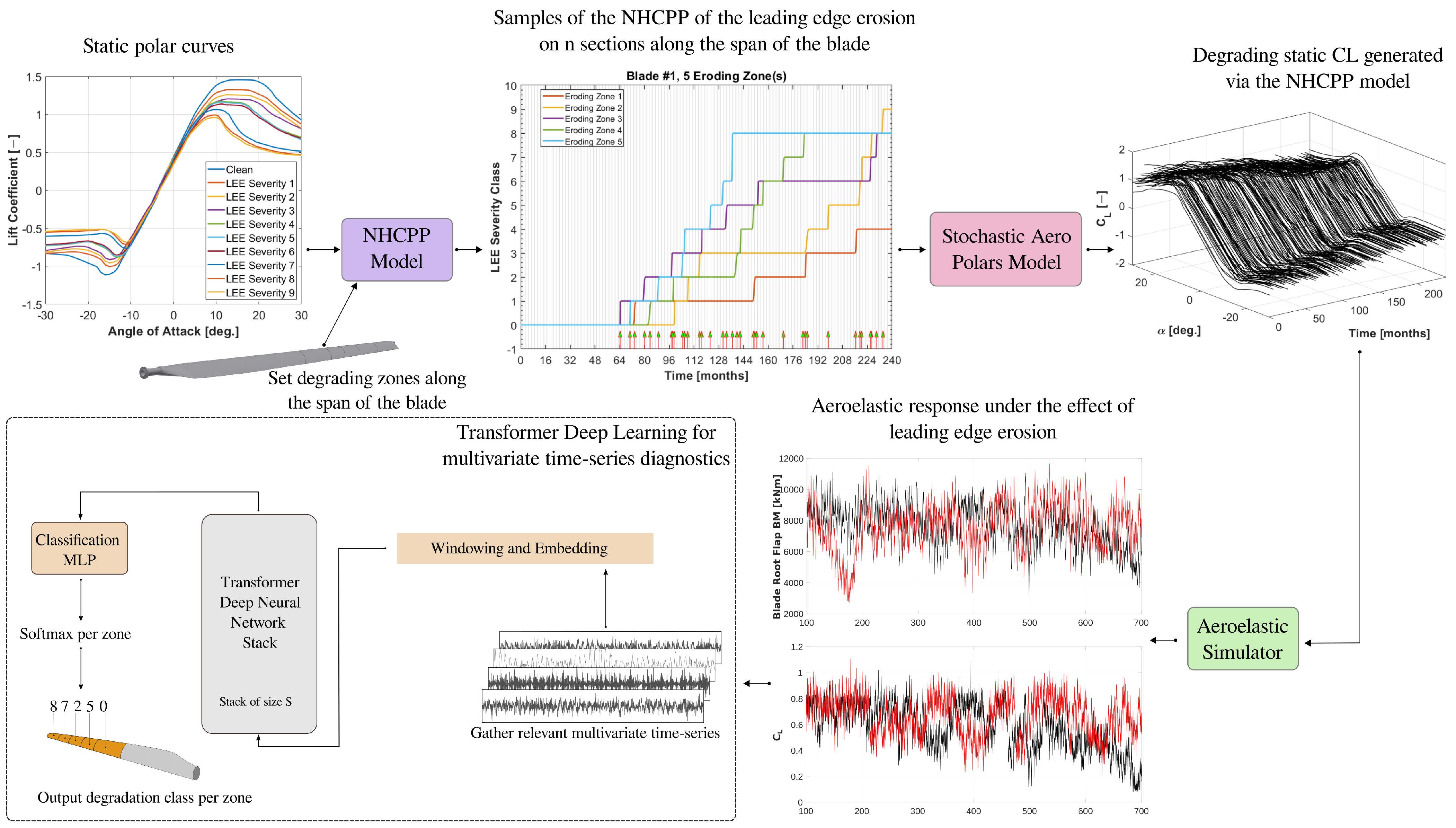
- We developed a stochastic spatio-temporal erosion model of the leading edge of wind turbine blades, which is characterized by a non-homogeneous compound Poisson process across discrete states, embedded in a generator of a stochastic ensemble of degrading airfoil aerodynamic polars for use in forward aero-servo-elastic simulations. The coupled model is able to compute the aeroelastic non-stationary response of a wind turbine, thus reflecting its behavior under the effect of leading edge erosion and varying turbulent input inflow conditions over a long period of degradation.
- We adapted a deep-learning multivariate time-series-based Transformer, which employs attention mechanisms to detect and classify long-term and slow leading edge erosion processes assuming the availability of on-blade sectional monitoring data, under short- and long-term wind inflow uncertainties and aerodynamic uncertainties on the lift and drag coefficients of the airfoil sections along the span of the blade.
2. Review of Prior Art
2.1. Modelling Leading-Edge Erosion
2.2. Diagnosing Leading Edge Erosion
3. Modeling Erosion of the Leading Edge
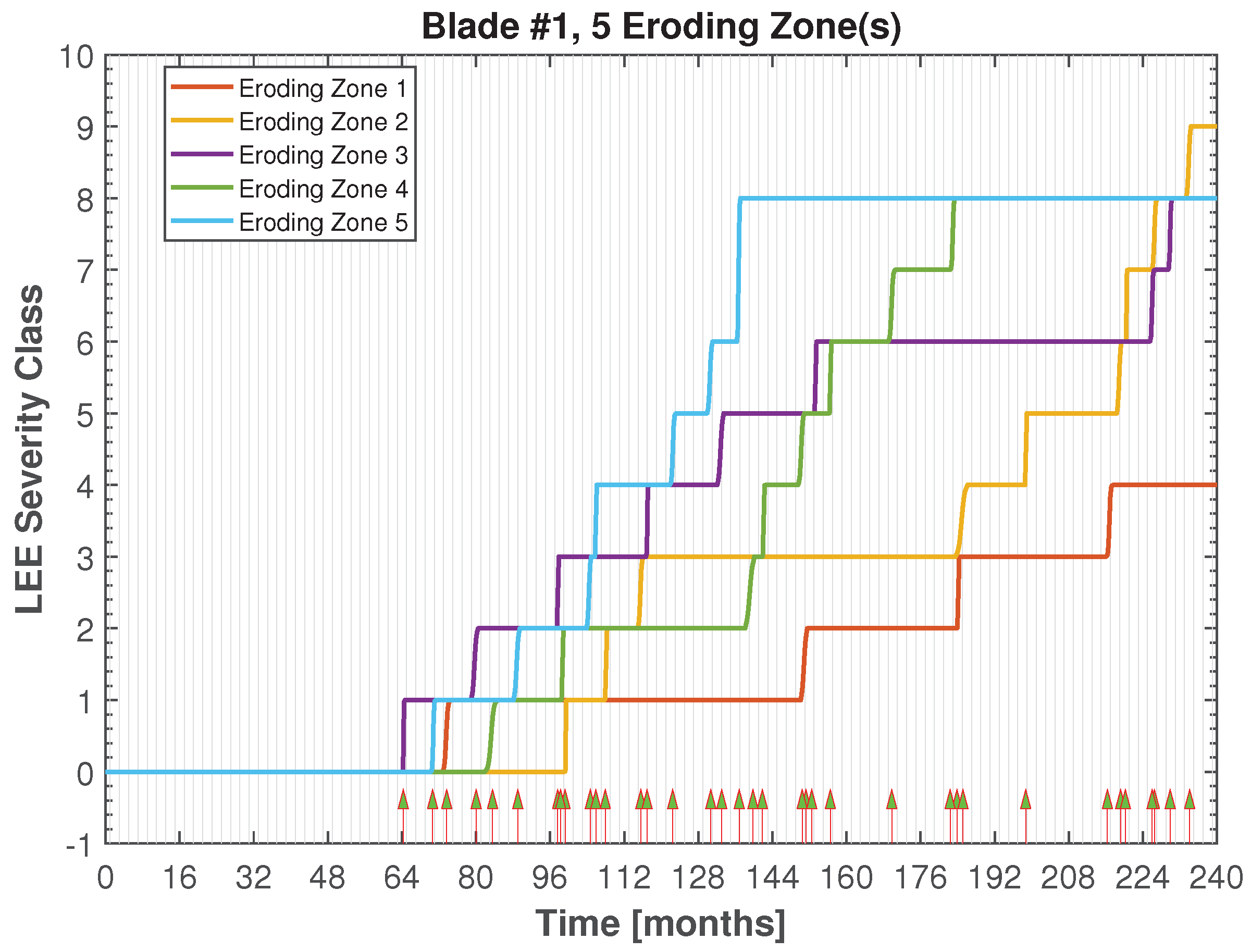
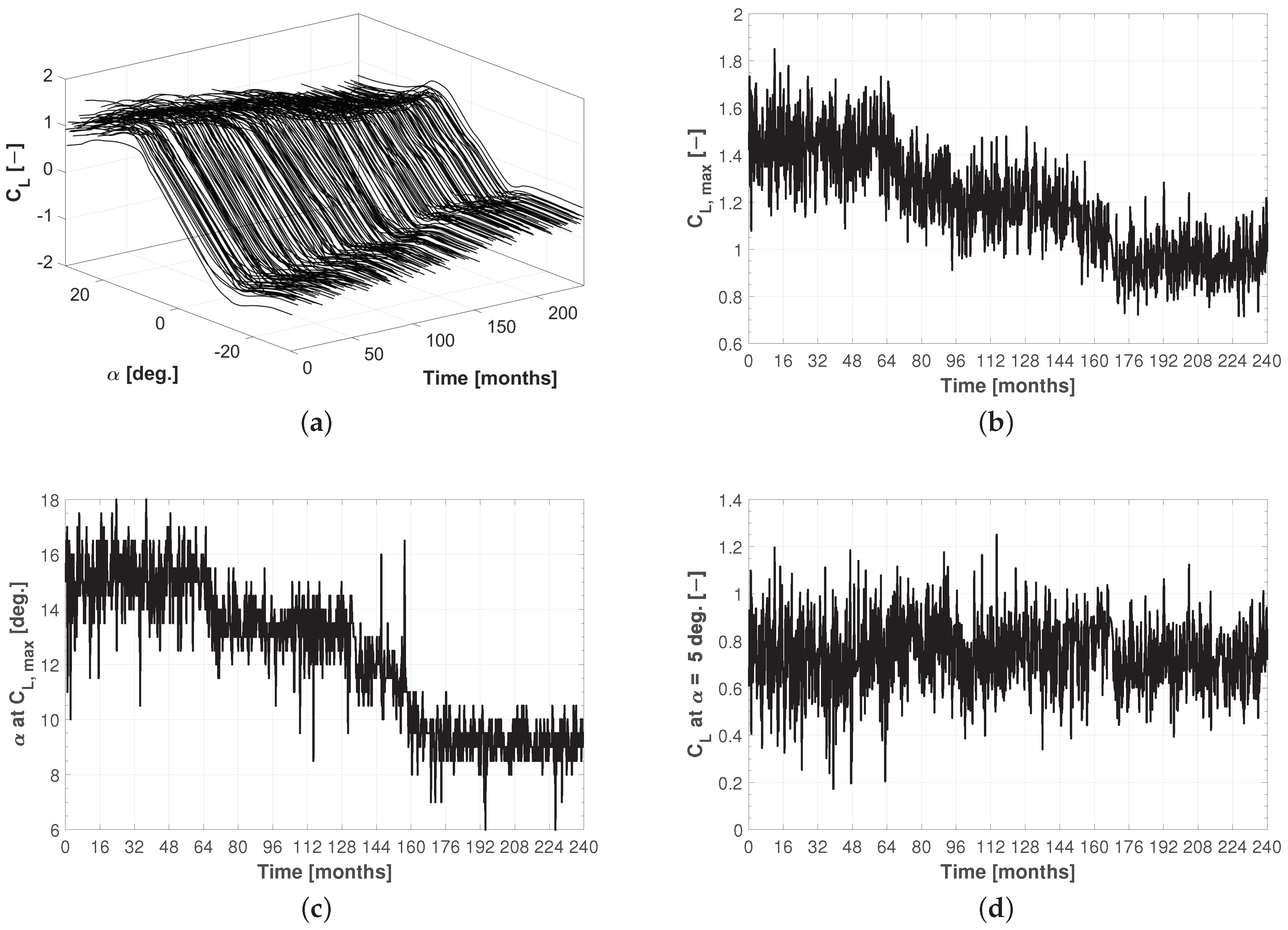
3.1. Non-Homogeneous Compound Poisson Process
- , , and , is independent of
- , ,
- , , , and
- , ,
- Choose such that
- Initialize and
- Generate
- Set
- If , stop; else go to next
- Generate , independent of
- If , set ;
- Go to Step 3
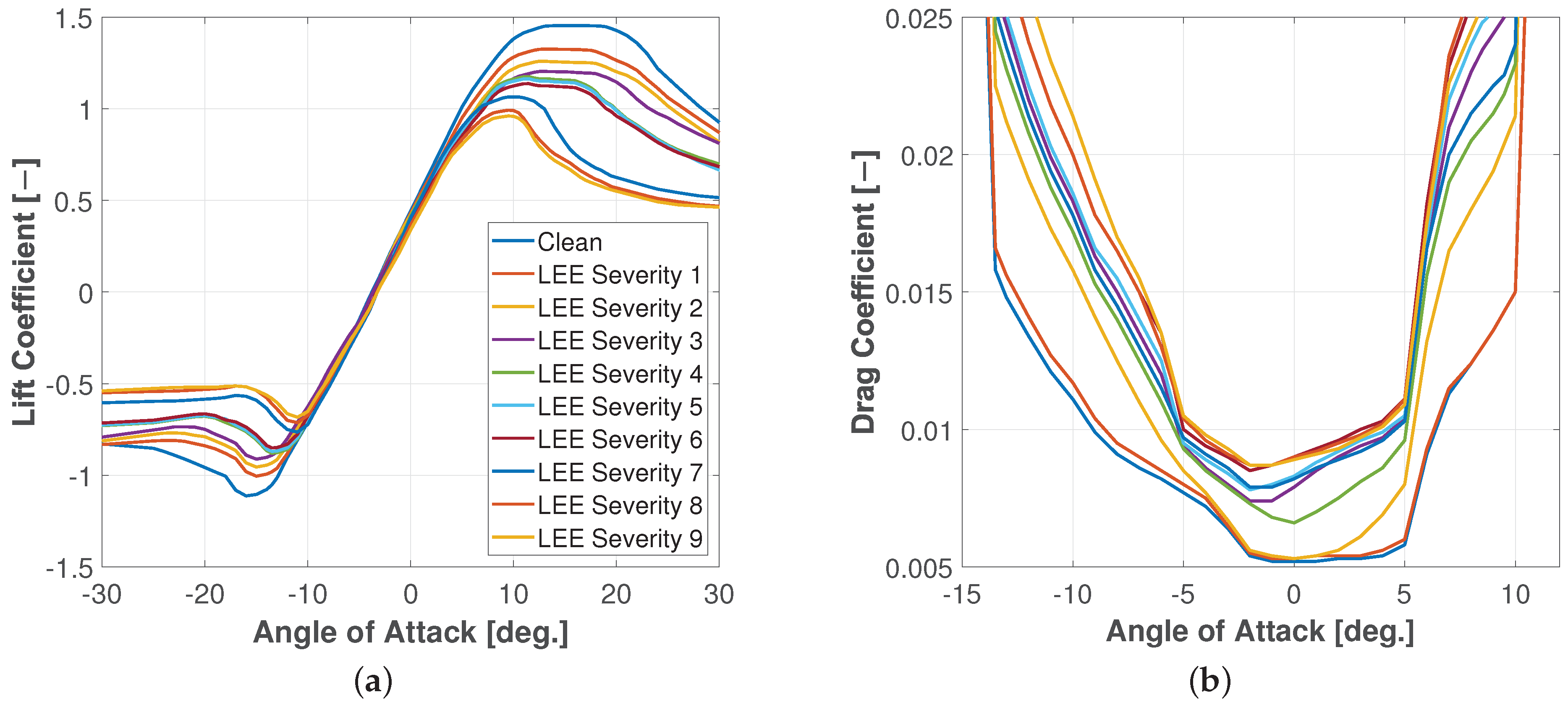
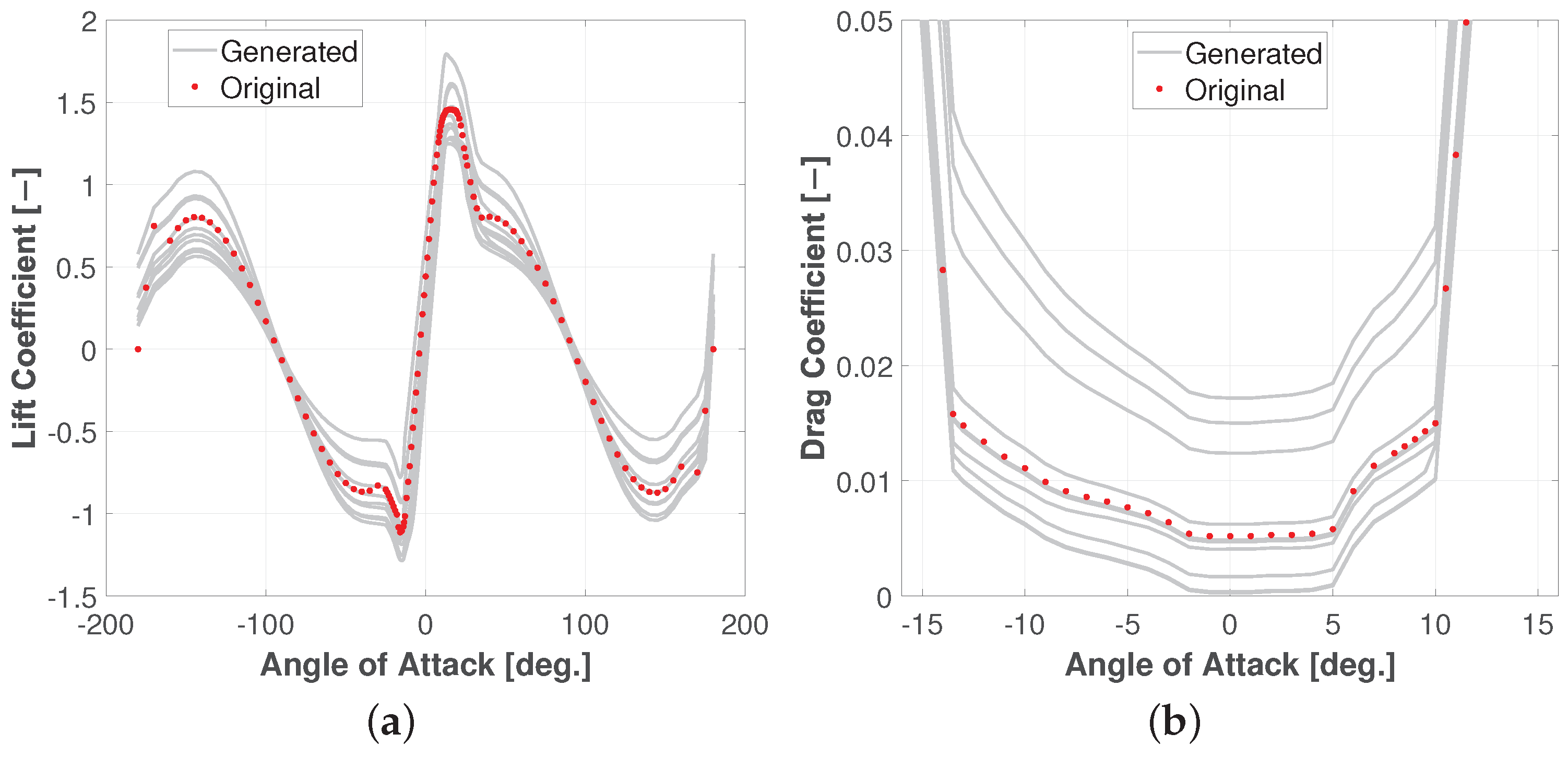
3.2. Stochastic Aerodynamic Polars Model
3.3. Overview of the Algorithm
| Algorithm 1: Spatio-temporal stochastic model of leading edge erosion. |
 |
4. Uncertainty Modeling and Aeroelastic Simulations
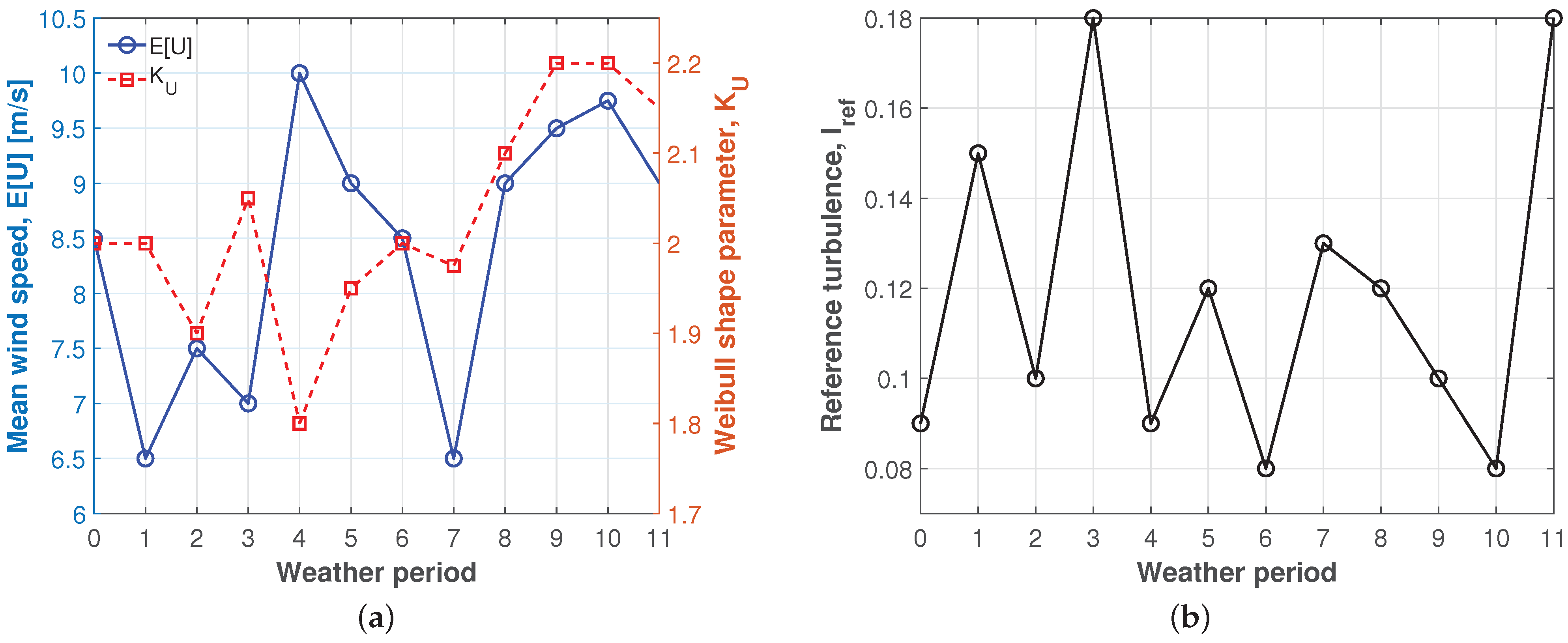
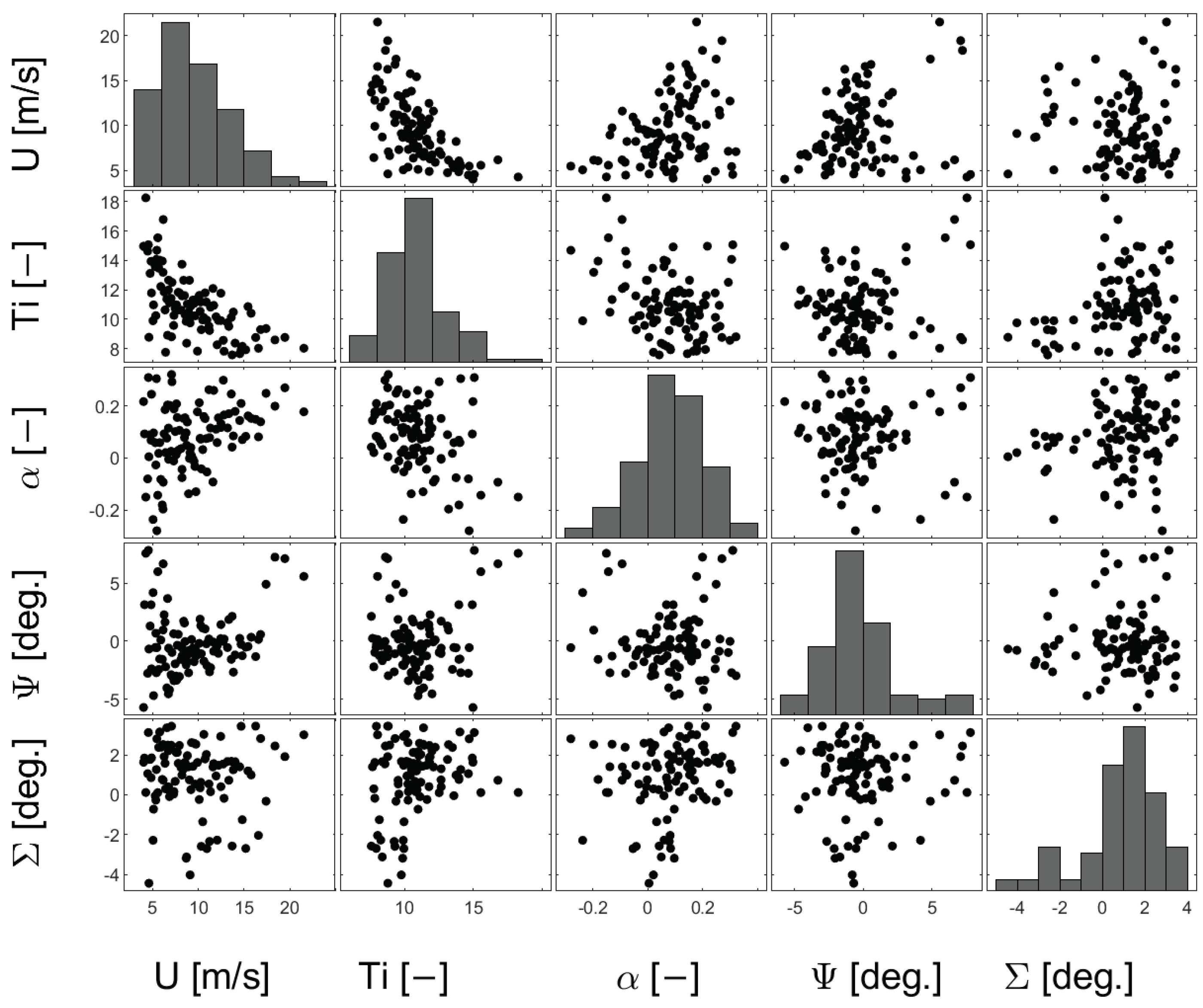
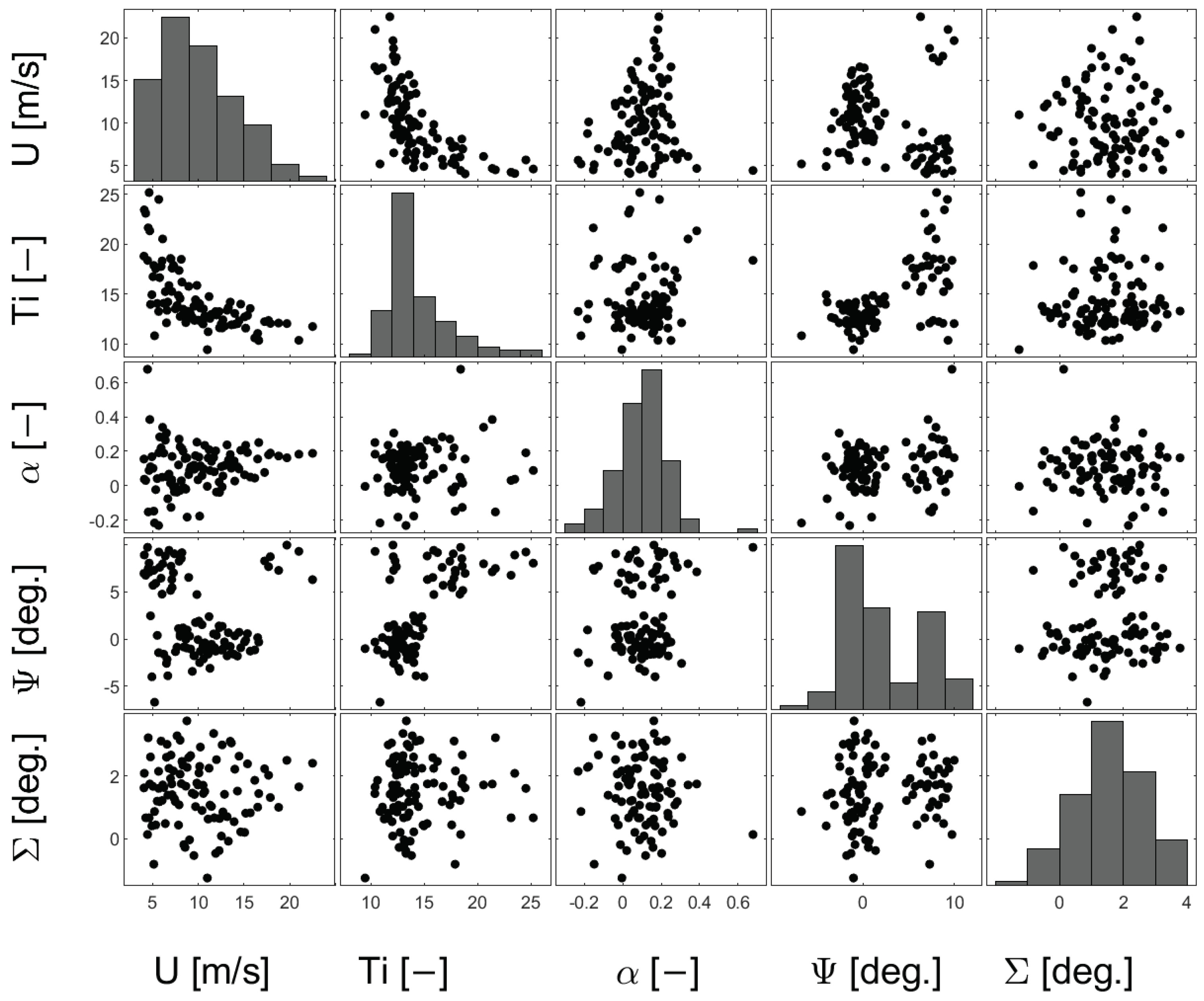
4.1. Stochastic Models of Inflow RVs
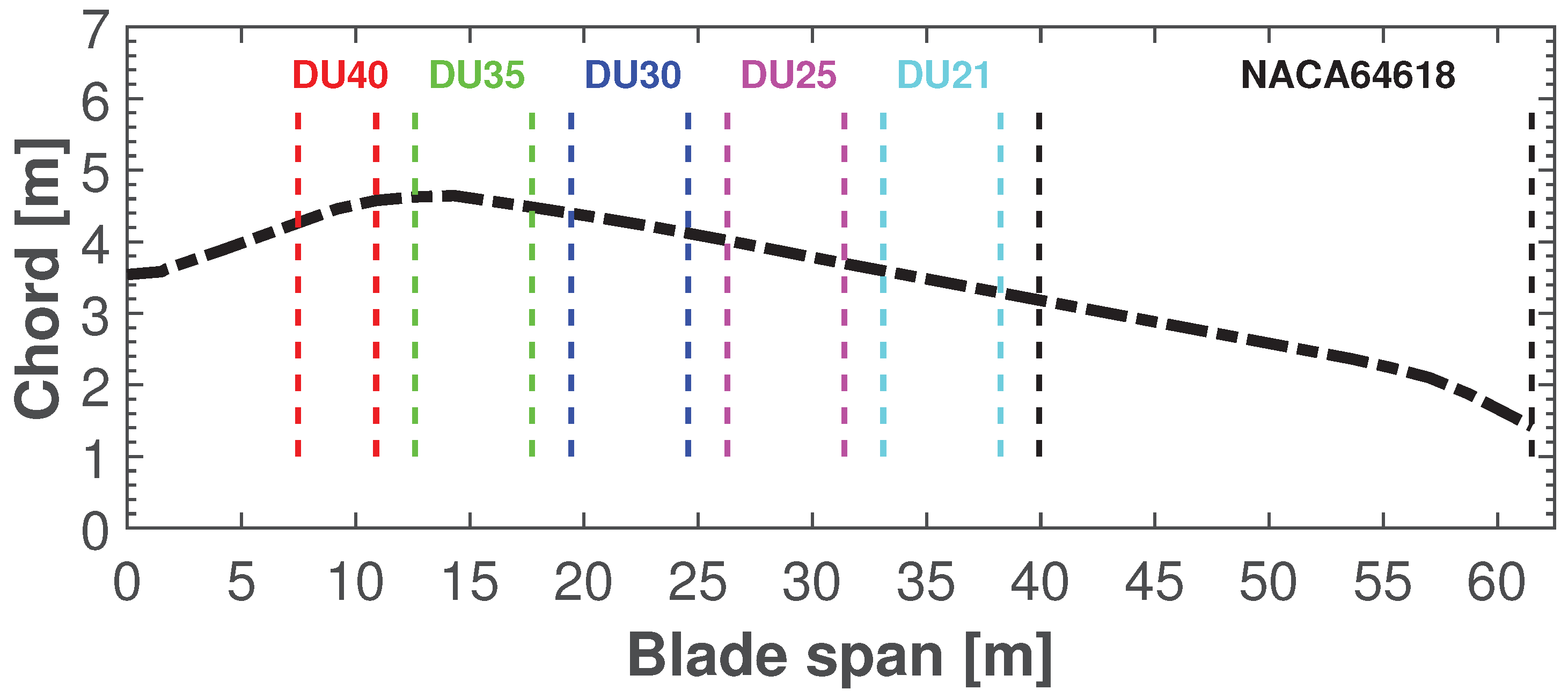
4.2. Setup of the Aero-Servo-Elastic Simulations
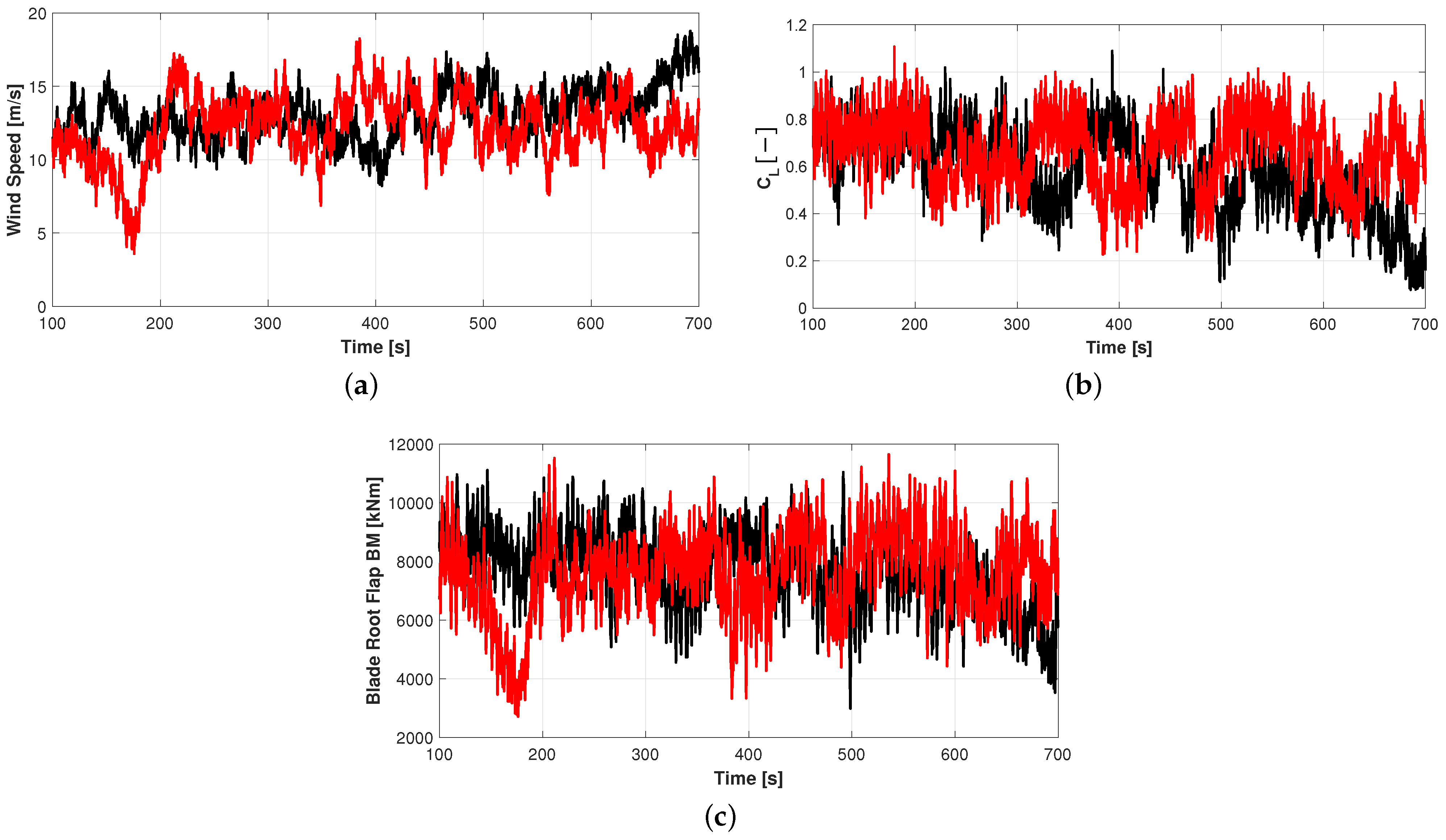
4.3. Retained Output from Aero-Servo-Elastic Simulations
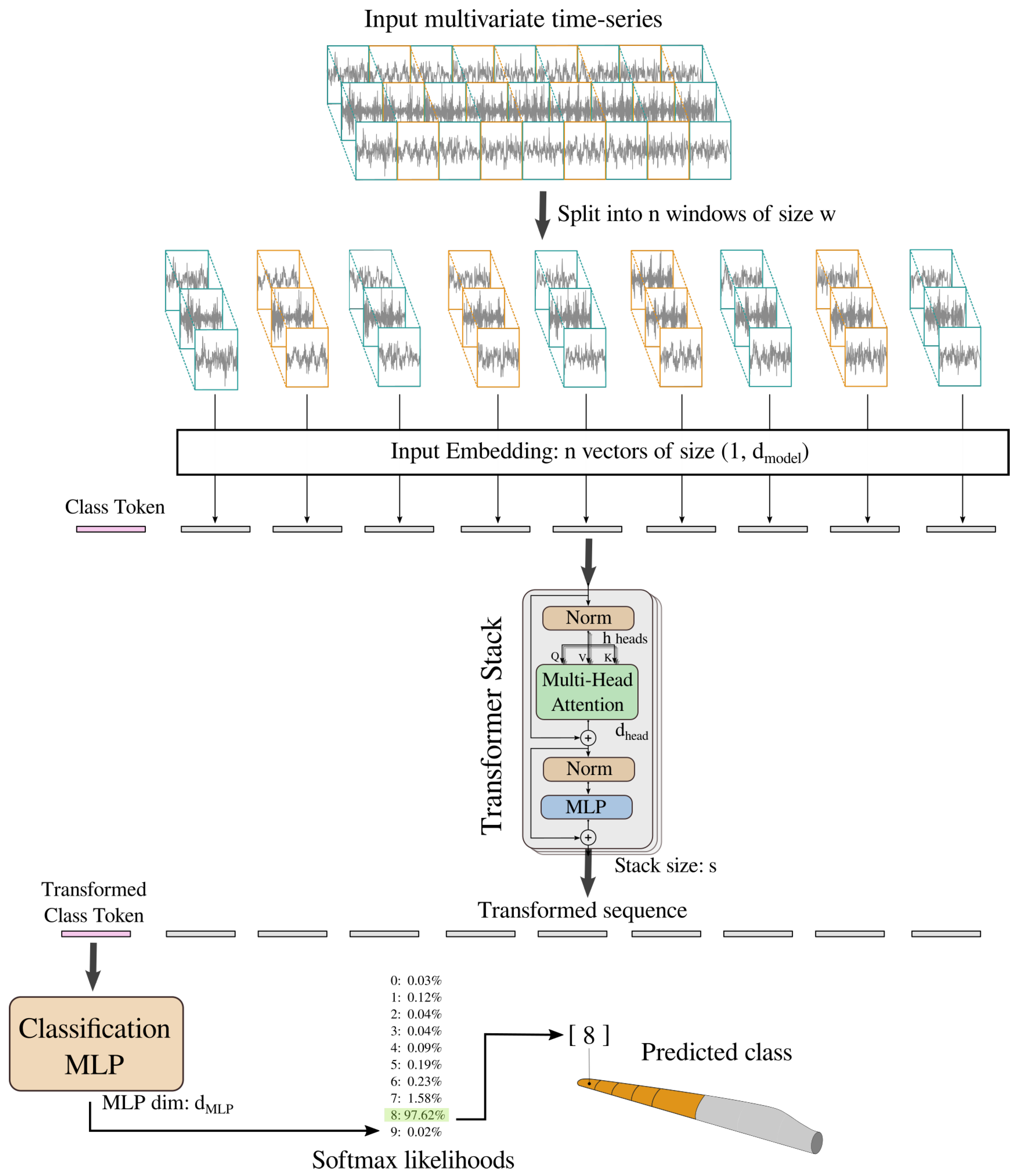
5. Diagnosing LEE via Transformers
- Labeled data for LEE are hard to acquire and are scarce; as a result, any method must be designed not to suffer from over-fitting under scarce labeled data availability.
- Diagnostics shall be done with remote streaming of sensor data. Human intervention and turbine down-time should be alleviated.
- The data used in the diagnostics method intend to emulate the sensory output of a single MEMS-based aerodynamic and aero-acoustic measurement node positioned in proximity to the tip of the wind turbine blade.
- The method shall be capable of ingesting 10-min-long multivariate time-series (industry standard SCADA recording length), sampled at 100 Hz, resulting in 60,000 data-point-long sequences. A sampling rate of 100 Hz may seem excessive, but the aim is to capture even small turbulence scales.
- A supervised scheme shall be used to train a Transformer-based network by utilizing labeled data resulting from aeroelastic simulations of a turbine combined with the degradation model, as presented earlier in the article.
- Physics-constraints shall be built into the loss or likelihood function.
- The output predictions should be probabilistic in nature.
5.1. Experiments and Datasets
- Are we able to learn the LEE severity classes from aerodynamic MTS data, in the general machine learning sense, with balanced data classes and no prior knowledge?
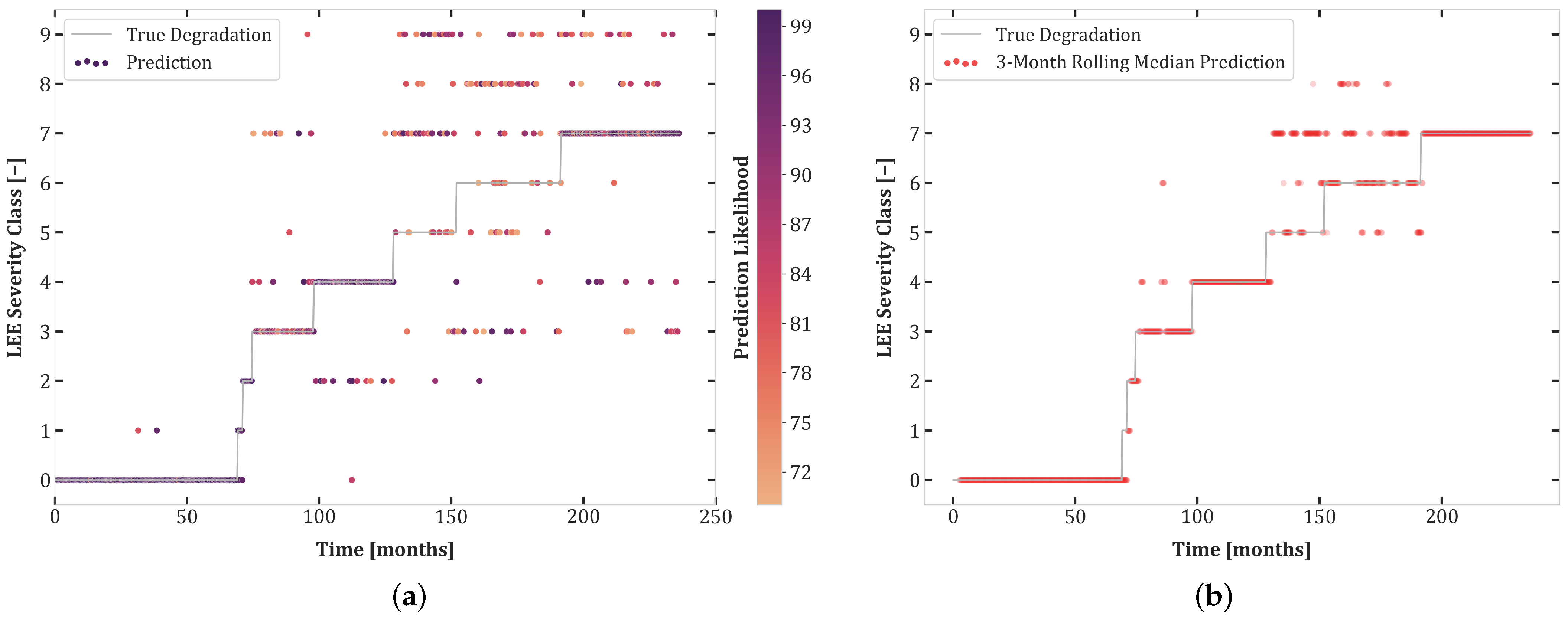
- In a continuous monitoring context, are we able to diagnose jumps in LEE severity and therefore identify the degradation path that the system takes?
- Are we able to do so in a realistic setting, with all previously described sources of uncertainty present in the simulations?
5.2. Transformer Architecture
5.3. Loss Functions
5.4. Training Regime
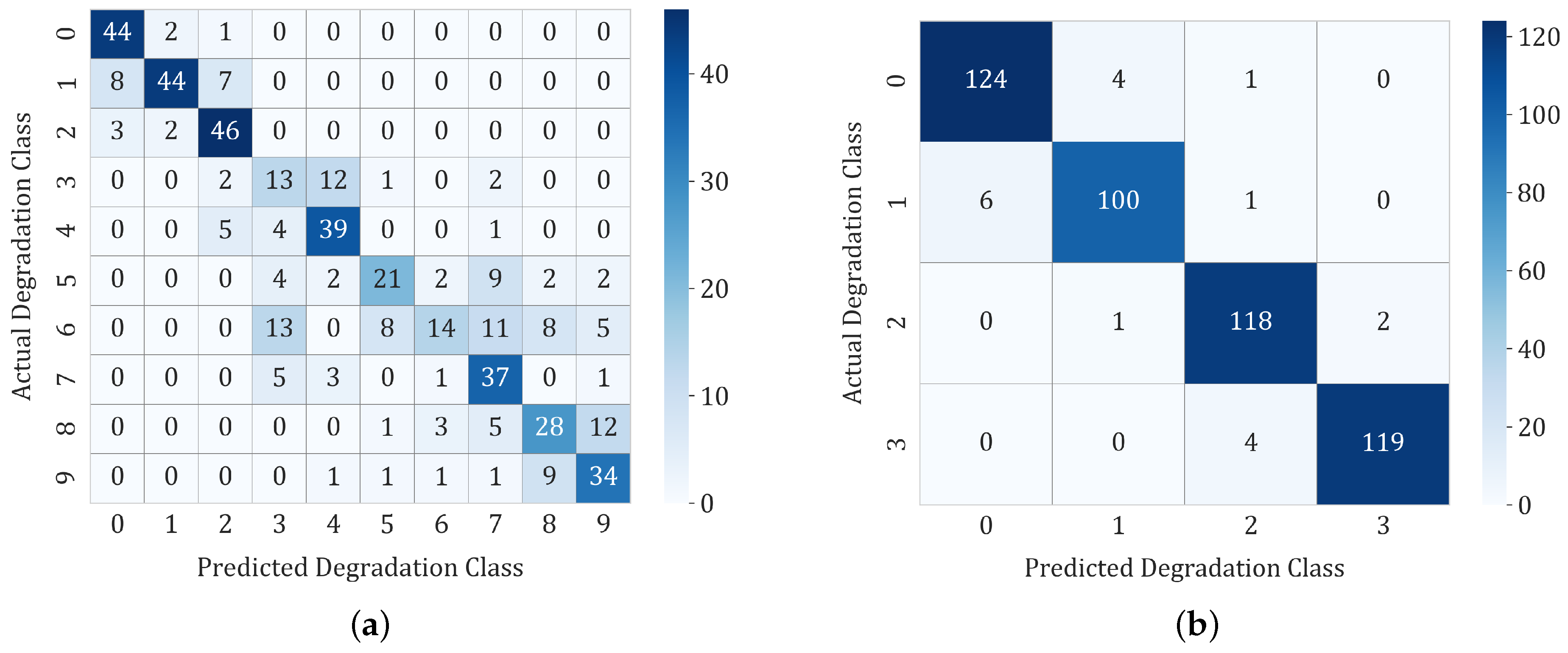
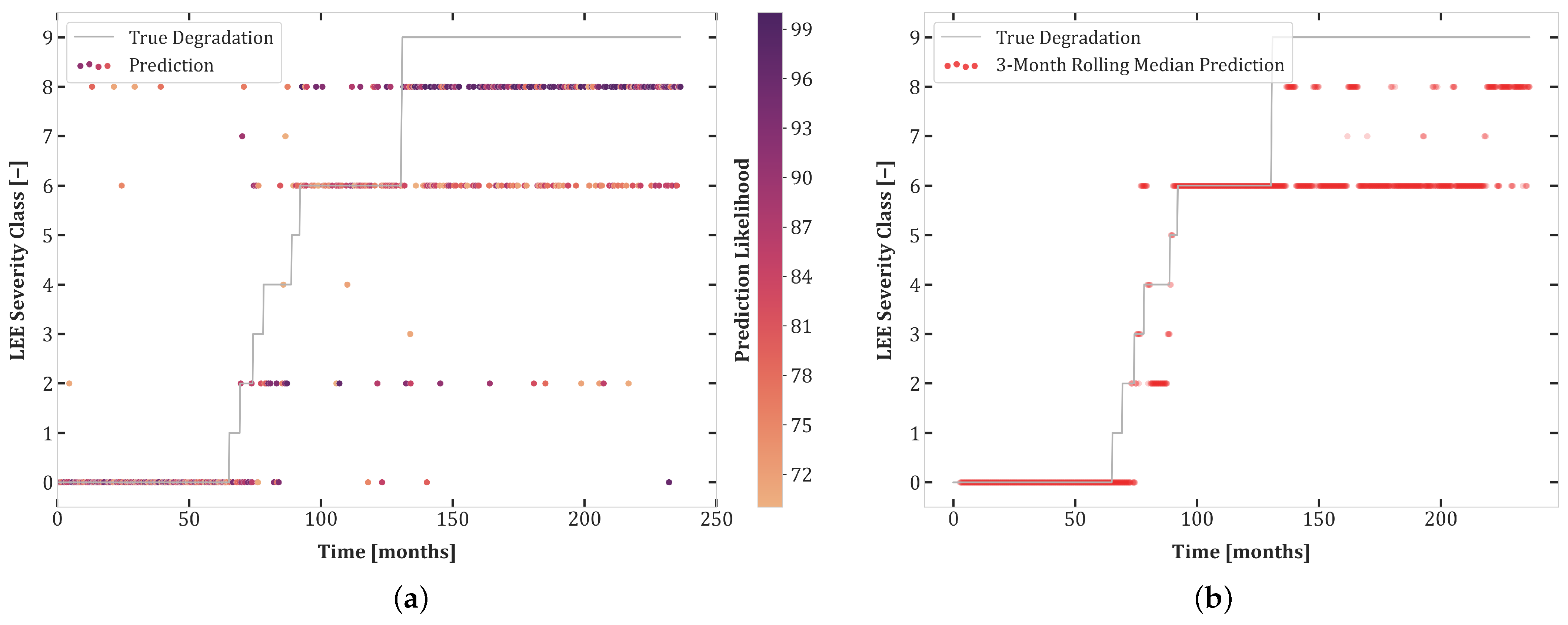
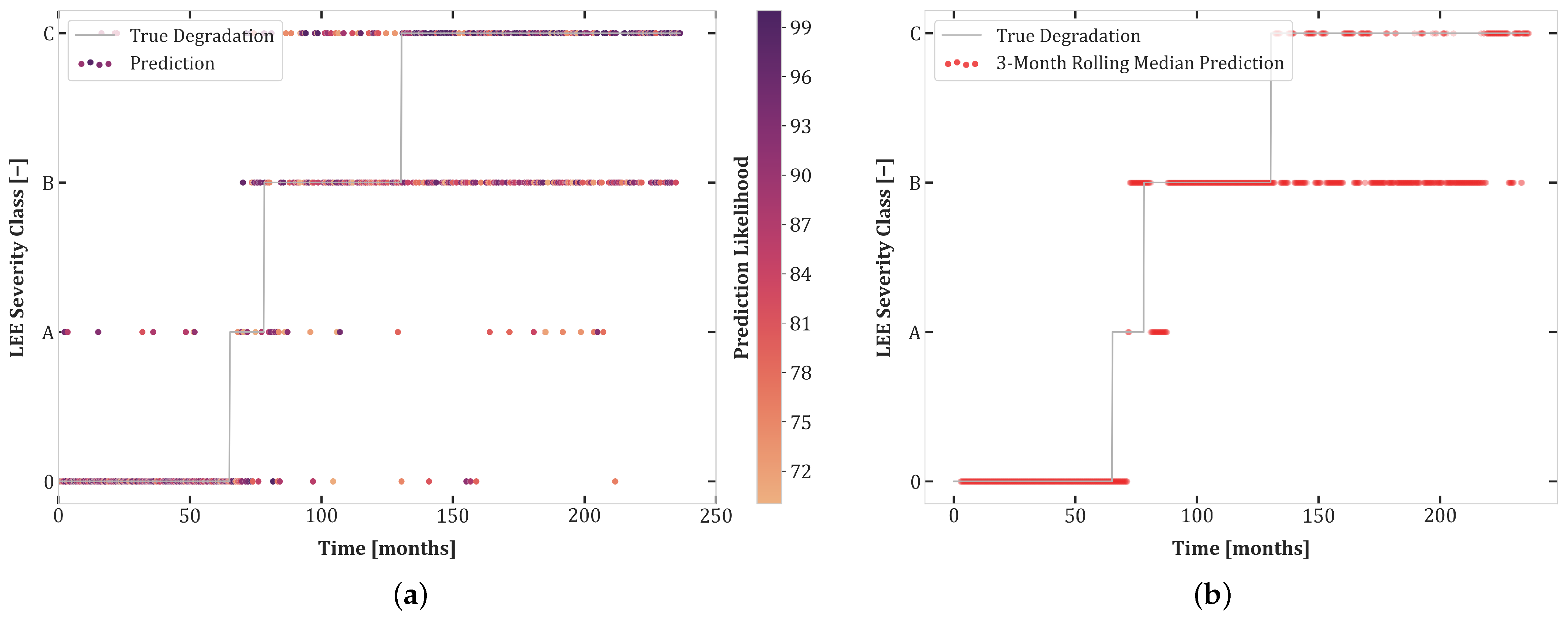
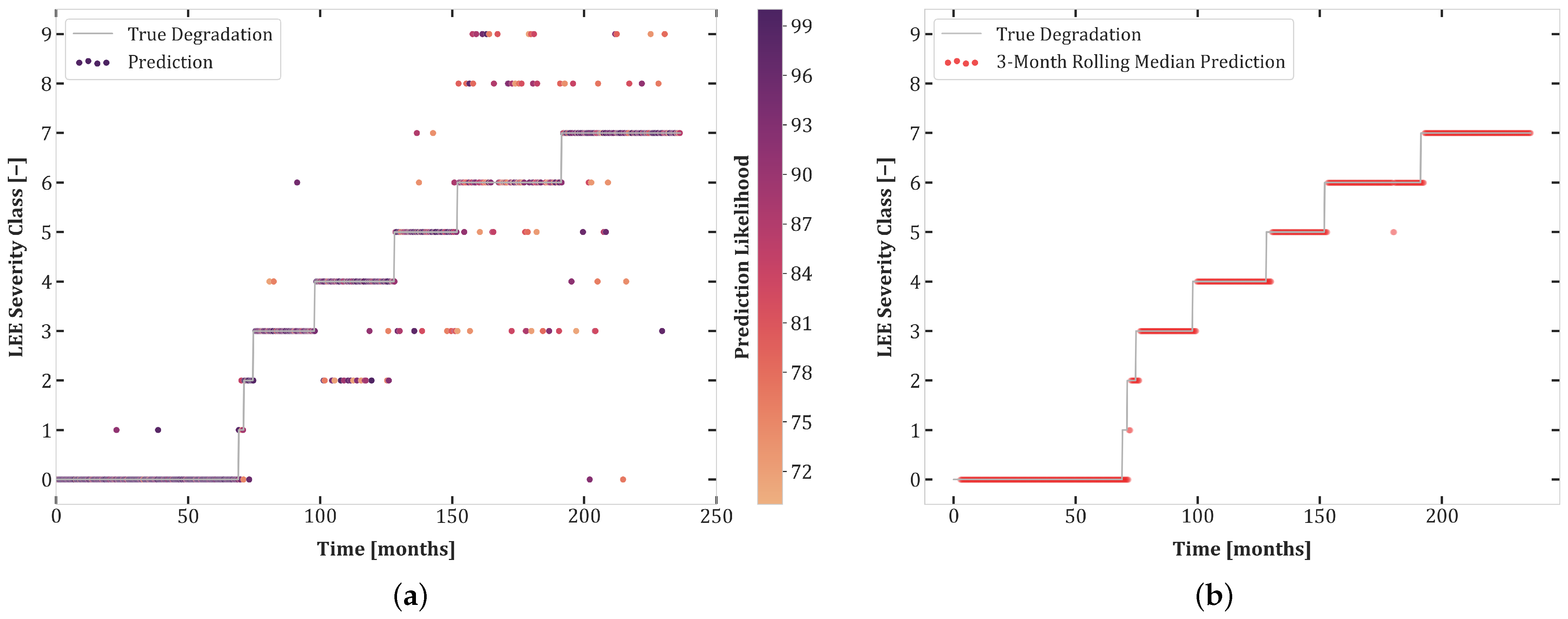
6. Results
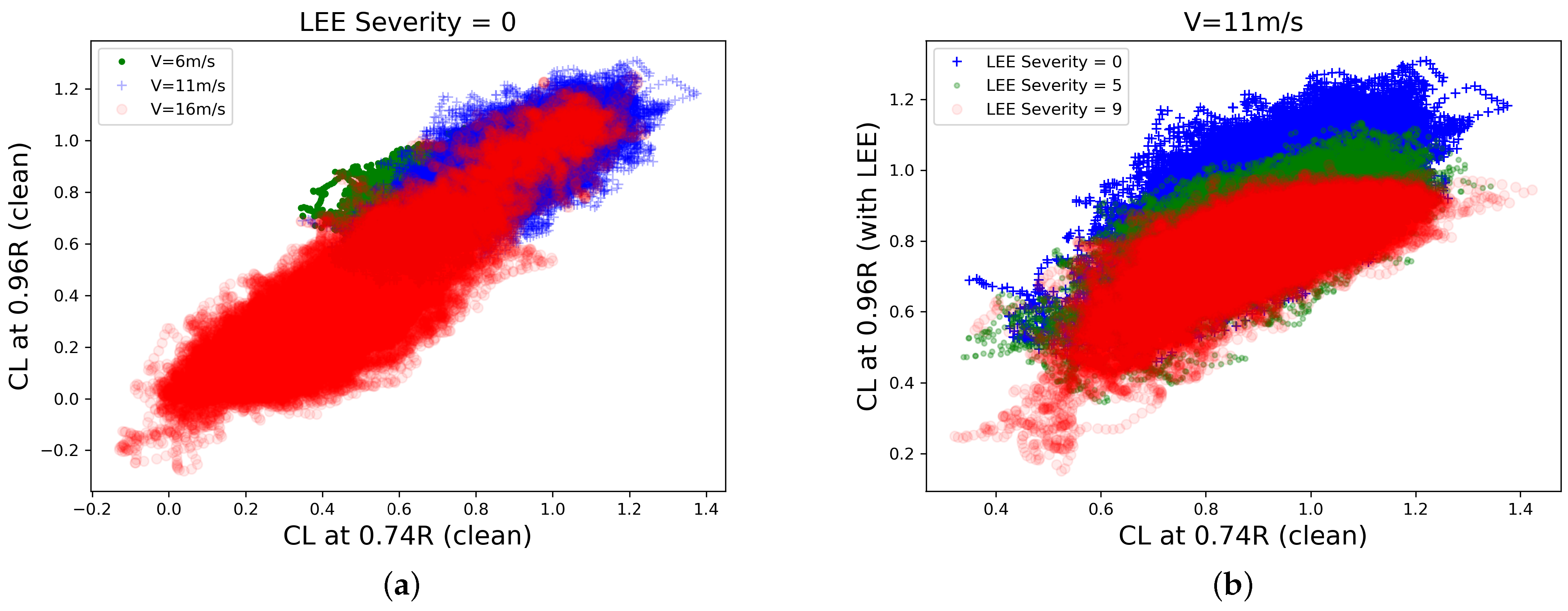
6.1. Experiment Set 1
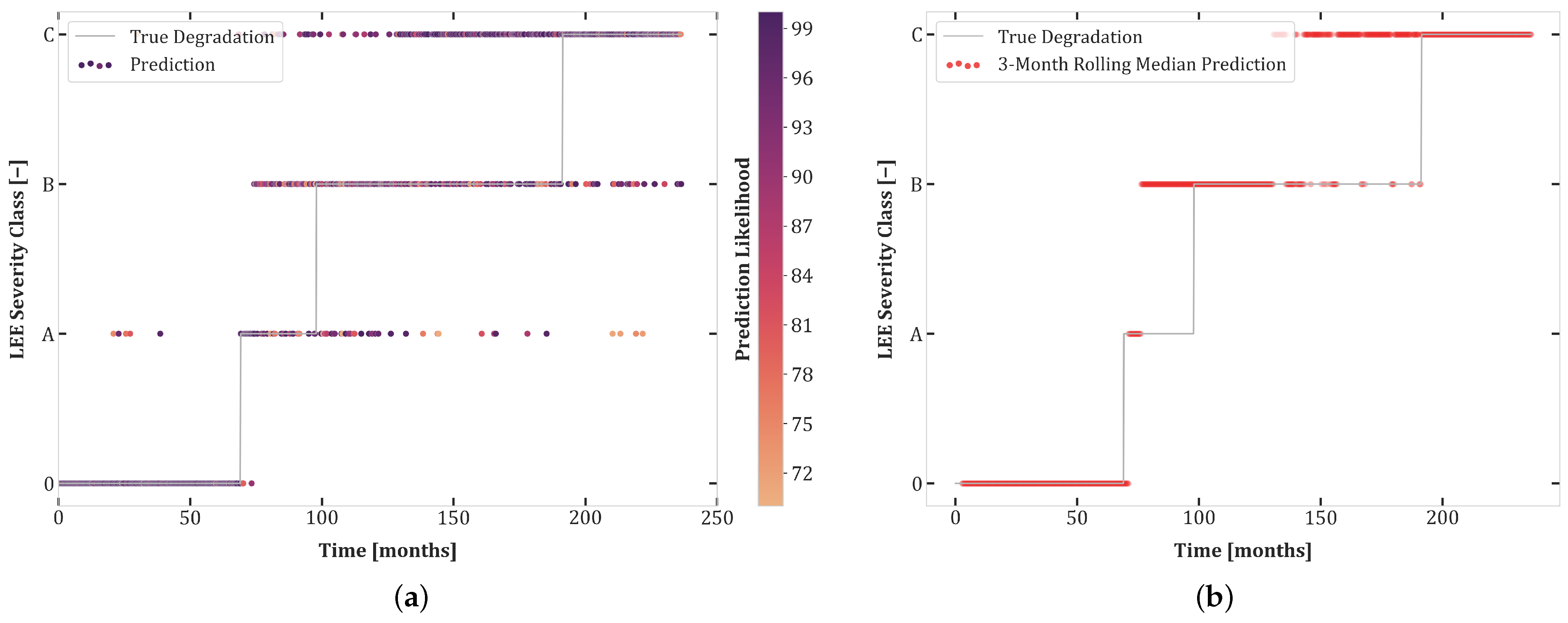
6.2. Experiment Set 2
6.3. Experiment Set 3
6.4. Transferability and Curriculum Learning
- The high accuracy of transferability tests between Experiments 1.1 and 2.1 highlights the similarity of these datasets. Moreover, the balanced dataset of Experiment 1.1 improves the prediction quality for Set 2.1.
- Although both Sets 1.1 and 2.1 contained all degradation classes, networks trained on these sets do not transfer well to Test Set 3.1, undoubtedly due to the uncertainty included in this experiment.
- There was better transferability between Sets 2.1 and 3.1 than between Sets 1.1 and 3.1. This can be explained by the extra loss component which enforces monotonicity in the second and third sets of experiments.
- The first curriculum learning experiment (Set 1.1 then 2.1) yielded a large performance boost for Test Sets 1.1 and 2.1. This was to be expected due to the data-intensive nature of Transformers and the similarity between these sets.
- The first curriculum learning experiment reduced transferability to Set 3.1. This is an indication of a loss of capacity to generalize to ambiguous data.
- The best test results on Set 3.1 were obtained in the second curriculum learning experiment. This suggests that pretraining on sets with reduced stochasticity followed by fine-tuning on uncertain data is an effective approach.
- The second curriculum learning experiment yielded the best high confidence accuracy for Sets 1.1 and 2.1. Thus, adding difficult, stochastic data points of Experiment 3.1 to the training dataset helps with regularization, enabling the model to construct a better internal representation of each severity class.
7. Limitations and Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Wind turbine | |
| Random variable | |
| U | Mean wind speed |
| Turbulence | |
| Wind shear exponent | |
| Turbulence intensity | |
| Expected value of a random variable | |
| Variance of a random variable | |
| Aerodynamic lift coefficient | |
| Aerodynamic drag coefficient | |
| Aerodynamic moment coefficient | |
| Aerodynamic pressure coefficient | |
| Multilayer perceptron | |
| Non-homogeneous Poisson process | |
| Non-homogeneous compound Poisson process | |
| R | Blade radius |
| Structural health monitoring | |
| Supervisory control and data acquisition | |
| Eroding zone | |
| Operation and maintenance | |
| Leading edge | |
| Leading edge erosion | |
| Convolutional neural network | |
| Recurrent neural network | |
| Multivariate time-series |
References
- Barber, S. Aerosense. Available online: https://www.aerosense.ai (accessed on 1 November 2021).
- Bech, J.I.; Hasager, C.B.; Bak, C. Extending the life of wind turbine blade leading edges by reducing the tip speed during extreme precipitation events. Wind. Energy Sci. 2018, 3, 729–748. [Google Scholar] [CrossRef] [Green Version]
- Bogdanoff, J.L.; Kozin, F. Probabilistic Models of Cumulative Damage; Wiley-Interscience: New York, NY, USA, 1985. [Google Scholar]
- Herring, R.; Dyer, K.; Martin, F.; Ward, C. The increasing importance of leading edge erosion and a review of existing protection solutions. Renew. Sustain. Energy Rev. 2019, 115, 109382. [Google Scholar] [CrossRef]
- Shihavuddin, A.; Chen, X.; Fedorov, V.; Nymark Christensen, A.; Andre Brogaard Riis, N.; Branner, K.; Bjorholm Dahl, A.; Reinhold Paulsen, R. Wind Turbine Surface Damage Detection by Deep Learning Aided Drone Inspection Analysis. Energies 2019, 12, 676. [Google Scholar] [CrossRef] [Green Version]
- Gertsen, T. Data-Driven Leading Edge Erosion Detection for Wind Turbine Blades Using SCADA Data. Master’s Thesis, TU Delft, Delft, The Netherlands, 2019. [Google Scholar]
- Shen, J. Classification of Wind Turbine Blade Performance State through Statistical Methods. Master’s Thesis, University of Windsor, Windsor, ON, Canada, 2019. [Google Scholar]
- Sareen, A.; Sapre, C.A.; Selig, M.S. Effects of leading edge erosion on wind turbine blade performance. Wind Energy 2014, 17, 1531–1542. [Google Scholar] [CrossRef]
- Gaudern, N. A practical study of the aerodynamic impact of wind turbine blade leading edge erosion. J. Phys. Conf. Ser. 2014, 524, 012031. [Google Scholar] [CrossRef]
- Groucott, S.; Pugh, K.; Zekos, I.; Stack, M.M. A Study of Raindrop Impacts on a Wind Turbine Material: Velocity and Impact Angle Effects on Erosion MAPS at Various Exposure Times. Lubricants 2021, 9, 60. [Google Scholar] [CrossRef]
- Prieto, R.; Karlsson, T. A model to estimate the effect of variables causing erosion in wind turbine blades. Wind Energy 2021, 24, 1031–1044. [Google Scholar] [CrossRef]
- Langel, C.M.; Chow, R.; Hurley, O.F.; Dam, C.C.P.V.; Maniaci, D.C.; Ehrmann, R.S.; White, E.B. Analysis of the Impact of Leading Edge Surface Degradation on Wind Turbine Performance. In Proceedings of the 33rd Wind Energy Symposium, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Corsini, A.; Castorrini, A.; Morei, E.; Rispoli, F.; Sciulli, F.; Venturini, P. Modeling of Rain Drop Erosion in a Multi-MW Wind Turbine. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 9. [Google Scholar]
- Zidane, I.F.; Saqr, K.M.; Swadener, G.; Ma, X.; Shehadeh, M.F. On the role of surface roughness in the aerodynamic performance and energy conversion of horizontal wind turbine blades: A review. Int. J. Energy Res. 2016, 40, 2054–2077. [Google Scholar] [CrossRef]
- Schramm, M.; Rahimi, H.; Stoevesandt, B.; Tangager, K. The Influence of Eroded Blades on Wind Turbine Performance Using Numerical Simulations. Energies 2017, 10, 1420. [Google Scholar] [CrossRef] [Green Version]
- Papi, F.; Cappugi, L.; Perez-Becker, S.; Bianchini, A. Numerical Modeling of the Effects of Leading-Edge Erosion and Trailing-Edge Damage on Wind Turbine Loads and Performance. J. Eng. Gas Turbines Power 2020, 142, 111005. [Google Scholar] [CrossRef]
- Doagou-Rad, S.; Mishnaevsky, L., Jr.; Bech, J.I. Leading edge erosion of wind turbine blades: Multiaxial critical plane fatigue model of coating degradation under random liquid impacts. Wind Energy 2020, 23, 1752–1766. [Google Scholar] [CrossRef]
- Bortolotti, P.; Canet, H.; Bottasso, C.L.; Loganathan, J. Performance of non-intrusive uncertainty quantification in the aeroservoelastic simulation of wind turbines. Wind. Energy Sci. 2019, 4, 397–406. [Google Scholar] [CrossRef] [Green Version]
- Dimitrov, N. Risk-based approach for rational categorization of damage observations from wind turbine blade inspections. J. Phys. Conf. Ser. 2018, 1037, 042021. [Google Scholar] [CrossRef]
- Ruiz, A.P.; Flynn, M.; Large, J.; Middlehurst, M.; Bagnall, A. The great multivariate time series classification bake off: A review and experimental evaluation of recent algorithmic advances. Data Min. Knowl. Discov. 2020, 35, 401–449. [Google Scholar] [CrossRef]
- Wang, Z.; Yan, W.; Oates, T. Time series classification from scratch with deep neural networks: A strong baseline. In Proceedings of the 2017 International joint conference on neural networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1578–1585. [Google Scholar]
- Middlehurst, M.; Large, J.; Bagnall, A. The Canonical Interval Forest (CIF) Classifier for Time Series Classification. arXiv 2020, arXiv:2008.09172. [Google Scholar]
- Stallone, A.; Cicone, A.; Materassi, M. New insights and best practices for the successful use of Empirical Mode Decomposition, Iterative Filtering and derived algorithms. Sci. Rep. 2020, 10, 15161. [Google Scholar] [CrossRef]
- Barbosh, M.; Singh, P.; Sadhu, A. Empirical mode decomposition and its variants: A review with applications in structural health monitoring. Smart Mater. Struct. 2020, 29, 093001. [Google Scholar] [CrossRef]
- Górecki, T.; Łuczak, M. Multivariate time series classification with parametric derivative dynamic time warping. Expert Syst. Appl. 2015, 42, 2305–2312. [Google Scholar] [CrossRef]
- Dempster, A.; Petitjean, F.; Webb, G.I. ROCKET: Exceptionally fast and accurate time series classification using random convolutional kernels. Data Min. Knowl. Discov. 2020, 34, 1454–1495. [Google Scholar] [CrossRef]
- Dempster, A.; Schmidt, D.F.; Webb, G.I. MINIROCKET: A Very Fast (Almost) Deterministic Transform for Time Series Classification. arXiv 2021, arXiv:2012.08791. [Google Scholar] [CrossRef]
- Dau, H.A.; Keogh, E.; Kamgar, K.; Yeh, C.C.M.; Zhu, Y.; Gharghabi, S.; Ratanamahatana, C.A.; Hu, B.; Begum, N.; Bagnall, A.; et al. The UCR Time Series Classification Archive. 2018. Available online: https://www.cs.ucr.edu/~eamonn/time_series_data_2018 (accessed on 1 November 2021).
- Yang, C.-L.; Chen, Z.-X.; Yang, C.-Y. Sensor Classification Using Convolutional Neural Network by Encoding Multivariate Time Series as Two-Dimensional Colored Images. Sensors 2020, 20, 168. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. Deep learning for time series classification: A review. arXiv 2019, arXiv:1809.04356. [Google Scholar]
- Liu, C.; Hsaio, W.; Tu, Y. Time Series Classification With Multivariate Convolutional Neural Network. IEEE Trans. Ind. Electron. 2019, 66, 4788–4797. [Google Scholar] [CrossRef]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. Evaluating surgical skills from kinematic data using convolutional neural networks. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2018; Volume 11073, pp. 214–221. [Google Scholar] [CrossRef] [Green Version]
- Fawaz, H.I.; Lucas, B.; Forestier, G.; Pelletier, C.; Schmidt, D.F.; Weber, J.; Webb, G.I.; Idoumghar, L.; Muller, P.A.; Petitjean, F. InceptionTime: Finding AlexNet for Time Series Classification. arXiv 2020, arXiv:1909.04939. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Lipton, Z.C.; Kale, D.C.; Elkan, C.; Wetzel, R. Learning to Diagnose with LSTM Recurrent Neural Networks. arXiv 2017, arXiv:1511.03677. [Google Scholar]
- Karim, F.; Majumdar, S.; Darabi, H.; Harford, S. Multivariate LSTM-FCNs for time series classification. Neural Netw. 2019, 116, 237–245. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. arXiv 2020, arXiv:2012.07436. [Google Scholar]
- Zerveas, G.; Jayaraman, S.; Patel, D.; Bhamidipaty, A.; Eickhoff, C. A Transformer-based Framework for Multivariate Time Series Representation Learning. arXiv 2020, arXiv:2010.02803. [Google Scholar]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The Graph Neural Network Model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, H.; Duan, Z.; Bai, Y.; Huang, Y.; Ren, A.; Yu, Q.; Zhang, Q.; Wang, Y.; Wang, X.; Sun, Y.; et al. Multivariate Time Series Classification with Hierarchical Variational Graph Pooling. arXiv 2020, arXiv:2010.05649. [Google Scholar]
- Yu, C.; Ma, X.; Ren, J.; Zhao, H.; Yi, S. Spatio-Temporal Graph Transformer Networks for Pedestrian Trajectory Prediction. arXiv 2020, arXiv:2005.08514. [Google Scholar]
- Li, C.; Zhang, S.; Qin, Y.; Estupinan, E. A systematic review of deep transfer learning for machinery fault diagnosis. Neurocomputing 2020, 407, 121–135. [Google Scholar] [CrossRef]
- Long, M.; Cao, Y.; Wang, J.; Jordan, M.I. Learning Transferable Features with Deep Adaptation Networks. arXiv 2015, arXiv:1502.02791. [Google Scholar]
- Du, Y.; Zhou, S.; Jing, X.; Peng, Y.; Wu, H.; Kwok, N. Damage detection techniques for wind turbine blades: A review. Mech. Syst. Signal Process. 2020, 141, 106445. [Google Scholar] [CrossRef]
- Dervilis, N.; Choi, M.; Taylor, S.; Barthorpe, R.; Park, G.; Farrar, C.; Worden, K. On damage diagnosis for a wind turbine blade using pattern recognition. J. Sound Vib. 2014, 333, 1833–1850. [Google Scholar] [CrossRef]
- Lei, J.; Liu, C.; Jiang, D. Fault diagnosis of wind turbine based on Long Short-term memory networks. Renew. Energy 2019, 133, 422–432. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, Z. A Conditional Convolutional Autoencoder Based Method for Monitoring Wind Turbine Blade Breakages. IEEE Trans. Ind. Inform. 2020, 17, 6390–6398. [Google Scholar] [CrossRef]
- Regan, T.; Beale, C.; Inalpolat, M. Wind Turbine Blade Damage Detection Using Supervised Machine Learning Algorithms. J. Vib. Acoust. 2017, 139, 061010. [Google Scholar] [CrossRef]
- Joshuva, A.; Sugumaran, V. A data driven approach for condition monitoring of wind turbine blade using vibration signals through best-first tree algorithm and functional trees algorithm: A comparative study. ISA Trans. 2017, 67, 160–172. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Liu, K.; Wang, Y.; Omariba, Z.B. Ice Detection Model of Wind Turbine Blades Based on Random Forest Classifier. Energies 2018, 11, 2548. [Google Scholar] [CrossRef] [Green Version]
- Weijtjens, W.; Avendaño-Valencia, L.D.; Devriendt, C.; Chatzi, E. Cost-effective vibration based detection of wind turbine blade icing from sensors mounted on the tower. In Proceedings of the 9th European workshop on structural health monitoring (EWSHM 2018), Manchester, UK, 10–13 July 2018; pp. 10–13. [Google Scholar]
- Jiang, J.R.; Lee, J.E.; Zeng, Y.M. Time Series Multiple Channel Convolutional Neural Network with Attention-Based Long Short-Term Memory for Predicting Bearing Remaining Useful Life. Sensors 2020, 20, 166. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jin, C.C.; Chen, X. An end-to-end framework combining time–frequency expert knowledge and modified Transformer networks for vibration signal classification. Expert Syst. Appl. 2021, 171, 114570. [Google Scholar] [CrossRef]
- Abdallah, I.; Natarajan, A.; Sørensen, J. Impact of uncertainty in airfoil characteristics on wind turbine extreme loads. Renew. Energy 2015, 75, 283–300. [Google Scholar] [CrossRef]
- Han, W.; Kim, J.; Kim, B. Effects of contamination and erosion at the leading edge of blade tip airfoils on the annual energy production of wind turbines. Renew. Energy 2018, 115, 817–823. [Google Scholar] [CrossRef]
- Billingsley, P. Probability and Measure, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1995. [Google Scholar]
- Sanchez-Silva, M.; Riascos-Ochoa, J. Seismic risk models for aging and deteriorating buildings and civil infrastructure. In Handbook of Seismic Risk Analysis and Management of Civil Infrastructure Systems; Tesfamariam, S., Goda, K., Eds.; Woodhead Publishing: Cambridge, UK, 2013; Chapter 15; pp. 387–409. [Google Scholar]
- Taylor, H.M.; Karlin, S. An Introduction to Stochastic Modeling, 3rd ed.; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Chen, C.; Savits, T. Some remarks on compound nonhomogeneous Poisson processes. Stat. Probab. Lett. 1993, 17, 179–187. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. Wind Turbines, Part 1 Design Requirements; Technical Report IEC 61400-1:2005(E); International Electrotechnical Commission: Geneva, Switzerland, 2005. [Google Scholar]
- Dimitrov, N.; Natarajan, A.; Kelly, M. Model of wind shear conditional on turbulence and its impact on wind turbine loads. Wind Energy 2014, 18, 1917–1931. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Jonkman, J.; Buhl, M. FAST User’s Guide; Technical Report NREL/EL-500-38230; National Renewable Energy Laboratory: Golden, CO, USA, 2005. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical Report NREL/TP-500-38060; National Renewable Energy Laboratory: Golden, CO, USA, 2009. [Google Scholar]
- Kaimal, J.C.; Wyngaard, J.C.; Izumi, Y.; Coté, O.R. Spectral characteristics of surface-layer turbulence. Q. J. R. Meteorol. Soc. 1972, 98, 563–589. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. arXiv 2019, arXiv:1810.04805. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Avendaño-Valencia, L.D.; Chatzi, E.N. Sensitivity driven robust vibration-based damage diagnosis under uncertainty through hierarchical Bayes time-series representations. Procedia Eng. 2017, 199, 1852–1857. [Google Scholar] [CrossRef]
- Bengio, Y.; Louradour, J.; Collobert, R.; Weston, J. Curriculum learning. In Proceedings of the 26th Annual International Conference on Machine Learning—ICML ’09, Montreal, QC, Canada, 14–18 June 2009; pp. 1–8. [Google Scholar] [CrossRef]
- Guida, M.; Calabria, R.; Pulcini, G. Bayes inference for a non-homogeneous Poisson process with power intensity law (reliability). IEEE Trans. Reliab. 1989, 38, 603–609. [Google Scholar] [CrossRef]
- Grabski, F. Nonhomogeneous compound Poisson process application to modeling of random processes related to accidents in the Baltic Sea waters and ports. J. Pol. Saf. Reliab. Assoc. 2018, 9, 21–30. [Google Scholar]
- Noortwijk, J. A survey of the application of gamma processes in maintenance. Reliab. Eng. Syst. Saf. 2009, 94, 2–21. [Google Scholar] [CrossRef]
- Mialon, G.; Chen, D.; Selosse, M.; Mairal, J. GraphiT: Encoding Graph Structure in Transformers. arXiv 2021, arXiv:2106.05667. [Google Scholar]

| Stage 1 | Stage 2 | Stage 3 | Stage 4 | Stage 5 | |
|---|---|---|---|---|---|
| Type A | 100P | 200P | 400P | — | — |
| Type B | — | 200P/100G | 400P/200G | 800P/400G | — |
| Type C | — | — | 400P/200G/DL | 800P/400G/DL+ | 1600P/800G/DL++ |
| Stage 1 | Stage 2 | Stage 3 | Stage 4 | Stage 5 | |
|---|---|---|---|---|---|
| Type A | 1 | 2 | 3 | — | — |
| Type B | — | 4 | 5 | 6 | — |
| Type C | — | — | 7 | 8 | 9 |
| Sensor Name | Description |
|---|---|
| Time steps of the simulations | |
| X-direction wind velocity at hub-height | |
| Lift force coefficient at Blade 1, Aerosense Node at | |
| Drag force coefficient at Blade 1, Aerosense Node at | |
| Angle of attack at Blade 1, Aerosense Node at |
| Parameter | Experiments | |||||
|---|---|---|---|---|---|---|
| 1.1 | 1.2 | 2.1 | 2.2 | 3.1 | 3.2 | |
| NHCPP severities | 0–9 | 0, 1, 6, 9 | 0–9 | 0–9 | 0–9 | 0–9 |
| Severity type grouping | - | - | - | 0, A, B, C | - | 0, A, B, C |
| Stochastic degradation | - | - | ✓ | ✓ | ✓ | ✓ |
| Inflow turbulence | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Aerodynamic uncertainty | - | - | - | - | ✓ | ✓ |
| Weather variability | - | - | - | - | ✓ | ✓ |
| Num. training samples | 3360 | 3360 | 2880 | 2880 | 2880 | 2880 |
| Num. validation samples | 960 | 960 | 720 | 720 | 720 | 720 |
| Num. testing samples | 480 | 480 | 1200 | 1200 | 1200 | 1200 |
| Parameter | Value |
|---|---|
| Number of windows, n | 300 |
| Window size, w | 200 |
| Internal Transformer dim., | 256 |
| Transformer stack size, s | 6 |
| Num. self-attention heads, h | 8 |
| Self-attention head dim., | 64 |
| Output MLP dim., | 2048 |
| Experiment | Testing Accuracy (%) | |
|---|---|---|
| All Predictions | >70% Likelihood | |
| Exp. 1.1 | 66.67 | 72.65 |
| Exp. 1.1 Large | 80.63 | 85.56 |
| Exp. 1.2 | 96.04 | 97.22 |
| Experiment | Testing Accuracy (%) | |
|---|---|---|
| All Predictions | >70% Likelihood | |
| Exp. 2.1 | 65.42 | 78.41 |
| Exp. 2.2 | 67.75 | 69.48 |
| Experiment | Testing Accuracy (%) | |
|---|---|---|
| All Predictions | >70% Likelihood | |
| Exp. 3.1 | 35.00 | 45.75 |
| Exp. 3.2 | 54.67 | 65.22 |
| Training Set(s) | Test Accuracy (%) | ||
|---|---|---|---|
| Set 1.1 | Set 2.1 | Set 3.1 | |
| Set 1.1 | – | 71.25 | 28.25 |
| Set 2.1 | 65.00 | – | 29.42 |
| Set 3.1 | 30.00 | 39.25 | – |
| Set 1.1, then 2.1 | 77.71 | 83.50 | 20.33 |
| Set 1.1, then 2.1 & 3.1 | 77.08 | 80.50 | 37.08 |
| Training Set(s) | >70% Likelihood Test Accuracy (%) | ||
|---|---|---|---|
| Set 1.1 | Set 2.1 | Set 3.1 | |
| Set 1.1 | – | 80.21 | 30.19 |
| Set 2.1 | 77.11 | – | 32.86 |
| Set 3.1 | 35.58 | 40.97 | – |
| Set 1.1, then 2.1 | 81.35 | 87.29 | 20.52 |
| Set 1.1, then 2.1 & 3.1 | 84.42 | 88.53 | 50.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duthé, G.; Abdallah, I.; Barber, S.; Chatzi, E. Modeling and Monitoring Erosion of the Leading Edge of Wind Turbine Blades. Energies 2021, 14, 7262. https://doi.org/10.3390/en14217262
Duthé G, Abdallah I, Barber S, Chatzi E. Modeling and Monitoring Erosion of the Leading Edge of Wind Turbine Blades. Energies. 2021; 14(21):7262. https://doi.org/10.3390/en14217262
Chicago/Turabian StyleDuthé, Gregory, Imad Abdallah, Sarah Barber, and Eleni Chatzi. 2021. "Modeling and Monitoring Erosion of the Leading Edge of Wind Turbine Blades" Energies 14, no. 21: 7262. https://doi.org/10.3390/en14217262
APA StyleDuthé, G., Abdallah, I., Barber, S., & Chatzi, E. (2021). Modeling and Monitoring Erosion of the Leading Edge of Wind Turbine Blades. Energies, 14(21), 7262. https://doi.org/10.3390/en14217262







