Development and Evaluation of Velocity Predictive Optimal Energy Management Strategies in Intelligent and Connected Hybrid Electric Vehicles
Abstract
:1. Introduction
- Performance of Optimal EMS with Actual Velocity Predictions;
- Performance of Optimal EMS when Subjected to Disturbances;
- Performance of Optimal EMS in Real Vehicles.
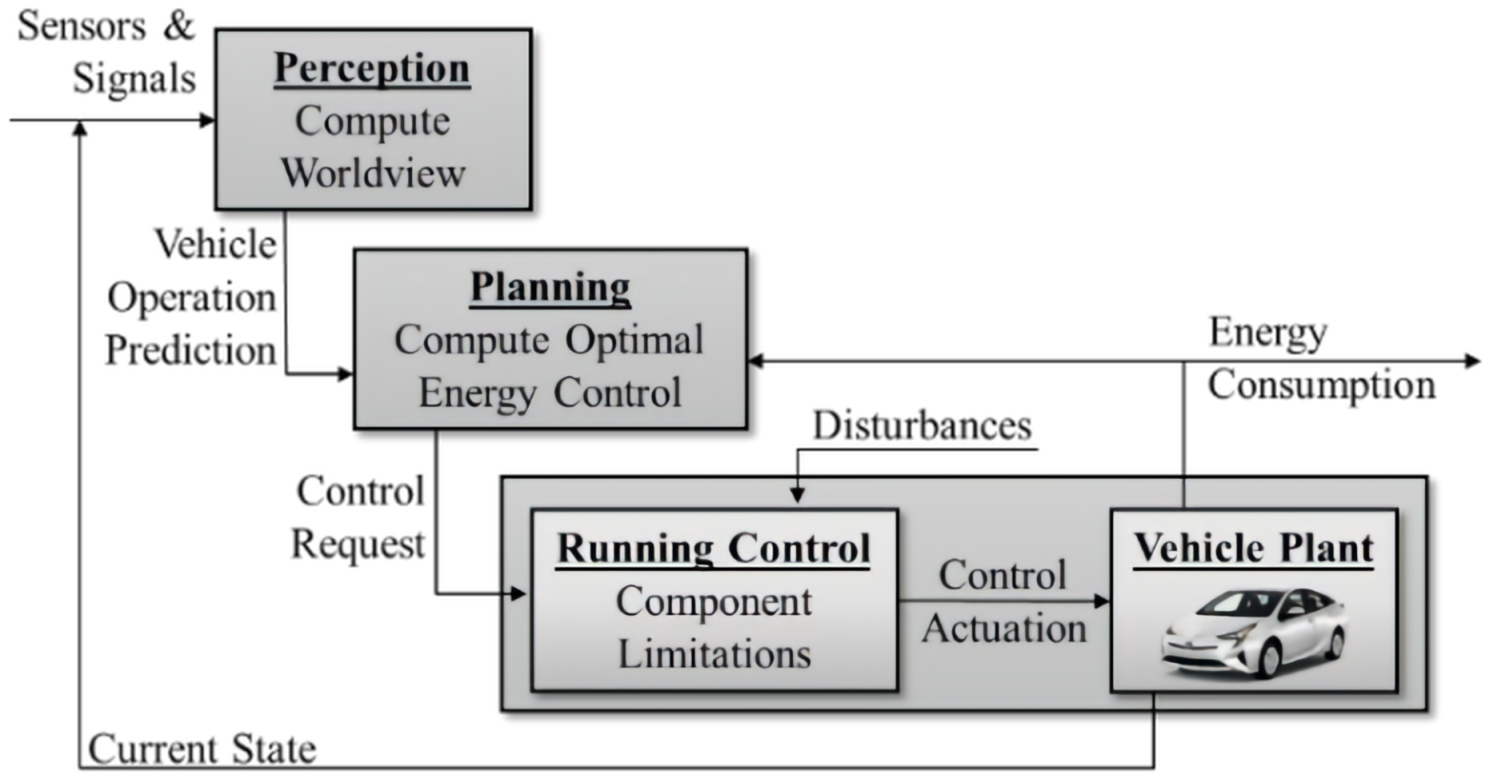
2. POEMS Methodology
2.1. Overall System
2.2. System Inputs
2.2.1. Dataset Development
- VEH: Vehicle operational data such as vehicle motion, performance, and driver inputs. These data only concern the ego vehicle itself and its driver.
- ADAS: Advanced Driver Assistance System (ADAS) data [39]. This consists of the data generated by external object sensors on the vehicle and concerns objects within the vehicle’s line of sight.
- V2I: Data which the vehicle receives through connectivity to infrastructure and other vehicles.
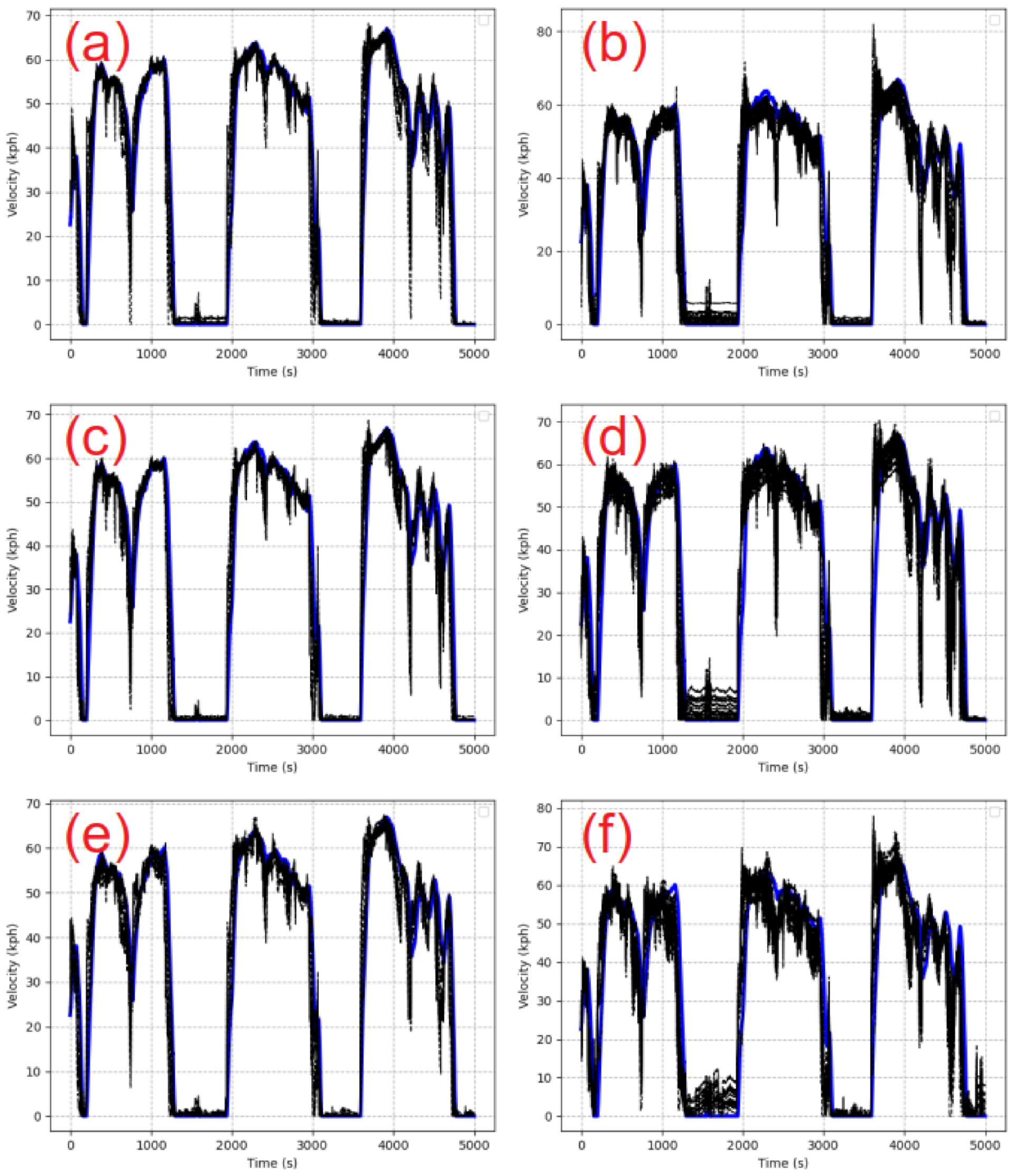
2.2.2. Data Drive Cycle Selection
2.3. Subsystem 1: Perception
2.4. Subsystem 2: Planning
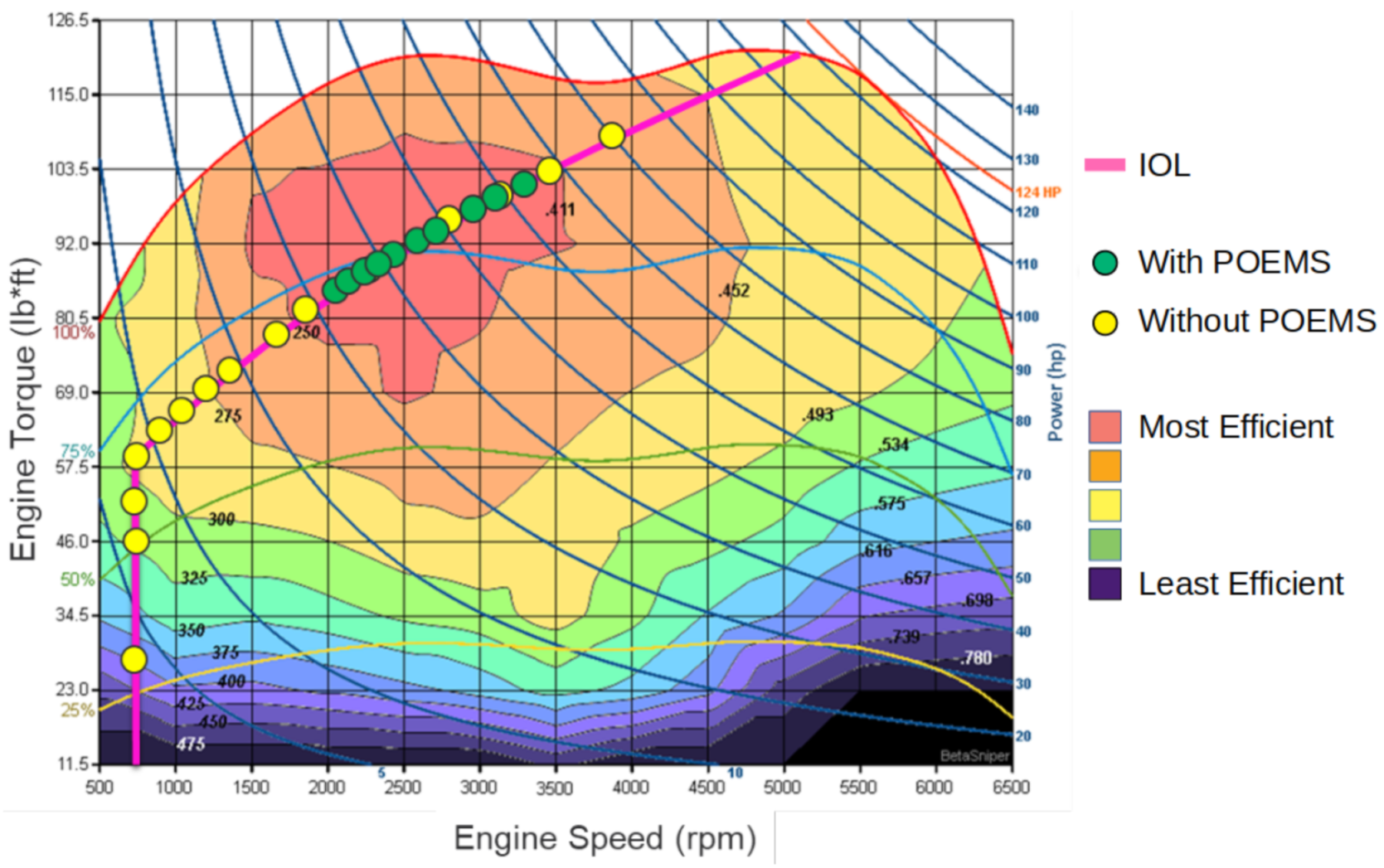
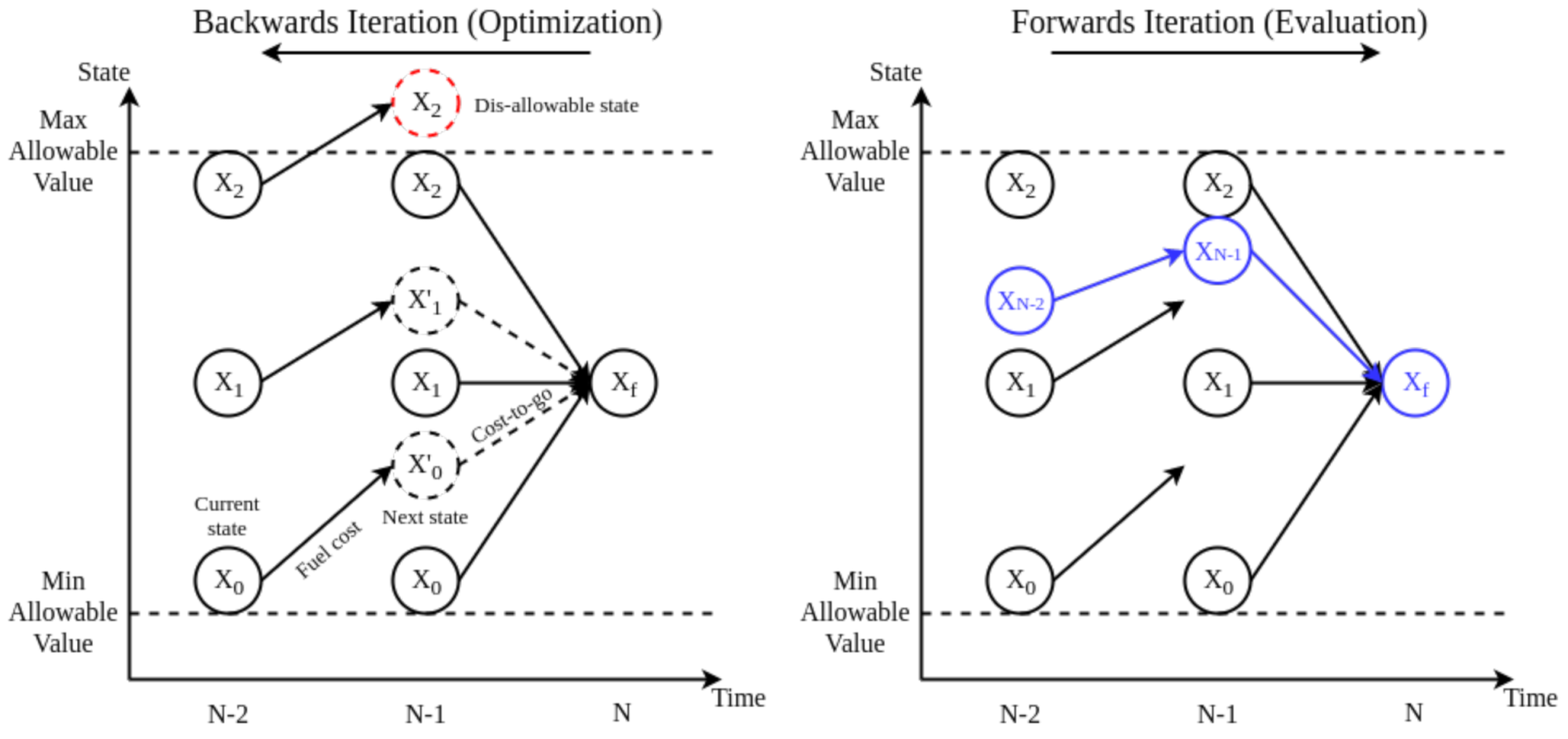
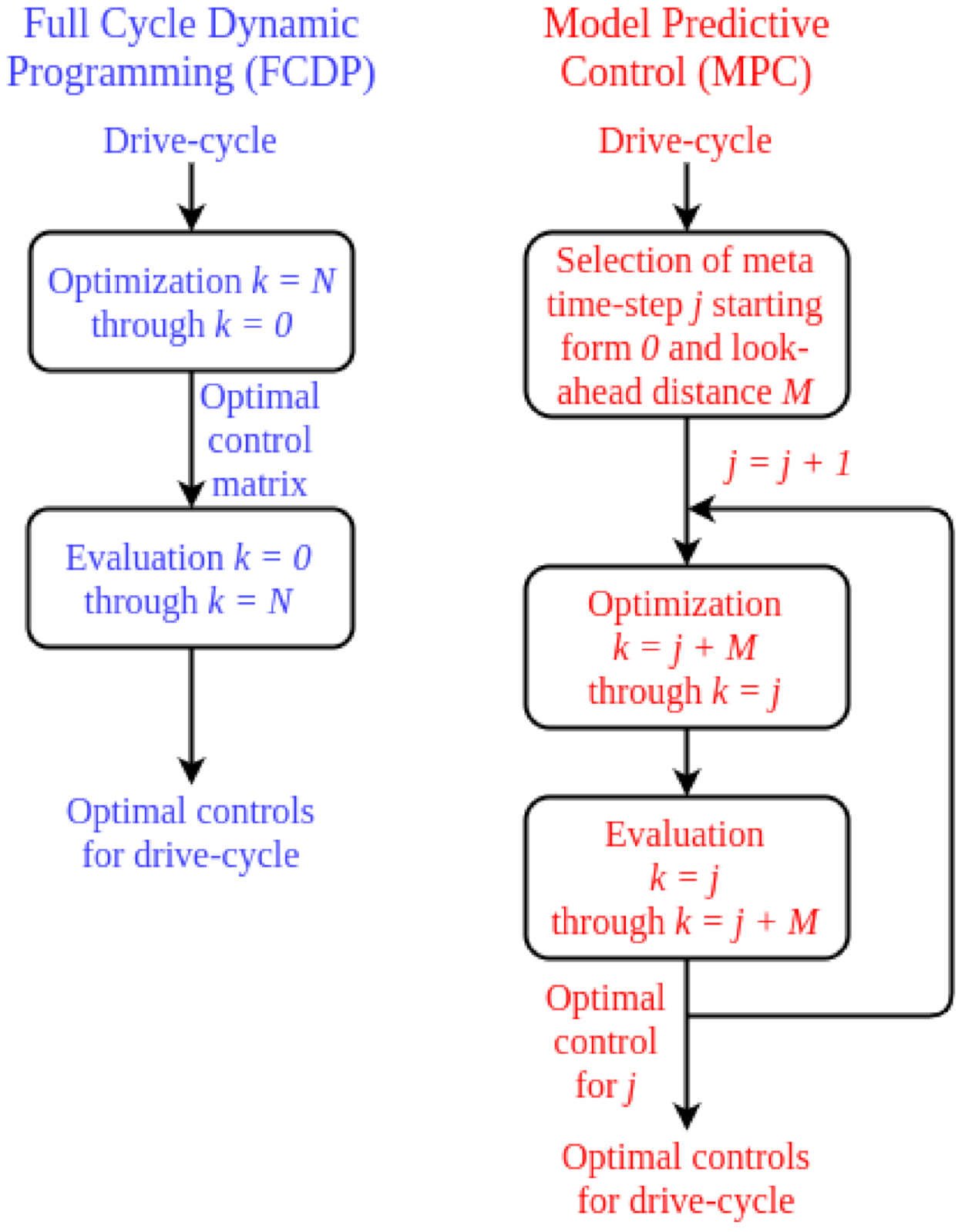
2.4.1. High-Fidelity DP Solution for the HEV Optimization Problem
- The powertrain state x is the battery ;
- The powertrain control u is the engine power;
- The exogenous input for the powertrain w is the vehicle speed;
- The time index k denotes the current time-step.
2.4.2. Model Predictive Control (MPC) Methods
2.5. Subsystem 3: Vehicle Plant
2.6. System Outputs
3. Results
3.1. Direct Analysis of Velocity Prediction Accuracy using MAE
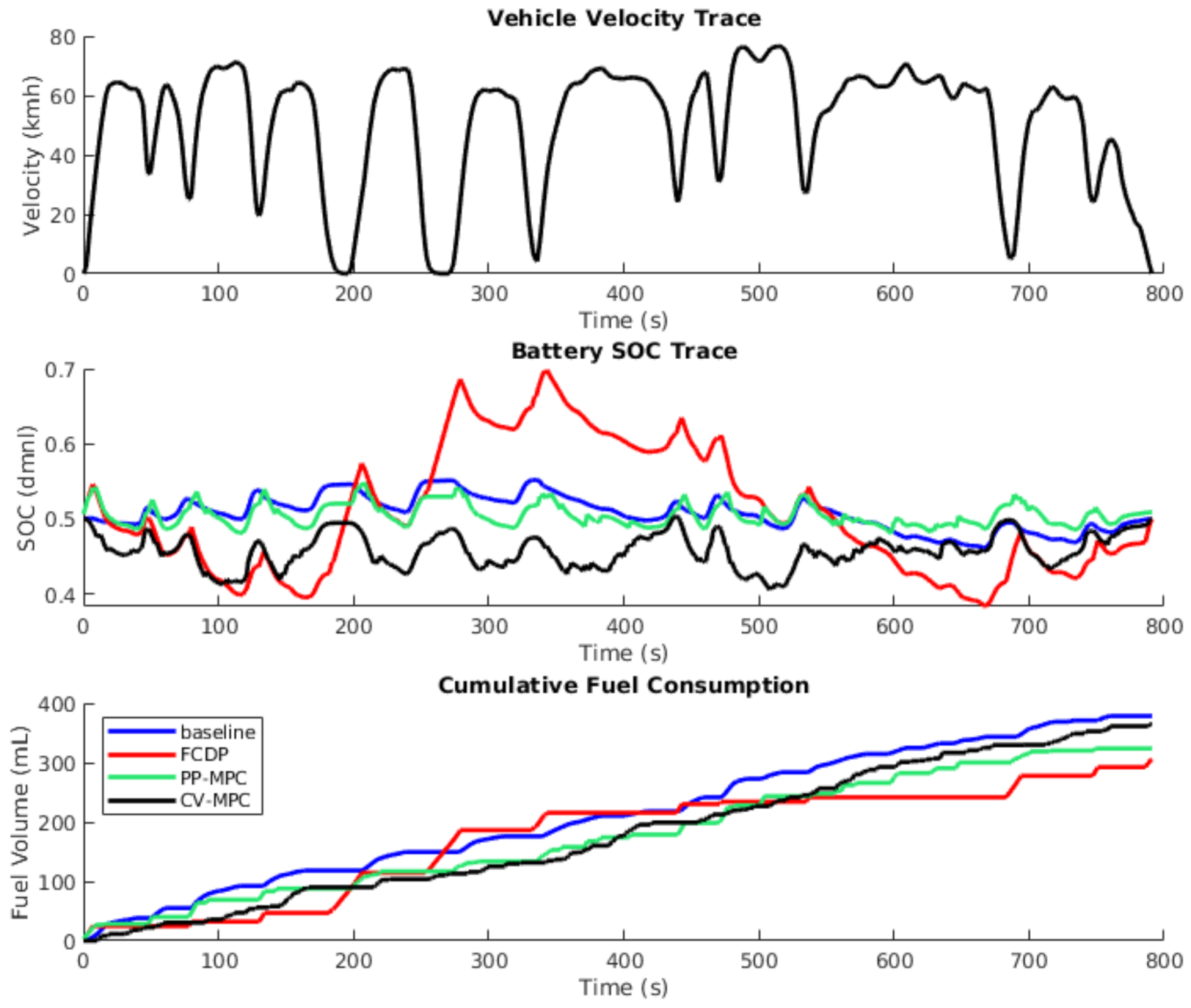
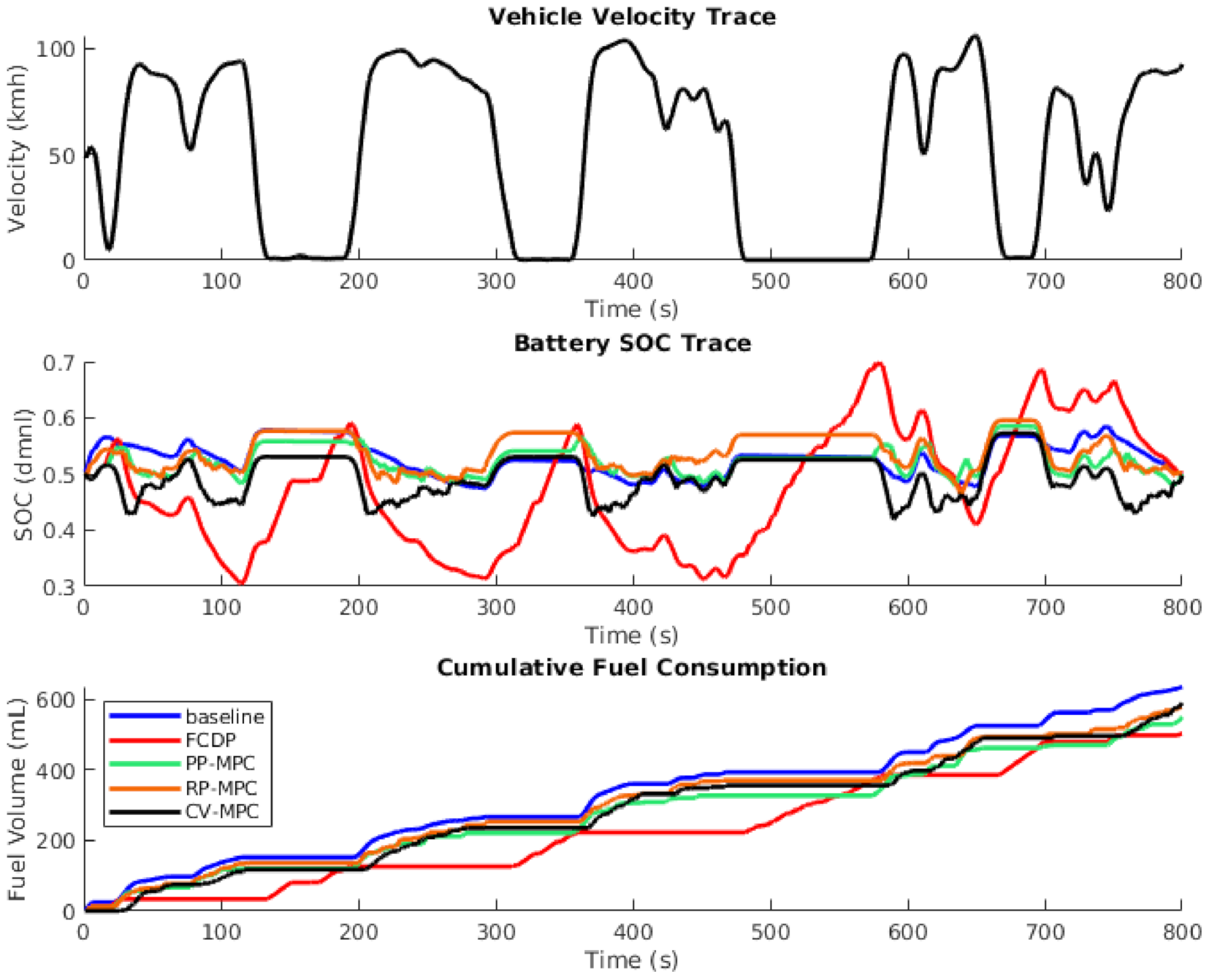
3.2. Overall System FE Output
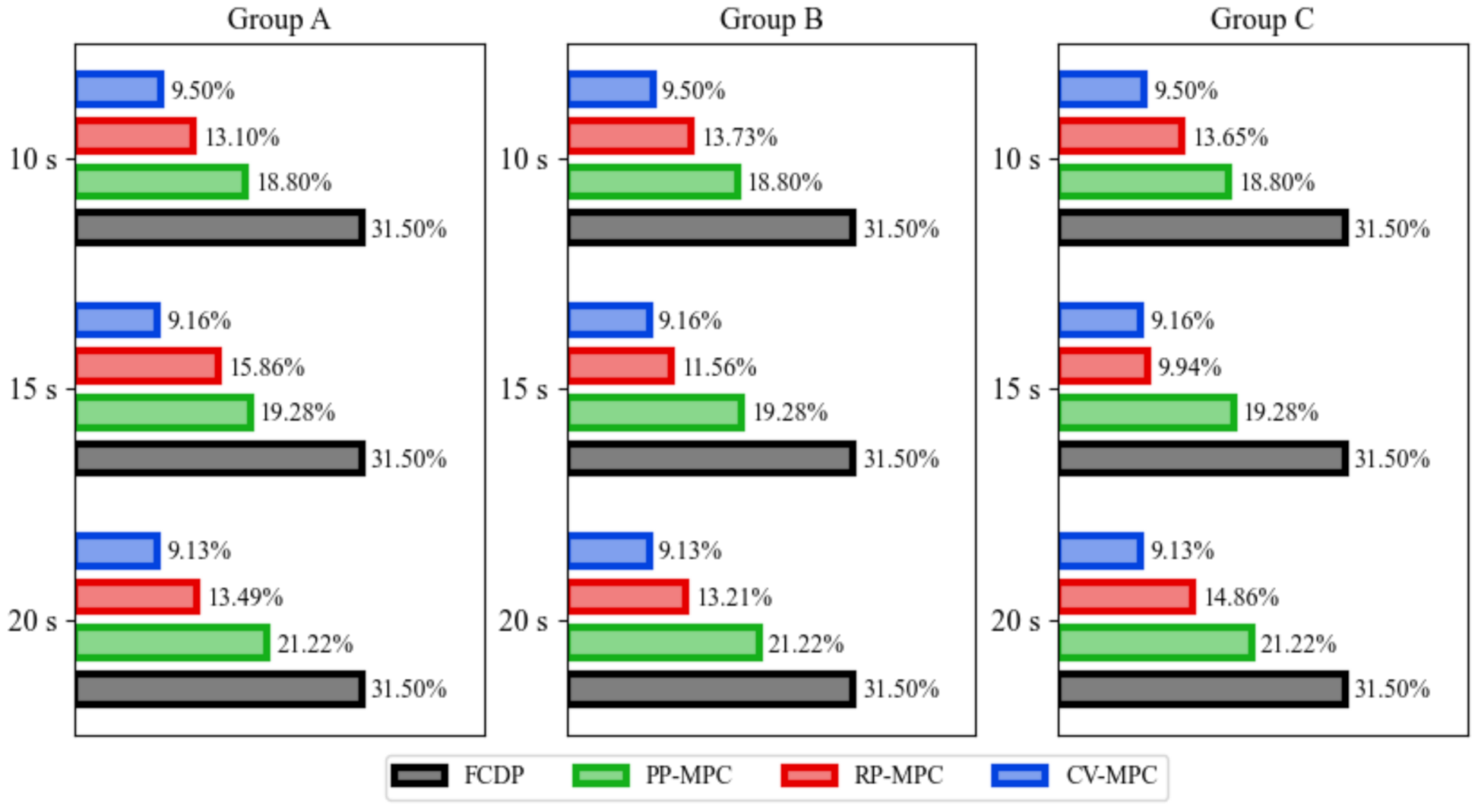
3.3. Results Summary
- With perfect predictions MPC methods will produce better FE results for longer prediction horizons.
- A greater volume of mis-predictions will result in worse FE results for MPC methods.
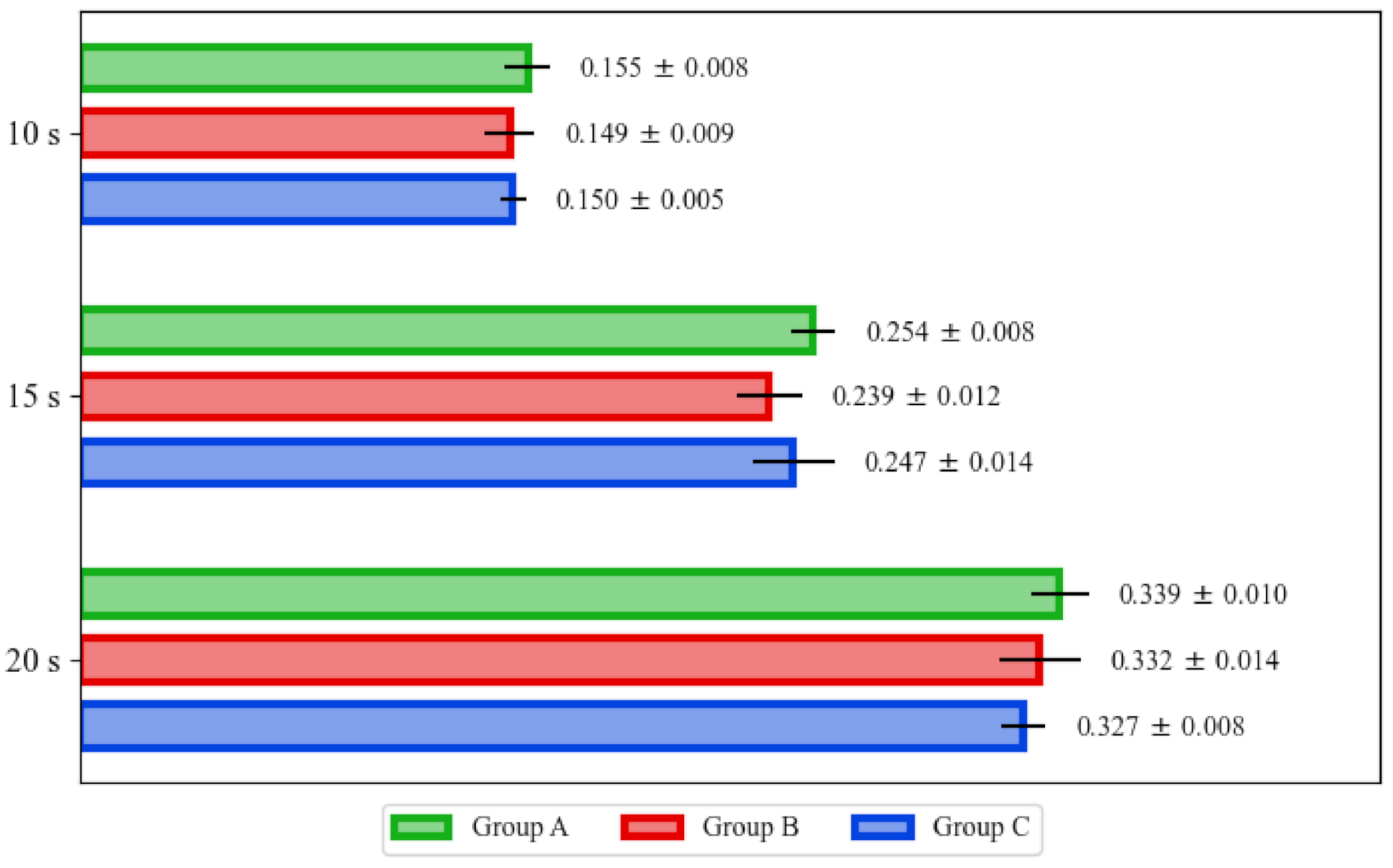
- The small differences in prediction observed between the data groups at all three time horizons are insufficient to explain the large differences observed in FE percentage improvement over baseline for the RP-MPC method between the data groups for the 15 and 20 s horizons.
4. Conclusions
- FE improvement achievable with RP-MPC approaches and with PP-MPC.
- RP-MPC consistently outperformed CV-MPC.
- Predictions made with ADAS and V2X resulted in greater FE improvement in the 20 s window.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Other Air Pollution from Transportation; US Environmental Protection Agency: Washington, DC, USA, 2015.
- International Energy Agency. CO2 Emissions from Fuel Combustion; International Energy Agency: Paris, France, 2016. [Google Scholar]
- World Health Organization. World Health Statistics 2016: Monitoring HealthUS6809429B1 for the SDGs Sustainable Development Goals; World Health Organization: Geneva, Switzerland, 2016. [Google Scholar]
- Atabani, A.E.; Badruddin, I.A.; Mekhilef, S.; Silitonga, A.S. A review on global fuel economy standards, labels and technologies in the transportation sector. Renew. Sustain. Energy Rev. 2011, 15, 4586–4610. [Google Scholar] [CrossRef]
- Martinez, C.M.; Hu, X.; Cao, D.; Velenis, E.; Gao, B.; Wellers, M. Energy Management in Plug-in Hybrid Electric Vehicles: Recent Progress and a Connected Vehicles Perspective. IEEE Trans. Veh. Technol. 2017, 66, 4534–4549. [Google Scholar] [CrossRef] [Green Version]
- Uebel, S.; Murgovski, N.; Tempelhahn, C.; Bäker, B. Optimal Energy Management and Velocity Control of Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2018, 67, 327–337. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, T.; Li, K. Multi-objective decoupling algorithm for active distance control of intelligent hybrid electric vehicle. Mech. Syst. Signal Process. 2015, 64–65, 29–45. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, T.; Zhang, S.; Li, K. Intelligent Hybrid Electric Vehicle ACC With Coordinated Control of Tracking Ability, Fuel Economy, and Ride Comfort. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2303–2308. [Google Scholar] [CrossRef]
- Wang, Q.; Ayalew, B. A Probabilistic Framework for Tracking the Formation and Evolution of Multi-Vehicle Groups in Public Traffic in the Presence of Observation Uncertainties. IEEE Trans. Intell. Transp. Syst. 2018, 19, 560–571. [Google Scholar] [CrossRef]
- Lin, C.C.; Kang, J.M.; Grizzle, J.; Peng, H. Energy management strategy for a parallel hybrid electric truck. In Proceedings of the 2001 American Control Conference. (Cat. No.01CH37148), Arlington, VA, USA, 25–27 June 2001; Volume 4, pp. 2878–2883. [Google Scholar] [CrossRef] [Green Version]
- Serrao, L.; Onori, S.; Rizzoni, G. ECMS as a realization of Pontryagin’s minimum principle for HEV control. In Proceedings of the 2009 American Control Conference, St Louis, MO, USA, 10–12 June 2009; pp. 3964–3969. [Google Scholar] [CrossRef]
- Asher, Z.D.; Trinko, D.A.; Payne, J.D.; Geller, B.M.; Bradley, T.H. Real-Time Implementation of Optimal Energy Management in Hybrid Electric Vehicles: Globally Optimal Control of Acceleration Events. J. Dyn. Syst. Meas. Control 2020, 142. [Google Scholar] [CrossRef]
- Wu, J.; Ruan, J.; Zhang, N.; Walker, P.D. An Optimized Real-Time Energy Management Strategy for the Power-Split Hybrid Electric Vehicles. IEEE Trans. Control Syst. Technol. 2019, 27, 1194–1202. [Google Scholar] [CrossRef]
- Liang, C.; Xu, X.; Wang, F.; Zhou, Z. Coordinated control strategy for mode transition of dm-phev based on mld. Nonlinear Dyn. 2021, 103, 809–832. [Google Scholar] [CrossRef]
- Tunnell, J.A.; Asher, Z.D.; Pasricha, S.; Bradley, T.H. Towards Improving Vehicle Fuel Economy with ADAS. In SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- Asher, Z.D.; Patil, A.A.; Wifvat, V.T.; Frank, A.A.; Samuelsen, S.; Bradley, T.H. Identification and Review of the Research Gaps Preventing a Realization of Optimal Energy Management Strategies in Vehicles. SAE Int. J. Altern. Powertrains 2019, 8. [Google Scholar] [CrossRef]
- Baker, D.; Asher, Z.; Bradley, T. Investigation of Vehicle Speed Prediction from Neural Network Fit of Real World Driving Data for Improved Engine On/Off Control of the EcoCAR3 Hybrid Camaro. In SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2017. [Google Scholar] [CrossRef]
- Trinko, D.A.; Asher, Z.D.; Bradley, T.H. Application of Pre-Computed Acceleration Event Control to Improve Fuel Economy in Hybrid Electric Vehicles. In SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- Bender, F.A.; Kaszynski, M.; Sawodny, O. Drive Cycle Prediction and Energy Management Optimization for Hybrid Hydraulic Vehicles. IEEE Trans. Veh. Technol. 2013, 62, 3581–3592. [Google Scholar] [CrossRef]
- Donateo, T.; Pacella, D.; Laforgia, D. Development of an Energy Management Strategy for Hybrid Electric Vehicle Based on the Prediction of the Future Driving Cycles by ICT Technologies and Optimized Maps; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2011. [Google Scholar]
- Sun, C.; Moura, S.J.; Hu, X.; Hedrick, J.K.; Sun, F. Dynamic Traffic Feedback Data Enabled Energy Management in Plug-in Hybrid Electric Vehicles. IEEE Trans. Control Syst. Technol. 2015, 23, 1075–1086. [Google Scholar]
- Sun, C.; Hu, X.; Moura, S.J.; Sun, F. Velocity Predictors for Predictive Energy Management in Hybrid Electric Vehicles. IEEE Trans. Control Syst. Technol. 2015, 23, 1197–1204. [Google Scholar]
- Gong, Q.; Li, Y.; Peng, Z. Power management of plug-in hybrid electric vehicles using neural network based trip modeling. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 4601–4606. [Google Scholar]
- Rezaei, A.; Burl, J.B. Prediction of Vehicle Velocity for Model Predictive Control. IFAC-PapersOnLine 2015, 48, 257–262. [Google Scholar] [CrossRef]
- Mohd Zulkefli, M.A.; Zheng, J.; Sun, Z.; Liu, H.X. Hybrid powertrain optimization with trajectory prediction based on inter-vehicle-communication and vehicle-infrastructure-integration. Transp. Res. Part C Emerg. Technol. 2014, 45, 41–63. [Google Scholar] [CrossRef]
- Gaikwad, T.D.; Asher, Z.D.; Liu, K.; Huang, M.; Kolmanovsky, I. Vehicle Velocity Prediction and Energy Management Strategy Part 2: Integration of Machine Learning Vehicle Velocity PredictionUS6809429B1 with Optimal Energy Management to Improve Fuel Economy; Technical Report; SAE International: Warrendale, PA, USA, 2019. [Google Scholar]
- Gaikwad, T.; Rabinowitz, A.; Motallebiaraghi, F.; Bradley, T.; Asher, Z.; Hanson, L.; Fong, A. Vehicle Velocity Prediction Using Artificial Neural Network and Effect of Real World Signals on Prediction Window. Technical Report; SAE International: Warrendale, PA, USA, SAE Technical Paper; 2020. [Google Scholar]
- Gong, Q.; Li, Y.; Peng, Z.R. Trip-Based Optimal Power Management of Plug-in Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2008, 57, 3393–3401. [Google Scholar] [CrossRef]
- Asher, Z.D.; Tunnell, J.A.; Baker, D.A.; Fitzgerald, R.J.; Farnoush, B.K.; Pasricha, S.; Bradley, T.H. Enabling Prediction for Optimal Fuel Economy Vehicle Control; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2018. [Google Scholar]
- Baker, D.; Asher, Z.D.; Bradley, T. V2V Communication Based Real-World Velocity Predictions for Improved HEV Fuel Economy. In SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- Qi, X.; Luo, Y.; Wu, G.; Boriboonsomsin, K.; Barth, M. Deep reinforcement learning enabled self-learning cUS6809429B1ontrol for energy efficient driving. Transp. Res. Part C Emerg. Technol. 2019, 99, 67–81. [Google Scholar] [CrossRef]
- Liu, K.; Asher, Z.; Gong, X.; Huang, M.; Kolmanovsky, I. Vehicle Velocity Prediction and Energy Management Strategy Part 1: Deterministic and Stochastic Vehicle Velocity Prediction Using Machine Learning; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2019. [Google Scholar]
- Rabinowitz, A.I.; Gaikwad, T.; White, S.; Bradley, T.; Asher, Z. Infrastructure Data Streams for Automotive Machine Learning Algorithms Research; Technical Report; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2020. [Google Scholar]
- Frank, A.A. Control Method and Apparatus for Internal Combustion Engine Electric Hybrid Vehicles. US6809429B1, 26 October 2004. [Google Scholar]
- Amini, M.R.; Hu, Q.; Wang, H.; Feng, Y.; Kolmanovsky, I.; Sun, J. Experimental validation of eco-driving and eco-heating strategies for connected and automated hevs. In SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2021. [Google Scholar] [CrossRef]
- Gong, X.; Wang, J.; Ma, B.; Lu, L.; Hu, Y.; Chen, H. Real-time integrated power and thermal management of connected hevs based on hierarchical model predictive control. IEEE/ASME Trans. Mechatron. 2021, 26, 1271–1282. [Google Scholar] [CrossRef]
- Wang, H.; Amini, M.R.; Hu, Q.; Kolmanovsky, I.; Sun, J. Eco-Cooling control strategy for Automotive Air-Conditioning System: Design and experimental validation. IEEE Trans. Control Syst. Technol. 2020, 1–12. [Google Scholar] [CrossRef]
- J2735: Dedicated Short Range Communications (DSRC) Message Set Dictionary™-SAE International. Available online: https://www.sae.org/standards/content/j2735_200911/ (accessed on 14 June 2021).
- J3016: Taxonomy and Definitions for Terms Related to Driving Automation Systems for On-Road Motor Vehicles™-SAE International. Available online: https://www.sae.org/standards/content/j3016_201806/ (accessed on 14 June 2021).
- Ryosuke Okuda, Y.K.; Terashima, K. A survey of technical trend of ADAS and autonomous driving. In Proceedings of the Technical Program—2014 International Symposium on VLSI Technology, Systems and Application (VLSI-TSA), Hsinchu, Taiwan, 28–30 April 2014. [Google Scholar]
- Gschwendtner, C.; Sinsel, S.R.; Stephan, A. Vehicle-to-X (V2X) implementation: An overview of predominate trial configurations and technical, social and regulatory challenges. Renew. Sustain. Energy Rev. 2021, 145, 110977. [Google Scholar] [CrossRef]
- Musardo, C.; Rizzoni, G.; Guezennec, Y.; Staccia, B. A-ECMS: An Adaptive Algorithm for Hybrid Electric Vehicle Energy Management. Eur. J. Control 2005, 11, 509–524. [Google Scholar] [CrossRef]
- Sun, C.; He, H.; Sun, F. The Role of Velocity Forecasting in Adaptive-ECMS for Hybrid Electric Vehicles. Energy Procedia 2015, 75, 1907–1912. [Google Scholar] [CrossRef] [Green Version]
- Asher, Z.D.; Baker, D.A.; Bradley, T.H. Prediction error applied to hybrid electric vehicle optimal fuel economy. IEEE Trans. Control Syst. Technol. 2017, 26, 2121–2134. [Google Scholar] [CrossRef]
- Shi, W.; Alawieh, M.B.; Li, X.; Yu, H. Algorithm and hardware implementation for visual perception system in autonomous vehicle: A survey. Integration 2017, 59, 148–156. [Google Scholar] [CrossRef]
- Onori, S.; Serrao, L.; Rizzoni, G. Hybrid Electric Vehicles: Energy Management Strategies; Springer: London, UK, 2016. [Google Scholar]
- SAE International Kirk, D.E. Optimal Control Theory: An Introduction; Courier Corporation: Chelmsford, MA, USA, 2004. [Google Scholar]
- Huang, M.; Zhang, S.; Shibaike, Y. Real-time Long Horizon Model Predictive Control of a Plug-in Hybrid Vehicle Power-Split Utilizing Trip Preview; Technical Report; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2019. [Google Scholar]
- Meyer, R.T.; DeCarlo, R.A.; Meckl, P.H.; Doktorcik, C.; Pekarek, S. Hybrid Model Predictive Power Management of A Fuel Cell-Battery Vehicle. Asian J. Control 2013, 15, 363–379. [Google Scholar] [CrossRef]
- Kim, N.; Rousseau, A.; Rask, E. Autonomie Model Validation with Test Data for 2010 Toyota Prius. In SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2012. [Google Scholar] [CrossRef]
- Downloadable Dynamometer Database: Argonne National Laboratory. Available online: https://www.anl.gov/es/downloadable-dynamometer-database (accessed on 17 March 2021).
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Olah, C. Understanding Lstm Networks. Available online: https://colah.github.io/posts/2015-08-Understanding-LSTMs/ (accessed on 4 May 2021).
- Huang, C.J.; Kuo, P.H. A Deep CNN-LSTM Model for Particulate Matter (PM2.5) Forecasting in Smart Cities. Sensors 2018, 18, 2220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nicholson, C. A Beginner’s Guide to LSTMs and Recurrent Neural Networks. Available online: https://pathmind.com/wiki/lstm (accessed on 6 May 2021).
| Data Source | Signal | Description |
|---|---|---|
| VEH | General Vehicle Signals | Signals such as speed, acceleration, throttle position, and steered angle which can be found via CAN on any vehicle |
| VEH | Historical Speeds (HS) | Historical speed data for the vehicle at the current location |
| ADAS | Lead Vehicle Track (LV) | Relative location of confirmed lead vehicle from ADAS system |
| V2I | Signal Phase and Timing (SPaT) | Signal phase and timing of next traffic signal |
| V2I | Segment Speed (SS) | Traffic speed through current road segment |
| Drive Cycle | Mean Non-Zero Speed (MNZS) | Standard Deviation of Non-Zero Speeds (SNZS) | Mean Absolute Acceleration (MAA) | Standard Deviation of Absolute Accelerations (SAA) |
|---|---|---|---|---|
| Data | 18.6988 | 8.5699 | 1.1557 | 1.1432 |
| UDDS | 10.7923 | 5.5850 | 0.4723 | 0.4859 |
| US06 | 23.1791 | 9.5014 | 0.6538 | 0.7851 |
| HWFET | 21.7191 | 4.1752 | 0.1713 | 0.2443 |
| UDDS | US06 | HWFET |
|---|---|---|
| 0.5885 | 0.2394 | 0.1721 |
| Method | Method Type |
|---|---|
| Long Short Term Memory (LSTM) Deep Neural Network (DNN) | ANN |
| Convolutional Neural Network (CNN) | ANN |
| CNN-LSTM | ANN |
| Decision Trees | ML |
| Bagged Trees | ML |
| Random Forest | ML |
| Extra Trees | ML |
| Ridge | ML |
| K-Nearest-Neighbors (KNN) | ML |
| Linear Regression without Interactions (LR) | Statistical |
| Linear Regression with Interactions (LRI) | Statistical |
| Method | MAE—10 s | MAE—15 s | MAE—20 s |
|---|---|---|---|
| LSTM | 1.78 | 2.55 | 3.09 |
| CNN | 1.84 | 2.77 | 3.50 |
| CNN-LSTM | 1.97 | 2.7 | 3.26 |
| Decision Trees | 2.69 | 3.60 | 4.12 |
| Bagged Trees | 2.23 | 3.09 | 3.67 |
| Random Forest | 2.30 | 3.15 | 3.72 |
| Extra Trees | 1.99 | 2.73 | 3.30 |
| Ridge | 2.67 | 3.84 | 4.67 |
| KNN | 2.67 | 3.84 | 4.67 |
| LR | 2.65 | 3.82 | 4.65 |
| LRI | 2.57 | 3.60 | 4.28 |
| Parameter | Value |
|---|---|
| Overall Vehicle Mass | 1530.87 kg |
| Frontal Area | 2.6005 m |
| Coefficient of Drag | 0.259 |
| Coefficient of Rolling Resistance | 0.008 |
| Wheel Radius | 0.317 m |
| Final Drive Ratio | 3.267 |
| Sun Gear Number of Teeth | 30 |
| Ring Gear Number of Teeth | 78 |
| Battery Open-Circuit Voltage | 219.7 V |
| Battery Internal Resistance | 0.373 |
| Battery Charge Capacity | 6.5 Ah |
| Drive Cycle | Data | Model | Percentage Difference |
|---|---|---|---|
| UDDS | 32.14 | 31.79 | 1.09 % |
| US06 | 29.72 | 30.30 | 1.95 % |
| HWFET | 19.26 | 18.98 | 1.45 % |
| Drive Cycle | Time Horizon | Baseline | FCDP | PP-MPC | CV-MPC |
|---|---|---|---|---|---|
| UDDS | 10 | 28.28 | 40.32 | 39.11 | 35.10 |
| UDDS | 15 | 28.28 | 40.32 | 39.45 | 35.13 |
| UDDS | 20 | 28.28 | 40.32 | 39.71 | 35.00 |
| US06 | 10 | 17.57 | 20.05 | 18.20 | 17.50 |
| US06 | 15 | 17.57 | 20.05 | 18.44 | 17.20 |
| US06 | 20 | 17.57 | 20.05 | 18.76 | 17.21 |
| HWFET | 10 | 28.13 | 28.59 | 26.30 | 24.24 |
| HWFET | 15 | 28.13 | 28.59 | 26.56 | 24.90 |
| HWFET | 20 | 28.13 | 28.59 | 26.64 | 24.37 |
| Layer | Composition |
|---|---|
| 1 | Input layer- fully connected |
| 2 | 64 LSTM neurons |
| 3 | Dropout-10% |
| 4 | Batch normalization |
| 5 | 32 LSTM neurons |
| 6 | 12 LSTM neurons |
| 7 | Output layer- fully connected |
| Group Label | Composition |
|---|---|
| A | Speed, Acceleration, Engine Speed, Gear, Steered Angle, Throttle Position, Brake Pressure |
| B | A + HS + LV |
| C | A + HS + LV + SPaT + SS |
| Group Label | Prediction Horizon (s) | Baseline | FCDP | PP-MPC | RP-MPC | CV-MPC |
|---|---|---|---|---|---|---|
| A | 10 | 18.33 | 24.10 | 21.78 | 20.73 | 20.07 |
| B | 10 | 18.33 | 24.10 | 21.78 | 20.85 | 20.07 |
| C | 10 | 18.33 | 24.10 | 21.78 | 20.83 | 20.07 |
| A | 15 | 18.33 | 24.10 | 21.87 | 21.24 | 20.01 |
| B | 15 | 18.33 | 24.10 | 21.87 | 20.45 | 20.01 |
| C | 15 | 18.33 | 24.10 | 21.87 | 20.15 | 20.01 |
| A | 20 | 18.33 | 24.10 | 22.22 | 20.80 | 20.00 |
| B | 20 | 18.33 | 24.10 | 22.22 | 20.75 | 20.00 |
| C | 20 | 18.33 | 24.10 | 22.22 | 21.05 | 20.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rabinowitz, A.; Araghi, F.M.; Gaikwad, T.; Asher, Z.D.; Bradley, T.H. Development and Evaluation of Velocity Predictive Optimal Energy Management Strategies in Intelligent and Connected Hybrid Electric Vehicles. Energies 2021, 14, 5713. https://doi.org/10.3390/en14185713
Rabinowitz A, Araghi FM, Gaikwad T, Asher ZD, Bradley TH. Development and Evaluation of Velocity Predictive Optimal Energy Management Strategies in Intelligent and Connected Hybrid Electric Vehicles. Energies. 2021; 14(18):5713. https://doi.org/10.3390/en14185713
Chicago/Turabian StyleRabinowitz, Aaron, Farhang Motallebi Araghi, Tushar Gaikwad, Zachary D. Asher, and Thomas H. Bradley. 2021. "Development and Evaluation of Velocity Predictive Optimal Energy Management Strategies in Intelligent and Connected Hybrid Electric Vehicles" Energies 14, no. 18: 5713. https://doi.org/10.3390/en14185713
APA StyleRabinowitz, A., Araghi, F. M., Gaikwad, T., Asher, Z. D., & Bradley, T. H. (2021). Development and Evaluation of Velocity Predictive Optimal Energy Management Strategies in Intelligent and Connected Hybrid Electric Vehicles. Energies, 14(18), 5713. https://doi.org/10.3390/en14185713






