Abstract
Battery storages are an essential element of the emerging smart grid. Compared to other distributed intelligent energy resources, batteries have the advantage of being able to rapidly react to events such as renewable generation fluctuations or grid disturbances. There is a lack of research on ways to profitably exploit this ability. Any solution needs to consider rapid electrical phenomena as well as the much slower dynamics of relevant electricity markets. Reinforcement learning is a branch of artificial intelligence that has shown promise in optimizing complex problems involving uncertainty. This article applies reinforcement learning to the problem of trading batteries. The problem involves two timescales, both of which are important for profitability. Firstly, trading the battery capacity must occur on the timescale of the chosen electricity markets. Secondly, the real-time operation of the battery must ensure that no financial penalties are incurred from failing to meet the technical specification. The trading-related decisions must be done under uncertainties, such as unknown future market prices and unpredictable power grid disturbances. In this article, a simulation model of a battery system is proposed as the environment to train a reinforcement learning agent to make such decisions. The system is demonstrated with an application of the battery to Finnish primary frequency reserve markets.
1. Introduction
Battery storages are an essential element of the emerging smart grid. Batteries are crucial for coping with increased photovoltaic [1] and wind penetration [2]. Schemes for introducing batteries are proposed at the level of buildings [3], wind farms [4] and the distribution grid [5]. Electric vehicle batteries can be used to temporarily store excess rooftop photovoltaic generation, which can be used to supply the load after photovoltaic generation has dropped [6]. Significant recent research has emerged on reinforcement learning (RL) applications for complex decision-making involving battery systems and energy markets. However, such works frequently ignore short-term electrical phenomena and employ RL frameworks with the simplifying assumption that renewable generation, power consumption and battery charging and discharging power remain constant throughout each market interval. Such assumptions are usually captured by a set of equations that specifies the environment of the RL agent. The environment is a system for interactive training of an RL agent: when the agent takes actions such as placing bids on a market, the environment gives feedback about the beneficial as well as the undesirable outcomes resulting from the action. If these simplifying assumptions could be eliminated, RL-powered battery systems could be a solution for managing short-term phenomena such as fluctuating renewable generation and power consumption, as well as sudden grid disturbances. To this end, this article presents an RL application working on two timescales: the timescale of the markets and the short-term timescale of electrical phenomena.
There are numerous applications for quickly reacting batteries. For example, batteries can support the extraction of maximum power generation from photovoltaic batteries with real-time maximum power point tracking control [7,8]. Battery applications for smoothing fluctuations of wind power generation require real-time control [9,10]. Without such smoothing applications, grid operations are required to take countermeasures to manage the resulting grid frequency variations [11]. One way to use batteries is to directly react to such frequency variations. Frequency reserves are energy resources that stand by to react to such frequency deviations by adjusting their production and consumption. Depending on the region, transmission system operators (TSO) or independent system operators (ISO) operate frequency reserve markets in which they procure frequency reserves and pay compensations for the provider of the reserve resource. Out of the various frequency reserve markets, primary frequency reserves (PFR) have the fastest response time requirements, which is reflected in the financial compensations paid to the reserve resource providers [12]. As batteries are easily capable of meeting such requirements, PFR participation allows batteries to contribute to coping with imbalances in the grid, regardless of whether such imbalances are caused by fluctuations in photovoltaic or wind generation, changes in electricity consumption or other disturbances [13].
PFR markets are generally auctions, in which the provider of the reserve resource has to specify the reserve capacity (adjustable MW of power production or consumption) for each market interval of the upcoming bidding period. A common market structure is that the bidding period is day-ahead and that the interval is one hour; this is also the case in the Finnish PFR market Frequency Containment Reserve for Normal Operation (FCR-N) [14], which will be the case study of this paper. Although revenues can be increased by bidding on as many intervals as possible, and with as much capacity as possible, the market will penalize participants that fail to provide the capacity specified in their bid. In the case of a battery storage, such failures will occur whenever the battery state of charge (SoC) reaches a minimum or maximum limit. As PFR requires the battery to react to frequency deviations on the order of seconds, it is an application operating on the two timescales identified above: the timescale of the markets and the short-term timescale of electrical phenomena. The contribution of this paper is an RL solution operating on these two timescales and using a simulation model to accurately capture the dynamics of the battery. The RL agent bids on the PFR market, and its training environment is a simulation model in which the battery reacts to grid frequency deviations with a one-second time step.
This paper is structured as follows: Section 2 reviews the state of the art. Section 3 presents a semiformal description of the solution. Section 4 describes the implementation of the simulation as well as the RL, with an application to the Northern European PFR market. Section 5 presents results of running the RL bidder on this market. Section 6 concludes the paper with an assessment of the obtained results and a discussion of further research directions.
2. Literature Review
There is a lack of research on using RL to trade batteries on PFR markets. However, there is a growing body of research on RL applications for batteries. There is also research on battery applications for frequency regulation.
2.1. Batteries in Primary Frequency Reserves
The increased reliance on renewable generation [15] and unreliabilities resulting from a rapid drive towards a smart grid [16] are increasing the demand for PFR, which has traditionally been provided by fossil fuel-based solutions [17]. There is a growing volume of research on solutions for providing PFR with distributed intelligent energy resources such as electric vehicles [18,19], domestic loads [20,21] and industrial processes [22]. The increased penetration of renewables is driving investments to battery-provided PFR [23]. However, since batteries can be exploited for a variety of grid support services, their penetration in PFR markets will depend on how prices on these markets develop [24]. Although batteries have been economically viable PFR assets for a long time [25], a growing body of research has emerged only in the last few years. The economic disadvantages caused by the battery degradation resulting from PFR participation are well understood and do not prevent economically profitable PFR participation [26,27]. Srinivasan et al. [28] propose the use of a virtual power plant to complement batteries with other intelligent distributed energy resources providing PFR.
2.2. Reinforcement Learning Applications for Batteries
In this section, RL applications for batteries are reviewed according to the timescale in which they operate. Three distinct timescales have been identified:
- •
- Real-time control.
- •
- Medium-term decision-making for optimizing some operational criteria such as electricity costs or photovoltaic self-consumption. In many cases, this involves decision-making once per electricity market interval, which in many cases is hourly.
- •
- Long-term studies to support investment decisions.
RL is broadly applied in real-time control, and research exists for a variety of battery applications. Maximizing photovoltaic generation requires a control algorithm such as mean power point tracking [29]. Real-time control with respect to driving speed is required for advanced battery management applications in electric vehicles [30] and plug-in hybrid electric vehicles (Chen et al. [31]). As a semi-real-time example, Sui and Song [32] used RL with a one-minute timestep to manage battery temperatures and thus battery lifetime in a battery pack.
Medium-term RL applications adjust the parameters of intelligent battery systems to optimize their operation. Muriithi and Chowdhury [33] optimized a battery and local photovoltaic to minimize electricity bills under variable electricity prices. Batteries have been used in conjunction with reschedulable loads to perform the rescheduling to exploit time-of-use and real-time energy pricing schemes [34,35,36] and variable intraday electricity market prices [37]. Whereas most works are aimed at existing electricity markets, a few authors have demonstrated the benefits of RL to optimize the emerging decentralized electricity system on novel markets [38,39]. The above works involved decision-making on electricity markets, which is the most common type of RL application in this category. However, other kinds of applications also exist. Mbuwir et al. [40] used a battery to maximize self-consumption of a local photovoltaic system. Finally, it is noted that for building HVAC systems, a thermal energy storage can be a competitor to a battery storage [41].
RL can be used at investment time to determine the parameters of a smart energy system that incorporates batteries. Diverse application contexts have been encountered, including wireless EV charging systems [42], wind farms [43], microgrids [44] and isolated villages with microgrids [45].
There is a lack of RL applications combining multiple timescales. In particular, the referenced works addressing the timescale of relevant markets ignore phenomena requiring real-time control actions, so there is a lack of research on how to financially exploit RL applications for batteries that try to solve the global problem of smoothing the fluctuations of renewable power generation. In this article, an RL agent is presented for trading on hourly PFR markets, so that the impact of power grid frequency fluctuations is considered on the timescale of seconds.
3. Battery Trading System
Figure 1 presents an overview of the proposed system. The bidding agent is implemented with a neural network, and it operates on the timescale of the market. The environment includes an offline implementation of the frequency market, based on market data, as well as a real-time battery simulation, which will detect if the battery goes out of bounds. The simulation has two modes: a PFR market participation mode and a resting mode, for hours with no PFR participation, during which the battery state of charge is driven to a value that is ideal with respect to upcoming PFR participation. Two items of state information are provided by the environment to the RL agent: battery state information and a market forecast. While battery state of charge information could be very useful for the RL, it would not be available at the timeframe when the bidding is done on the previous day. Thus, the only battery state information that is available is the information of when the battery last rested—this information can readily be extracted from the bidding plans. The PFR market forecast is also relevant, since it may be beneficial to concentrate bidding on high-price hours and resting on low-price hours. The day-ahead PFR forecasting method presented in [14] is used.
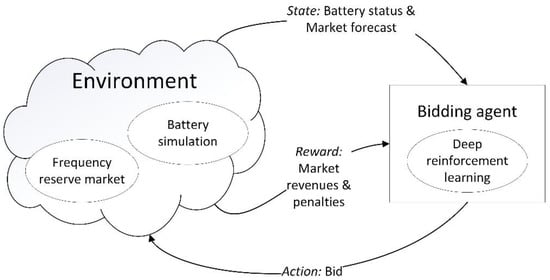
Figure 1.
System overview.
Several formulations of the reinforcement learning mechanism exist, and these have been applied in the battery energy management domain. The simplest is q-learning, which involves a table for mapping states and actions [46]. As our problem formulation involves a small state space, q-learning could have been used in this work. However, the use of q-learning would have introduced scalability problems in further work involving more complex state spaces. Reinforcement learning methods using a neural network instead of a q-table are a more scalable approach. Such methods are called deep reinforcement learning in case there is more than one hidden layer [30]. In our case, a neural network with one hidden layer was used, since experimentation with a second hidden layer did not result in improved performance. Advanced variations of deep reinforcement learning involve the use of several interdependent neural networks. This is a beneficial approach when the state space becomes significantly more complicated, as in the case of Zhang et al. [47], who consider a system with several resources in each of the following categories: batteries, wind and photovoltaic generation, water purification plants and diesel generators.
In order to support a problem formulation of the concept in Figure 1, Table 1 defines relevant symbols and Table 2 defines functions, which are used by the algorithm for training the reinforcement learning agent. Figure 2 formalizes the concept in Figure 1 using these symbols. Figure 3 presents the algorithm for training the reinforcement learning agent (‘bidding agent’) in the environment of Figure 2. The algorithm is based on established reinforcement learning techniques and integrates a real-time simulation of the battery on a primary frequency reserves market. A time range of days is selected for the training. One epoch is one iteration of the outer loop in Figure 3 and involves running the agent for each day in the training period. One state–action pair of the reinforcement learning agent is one hour, since that is the primary frequency reserves market interval. One state–action pair is taken by one iteration of the inner loop of the unshaded area in Figure 3 (i.e., the loop with the condition ‘h < 24’, which iterates through each hour of the day). The shaded area of Figure 3 involves calling the battery simulation with a one-second timestep. The purpose of this is to determine whether the battery state of charge goes out of bounds, which involves a penalty from the primary frequency reserves market, since the battery is not available to provide the primary frequency reserves in such a state.

Table 1.
Symbols.

Table 2.
Functions used in the procedure for training the reinforcement learning agent (Figure 3).
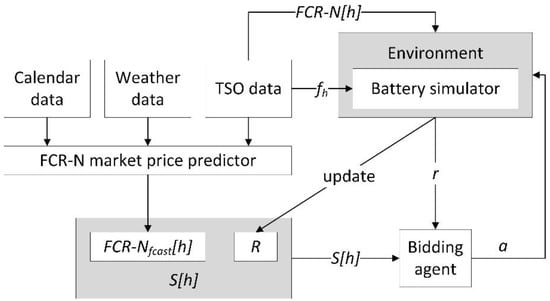
Figure 2.
Setup for training the bidding agent.
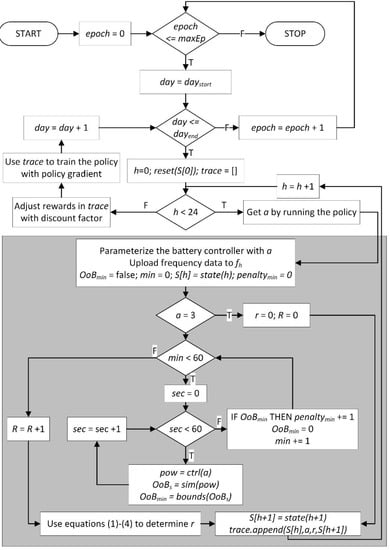
Figure 3.
Procedure for training the bidding agent using the environment in Figure 2. The shaded area is the step (a) function discussed in Section 4.1.
Finally, the environment needs to provide feedback to the RL agent in the form of a reward. The compensation from the PFR markets and the penalties for failing to provide the reserve are elements of the reward. For a particular hour, the compensation from the market is the product of the market price EUR/MW and the reserve capacity in MW. The FCR-N technical specification states that the compensation is only received for those minutes when the reserve was available [49]:
For each hour, the compensation is paid only for those minutes during which the system did not violate the penalty criteria. For this reason, Equations (1) and (2) include the fraction (60_penalty_min)/60 [49]:
The terms and conditions for providers of FCR state that if the reserve resource is unavailable too often, the frequency reserve market operator may, at its discretion, temporarily ban the reserve provider from participating in the market [50]. In order to include such considerations in the learning process of the reinforcement learning agent, a reputationdamage is defined. This differs from the penalty in Equation (2) in two respects. Firstly, it is not dependent on the FCR-N price for the hour in question [50]. Secondly, since the market operator does not provide any quantitative criteria for banning the reserve provider [50], a reputationfactor coefficient is defined, which can be adjusted by the reserve provider in order to make the tradeoff between increasing revenues versus bidding prudently to avoid penalties:
Therefore, the reward for the reinforcement learning agent is the formula for the net revenue with an additional element to further penalize the agent for failing to provide the reserve and thus damaging the reputation of the reserve provider:
4. Implementation
4.1. Enviroment
The battery model in Figure 4 is used to simulate the behavior of the battery’s SoC when it is charged or discharged as it participates on PFR. The battery model is a Simulink model and receives its inputs from the MATLAB function that implements the ctrl(a) function in Table 2. The implementation is done according to the rules of the Finnish PFR market FCR-N [48]. The same rules apply to PFR markets in Sweden, Norway and Denmark. In these countries, the nominal power grid frequency is 50 Hz with a maximum permitted deadband zone when the grid frequency is in the range 49.99–50.01 Hz. Equation (5) defines the discharging power when the frequency is in the range 49.9–49.99 Hz. A one-second simulation step is used, so fh[s] in Equation (5) is the power grid frequency for the current second, which corresponds to sec in Figure 3. When the frequency is under 49.9 Hz, the full power capacity of the bid, negative of capacity(a), is the discharge power.
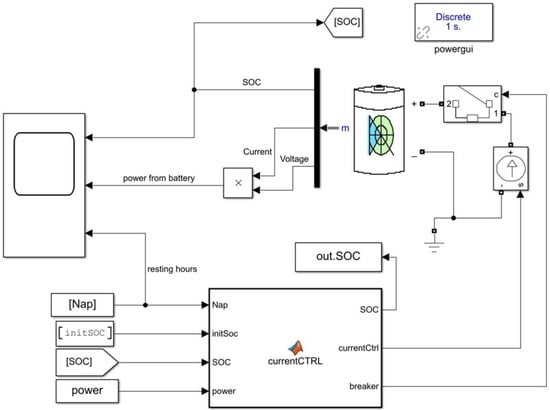
Figure 4.
Battery simulation model.
The case of frequency in the range 50.01–50.1 Hz is symmetric and is described by Equation (6).
ctrl(a) from Equations (5) and (6) is the ‘power’ input in Figure 4. Figure 5 shows how ‘power’ is computed from the frequency according to a software implementation of Equations (5) and (6). In this example, a = 0, so maximum capacity(a) is 1 MW. The slight differences between the red and blue curves are due to the deadband, e.g., according to Equation (5), ‘power’ is 0 when the frequency is 49.99 Hz. When frequency exceeds 50.1 Hz, Equation (6) no longer applies, and the ‘power’ remains at 1 MW.
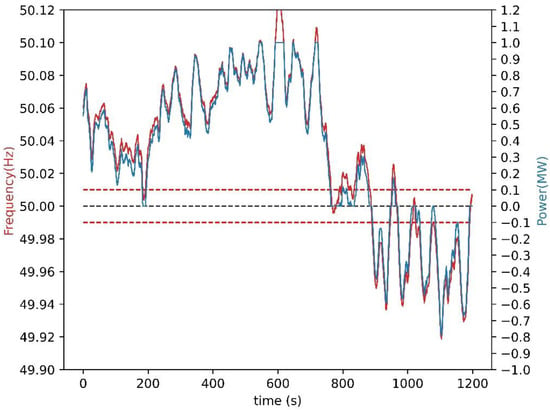
Figure 5.
Power as a function of frequency (Equations (5) and (6)) for the time period 4 September 2020 00:32:59–00:52:59. Red horizontal lines are the deadband limits. Black horizontal line is the nominal frequency and the battery idle state.
The battery in Figure 4 is an instance of the ‘Battery’ from Simulink’s Simscape library [51]. The charging and discharging losses of the battery simulation component are according to the equations for the lithium-ion battery type in [51]. The battery has been parameterized as specified in Table 3. The OoB limits for the function sim(pow) in Table 2 are defined as 5% and 95% SoC.

Table 3.
Parameters of the battery in Simulink.
The battery simulation model is an open-loop system, where the battery’s behavior is controlled with a controlled current source. The controlled current source receives its control signal from the ‘CurrentCTRL’ (see Figure 4) MATLAB function. Its main purpose is to convert the ‘power’ input to a current signal for the controlled current source. This is done by dividing the signal by the battery’s ‘nominal voltage’ (Table 3) when there is a bid for that hour. Otherwise, the battery rests, which is indicated by the ‘Nap’ input to ‘CurrentCTRL’. During rest hour, the battery will charge or discharge towards SOC 50% with constant current. The charging and discharging are configured so that the SoC has time to reach 50% by the end of the rest hour, regardless of the initial SoC. ‘CurrentCTRL’ also keeps track of the SoC during the simulation. The SoC vector is passed to the MATLAB function that implements the bounds(OoBs) function in Table 2.
The battery simulation model was wrapped in custom Python code that implements an interface similar to the environments in the OpenAI Gym collection [52], which has been used in several recent publications on RL applications in the energy domain [53,54,55,56,57,58]. This interface defines the functions reset(S[0]) and step(a). reset(S[0]) is called in Figure 3 at the beginning of each day and assigns a random value to the SoC, which ensures that the RL can continue to gain new experiences when the same day is used several times in the training phase. In our implementation, the SoC is assigned a random value from a continuous uniform distribution with bounds 35% and 65%. The shaded area in Figure 3 is the step(a) function, which receives the action from the RL agent and returns the reward and the next state.
4.2. Bidding Agent
The RL agent is implemented as a densely connected neural network. Its hyperparameters were determined experimentally and are presented in Table 4. The input layer has two nodes, since the state vector S[h] has two elements. The output layer has four nodes, one for each possible value of the action a. An epsilon greedy exploration strategy is used, so the probability of selecting a random action is initially 1 and is decreased by the epsilon decay factor at the end of each day in the algorithm of Figure 3. The algorithm in Figure 3 collects all 24 experiences gained over one day into an experience trace, which is used to train the neural network, and a discount of 0.5 is applied to the trace.

Table 4.
Hyperparameters of the neural network.
Further work is possible for the optimization of hyperparameters. Automated machine learning methods for neural architecture search can identify the optimal set of layers for a deep neural network. Once the architecture has been fixed, automatic hyperparameter tuning methods can optimize the remaining hyperparameters. However, these techniques are in general not directly applicable to reinforcement learning [59]. Recent applications to deep reinforcement learning are a promising approach for improving our neural network architecture and hyperparameters [60].
The time range of 1 September 2020–31 October 2020 was used for training and validation. A value of 110 was used for reputationfactor. Out of these 61 days, 11 randomly selected days were used for validation and the rest were used for training. A random seed was defined to ensure the repeatability of the results. Figure 6 shows some insights into the training process after 2, 4, 6, 8 and 10 epochs.
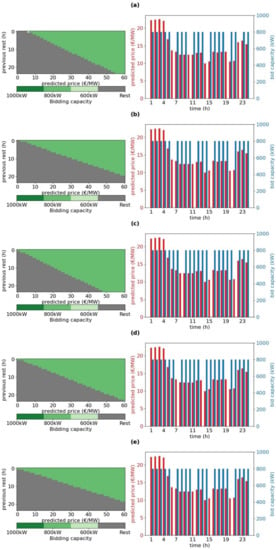
Figure 6.
The actions taken by the trained reinforcement learning agent (left) and the resulting bidding behavior on 4 September 2020 (right) after epochs 2 (a), 4 (b), 6 (c), 8 (d) and 10 (e).
On the left of Figure 6, the actions selected by the trained RL agent are shown for each state (the state is defined by the combination of R on the vertical axis and FCR-Nfcast on the horizontal axis). Analyzing Equations (2)–(4), it can be seen that the positive component of the reward is directly proportional to the price of the FCR-N market, which is approximated by FCR-Nfcast. However, the negative component of the reward is only partially proportional to the price. Thus, at higher prices, the benefits should outweigh the penalties, so it is expected that the agent will learn to prefer resting during low-price hours. Accordingly, in Figure 6, it is observed that resting actions concentrate on the left of the price forecast axis. With respect to the vertical axis, it is expected that the likelihood of penalties increases when the battery has operated for several hours without resting, so it is expected that the agent will learn to prefer resting on the lower part of the vertical axis. The combined effect of these two learning outcomes is that the best states for resting are in the bottom-left corner and the best states for bidding are in the top-right corner. By observing the progression of the left-hand charts in Figure 6, it is evident that the agent has learned this behavior.
On the right of Figure 6, the bidding actions taken by the agent are shown for one of the validation days, 4 September 2020. After epoch 2 (Figure 6a), the chart on the left shows that the agent has learned to use three actions: rest, bid 600 kW and bid 800 kW. Only the rest and 800 kW actions are used in the chart on the left (the blue bars show the bid size with 0 meaning rest). The red prices are the forecasted market price. As training progresses over subsequent epochs 4, 6, 8 and 10 (Figure 6b-e), the agent learns to use only two actions: resting and 800 kW bid. The agent also learns to schedule the rest actions for hours with low price. The figure does not show penalties and rewards, which are discussed next in Section 5. The purpose of the discussion in this section was to give insights into the RL training process and the behavior learned by the RL agent.
5. Result
Figure 7 shows the cumulative reward for all of the days in the training set, and Figure 8 shows the cumulative reward for the days in the validation set. The results for the training and validation sets start to stabilize after 20 epochs, so training was stopped after 35 epochs.
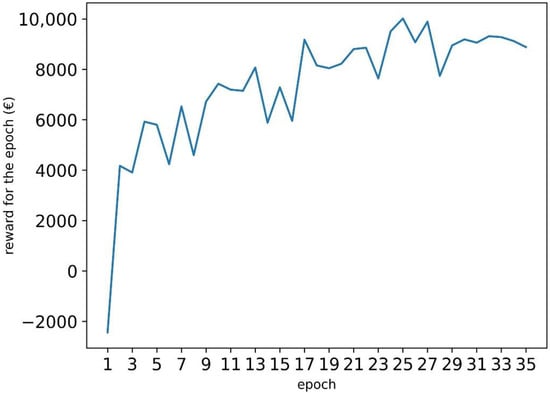
Figure 7.
The cumulative reward for all of the training days.
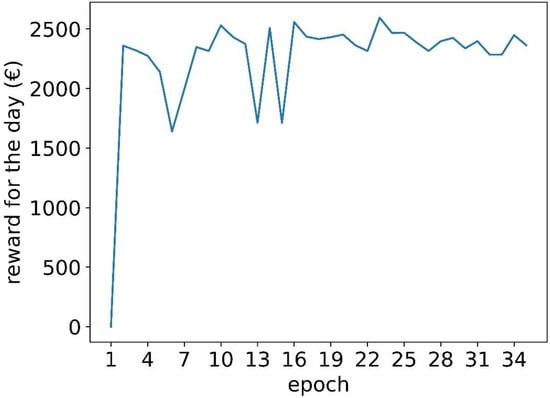
Figure 8.
The cumulative reward for all the validation days.
Figure 9 shows the cumulative reward for one of the validation days, 4 September 2020. This is the sum of the rewards for each hour of the day. At nine epochs, there is a relatively low reward. This epoch is analyzed further in Figure 10. The chart in Figure 10a is similar to the charts on the right in Figure 6. The chart in Figure 10b is the reward and the actual market price. The chart in Figure 10c is the penalties. It is observed that due to only three resting hours for the entire day, the battery fails to provide the reserve capacity and incurs significant penalties on hour 17, which explains the low reward for epoch 9 in Figure 9. Figure 11 shows a similar chart after 35 epochs of training. The chart in Figure 11a shows that the agent has learned to rest more frequently, and generally, the rest occurs when there is a low price forecast. Although the increased resting reduces the market revenues (Figure 11b), there are no penalties (Figure 11c). Thus, the agent at 35 epochs plays safer than the agent at 10 epochs, resulting in a fairly good reward at 35 epochs, although the reward is not as high as in some of the earlier epochs, when the agent was resting less and thus making riskier bids. The risks are due to the unpredictable need to charge or discharge the battery when participating in PFR. The need depends on the occurrence of grid frequency deviations. There is a lack of research for predicting such deviations day-ahead (which is when the PFR bids must be placed), so our agent does not have information to learn the likelihood of charging or discharging needs for any particular hour. However, the results show that based on the available market forecasts, the agent learns to bid intelligently under uncertainty, balancing revenues and risk of penalties.
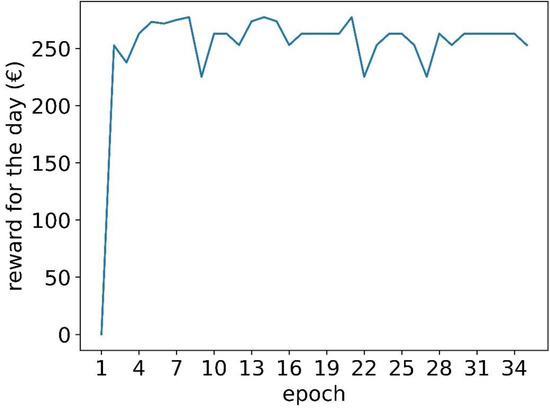
Figure 9.
The cumulative reward for all of the hours for one of the validation days (4 September 2020).
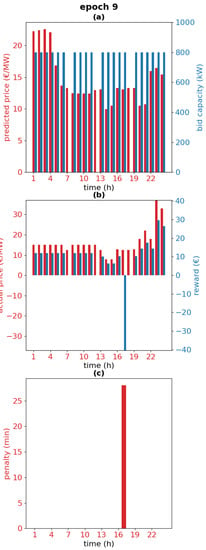
Figure 10.
Bids and predicted price (a), reward and actual market price (b) and penalties (c) for the validation day 4 September 2020 at 9 epochs.
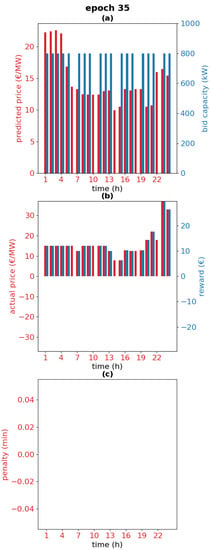
Figure 11.
Bids and predicted price (a), reward and actual market price (b) and penalties (c) for the validation day 4 September 2020 at 35 epochs.
The results shown in this paper have been obtained by using a value of 110 for the reputationfactor. Figure 12 shows how the results would change if the value of reputationfactor is varied. The experiment described in this paper was repeated for the following values: 10, 30, 50, 70, 90, 110, 130, 150, 170 and 190. Each repetition of the experiment resulted in one dot in the figure, labeled with the value of reputationfactor. According to Equations (3) and (4), a higher value of reputationfactor will result in a large negative component in the reward whenever the battery is unavailable. The duration of this unavailability is penaltymin on the x-axis. The compensation on the y-axis is according to Equation (1). As reputationfactor is increased, it is expected that the RL agent learns to be more careful in avoiding penalties, either by resting more or by bidding a lower capacity, thus reducing the likelihood of the battery being unavailable. The result of this should be decreasing compensation and decreasing penalties as reputationfactor increases. This trend is visible in Figure 12. The dots for 10, 30 and 50 are very close to each other and overlap in the figure. This is because the compensation outweighs the penalties, so the agent learns to ignore the penalties and only tries to maximize the compensation. At a value of 70, the penalties are drastically reduced, without a loss of compensation. In fact, the compensation is slightly higher, which can be understood from Equation (1): there is no compensation for the minutes during which the battery is unavailable. As reputationfactor is increased to 90 and beyond, the trend that was mentioned above is observed: the agent bids more carefully, resulting in a slight decrease in compensation as well as in the penalties. Looking at the relative vertical positions of the dots, 130 is an outlier in this trend. Further, 110 and 150 do not fully fit into the trend. The validation set is 11 days, so a longer set would be expected to result in a clearer trend. From the results, it is concluded that it is advantageous to use a reputationfactor of at least 70. The use of a higher value is a business decision, depending on whether a decrease in compensation is considered desirable in order to decrease the penalties. As has been explained in the context of Equation (3), the potential business impact of incurring excessive penalties is very severe, but the market operator does not publish any quantitative criteria for what it considers to be excessive penalties, so for that reason, the choice of value for reputationfactor is left as a business decision.
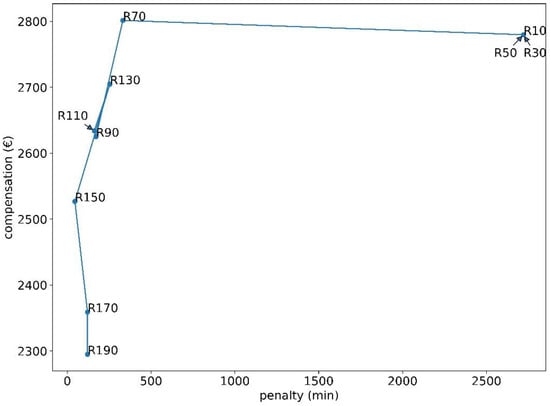
Figure 12.
Compensation versus penaltymin. The dots show the result of running the experiment with different values of reputationfactor. Each dot is labeled with the corresponding value of reputationfactor.
6. Conclusions
In the literature review, a research gap was identified for RL-based energy management solutions that take into account market participation and cope with real-time requirements for the energy resources that participate in the markets. In this paper, PFR was selected as an application in which revenues depend on battery capacity that is bid on hourly markets, as well as penalties that occur on the timeframe of seconds if the battery is unavailable due to its SoC being OoB. The problem formulation addressed the realities of an online deployment, in which bids on the PFR market must be done on the day before, when it is not possible to accurately predict the SoC, as the requirement to discharge and charge the battery on a PFR market is dependent on power grid frequency deviations, which cannot be accurately predicted day-ahead. Thus, the state information for the RL was limited to information that is available at bidding time. It was observed that the agent learned behavior that took into account the benefits of bidding on high-price hours and the increased risk of penalties of participating in PFR markets for several hours without allowing the battery to rest.
A novel methodology integrating a real-time battery simulation with a reinforcement learning agent bidding on hourly markets was proposed in this article. The main finding is that this approach promises to achieve the dual goal of maximizing market revenues while minimizing penalties caused by short-term failures to provide the frequency reserve. In further work, the reliability of the methodology can be improved by addressing the following limitations: Firstly, a 2-month dataset was used, so market and grid frequency data for a longer time-period can be collected and preprocessed. Secondly, the state space can be broadened with any variables that may have an impact on the power grid frequency. Although it is not possible to accurately predict the grid frequency in a day-ahead bidding scenario, some feature engineering based on historical frequency data is an avenue of further research. Finally, automated machine learning methods that have recently emerged for reinforcement learning applications can be used to search for the optimal neural network architecture and hyperparameters.
For further work, batteries for supporting photovoltaic installations in residential and commercial buildings are an application area that would benefit from optimization on the two timescales that have been considered in this paper. Maximum power point tracking (MPPT) algorithms have been proposed to control the battery and thus create an ideal load for photovoltaic generation. However, such batteries have other uses related to shifting power consumption from the grid and possible photovoltaic power sales to the grid, taking into account variable electricity prices. The MPPT and variable electricity price exploitation are two optimization tasks that occur on two different timescales but cannot be addressed separately, since they both affect the SoC of the same battery.
Author Contributions
Conceptualization, H.A. and S.S.; methodology, H.A. and S.S.; software, H.A. and R.S.; validation, H.A., R.S., S.S. and V.V.; investigation, H.A., R.S. and S.S.; resources, H.A., R.S., S.S. and V.V.; data curation, H.A.; writing—original draft preparation, H.A. and S.S.; visualization, H.A. and R.S.; supervision, S.S. and V.V.; project administration, S.S. and V.V.; funding acquisition, S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Business Finland grant 7439/31/2018.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors thank Kalle Rantala for technical support with high-performance computing infrastructure.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Peters, I.M.; Breyer, C.; Jaffer, S.A.; Kurtz, S.; Reindl, T.; Sinton, R.; Vetter, M. The role of batteries in meeting the PV terawatt challenge. Joule 2021, 5, 1353–1370. [Google Scholar] [CrossRef]
- de Siqueira Silva, L.M.; Peng, W. Control strategy to smooth wind power output using battery energy storage system: A review. J. Energy Storage 2021, 35, 102252. [Google Scholar] [CrossRef]
- Sepúlveda-Mora, S.B.; Hegedus, S. Making the case for time-of-use electric rates to boost the value of battery storage in commercial buildings with grid connected PV systems. Energy 2021, 218, 119447. [Google Scholar] [CrossRef]
- Loukatou, A.; Johnson, P.; Howell, S.; Duck, P. Optimal valuation of wind energy projects co-located with battery storage. Appl. Energy 2021, 283, 116247. [Google Scholar] [CrossRef]
- Akagi, S.; Yoshizawa, S.; Ito, M.; Fujimoto, Y.; Miyazaki, T.; Hayashi, Y.; Tawa, K.; Hisada, T.; Yano, T. Multipurpose control and planning method for battery energy storage systems in distribution network with photovoltaic plant. Int. J. Electr. Power Energy Syst. 2020, 116, 105485. [Google Scholar] [CrossRef]
- Nefedov, E.; Sierla, S.; Vyatkin, V. Internet of energy approach for sustainable use of electric vehicles as energy storage of prosumer buildings. Energies 2018, 11, 2165. [Google Scholar] [CrossRef] [Green Version]
- Ge, X.; Ahmed, F.W.; Rezvani, A.; Aljojo, N.; Samad, S.; Foong, L.K. Implementation of a novel hybrid BAT-Fuzzy controller based MPPT for grid-connected PV-battery system. Control. Eng. Pract. 2020, 98, 104380. [Google Scholar] [CrossRef]
- Aldosary, A.; Ali, Z.M.; Alhaider, M.M.; Ghahremani, M.; Dadfar, S.; Suzuki, K. A modified shuffled frog algorithm to improve MPPT controller in PV System with storage batteries under variable atmospheric conditions. Control. Eng. Pract. 2021, 112, 104831. [Google Scholar] [CrossRef]
- Ciupageanu, D.; Barelli, L.; Lazaroiu, G. Real-time stochastic power management strategies in hybrid renewable energy systems: A review of key applications and perspectives. Electr. Power Syst. Res. 2020, 187, 106497. [Google Scholar] [CrossRef]
- Lin, L.; Jia, Y.; Ma, M.; Jin, X.; Zhu, L.; Luo, H. Long-term stable operation control method of dual-battery energy storage system for smoothing wind power fluctuations. Int. J. Electr. Power Energy Syst. 2021, 129, 106878. [Google Scholar] [CrossRef]
- Ryu, A.; Ishii, H.; Hayashi, Y. Battery smoothing control for photovoltaic system using short-term forecast with total sky images. Electr. Power Syst. Res. 2021, 190, 106645. [Google Scholar] [CrossRef]
- Subramanya, R.; Yli-Ojanperä, M.; Sierla, S.; Hölttä, T.; Valtakari, J.; Vyatkin, V. A virtual power plant solution for aggregating photovoltaic systems and other distributed energy resources for northern european primary frequency reserves. Energies 2021, 14, 1242. [Google Scholar] [CrossRef]
- Koller, M.; Borsche, T.; Ulbig, A.; Andersson, G. Review of grid applications with the Zurich 1MW battery energy storage system. Electr. Power Syst. Res. 2015, 120, 128–135. [Google Scholar] [CrossRef]
- Giovanelli, C.; Sierla, S.; Ichise, R.; Vyatkin, V. Exploiting artificial neural networks for the prediction of ancillary energy market prices. Energies 2018, 11, 1906. [Google Scholar] [CrossRef] [Green Version]
- Lund, H.; Hvelplund, F.; Østergaard, P.A.; Möller, B.; Mathiesen, B.V.; Karnøe, P.; Andersen, A.N.; Morthorst, P.E.; Karlsson, K.; Münster, M.; et al. System and market integration of wind power in Denmark. Energy Strategy Rev. 2013, 1, 143–156. [Google Scholar] [CrossRef] [Green Version]
- Bialek, J. What does the GB power outage on 9 August 2019 tell us about the current state of decarbonised power systems? Energy Policy 2020, 146, 111821. [Google Scholar] [CrossRef]
- Papadogiannis, K.A.; Hatziargyriou, N.D. Optimal allocation of primary reserve services in energy markets. IEEE Trans. Power Syst. 2004, 19, 652–659. [Google Scholar] [CrossRef]
- Pavić, I.; Capuder, T.; Kuzle, I. Low carbon technologies as providers of operational flexibility in future power systems. Appl. Energy 2016, 168, 724–738. [Google Scholar] [CrossRef]
- Zecchino, A.; Prostejovsky, A.M.; Ziras, C.; Marinelli, M. Large-scale provision of frequency control via V2G: The Bornholm power system case. Electr. Power Syst. Res. 2019, 170, 25–34. [Google Scholar] [CrossRef]
- Malik, A.; Ravishankar, J. A hybrid control approach for regulating frequency through demand response. Appl. Energy 2018, 210, 1347–1362. [Google Scholar] [CrossRef]
- Borsche, T.S.; de Santiago, J.; Andersson, G. Stochastic control of cooling appliances under disturbances for primary frequency reserves. Sustain. Energy Grids Netw. 2016, 7, 70–79. [Google Scholar] [CrossRef]
- Herre, L.; Tomasini, F.; Paridari, K.; Söder, L.; Nordström, L. Simplified model of integrated paper mill for optimal bidding in energy and reserve markets. Appl. Energy 2020, 279, 115857. [Google Scholar] [CrossRef]
- Ramírez, M.; Castellanos, R.; Calderón, G.; Malik, O. Placement and sizing of battery energy storage for primary frequency control in an isolated section of the Mexican power system. Electr. Power Syst. Res. 2018, 160, 142–150. [Google Scholar] [CrossRef]
- Killer, M.; Farrokhseresht, M.; Paterakis, N.G. Implementation of large-scale li-ion battery energy storage systems within the EMEA region. Appl. Energy 2020, 260, 114166. [Google Scholar] [CrossRef]
- Oudalov, A.; Chartouni, D.; Ohler, C. Optimizing a battery energy storage system for primary frequency control. IEEE Trans. Power Syst. 2007, 22, 1259–1266. [Google Scholar] [CrossRef]
- Andrenacci, N.; Pede, G.; Chiodo, E.; Lauria, D.; Mottola, F. Tools for life cycle estimation of energy storage system for primary frequency reserve. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 20–22 June 2018; pp. 1008–1013. [Google Scholar] [CrossRef]
- Karbouj, H.; Rather, Z.H.; Flynn, D.; Qazi, H.W. Non-synchronous fast frequency reserves in renewable energy integrated power systems: A critical review. Int. J. Electr. Power Energy Syst. 2019, 106, 488–501. [Google Scholar] [CrossRef]
- Srinivasan, L.; Markovic, U.; Vayá, M.G.; Hug, G. Provision of frequency control by a BESS in combination with flexible units. In Proceedings of the 5th IEEE International Energy Conference (ENERGYCON), Limassol, Cyprus, 3–7 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Phan, B.C.; Lai, Y. Control strategy of a hybrid renewable energy system based on reinforcement learning approach for an isolated microgrid. Appl. Sci. 2019, 9, 4001. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Cui, H.; Nemeth, T.; Jansen, J.; Ünlübayir, C.; Wei, Z.; Zhang, L.; Wang, Z.; Ruan, J.; Dai, H.; et al. Deep reinforcement learning-based energy management of hybrid battery systems in electric vehicles. J. Energy Storage 2021, 36, 102355. [Google Scholar] [CrossRef]
- Chen, Z.; Hu, H.; Wu, Y.; Xiao, R.; Shen, J.; Liu, Y. Energy management for a power-split plug-in hybrid electric vehicle based on reinforcement learning. Appl. Sci. 2018, 8, 2494. [Google Scholar] [CrossRef] [Green Version]
- Sui, Y.; Song, S. A multi-agent reinforcement learning framework for lithium-ion battery scheduling problems. Energies 2020, 13, 1982. [Google Scholar] [CrossRef] [Green Version]
- Muriithi, G.; Chowdhury, S. Optimal energy management of a grid-tied solar pv-battery microgrid: A reinforcement learning approach. Energies 2021, 14, 2700. [Google Scholar] [CrossRef]
- Kim, S.; Lim, H. Reinforcement learning based energy management algorithm for smart energy buildings. Energies 2018, 11, 2010. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Choi, D. Reinforcement learning-based energy management of smart home with rooftop solar photovoltaic system, energy storage system, and home appliances. Sensors 2019, 19, 3937. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Choi, D. Energy management of smart home with home appliances, energy storage system and electric vehicle: A hierarchical deep reinforcement learning approach. Sensors 2020, 20, 2157. [Google Scholar] [CrossRef] [Green Version]
- Roesch, M.; Linder, C.; Zimmermann, R.; Rudolf, A.; Hohmann, A.; Reinhart, G. Smart grid for industry using multi-agent reinforcement learning. Appl. Sci. 2020, 10, 6900. [Google Scholar] [CrossRef]
- Kim, J.; Lee, B. Automatic P2P Energy trading model based on reinforcement learning using long short-term delayed reward. Energies 2020, 13, 5359. [Google Scholar] [CrossRef]
- Wang, N.; Xu, W.; Shao, W.; Xu, Z. A q-cube framework of reinforcement learning algorithm for continuous double auction among microgrids. Energies 2019, 12, 2891. [Google Scholar] [CrossRef] [Green Version]
- Mbuwir, B.V.; Ruelens, F.; Spiessens, F.; Deconinck, G. Battery energy management in a microgrid using batch reinforcement learning. Energies 2017, 10, 1846. [Google Scholar] [CrossRef] [Green Version]
- Zsembinszki, G.; Fernández, C.; Vérez, D.; Cabeza, L.F. Deep Learning optimal control for a complex hybrid energy storage system. Buildings 2021, 11, 194. [Google Scholar] [CrossRef]
- Lee, H.; Ji, D.; Cho, D. Optimal design of wireless charging electric bus system based on reinforcement learning. Energies 2019, 12, 1229. [Google Scholar] [CrossRef] [Green Version]
- Oh, E. Reinforcement-learning-based virtual energy storage system operation strategy for wind power forecast uncertainty management. Appl. Sci. 2020, 10, 6420. [Google Scholar] [CrossRef]
- Tsianikas, S.; Yousefi, N.; Zhou, J.; Rodgers, M.D.; Coit, D. A storage expansion planning framework using reinforcement learning and simulation-based optimization. Appl. Energy 2021, 290, 116778. [Google Scholar] [CrossRef]
- Sidorov, D.; Panasetsky, D.; Tomin, N.; Karamov, D.; Zhukov, A.; Muftahov, I.; Dreglea, A.; Liu, F.; Li, Y. Toward zero-emission hybrid AC/DC power systems with renewable energy sources and storages: A case study from Lake Baikal region. Energies 2020, 13, 1226. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Shi, J.; Li, S.; Li, H.; Wang, Z. Energy consumption and battery aging minimization using a q-learning strategy for a battery/ultracapacitor electric vehicle. Energy 2021, 229, 120705. [Google Scholar] [CrossRef]
- Zhang, G.; Hu, W.; Cao, D.; Liu, W.; Huang, R.; Huang, Q.; Chen, Z.; Blaabjerg, F. Data-driven optimal energy management for a wind-solar-diesel-battery-reverse osmosis hybrid energy system using a deep reinforcement learning approach. Energy Convers. Manag. 2021, 227, 113608. [Google Scholar] [CrossRef]
- Fingrid. The Technical Requirements and the Prequalification Process of Frequency Containment Reserves (FCR). Available online: https://www.fingrid.fi/globalassets/dokumentit/en/electricity-market/reserves/appendix3---technical-requirements-and-prequalification-process-of-fcr.pdf (accessed on 6 July 2021).
- Fingrid. Fingridin reservikaupankäynti ja tiedonvaihto -ohje. Available online: https://www.fingrid.fi/globalassets/dokumentit/fi/sahkomarkkinat/reservit/fingridin-reservikaupankaynti-ja-tiedonvaihto--ohje.pdf (accessed on 6 July 2021).
- Fingrid. Ehdot ja edellytykset taajuudenvakautusreservin (FCR) toimittajalle. Available online: https://www.fingrid.fi/globalassets/dokumentit/fi/sahkomarkkinat/reservit/fcr-liite1---ehdot-ja-edellytykset.pdf (accessed on 6 July 2021).
- MathWorks. Battery—Generic Battery Model. Available online: https://se.mathworks.com/help/physmod/sps/powersys/ref/battery.html (accessed on 6 July 2021).
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. Openai gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
- Avila, L.; De Paula, M.; Trimboli, M.; Carlucho, I. Deep reinforcement learning approach for MPPT control of partially shaded PV systems in Smart Grids. Appl. Soft Comput. 2020, 97, 106711. [Google Scholar] [CrossRef]
- Zhang, Z.; Chong, A.; Pan, Y.; Zhang, C.; Lam, K.P. Whole building energy model for HVAC optimal control: A practical framework based on deep reinforcement learning. Energy Build. 2019, 199, 472–490. [Google Scholar] [CrossRef]
- Azuatalam, D.; Lee, W.; de Nijs, F.; Liebman, A. Reinforcement learning for whole-building HVAC control and demand response. Energy AI 2020, 2, 100020. [Google Scholar] [CrossRef]
- Brandi, S.; Piscitelli, M.S.; Martellacci, M.; Capozzoli, A. Deep reinforcement learning to optimise indoor temperature control and heating energy consumption in buildings. Energy Build. 2020, 224, 110225. [Google Scholar] [CrossRef]
- Nakabi, T.A.; Toivanen, P. Deep reinforcement learning for energy management in a microgrid with flexible demand. Sustain. Energy Grids Netw. 2021, 25, 100413. [Google Scholar] [CrossRef]
- Schreiber, T.; Eschweiler, S.; Baranski, M.; Müller, D. Application of two promising reinforcement learning algorithms for load shifting in a cooling supply system. Energy Build. 2020, 229, 110490. [Google Scholar] [CrossRef]
- He, X.; Zhao, K.; Chu, X. AutoML: A survey of the state-of-the-art. Knowl. Based Syst. 2021, 212, 106622. [Google Scholar] [CrossRef]
- Franke, J.K.; Köhler, G.; Biedenkapp, A.; Hutter, F. Sample-efficient automated deep reinforcement learning. arXiv 2020, arXiv:2009.01555. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).