Abstract
Heat transport guided by the combined dynamics of surface phonon-polaritons (SPhPs) and phonons propagating in a polar nanowire is theoretically modeled and analyzed. This is achieved by solving numerically and analytically the Boltzmann transport equation for SPhPs and the Fourier’s heat diffusion equation for phonons. An explicit expression for the SPhP thermal conductance is derived and its predictions are found to be in excellent agreement with its numerical counterparts obtained for a SiN nanowire at different lengths and temperatures. It is shown that the SPhP heat transport is characterized by two fingerprints: (i) The characteristic quantum of SPhP thermal conductance independent of the material properties. This quantization appears in SiN nanowires shorter than 1 m supporting the ballistic propagation of SPhPs. (ii) The deviation of the temperature profile from its typical linear behavior predicted by the Fourier’s law in absence of heat sources. For a 150 m-long SiN nanowire maintaining a quasi-ballistic SPhP propagation, this deviation can be as large as 1 K, which is measurable by the current state-of-the-art infrared thermometers.
1. Introduction
One-dimensional (1D) heat conduction at low temperatures has been extensively investigated due to the existence of a quantum of thermal conductance. This quantization is related to the heat flux carried by ballistic phonons or electrons in a single polarization and is given by , where and h are the respective Boltzmann and Planck constants, and T is the temperature [,,,,]. This minimal and universal amount of heat, for a given T, holds for both electrons and phonons, as was theoretically predicted [,] and experimentally validated [,]. Given that the mean free paths of electrons and phonons are typically smaller than 1 m at room temperature, with lower temperatures leading to longer mean free paths, the observation of this quantization in the ballistic regime typically requires the utilization of nanostructures at temperatures lower than 1 K [,].
The limitations of phonons and electrons to exhibit 1D ballistic heat conduction at temperatures comparable to room temperature, can be overcome with surface phonon-polaritons (SPhPs), which are evanescent electromagnetic waves generated by the hybridization of photons and phonons at the interface of polar materials [,,,,,,,,]. This ballistic behavior appears due to the huge SPhP propagation length that was found to be as long as 1 m [,,,] and is hence orders of magnitude longer than the typical mean free paths of electrons and phonons. The spectral values of this propagation length is mainly determined by the material permittivity, which is nearly independent of temperature, within a wide range of temperatures lower and higher than room temperature []. Therefore, the ballistic heat transport of SPhPs is not necessarily restricted to low temperatures, as is the case of electrons and phonons. On the other hand, the wavelength of SPhPs propagating along nanowires can be much longer than the nanowire diameter [] and hence these energy carriers can be considered as a 1D quantum gas. As a result of these relatively long values of the propagation length and wavelength of SPhPs, their contribution to the axial heat transport was predicted to be comparable to or even higher than that of phonons. In fact, in the pure ballistic regime, the quantum of thermal conductance due to phonons and electrons in a nanowire at cryogenic temperature also holds for the SPhPs at room temperature []. Even though the phonon, electron, and SPhP quantum of thermal conductance of nanowires were already quantified separately, the heat transport driven by the simultaneous propagation of phonons and SPhPs along a polar dielectric nanowire has been not explored yet.
The purpose of this work is to theoretically study the temperature and heat flux profiles generated by the coupling of SPhPs and phonons along the surface of a polar nanowire at a temperature comparable to or lower than room temperature. This is achieved by solving, numerically and analytically, the Boltzmann transport Equation (BTE) and combining its prediction for the SPhP heat flux with the principle of energy conservation. An explicit expression for the SPhP thermal conductance valid for both the ballistic and diffusive regimes is derived and analyzed. The critical nanowire length at which the quantization of the thermal conductance appears is thus determined.
2. Theoretical Models
Let us consider a polar nanowire supporting the simultaneous propagation of SPhPs and phonons due to the temperature difference set by two thermal baths, as shown in Figure 1. The resulting steady-state heat transport along the z axis is thus driven by the heat fluxes generated by these two types of energy carriers.
Figure 1.
Scheme of a polar nanowire supporting the propagation of both SPhPs and phonons due to the temperature difference imposed by two thermal baths.
Considering that the phonon heat conduction can be described by an effective thermal conductivity [], the principle of energy conservation along with the Fourier’s law establishes that the temperature T inside the nanowire is given by
where q is the SPhP heat flux and is the total heat flux, a constant independent of position z (i.e., ), which yields the following heat diffusion equation:
with being an effective heat source term that stands for the coupling between SPhPs and phonons. Physically, represents the heat source (sink) due to the thermal absorption (emission) of SPhPs at the nanowire surface. Taking into account that SPhPs can be treated like bosonic particles [,], q can be determined by means of the BTE under the relaxation time approximation in the intensity representation [,]. The validity of BTE for describing the energy transport by SPhPs still remains under debate as its predictions showed mixed results with respect to the fluctuational electrodynamic theory [,]. In thin films, the predictions of the BTE for the SPhP thermal conductivity showed a good agreement with the corresponding ones of this theory [] and, therefore, in this work, we assume its validity for describing the propagation of SPhPs along a nanowire. For the steady-state heat transport along the z axis shown in Figure 1, the BTE for the 1D SPhP gas takes the two-component form:
where the SPhP intensity and its equilibrium counterpart are defined by and , respectively, the superscript “” stands for the SPhP propagation along () direction, while the SPhP distribution function, group speed and propagation length are respectively denoted by f, V and , with , , and being the Planck constant, Bose–Einstein equilibrium distribution function and SPhP density of states per unit frequency interval per unit length, respectively. The group speed and propagation length are determined by the dispersion relation of SPhP and generally depends on frequency, as shown below. Since SPhPs propagate along the surface of the nanowire and span over its surface, their 1D density of states is given by []: . After solving Equation (3a,b) for the intensity distribution , the SPhP heat flux can be determined by
where a is the radius of the nanowire. According to Figure 1, Equations (1)–(3) are going to be solved either numerically or analytically under the following boundary conditions:
2.1. Numerical Approach
To numerically solve Equations (1)–(4), which are coupled, for the heat transport driven by SPhPs and phonons in a polar nanowire, the discrete-ordinate method (DOM) (see, for instance, [,]) and the finite difference method (FDM) are adopted for the SPhP BTE and the heat diffusion equation, respectively. This FDM scheme is exactly the same as that in our previous work []. The DOM scheme for the 1D SPhP BTE will be introduced here. Under this approach, the numerical integration for the SPhP heat flux in Equation (4) can be written as follows
where the rectangular scheme is adopted with a uniform frequency interval and the index of discrete frequency points . The spectral discretization of the SPhP BTE in Equation (3) then takes the form
The step scheme is adopted for the spatial discretization of the SPhP BTE to ensure both efficiency and accuracy. For the positive () propagation, the forward difference scheme is applied to Equation (7a):
where denotes the index of spatial nodes, with the spatial step . For the negative () propagation, on the other hand, the backward difference scheme is applied to Equation (7b):
The evolution equations of the discrete SPhP intensity can then be obtained from Equations (8) and (9), as follows
where is introduced for short notation. The positive component in Equation (10a) is updated from the left-hand hot () boundary, whereas the negative component in Equation (10b) is updated from the right-hand cold () boundary.
Once the discrete SPhP intensity distribution is resolved, the SPhP heat flux distribution is computed based on Equation (6). The temperature distribution is then calculated through a numerical solution of the heat diffusion Equation (2) by the FDM scheme. The equilibrium SPhP intensity is thus updated and the SPhP BTE is solved again. The solution of the coupled model is obtained through an iterative procedure until the solutions of the SPhP BTE and the heat diffusion equation are consistent with each other. More details of the solution procedure can be found in our previous work [].
2.2. Analytical Approach
The analytical solutions of the BTE in Equation (3a,b) for the intensities and of the SPhPs leaving the surfaces and are given by
where , . In writing Equation (11a,b), we have used the boundary conditions in Equation (5): and established by the thermal equilibrium of the external surfaces and set at the temperatures and , respectively. After inserting Equation (11a,b) into Equation (4), one obtains
For simplicity, Equation (12) can be rewritten in terms of the normalized equilibrium intensity , as follows
which indicates that the SPhP heat flux q results from the intensity difference driven by the temperature difference , as expected. Considering that the nanowire undergoes small temperature gradients (), the temperature dependence of the equilibrium intensity can be linearized. In addition, given that the temperature profile exhibits a nearly linear dependence on position, as shown below, the first-order approximation of the equilibrium intensity can be written as , with and being two parameters independent of position. Under this approximation, and Equation (13) takes the form
Note that the SPhP heat flux at two equidistant positions from the external nanowire surfaces () takes the same value (), such that its maximum appears at the middle of the nanowire (). This behavior arises from the non-local dependence of the heat flux on the temperature profile, as established by Equation (12). The integration of Equation (1) for the SPhP heat flux in Equation (14) yields the following temperature profile and total heat flux
where , and the spectral SPhP thermal conductivity is defined in terms of its integrated counterpart given by
Equation (16) was derived by considering that the average temperature , such that . According to Equation (15a), the deviation of the temperature profile from the usual linear dependence (first two terms) on position is driven by the ratio between the SPhP and phonon thermal conductivities. Interestingly, regardless of the values of this ratio, the SPhP contribution to the temperature profile disappears at the middle of the nanowire (). This behavior is related to the symmetry of the SPhP heat flux around this position and is well confirmed by accurate numerical results, as shown below. As a result of this symmetry, the sum of temperatures at two equidistant points from the external nanowire surfaces is an invariant of heat conduction given by , as established by Equation (15a). This feature of temperature is generated by the non-local behavior of the heat conduction and is analogous to the characteristic temperature profiles found in radiative heat transfer [].
As the heat transport in a polar nanowire is driven by both phonons and SPhPs, the total heat flux is determined by the sum of thermal conductivities related to these two energy carriers, as established by Equation (15b). This fact indicates that, as the nanowire radius a scales down, the usual reduction in could be offset by the increasing values of , due to the predominant surface effects driving the propagation of SPhPs. In the SPhP diffusive approximation (), the ratio and Equation (16) becomes independent of the nanowire length l defining the parameter . In the ballistic limit (), on the other hand, and the SPhP thermal conductivity becomes independent of the propagation length . For both cases, Equation (16) can conveniently be rewritten as the following Landauer formula for the SPhP thermal conductance of the nanowire
where is the probability of SPhPs to transmit from one thermal bath to the other through the nanowire (Figure 1). For long nanowires (), the transmission probability goes to zero () and therefore G vanishes. By contrast, for short nanowires (), and Equation (17) reduces to the quantum of thermal conductance () of nanowires supporting the ballistic propagation of SPhPs [], as expected. The ratio between the nanowire length and SPhP propagation length thus drives the SPhP thermal conductance G, which takes higher values for shorter wires.
3. Results and Discussions
The propagation and heat transport of the SPhPs along a SiN nanowire is quantified and analyzed in this section. SiN is a typical polar material able to support the propagation of SPhPs in a wide frequency range [,] and therefore can be considered as a good SPhP conductor. By solving the Maxwell equations under proper boundary conditions for the transverse magnetic polarization required for the existence of SPhPs [,], the following dispersion relation for the SPhP wavevector along the wire axis is obtained []
where and are the modified Bessel functions, the prime () indicates derivative with respect to their arguments, accounts for the contribution of the azimuthal modes, and are the relative permittivity of the respective wire and its surrounding medium, and and are the corresponding radial wavevectors, with and c being the speed of light in vacuum. For thin enough wires (), which is of interest in this work to enhance the SPhP propagation along the wire, Equation (18) becomes independent of the radius a and branch n, as follows . For nanowires of SiN, this condition is well satisfied for [] and establishes that the azimuthal modes does not contribute to the thermal transport through nanowires. The solution of this symmetric relation for is
Equation (19) differs from the dispersion relation of the single plane interface [] by just a factor of , due to the geometry effect.
The frequency spectrum of the real () and imaginary () parts of the SiN relative permittivity are shown in Figure 2. The main resonance peak of at 155 Trad/s indicates that SiN absorbs a significant amount of energy from the electromagnetic field and therefore limits the propagation of SPhPs, at that frequency. By contrast, the dip of occurs at 175 Trad/s, which represents the frequency at which the SPhPs exhibit the strongest confinement to the interface []. The yellow zone (), on the other hand, stands for the Reststrahlen band determined by the frequency interval (167.0; 199.5) Trad/s that contains the range of frequencies () that would support the propagation of SPhPs in absence of absorption (), as established by Equation (18). However, given that SiN is an absorbing material (), SPhPs are expected to propagate with frequencies inside and outside of this band, as reported in the literature [] for nanofilms and is shown in Figure 3 for a SiN nanowire.
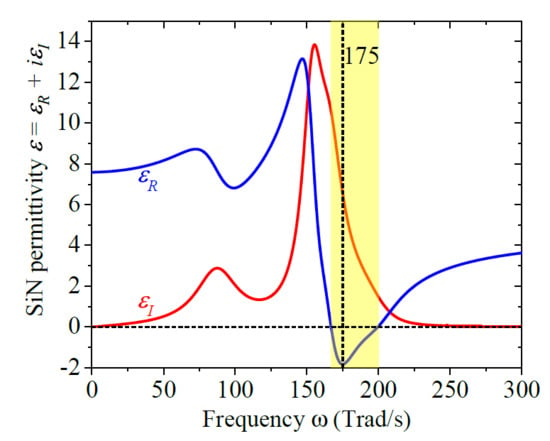
Figure 2.
Real and imaginary parts of the relative permittivity of SiN, as a function of frequency []. The yellow zone stands for the band in which .
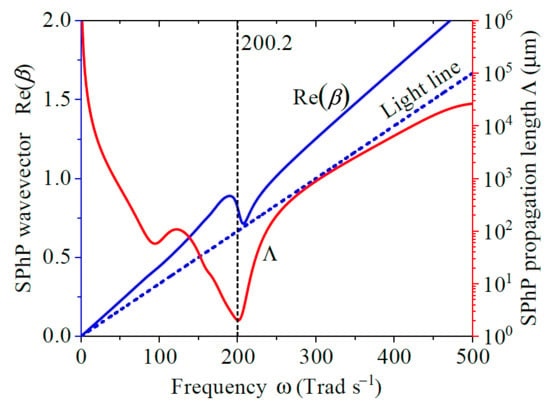
Figure 3.
Frequency spectrum of the wavevector and propagation length of SPhPs propagating along a SiN nanowire suspended in air (). The blue dashed line stands for the wavevector of light in vacuum.
The wavevector Re() and propagation length [2Im of SPhPs propagating along the surface of a SiN nanowire suspended in air are shown in Figure 3, as functions of frequency. Note that Re() increases almost linearly with frequency, through values generally higher than those of the light line (). The deviations from this behavior characterized by a SPhP group velocity Re() close to but smaller than c, show up around 200.2 Trad/s, which is close to the frequency (199.5 Trad/s) where changes its sign. The relatively weak absorption of the thin nanowire ( nm) enables SPhPs to propagate distances as long as 2.7 cm at high frequency (500 Trad/s), as shown in Figure 3. The dip of is related to the maximum of energy absorption driven by and negligible value of at 200.2 Trad/s, as shown in Figure 2. In addition, the fact that m, indicates that SPhPs propagate ballistically along a SiN nanowire shorter than 1 m, which is a condition to reach the 1D quantum of thermal conductance reported in the literature [].
The temperature and heat flux profiles along a SiN nanowire supporting the simultaneous propagation of SPhPs and phonons are shown in Figure 4a and Figure 4b, respectively, for three nanowire lengths. For the shortest nanowire with a length (10 m) much smaller than the propagation length of most SPhPs (see Figure 3), SPhPs propagate ballistically with weak adsorption and low energy exchange with phonons. The SPhP heat generation inside the nanowire is therefore small and T exhibits pretty much the same linear behavior predicted by the heat diffusion Equation (2), without a heat source term. This is confirmed by the relatively low SPhP heat flux shown in Figure 4b via the blue lines, which are nearly independent of position due to the independence of the phonon and SPhP heat transport. On the other hand, for longer nanowires with a length ( and 150 m) comparable to the propagation length of some SPhPs, the quasi-ballistic propagation of SPhPs fosters their energy exchange with phonons, which generates a non-linear temperature profile similar to that predicted by the heat diffusion equation with a heat sink for and a heat source for , as seen in Figure 4a. The apparent heat sink and heat source terms in the nanowire arise from the predominant emission and adsorption of SPhPs near its hot and cold sides, respectively. Therefore, the SPhP heat flux increases with position until and decreases afterwards, while the phonon counterpart shows the opposite trend, as established by the principle of energy conservation in Equation (1). The increase in the SPhP heat flux with the nanowire length provides a pathway to enhance the heat transport along polar nanowires by means of the coupling of SPhPs and phonons, as is the case in polar nanofilms []. Furthermore, as the non-linearity of the temperature profile represents the fingerprints of SPhPs, its experimental observation can provide an intuitive and conclusive way to detect the SPhP heat transport. For instance, for the 150 m-long SiN nanowire shown in Figure 4a, the largest temperature deviation from the linear profile is about 1 K, which is measurable by the current state-of-the-art infrared thermometers.
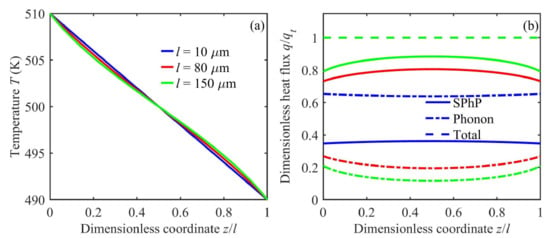
Figure 4.
(a) Temperature and (b) heat flux profiles in a SiN nanowire with representative lengths l. The solid and dashed-dot lines in (b) represent the respective SPhP and phonon heat fluxes, whereas the dashed one stands for the total heat flux . Calculations were carried out for a SiN nanowire with a radius nm and a typical phonon thermal conductivity of = 1 W/m·K.
Figure 5 shows the frequency spectrum of the SPhP transmission probability for four SiN nanowire lengths. Note that shorter nanowires exhibit a higher transmissivity, whose lowest value at 201.6 Trad/s is related to the minimum value of the SPhP propagation length shown in Figure 3. By contrast, for other sufficiently low and high frequencies, tends to unity as a result of the long propagation lengths of SPhPs. According to Equation (17), these lowest and highest values of the SPhP transmissivity drive the behavior of the thermal conductivity spectrum, which takes higher values for shorter nanowires, as shown in Figure 6a. At high enough frequencies, this spectrum becomes independent of the nanowire length and decays exponentially due to the insufficient thermal energy required to excite them, as established by the Bose–Einstein distribution function involved in Equation (17). At very low frequencies, on the other hand, the thermal conductance spectrum takes its highest values due to the high transmissivity of SPhPs. The integration of the spectra in Figure 6a yields the SPhP thermal conductance G shown in Figure 6b,c, as a function of the nanowire length and temperature, respectively. As a result of the predominance of ballistic regime characterized by a high transmissivity, shorter nanowires exhibit a higher G, whose values increase with temperature. The analytical (solid lines) and numerical (dots) predictions exhibit a very good agreement for the three temperatures and lengths, which confirms the high accuracy of Equation (17) for predicting the thermal conductance of SPhPs. More importantly, the upper bound of G, in the ballistic regime ( m), is well confirmed by the analytical and numerical solutions and its values coincide with the quantum of thermal conductance . Even though the transmissivity of a 1 m-long SiN nanowire is not unity over the full frequency spectrum (see Figure 5), the corresponding SPhP thermal conductance is pretty much equal to . The quantization of the SPhP thermal conductance is thus expected to be observed in SiN nanowires with a length comparable to or shorter than 1 m.
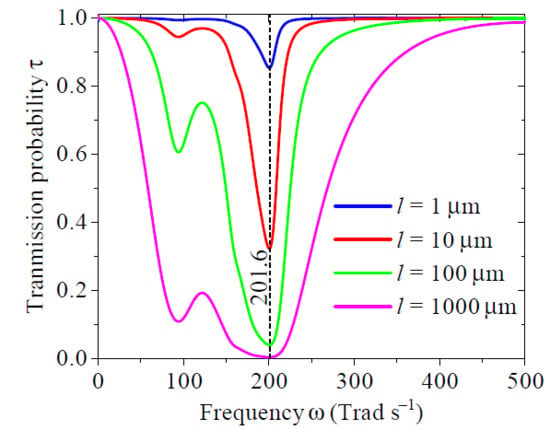
Figure 5.
Frequency spectrum of the transmission probability of SPhPs propagating along a SiN nanowire of different lengths.
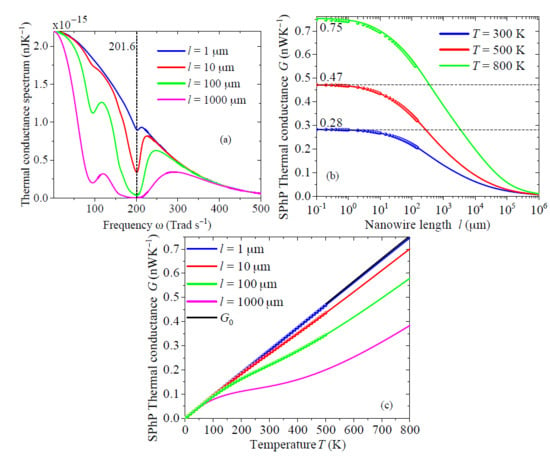
Figure 6.
(a) SPhP thermal conductance spectrum along with its integrated counterpart as a function of the (b) length and (c) temperature of a SiN nanowire suspended in air with a radius nm. The solid lines represent the predictions of Equation (17) and the dots the stand for the numerical results obtained with the DOM+FDM described in Section 2.1. Calculations in (a) were carried out for K.
4. Conclusions
Based on the Boltzmann transport equation, we have theoretically demonstrated that the heat transport by surface phonon-polaritons propagating along a nanowire is characterized by two fingerprints: (i) The characteristic quantum of thermal conductance independent of the material properties. This quantization appears in SiN nanowires shorter than 1 m, supporting the ballistic propagation of polaritons. (ii) The deviation of the temperature profile from its typical linear behavior predicted by Fourier’s law of heat conduction in the absence of heat sources. For a 150 m-long SiN nanowire keeping up a quasi-ballistic polariton propagation, this deviation can be as large as 1 K, which can be observed by the current state-of-the-art infrared thermometers. Furthermore, we have derived an explicit formula for the polariton thermal conductance that is able to accurately predict the energy transport of polaritons for different lengths and temperatures of a polar nanowire. The obtained results can thus be useful for understanding and quantifying the thermal performance of surface phonon-polaritons in 1D structures.
Author Contributions
Conceptualization, J.O.-M.; methodology, Y.G. and J.O.-M.; validation, J.O.-M., Y.G., M.N. and S.V.; writing—original draft preparation, Y.G. and J.O.-M.; writing—review and editing, M.N. and S.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the postdoctoral fellowship of the Japan Society for the Promotion of Science, grant n° P19353, CREST Japan Science and Technology Agency, grants n° JPMJCR19Q3 and JPMJCR19I1, and French project ANR-19-CE09-0005 “EPolariton”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data supporting the conclusions are provided in the article.
Conflicts of Interest
The authors declare no conflict of interest.The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Rego, L.G.C.; Kirczenow, G. Quantized Thermal Conductance of Dielectric Quantum Wires. Phys. Rev. Lett. 1998, 81, 232. [Google Scholar] [CrossRef] [Green Version]
- Yamamoto, T.; Watanabe, S.; Watanabe, K. Universal Features of Quantized Thermal Conductance of Carbon Nanotubes. Phys. Rev. Lett. 2004, 92, 075502. [Google Scholar] [CrossRef] [Green Version]
- Glavin, B.A. Low-Temperature Heat Transfer in Nanowires. Phys. Rev. Lett. 2001, 86, 4318. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chalopin, Y.; Gillet, J.-N.; Volz, S. Predominance of thermal contact resistance in a silicon nanowire on a planar substrate. Phys. Rev. B 2008, 77, 233309. [Google Scholar] [CrossRef]
- Venkatesh, R.; Amrit, J.; Chalopin, Y.; Volz, S. Thermal resistance of metal nanowire junctions in the ballistic régime. Phys. Rev. B 2011, 83, 115425. [Google Scholar] [CrossRef]
- Büttiker, M. Four-Terminal Phase-Coherent Conductance. Phys. Rev. Lett. 1986, 57, 1761. [Google Scholar] [CrossRef]
- Rego, L.G.C.; Kirczenow, G. Fractional exclusion statistics and the universal quantum of thermal conductance: A unifying approach. Phys. Rev. B 1999, 59, 13080. [Google Scholar] [CrossRef] [Green Version]
- Chiatti, O.; Nicholls, J.T.; Proskuryakov, Y.Y.; Lumpkin, N.; Farrer, I.; Ritchie, D.A. Quantum Thermal Conductance of Electrons in a One-Dimensional Wire. Phys. Rev. Lett. 2006, 97, 056601. [Google Scholar] [CrossRef] [Green Version]
- Schwab, K.; Henriksen, E.A.; Worlock, J.M.; Roukes, M.L. Measurement of the quantum of thermal conductance. Nature 2000, 404, 974. [Google Scholar] [CrossRef] [PubMed]
- Biehs, S.A.; Messina, R.; Venkataram, P.S.; Rodriguez, A.W.; Cuevas, J.C.; Ben-Abdallah, P. Near-field radiative heat transfer in many-body systems. Rev. Mod. Phys. 2021, 93, 025009. [Google Scholar] [CrossRef]
- Dong, J.; Zhao, J.; Liu, L. Long-distance near-field energy transport via propagating surface waves. Phys. Rev. B 2018, 97, 075422. [Google Scholar] [CrossRef] [Green Version]
- Agranovich, V.M. Surface Polaritons, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Zayats, A.V.; Smolyaninov, I.I.; Maradudin, A.A. Nano-optics of surface plasmon polaritons. Phys. Rep. 2005, 408, 0370. [Google Scholar] [CrossRef]
- Jiunn-Woei, L.; Szu-Yao, M.; Jia-Yun, L.; Yun-Cheng, K.; Mao-Kuen, K. Nano-optics of surface plasmon polaritons. Opt. Express 2021, 29, 18876. [Google Scholar]
- Ordonez-Miranda, J.; Tranchant, L.; Antoni, T.; Chalopin, Y.; Volz, S. Thermal conductivity of nano-layered systems due to surface phonon-polaritons. J. Appl. Phys. 2014, 115, 054311–054315. [Google Scholar] [CrossRef] [Green Version]
- Gluchko, S.; Palpant, B.; Volz, S.; Braive, R.; Antoni, T. Thermal excitation of broadband and long-range surface waves on SiO2 submicron films. Appl. Phys. Lett. 2017, 110, 263108. [Google Scholar] [CrossRef] [Green Version]
- Tranchant, L.; Hamamura, S.; Orrdonez-Miranda, J.; Yabuki, T.; Vega-Flick, A.; Cervantes-Alvarez, A.; Alvarado-Gil, J.J.; Volz, S.; Miyazaki, K. Two-Dimensional Phonon Polariton Heat Transport. Nano Lett. 2019, 19, 6924–6930. [Google Scholar] [CrossRef]
- Ordonez-Miranda, J.; Tranchant, L.; Kim, B.; Chalopin, Y.; Antoni, T.; Volz, S. Effects of anisotropy and size of polar nano thin films on their thermal conductivity due to surface phonon-polaritons. Appl. Phys. Express 2014, 7, 035201–035204. [Google Scholar] [CrossRef] [Green Version]
- Ordonez-Miranda, J.; Tranchant, L.; Joulain, K.; Ezzahri, Y.; Drevillon, J.; Volz, S. Thermal energy transport in a surface phonon-polariton crystal. Phys. Rev. B 2016, 93, 035428. [Google Scholar] [CrossRef]
- Ordonez-Miranda, J.; Tranchant, L.; Tokunaga, T.; Kim, B.; Palpant, B.; Chalopin, Y.; Antoni, T.; Volz, S. Anomalous thermal conductivity by surface phonon-polaritons of polar nano thin films due to their asymmetric surrounding media. J. Appl. Phys. 2013, 113, 084311–084318. [Google Scholar] [CrossRef]
- Ordonez-Miranda, J.; Tranchant, L.; Kim, B.; Chalopin, Y.; Antoni, T.; Volz, S. Quantized thermal conductance of nanowires at room temperature due to Zenneck surface-phonon polaritons. Phys. Rev. Lett. 2014, 112, 055901–055905. [Google Scholar] [CrossRef] [Green Version]
- Ordonez-Miranda, J.; Tranchant, L.; Gluchko, S.; Volz, S. Energy transport of surface phonon polaritons propagating along a chain of spheroidal nanoparticles. Phys. Rev. B 2015, 92, 115409–115413. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Ordonez-Miranda, J.; Gluchko, S.; Anufriev, R.; Meneses, D.D.S.; Del Campo, L.; Volz, S.; Nomura, M. Enhanced thermal conduction by surface phonon-polaritons. Sci. Adv. 2020, 6, eabb4461. [Google Scholar] [CrossRef]
- Li, X.; Lee, S. Crossover of ballistic, hydrodynamic, and diffusive phonon transport in suspended graphene. Phys. Rev. B 2019, 99, 085202. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.-Z.A.; Narayanaswamy, A.; Chen, G. Surface phonon-polariton mediated thermal conductivity enhancement of amorphous thin films. Phys. Rev. B 2005, 72, 155435. [Google Scholar] [CrossRef] [Green Version]
- Majumdar, A. Microscale heat conduction in dielectric thin films. ASME J. Heat Transf. 1993, 115, 7–16. [Google Scholar] [CrossRef]
- Minnich, A.J.; Chen, G.; Mansoor, S.; Yilbas, B.S. Quasiballistic heat transfer studied using the frequency-dependent Boltzmann transport equation. Phys. Rev. B 2011, 84, 235207. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.Z.A.; Chen, G. Heat flow in thin films via surface phonon-polaritons. Front. Heat Mass Transf. 2010, 1, 023005. [Google Scholar] [CrossRef]
- Kathmann, C.; Messina, R.; Ben-Abdallah, P.; Biehs, S.A. Limitations of kinetic theory to describe near-field heat exchanges in many-body systems. Phys. Rev. B 2018, 98, 115434. [Google Scholar] [CrossRef] [Green Version]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2005; pp. 108–111. [Google Scholar]
- Guo, Y.; Wang, M. Heat transport in two-dimensional materials by directly solving the phonon Boltzmann equation under Callaway’s dual relaxation model. Phys. Rev. B 2017, 96, 134312. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Tachikawa, S.; Volz, S.; Nomura, M.; Ordonez-Miranda, J. Quantum of Thermal Conductance of Nanofilms due to Surface-Phonon Polaritons. Under Rev. 2021. [Google Scholar]
- Kourganoff, V. Basic Methods in Transfer Problems, 1st ed.; Dover Publications: New York, NY, USA, 1963. [Google Scholar]
- Ordonez-Miranda, J.; Volz, S.; Nomura, M. Surface Phonon-Polariton Heat Capacity of Polar Nanofilms. Phys. Rev. Appl. 2021, 15, 054068. [Google Scholar] [CrossRef]
- Yeh, C.; Shimabukuro, F.I. The Essence of Dielectric Waveguides; Springer: New York, NY, USA, 2008. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).