Short Survey of Architectures of Photovoltaic Arrays for Solar Power Generation Systems
Abstract
:1. Introduction
2. Static PV Arrays
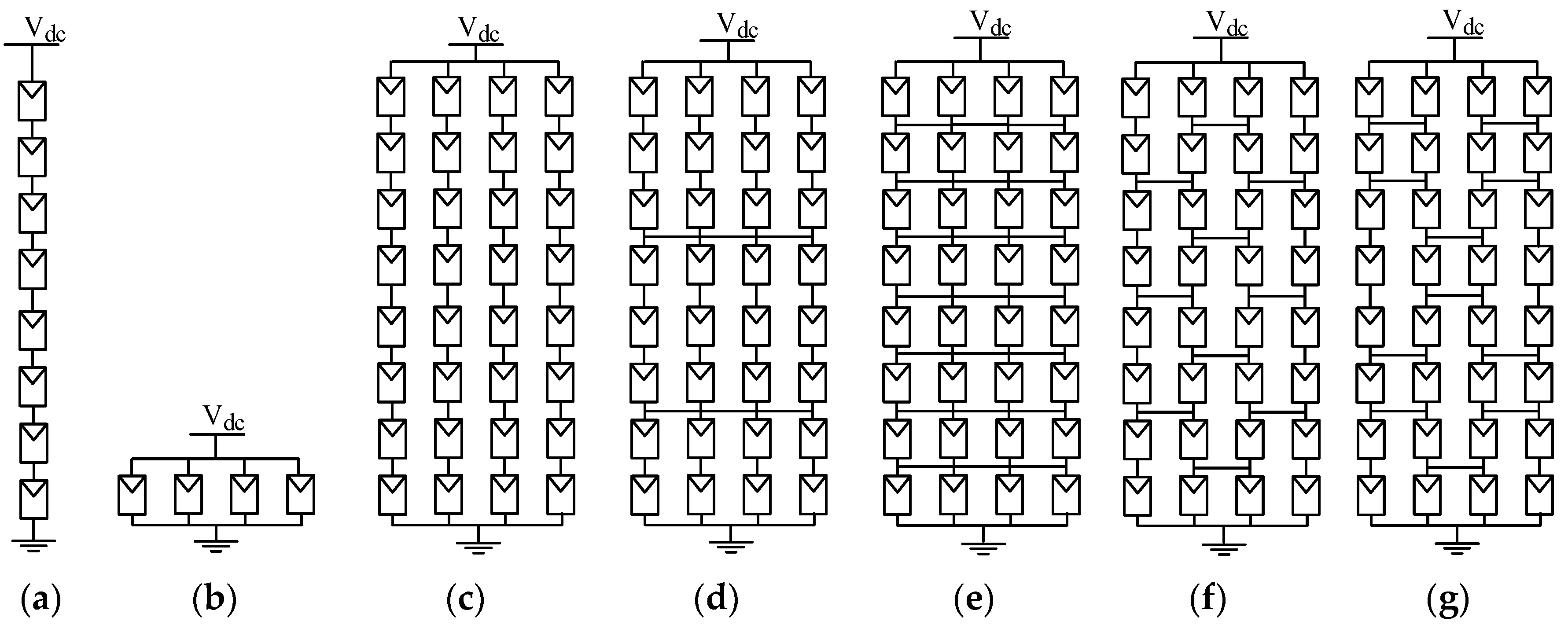
2.1. Common Interconnection Patterns of PV Cells and Modules
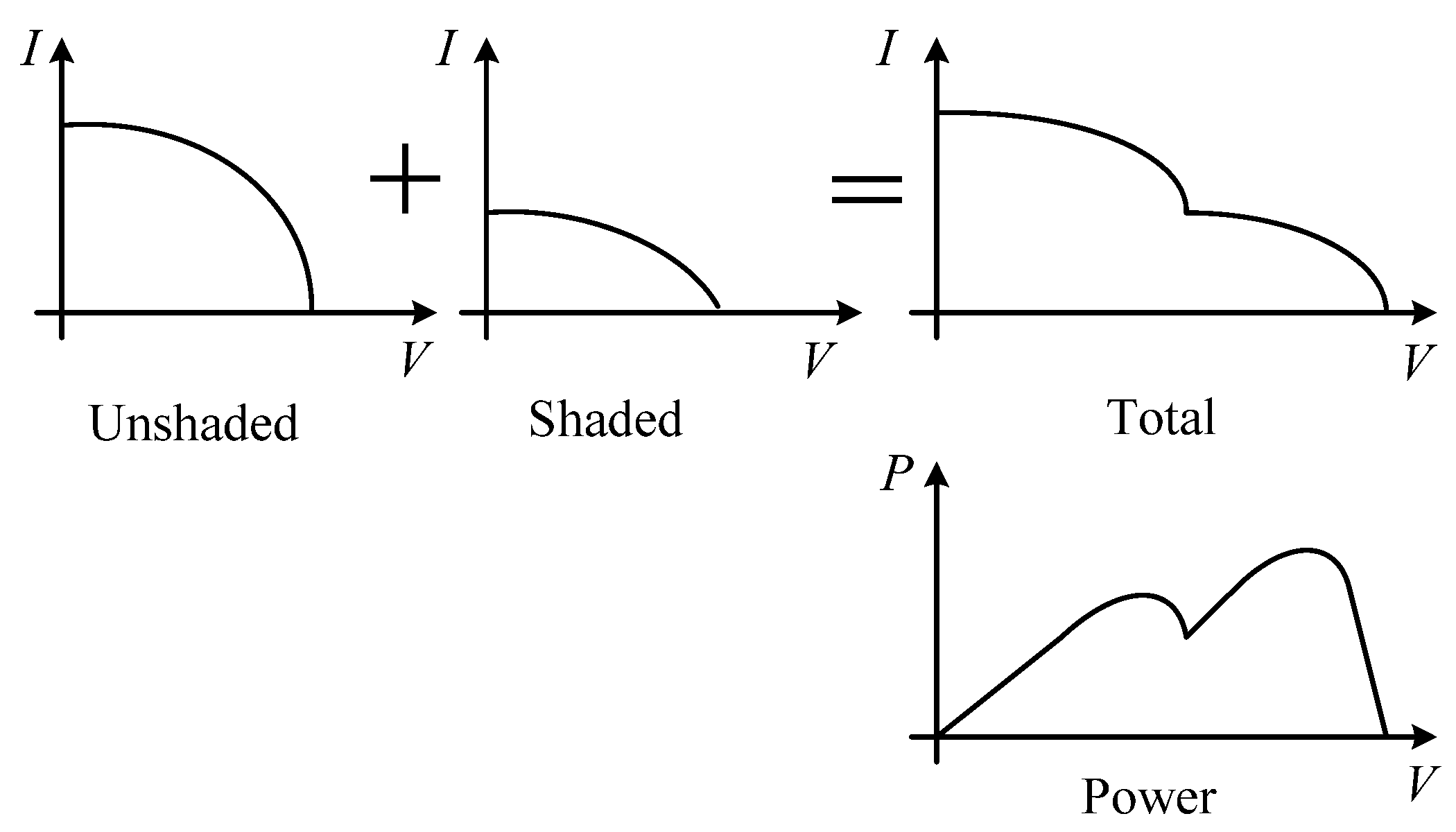
2.2. Tolerance of Commonly Used Arrays to Shading
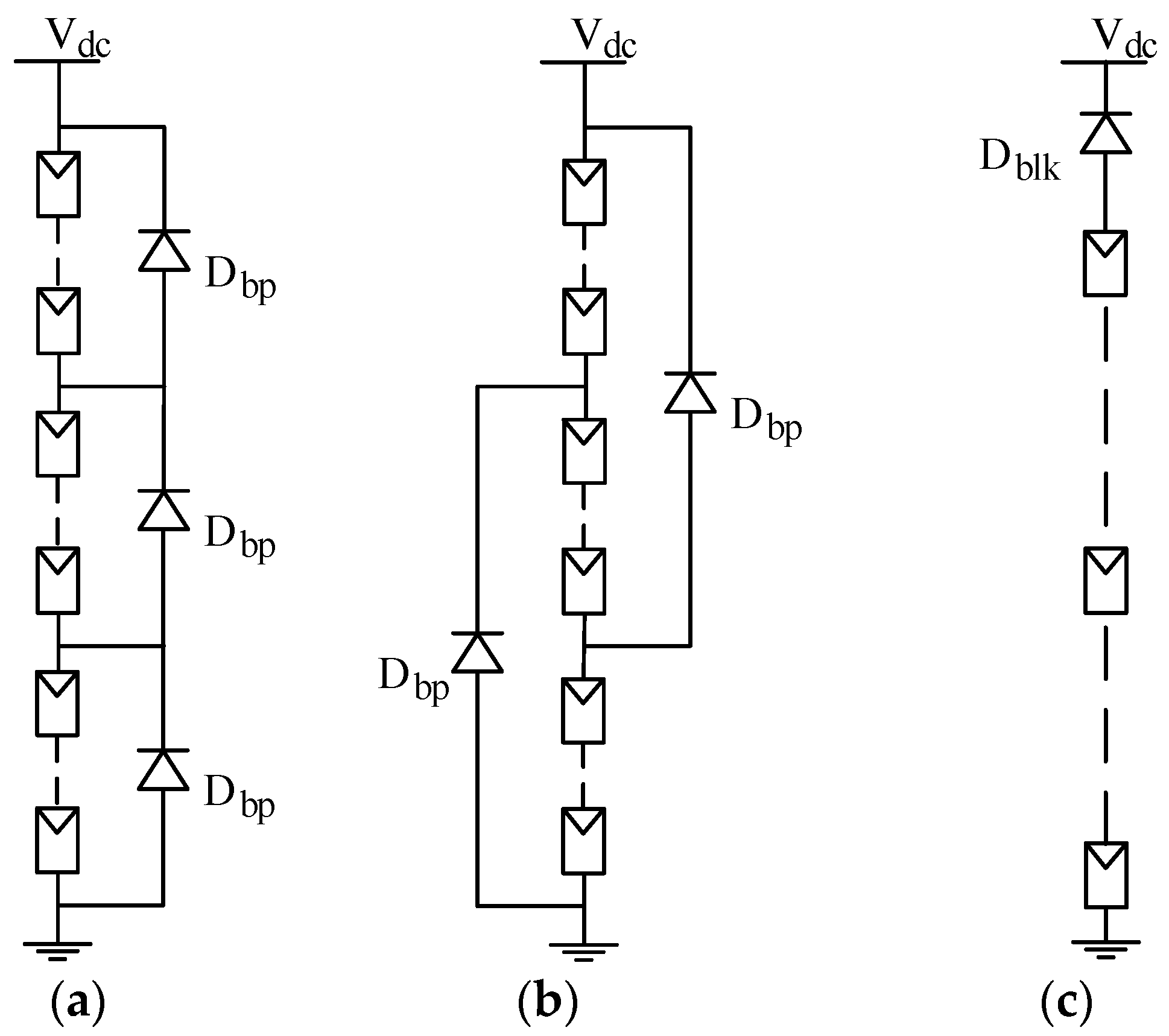
2.3. Bypass Diodes
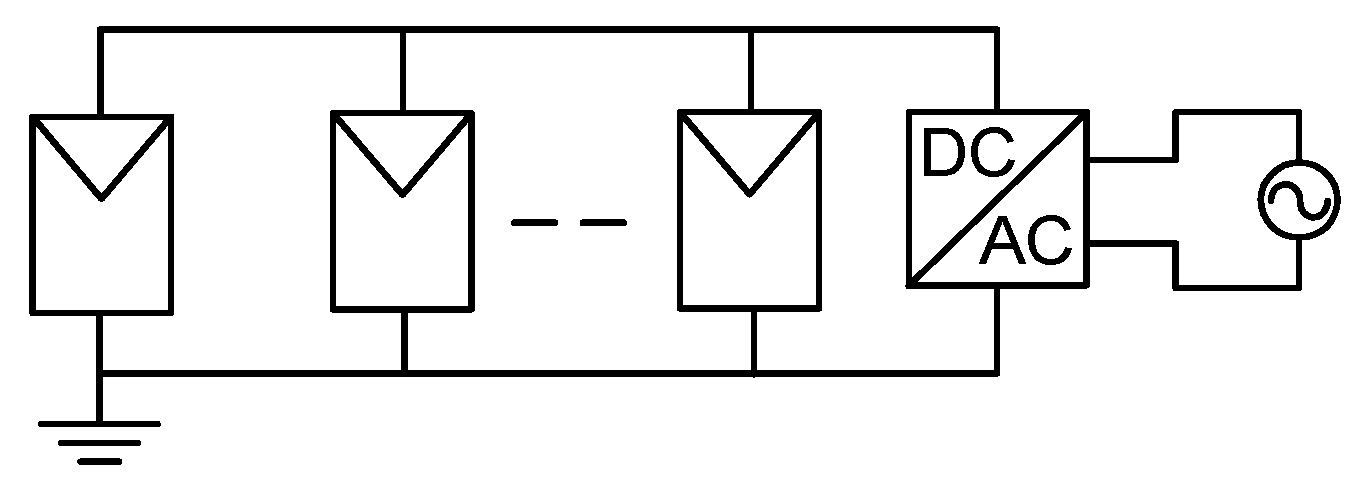
2.4. Blocking Diodes
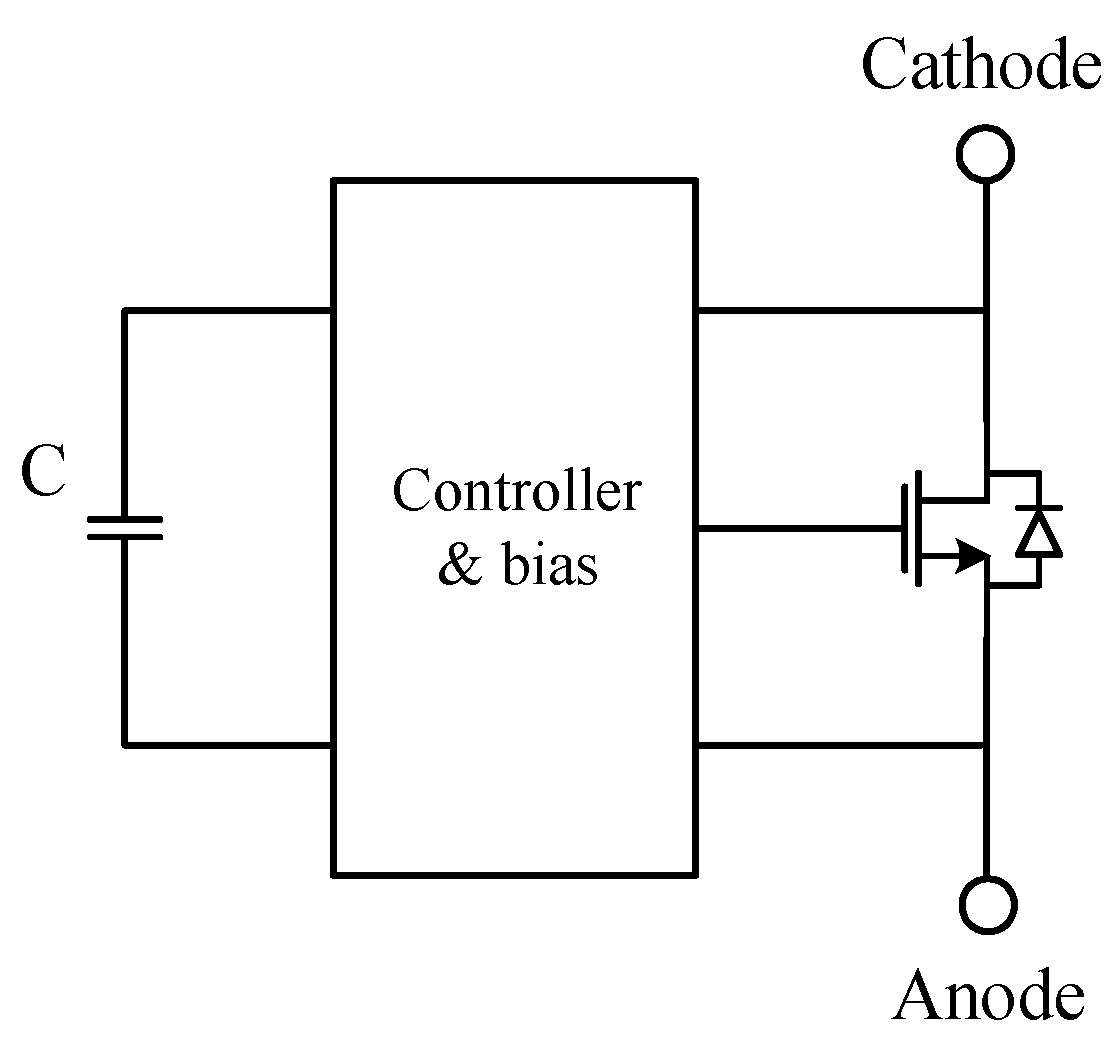
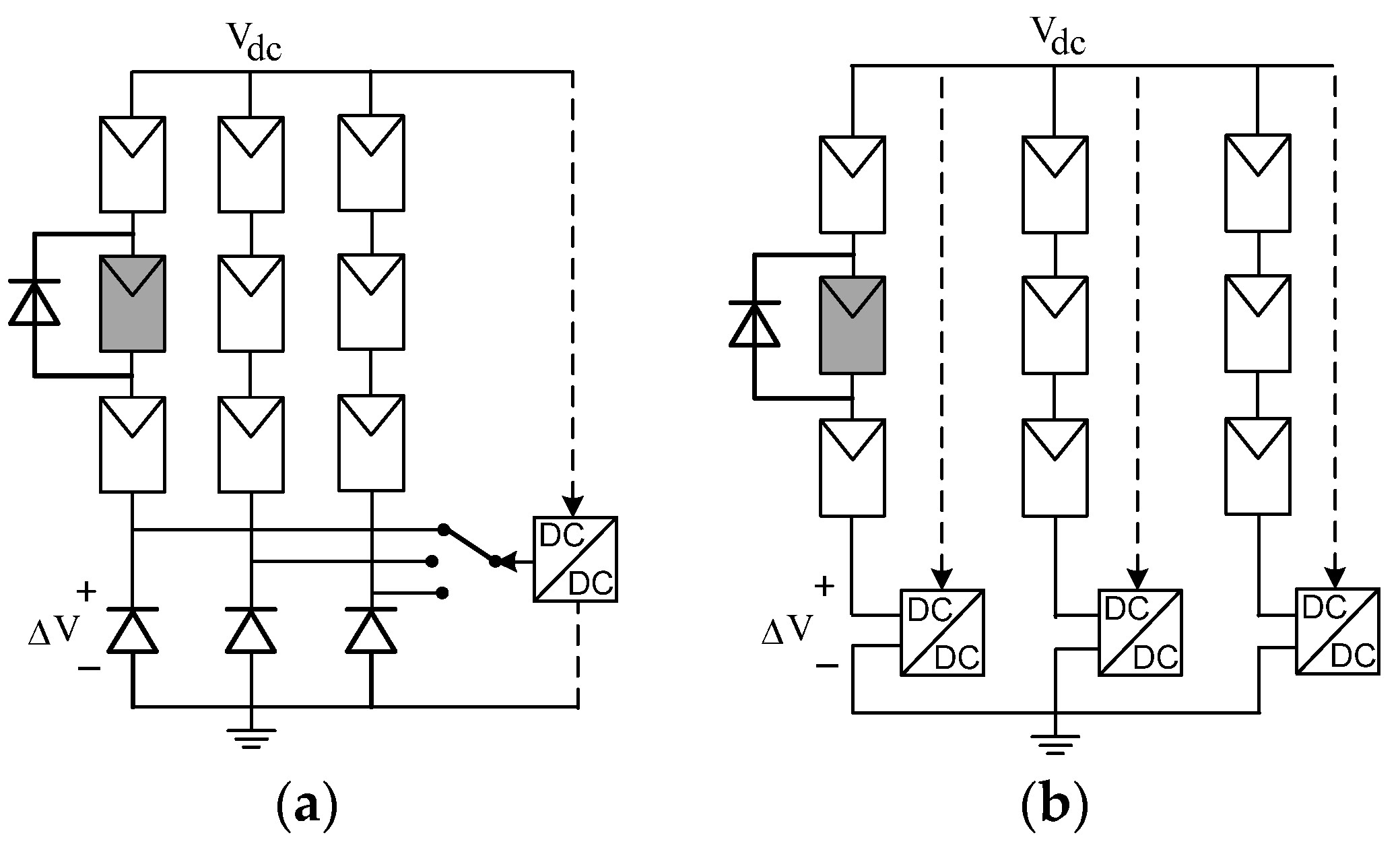
2.5. Active Bypass Diode
2.6. Hotspots
3. Variable Structure Arrays
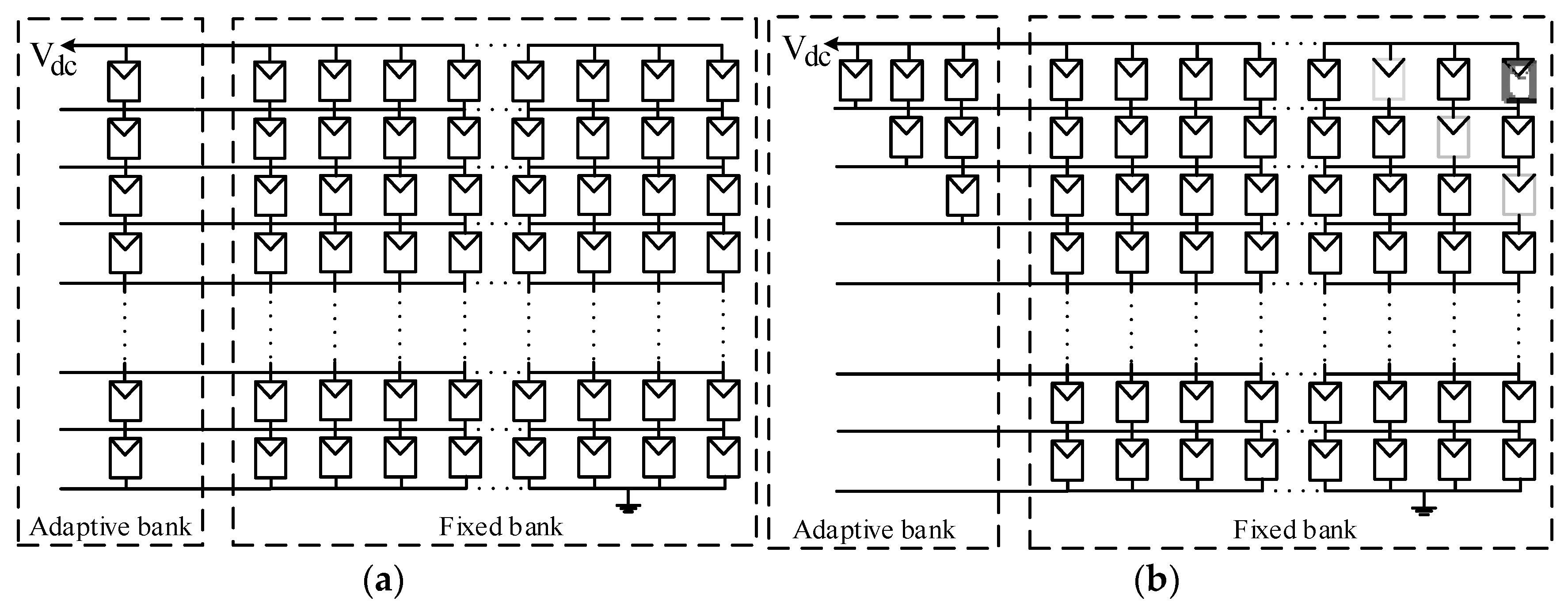
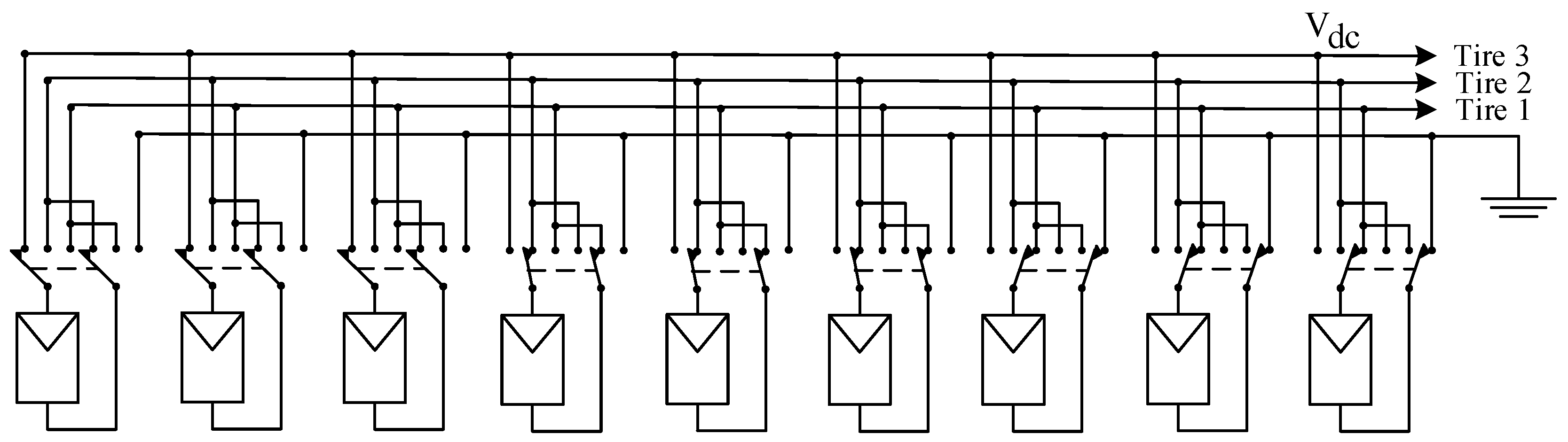
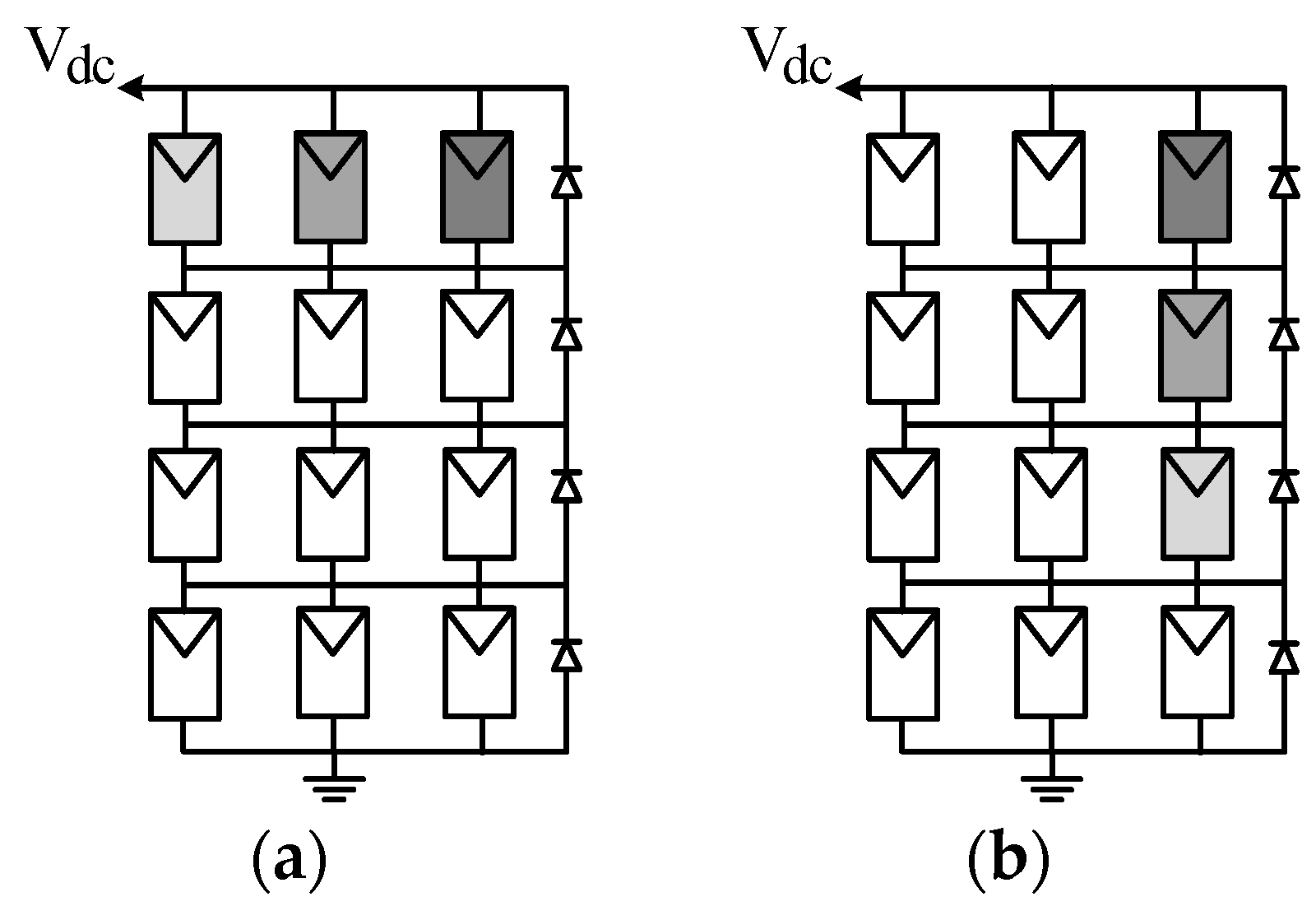
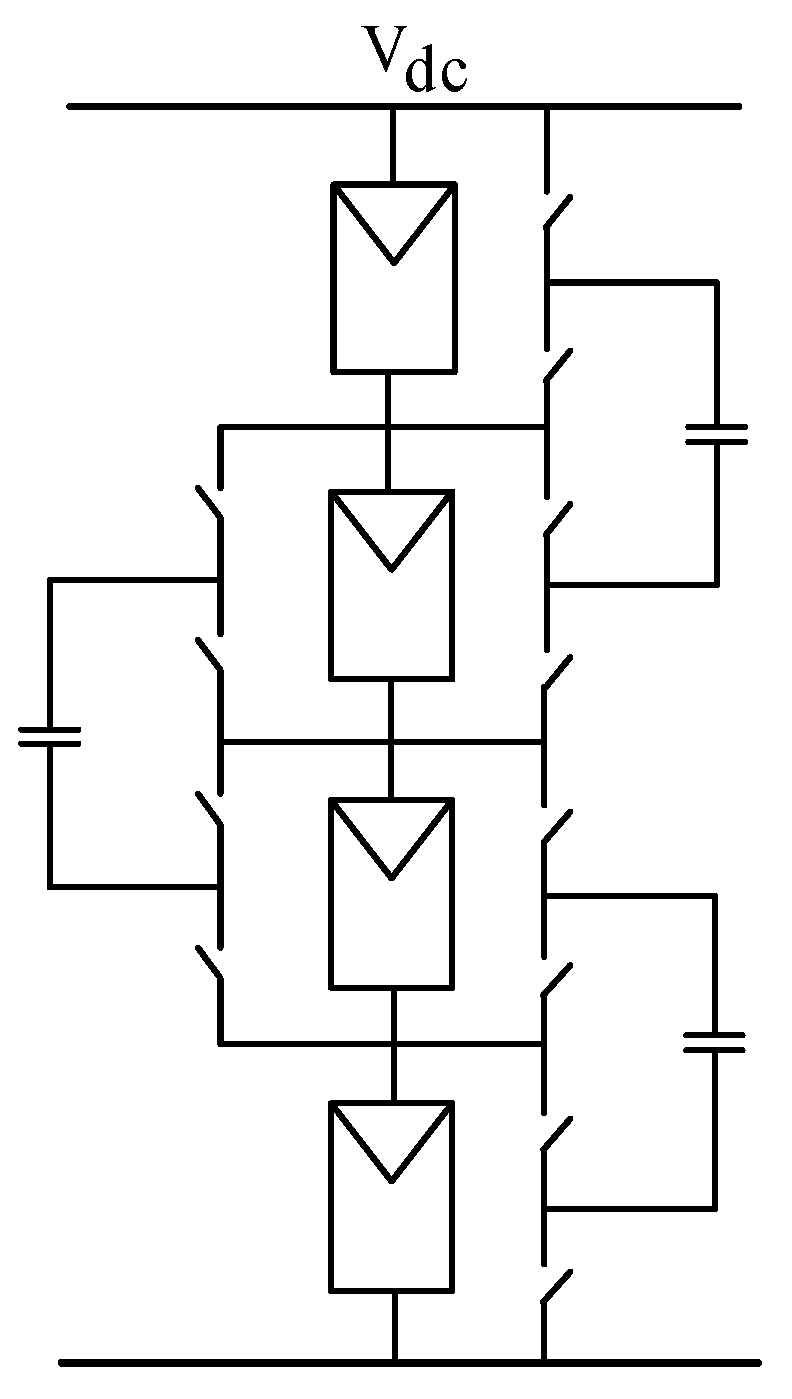
3.1. Reconfigurable Array with an Adaptive Bank
3.2. Dynamic Arrays
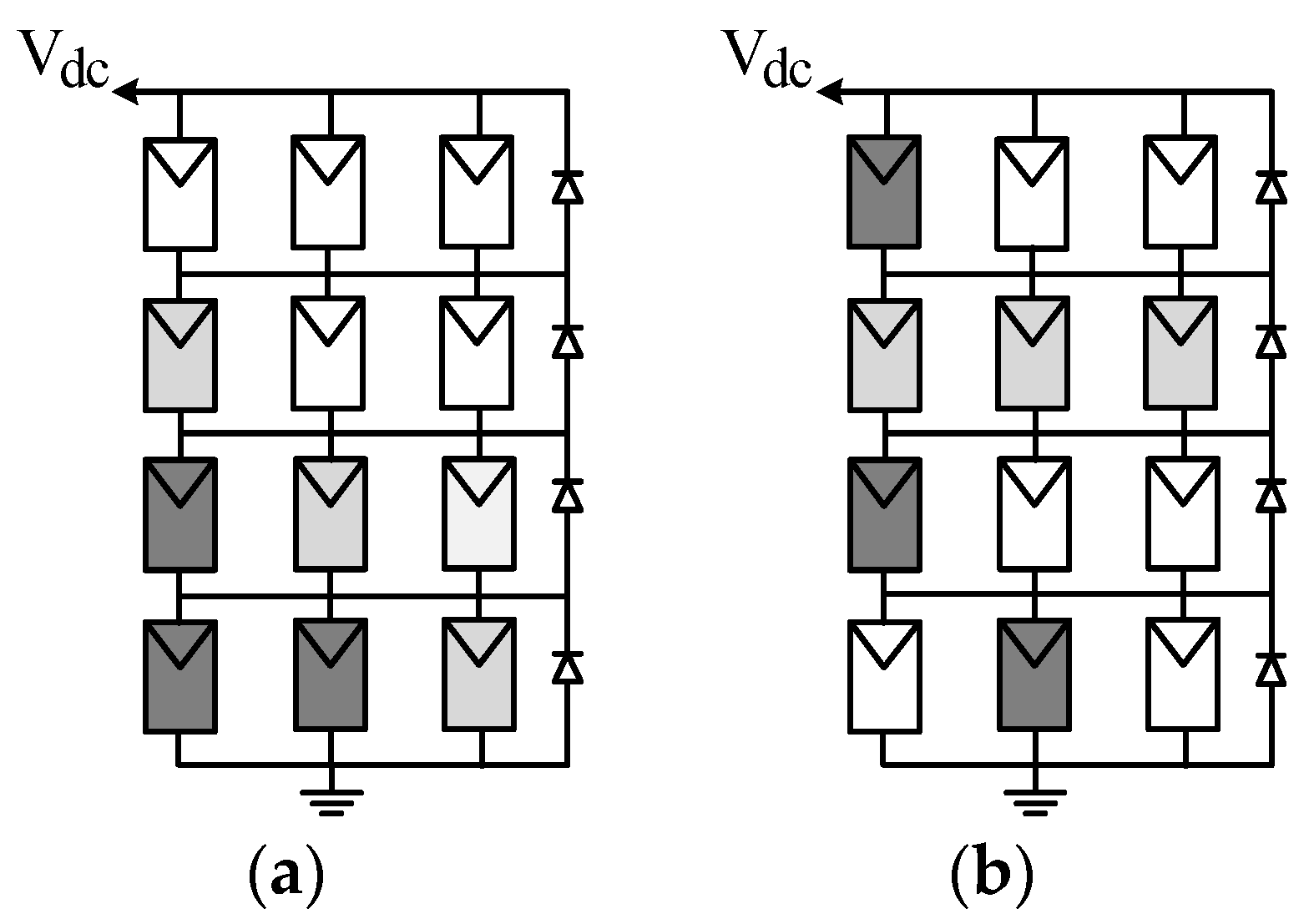
3.2.1. SC-DPVA: “String-Configured DPVA’s”
OS-DPVA “Optimized-String DPVA”
3.2.2. Reconfiguration Strategies
4. Power Processing Architectures for PV Arrays
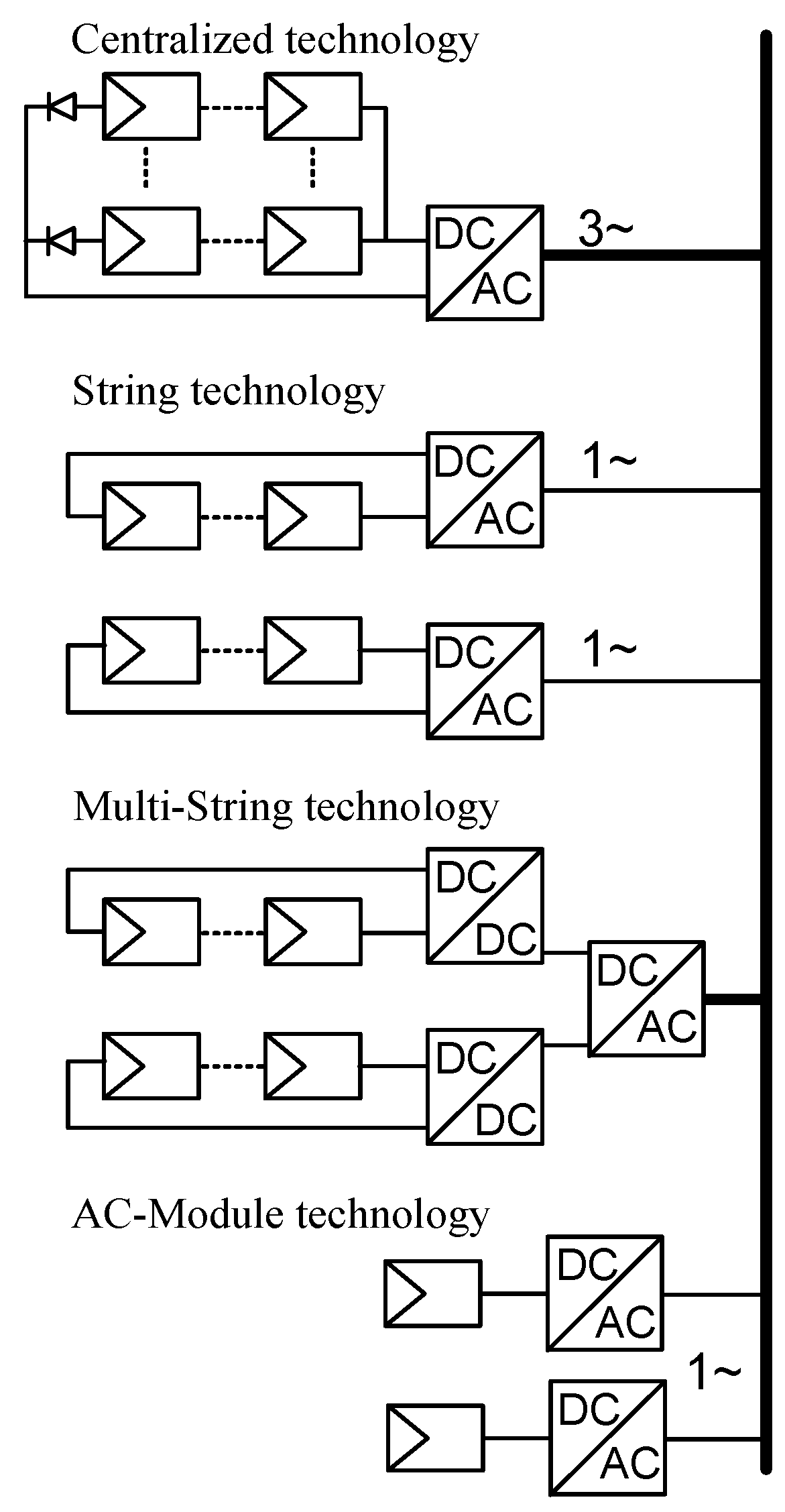
4.1. System Architectures
4.2. String PE Architecture
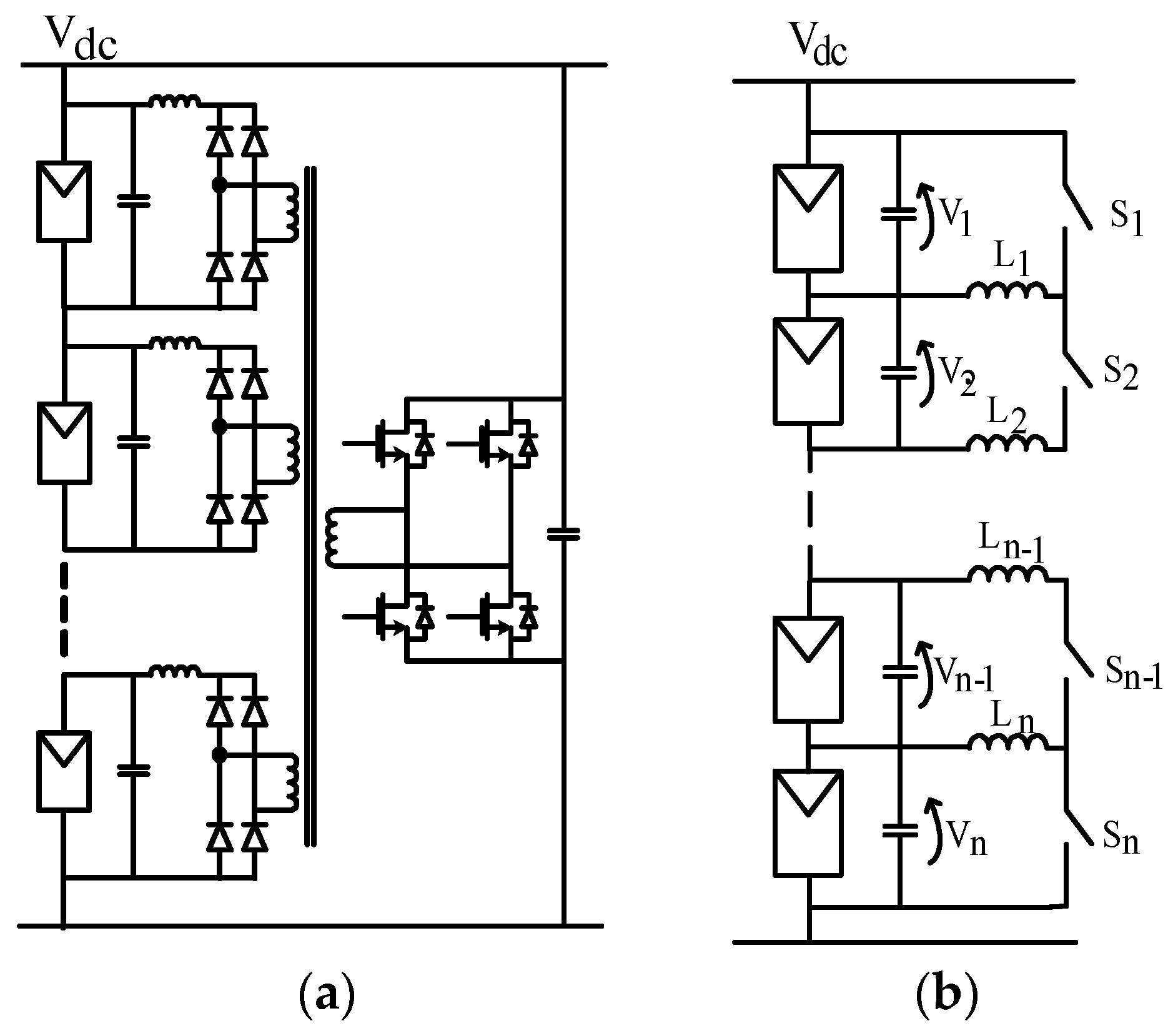
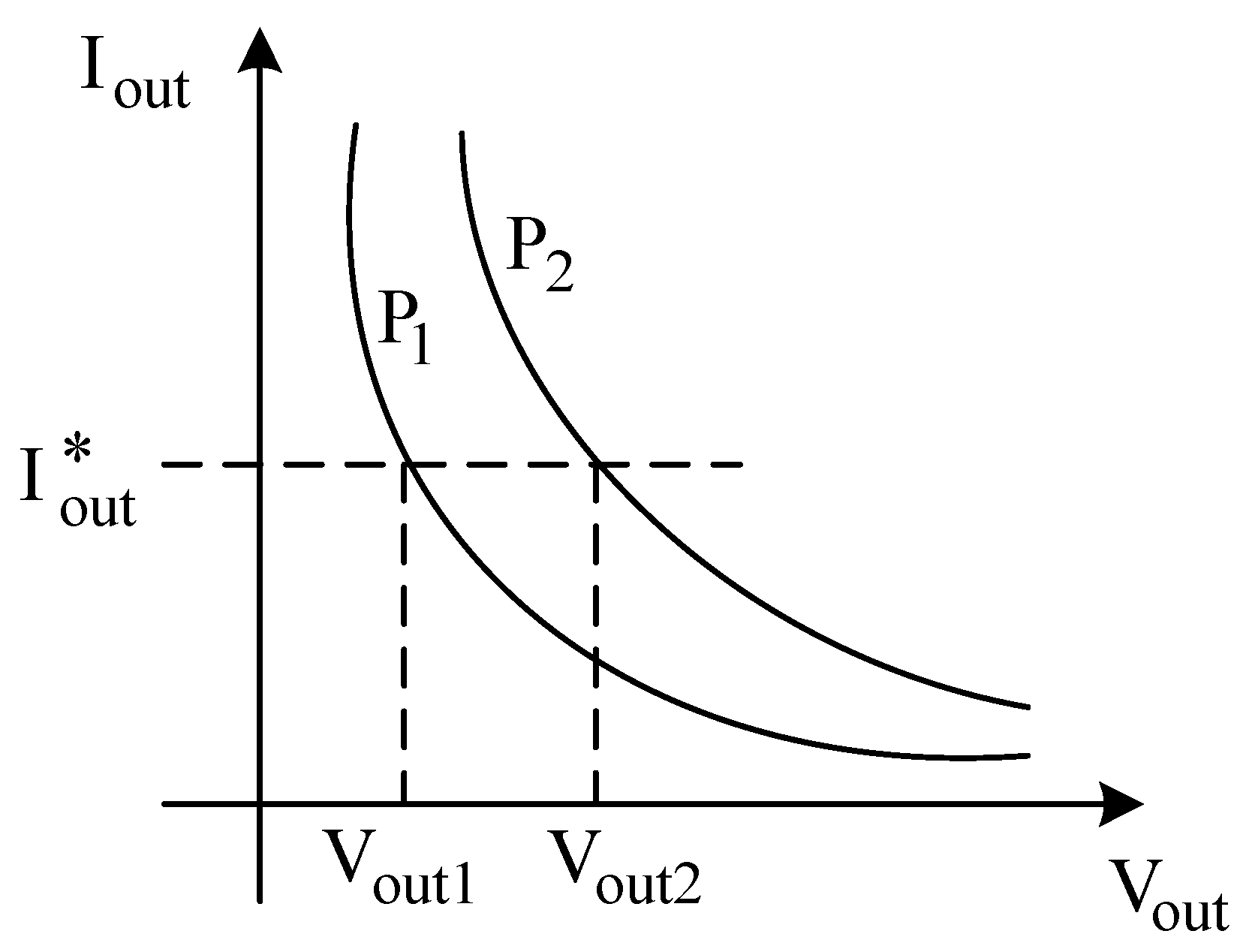
4.2.1. Series Compensation
4.2.2. Shunt Compensation
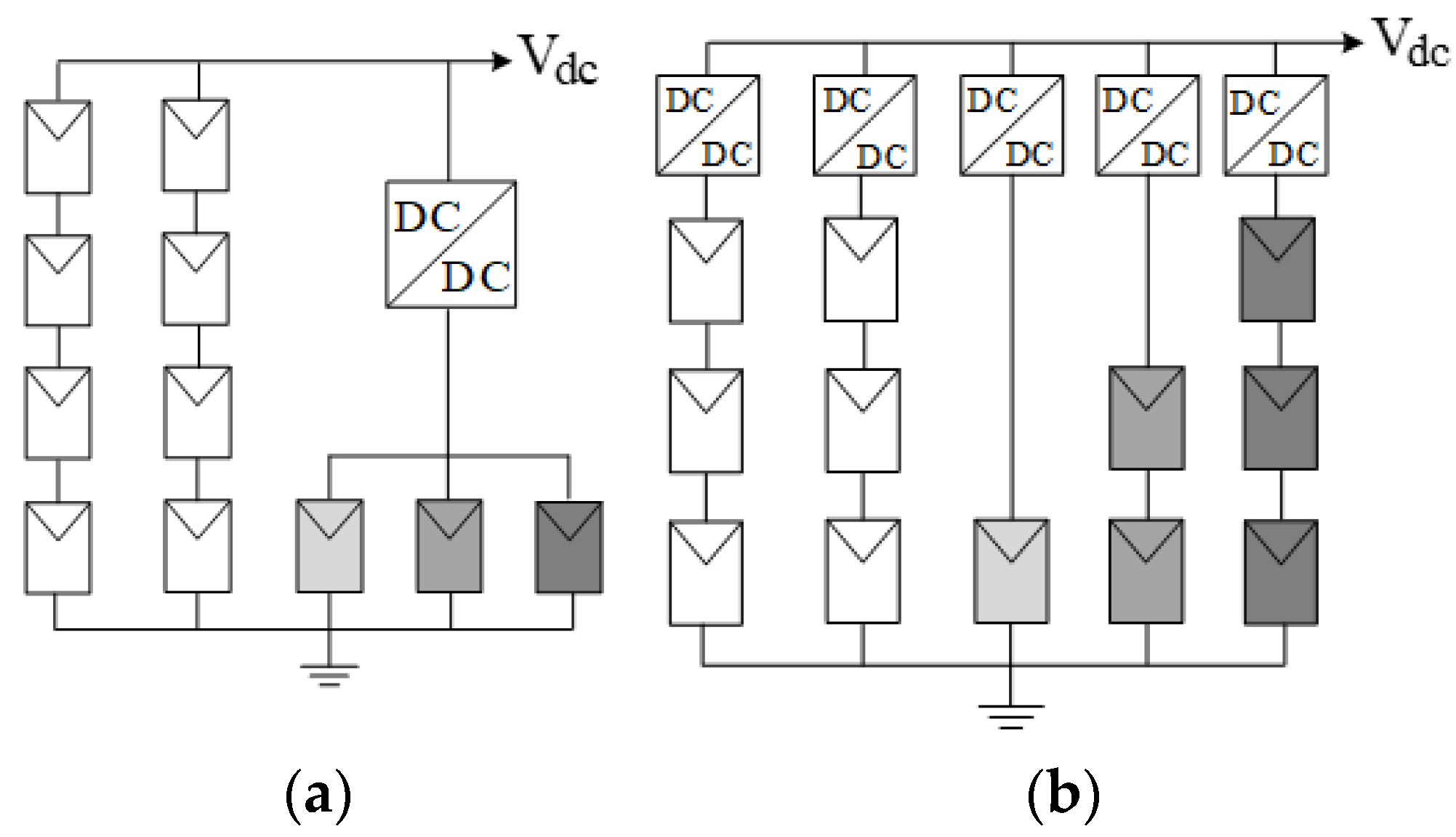
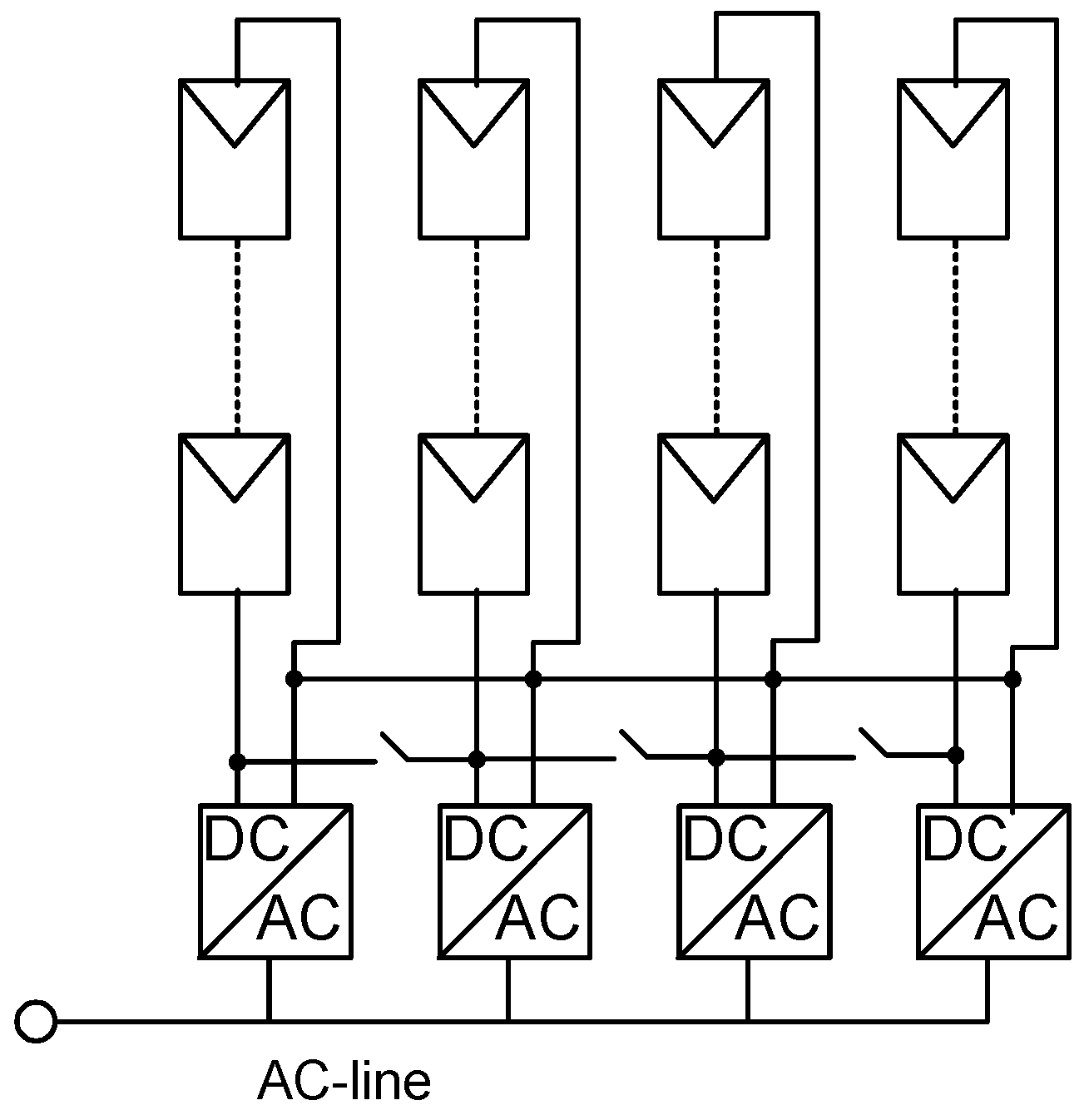
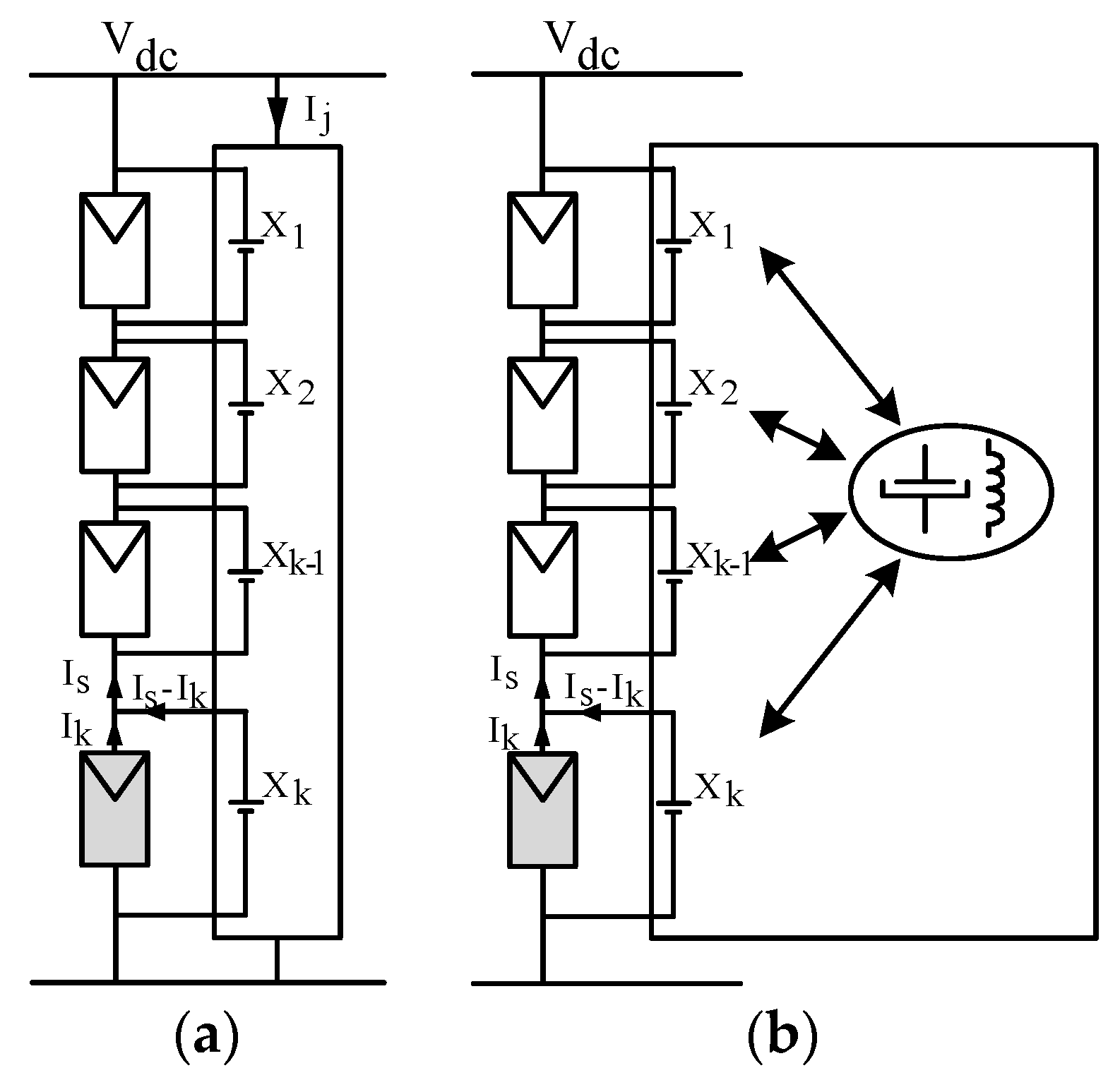
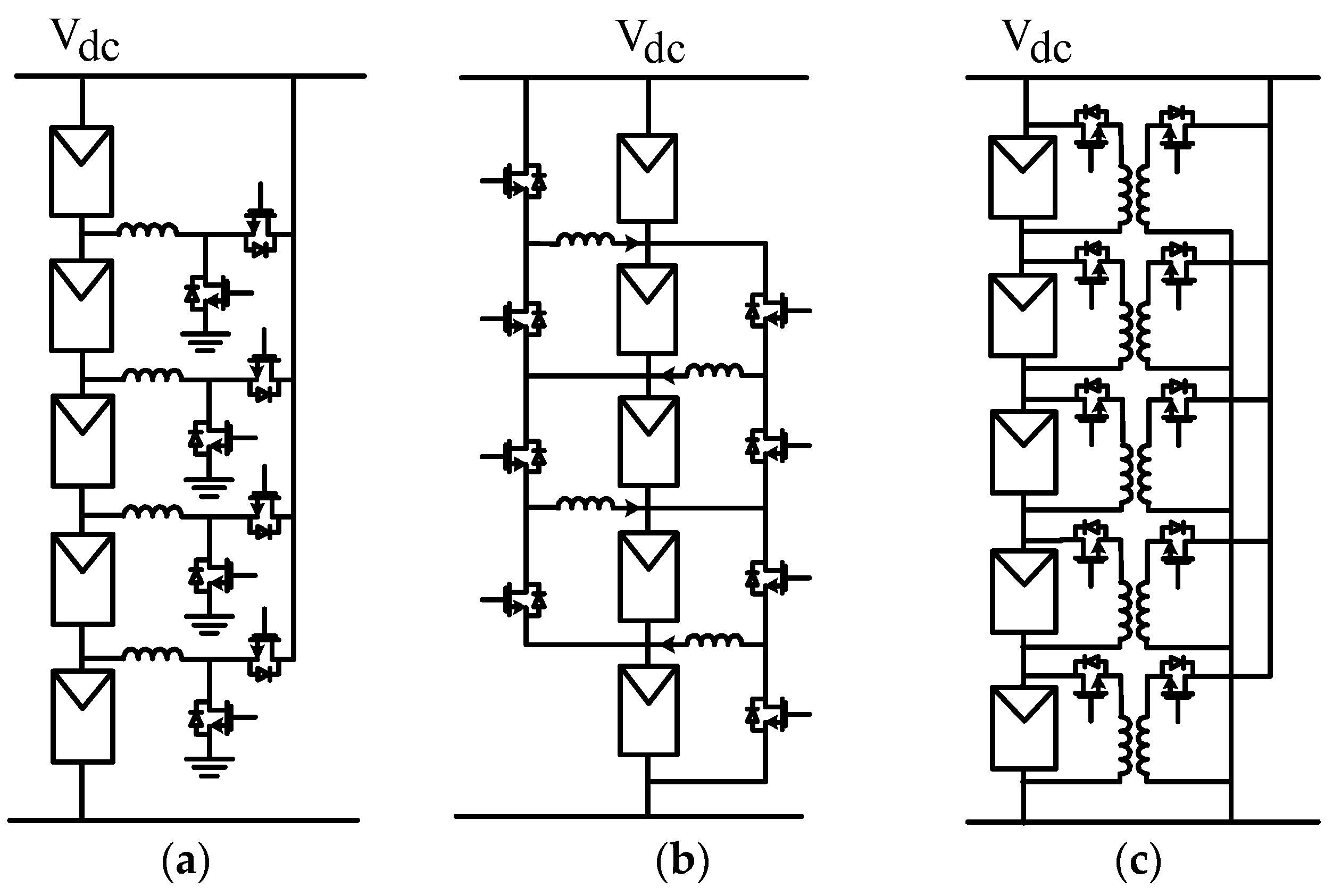
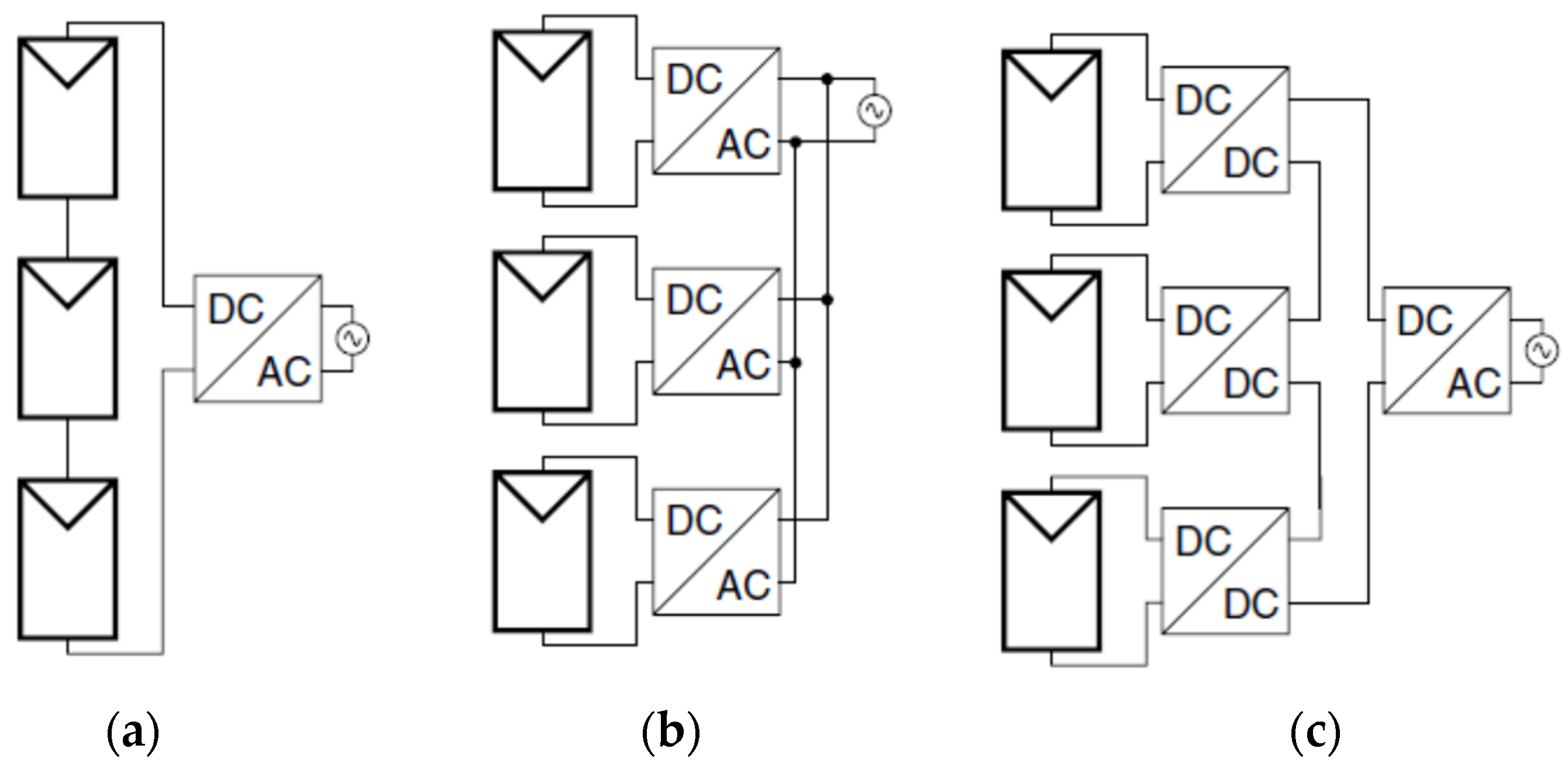
4.3. Module-Integrated Architectures
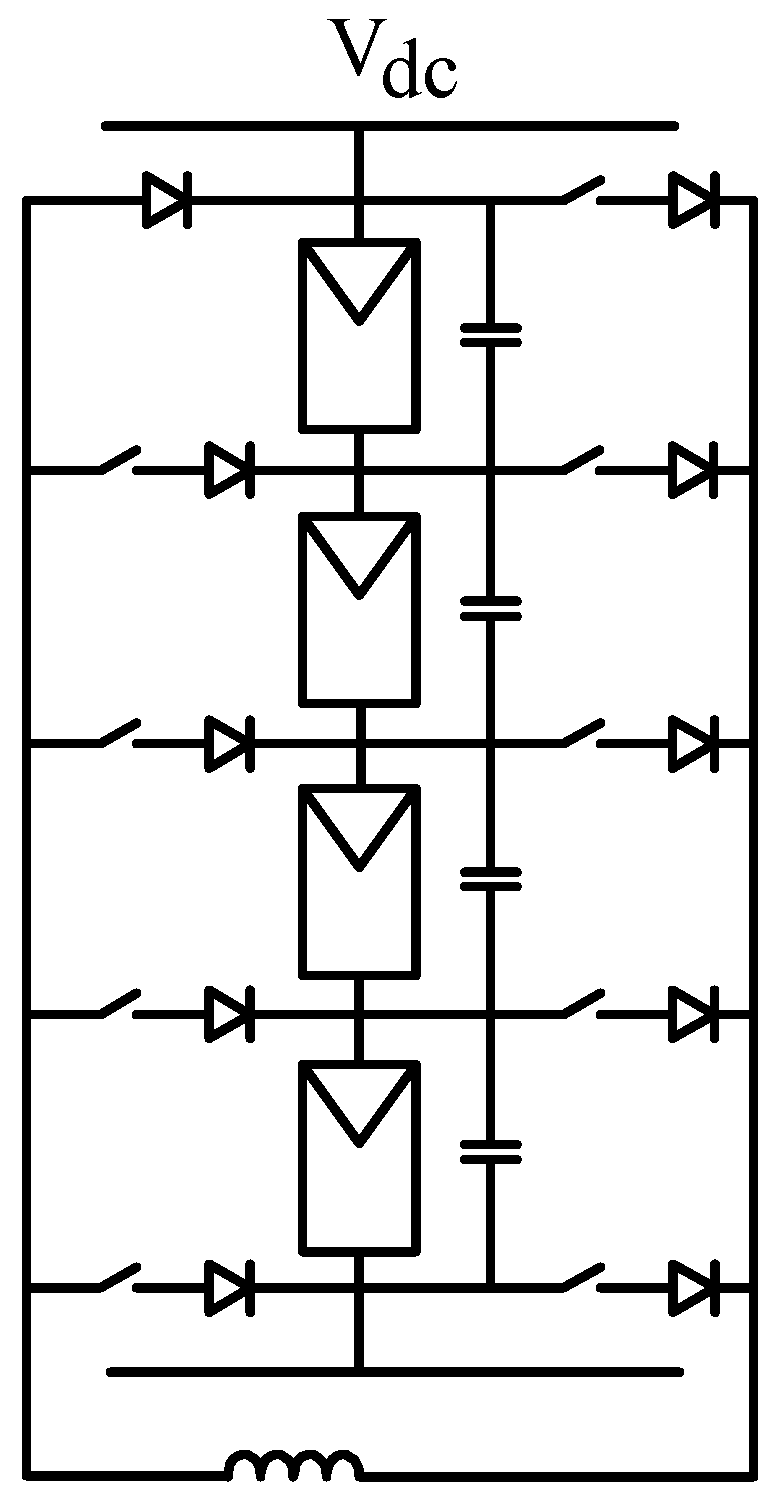
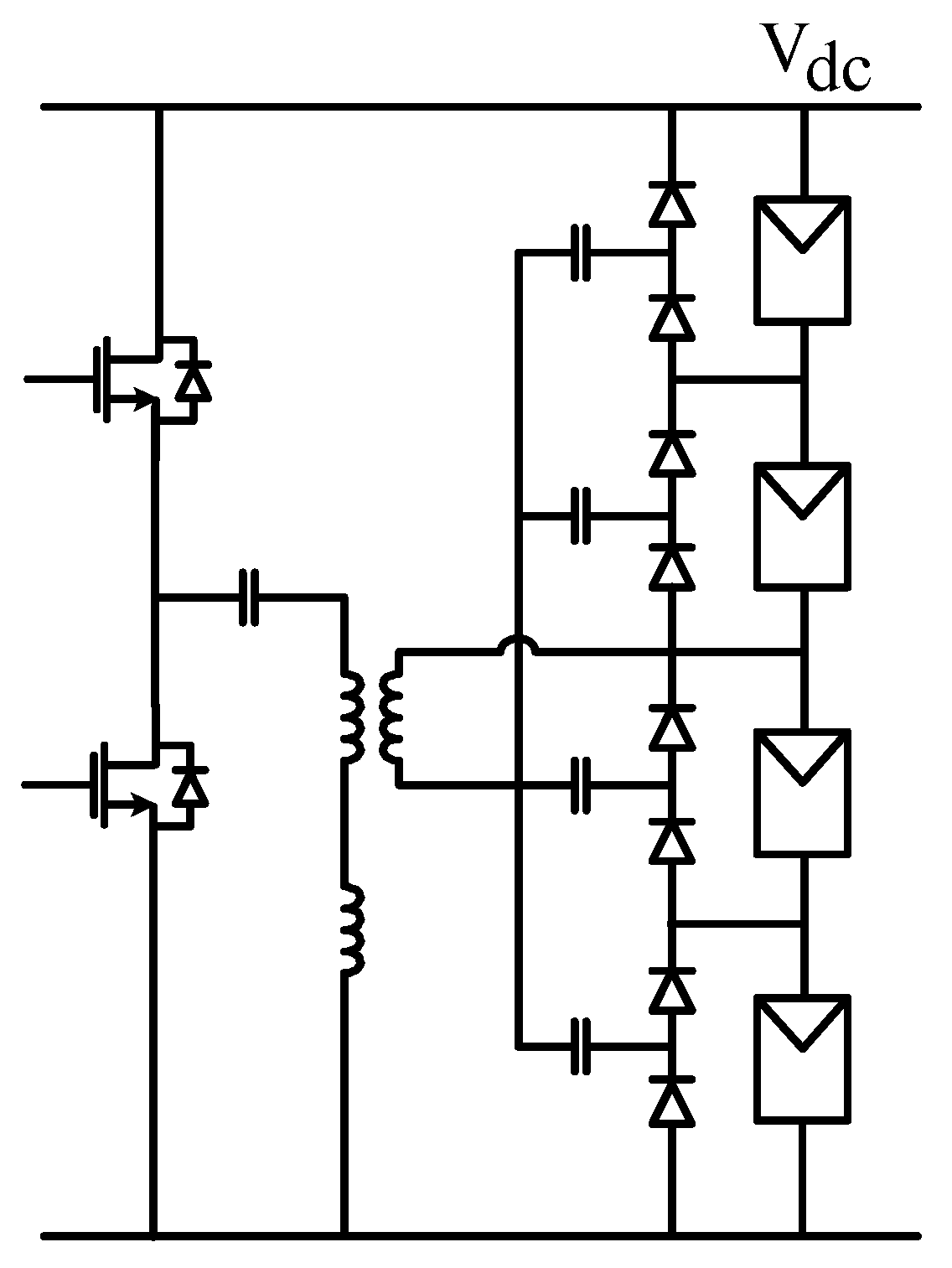
4.4. Sub-Module-Integrated Architectures
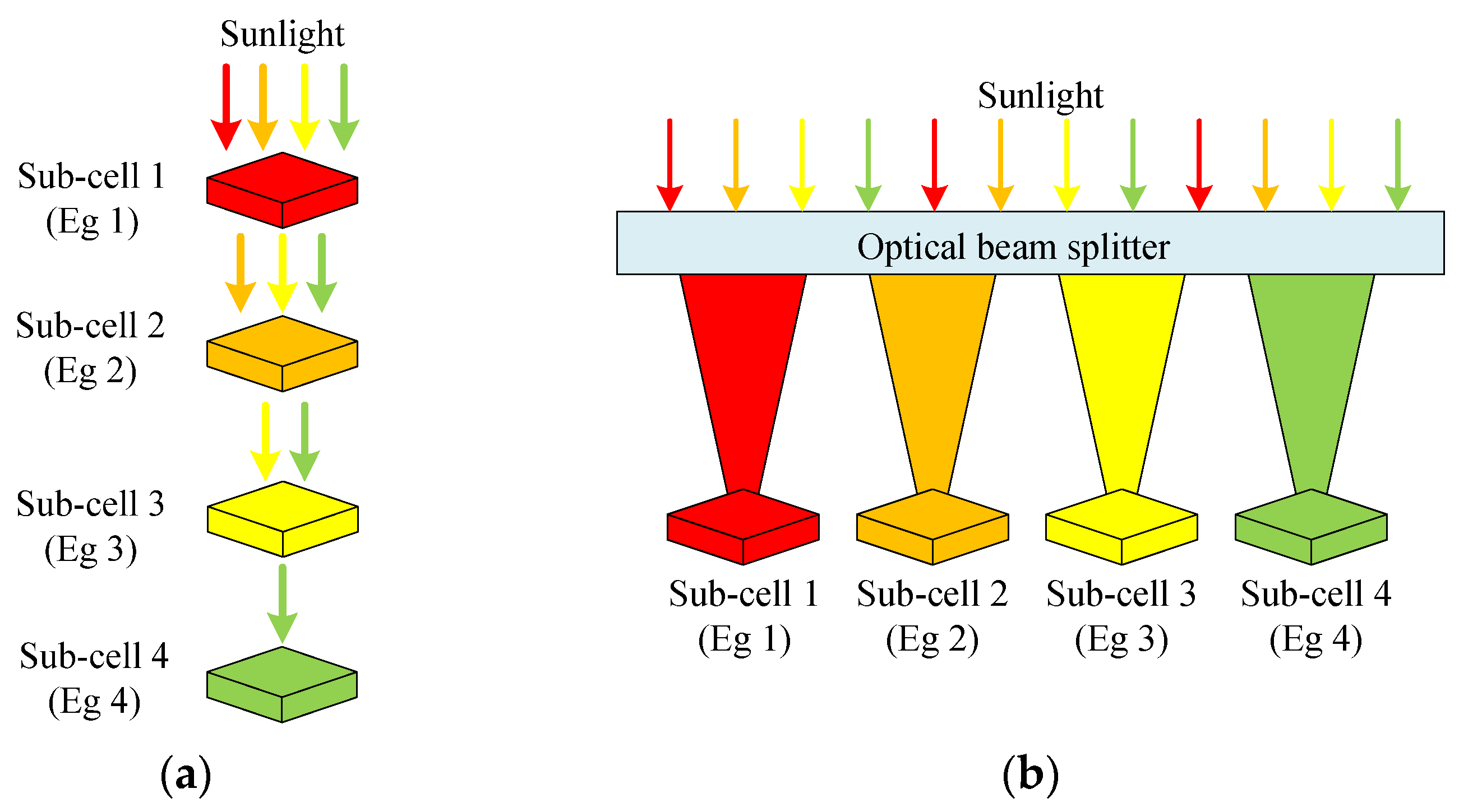
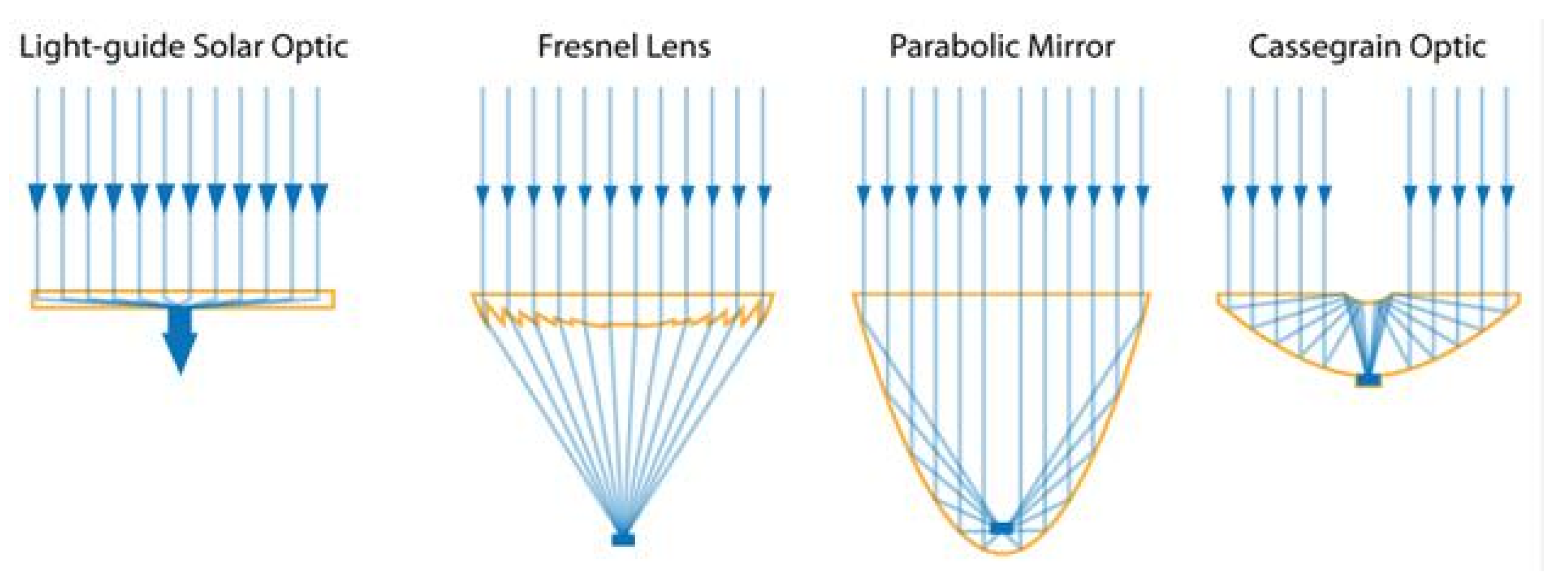
5. Emerging Multi-Junction and Concentrated PV
6. Adoption by the Public
7. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- The Nobel Prize in Physics 1921. Available online: https://www.nobelprize.org/prizes/physics/1921/summary/ (accessed on 8 August 2021).
- Solar Cell Central. Solar Electricity Costs. Available online: http://solarcellcentral.com/cost_page.html (accessed on 8 August 2021).
- Photovoltaic System. Available online: https://en.wikipedia.org/wiki/Photovoltaic_system (accessed on 8 August 2021).
- Esram, T.; Chapman, P.L. Comparison of photovoltaic array maximum power point tracking techniques. IEEE Trans. Energy Convers. 2007, 22, 439–449. [Google Scholar] [CrossRef] [Green Version]
- Trends in PV Applications 2020. Available online: https://iea-pvps.org/trends_reports/trends/ (accessed on 8 August 2021).
- Kajihara, A.; Harakawa, A.T. Model of photovoltaic cell circuits under partial shading. In Proceedings of the 2005 IEEE International Conference on Industrial Technology, Hong Kong, China, 14–17 December 2005; pp. 866–870. [Google Scholar]
- Feldman, J.; Singer, S.; Braunsten, A. Solar cell interconnections and shadow problem. Sol. Energy 1981, 26, 419–428. [Google Scholar] [CrossRef]
- Wang, Y.J.; Hsu, P.C. An investigation on partial shading of PV modules with different connection configurations of PV cells. Int. J. Energy 2011, 36, 3069–3078. [Google Scholar] [CrossRef]
- Bishop, J.W. Computer simulation of the effects of electrical mismatches in photovoltaic cell interconnection circuit. Solar Cells 1988, 25, 73–89. [Google Scholar] [CrossRef]
- Moballegh, S.; Jiang, J. Modeling, Prediction, and Experimental Validations of Power Peaks of PV Arrays Under Partial Shading Conditions. IEEE Trans. Sustain. Energy 2014, 5, 293–300. [Google Scholar] [CrossRef]
- Storey, J.; Wilson, P.R.; Bagnall, D. Simulation platform for dynamic photovoltaic arrays. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition (ECCE 2013), Denver, CO, USA, 15–19 September 2013; pp. 1617–1622. [Google Scholar]
- Gao, L.; Dougal, R.A.; Liu, S.; Iotova, A.P. Parallel-Connected Solar PV System to Address Partial and Rapidly Fluctuating Shadow Conditions. IEEE Trans. Ind. Electron. 2009, 56, 1548–1556. [Google Scholar]
- Teo, J.C.; Tan, R.H.; Mok, V.H.; Ramachandaramurthy, V.K.; Tan, C. Impact of Partial Shading on the P-V Characteristics and the Maximum Power of a Photovoltaic String. Energies 2018, 11, 1860. [Google Scholar] [CrossRef] [Green Version]
- Maki, A.; Valkealahti, S. Power Losses in Long String and Parallel-Connected Short Strings of Series-Connected Silicon-Based Photovoltaic Modules Due to Partial Shading Conditions. IEEE Trans. Energy Convers. 2012, 27, 173–183. [Google Scholar] [CrossRef]
- Gautam, N.K.; Kaushika, N.D. Network analysis of fault-tolerant solar photovoltaic arrays. Sol. Energy Mater. Solar Cells 2001, 69, 25–42. [Google Scholar] [CrossRef]
- Díaz-Dorado, E.; Suárez-García, A.; Carrillo, C.; Cidrás, J. Influence of the shadows in photovoltaic systems with different configurations of bypass diodes. In Proceedings of the 2010 International Symposium on Power Electronics Electrical Drives Automation and Motion (SPEEDAM), Pisa, Italy, 14–16 June 2010; pp. 134–139. [Google Scholar]
- Silvestre, S.; Boronat, A.; Chouder, A. Study of bypass diodes configuration on pv modules. Appl. Energy 2009, 86, 1632–1640. [Google Scholar] [CrossRef]
- Miyatake, M.; Toriumi, F.; Endo, T.; Fujii, N. A Novel maximum power point tracker controlling several converters connected to photovoltaic arrays with particle swarm optimization technique. In Proceedings of the European Conference on Power Electronics and Applications, Aalborg, Denmark, 2–5 September 2007; pp. 1–10. [Google Scholar]
- Boztepe, M.; Guinjoan, F.; Velasco-Quesada, G.; Silvestre, S.; Chouder, A.; Karatepe, E. Global MPPT Scheme for Photovoltaic String Inverters Based on Restricted Voltage Window Search Algorithm. IEEE Trans. Ind. Electron. 2014, 61, 3302–3312. [Google Scholar] [CrossRef]
- Acciari, G.; Graci, D.; La Scala, A. Higher PV module efficiency by a novel CBS bypass. IEEE Trans. Power Electron. 2011, 26, 1333–1336. [Google Scholar] [CrossRef]
- Swaleh, M.S.; Green, M.A. Effect of shunt resistance and bypass diode on the shadow tolerance of solar cell modules. Sol. Cells 1982, 5, 183. [Google Scholar] [CrossRef]
- Dzung, N.; Lehman, B. An Adaptive Solar Photovoltaic Array Using Model Based Reconfiguration Algorithm. IEEE Trans. Ind. Electron. 2008, 55, 2644–2654. [Google Scholar]
- Velasco-Quesada, G.; Guinjoan-Gispert, F.; Pique-Lopez, R.; Roman-Lumbreras, M.; Conesa-Roca, A. Electrical PV Array Reconfiguration Strategy for Energy Extraction Improvement in Grid-Connected PV Systems. IEEE Trans. Ind. Electron. 2009, 56, 4319–4331. [Google Scholar] [CrossRef] [Green Version]
- Storey, J.; Wilson, P.R.; Bagnall, D. The Optimized-String Dynamic Photovoltaic Array. IEEE Trans. Power Electron. 2014, 29, 1768–1776. [Google Scholar] [CrossRef] [Green Version]
- Storey, J.P.; Wilson, P.R.; Bagnall, D. Improved Optimization Strategy for Irradiance Equalization in Dynamic Photovoltaic Arrays. IEEE Trans. Power Electron. 2013, 28, 2946–2956. [Google Scholar] [CrossRef]
- Kjaer, S.B.; Pedersen, J.K.; Blaabjerg, F. A review of single-phase grid connected inverters for photovoltaic modules. IEEE Trans. Ind. Appl. 2005, 41, 1292–1306. [Google Scholar] [CrossRef]
- Myrzik, J.M.A.; Calais, M. String and module integrated inverters for single phase grid connected photovoltaic systems–A review. In Proceedings of the 2003 IEEE Bologna Power Tech Conference, Bologna, Italy, 23–26 June 2003; Volume 2. [Google Scholar]
- Yogesh, R.N.; Thorat, A.R. A review on photovoltaic module based grid connected power inverter. In Proceedings of the 2013 International Conference on Power, Energy and Control (ICPEC), Dindigul, India, 6–8 February 2013; pp. 272–276. [Google Scholar]
- Hu, H.; Harb, S.; Kutkut, N.; Batarseh, I.; Shen, Z.J. Power decoupling techniques for micro-inverters in PV systems-a review. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition (ECCE), Atlanta, GA, USA, 12–16 September 2010; pp. 3235–3240. [Google Scholar]
- Scholten, D.M.; Ertugrul, N.; Soong, W.L. Micro-inverters in small scale PV systems: A review and future directions. In Proceedings of the 2013 Australasian Universities Power Engineering Conference (AUPEC), Hobart, TAS, Australia, 29 September–3 October 2013; pp. 1–6. [Google Scholar]
- Oldenkamp, H.; de Jong, I.; van der Borg, N.; de Boer, B.; de Moor, H.; Sinke, W.C. PV-Wirefree versus Conventional Pv-Systems: Detailed Analysis of Difference in Energy Yield between Series and Parallel Connected Pv-Modules. Available online: http://www.oke-services.nl/pages/pvwirefree.htm (accessed on 8 August 2021).
- Daher, S.; Schmid, J.; Antunes, F.L.M. Multilevel Inverter Topologies for Stand-Alone PV Systems. IEEE Trans. Ind. Electron. 2008, 55, 2703–2712. [Google Scholar] [CrossRef]
- Malathy, S.; Ramaprabha, R.; Mathur, B.L. Asymmetrical multilevel inverters for partially shaded PV systems. In Proceedings of the 2013 International Conference on Circuits, Power and Computing Technologies (ICCPCT), Nagercoil, India, 20–21 March 2013; pp. 579–583. [Google Scholar]
- Echeverria, J.; Kouro, S.; Perez, M.; Abu-Rub, H. Multi-modular cascaded DC-DC converter for HVDC grid connection of large-scale photovoltaic power systems. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 6999–7005. [Google Scholar]
- Mishima, T.; Ohini, T. A Power Compensation and Control System for a Partially Shaded PV Array. Electr. Eng. Jpn. 2004, 146, 74–82. [Google Scholar] [CrossRef]
- Karatepe, E.; Hiyama, T.; Boztepe, M.; Colak, M. Voltage based power compensation system for photovoltaic generation system under partially shaded insolation conditions. Energy Convers. Manag. 2008, 49, 2307–2316. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, J.; Han, Y. PV Balancers: Concept, Architectures, and Realization. IEEE Trans. Power Electron. 2015, 30, 3479–3487. [Google Scholar] [CrossRef]
- Shimizu, T.; Hirakata, M.; Kamezawa, T.; Watanabe, H. Generation Control Circuit for Photovoltaic Modules. IEEE Trans. Power Electron. 2001, 16, 293–300. [Google Scholar] [CrossRef] [Green Version]
- Walker, G.; Xue, J.; Sernia, P. PV string per-module maximum power point enabling converters. In Proceedings of the Australasian Universities Power Engineering Conference, AUPEC’03, Christchurch, New Zealand, 28 September–1 October 2003. [Google Scholar]
- Walker, G.R.; Pierce, J.C. Photovoltaic Dc-Dc module integrated converter for novel cascaded and bypass grid connection topologies—design and optimisation. In Proceedings of the 37th IEEE Power Electronics Specialists Conference, Jeju, Korea, 18–22 June 2006; pp. 1–7. [Google Scholar]
- Nimni, Y.; Shmilovitz, D. A returned energy architecture for improved photovoltaic systems efficiency. In Proceedings of the 2010 IEEEE Symposium on Circuits and Systems (ISCAS), Paris, France, 30 May–2 June 2010; pp. 2191–2194. [Google Scholar]
- Ben-Yaakov, S.; Blumenfeld, A.; Cervera, A.; Evzelman, M. Design and evaluation of a modular resonant switched capacitors equalizer for PV panels. In Proceedings of the Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 4129–4136. [Google Scholar]
- Ball, N.E. Parallel and Virtual Parallel Interconnection of Solar Cells in Solar Panel. U.S. Patent 7,521,630, 21 April 2007. [Google Scholar]
- Pascual, C.; Krein, P.T. Switched capacitor system for automatic series battery equalization. In Proceedings of the Applied Power Electronics Conference and Exposition, Atlanta, GA, USA, 27 February 1997; Volume 2, pp. 848–854. [Google Scholar]
- Yuanmao, Y.; Cheng, K.W.E.; Yeung, Y.P.B. Zero-Current Switching Switched-Capacitor Zero-Voltage-Gap Automatic Equalization System for Series Battery String. IEEE Trans. Power Electron. 2012, 27, 3234–3242. [Google Scholar] [CrossRef]
- Shenoy, P.S.; Kim, K.A.; Johnson, B.B.; Krein, P.T. Differential Power Processing for Increased Energy Production and Reliability of Photovoltaic Systems. IEEE Trans. Power Electron. 2013, 28, 2968–2979. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, X.; Zhong, Y.; Matsui, M. A novel topology for solving the partial shading problem in photovoltaic power generation system. In Proceedings of the 2009 IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009; pp. 2130–2135. [Google Scholar]
- Sharma, P.; Agarwal, V. Exact Maximum Power Point Tracking of Grid-Connected Partially Shaded PV Source Using Current Compensation Concept. IEEE Trans. Power Electron. 2014, 29, 4684–4692. [Google Scholar] [CrossRef]
- Debnath, D.; De, P.; Chatterjee, K. Simple scheme to extract maximum power from series connected photovoltaic modules experiencing mismatched operating conditions. IEEE Trans. Power Electron. 2016, 9, 408–416. [Google Scholar] [CrossRef]
- Villa, L.F.L.; Ho, T.-P.; Crebier, J.-C.; Raison, B. A Power Electronics Equalizer Application for Partially Shaded Photovoltaic Modules. IEEE Trans. Power Electron. 2013, 6, 1179–1190. [Google Scholar]
- Villa, L.F.L.; Pichon, X.; Sarrafin-Ardelibi, F.; Raison, B.; Crebier, J.C.; Labonne, A. Toward the Design of Control Algorithms for a Photovoltaic Equalizer: Choosing the Optimal Switching Strategy and the Duty Cycle. IEEE Trans. Power Electron. 2014, 29, 1447–1460. [Google Scholar] [CrossRef]
- Villa, L.F.L.; Raison, B.; Crebier, J.-C. Toward the Design of Control Algorithms for a Photovoltaic Equalizer: Detecting Shadows through Direct Current Sampling. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 893–906. [Google Scholar] [CrossRef]
- Uno, M.; Kukita, A. Single-switch voltage equalizer using multi-stacked SEPIC for partially shaded series-connected PV modules. In Proceedings of the of 35th International Telecommunications Energy Conference Smart Power and Efficiency (INTELEC), Hamburg, Germany, 13–17 October 2013; pp. 1–6. [Google Scholar]
- Uno, M.; Kukita, A. Two-switch voltage equalizer using series-resonant inverter and voltage multiplier for partially-shaded series-connected photovoltaic modules. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition (ECCE), Denver, CO, USA, 15–19 September 2013; pp. 1311–1318. [Google Scholar]
- Sharma, P.; Agarwal, V. Maximum Power Extraction from a Partially Shaded PV Array Using Shunt-Series Compensation. IEEE J. Photovolt. 2014, 4, 1128–1137. [Google Scholar] [CrossRef]
- Kim, K.A.; Shenoy, P.S.; Krein, P.T. Converter Rating Analysis for Photovoltaic Differential Power Processing Systems. IEEE Trans. Power Electron. 2015, 30, 1987–1997. [Google Scholar] [CrossRef]
- Walker, G.R.; Sernia, P.C. Cascaded DC-DC converter connection of photovoltaic modules. IEEE Trans. Power Electron. 2004, 19, 1130–1139. [Google Scholar] [CrossRef]
- Femia, N.; Lisi, G.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Distributed Maximum Power Point Tracking of Photovoltaic Arrays: Novel Approach and System Analysis. IEEE Trans. Ind. Electron. 2008, 55, 2610–2621. [Google Scholar] [CrossRef] [Green Version]
- Roman, E.; Alonso, R.; Ibanez, P.; Elorduizapatarietxe, S.; Goitia, D. Intelligent PV module for grid-connected PV systems. IEEE Trans. Ind. Electron. 2006, 53, 1066–1073. [Google Scholar] [CrossRef]
- Xiao, W.; Ozog, N.; Dunford, W.G. Topology study of photovoltaic interface for maximum power point tracking. IEEE Trans. Ind. Electron. 2007, 54, 1696–1704. [Google Scholar] [CrossRef]
- Kim, K.A.; Krein, P.T. Photovoltaic converter module configurations for maximum power point operation. In Proceedings of the Power and Energy Conference at Illinois (PECI), Urbana, IL, USA, 12–13 February 2010; pp. 77–82. [Google Scholar]
- Linares, L.; Erickson, R.W.; MacAlpine, S.; Brandemuehl, M. Improved Energy Capture in Series String Photovoltaics via Smart Distributed Power Electronics. In Proceedings of the Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Exposition (APEC 2009), Washington, DC, USA, 15–19 February 2009; pp. 904–910. [Google Scholar]
- Svarc, J. Solar Panel Construction. Available online: https://www.cleanenergyreviews.info/blog/solar-panel-components-construction (accessed on 8 August 2021).
- Canadian Solar. Products and Solutions. Available online: https://www.csisolar.com/na/module/ (accessed on 8 August 2021).
- Yanzhi, W.; Xue, L.; Massoud, P.; Jaemin, K.; Naehyuck, C. Capital cost-aware design and partial shading-aware architecture optimization of a reconfigurable photovoltaic system. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 18–22 March 2013; pp. 909–912. [Google Scholar]
- Pilawa-Podgurski, R.C.N.; Perreault, D.J. Submodule Integrated Distributed Maximum Power Point Tracking for Solar Photovoltaic Applications. IEEE Trans. Power Electron. 2013, 28, 2957–2967. [Google Scholar] [CrossRef] [Green Version]
- Qin, S.; Barth, C.B.; Pilawa-Podgurski, R.C.N. Enhancing Microinverter Energy Capture with Submodule Differential Power Processing. IEEE Trans. Power Electron. 2016, 31, 3575–3585. [Google Scholar] [CrossRef]
- Dhople, S.V.; Ehlmann, J.L.; Davoudi, A.; Chapman, P.L. Multiple-input boost converter to minimize power losses due to partial shading in photovoltaic modules. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Atlanta, GA, USA, 12–16 September 2010; pp. 2633–2636. [Google Scholar]
- Feng, W.; Xinke, W.; Lee, F.C.; Fang, Z. Analysis of unified output MPPT control in Sub-Panel PV converter system. IEEE Trans. Power Electron. 2013, 29, 1275–1284. [Google Scholar] [CrossRef]
- Olalla, C.; Clement, D.; Rodriguez, M.; Maksimovic, D. Architectures and Control of Submodule Integrated DC–DC converters for photovoltaic applications. IEEE Trans. Power Electron. 2013, 28, 2980–2997. [Google Scholar] [CrossRef]
- Wang, F.; Zhu, T.; Zhuo, F.; Yi, H.; Shi, S.; Zhang, X. Analysis and Optimization of Flexible MCPT Strategy in Submodule PV Application. IEEE Trans. Sustain. Energy 2017, 8, 249–257. [Google Scholar] [CrossRef]
- Barnett, A.; Honsberg, C.; Kirkpatrick, D.; Kurtz, S.; Moore, D.; Salzman, D.; Schwartz, R.; Gray, J.; Bowden, S.; Goossen, K.; et al. 50% efficient solar cell architectures and designs. In Proceedings of the Conference Record of the IEEE 4th World Conference on Photovoltaic Energy Conversion, Waikoloa, HI, USA, 7–12 May 2006; Volume 2, pp. 2560–2564. [Google Scholar]
- Alam, M.K.; Khan, F.; Imtiaz, A.M. Optimization of subcell interconnection for multi junction solar cells using switching power converters. IEEE Trans. Sustain. Energy 2013, 4, 340–349. [Google Scholar] [CrossRef]
- Alam, M.K.; Khan, F.; Imtiaz, A.M. An efficient power electronics solution for lateral multi-junction solar cell systems. In Proceedings of the IECON 2011—37th Annual Conference on IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011; pp. 4373–4378. [Google Scholar]
- Khan, O.; Xiao, W.; Zeineldin, H.H. Gallium-Nitride-Based Submodule Integrated Converters for High-Efficiency Distributed Maximum Power Point Tracking PV Applications. IEEE Trans. Ind. Electron. 2016, 63, 966–975. [Google Scholar] [CrossRef]
- Morgan, N. New Ideas for Solar Power. Available online: https://slideplayer.com/slide/5220131/ (accessed on 8 August 2021).
- Sherif, R.; Paredes, A.; Cotal, H.; Hayden, H. A 2-kW concentrating PV array using triple junction cells. In Proceedings of the IEEE Photovoltaic Specialists Conference, New Orleans, LA, USA, 19–24 May 2002; pp. 1380–1383. [Google Scholar]
- Cotal, H.; Fetzer, C.; Boisvert, J.; Kinsey, G.; King, R.; Hebert, P.; Yoon, H.; Karam, N. III-V multijunction solar cells for concentrating photovoltaics. Energy Environ. Sci. 2009, 2, 174–192. [Google Scholar] [CrossRef]
- Seshan, C. CPV: Not just for hot deserts! In Proceedings of the IEEE Photovoltaic Specialists Conference, Honolulu, HI, USA, 20–25 June 2010; pp. 3075–3080. [Google Scholar]
- Zaman, M.S.; Poshtkouhi, S.; Palaniappan, V.; Li, K.W.; Bergveld, H.J.; Myskorg, S.; Trescases, O. Distributed Power-Management Architecture for a Low-Profile Concentrating-PV System. In Proceedings of the 15th International Power Electronics and Motion Control Conference (EPE-PEMC), Novi Sad, Serbia, 4–6 September 2012. [Google Scholar]
- Panchenko, P.; Kharchenko, V.; Vasant, P. Modeling of Solar Photovoltaic Thermal Modules. In Advances in Intelligent Systems and Computing; Springer Nature Switzerland AG: Cham, Switzerland, 2019; Volume 866, pp. 108–116. [Google Scholar] [CrossRef]
- Panchenko, V. Photovoltaic Thermal Module with Paraboloid Type Solar Concentrators. Int. J. Energy Optim. Eng. 2021, 10, 1–23. [Google Scholar] [CrossRef]
- Zsiborács, H.; Zentkó, L.; Pintér, G.; Vincze, A.; Baranyai, N.H. Assessing shading losses of photovoltaic power plants based on string data. Energy Rep. 2021, 7, 3400–3409. [Google Scholar] [CrossRef]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abramovitz, A.; Shmilovitz, D. Short Survey of Architectures of Photovoltaic Arrays for Solar Power Generation Systems. Energies 2021, 14, 4917. https://doi.org/10.3390/en14164917
Abramovitz A, Shmilovitz D. Short Survey of Architectures of Photovoltaic Arrays for Solar Power Generation Systems. Energies. 2021; 14(16):4917. https://doi.org/10.3390/en14164917
Chicago/Turabian StyleAbramovitz, Alexander, and Doron Shmilovitz. 2021. "Short Survey of Architectures of Photovoltaic Arrays for Solar Power Generation Systems" Energies 14, no. 16: 4917. https://doi.org/10.3390/en14164917
APA StyleAbramovitz, A., & Shmilovitz, D. (2021). Short Survey of Architectures of Photovoltaic Arrays for Solar Power Generation Systems. Energies, 14(16), 4917. https://doi.org/10.3390/en14164917





