Long-Term Natural Gas Consumption Forecasting Based on Analog Method and Fuzzy Decision Tree
Abstract
1. Introduction
2. Literature Review
3. Analog Forecasting
- The method of biological analogies,
- The method of spatial analogies,
- Historical analogy method,
- The method of space-time analogies.
- Determining the number of classes (clusters).
- Selection of class centers (centroids) by random selection of k observations, selection of the first k observations from a set, or selection that allows to maximize the distance of the clusters.
- Assigning points to the nearest centroids—each element is assigned to the class (cluster) to the center of which it has the closest (the measure of similarity here is the distance between the element and the centroid).
- Calculation of new cluster centers—most often the new center of the class is the point whose coordinates are the arithmetic mean of the coordinates of the elements belonging to this class.
- Repeating the algorithm until reaching the convergence criterion (usually it is a step in which the allocation of points has not changed or after the algorithm has reached the number of adopted iterations).
4. Fuzzy Approach in Learning Decision Trees
4.1. Basic Concepts of Fuzzy Learning
- partitioning,
- fuzzification,
- pruning tree.
4.2. Partitioning
4.3. Fuzzification
4.4. Pruning and Inducing Fuzzy Decision Tree
| Algorithm 1. Algorithm for fuzzy decision tree induction |
| Input: –a training set, –Input feature set, –target feature, –thresholds for control of growth of the tree |
| Output: Fuzzy Decision Tree FDT |
| START |
| 1: Create fuzzy decision tree FDT with a single root node |
| 2: if is empty or one of the ’s is below critical value then |
| 3: Mark DFT as leaf with the most common value of from as label |
| 4: Return DFT |
| 5: end if |
| 6: For each find with the smallest classification ambiguity |
| 7: for each outcome of do |
| 8: Recursively call procedure with corresponding partition |
| 9: Connect the root node to the returned subtree with an edge that is labelled as |
| 10: end for |
| 11: Return DFT |
| STOP |
- Converted FDT into set of rules.
- For each rule, calculate the membership of the object for the premise of rule.
- For each class, aggregate membership derived from all rules.
5. Data
5.1. Data Description
- Historical gas prices (local, global, current, and future),
- Weather data (temperature, wind, precipitation, and sunshine),
- Number and consumption of gas of individual customers (also price and income elasticity coefficients),
- Data on construction and renovation activities (construction of new houses, changes in energy consumption, and others),
- The number and consumption of gas by large consumers (size and characteristics of off-take, flexibility factors),
- Macroeconomic data (GDP, inflation, wages, unemployment rate, and others),
- Political situation
- Metadata (data of local government, statistical offices, and others).
5.2. Correlation Analysis
6. Methodology
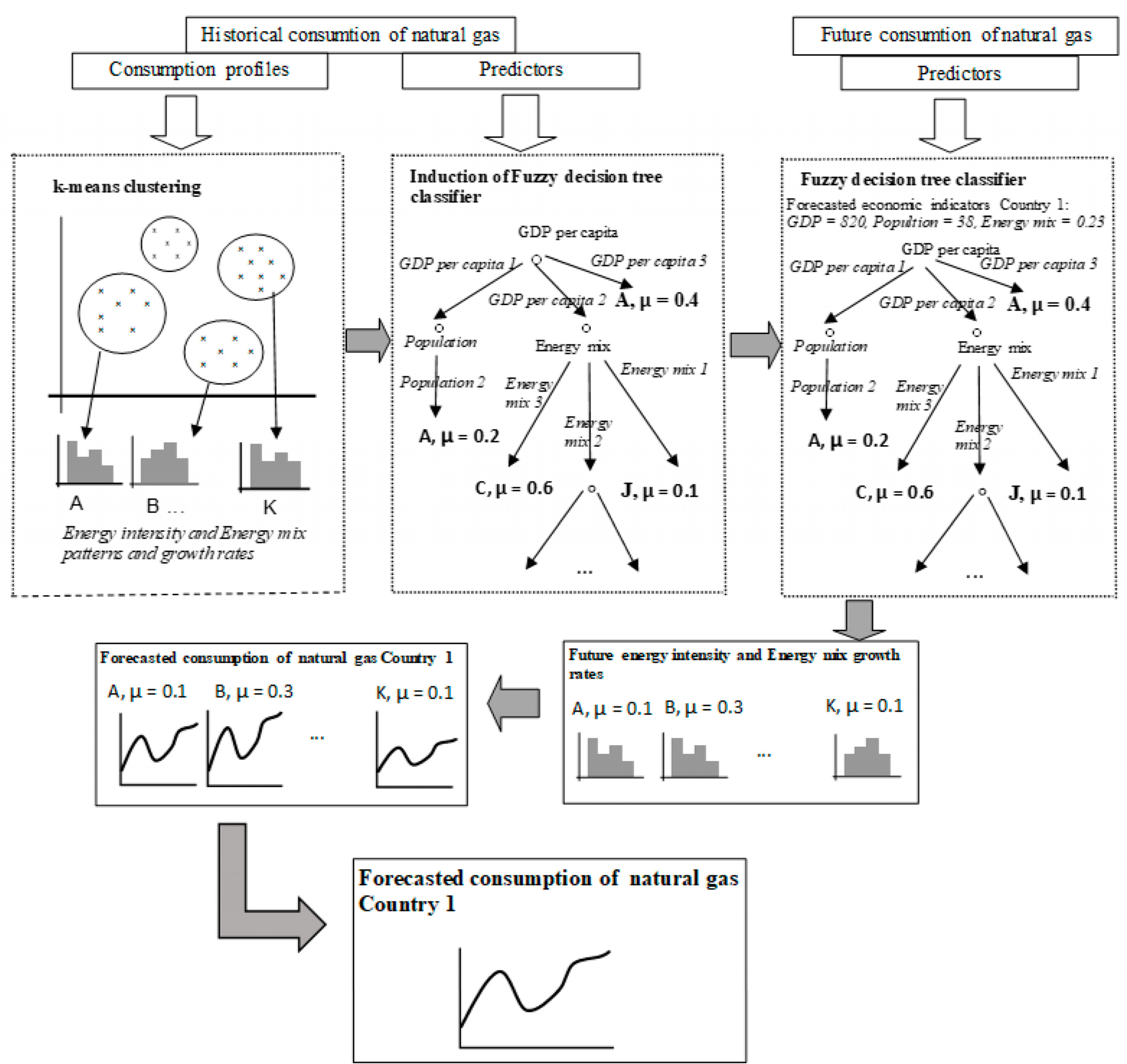
6.1. Finding Analogies Using Clustering
6.2. Fuzzy Decision Tree Learning
- Transformation of explanatory variables of crisp type into fuzzy variables.
- Extraction of knowledge from a dataset containing explanatory variables and explained variable with the help of a decision tree.
- Building a forecast based on the acquired knowledge.
6.3. Final Analog Forecasting of Natural Gas Consuption
| Algorithm 2. Algorithm for forecasting the annual consumption of natural gas |
| Input: S(B)—collection of m observations containing attributes—annual economic indicators for ms territorial units from the period of T years, where m = msT |
| Ster—set of forecasts of n economic indicators for ms territorial units for period of T years |
| Output: Sf—set of annual natural gas consumption forecasts for ms territorial units in h years |
| START |
| 1: Calculate the growth rates of the economy’s energy consumption indicators and the share of gas in the Energy mix for each ms territorial units in the subsequent years of the T period |
| 2: Assign observations from the set S(B) to k subsets Each subset contais selected energy carrier consumption indices, where the number of clusters k is determined by the cross-validation method for the declining cost function |
| 3: Calculate the average growth rates of the economy energy consumption indices and the share of gas in the Energy mix in period T for each of the k clusters |
| 4: Fuzzy the s selected attributes (economic and social indicators) from the set S(B) |
| 5: Build the fuzzy decision tree describing the relationship between s attributes and k analogy groups (clusters) |
| 6: Fuzzy input variable in test set Stest |
| 7: Build a collection of membership functions that define the similarity to particular groups of analogies using the fuzzy decision tree obtained in step 5 |
| 8: Build gas consumption forecasts for each territorial unit by relative chain increments using average growth rates for all clusters to which each observation belongs |
| 9: Calculate the forecasts for each territorial unit by sharpening the center of gravity method. Repeat the calculation for each unit in subsequent years of the forecast |
| STOP |
7. Results
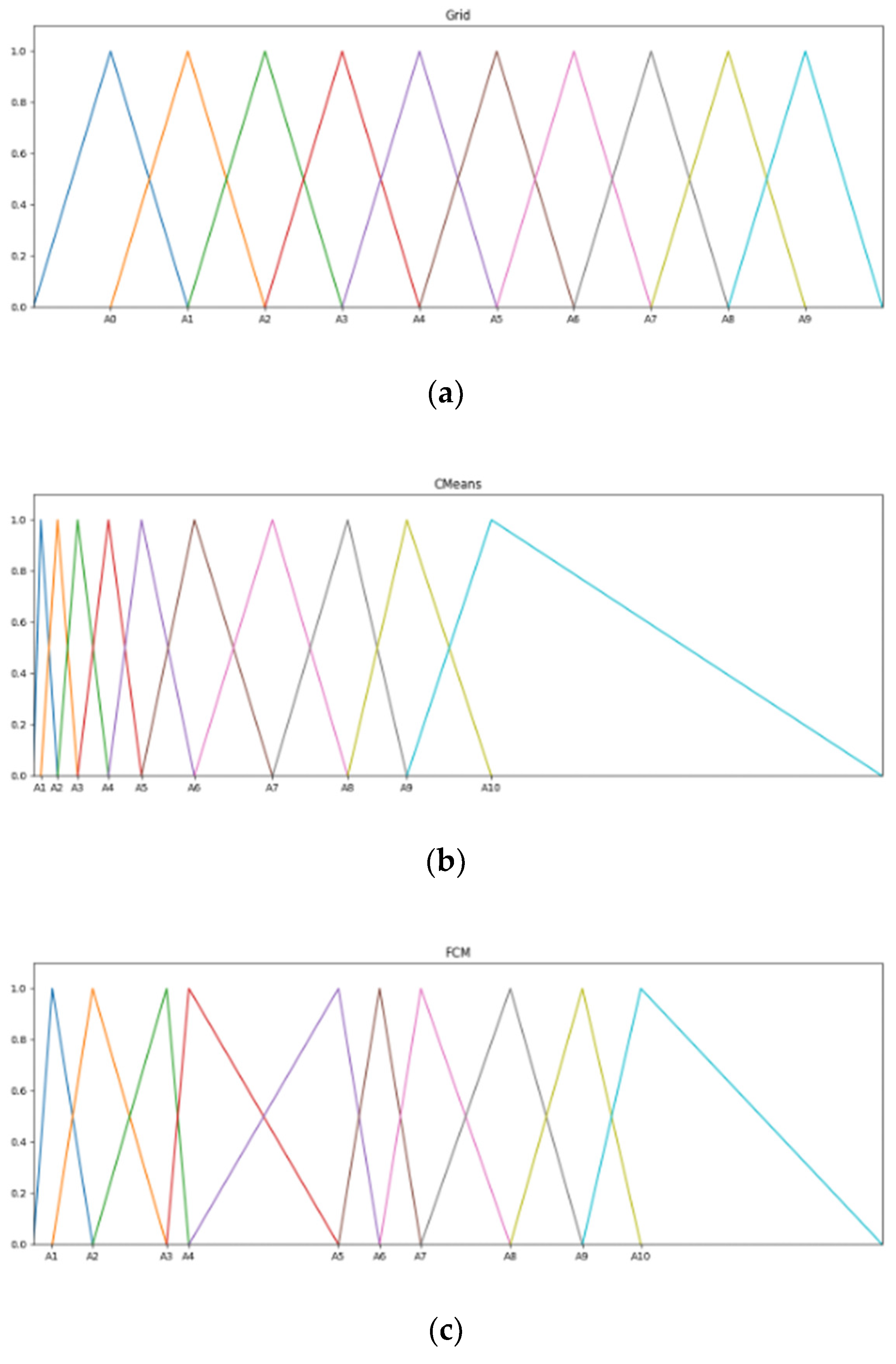
7.1. Hyper-Parameters Selection
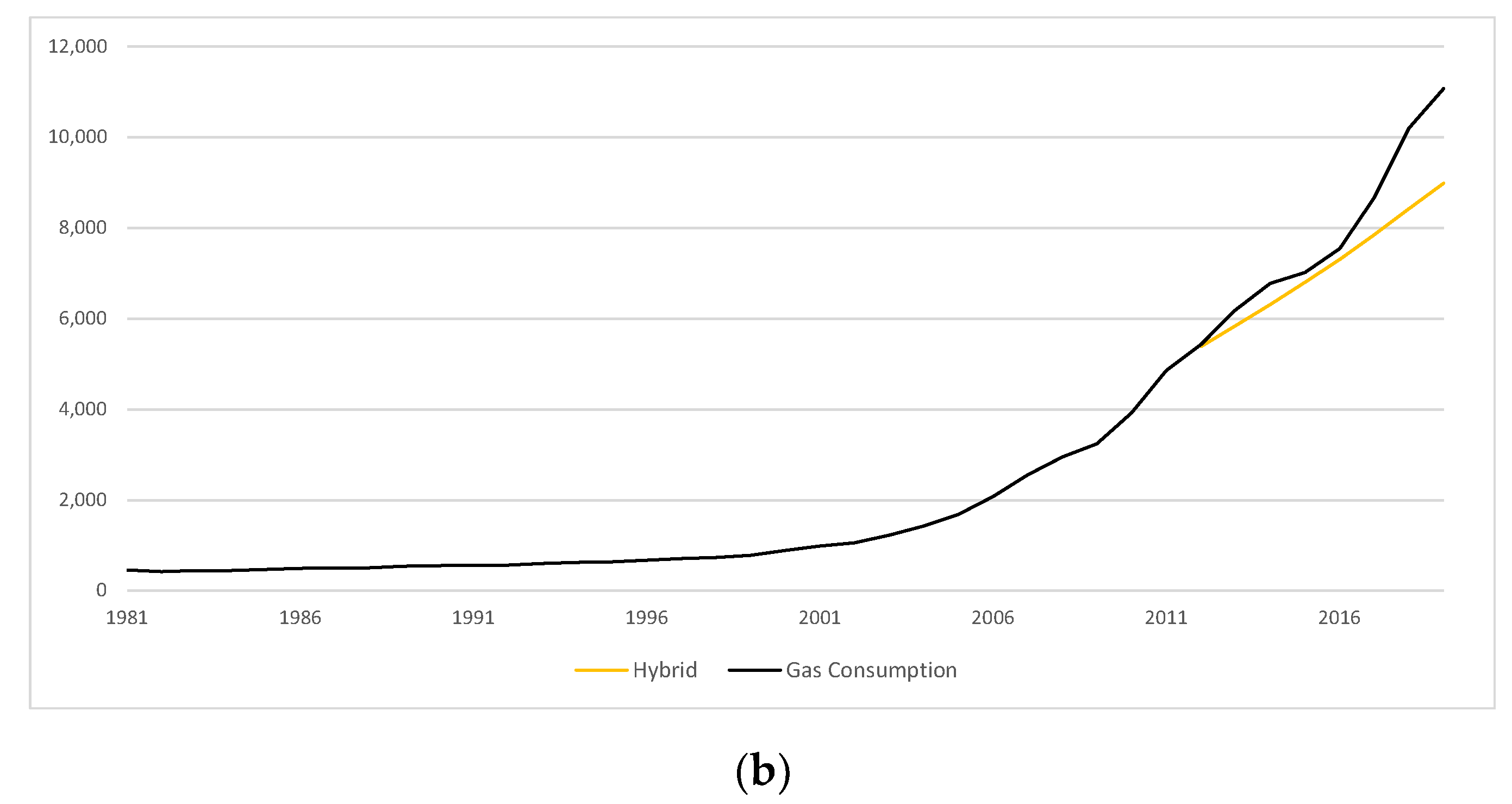
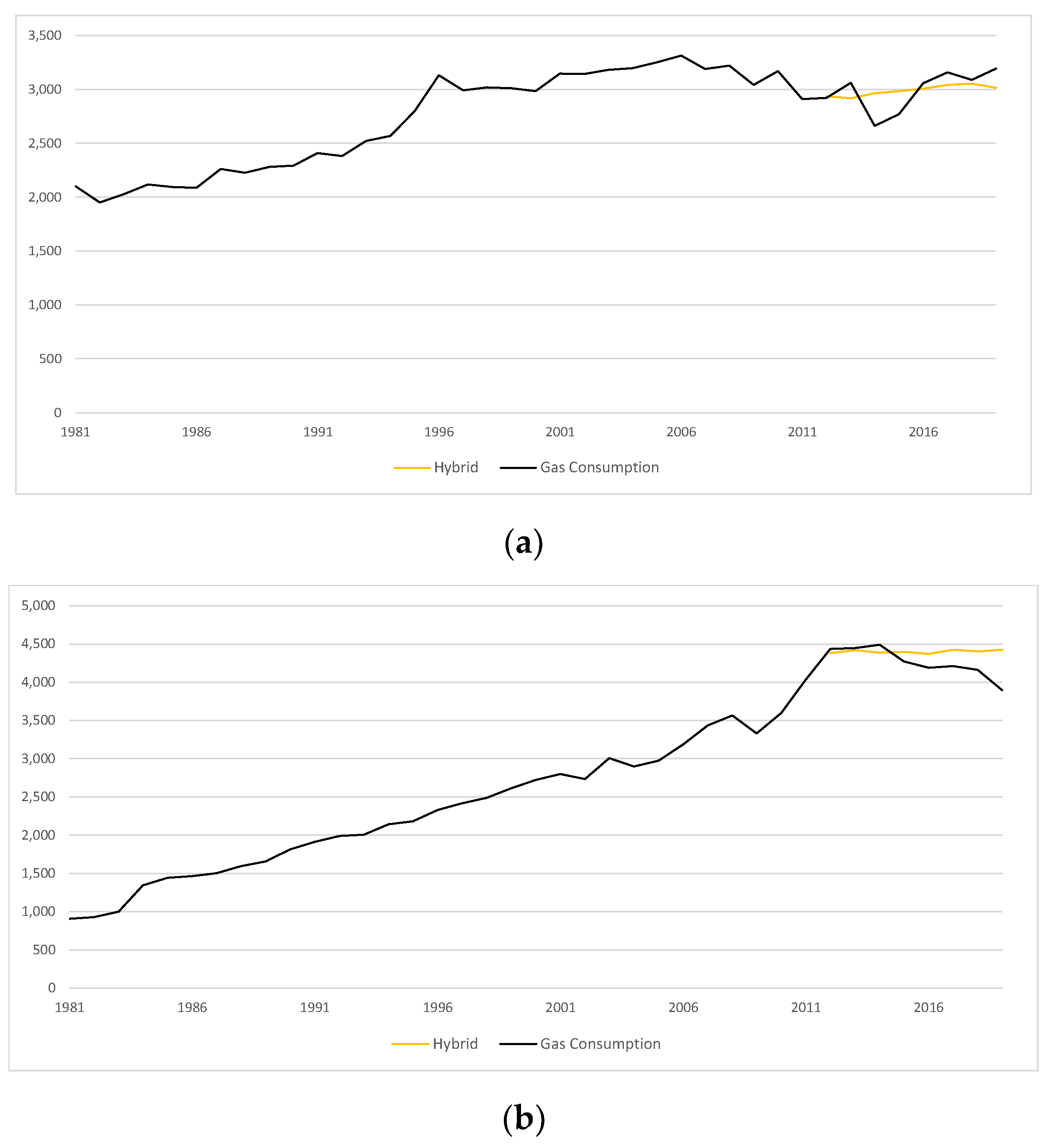
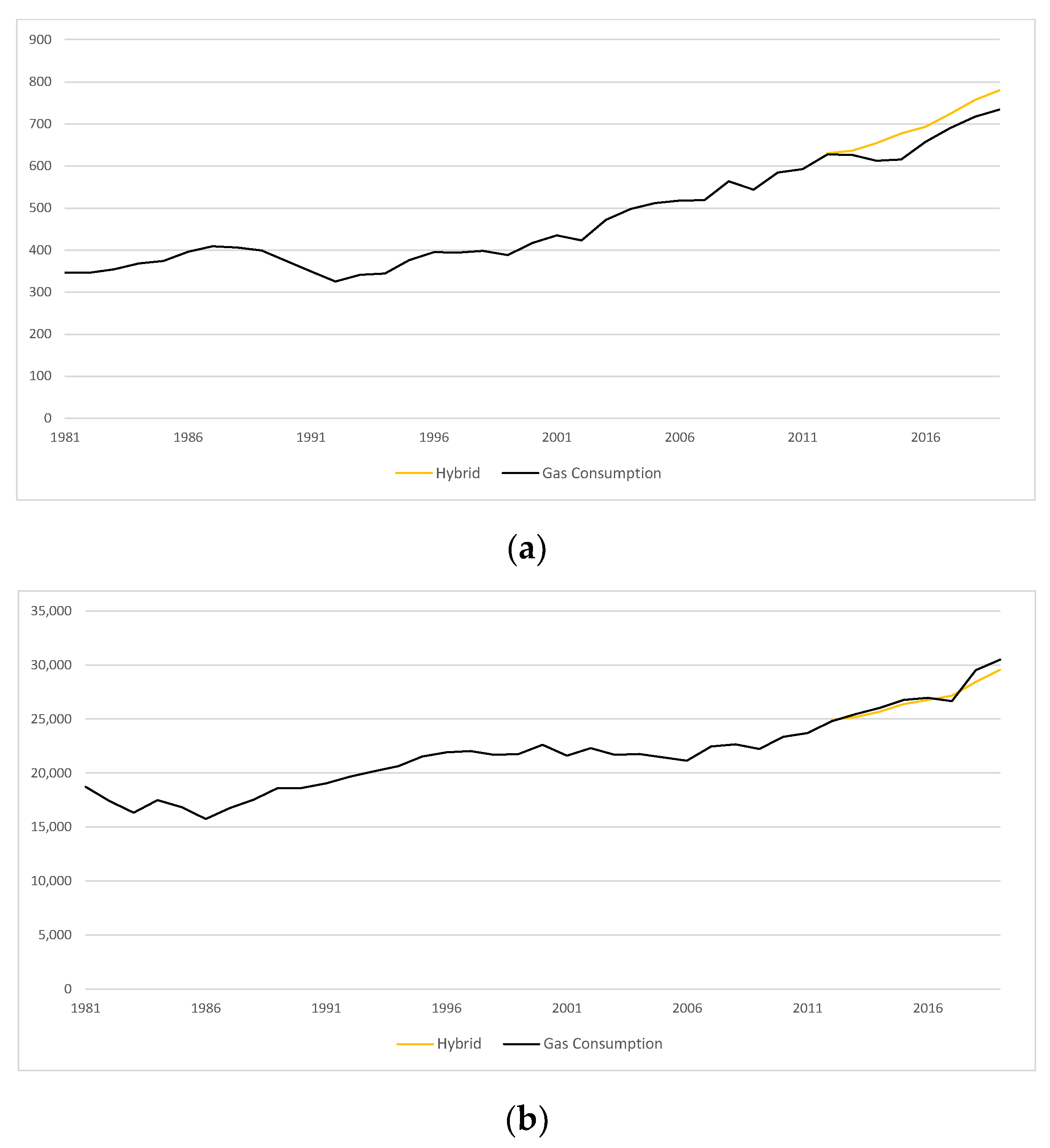
7.2. Comparison of Results
8. Discussion
8.1. Long-Term Natural Gas Consuption Forecasting for Teritiral Units
8.2. Methodology for Forecasting Long-Term Annual Gas Consumption with Low Forecast Error for Territorial Units
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sangrody, H.; Zhou, N.; Tutun, S.; Khorramdel, B.; Motalleb, M.; Sarailoo, M. Long term forecasting using machine learning methods. In Proceedings of the 2018 IEEE Power and Energy Conference at Illinois (PECI), Champaign, IL, USA, 22–23 February 2018; pp. 1–5. [Google Scholar]
- Choi, E.; Cho, S.; Kim, D.K. Power demand forecasting using long short-term memory (LSTM) deep-learning model for monitoring energy sustainability. Sustainability 2020, 12, 1109. [Google Scholar] [CrossRef]
- Wei, N.; Li, C.; Peng, X.; Li, Y.; Zeng, F. Daily natural gas consumption forecasting via the application of a novel hybrid model. Appl. Energy 2019, 250, 358–368. [Google Scholar] [CrossRef]
- Hribar, R.; Potočnik, P.; Šilc, J.; Papa, G. A comparison of models for forecasting the residential natural gas demand of an urban area. Energy 2019, 167, 511–522. [Google Scholar] [CrossRef]
- Marziali, A.; Fabbiani, E.; De Nicolao, G. Forecasting residential gas demand: Machine learning approaches and seasonal role of temperature forecasts. Int. J. Oil Gas Coal Technol. 2021, 26, 202. [Google Scholar] [CrossRef]
- Keijzer, B.; Visser, P.; Romillo, V.G.; Muñoz, V.G.; Boesten, D.; Meezen, M.; Rahola, T.B.S. Forecasting residential gas consumption with machine learning algorithms on weather data. E3S Web Conf. 2019, 111, 05019. [Google Scholar] [CrossRef]
- Panapakidis, I.P.; Dagoumas, A.S. Day-ahead natural gas demand forecasting based on the combination of wavelet transform and ANFIS/genetic algorithm/neural network model. Energy 2017, 118, 231–245. [Google Scholar] [CrossRef]
- Soldo, B. Forecasting natural gas consumption. Appl. Energy 2012, 92, 26–37. [Google Scholar] [CrossRef]
- Tamba, J.G.; Essiane, S.N.; Sapnken, E.F.; Koffi, F.D.; Nsouandélé, J.L.; Soldo, B.; Njomo, D. Forecasting natural gas: A literature survey. Int. J. Energy Econ. Policy 2018, 8, 216–249. [Google Scholar]
- Peak Hydrocarbons. Available online: https://eto.dnv.com/2019/peak-hydrocarbons (accessed on 17 July 2021).
- Maggio, G.; Cacciola, G. When will oil, natural gas, and coal peak? Fuel 2012, 98, 111–123. [Google Scholar] [CrossRef]
- Hubbert, M.K. Energy from fossil fuels. Science 1949, 109, 103–109. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, H.; Zhou, Q.; Wu, J.; Qin, S. China’s natural gas production and consumption analysis based on the multicycle Hubbert model and rolling grey model. Renew. Sustain. Energy Rev. 2016, 53, 1149–1167. [Google Scholar] [CrossRef]
- Siemek, J.; Nagy, S.; Rychlicki, S. Estimation of natural-gas consumption in Poland based on the logistic-curve interpretation. Appl. Energy 2003, 75, 1–7. [Google Scholar] [CrossRef]
- Mohr, S.H.; Wang, J.; Ellem, G.; Ward, J.; Giurco, D. Projection of world fossil fuels by country. Fuel 2015, 141, 120–135. [Google Scholar] [CrossRef]
- Espinoza, V.S.; Fontalvo, J.; Martí-Herrero, J.; Ramírez, P.; Capellán-Pérez, I. Future oil extraction in Ecuador using a Hubbert approach. Energy 2019, 182, 520–534. [Google Scholar] [CrossRef]
- Rehman, S.A.U.; Cai, Y.; Mirjat, N.H.; Walasai, G.D.; Shah, I.A.; Ali, S. The future of sustainable energy production in Pakistan: A system dynamics-based approach for estimating Hubbert peaks. Energies 2017, 10, 1858. [Google Scholar] [CrossRef]
- Cavallo, A.J. Hubbert’s petroleum production model: An evaluation and implications for world oil production forecasts. Nat. Resour. Res. 2004, 13, 211–221. [Google Scholar] [CrossRef]
- Sanchez-Ubeda, E.F.; Berzosa, A. Modeling and forecasting industrial end-use natural gas consumption. Energy Econ. 2007, 29, 710–742. [Google Scholar] [CrossRef]
- Suykens, J.; Lemmerling, P.; Favoreel, W.; de Moor, B.; Crepel, M.; Briol, P. Modelling the Belgian gas consumption using neural networks. Neural Process. Lett. 1996, 4, 157–166. [Google Scholar] [CrossRef]
- Gutiérrez, R.; Nafidi, A.; Gutiérrez Sánchez, R. Forecasting total natural-gas consumption in Spain by using the stochastic gompertz innovation diffusion model. Appl. Energy 2005, 80, 115–124. [Google Scholar] [CrossRef]
- Erdogdu, E. Natural gas demand in Turkey. Appl. Energy 2010, 87, 211–219. [Google Scholar] [CrossRef]
- Olgun, M.; Özdemir, G.; Aydemir, E. Forecasting of Turkey’s natural gas demand using artifical neural networks and support vector machines. Energy Sources Econ. Plan. Policy 2012, 11, 295–302. [Google Scholar]
- Boran, F.E. Forecasting natural gas consumption in Turkey using grey prediction. Energy Sources Econ. Plan. Policy 2015, 10, 208–213. [Google Scholar] [CrossRef]
- Gil, S.; Deferrari, J. Generalized model of prediction of natural gas consumption. J. Energy Resour. Technol. 2004, 126, 90–98. [Google Scholar] [CrossRef]
- Wu, L.; Liu, S.; Chen, H.; Zhang, N. Using a novel grey system model to forecast natural gas consumption in China. Math. Probl. Eng. 2015, 2015, 1–7. [Google Scholar] [CrossRef]
- Zeng, B.; Li, C. Forecasting the natural gas demand in China using a self-adapting intelligent grey model. Energy 2016, 112, 810–825. [Google Scholar] [CrossRef]
- Xu, G.; Wang, W. Forecasting China’s natural gas consumption based on a combination model. J. Nat. Gas. Chem. 2010, 19, 493–496. [Google Scholar] [CrossRef]
- Szoplik, J. Forecasting of natural gas consumption with artificial neural networks. Energy 2015, 85, 208–220. [Google Scholar] [CrossRef]
- Scarpa, F.; Bianco, V. Assessing the quality of natural gas consumption forecasting: An application to the Italian residential sector. Energies 2017, 10, 1879. [Google Scholar] [CrossRef]
- Forouzanfar, M.; Doustmohammadi, A.; Menhaj, M.B.; Hasanzadeh, S. Modeling and estimation of the natural gas consumption for residential and commercial sectors in Iran. Appl. Energy 2010, 87, 268–274. [Google Scholar] [CrossRef]
- Khan, M.A. Modelling and forecasting the demand for natural gas in Pakistan. Renew. Sustain. Energy Rev. 2015, 49, 1145–1159. [Google Scholar] [CrossRef]
- Levenberg, A.; Levenberg, A.; Pulman, S.; Moilanen, K.; Simpson, E.; Roberts, S. Predicting economic indicators from web text using sentiment composition. Int. J. Comput. Commun. Eng. 2014, 3, 109–115. [Google Scholar] [CrossRef][Green Version]
- Merkel, G.D.; Povinelli, R.J.; Brown, R.H. Short-term load forecasting of natural gas with deep neural network regression. Energies 2018, 11, 2008. [Google Scholar] [CrossRef]
- Bianco, V.; Scarpa, F.; Tagliafico, L.A. Scenario analysis of nonresidential natural gas consumption in Italy. Appl. Energy 2014, 113, 392–403. [Google Scholar] [CrossRef]
- Bianco, V.; Scarpa, F.; Tagliafico, L.A. Analysis and future outlook of natural gas consumption in the Italian residential sector. Energy Convers. Manag. 2014, 87, 754–764. [Google Scholar] [CrossRef]
- Šebalj, D.; Mesarić, J.; Dujak, D. Predicting natural gas consumption—A literature review. In Proceedings of the Central European Conference on Information and Intelligent Systems; Faculty of Organization and Informatics Varazdin, Zagreb, Croatia, 27–29 September 2017; pp. 293–300. [Google Scholar]
- Paliński, A. Data warehouses and data mining in forecasting the demand for gas and gas storage services. Naft. Gaz 2018, 74, 283–289. [Google Scholar] [CrossRef]
- Paliński, A. Forecasting gas demand using artificial intelligence methods. Naft. Gaz 2019, 75. [Google Scholar] [CrossRef]
- Bartels, R.; Fiebig, D.G.; Nahm, D. Regional end-use gas demand in Australia. Econ. Rec. 1996, 72, 319–331. [Google Scholar] [CrossRef]
- Behrouznia, A.; Saberi, M.; Azadeh, A.; Asadzadeh, S.M.; Pazhoheshfar, P. An adaptive network based fuzzy inference system-fuzzy data envelopment analysis for gas consumption forecasting and analysis: The case of South America. In Proceedings of the International Conference on Intelligent and Advanced Systems, Manila, Philippines, 15–17 June 2010. [Google Scholar] [CrossRef]
- Elragal, H. Improving neural networks prediction using fuzzy-genetic model. In Proceedings of the Twenty-First National Radio Science Conference, Cairo, Egypt, 18 March 2004; p. C12-1. [Google Scholar]
- Hambali, M.A. Electric power load forecast using decision tree algorithms. Comput. Inf. Syst. Dev. Inform. Allied Res. J. 2016, 7, 29–42. [Google Scholar]
- Fiordaliso, A.A. Constrained Takagi–Sugeno fuzzy system that allows for better interpretation and analysis. Fuzzy Sets Syst. 2001, 118, 307–318. [Google Scholar] [CrossRef]
- Vitullo, S.; Brown, R.; Corliss, G.; Marx, B. Mathematical models for natural gas forecasting. Can. Appl. Math. Q. 2009, 17, 1005–1013. [Google Scholar]
- Liu, J.; Wang, S.; Wei, N.; Chen, X.; Xie, H.; Wang, J. Natural gas consumption forecasting: A discussion on forecasting history and future challenges. J. Nat. Gas. Sci. Eng. 2021, 90, 103930. [Google Scholar] [CrossRef]
- Azadeh, A.; Asadzadeh, S.M.; Saberi, M.; Nadimi, V.; Tajvidi, A.; Sheikalishahi, M. A neuro-fuzzy-stochastic frontier analysis approach for long-term natural gas consumption forecasting and behavior analysis: The cases of Bahrain, Saudi Arabia, Syria, and UAE. Appl. Energy 2011, 88, 3850–3859. [Google Scholar] [CrossRef]
- Thomassey, S.; Fiordaliso, A. A hybrid sales forecasting system based on clustering and decision trees. Decis. Support. Syst. 2006, 42, 408–421. [Google Scholar] [CrossRef]
- Basallo-Triana, M.J. Analogue-based demand forecasting of short life-cycle products: A regression approach and a comprehensive assesment. Int. J. Prod. Res. 2017, 55, 2336–2350. [Google Scholar] [CrossRef]
- Skalna, I.; Rębiasz, B.; Gaweł, B.; Basiura, B.; Duda, J.; Opiła, J.; Pełech-Pilichowski, T. Advances in Fuzzy Decision Making: Theory and Practice, Studies in Fuzziness and Soft Computing; Springer: New York, NY, USA, 2015; ISBN 978-3-319-26492-9. [Google Scholar]
- Gaweł, B.; Rębiasz, B.; Skalna, I. Data mining methods for long-term forecasting of market demand for industrial goods. In Information Systems Architecture and Technology; Wilimowska, Z., Borzemski, L., Grzech, A., Świątek, J., Eds.; Springer: Cham, Germany, 2016; pp. 3–13. [Google Scholar]
- Lorenz, E.N. Atmospheric predictability as revealed by naturally occurring analogues. J. Atmos. Sci. 1969, 26, 636–646. [Google Scholar] [CrossRef]
- Rogers, D.S.; Green, H.L. A new perspective on forecasting store sales: Applying statistical models and techniques in the analog approach. Geogr. Rev. 1979, 69, 449–458. [Google Scholar] [CrossRef]
- Sidle, R.E.E.; Lee, W.J.J. An update on the use of reservoir analogs for the estimation of oil and gas reserves. SPE Econ. Manag. 2010, 2, 80–85. [Google Scholar] [CrossRef]
- Szozda, N. Analogous forecasting of products with a short life cycle. DMMS 2010, 4, 71–85. [Google Scholar] [CrossRef]
- Zeliaś, A.; Pawełek, B.; Wanat, S. Prognozowanie Ekonomiczne Teoria Przykłady Zadania; PWN: Warszawa, Poland, 2020; ISBN 83-01-14043-7. [Google Scholar]
- Macqueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June–18 July 1967; pp. 281–297. [Google Scholar]
- Rokach, L.; Maimon, O. Data mining with decision trees: Theory and applications. In Machine Perception and Artificial Intelligence, 2nd ed.; World Scientific: Singapore, 2014; Volume 81, ISBN 978-981-4590-07-5. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Yuan, Y.; Shaw, M.J. Induction of fuzzy decision trees. Fuzzy Sets Syst. 1995, 69, 125–139. [Google Scholar] [CrossRef]
- Silva, P.C.D.L.E.; Júnior, C.A.S.; Alves, M.A.; Silva, R.C.P.; Vieira, G.L.; Lucas, P.D.O.E.; Sadaei, H.J.; Guimarães, F.G. PYFTS/pyFTS: Stable Version 1.6; Zenodo: Geneva, Switzerland, 2019; Available online: https://zenodo.org/record/2669398 (accessed on 17 July 2021).
- Statistical Review of World Energy. Available online: https://www.bp.com/en/global/corporate/energy-economics/statistical-review-of-world-energy.html (accessed on 11 February 2021).
- World Development Indicators. Available online: https://datacatalog.worldbank.org/dataset/world-development-indicators (accessed on 11 February 2021).
- KAPSARC Data Portal. Available online: https://datasource.kapsarc.org/pages/home/ (accessed on 12 February 2021).
- Balfe, P.; Kelp, O. Gas consumption forecasting. A methodology. Acil Allen Consulting: Brisbane, Australia, 2014. Available online: https://www.aemo.com.au/-/media/files/gas/national_planning_and_forecasting/ngfr/gas-consumption-forecasting-methodology.pdf (accessed on 9 August 2021).
- Hafezi, R.; Akhavan, A.N.; Zamani, M.; Pakseresht, S.; Shamshirband, S. Developing a data mining based model to extract predictor factors in energy systems: Application of global natural gas demand. Energies 2019, 12, 4124. [Google Scholar] [CrossRef]
- Azadeh, A.; Zarrin, M.; Rahdar Beik, H.; Aliheidari Bioki, T. A neuro-fuzzy algorithm for improved gas consumption forecasting with economic, environmental and IT/IS indicators. J. Pet. Sci. Eng. 2015, 133, 716–739. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. The M4 competition: 100,000 time series and 61 forecasting methods. Int. J. Forecast. 2020, 36, 54–74. [Google Scholar] [CrossRef]
- Hyndman, R.; Koehler, A.B.; Ord, J.K.; Snyder, R.D. Forecasting with Exponential Smoothing: The State Space Approach; Springer Science and Business Media: Berlin, Germany, 2008. [Google Scholar]
- Hyndman, R.J.; Khandakar, Y. Automatic time series forecasting: The forecast package for R. J. Stat. Softw. 2008, 27, 1–22. [Google Scholar] [CrossRef]

| Energy_GDP | — | Energy intensity of GDP–ratio of annual energy consumption to GDP in TJ/billion USD at constant prices 2010 |
| NG_mix | — | Share of natural gas consumption in the Energy mix (in total annual consumption of primary energy carriers) |
| GDP_PC | — | GDP per capita in USD at constant prices 2010 |
| Industry_GDP | — | The share of industrial production in generating GDP |
| HeatingDays | — | Heating Degree Days (HDD) index for 15 degrees Celsius |
| Population | — | The country’s population in millions |
| CO2_GDP | — | Relation of CO2 emissions to GDP in million tons/billion USD at constant prices 2010 |
| GDP | — | Annual GDP in USD billion at constant prices 2010 |
| NG | — | Annual consumption of natural gas in TJ |
| Mean | Median | Standard Deviation | Kurtosis | Skewness | Min | Max | Number of Observations | |
|---|---|---|---|---|---|---|---|---|
| Energy_GDP | 10.7 | 7.2 | 10.3 | 17.7 | 3.7 | 0.0 | 92.8 | 3668 |
| NG_mix | 0.2 | 0.2 | 0.2 | 0.9 | 1.2 | 0.0 | 0.9 | 4064 |
| GDP_PC | 19,036.0 | 11,969.0 | 19,560.0 | 3.0 | 2.0 | 173.0 | 116,233.0 | 3665 |
| Industry_GDP | 31.7 | 29.2 | 11.9 | 2.1 | 1.1 | 0.0 | 84.8 | 3063 |
| HeatingDays | 898.0 | 9455.0 | 6729.0 | −1.0 | 0.0 | 0.0 | 25,416.0 | 4345 |
| Population | 58.3 | 14.20 | 167.6 | 36.40 | 5.9 | 0.0 | 1397.7 | 4345 |
| CO2_GDP | 0.7 | 0.4 | 0.7 | 13.80 | 3.3 | 0.0 | 5.5 | 3634 |
| GDP | 602.4 | 169.7 | 1567.1 | 50.10 | 6.3 | 0.0 | 18,273.0 | 3703 |
| NG | 1080.0 | 262.5 | 3016.3 | 35.50 | 5.7 | 0.0 | 30,479.0 | 3564 |
| Variable | Energy_ GDP | NG_mix | GDP_PC | Industry_ GDP | Heating Days | Population | CO2_GDP | GDP | NG |
|---|---|---|---|---|---|---|---|---|---|
| Energy_GDP | 1.00 | 0.39 | −0.37 | 0.22 | 0.06 | 0.19 | 0.96 | −0.12 | 0.06 |
| NG_mix | 0.39 | 1.00 | −0.05 | 0.26 | −0.08 | −0.18 | 0.30 | −0.06 | 0.18 |
| GDP_PC | −0.37 | −0.05 | 1.00 | −0.17 | 0.34 | −0.20 | −0.42 | 0.22 | 0.11 |
| Industry_GDP | 0.22 | 0.26 | −0.17 | 1.00 | −0.23 | 0.03 | 0.27 | −0.15 | −0.07 |
| HeatingDays | 0.06 | −0.08 | 0.34 | −0.23 | 1.00 | −0.11 | 0.04 | 0.07 | 0.14 |
| Population | 0.19 | −0.18 | −0.20 | 0.03 | −0.11 | 1.00 | 0.28 | 0.33 | 0.19 |
| CO2_GDP | 0.96 | 0.30 | −0.42 | 0.27 | 0.04 | 0.28 | 1.00 | −0.11 | 0.05 |
| GDP | −0.12 | −0.06 | 0.22 | −0.15 | 0.07 | 0.33 | −0.11 | 1.00 | 0.80 |
| NG | 0.06 | 0.18 | 0.11 | −0.07 | 0.14 | 0.19 | 0.05 | 0.80 | 1.00 |
| Cluster | Energy_GDP (TJ/USD Billion) | NG_mix (%) | Number of Cases | Percent (%) |
|---|---|---|---|---|
| 1 | 69.09 | 0.73 | 14 | 0.62 |
| 2 | 15.66 | 0.05 | 196 | 8.64 |
| 3 | 31.90 | 0.11 | 53 | 2.34 |
| 4 | 44.67 | 0.40 | 27 | 1.19 |
| 5 | 61.34 | 0.45 | 13 | 0.57 |
| 6 | 37.01 | 0.85 | 30 | 1.32 |
| 7 | 6.31 | 0.13 | 431 | 19.00 |
| 8 | 9.74 | 0.46 | 131 | 5.77 |
| 9 | 10.85 | 0.65 | 115 | 5.07 |
| 10 | 87.90 | 0.79 | 11 | 0.48 |
| 11 | 9.78 | 0.35 | 270 | 11.90 |
| 12 | 6.24 | 0.02 | 475 | 20.93 |
| 13 | 23.31 | 0.52 | 45 | 1.98 |
| 14 | 39.69 | 0.64 | 33 | 1.45 |
| 15 | 7.42 | 0.23 | 425 | 18.73 |
| Partition | Grid | c-Means | Fuzzy c-Means |
|---|---|---|---|
| A1 | [−12441; 312; 13,066] | [312; 1502; 4474] | [312; 3127; 6129] |
| A2 | [312; 13,066; 25,821] | [1502; 4474; 8332] | [3127; 6129; 6461] |
| A3 | [13,066; 25,821; 38,575] | [4474; 8332; 13,337] | [6129; 6461; 13,511] |
| A4 | [25,821; 38,575; 51,329] | [8332; 13,337; 19,226] | [6461; 13,511; 14,920] |
| A5 | [38,575; 51,329; 64,084] | [13,337; 19,226; 26,060] | [13,511; 14,920; 24,823] |
| A6 | [51,329, 64,084; 76,838] | [19,226; 26,060; 32,233] | [14,920; 24,823; 33,456] |
| A7 | [64,084; 76,838; 89,592]) | [26,060; 32,233; 39,576] | [24,823; 33,456; 38,081] |
| A8 | [76,838; 89,592; 102,347] | [32,233; 39,576; 48,189] | [33456; 38,081; 39,270] |
| A9 | [89,592; 102,347, 115,101] | [39,576; 48,189; 62,294] | [38,081; 39,270; 53,481] |
| A10 | [102,347; 115,101; 127,856] | [48,189; 62,294; 127,856] | [39,270; 53,481;127,856] |
| Method | RMSE | MAPE (%) |
|---|---|---|
| Naïve approach 1 | 1259 | 16.8 |
| Classical approach (ETS, ARIMA) 1 | 1203 | 16.3 |
| ML benchmark (NARR) | 534 | 15.3 |
| Linear regression (pooled) | 923 | 100.0 |
| Individual linear trend for each country | 567 | 13.0 |
| Hybrid with crisp decision tree | 271 | 7.8 |
| Hybrid with crisp decision tree and random term | ~552 | ~12.7 |
| Hybrid with fuzzy decision tree | 395 | 9.5 |
| Country | Our Hybrid Approach (MAPE) | Classical (MAPE) |
|---|---|---|
| United States | 1.80% | 3.12% |
| China | 9.50% | 4.94% |
| Japan | 4.30% | 5.60% |
| Mexico | 4.10% | 4.39% |
| Germany | 4.40% | 6.08% |
| Algeria | 5.80% | 7.38% |
| Poland | 5.10% | 4.14% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaweł, B.; Paliński, A. Long-Term Natural Gas Consumption Forecasting Based on Analog Method and Fuzzy Decision Tree. Energies 2021, 14, 4905. https://doi.org/10.3390/en14164905
Gaweł B, Paliński A. Long-Term Natural Gas Consumption Forecasting Based on Analog Method and Fuzzy Decision Tree. Energies. 2021; 14(16):4905. https://doi.org/10.3390/en14164905
Chicago/Turabian StyleGaweł, Bartłomiej, and Andrzej Paliński. 2021. "Long-Term Natural Gas Consumption Forecasting Based on Analog Method and Fuzzy Decision Tree" Energies 14, no. 16: 4905. https://doi.org/10.3390/en14164905
APA StyleGaweł, B., & Paliński, A. (2021). Long-Term Natural Gas Consumption Forecasting Based on Analog Method and Fuzzy Decision Tree. Energies, 14(16), 4905. https://doi.org/10.3390/en14164905






