Abstract
This paper presents a review of the existing models for the estimation of explosion-induced crushed and cracked zones. The control of these zones is of utmost importance in the rock explosion design, since it aims at optimizing the fragmentation and, as a result, minimizing the fine grain production and recovery cycle. Moreover, this optimization can reduce the damage beyond the set border and align the excavation plan with the geometric design. The models are categorized into three groups based on the approach, i.e., analytical, numerical, and experimental approaches, and for each group, the relevant studies are classified and presented in a comprehensive manner. More specifically, in the analytical methods, the assumptions and results are described and discussed in order to provide a useful reference to judge the applicability of each model. Considering the numerical models, all commonly-used algorithms along with the simulation details and the influential parameters are reported and discussed. Finally, considering the experimental models, the emphasis is given here on presenting the most practical and widely employed laboratory models. The empirical equations derived from the models and their applications are examined in detail. In the Discussion section, the most common methods are selected and used to estimate the damage size of 13 case study problems. The results are then utilized to compare the accuracy and applicability of each selected method. Furthermore, the probabilistic analysis of the explosion-induced failure is reviewed using several structural reliability models. The selection, classification, and discussion of the models presented in this paper can be used as a reference in real engineering projects.
1. Introduction
To fracture in-situ rock mass and prepare it for subsequent drilling and transport, explosion is widely used in the mining industry. In such conditions, run of mine fragmentation is assumed to be good when it is fine and loose enough to provide an efficient digging and loading operation [1]. Thus, significant attention has been drawn to estimating explosion-induced damage size in rock mass. The primary objective of research in this area has been to tailor blast fragmentation as well as to optimize mineral extraction and recovery cycle [2].
It should be noted that large amounts of fine materials are also produced by the crushed zone induced around the blast hole [3]. Thus, increasing the amount of fines multiplies handling and processing costs and, in many cases, reduces product value. Additionally, in some cases, such as quarry production, generated fines are recognized as waste. The volume of such wasted fines in Europe alone has been estimated to be about 500 million tons per year [4]. Thus, determining the size of the crushed zone and produced fines appears to be necessary [5]. Moreover, damage size at the perimeter of an excavation is of importance once the so-called drill and blast techniques are used for rock excavation [6]. In this area, minimizing explosion-induced damage is the main objective. This principle also needs to be considered, for example, in walls of drifts and other underground openings as well as slopes of surface mines. The damage penetrated through the walls and slopes is taken into account as unwanted damage or overbreak. This type of damage caused by explosion can thus have a direct impact on the stability and performance of the main structure [7]. Accordingly, diminishing such damages can:
- prevent possible damage to adjacent structures [8],
- enhance the stability of roof and side walls [9],
- improve excavation rate,
- reduce manufacturing expenses, and
- cut down operating costs [10].
In summary, by controlling the size of the crushed zone, one can optimize blasting fragmentation and minimize produced fine materials and recovery cycle. At the same time, optimizing the cracked zone can lead to a reduction in damage beyond the expected excavation boundary, control undesirable damage, and fit the explosion scheme to the geometric design [11]. That is why one main objective in rock blasting operations has been to keep unwanted damage under control [12]. To meet this objective, it is essential to understand and predict destruction caused by explosion [13].
In this paper, various methods associated with measuring and estimating explosion-induced rock damage are carefully studied and classified into different groups. To this end, this review is organized as follows: (1) the whole process of single-hole blasting is described from detonation initiation to wave propagation and rock vibration, and details are separately provided for each step (Section 2); (2) rock explosion damage is classified into different groups and illustrated schematically (Section 3); (3) different models are classified for assessing the size and severity of rock damage and presented in three different groups of analytical, numerical, and laboratory methods (Section 4); (4) the most commonly used methods are adopted in 13 case studies, and their results are compared (Section 5.1); (5) probabilistic methods are examined for calculating failure probability caused by rock explosion, and their potential differences are described compared to deterministic methods (Section 5.2).
2. A Review on Explosion Mechanism
In this section, the single-hole blasting process is examined and then the impact of induced detonation wave is described on surrounding rock medium. For this purpose, consider a single blast hole containing an explosive charge, as shown in Figure 1. Assume that a gauge is placed at point B to record explosion history. The results would be similar to those plotted in Figure 2a,b, wherein pressure–time (p–t) and pressure–distance (p–y) graphs induced by the explosion are schematically presented [4].
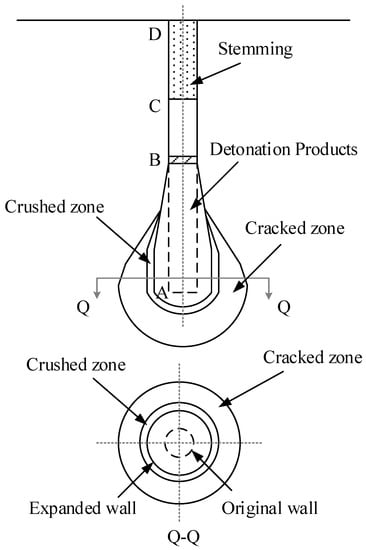
Figure 1.
The blast hole and surrounding damages.
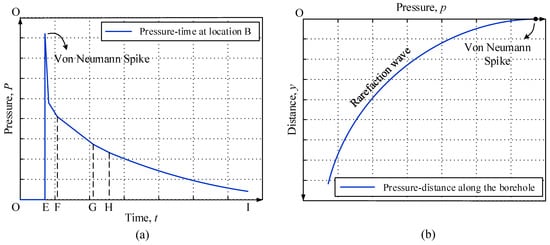
Figure 2.
The rock mass response to explosion wave in the form of (a) p–t and (b) p–y graphs.
Detonation begins from the bottom of the borehole, i.e., point A, which corresponds to point O in the p–t graph. At this moment, the detonation pressure is still zero because a portion of the explosion is yet to be recorded at point B. Then, the detonation wave travels from the bottom of the hole to point B. This part corresponds to on the p–t graph, wherein the pressure is still zero. Once the wave front arrives at point B, the p–t graph encounters a sudden peak and the induced pressure reaches its maximum value. This peak point is called the Von-Neumann spike. Next, the detonation wave passes point B toward point C. Consequently, the p–t graph drops sharply from E to F. Once the detonation wave touches point C, some part of the wave goes through stemming, with the remaining part reflecting back into the blast hole. Afterwards, the detonation wave moves through stemming, reaches the collar, and subsequently moves back from point D to point C. In the meantime, the pressure at point B decreases from F to G. After that, the induced wave travels toward point B and consequently the pressure drops from G to H. Following this step, the detonation wave moves toward the bottom of the blast hole and then gradually dissipates through the surrounding cracks and damages and leaks away from the system. This process continues until the borehole pressure reaches the atmospheric pressure. Correspondingly, the p–t graph is slowly reduced from point H to zero.
Pressure changes for different positions along the borehole from point B (wherein the p–t graph is at the maximum point) downward are illustrated in Figure 2b. As demonstrated, the pressure decreases sharply as it goes farther from point B due to borehole expansion, crushing and cracking of surrounding rock medium, explosion-induced gas leakage, etc.
It should be also noted that the process described above is more accurate for cases, in which the blast hole is long enough and the reflected wave in the borehole is neglected. In practice, multiple reflections of the wave from the bottom and the collar as well as the interaction between the wave and the lateral boundaries of the borehole can produce some fluctuations in pressure history. Thus, the actual p–t and p–y graphs are not perfectly smooth and exhibit some fluctuations. The next point to highlight is the role of stemming in the extension of the p–t graph. In fact, stemming causes the detonation wave to trap into the blast hole, making the detonation energy focused on fragmentation and breakage; this issue extends pressure history and consequently enhances explosion efficiency. More precisely, denoting stemming wave velocity and stemming length by and , respectively, the time duration of pressure history increases as , provided that stemming is correctly placed. Without stemming, the explosion-induced gas tends to escape from the collar and the described t cannot be saved anymore. It will then waste energy and decrease explosion efficiency [4,14,15]. However, it should be noted that calculating the exact optimal stemming length is very difficult and challenging as the flow of energy during the explosion cannot be modeled accurately and usually accompanies with a margin of uncertainty. What can be mentioned with certainty is that the more the so-called energy leakage gaps are reduced, the better the energy released by the explosion can be used for fragmentation purposes [16].
3. Damage Pattern
Following the explosion, the pressure waves are rapidly released and strongly vibrate the rock environment [11,17]. The resulting vibration, occurring in a fraction of a second, stimulates mechanical and dynamic characteristics of rock mass [18]. This stimulation correspondingly generates a series of tensions and stresses on existing discontinuities, and also contributes to the opening and expansion of joints, depending on rock toughness [19,20].
First, the blast hole is relatively expanded [21,22]. Then, discontinuities increase and lead to formation of an unstable crushed zone due to the growth of fine cracks [23]. On the other hand, cracks affected more by the blast shock go beyond the crushed zone and penetrate radially into the surrounding environment [24,25]. Beyond the crushed zone and radial cracks, the effects of the explosion are observed in the form of ground vibration [26,27]. These three sections are shown in Figure 3.
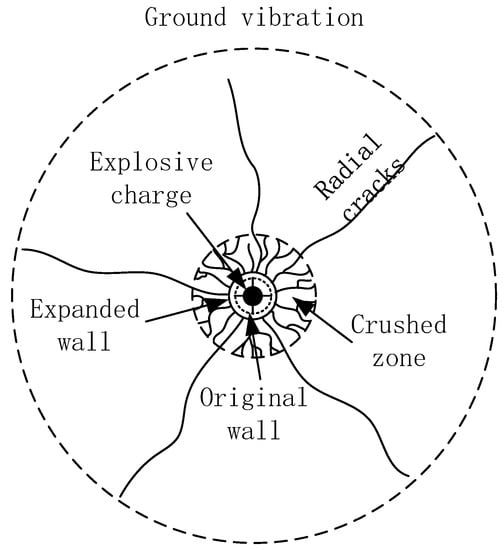
Figure 3.
Crack formation around a blast hole.
Thus, the effects of single-hole explosion can be summarized in four steps:
- The blast hole is expanded.
- A crushed zone is formed surrounding the blast hole.
- Radial cracks penetrate through the rock, causing a cracked zone.
- Explosion-induced waves affect the surrounding environment, producing some ground vibrations.
The pattern of damage generated around the explosion point is initially found in practical projects but later proved in experimental models. For instance, Olsson and Ouchterlony [28] showed the pattern generated in experimental models. However, it should be noted that, in practice, the zones mentioned above are interconnected without any sharp boundaries that help in distinguishing them from one another. However, the definition provided for damage pattern can greatly help in establishing models and calculating results.
4. Estimation of Induced Damage
A shock wave is initially generated once an explosion charge is fired. Subsequently, a stress wave affects the surrounding environment, creating two damage zones near the blast hole, namely crushed and cracked zones. As discussed, sizes of these two damage zones are of importance for an optimal blast design. As far as the project client can estimate the size of damage zones (i.e., crushed and cracked zones) as a function of input parameters such as rock properties and explosive characteristics, the optimal values of input parameters can be obtained using a blast design optimization. This optimization can be done through a try-and-error process to obtain the optimal values of target parameters or can be mathematically implemented in an optimization algorithm [29,30,31].
Different researchers have proposed various methods to approximate the induced damage. In a general case, the size of a damage zone can be assumed as a function of input parameters such as:
where r is the damage zone radius and to represent the input parameters (either rock or explosion characteristics). The most important input parameters are outlined in Table 1.

Table 1.
Main parameters involved in explosion-induced rock damages.
This form of damage estimation can be simply applied to a particular case study with virtually no complexities. However, it is not always easy to provide a close-form function such as since several sources of uncertainties are included in explosion-associated problems [32,33,34]. Numerous research studies are also available in the related literature to estimate damage in rock and soil media [35,36,37]. In an overall view, these methods can be categorized into three main groups: analytical, numerical [38], and experimental [39].
Approaches toward problems in each of these three methods are not the same. In analytical techniques, a parameter such as peak particle velocity (PPV) [40,41,42], borehole pressure [43,44], or explosion pressure [45] is generally presented as a critical factor to estimate the size of a damage zone. Next, two different approaches are used to provide a solution; either an analytical calculation is employed to directly determine both the critical parameter and the damage zone, or the relationship between the parameter and the damage zone is estimated and the rest of the problem remains unsolved for the reader. In numerical methods, however, an algorithm such as finite element method (FEM), finite difference method (FDM), discrete element method (DEM), etc. is used to evaluate changes in the stress field surrounding an explosion point and examine consequent issues including induced cracks and damages [46,47,48]. In experimental approaches, some laboratory or in-situ tests are utilized to develop an empirical relationship to estimate the size and dimension of damages [49].
In the following, each of these three methods is separately addressed, and then related previously developed research works are listed and explained in more detail.
4.1. Analytical Approach
As previously described, in analytical approaches, a feature of a model is selected as a main parameter, and it is determined how this parameter is distributed around the blast hole. The relationship between the parameter and rock damage is then examined so that damage size can be measured for each parameter value. Peak ground velocity and borehole pressure are assumed as two parameters widely used for this purpose [50]. Analytical approaches based on PPV and borehole pressure are discussed in Section 4.1.1 and Section 4.1.2, respectively.
4.1.1. Damage Prediction Using PPV
PPV is known as one of the critical parameters, used by several researchers, to estimate damage zones [51]. Accordingly, damage rate can be predicted if PPV is estimated in different areas in rock environments. Some of the PPV-based criteria for blast-induced damage in rocks are presented in Table 2 and Table 3.

Table 2.
PPV-based criteria for blast-induced damage in rock (adopted from Bauer and Calder [52]).

Table 3.
PPV-based criteria for blast-induced damage in rock (adopted from Mojtabai and Beattie [53]).
Two requirements need to be met when using PPV in damage estimation and structural control: (1) the PPV at the desired location should be predicted; (2) the relationship between the PPV and the damage state (i.e., fragility curve) should be provided. In practice, PPV vectors surrounding a blast hole are difficult to be developed, and there are not many sources available in this area. To further explain this issue, the proposed model by Holmberg and Persson can be noted [40,54], since they offered the following equation to estimate PPV:
where V shows PPV, K, , and are the empirical constants, W is the charge weight unit, and R denotes the distance unit from the charge. However, this equation is developed for areas far from the explosion point. In fact, the given equation is applicable for areas, in which R is so large that it makes blast hole dimension negligible, and cannot be used for areas close to the explosion point, where a blast hole dimension should be considered.
To solve this problem, Holmberg and Persson [54] assumed that the explosive charge has a cylindrical shape. Accordingly, they divided the explosive charge into small pieces so that each of the pieces has a length of and unit charge concentration of q (kg/m). Then, they stated that PPV in an arbitrary point such as (, ) can be calculated as follows:
where T is the stemming depth (m) [55], H is the charge length (m), and J is the subdrill (m) [56], as demonstrated in Figure 4.
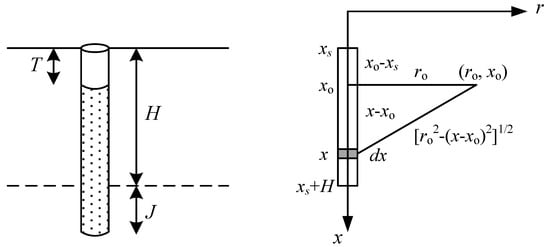
Figure 4.
The explosive charge and partitioning.
The parameter was assumed as follows:
After integrating from Equation (3), PPV was explicitly presented as follows:
The values of K, , and for hard rock mass are 700, 0.7, and 1.4, respectively. Thus, by having q, the PPV amount can be calculated for any desired distance (r). In this respect, Changshou Sun [6] presented Table 4 for Scandinavian bedrock to approximate rock damage based on the induced PPV.

Table 4.
Damage type based on induced PPV in a Scandinavian bedrock.
Although this appears to be a very simple and practical method, later, Hustrulid and Lu [57] reiterated that the main integral suffered from a basic mistake and the accurate form of the integral was:
which could not be solved obviously in an analytic manner. Moreover, the proposed method has other problems; for instance:
- Only the magnitude of the PPV is considered and the direction of the PPV is neglected.
- Only the explosive weight is taken into account, and other characteristics are ignored.
- To determine the parameters K, , and , further laboratory or in-situ tests are required, which are difficult to conduct.
For such reasons, these types of approaches have not been highly welcomed by research communities.
4.1.2. Damage Prediction Using Borehole Pressure
Borehole pressure is known as one of the common parameters in the estimation of rock damage. Accordingly, it is believed that the initiation and propagation of cracks in rocks are due to severe stress caused by explosion waves. Thus, borehole pressure is being used by many researchers to directly estimate the crushed zone size in rock environments. The next sections present a summary of such studies.
Mosinets’ Model
Mosinets et al. [58] expressed the radius of damage zones (either cracked or crushed ones) surrounding the blast hole by the following equation:
where r is the damage zone radius, k represents the proportionality coefficient, and q refers to the charge weight in the TNT equivalent. Each damage zone also has its own coefficient k. For the crushed zone, the coefficient k is as follows:
where shows the longitudinal wave velocity and denotes the transverse wave velocity.
Drukovanyi’ Model
Assuming an isotropic and incompressible granular medium with cohesion (derived from Il’yushin’s model [59]), Drukovanyi et al. [60] examined behaviors of rocks in the zone of fine crushing. Considering a plane strain for detonation of a column of explosive material in rock mass, they theoretically developed the following relation to determine the crushed zone radius () close to the blast hole:
where stands for the borehole radius (mm), is the borehole pressure (Pa), C shows cohesion (Pa), f refers to the internal friction coefficient (), is the uniaxial (unconfined) compressive strength (Pa), denotes the adiabatic expansion constant of explosive, and L represents a constant defined by:
where E is the Young’s modulus (Pa), refers to the Poisson’s ratio, and T shows the tensile strength (Pa) of the rock. Drukovanyi’s model assumes that the borehole pressure is calculated as follows:
where shows the explosive density and D is the detonation velocity. They also referred to Il’yushin’s model and considered , , and D = 4000–6000 m/s.
It was noted by Drukovanyi et al. [60] that damage predicted using this model can give values higher than reality to rocks by the compressive strength less than 100 MPa. Moreover, it has been reported in the related literature that this approach is limited to cases, where the main mode of failure is compression [6].
Senuk’s Model
Senuk [61] developed the following relation to estimate the cracked zone radius in the vicinity of a cylindrical explosive charge:
where k is the stress concentration factor in sharp cracks and joints, which is assumed to be approximately equal to 1.12, shows the blast hole pressure approximated by , and T represents the rock tensile strength. Thus, Equation (12) can be rewritten as follows:
Szuladzinski’s Model
According to the hydrodynamic theory for rock explosion, Szuladzinski [62] proposed a model to predict the crushed zone radius around a blast hole. In this model, the rock environment in the vicinity of the blast hole was assumed as an elastic medium with cracking and crushing capabilities. The effective explosion energy in the model was also roughly assumed as two-thirds of the total explosive energy, and decoupling effects were ignored. The relation presented in this study for the crushed zone radius is as follows:
where (mm) is the borehole radius, () shows the explosive density, (Nmm/g) represents the effective explosive energy (assumed to be two-thirds of the complete reaction heat), and (MPa) refers to the confined dynamic compressive strength of rock mass (assumed to be approximately eight times of the unconfined static compressive strength, [63,64,65,66]).
SveBeFo Model
The Swedish Engineering Research Organization (SveBeFo) conducted several studies on the initiation and propagation of cracks in rock environments under explosion load. Based on the results of these studies, Ouchterlony [67] presented the following relation to calculate the length of induced radial cracks:
where denotes the unanchored radius of the cracked zone, shows the borehole diameter, is the borehole pressure, D represents the velocity of detonation (VOD), c is the sound speed in a rock environment, and denotes an experimental parameter showing critical borehole pressure which can be estimated by the following equation:
where is the fracture toughness of rock mass and shows the borehole diameter. Accordingly, Ouchterlony [67] introduced the following equation to estimate the borehole pressure:
where is an isotropic exponent for a specific explosive (1.254–2.154), denotes the explosive density, D stands for VOD, and represents the ratio of explosive diameter to borehole diameter called the decoupling ratio. Later, Ouchterlony et al. [68] provided the following correction coefficients to improve the given method:
where stands for the corrected damage zone radius, is correction for hole spacing, shows correction for time spread in initiation, stands for correction for wet holes, and is correction for fracturing. These coefficients could be determined based on the concept of fracture mechanics, which is complicated for conventional engineering design. Moreover, it is not easy to determine rock fracture toughness, i.e., , especially for weak rocks. These issues led to limited applications of the given method in research works and consequently no extensive use of the method in practical designs.
Quasi-Static Model
Assuming a balance between borehole pressure and stress distributed in the surrounding rock medium, Sher and Aleksandrova [69,70] provided a model to predict crack size around a cylindrical borehole. In this model, a dynamic process was approximated by a quasi-static method, and the following equations were then proposed to estimate the radius of the cracked zone:
where denotes the initial hole radius, r shows the final hole radius, is the elastic deformation of rock, represents the ratio of final radius to initial radius of hole, refers to the radius at which the adiabatic constant changes, is the initial adiabatic expansion constant (), and signifies the final adiabatic expansion constant (). Both and parameters can be calculated as follows:
where c is the cohesion and refers to the internal friction angle. Based on the equations presented above, Hustrulid [71] provided the following process to determine the cracked zone radius:
- Step 1
- Calculate from Equation (20)
- Step 2
- Approximate a value for (this value is approximated in this step and later modified in a cyclic process)
- Step 3
- Substitute and in Equation (21) and calculate
- Step 4
- Substitute in Equation (22) and determine
- Step 5
- Step 6
- Substitute in Equation (19) to assess if equality is achieved (if so, is the final answer. Otherwise, the steps 2–6 should be repeated until the final answer is reached).
Djordjevic’s Model
Based on the Griffith’s failure criterion, Djordjevic [72] developed a model mostly applicable for brittle rocks [2]. The crushed zone radius proposed in this study is:
where (mm) is the blast hole radius, T (Pa) shows the tensile strength of rock material, and (Pa) represents the borehole pressure.
Kanchibotla Model
Kanchibotla et al. [73] considered damage around a blast hole as a function of blast hole radius, explosion pressure, and uniaxial compressive strength of rock mass. Using these parameters, they proposed a relation to estimate the crushed zone radius as follows:
where (mm) is the borehole radius, (Pa) refers to the detonation pressure, and (Pa) denotes the unconfined compressive strength of rock.
Johnson’s Model
Johnson [74] considered four different zones near a blast point including borehole, crushed zone, cracked zone (also named as transition zone), and no-damage zone (also labeled as seismic zone). To calculate the crushed zone radius in this study, the following formula was proposed:
where is the dynamic compressive strength of rock, represents the borehole pressure, shows the crushed zone radius, stands for the borehole radius, and is the crush damage decay constant determined by laboratory experiments.
Modified Ash’s Model
Hustrulid [71] improved the Ash’s model [63,64,65,66] and provided the following equation to approximate the size of the cracked zone around a blast hole:
where is the borehole radius, shows the decoupling ratio, stands for the relative bulk strength (compared with ammonium nitrate/fuel oil (ANFO)), and refers to the rock density. can be calculated as follows:
where is the weight strength of explosive relative to ANFO, stands for the density of ANFO, and shows the explosive density.
4.2. Numerical Approach
When a rock is idealized as a continuous medium, continuum-based approaches such as FEM [75,76,77,78,79,80,81] or FDM [82,83,84,85,86,87] are usually employed to simulate the model. However, the rock is modeled as a set of structural units (such as springs, beams, etc.) or as separate particles bonded at contact point if modeling of discontinuities is required. In such cases, DEM [88,89,90,91,92,93], the bonded particle model [94] or hybrid methods [95,96,97,98,99] are used for numerical analysis. Typically, due to the high volume of calculations required in such methods, calculations are performed using software packages to simulate the model. Various packages have thus been developed for geotechnical modeling. In this regard, two famous DEM codes, UDEC and 3DEC, are widely utilized for modeling two- and three-dimensional cases of jointed rock, respectively.
Wang and Konietzky [46] used UDEC to study the initiation and propagation of damage around the blast hole in rock. They first used general-purpose multiphysics simulation software package (LS-DYANA) to model an explosion in intact rock and calculate the explosion load imposed on the borehole wall. Then, they returned to UDEC and modeled a jointed rock environment. They assigned the obtained load as a radial velocity history to the borehole wall and studied the damage evolution. Their coupled model is schematically shown in Figure 5.

Figure 5.
Coupled method illustrating the (a) physical model of explosion in jointed rock mass, (b) explosion history obtained via LS-DYNA, and (c) input of converted explosion history for UDEC simulation.
To model the jointed rock environment in UDEC, Wang and Konietzky [46] used two sets of joints: a randomly-generated series of polygonal joints (e.g., Voronoi joints) and two series of orthogonally aligned joints dipping at and . Having the load exerted on the blast hole, they began to study the growth of damage in rock. It was observed that some small damage formed around the blast hole and then penetrated through outer layers. By passing the time, the damage size continuously increased until ms that it stopped growing further and reached at its maximum size. Later, it was noted that, at the time ms, the maximum length of cracks reached to 2.5 m while the crushed zone radius varied between 7 to 9 times of the blast hole radius. This estimation is moderately higher than that in similar studies approximating the ratio below 5 between the crushed zone radius and the borehole radius ().
Using the analytical code of the Realistic Failure Process Analysis 2D (RFPA2D), Liu et al. [100] analyzed rock mass behavior under explosion assuming different geometrical properties for joints including average distance from blast site to joints, length of joints, number of joints, and relative angles of joints. These properties are schematically shown in Figure 6.

Figure 6.
Single hole blasting model illustrating the model parameters including joints, the length of joints (L), distance from joints to blasting hole (), and joint angle ().
The results of this study showed that the effect of joints on blast-induced damage is slowly reduced as the average distance of joints from the blast hole increases. It was also observed that rock masses with long joints could experience more damage than those having short joints. Their results also revealed that the damage caused by the blast was significantly greater in rock masses with joints than in cases without joints. However, little change might be observed in damage intensity caused by an explosion when the number of joints exceeded 3. It was also concluded that joints could highly facilitate the propagation of cracks and play a significant role in determining their shapes, dimensions, and directions of propagation.
Moreover, Lak et al. [101] used a hybrid finite difference-boundary element method to investigate the propagation of blast-induced cracks around a wellbore. To this end, they planned two separate steps. First, they investigated the formation of radial cracks due to the propagation of shock waves caused by explosion using the dynamic finite difference method. Importing outputs into the second step, they then modeled the propagation of cracks caused by gas expansion using the quasi-static boundary element method.
Two types of cracks were considered in this study: type I and type II. The cracks along the direction of maximum horizontal stress () were considered as type I, and those along the direction of minimum horizontal stress () are marked as type II. The results of this study showed that the ratio of has an obvious effect on the radial cracks propagation. When has a small value near 0, the length of type I cracks is larger than that of type II cracks (roughly about twice, ). With the increase of the ratio of , the length of type I cracks decreases and the length of type II cracks increases. Finally, in hydrostatic stress conditions, i.e., cases where , the length of type I and type II cracks turn out to be equal ().
4.3. Experimental Approach
Explosion-induced damage in rocks occurs through a complex process. Therefore, laboratory studies have been exploited as one of the main methods to investigate this problem in the past few decades given the complexity of research in this area [102]. It should be noted that experimental studies of explosion phenomena as well as subsequent failures mainly deal with two main aspects [103]:
- Primary cracks due to the high amplitude of stress waves
- Further development of cracks due to gas penetration
In a study on stress-wave, Lownds [104] conducted a set of reduced-scale experiments in granite. A sensor hole was also placed at a distance of 150 mm away from a borehole with a diameter of 32 mm. A pressure transducer was subsequently placed in a water-coupled sensor hole with the same diameter as the borehole to measure stress waves. They recorded the effect of different coupling media on stress waves using the installed pressure transducer. In a similar study, Talhi et al. [105] measured the relative magnitude of stress pulses by placing a pressure gauge in a water-coupled sensor hole with a diameter of 8 mm to check the variation of stress waves caused by changes in decoupling ratio and borehole length. Through these methods, peak pressure at a relatively close distance to the borehole was measured providing a database of relative measurement for different borehole conditions. In addition, Teowee and Papilon [106,107] utilized piezoelectric sensors to measure the sympathetic pressure of adjacent deck charges and boreholes. For this purpose, they compared peak pressure between these piezoelectric gauges and concluded that the given sensors could measure peak pressure up to 138 MPa. Due to the relative size of the manometer and the applicability of measuring high pressure, piezoresistive gauges, such as carbon composite resistors, have been employed by different researchers to investigate pressure pulse caused by stress wave propagation [44,108].
Measuring damage size and pattern using induced gas pressure and penetration has also been investigated by different researchers. For example, the direct measurement of crack length was performed by Olsson and Bergqvist [109,110], Deghan Banadaki [111], and Nariseti [112] to reflect on blasting-induced rock fractures. Paventi and Mohanty [113] also shed light on the effect of coupling medium on crack pattern through laboratory-scale tests of samples with 10-cm diameter. Boreholes with diameters of 6 mm and 10 mm were thus equipped with pentaerythritol tetranitrate explosive in central position while containing different coupling media such as air, water, and clay. The results showed that fracture intensity was smallest in air-coupled boreholes followed by clay-coupled boreholes. Additionally, they reported that water-coupled boreholes led to intense fracturing near boreholes. Furthermore, Yamin [114] conducted reduced-scale experiments to examine damage extent around boreholes. To this end, pressure sensors were placed in sensor holes on concentric circles at different distances surrounding a borehole to measure gas pressure. It was consequently reported that gas penetration was observed from a 75-mm blast hole charged with a 40-mm emulsion cartridge up to a distance of about 15 borehole diameters. Additionally, Yamin [114], McHugh [115], and Brinkmann [116] investigated rock damage following gas penetration.
It should be noted that laboratory and experimental models to directly determine damage zones in rock under explosion load are difficult and costly [117]. The test site should also be safe and equipped with required facilities to measure rock behavior. Providing such conditions, however, is not simple. Therefore, there are few studies available in this area.
One of the existing approaches in this field is Esen’s model [2]. To measure the crushed zone size around a blast hole, Esen et al. conducted a detailed laboratory test on 92 samples mostly made up of concrete with dimensions of 1.5 m × 1 m × 1.1 m. They consequently defined a crushing zone index () based on the crushing process around the explosion point as follows:
where is the blast hole pressure (Pa), K stands for the stiffness of rock mass (Pa), and shows the uniaxial compressive strength of rock (Pa). The values of and K are calculated as follows:
where is the ideal blast pressure (Pa), shows the unexploded explosive density (kg/m3), represents the ideal detonation velocity (m/s), denotes the dynamic Young’s modulus of rock (Pa), and refers to the dynamic Poisson’s ratio of rock. These relationships are also used to approximate blast hole pressure and rock stiffness. Where more accurate values of these parameters are available through direct measurement or numerical modeling, they can be used instead of the presented equations [118]. After calculating , Essen et al. [2] found a power relationship between this factor and the crushed zone radius as follows:
where is the crushing zone index, represents the crushed zone radius, and shows the blast hole radius. The crushed zone radius is then calculated as follows:
5. Discussion
5.1. Comparison of Different Models
Various methods have been described to estimate sizes of damage zones around blast holes. In this section, the most commonly used methods are listed and their results are compared through several case studies. For this purpose, 13 rock explosion samples were selected from various studies, in which explosions were carried out in two different types of rocks, including clayey-limestone and basalt, with two types of explosives including ANFO and water-resistant ANFO. The details of these samples including the characteristics of the rocks, explosives, and blast holes are outlined in Table 5.

Table 5.
The characteristics of the rocks, explosives, and blast holes in the 13 studied samples.
In the following, five different methods were selected, including Esen’s [2], Il’yushin’s [59], Szuladzinski’s [62], Djordjevic’s [72], and Kanchibotla’s [73] models, to calculate damage size corresponding to each of the 13 samples presented. The results of these models for the introduced case studies are displayed in the columns 2–6 of Table 6. The results are also plotted in Figure 7.

Table 6.
Results of the selected methods in estimating damage radius for the 13 studied samples.

Figure 7.
Comparison of different models in estimating damage radius obtained from the 13 studied samples.
As can be observed from Figure 7, in almost all the 13 cases, Il’yushin’s and Kanchibotla’s models yielded relatively larger results than the other models. One possible reason for this issue is that both models used an ideal explosion assumption in their relationships, while the real cases are closer to a non-ideal one. This issue has been pointed out by other researchers as well. It has been argued in the related literature that the purpose of Kanchibotla’s model is to study mine fragmentation and optimize mine excavation [2]. Therefore, it may not be able to provide a precise crack propagation estimation and damage zone determination. The other three models, i.e., Esen’s, Szuladzinski’s, and Djordjevic’s models, correspondingly provide relatively close estimations. However, Esen’s model is preferred to the other models in the literature. The advantage of using Esen’s model compared with other ones is its development based on experimental and real-scale samples, whose results have also been validated by rock blasting real projects. However, the other three models have been developed theoretically through several simplifications and simple assumptions. Moreover, there are several comparisons between these models available in the literature, and almost all of them have addressed Esen’s model as the most accurate approach to predict the crushed zone size. For instance, Amnieh and Bahadori [119,120] conducted several single-hole explosion tests at the Gotvand Olya Dam and compared the results with those of Ash’s, Djordjevic’s, Szuladzinski’s, Kanchibotla’s, and Esen’s models. Eventually, they concluded that the results obtained from Esen’s model were closer to real values compared with the other models in all the cases observed. Additionally, studying the crushed zone radius around a blast hole using laboratory tests, Changshou Sun [6] introduced Esen’s model as the most complete set of data for the crushed zone extent and then applied it to validate their laboratory test results.
5.2. Probabilistic Approaches
The models investigated in this review up to now have been addressing single-hole rock blasting in terms of a deterministic problem. Although the deterministic estimation of damage has been incorporated in a simple algorithm without any certain complexity, some uncertainties have remained unnoticed in the problem. Neither rock medium nor blast load characteristic values are deterministic and consequently cannot be determined with certainty. The deterministic estimation of damage zone is similar to assuming a 100% probability for a specific failure size, which does not appear to be a rational workaround. A better solution in this regard is to match each damage zone radius with a failure probability. In other words, instead of the deterministic estimation of damage zone, an exceedance probability is assumed as the goal of analysis. In fact, determinacy should be left aside and uncertainty needs to be modeled using random variables. As a result, one could estimate the probability required for a crack to exceed a certain length value. This issue has been formulated as a reliability problem in the related literature and investigated in some research works.
Defining the involved parameters as random variables with certain mean and standard deviation and establishing a limit state function for crush and crack zone radii, Shadabfar et al. [121,122,123] incorporated the Monte Carlo method to calculate failure probability. Based on their results, they concluded that exceedance probability was severely reduced following an increase in the crushed zone radius. Accordingly, the probability of the crushed zone radius longer than 0.5 m was reported to be less than 1%. Moreover, the comparison of different probabilistic models developed based on Esen’s, Szuladzinski’s, Djordjevic’s, and Kanchinotla’s models revealed that the results of Esen’s model could exhibit a lower failure probability than those of the other models. In other words, Esen’s model has a more optimistic estimation of the bearing capacity of rock mass compared with the other models.
Additionally, it was observed that Kanchibotla’s model was much more different than the other models, yielding a much higher failure probability. This issue has also been noticed by other researchers [124]. It is reasoned that the objective of Kanchibotla’s model is to study mine fragmentation and optimize mine drilling. Hence, it may not yield a precise crack propagation estimation and damage zone determination.
Furthermore, defining both the crushed and cracked zones in terms of a reliability problem in another study, Shadabfar et al. [125] took advantage of the first-order reliability method and calculated explosion-induced failure probability. The obtained results of this study were then represented in terms of exceedance probability versus damage zone radius (Figure 8).
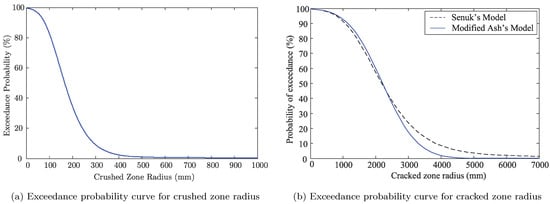
Figure 8.
The exceedance probability curve for (a) crushed and (b) cracked zones.
The diagram was then drawn for all the points in the vicinity of the blast location and presented as exceedance probability contours (Figure 9).

Figure 9.
The contour plot of exceedance probability for (a) crushed and (b) cracked zones.
As shown in Figure 9, failure probability is reduced via distancing from the blast location. Thus, failure probability for the crushed zone approaches 0 by exceeding 0.5 m.
In addition, using a parametric study, ShadabFar et al. [125] investigated the effects of decoupling on resulting failures. For this purpose, a number of reliability analyses were conducted and changes in failure probability were recorded accurately through incorporating different ratios of explosive charge to blast hole radii in the governing equation. According to their results, failure probability declined and the exceedance probability diagram showed a lower level of probability as the decoupling ratio was reduced. The reason is that the distance between explosive charge and blast hole wall increased through a reduction in the decoupling ratio, leading to the sharp damping of blast wave before propagating in the rock medium. Additionally, the results revealed that the highest impact of the decoupling ratio occurred in the range of small damage zone radii. More precisely, the decoupling ratio mostly affected failure radii in the range of 300–2350 mm, while its impact was severely reduced for larger failure radii.
Performing a set of reliability sensitivity analyses, ShadabFar et al. [125] also compared the influence of parameters involved in different models. The results of their study showed that the main parameters affecting the crushed zone radius in Esen’s model were the uniaxial compressive strength of rock and the blast hole radius. Furthermore, according to Senuk’s model, two main parameters influencing the cracked zone radius were the blast hole radius and the tensile stress of rock mass. The results of this analysis were then presented in a diagram in terms of sensitivity vector for each parameter involved in different models (Figure 10). This diagram presents the relative importance of each parameter in comparison with other parameters. Load variables (i.e., components whose growth would increase failure probability) are marked with a dark color, whereas resistance variables (i.e., components whose rising trend would decrease failure probability) are marked with a bright color.

Figure 10.
The relative importance of parameters involved in various models.
6. Conclusions
In this review, the most important existing models for the estimation of explosion-induced crushed and cracked zones were investigated. The models were categorized into three groups, i.e., analytical, numerical, and experimental approaches. First, the rock explosion mechanism was described from the detonation initiation and stress wave propagation to the rock failure. Subsequently, the induced damage was grouped into two forms of crushed and cracked zones and the most important parameters affecting these zones were reported. Then, the most important methods for estimating the dimensions of each damage zone were examined.
More specifically, the analytical models were presented based on the two main parameters of PPV and blast hole pressure. The numerical methods were addressed via the commonly used numerical codes, including the FEM, DEM, and FDM methods. The experimental models were divided into two general categories of primary cracks due to high-stress waves and deep cracks caused by gas penetration and discussed in detail. Finally, a number of empirical models drawn from laboratory results were used in a step-by-step approach.
The most commonly utilized models described in this review were selected to separately calculate the damage dimensions in 13 case studies, which were collected from the related literature and presented in an integrated form. All the results were compared, and their differences or similarities were discussed.
Thereafter, the probabilistic models available for analyzing the failure probability induced by the rock explosion were deliberated, and their advantages over the deterministic models were described. The comparisons were made between different models, and the relative importance of the involved parameters was investigated via the reliability sensitivity analysis.
This review categorized and reported the most important assumptions and key points of the related literature along with their prominent results to allow for more coherent and accurate use of their content. Hence, the results of the present study can be used as a comprehensive and categorized source for estimating the blast-induced damage in rocks. However, for the practical use of the methods presented here, their main sources should be utilized for more details. Finally, this paper only covered the single-hole blasting. In cases with multiple blasting, due to the interaction between the explosion waves released from each blast hole, a system of damage zones is generated, which can potentially overlap and cause more complex failure in the environment. This topic remains as the authors’ concern for future research works.
Author Contributions
Conceptualization, data curation, formal analysis, investigation, methodology, project administration, resources, software, supervision, validation, visualization, writing—original draft, and writing—review & editing are done by M.S.; Funding acquisition, methodology, resources, validation, visualization, writing—original draft, and writing—review & editing are done by C.G.; Funding acquisition, validation, visualization, and writing—review & editing are done by M.Z.; Data curation, investigation, methodology, resources, validation, visualization, and writing—original draft are done by H.K.; Investigation, methodology, resources, validation, visualization, writing—original draft, and writing—review & editing are done by E.V.M. All authors have read and agreed to the published version of the manuscript.
Funding
The research presented in this paper was conducted with support from the Natural Science Foundation of China (NSFC) under the project number 02302340347.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kanchibotla, S.; Morrell, S.; Valery, W.; Loughlin, P.O. Exploring the effect of blast design on SAG mill throughput at KCGM. In Proceedings of the Mine to Mill Conference, Brisbane, Australia, 11–14 October 1998. [Google Scholar]
- Esen, S.; Onederra, I.; Bilgin, H. Modelling the size of the crushed zone around a blasthole. Int. J. Rock Mech. Min. Sci. 2003, 40, 485–495. [Google Scholar] [CrossRef]
- Ouchterlony, F.; Moser, P. Lessons from single-hole blasting in mortar, concrete and rocks. In Rock Fragmentation by Blasting; Singh, P.K., Sinha, A., Eds.; CRC Press: London, UK, 2012; pp. 3–14. [Google Scholar]
- Zhang, Z.X. Rock Fracture and Blasting, Theory and Applications; Butterworth-Heinemann: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Chi, L.Y.; Zhang, Z.X.; Aalberg, A.; Yang, J.; Li, C.C. Fracture processes in granite blocks under blast loading. Rock Mech. Rock Eng. 2019, 52, 853–868. [Google Scholar] [CrossRef]
- Sun, C. Damage Zone Prediction for Rock Blasting. Ph.D. Thesis, University of Utah, Salt Lake City, UT, USA, 2013. [Google Scholar]
- Zou, D. Theory and Technology of Rock Excavation for Civil Engineering, 1st ed.; Springer: Singapore, 2017. [Google Scholar]
- Singh, S. Blast damage control in jointed rock mass. Fragblast Int. J. Blasting Fragm. 2005, 9, 175–187. [Google Scholar] [CrossRef]
- Chen, M.; Lu, W.B.; Yan, P.; Hu, Y.G. Blasting excavation induced damage of surrounding rock masses in deep-buried tunnels. KSCE J. Civ. Eng. 2015, 20, 933–942. [Google Scholar] [CrossRef]
- Kanchibotla, S. Optimum Blasting? Is it Minimum Cost Per Broken Rock or Maximum Value Per Broken Rock? Fragblast Int. J. Blasting Fragm. 2003, 7, 35–48. [Google Scholar] [CrossRef]
- Performance of Explosives and New Developments, 1st ed.; Mohanty, B., Singh, V.K., Eds.; CRC Press: New Delhi, India, 2012. [Google Scholar]
- Leng, Z.; Lu, W.; Chen, M.; Yan, P.; Hu, Y. A new theory of rock-explosive matching based on the reasonable control of crushed zone. Engineering 2014, 12, 32–38. [Google Scholar]
- Trivino, L.; Mohanty, B. Assessment of crack initiation and propagation in rock from explosion-induced stress waves and gas expansion by cross-hole seismometry and FEM-DEM method. Int. J. Rock Mech. Min. Sci. 2015, 77, 287–299. [Google Scholar] [CrossRef]
- Bhandari, S. Engineer Rock Blasting Operations, 1st ed.; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Fairhurst, C. Comprehensive Rock Comprehensive Rock Engineering: Principles, Practice and Projects, Analysis and Design Methods, 2nd ed.; Pergamon Pr: Oxford, UK, 1995. [Google Scholar]
- Qiu, X.; Shi, X.; Zhang, S.; Liu, B.; Zhou, J. Experimental Study on the Blasting Performance of Water-Soil Composite Stemming in Underground Mines. Adv. Mater. Sci. Eng. 2018, 2018. [Google Scholar] [CrossRef]
- Xia, Y.; Jiang, N.; Zhou, C.; Luo, X. Safety assessment of upper water pipeline under the blasting vibration induced by Subway tunnel excavation. Eng. Fail. Anal. 2019, 104, 626–642. [Google Scholar] [CrossRef]
- Ouchterlony, F.; Nyberg, U.; Olsson, M.; Bergqvist, I.; Granlund, L.; Grind, H. Where does the explosive energy in rock blasting rounds go? Sci. Technol. Energetic Mater. 2004, 65, 54–63. [Google Scholar]
- Souissi, S.; Hamdi, E.; Sellami, H. Microstructure effect on hard rock damage and fracture during indentation process. Geotech. Geol. Eng. 2015, 33, 1539–1550. [Google Scholar] [CrossRef]
- Fourney, W.L. The role of stress waves and fracture mechanics in fragmentation. In Proceedings of the 11th International Symposium on Rock Fragmentation by Blasting, Sydney, Australia, 24–26 August 2015; The Australasian Institute of Mining and Metallurgy: Carlton, Australia, 2015; pp. 27–40. [Google Scholar]
- Persson, P.; Ladegaard-Pedersen, A.; Kihlstrom, B. The influence of borehole diameter on the rock blasting capacity of an extended explosive charge. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1969, 6, 277–284. [Google Scholar] [CrossRef]
- Brinkmann, J. An experimental study of the effects of shock and gas penetration in blasting. In Proceedings of the 3rd International Symposium on Rock Fragmentation by Blasting, Brisbane Australia, 26–31 August 1990; pp. 55–66. [Google Scholar]
- Wang, C.; Zhu, Z.M.; Zheng, T. The fracturing behavior of detected rock under blasting loads. In Applied Mechanics and Materials; Trans Tech Publications: Stafa-Zurich, Switzerland, 2012; Volume 142, pp. 193–196. [Google Scholar] [CrossRef]
- Saharan, M.; Mitri, H.; Jethwa, J. Rock fracturing by explosive energy: Review of state-of-the-art. Fragblast Int. J. Blasting Fragm. 2006, 10, 61–81. [Google Scholar] [CrossRef]
- Banadaki, M.D.; Mohanty, B. Numerical simulation of stress wave induced fractures in rock. Int. J. Impact Eng. 2012, 40–41, 16–25. [Google Scholar] [CrossRef]
- Adhikari, G.; Theresraj, A.; Venkatesh, H.; Balachander, R.; Gupta, R. Ground vibration due to blasting in limestone quarries. Fragblast Int. J. Blasting Fragm. 2010, 8, 85–94. [Google Scholar] [CrossRef]
- Chi, L.Y.; Zhang, Z.X.; Aalberg, A.; Yang, J.; Li, C.C. Measurement of shock pressure and shock-wave attenuation near a blast hole in rock. Int. J. Impact Eng. 2019, 125, 27–38. [Google Scholar] [CrossRef]
- Olsson, M.; Ouchterlony, F. New Formula for Blast Induced Damage in the Remaining Rock (Title in Swedish: Ny skadezonsformel for skonsam sprangning); Technical Report SveBeFo Rapport 65; Swedish Rock Engineering Research: Stockholm, Sweden, 2003. [Google Scholar]
- Asl, P.F.; Monjezi, M.; Hamidi, J.K.; Armaghani, D.J. Optimization of flyrock and rock fragmentation in the Tajareh limestone mine using metaheuristics method of firefly algorithm. Eng. Comput. 2018, 34, 241–251. [Google Scholar] [CrossRef]
- Leng, Z.; Fan, Y.; Gao, Q.; Hu, Y. Evaluation and optimization of blasting approaches to reducing oversize boulders and toes in open-pit mine. Int. J. Min. Sci. Technol. 2020, 30, 373–380. [Google Scholar] [CrossRef]
- Ma, L.; Lai, X.; Zhang, J.; Xiao, S.; Zhang, L.; Tu, Y. Blast-Casting Mechanism and Parameter Optimization of a Benched Deep-Hole in an Opencast Coal Mine. Shock Vib. 2020, 2020. [Google Scholar] [CrossRef]
- Verma, H.; Samadhiya, N.; Singh, M.; Goel, R.; Singh, P. Blast induced rock mass damage around tunnels. Tunn. Undergr. Space Technol. 2018, 71, 149–158. [Google Scholar] [CrossRef]
- Jang, H.; Kawamura, Y.; Shinji, U. An empirical approach of overbreak resistance factor for tunnel blasting. Tunn. Undergr. Space Technol. 2019, 92. [Google Scholar] [CrossRef]
- Silva, J.; Worsey, T.; Lusk, B. Practical assessment of rock damage due to blasting. Int. J. Min. Sci. Technol. 2019, 29, 379–385. [Google Scholar] [CrossRef]
- Srirajaraghavaraju, R.R. Transmitted Pressure and Resulting Crack Network in Selected Rocks from Single-Hole Blasts in Laboratory-Scale Experiments. Master’s Thesis, University of Toronto, Toronto, ON, Canada, 2014. [Google Scholar]
- Johnson, C.E. Fragmentation Analysis in the Dynamic Stress Wave Collision Regions in Bench Blasting. Ph.D. Thesis, University of Kentucky, Lexington, KY, USA, 2014. [Google Scholar]
- Guo, Y.; Han, Z.; Guo, H.; Wang, T.; Liu, B.; Wang, D. Numerical simulation damage analysis of pipe-cement-rock combination due to the underwater explosion. Eng. Fail. Anal. 2019, 105, 584–596. [Google Scholar] [CrossRef]
- Wei, X.; Zhao, Z.; Gu, J. Numerical simulations of rock mass damage induced by underground explosion. Int. J. Rock Mech. Min. Sci. 2009, 46, 1206–1213. [Google Scholar] [CrossRef]
- Yang, R.; Wang, Y.; Ding, C. Laboratory study of wave propagation due to explosion in a jointed medium. Int. J. Rock Mech. Min. Sci. 2016, 81, 70–78. [Google Scholar] [CrossRef]
- Persson, P.A.; Holmberg, R.; Lee, J. Rock Blasting and Explosives Engineering, 1st ed.; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Jommi, C.; Pandolf, A. Vibrations induced by blasting in rock: A numerical approach. Riv. Ital. Geotec. 2008, 2, 77–94. [Google Scholar]
- Fleetwood, K.G.; Villaescusa, E.; Li, J. Limitations of using ppv damage models to predict rock mass damage. In Proceedings of the Thirty-Fifth Annual Conference on Explosives and Blasting Technique, Denver, CO, USA, 8–11 February 2009; International Society of Explosives Engineers: Denver, CO, USA, 2009; Volume 1, pp. 1–15. [Google Scholar]
- Duan, K.; Kwok, C.Y. Evolution of stress-induced borehole breakout in inherently anisotropic rock: Insights from discrete element modeling. J. Geophys. Res. Solid Earth 2016, 121, 2361–2381. [Google Scholar] [CrossRef]
- Parra, L.F.T. Study of Blast-Induced Damage in Rock with Potential Application to Open Pit and Underground Mines. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2012. [Google Scholar]
- Ma, G.; Hao, H.; Wang, F. Simulations of explosion-induced damage to underground rock chambers. J. Rock Mech. Geotech. Eng. 2011, 3, 19–29. [Google Scholar] [CrossRef]
- Wang, Z.; Konietzky, H. Modelling of blast-induced fractures in jointed rock masses. Eng. Fract. Mech. 2009, 76, 1945–1955. [Google Scholar] [CrossRef]
- Mitelman, A.; Elmo, D. Modelling of blast-induced damage in tunnels using a hybrid finite-discrete numerical approach. J. Rock Mech. Geotech. Eng. 2014, 6, 565–573. [Google Scholar] [CrossRef]
- Bendezu, M.; Romanel, C.; Roehl, D. Finite element analysis of blast-induced fracture propagation in hard rocks. Comput. Struct. 2017, 182, 1–13. [Google Scholar] [CrossRef]
- Onederra, I.A.; Furtney, J.K.; Sellers, E.; Iverson, S. Modelling blast induced damage from a fully coupled explosive charge. Int. J. Rock Mech. Min. Sci. 2013, 58, 73–84. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.g.; Liu, M.s.; Wu, X.x.; Zhao, G.; Li, P. Damage-vibration couple control of rock mass blasting for high rock slopes. Int. J. Rock Mech. Min. Sci. 2018, 103, 137–144. [Google Scholar] [CrossRef]
- Sun, X.J.; Sun, J.S. Research on the damage fracture of rock blasting based on velocity response spectrum. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2012; Volume 105, pp. 1521–1527. [Google Scholar] [CrossRef]
- Bauer, A.; Calder, P. Open Pit and Blast Seminar; Course No. 63321; Mining Engineering Department, Queens University: Kingston, ON, Canada, 1978. [Google Scholar]
- Mojtabai, N.; Beatty, S. An empirical approach to assessment of and prediction of damage in bench blasting. Trans. Inst. Min. Metall. 1995, 105, A75–A80. [Google Scholar]
- Holmberg, R.; Persson, P. The Swedish approach to contour blasting. In Proceedings of the Annual Conference on Explosives and Blasting Technique, New Orleans, LA, USA, 1–3 February 1978; International Society of Explosives Engineers: New Orleans, LA, USA, 1978; pp. 113–127. [Google Scholar]
- Aleksandrova, N.I.; Sher, Y.N. Effect of stemming on rock breaking with explosion of a cylindrical charge. J. Min. Sci. 1999, 35, 483–493. [Google Scholar] [CrossRef]
- Wang, M.; Yue, S.; Zhang, N.; Gao, K.; Wang, D. A method of calculating critical depth of burial of explosive charges to generate bulging and cratering in rock. Shock Vib. 2016, 1–11. [Google Scholar] [CrossRef]
- Hustrulid, W.; Lu, W. Some general design concepts regarding the control of blast-induced damage during rock slope excavation. In Proceedings of the 7th International Symposium on Rock Fragmentation by Blasting, Beijing, China, 11–15 August 2002; pp. 595–604. [Google Scholar]
- Mosinets, V.; Gorbacheva, N. A seismological method of determining the parameters of the zones of deformation of rock by blasting. Sov. Min. 1972, 8, 640–647. [Google Scholar] [CrossRef]
- Ilyushin, A. The Mechanics of a Continuous Medium; Izd-vo MGU: Moscow, Russia, 1971. (In Russian) [Google Scholar]
- Drukovanyi, M.F.; Kravtsov, V.; Chernyavskii, Y.; Shelenok, V.; Reva, N.; Zverkov, S. Calculation of fracture zones created by exploding cylindrical charges in ledge rocks. Sov. Min. 1976, 12, 292–295. [Google Scholar] [CrossRef]
- Senuk, V. The impulse from an explosion, and conditions for its greater utilization in crushing hard rock masses in blasting. Sov. Min. 1979, 15, 22–27. [Google Scholar] [CrossRef]
- Szuladzinski, G. Response of rock medium to explosive borehole pressure. In Rock Fragmentation by Blasting, Proceedings of The Fourth International Symposium on Rock Fragmentation by Blasting, FRAGBLAST-4, Vienna, Austria, 5–8 July 1993; Balkema: Rotterdam, The Netherland, 1993; pp. 17–23. [Google Scholar]
- Ash, R. The mechanics of rock breakage (part 1). Pit Quarry 1963, 56, 98–100. [Google Scholar]
- Ash, R. The mechanics of rock breakage (part 2)-standards blasting design. Pit Quarry 1963, 56, 119–122. [Google Scholar]
- Ash, R. The mechanics of rock breakage (part 3)-characteristics of explosives. Pit Quarry 1963, 56, 126–131. [Google Scholar]
- Ash, R. The mechanics of rock breakage (part 4)-material properties, powder factor, blasting cost. Pit Quarry 1963, 56, 109–118. [Google Scholar]
- Ouchterlony, F. Prediction of crack lengths in rock after cautious blasting with zero inter-hole delay. Int. J. Blasting Fragm. Fragblast 1997, 1, 417–444. [Google Scholar] [CrossRef]
- Ouchterlony, F.; Olsson, M.; Bergqvist, I. Towards new Swedish recommendations for cautious perimeter blasting. Int. J. Blasting Fragm. Fragblast 2002, 6, 235–261. [Google Scholar] [CrossRef]
- Sher, E.; Aleksandrova, N. Dynamics of development of crushing zone in elastoplastic medium in camouflet explosion of string charge. J. Min. Sci. 1997, 33, 529–535. [Google Scholar] [CrossRef]
- Sher, E.; Aleksandrova, N. Effect of borehole charge structure on the parameters of a failure zone in rocks under blasting. J. Min. Sci. 2007, 43, 409–417. [Google Scholar] [CrossRef]
- Hustrulid, W. Some comments regarding development drifting practices with special emphasis on caving applications. In Second International Symposium on Block and Sublevel Caving; Potvin, Y., Ed.; Australian Centre for Geomechanics: Perth, Australia, 2010; pp. 3–43. [Google Scholar]
- Djordjevic, N. A two-component model of blast fragmentation. In Proceedings of the 6th International Symposium for Rock Fragmentation by Blasting-Fragblast, Johannesburg, South Africa, 8–12 August 1999; pp. 213–219. [Google Scholar]
- Kanchibotla, S.; Valery, W.; Morrell, S. Modelling fines in blast fragmentation and its impact on crushing and grinding; Australasian Institute of Mining and Metallurgy Publication Series. In Proceedings of the Explo 99: A Conference on Rock Breaking, Kalgoorlie, WA, USA, 7–11 November 1999. [Google Scholar]
- Johnson, J. The Hustrulid Bar—A Dynamic Strength Test and Its Application to the Cautious Blasting of Rock. Ph.D. Thesis, The Unversity of Utah, Salt Lake, UT, USA, 2010. [Google Scholar]
- Saharan, M.R.; Mitri, H.S. Numerical Procedure for Dynamic Simulation of Discrete Fractures Due to Blasting. Rock Mech. Rock Eng. 2008, 41, 641–670. [Google Scholar] [CrossRef]
- Zhu, W.; Wei, J.; Zhao, J.; Niu, L. 2D numerical simulation on excavation damaged zone induced by dynamic stress redistribution. Tunn. Undergr. Space Technol. 2014, 43, 315–326. [Google Scholar] [CrossRef]
- Goodarzi, M.; Mohammadi, S.; Jafari, A. Numerical analysis of rock fracturing by gas pressure using the extended finite element method. Pet. Sci. 2015, 12, 304–315. [Google Scholar] [CrossRef]
- Hu, Y.; Lu, W.; Chen, M.; Yan, P.; Zhang, Y. Numerical simulation of the complete rock blasting response by SPH–DAM–FEM approach. Simul. Model. Pract. Theory 2015, 56, 55–68. [Google Scholar] [CrossRef]
- Yang, J.; Yao, C.; Jiang, Q.; Lu, W.; Jiang, S. 2D numerical analysis of rock damage induced by dynamic in-situ stress redistribution and blast loading in underground blasting excavation. Tunn. Undergr. Space Technol. 2017, 70, 221–232. [Google Scholar] [CrossRef]
- Hu, Y.; Lu, W.; Wu, X.; Liu, M.; Li, P. Numerical and experimental investigation of blasting damage control of a high rock slope in a deep valley. Eng. Geol. 2018, 237, 12–20. [Google Scholar] [CrossRef]
- Jayasinghe, L.; Shang, J.; Zhao, Z.; Goh, A. Numerical investigation into the blasting-induced damage characteristics of rocks considering the role of in-situ stresses and discontinuity persistence. Comput. Geotech. 2019, 116, 1–13. [Google Scholar] [CrossRef]
- Yilmaz, O.; Unlu, T. Three dimensional numerical rock damage analysis under blasting load. Tunn. Undergr. Space Technol. 2013, 38, 266–278. [Google Scholar] [CrossRef]
- Hu, R.; Zhu, Z.; Xie, J.; Xiao, D. Numerical study on crack propagation by using softening model under blasting. Adv. Mater. Sci. Eng. 2015, 2015, 1–9. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, T.; Zhang, P.; Zhou, J.; Yu, Q.; Deng, W. The analysis of rock damage process based on the microseismic monitoring and numerical simulations. Tunn. Undergr. Space Technol. 2017, 69, 1–17. [Google Scholar] [CrossRef]
- Jessu, K.; Spearing, A.; Sharifzadeh, M. A Parametric Study of Blast Damage on Hard Rock Pillar Strength. Energies 2018, 11, 1901. [Google Scholar] [CrossRef]
- Lak, M.; Fatehi Marji, M.; Yarahmadi Bafghi, A.; Abdollahipour, A. Analytical and numerical modeling of rock blasting operations using a two-dimensional elasto-dynamic Green’s function. Int. J. Rock Mech. Min. Sci. 2019, 114, 208–217. [Google Scholar] [CrossRef]
- Zhou, M.; Shadabfar, M.; Huang, H.; Leung, Y.F.; Uchida, S. Meta-modelling of coupled thermo-hydro-mechanical behaviour of hydrate reservoir. Comput. Geotech. 2020, 128, 103848. [Google Scholar] [CrossRef]
- Aliabadian, Z.; Sharafisafa, M.; Mortazavi, A.; Maarefvand, P. Wave and fracture propagation in continuum and faulted rock masses: Distinct element modeling. Arab. J. Geosci. 2014, 7, 5021–5035. [Google Scholar] [CrossRef]
- Deng, X.; Zhu, J.; Chen, S.; Zhao, Z.; Zhou, Y.; Zhao, J. Numerical study on tunnel damage subject to blast-induced shock wave in jointed rock masses. Tunn. Undergr. Space Technol. 2014, 43, 88–100. [Google Scholar] [CrossRef]
- Sharafisafa, M.; Aliabadian, Z.; Alizadeh, R.; Mortazavi, A. Distinct element modelling of fracture plan control in continuum and jointed rock mass in presplitting method of surface mining. Int. J. Min. Sci. Technol. 2014, 24, 871–881. [Google Scholar] [CrossRef]
- Bai, Q.S.; Tu, S.H.; Zhang, C. DEM investigation of the fracture mechanism of rock disc containing hole(s) and its influence on tensile strength. Theor. Appl. Fract. Mech. 2016, 86, 197–216. [Google Scholar] [CrossRef]
- Yin, T.; Zhang, S.; Li, X.; Bai, L. A numerical estimate method of dynamic fracture initiation toughness of rock under high temperature. Eng. Fract. Mech. 2018, 204, 87–102. [Google Scholar] [CrossRef]
- Yuan, W.; Su, X.; Wang, W.; Wen, L.; Chang, J. Numerical study of the contributions of shock wave and detonation gas to crack generation in deep rock without free surfaces. J. Pet. Sci. Eng. 2019, 177, 699–710. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Fakhimi, A.; Lanari, M. DEM-SPH simulation of rock blasting. Comput. Geotech. 2014, 55, 158–164. [Google Scholar] [CrossRef]
- An, H.; Liu, H.; Han, H.; Zheng, X.; Wang, X. Hybrid finite-discrete element modelling of dynamic fracture and resultant fragment casting and muck-piling by rock blast. Comput. Geotech. 2017, 81, 322–345. [Google Scholar] [CrossRef]
- Zhu, J.B.; Li, Y.S.; Wu, S.Y.; Zhang, R.; Ren, L. Decoupled explosion in an underground opening and dynamic responses of surrounding rock masses and structures and induced ground motions: A FEM-DEM numerical study. Tunn. Undergr. Space Technol. 2018, 82, 442–454. [Google Scholar] [CrossRef]
- Wang, Z.l.; Li, Y.c.; Wang, J. Numerical analysis of blast-induced wave propagation and spalling damage in a rock plate. Int. J. Rock Mech. Min. Sci. 2008, 45, 600–608. [Google Scholar] [CrossRef]
- Wang, Z.; Konietzky, H.; Shen, R. Coupled finite element and discrete element method for underground blast in faulted rock masses. Soil Dyn. Earthq. Eng. 2009, 29, 939–945. [Google Scholar] [CrossRef]
- Liu, C.; Yang, M.; Han, H.; Yue, W. Numerical simulation of fracture characteristics of jointed rock masses under blasting load. Eng. Comput. 2019, 36, 835–1851. [Google Scholar] [CrossRef]
- Lak, M.; Marji, M.F.; Bafghi, A.Y.; Abdollahipour, A. A coupled finite difference-boundary element method for modeling the propagation of explosion-induced radial cracks around a wellbore. J. Nat. Gas Sci. Eng. 2019, 64, 41–51. [Google Scholar] [CrossRef]
- Chi, L.Y.; Zhang, Z.X.; Aalberg, A.; Li, C.C. Experimental investigation of blast-induced fractures in rock cylinders. Rock Mech. Rock Eng. 2019, 52, 2569–2584. [Google Scholar] [CrossRef]
- Ge, J.; Li, G.Q.; Chen, S.W. Theoretical and experimental investigation on fragment behavior of architectural glass panel under blast loading. Eng. Fail. Anal. 2012, 26, 293–303. [Google Scholar] [CrossRef]
- Lownds, M. Measurement shock pressures in splitting of dimensional stone. In Proceedings of the 1st World Conference on Explosives and Blasting Technique, Munich, Germany, 6–8 September 2000; pp. 241–246. [Google Scholar]
- Talhi, K.; Hadjaj-Aoul, E.; Hannachi, E.B. Design of a model blasting system to measure peak P-wave stress. Acta Geod. Geophys. Hung. 2004, 39, 427–438. [Google Scholar] [CrossRef]
- Teowee, G.; Papillon, B. Measurement of borehole pressure during blasting. In Proceedings of the Rock Fragmentation by Blasting: Fragblast 10, New Delhi, India, 26–29 November 2012; pp. 599–605. [Google Scholar]
- Teowee, G.; Papillon, B. Monitoring of dynamic borehole pressures. In Proceedings of the 39th Annual Conference on Explosives and Blasting Techniques, Fort Worth, TX, USA, 10–13 February 2013; pp. 1–10. [Google Scholar]
- Austing, J.L.; Tulis, A.J.; Hrdina, D.J.; Baker, D.E.; Martinez, R. Carbon resistor gauges for measuring shock and detonation pressures. I. Principles of functioning and calibration. Propellants Explos. Pyrotech. 1991, 16, 205–215. [Google Scholar] [CrossRef]
- Olsson, M.; Bergqvist, I. Crack lengths from explosives in small diameter boreholes. In Proceedings of the 4th International symposium on Rock Fragmentation by Blasting, Vienna, Austria, 5–8 July 1993; pp. 193–196. [Google Scholar]
- Olsson, M.; Bergqvist, I. Crack lengths from explosives in multiple hole blasting. In Proceedings of the 5th International symposium on Rock Fragmentation by Blasting, Montreal, QC, Canada, 25–29 August 1996; pp. 187–193. [Google Scholar]
- Dehghan-Banadaki, M. Stress-Wave Induced Fracture in Rock due to Explosive Action. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2010. [Google Scholar]
- Nariseti, C. Quantification of Damage in Selected Rocks due to Impact with Tungsten Carbide Bits. Master’s Thesis, University of Toronto, Toronto, ON, Canada, 2013. [Google Scholar]
- Paventi, M.; Mohanty, B. Mapping of blast-induced fractures in rock. In Proceedings of the 7th International Symposium of Rock Fragmentation by Blasting, Beijing, China, 11–15 August 2002; Metallurgical Industry Press: Beijing, China, 2002; pp. 166–172. [Google Scholar]
- Yamin, G. Field Measurements of Blast Induced Damage in Rock. Master’s. Thesis, University of Toronto, Toronto, ON, Canada, 2005. [Google Scholar]
- McHugh, S. Crack extension caused by internal gas pressure compared with extension caused by tensile stress. Int. J. Fract. 1983, 21, 163–176. [Google Scholar] [CrossRef]
- Brinkmann, J. Separating shock wave and gas expansion breakage mechanism. In Proceedings of the 2nd International Symposium on Rock Fragmentation by Blasting, Keystone, CO, USA, 23–26 August 1987; pp. 6–15. [Google Scholar]
- Fullelove, I.; Onederra, I.; Villaescusa, E. Empirical approach to estimate rock mass damage from long-hole winze (LHW) blasting. Min. Technol. 2017, 126, 34–43. [Google Scholar] [CrossRef]
- Hu, Y.; Lu, W.; Chen, M.; Yan, P.; Yang, J. Comparison of blast-induced damage between presplit and smooth blasting of high rock slope. Rock Mech. Rock Eng. 2014, 47, 1307–1320. [Google Scholar] [CrossRef]
- Amnieh, H.B.; Bahadori, M. Numerical analysis for effects of single blast hole in mudstone rock-mass at Gotvand Olya dam. Iran. J. Geophys. (IJG) 2012, 6, 56–72. [Google Scholar]
- Amnieh, H.B.; Bahadori, M. Numerical and field analysis of single-hole blasting mechanism in conglomerate rock mass of Gotvand Olya Dam. Energy Eng. Manag. 2012, 2, 22–31. [Google Scholar]
- Shadab Far, M.; Wang, Y. Probabilistic analysis of crushed zone for rock blasting. Comput. Geotech. 2016, 80, 290–300. [Google Scholar] [CrossRef]
- Shadab Far, M.; Wang, Y. Approximation of the Monte Carlo Sampling Method for Reliability Analysis of Structures. Math. Probl. Eng. 2016, 2016, 1–9. [Google Scholar] [CrossRef]
- Shadabfar, M.; Huang, H.; Wang, Y.; Wu, C. Monte Carlo analysis of the induced cracked zone by single-hole rock explosion. Geomech. Eng. 2020, 21, 289–300. [Google Scholar] [CrossRef]
- Lu, W.; Leng, Z.; Chen, M.; Yan, P.; Hu, Y. A modified model to calculate the size of the crushed zone around a blast-hole. J. S. Afr. Inst. Min. Metall. 2016, 116, 413–422. [Google Scholar] [CrossRef]
- Shadab Far, M.; Wang, Y.; Dallo, Y.A.H. Reliability analysis of the induced damage for single-hole rock blasting. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2019, 13, 82–98. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).