An Accurate Discrete Current Controller for High-Speed PMSMs/Gs in Flywheel Applications

Abstract

High-speed Permanent-Magnet Synchronous Motors/Generators (PMSMs/Gs) in a Flywheel Energy Storage System (FESS) are faced with high cross-coupling voltages and low switching-to-fundamental frequency ratios. High cross-coupling voltages between d-q axis current loops lead to transient current errors, which is more serious at lower switching-to-fundamental-frequency ratios. If the delays are not properly considered during the current controller design in a digital control system, the low switching-to-fundamental-frequency ratios may result in oscillatory or unstable responses. In this study, an accurate discrete current controller for high-speed PMSMs/Gs is proposed based on an accurate discrete model that takes the phase and magnitude errors generated during the sampling period into consideration, and an Extended State Observer (ESO) is applied to estimate and compensate the back EMF error. The cross-coupling problem is well settled, and the current loop dynamic at lower switching-to-fundamental frequency ratios is improved. Finally, the proposed discrete controller is validated on a 12,000 rpm PMSM/G prototype.

1. Introduction

A Flywheel Energy Storage System (FESS) is a mechanical energy storage system that stores energy through a high-speed rotational flywheel driven by an integrated motor/generator and a power converter [1]. Due to its high-energy transfer efficiency, high instantaneous power, fast dynamic response, long cycle lifetime, and low pollution to environments [2,3], the application of FESS has been widely researched within a wide range of fields including electrical vehicles, naval warships, aerospace applications, micro grids, wind power plants, and so on [4,5,6,7].

The High-speed Permanent Magnet Synchronous Motor/Generator (PMSM/G) is a good candidate for the FESS machine thanks to its efficiency, power density, reliability, and flexibility of bidirectional power flow [8]. However, the high speed leads to a high cross-coupling voltage between d-q axes current loops, which leads to transient errors during dynamic process. Moreover, the wide speed range operation of the high-speed PMSM/G and the switching frequency limitation of power electronic devices results in low switching-to-fundamental-frequency ratios. At low ratios, oscillation or instability can be caused by high cross-coupling between d-q axis currents and intolerable digital delays between the variable sampling and reference signal implementation if the discrete nature of the Pulse Width Modulation (PWM) modulation method is not properly considered during the current controller design [9].

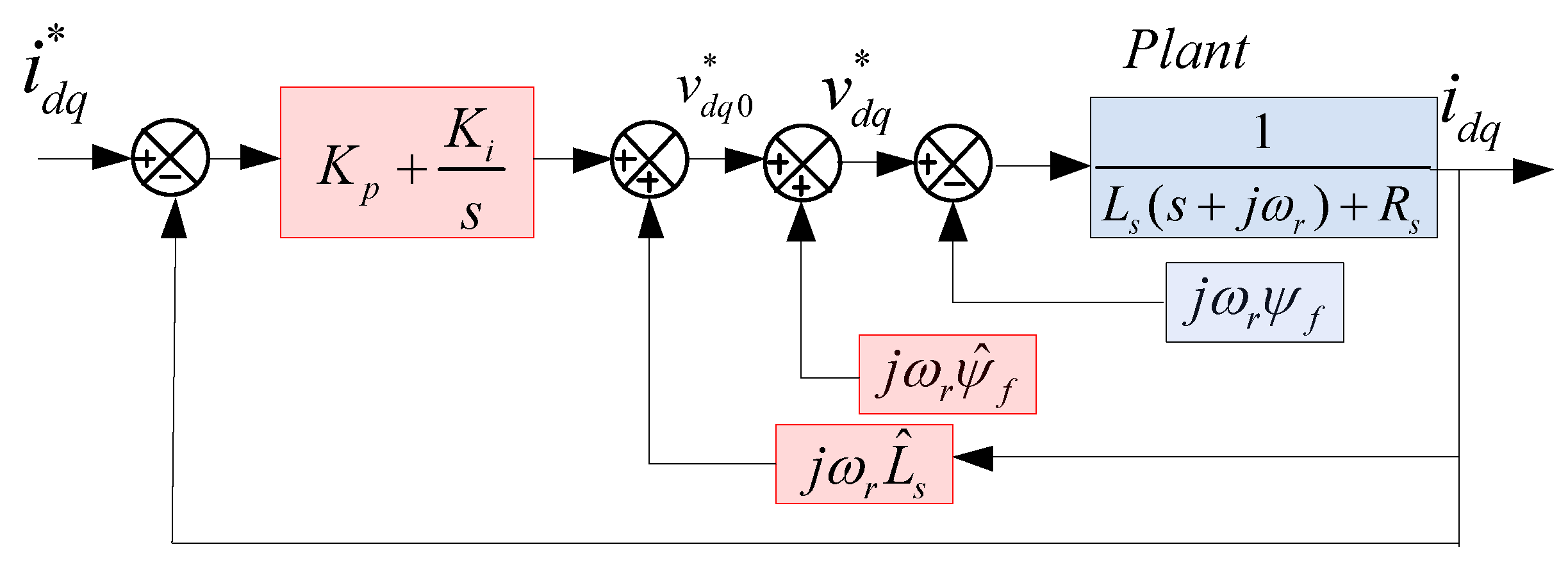
To solve the cross-coupling problem, the most direct and commonly used decoupling method is the state feedback method, which calculates and compensates cross-coupling terms according to the sampled current and speed in the current controller [10,11]. However, the drawback is that the calculation of decoupling terms is highly dependent on inductance parameters. With the intolerant sampling delays, the effectiveness of the decoupling is greatly reduced. Another commonly used decoupling method is based on the complex vector model [12], the essence of which is zero-pole cancellation. The final compensation term comes from the output of an integrator, so the requirement for the parameter accuracy is reduced, and the robustness to the parameter perturbation is enhanced. The drawback is that the oscillation of synchronous frequencies is superimposed on the transient current waveform before the controller enters a steady state [13]. Two Proportional-Integral (PI) cross-decoupling terms are used in [14] to compensate the reference voltage, which improved the robustness, but the bandwidth of the current controller needs to be increased to ensure the current tracking performance, resulting in a larger noise in the output voltage of the current controller. A sliding mode control decoupling algorithm is proposed in [15] that improves the robustness of the system to the parameter variation to a certain extent, but also induced the chattering problem.

All the methods above are discussed in the continuous time domain, where a current controller is normally designed based on a continuous model. When applied to discrete control systems, the controller has to be transferred to its discrete form though approximation methods, among which the Euler difference method and Tustin transformation are the most widely used options. However, inevitable performance degradation occurs because the intrinsic delay of the digital controller is not taken in to consideration during the design procedure, which results in sensitivity to the rotation speed [16,17].

The digital delays can be roughly modeled with a first-order low-pass filter with a time constant of 3Ts/2 [18], but this approach is only reasonable when the digital delays are much smaller than the fundamental period of the electrical machines [19]. However, when faced with lower switching-to-fundamental-frequency ratios, the magnitude and phase errors generated during the sampling period should be analyzed though a more complex and accurate model such as a higher-order Padé approximations [20,21].

In our previous conference publication [22], an accurate discrete current loop model with a complex vector expression was built, and an accurate discrete controller was designed that accounted for the magnitude and phase errors generated during the sampling period. This allowed classical analysis tools to be applied in the stability and performance evaluation of a closed-loop system in discrete time [23,24], but the elaboration was not complete and the rough simulation and experimental results given were based on a low-speed machine with a switching frequency of 5 kHz and fundamental frequency of 50 Hz at 1000 rpm, which was not convincing enough. 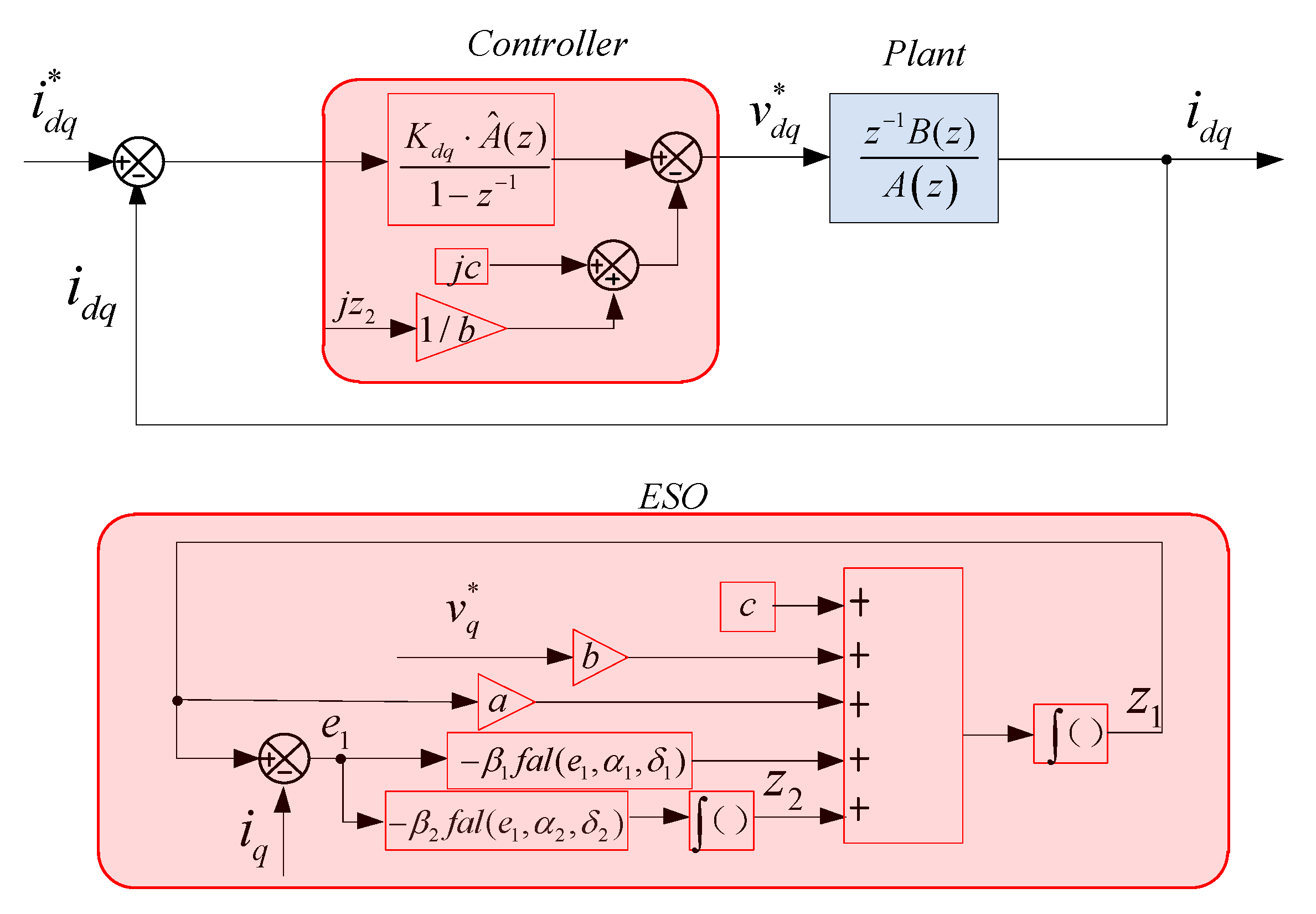Following the work in [13], an Extended State Observer (ESO) was added in the current loop to estimate and compensate the back-Electromotive Force (back-EMF) error in this paper, and simulation and experimental results were obtained on a real high-speed PMSM/G prototype with rated speed of 12,000 rpm.

The controller design and performance analysis are presented in Section 2. Simulation and experiment validation are presented in Section 3 and Section 4. Finally, a conclusion is drawn in Section 5.

2. Design of the Proposed Current Controller

The simplified schematic of the FESS studied in this paper is presented in Figure 1, consisting of a flywheel driven by a PMSM/G and a bidirectional converter connected to the DC link with a resistive DC load.

The model of a non-salient PMSM/G is expressed in the stationary frame and rotor frame as

$$v_{\alpha }{}_{\beta }=R_{\mathrm{s}}{i}_{\alpha \beta }+L_{\mathrm{s}}\frac{d{i}_{\alpha \beta }}{dt}+e_{\alpha \beta }$$

(1)

and

$$v_{dq}=R_{\mathrm{s}}{i}_{dq}+L_{\mathrm{s}}\frac{d{i}_{dq}}{dt}+j{\omega }_r{L}_s{i}_{dq}+j{\omega }_r{\psi }_f$$

(2)

respectively, where $v_{\alpha \beta }=v_{\alpha }+{jv}_{\beta }$, $i_{\alpha \beta }=i_{\alpha }+{ji}_{\beta }$, $v_{dq}=v_d+{jv}_q$, and $i_{dq}=i_d+{ji}_q$ represent the machine voltage and current vectors; ${\psi }_f$ is the flux linkage; ${\omega }_r$ and ${\theta }_r$ represent the rotor electrical angular speed and position, respectively; Ls and Rs are the phase inductance and resistance, respectively; and the back EMF vector in the stationary frame is $e_{\alpha \beta }={-\omega \psi }_f\sin {\theta }_r+{j\omega \psi }_f\cos {\theta }_r$.

2.1. Decoupling of Current Loop Based on the Accurate Discrete-time Domain Model of PMSMs

In a digital system, a zero-order holder is applied to each variable to model the sampling process. The two independent excitation sources of PMSMs/Gs—the input voltage and back EMF—exhibit different sampling retention characteristics. As Space Vector Pulse Width Modulation (SVPWM) modulation of the input voltage is realized in the stationary frame, it is more reasonable to hold the input voltage in the stationary frame, where the amplitude and phase of $v_{\alpha }$, $v_{\beta }$ are constant within one sampling period [9,13]. However, it is advisable to hold the back EMF in the rotor frame where it is a DC variable. Consider all of the above, the superposition principle is employed to discretize the input voltage and back EMF separately as follows.

With only the excitation of the input voltage considered, the continuous voltage Equation (2) of a PMSM in the stationary frame is simplified to

$$v_{\alpha \beta }=R_{\mathrm{s}}{i}_{\alpha \beta }+L_{\mathrm{s}}\frac{d{i}_{\alpha \beta }}{dt},$$

(3)

With the differential Equation (3) solved and the digital delay of one sampling period Ts considered, the discrete current loop model of a PMSM in the stationary frame is derived as

$$i_{\alpha \beta }[k]=i_{\alpha \beta }[k-1]e^{-R_{\mathrm{s}}{T}_s/L_s}+v_{\alpha \beta }[k-2]\frac{1-e^{-R_{\mathrm{s}}{T}_s/L_s}}{R_s},$$

(4)

Applying the Park transformation by substituting $i_{\alpha \beta }\left[k\right]=i_{dq}\left[k\right]·e^{j{\theta }_r[k]}$ and $v_{\alpha \beta }\left[k\right]=v_{dq}\left[k\right]·e^{j{\theta }_r[k]}$ into Equation (4), the discrete current loop dynamic of a PMSM in the rotor frame only excited by the input voltage is derived as

$$i_{dq}[k]=i_{dq}[k-1]e^{-j{\omega }_r{T}_s}{e}^{-R_{\mathrm{s}}{T}_s/L_s}+v_{dq}[k-2]e^{-j2{\omega }_r{T}_s}\frac{1-e^{-R_{\mathrm{s}}{T}_s/L_s}}{R_s},$$

(5)

With only the back EMF considered, the continuous current loop dynamics of a PMSM in the rotor frame are expressed as

$$L_{\mathrm{s}}\frac{d{i}_{dq}}{dt}=-(R_{\mathrm{s}}+j{\omega }_r{L}_s)i_{dq}-j{\omega }_r{\psi }_f,$$

(6)

With the differential Equation (6) solved, the discrete solution is expressed as

$$i_{dq}[k]=i_{dq}[k-1]e^{-(R_{\mathrm{s}}+j{\omega }_r{L}_s)T_s/L_s}-j{\omega }_r{\psi }_{\mathrm{f}}\frac{1-e^{-(R_{\mathrm{s}}+j{\omega }_r{L}_s)T_s/L_s}}{R_s+j{\omega }_r{L}_s},$$

(7)

The first terms on the right hand of Equations (5) and (7) are the same, whereas the second terms are the dynamics due to the input voltage and back EMF excitation, respectively. According to the superposition principle, the integrated discrete current loop model of the PMSM with both input voltage and back EMF considered is expressed as

$$i_{dq}[k]=i_{dq}[k-1]e^{-(R_{\mathrm{s}}+j{\omega }_r{L}_s)T_s/L_s}+v_{dq}[k-2]e^{-j2{\omega }_r{T}_s}\frac{1-e^{-R_s{T}_s/L_s}}{R_s}-j{\omega }_r{\psi }_{\mathrm{f}}\frac{1-e^{-(R_{\mathrm{s}}+j{\omega }_r{L}_s)T_s/L_s}}{R_s+j{\omega }_r{L}_s},$$

(8)

where the last term on the right hand can be regarded as a system disturbance to be canceled by feedforward compensation.

The disturbance compensation with an ESO will be illustrated in the following section. Here the last term of Equation (8) is assumed to be completely compensated, and the discrete transfer function from the input voltage to the output current is derived as [13]

$$G_p(z)=\frac{i_{dq}(z)}{v_{dq}(z)}=\frac{1}{R_s}\frac{e^{-j2{\omega }_r{T}_s}{z}^{-2}(1-e^{-R_s{T}_s/L_s})}{1-e^{-(R_s+j{\omega }_r{L}_s)T_s/L_s}{z}^{-1}}\triangleq \frac{z^{-1}B(z)}{A(z)},$$

(9)

where $A(z)$ and $B(z)$ are the denominator and numerator of the plant, respectively; and $G_p(z)$ contains a complex pole $p=e^{-(R_{\mathrm{s}}+j{\omega }_r{L}_s)T_s/L_s}$ that is prone to move with the speed variation.

To cancel the speed sensitive pole, a complex zero $z=e^{-(R_{\mathrm{s}}+j{\omega }_r{L}_s)T_s/L_s}$ is introduced in the control law as

$$v_{dq}^{*}=(i_{dq}^{*}-i_{dq})\frac{K_{dq}\widehat{A}(z)}{1-z^{-1}}=(i_{dq}^{*}-i_{dq})\frac{K_{dq}{e}^{j2{\omega }_r{T}_s}\left(1-e^{-(R_s+j{\omega }_r{L}_s)T_s/L_s}{z}^{-1}\right)}{1-z^{-1}},$$

(10)

where $\widehat{A}(z)$ is the estimation of $A(z)$, and K_dq represents the proportional gain of the controller.

2.2. Back-EMF Compensation Based on an Extended State Observer

The fundamental idea of an ESO is estimate and compensate real-time internal uncertainties and external disturbances [25,26,27]. All the internal uncertainties and external disturbances are integrated as a total disturbance and regarded as an extended variable. The ESO is able to observe the state variables with only the inputs and outputs of the system known.

For a second-order Single Input Single Output (SISO) system,

$$\{\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=f(x_1,x_2,\omega (t),t)+bu\\ y=x_1\end{array},$$

(11)

where y is the output, measured and to be controlled, whereas u is the input, and x₁, x₂ are the state variables. $f(x_1,x_2,\omega (t),t)$ is a multivariable function of the states, external disturbances, and time, which is not necessary to be expressively known. Treating $x_3=f(x_1,x_2,\omega (t),t)$ as the total disturbance, let $G(t)=\dot{f}(x_1,x_2,\omega (t),t)=f^{\prime }(x_1,x_2,\omega (t),t)$ and transform the original plant to an extended system using

$$\{\begin{array}{l}{e}_1=z_1-y\\ {\dot{z}}_1=z_2-{\beta }_{1}fal(e_1,{\alpha }_1,{\delta }_1)\\ {\dot{z}}_2=z_3+bu-{\beta }_{2}fal(e_1,{\alpha }_2,{\delta }_2)\\ {\dot{z}}_3=-{\beta }_{3}fal(e_1,{\alpha }_3,{\delta }_3)\end{array},$$

(12)

Equation (10) is observable through an ESO

$$\{\begin{array}{l}{e}_1=z_1-y\\ {\dot{z}}_1=z_2-{\beta }_{1}fal(e_1,{\alpha }_1,{\delta }_1)\\ {\dot{z}}_2=z_3+bu-{\beta }_{2}fal(e_1,{\alpha }_2,{\delta }_2)\\ {\dot{z}}_3=-{\beta }_{3}fal(e_1,{\alpha }_3,{\delta }_3)\end{array},$$

(13)

where z₁, z₂, z₃ are the observed values of x₁, x₂, x₃, respectively; and $fal(e,\alpha ,\delta )$ is a nonlinear function defined as

$$fal(e,\alpha ,\delta )=\{\begin{array}{l}{\delta }^{\alpha -1}e\\ {\left|e\right|}^{\alpha }sign(e),\left|e\right|>\delta \end{array},$$

(14)

where e is the input variable, and $0<\alpha <1$ and $\delta$ are the parameters. According to [26], if the parameters are properly tuned, the ESO (Equation (13)) is able to estimate the state variables in real time with a satisfying accuracy, that is, z₁ → x₁, z₂ → x₂.

The q-axis voltage equation is written as

$$\frac{d}{dt}{i}_q=-\frac{{\widehat{R}}_{\mathrm{s}}}{{\widehat{L}}_s}{i}_q+\frac{1}{{\widehat{L}}_s}{u}_q-{\omega }_r\frac{{\widehat{\psi }}_f}{{\widehat{L}}_s}-{\omega }_r\frac{{\widehat{L}}_s}{L_s}{i}_d-(\frac{R_{\mathrm{s}}}{L_s}-\frac{{\widehat{R}}_{\mathrm{s}}}{{\widehat{L}}_s})i_q+(\frac{1}{L_s}-\frac{1}{{\widehat{L}}_s})u_q-{\omega }_r(1-\frac{{\widehat{L}}_s}{L_s})i_d-{\omega }_r(\frac{{\psi }_f}{L_s}-\frac{{\widehat{\psi }}_f}{{\widehat{L}}_s}),$$

(15)

where ${\widehat{L}}_s,{\widehat{R}}_s,{\widehat{\psi }}_f$ are the estimated values of $L_s,R_s,{\psi }_f$, respectively.

As the cross-coupling term ${\omega }_r\frac{{\widehat{L}}_s}{L_s}{i}_d$ has been canceled by the proposed control law (Equation (10)), Equation (15) can be simplified to

$$\frac{d}{dt}{i}_q=-\frac{{\widehat{R}}_{\mathrm{s}}}{{\widehat{L}}_s}{i}_q+\frac{1}{{\widehat{L}}_s}{u}_q-{\omega }_r\frac{{\widehat{\psi }}_f}{{\widehat{L}}_s}-(\frac{R_{\mathrm{s}}}{L_s}-\frac{{\widehat{R}}_{\mathrm{s}}}{{\widehat{L}}_s})i_q+(\frac{1}{L_s}-\frac{1}{{\widehat{L}}_s})u_q-{\omega }_r(1-\frac{{\widehat{L}}_s}{L_s})i_d-{\omega }_r(\frac{{\psi }_f}{L_s}-\frac{{\widehat{\psi }}_f}{{\widehat{L}}_s}),$$

(16)

when considering the ESO.

Denoting state variables $x_1=i_q$ and $x_2=-(\frac{R_{\mathrm{s}}}{L_s}-\frac{{\widehat{R}}_{\mathrm{s}}}{{\widehat{L}}_s})i_q+(\frac{1}{L_s}-\frac{1}{{\widehat{L}}_s})u_q-{\omega }_r(1-\frac{{\widehat{L}}_s}{L_s})i_d-{\omega }_r(\frac{{\psi }_f}{L_s}-\frac{{\widehat{\psi }}_f}{{\widehat{L}}_s}),$ Equation (16) transforms to an extended system:

$$\{\begin{array}{l}{\dot{x}}_1=a{x}_1+x_2+bu+c\\ {\dot{x}}_2=G(t)\\ y=x_1\end{array},$$

(17)

where $a=-\frac{{\widehat{R}}_s}{{\widehat{L}}_s},b=\frac{1}{{\widehat{L}}_s},c=-\frac{{\omega }_r}{{\widehat{L}}_s}{\widehat{\psi }}_f$, and G(t) is an unknown differential function of x₂.

Equation (17) is not a standard extended system as Equation (12) is, but it can be observed by a modified ESO:

$$\{\begin{array}{l}{e}_1=z_1-y\\ {\dot{z}}_1=a{z}_1+z_2+bu+c-{\beta }_{1}fal(e_1,{\alpha }_1,{\delta }_1)\\ {\dot{z}}_2=-{\beta }_{2}fal(e_1,{\alpha }_2,{\delta }_2)\end{array},$$

(18)

whose discrete form is

$$\{\begin{array}{l}{e}_1[k]=z_1[k-1]-y[k-1]\\ z_2[k]=z_2[k-1]-{\beta }_{2}fal(e_1[k],{\alpha }_2,{\delta }_2)T_s\\ z_1[k]=z_1[k-1]+\\ \left(a{z}_1[k-1]+z_2[k]+bu[k-1]+c-{\beta }_{1}fal(e_1[k],{\alpha }_1,{\delta }_1)\right)T_s\end{array},$$

(19)

with T_s as the sampling period.

Applying the observed total disturbance compensation, the proposed discrete current controller designed with ESO-based back-EMF compensation is expressed as

$${v_{dq}^{*}}^{\prime }=v_{dq}^{*}-\frac{c+z_2}{b}=v_{dq}^{*}+{\omega }_r{\widehat{\psi }}_f-\frac{z_2}{b},$$

(20)

whereas the block diagram of is presented in Figure 2.

2.3. Performance Analysis

The most commonly used conventional continuous current controller,

$$v_{dq}^{*}=v_{dq0}^{*}+j{\omega }_r{\widehat{\psi }}_f=(i_{dq}^{*}-i_{dq})(K_p+\frac{K_i}{s})+j{\omega }_r{\widehat{L}}_s{i}_{dq}+j{\omega }_r{\widehat{\psi }}_f,$$

(21)

is illustrated in Figure 3, in which a typical PI controller is used, and the state feedback decoupling is realized by using the instantaneous feed forward of $j\omega {\widehat{L}}_s{i}_{dq}$ to cancel the cross-coupling term and obtain a decoupled plant model to be appropriately regulated by the PI controller. However, the d-q axis current loop cannot be accurately decoupled through this method when approximation methods such as the Euler difference method or Tustin transformation are used to transform the controller to discrete forms due to the error generated by the approximations.

Considering the PMSM current loop model in the discrete-time domain (Equation (9)), the conventional current controller (Equation (21)) is transformed to its discrete form as

$$v_{dq}^{*}=(i_{dq}^{*}-i_{dq})(K_p+\frac{K_i}{1-z^{-1}})+j{\omega }_r{\widehat{L}}_s{i}_{dq}+j{\omega }_r{\widehat{\psi }}_f,$$

(22)

Assuming the back EMF is completely compensated, and substituting the Gp(z) into Equation (22), the real closed-loop transfer function for the current controller (Equation (21)) in the discrete-time domain is derived as

$$\begin{array}{l}{H}_{cl}(z)=\frac{\left(K_p+\frac{K_i}{1-z^{-1}}\right)G_p(z)}{1+\left(K_p+\frac{K_i}{1-z^{-1}}-\mathrm{j}{\omega }_r{\widehat{L}}_s\right)G_p(z)}\\ =\frac{\frac{1}{R_s}\left(K_p+\frac{K_i}{1-z^{-1}}\right)e^{-j2{\omega }_r{T}_s}{z}^{-2}\left(1-e^{-R_s{T}_s/L_s}\right)}{\left(1-e^{-(R_s+j{\omega }_r{L}_s)T_s/L_s}{z}^{-1}\right)+\frac{1}{R_s}\left(K_p+\frac{K_i}{1-z^{-1}}-\mathrm{j}{\omega }_r{\widehat{L}}_s\right)e^{-j2{\omega }_r{T}_s}{z}^{-2}\left(1-e^{-R_s{T}_s/L_s}\right)}\end{array}$$

(23)

Applying Taylor’s Formula to Equation (22) and keeping the first two terms, Equation (23) is transformed to

$$H_{cl}(z)=\frac{\left(K_p+\frac{K_i}{1-z^{-1}}\right)\frac{T_s}{L_s}{e}^{-j2{\omega }_r{T}_s}{z}^{-2}}{1-\left(1-\frac{R_s{T}_s}{L_s}-j{\omega }_r{T}_s\right)z^{-1}+\left(K_p+\frac{K_i}{1-z^{-1}}-\mathrm{j}{\omega }_r{\widehat{L}}_s\right)\frac{T_s}{L_s}{e}^{-j2{\omega }_r{T}_s}{z}^{-2}},$$

(24)

where the complex cross-coupling term still exists due to the delays.

In contrast, the closed transfer function of the discrete current controller (Equation (10)) directly designed in the discrete-time domain is derived as

$$H_{cl}(z)=\frac{K_{dq}(1-e^{-R_s{T}_s/L_s})z^{-2}}{R_s(1-z^{-1})+K_{dq}(1-e^{-R_s{T}_s/L_s})z^{-2}},$$

(25)

where the speed-sensitive complex pole is completely canceled, and consequently the cross-coupling problem is well settled.

3. Simulation Results

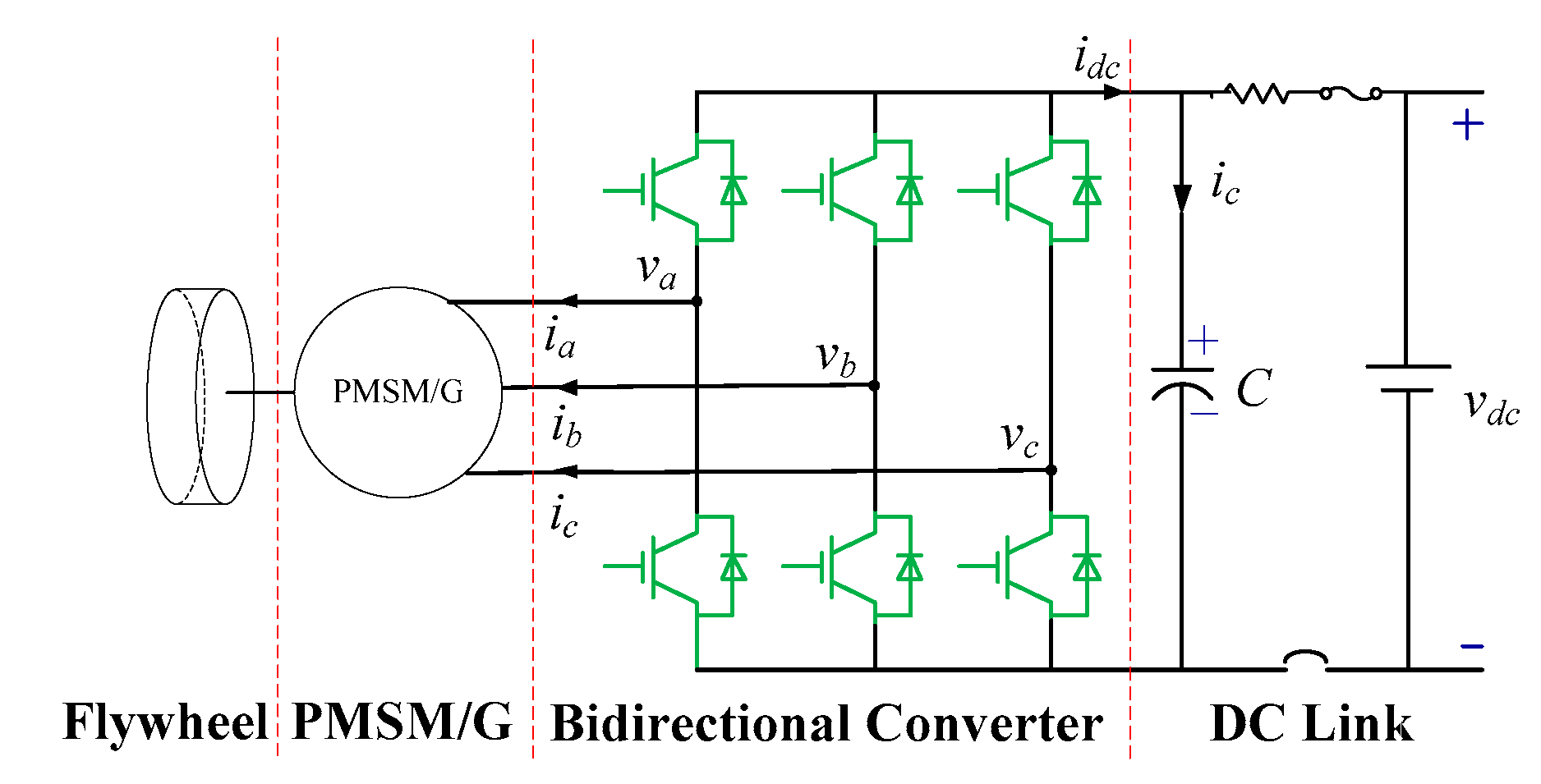
Performance of the proposed current controller (Equation (20)) was compared with the discrete form (Equation (22)) of the conventional controller with and without feedback decoupling term $j\omega {\widehat{L}}_s{i}_{dq}$ using MATLAB/SIMUINK simulations. The parameters of the PMSM/G and converter obtained from a high-speed prototype in Figure 4 are listed in

Table 1. Parameters of the PMSM/G and converter.

Rated Voltage (V)	141
Rated Power (kW)	2.5
Pole Pairs	1
Rated Speed (rpm)	12,000
Flux Linkage (V.s)	0.091
Stator Resistance (Ω)	0.17
Stator Inductance (mH)(Ld=Lq)	3.52
Inertia (kg·m2)	0.011
DC-link Voltage (V)	300
Capacitance (mF)	25.0
Switching Frequency (kHz)	2.5 (simulation) 5.0 (experiment)

.

The switching frequency was set to 2.5 kHz in the simulation, but kept as 5.0 kHz in the experiments. The bandwidth f_cl of three controllers was set as 500 Hz. For comparison, simulation results of the current controllers without decoupling and with state feedback decoupling are presented. The PMSM/G worked in generation mode at a constant speed. The DC link was fed by a DC voltage source, and no load was connected to the DC link. The q-axis current reference changed from 0A to −15A, then from −15A to 15A at 6000 rpm (100 Hz, fs/fe = 25) and 12,000 rpm (200 Hz, fs/fe = 12.5), where fs and fe were the switching frequency and fundamental electrical frequency, respectively. The results are shown in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10.

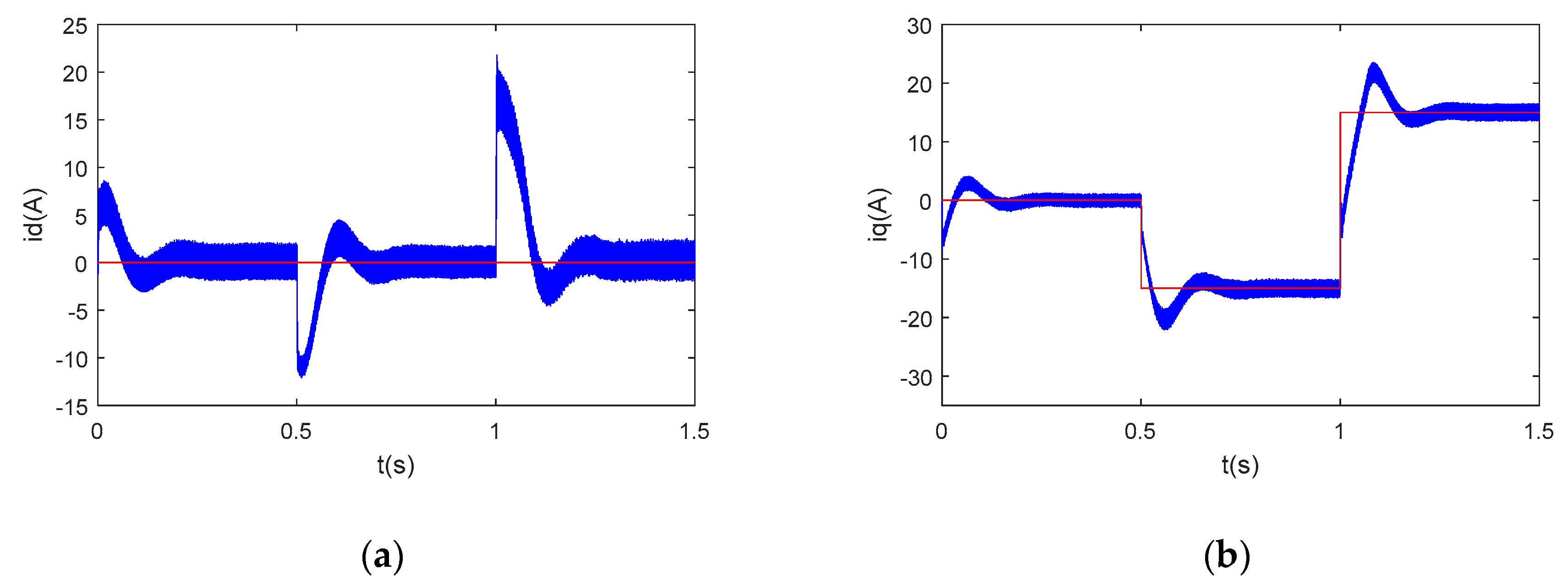
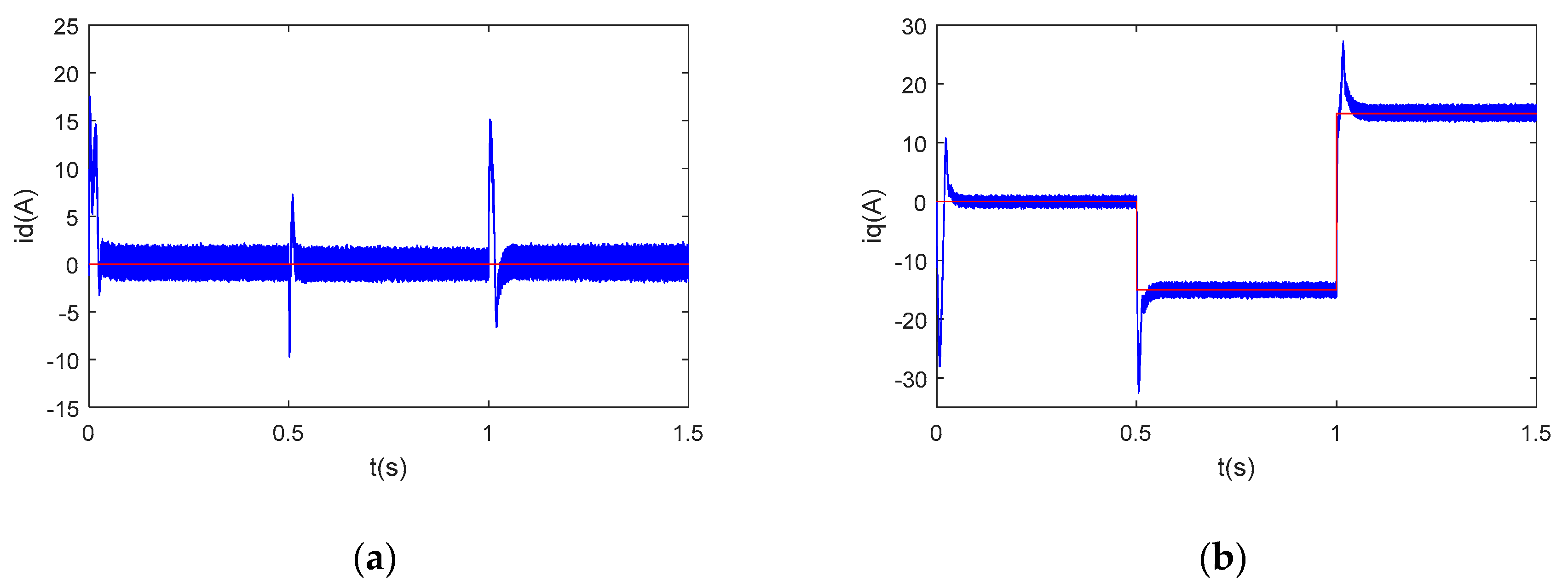
Figure 5, Figure 6 and Figure 7 present the simulation results of the three current controllers at 6000 rpm. In Figure 5, a transient error −7A is shown to have occurred when the q-axis current changed from 0A to −15A, whereas another 14A error occurred when the q-axis reference changed from −15A to 15A. The recovery time was around 0.1s. When feedback decoupling was applied, the transient errors reduced to −4A and 7A, respectively, and the recovery time was around 0.02 s (Figure 6). However, there was no obvious transient error in Figure 7 when the q-axis current reference changed. As for the q-axis currents, an overshoot of 2.5A and 3A can be seen in Figure 5 and Figure 6, but almost no overshoot can be seen in Figure 7.

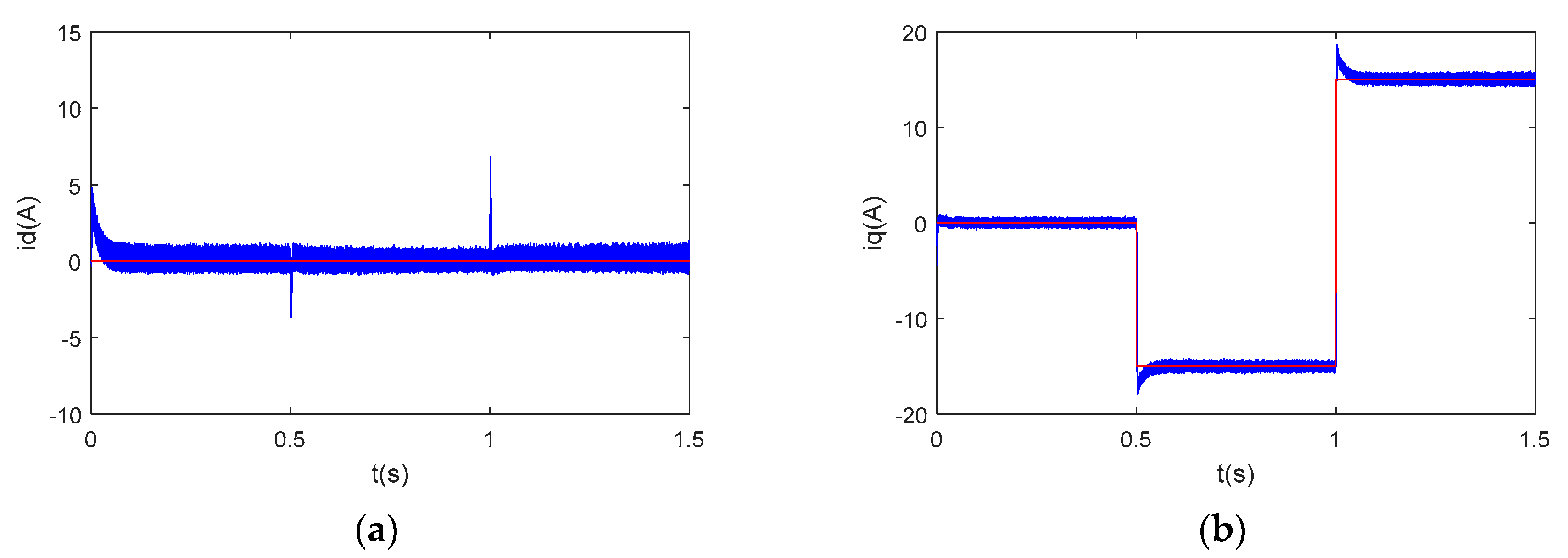
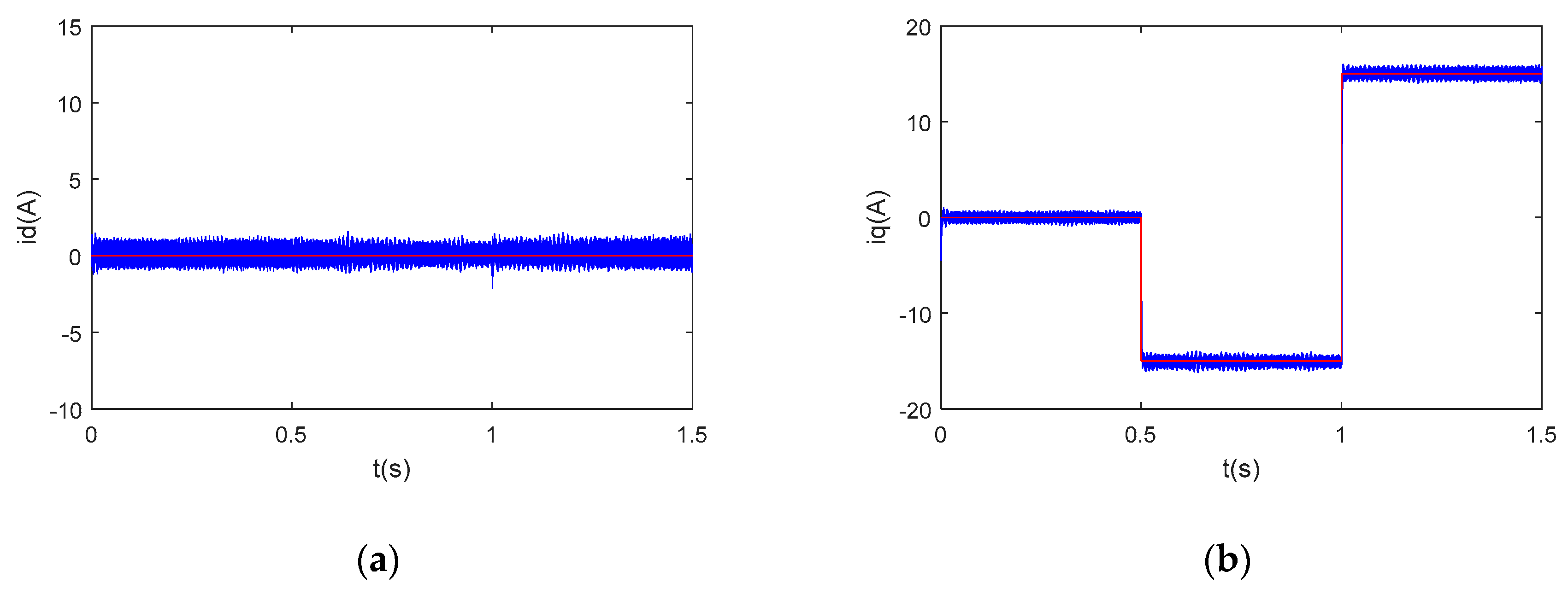
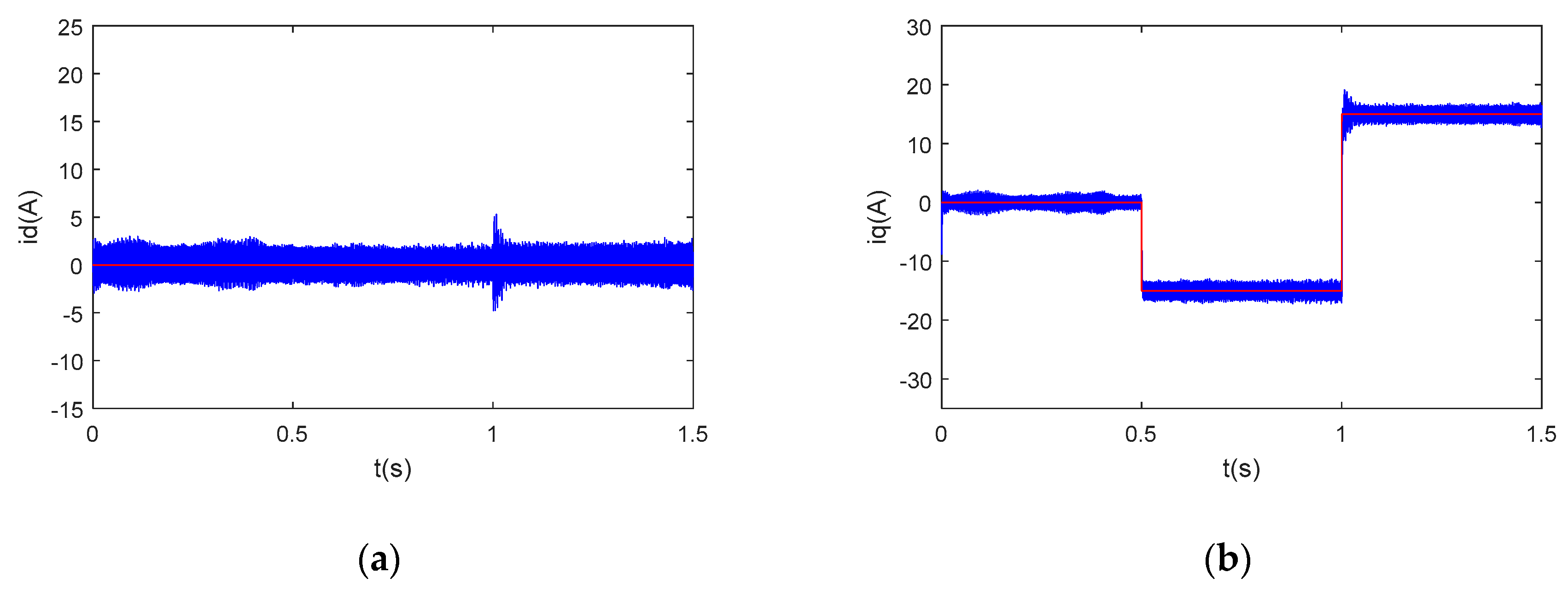
Figure 8, Figure 9 and Figure 10 present the simulation results of the three current controllers at 12,000 rpm, where the advantage of the proposed accurate current controller was most significant. In Figure 8, a transient error −12A occurred when the q-axis current changed from 0A to −15A, whereas another 20A error occurred when the q-axis reference changed from −15A to 15A. The recovery time was around 0.2 s. In Figure 9, the transient errors were reduced to −10A and 15A, respectively, when the feedback decoupling was applied, with a recovery time of around 0.1 s. However, there is no obvious transient error present in Figure 10 when the q-axis current reference changed from 0A to −15A, and a 5A error can be seen when the reference changed from −15A to 15A. As for the q-axis currents, an overshoot of 6A and 10A can be seen in Figure 8 and Figure 9, with recovery times of 0.2 and 0.1 s, respectively. However, no obvious overshoot can be seen in Figure 10.

Therefore, the simulation results prove that the proposed accurate discrete controller has better decoupling capability and dynamic performance than conventional controllers when applied with the same proportional gain to ensure the same current loop bandwidth, especially at higher speeds with lower switching-to-fundamental-frequency ratios.

4. Experimental Results

Dynamic performance of the three controllers was also experimentally tested on the high-speed prototype shown in Figure 4, which consisted of a high-speed PMSM/G with a rated speed of 12,000 rpm and a converter based on the TI DSP TMS32028335. The switching frequency was 5.0 kHz. To test the transient performance of the three controllers, step references of the q-axis current were given to compare the tracking performance of q-axis current and transient errors of d-axis current. The PMSM/G operated on generation mode at a constant speed clamped by the prime motor. The voltage loop was uncontrolled as the DC link was fed by a bidirectional DC source. The initial q-axis current reference was 0A, followed by two reduced steps −6A at 20 ms and −12A at 70 ms, respectively. The references increased to −6A at 120 ms and 0A at 170 ms, respectively. The experiments were conducted at two different speeds, 6000 rpm (100 Hz, fs/fe = 50) and 12,000 rpm (200 Hz, fs/fe = 25), with different proportional gains of 500πLs and 1000πLs, respectively. The waveforms of d-axis current i_d, q-axis current i_q, q-axis current reference i_qref, and phase current i_a for each condition are presented in Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21 and Figure 22, respectively.

Figure 11, Figure 12 and Figure 13 present the experimental results of the three current controllers at 6000 rpm with a proportional gain of 500πLs. In Figure 11, a transient error −3A can be seen when the q-axis current changed from 0A to −6A, whereas another −6A error occurred when the q-axis reference changed from −6A to −12A. The recovery time was more than 50 ms. In Figure 12, transient errors were reduced to −1.6A and −3.2A, respectively, when feedback decoupling was applied, and the recovery time was around 20 ms. However, there is no obvious transient error shown in Figure 13. As for the q-axis currents, the average times for the q-axis current to reach the reference in Figure 11 and Figure 12 were 20 and 2 ms, respectively. However, these values are less than the 1 ms seen in Figure 13.

Figure 14, Figure 15 and Figure 16 present the experimental results of the three current controllers at 6000 rpm with a proportional gain of 1000πLs. In general, the results were similar to Figure 11, Figure 12 and Figure 13, and the transient error of the d-axis currents and the time for the q-axis current to reach the reference were reduced for all three controllers as the bandwidth increased. However, the performance of the proposed accurate discrete current controller with Kdq = 500πLs proportional gain was better than the other two controllers with a higher proportional gain of Kp = 1000πLs, indicating the suitability in systems with bandwidth limitations.

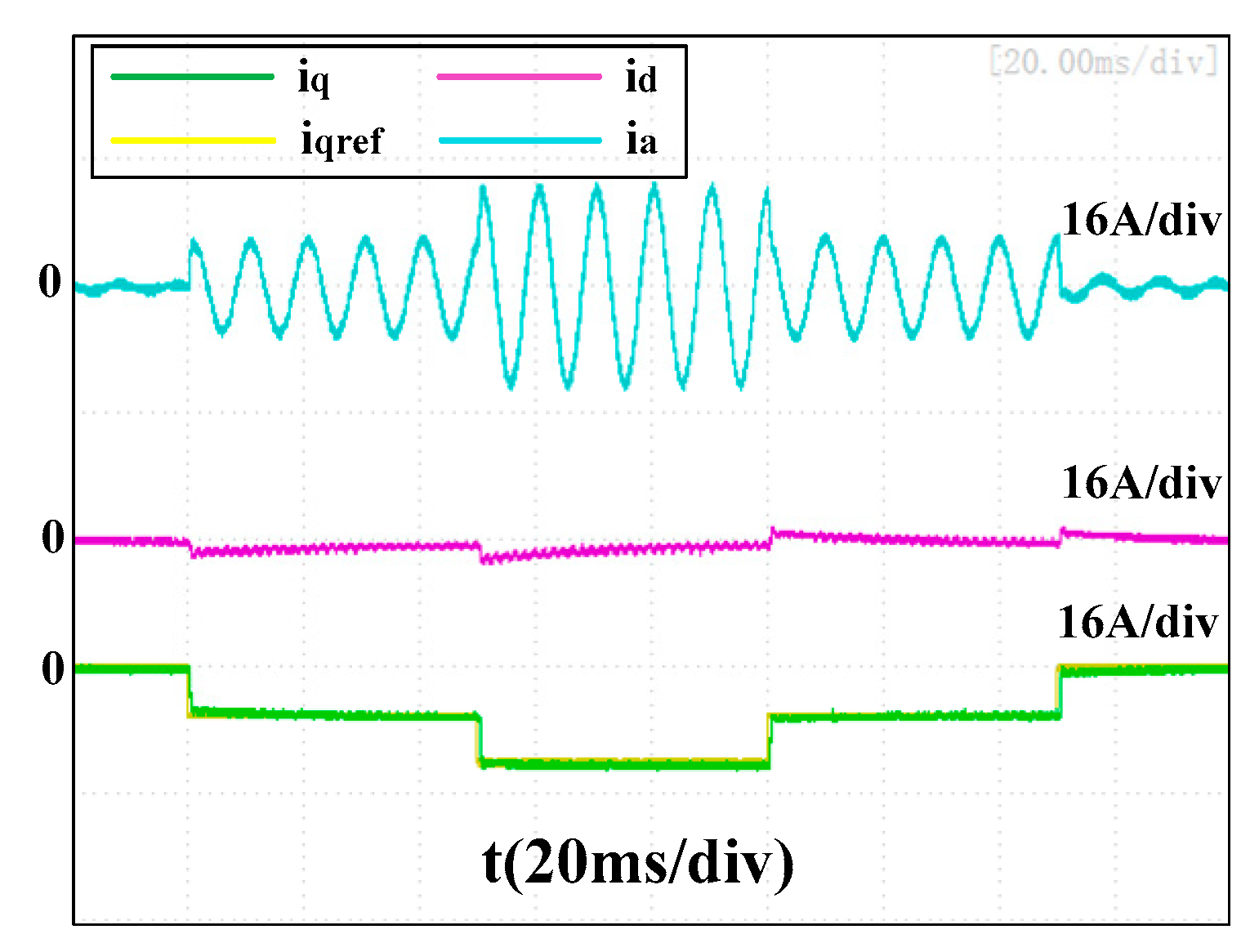
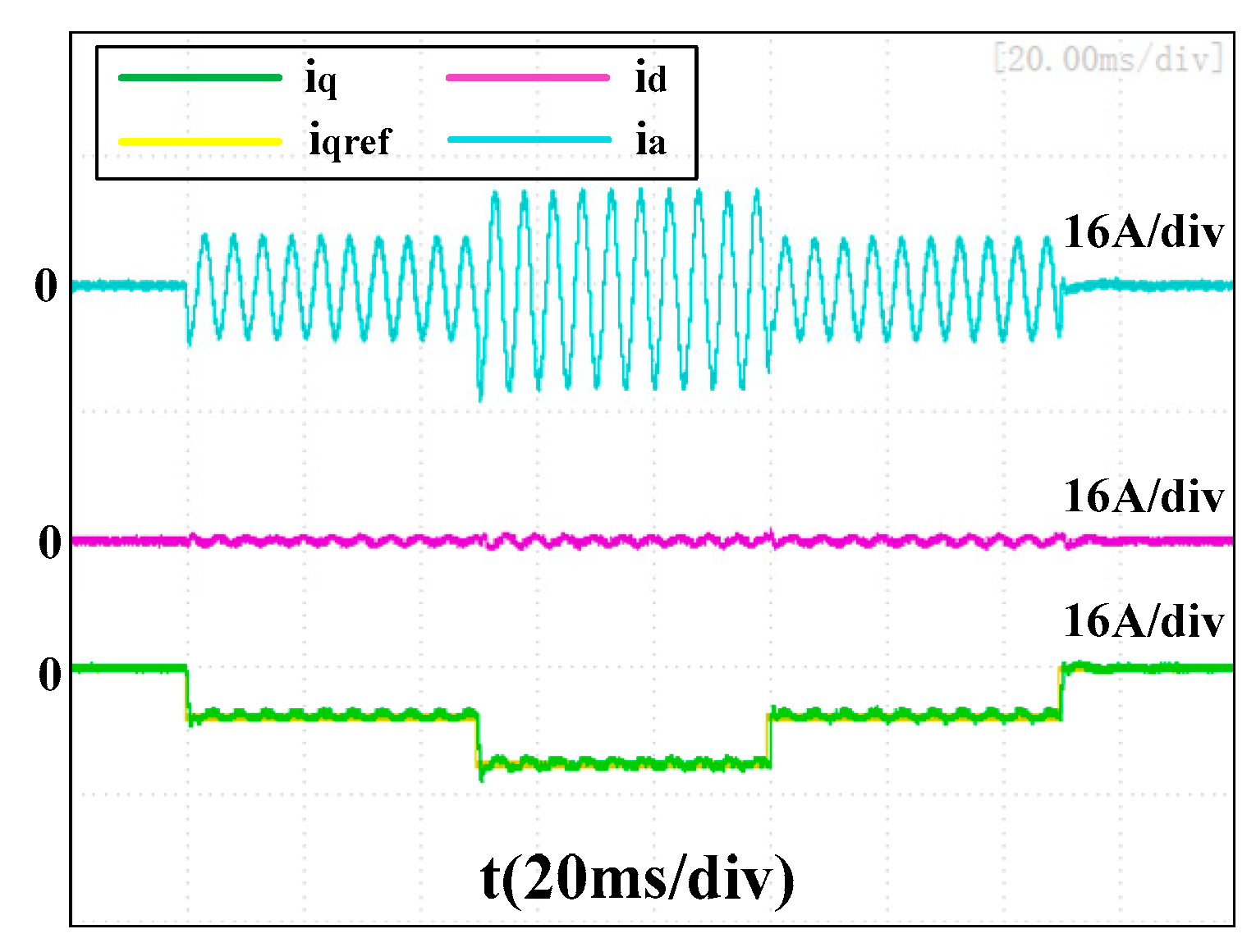
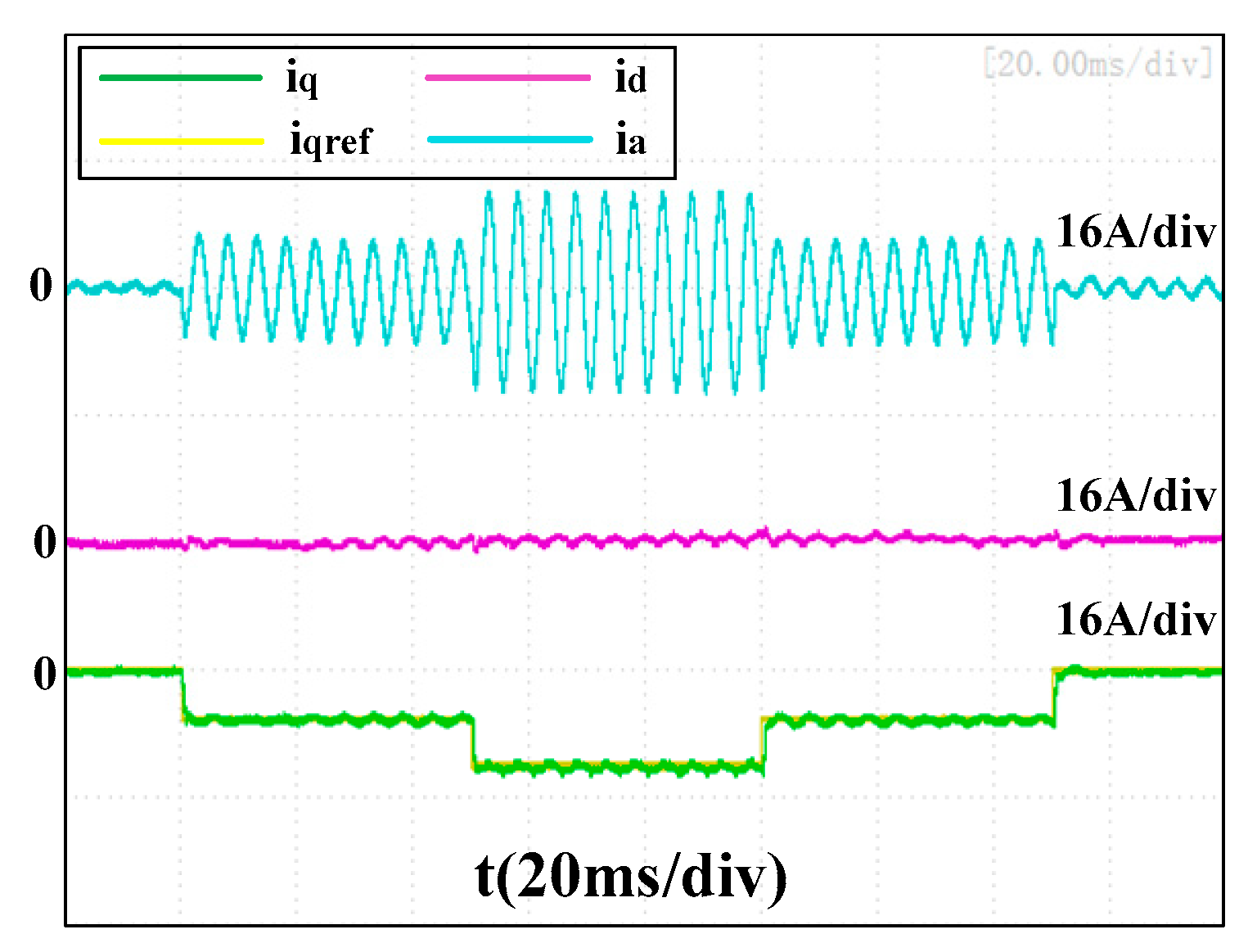
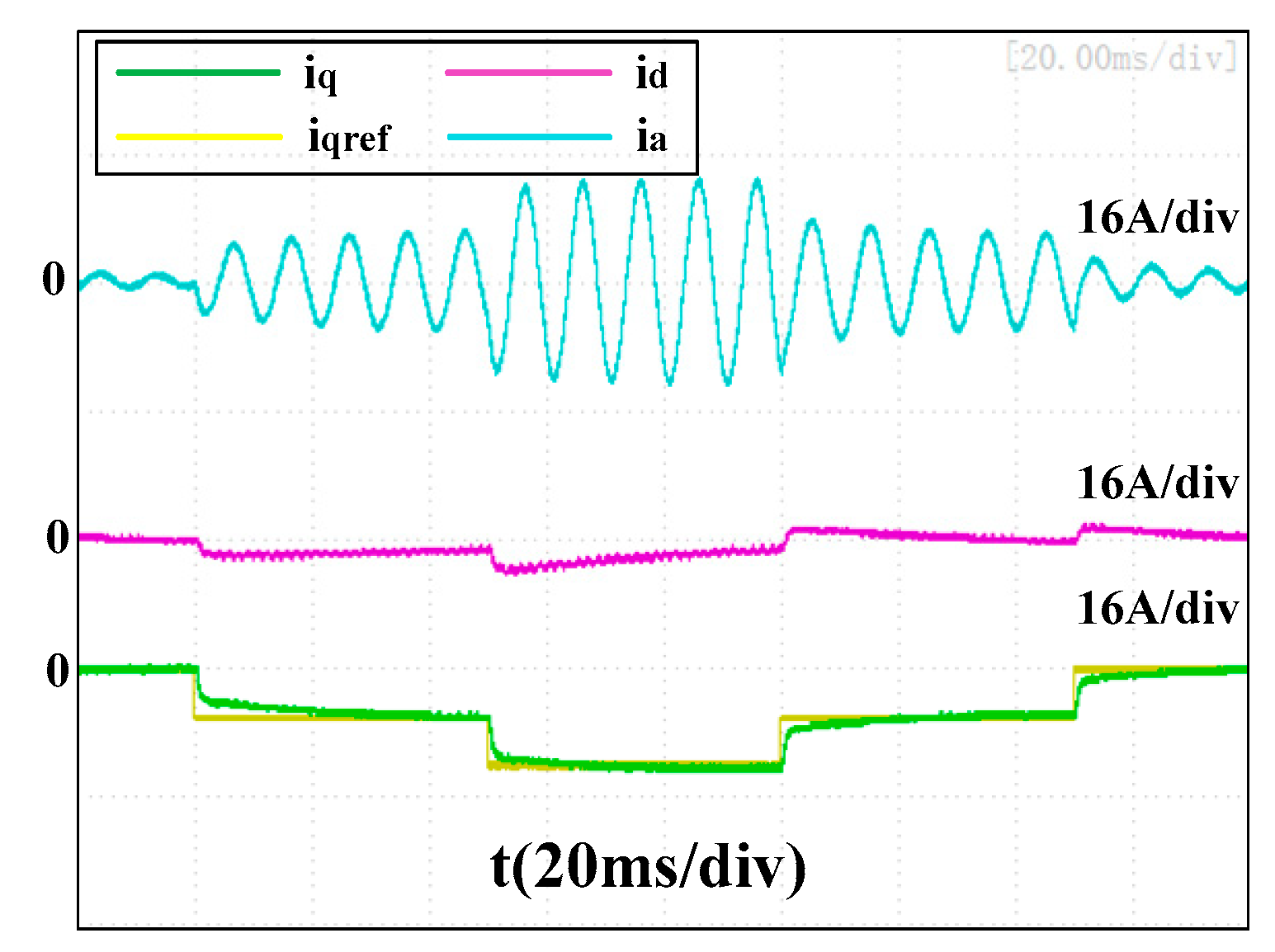
Figure 17, Figure 18 and Figure 19 present the experimental results of the three current controllers at 12,000 rpm with a proportional gain of 500πLs. As fs/fe = 25 in this case, the performances were much worse than with fs/fe = 50 (Figure 11, Figure 12 and Figure 13). In Figure 17, the q-axis current was not able to reach its reference and the transient error of the d-axis current was not able to recover to 0 within 50 ms. 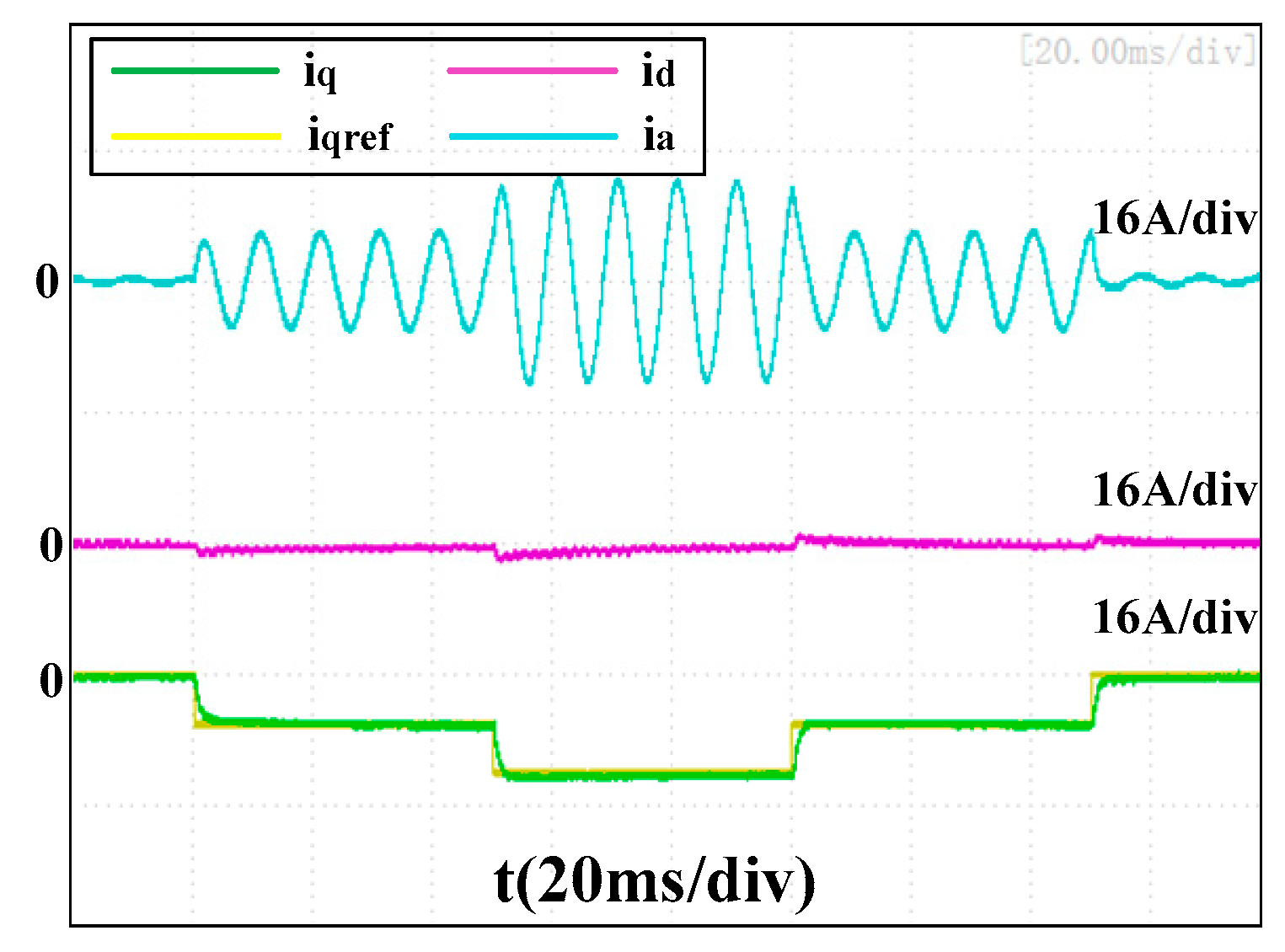In Figure 18, the transient errors of the d-axis current were reduced to −3.2A and −6.4A, respectively, and the average recovery time was around 30 ms. An overshoot of 3.0 A occurred to the q-axis current when its reference changed from −6A to −12A, and the recovery time was also around 30 ms. 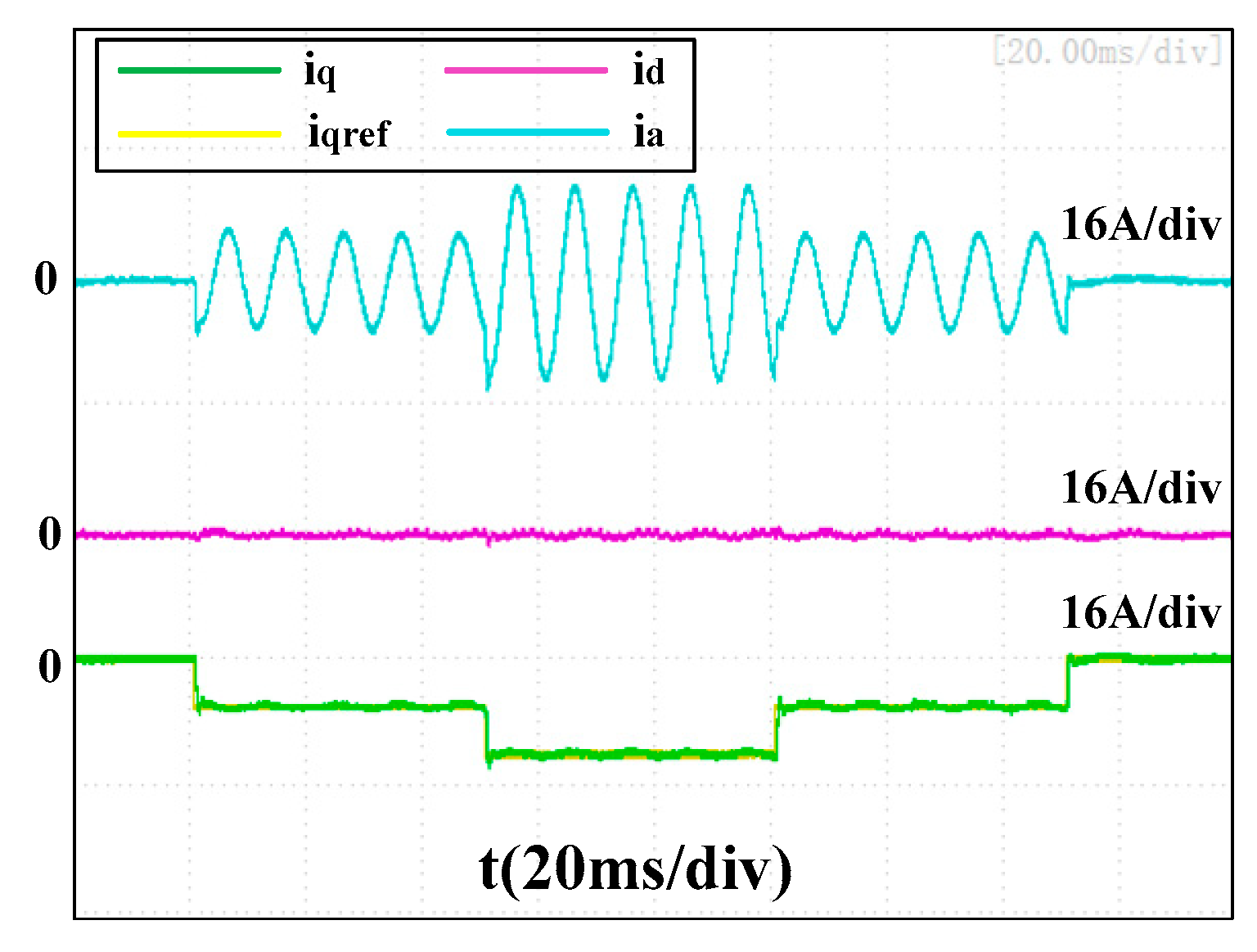However, there is still no obvious transient error of the d-axis current present in Figure 19, and the q-axis currents tracked their references well, although a tiny low-frequency vibration occurred in phase with the current.

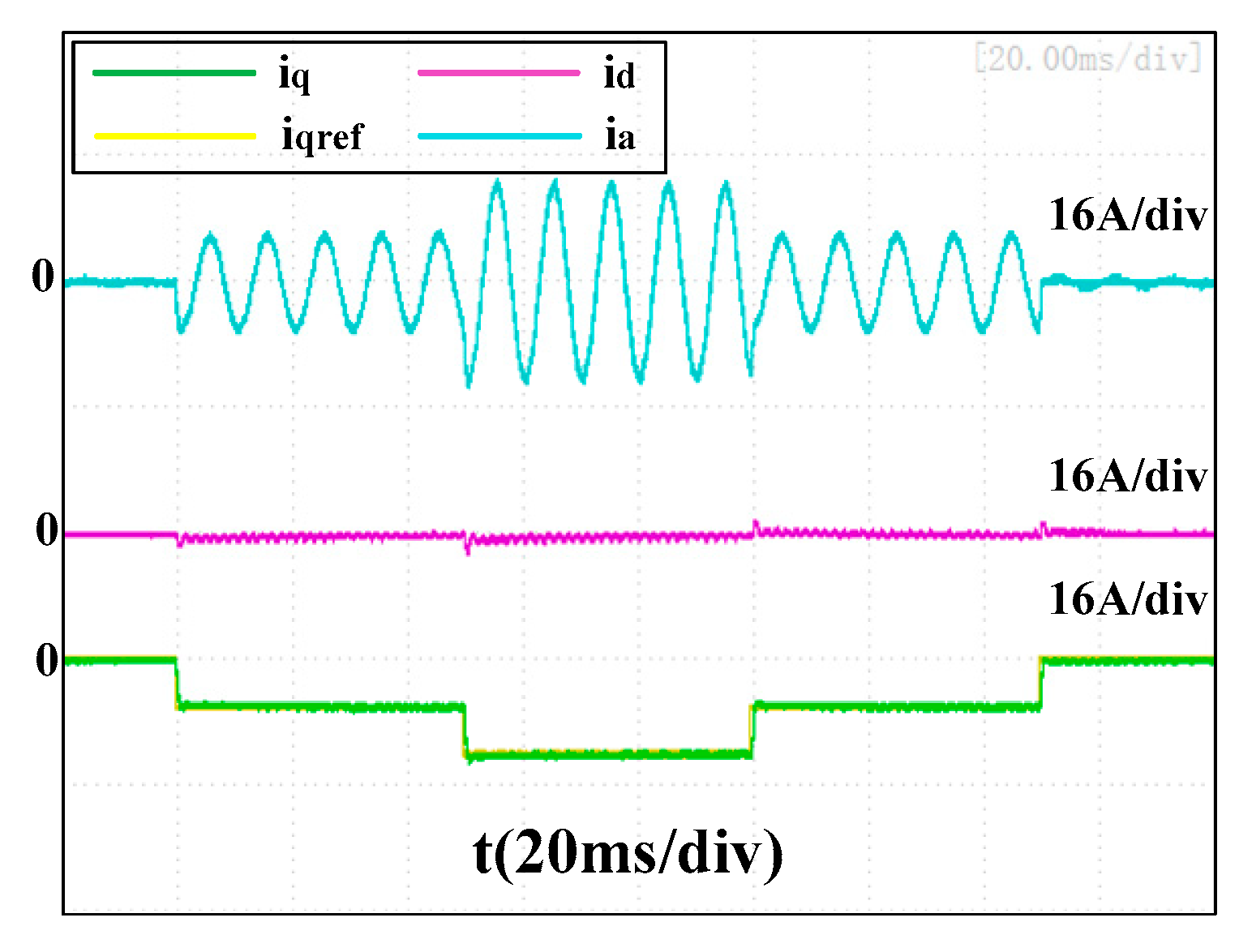
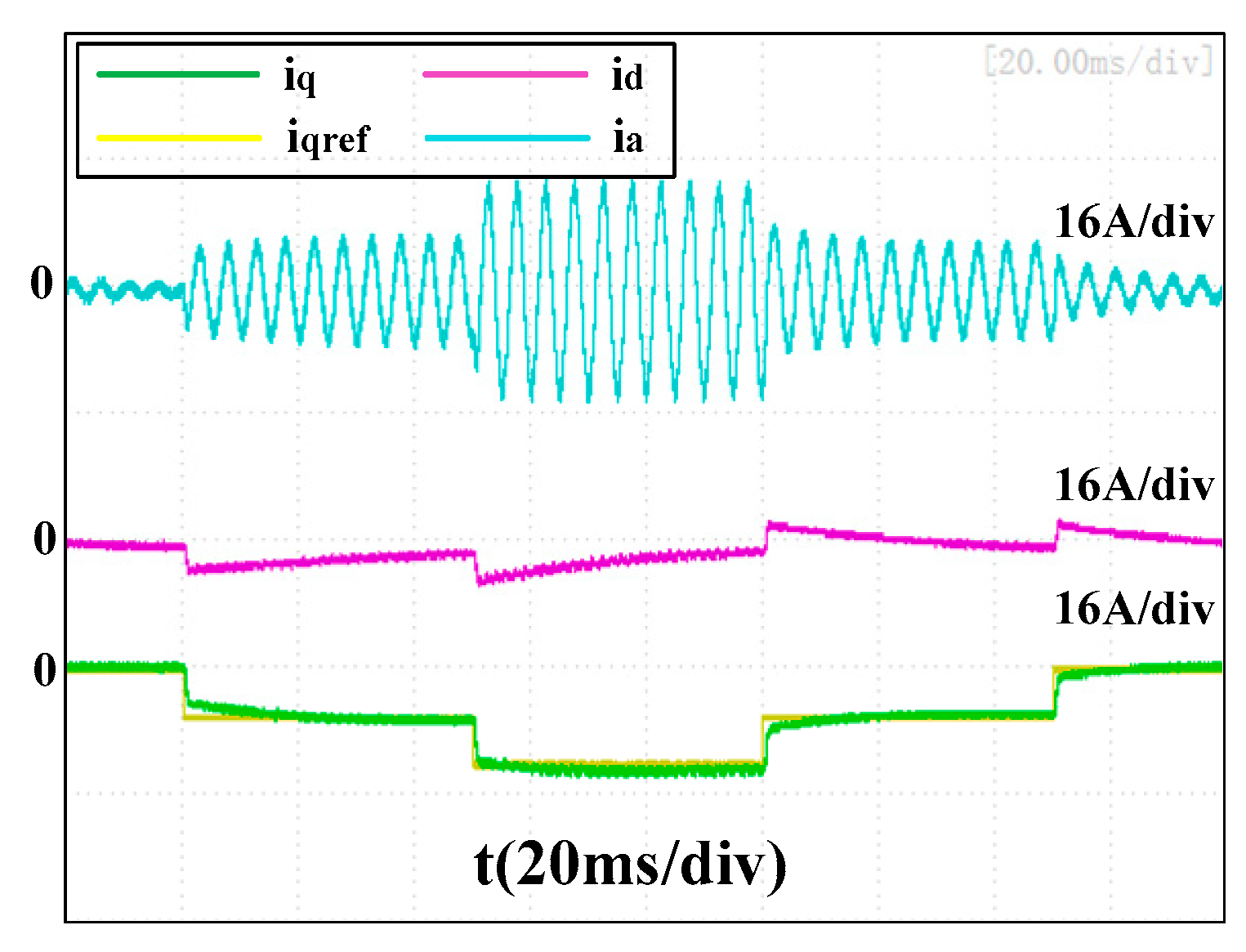
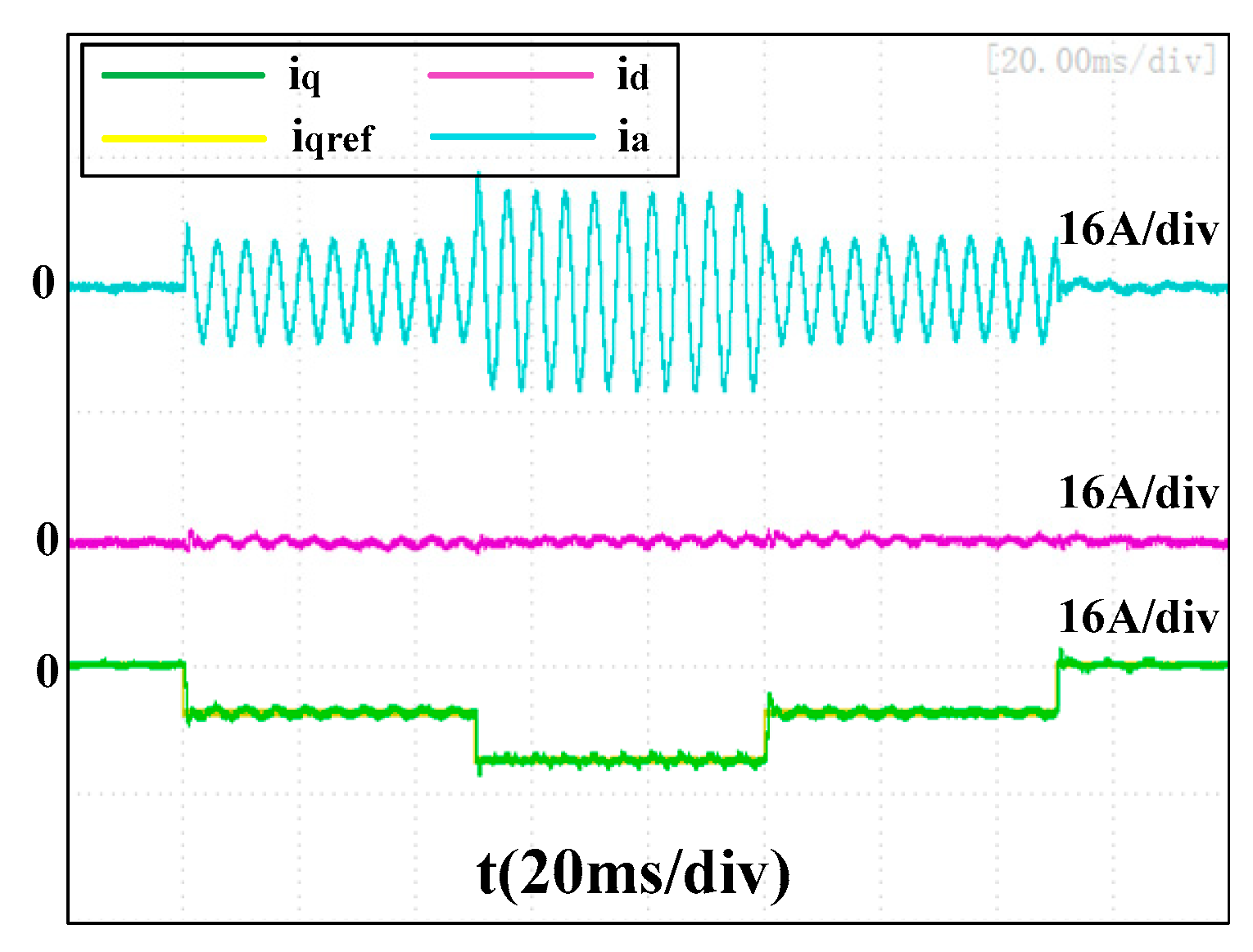
Figure 20, Figure 21 and Figure 22 present the experimental results of the three current controllers at 12,000 rpm with a proportional gain of 1000πLs. The performances of the two conventional controllers were improved compared to Figure 17 and Figure 18. The transient errors and recovery time were reduced. The q-axis current seen in Figure 22 was faced with a small overshoot when its reference changed, but the performance of the proposed accurate discrete current controller with a lower proportional gain of Kdq = 500πLs was still much better than that of the two conventional controllers with Kp = 1000πLs. 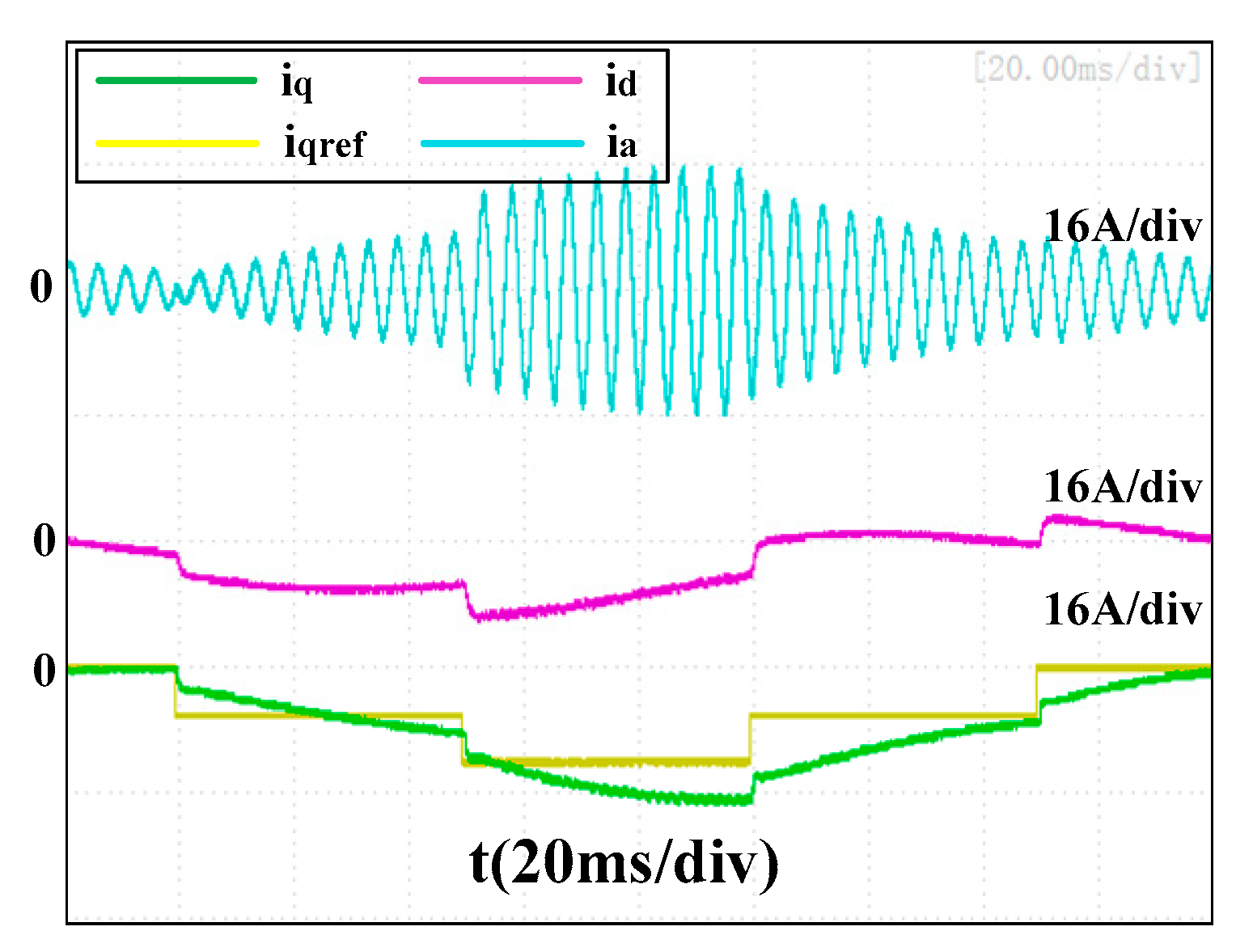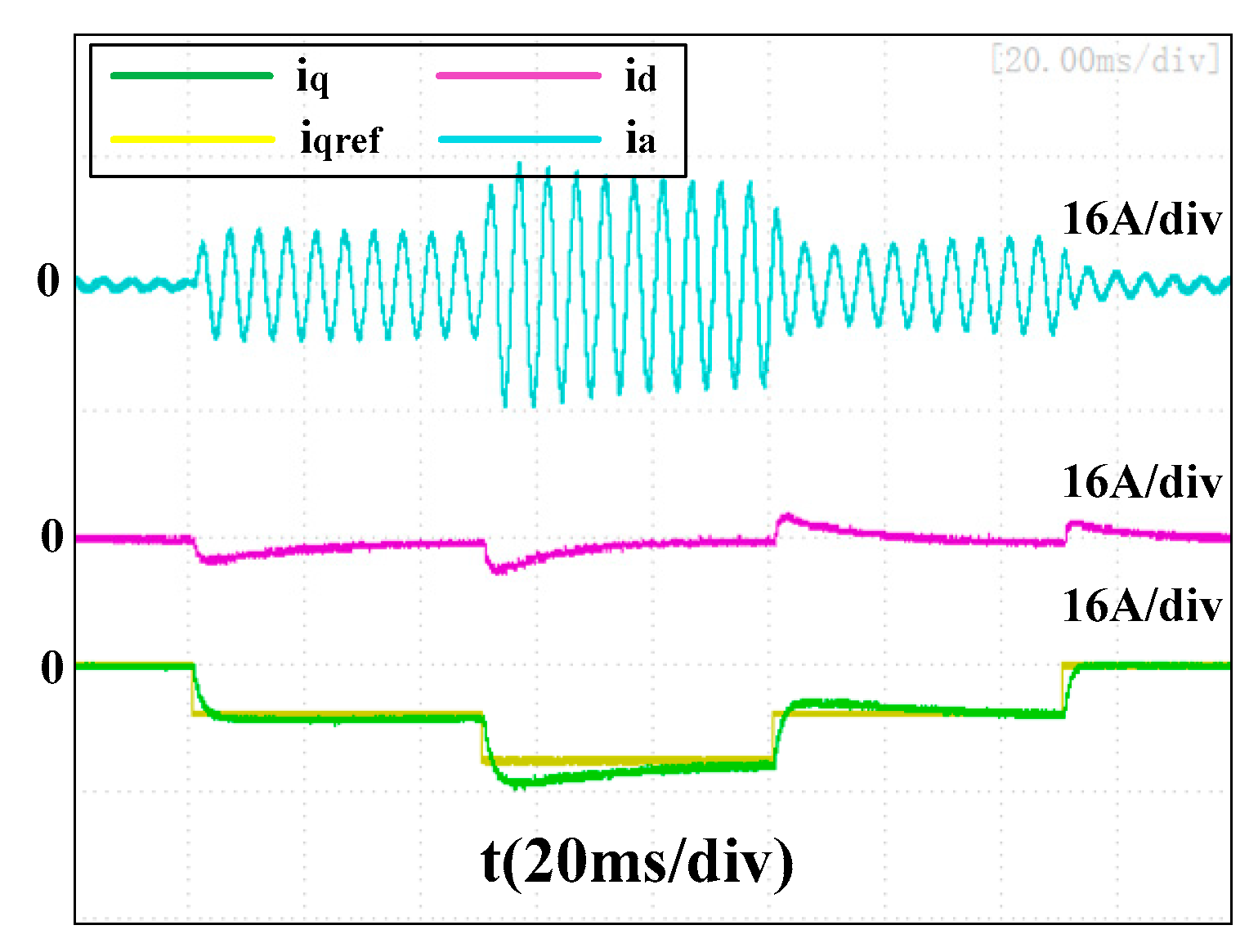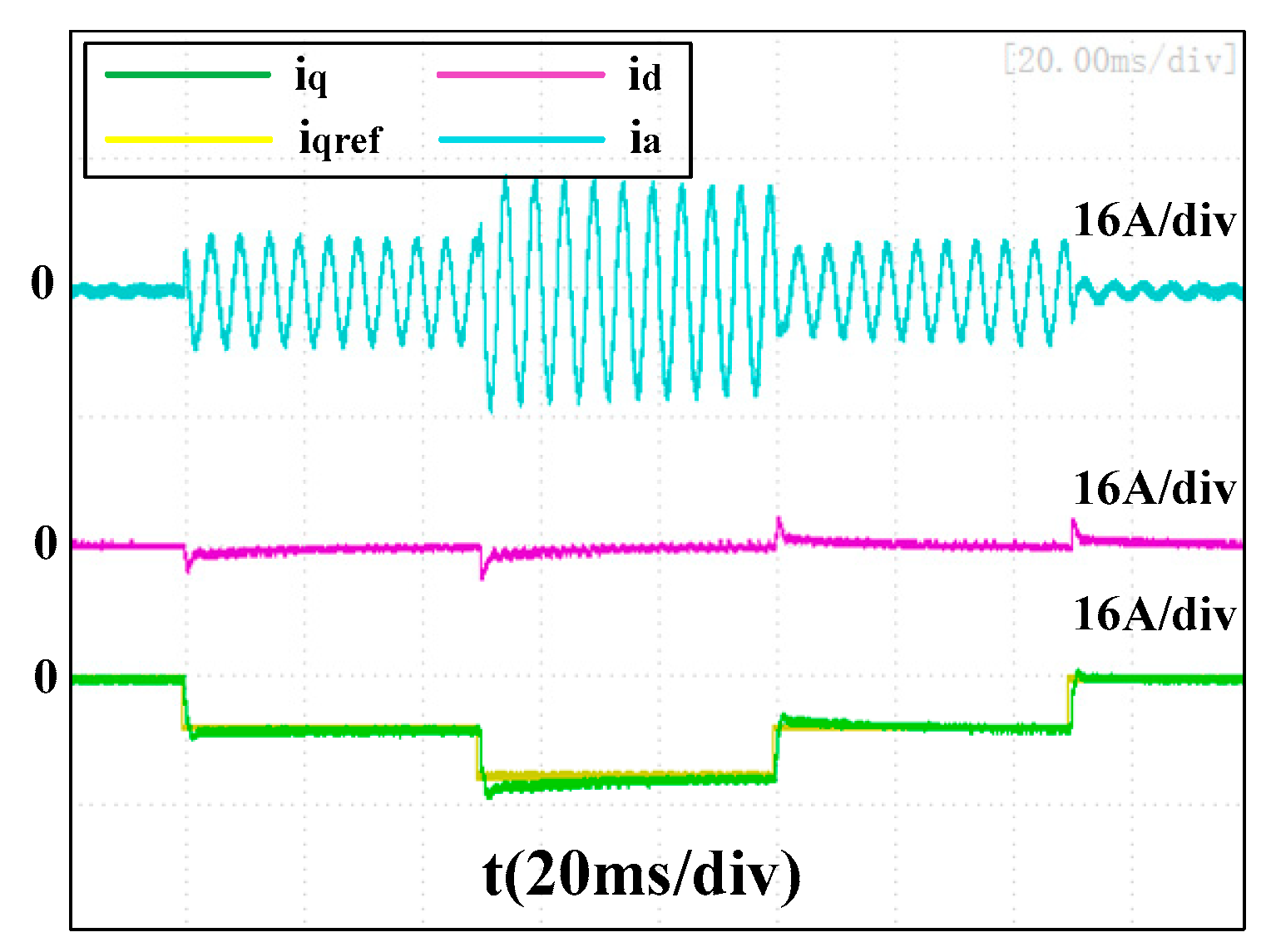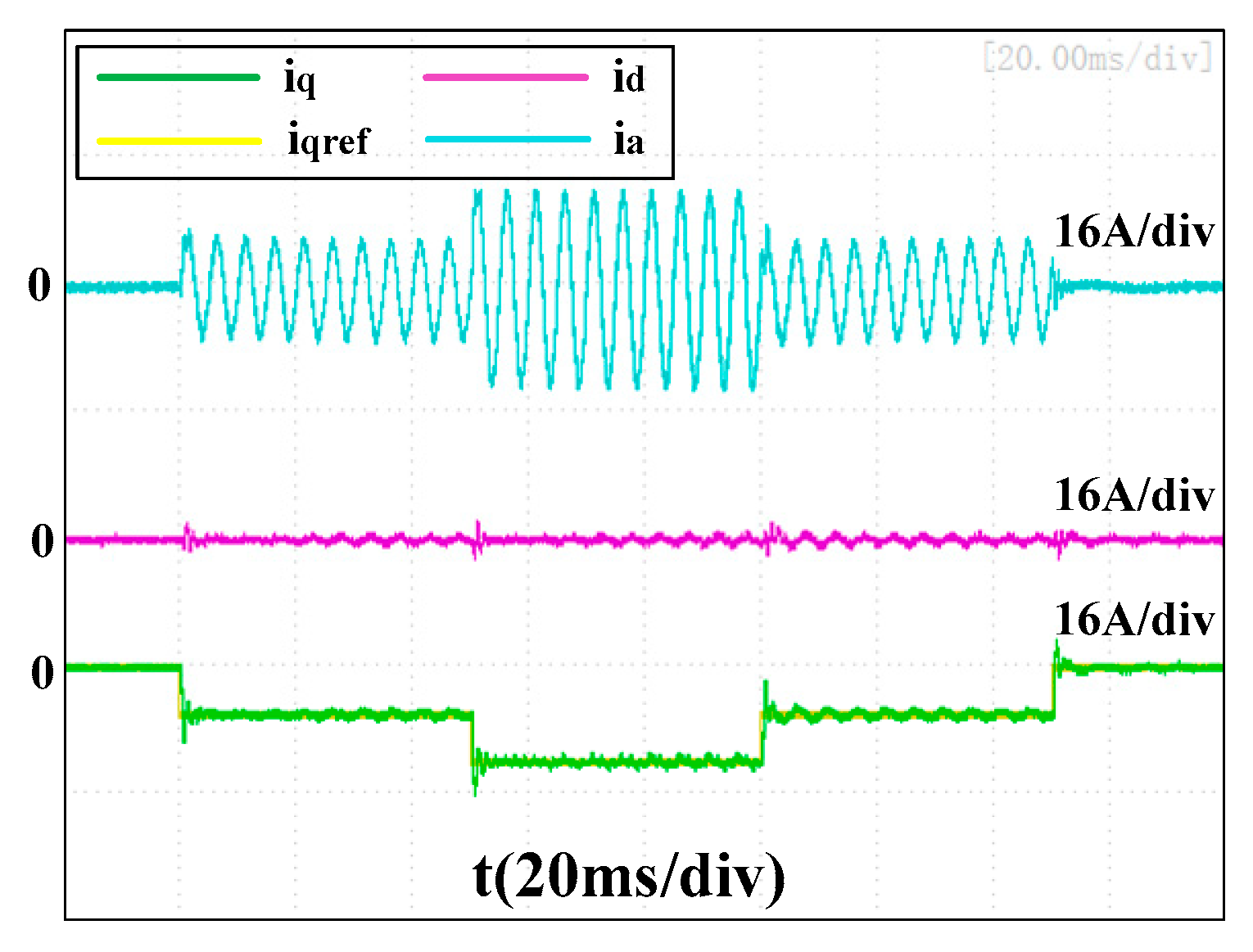Figure 23 and Figure 24 present the experimental results of the proposed controller at 12,000 rpm when faced with parameter errors of ${\widehat{L}}_s=0.8L_s$ and ${\widehat{L}}_s=1.2L_s$, respectively. No obvious difference was found compared to Figure 22 with the accurate parameter, which indicated it was robust to ±20% Ls errors.

In general, the experimental results matched the simulation results well, and demonstrated the advantage of the proposed accurate discrete current controller with better decoupling and dynamic performance, especially at higher speeds and lower switching-to-fundamental-frequency ratios. In particular, the performance of the proposed controller was much better than that of the conventional controllers with double bandwidth, which again proves its suitability for systems with lower bandwidths limited by the switching frequency.

.

.

5. Conclusions

High-speed PMSMs/Gs in a FESS are faced with a high cross-coupling voltage and low sampling-to-fundamental frequency ratio. High cross-coupling voltage leads to transient errors during dynamic processing of the current loop. Conventional current controllers initially designed in the continuous-time domain and subsequently transformed to their discrete forms with approximation methods are sensitive to speed variations, since the discrete nature of digital systems is not properly incorporated and may result in oscillatory or unstable responses. In this paper, an accurate discrete current loop model with complex vector expression was built, and an accurate discrete controller was designed while considering phase and magnitude errors generated during the sampling period. Further, an Extended State Observer (ESO) was applied to estimate and compensate the back-EMF error. The cross-coupling problem of the current loop was settled well, and the current loop dynamics at low switching-to-fundamental frequency ratios were improved. Performance of the proposed accurate discrete current controller was validated and compared with that of two conventional current controllers through simulations and experimental results obtained on a 12,000 rpm PMSM/G prototype. The results prove that the proposed controller has much better decoupling capability and an improved dynamic response compared with the two conventional controllers with double bandwidth, especially at higher speeds with lower-to-switching-frequency ratios. The low-frequency ripples found in the experimental results of the proposed method were due to the nature of this method, which it is sensitive to DC disturbances, and elimination of this will be the focus of future research. Efficiency improvement based on system level analysis will also be a promising research focus due to the requirements of energy storage in flywheel applications.