1. Introduction
District heating systems (DHS) are a standard solution for the supply of heat to buildings and technologies in urban areas. The proper operation of DHS can offer several synergistic advantages: higher efficiency of the central source compared to small decentralized sources, application of efficient large-scale cogeneration, reduction of specific emissions, better control over the amount of produced emissions, and use of waste heat from technologies located in different parts of the city. In recent decades, the main trends in district heating are lowering the temperature of distributed heating water, application of sophisticated systems of automatic control of DHS, utilizing renewable energy sources, development of cooperation of heating and cooling supply systems, and increasing storage capacity. Depending on heat production technology and the parameters of heat distribution, the so-called generations of heat supply systems have been defined [
1]. Generations 1 to 3 include the current historical development of heating systems.
Proposals of the new 4th and recently recognized 5th generation of district heating and cooling supply systems are part of the overall answer for lowering carbon emissions. These proposals attempt to address the problem by focusing on the utilization of multiple sources of waste heat and renewables. Many of the considered sources can only provide low potential heat. This calls for lower operational temperatures in the whole DHS. It needs to be combined with some form of temperature boosting (i.e., using devices such as heat pumps) to satisfy demands for higher temperature potentials, such as those associated with domestic hot water production. The 5th generation of district heating and cooling supply goes as far as suggesting neutral temperature levels and potentially lowering the requirements for insulation of the pipes in the distribution network [
2]. For efficient utilization of all possible sources, it is also necessary to deal with the temporal mismatch of demand and production. In principle, this can be realized with the help of hot and cold water storage, given that there is an efficient control strategy. The demands on control algorithms further increase with the requirements for predictive control of DHS. This requires testing a larger number of alternative scenarios, which places extreme demands on the speed of partial calculations.
If these proposals are to be fulfilled, there needs to be a systematic approach through which the behavior of these complicated systems can be studied, where new ideas can be tested in the context of the whole system and their implementation optimized, so their real potential can be assessed accurately and holistically.
It is quite straightforward to model the physics of the components (for example, using proprietary solvers for partial differential equations such as ANSYS, COMSOL, and STAR-CCM+), but it is not so straightforward to make them progress quickly as well (the exception here might be quasi-stationary models, but those are not considered strict dynamics by definition).
There are several relatively recent papers dealing with thermal modeling and optimization of district heating pipes. Teleszewski et al. presented a comparison of heat loss of a quadruple pre-insulated heating network, four pre-insulated single-pipe networks, and two twin-pipe networks. A simplified 2D steady-state model based on the boundary element method was used for calculations [
3]. Krawczyk and Teleszewski also presented possible variants of heat loss reduction by analyzing possible changes in cross-sectional geometry [
4,
5]. Ocłon et al. studied steady-state heat losses of the pre-insulated pipe and twin-pipe in the heating network using an analytical 1D model and a numerical 2D steady-state model [
6]. Heijde et al. presented the derivation of the steady-state heat losses and temperature changes for a double pipe network, which was implemented in Modelica software [
7]. The authors used equivalent thermal resistances previously derived by Wallenten [
8]. Danielewicz et al. developed a model for heat loss calculations in pre-insulated district heating network pipes using computational fluid dynamics (CFD) [
9]. Sommer et al. compared efficiency, investment costs, and flexibility of advanced district heating systems, namely, the double-pipe bidirectional network and the single-pipe reservoir network, using Modelica simulations [
10]. Arabkooshar et al. analyzed the performance of a triple-pipe system in district heating and compared it with a twin-pipe system employing CFD [
11]. To combine these models into a single complex simulation of a grid might be very challenging. A fast dynamical model of a grid where the simulated physical behavior of each component is close to their real behavior opens up an opportunity for discovery and assessment of new control strategies. Such a model used to be referred to as a virtual system or digital twin, if it is a simulation of installation.
In order to bring these ideas closer to life, there needs to be an open exchange of tools, software, and data among researchers. The thriving discipline of machine learning is one example, where this attitude helps develop the technology significantly. The approach to district heating needs to be similarly bottom-up. It means that the components of the district heating and cooling systems must be modeled first. Further, they must be easy to combine into more complex simulations and the tools should be available to anyone who chooses to contribute. A recent review of open-source tools for energy-related modelling and optimization concluded that open-source development has received more attention but its success is still relatively limited [
12].
Two programming languages seem to be most appropriate to the above. The first is Python, which is a general-purpose language, highly suitable for scientific computing. There is a vast amount of very competent libraries available. The other is Modelica, which is highly suitable for modelling multi-component and multi-physics dynamical systems. There is a library for modelling of district heating networks written in Modelica language called DisHeatLib [
13], but it is not compatible with the open-source environment OpenModelica.
The presented research addresses the problem of generating efficient dynamical models (using open-source tools) as the means by which faster and more complex simulations of DHS can be constructed efficiently. Human engineering intuition can be efficiently combined with machine-learning algorithms into an efficient process of developing the models. An optimization tool capable of interfacing with OpenModelica as well as other software is presented in this contribution. It is capable of learning the parameters of nested Modelica models, so the models acquire the desired dynamical behavior. It can run on distributed hardware, which allows it to scale quite well for more-complicated models.
In this paper, the authors present a functional example of semi-automated model complexity reduction. First, the cross-sectional thermal dynamics behavior was modeled using the open-source tool FEniCS. Then, simple components representing thermal capacities and heat conductors were created in Modelica and a simple equivalent scheme was built from them. Then, the values of the parameters of the capacitors and heat conductors were learned, so the simplified model approximated the results of the complex model. These steps create an innovative solution process that is characterized by short computational time and robustness, corresponding to DHS needs.
2. Materials and Methods
This chapter describes the individual steps of the used calculation solution procedure. The solution to the problem can be divided into three main stages. At first, the data needs to be generated. This is achieved using an open-source platform for solving partial differential equations called the FEniCS project [
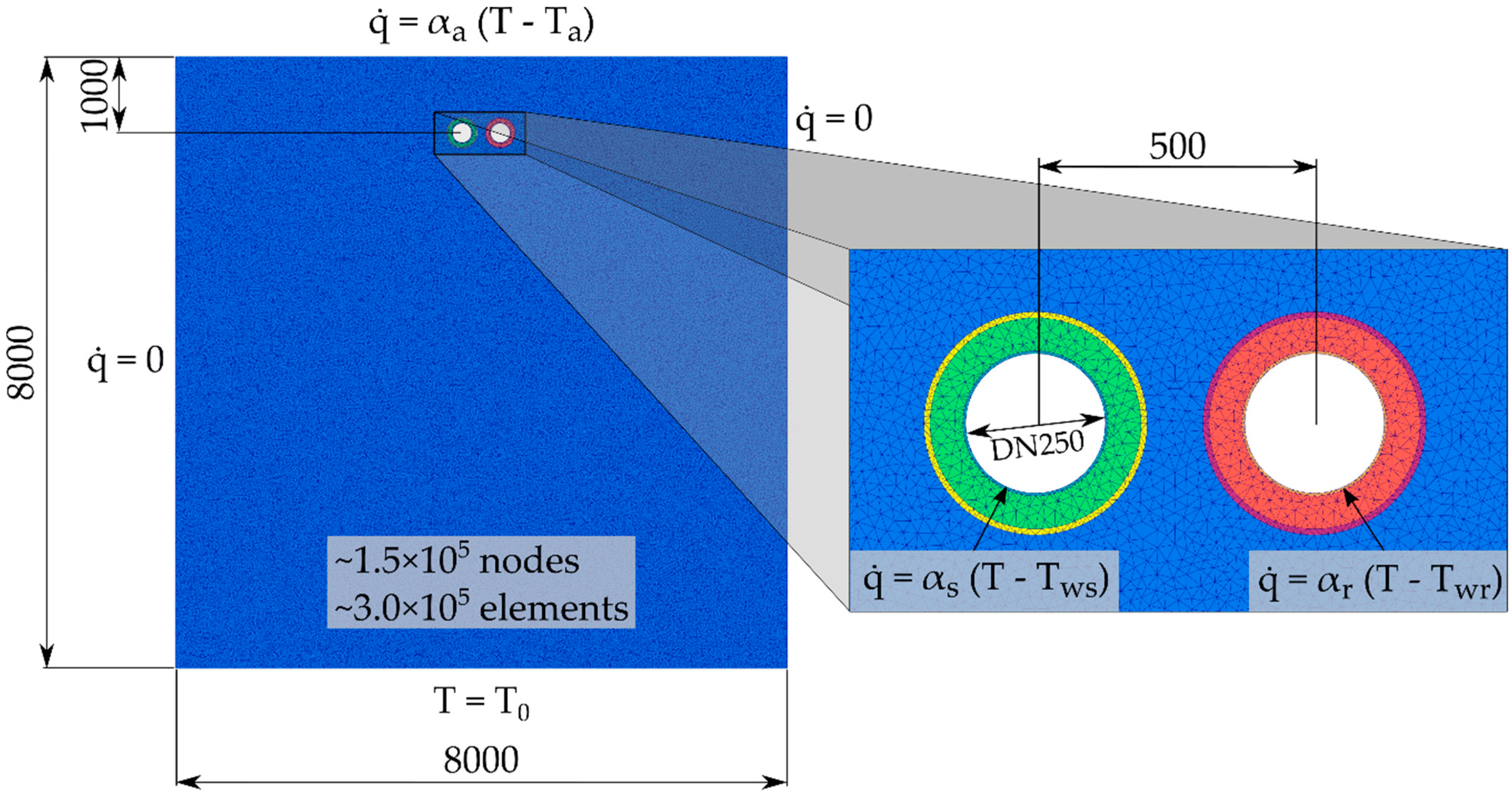
14]. A serial topology generator was created for this purpose. It takes the geometry and its material properties (temperature-independent) as input and outputs topology containing mesh and its relevant annotations (see
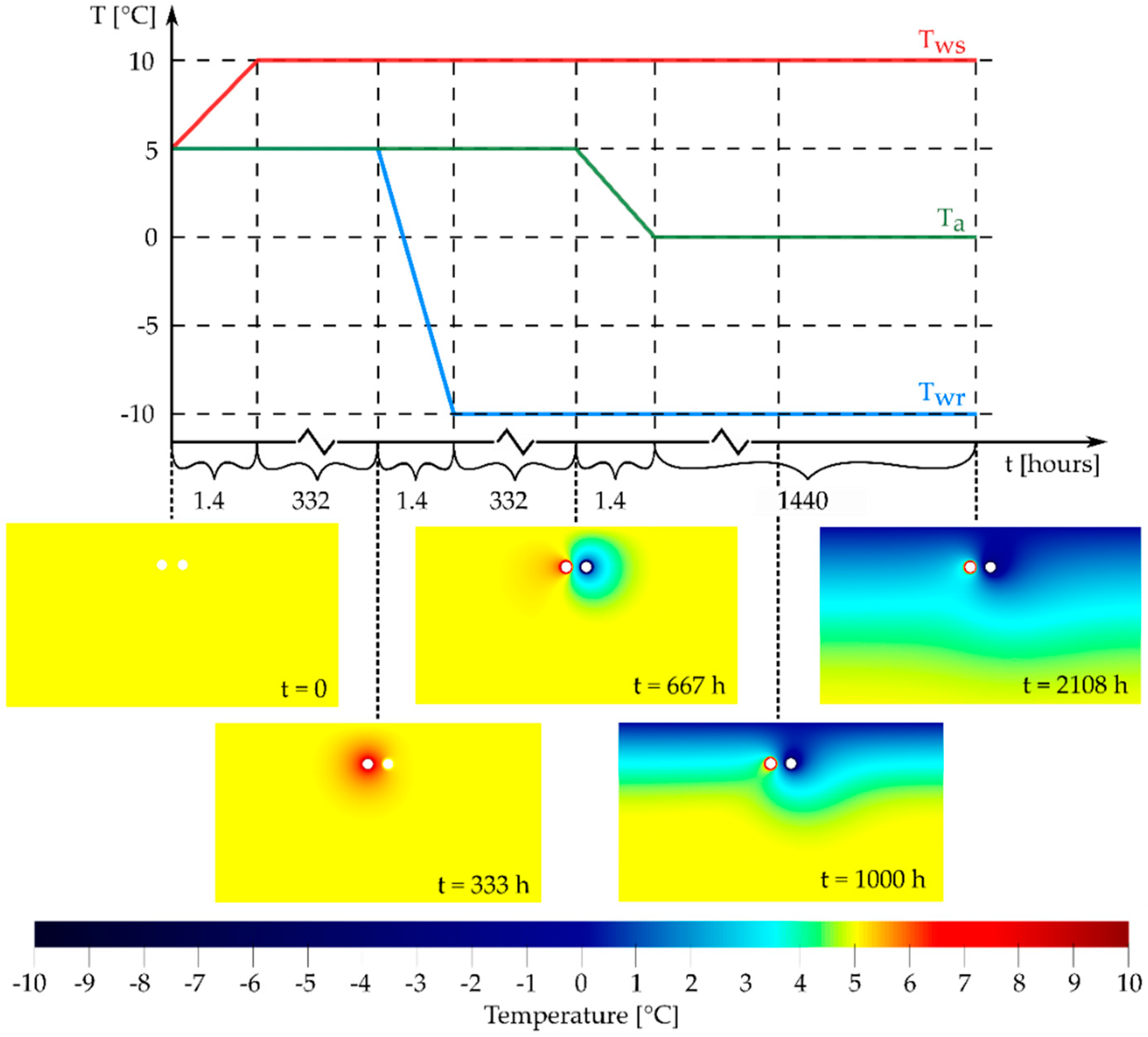
Figure 1). This topology is then loaded and passed into a finite element method assembler along with input data (driving temperatures of the water and air). An assembly object is produced, containing objects such as mass matrix, conductivity matrix, and boundary condition-related mathematical entities. The boundary conditions applied during this process are also shown in
Figure 1. The open-source application ParaView is used for visualization of the domain and the spatial data.
This assembly is then passed to an adaptive time step solver. The adaptation is governed by the measurement of violation of the conservation of energy. The progress of the simulation is recorded in a comma-separated value file (CSV). The data recorded in this file are explained in
Table 1. The CSV file is then converted into a Modelica package with highly efficient interpolation kernels wrapped around the data (constant computational complexity), so it can be used conveniently in the graphical OpenModelica environment and directly compiled into the executable model. This whole process is later referred to as data mining. If set, the simulator can also store snapshots of the whole domain after each time step.
The output data of this rather complex simulation must contain enough relevant dynamics. The driving temperatures used in the training dataset along with several explanatory snapshots are shown in
Figure 2. It includes fast dynamics as well as long periods of equalization, so the heat has enough time to spread and affect the relevant areas if they are thermally distant from each other. Steady-state behavior is implicitly present.
In the second stage, a simplified model was implemented in Modelica. It consisted mainly of two components. The first is a thermal capacitor with a parameter, M, which represents its thermal mass. The governing equation is a simple ordinary differential equation (ODE):
where
M (J·K
−1) is a thermal mass of the node,
T (K) is a temperature of a node,
t (s) is time, and
(W) and
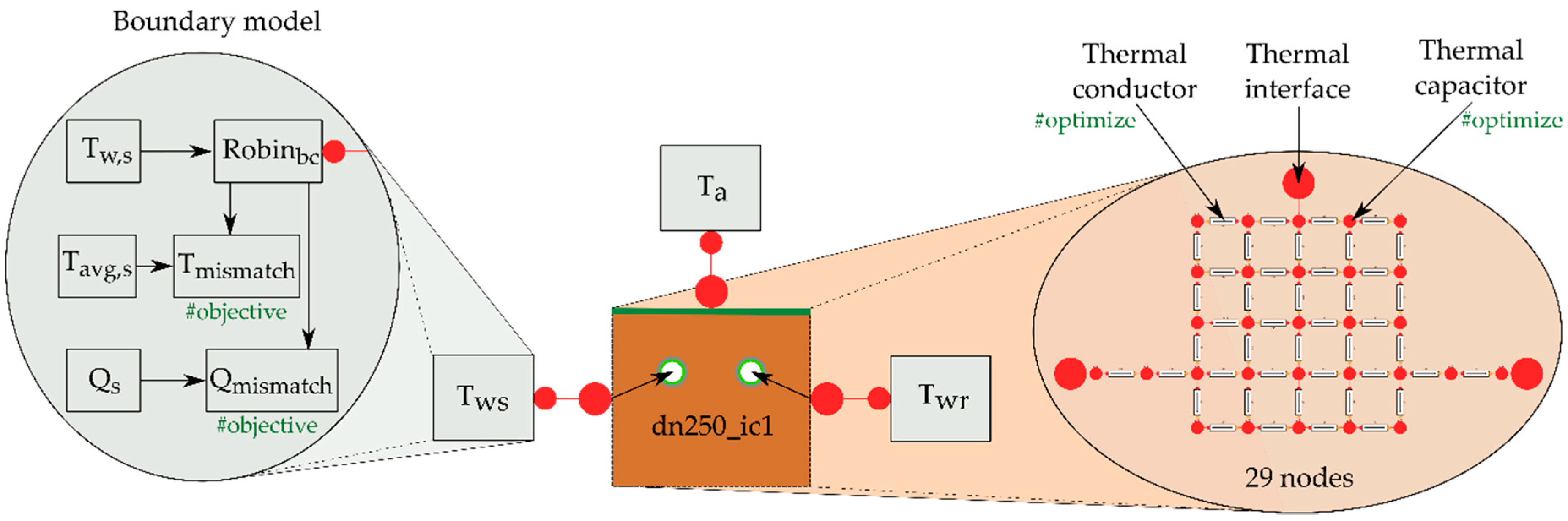
(W) are incoming and outgoing heat flow, respectively. The initial condition associated with this ODE is simply an initial value (unlike the complex model, the simple model cannot be initialized to a steady-state solution prior to the training process). The other component is the thermal conductor (or resistor, if preferred). It has a parameter,
K, that represents its thermal conductance. The following equation describes its behavior:
where
(W) is a heat flow through the conductor in direction 1–2,
K (W·K
−1) is a thermal conductance, and
T1 (K) and
T2 (K) are temperatures of the adjacent points 1 and 2, respectively. Along with these two components, there are also models representing the boundary conditions (for supply pipe, return pipe, and ground-level surface). These boundary models look up the corresponding data from the data package generated during the data-mining process. They also evaluate absolute errors between temperature and heat flow at the boundary interfaces. The total loss for training is the weighted sum of those errors from all instances of these boundary models accumulated over time.
where
(W) is a boundary heat flow evaluated inside the simplified model,
Tdata_medium (K) is a driving temperature of the media (one of
Tws,
Twr or
Ta), which is the only input to the simplified model, and
Tmodel_surface (K) is the average temperature also evaluated inside the simplified model.
where
L (which has no meaningful units) is actual weighted loss or mismatch for a given surface,
w1 and
w2 are dimensionless weights,
Tdata_surface (K) and
Tmodel_surface (K) are temperatures of a corresponding surface, and
Qdata_surface (K) and
Qmodel_surface (K) are heat flow through the corresponding surface evaluated by complex and simplified model, respectively.
These models are then assembled into a simple grid (see
Figure 3). The sparsity of the model is mostly resolved in this step. In a matrix form, the typical row would therefore have five non-zero entries, since the typical thermal capacitor is connected to four other thermal capacitors. A mathematical model of this kind should be enough to capture the macroscopic relations between variables that are recorded during the complex simulation.
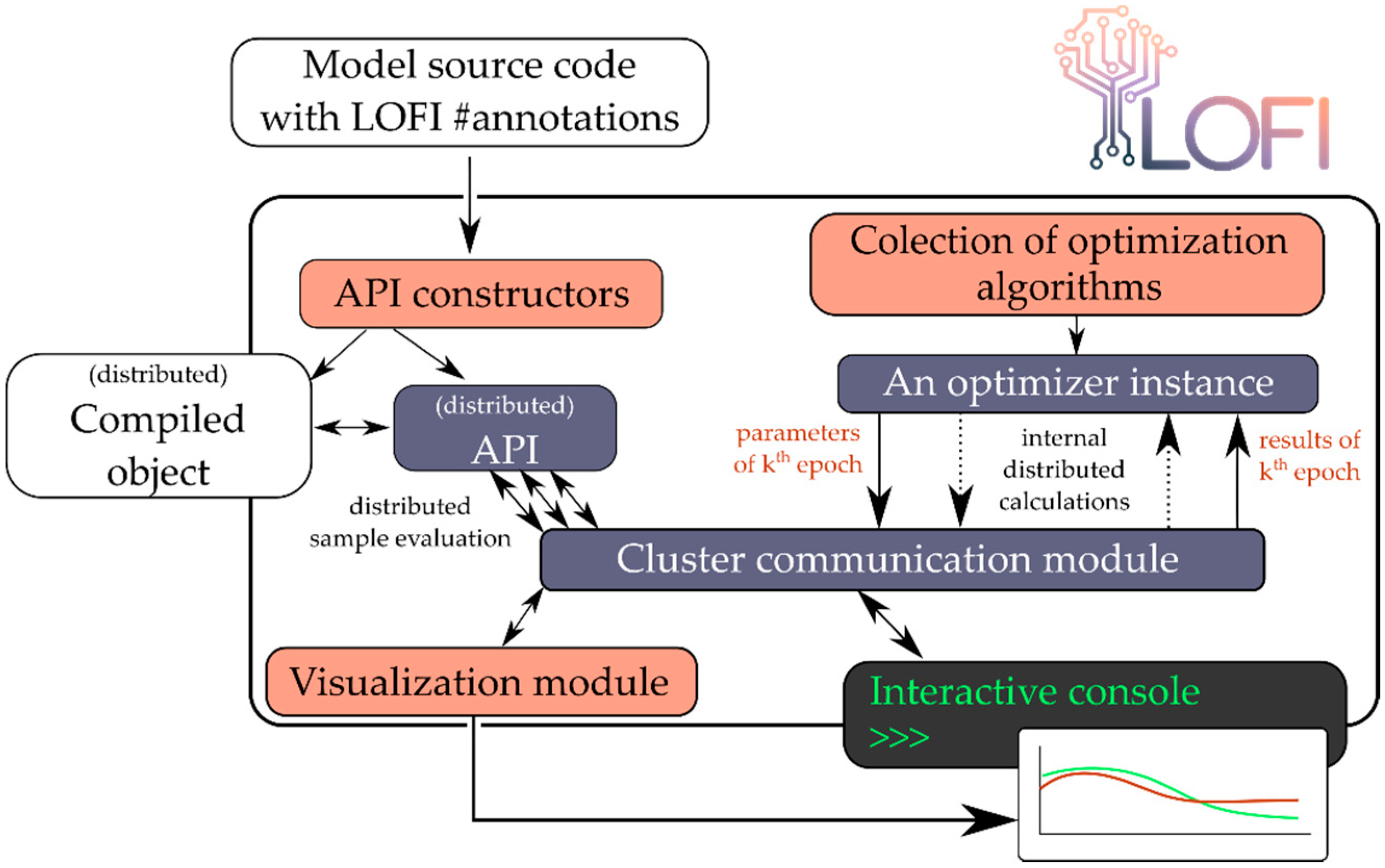
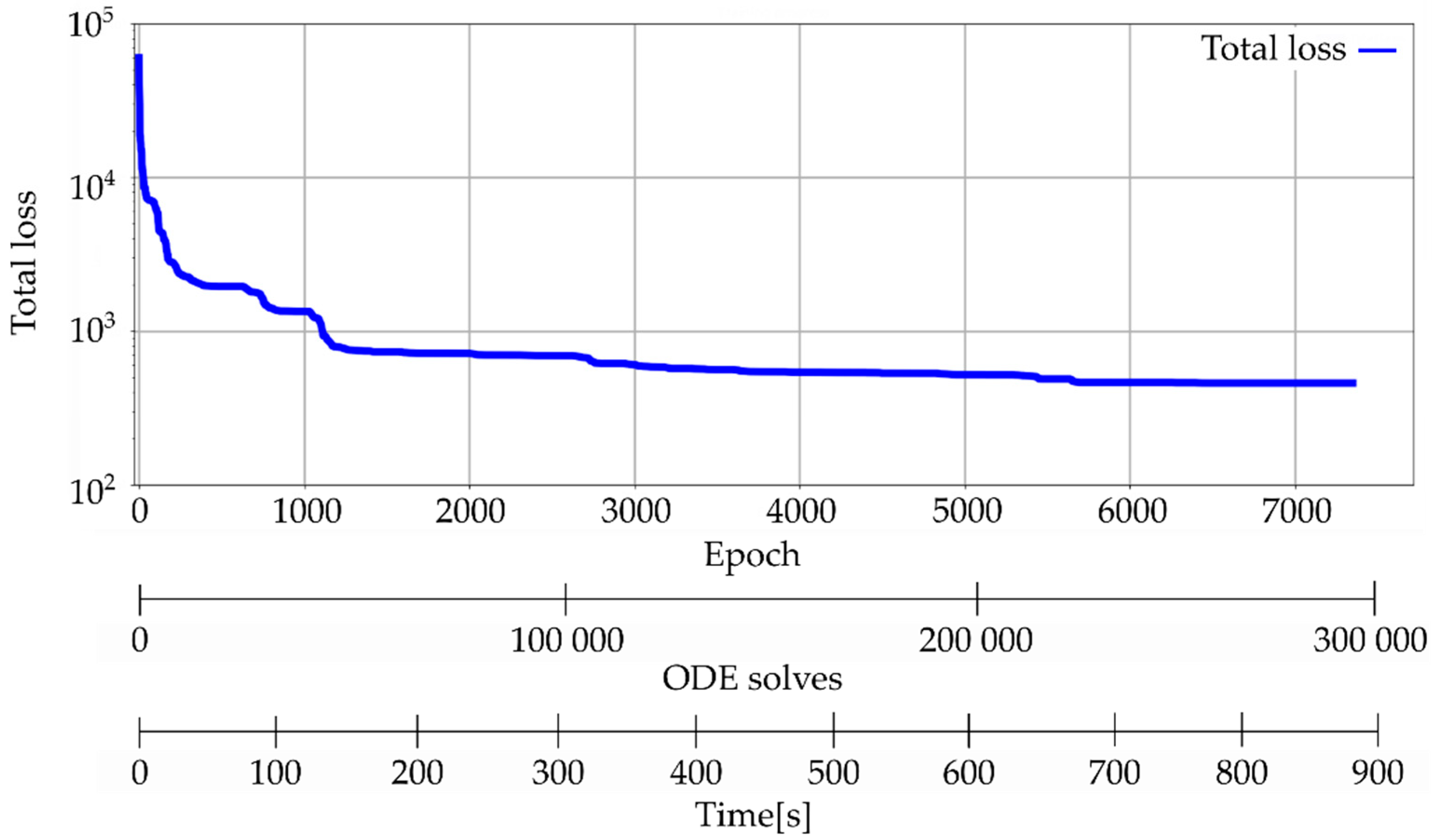
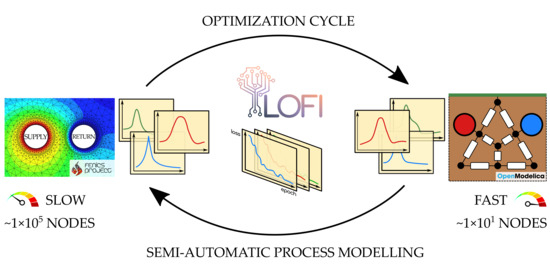
The third stage is the learning and training process. For this purpose, a custom optimization tool called Lofi was written from scratch in Python. It contains an application interface (API) to the OpenModelica compiler and several derivative-free optimizers that were also written from scratch. So far, the optimizers that were included are based on swarm intelligence and evolutionary strategies. Lofi is fully parallelized and capable of running on a distributed hardware (within a message-passing environment such as Open MPI or MPICH). Objectives and parameters subjected to optimization are annotated inside the Modelica code using the hashtags/keywords #objective and #optimize in the description of the variables (at this stage, only type Real is supported with the #optimize keyword). This overall architecture of Lofi is presented in
Figure 4. The capability of Lofi is not at all limited to the problems presented in the main text of this article (see
Appendix A for a short summary).