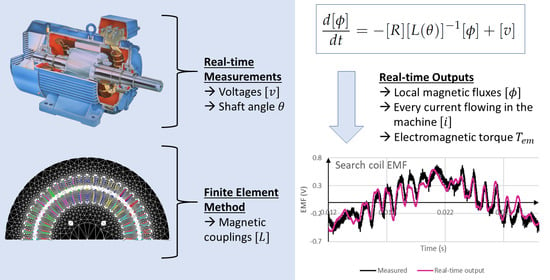
Real-Time Digital Twin of a Wound Rotor Induction Machine Based on Finite Element Method
Abstract
1. Introduction
- It considers space harmonics and magnetic imbalances since any machine geometry can be modeled in a FEM software;
- Any number of electrical circuits can be added to the models, including phase windings of course, but also bars, dampers and even search coils. This means the model can output actual currents flowing in bars and dampers and also local magnetic fluxes by using search coils.
2. CFE-CC Model Construction of a Wound Rotor Induction Machine
2.1. Model’s Equations
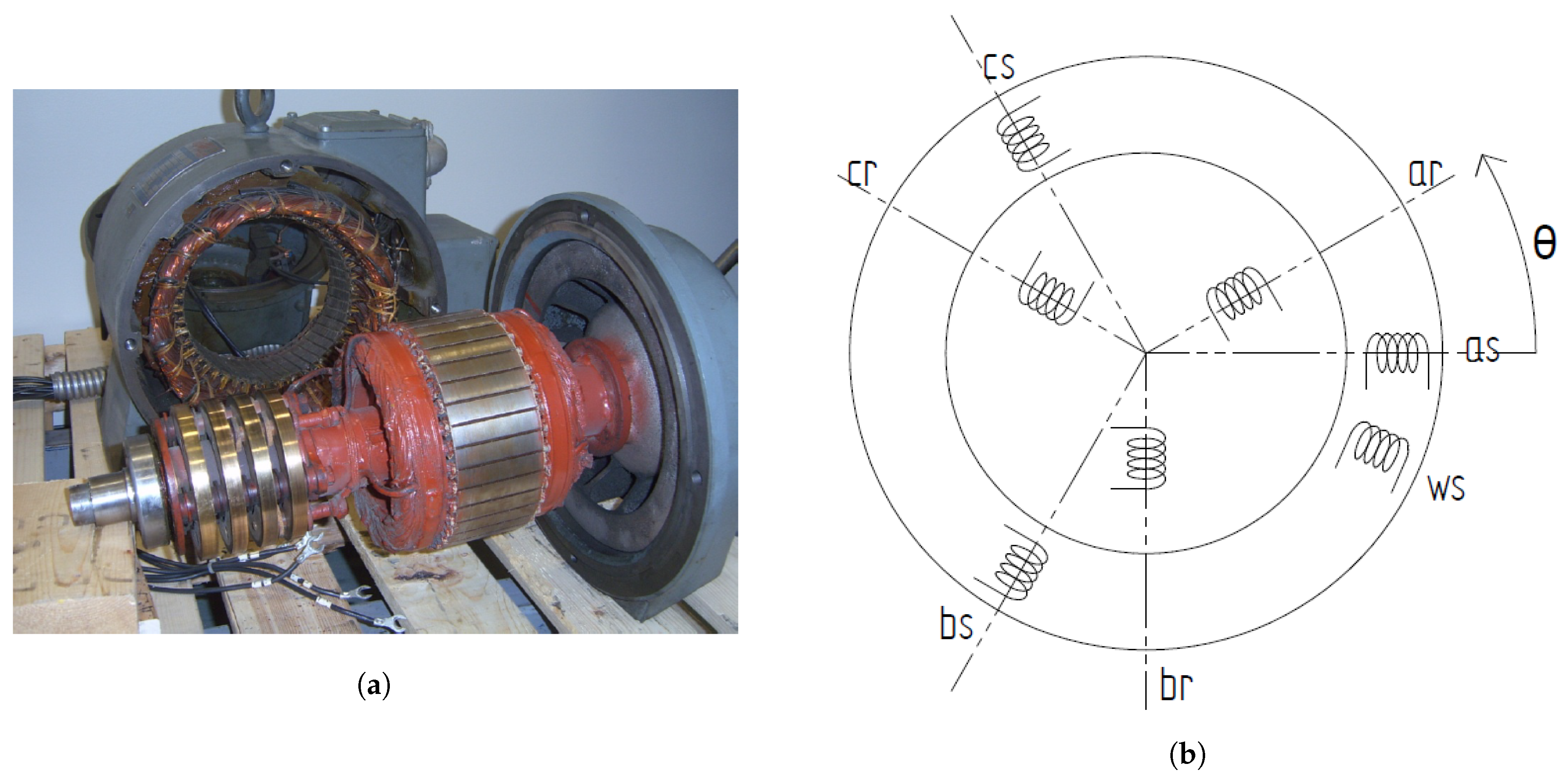
2.2. Identification of Electrical Circuits
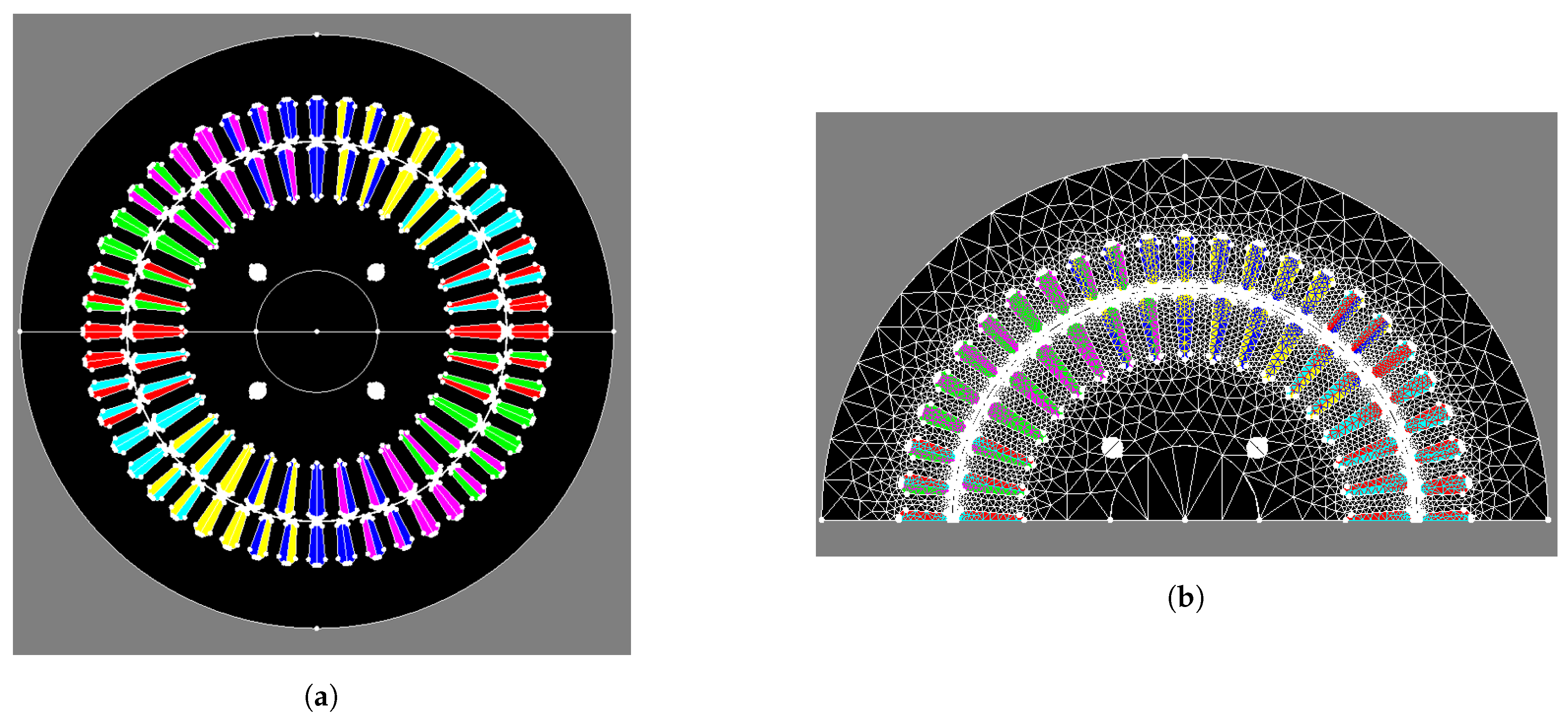
2.3. Computation of the Inductance Matrix Using FEM
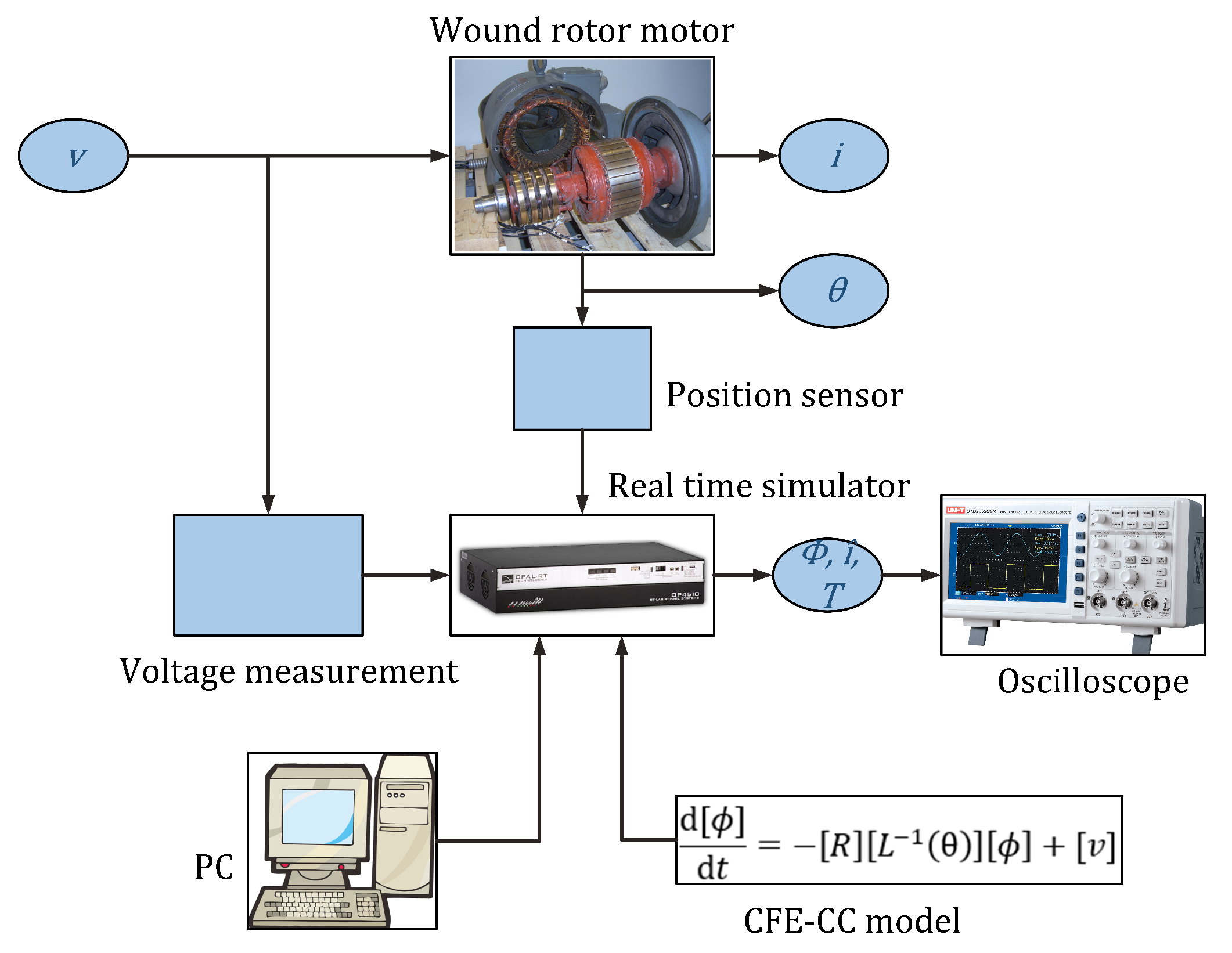
3. Hardware Setup
3.1. Real-Time Simulator And RT-Lab
- Modify execution state of the program (run, stop, pause);
- Change parameters in real-time of the running model;
- Receive data from the running model.
3.2. Voltage and Current Measurement
3.3. Angular Position Sensor
3.4. Setup Overview
4. Implementation on Real-Time Simulator
4.1. Programming Method
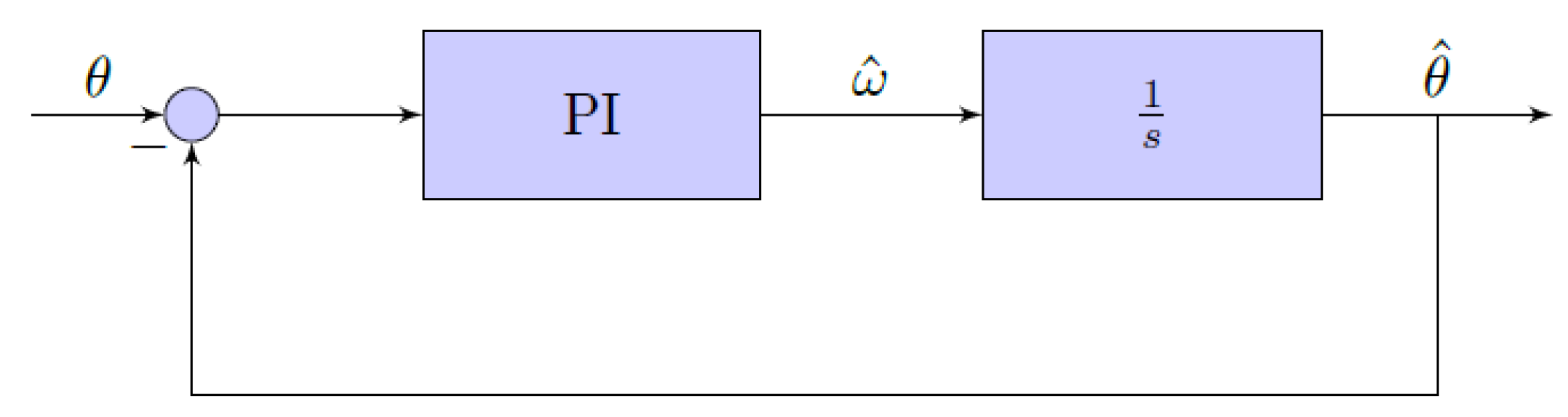
4.2. Position Tracking Scheme
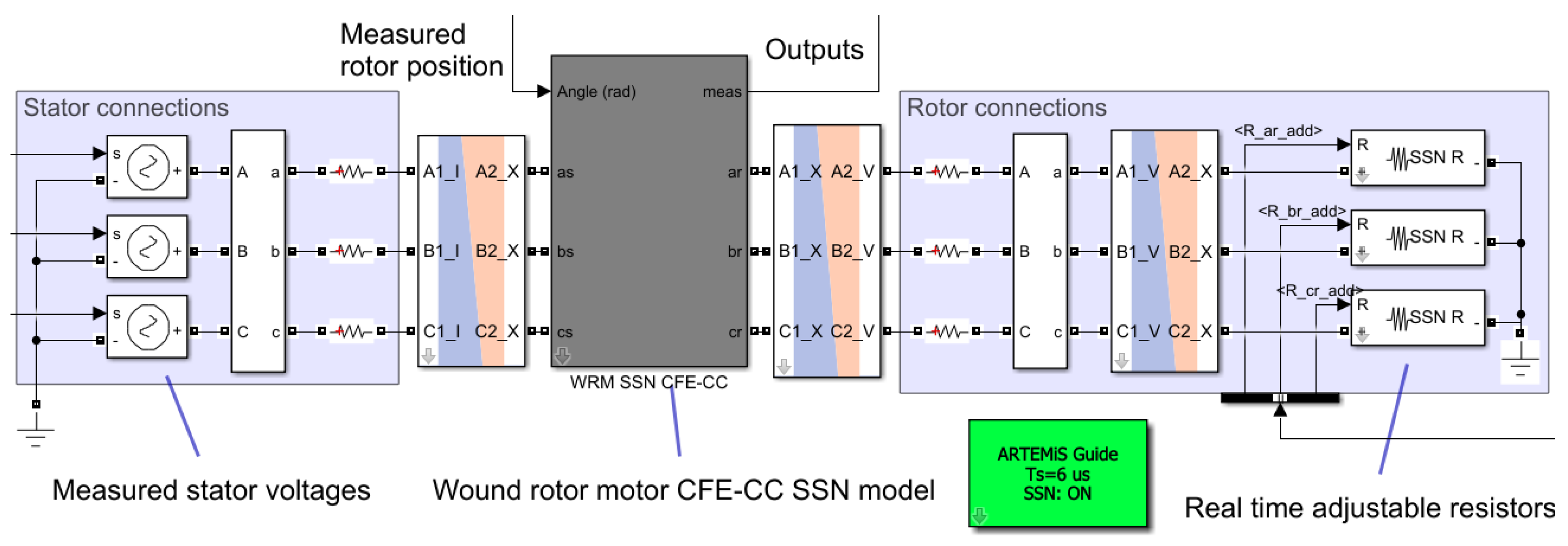
4.3. CFE-CC Model Implementation for Real-Time Execution
4.4. Time Step Selection
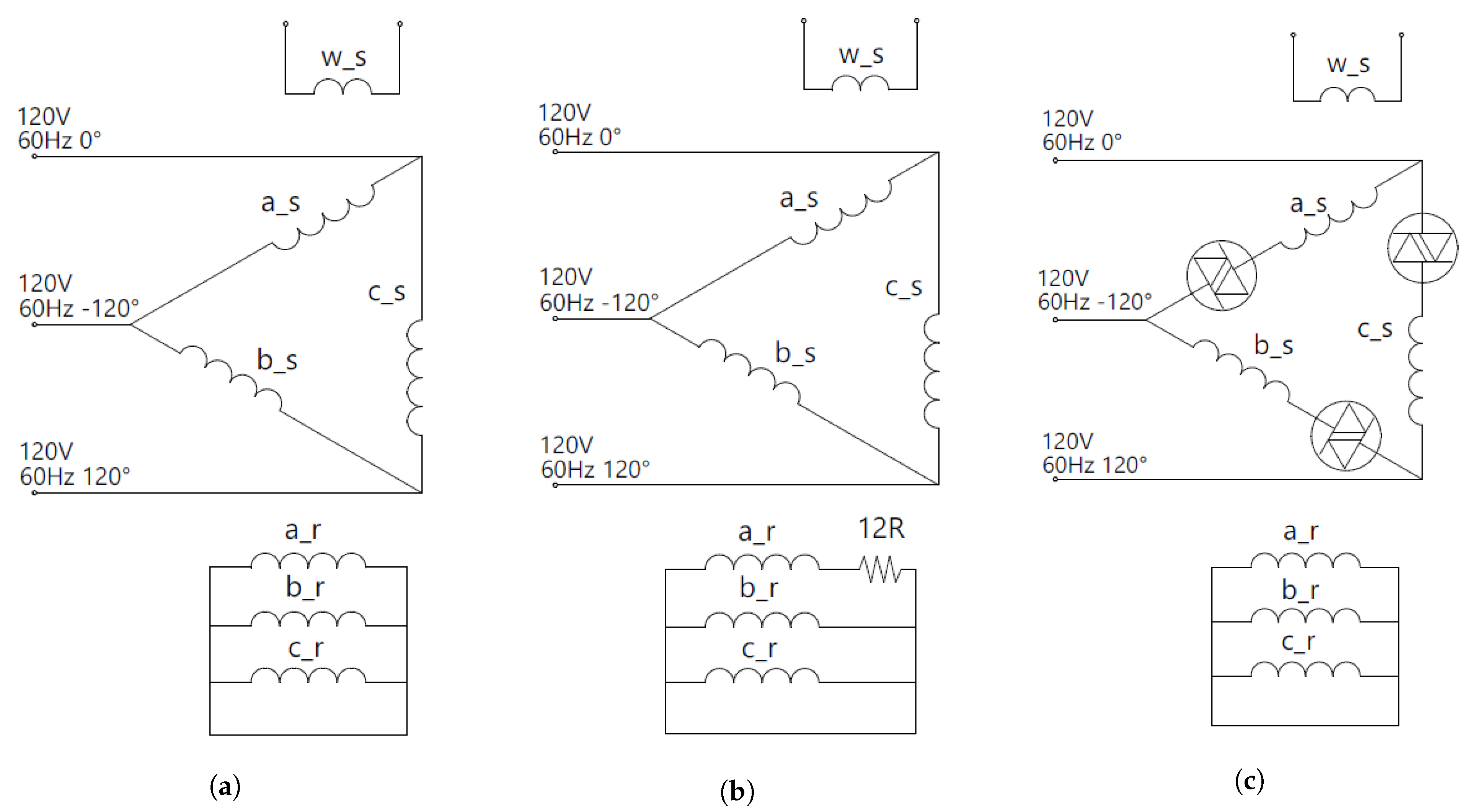
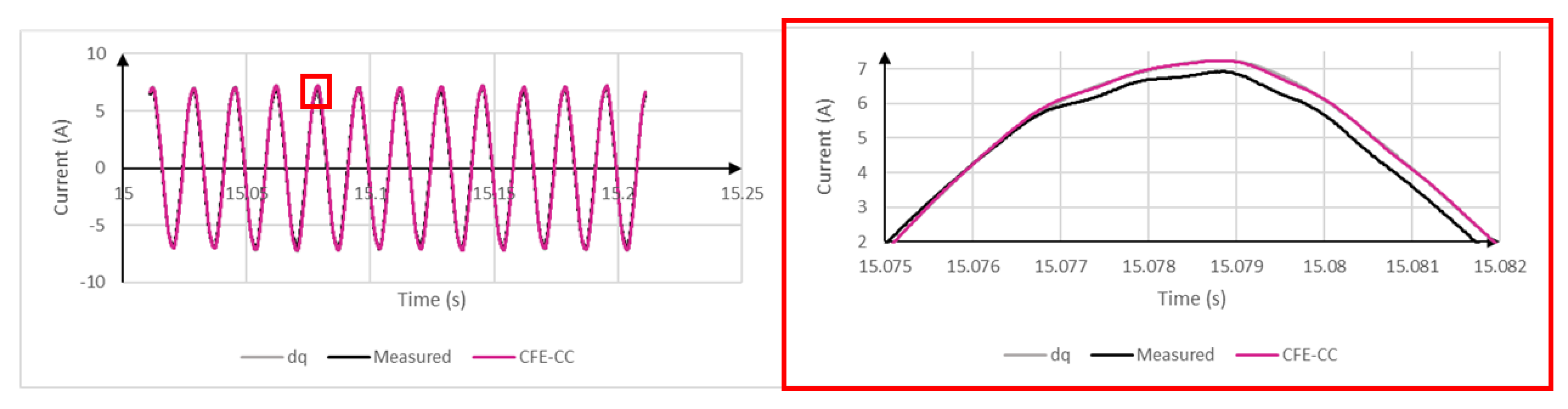
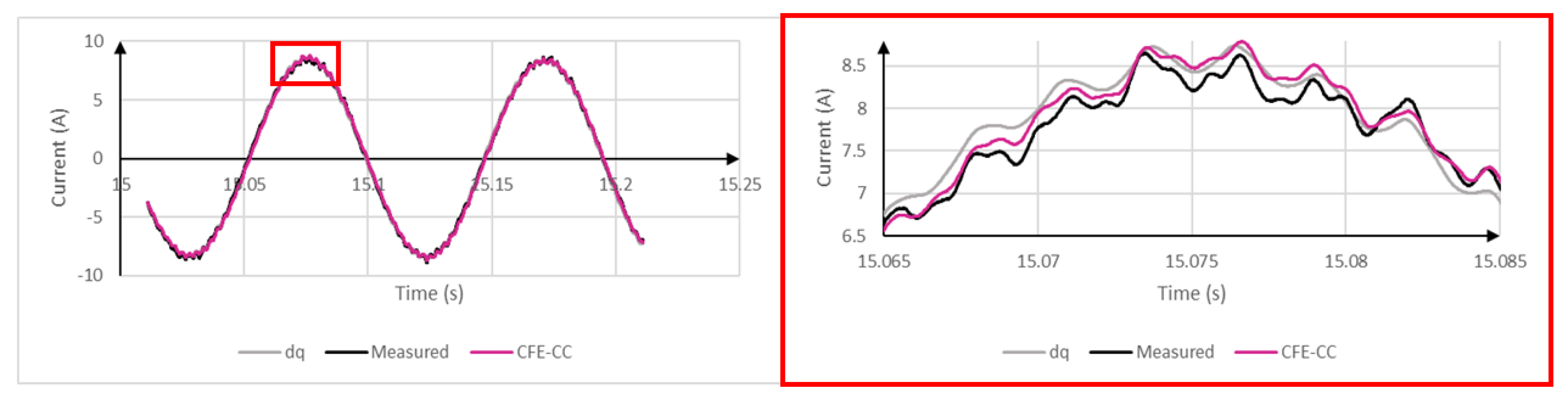
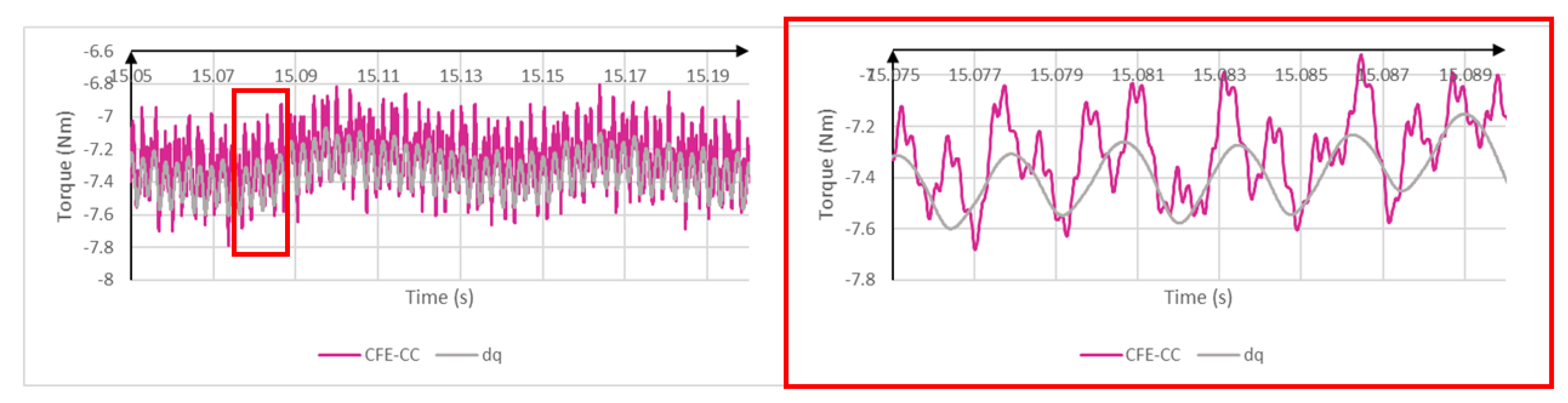
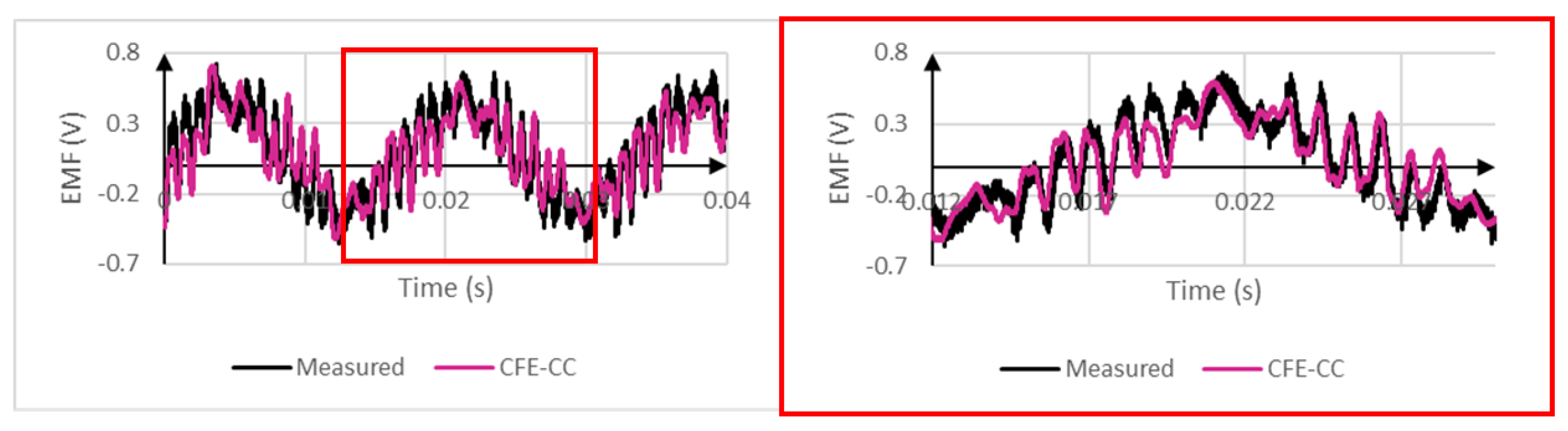
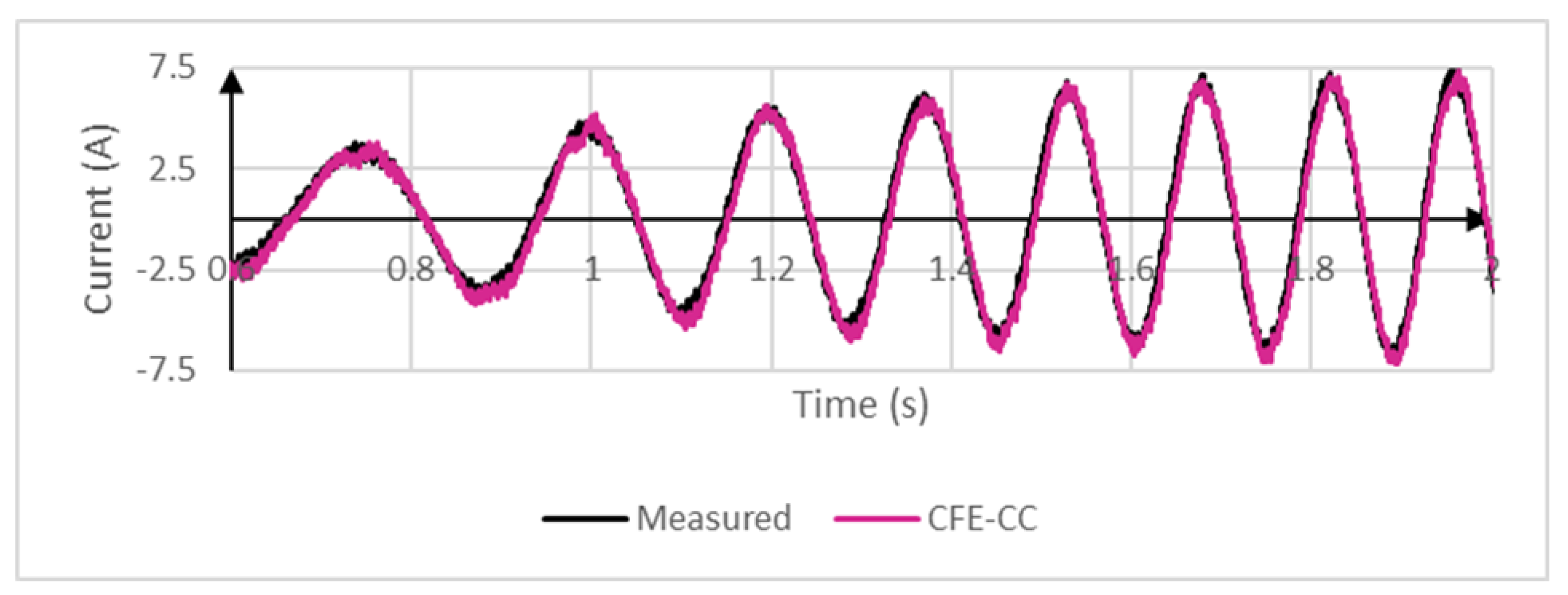
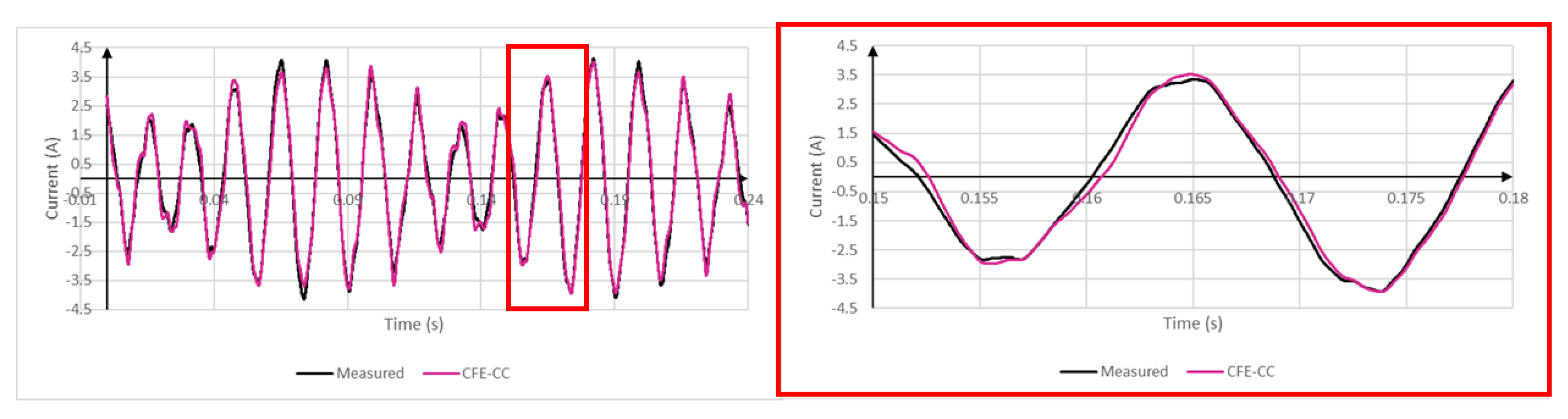
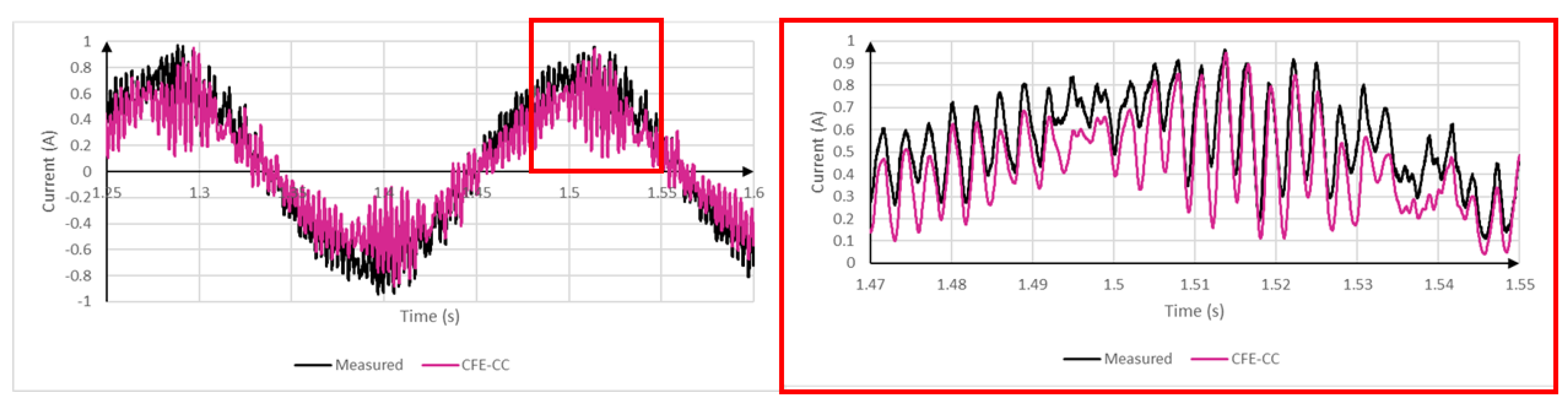
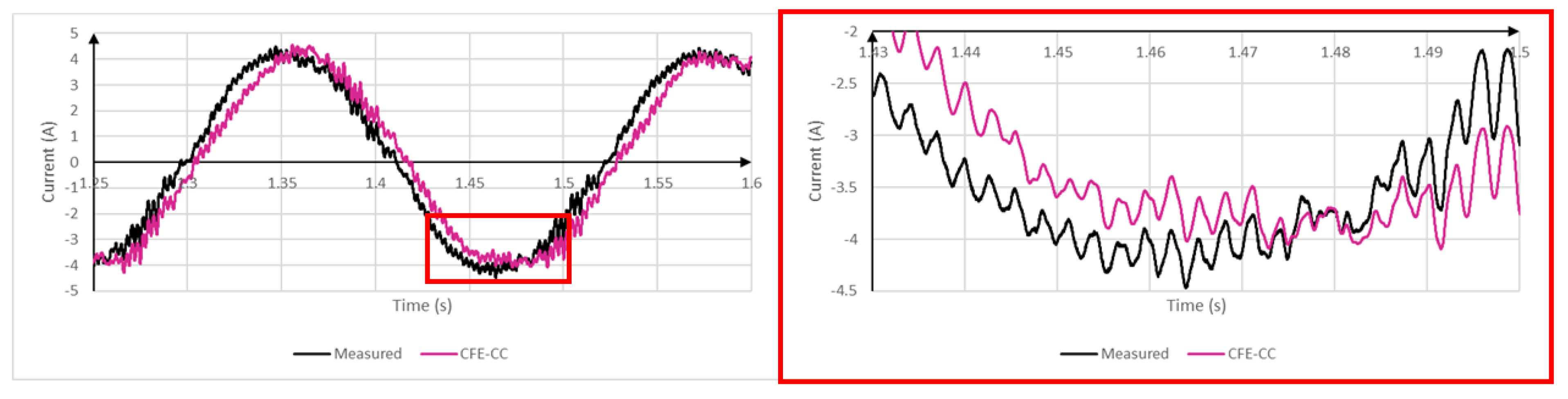
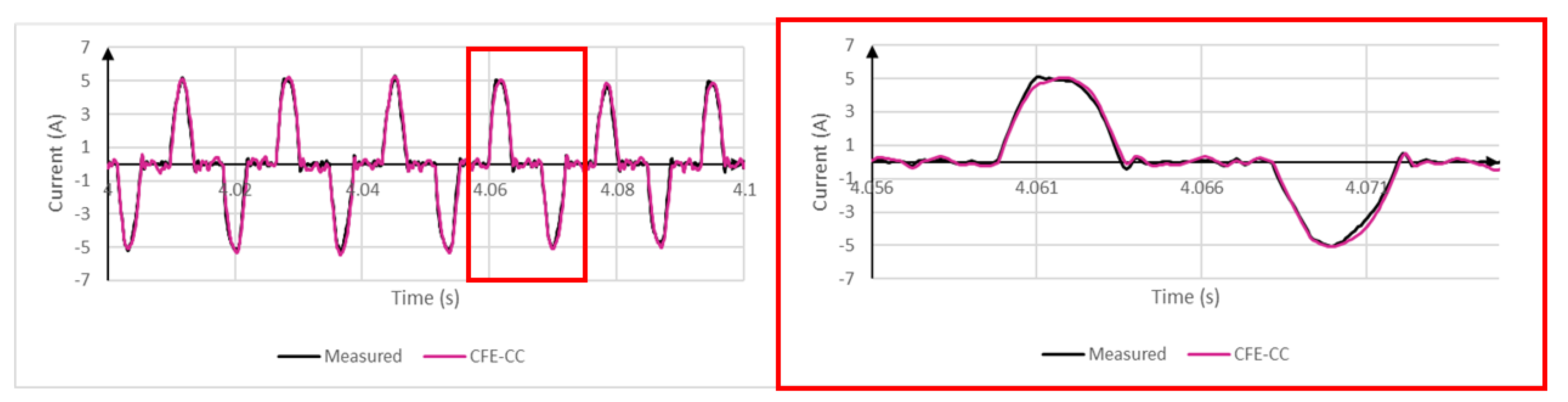
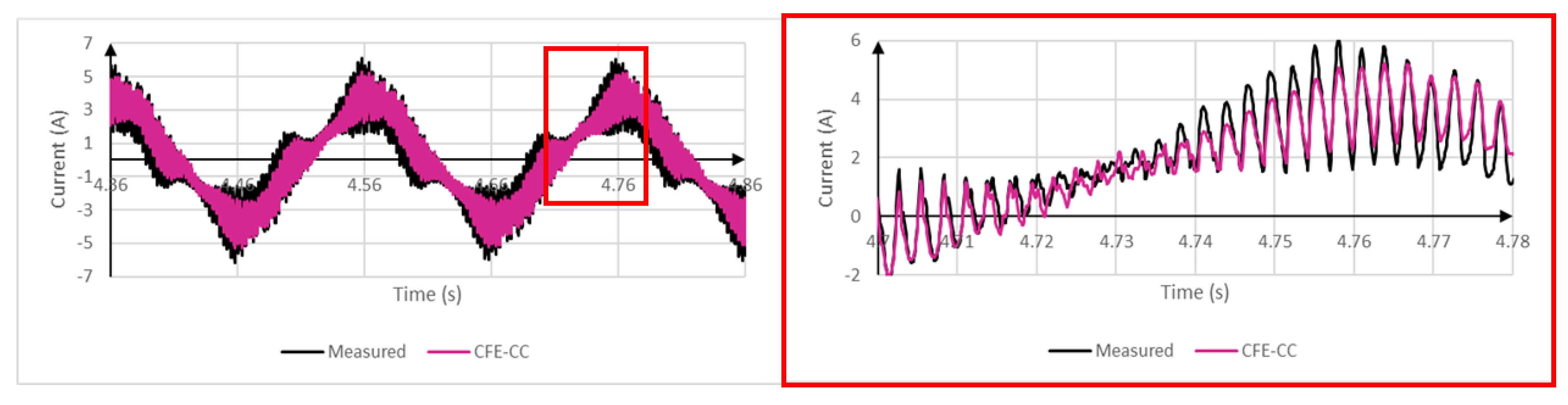
5. Validation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| WRIM | Wound rotor induction machine |
| DRTS | Digital real-time simulator |
| RTDT | Real-time digital twin |
| CFE-CC | Combination of finite element and coupled circuits |
| FEM | Finite element method |
| SSN | State-Space-Nodal |
| SPS | SimPowerSystems |
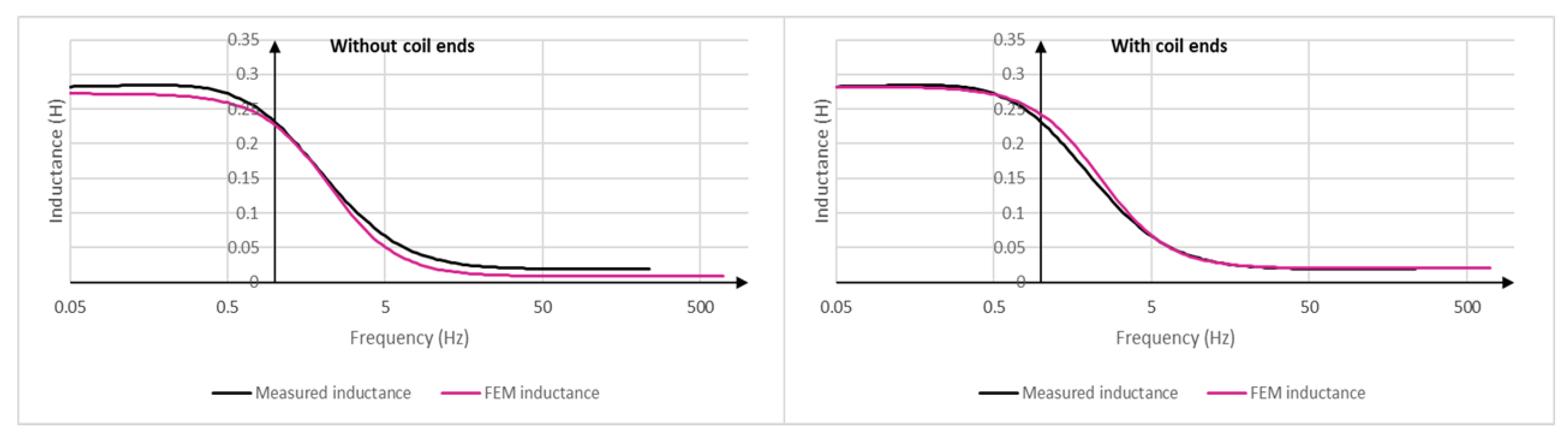
Appendix A. Alteration of Inductance Matrix to Consider Rotor Skew and Coil Ends
Appendix A.1. Rotor Skewing

Appendix A.2. Coil Ends
References
- Ebrahimi, A. Challenges of developing a digital twin model of renewable energy generators. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; pp. 1059–1066. [Google Scholar]
- Wang, J.; Ye, L.; Gao, R.X.; Li, C.; Zhang, L. Digital Twin for rotating machinery fault diagnosis in smart manufacturing. Int. J. Prod. Res. 2019, 57, 3920–3934. [Google Scholar] [CrossRef]
- Boschert, S.; Heinrich, C.; Rosen, R. Next generation digital Twin. In Proceedings of the TMCE, Las Palmas de Gran Canaria, Spain, 7–11 May 2018. [Google Scholar]
- Fuller, A.; Fan, Z.; Day, C.; Barlow, C. Digital Twin: Enabling Technologies, Challenges and Open Research. IEEE Access 2020, 8, 108952–108971. [Google Scholar] [CrossRef]
- Roshandel Tavana, N.; Dinavahi, V. A General Framework for FPGA-Based Real-Time Emulation of Electrical Machines for HIL Applications. IEEE Trans. Ind. Electron. 2015, 62, 2041–2053. [Google Scholar] [CrossRef]
- Kłosowski, Z.; Cieślik, S. Real-time simulation of power conversion in doubly fed induction machine. Energies 2020, 13, 673. [Google Scholar] [CrossRef]
- Sidwall, K.; Forsyth, P. Advancements in Real-Time Simulation for the Validation of Grid Modernization Technologies. Energies 2020, 13, 4036. [Google Scholar] [CrossRef]
- Mojlish, S.; Erdogan, N.; Levine, D.; Davoudi, A. Review of Hardware Platforms for Real-Time Simulation of Electric Machines. IEEE Trans. Transp. Electrif. 2017, 3, 130–146. [Google Scholar] [CrossRef]
- Sudhoff, S.D.; Kuhn, B.T.; Corzine, K.A.; Branecky, B.T. Magnetic Equivalent Circuit Modeling of Induction Motors. IEEE Trans. Energy Convers. 2007, 22, 259–270. [Google Scholar] [CrossRef]
- Fleming, F.E.; Edrington, C.S. Real-Time Emulation of Switched Reluctance Machines via Magnetic Equivalent Circuits. IEEE Trans. Ind. Electron. 2016, 63, 3366–3376. [Google Scholar] [CrossRef]
- Jandaghi, B.; Dinavahi, V. Real-Time HIL Emulation of Faulted Electric Machines Based on Nonlinear MEC Model. IEEE Trans. Energy Convers. 2019, 34, 1190–1199. [Google Scholar] [CrossRef]
- Luo, X.; Liao, Y.; Toliyat, H.; El-Antably, A.; Lipo, T.A. Multiple Coupled Circuit Modeling of Induction Machines. In Proceedings of the Conference Record of the 1993 IEEE Industry Applications Conference Twenty-Eighth IAS Annual Meeting, Toronto, ON, Canada, 2–8 October 1993; pp. 203–210. [Google Scholar] [CrossRef]
- Dehkordi, A.B.; Neti, P.; Gole, A.; Maguire, T. Development and validation of a comprehensive synchronous machine model for a real-time environment. IEEE Trans. Energy Convers. 2009, 25, 34–48. [Google Scholar] [CrossRef]
- Gbégbé, A.Z.; Rouached, B.; Cros, J.; Bergeron, M.; Viarouge, P. Damper Currents Simulation of Large Hydro-Generator Using the Combination of FEM and Coupled Circuits Models. IEEE Trans. Energy Convers. 2017, 32, 1273–1283. [Google Scholar] [CrossRef]
- Quéval, L.; Ohsaki, H. Study on the implementation of the phase-domain model for rotating electrical machines. In Proceedings of the 2012 15th International Conference on Electrical Machines and Systems (ICEMS), Sapporo, Japan, 21–24 October 2012; pp. 1–6. [Google Scholar]
- Rouached, B.; Cros, J.; Clénet, S.; Viarouge, P. Estimation of Damper Bars Losses in Large Synchronous Alternator using Bar Current Waveforms; Electrimacs: Toulouse, France, 2017. [Google Scholar]
- Demetriades, G.D.; de la Parra, H.Z.; Andersson, E.; Olsson, H. A Real-Time Thermal Model of a Permanent-Magnet Synchronous Motor. IEEE Trans. Power Electron. 2010, 25, 463–474. [Google Scholar] [CrossRef]
- Mathault, J.; Bergeron, M.; Rakotovololona, S.; Cros, J.; Viarouge, P. Influence of Discrete Inductance Curves on the Simulation of a Round Rotor Generator Using Coupled Circuit Method; Electrimacs: Valencia, Spain, 2014. [Google Scholar]
- Dufour, C.; Mahseredjian, J.; Belanger, J. A Combined State-Space Nodal Method for the Simulation of Power System Transients. IEEE Trans. Power Deliv. 2011, 26, 928–935. [Google Scholar] [CrossRef]
- Wang, L.; Jatskevich, J.; Dinavahi, V.; Dommel, H.W.; Martinez, J.A.; Strunz, K.; Rioual, M.; Chang, G.W.; Iravani, R. Methods of Interfacing Rotating Machine Models in Transient Simulation Programs. IEEE Trans. Power Deliv. 2010, 25, 891–903. [Google Scholar] [CrossRef]
- Dufour, C.; Nasrallah, D.S. State-space-nodal rotating machine models with improved numerical stability. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 4368–4375. [Google Scholar] [CrossRef]
- Mohr, M.; Bíró, O.; Stermecki, A.; Diwoky, F. A Finite Element-Based Circuit Model Approach for Skewed Electrical Machines. IEEE Trans. Magn. 2014, 50, 837–840. [Google Scholar] [CrossRef]
| Parameter | Value | Unit |
|---|---|---|
| Power rating | 1864 | W |
| Rated voltage | 208 | V |
| Number of phases | 3 | |
| Number of poles | 4 | |
| Number of stator slots | 48 | |
| Number of rotor slots | 36 | |
| Frequency | 60 | Hz |
| Speed | 1690 | RPM |
| Power factor | 0.81 |
| CPU | Intel Xeon E3 v5 CPU (4 core, 8 MB cache, 2.1 or 3.5 GHz) |
| Dynamic memory | 16 GB RAM |
| Storage | 128 GB SSD |
| Digital outputs | 32 channels, 5 V to 30 V adjustable by a user-supplied voltage |
| Digital inputs | 32 channels, 4 V to 50 V |
| Analog inputs | 16 channels, 16 bits, ±20 V true differential |
| Analog outputs | 16 channels, 16 bits, ±16 V |
| Frequency (Hz) | Measurements (V) |
|---|---|
| 60 | 156.5 |
| 180 | 1.0 |
| 300 | 3.9 |
| 420 | 1.8 |
| Frequency (Hz) | Measurements (A) | CFE-CC (A) | dq (A) |
|---|---|---|---|
| 60 | 5.780 | 5.865 | 5.916 |
| 180 | 0.050 | 0.068 | 0.102 |
| 300 | 0.119 | 0.102 | 0.102 |
| 420 | 0.051 | 0.051 | 0.051 |
| 588 | 0.010 | 0.010 | n/a |
| 913 | 0.015 | 0.013 | n/a |
| 1033 | 0.017 | 0.015 | n/a |
| Frequency (Hz) | Measurements (A) | CFE-CC (A) | dq (A) |
|---|---|---|---|
| 6.4 | 7.130 | 7.286 | 7.384 |
| 114 | 0.183 | 0.116 | 0.117 |
| 354 | 0.139 | 0.125 | 0.129 |
| 367 | 0.055 | 0.044 | 0.045 |
| 642 | 0.014 | 0.013 | n/a |
| 655 | 0.014 | 0.015 | n/a |
| 967 | 0.018 | 0.015 | n/a |
| 979 | 0.023 | 0.021 | n/a |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouzid, S.; Viarouge, P.; Cros, J. Real-Time Digital Twin of a Wound Rotor Induction Machine Based on Finite Element Method. Energies 2020, 13, 5413. https://doi.org/10.3390/en13205413
Bouzid S, Viarouge P, Cros J. Real-Time Digital Twin of a Wound Rotor Induction Machine Based on Finite Element Method. Energies. 2020; 13(20):5413. https://doi.org/10.3390/en13205413
Chicago/Turabian StyleBouzid, Sami, Philippe Viarouge, and Jérôme Cros. 2020. "Real-Time Digital Twin of a Wound Rotor Induction Machine Based on Finite Element Method" Energies 13, no. 20: 5413. https://doi.org/10.3390/en13205413
APA StyleBouzid, S., Viarouge, P., & Cros, J. (2020). Real-Time Digital Twin of a Wound Rotor Induction Machine Based on Finite Element Method. Energies, 13(20), 5413. https://doi.org/10.3390/en13205413