Model-Independent Derivative Control Delay Compensation Methods for Power Systems
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
1.2.1. Communication Delays in Power Systems
1.2.2. Compensation of Delays in Control Loops
1.2.3. Compensation of Delays in on-Line Monitoring
1.2.4. D-Term-Based Delay Compensation
1.3. Contributions
- A discussion on the maximum fidelity that the two delay-compensation methods for wide-area controllers can achieve is presented.
- A technique to solve small-signal stability analysis of power systems with inclusion of either constant or realistically-modeled communication delays in the derivatives of the state variables is proposed.
- A new theorem on the stability of the NTDS is derived.
- A thorough comparison of the performance of PD and predictor-based delay compensation methods in power systems, including both open-loop and closed-loop scenarios, is shown.
1.4. Organization
2. D-Based Delay Compensation Methods and Small Signal Stability
2.1. Power System Model with Inclusion of Delays
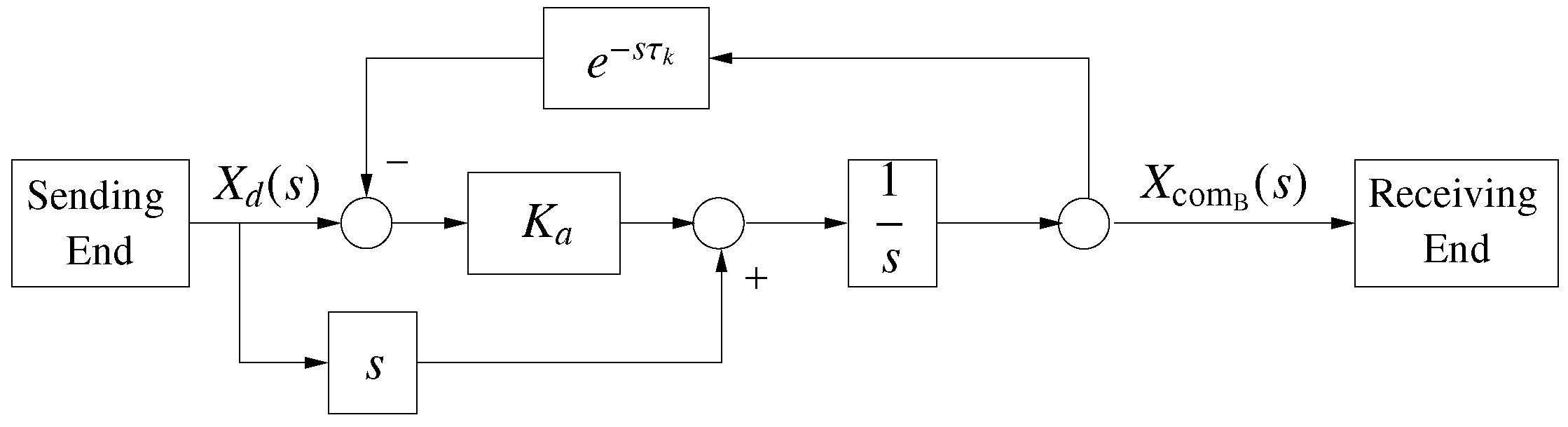
2.2. PD Delay Compensation
2.3. Predictor-Based Delay Compensation
2.4. Power System Model with Inclusion of Delay Compensation
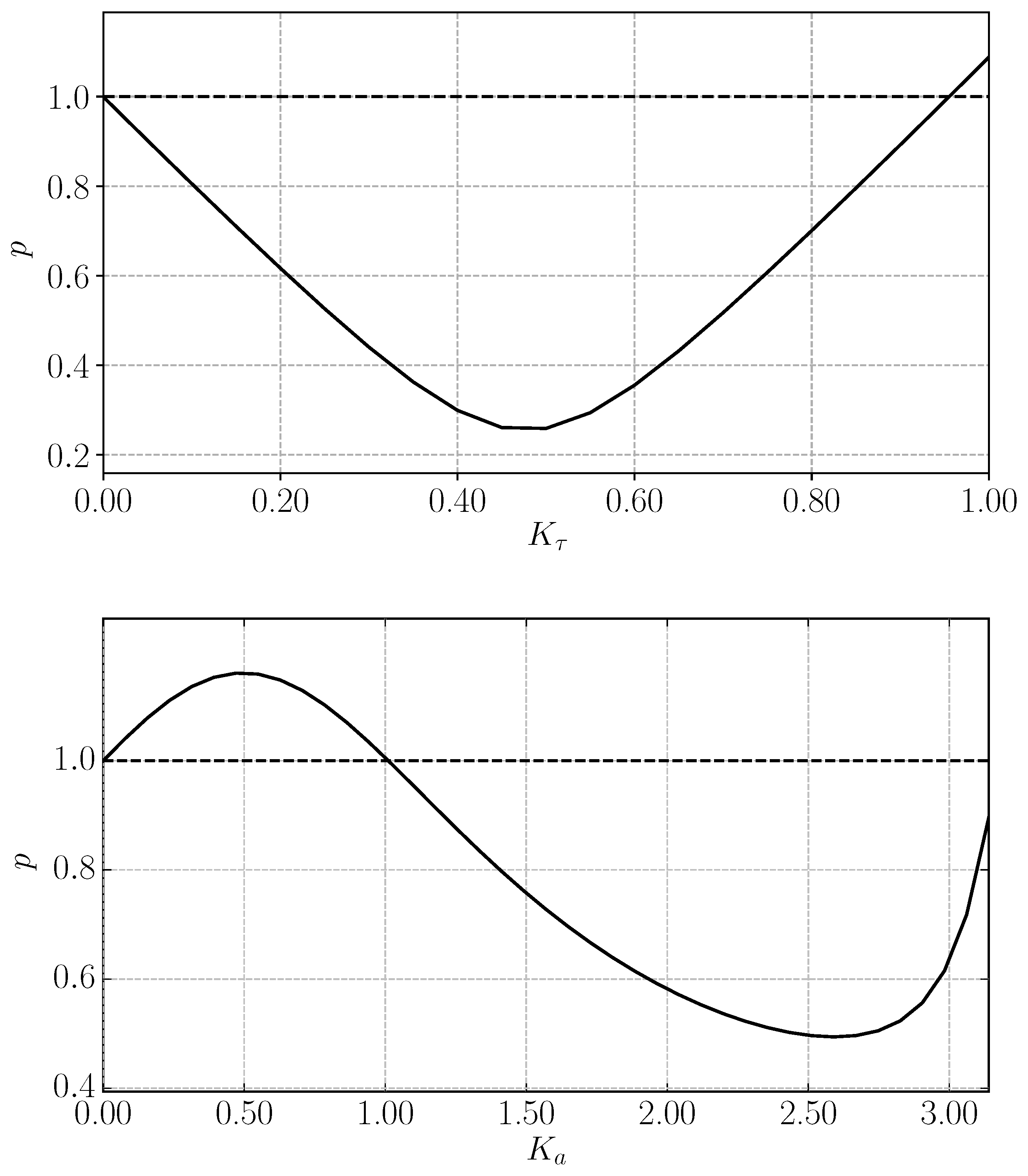
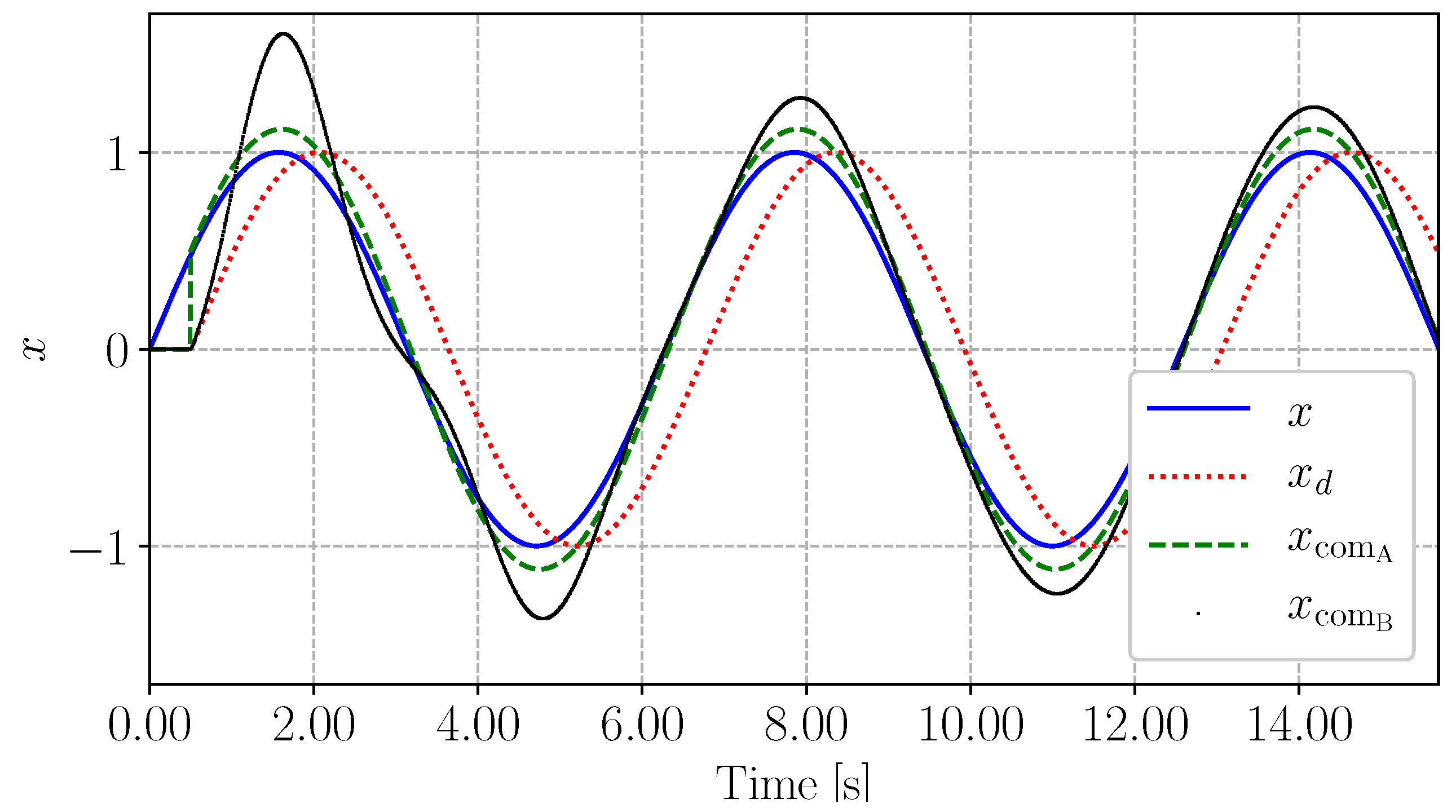
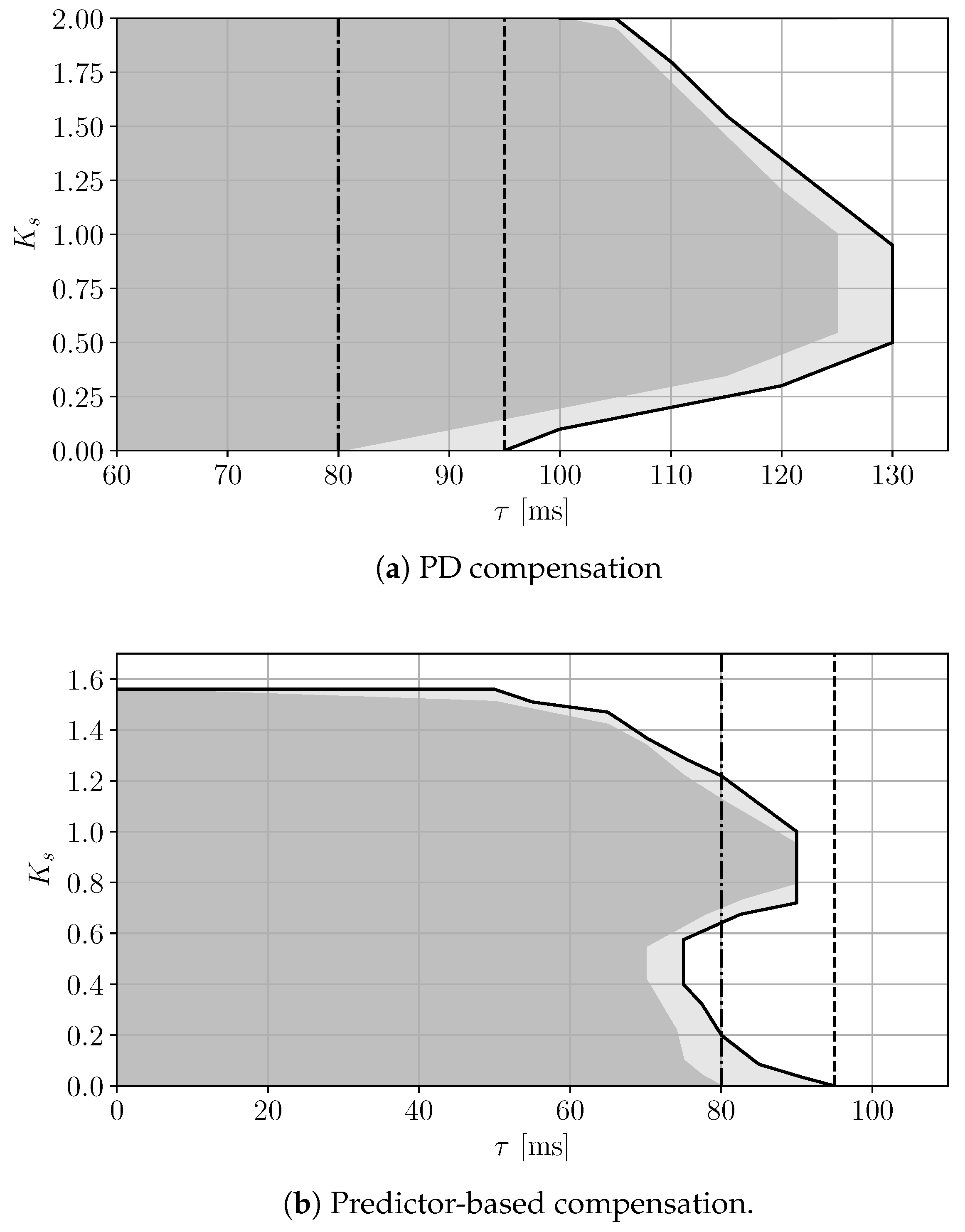
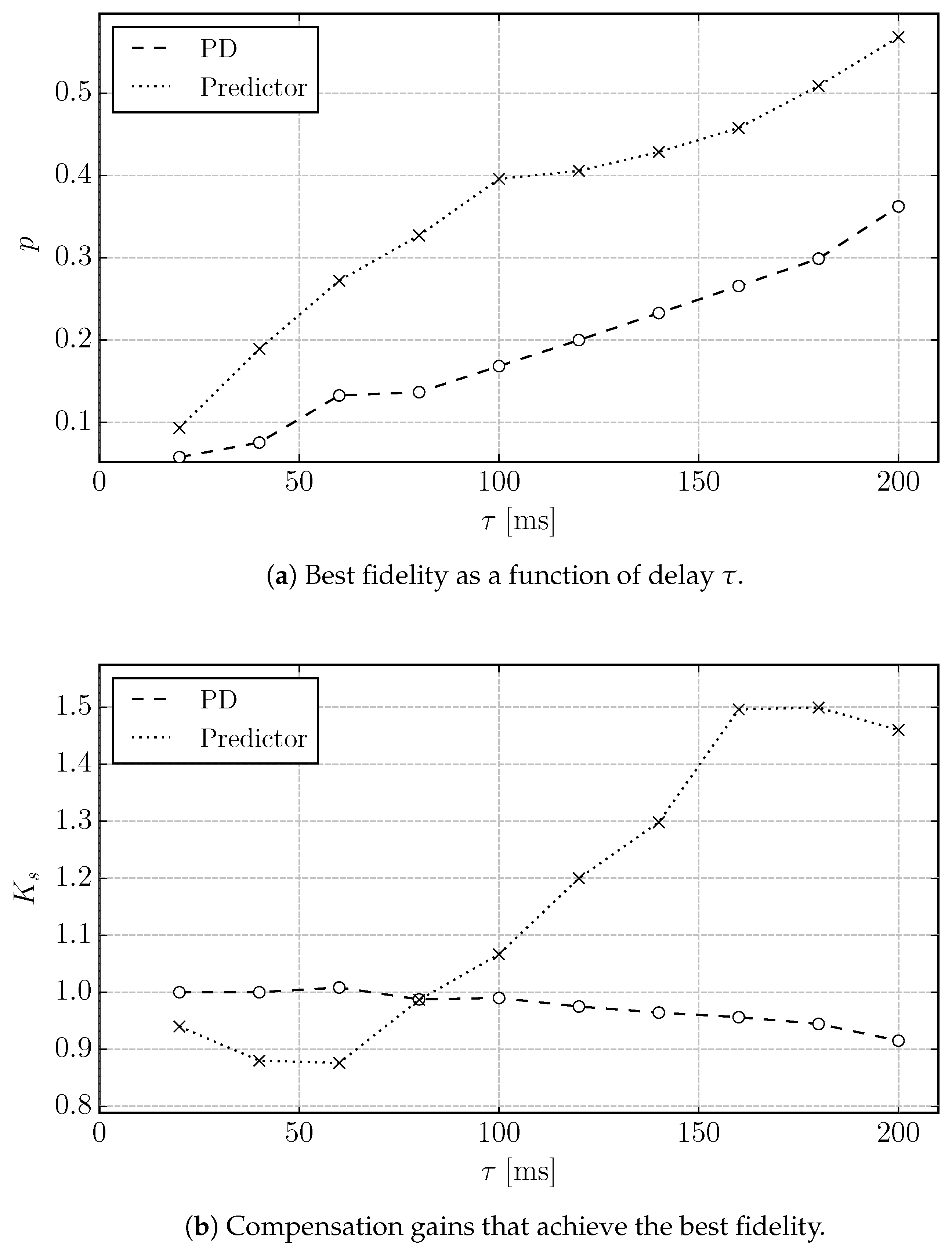
3. Fidelity Comparison
Illustrative Example
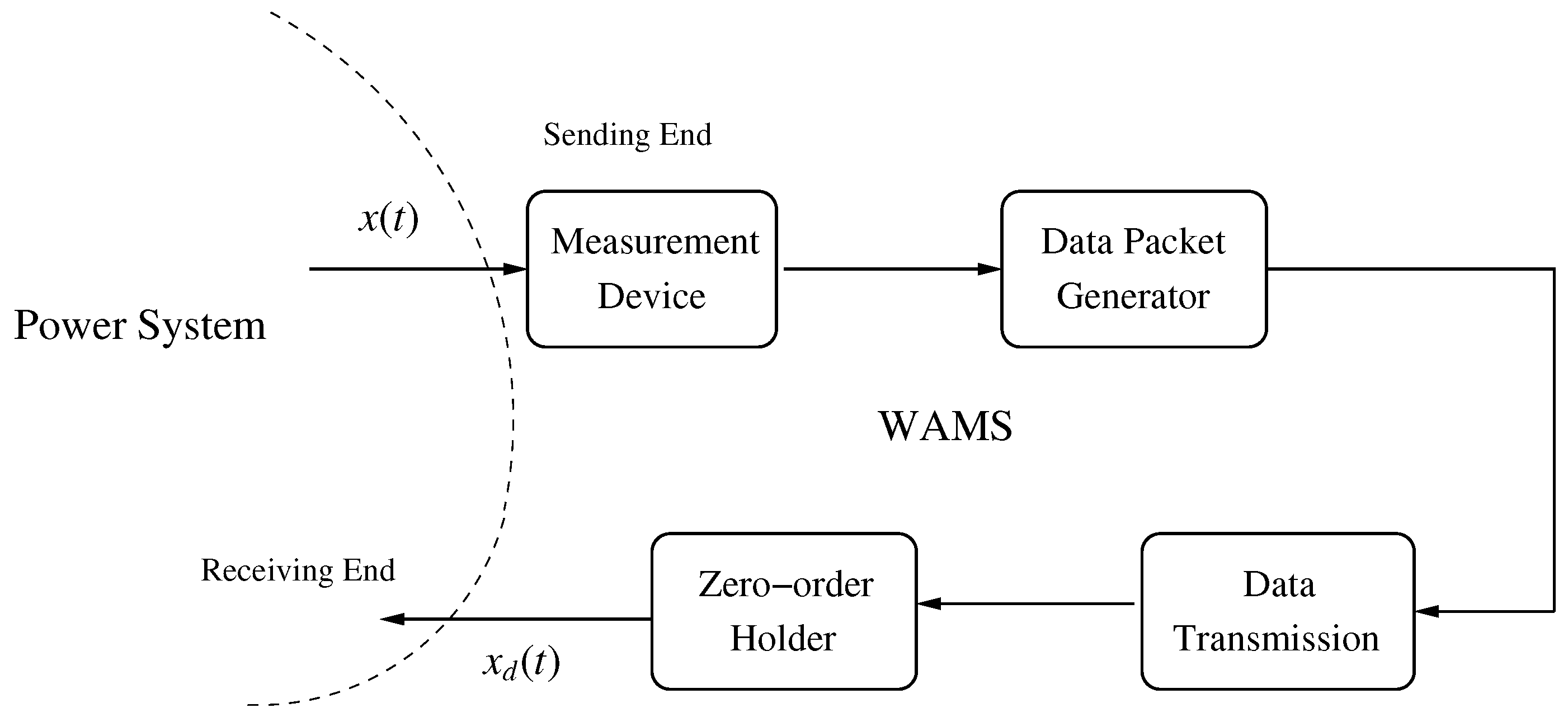
4. Wide-Area Measurement Delay Compensation
4.1. Wide-Area Measurement Delay Model
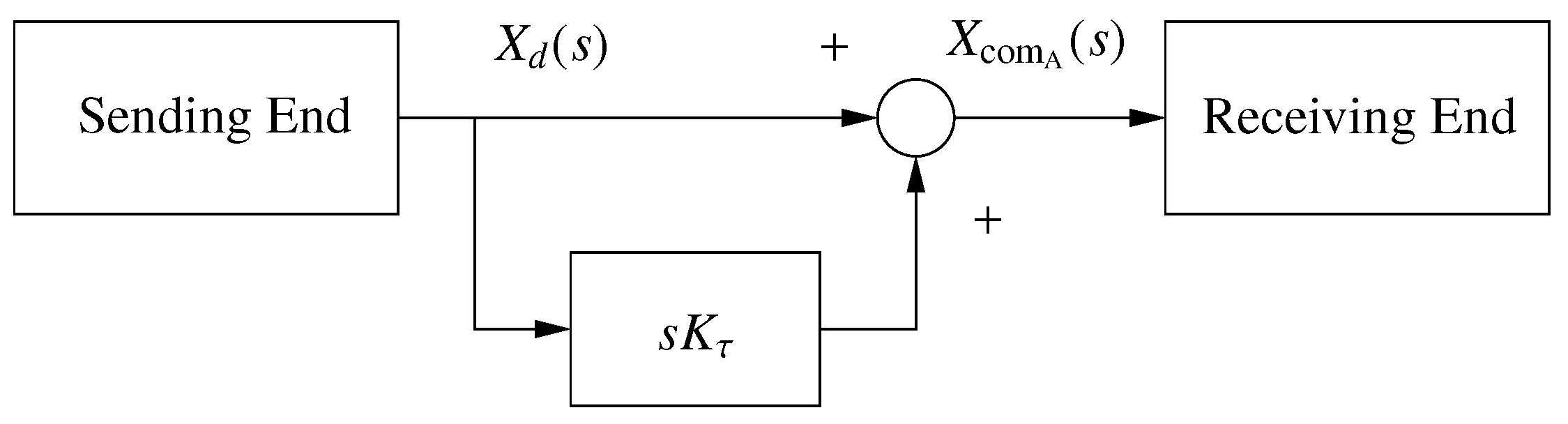
4.2. Implementation of the Delay Compensation
5. Case Study
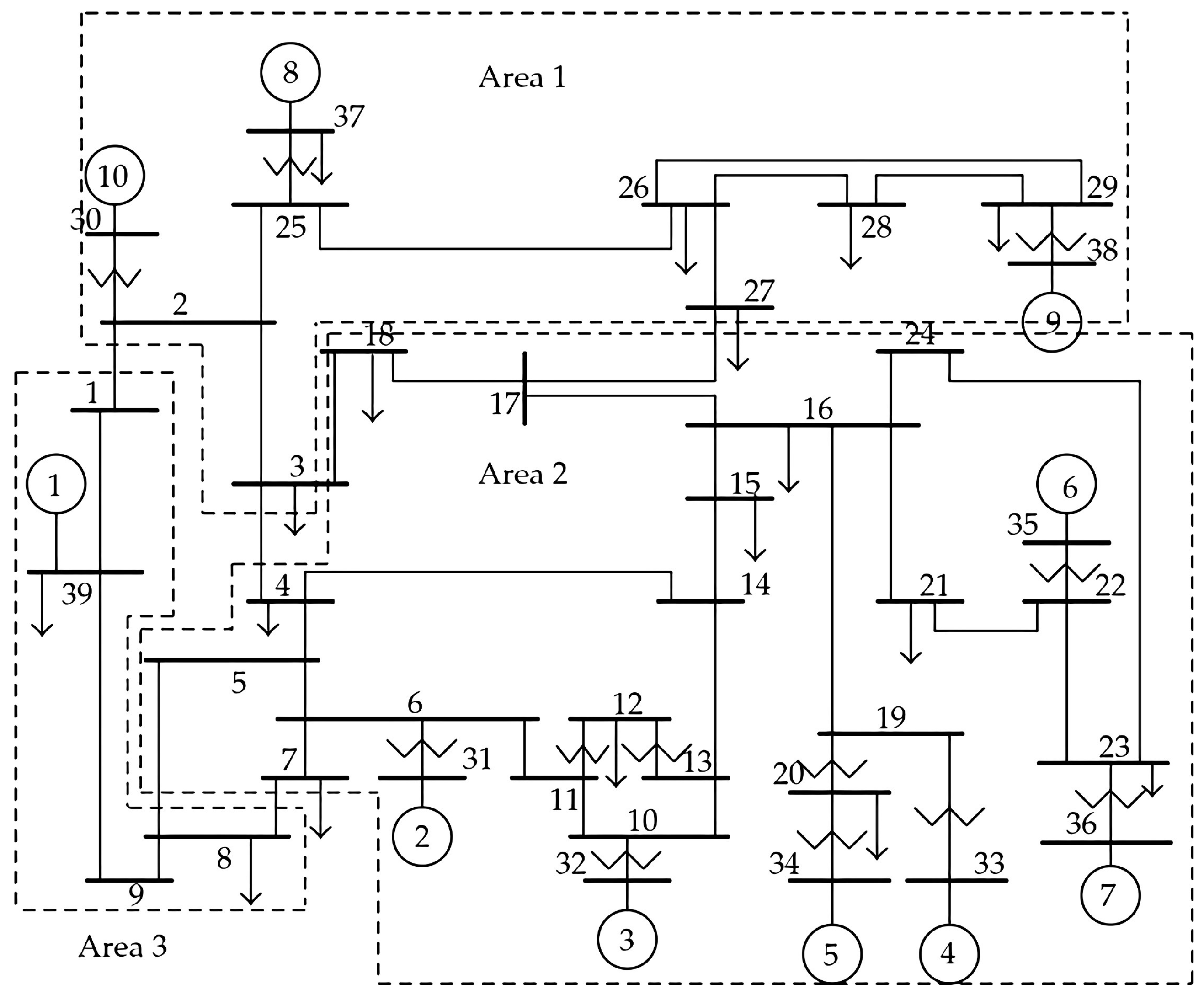
5.1. IEEE 14-Bus System
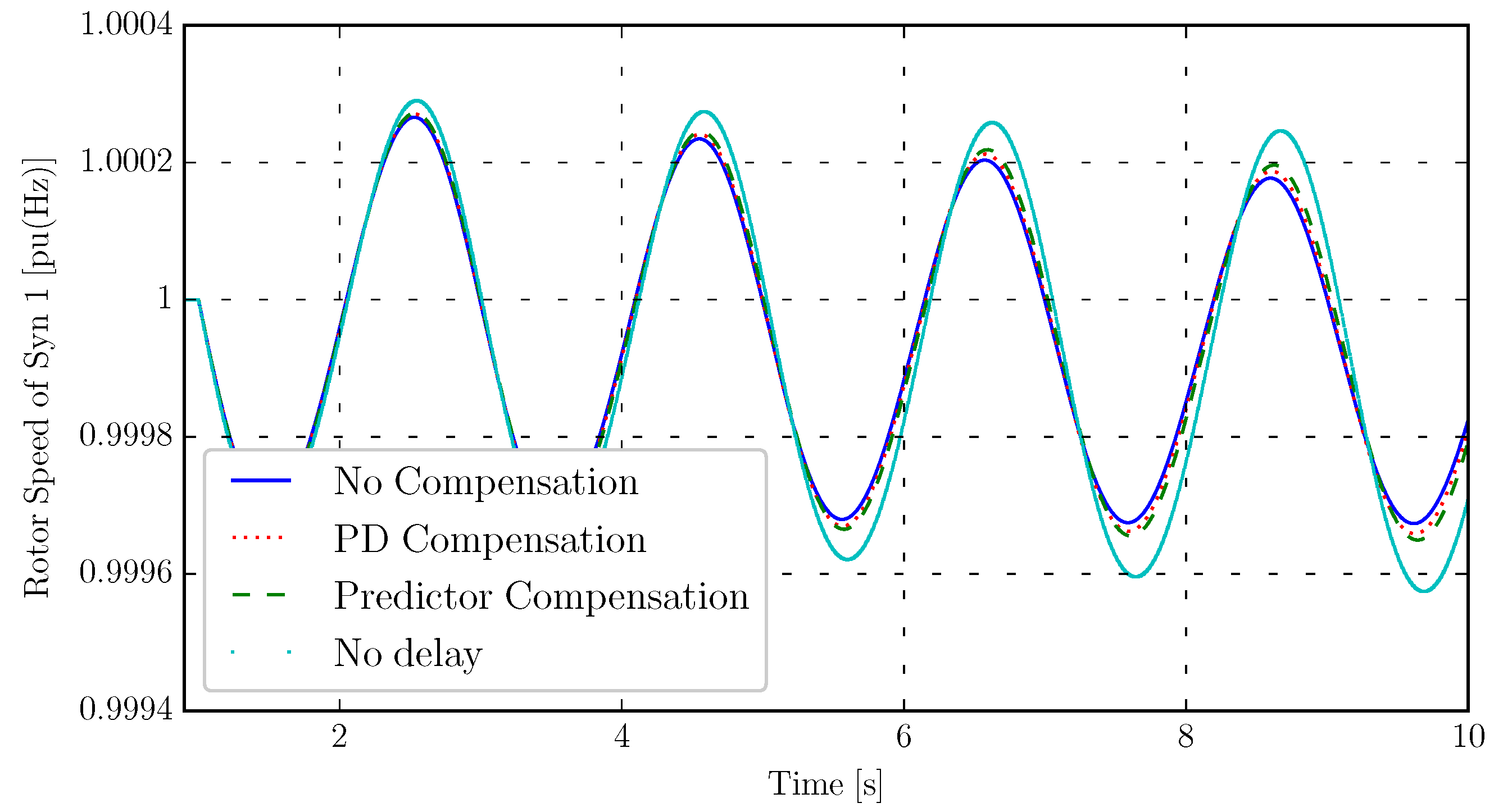
5.1.1. Constant Delay
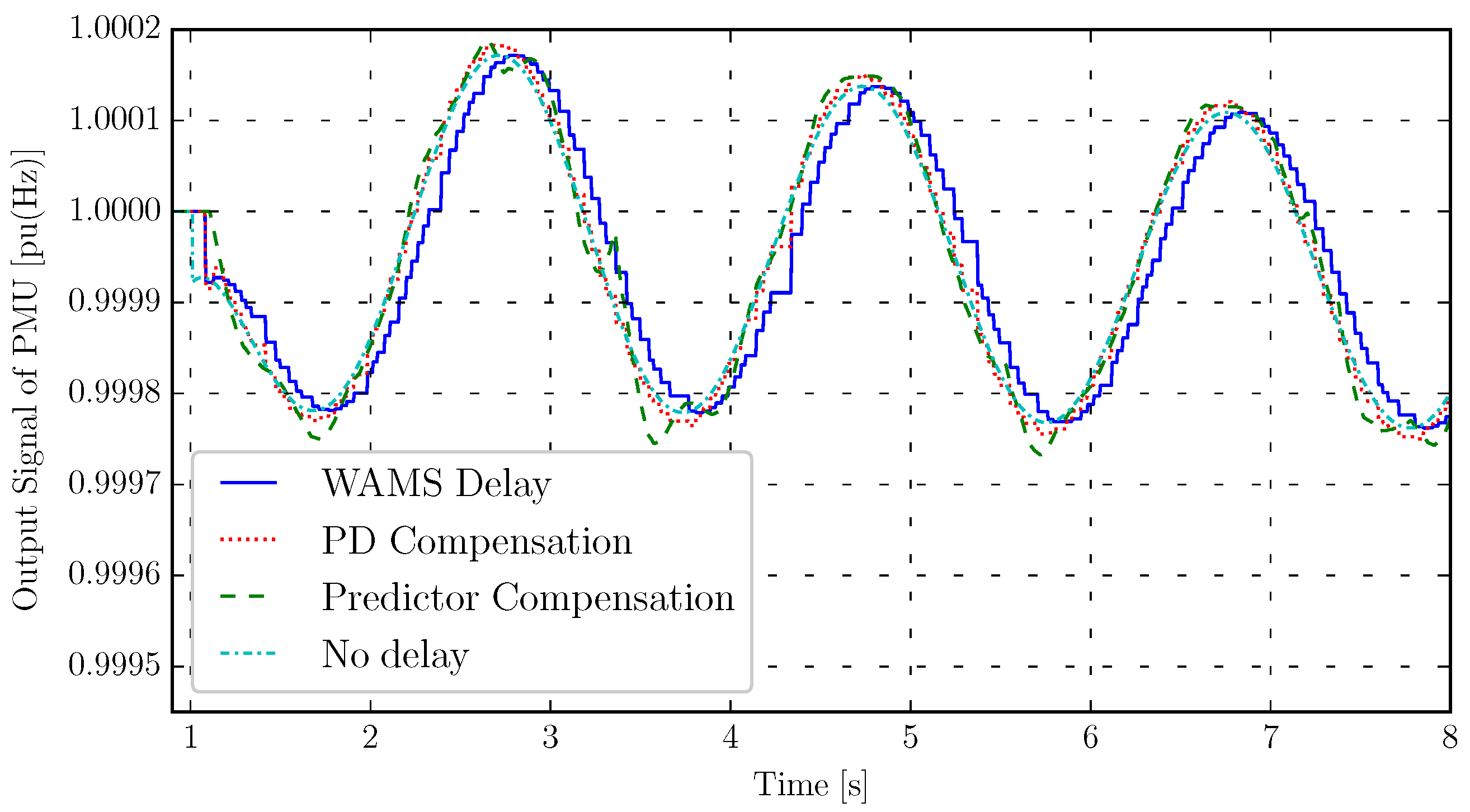
5.1.2. WAMS Delay
5.2. New England System
5.2.1. Constant Delay
5.2.2. WAMS Delay
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Zhang, Y.; Bose, A. Design of wide-area damping controllers for interarea oscillations. IEEE Trans. Power Syst. 2008, 23, 1136–1143. [Google Scholar] [CrossRef]
- Mokhtari, M.; Aminifar, F.; Nazarpour, D.; Golshannavaz, S. Wide-area power oscillation damping with a fuzzy controller compensating the continuous communication delays. IEEE Trans. Power Syst. 2013, 28, 1997–2005. [Google Scholar] [CrossRef]
- Milano, F.; Ortega, Á.; Conejo, A.J. Model-agnostic linear estimation of generator rotor speeds based on phasor measurement units. IEEE Trans. Power Syst. 2018, 33, 7258–7268. [Google Scholar]
- Zhao, L.; Abur, A. Multi area state estimation using synchronized phasor measurements. IEEE Trans. Power Syst. 2005, 20, 611–617. [Google Scholar] [CrossRef]
- Zhu, L.; Lu, C.; Dong, Z.Y.; Hong, C. Imbalance learning machine-based power system short-term voltage stability assessment. IEEE Trans. Ind. Inform. 2017, 13, 2533–2543. [Google Scholar] [CrossRef]
- Yu, J.J.Q.; Lam, A.Y.S.; Hill, D.J.; Li, V.O.K. Delay aware intelligent transient stability assessment system. IEEE Access 2017, 5, 17230–17239. [Google Scholar] [CrossRef]
- Tian, Y.C.; Levy, D. Compensation for control packet dropout in networked control systems. Inf. Sci. 2008, 178, 1263–1278. [Google Scholar] [CrossRef]
- Roy, S.; Patel, A.; Kar, I.N. Analysis and design of a wide-area damping controller for inter-area oscillation with artificially induced time delay. IEEE Trans. Smart Grid 2019, 10, 3654–3663. [Google Scholar] [CrossRef]
- Zheng, Y.; Brudnak, M.J.; Jayakumar, P.; Stein, J.L.; Ersal, T. A predictor-based framework for delay compensation in networked closed-loop systems. IEEE/ASME Trans. Mechatron. 2018, 23, 2482–2493. [Google Scholar] [CrossRef]
- Wang, S.; Meng, X.; Chen, T. Wide-area control of power systems through delayed network communication. IEEE Trans. Power Syst. 2012, 20, 495–503. [Google Scholar]
- Naduvathuparambil, B.; Valenti, M.C.; Feliachi, A. Communication delays in wide area measurement systems. In Proceedings of the 34th Southeastern Symposium on System Theory, Huntsville, LA, USA, 19 March 2002; pp. 118–122. [Google Scholar]
- Ye, H.; Liu, Y.; Zhang, P. Efficient eigen-analysis for large delayed cyber-physical power system using explicit infinitesimal generator discretization. IEEE Trans. Power Syst. 2016, 31, 2361–2370. [Google Scholar] [CrossRef]
- Milano, F.; Anghel, M. Impact of time delays on power system stability. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 889–900. [Google Scholar] [CrossRef]
- Stahlhut, J.W.; Browne, T.J.; Heydt, G.T. Latency viewed as a stochastic process and its impact on wide area power system control signals. IEEE Trans. Power Syst. 2008, 23, 84–91. [Google Scholar] [CrossRef]
- Yao, W.; Jiang, L.; Wu, Q.H.; Wen, J.Y.; Cheng, S.J. Delay-dependent stability analysis of the power system with a wide-area damping controller embedded. IEEE Trans. Power Syst. 2011, 26, 233–240. [Google Scholar] [CrossRef]
- Papachristodoulou, A.; Peet, M.M.; Niculescu, S. Stability analysis of linear system with time-varying delays: Delay uncertainty and quenching. In Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 2117–2118. [Google Scholar]
- Liu, M.; Ortega, Á.; Milano, F. PMU-based Estimation of the Frequency of the Center of Inertia and Generator Rotor Speeds. In Proceedings of the IEEE PES General Meeting, Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar]
- Lu, C.; Zhang, X.; Wang, X.; Han, Y. Mathematical expectation modeling of wide-area controlled power systems with stochastic time delay. IEEE Trans. Smart Grid 2015, 6, 1511–1519. [Google Scholar] [CrossRef]
- Liu, M.; Dassios, I.; Tzounas, G.; Milano, F. Stability analysis of power systems with inclusion of realistic-modeling wams delays. IEEE Trans. Power Syst. 2019, 34, 627–636. [Google Scholar] [CrossRef]
- Padhy, B.P.; Srivastava, S.C.; Verma, N.K. A wide-area damping controller considering network input and output delays and packet drop. IEEE Trans. Power Syst. 2017, 32, 166–176. [Google Scholar] [CrossRef]
- Ghosh, S.; Folly, K.A.; Patel, A. Synchronized versus non-synchronized feedback for speed-based wide-area pss: Effect of time-delay. IEEE Trans. Smart Grid 2018, 9, 3976–3985. [Google Scholar] [CrossRef]
- Yao, W.; Jiang, L.; Wen, J.; Wu, Q.; Cheng, S. Wide-area damping controller for power system interarea oscillations: A networked predictive control approach. IEEE Trans. Control Syst. Technol. 2015, 23, 27–36. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, G.; Rees, D. Networked predictive control systems based on the hammerstein model. IEEE Trans. Circuits Syst. II Express Briefs 2008, 55, 469–473. [Google Scholar] [CrossRef]
- Yu, X.; Jiang, J. Analysis and compensation of delays in ff h1 fieldbus control loop using model predictive control. IEEE Trans. Instrum. Meas. 2014, 63, 2432–2446. [Google Scholar] [CrossRef]
- Chaudhuri, N.R.; Ray, S.; Majumder, R.; Chaudhuri, B. A new approach to continuous latency compensation with adaptive phasor power oscillation damping controller (pod). IEEE Trans. Power Syst. 2010, 25, 939–946. [Google Scholar] [CrossRef]
- Sarkar, T.K.; Ji, Z.; Kim, K.; Medouri, A.; Salazar-Palma, M. A survey of various propagation models for mobile communication. IEEE Antennas Propag. Mag. 2003, 45, 51–82. [Google Scholar] [CrossRef]
- Huang, Z.; Schneider, K.; Nieplocha, J. Feasibility studies of applying kalman filter techniques to power system dynamic state estimation. In Proceedings of the 2007 International Power Engineering Conference (IPEC 2007), Singapore, 3–6 December 2007; pp. 376–382. [Google Scholar]
- Zhou, N.; Meng, D.; Lu, S. Estimation of the dynamic states of synchronous machines using an extended particle filter. IEEE Trans. Power Syst. 2013, 28, 4152–4161. [Google Scholar] [CrossRef]
- Zhao, J. Dynamic state estimation with model uncertainties using h∞ extended kalman filter. IEEE Trans. Power Syst. 2018, 33, 1099–1100. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.; Zhang, Y.; Guo, J.; Zhou, D. Wide Area Monitoring through Synchrophasor Measurement. In Smart Grid Handbook; Liu, C., McArthur, S., Lee, S., Eds.; Wiley: Hoboken, NJ, USA, 2016; pp. 1–18. [Google Scholar]
- Michiels, W.; Niculescu, S.I. Time-delay systems of neutral type. In Stability and Stabilization of Time-Delay Systems: An Eigenvalue-based Approach; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007; pp. 15–31. [Google Scholar]
- Milano, F.; Dassios, I. Small-Signal Stability Analysis for Non-Index 1 Hessenberg Form Systems of Delay Differential-Algebraic Equations. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 1521–1530. [Google Scholar] [CrossRef]
- Liu, M.; Dassios, I.; Milano, F. On the stability analysis of systems of neutral delay differential equations. Circuits Syst. Signal Process. 2019, 38, 1639–1653. [Google Scholar] [CrossRef]
- Liu, M.; Tzounas, G.; Milano, F. A model-independent delay compensation method for power systems. In Proceedings of the Milan PowerTech, Milano, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar]
- Milano, F. A Python-based software tool for power system analysis. In Proceedings of the IEEE PES General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Milano, F. Power System Modeling and Scripting; Springer: London, UK, 2010. [Google Scholar]
- Milano, F.; Ortega, Á. Converter-Interfaced Energy Storage Systems: Context, Modelling and Dynamic Analysis; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]


| Compensation Gain | PD | Predictor-Based |
|---|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Dassios, I.; Tzounas, G.; Milano, F. Model-Independent Derivative Control Delay Compensation Methods for Power Systems. Energies 2020, 13, 342. https://doi.org/10.3390/en13020342
Liu M, Dassios I, Tzounas G, Milano F. Model-Independent Derivative Control Delay Compensation Methods for Power Systems. Energies. 2020; 13(2):342. https://doi.org/10.3390/en13020342
Chicago/Turabian StyleLiu, Muyang, Ioannis Dassios, Georgios Tzounas, and Federico Milano. 2020. "Model-Independent Derivative Control Delay Compensation Methods for Power Systems" Energies 13, no. 2: 342. https://doi.org/10.3390/en13020342
APA StyleLiu, M., Dassios, I., Tzounas, G., & Milano, F. (2020). Model-Independent Derivative Control Delay Compensation Methods for Power Systems. Energies, 13(2), 342. https://doi.org/10.3390/en13020342








