Abstract
In this paper, energy management and control of a microgrid is developed through supervisor and adaptive neuro-fuzzy wavelet-based control controllers considering real weather patterns and load variations. The supervisory control is applied to the entire microgrid using lower–top level arrangements. The top-level generates the control signals considering the weather data patterns and load conditions, while the lower level controls the energy sources and power converters. The adaptive neuro-fuzzy wavelet-based controller is applied to the inverter. The new proposed wavelet-based controller improves the operation of the proposed microgrid as a result of the excellent localized characteristics of the wavelets. Simulations and comparison with other existing intelligent controllers, such as neuro-fuzzy controllers and fuzzy logic controllers, and classical PID controllers are used to present the improvements of the microgrid in terms of the power transfer, inverter output efficiency, load voltage frequency, and dynamic response.
1. Introduction
Distributed generation (DG) systems based on renewable energy sources (RES), such as solar, wind, biomass, and hydropower, which are increasing steadily across the globe, are important in the generation of clean energy. In DG, energy conversion systems are placed near to the end consumers and large units are replaced with smaller ones. DG enables lower active power losses and operational costs, increased operational performance, and increased energy efficiency of the power system. Power system regulators are turning towards RES-based DG systems, along with the conventional centralized generation systems [1].
In DG and microgrid systems, one of the most critical parts is the inverter, because of its extensive range of functions [2]. Their operation is standardized by many international industrial standards and requirements such as IEEE 929-2000, EN61000-3-2, U.S. National Electrical Code 690, and IEEE 1547. These standards describe some important parameters and properties of grid-coupled inverter, such as total harmonic distortion (THD), electromagnetic interference, voltage fluctuation, power quality, and power factor [3,4,5].
Owing to the expansion of DG and/or microgrid systems, many inverter designs and their control strategies have been published in the literature. For instance, fixed gain controllers (PI/PID) have been adopted by many researchers. For example, a PI controller with grid voltage feed-forward was used by the authors of [6,7], but some well-known drawbacks, such as a poor performance due to the integral action and the inability to track a sinusoidal signal, appeared in this method. These drawbacks have been addressed in the literature [8] by using a second order integrator. This approach is the most promising in terms of frequency synchronization, but the estimated frequency holds low frequency oscillations in case of DC offset being present in the grid voltage [9]. Similarly, in the literature [10], an adaptive control method was suggested using a direct current control scheme. The main drawback of the direct current control scheme is that there is no fixed systematic methodology to tune the PI controller, and therefore, an optimal direct current control is challenging to achieve.
Some researchers have preferred the applications of multilevel inverters (e.g., flying-capacitor and cascade H-Bridge neutral-point-clamped) in RES technologies [11,12,13,14]. However, the main problem of multilevel topologies is the unbalanced voltage between the capacitors across the DC link [15]. Similarly, numerous control strategies and algorithms on grid interactive inverters have been investigated and developed by different authors in past literature.
Some other techniques/controllers applied to inverters are predictive control [16,17], fuzzy control [18,19], sliding mode control [20], neural network (NN)-based control [21], and neuro-fuzzy (NF) [22]. All of the aforementioned techniques have their own advantages and drawbacks. For example, predictive control needs high computation efforts [23], while chattering limits the applications of the sliding mode control [24]. Fuzzy control has suffered of criticism for lacking a systematic strategy and a stability analysis technique. Similarly, in NN, each unit of the plant must be turned to produce control rules, and therefore its limitation is versatility [25]. Moreover, the NF method stays in the initial local minima during the search space [26]. This drawback in the existing NF controller motivates us to present a new controller based on the Jacobi wavelet. In the literature, many studies have shown that the use of a wavelet improves the performance of the NF network in RES [27,28,29,30,31,32,33,34,35,36].
Furthermore, an autonomous operation via distributed power sources improves its performance in terms of power sharing and voltage regulation. This operation can be obtained using energy management to supervise and control the power flow in the microgrid. For example, many authors have used different energy management systems for microgrids [37,38,39]. The authors of [37] controlled the microgrid via centralized management control, and therefore, the overall system could get away from communication when failure happened at a single location. The drawback of [38] was the absence of a countermeasure in the lower–top layers in its energy management strategy. Similarly, the researchers in [39] developed energy management of a microgrid using multiple-time optimization problems, but it could only give a day-ahead forecast, and power fluctuations and other related regulation schemes in the microgrid were not considered.
The main contributions of this research work are as follows:
(1) A supervisory energy management based on a two-level setting. The top-level controller determines set points for individual microgrid subsystems/components, i.e., a photovoltaic (PV), ultra-capacitor (UC), battery, and inverter, using weather statistics and load conditions. The lower level ensures that the top-level set points are accurately followed by the microgrid components. The operation of the microgrid is checked using real-world records of weather patterns and load fluctuations.
(2) A new adaptive controller based on the Jacobi wavelet neuro-fuzzy structure is developed for the grid coupled inverter, which yields a better THD, active and reactive power tracking, frequency, and efficiency than those achieved by other controllers that have appeared in the literature.
The rest of this research work is arranged as follows. The structure and control of the microgrid is given in Section 2. In Section 3, the supervisory algorithm is discussed. Section 4 provides the results and a comparison with the other existing intelligent and classical controllers. Finally, Section 5 draws the conclusions of this research.
2. Structure and Control of Microgrid
2.1. Structure of the System
Figure 1 illustrates the general structure of the proposed microgrid under analysis. It consists of a PV array, UC, and battery storage system. The PV array is capable of generating 261 kW under variable weather patterns and the UC/battery storage system are integrated for backup during excess power demand and as an energy storage system for surplus power. A DC–DC boost converter connects the PV array to the inverter. Similarly, two non-isolated buck boost converters connect the UC/battery to the DC bus, followed by the inverter. The inverter is controlled using a new wavelet-based adaptive controller. The adaptive-based controlled inverter is then coupled to the AC link at the grid and load. Energy management, power sharing, and transferring among PV, UC, and the battery with the rest of the microgrid are performed via energy management and supervisory control system (EMSCS).
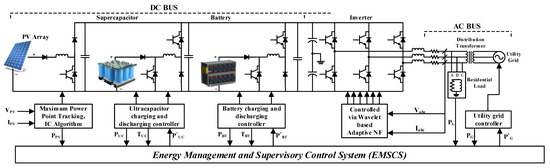
Figure 1.
Structure of the proposed microgrid.
2.2. Control of PV
The power of PV varies according to the weather patterns; therefore, its output is controlled by using an incremental conductance (IC) maximum power point tracking (MPPT) method, and is then regulated via a DC–DC boost converter, as illustrated in Figure 2. In PV, the optimal terminal voltage is determined by minimizing the MPPT error, which is shown as “e” in Figure 2, which is determined on a P/V curve through the IC method. The boost converter is controlled using PID controllers through the control of the duty cycle.
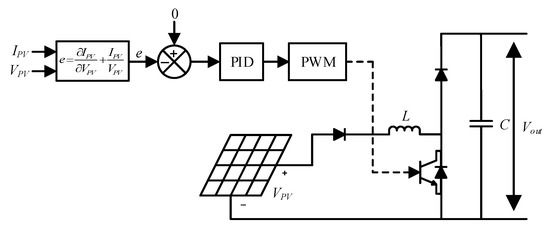
Figure 2.
Control of photovoltaic (PV).
2.3. Control of Ultra-Capacitor/Battery
Both the UC and battery are controlled through PIDs embedded in DC–DC buck-boost converters. The boost mode permits power flow from the UC and/or battery to the DC during power demand bus, and the buck mode is utilized to charge the UC and/or battery from the DC bus during surplus power. Another advantage of the UC/battery is to regulate the DC bus voltage during abrupt weather variations and load changes. The control diagrams of the UC and battery are illustrated in Figure 3 and Figure 4, respectively.
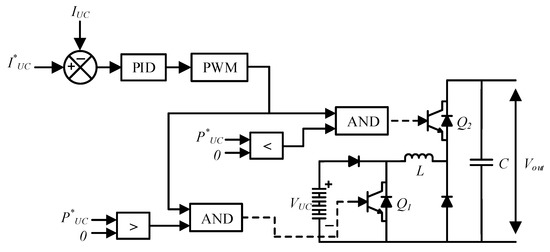
Figure 3.
Control of UC.
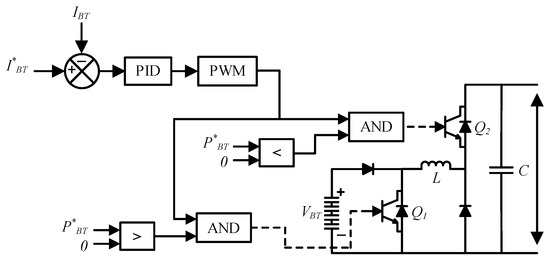
Figure 4.
Control of the battery.
2.4. Control of Inverter
Inverters are critical for injecting power from the DG or microgrid into the grid or grid-coupled load.
The control law for the proposed problem is written as follows:
where P and Q stand for the active and reactive powers, respectively. According to the control law, the amount of P and Q injected into the load and grid from the inverter must be done according to the desired powers defined to the controller, provided that the maximum efficiency () is obtained while keeping the power quality constraints, i.e., THD and frequency (f), according to the IEEE standards [3,4,5]. The value of the power quality constraints must be kept smaller in order to reduce the power losses in the system.
In this work, the inverter was controlled through two adaptive neuro-fuzzy Jacobi wavelet (ANFJW)-based controllers—one controller used for controlling the active power, and another for controlling the reactive power delivered by the inverter to the grid. During operation, both the P and Q generated by the plant (microgrid) were compared with the references for P and Q. These differences were provided to the respective ANFJW controllers. Both ANFJW controllers operated on the difference and generated the corresponding reference currents (id* for active power and iq* for reactive power). Finally, the inverter switching commands/signals were generated using hysteresis current control method as shown in Figure 5.
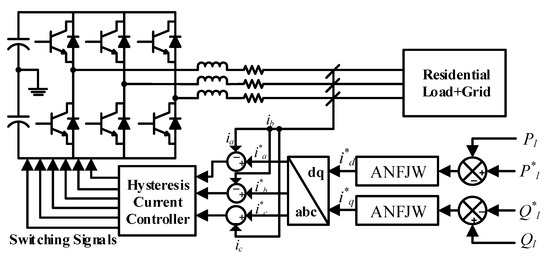
Figure 5.
Working of the proposed strategy.
Each controller was modelled in seven layers, as shown in Figure 6. The first three layers formed the antecedent part, and the next four layers formed the consequent part of the ANFJW controller. The number of inputs in the first layer was equivalent to the number of nodes, which were used for further distribution as inputs.
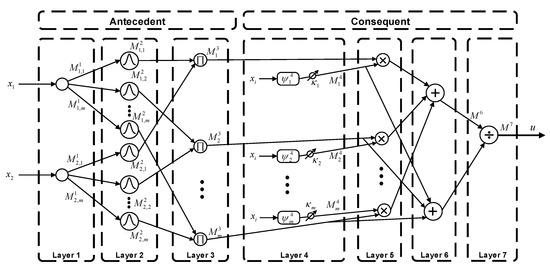
Figure 6.
Structure of the adaptive neuro-fuzzy Jacobi wavelet (ANFJW) controller.
and describe the input and output of a node in kth layer, respectively.
- First Layer:
It combines the numbers of the input variables, and are then transferred to the next layer by the nodes from the first layer, which is written as follows:
where i = 1, 2, …, m and k stands for the number of nodes and iteration, respectively.
- Second Layer:
In this layer, the fuzzy system receives the linguistic terms and their degree of membership of each input. The Gaussian membership function (GMF) is used for computing the linguistic terms of each input.
where and denote the center and variance of GMF, respectively.
- Third Layer:
In this layer, the product of membership function is performed, where the Min operator is used to find the output value.
- Fourth Layer:
The Jacobi wavelet function is used in this layer, which is written as follows:
where
here,, where the input of this layer is , and the output of this layer is written as follows:
The main objective is to reduce the error between the reference power and desire power. The proposed controller works on the error, e, which is the difference between the reference power and desire power, as illustrated in Figure 7. The proposed control strategy processes the error, and it is written as follows:
Figure 7.
Working of the proposed strategy.
- Fifth Layer:
In this layer, the output of the antecedent and consequents parts is multiplied, and then added for each input.
- Sixth Layer:
The summation of rules (third layer output) is performed in this layer.
- Seven Layer:
In this layer, the output of ANFJW is calculated as follows:
This output is used in the duty cycle to generate the control commands to the switches of the inverter.
Below, it is explained how the parameters of ANFJW controller are updated. The output of the proposed controller is given as follows:
and the objective function to be minimized is given as follows:
The parameters to be updated are the following:
These parameters are updated online through the gradient back propagation method. The gradient-based update equations are given as follows:
where e = yd − y
Now, for simplification, , and is evaluated using the chain rule. The updated equations are written as follows:
By calculating the partial derivative for the individual parameters, it is obtained as follows:
where
So, Equation (31) becomes:
Similarly,
Using the values of Equations (20), (33), and (34) in Equations (25)–(27), the following final updated equations are obtained.
3. Energy Management and Supervisory Control System
A supervisory control approach was designed to provide the required power demand during the day and after sunset by using the proposed algorithm, as illustrated in Figure 8.
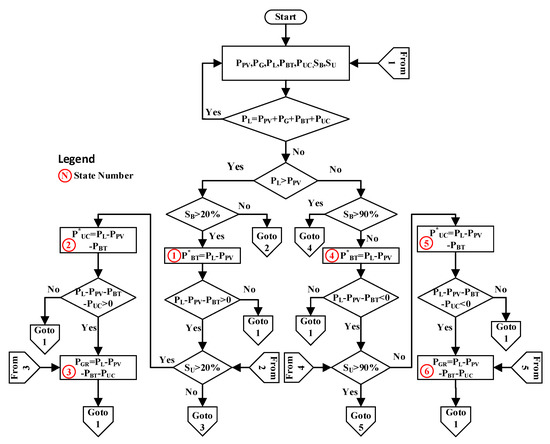
Figure 8.
Flowchart of the energy management and supervisory control system (EMSCS).
The proposed supervisory control system controls the subsystems (PV, UC, battery, and power converters), as well as the whole microgrid. According to the implemented algorithm, the net load demand must be satisfied from the generation of the PV array. If PV cannot satisfy the net demand, then battery bank will supply the remaining power, if its charge level is sufficient, i.e., above 20% (state 1). If the PV and battery bank cannot provide the total demand, then the remaining power will be taken from the SC if its charge level is above 20% (state 2), followed by the utility grid (state 3). Similarly, if PV generates more power than the demand, the remaining power will be used to charge the battery and then the SC, if their states of charges are below 90% (state 4 and state 5). If the battery and SC are charged, then the remaining power will be transferred to the public grid (state 6).
The EMSCS layer power provides the required control signals to the power converters connected to the inputs/outputs of the components used in the microgrid. The descriptions of the parameters are defined in Table 1.

Table 1.
Inputs/outputs of the proposed EMSCS.
The working of the algorithm is discussed as below.
- All of the control signals are generated, i.e., PPV, PG, PL, PB, PU, SB, and SU.
- Check , go to 1 if this condition is true, and if not then follow next step.
- Check PL > , if it is true, go to step 9, and if not then check the next condition.
- Check SB > 20%, if it is true, then discharge the battery, and go to next step, otherwise go to step 2.
- Check the condition , if this is true, then go to the next step, otherwise go to step 6.
- Check SU > 20%, if it is true, then discharge the UC, and go to the next step, otherwise go to step 8.
- Check the condition , if it is true, then go to the next step, otherwise go to step 1.
- Using all of the remaining deficient power reference to the grid and go to step 1.
- Check SB > 90%, if it is not true, then charge the battery and go to the next step, otherwise go to step 11.
- Check the condition , if true, then go to the next step, otherwise go to step 1.
- Check SU > 90%, if it is not true, then charge the UC and go to the next step, otherwise go to step 13.
- Check the condition , if true, then go to the next step, otherwise step 1.
- Provide all of the net surplus power to the utility grid and go to step 1.
4. Simulations
The proposed microgrid was simulated for a complete full day under real weather patterns, i.e., ambient temperature (°C) and solar irradiance (W/m2), taken at Islamabad, Pakistan. Both parameters were recorded on an hourly basis, as presented in Figure 9. The intensity of irradiance fluctuated during the day, depending on the sunrise and sunset. From Figure 9, the sun appeared at 07:00 a.m. and set at 17:20 p.m. The average solar irradiance during the daytime was 990 (W/m2). Likewise, the average temperature during the daytime reached 40 °C, while at night, it went down to 19 °C.
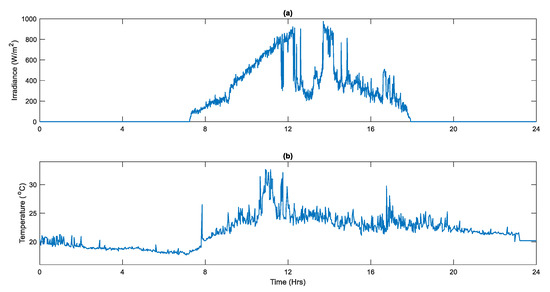
Figure 9.
Weather data: (a) irradiance and (b) temperature.
Figure 10 illustrates the power generated by the PV (denoted as violet), battery (denoted as red) main inverter (denoted as dark goldenrod), UC (denoted as light green), utility grid (denoted as black), and total demand (denoted as light blue). In order to explain Figure 10, it is divided into six states, as indicated in the flow chart (Figure 8). From t = 00:00 to 07:10 a.m., the PV output power was zero because of the nonappearance of sun irradiance. The overall demand was applied on the battery system. During this interval, the proposed EMSCS checked the state of charge (SoC) of the battery, and as its SoC was greater than 20%, the battery provided the required net power (around 150 kW). The battery SoC was reduced to 68%, as shown in Figure 11. The EMSCS was operating in state 1. At t = 07:10 to 09:00 a.m., the PV system started producing power, but it was still not enough to overcome the demand. Meanwhile, the output power of the PV started to increase. At the end of the interval, the PV and battery provided 90 kW each with the battery SoC at 62%. The EMSCS was still operating in state 1. At t = 09:00 to 09:48 a.m., because of the slow response time of the battery, the cumulative power supply (battery (52 kW) + PV system (179 kW)) exceeded the power demand (198 kW). Therefore, the UC started charging using 33 kW of power when the SoC went from to 84% from 73%, and the EMSCS was shifted to state 5.
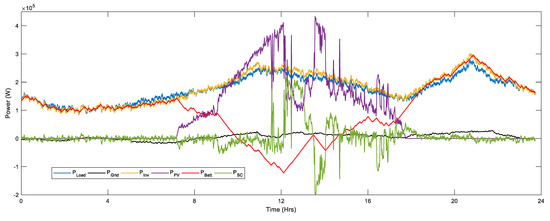
Figure 10.
Power exchange and sharing among energy sources.
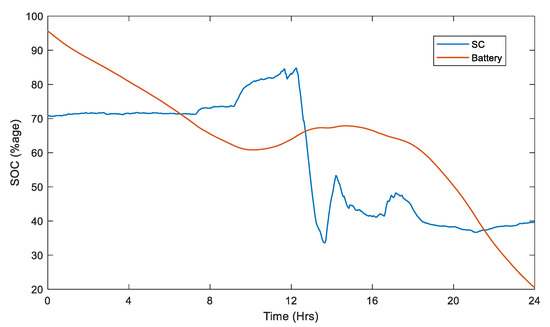
Figure 11.
States of charge (SoCs) of the ultra-capacitor (UC) and battery.
At t = 09:48 to 11:30 a.m., the PV not only provided sufficient power to the load, but also charged the battery and UC. In this interval, the EMSCS was in states 4 and 5. At t = 11:30 to 11:39 a.m., 12:10 to 13:27 p.m., and 14:03 to 14:40 p.m., the PV output power suddenly dropped due to partially clouded conditions. In this crucial time, the UC assisted the microgrid and fulfilled the power gap with slight support from the grid station. In this interval, the EMSCS rapidly shifted to states 2 and 3. At t = 14:40 to 17:36 p.m., the PV output power started decreasing because of the evening time. The battery could fulfil the power deficiency and kept the EMSCS in state 1. At t =17:36 to 18:15 p.m., the battery, UC, and grid station provided backup to the microgrid because of the deficient power. The EMSCS shifted between states 1, 2, and 3. Whereas at t= 18:15 to 24:00 p.m., with no PV power and also because of the non-peak hours, the grid and battery fulfilled the load demand, and the battery SoC dropped to 21%. In this interval, the EMSCS moved between states 1 and 3. The operating states for 24 h are shown in Figure 12. In this manner, the power exchange and sharing among PV, battery, UC, utility grid, and domestic load happened for 24 h under EMSCS.
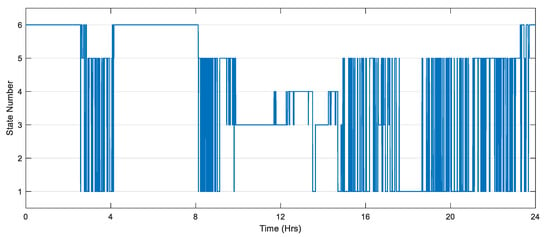
Figure 12.
Operating states.
For better power quality and power flow from the DC link to the rest of the system, the inverter was controlled via ANFJW controllers. The results of the proposed ANFJW controllers were compared with the existing intelligent controllers, such as NFC and fuzzy logic controller (FLC), as well as the classical controller (i.e., PID), using the same weather and load conditions. Figure 13 shows the performance of the inverter (active power) for the different controllers in terms of power transfer. The load condition had two peaks of 275 kW and 307 kW at t = 11:00 a.m. and 21:00 p.m., respectively. The zoomed figures show the performance of the difference controllers in detail. It can be clearly noticed from the zoomed figures (Figure 13) that the proposed controller, ANFJW (denoted as red), and reference signal (donated as dashed-blue) superimposed each other, while the other controllers also tried to track the reference signal, but were unable to because of overshoots. Similarly, Figure 14 gives the performance of the inverter in terms of the reactive power transfer. For instance, from the zoomed portion (i.e., at 04:45 to 04:48 a.m.) in Figure 14, the proposed controller tracked the reference power very quickly, while the other controllers took some time with the overshoots. The same performance can also be seen at 19:57 to 20:03 p.m. in the zoomed portion. Hence, the proposed ANFJW controllers show a better performance at different intervals for both real and reactive power transfer.
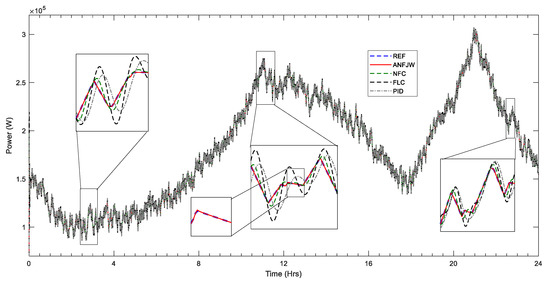
Figure 13.
Output real power comparison at different intervals.
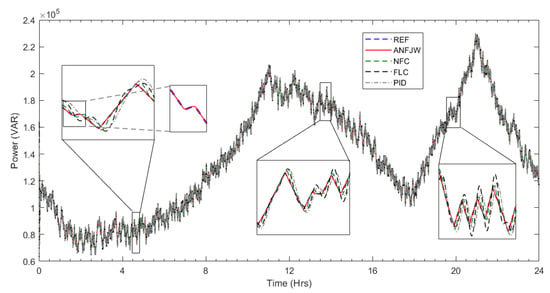
Figure 14.
Output reactive power comparison at different intervals.
Furthermore, the power quality analyses in terms of the THD and frequency of all of controllers was performed and are illustrated in Figure 15 and Figure 16, respectively. According to IEEE standards, the standard limits for frequency and THD are ±0.8% and 5%, respectively. In this work, the operating load voltage RMS and frequency were 440 V and 50 Hz, respectively. The THD shown in Figure 15 is small with the proposed controller, which is around 2.37%. Similarly, the change in frequency was below 0.02%, as it can be seen at different intervals in the zoomed windows in Figure 16.
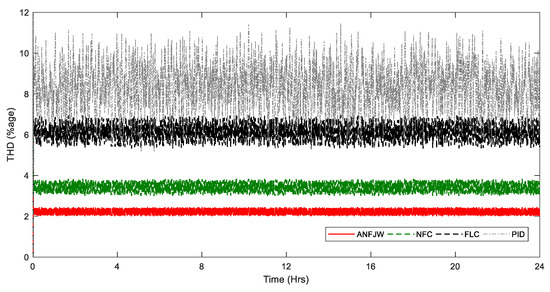
Figure 15.
Total harmonic distortion (THD) comparison.
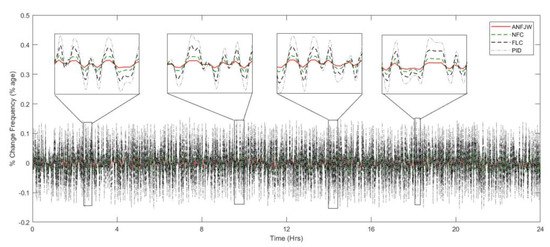
Figure 16.
Comparison of change in frequency.
To show further better the performance, the efficiency of the inverter for all controllers using Equation (1) was calculated for 24 h and is shown in Figure 17. The real and reactive power transfer efficiencies of the inverter with the ANFJW controllers was greater, i.e., 99.05% and 99.08%, followed by NFC, FLC, and then PID.
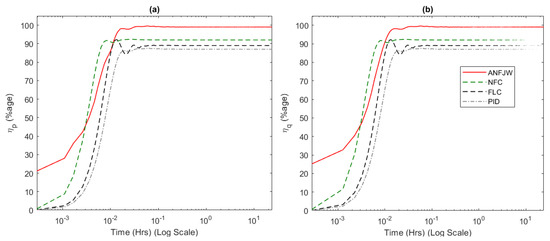
Figure 17.
Power efficiency comparison of different controllers: (a) real power and (b) reactive power.
For further analysis, the dynamic performance of all of the controllers through the index parameters, i.e., integral absolute error (IAE), integral square error (ISE), integral time absolute error (ITAE), integral time square error (ITSE), and mean relative error (MRE), under the same operating conditions, were calculated using Equations (38)–(41) for active power, and using Equations (42)–(45) for reactive power, and are illustrated in Figure 18 and Figure 19, respectively. All of the index parameters were much smaller in the case of the proposed controller, which showed a superior dynamic performance. All of the comparisons are summarized in Table 2.
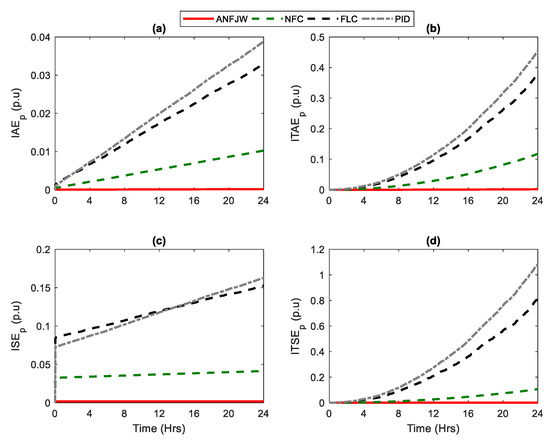
Figure 18.
Dynamic performance comparison using active power: (a) integral absolute error (IAE), (b) integral time absolute error (ITAE), (c) integral square error (ISE), and (d) integral time square error (ITSE).
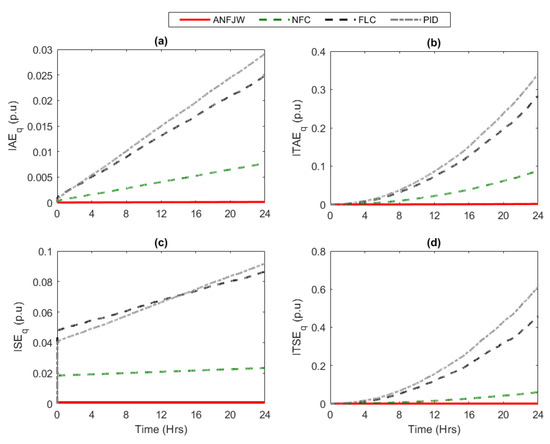
Figure 19.
Dynamic performance comparison using reactive power: (a) IAE, (b) ITAE, (c) ISE, and (d) ITSE.

Table 2.
Comparison of efficiencies and dynamic response.
5. Conclusions
This paper presented a novel improved adaptive NFC of inverter and supervisory energy management of a microgrid. The improvement in the existing NFC was performed by the integration of the Jacobi wavelet. Because of the excellent time-localized behavior of the Jacobi wavelet, the proposed controller did not stop in the first local minima, but it searched for the optimal minima. This yielded excellent results in terms of power transfer, inverter output efficiency, and load voltage frequency. The EMSCS controlled the individual components as well as the entire system to ensure the following: (1) maximize output power, (2) appropriate sharing of UC/battery power and energy sources, and (3) continuity of power for a 24 h power supply with reliability and lessening the differences in output power under unfavorable weather conditions and inadequate storage.
Author Contributions
Conceptualization, T.K. and S.Z.H.; methodology, T.K., M.K., and S.Z.H.; software, T.K.; validation, T.K. and S.Z.H.; formal analysis, M.K., V.S.P., and L.M.F.-R.; investigation, T.K. and M.K.; resources, S.Z.H.; data curation, S.Z.H.; writing (original draft preparation), T.K., M.K., and S.Z.H.; writing (review and editing), V.S.P. and L.M.F.-R.; visualization, T.K. and S.Z.H.; supervision, M.K., V.S.P., and L.M.F.-R.; project administration, M.K., V.S.P., and L.M.F.-R.; funding acquisition, M.K., V.S.P., and L.M.F.-R. All authors have read and agreed to the published version of the manuscript.
Funding
The work of Murat Karabacak and Tariq Kamal is sponsored by the Scientific and Technological Research Council of Turkey under project number 5190011. The work of Vedran S. Perić is supported by the Bavarian Government and Deutsche Forschungsgemeinschaft (DFG) under project number 350746631. The work of Luis M. Fernández-Ramírez and Tariq Kamal is sponsored by the Spanish Ministry of Science, Innovation, and Universities under project number RTI2018-095720-B-C32.
Acknowledgments
Authors are thankful to all organizations stated in the funding portion.
Conflicts of Interest
There is no conflict of interest.
Abbreviations
| ANFJW | Adaptive neuro-fuzzy Jacobi wavelet |
| EMSCS | Energy management and supervisory control system |
| FLC | Fuzzy logic controller |
| GMF | Gaussian membership function |
| IAE | Integral absolute error |
| IC | Incremental conductance |
| ISE | Integral square error |
| ITAE | Integral time absolute error |
| ITSE | Integral time square error |
| MPPT | Maximum power point tracking |
| MRE | Mean relative error |
| NF | Neuro-fuzzy |
| NN | Neural network |
| PV | Photovoltaic |
| RES | Renewable energy sources |
| THD | Total harmonic distortion |
| UC | Ultra-capacitor |
References
- Ozdemir, S.; Kaplan, O.; Sefa, I.; Altin, N. Fuzzy PI controlled inverter for grid interactive renewable energy systems. IET Renew. Power Gener. 2015, 9, 729–738. [Google Scholar]
- Hossain, M.; Pota, H.; Issa, W.; Hossain, M.; Hossain, M.A.; Pota, H.R.; Issa, W.; Hossain, M.J. Overview of AC Microgrid Controls with Inverter-Interfaced Generations. Energies 2017, 10, 1300. [Google Scholar] [CrossRef]
- Altin, N.; Ozdemir, S. Three-phase three-level grid interactive inverter with fuzzy logic based maximum power point tracking controller. Energy Convers. Manag. 2013, 69, 17–26. [Google Scholar] [CrossRef]
- Alsayari, N.; Chilipi, R.; Al Hosani, K.; Almaskari, F. Grid synchronization and control of distributed generation unit with flexible load compensation capabilities using multi-output LMS-filter. Int. J. Electr. Power Energy Syst. 2017, 93, 253–265. [Google Scholar] [CrossRef]
- Al Sayari, N.; Chilipi, R.; Barara, M. An adaptive control algorithm for grid-interfacing inverters in renewable energy based distributed generation systems. Energy Convers. Manag. 2016, 111, 443–452. [Google Scholar] [CrossRef]
- Cecati, C.; Dell’Aquila, A.; Liserre, M.; Monopoli, V.G. Design of H-bridge multilevel active rectifier for traction systems. IEEE Trans. Ind. Appl. 2003, 39, 1541–1550. [Google Scholar] [CrossRef]
- Kazźmierkowski, M.P.; Krishnan, R.; Blaabjerg, F. Control in Power Electronics: Selected Problems; Academic Press: San Diego, CA, USA, 2002; ISBN 9780080490786. [Google Scholar]
- Yuan, X.; Merk, W.; Stemmler, H.; Allmeling, J. Stationary-frame generalized integrators for current control of active power filters with zero steady-state error for current harmonics of concern under unbalanced and distorted operating conditions. IEEE Trans. Ind. Appl. 2002, 38, 523–532. [Google Scholar] [CrossRef]
- Ren, X.; Lyu, Z.; Li, D.; Zhang, Z.; Zhang, S. Synchronization signal extraction method based on enhanced DSSOGI-FLL in power grid distortion. Syst. Sci. Control Eng. 2018, 6, 305–313. [Google Scholar] [CrossRef]
- Li, S.; Haskew, T.A.; Hong, Y.K.; Xu, L. Direct-current vector control of three-phase grid-connected rectifier-inverter. Electr. Power Syst. Res. 2011, 81, 357–366. [Google Scholar] [CrossRef]
- Sędłak, M.; Styński, S.; Kaźmierkowski, M.P.; Malinowski, M. Three-level four-leg flying capacitor converter for renewable energy sources. Przeglad Elektrotechniczny 2012, 88, 6–11. [Google Scholar]
- Chandran, B.P.; Selvakumar, A.I.; Mathew, F.M. Integrating multilevel converters application on renewable energy sources—A survey. J. Renew. Sustain. Energy 2018, 10, 065502. [Google Scholar] [CrossRef]
- Verdugo, C.; Kouro, S.; Rojas, C.A.; Perez, M.A.; Meynard, T.; Malinowski, M. Five-Level T-type Cascade Converter for Rooftop Grid-Connected Photovoltaic Systems. Energies 2019, 12, 1743. [Google Scholar] [CrossRef]
- Mishra, N.; Singh, B. Solar PV Grid Interfaced System with Neutral Point Clamped Converter for Power Quality Improvement. J. Inst. Eng. Ser. B 2018, 99, 605–612. [Google Scholar] [CrossRef]
- Carrasco, J.M.; Franquelo, L.G.; Bialasiewicz, J.T.; Galvan, E.; PortilloGuisado, R.C.; Prats, M.A.M.; Leon, J.I.; Moreno-Alfonso, N. Power-Electronic Systems for the Grid Integration of Renewable Energy Sources: A Survey. IEEE Trans. Ind. Electron. 2006, 53, 1002–1016. [Google Scholar] [CrossRef]
- Shadmand, M.B.; Li, X.; Balog, R.S.; Rub, H.A. Model predictive control of grid-tied photovoltaic systems: Maximum power point tracking and decoupled power control. In Proceedings of the 2015 First Workshop on Smart Grid and Renewable Energy (SGRE), Doha, Qatar, 22–23 March 2015; pp. 1–6. [Google Scholar]
- Hu, J.; Zhu, J.; Dorrell, D.G. Model-predictive control of grid-connected inverters for PV systems with flexible power regulation and switching frequency reduction. IEEE Trans. Ind. Appl. 2015, 51, 587–594. [Google Scholar] [CrossRef]
- Cecati, C.; Ciancetta, F.; Siano, P. A Multilevel Inverter for Photovoltaic Systems with Fuzzy Logic Control. IEEE Trans. Ind. Electron. 2010, 57, 4115–4125. [Google Scholar] [CrossRef]
- Hannan, M.A.; Ghani, Z.A.; Hoque, M.M.; Ker, P.J.; Hussain, A.; Mohamed, A. Fuzzy Logic Inverter Controller in Photovoltaic Applications: Issues and Recommendations. IEEE Access 2019, 7, 24934–24955. [Google Scholar] [CrossRef]
- Mao, Y.; Yang, Y. Backstepping sliding mode control of grid-connected inverters. Int. J. Electron. Lett. 2017, 5, 314–326. [Google Scholar] [CrossRef]
- Sun, Y.; Li, S.; Lin, B.; Fu, X.; Ramezani, M.; Jaithwa, I. Artificial Neural Network for Control and Grid Integration of Residential Solar Photovoltaic Systems. IEEE Trans. Sustain. Energy 2017, 8, 1484–1495. [Google Scholar] [CrossRef]
- Altin, N.; Sefa, İ. dSPACE based adaptive neuro-fuzzy controller of grid interactive inverter. Energy Convers. Manag. 2012, 56, 130–139. [Google Scholar] [CrossRef]
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Carrasco, J.M.; Martinez, O.; Rodriguez, J.; Cortes, P.; Kouro, S. Model Predictive Control with constant switching frequency using a Discrete Space Vector Modulation with virtual state vectors. In Proceedings of the 2009 IEEE International Conference on Industrial Technology, Gippsland, VIC, Australia, 10–13 February 2009; pp. 1–6. [Google Scholar]
- Lee, H.; Utkin, V.I. Chattering suppression methods in sliding mode control systems. Annu. Rev. Control 2007, 31, 179–188. [Google Scholar] [CrossRef]
- Liu, Y.-H.; Liu, C.-L.; Huang, J.-W.; Chen, J.-H. Neural-network-based maximum power point tracking methods for photovoltaic systems operating under fast changing environments. Sol. Energy 2013, 89, 42–53. [Google Scholar] [CrossRef]
- Badar, R.; Khan, L. Adaptive Neuro Fuzzy Wavelet Based SSSC Damping Control Paradigm. In Proceedings of the 2012 10th International Conference on Frontiers of Information Technology, Islamabad, Pakistan, 17–19 December 2012; pp. 101–106. [Google Scholar]
- Kamal, T.; Karabacak, M.; Hassan, S.Z.; Fernández-Ramírez, L.M.; Roasto, I.; Khan, L. An indirect adaptive control paradigm for wind generation systems. In Advanced Control and Optimization Paradigms for Wind Energy Systems; Springer: Singapore, 2019; pp. 235–257. [Google Scholar]
- Hassan, S.; Li, H.; Kamal, T.; Arifoğlu, U.; Mumtaz, S.; Khan, L. Neuro-Fuzzy Wavelet Based Adaptive MPPT Algorithm for Photovoltaic Systems. Energies 2017, 10, 394. [Google Scholar] [CrossRef]
- Banakar, A.; Azeem, M.F. Artificial wavelet neural network and its application in neuro-fuzzy models. Appl. Soft Comput. J. 2008, 8, 1463–1485. [Google Scholar] [CrossRef]
- Yusuf, O.; Yilmaz, S. An Adaptive Fuzzy Wavelet Network with Gradient Learning for Nonlinear Function Approximation. J. Intell. Syst. 2014, 23, 201–212. [Google Scholar]
- Hassan, S.Z.; Kamal, T.; Mumtaz, S.; Khan, L. An online self recurrent direct adaptive neuro-fuzzy wavelet based control of photovoltaic systems. In Solar Photovoltaic Power Plants. Advanced Control and Optimization Techniques; Springer: Singapore, 2019; pp. 233–250. [Google Scholar]
- Kumar, S.A.; Subathra, M.S.P.; Kumar, N.M.; Malvoni, M.; Sairamya, N.J.; George, S.T.; Suviseshamuthu, E.S.; Chopra, S.S. A Novel Islanding Detection Technique for a Resilient Photovoltaic-Based Distributed Power Generation System Using a Tunable-Q Wavelet Transform and an Artificial Neural Network. Energies 2020, 13, 4238. [Google Scholar] [CrossRef]
- Frizzo Stefenon, S.; Zanetti Freire, R.; dos Santos Coelho, L.; Meyer, L.H.; Bartnik Grebogi, R.; Gouvêa Buratto, W.; Nied, A. Electrical Insulator Fault Forecasting Based on a Wavelet Neuro-Fuzzy System. Energies 2020, 13, 484. [Google Scholar] [CrossRef]
- Zhu, H.; Li, X.; Sun, Q.; Nie, L.; Yao, J.; Zhao, G. A Power Prediction Method for Photovoltaic Power Plant Based on Wavelet Decomposition and Artificial Neural Networks. Energies 2016, 9, 11. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Campilongo, S.; Ficarella, A.; Congedo, P.M. Comparison Between Wind Power Prediction Models Based on Wavelet Decomposition with Least-Squares Support Vector Machine (LS-SVM) and Artificial Neural Network (ANN). Energies 2014, 7, 5251–5272. [Google Scholar] [CrossRef]
- Kamal, T.; Karabacak, M.; Blaabjerg, F.; Hassan, S.Z.; Fernández-Ramírez, L.M. A Novel Lyapunov Stable Higher Order B-spline Online Adaptive Control Paradigm of Photovoltaic Systems. Sol. Energy 2019, 194, 530–540. [Google Scholar] [CrossRef]
- Tan, K.T.; So, P.L.; Chu, Y.C.; Chen, M.Z.Q. Coordinated Control and Energy Management of Distributed Generation Inverters in a Microgrid. IEEE Trans. Power Deliv. 2013, 28, 704–713. [Google Scholar] [CrossRef]
- Zhu, D.; Yang, R.; Hug-Glanzmann, G. Managing microgrids with intermittent resources: A two-layer multi-step optimal control approach. In Proceedings of the North American Power Symposium 2010, Arlington, TX, USA, 26–28 September 2010. [Google Scholar]
- Chen, C.; Duan, S.; Cai, T.; Liu, B.; Hu, G. Optimal allocation and economic analysis of energy storage system in microgrids. IEEE Trans. Power Electron. 2011, 26, 2762–2773. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).