Solution to the Economic Emission Dispatch Problem Using Numerical Polynomial Homotopy Continuation

Abstract

The economic emission dispatch (EED) is a highly constrained nonlinear multiobjective optimization problem with a convex (or nonconvex) solution space. These characteristics and constraints make the EED a difficult problem to solve. Several approaches for a solution have been proposed, such as deterministic techniques, stochastic techniques, or a combination of both. This work presents the use of an algebraic (deterministic) technique, the numerical polynomial homotopy continuation (NPHC) method, to solve the EED problem. A comparison with the sequential quadratic programming (SQP) algorithm and the nondominated sorting genetic algorithm II (NSGA-II) is also presented. Results show that the NPHC algorithm finds all the roots (solutions) of the problem starting from any initial point and assures an accurate solution with a good convergence time. In addition, the NPHC algorithm provides a more accurate solution than the SQP algorithm and the NSGA-II.

1. Introduction

Power dispatch is a complicated task for the energy industry because a highly variable and unpredictable load demand from the customers needs to be satisfied using the most suitable (less expensive) mix of producers [1,2]. The available producers use different types of fuel (including fossil and renewable energy sources), have different capacities, have different efficiencies, and there is the need to decide whether to operate them at full- or part-load [3,4]. In addition, the highest percentage of electricity is generated using fossil fuels, which increases the problem of pollutant emissions to the environment, of which CO₂, SO₂, and NO_x are of most concern [5,6]. Thus, the goal of the energy production industry is to simultaneously minimize both, fuel costs and emissions to the environment [7].

Fuel costs and emissions to the environment are objectives competing with each other; that is, the use of a cheap coal-fired power plant produces high amounts of emissions to the environment, and the use of a clean natural gas power plant is expensive to operate [8,9]. Thus, the optimization problem is formulated to be multiobjective with competing and non-commensurable objectives, in which a set of optimum producer configurations is obtained [10]. The problem can be solved using a fixed load demand (static economic emission dispatch, SEED) [11], or using a variable load demand (dynamic economic emission dispatch DEED) [12]. The SEED has the limitation that it does not consider the look ahead variations of the load demand as well as the dynamic behavior of the producers, something which is fully considered in the DEED. The characteristics of the producers are modeled by considering linear/nonlinear [11,13] or smooth/nonsmooth [11,14,15] objective functions, and by including valve point effects [12], ramp rate limits [16], generation limits [17], prohibited operating zones [18], spinning reserve [13], among others. These characteristics may turn the problem convex or nonconvex [11,18,19].

Three main different approaches are commonly used to solve the economic emission dispatch problem, i.e., deterministic techniques, stochastic techniques, and combinations of these two techniques. Deterministic techniques [3,4,11,15,20] have the advantage that can solve large scale systems with good accuracy [15,20] in a short convergence time [12,15]. However, these techniques can get stuck at local optimum points easily, are very sensitive to the starting point [21,22], and have difficulties with solving nonconvex problems as well as those with nonsmooth objective functions [21,23]. Stochastic techniques have the advantage that can solve nonconvex problems and those with nonsmooth objective functions [14,16,17,18,24,25,26,27,28,29,30]. However, these techniques find a solution close to the Pareto set only [31], as opposed to the exact solution [14,16], and require a very long time of computation, especially when dealing with large problems [1,15,24], and the control parameters and diversity of the population introduce several degrees of freedom to the solution approach [14,15]. Methods that use a combination of mathematical programming and artificial intelligent techniques use the best features of both, and have proven to be good methods for the solution of complex problems [23,32]; however, the number of operations and its associated computational burden are still areas of improvement.

The Numerical Polynomial Homotopy Continuation (NPHC) method is an analytical (deterministic) approach based on a combination of the Homotopy Analysis (HA) method and the fundamental theorem of algebra. The NPHC method finds all possible solutions, even the isolated ones [33], of a system of non-linear equations, i.e., algebraic, differential, partial differential, etc., or a combination of them [34]. This method assures convergence and the finding of the exact solution independently of the initial point and the constraints associated with a variety of parameters that affect the system [35,36]. The NPHC method has been applied to solve problems in physics and mathematics such as in industrial robotics [37], experimental dynamics [38], topology [39], high energy physics [40,41], among others [42,43,44].

To the best knowledge of the authors, the NPHC method has been used in power engineering to solve voltage instabilities [45] and power flow problems [46] only. The novelty of the work presented here is the use of the NPHC method to solve the economic emission dispatch problem, which deals with the combined economic and environmental dispatch of a power network. In addition, the solution of the NPHC algorithm is compared with the solutions of a Sequential Quadratic Programming (SQP) algorithm [47] and a Nondominated Sorting Genetic Algorithm II (NSGA-II) [48].

The remainder of this paper is organized as follows: Section 2 presents a description of the problem; Section 3 presents a description of the NPHC method; Section 4 presents the results and discussion of the findings; and finally Section 5 concludes the paper.

2. Problem Description

2.1. Principle of Multiobjective Optimization

The multiobjective optimization problem is formulated as [24]

Minimize:

$$F\left(X\right)=\{f_1\left(X\right),f_2\left(X\right),\dots ,f_M\left(X\right)\}$$

(1)

with respect to nonnegative X, and subject to:

$$g_l\left(X\right)=0\mathrm{for}\mathrm{all}l$$

(2)

$$h_k\left(X\right)\le 0\mathrm{for}\mathrm{all}k$$

(3)

where $F=\left\{f_m\right\}$ is the set of objective functions and $M\in {\mathbb{Z}}^{+}$, $X=\left\{x_i\right\}$ is the set of decision variables, $g_l$ are the equality constraints, and $h_k$ are the inequality constraints.

2.2. Economic Emission Dispatch Problem

The economic emission dispatch (EED) problem is expressed as a nonlinear constrained multiobjective optimization problem with competing and non-commensurable objectives. Mathematically the problem is formulated as [24,49];

Minimize:

$$f_m=\sum _{i=1}^3{a}_{i,m}+b_{i,m}{x}_i+c_{i,m}{x}_i^2,m=1,\dots ,3$$

(4)

with respect to nonnegative $x_i$, and subject to

$$\sum _{i=1}^3{x}_i-D-L=0$$

(5)

$$x_i^{\min }\le x_i\le x_i^{\max },i=1,\dots ,3$$

(6)

Equation (4) represents the objective functions, where the first objective function ($m=1$) corresponds to the total fuel cost ($/hr), the second objective function ($m=2$) corresponds to the total SO₂ emissions (ton/hr), and the third objective function ($m=3$) corresponds to the total NO_x emissions (ton/hr); $x_i$ is the real power generated by each producer; and $a_{i,m}$, $b_{i,m}$, and $c_{i,m}$ are real non-negative constants particular to each producer which allow the model to account for the part-load behavior of the producers and to maintain the convexity of the objective functions. Equation (5) is the equality constraint which represents the real power balance, where D is the fixed load demand and L the real power flow losses in the transmission lines given as

$$L=X\mathbf{B}{X}^T$$

(7)

where $\mathbf{B}$ is the transmission loss matrix and $X=\left[x_1{x}_2{x}_3\right]$ is the row vector formed by the real power generated by the producers. Equation (6) is the inequality constraint, which represents the generation limits of the producers.

The values of the characteristics of the producers, the load demand, and the transmission loss matrix are obtained from [49].

3. Numerical Polynomial Homotopy Continuation Formulation

3.1. Description of the NPHC Method

The NPHC method [50,51] aims to find all the roots (real and imaginary) of a system of N multivariate polynomial equations $P\left(X\right)=\left\{p_n\left(X\right)\right\}$ in N variables $X=\left\{x_n\right\}$, which has isolated solutions.

For the solution of the problem, an upper bound on the number of solutions of this system is established using the Classical Bézout Theorem. Then, the homotopy is constructed as

$$H(X,\theta )=\sigma (1-\theta )Q\left(X\right)+\theta P\left(X\right)=0$$

(8)

where $\sigma$ is a convergence parameter, $\theta \in [0,1)$ is the tracking parameter, and $Q\left(X\right)$ is a system of polynomial equations (start system) from which the roots (solutions) are known and selected using the Classical Bézout Bound (CBB) at $H(X,0)=Q\left(X\right)=0$, such as

$$Q\left(X\right)=\left(\begin{array}{c}{x}_1^{q_1}-1\\ x_2^{q_2}-1\\ ⋮\\ x_N^{q_N}-1\end{array}\right)=0$$

(9)

which has a maximum number of ${\prod }_{n=1}^N{q}_n$ solutions in ${\mathbb{C}}^N$, where $q_n$ is the degree of the n-th polynomial of $P\left(X\right)$ [46]. Finally, the paths corresponding to all the solutions of the system are tracked through all the solution space starting from $H(X,0)=Q\left(X\right)=0$ when $\theta =0$, and finishing at $H(X,1)=P\left(X\right)=0$ when $\theta =1$. The tracking of the solutions is developed using the corrector-predictor method.

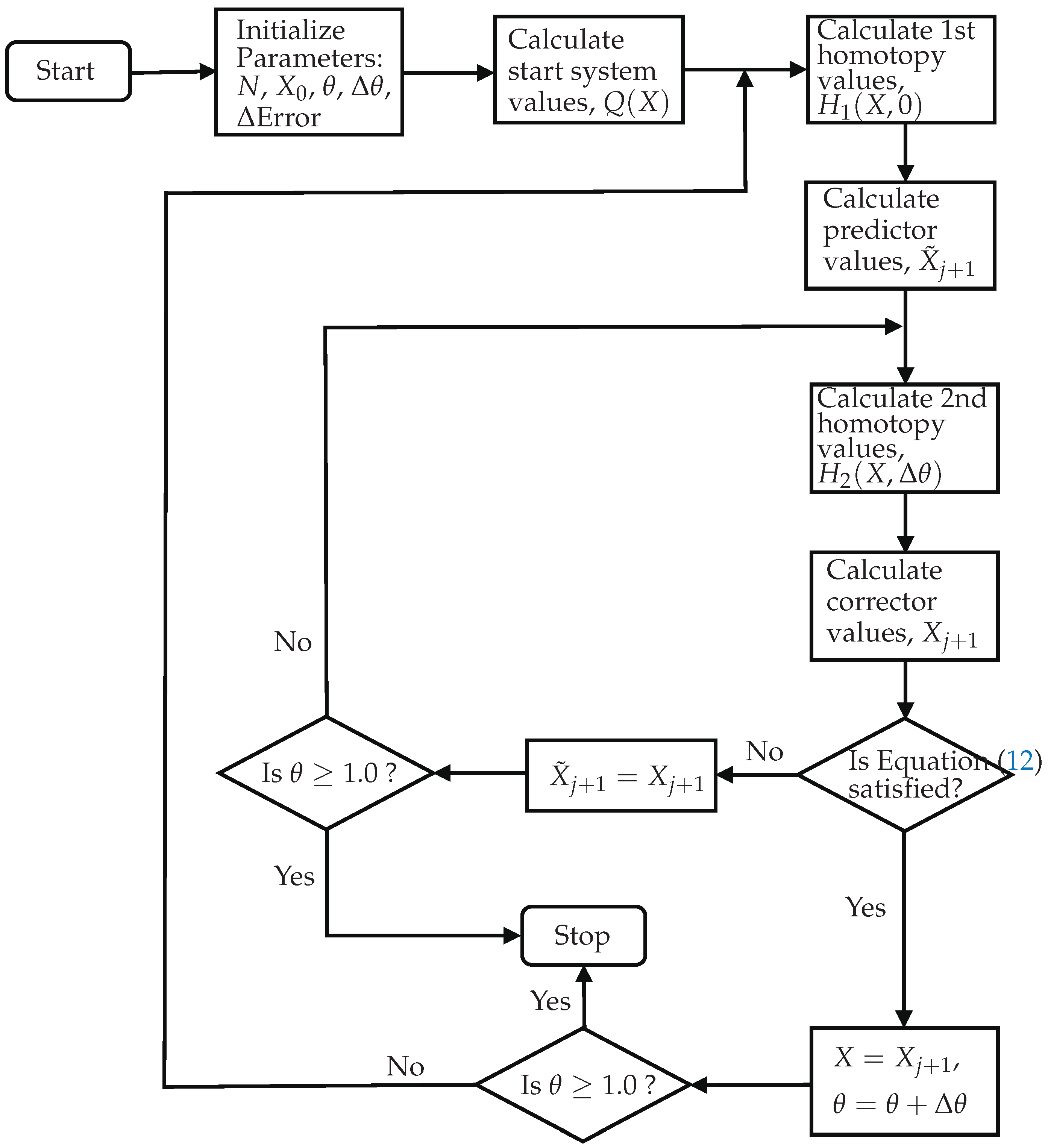
3.2. Computational Flow

The NPHC optimization algorithm is shown in Figure 1 and is described in the following steps:

Step 1: Initialize the model parameters.

Step 2: Obtain the start system using Equation (9).

Step 3: Develop a first evaluation of the homotopy, $H_1\left(X\right)$, using the value of $X_0$ from Step 1.

Step 4: Calculate the values of Newton’s predictor, ${\tilde{X}}_{j+1}$, using the values of $H_1\left(X\right)$ from Step 3, such as [52]

$${\tilde{X}}_{j+1}=x_j+\Delta zP\left(X_j\right)$$

(10)

where j is the corresponding iteration and $\Delta z$ is the increment step.

Step 5: Develop a second evaluation of the homotopy, $H_2\left(X\right)$, using the values of the predictor, ${\tilde{X}}_{j+1}$, from Step 4.

Step 6: Adjust the predictor set by means of a corrector. The values of Newton’s corrector, $X_{j+1}$, are calculated using the values of $H_2\left(X\right)$ from Step 5, such as [52]

$$X_{j+1}={\tilde{X}}_{j+1}-P({\tilde{X}}_{j+1}){\mathbf{J}}_X^{-1}$$

(11)

where ${\mathbf{J}}_X$ is the Jacobian matrix of Equation (8).

Step 7: Evaluate the converge criteria, given as [52]

$$|X_{j+1}-{\tilde{X}}_{j+1}|\le \Delta \mathrm{Error}$$

(12)

where $\Delta \mathrm{Error}$ is a constant decimal value that defines the precision of the solution.

Step 8: If the converge criteria is not satisfied, the value of the corrector is given to the predictor, and (i) if the value of $\theta$ is smaller than 1.0, the cycle continues at Step 5 using the new value of the predictor ${\tilde{X}}_{j+1}$; (ii) if the value of $\theta$ is equal or bigger than 1.0 the cycle is considered to be completed, and the final result is the value of the corrector, $X_{j+1}$.

Step 9: If the converge criteria is satisfied, the values of the start system, X, are substituted by the values of the corrector, $X_{j+1}$, the value of $\theta$ is increased by $\Delta \theta$, and (i) if the value of $\theta$ is smaller than 1.0, the cycle continues at Step 3 using the new value of X; (ii) if the value of $\theta$ is equal or bigger than 1.0, the cycle is considered to be completed, and the final result is the value of the corrector, $X_{j+1}$.

3.3. Application of the Algorithms to the EED Problem

The NPHC method works with closed systems of equations only. That is, the number of equations of the system must equal to the number of unknown variables. Thus, for the EED problem, the objective functions and equality constraints are grouped in a linear combination form, such as [21]

$$f={\varphi }_1{f}_1+(1-{\varphi }_1)({\varphi }_2{\omega }_2{f}_2+{\varphi }_3{\omega }_3{f}_3)-\lambda g$$

(13)

where $f_m$ are the objective functions; ${\varphi }_m$ are weights of the linear combination corresponding to each of the objective functions, where $0\le {\varphi }_m\le 1$; ${\omega }_2=600$ and ${\omega }_3=50,000$ are scaling factors to convert SO₂ and NO_x emission units to cost units, respectively, selected to have the result of the three objective functions at the same order of magnitude to avoid numerical instabilities during the computational process; g is the equality constraint which represents the real power balance; $\lambda$ is the Lagrange multiplier of the problem associated with the equality constraint [31], i.e., Equation (5).

For the SQP algorithm, the multiobjective optimization is developed in a constrained manner; that is, the first objective function is used as a constrain to obtain the minimum of a second objective function, and the results of the first and second objective functions are used as constraints to minimize a third objective function.

For the NSGA-II algorithm, the objective functions are evaluated at the same time, as a true multiobjective optimization, obtaining the solution of all the objective functions in a single run of the algorithm. The crossover and mutation probabilities are 0.99 and 0.01, respectively; the distribution index for crossover and mutation are 5 and 50, respectively; the algorithm is run for 20,000 generations, as suggested in [49].

The simulations are run in a computer with 16 GB of RAM and 8 cores Intel i7 6700-K at 4 GHz.

4. Results and Discussion

For the present work, the NPHC searching space is reduced to real positive roots only, which are related to the physical aspect of the power generated by the producers. This physical assumption helps to reduce considerably the computational effort.

An independence analysis for the homotopy parameters, $\Delta \mathrm{Error}$ and $\Delta \theta$, is developed based on the criteria [53]

$$\left|{\displaystyle \frac{X_{\tilde{j}-1}-X_{\tilde{j}}}{X_{\tilde{j}-1}}}\right|<5\times {10}^{-3}$$

(14)

where $X_{\tilde{j}}$ is the result of the current optimization and $X_{\tilde{j}-1}$ the result of the previous optimization, finding that the values of $\Delta \mathrm{Error}=0.01$ and $\Delta \theta =0.1$ do not alter the final result of the NPHC optimizations.

4.1. Using 25 Elements to Construct the Pareto Set

The results of the optimization of a single objective function using 25 elements or individuals to construct the Pareto set are given in

Table 1. Minimization of fuel cost.

Method	Value ($/h)	Producers (MW)	Time
SQP	8344.593	435.198, 299.970, 130.661	0.090
NSGA-II	8357.559	473.832, 244.248, 146.605	57.442
NPHC	8344.593	435.198, 299.970, 130.661	0.006

for the fuel cost,

Table 2. Minimization of SO₂ emissions.

Method	Value (ton/h)	Producers (MW)	Time
SQP	8.9659	550.603, 220.760, 93.160	0.341
NSGA-II	8.9786	575.635, 236.714, 52.971	57.065
NPHC	8.9659	552.112, 219.444, 92.960	0.010

for the SO₂ emissions, and

Table 3. Minimization of NO_x emissions.

Method	Value (ton/h)	Producers (MW)	Time
SQP	0.095925	493.075, 265.802, 106.127	0.394
NSGA-II	0.096389	540.950, 225.798, 97.766	57.467
NPHC	0.095924	508.580, 250.443, 105.723	0.007

for the NO_x emissions. It is observed that the NPHC and the SQP algorithms provide the best result for the minimization of fuel cost and SO₂ emissions, and the NSGA-II algorithm provides the worst result. For the minimization of NO_x emissions, the NPHC algorithm provides the best result, followed by the SQP algorithm, and the NSGA-II algorithm provides the worst result.

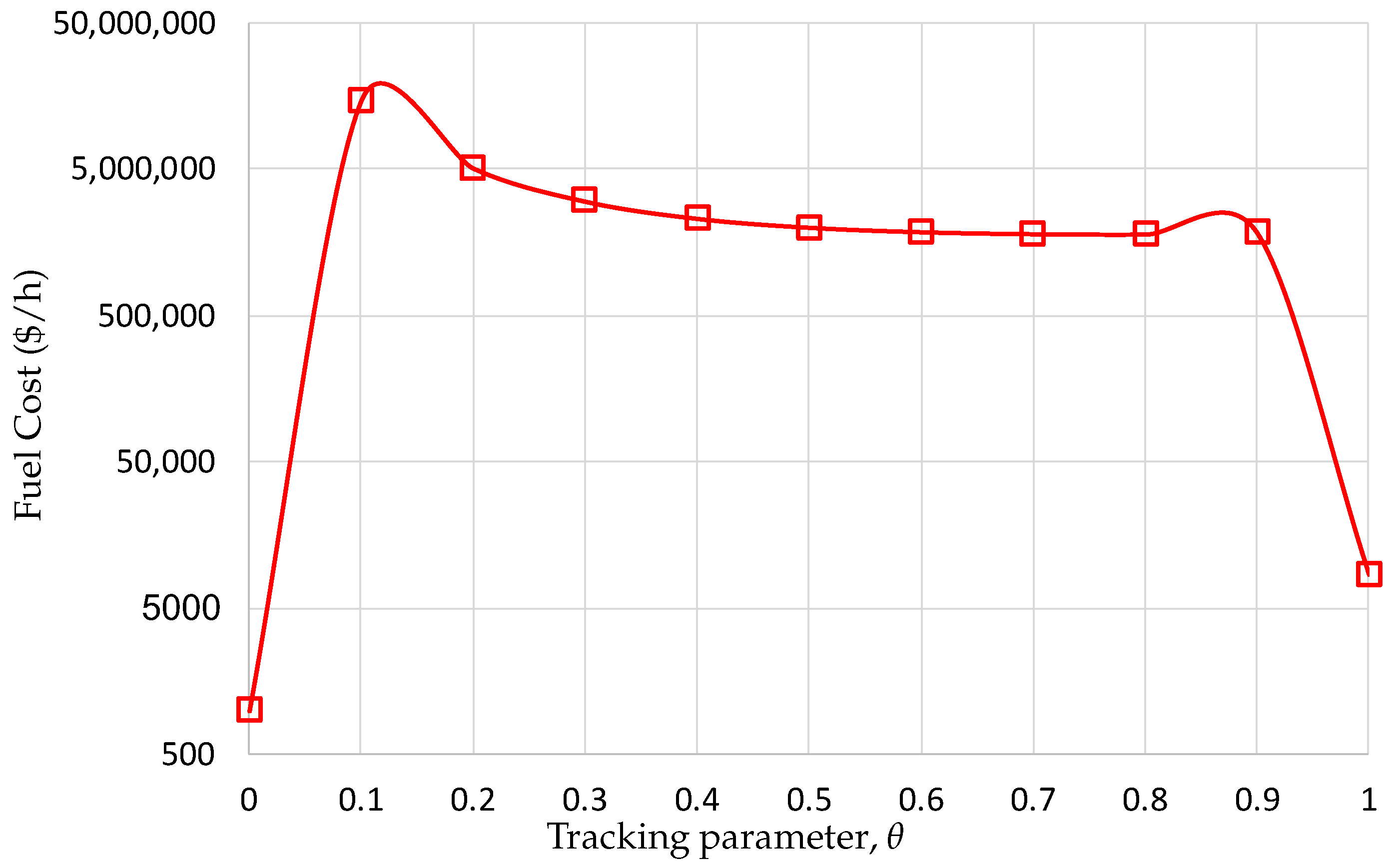
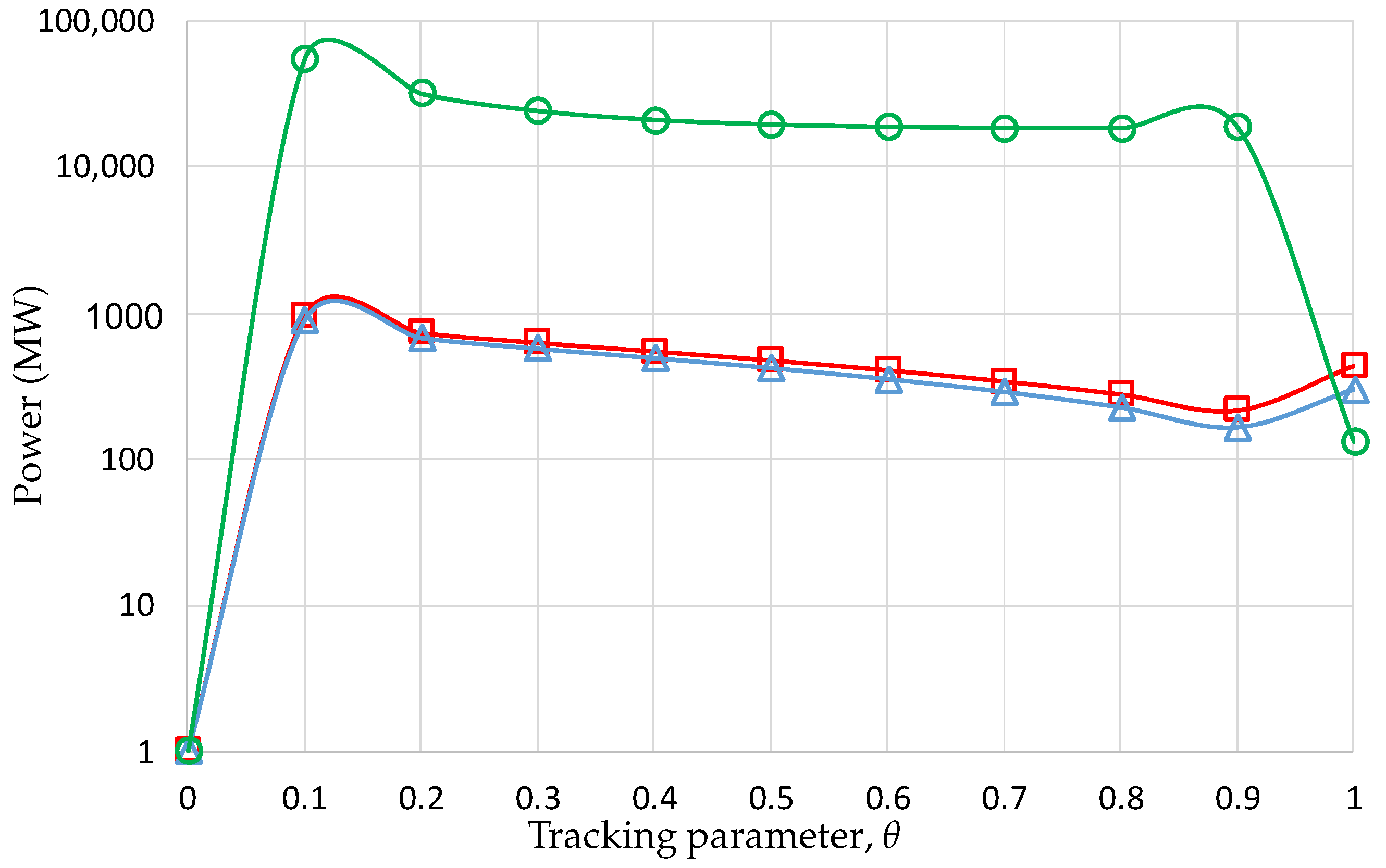
Figure 2 shows the trajectory of the minimization of the fuel cost objective function using the NPHC algorithm with respect to the tracking parameter. It is observed that the trajectory of the solution is very smooth, which helps to reduce the time of computation. It is observed that the solution is always reached at $\theta =1$. Figure 3 shows the trajectory of the roots (solutions) corresponding to the three producers, for the minimization of the fuel cost objective function. It is observed that the trajectory of the roots is also very smooth, following a similar shape than the objective function towards the solution at $\theta =1$. This smoothness is a characteristic of the NPHC method to avoid getting stuck at local optimums, assuring the finding of the global optimum.

In terms of the time of computation, the NPHC algorithm provides the shortest time for the individual minimization of the three objective functions. Compared with the SQP algorithm, the response of the NPHC algorithm is one order of magnitude faster for the minimization of fuel cost, and SO₂ emissions, and two orders of magnitude faster for the minimization of NO_x emissions. Compared with the NSGA-II algorithm, the response of the NPHC algorithm is four orders of magnitude faster for the individual minimization of the three objective functions.

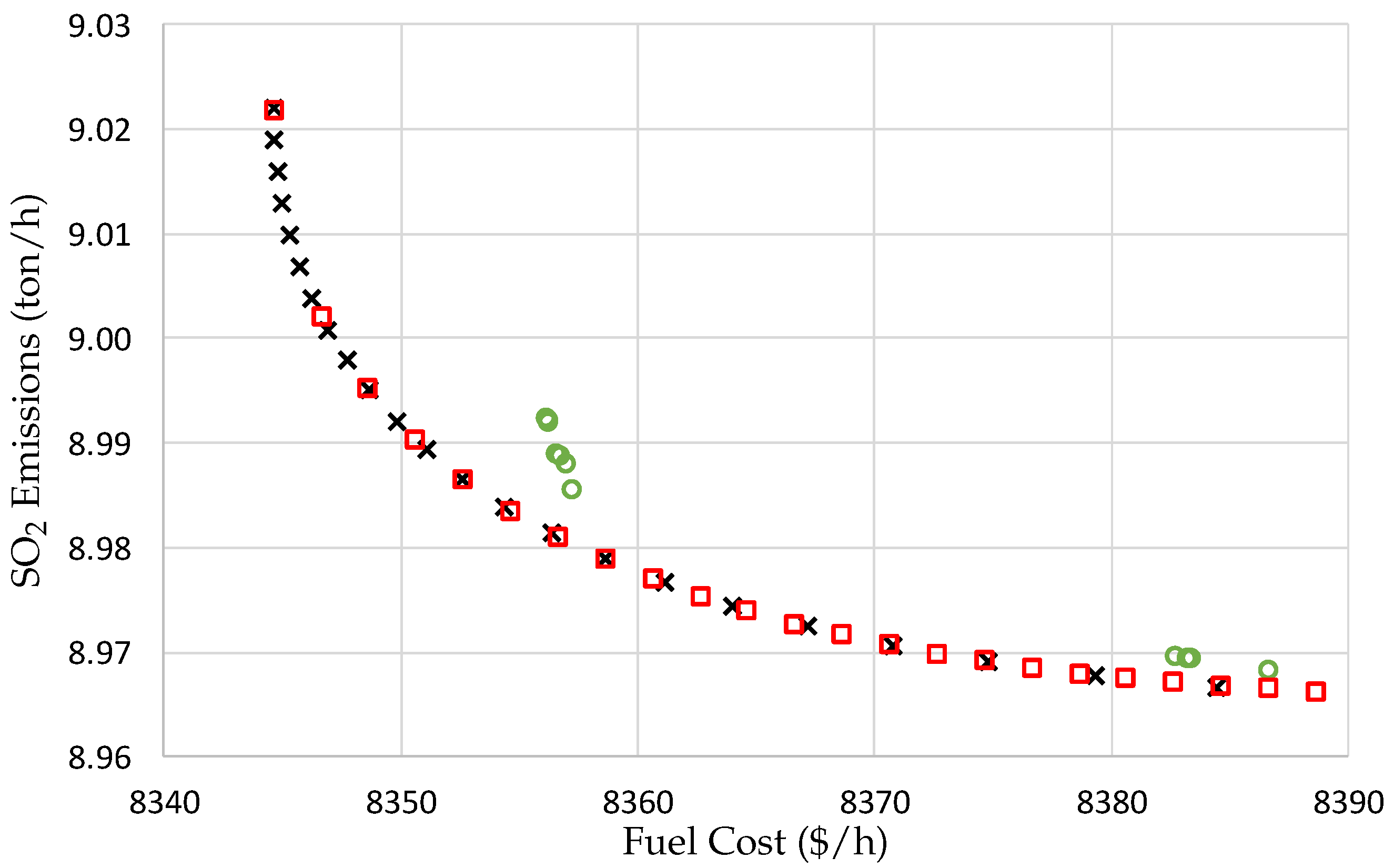
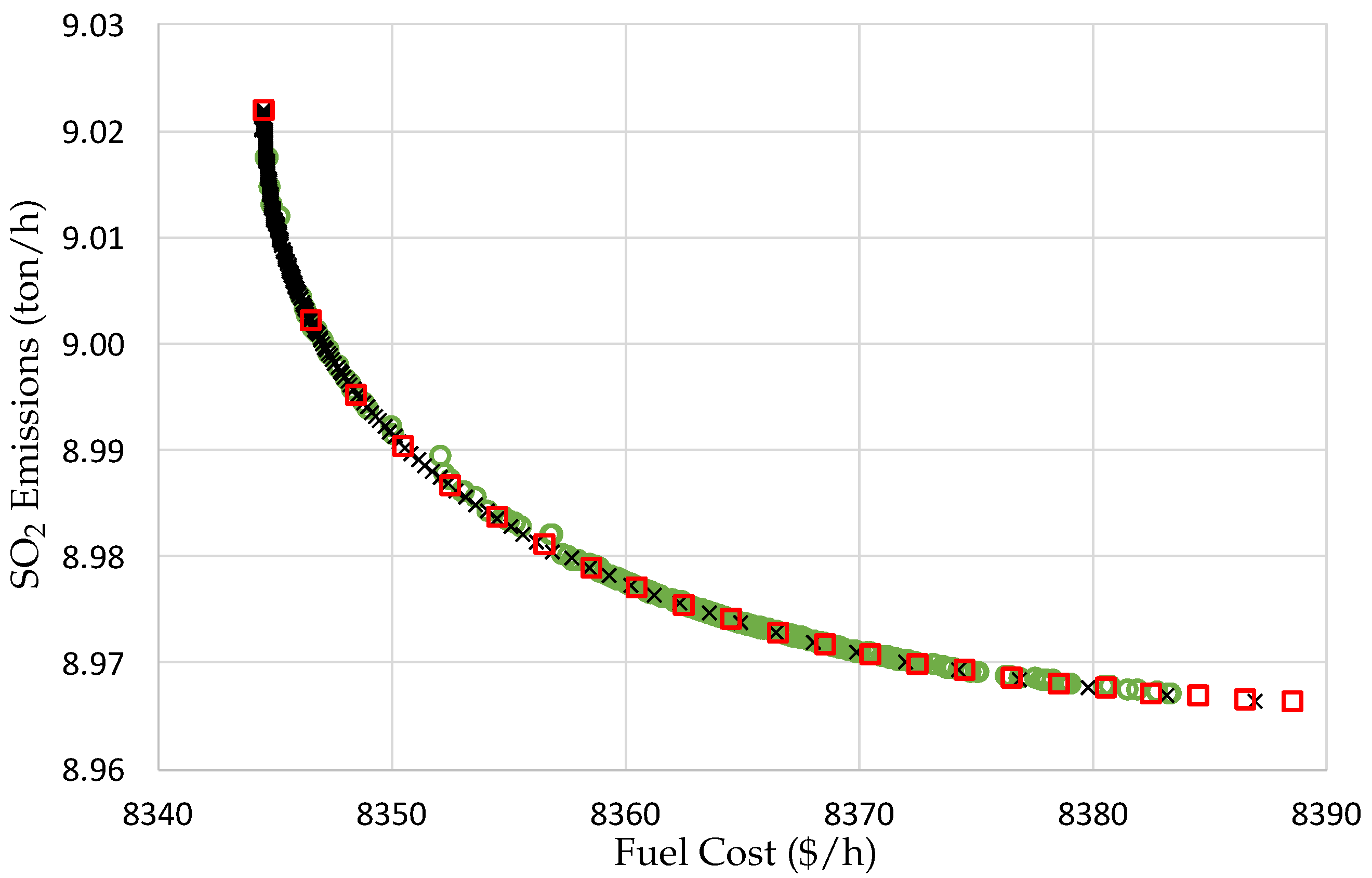
Figure 4 shows the Pareto set for fuel cost and SO₂ emissions. It is observed that the NPHC and SQP algorithms provide an accurate solution, as well as a good distribution of the elements on the solution space. Also, the figure shows that the NSGA-II algorithm has problems in obtaining both, a good solution and a good distribution of the results on the solution space. In terms of the time of computation, the SQP algorithm needs 14.229 s to obtain the Pareto set, the NSGA-II algorithm needs 58.212 s to obtain the Pareto set, and the NPHC algorithm needs 0.150 s only to obtain the Pareto set.

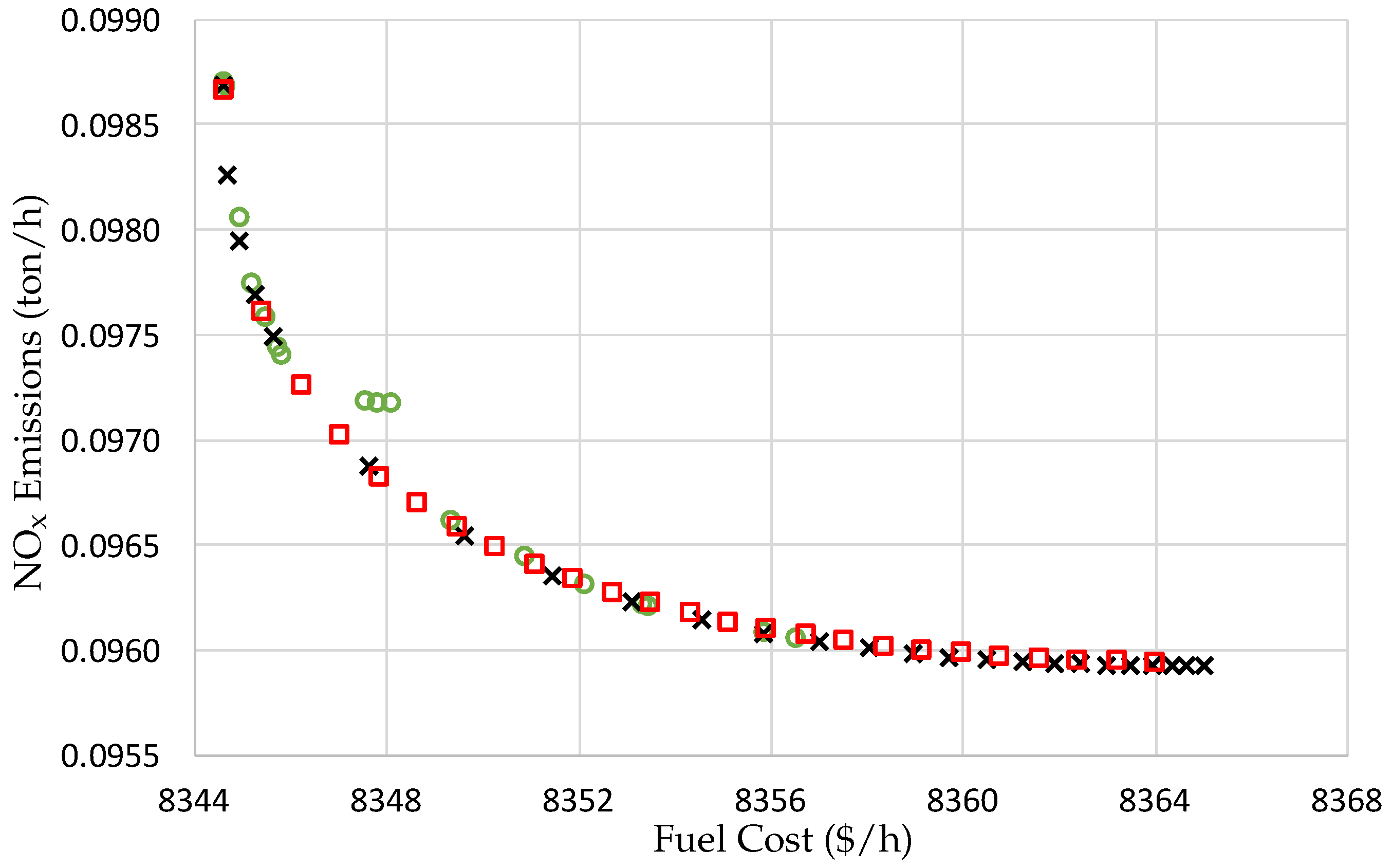
Figure 5 shows the Pareto set for fuel cost and NO_x emissions. The figure shows that the NPHC and SQP algorithms provide an accurate solution, as well as a good distribution of the elements on the solution space. The figure shows that the NSGA-II algorithm provides a good solution, although some individuals are still far from the Pareto set. It is also observed that the NSGA-II algorithm does not populate the solution space for values of fuel cost higher than 8357. In terms of the time of computation, the SQP algorithm needs 25.711 s to obtain the Pareto set, the NSGA-II algorithm needs 57.679 s to obtain the Pareto set, and the NPHC algorithm needs 0.156 s only to obtain the Pareto set.

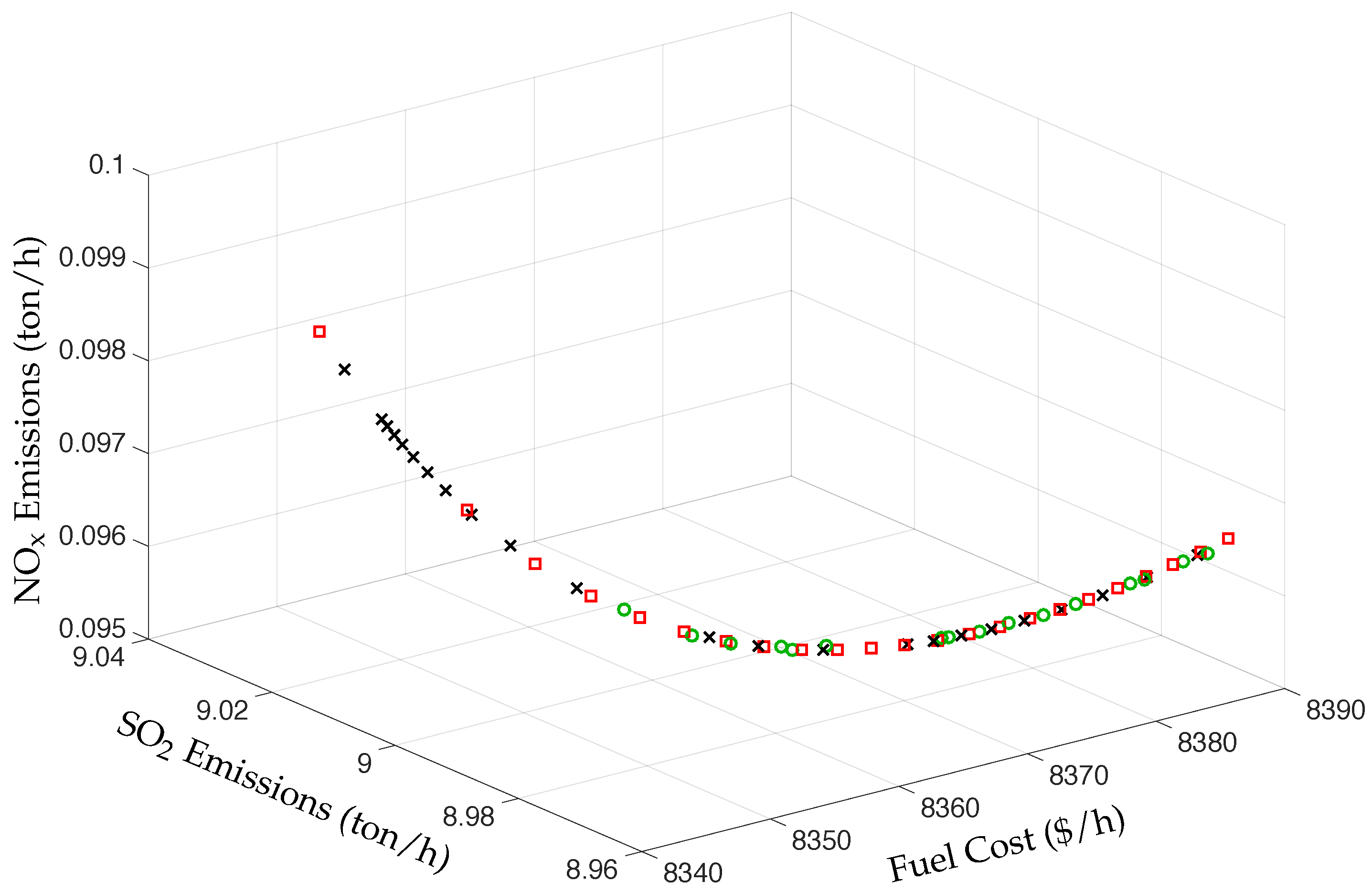
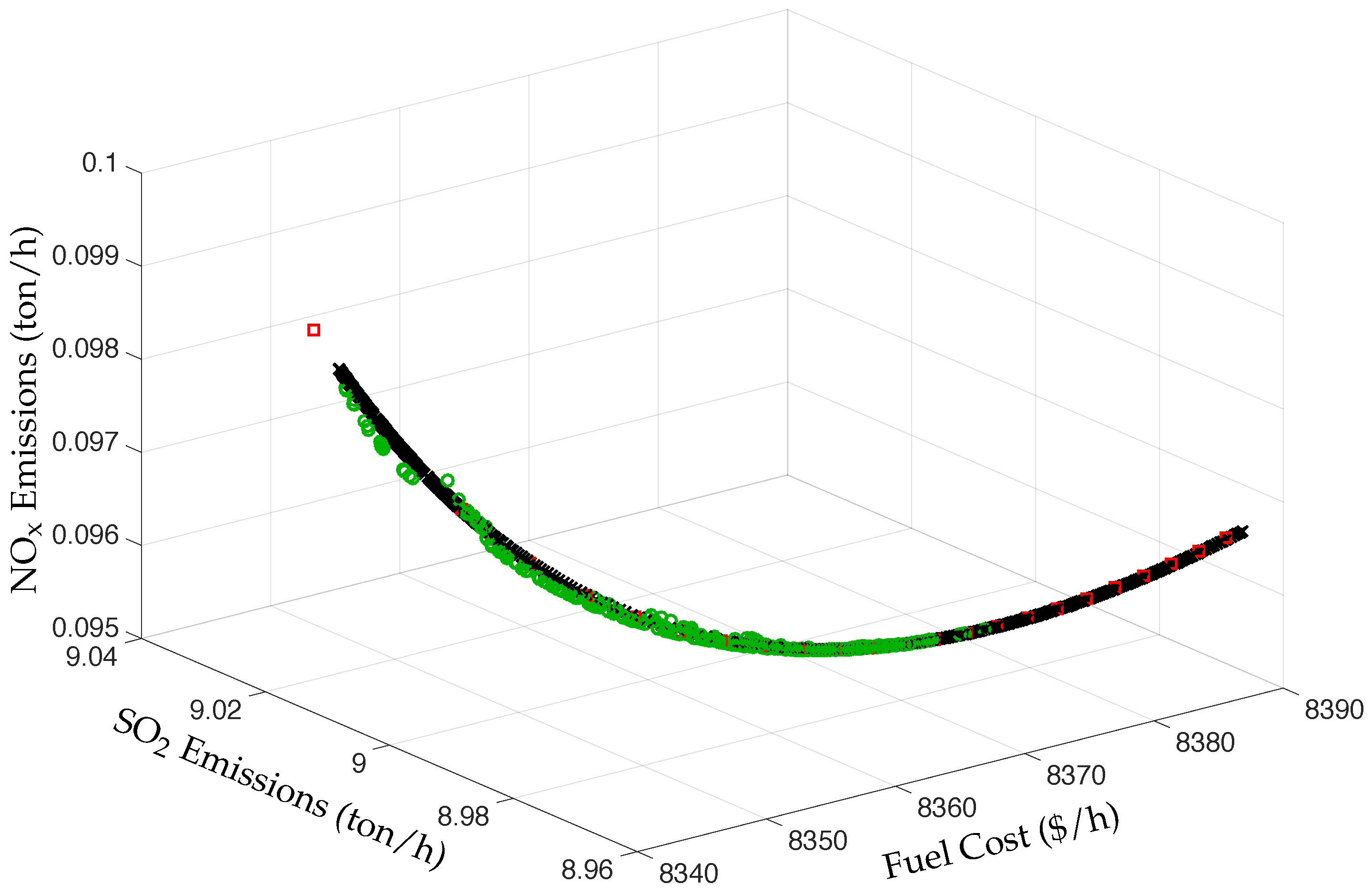
Figure 6 shows the Pareto set for fuel cost, SO₂ emissions, and NO_x emissions. The figure shows that the NPHC and SQP algorithms provide an accurate solution as well as a good distribution of the elements on the solution space. It is also observed that the NSGA-II algorithm populates well the Pareto set for high fuel cost only, but leaves unpopulated the other part of the Pareto set. In terms of the time of computation, the SQP algorithm needs 17.580 s to obtain the Pareto set, the NSGA-II algorithm needs 59.063 s to obtain the Pareto set, and the NPHC algorithm needs 0.174 s only to obtain the Pareto set.

4.2. Using 500 Elements to Construct the Pareto Set

The results of the optimization of a single objective function using 500 elements or individuals to construct the Pareto set are given in

Table 4. Minimization of fuel cost.

Method	Value ($/h)	Producers (MW)	Time
SQP	8344.593	435.198, 299.970, 130.661	0.090
NSGA-II	8344.832	431.532, 307.204, 127.289	403.250
NPHC	8344.593	435.198, 299.970, 130.661	0.006

for the fuel cost,

Table 5. Minimization of SO₂ emissions.

Method	Value (ton/h)	Producers (MW)	Time
SQP	8.9659	550.603, 220.760, 93.160	0.341
NSGA-II	8.9662	557.153, 211.829, 95.463	432.091
NPHC	8.9659	552.112, 219.444, 92.960	0.010

for the SO₂ emissions, and

Table 6. Minimization of NO_x emissions.

Method	Value (ton/h)	Producers (MW)	Time
SQP	0.095925	493.075, 265.802, 106.127	0.394
NSGA-II	0.095926	510.543, 248.199, 105.969	430.515
NPHC	0.095924	508.580, 250.443, 105.723	0.007

for the NO_x emissions. It is observed that the result of the NPHC and the SQP algorithms are as accurate as those obtained using 25 elements or individuals, with the only difference that the solution space is more populated because of the increase in the number of elements used. Also, the NSGA-II algorithm obtains a very close solution to those provided by the NPHC and SQP algorithms, increasing the accuracy when compared with the results obtained using 25 individuals only. However, this increase in accuracy of the NSGA-II algorithm comes with the price of a longer time of computation, increasing it from about 57 s to more than 400 s for each of the optimizations. The time needed by the NPHC and the SQP algorithms is the same as the case when 25 elements are used.

Figure 7 shows the Pareto set for fuel cost and SO₂ emissions. As for the case of 25 elements, the NPHC and SQP algorithms provide an accurate solution as well as a good distribution of the elements on the solution space. The figure also shows that the NSGA-II algorithm provides a very close solution to those of the NPHC and SQP algorithms, and covers well the solution space except for fuel cost values higher than 8391. In terms of the time of computation, the SQP algorithm needs an average of 0.569 s to obtain a single point, thus it needs 284.580 s to obtain the 500 elements of the Pareto set; the NSGA-II algorithm needs 379.879 s to obtain the Pareto set using 500 individuals; the NPHC algorithm needs 2.844 s only to obtain the Pareto set using 500 elements.

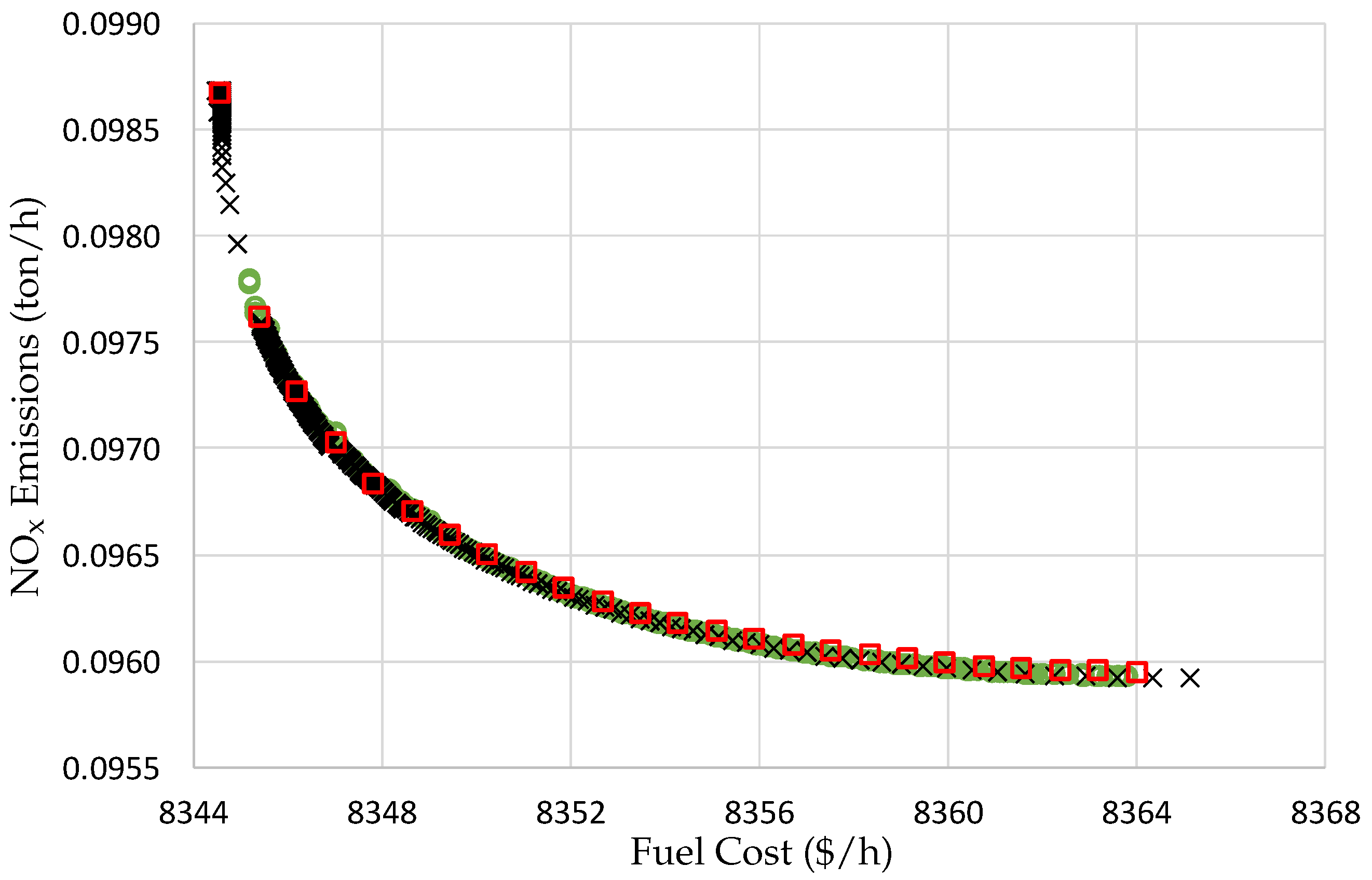
Figure 8 shows the Pareto set for fuel cost and NO_x emissions. As for the case of 25 elements, the NPHC and SQP algorithms provide an accurate solution as well as a good distribution of the elements on the solution space. The figure also shows that the NSGA-II algorithm provides a very close solution to those of the NPHC and SQP algorithms, and covers well the solution space except for fuel cost values smaller than 8345. In terms of the time of computation, the SQP algorithm needs an average of 1.0284 s to obtain a single point; thus, it needs 514.220 s to obtain the 500 elements of the Pareto set; the NSGA-II algorithm needs 385.152 s to obtain the Pareto set using 500 individuals; the NPHC algorithm needs 2.877 s only to obtain the Pareto set using 500 elements.

Figure 9 shows the Pareto set for fuel cost, SO₂ emissions, and NO_x emissions. It is observed that the NPHC and SQP algorithms provide an accurate solution as well as a good distribution of the elements on the solution space. It is observed that again the NSGA-II algorithm covers well the solution space, although it has problems to reach the exact solution for small fuel cost values. In terms of the time of computation, the SQP algorithm needs an average of 0.703 s to obtain a single point; thus, it needs 351.6 to obtain the 500 elements of the Pareto set; the NSGA-II algorithm needs 474.36 s to obtain the Pareto set using 500 individuals; the NPHC algorithm needs 3.206 s only to obtain the Pareto set using 500 elements.

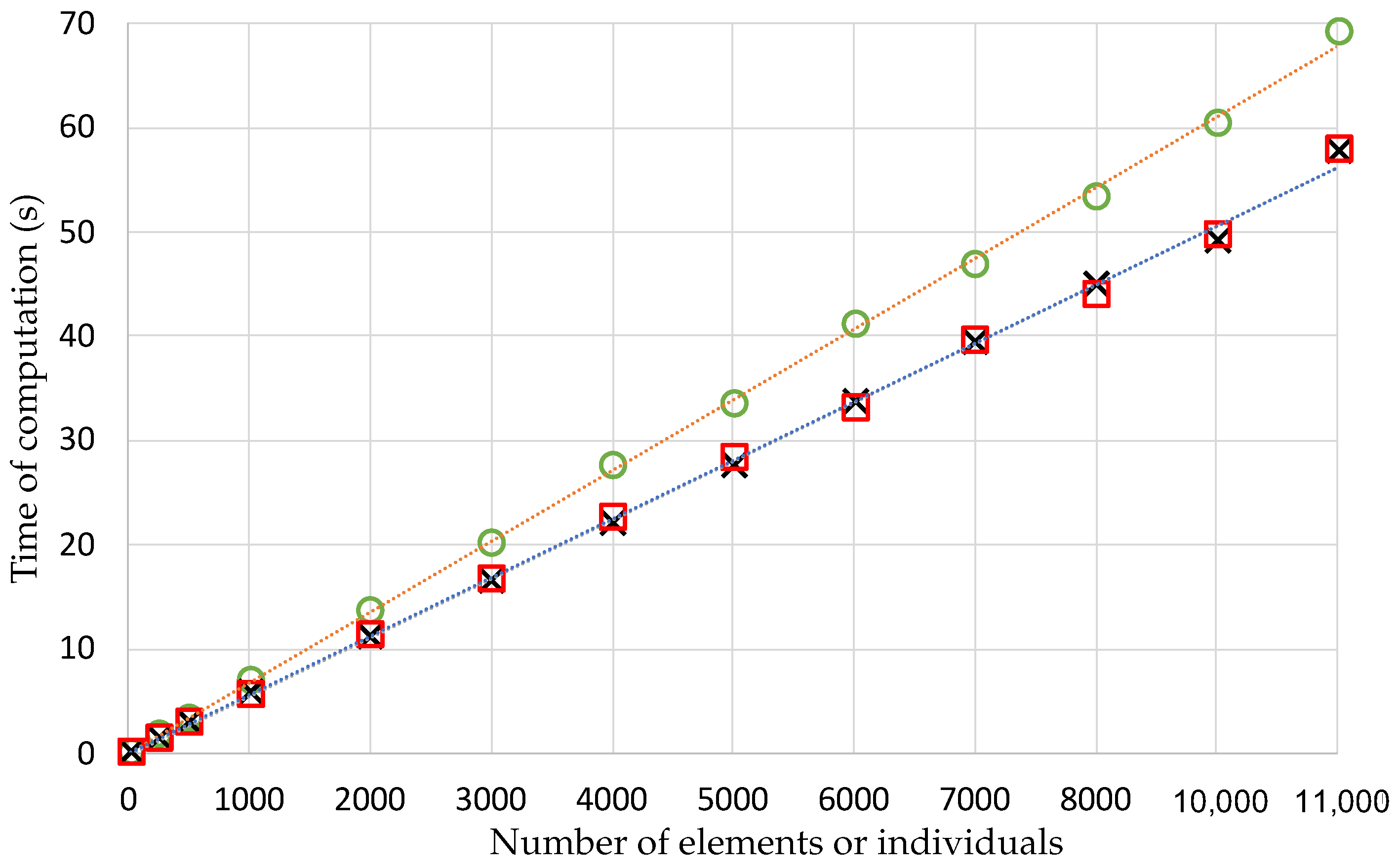
4.3. Time of Computation Required by the NPHC Algorithm

Figure 10 shows the time of computation used by the NPHC algorithm to obtain a simultaneous solution of two and three objective functions with respect to the number of elements or individuals used. For the three cases, i.e., fuel cost–SO₂, fuel cost–NO_x, and fuel cost–SO₂–NO_x, the time of computation increases as a linear function of the number of elements used. It is also observed that the optimizations are obtained very fast, even when a large number of elements or individuals are used. This result shows that the NPHC is a very efficient algorithm.

5. Conclusions

In this work, the Numerical Polynomial Homotopy Continuation (NPHC) method has been successfully applied to solve the Economic Emission Dispatch problem. The NPHC algorithm is compared with the SQP algorithm, which is based on a deterministic approach, and the NSGA-II algorithm, which is based on a stochastic approach.

The work shows that the NPHC algorithm performs well at obtaining an accurate solution of the multiobjective optimization problem by guaranteeing to find all the roots (solutions) of the problem by searching through all the solution space. The NPHC algorithm is very easy to implement because it is constructed based on the Homotopy Analysis method and the fundamental theorem of algebra. The NPHC algorithm obtains the solution of the problem in a very short period of time when compared to other deterministic and probabilistic algorithms. For the minimization of a single objective function, the time of computation required by the NPHC algorithm is independent of the number of elements used because the trajectory of a single objective function is followed through the optimization process. For the simultaneous minimization of two and three objective functions, the time of computation required by the NPHC algorithm varies linearly with respect to the number of elements used to construct the Pareto set, suggesting that the NPHC is a very efficient algorithm.

These findings show that the NPHC method is a good alternative to solve multiobjective optimization models to help the power industry to deal with the dispatch of electricity considering the reduction of both, fuel cost and emissions to the environment.