Abstract
In many developing countries, electricity outages occur frequently with consequences for sustainable development. Moreover, within a country, region or city, the distribution of outages and their resultant impacts often vary from one locality to another. However, due to data constraints, local-scale variations in outage experiences have seldom been examined in African countries. In this study, a spatial approach is used to estimate and compare exposure to electricity load shedding outages across communities in the city of Accra, Ghana. Geographic Information System and statistics from the 2015 rolling blackouts are used to quantify neighborhood-level load shedding experiences and examine for spatial patterns. The results show that annual load shedding exposure varied greatly, ranging from 1117 to 3244 h. The exposure values exhibit statistically significant spatial clustering (Moran’s I = 0.3329, p < 0.01). Several neighborhoods classified as load shedding hot or cold spots, clusters and outliers are also identified. Using a spatial approach to quantify load shedding exposure was helpful for overcoming the limitations of lack of fine-grained, micro-level outage data that is often necessary for such an analysis. This approach can therefore be used in other data-constrained cities and regions. The significant global spatial autocorrelation of load-shedding exposure values also suggests influence by underlying spatial processes in shaping the distribution of load shedding experiences. The resultant exposure maps provide vital information on spatial disparities in load shedding implementation, which can be used to influence decisions and policies towards all-inclusive and sustainable electrification.
1. Introduction
Power outages in electricity supply systems occur both in developed and developing countries. The threat of electricity blackouts and brownouts has increased in recent times, with components of the electricity system—generation, transmission and distribution—being increasingly vulnerable to both natural and manmade phenomena. Several studies have documented the occurrence of outages in developed nations, often caused by extreme weather events or other natural hazards [1,2,3,4]. The impacts associated with outages in these countries is often substantial due to high societal reliance on electricity. Even then, concern about power outages in the developed world is low because of their limited scope in terms of frequency, duration and affected area [5].
On the contrary, power outages in developing countries are frequent and last for extended periods of time. Most of the outages occur on the low voltage distribution network due to faults associated with aging infrastructure, poor maintenance, illegal connections and adverse weather. Many developing countries also experience another, more serious type of power outage: mandatory rolling blackouts or load shedding. Mandatory load shedding is usually triggered by a supply–demand mismatch due to shortfalls in electricity generation and/or spike in electricity demand. Load shedding sometimes affects large geographic areas (entire regions or countries) and can last for years. Ghana is one of the countries in Africa that has been through several acute, multi-year electricity supply shortages over the past four decades, which have resulted into nation-wide load shedding (also known as “dumsor” in the local “Twi” language). The most recent mandatory load shedding in Ghana lasted for about four years, from 2013 to 2016. At the peak of the power supply crisis, electricity users experienced up to 16 h of no power on a daily basis (or 24 h of power outage for every 12 h of power) [6,7].
Frequent and prolonged electricity outages—including load shedding outages—have significant negative consequences in the affected areas. The impacts cut across the social, economic and environmental aspects of society. Across several African countries, power outages have been found to have a substantial drag effect on economic growth [8]. Power outages are negatively correlated with the performance of firms, measured as firm sales [9], firm productivity [10] and also cause significant monetary losses related to equipment damage and damage to raw materials [11]. Power outages also have negative implications for social and sustainability issues, such as health, employment, education, population growth and poverty eradication. The use of back-up diesel generators to mitigate power outage impacts often drives up consumer expenditure on electricity and also reduces air quality due to increased local emissions [12]. Power outages also discourage entrepreneurship and reduce demand for labor thereby limiting the chances of finding employment [13]. In Ghana, up to USD 3 billion of economic activity and thousands of jobs are reported to have been lost during the recent electricity supply crisis [14]. These load shedding outages were also linked to increased tax evasion by firms [15] and the non-payment of utility bills by household-level consumers [16]. Load shedding is also reported to have increased the risk of in-facility mortality, especially for healthcare facilities situated in Ghana’s urban centers [17]. “Dumsor”-themed public demonstrations were also held in the leading cities of Accra and Kumasi to protest the government’s failure to deal with the power supply shortages [18].
In Africa and other developing regions, power outages and their impacts are arguably most felt in urban areas since cities often have high electricity access and consumption rates as compared to rural areas. However, even within a city, electricity supply and (un)reliability can significantly vary from one locality to another. There are some studies that have examined electricity outage experiences within cities/urban areas, albeit mostly for developed nations. Some of these studies have also identified the factors that influence the distribution of power outages across small communities within a city [19,20]. For example, during times of limited electricity supply, high priority facilities such as hospitals may continue to receive uninterrupted power due to the criticality of the services that they provide [20]. This may indirectly benefit local communities within the vicinity of such critical facilities. Sometimes, areas with industrial and large commercial establishments also maintain a continuous supply of electricity (even during times of shortages) due their perceived importance to the national economy [21]. Additionally, in the case of Ghana, the distribution of electricity during the recent power crisis has been said to have political and wealth leanings. Min [22] showed that improvements in electricity service quality after the recent power supply shortages were more noticeable in communities with high support for the ruling elite. Aidoo and Briggs [6] found a relationship between electricity availability and wealth in Accra, Ghana, where residents in ‘poor communities’ were more likely to experience longer load shedding outages than those in ‘wealthier ones.’
Spatial Approaches in Energy Studies
Spatial approaches are useful both for the analysis and presentation of useful information on various geographic scales. Spatial methods have been used in many studies across different fields and countries, for example, to study crime rates in Brazil [23], prevalence of low birth weight in Georgia, USA [24], regional distribution of educational attainment in Western Europe [25], adult in-migration patterns in North Carolina, USA [26], differences in secondary school education achievement in Australia [27], distribution and drivers of forest fires in Portugal [28], and for identification and pattern analysis of health care hot spots in Taiwan [29], among many others. In Africa, spatial analysis has been used to examine the link between shifting population trends and climate change revealing hotspots of vulnerability to climate change impacts in central, southern and East Africa [30]. Spatial regression has also been used to examine the effect of topographical parameters on rainfall distribution in East Africa [31]. A study by Ansong et al., [32] on space and time-varying trends in academic performance at junior high school level in Ghana, employed spatial grouping analysis to depict growth trajectories across the rural–urban divide. On the health front, a scoping review on the use of Geographic Information System (GIS) and spatial analysis in HIV-related research in Africa has been done showing widespread use of these approaches [33]. There is similarly relative widespread use of spatial techniques within other research fields in Africa. However, the use of such techniques in energy-related studies on the continent has remained relatively low.
In other countries, especially developed countries, spatial methods have been employed to study various energy topics including energy resource potential, energy consumption and demand, and energy prices. GIS techniques have been used to assess the potential and use of various renewable energy resources in India [34], Turkey [35] and southern Appalachian region in USA [36]. Cluster and Outlier analysis together with GeoDetector have been used to assess the distribution and drivers of renewable energy industries on a national level in China [37]. Spatial autocorrelation and spatial regression modelling have been used in a study by Xie et al. [38] to examine the spatial patterns and the driving factors behind changing energy consumption across regions in China. Spatial auto-regression was able to reveal more determinants of energy consumption change than a standard regression model. Walker et al. [39], has also used local measures of spatial autocorrelation to assess local variations in the prices of heating oil in Northern Ireland and found significant local spatial variations. Dar-Mousa and Makhamreh [40] used Global Moran’s I analysis, a spatial statistical approach to assess patterns in electricity consumption in Amman city, Jordan and found a positive and significant autocorrelation with nearby areas having similar per capita electricity consumption values. A study by Tyralis et al. [41] also employed hotspot analysis, cluster and outlier analysis as well as grouping analysis to identify spatial patterns in electricity demand across administrative divisions in Greece. Spatial modelling approaches have also been used to examine and model electricity outages and their relationship with socio-economic and environmental factors at different spatial scales (state, region, county, census block) in the US [2,19,20]. Spatial visualization using maps has also found application in improving the communication of load shedding schedules in South Africa, enabling users to easily visualize and better plan for load shedding [42]. These and other related studies demonstrate the usefulness of spatial analytical techniques in examining and communicating spatial characteristics of energy parameters on both local and national scales. In order to undertake such analyses, sufficiently detailed spatial data on energy (electricity) parameters on a spatial level of interest is required. While this data is usually available in developed countries, in developing countries (including in Africa), detailed granular data is often not collected, is inaccessible or unusable due to its poor quality. Moreover, efforts to collect such data by any researcher can be difficult because of restrictive bureaucratic and financial requirements. This potentially explains why very few spatial analyses on energy (electricity) parameters have been carried out in Africa, especially on a local level.
In the present study, the objective is to spatially present and analyze electricity outage (load shedding) experiences in Accra, Ghana. In particular, the study aims to: (1) spatially quantify and map electricity load shedding outages across local communities; and (2) examine the global and local spatial patterns of these load shedding outages. The study utilizes a comprehensive outage dataset from the utility company to calculate community load shedding levels over a one-year period. A Geographic Information System (GIS) approach is used to disaggregate and link available macro-level load shedding outage data to corresponding local communities. Furthermore, spatial statistical tools are applied to examine the spatial patterns and relationships among load shedding variables across the communities. This is a first step towards integrating spatial dependency in modelling societal drivers to load shedding experiences in Accra, Ghana [20]. The study is motivated by the need to provide community-scale spatial information to utility-level decision makers for better planning of electricity distribution during times of supply shortages. Subsequent sections are structured as follows: Section 2 presents the study area and data used, methods used in the study are described in Section 3, Section 4 presents and discusses the study results, while the final study conclusions, including limitations and areas of future research, are given in Section 5.
2. Study Area and Data
2.1. Study Area
The Accra Metropolitan Area (AMA), also known as, Accra Metropolis (or simply, Accra) is the capital city of Ghana and one of the districts in the Greater Accra Region. Its total surface area is approximately 200 km2. In 2010, the Accra metropolitan area was home to 1,665,086 people but the population was projected to reach in excess of 2 million people in 2019 [43]. The Accra metropolitan area is divided into several sub-metropolitan areas, including: Okaikoi, Ashiedu Keteke, Ayawaso, Kpeshie, Osu Klotey and Ablekuma. Within the sub-metropolitan areas, there are several smaller communities whose informal boundaries mainly follow natural barriers, such as roads and drainage channels. These communities are herein referred to as neighborhoods. A neighborhood has been defined as “a geographic unit of limited size, with relative homogeneity in housing and population, as well as some level of social interaction and symbolic significance to residents.” [44] This definition presents a neighborhood both as a social entity—with similar characteristics and a sense of cohesion—and as a physical/geographical area of known boundaries. The boundaries of the Accra neighborhoods have been delineated in the Accra neighborhood map produced by Engstrom et al. [44]. The map was developed by first georeferencing a local tourist map—containing local vernacular names of the communities—onto an enumeration area map. Each enumeration area (EA) was then ‘dissolved’ into an associated neighborhood such that no EA was shared by two neighborhoods. The resultant neighborhood map was validated by local residents as well as by public officials [44].
This study employs a neighborhood as the spatial unit of analysis and uses a part of the above-mentioned Accra neighborhood map as the study area. The part of the map used in this study covers 47 neighborhoods in the western part of the Accra metropolitan area (see Figure 1). The neighborhoods were selected because they are served by a single electricity utility branch, which availed relevant data useful to this study. The selected neighborhoods cover 31% of the total area of Accra metropolis and are home to about 56% of the city’s total population. The average population density of these neighborhoods is 19,930 people per square kilometer. The average size of the selected neighborhoods is 1.48 km2, ranging from 0.26–5.12 km2 and a standard deviation of 0.95. The average population in these neighborhoods is 24,505 people, ranging from 2050–58,120 people. Dansoman estate is the neighborhood with the largest population and surface area, covering about 7% of the total area of the selected neighborhoods. Awudome estate is the neighborhood with the least population and surface area. At 65,838 people per square kilometer, Sabon Zongo has the highest population density among all the selected neighborhoods, while Victoriaborg has the lowest population density [44].
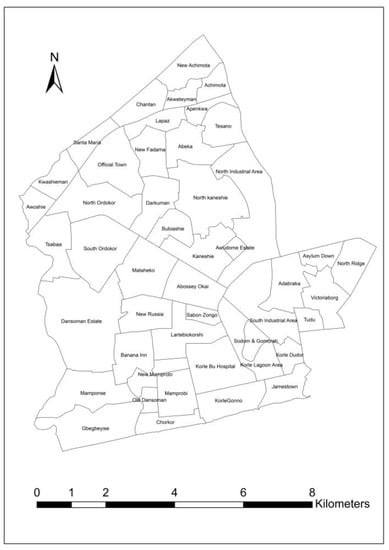
Figure 1.
Map of the study area showing neighborhoods.
2.2. Data and Data Sources
Together with the neighborhood map, the study utilized several datasets, including: electricity network (feeder) drawing, electricity outage statistics, and socio-demographic data. Socio-demographic data was obtained from Ghana Statistical Services (GSS) and Engstrom et al. [44]. The electricity network drawing—in AutoCAD format—was obtained from the electricity utility company together with the electricity outage statistics. The electricity network drawing was first converted into shapefile format in ArcGIS and georeferenced. Only the 11 kV feeder network was used in this study because electricity load shedding was mostly carried out on the 11 kV feeder level. The electricity outage statistics obtained from the electricity utility company consist of information about different outage types, including planned, unplanned, national load shedding and emergency outages. For most outage segments, information on outage start date and time, outage end date and time, the duration of outage, affected feeder name and voltage, and the number of affected customers was recorded. The outage statistics selected for this analysis are load shedding statistics recorded over the year 2015. The 2015 load shedding statistics are one of the most comprehensive outage statistics collected by the utility in the study area. Over 10,000 load shedding segments were recorded in that year at the peak of an acute electricity supply crisis. This represented about 70% of the total outages reported within the utility service area over a four-year period, 2013–2016.
2.3. Mapping Neighborhood Load Shedding Outage Experiences
In order to assess the load shedding experience of each neighborhood, the georeferenced 11 kV electricity network drawing was overlaid onto the neighborhood map within ArcGIS Desktop software (Release 10.5.1, ESRI, Redlands, CA, USA) (Figure 2). Each neighborhood in the study area was associated with one or more 11 kV electricity network feeders that intersected it. A feeder that crosses a neighborhood potentially supplies electricity to that neighborhood and therefore contributes to its load shedding experience. However, it is also possible that a feeder might pass through a neighborhood without necessarily supplying electricity to it (going to another place). Therefore, in determining whether a feeder contributed to the load shedding experience of any given neighborhood, we only considered feeders that were connected to 11 kV stepdown distribution transformers located in that neighborhood (Figure 3). Knowing which feeder(s) supply electricity to a neighborhood is essential for tagging load shedding outage statistics to corresponding neighborhoods.
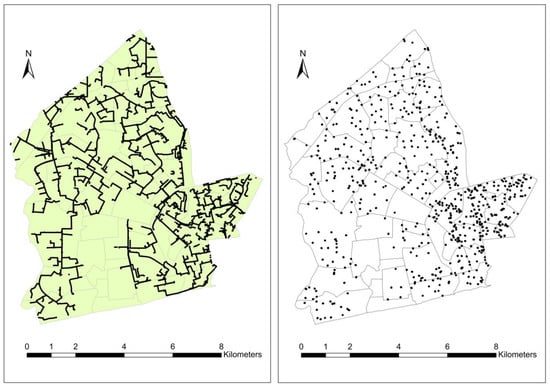
Figure 2.
Map of neighborhoods overlaid with an 11 kV power distribution network (left) and overlaid with 11 kV distribution transformers (right).
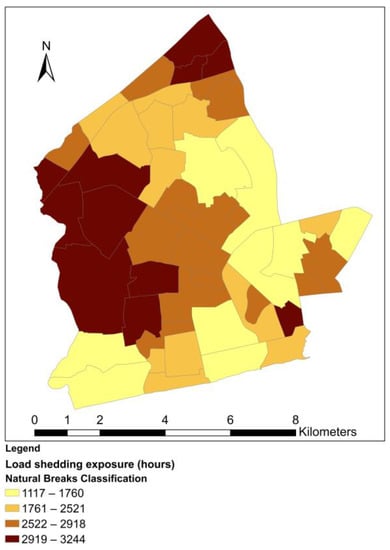
Figure 3.
Neighborhood exposure to electricity load shedding.
From Figure 2, it can be seen that some neighborhoods were not intersected by any 11 kV electricity feeder. A case in point is Chorkor and Old Dansoman in the south of the study area. This—according to utility officials—was a case of missing data and did not imply that those particular neighborhoods are not supplied by an 11kV electricity network. This was also verified by the author (PN) who physically visited the neighborhoods and found that there was a functional electricity distribution network. During the validation process of the overlaid network map, the electricity feeders that serve these neighborhoods were identified basing on the knowledge of technical personnel from the utility company. As such, all the neighborhoods are included in the subsequent calculations and analyses.
3. Methods
3.1. Calculating Neighbourhood Load Shedding Exposure and Normalization
In order to determine load shedding experiences across the neighborhoods in the study area, a variable called load shedding exposure, sometimes known as outage exposure, was used. Load shedding exposure is defined here as the cumulative number of load shedding outage hours (or minutes) experienced on any single electricity feeder serving a given neighborhood in the study area. The load-shedding exposure variable is a standardized variable and is therefore suitable for avoiding potential bias of comparing total neighborhood outage hours—since neighborhoods are served by a different number of electricity feeders. Load shedding exposure, , for each neighborhood was calculated according to the following equation:
where is the average load shedding frequency; is the average load shedding duration.
Average load shedding frequency,, refers to the number of times that a single electricity feeder serving a given neighborhood was under load shedding (experienced load shedding outages). Average load shedding duration, , is the average length of time that a single load shedding outage, experienced on a single feeder serving a given neighborhood, lasted. and are calculated according to the following equations.
where is the total number of load shedding outages experienced on all feeders serving a neighborhood, is the sum of the duration of all load shedding outages experienced in a neighborhood, and N is the total number of electricity feeders serving the neighborhood.
The load-shedding exposure values obtained using Equation (1) can show which neighborhood is experiencing more (or less) load shedding hours than others. But the load-shedding exposure variable does not take into account the external (societal) factors that often influence the observed load shedding distribution patterns. Electricity distribution decisions especially under conditions of limited supply are usually shaped by societal factors such as socio-economic and political factors [6,22]. In order to fully explain load shedding distribution dynamics, these factors should be taken into account. Through normalization, the load-shedding exposure values can be adjusted to integrate societal perspectives. As a further step in exploring neighborhood-level load shedding experiences, load-shedding exposure values were transformed using surface area, population and population density variables. A list of the variables involved in this step is given in Table 1. Hereafter, we focus our attention on analyzing the spatial patterns of the four load-shedding exposure variables (, , , and ).

Table 1.
Normalizing and transformed variables for assessing neighborhood load shedding experiences.
3.2. Spatial Analysis
In this sub-section, we present a two-step spatial analytical process. First, we visualize the load-shedding exposure values and their transformations on the neighborhood map. Secondly, we apply spatial statistical tools to assess for global and local patterns of spatial association in the load-shedding exposure variables.
3.2.1. Visualization
Data visualization is a useful way for easily identifying patterns in a given dataset. When visualization is done using a map, it is easy to identify how certain attributes vary at a given spatial scale. In this study, the load-shedding exposure variable and its transformations are visualized in order to generate an initial picture of their spatial characteristics. However, data visualization alone cannot be relied upon to make spatial inference [41]. As a step towards making complete spatial inference, we further apply spatial statistics tools to the visualized variables. In particular, we analyze for significant global spatial autocorrelation, and the presence/location of hot/cold spots, clusters and outliers. The visualization and analysis were carried out in ArcGIS Desktop software (Release 10.5.1, ESRI, Redlands, CA, USA).
3.2.2. Global index of Spatial Autocorrelation
Autocorrelation is the measure of the similarity of one value relative to other values surrounding it. In most traditional (nonspatial) statistical analysis, autocorrelation in a dataset is undesirable because it violates the principle of independence/stationarity of data. However, significant spatial autocorrelation, which points to the presence of spatial structuring in a dataset, is a basic indicator that some underlying spatial processes could be influencing the patterns, thus necessitating further examination. In this study, we apply the global Moran’s I statistic to evaluate the global spatial autocorrelation (GSA) of the four load-shedding exposure variables. Moran’s I statistic is related to the Pearson’s Correlation Coefficient [45] and is represented by the following equation [46]:
where is the deviation of an attribute for feature from its mean is the spatial weight between feature and ; is the total number of features; and is the aggregate of all the spatial weights:
The -score for Moran’s I statistic is calculated as:
where:
and
From the analysis, a positive and statistically significant Moran’s I (z-score > 1.65, p-value < 0.10) indicates spatial clustering in a dataset while a negative and statistically significant Moran’s I (z-score <-1.65, p-value < 0.10) indicates spatial dispersion. A positive or negative Moran’s I value that is not statistically significant (z-score between -1.65 and 1.65, p-value > 0.10) implies spatial randomness [46]. While global Moran’s I statistic is important for examining the presence of spatial patterns within a dataset, it does not tell specifically where the patterning occurs. To investigate the locations of spatial patterns in the load-shedding exposure variables, local indicators of spatial association were used.
3.2.3. Local Indicators of Spatial Autocorrelation
Local indicators of spatial association (LISA) are important for pinpointing the locations of spatial hot spots, cold spots, clusters and outliers [45,46]. The two most common local indicators, namely Getis-Ord Gi* statistic and Anselin Local Moran’s I statistic were used in this study.
Briefly, the Getis-Ord Gi* statistic is useful for identifying statistically significant hot spots and cold spots from a set of weighted features. The Getis-Ord Gi* statistic is a z-score and is calculated according to Equation (9) [47]. Features with high/low values can only be hot/cold spots if they are surrounded by other features with similarly high/low values in a statistically significant way. For a given set of features and variables, the Gi* statistic tool generates a set of z-scores and p-values for each feature. The limits of the z-scores and p-values necessary for identifying statistically significant hot/cold spots are described in Table 2.
where is the attribute value for feature ; is the spatial weight between feature and ; is the mean of the corresponding attribute; is the standard deviation of the corresponding attribute; and is the total number of features.

Table 2.
Hot/cold spot classification.
Anselin Local Moran’s I statistic is used to identify spatial clusters and outliers among the features and their corresponding variables. Akin to hot/cold spots, clusters are neighborhoods that are surrounded by other neighborhoods with similarly high or low load-shedding exposure values. Outliers are neighborhoods that are surrounded by other neighborhoods with dissimilar load-shedding exposure values. The possible combinations of cluster/outlier neighborhoods are given in Table 3. The calculation for Anselin Local Moran’s I statistic is based on the following equation [48]:
where is an attribute for feature ; is the mean of the corresponding attribute; is the standard deviation of the corresponding attribute; and is the spatial weight between the feature and .

Table 3.
Cluster and outlier classification.
3.2.4. Conceptualization of Spatial Relationships
To better analyze the spatial associations amongst the study variables, it is necessary to first conceptualize how the neighborhoods interact within space. Various methodological options for defining spatial relationships among features exist within ArcGIS platform. Selecting an appropriate approach depends on the perceived spatial associations among the features under analysis. In this study, we use the polygon contiguity method, particularly the first-order contiguity edges and corners (Queen’s case) spatial weights matrix. The Queen’s case has been shown to better represent the spatial interaction of irregularly shaped and sized polygons than distance-based methods [29]. For this reason, we argue that it better represents the interaction among the study area neighborhoods. Subsequent to the use of the first-order queen’s case, we also utilize the row standardization option—where applicable—to minimize bias due to effects of aggregation and sampling that could result in neighborhoods having different numbers of neighbors.
4. Results and Discussion
4.1. Calculating, Normalizing and Visualizing Load Shedding Exposure
The calculated neighborhood-level load shedding exposure, , values are shown in Figure 3. The values range from 1117 to 3244 h for the year 2015. The descriptive statistics of load shedding exposure, together with those for the normalized variables are given in Table 4. From the results, it can be seen that experiences with load shedding vary markedly across neighborhoods in Accra. This is in agreement with the findings of a study carried out by Aidoo & Briggs [6]. Neighborhoods in the North, Central and Western parts of the study area generally experienced more load shedding exposure than those in the South and Eastern parts. Eleven neighborhoods have load-shedding exposure values in the highest classification range (2919 to 3244 h), two more than those in the lowest classification range (1117 to 1760 h). Each of the neighborhoods in the highest classification range, apart from Korle Dudor, shares a physical boundary with at least one of the other neighborhoods with which it occupies the same classification range. This indicates the potential clustering of neighborhoods with similarly high values. The same can be said for the neighborhoods with values classified under lower classification ranges.

Table 4.
Descriptive statistics of the study variables.
Through the normalization of load shedding exposure, we have introduced factors of surface area, population and population density to control for size and compositional differences among the neighborhoods. The spatial distribution of normalization factors is given in Figure 4, Figure 5 and Figure 6, while the resultant normalized load-shedding exposure values are visualized in Figure 7, Figure 8 and Figure 9. From the maps, it is evident that the spatial distribution of load shedding exposure is markedly altered by the normalization. For all normalized load-shedding exposure variables, most of their values fall within the two lowest classification ranges. For example, for , only six neighborhoods have values in the two highest classification ranges combined (17.43 to 84.59 min/capita). This can be attributed to the presence of a few outlier neighborhoods with very high normalized values. Because of this, there is also a very high likelihood of finding significant spatial clustering of neighborhoods with low values. From Figure 7, normalization with surface area confers higher values to neighborhoods with smaller surface areas. For both and , only one neighborhood (Awudome estate and Victoriaborg, respectively) has a very high value, classified under the highest classification range. The fact that there are a few, scattered high exposure neighborhoods surrounded by low exposure neighborhoods also hints at the potential presence of spatial outliers.
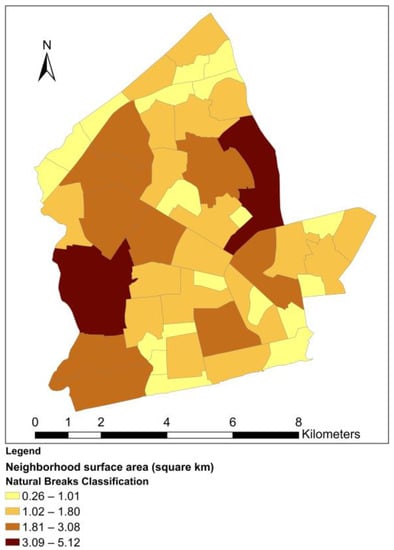
Figure 4.
Distribution of neighborhood surface area.
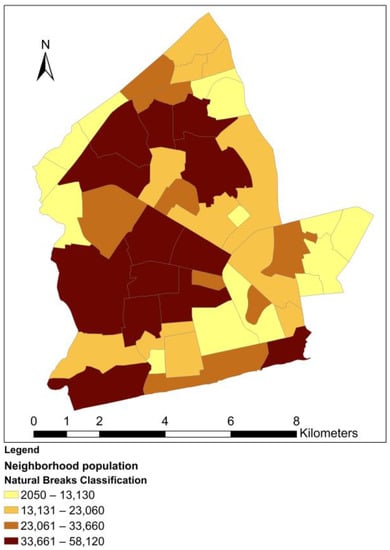
Figure 5.
Distribution of neighborhood population.
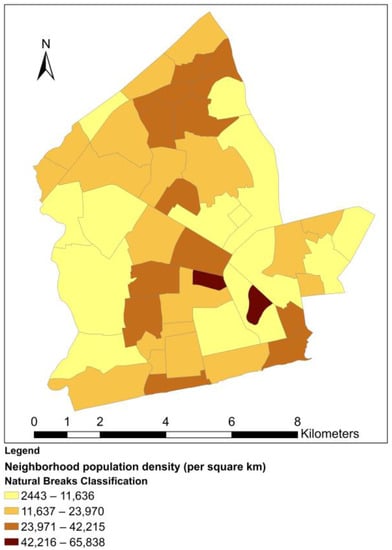
Figure 6.
Distribution of neighborhood population density.
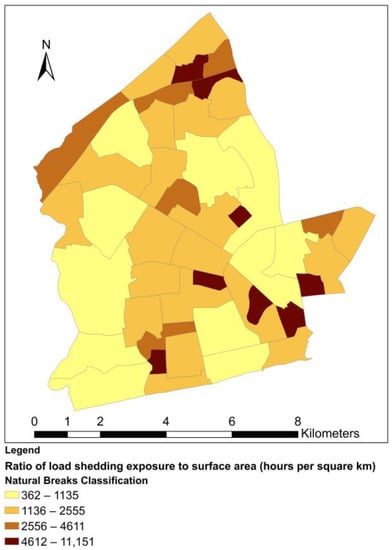
Figure 7.
Neighborhood exposure to electricity load shedding per unit area.
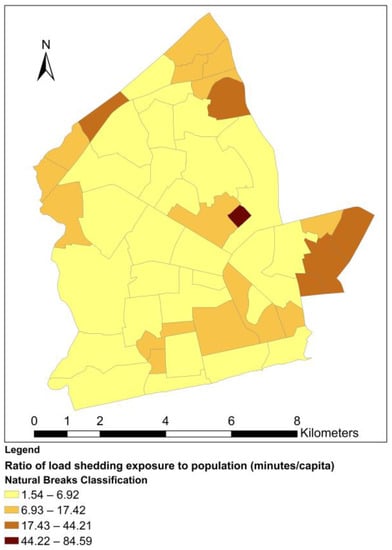
Figure 8.
Neighborhood ratio of load shedding exposure to population.
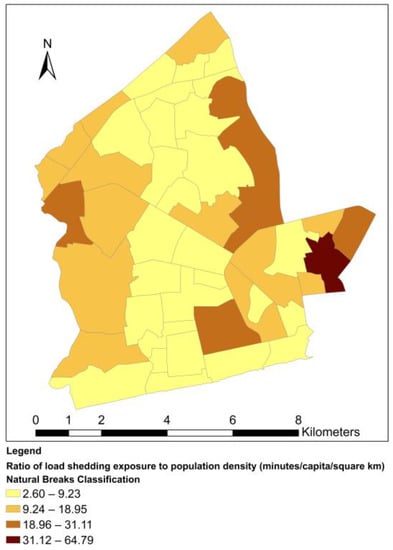
Figure 9.
Neighborhood ratio of load shedding exposure to population density.
4.2. Global Spatial Autocorrelation of Load Shedding Exposure
The results from the analysis of global spatial association for the load-shedding exposure variables are presented in this subsection (see Table 5). As explained in Section 3.2.2, the global Moran’s index is useful for investigating the (non-)existence of global spatial patterns. Load shedding exposure, and values exhibited statistically significant Moran’s I results (p < 0.05), while the Moran’s I results for and values were not significant (p > 0.1).

Table 5.
Global Moran’s I result for load-shedding exposure variables.
The statistical significance of the global Moran’s I results for load shedding exposure, and is at 99% and 95% confidence levels, respectively. This implies that the likelihood of the spatial distribution of their values in the study area being as a result of random chance is 1% and 5%, respectively. Furthermore, the positive z-score results of 3.84 and 2.57 obtained for and , respectively, confirm the spatial patterns as clustering of similar values. This means that, for both these variables, neighborhoods with similar values tend to be located more closely together than would be expected out of random chance. Consequently, the null hypothesis of complete spatial randomness can be rejected for both load shedding exposure, and . It can be concluded that spatial processes, other than random chance, influence the distribution of load shedding exposure, and values across the neighborhoods.
The spatial clustering of load shedding exposure, values can be explained by several factors. Firstly, in the study area, one 11 kV electricity feeder can serve electricity to several (bordering) neighborhoods. Therefore, nearby neighborhoods can potentially have the same or similar load shedding experience. Secondly, nearby neighborhoods also potentially have similar socio-economic characteristics. Considering that electricity (un)availability can be targeted basing on economic conditions [6], neighborhoods within the vicinity of each other can experience similar load shedding exposure.
The z-scores of all the transformed load-shedding exposure variables are smaller in magnitude compared to the unnormalized variable. This indicates that normalization has had a diminishing effect on the intensity of spatial patterning of load shedding exposure. Precisely, normalization with population density weakens but retains a statistically significant level of spatial clustering (z-score = 2.57; p < 0.05) of load shedding exposure. Normalization with population also reduces the clustering intensity of load shedding exposure (z-score = 1.60), but to a level where the clustering pattern is no longer statistically significant (p > 0.1). On the other hand, the negative z-score (−0.745) obtained for the variable indicates spatial dispersion rather than clustering. However, the pattern is also not statistically significant.
4.3. Hot Spot Analysis
Figure 10, Figure 11, Figure 12 and Figure 13 show the results from the hot spot analysis for the load-shedding exposure variables. Across all the variables, 16 different neighborhoods were identified as hot spots, and 10 neighborhoods as cold spots. Hot spots were identified in three of the four variables while cold spots were found in only two variables. Some neighborhoods were identified as hot spots in more than one variable while in another instance, a neighborhood classified as a hot spot in one variable was identified as a cold spot in another variable. A summary of the cross-cutting hot/cold spot neighborhoods is given in Table 6. For the unnormalized load shedding exposure,, (Figure 10), a total of 18 out of the 47 neighborhoods were identified as either hot spots or cold spots at different confidence levels. Ten neighborhoods are classified as hot spots while eight neighborhoods are cold spots. Only two neighborhoods—Tsaabaa (a hot spot) and Korle Gonno (a cold spot)—are spots at the highest confidence level of 99%. Ten neighborhoods are hot/cold spots at the 95% confidence level. With regard to the normalized load-shedding exposure variables (Figure 11, Figure 12 and Figure 13), not many hot/cold spots were identified. Darkuman and South Ordokor are the only significant (cold) spots—at a 90% confidence level—for . For and , four and five hot spot neighborhoods, respectively, have been identified, being mostly located in the eastern tip of the study area. No cold spot neighborhoods were returned for these two variables. Awudome estate is a highly significant (99% confidence level) hot spot for . Both Adabraka and Tudu are moderately significant (95% confidence level) hot spots for
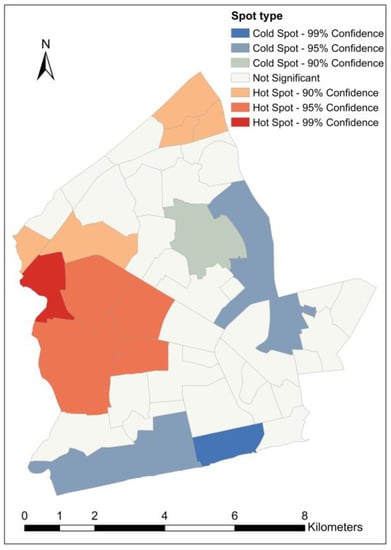
Figure 10.
Hot/cold spot neighborhoods for load shedding exposure.
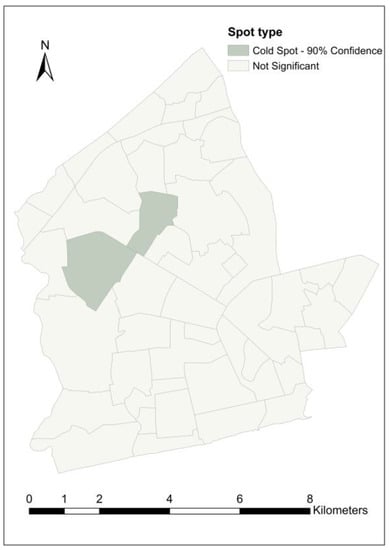
Figure 11.
Cold spot neighborhoods for load shedding exposure per unit area.
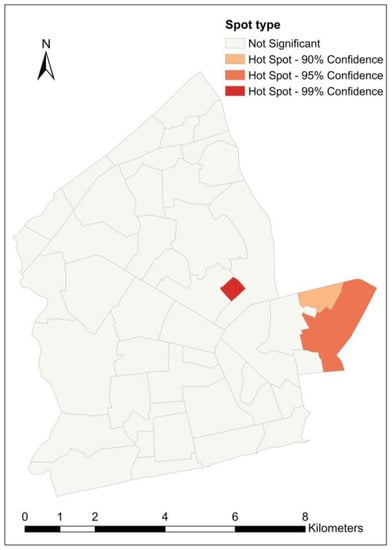
Figure 12.
Hot spot neighborhoods for ratio of load shedding exposure to population.
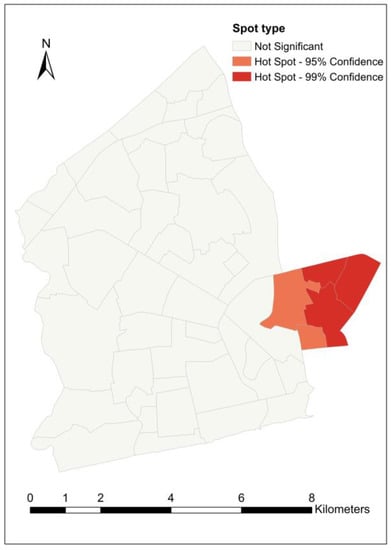
Figure 13.
Hot spot neighborhoods for ratio of load shedding exposure to population density.

Table 6.
Intersecting hot/cold spot neighborhoods for different load-shedding exposure variables.
4.4. Cluster and Outlier Analysis
Cluster and outlier analysis was carried out to complement the results from the hot spot analysis. Beyond this, however, cluster and outlier analysis was also useful for identifying outlier neighborhoods whose load-shedding exposure values significantly differ from those of their surrounding neighborhoods. Across all variables, a total of eight (08) different neighborhoods were identified as high-high clusters, ten (10) as low-low clusters, two (02) as high-low outliers and three (03) as low-high outliers. Each variable returned at least two low-low clusters while high-high cluster neighborhoods were identified in all variables except . Neighborhoods that were identified as clusters in more than one variable are given in Table 7. From Figure 14, the unnormalized load shedding exposure, , has the highest number of clusters—both high-high (07) and low-low (05) clusters. However, no significant outlier was identified in this variable. With regard to the , two neighborhoods—Darkuman and South Ordokor—were identified as low-low clusters and Bubiashie as a high-low outlier (see Figure 15). In Figure 16, four neighborhoods, including Darkuman, Mataheko, New Fadama and New Russia, are low-low clusters for , while the Korle Lagoon area is a high-low outlier. The clusters for are Chorkor, Lapaz and New Fadama (all low-low clusters), while Adabraka, Asylum Down and Tudu are low-high outliers (see Figure 17). North Ridge is a high-high cluster for both and .

Table 7.
Neighborhoods showing more than one clustering tendency for different load-shedding exposure variables.
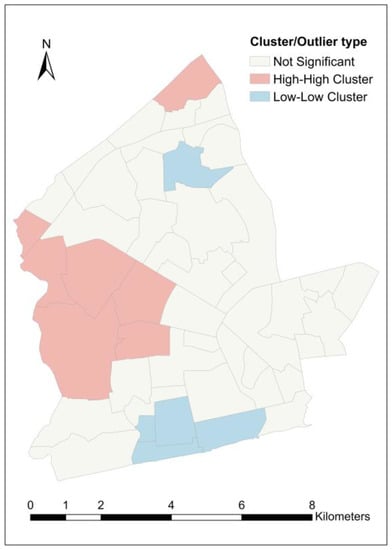
Figure 14.
Cluster neighborhoods for load shedding exposure.
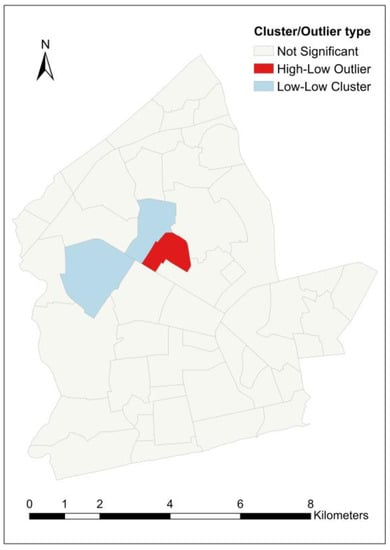
Figure 15.
Cluster and outlier neighborhoods for load shedding exposure per unit area.
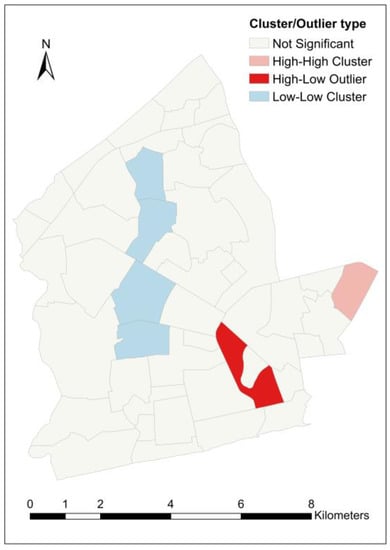
Figure 16.
Cluster and outlier neighborhoods for ratio of load shedding exposure to population.
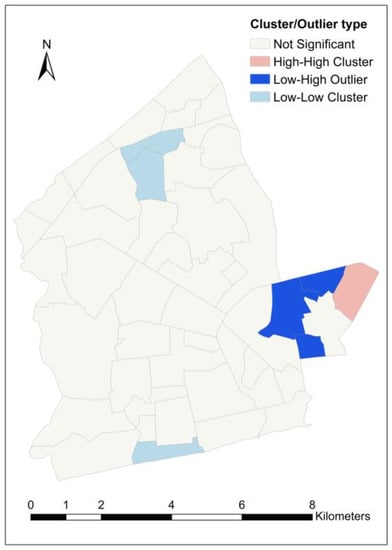
Figure 17.
Cluster and outlier neighborhoods for ratio of load shedding exposure to population density.
4.5. Comparing Results from Local Indicators of Spatial Association (LISA) Analyses
Table 8 is a comparative presentation of results from both hot spot analysis and cluster and outlier analysis. Several neighborhoods that intersect as spots and clusters/outliers are identified. There are eight (08) neighborhoods categorized both as hot spots and high-high clusters. Seven of these were identified under load shedding exposure, . The other neighborhood categorized both as a hot spot and a high-high cluster is North Ridge under both and . Several neighborhoods that were identified as hot spots fall under outlier category when using cluster and outlier analysis. Particularly, Adabraka, Asylum Down and Tudu, which are hot spot neighborhoods for , are identified as low-high outliers under the same variable. Other hot spot neighborhoods under , and are categorized as “insignificant” when using cluster and outlier analysis.

Table 8.
Neighborhoods at the intersection of different spot and cluster/outlier types.
Several neighborhoods identified as cold spots also turned out as low-low clusters. Six (06) neighborhoods under and fall within this characterization. For , four (04) neighbourhoods, which are cold spots, are categorized as “insignificant” when using cluster and outlier analysis. Under all variables, some neighborhoods that were categorized as “insignificant” under hot spot analysis were found to be significant clusters/outliers and vice versa. However, in general, most of the neighborhoods remained “insignificant” when using both hot spot analysis, and cluster and outlier analysis.
From the above results, hot spot analysis and cluster and outlier analysis can generally be said to be complimentary approaches, particularly for identifying spatial clusters. While some differences have been observed in the cluster and spot results under the same variable, these may be attributed to the fact that clusters (and outliers) are only considered significant at p < 0.05, while hot/cold spots are classified from a 90% confidence level. This highlights the uniqueness of the underlying calculations upon which the two local indicators of spatial association (LISA) approaches are based [48]. Therefore, depending on the purpose of the study, it may be beneficial to use both methods and compare their results. Additionally, both methods are useful for any study—including the present study—which is interested in identifying spatial clusters at varying confidence intervals (possible by hot spot analysis) as well as spatial outliers (possible by cluster and outlier analysis). In this case, the two methods play a supplementary role.
4.6. Comparing Visualization and Spatial Statistical Analysis Results
For load shedding exposure, , there was a general agreement between the spatial characteristics inferred from both visualization and spatial statistical tools. However, for normalized variables, this was not the case. For all normalized variables, visualization categorized most neighborhoods under the two lowest classification ranges on their respective maps. This seemed to suggest a higher possibility of finding many low-low clusters as well as a high likelihood of finding spatial outliers, especially high-low outliers. However, several neighborhoods that appeared to be cold spots, low-low clusters or high-low outliers from the visualized data were not identified as such when using spatial statistical tools. Therefore, while spatial visualization is a useful tool for data exploration, it should not be entirely relied upon for making concrete spatial interpretation [41]. It should be used in conjunction with other more robust spatial tools.
5. Conclusions, Limitations and Future Research
In this study, electricity outage segments from the 2015 load shedding outages were spatially linked to 47 corresponding neighborhoods in Accra, Ghana. Using a load-shedding exposure variable, the extent of electricity outages experienced in each neighborhood was quantified. The load-shedding exposure values were then transformed using relevant factors, examined for spatial patterns and relevant maps produced. The mapped results are very easy to understand by a wide range of stakeholders including utility-level decision makers, local leaders and residents. To the best of our knowledge, no previous study has used such a spatial approach to comprehensively quantify, analyze and present outage exposure in Ghana at such a small geographical scale. By using an extensive outage dataset from the electricity utility company, this study has presented a more complete picture of neighborhood load shedding experiences, beyond what was previously reported in other studies. In particular, the study results reveal the following:
Firstly, there are considerable variations in load shedding experiences across neighborhoods in Accra. Some neighborhoods were exposed to twice as many load shedding hours as others during the 2015 nationwide electricity crisis. Neighborhoods having similarly high or low load shedding exposure are more spatially clustered together than would be expected by random chance. This indicates that other spatial processes (socioeconomic, political, demographic and other factors) influenced the distribution of load shedding outages in the study area. Secondly, normalizing load-shedding exposure values with surface area, population and population density significantly altered the spatial distribution characteristics of load shedding exposure in Accra neighborhoods. Specifically, the strength of the spatial association of load shedding exposure was diminished when normalization was carried out. In any case, normalization was useful for transforming the absolute load-shedding exposure values to ensure some form of standardized comparison of experiences across neighborhoods. Moreover, societal factors introduced into the analysis through normalization helped to explore the distribution of load shedding experiences from different perspectives. Lastly, there are several hot/cold spot, cluster and outlier neighborhoods across both the normalized and unnormalized load-shedding exposure variables. By pinpointing the location of hot/cold spots and clusters, the study has provided useful spatial information to utility-level decision makers. In case of future electricity supply shortages, the electricity utility company can utilize these results to improve load shedding planning in the study area towards achieving sustainable electrification. Hot spots, high-high clusters and high-low outliers also point to potential priority neighborhoods for implementing targeted interventions to build resilience against load shedding impacts, including information campaigns about coping measures. Moreover, a further investigation of any unique features in the low-high outlier neighborhoods, may provide useful information about potential drivers of outage decisions made by utility managers, such as, the prioritization of critical infrastructure (for example, hospitals).
Whereas every effort was made to undertake a comprehensive study covering the whole city of Accra, ultimately the study was limited to neighborhoods in the western part of the Accra metropolis, which are under the jurisdiction of a single electricity utility branch. Therefore, the results can only be interpreted within the context of the study area and may not necessarily represent the experiences across the entire city of Accra. Analyzing load shedding experiences across all the neighborhoods in Accra may offer a complete picture of city-wide experiences. However, extra caution should be taken when carrying out a city-wide assessment for Accra using this approach. Since the Accra metropolis is served by two branches of the utility company, there is a potential risk of introducing data-related errors into the analysis. There is no guarantee that both utility branches consistently collect all the outage statistics over a long period of time. Furthermore, for normalization, a few select societal factors have been used because their data was readily available. Future studies should utilize other relevant variables and explore their effect on outage experiences. Beyond normalization, other methods, such as regression analyses may be used, for example, to assess and model the relationship between outage exposure and socioeconomic or demographic factors, while taking into account spatial aspects. Finally, other studies should also seek to understand how neighborhoods experience other types of electricity outages, such as unplanned outages and the underlying causes of these recurrent outages. This could shed more light on the persistent challenges in electricity distribution in developing countries, for example, aging infrastructure, electricity pricing, maintenance scheduling, and governance challenges.
Author Contributions
Conceptualization, P.N. and M.G.; methodology, P.N.; software, P.N.; validation, P.N.; formal analysis, P.N.; investigation, P.N.; data curation, P.N.; writing—original draft preparation, P.N.; writing—review and editing, A.Z. and M.G.; visualization, P.N.; supervision, A.Z. and M.G. All authors have read and agree to the published version of the manuscript.
Funding
This research was carried out under the Water and Energy Security for Africa (WESA) project funded by the Germany Federal Ministry of Education and Research (BMBF) through the DLR project management agency.
Acknowledgments
The authors highly appreciate the support received from personnel of the Electricity Company of Ghana (ECG), who granted access to relevant data without which this study would not have been possible. The authors also thank John Weeks, Christopher D. Lippitt and others in the team that developed the Accra neighborhood map. Their willingness to share their work greatly benefitted this study. Special mention also goes to Richard Ampadu-Ameyaw of CSIR-STEPRI in Accra, Ghana for the valuable all-round support during the fieldwork. All the views, opinions, and conclusions in this article are entirely the authors’ and do not necessarily represent the views of the above-mentioned individuals or institutions.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in writing of the manuscript, or in the decision to publish the results.
References
- Ghanem, D.A.; Mander, S.; Gough, C. “I think we need to get a better generator”: Household resilience to disruption to power supply during storm events. Energy Policy 2016, 92, 171–180. [Google Scholar] [CrossRef]
- Mitsova, D.; Esnard, A.-M.; Sapat, A.; Lai, B.S. Socioeconomic vulnerability and electric power restoration timelines in Florida: The case of Hurricane Irma. Nat. Hazards 2018, 94, 689–709. [Google Scholar] [CrossRef]
- Hines, P.; Apt, J.; Talukdar, S. Large blackouts in North America: Historical trends and policy implications. Energy Policy 2009, 37, 5249–5259. [Google Scholar] [CrossRef]
- Panteli, M.; Mancarella, P. Influence of extreme weather and climate change on the resilience of power systems: Impacts and possible mitigation strategies. Electr. Power Syst. Res. 2015, 127, 259–270. [Google Scholar] [CrossRef]
- Hiete, M.; Merz, M.; Schultmann, F. Scenario-based impact analysis of a power outage on healthcare facilities in Germany. Int. J. Disaster Resil. Built Environ. 2011, 2, 222–244. [Google Scholar] [CrossRef]
- Aidoo, K.; Briggs, R.C. Underpowered: Rolling blackouts in Africa disproportionately hurt the poor. Afr. Stud. Rev. 2019, 62, 112–131. [Google Scholar] [CrossRef]
- Paradi-Guilford, C. How Ghana Is Tackling Energy Shortages. Available online: https://www.weforum.org/agenda/2015/03/how-ghana-is-tackling-energy-shortages/ (accessed on 25 March 2015).
- Andersen, T.B.; Dalgaard, C.-J. Power outages and economic growth in Africa. Energy Econ. 2013, 38, 19–23. [Google Scholar] [CrossRef]
- Cole, M.A.; Elliott, R.J.; Occhiali, G.; Strobl, E. Power outages and firm performance in Sub-Saharan Africa. J. Dev. Econ. 2018, 134, 150–159. [Google Scholar] [CrossRef]
- Moyo, B. Power infrastructure quality and manufacturing productivity in Africa: A firm level analysis. Energy Policy 2013, 61, 1063–1070. [Google Scholar] [CrossRef]
- Diboma, B.; Tatietse, T.T. Power interruption costs to industries in Cameroon. Energy Policy 2013, 62, 582–592. [Google Scholar] [CrossRef]
- Farquharson, D.; Jaramillo, P.; Samaras, C. Sustainability implications of electricity outages in sub-Saharan Africa. Nat. Sustain. 2018, 1, 589–597. [Google Scholar] [CrossRef]
- Mensah, J.T. Jobs! Electricity Shortages and Unemployment in Africa; World Bank Group: Washington, DC, USA, 2018. [Google Scholar]
- PULSE. Dumsor Cost Us $3Billion—Nana Addo. Available online: https://www.pulse.com.gh/news/business/power-crisis-dumsor-cost-us-dollar3billion-nana-addo/m0ye2mc (accessed on 17 August 2017).
- Kamasa, K.; Adu, G.; Oteng-Abayie, E. Business environment and firms’ decisions to evade taxes: Evidence from Ghana. Afr. J. Bus. Econ. Res. 2019, 14, 135–155. [Google Scholar] [CrossRef]
- Dzansi, J.; Puller, S.L.; Street, B.; Yebuah-Dwamena, B. The Vicious Circle of Blackouts and Revenue Collection in Developing Economies: Evidence from Ghana (E-89457-GHA-1); International Growth Centre: London, UK, 2018. [Google Scholar]
- Apenteng, B.A.; Opoku, S.T.; Ansong, D.; Akowuah, E.A.; Afriyie-Gyawu, E. The effect of power outages on in-facility mortality in healthcare facilities: Evidence from Ghana. Glob. Public Health 2018, 13, 545–555. [Google Scholar] [CrossRef] [PubMed]
- Bayor, I.; Yelyang, A. The Ghana “Dumsor” Energy Setbacks and Sensitivities: From Confrontation to Collaboration; West Africa Network for Peacebuilding (WANEP): Accra, Ghana, 2015. [Google Scholar]
- Liévanos, R.S.; Horne, C. Unequal resilience: The duration of electricity outages. Energy Policy 2017, 108, 201–211. [Google Scholar] [CrossRef]
- Maliszewski, P.J.; Perrings, C. Factors in the resilience of electrical power distribution infrastructures. Appl. Geogr. 2012, 32, 668–679. [Google Scholar] [CrossRef]
- Kesselring, R. The electricity crisis in Zambia: Blackouts and social stratification in new mining towns. Energy Res. Soc. Sci. 2017, 30, 94–102. [Google Scholar] [CrossRef]
- Min, B. Political Favoritism and the Targeting of Power Outages; International Growth Centre: London, UK, 2019. [Google Scholar]
- De Oliveira, V.H.; de Medeiros, C.N.; Carvalho, J.R. Violence and local development in Fortaleza, Brazil: A spatial regression analysis. Appl. Spat. Anal. 2019, 12, 147–166. [Google Scholar] [CrossRef]
- Tu, W.; Tedders, S.; Tian, J. An exploratory spatial data analysis of low birth weight prevalence in Georgia. Appl. Geogr. 2012, 32, 195–207. [Google Scholar] [CrossRef]
- Rodríguez-Pose, A.; Tselios, V. Mapping the European regional educational distribution. Eur. Urban Reg. Stud. 2011, 18, 358–374. [Google Scholar] [CrossRef]
- Sharma, A. Exploratory spatial data analysis of older adult migration: A case study of North Carolina. Appl. Geogr. 2012, 35, 327–333. [Google Scholar] [CrossRef]
- Vidyattama, Y.; Li, J.; Miranti, R. Measuring spatial distributions of secondary education achievement in Australia. Appl. Spat. Anal. 2019, 12, 493–514. [Google Scholar] [CrossRef]
- Nunes, L.; Lourenço, L.; Meira, A.C. Exploring spatial patterns and drivers of forest fires in Portugal (1980–2014). Sci. Total Environ. 2016, 573, 1190–1202. [Google Scholar] [CrossRef] [PubMed]
- Tsai, P.-J.; Lin, M.-L.; Chu, C.-M.; Perng, C.-H. Spatial autocorrelation analysis of health care hotspots in Taiwan in 2006. BMC Public Health 2009, 9, 464. [Google Scholar] [CrossRef] [PubMed]
- López-Carr, D.; Pricope, N.G.; Aukema, J.E.; Jankowska, M.M.; Funk, C.; Husak, G.; Michaelsen, J. Spatial analysis of population dynamics and climate change in Africa: Potential vulnerability hot spots emerge where precipitation declines and demographic pressures coincide. Popul. Environ. 2014, 35, 323–339. [Google Scholar] [CrossRef]
- Hession, S.L.; Moore, N. A spatial regression analysis of the influence of topographyon monthly rainfall in East Africa. Int. J. Climatol. 2011, 31, 1440–1456. [Google Scholar] [CrossRef]
- Ansong, D.; Ansong, E.K.; Ampomah, A.O.; Afranie, S. A spatio-temporal analysis of academic performance at the Basic Education Certificate Examination in Ghana. Appl. Geogr. 2015, 65, 1–12. [Google Scholar] [CrossRef]
- Boyda, D.C.; Holzman, S.B.; Berman, A.; Grabowski, M.K.; Chang, L.W. Geographic information systems, spatial analysis, and HIV in Africa: A scoping review. PLoS ONE 2019, 14, e0216388. [Google Scholar] [CrossRef]
- Ramachandra, T.; Shruthi, B. Spatial mapping of renewable energy potential. Renew. Sustain. Energy Rev. 2007, 11, 1460–1480. [Google Scholar] [CrossRef]
- Güngör-Demirci, G. Spatial analysis of renewable energy potential and use in Turkey. J. Renew. Sustain. Energy 2015, 7, 013126(1)–013126(17). [Google Scholar]
- Arnette, N.; Zobel, C.W. Spatial analysis of renewable energy potential in the greater southern Appalachian mountains. Renew. Energy 2011, 36, 2785–2798. [Google Scholar] [CrossRef]
- Wang, Q.; Kwan, M.-P.; Fan, J.; Zhou, K.; Wang, Y.-F. A study on the spatial distribution of the renewable energy industries in China and their driving factors. Renew. Energy 2019, 139, 161–175. [Google Scholar] [CrossRef]
- Xie, H.; Liu, G.; Liu, Q.; Wang, P. Analysis of spatial disparities and driving factors of energy consumption change in China based on spatial statistics. Sustainability 2014, 6, 2264–2280. [Google Scholar] [CrossRef]
- Walker, R.; McKenzie, P.; Liddell, C.; Morris, C. Spatial analysis of residential fuel prices: Local variations in the price of heating oil in Northern Ireland. Appl. Geogr. 2015, 63, 369–379. [Google Scholar] [CrossRef]
- Dar-Mousa, R.N.; Makhamreh, Z. Analysis of the pattern of energy consumptions and its impact on urban environmental sustainability in Jordan: Amman City as a case study. Energy Sustain. Soc. 2019, 9, 15. [Google Scholar] [CrossRef]
- Tyralis, H.; Mamassis, N.; Photis, Y.N. Spatial analysis of the electrical energy demand in Greece. Energy Policy 2017, 102, 340–352. [Google Scholar] [CrossRef]
- Parry, D.; Cowley, C. Maps as a technique for visualizing load-shedding schedules. In Proceedings of the 2015 Annual Conference of the South African Institute of Computer Scientists and Information Technologists: Knowledge through Technology (SAICSIT 2015), Stellenbosch, South Africa, 28–30 September 2015. [Google Scholar]
- GSS. Demography: Population Projection. Available online: http://www.statsghana.gov.gh/nationalaccount_macros.php?Stats=MTA1NTY1NjgxLjUwNg==/webstats/s679n2sn87 (accessed on 14 August 2019).
- Engstrom, R.; Ofiesh, C.; Rain, D.; Jewell, H.; Weeks, J. Defining neighborhood boundaries for urban health research in developing countries: A case study of Accra, Ghana. J. Maps 2013, 9, 36–42. [Google Scholar] [CrossRef]
- Waller, L.A.; Gotway, C.A. Applied Spatial Statistics for Public Health Data; John Wiley and Sons: New York, NY, USA, 2004. [Google Scholar]
- ESRI. How Spatial Autocorrelation (Global Moran’s I) Works: ArcMap. Available online: https://desktop.arcgis.com/en/arcmap/10.5/tools/spatial-statistics-toolbox/h-how-spatial-autocorrelation-moran-s-i-spatial-st.htm (accessed on 10 May 2018).
- Getis, A.; Ord, J.K. The analysis of spatial association by use of distance statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Anselin, L. Local Indicators of Spatial Association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).