An Energy Efficient Message Dissemination Scheme in Platoon-Based Driving Systems
Abstract
1. Introduction
2. Related Works
3. Energy Efficient Message Dissemination
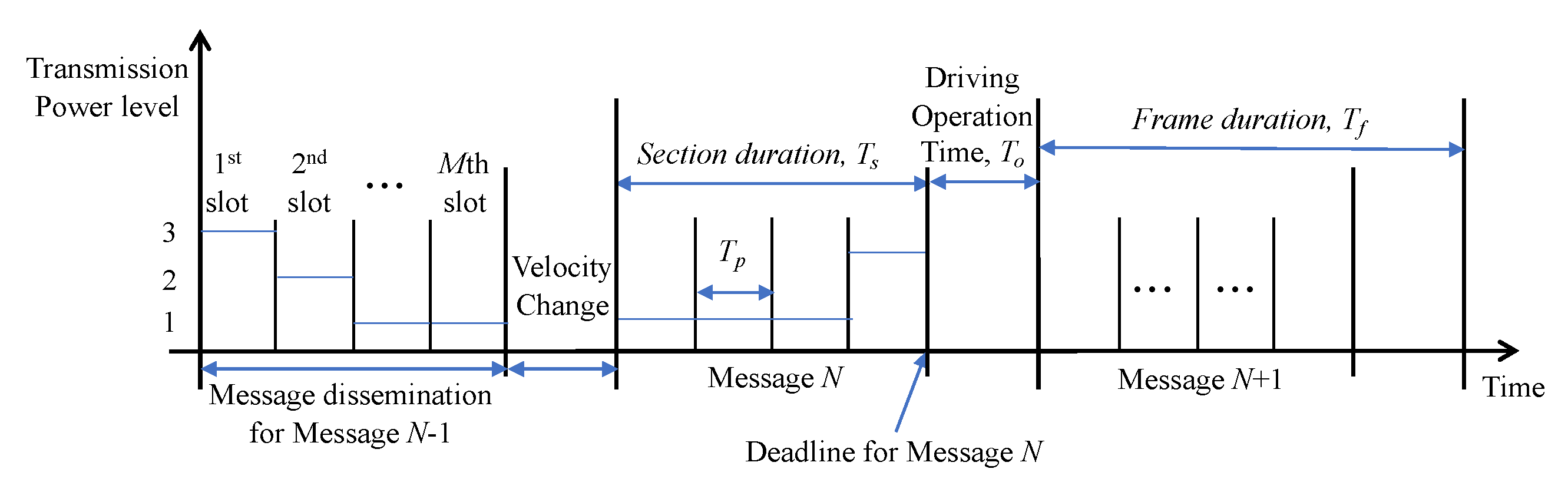
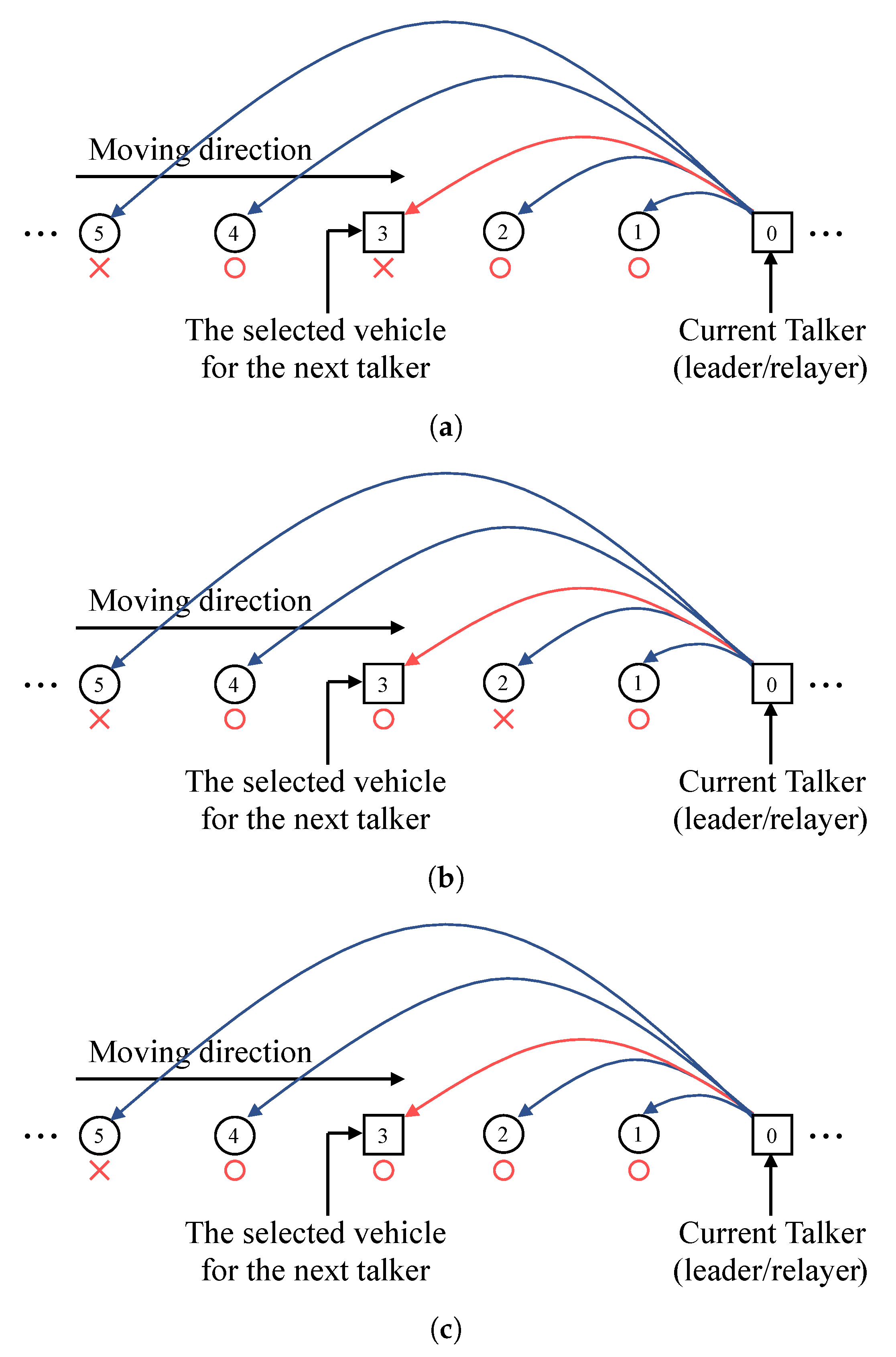
3.1. Arq-Based Relay Protocol
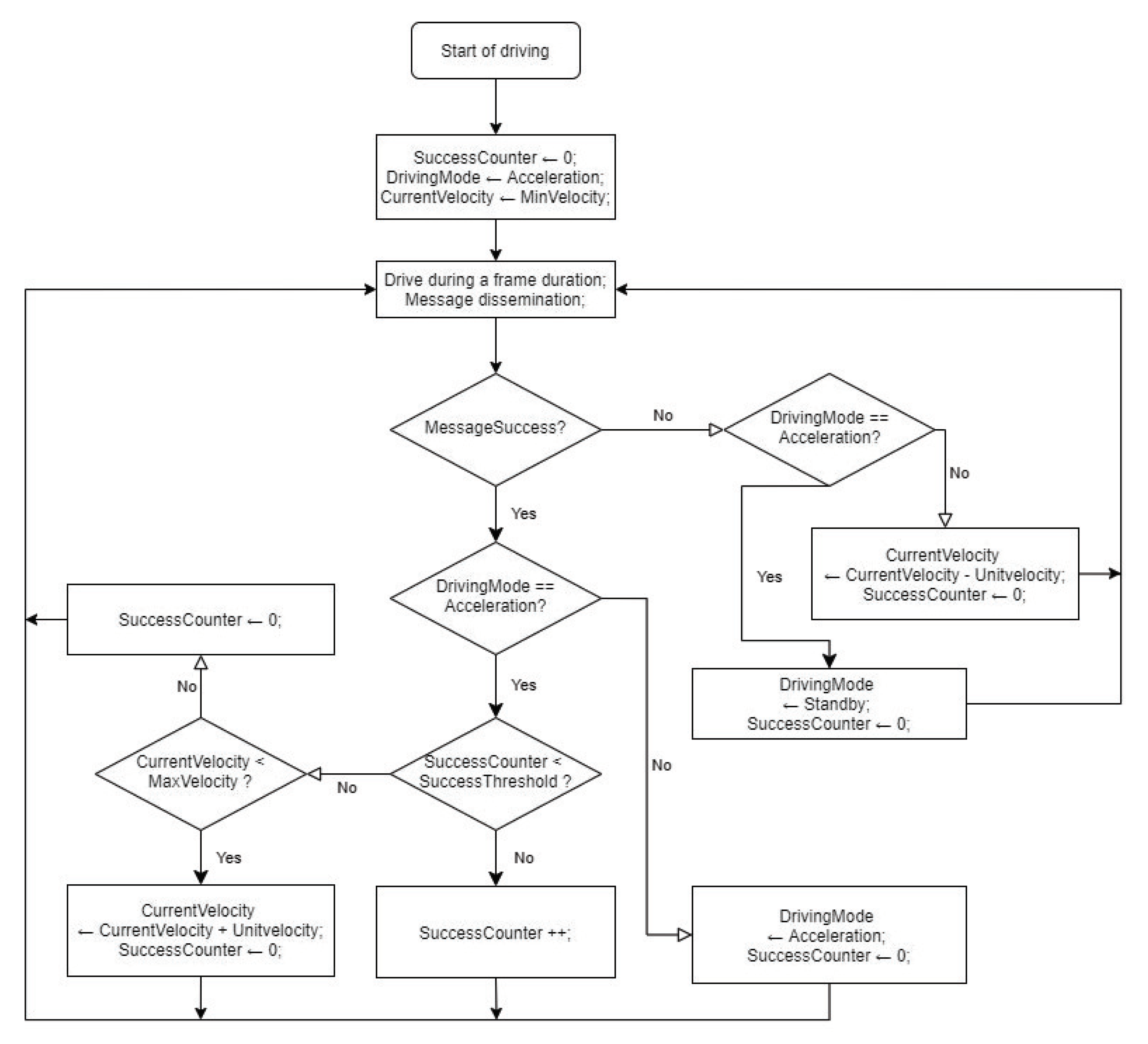
3.2. Adaptive Platoon Velocity Control Scheme
4. Mdp Formulation
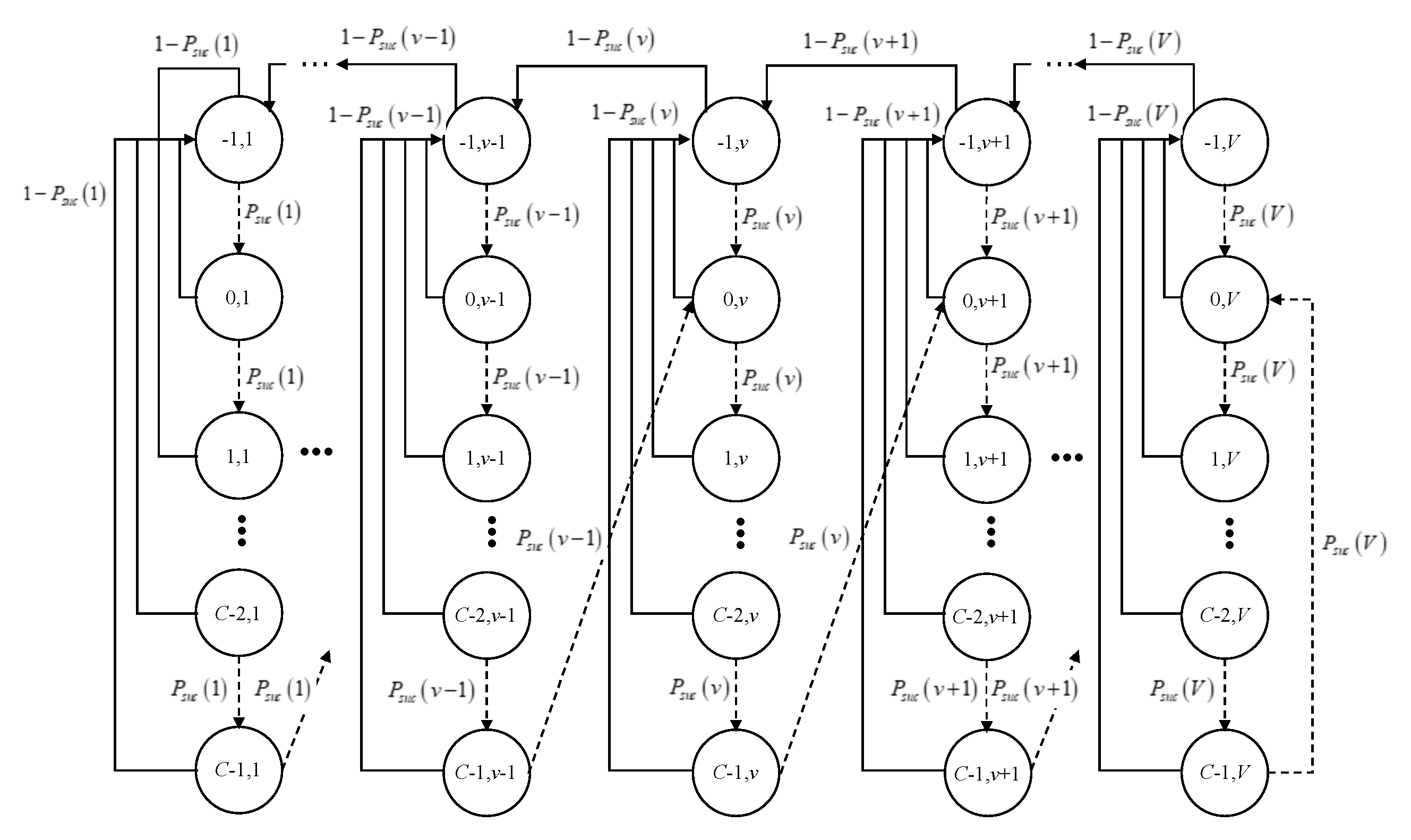
4.1. State Space
- denotes the state of the platoon velocity, where is the maximum platoon velocity. All the velocities are normalized with respect to a unit platoon velocity, . Thus, the velocity of the platoon is considered to be an integer multiple of and can be defined as .
- is the set of driving modes of the platoon. The platoon takes the value 1 when it tries to accelerate the platoon velocity. On the contrary, the platoon takes the value 0 when it enters to the standby mode.
- is the state of the counter of the successful message dissemination, where C is a given threshold for the counter regarding consecutive successful message dissemination.
- is the set of time-slots in the duration of a frame for the operation of platoon-based driving. That is to say, is the union of two sets and , where is the set of slots in the duration of a section and is the driving operation time, in which the platoon changes its velocity after the finish of the message dissemination. There are totally M slots in a section; thus, the number of possible packet transmission attempt is M. In conclusion, a message dissemination is conducted in first M slot times of . After that, the change of the platoon velocity is performed in the th slot in .
- is the set of packet reception states, where P is the total number of possible combinations of cumulative status of ACK reception from every non-leader vehicles, i.e., , if there are totally vehicles in the platoon except the leader. Also, a possible case for the cumulative ACK reception is represented by a vector, which is represented by where is an index variable. That is, if ACK has been received from the the th follower vehicle within current slot, . Otherwise, . For example, if the total number of non-leader vehicle is 5 and the first and third follower vehicles have sent their ACKs until the current slot, . In addition, if .
- is the set of possible talkers, where total number of the vehicles in the platoon is N. Since talkers are vehicles who forward the control packets, tail is not included in the set of talkers.
4.2. Action Space
4.3. State Transition Function
4.4. Reward and Cost Functions
4.5. Optimal Equation
| Algorithm 1: Value iteration algorithm. |
 |
5. Performance Measures
6. Evaluation Results
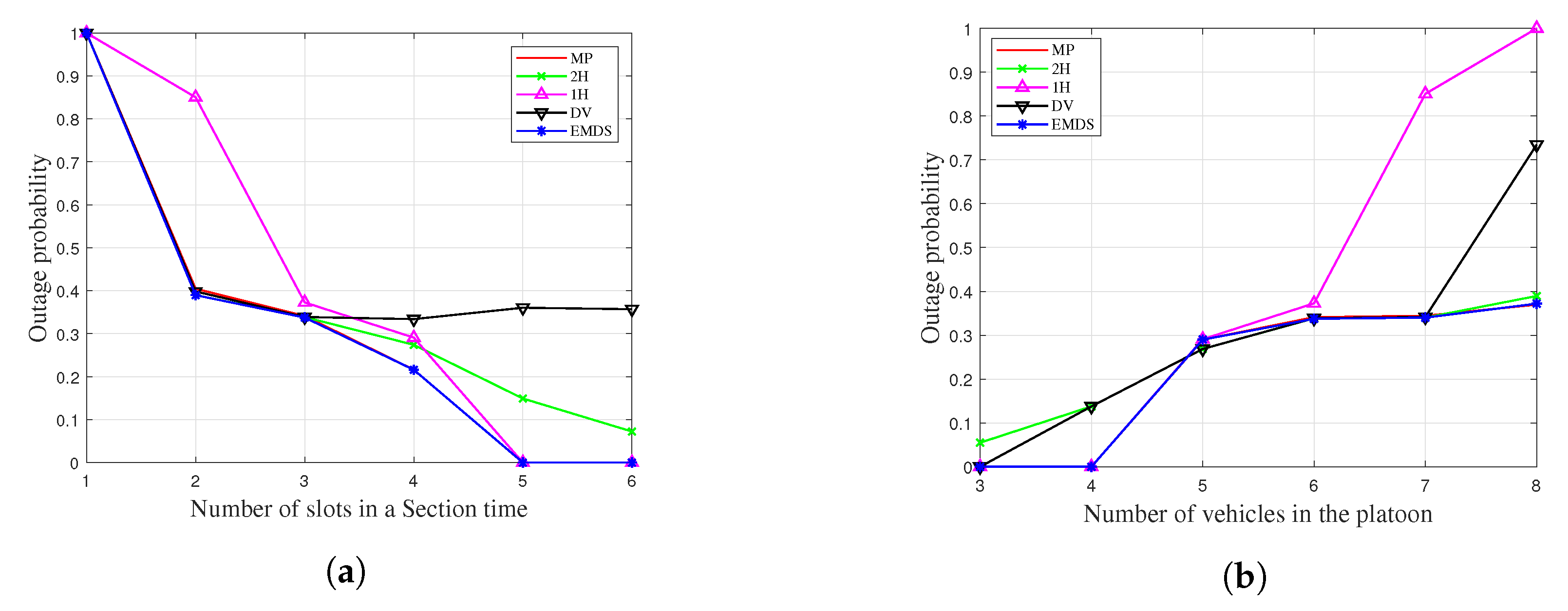
6.1. Outage Probability
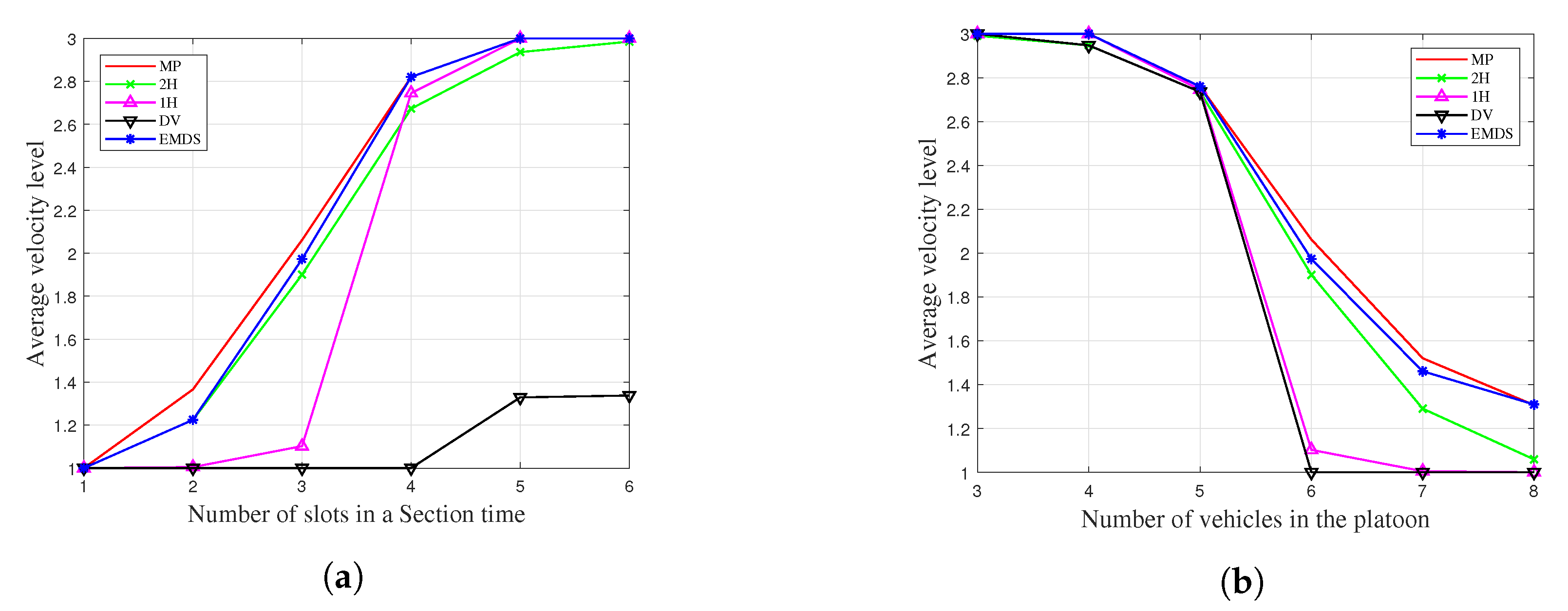
6.2. Average Velocity Level
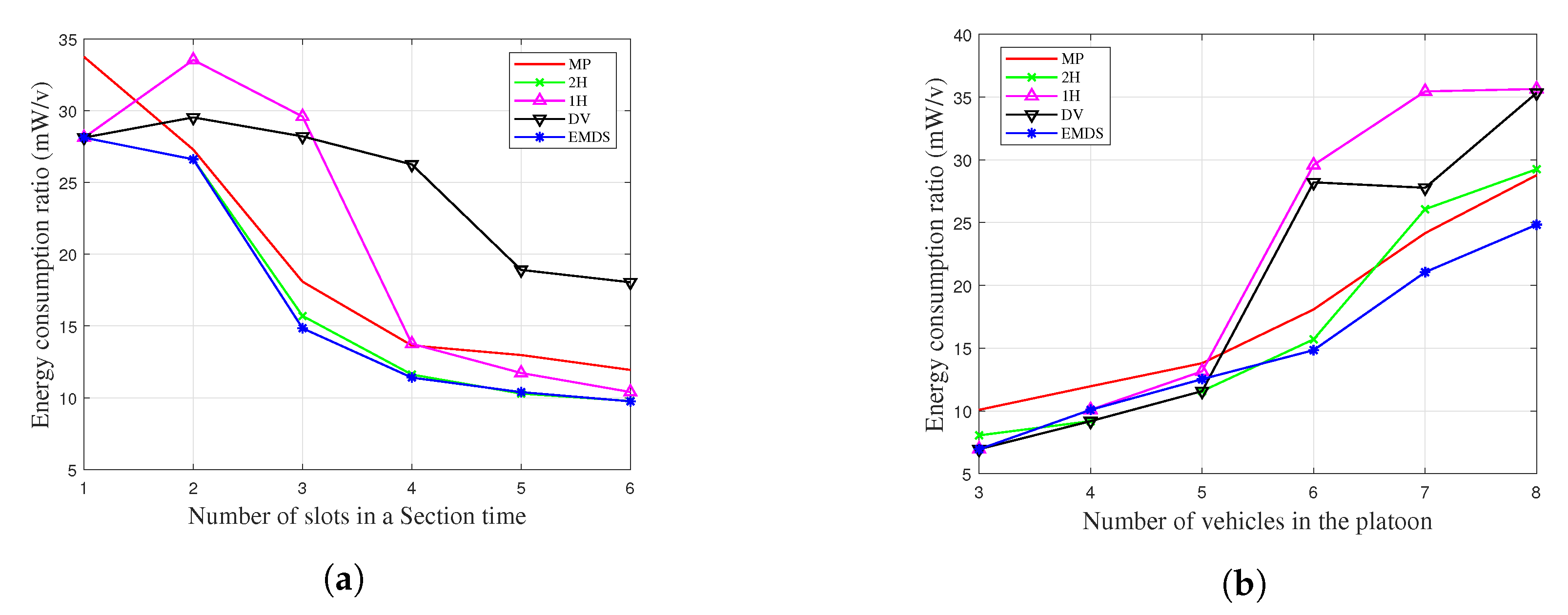
6.3. Energy Efficiency
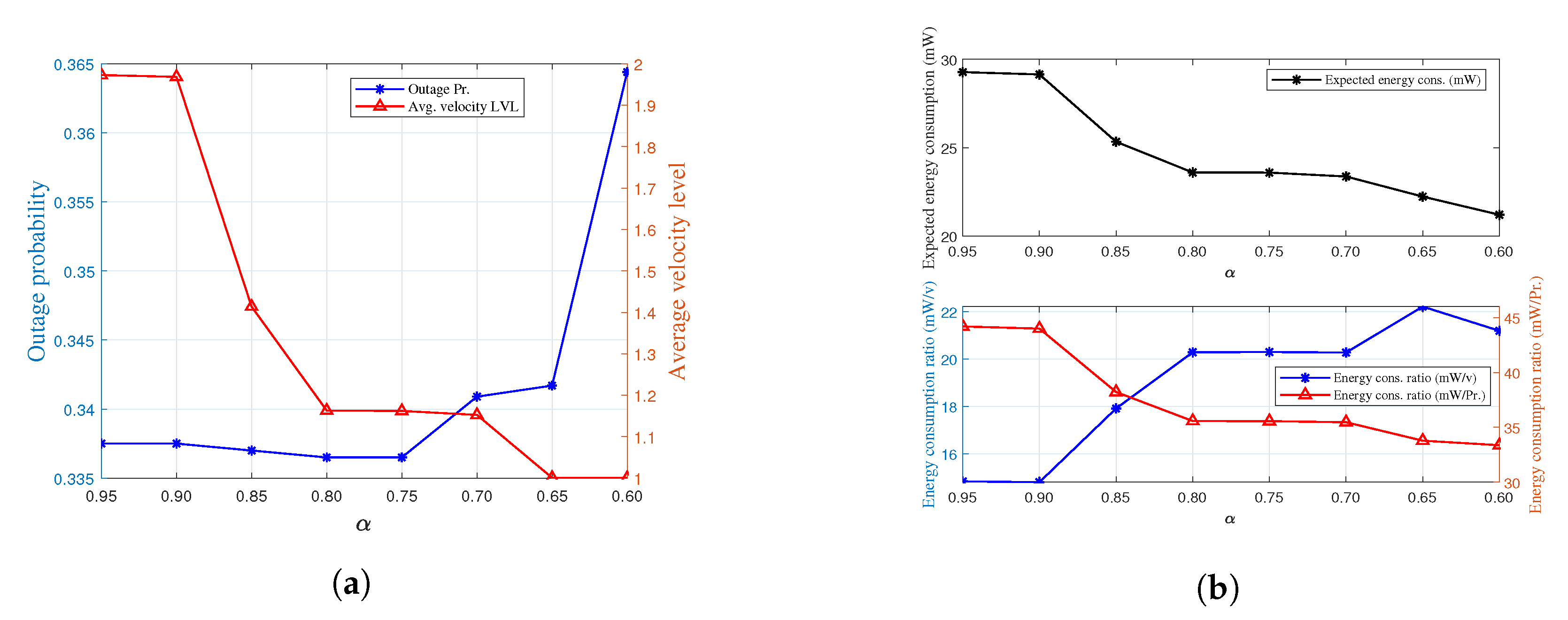
6.4. Effect of
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Peng, H.; Li, D.; Abboud, K.; Zhou, H.; Zhao, H.; Zhuang, W.; Shen, X.S. Performance Analysis of IEEE 802.11 p DCF for Multiplatooning Communications With Autonomous Vehicles. IEEE Trans. Veh. Technol. 2017, 66, 2485–2498. [Google Scholar] [CrossRef]
- Alam, A.; Gattami, A.; Johansson, K. An experimental study on the fuel reduction potential of heavy duty vehicle platooning. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems, Funchal, Portugal, 19–22 September 2010; pp. 306–311. [Google Scholar]
- Marzbani, H.; Khayyam, H.; Quoc, C.N.T.O.Đ.; Jazar, R.N. Autonomous Vehicles: Autodriver Algorithm and Vehicle Dynamics. IEEE Trans. Veh. Technol. 2019, 68, 3201–3211. [Google Scholar] [CrossRef]
- Wu, Q.; Nie, S.; Fan, P.; Liu, H.; Qiang, F.; Li, Z. A Swarming Approach to Optimize the One-Hop Delay in Smart Driving Inter-Platoon Communications. Sensors 2018, 18, 3307. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Dai, Y.; Xia, J. A CAV Platoon Control Method for Isolated Intersections: Guaranteed Feasible Multi-Objective Approach with Priority. Energies 2020, 13, 625. [Google Scholar] [CrossRef]
- Dey, K.C.; Yan, L.; Wang, X.; Wang, Y.; Shen, H.; Chowdhury, M.; Soundararaj, V. A Review of Communication, Driver Characteristics, and Controls Aspects of Cooperative Adaptive Cruise Control (CACC). IEEE Trans. Intell. Transp. Syst. 2016, 17, 491–509. [Google Scholar] [CrossRef]
- Zhou, T.; Sharif, H.; Hempel, M.; Mahasukhon, P.; Wang, W.; Ma, T. A novel adaptive distributed cooperative relay MAC protocol for vehicular networks. IEEE J. Sel. Areas Commun. 2011, 29, 72–82. [Google Scholar] [CrossRef]
- Fasolo, E.; Zanella, A.; Zorzi, M. An effective broadcast scheme for alert message propagation in vehicular ad hoc networks. Proc. IEEE ICC 2006, 3960–3965. [Google Scholar]
- Tonguz, O.K.; Wisitpongphan, N.; Fan, B. DV-CAST: A distributed vehicular broad- cast protocol for vehicular ad hoc networks. IEEE Wirel. Commun. 2010, 17, 47–57. [Google Scholar] [CrossRef]
- Kaul, S.; Gruteser, M.; Rai, V.; Kenney, J. Minimizing age of information in vehicular networks. In Proceedings of the 2011 8th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks, Salt Lake City, UT, USA, 27–30 June 2011; pp. 350–358. [Google Scholar]
- Bharati, S.; Zhuang, W. CAH-MAC: Cooperative ADHOC MAC for vehicular networks. IEEE J. Sel. Areas Commun. 2013, 31, 470–479. [Google Scholar] [CrossRef]
- Yang, F.; Tang, Y. Cooperative clustering-based medium access control for broadcasting in vehicular ad-hoc networks. IET Commun. 2014, 8, 3136–3144. [Google Scholar] [CrossRef]
- Zhang, T.; Zhu, Q. A TDMA based cooperative communication MAC protocol for vehicular ad hoc networks. In Proceedings of the 2016 IEEE 83rd Vehicular Technology Conference (VTC Spring), Nanjing, China, 15–18 May 2016; pp. 1–6. [Google Scholar]
- Jia, D.; Lu, K.; Wang, J. A Disturbance-Adaptive Design for VANET-Enabled Vehicle Platoon. IEEE Trans. Veh. Technol. 2014, 63, 527–539. [Google Scholar] [CrossRef]
- Hoang, L.-N.; Uhlemann, E.; Jonsson, M. An Efficient Message Dissemination Technique in Platooning Applications. IEEE Commun. Lett. 2015, 19, 1017–1020. [Google Scholar] [CrossRef]
- Falkoni, A.; Pfeifer, A.; Krajačić, G. Vehicle-to-Grid in Standard and Fast Electric Vehicle Charging: Comparison of Renewable Energy Source Utilization and Charging Costs. Energies 2020, 13, 1510. [Google Scholar] [CrossRef]
- Kim, H.; Kim, T. Vehicle-to-Vehicle (V2V) Message Content Plausibility Check for Platoons through Low-Power Beaconing. Sensors 2019, 19, 5493. [Google Scholar] [CrossRef] [PubMed]
- Kamerman, A.; Monteban, L. WaveLAN-II: A high-performance wireless LAN for the unlicensed band. Bell Labs Tech. J. 1997, 2, 118–133. [Google Scholar] [CrossRef]
- Ni, S.; Tseng, Y.; Chen, Y.; Sheu, J. The broadcast storm problem in a mobile ad hoc network. Wirel. Netw. 2002, 8, 151–167. [Google Scholar]
- Palombara, C.L.; Tralli, V.; Masini, B.M.; Conti, A. Relay-Assisted Diversity Communications. IEEE Trans. Veh. Technol. 2013, 62, 415–421. [Google Scholar] [CrossRef]
- Karabulut, M.A.; Shah, A.F.M.S.; Ilhan, H. OEC-MAC: A Novel OFDMA Based Efficient Cooperative MAC Protocol for VANETS. IEEE Access 2020, 8, 94665–94677. [Google Scholar] [CrossRef]
- IEEE Draft Standard for Information Technology—Telecommunications and Information Exchange Between Systems Local and Metropolitan Area Networks—Specific Requirements Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications Amendment Enhancements for High Efficiency WLAN; IEEE P802.11ax/D6.0; IEEE: Piscataway, NJ, USA, 2019.
- Puterman, M.L. Problem Definition and Notation. In Markov Decision Processes: Discrete Stochastic Dynamic Programming; Wiley: Hoboken, NJ, USA, 1994; pp. 1–684. [Google Scholar]
- Bertsekas, D.P. Dynamic Programming. In Dynamic Programming and Optimal Control; Athena Scientific: Nashua, NH, USA, 2012; pp. 1–712. [Google Scholar]
- Stevens-Navarro, E.; Lin, Y.; Wong, V.W.S. An MDP-based vertical handoff decision algorithm for heterogeneous wireless networks. IEEE Trans. Veh. Technol. 2008, 57, 1243–1254. [Google Scholar] [CrossRef]
- Choi, J.; Park, K.; Kim, C.-K. Cross-Layer Analysis of Rate Adaptation, DCF and TCP in Multi-Rate WLANs. In Proceedings of the IEEE INFOCOM 2007—26th IEEE International Conference on Computer Communications, Barcelona, Spain, 6–12 May 2007; pp. 1–9. [Google Scholar]
- IEEE Standard for Information Technology– Local and mEtropolitan Area Networks– Specific Requirements– Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications Amendment 6: Wireless Access in Vehicular Environments; IEEE 802.11p; IEEE: Piscataway, NJ, USA, 2010.
- IEEE P802.11 Next Generation V2X Study Group. Available online: http://www.ieee802.org/11/Reports/tgbd_update.htm (accessed on 9 July 2020).

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, T.; Song, T.; Pack, S. An Energy Efficient Message Dissemination Scheme in Platoon-Based Driving Systems. Energies 2020, 13, 3940. https://doi.org/10.3390/en13153940
Kim T, Song T, Pack S. An Energy Efficient Message Dissemination Scheme in Platoon-Based Driving Systems. Energies. 2020; 13(15):3940. https://doi.org/10.3390/en13153940
Chicago/Turabian StyleKim, Taeyoon, Taewon Song, and Sangheon Pack. 2020. "An Energy Efficient Message Dissemination Scheme in Platoon-Based Driving Systems" Energies 13, no. 15: 3940. https://doi.org/10.3390/en13153940
APA StyleKim, T., Song, T., & Pack, S. (2020). An Energy Efficient Message Dissemination Scheme in Platoon-Based Driving Systems. Energies, 13(15), 3940. https://doi.org/10.3390/en13153940






