An Inverse Design Method for Airfoils Based on Pressure Gradient Distribution
Abstract
:1. Introduction
2. Numerical Methods
2.1. Computational Method
2.2. Adjoint Method
2.3. Optimization Method and Design Variable
3. Inverse Design Based on the Target Pressure Gradient
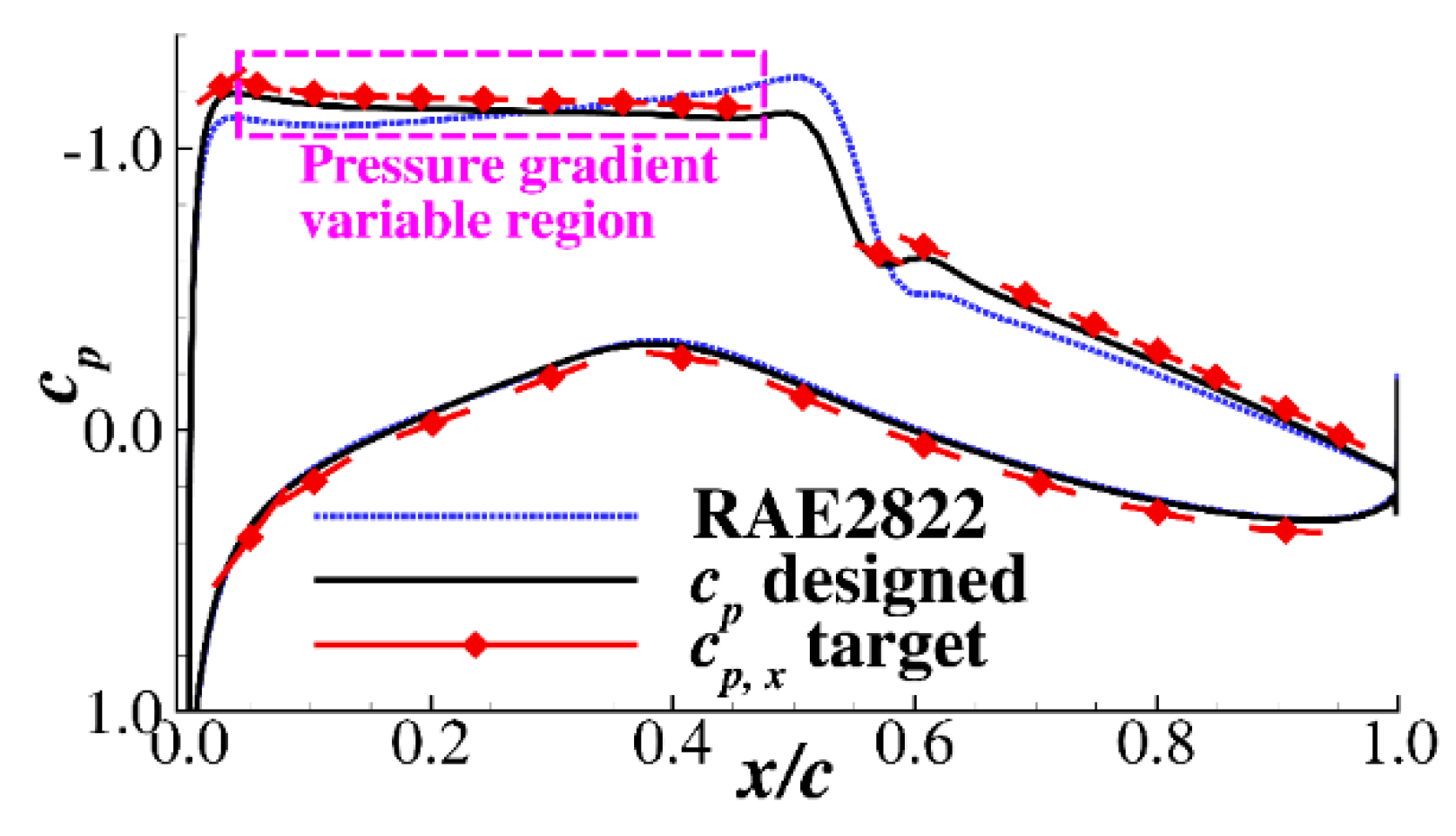
3.1. Supercritical Airfoil Design
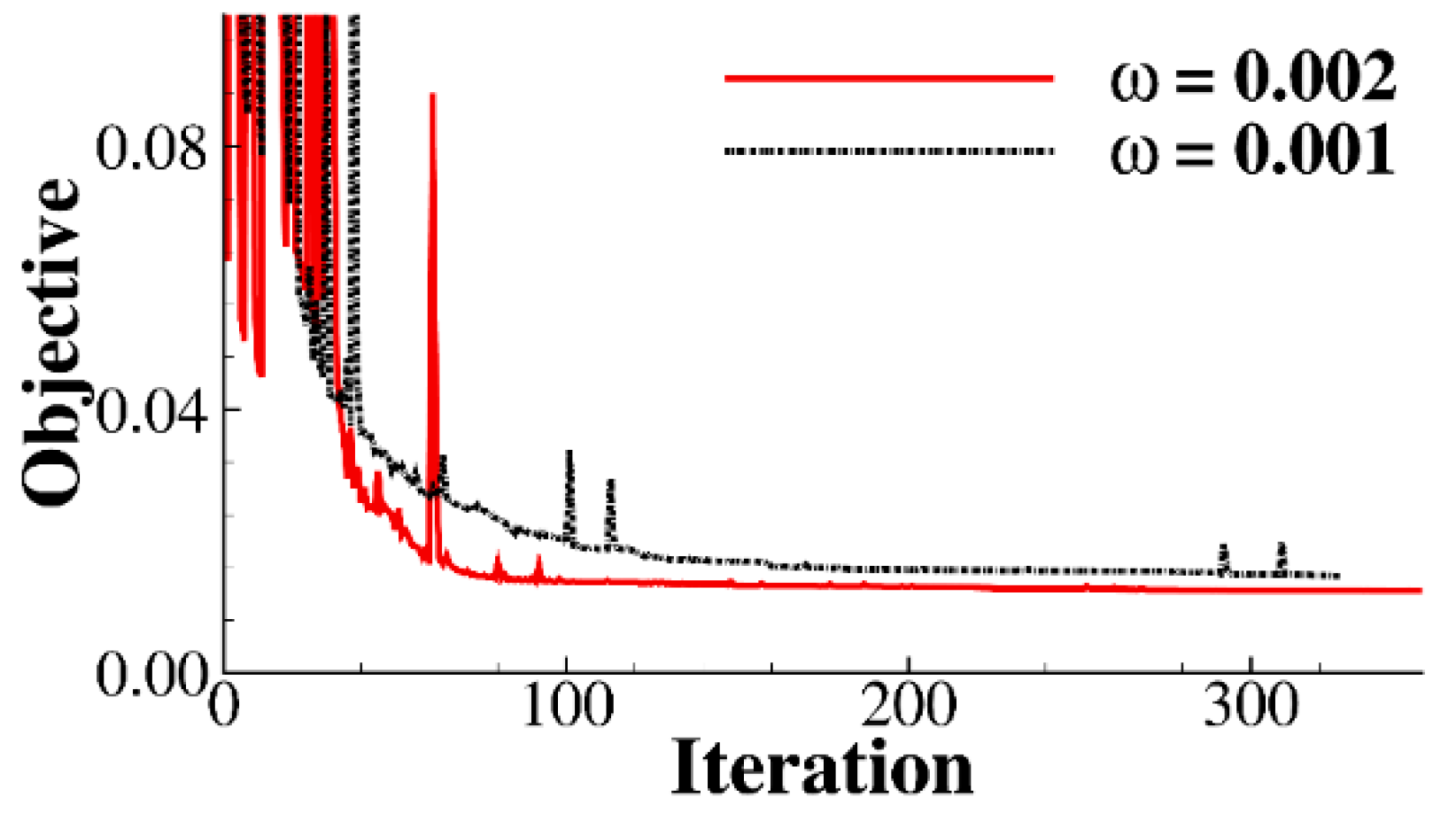
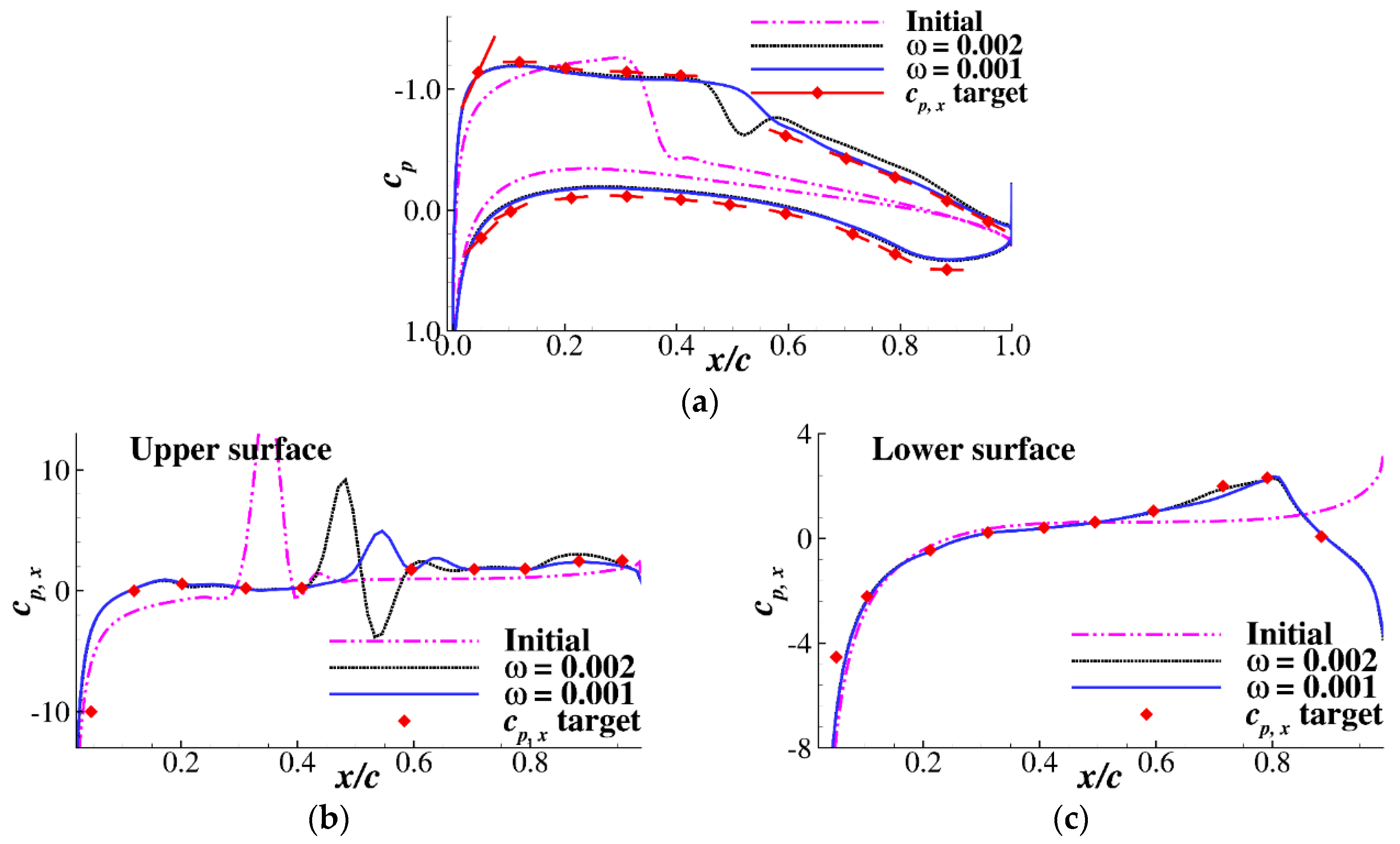
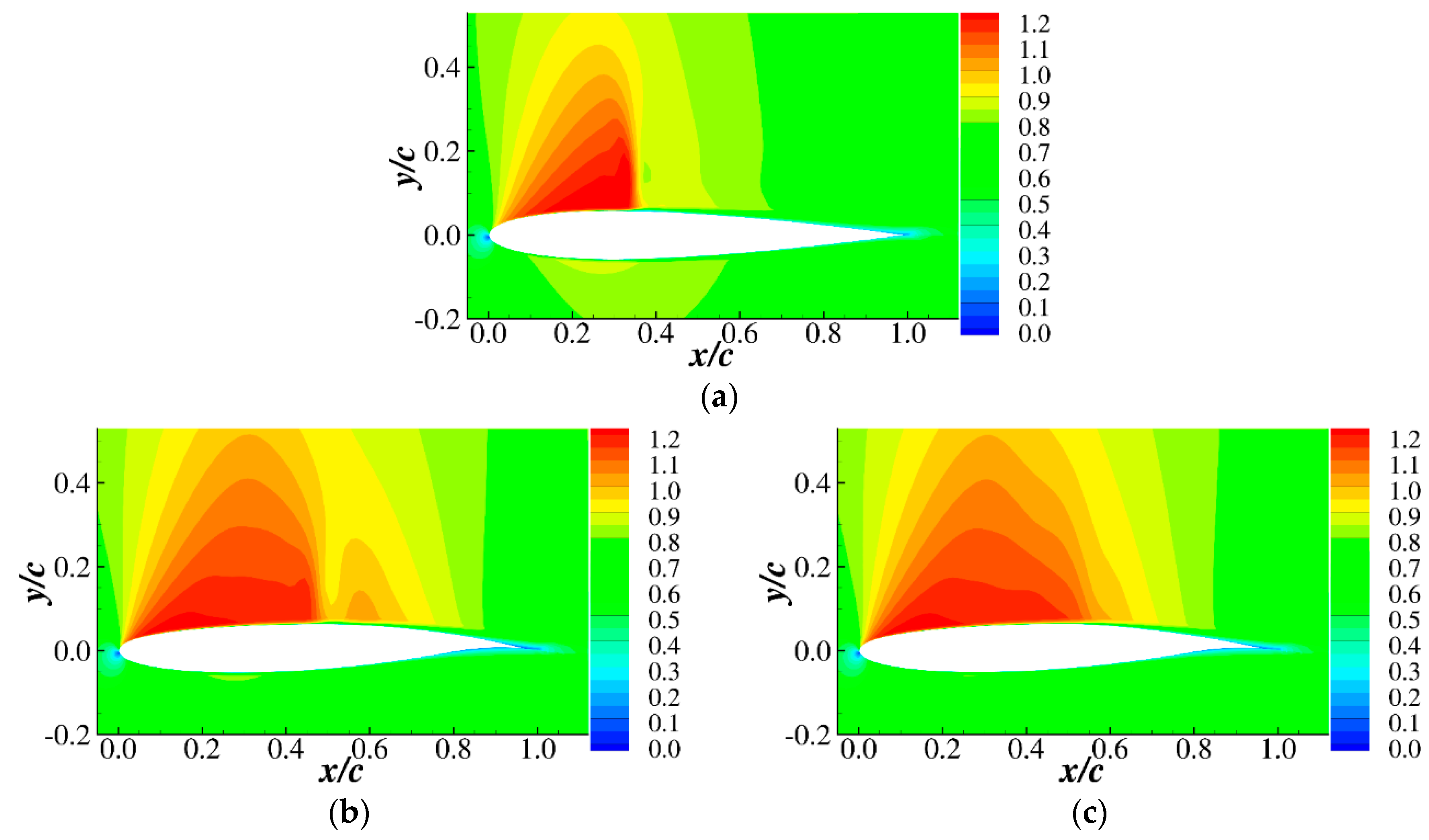
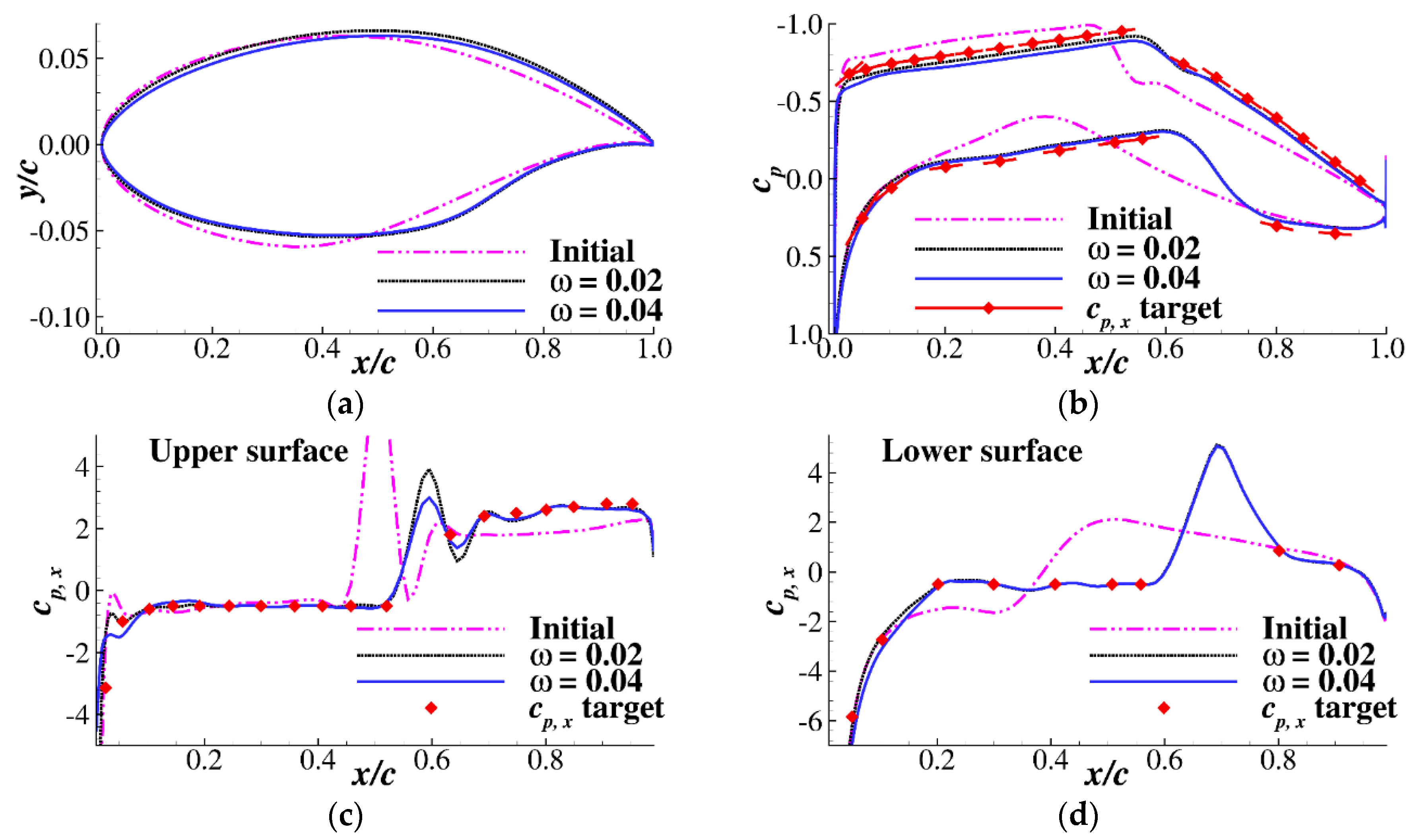
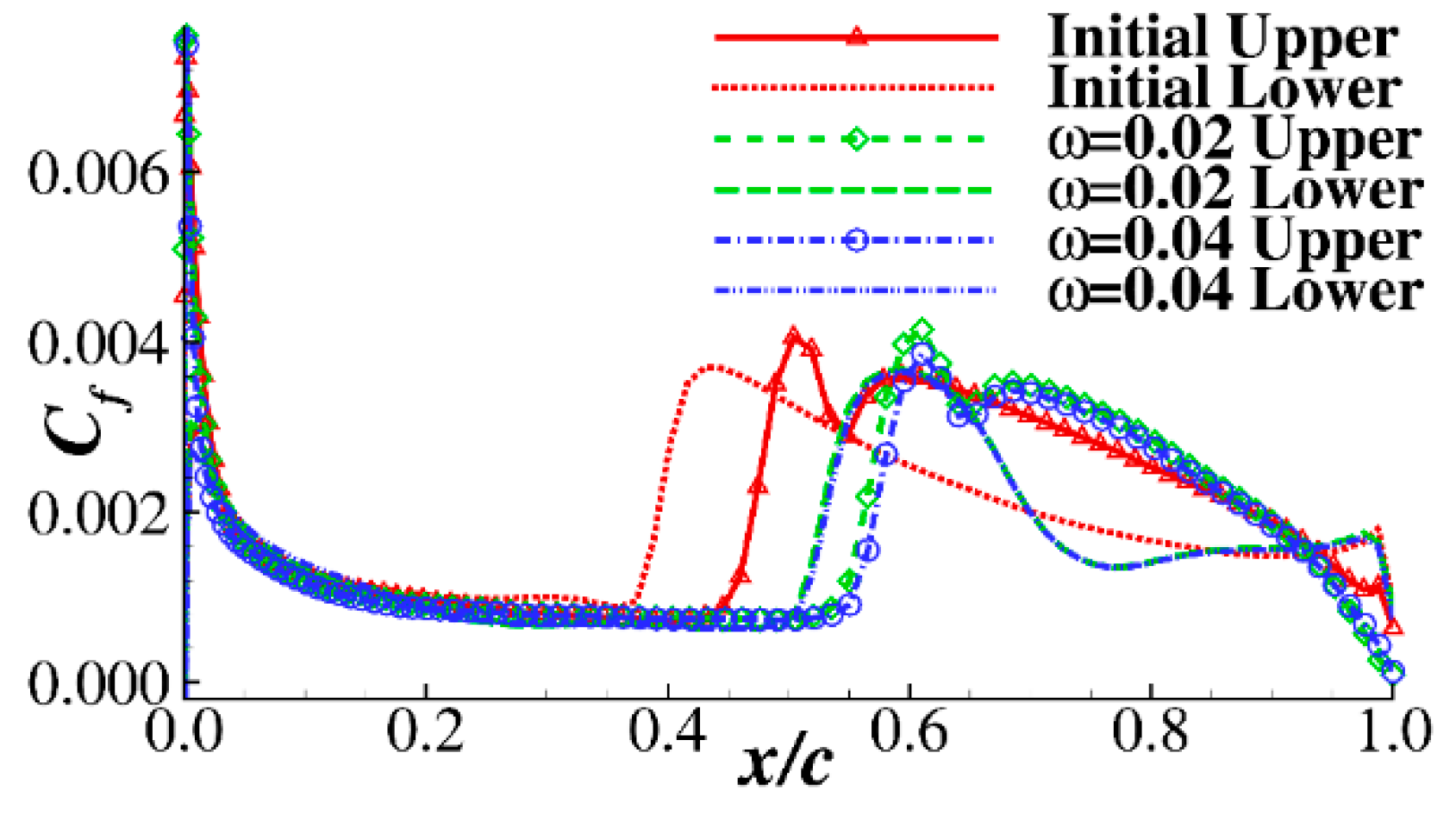
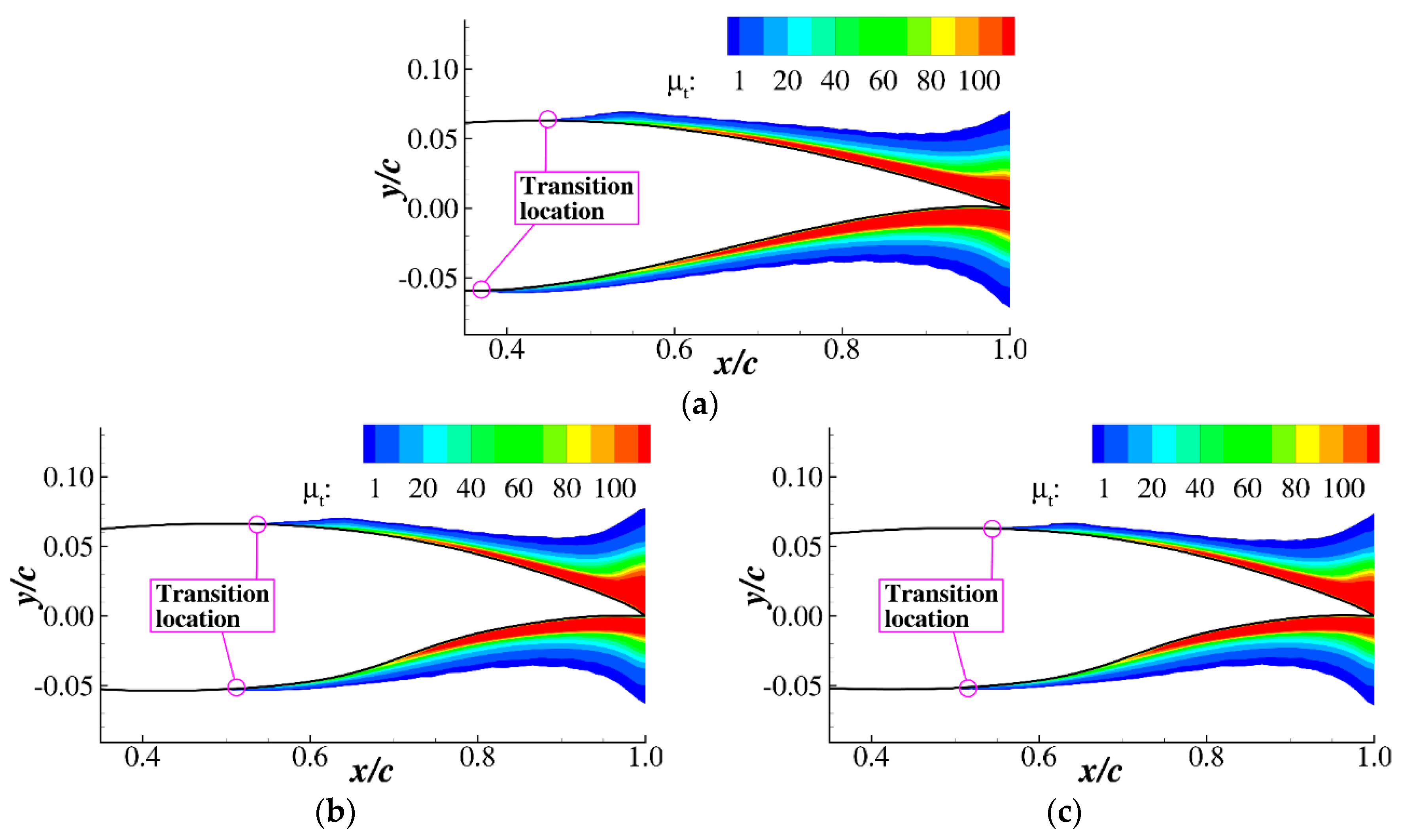
3.2. Supercritical Natural Laminar Flow Airfoil Design
4. Influence of Pressure Gradient on Supercritical Airfoil Performance
4.1. Target Pressure Gradient of Supercritical Airfoil
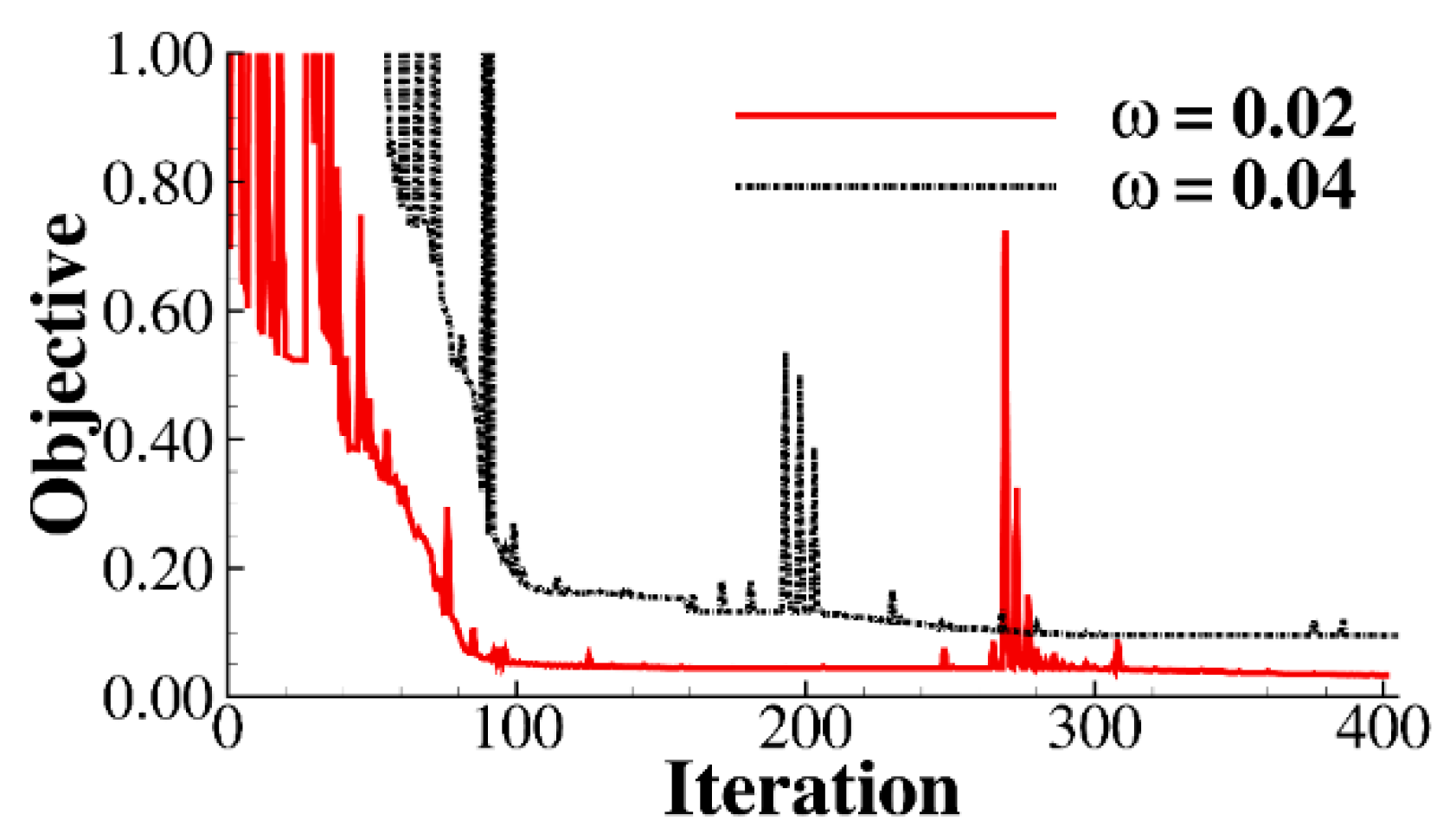
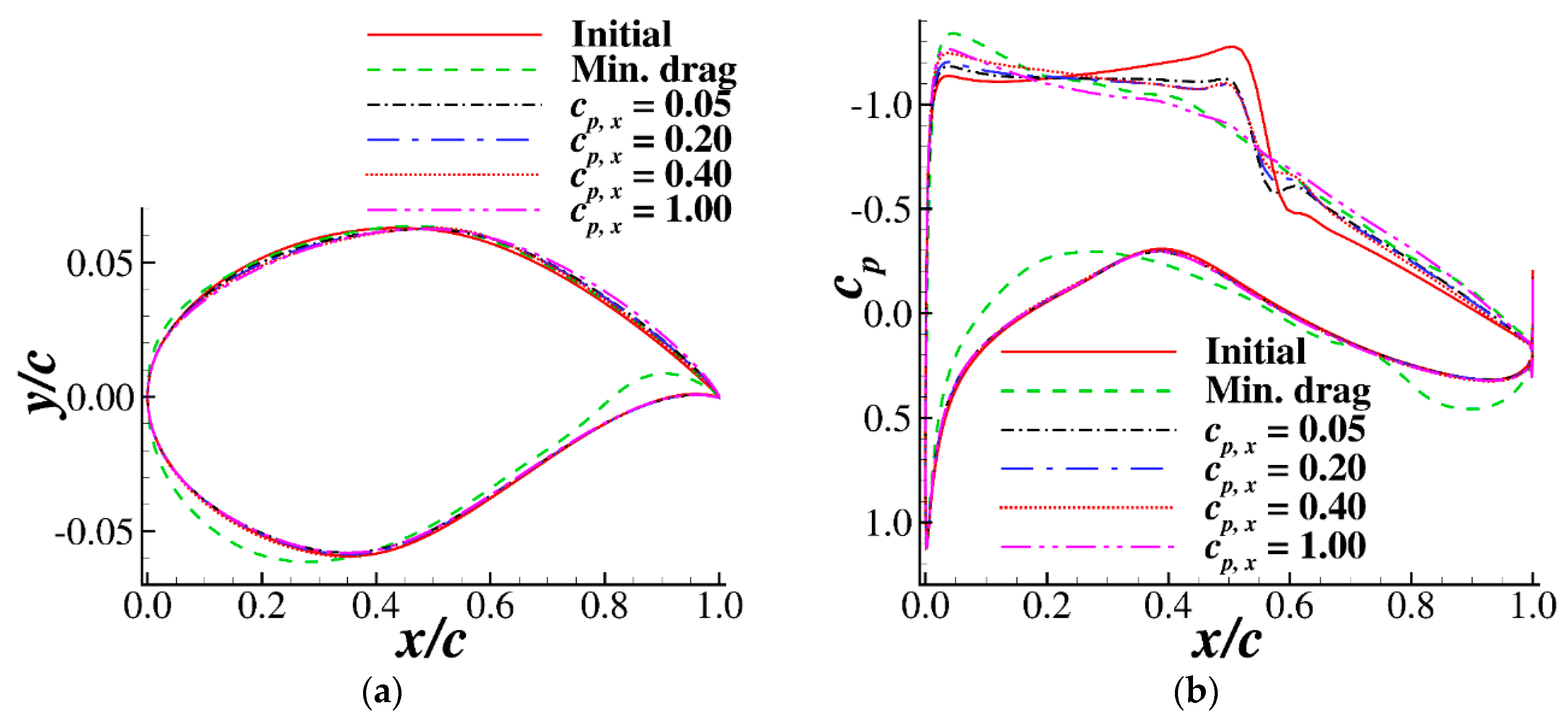
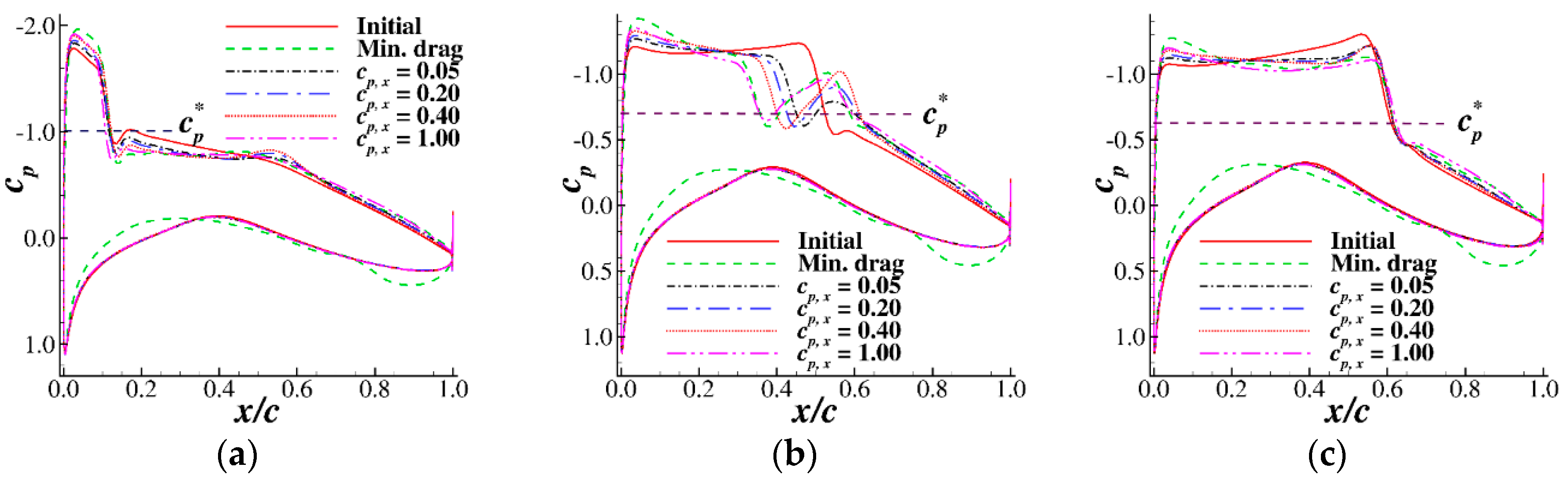
4.2. Characteristics of Airfoils with Different Upper Surface Pressure Gradients
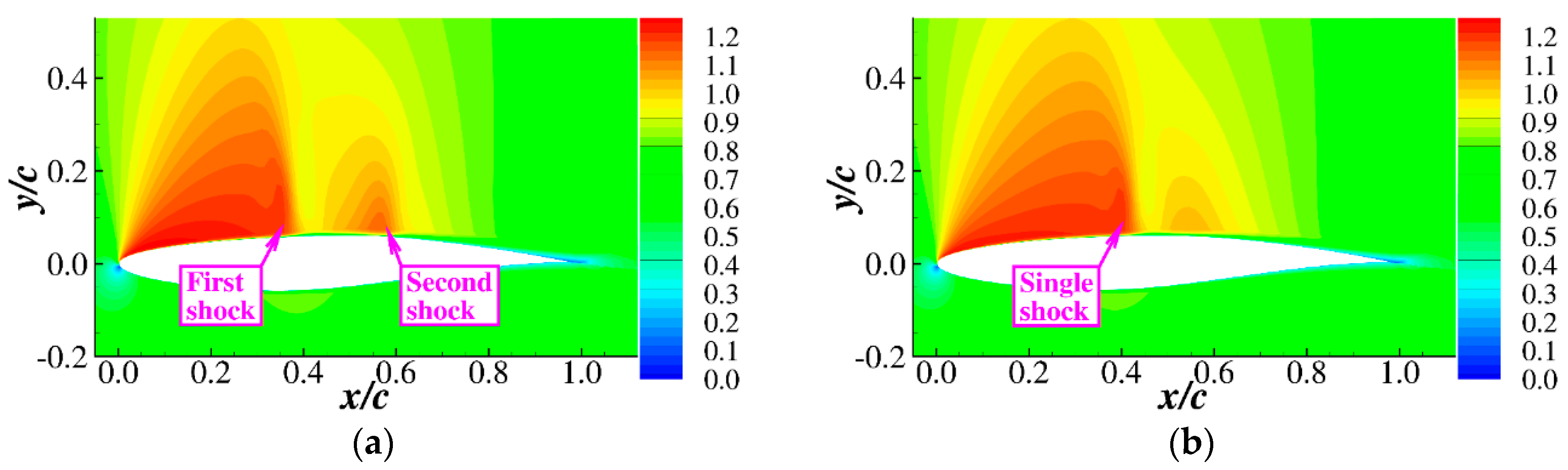
4.3. Drag Divergence Performance of Airfoils with Different Pressure Gradients
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Yin, Y. Study on Riblet Drag Reduction Considering the Effect of Sweep Angle. Energies 2019, 12, 3386. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Saleh, J.H.; Yang, V. Optimization of Supercritical Airfoil Design with Buffet Effect. AIAA J. 2019, 57, 4343–4353. [Google Scholar] [CrossRef]
- Driver, J.; Zingg, D.W. Optimized Natural-Laminar-Flow Airfoils. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar]
- Raheem, M.A.; Edi, P.; Pasha, A.A.; Rahman, M.M.; Juhany, K.A. Numerical Study of Variable Camber Continuous Trailing Edge Flap at Off-Design Conditions. Energies 2019, 12, 3185. [Google Scholar] [CrossRef] [Green Version]
- Zhao, T.; Zhang, Y.; Chen, H.; Chen, Y.; Zhang, M. Supercritical Wing Design Based on Airfoil Optimization and 2.75D Transformation. Aerosp. Sci. Technol. 2016, 56, 168–182. [Google Scholar] [CrossRef]
- Zhang, Y.; Fang, X.; Chen, H.; Fu, S.; Duan, Z.; Zhang, Y. Supercritical Natural Laminar Flow Airfoil Optimization for Regional Aircraft Wing Design. Aerosp. Sci. Technol. 2015, 43, 152–164. [Google Scholar] [CrossRef]
- Edi, P.; Fielding, J.P. Civil-Transport Wing Design Concept Exploiting New Technologies. J. Aircr. 2006, 43, 932–940. [Google Scholar] [CrossRef]
- Gopalarathnam, A.; Selig, M.S. Hybrid Inverse Airfoil Design Method for Complex Three-Dimensional Lifting Surfaces. J. Aircr. 2002, 39, 409–417. [Google Scholar] [CrossRef] [Green Version]
- Selig, M.S.; Maughmert, M.D. Multipoint Inverse Airfoil Design Method Based on Conformal Mapping. AIAA J. 1992, 30, 1162–1170. [Google Scholar] [CrossRef]
- Malone, J.B.; Narramoret, J.C.; Sankar, L.N. Airfoil Design Method Using the Navier-Stokes Equations. J. Aircr. 1991, 28, 216–224. [Google Scholar] [CrossRef]
- Dadone, A.; Grossman, B. Fast Convergence of Viscous Airfoil Design Problems. AIAA J. 2002, 40, 1997–2005. [Google Scholar] [CrossRef]
- Gopalarathnam, A.; Selig, M.S. Low-Speed Natural-Laminar-Flow Airfoils: Case Study in Inverse Airfoil Design. J. Aircr. 2001, 38, 57–63. [Google Scholar] [CrossRef] [Green Version]
- Eyi, S.; Lee, K.D. Inverse Airfoil Design Using the Navier-Stokes Equations. In Proceedings of the 7th Applied Aerodynamics Conference, Irvine, CA, USA, 16–19 February 1993. [Google Scholar]
- Gardner, B.A.; Selig, M.S. Airfoil Design Using a Genetic Algorithm and an Inverse Method. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003. [Google Scholar]
- Hacioglu, A. Fast Evolutionary Algorithm for Airfoil Design via Neural Network. AIAA J. 2007, 45, 2196–2203. [Google Scholar] [CrossRef]
- Bui-Thanh, T.; Damodaran, M.; Willcox, K. Aerodynamic Data Reconstruction and Inverse Design Using Proper Orthogonal Decomposition. AIAA J. 2004, 42, 1505–1516. [Google Scholar] [CrossRef] [Green Version]
- Ylmaz, E.; German, B.J. A Deep Learning Approach to an Airfoil Inverse Design Problem. In Proceedings of the 2018 Multidisciplinary Analysis and Optimization Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Sekar, V.; Zhang, M.; Shu, C.; Khoo, B.C. Inverse Design of Airfoil Using a Deep Convolutional Neural Network. AIAA J. 2019, 57, 993–1003. [Google Scholar] [CrossRef]
- Tang, H.; Lei, Y.; Li, X.; Gao, K.; Li, Y. Aerodynamic Shape Optimization of a Wavy Airfoil for Ultra-Low Reynolds Number Regime in Gliding Flight. Energies 2020, 13, 467. [Google Scholar] [CrossRef] [Green Version]
- Jameson, A. Aerodynamic Design via Control Theory. J. Sci. Comput. 1988, 3, 233–260. [Google Scholar] [CrossRef] [Green Version]
- Mader, C.A.; Martins, J.R.R.A.; Alonso, J.J.; Weide, E. ADjoint: An Approach for the Rapid Development of Discrete Adjoint Solvers. AIAA J. 2008, 46, 863–873. [Google Scholar] [CrossRef]
- He, P.; Mader, C.A.; Martins, J.R.R.; Maki, J. DAFoam: An Open-Source Adjoint Framework for Multidisciplinary Design Optimization with OpenFOAM. AIAA J. 2019, 58, 1304–1319. [Google Scholar] [CrossRef]
- Li, R.; Deng, K.; Zhang, Y.; Chen, H. Pressure Distribution Guided Supercritical Wing Optimization. Aeronaut. J. 2018, 31, 1842–1854. [Google Scholar] [CrossRef]
- Kenway, G.K.W.; Mader, C.A.; He, P.; Martins, J.R.R.A. Effective Adjoint Approaches for Computational Fuid Dynamics. Prog. Aerosp. Sci. 2019, 110, 100542. [Google Scholar] [CrossRef]
- Jameson, A.; Schmidt, W.; Turkel, E. Numerical Solution of the Euler Equations by Finite Volume Methods Using Runge–Kutta Time Stepping Schemes. In Proceedings of the 14th Fluid and Plasma Dynamics Conference, Palo Alto, CA, USA, 13–25 June 1981. [Google Scholar]
- Spalart, P.; Allmaras, S. A One-Equation Turbulence Model for Aerodynamic Flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar]
- Cook, P.H.; McDonald, M.A.; Firmin, M.C.P. Experimental Data Base for Computer Program Assessment; Aerofoil RAE 2822—Pressure Distributions, and Boundary Layer and Wake Measurements; AGARD Advisory Report No. 138; Advisory Group for Aerospace Research and Development: Neuilly sur Seine, France, 1979. [Google Scholar]
- Hascoet, L.; Pascual, V. The Tapenade Automatic Differentiation Tool: Principles, Model, and Specification. ACM Trans. Math. Softw. 2012, 7957. [Google Scholar] [CrossRef] [Green Version]
- Gill, P.E.; Murray, W.; Saunders, M.A. SNOPT: An SQP Algorithm for Large-Scale Constrained Optimization. Siam. Rev. 2005, 47, 99–131. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Z.; Huang, W.; Yan, L. A Review of Parametric Approaches Specific to Aerodynamic Design Process. Acta. Astronaut. 2018, 145, 319–331. [Google Scholar] [CrossRef]
- Zhao, K.; Gao, Z.; Huang, J.; Li, Q. Aerodynamic Optimization of Rotor Airfoil Based on Multi-Layer Hierarchical Constraint Method. Chin. J. Aeronaut. 2016, 29, 1541–1552. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Gao, Z.; Huang, J.; Zhao, K. Robust Design of NLF Airfoils. Chin. J. Aeronaut. 2013, 26, 309–318. [Google Scholar] [CrossRef] [Green Version]
- Han, Z.H.; Chen, J.; Zhang, K.S.; Xu, Z.M.; Zhu, Z.; Song, W.P. Aerodynamic Shape Optimization of Natural-Laminar-Flow Wing Using Surrogate-Based Approach. AIAA J. 2018, 56, 2579–2593. [Google Scholar] [CrossRef]
- Hepperle, M. JavaFoil—Analysis of Airfoils. Available online: http://www.mh-aerotools.de/airfoils/javafoil.htm (accessed on 2 July 2020).
- Menter, F.R.; Langtry, R.B.; Likki, S.R.; Suzen, Y.B.; Huang, P.G.; Völker, S. A Correlation-Based Transition Model Using Local Variables-Part I: Model Formulation. J. Turbomach. 2006, 128, 413–422. [Google Scholar] [CrossRef]
- Harris, C.D. NASA Supercritical Airfoils: A Matrix of Family-Related Airfoils; NASA-TP-2969; NASA Langley Research Center: Hampton, VA, USA, 1990.
- Liepmann, H.W.; Roshko, A. Elements of gasdynamics. In Waves in Supersonic Flow; Dover Publications: New York, NY, USA, 2001; Chapter 4; pp. 84–123. [Google Scholar]
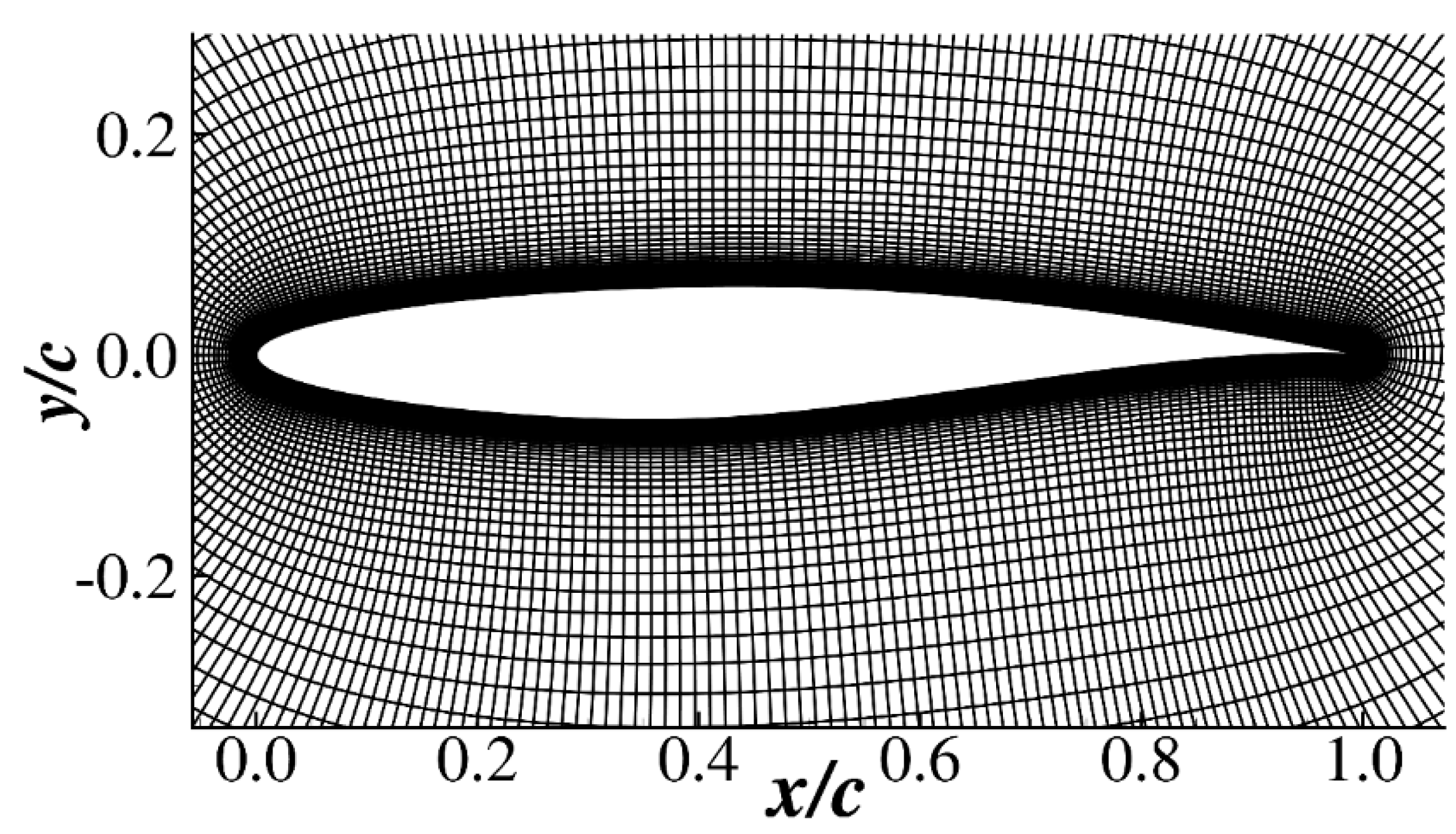
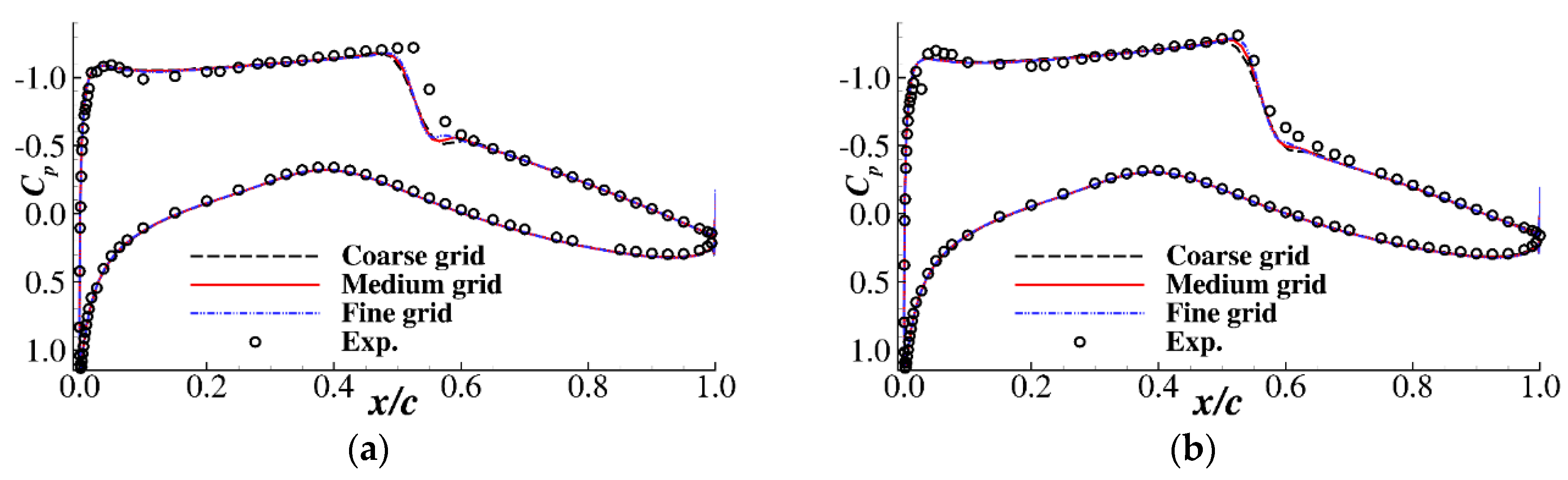
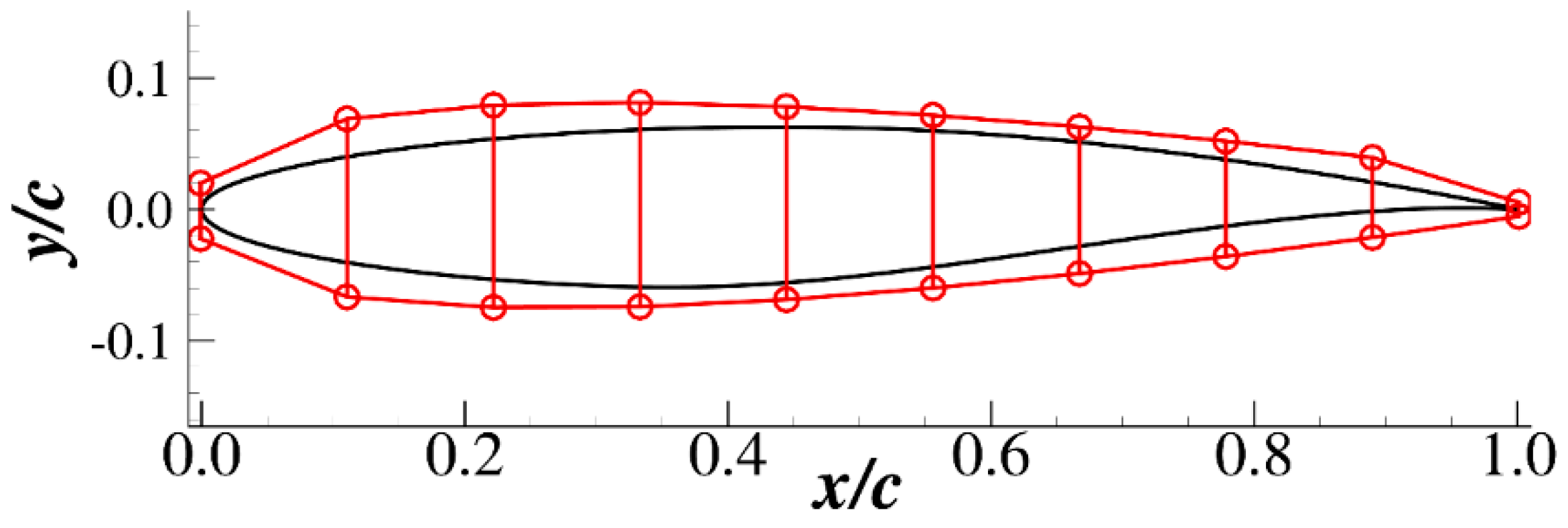
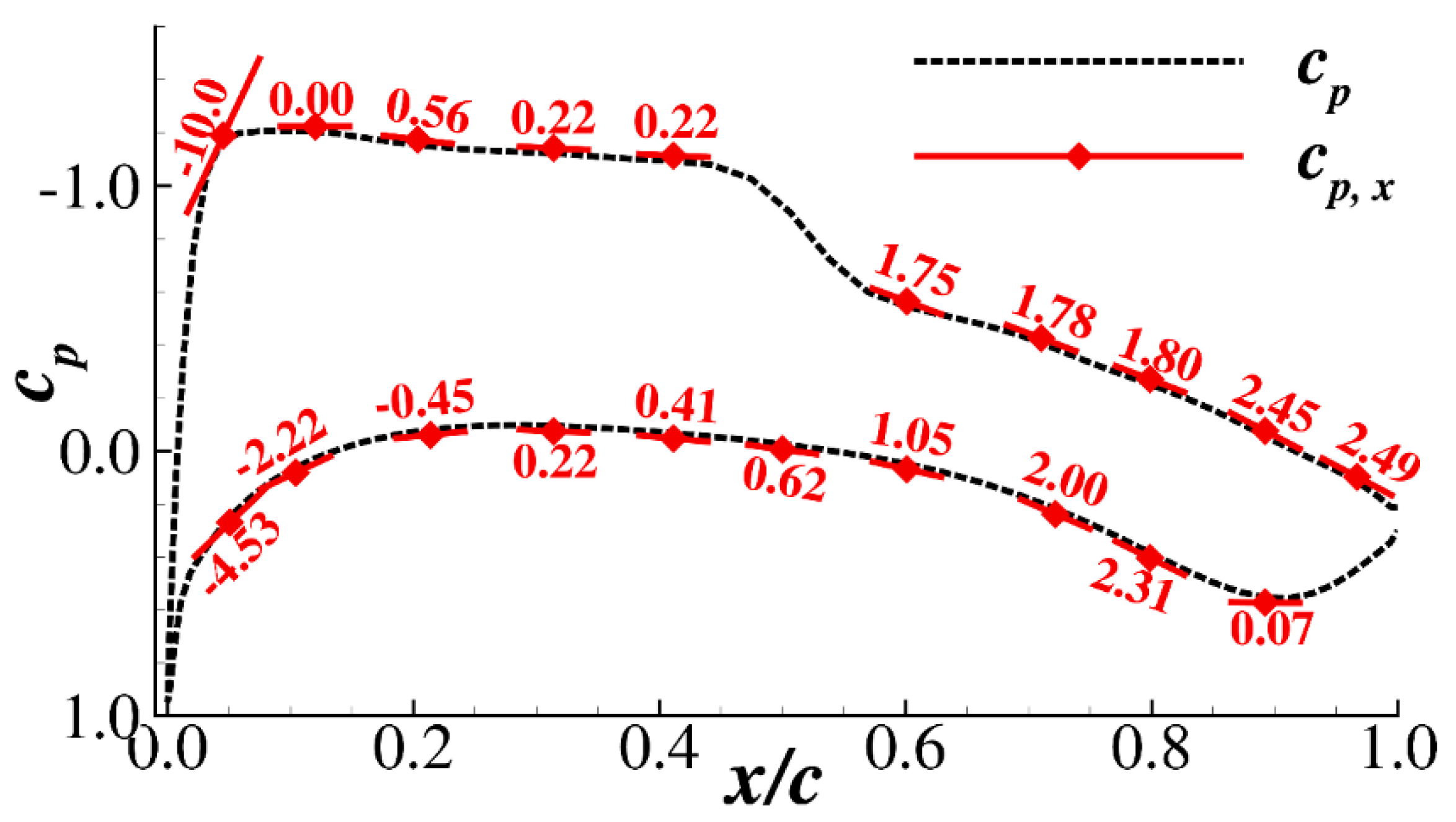


| Case | Configuration | α (°) | Lift Coefficient CL | Drag Coefficient CD |
|---|---|---|---|---|
| Case 6 | Experiment [27] | 2.92 | 0.743 | 0.0127 |
| Coarse grid | 2.34 | 0.743 | 0.01245 | |
| Medium grid | 2.31 | 0.743 | 0.01219 | |
| Fine grid | 2.29 | 0.743 | 0.01215 | |
| Case 9 | Experiment [27] | 3.19 | 0.803 | 0.0168 |
| Coarse grid | 2.66 | 0.803 | 0.01679 | |
| Medium grid | 2.60 | 0.803 | 0.01628 | |
| Fine grid | 2.57 | 0.803 | 0.01613 |
| No. | Target cp,x at 0.10 ≤ x/c ≤ 0.45 | Alpha | Lift Coefficient | Drag Coefficient | Lift-To-Drag Ratio |
|---|---|---|---|---|---|
| Initial | --- | 2.61 | 0.800 | 0.01618 | 49.44 |
| 1 | -0.05 | 2.33 | 0.800 | 0.01242 | 64.41 |
| 2 | 0.05 | 2.40 | 0.800 | 0.01227 | 65.20 |
| 3 | 0.1 | 2.44 | 0.800 | 0.01217 | 65.74 |
| 4 | 0.2 | 2.40 | 0.800 | 0.01157 | 69.14 |
| 5 | 0.4 | 2.43 | 0.800 | 0.01116 | 71.68 |
| 6 | 0.6 | 2.42 | 0.800 | 0.01121 | 71.36 |
| 7 | 0.8 | 2.36 | 0.800 | 0.01111 | 72.01 |
| 8 | 1.0 | 2.31 | 0.800 | 0.01107 | 72.27 |
| 9 | Without cp,x target | 1.75 | 0.800 | 0.01077 | 74.28 |
| Initial Airfoil | Optimized with ω = 0.001 | Optimized with ω = 0.002 | |
|---|---|---|---|
| Angle of attack α | 2.00 | 1.69 | 1.61 |
| Lift coefficient CL | 0.359 | 0.791 | 0.792 |
| Drag coefficient CD | 0.01318 | 0.01089 | 0.01165 |
| Lift-to-drag ratio | 27.24 | 72.63 | 67.98 |
| Pressure gradient deviation | 49.96 | 1.66 | 1.57 |
| Airfoil volume | 0.0674 | 0.0642 | 0.0654 |
| Original Airfoil | Optimized with ω = 0.02 | Optimized with ω = 0.04 | |
|---|---|---|---|
| Angle of attack α | 1.50 | 1.39 | 1.46 |
| Lift coefficient CL | 0.592 | 0.601 | 0.595 |
| Drag coefficient CD (Full turbulent) | 0.01004 | 0.01084 | 0.01047 |
| Lift-to-drag ratio (Full turbulent) | 58.96 | 55.44 | 56.83 |
| Pressure gradient deviation | 37.42 | 1.12 | 2.10 |
| Airfoil volume | 0.0649 | 0.0681 | 0.0650 |
| Original Airfoil | Optimized with ω = 0.02 | Optimized with ω = 0.04 | |
|---|---|---|---|
| Angle of attack α | 1.17 | 0.99 | 1.05 |
| Lift coefficient CL | 0.600 | 0.600 | 0.600 |
| Drag coefficient CD | 0.00624 | 0.00609 | 0.00599 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Yan, C.; Chen, H. An Inverse Design Method for Airfoils Based on Pressure Gradient Distribution. Energies 2020, 13, 3400. https://doi.org/10.3390/en13133400
Zhang Y, Yan C, Chen H. An Inverse Design Method for Airfoils Based on Pressure Gradient Distribution. Energies. 2020; 13(13):3400. https://doi.org/10.3390/en13133400
Chicago/Turabian StyleZhang, Yufei, Chongyang Yan, and Haixin Chen. 2020. "An Inverse Design Method for Airfoils Based on Pressure Gradient Distribution" Energies 13, no. 13: 3400. https://doi.org/10.3390/en13133400
APA StyleZhang, Y., Yan, C., & Chen, H. (2020). An Inverse Design Method for Airfoils Based on Pressure Gradient Distribution. Energies, 13(13), 3400. https://doi.org/10.3390/en13133400





