Maximizing Distributed Energy Resource Hosting Capacity of Power System in South Korea Using Integrated Feeder, Distribution, and Transmission System
Abstract
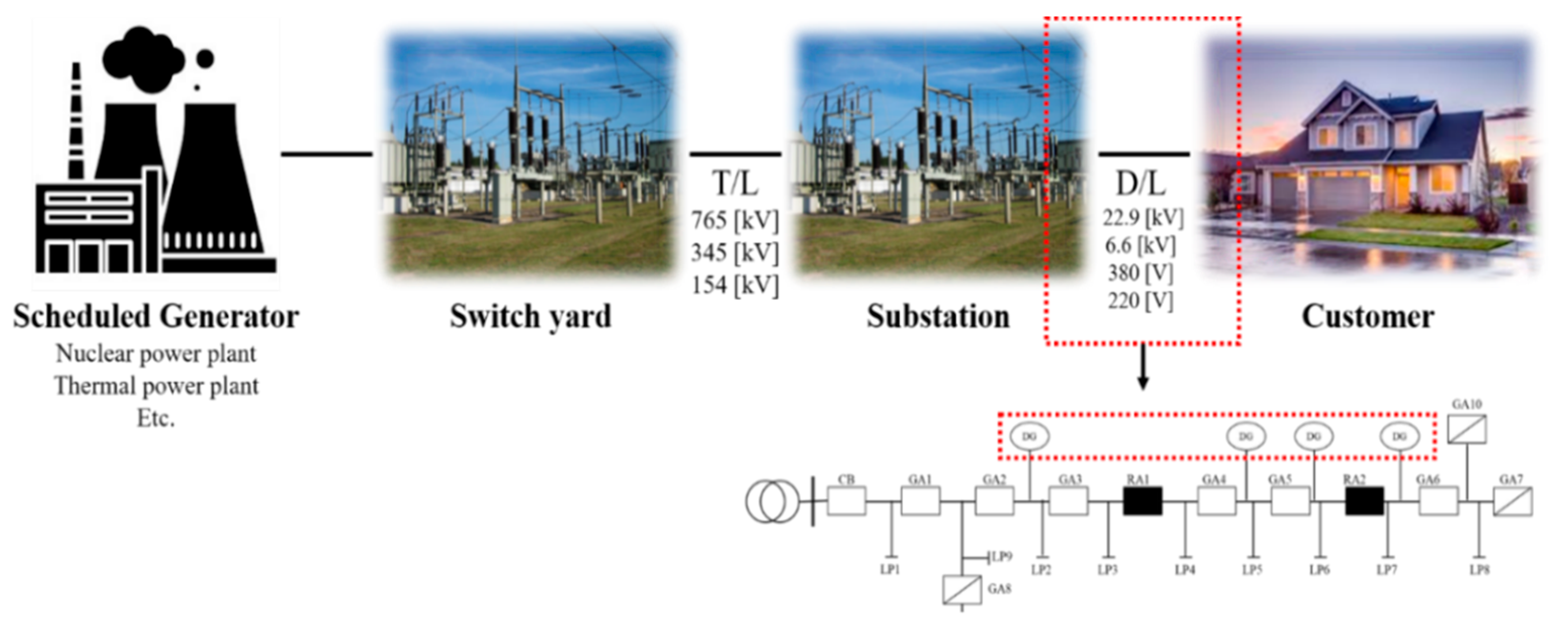
1. Introduction
2. South Korea’s Standard for DER in the Power System
3. Fast Voltage Stability Index
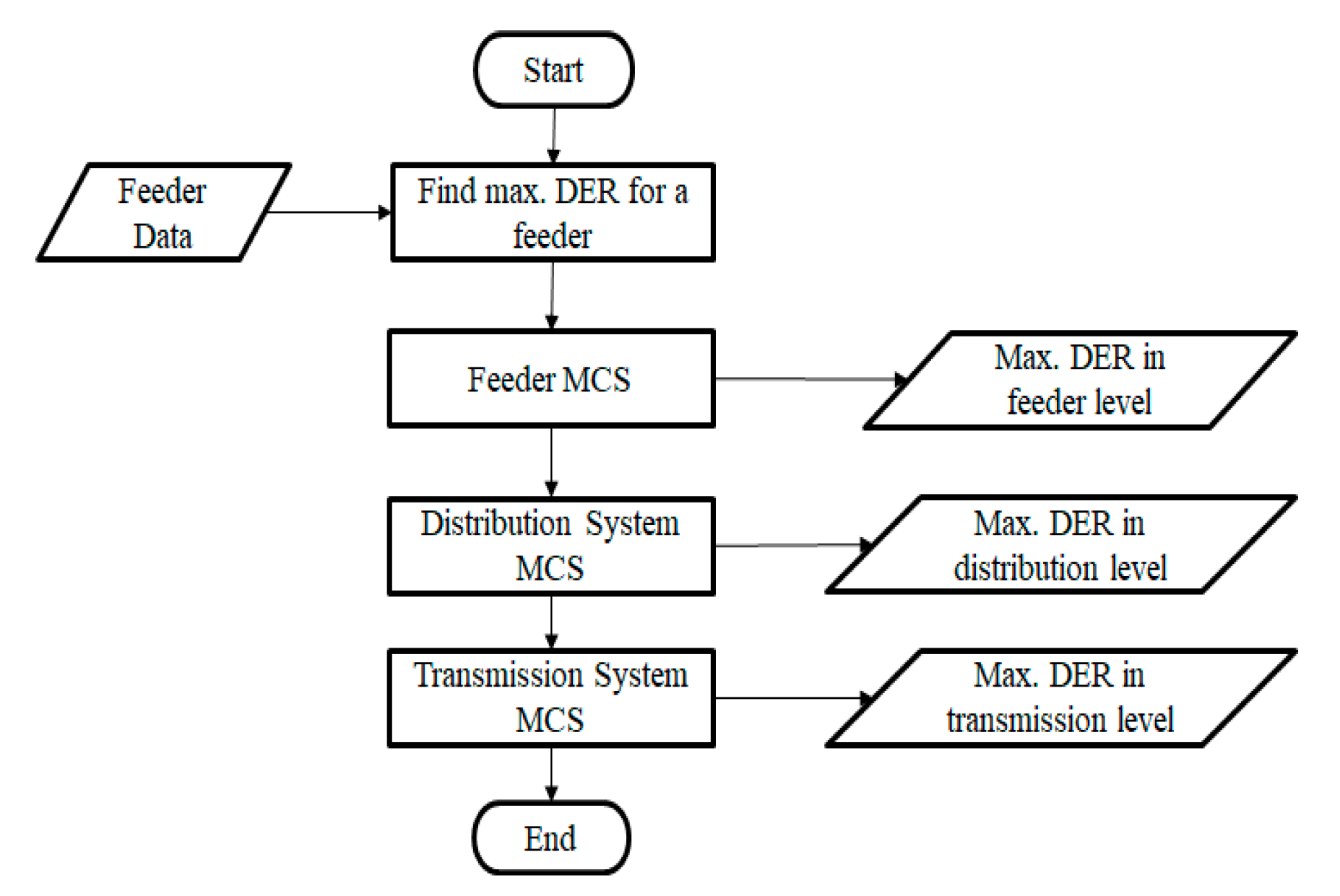
4. Maximizing the Hosting Capacity with Monte Carlo Simulation
4.1. Monte Carlo Simulation
4.2. Proposed Algorithm to Increase DER Hosting Capacity
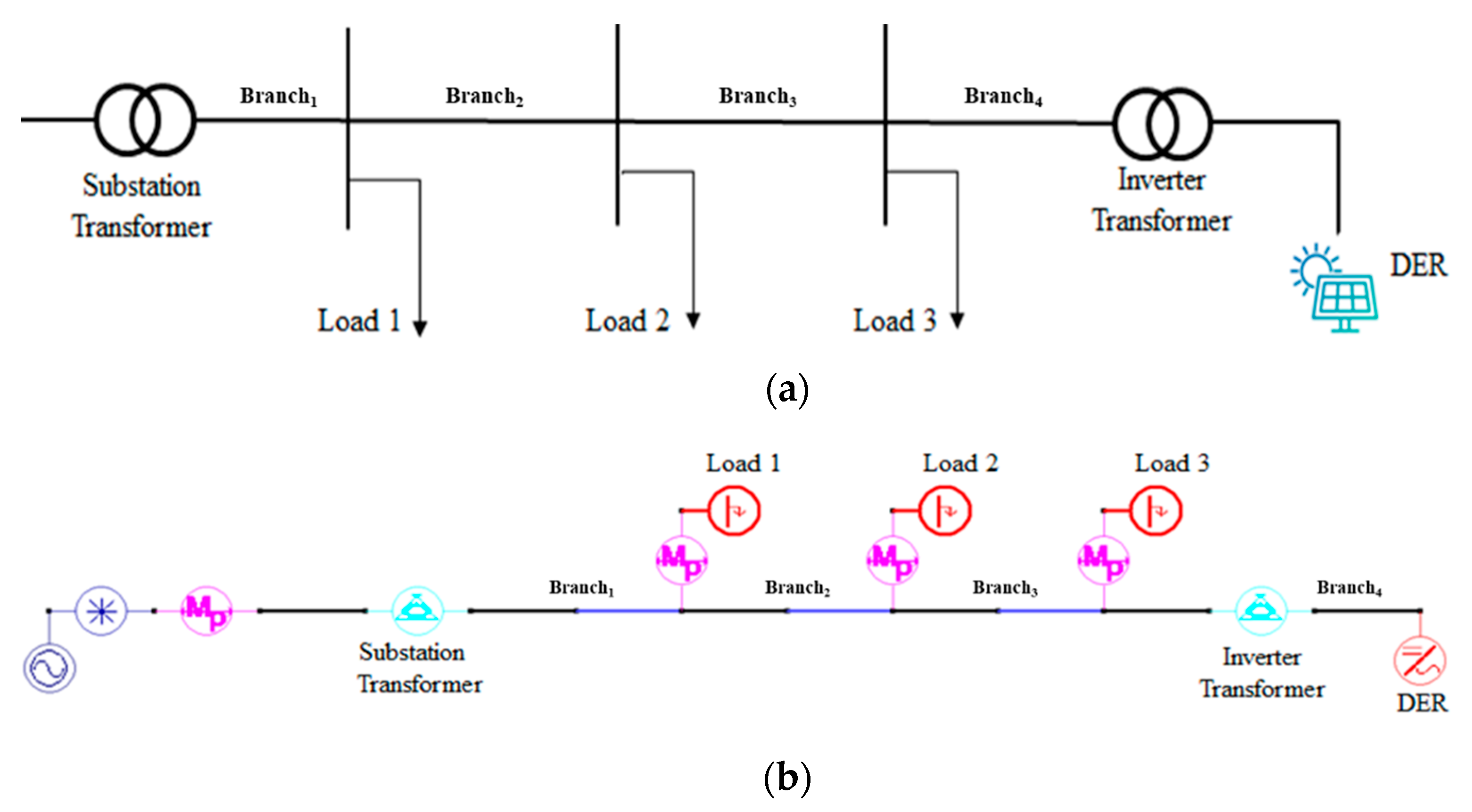
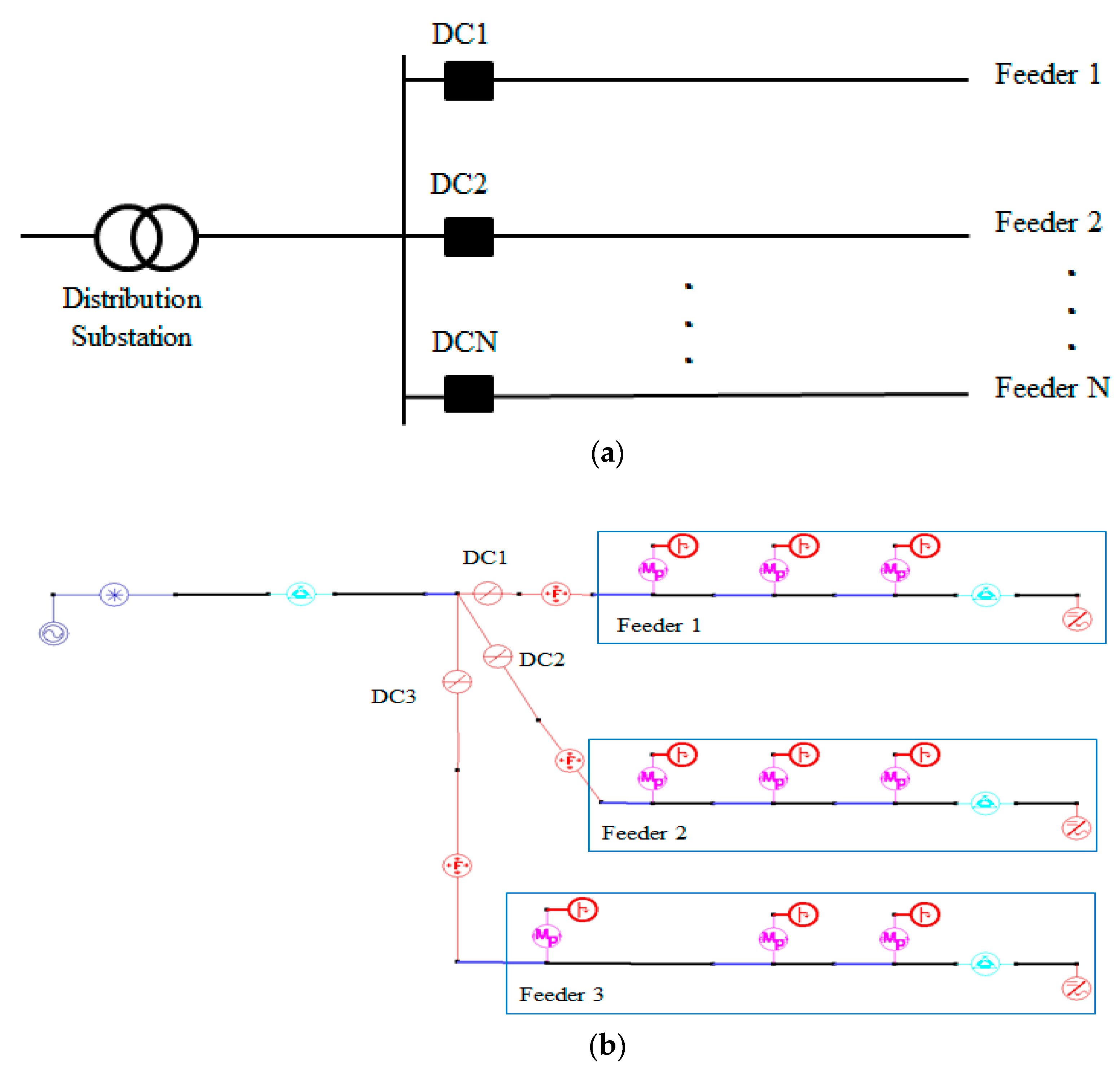
5. Case Study
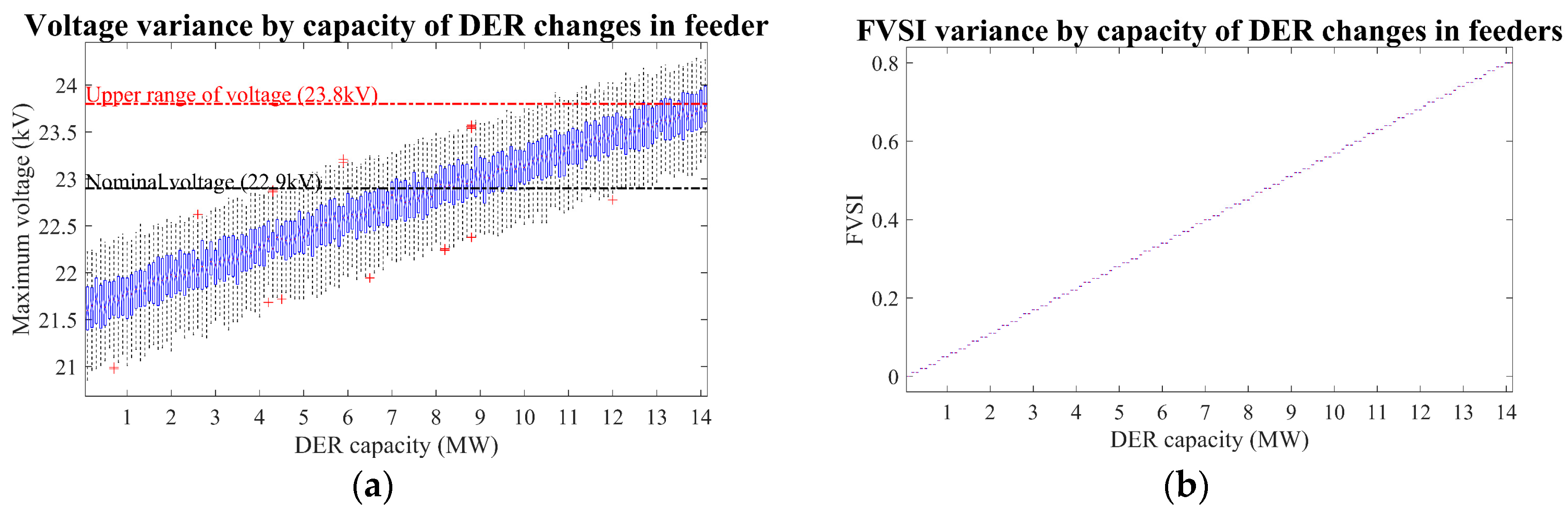
5.1. Result for Momentary Situation
5.2. Result for Various Power Shares and Power Factors of DER and Estimation Model
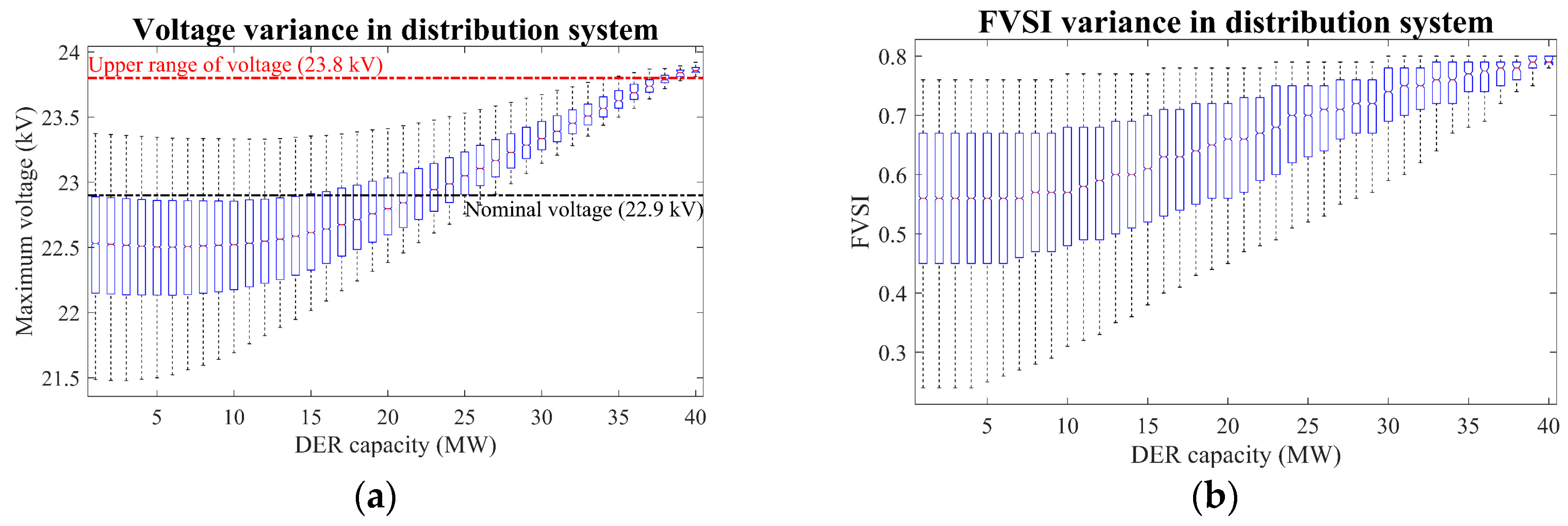
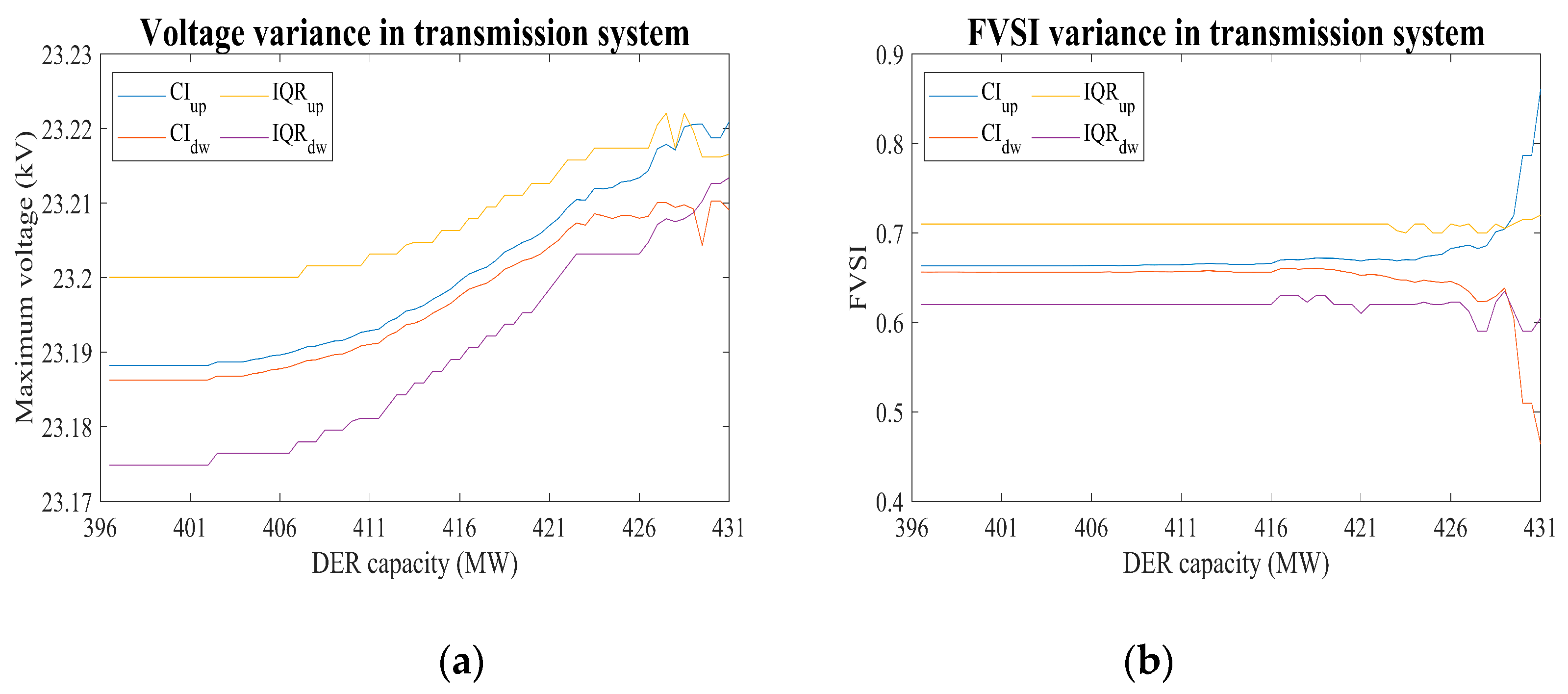
6. Monthly Simulation under Various DER Penetration Levels
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994; ISBN 007035958X. [Google Scholar]
- Mortazavi, H.; Mehrjerdi, H.; Saad, M.; Lefebvre, S.; Asber, D.; Lenoir, L. A Monitoring Technique for Reversed Power Flow Detection with High PV Penetration Level. IEEE Trans. Smart Grid 2015, 6, 2221–2232. [Google Scholar] [CrossRef]
- Kim, S. Increasing Hosting Capacity of Distribution Feeders by Analysis of Generation and Consumption. KEPCO J. Electr. Power Energy 2019, 5, 295–309. [Google Scholar] [CrossRef]
- Cho, S.; Sim, J.; Lim, H.; Kim, H.; Kim, S.; Ju, S.; Song, J. Increasing Hosting Capacity in KEPCO Distribution Feeders. KEPCO J. Electr. Power Energy 2019, 5, 311–321. [Google Scholar]
- IEEE Standard Association IEEE Std. 1547-2018. Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces; IEEE: New York, NY, USA, 2018; ISBN 9781504446396. [Google Scholar]
- Kong, J.; Kim, S.T.; Kang, B.O.; Jung, J. Determining the size of energy storage system to maximize the economic profit for photovoltaic and wind turbine generators in South Korea. Renew. Sustain. Energy Rev. 2019, 116, 109467. [Google Scholar] [CrossRef]
- Africano, Y.; Celeita, D.; Ramos, G. Co-simulation strategy of PV hosting capacity applying a stochastic analysis. In Proceedings of the 2017 IEEE Workshop on Power Electronics and Power Quality Applications (PEPQA), Bogota, Colombia, 31 May–2 June 2017. [Google Scholar] [CrossRef]
- Song, Y.; Hill, D.J.; Liu, T. Static voltage stability analysis of distribution systems based on network-load admittance ratio. IEEE Trans. Power Syst. 2019, 34, 2270–2280. [Google Scholar] [CrossRef]
- Matavalam, A.R.R.; Ajjarapu, V. Calculating the long term voltage stability margin using a linear index. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 1–5 September 2015. [Google Scholar] [CrossRef]
- ARENA. DEIP Access and Pricing; ARENA: Canberra, Australia, 2020. [Google Scholar]
- CEPA. Distributed Energy Resources Integration Program-Access and Pricing Reform Options; CEPA: London, UK, 2020. [Google Scholar]
- Elrayyah, A.Y.; Wanik, M.Z.C.; Bouselham, A. Simplified approach to analyze voltage rise in LV systems With PV installations using equivalent power systems diagrams. IEEE Trans. Power Deliv. 2017, 32, 2140–2149. [Google Scholar] [CrossRef]
- Jain, H.; Palmintier, B.; Krad, I.; Krishnamurthy, D. Studying the Impact of Distributed Solar PV on Power Systems Using Integrated Transmission and Distribution Models. In Proceedings of the 2018 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Denver, CO, USA, 1–5 April 2018. [Google Scholar] [CrossRef]
- Kim, J.; Baek, S.-M.; Park, J. Allowable Capacity Estimation of DGs for High Renewable Penetration to Distribution System. In Proceedings of the 2018 IEEE Industry Applications Society Annual Meeting (IAS), Portland, OR, USA, 23–27 September 2018; pp. 1–8. [Google Scholar]
- Ministry of Trade, Industry and Energy. Available online: http://english.motie.go.kr/ (accessed on 1 May 2020).
- Musirin, I.; Abdul Rahman, T.K. Novel fast voltage stability index (FVSI) for voltage stability analysis in power transmission system. In Proceedings of the Student Conference on Research and Development, Shah Alam, Malaysia, 17 July 2002. [Google Scholar] [CrossRef]
- Kim, J.C.; Cho, S.M.; Shin, H.S. Advanced power distribution system configuration for smart grid. IEEE Trans. Smart Grid 2013, 4, 353–358. [Google Scholar] [CrossRef]
- Afamefuna, D.; Chung, I.Y.; Hur, D.; Kim, J.Y.; Cho, J. A techno-economic feasibility analysis on LVDC distribution system for rural electrification in South Korea. J. Electr. Eng. Technol. 2014, 9, 1501–1510. [Google Scholar] [CrossRef]
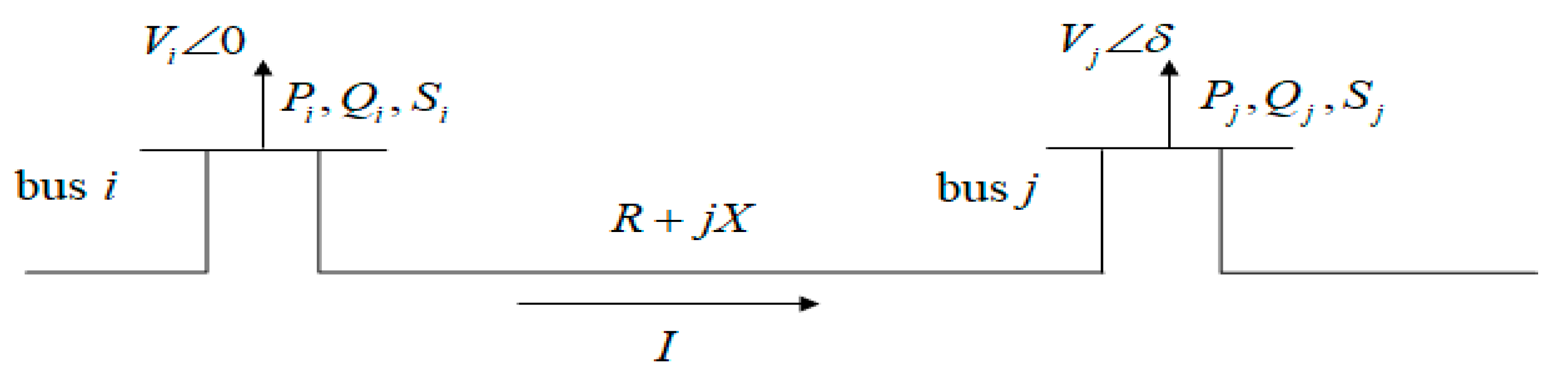

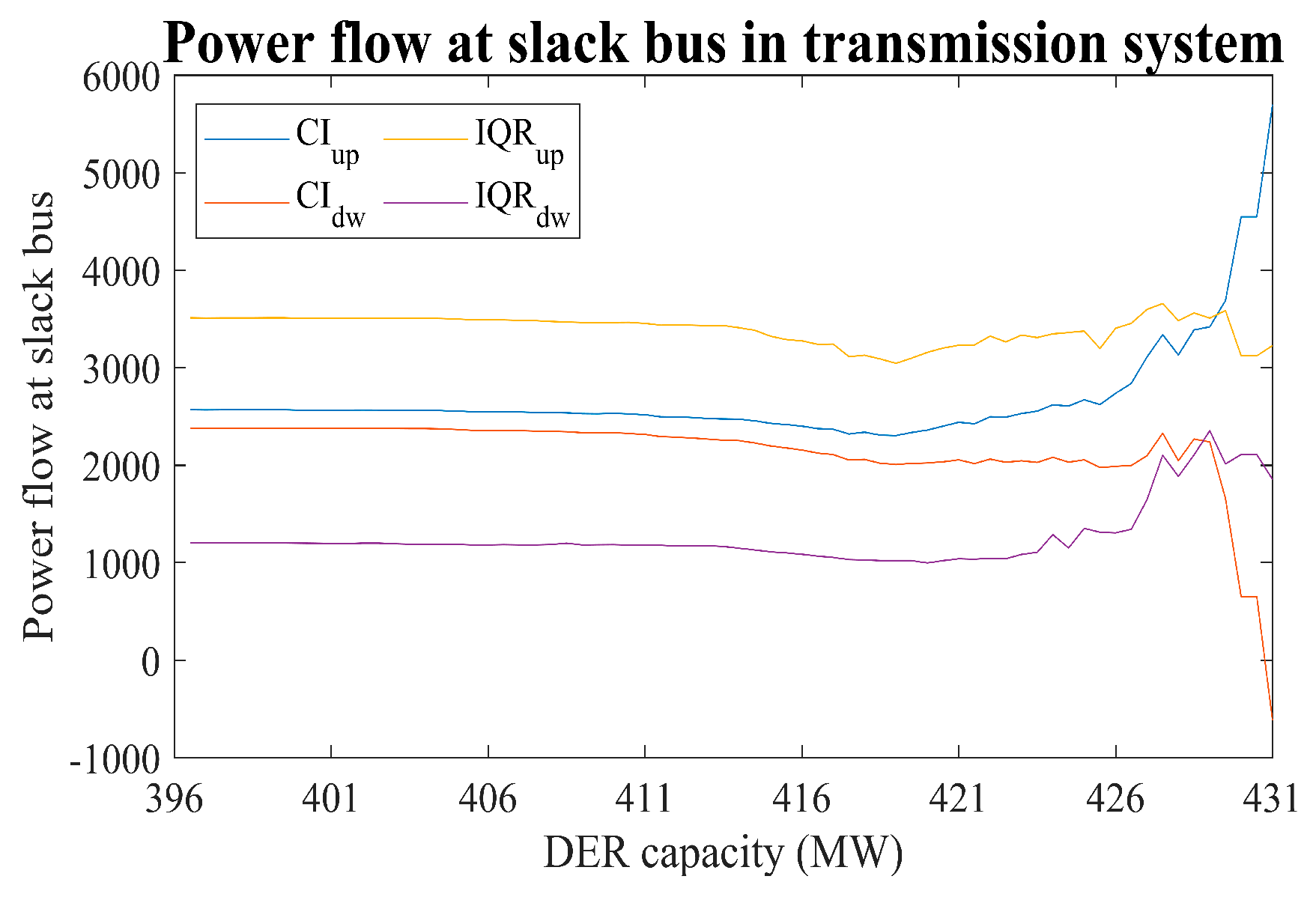
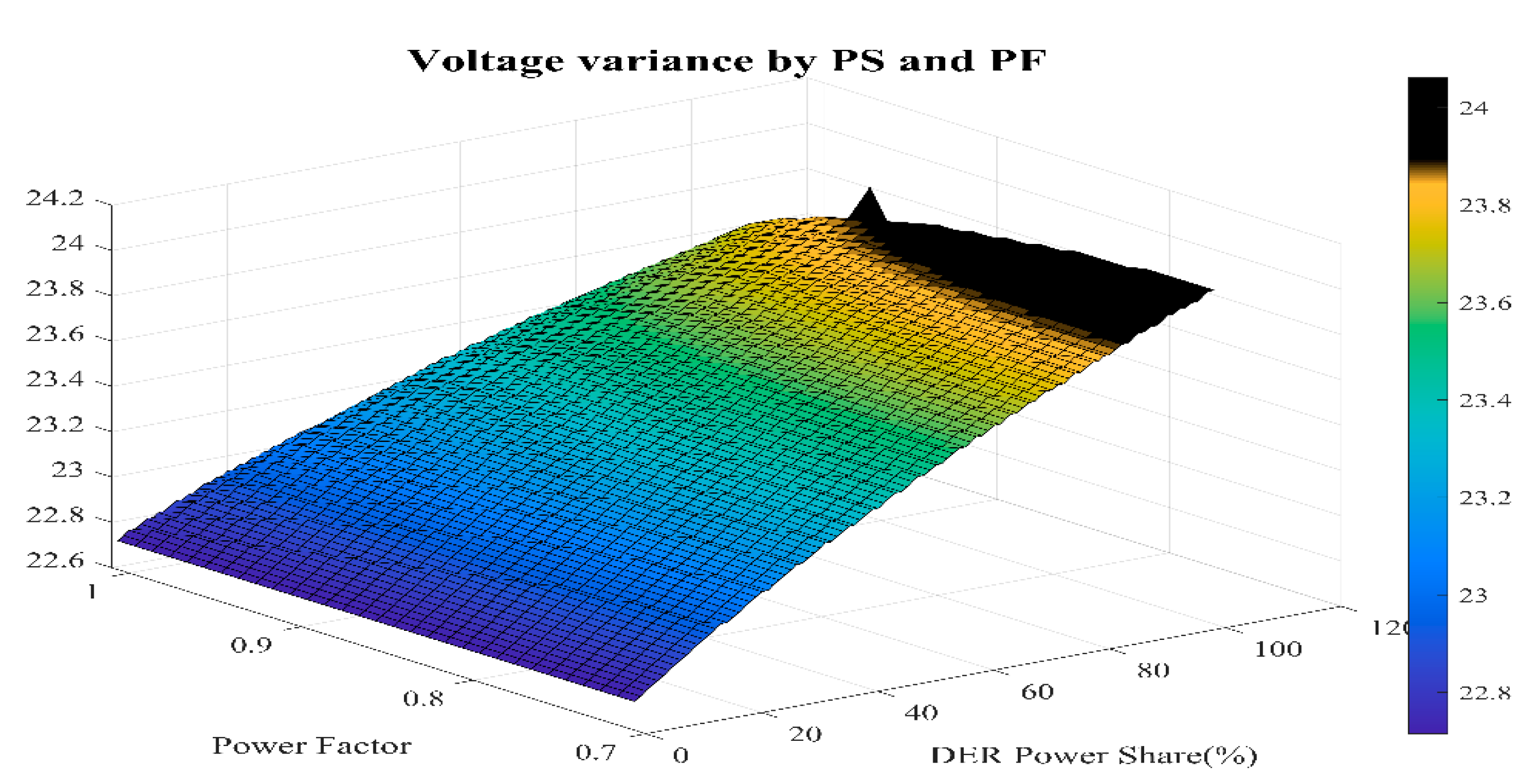
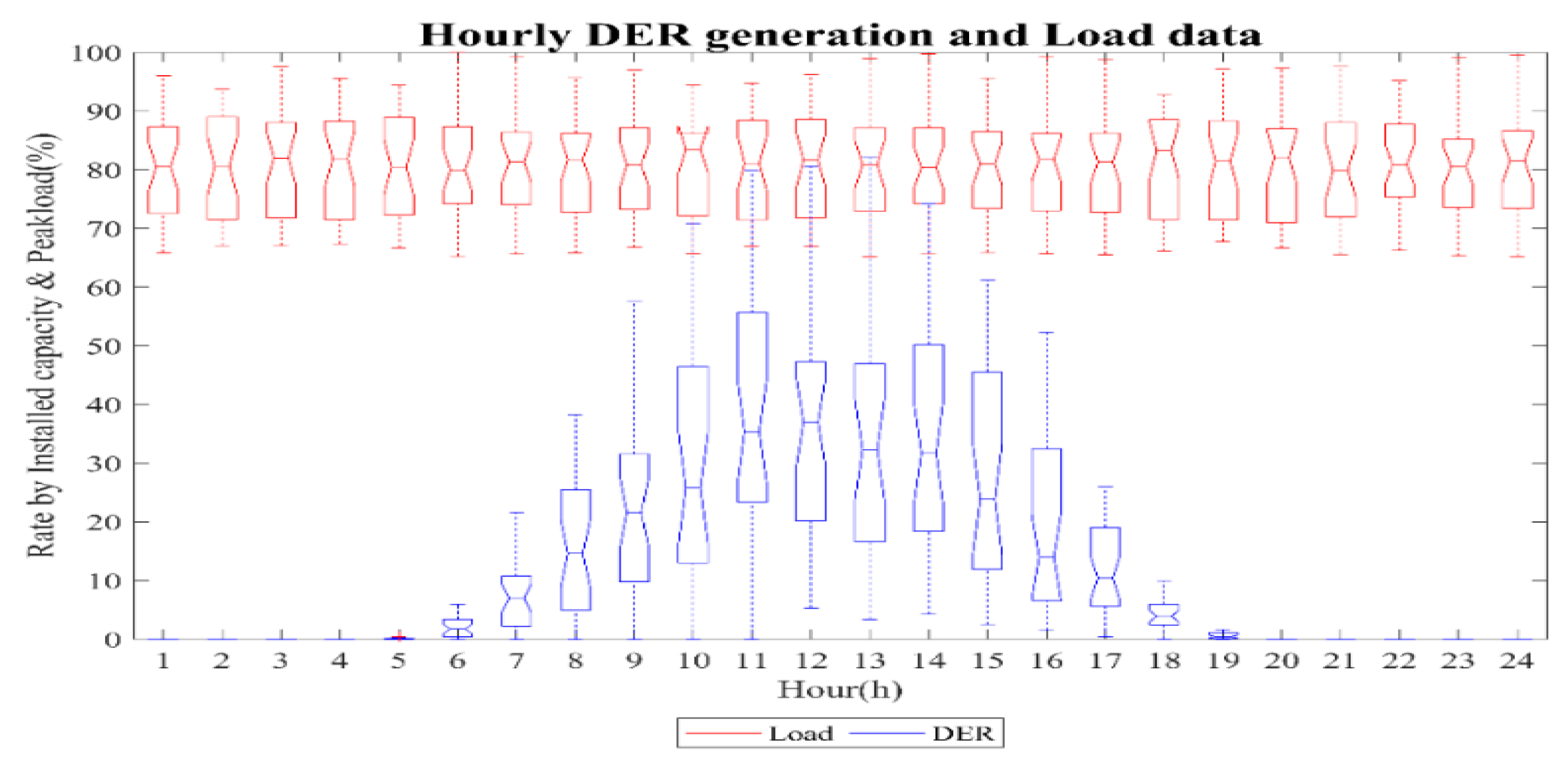
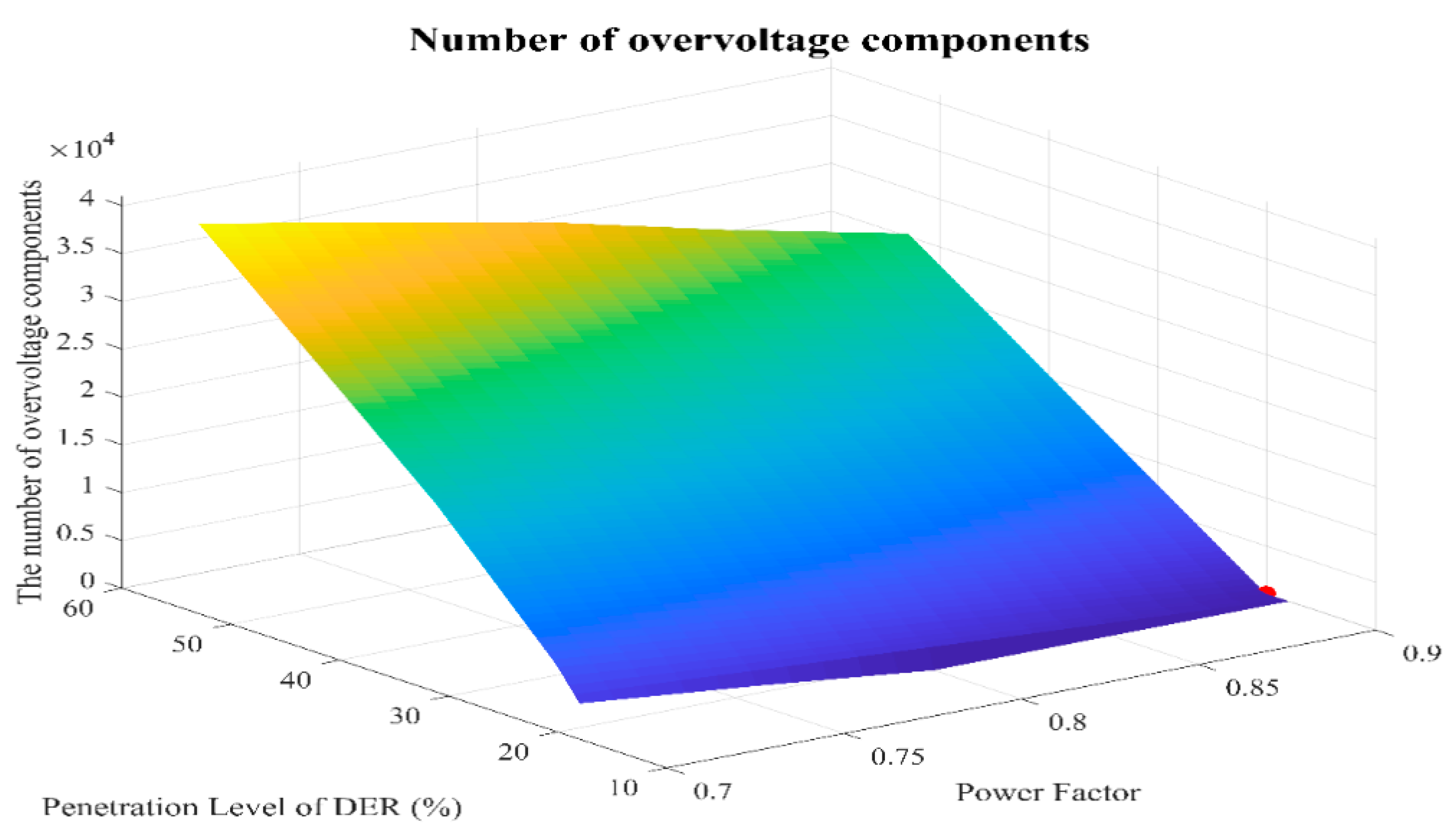

| Type | Nominal Voltage | Voltage by Distribution Type (V) | Maximum Voltage | ||
|---|---|---|---|---|---|
| Single-Phase Two-Wire | Three-Phase Three-Wire | Three-Phase Four-Wire | |||
| Low voltage | 220 | 220 | - | - | - |
| 380 | - | - | 220/380 | - | |
| High voltage | 22,900 | 13,200 | - | 13,200/22,900 | 25,800 |
| Nominal Voltage (V) | Maintenance Range (V) | ||
|---|---|---|---|
| Min | Max | ||
| Low voltage | 220 | 207 | 233 |
| 380 | 342 | 418 | |
| High voltage | 13,200 | 12,000 | 13,800 |
| 22,900 | 20,800 | 23,800 | |
| Type | Voltage (kV) | Allowable Capacity (kVA) | |
|---|---|---|---|
| Steady State | Emergency State | ||
| Normal distribution line | 22.9 | 10,000 | 14,000 |
| Large-capacity distribution line | 15,000 | 20,000 | |
| Type | Application Standard | Allowable Current (A) | Condition |
|---|---|---|---|
| ASCR-OC 160 mm2 | Continuous allowable current | 395 | 90 °C |
| Object | Range | Distribution Type |
|---|---|---|
| Load | [3000–3500] kVA | Uniform |
| DER | [0–14] kVA | |
| Feeder length | 10 km [Fixed] | - |
| Capacity (MW) | Penetration Level (%) | Overvoltage Component | Max. Power Share (%) |
|---|---|---|---|
| 37.5 | 53.2651 | 744 | 233.38 |
| 20 | 31.0897 | 248 | 158.88 |
| 12.5 | 20.1191 | 0 | 114.91 |
| 10 | 17.9558 | 0 | 97.26 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Widiputra, V.; Kong, J.; Yang, Y.; Jung, J.; Broadwater, R. Maximizing Distributed Energy Resource Hosting Capacity of Power System in South Korea Using Integrated Feeder, Distribution, and Transmission System. Energies 2020, 13, 3367. https://doi.org/10.3390/en13133367
Widiputra V, Kong J, Yang Y, Jung J, Broadwater R. Maximizing Distributed Energy Resource Hosting Capacity of Power System in South Korea Using Integrated Feeder, Distribution, and Transmission System. Energies. 2020; 13(13):3367. https://doi.org/10.3390/en13133367
Chicago/Turabian StyleWidiputra, Victor, Junhyuk Kong, Yejin Yang, Jaesung Jung, and Robert Broadwater. 2020. "Maximizing Distributed Energy Resource Hosting Capacity of Power System in South Korea Using Integrated Feeder, Distribution, and Transmission System" Energies 13, no. 13: 3367. https://doi.org/10.3390/en13133367
APA StyleWidiputra, V., Kong, J., Yang, Y., Jung, J., & Broadwater, R. (2020). Maximizing Distributed Energy Resource Hosting Capacity of Power System in South Korea Using Integrated Feeder, Distribution, and Transmission System. Energies, 13(13), 3367. https://doi.org/10.3390/en13133367





