2.1. Power System Stability
All generators in an interconnected power system are working with the same frequency and the rotor mechanical speed is synchronized to this frequency. In technical terminology it is said that the generators are “in step”. This electrical connection between synchronous generators is elastic and allows angle fluctuations between them. Following some disturbances like short circuits which lead to line losses, the rotors of some generators will start to oscillate. The ability of the generators in the power system to remain in synchronicity those oscillations is referred to as rotor angle stability [
10]. If a short circuit occurs and before the protection trips, a balance between mechanical power applied on the turbine and electrical power delivered to the system exists on each generator. When the protection trip occurs, the load in the system is changed rapidly but the change of mechanical power on the prime mover is much slower. This produces differences between mechanical and electrical torque in generators, and thus the rotor angle changes. The simplified relationship between the power output on generators and the rotor angle positions of the synchronous generators is represented by the following equation:
where
Eg is induced generator voltage,
Us is voltage at generator terminals,
X is generator reactance and
δ is the angle between voltages or load angle. A graphical representation of this nonlinear equation is shown in
Figure 1.
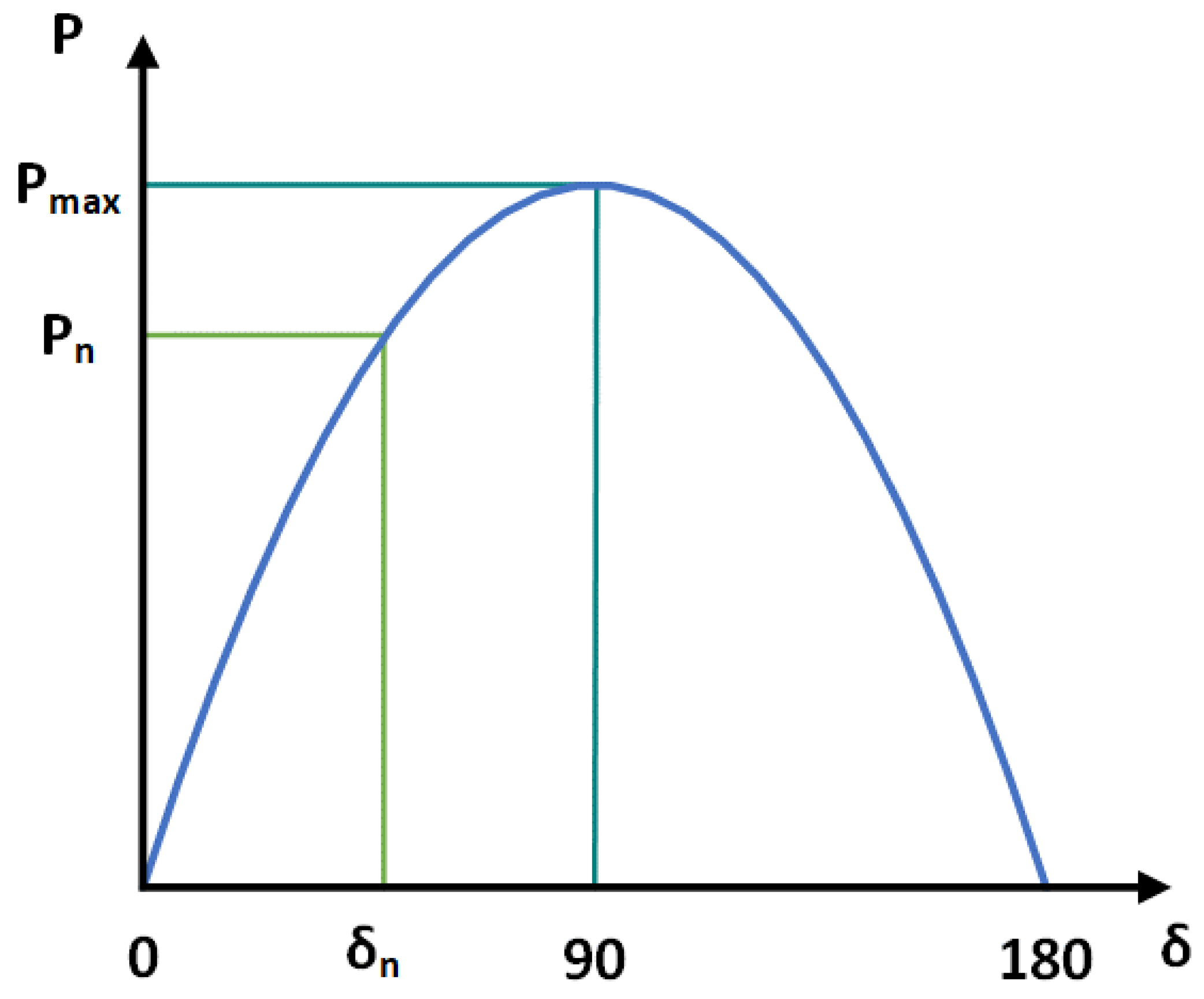
This is an idealized equation and representation, but it can be used to describe the system behavior. Therefore, in
Figure 1 the transferred power rises with angle difference, but only to a certain point. The maximum transferred power is reached at an angle of 90° and any further increase in the angle will result in a decrease of transferred power. The power transferred at 90° is at its maximum under steady state conditions.
The same characteristic can be used to describe what happens during transient conditions. Initially, the system is in balance with transferred power
Pn at the load angle of
δn. After the protection trip occurs and the breaker is opened, the transferred power is reduced instantaneously and the mechanical power remains the same. Due to this difference, the rotor starts to accelerate and the angle
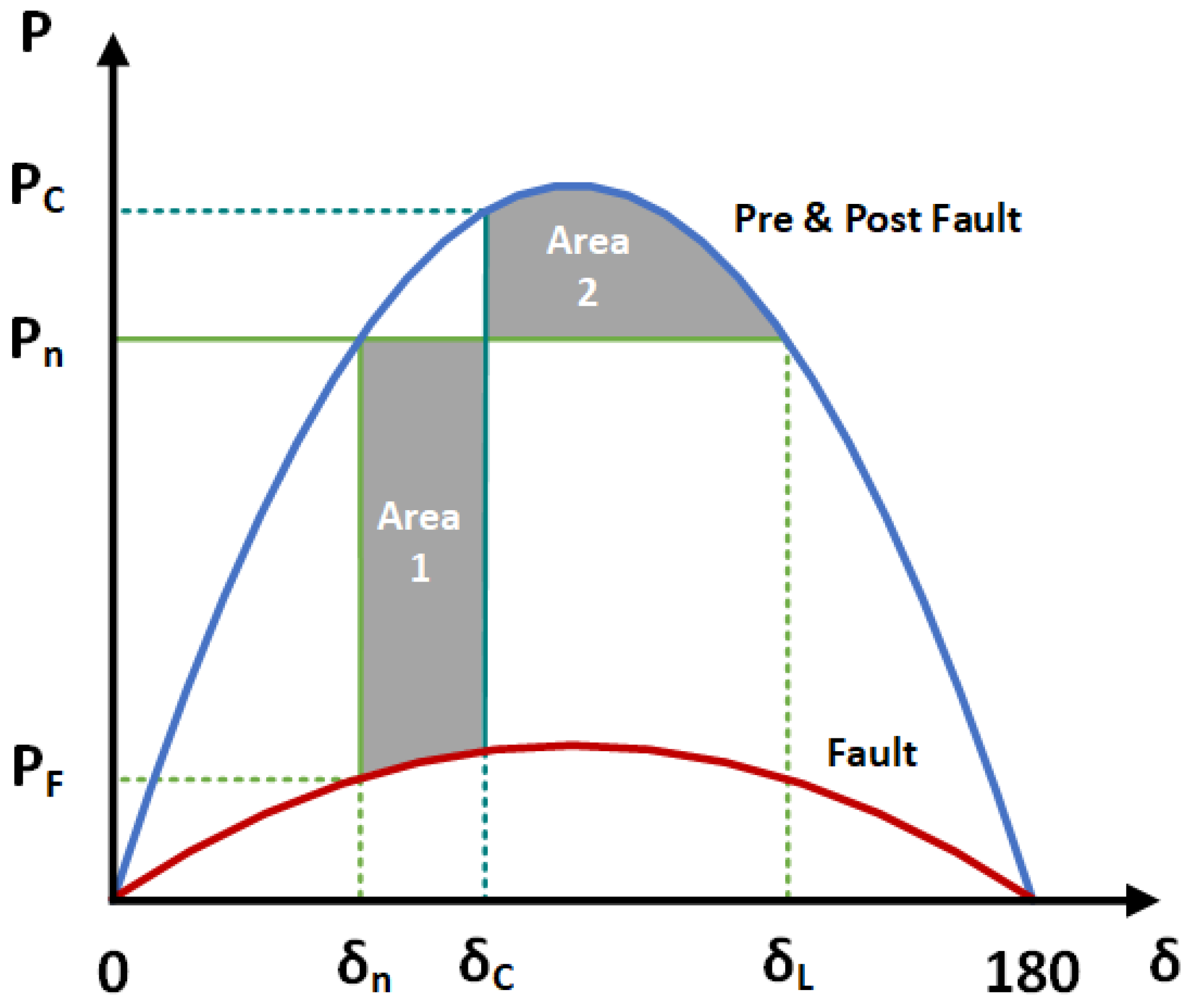
δ increases. When the fault is cleared, the reached angle is
δC but the rotor continues to accelerate since there is accumulated kinetic energy in it. At this point the rotor starts to decelerate since the electric torque is higher than the mechanical. The rotor decelerates till the angle
δF is reached and all accumulated kinetic energy is used up. In
Figure 1 and
Figure 2 it can be noticed that a critical angle
δL exists, above which further increase in the angle results in lower electrical power and the generator starts to accelerate with no recovery. It can be concluded that the generator will maintain its stability if there is sufficient decelerating energy to oppose the acceleration. This is called the equal area criterion.
From the mentioned criterion it is also obvious that a critical time exists in which the fault must be cleared in order to maintain the stability of the generator. This time depends on the generator reactance and inertia constants. Since the size of the machines has increased and the inertia constants have decreased in the last decade, the critical times are reduced as well. If the loss of generator synchronicity occurs, high amplitude currents cause strains in generator windings as well as mechanical strains that can lead to generator and turbine damages. Therefore, it is important to clear the fault as soon as possible.
2.2. Load Angle Definition and Measurement
Hydrogenerators and turbogenerators can be described by a distinctive standard two-axis mathematical model. In order to describe the synchronous generator with this mathematical model, the generator parameters have to be known. The load angle is one of the main synchronous generator parameters and the precise load angle measurement is imperative for determining the mathematical model. The load angle is mostly used in the generator monitoring systems, but its measurement in such systems is not conducted in real time [
12]. The motivation behind this research was to evaluate if these measurements, conducted in real time, can be used for generator protection. Additionally, the load angle can be used for power system stability analysis and to determine losses of a generator. In these cases, the load angle must be measured in real time and in both static and transient generator operation modes.
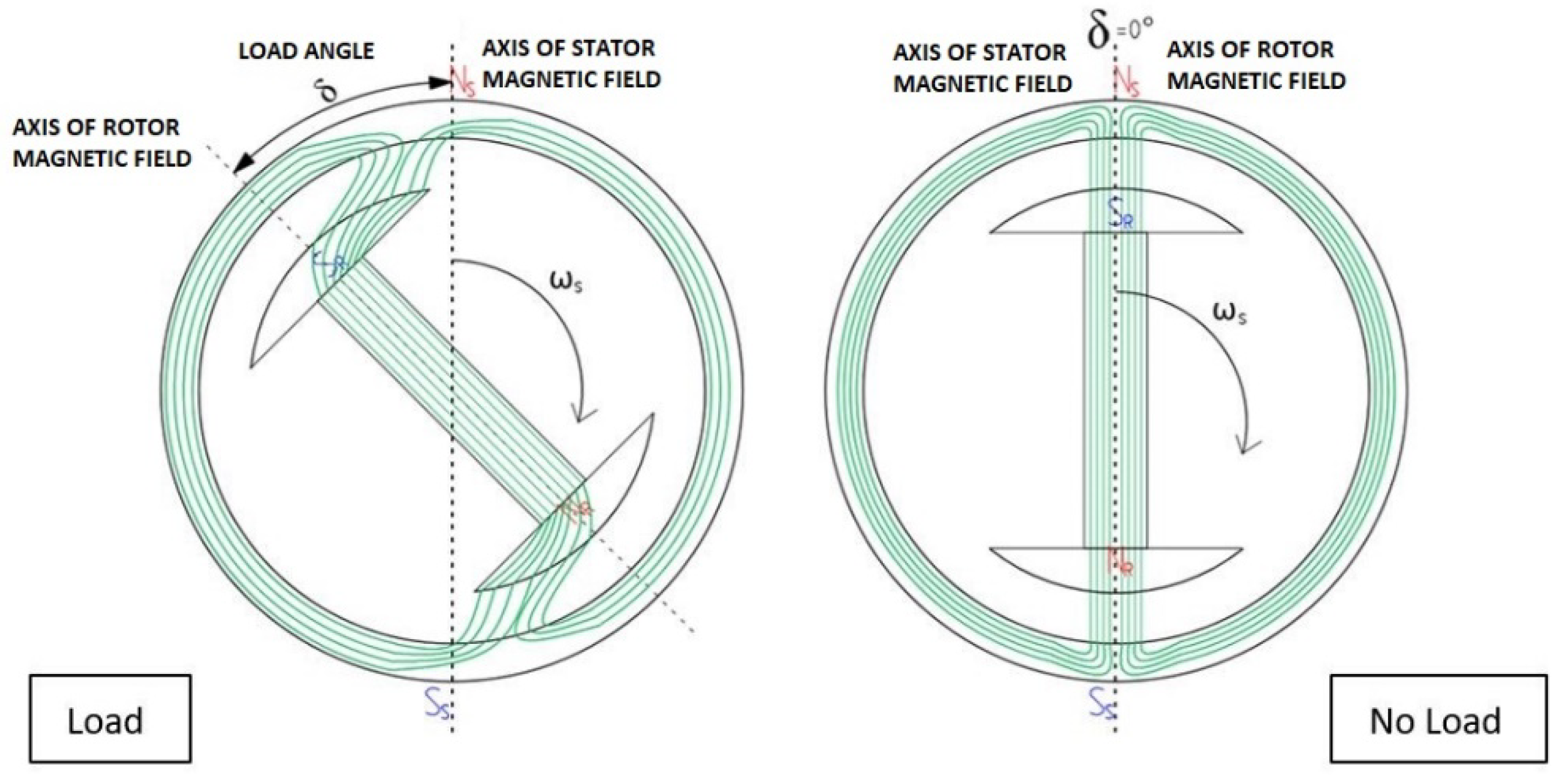
The electrical load angle
δ is the angle between induced EMF and terminal voltage or the angle between rotor and stator magnetic fields. The magnetic field of a synchronous generator rotates at synchronous speed and induces a rotating magnetic field in a stator but they are not completely aligned as the stator field lags behind the rotor field. This lagging is expressed in the load angle, as shown in
Figure 3. The generated power is directly proportional to the sine value of this angle.
When combined with the on-line capability chart (P-Q chart), the real time (on-line) measurement of the load angle (static and dynamic) is very important for determining the actual working parameters of a generator. Furthermore, the load angle is a key parameter in understanding torsional dynamics of a generator where magnetic field stiffness influences dynamic response of the generator.
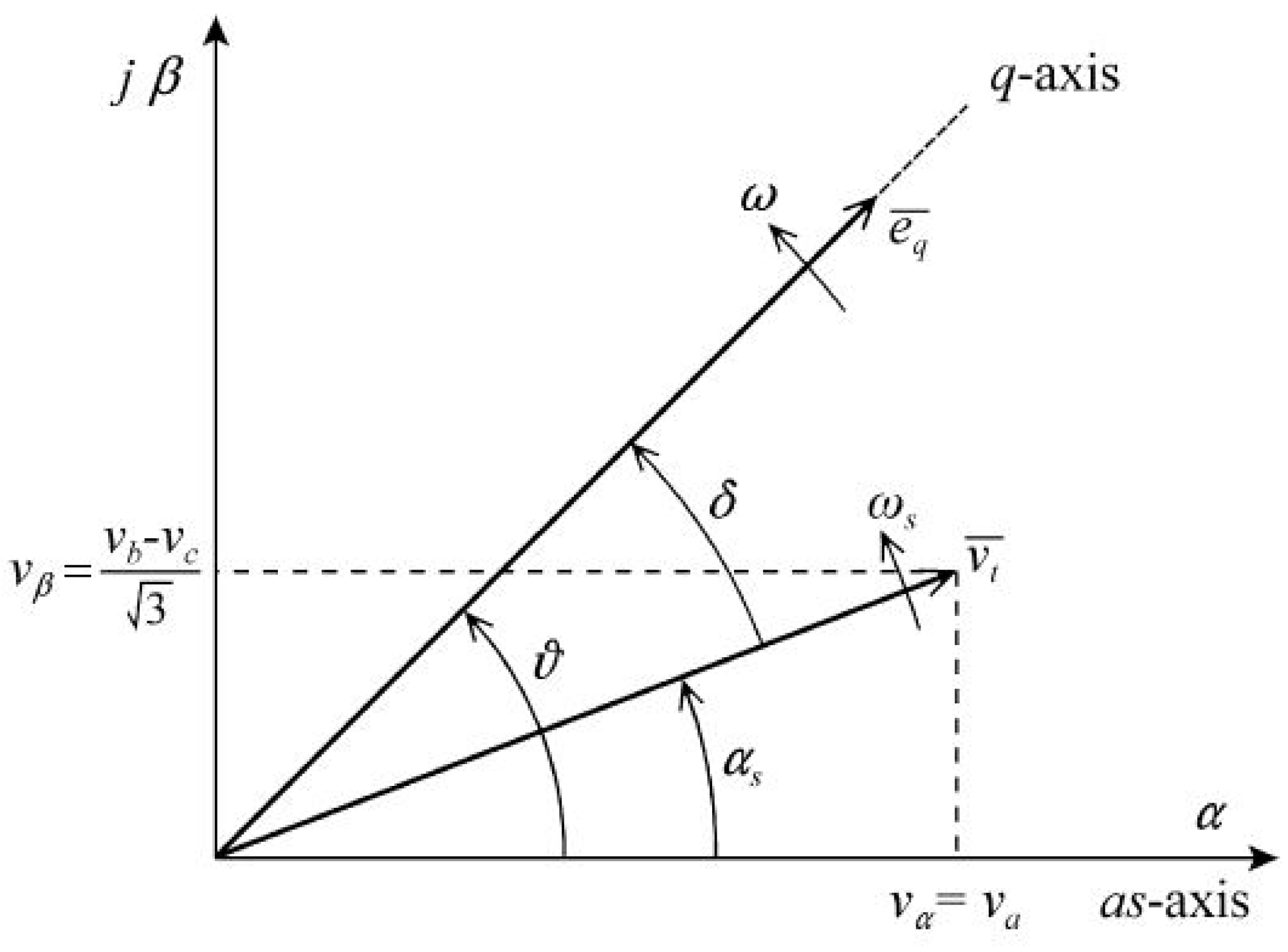
As mentioned before, hydrogenerators and turbogenerators can be described by a distinctive standard two-axis mathematical model. The vector diagram in
Figure 4 and Equations (2)−(5) [
12] are based on the mentioned
dq mathematical model of the synchronous generator. In this representation the load angle is defined as the electrical angle between the space vector of the excitation voltage
ēq and the terminal voltage space vector
. Since
ēq lies along the positive
q axis, the load angle can also be defined as the electrical angle between the
q axis and the voltage vector
. At no-load condition
ēq and
are identical and the load angle equals zero.
The resulting vector
is defined in the stator coordination system
αβ where the real axis of this system corresponds to the phase of a winding axis
as. When instantaneous values of generator terminal line voltages are known, the vector
can be calculated from Equations (2) and (3). Based on this, the angle
which is the angle between vector
and the axis
as is defined in Equation (4) [
12]:
Therefore, at symmetrical terminal voltage conditions the position of can be obtained by the phase angle of any line terminal voltage. The load angle can be obtained by measuring the rotor reference axis displacement referenced to the fundamental component of the line voltage, which is selected as the reference one, at load and no-load conditions respectively, as defined in Equation (5).
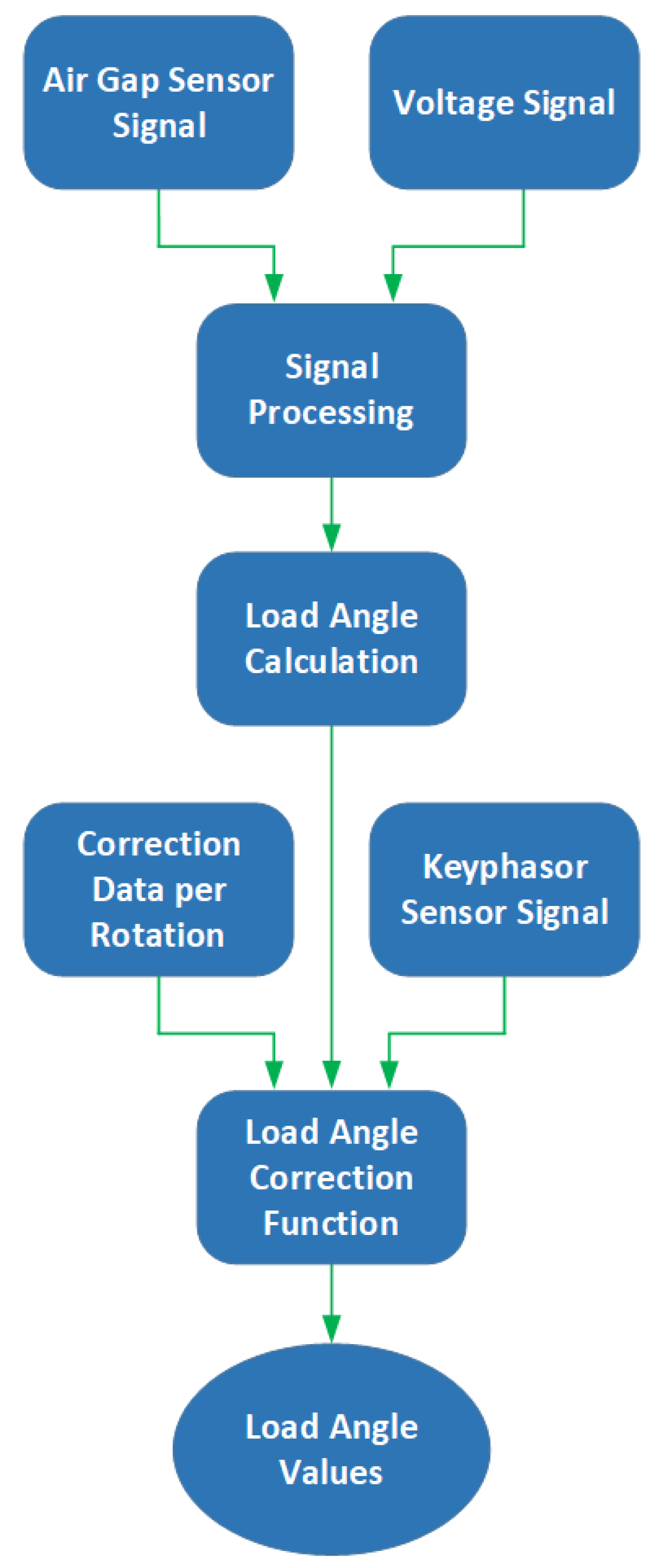
The load angle is determined by the terminal voltage signal of one phase and by the information on rotor position. Since the information on rotor position can be obtained in several different ways, different methods for determining the load angle also exist. The quality of the load angle measurements corresponds to the accuracy of determining the rotor position, and the rotor position is usually determined in practice by different methods like the incremental encoder, inductive sensor and the capacitive air gap sensor.
The principle behind determining the rotor position by the inductive sensor is to use the inductive sensor for recording the passes of the gear teeth which are mounted on the generator shaft. The gear holds the same number of teeth as the pairs of poles, meaning that one impulse from the sensor appears in each period. An approximately sine signal is obtained at the output of the inductive sensor, and this signal is further modulated in frequency by the rotational speed of the rotor.
Measuring the load angle by using the incremental encoder is based on measuring the time difference between the reference marker and the incremental passage of the terminal voltage signal through zero-crossing.
The results shown in [
12] suggest that the methods for determining the rotor position based on the incremental encoder and inductive sensor are very sensitive to vibrations and precession of the generator shaft. The capacitive air gap sensor method for determining the rotor position, or in other words for measuring the load angle, was developed to overcome these problems.
The capacitive air gap sensor measures the distance between the stator and rotor poles. The measurement of the distance between the stator and rotor poles is contactless and based on the capacitive flat-shaped probe which is mounted by simply being glued onto stator laminations. The capacitive air gap sensor for measuring the air gap width is in fact a measuring chain consisting of the probe and the linearization module (LM) [
13,
14]. An example of the capacitive air gap sensor is shown in
Figure 5 [
15]. The probe is connected to the linearization module via a triaxial cable and the linearization module sends a high frequency signal to the probe through the triaxial cable. The capacity is measured by a change in the phase of this signal, and the capacity directly depends on the air gap width. The linearization module is powered by DC voltage. On the output it produces a signal whose frequency is twice the grid frequency and is a good representation of the rotor position. After the signal is processed in the linearization module, a direct current output signal (4 to 20 mA) is obtained. This output signal is proportional to the generator air gap width.
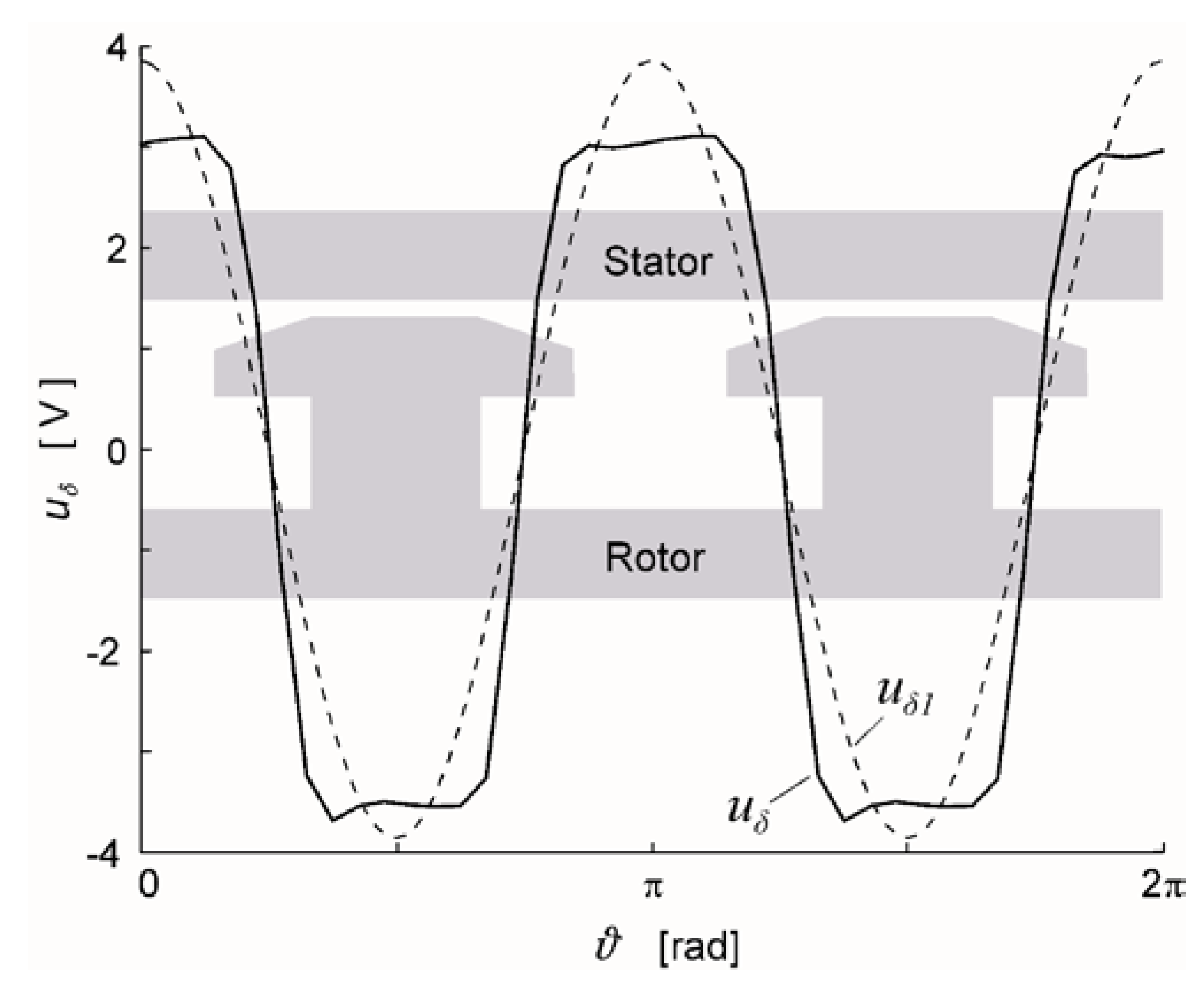
Figure 6 shows this signal
uδ recorded at a constant rotor speed and a sketch of the air gap width configuration [
12]. The signal
uδ1 is a fundamental component of the
uδ signal and both signals are expressed in volts, while the angle
is expressed in electrical radians. The load angle measurements require the air gap sensor signal to be tightly bound to the rotor position. If the rotor position correlates with the induced EMF, it can be used to determine the value of the load angle together with a terminal voltage signal. It can also be said that the phase shift of the capacitive air gap sensor signal towards the terminal voltage signal represents the load angle.
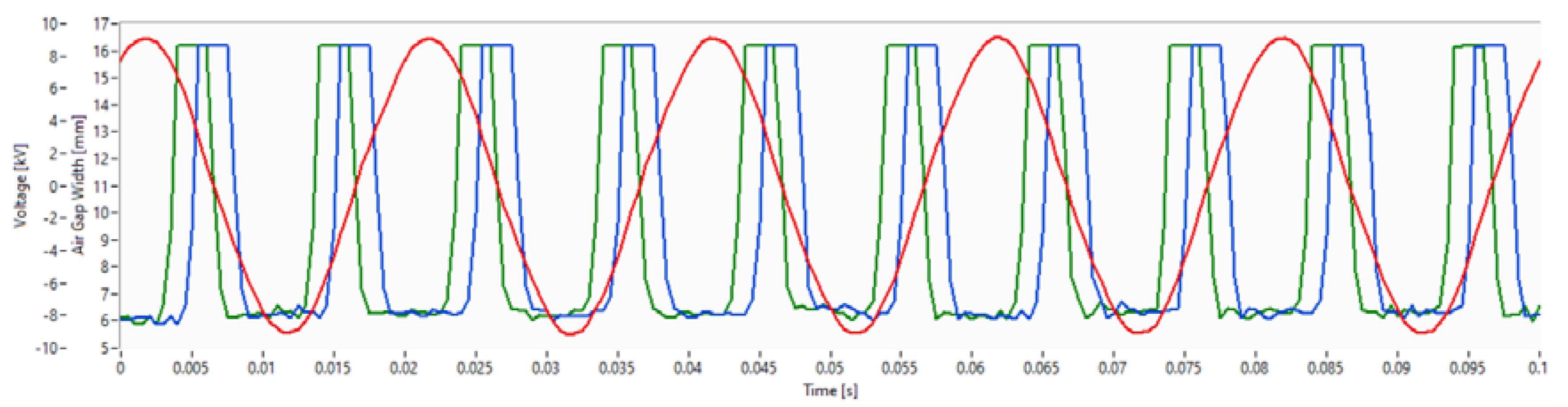
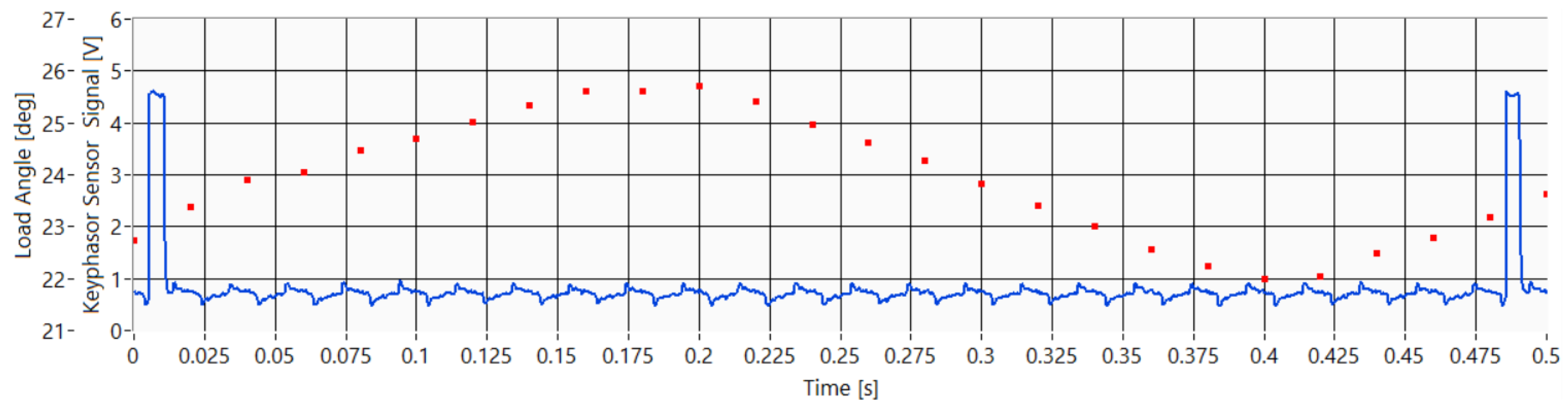
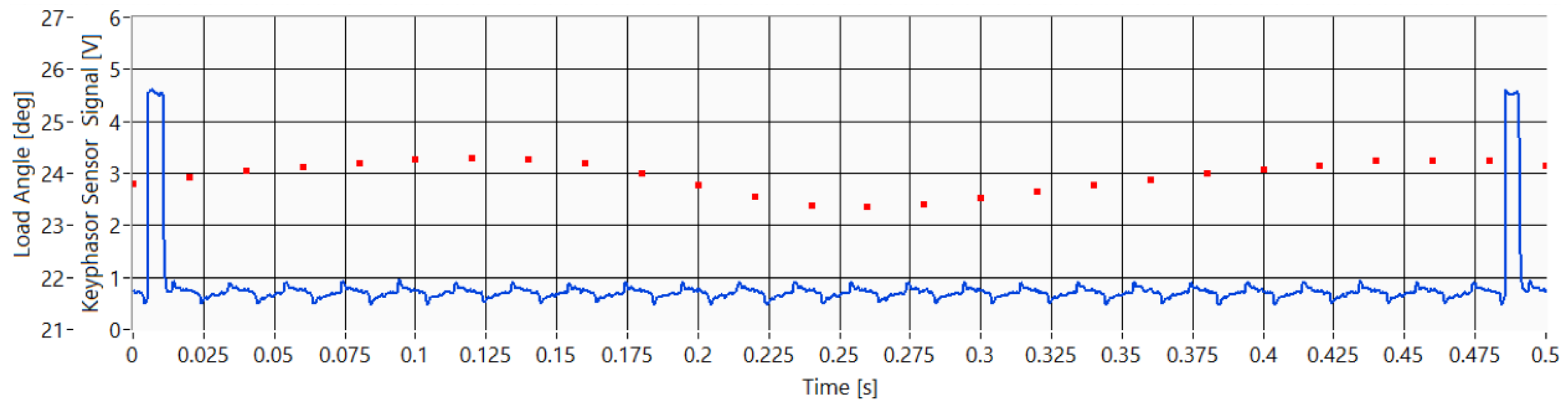
Figure 7 shows the measurement results and the relationship between the terminal voltage signal and the capacitive air gap sensor signal. As the load angle increases, the air gap sensor signal starts leading in front of the voltage signal which is clearly shown in
Figure 7. The blue curve represents the air gap sensor signal when the generator is excited but operates in the no-load mode. In this operation mode the active power and load angle values both equal zero. The green curve represents the air gap sensor signal when the generator is loaded and when the active power and load angle values are greater than zero.
When compared to the shaft encoder, the capacitive air gap sensor gives more stable and precise information on the rotor position because of the small radius of the shaft encoder ring compared to the rotor radius [
16,
17,
18,
19]. The research results shown in [
12] confirm that the air gap sensor method for measuring the load angle is the most reliable, most precise and cheapest way of measuring the load angle. In the here presented research, the air gap sensor method is used for measuring the load angle.
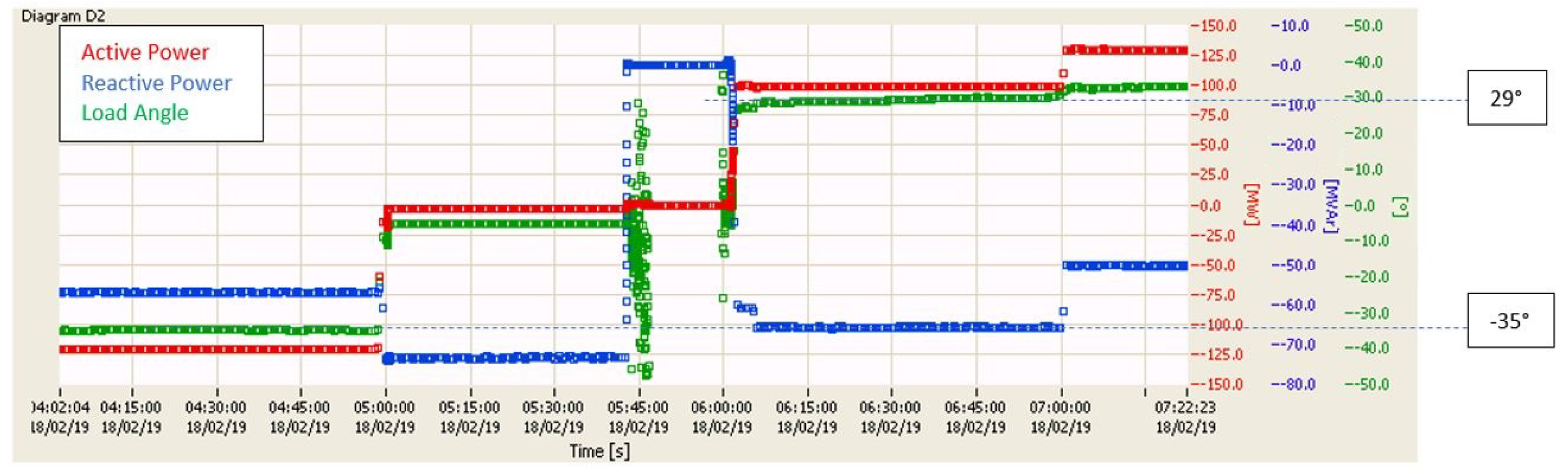
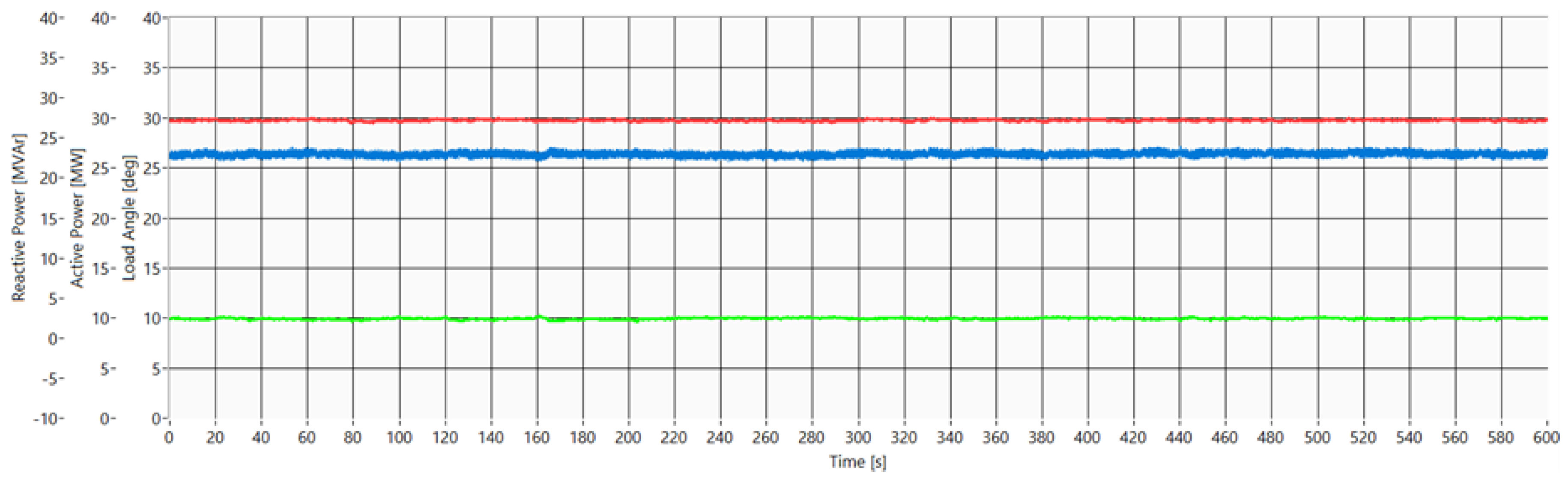
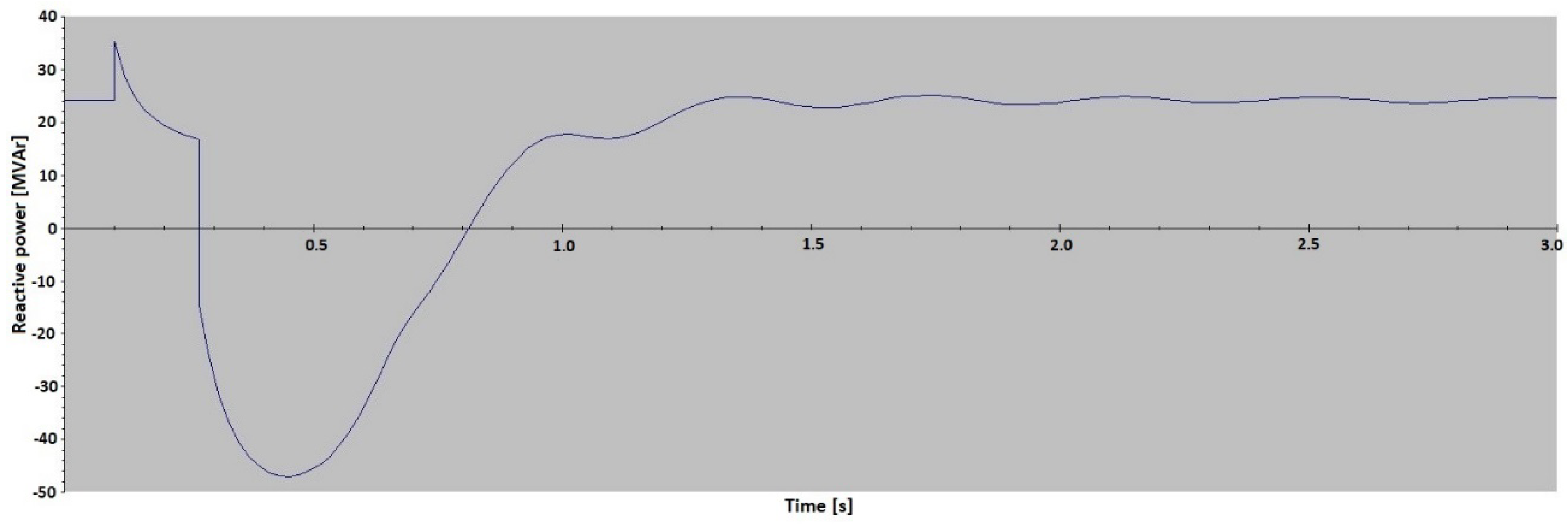
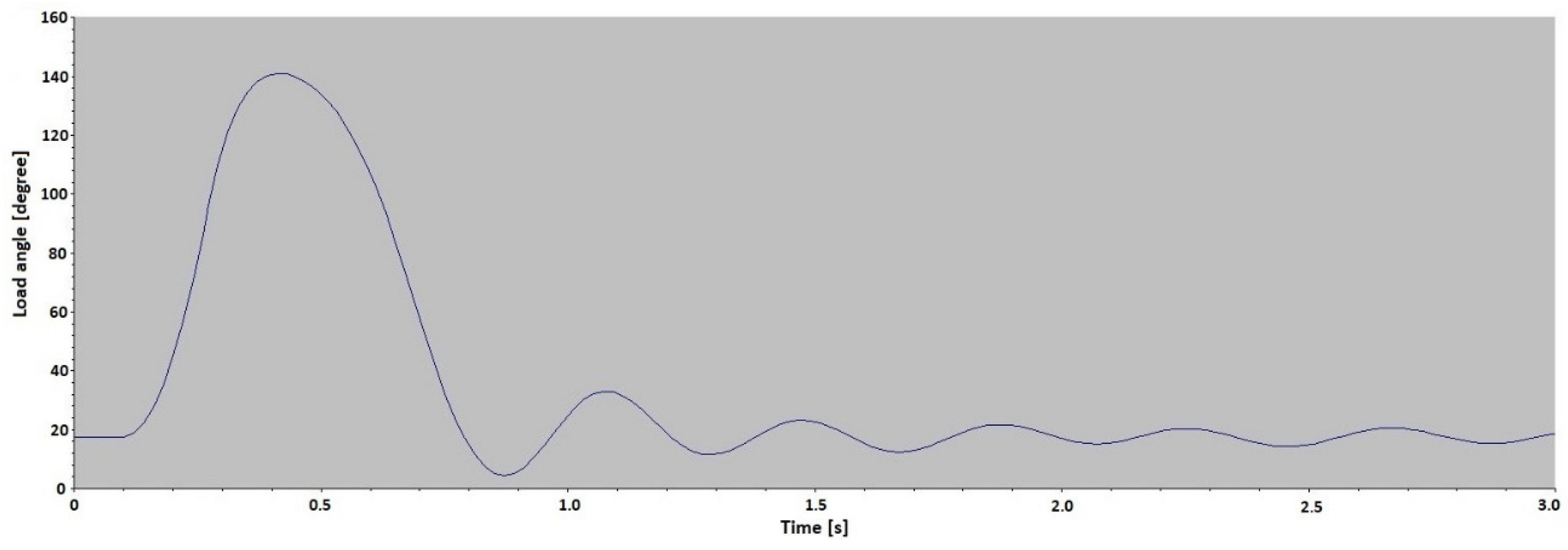
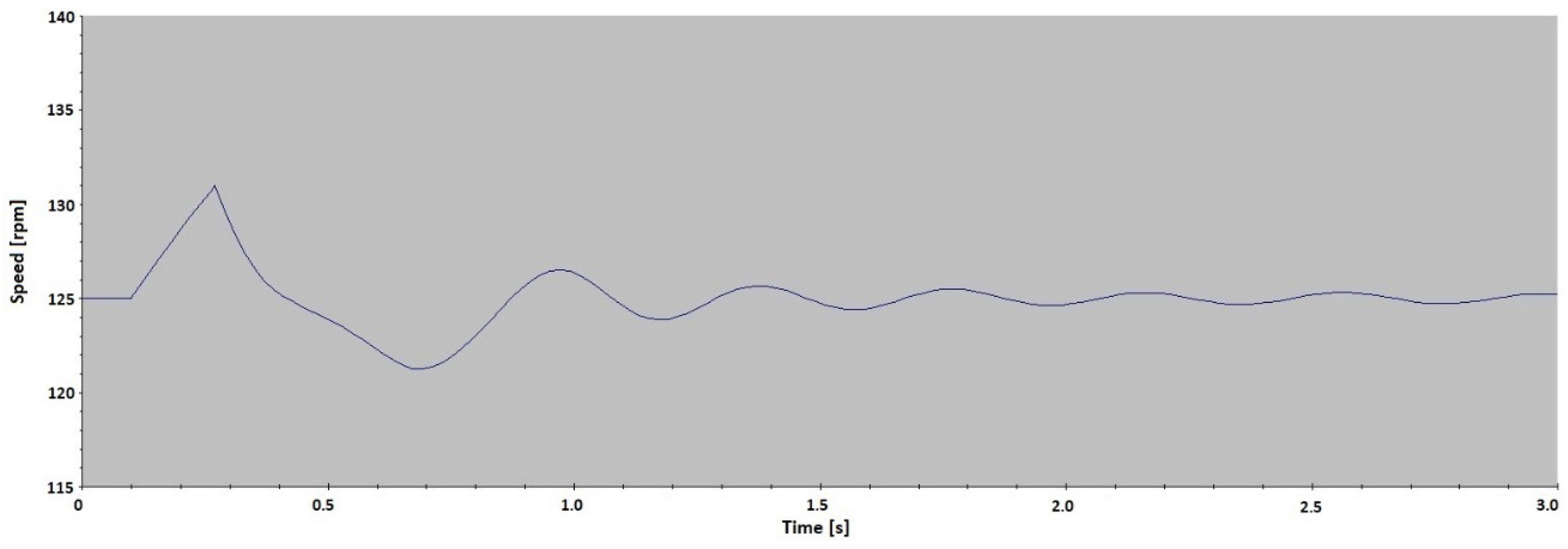
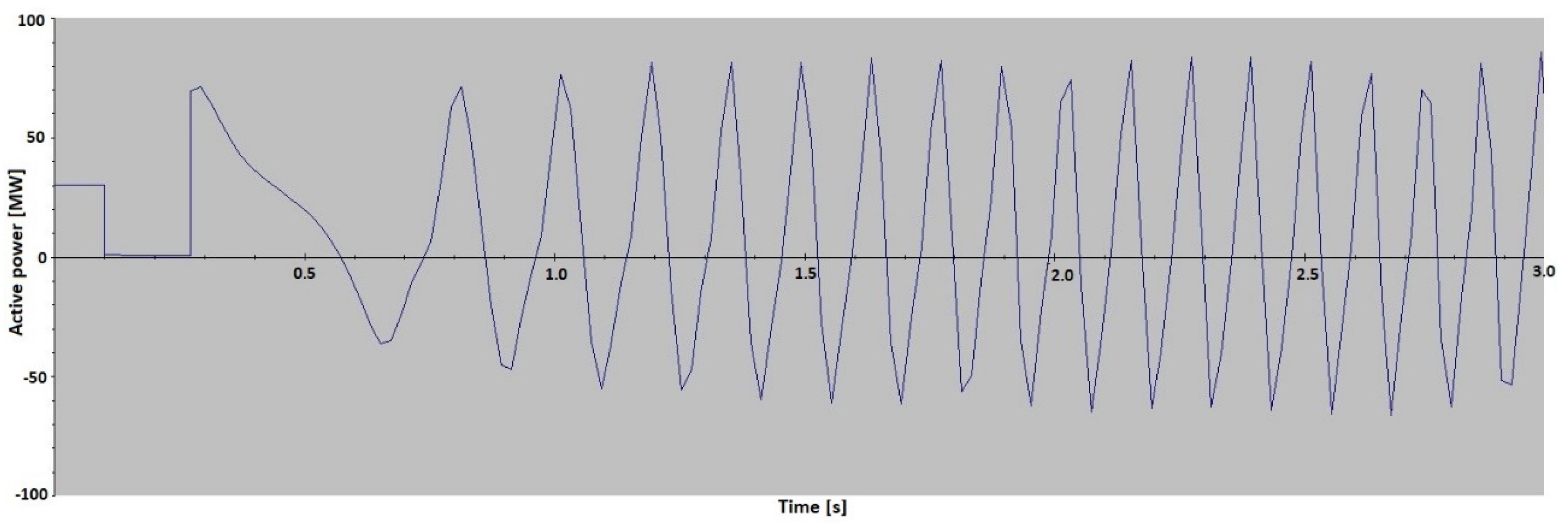
Figure 8 confirms that this method gives stable results, as it shows the change of the load angle of the pumped-storage hydro unit under three operation modes: synchronous condenser, pumping and generator, with different active and reactive power. The measurements shown in
Figure 8 were taken from the monitoring system of a pumped-storage hydro unit.
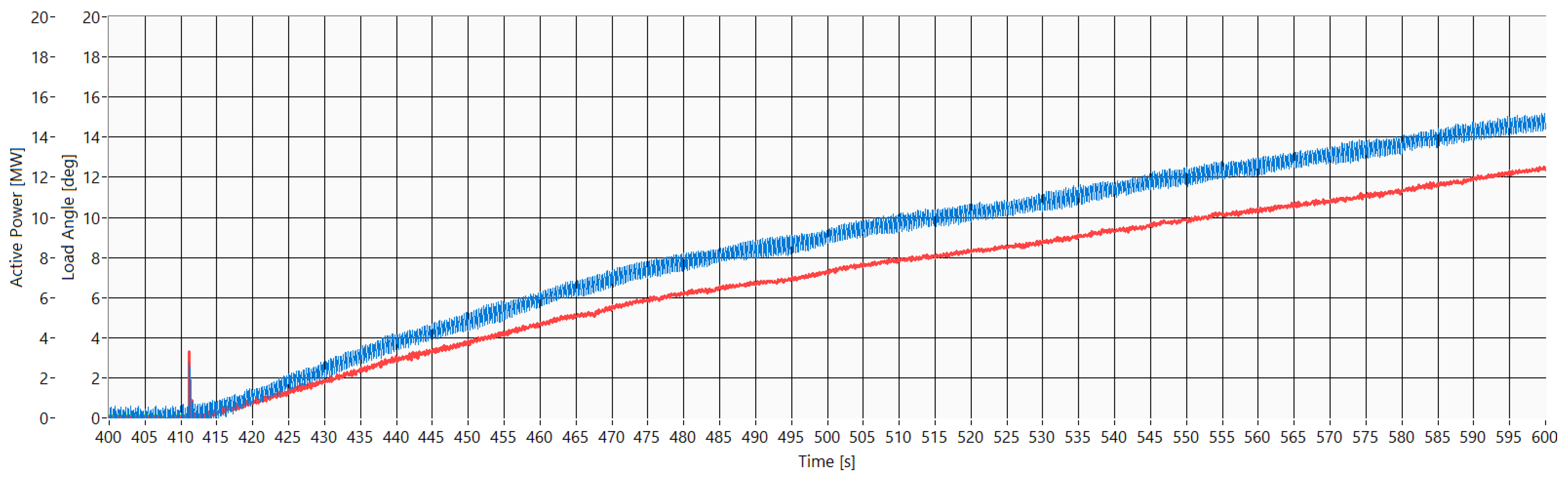
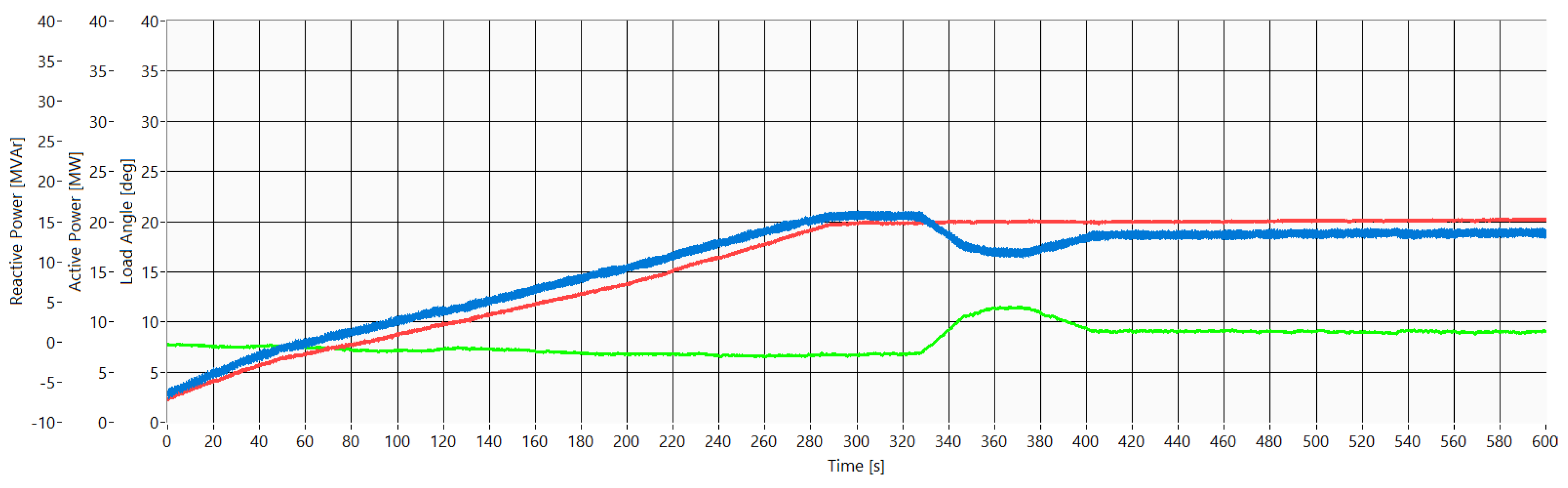
Figure 8 shows the values of active power (red dots), reactive power (blue dots) and the load angle (green dots) over a period of 3 h and 20 min. The interdependence of the load angle values and the active/reactive power values is clearly shown. In the period from 4:02 to 5:00 a.m. the pumped-storage hydro unit works under the pumping (motor) operation mode, so the values of the load angle are negative. In the period from 5:00 to 5:45 a.m. the pumped-storage hydro unit works under the synchronous condenser operation mode (active power is 0 MW, and reactive power is about −75 MVAr). Under this operation mode the load angle almost equals zero degrees because there is no load. At 5:45 a.m. the pumped-storage hydro unit is turned off and turned on again at 6:00 a.m. When the pumped-storage hydro unit is turned off and on, the load angle measurement loses its stability because the excitation is turned off. This instability is shown in
Figure 8 in the time period between 5:45 and 6:00 a.m. After 6:00 a.m. the pumped-storage hydro unit works under the generator operation mode, where the load angle values are positive. At 7:00 a.m., when the active power increases, the load angle increases as well.
Measuring the load angle in real time is a relatively new procedure yet to be researched, and the full potential of this parameter of synchronous generator has not been used in practice. To date, it is most commonly used in generator monitoring systems. Different types of sensors are used for measuring the load angle, and because these measurements are very specific, one universal solution does not exist.
2.3. Loss of Synchronicity Detection Methods
A substantial amount of research has been conducted, as well as articles written, about the loss of synchronicity detection. The most commonly used detection method in today’s numerical protection relays is based on the monitoring of impedance change at the generator terminals [
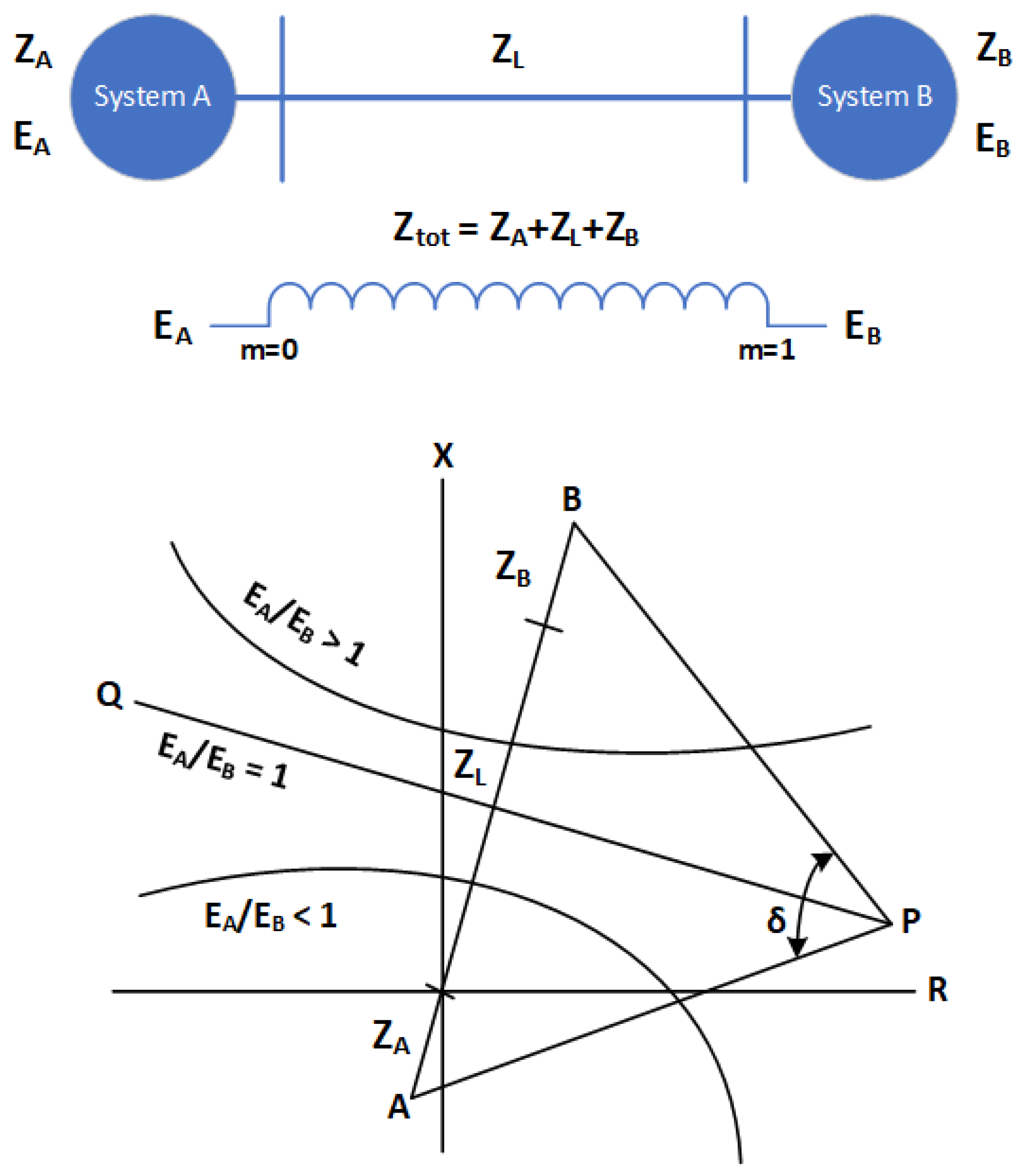
20]. When using a simple example which consists of two systems A and B, their impedances
ZA and
ZB and the line impedance
ZL, then the impedance characteristic is presented in
Figure 9.
If the voltages
EA and
EB are equal, i.e.,
EA/
EB = 1 then the impedance characteristic is represented by the line PQ, and the angle between lines AP and BP is the load angle between the two systems
δ. The line AB stands for total impedance. If system B is used as the reference system and it is assumed that
EA is leading
EB, then the impedance is changing from point A towards point B. During the loss of synchronicity, the impedance travels from point P to point Q. When the impedance intersects total impedance, the angle between two systems is 180° and it can be said that the systems are out of step. This point of intersection is known as the electrical center of the system. The impedance continues to travel and reaches again the point when the systems are in phase. At this point it is said that one out of step cycle has been completed. When the ratio
EA/
EB is not equal to 1, the impedance characteristics are represented by the curves as can be seen in
Figure 9.
The total impedance of the system consists of system A with impedance
ZA, line impedance
ZL and system B with impedance
ZB. The position of the loss of synchronicity protection relay is usually at the generator terminals and it divides total impedance into
m⋅Ztot and (1 −
m)⋅
Ztot [
21]. Impedance at the measurement location can be calculated by Equation (6):
All methods for detecting the loss of synchronicity are based on impedance monitoring. There are several different implementations of this method, such as:
The common characteristic of these schemes is that they require extensive stability studies to determine loss of synchronicity characteristics, maximum generator slip, characteristic of stable swings and expected current levels in relays [
3]. Because of this, there have been attempts of different researchers to propose some other methods to detect the out of step. The schemes can be divided into schemes that use only local measurement and the ones that use wide area measurement for decision-making. The authors in [
22] are proposing a method that uses a change of rate of swing center voltage (SCV). This method does not require extensive analysis but uses some approximations for the calculation of SCV. The approach that combines time-domain analysis in Clarke’s domain with the SCV method is presented in [
23]. The algorithm that uses the well-known equal area criterion is presented in [
24,
25]. This method uses reactive power, real power, and the rate of change of real power to predict the out of step condition. Since the setting of the change of real power is based on the maximum slip, it requires extensive simulation studies [
26]. Equal-Area Criterion combined with the least-squares method is used in [
27]. The algorithm based on the same criterion but applied in the time domain is described in [
28]. Reference [
29] presents the R-Rdot algorithm that measures the resistance at generator terminals, and the rate of change of this resistance to detect unstable swings. The disadvantage of this scheme is that it does not control the angle at which the tripping is issued. As the synchrophasor technology develops, some methods that use this technology are also being proposed [
30]. For the methods using PMUs, communication and measurement equipment is needed at all relevant locations in the system. An interesting approach using wide-area measurements and generators’ coherency identification in real time for system splitting decision is presented in [
31]. The common characteristic of many of the methods used for the loss of synchronicity is the indirect prediction and/or detection of load angle behavior following disturbances in the power system.
Despite all of the newly proposed methods for the loss of synchronicity detection, the most commonly used algorithm in today’s practice is still the detection of impedance change, as already mentioned at the beginning of this chapter. The impedance characteristic is presented in
Figure 9 and the angle
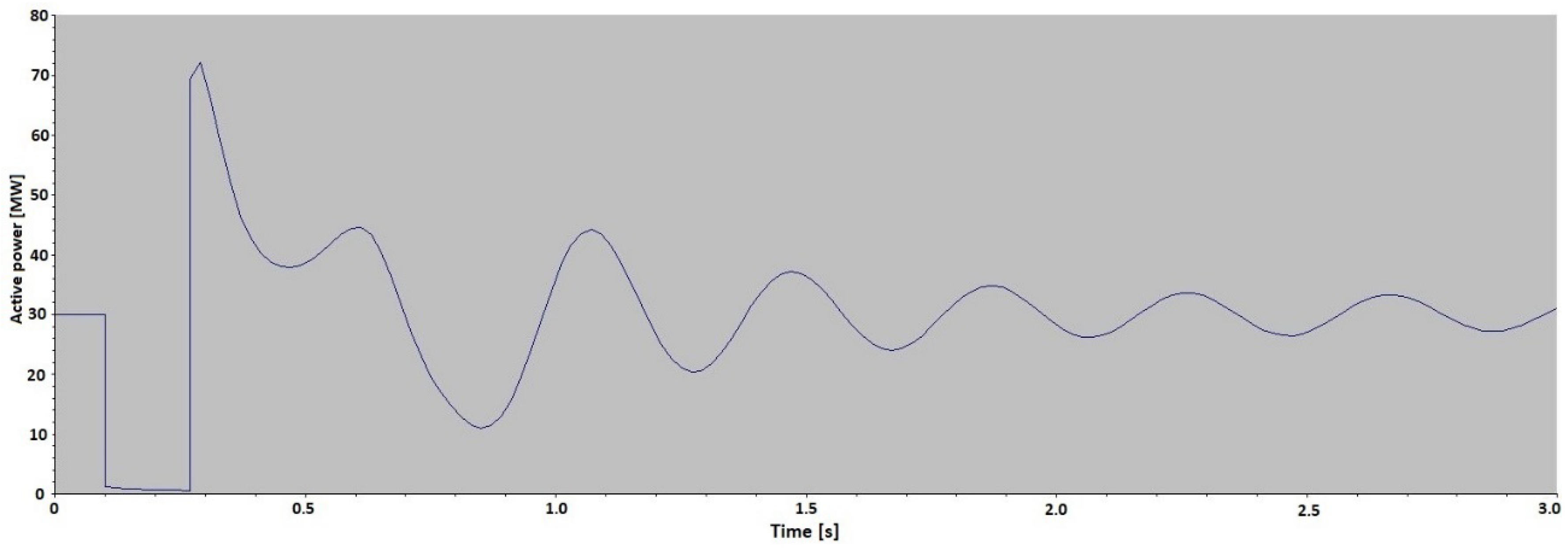
δ between lines AP and BP is the same angle that can be obtained by direct load angle measurement. In the impedance measurement method, the load angle change is supervised through the detection of impedance vector change and when this vector passes through the relay characteristic then the pole slip is detected. During the transient, the load angle changes from the start value (normally 30° to 40°), passes 180° and then comes back to the first value.
The dynamical behavior of the generator can be described by the following equations:
where
H is the generator inertia constant and
ω0 is the rated angular velocity.
Pm and
Pe are the mechanical input power and electrical output power respectively,
δ is the load angle and
ω is generator angular speed. From the equations and from what is stated in this chapter it can be concluded that if the load angle would be measured in real time, it could be used for generator loss of synchronicity protection purposes.