Abstract
The importance of efficient utilization of biomass as renewable energy in terms of global warming and resource shortages are well known and documented. Biomass gasification is a promising power technology especially for decentralized energy systems. Decisive progress has been made in the gasification technologies development during the last decade. This paper deals with the control and optimization problems for an isolated microgrid combining the renewable energy sources (solar energy and biomass gasification) with a diesel power plant. The control problem of an isolated microgrid is formulated as a Markov decision process and we studied how reinforcement learning can be employed to address this problem to minimize the total system cost. The most economic microgrid configuration was found, and it uses biomass gasification units with an internal combustion engine operating both in single-fuel mode (producer gas) and in dual-fuel mode (diesel fuel and producer gas).
1. Introduction
Hybrid energy systems development based on renewable energy sources (RES) leads to the need of solving many practical problems, including the problem of optimal power systems’ structure selection (the ratio of capacities in the energy system of energy sources and storage systems) and their control. These characteristics of the system depend both on the technical and economic indicators of energy sources, as well as on the availability and energy potential of renewable energy resources in a given area, including the distribution of this potential (wind speed and solar radiation intensity) over time. These problems attract a lot of specialists [1,2,3], including experts in data driven unit commitment problem solvers development. Various software packages have been developed (Homer, Calliope, RETScreen, DER-CAM, Compose, iHOGA, and others) to calculate the potential of renewable energy and to support the best choice of the hybrid system’s components [4]. Optimization of the power and components of a hybrid system with renewable energy sources in most cases is carried out to minimize the cost of generated energy, taking into account all costs, to provide 100% reliability of energy supply. The following optimization criteria were employed: energy efficiency, maximum energy production on a specific source of renewable energy, maximum use of installed renewable energy generation capacity, exergy efficiency, minimizing the payback period, minimizing capital costs, environmental impact such as CO2 emissions, and various social criteria: creating jobs, effects on human health, human development index, etc. [5,6,7].
In [8], a technological scheme is considered, which includes the generation of thermal energy from solar collectors and direct biomass burning in a boiler, the production of superheated water vapor, and energy generation in a steam turbine. In [9], the authors presented a technological scheme for the production of heat and electric energy through the utilization of pyrolysis gases using the regular and organic Rankine cycle. Pyrolysis gas is a by-product of charcoal production. At the same time, the application of biomass gasification technology in hybrid power systems remains little studied. The main problem is that when analyzing the operation of a hybrid power system with biomass gasification, the gasification unit is considered oversimplified [10,11,12,13,14,15,16,17]. The technological mode of the hybrid renewable energy system with biomass gasification has not yet been studied, especially the transient processes when starting, stopping, and regulating the system.
Due to the variable energy input from renewable energy sources and the variability of the consumer’s electrical load schedule in a hybrid system, it is necessary to have maneuvering energy sources such as diesel generator and energy storage systems, e.g., rechargeable batteries. The cost of the battery is extremely high and can reach up to 50% of the total cost of the hybrid system [18]. In the scheme with gasification of biomass as the main source of energy to provide a buffer and reserve supply of producer gas, it is possible to use gas holders. Comparative studies are presented in [19], which demonstrated that a hybrid system containing sources of wind energy and biomass gasification is more economic in comparison with the wind–diesel systems. In [20,21], it was concluded that a biomass gasifier is a more preferable option for powering remote isolated rural areas comparing to the solar power plants. One of the ongoing projects is the creation of a micro hybrid system on Mount Athos (Greece). The system is mounted on the basis of solar panels and several biomass gasification reactors [22].
The main problem of hybrid power systems is the intermittency and stochastic character of some renewable energy sources. Therefore, combining two or more sources of energy makes it possible to counteract the stochastic nature of renewable energy, using, among other things, the stable nature of traditional generation and electric energy storage systems. However, for the reliable operation of hybrid energy complexes, effective management of such systems is required, which would take into account various internal and external input factors including energy volumes, tariffs, weather, reliability indicators, and other factors. Many companies including Siemens, HOMER Energy, Tendril, Opower, and Vivint, have developed their own concept of a hybrid power system with different control schemes [23]. For example, using HOMER, it was found that the Photovoltaic system (PV)/wind/diesel hybrid power system is most preferable for providing electricity to consumers on Masirah Island, Oman [24].
The hybrid energy systems control strategies are divided into three main groups: centralized, decentralized, and hybrid (centralized–decentralized). The following two families of mathematical methods are widely employed for such control: linear programming methods and artificial intelligence technologies (machine learning, multi-agent systems, fuzzy logic, etc.) [25,26]. At the same time, it was noted in [27] that the use multivariate of optimization methods together with artificial intelligence technologies is an effective approach to control the hybrid power systems with biomass gasifiers.
Biomass is an available and renewable source of energy, which leads to a high interest in the development of gasification technologies [28,29]. It is possible to efficiently employ the internal combustion engines and biomass Integrated Gasification Combined Cycle (BIGCC) system with high efficiency, much higher than that of the biomass Rankine cycle or the Organic Rankine Cycle (ORC) The huge energy potential of biomass and waste (primarily forestry and agriculture) is currently used only to a small extent, although technically and economically it can be beneficial for various energy systems [30,31]. To solve this challenge, it is necessary to study and test the novel methods, as well as to study known, and to master, state-of-the-art methods. The creation of reliable technologies based on these methods is possible only through deep scientific study of all stages of the process: from the selection of suitable raw materials, to the control of processes in the reactor and the disposal of emissions [32,33,34].
Biomass is characterized by a high moisture content and variable size distribution of the source material; high reactivity compared to fossil coal [35]; variability of the mechanical properties of particles (tendency to agglomerate [34,36] or, conversely, to destruction [37,38]); the formation of significant amounts of tarry products during heating and oxidation [33]; and low ash content. The latter, however, often have increased corrosion properties and a tendency to form fly ash [34,37,38]. Many processes of biomass processing have been proposed [28,33], but their efficiency is very sensitive to the conditions of their implementation. There are more specific conversion processes: plasma processing [39,40] or the use of supercritical water [33,41], but they are technologically more complicated and require higher energy costs.
The pyrolysis and gasification are potentially applicable in small and medium capacity generation [42,43], usually working with an internal combustion engine [44,45], a microturbine [46], or a gas burner [47]. However, the combustion and gasification of biomass can be applied at large thermal stations to partially replace coal and reduce emissions [48,49,50]. The processes of co-combustion of coal and biomass were also considered in [36,51,52,53,54].
A promising solution for the optimal control of hybrid microgrids with various flexible and inflexible power sources is the modeling and control of the operating modes of such systems as the Markov decision process (MDP). Such a formulation, in fact, allows one to obtain a rather realistic model of a hybrid microgrid with various states, control actions, and probabilistic transitions between them. The most advanced methods for solving MDP problems are reinforcement learning (RL). Trained RL agents, knowing most of the optimal solutions, can be employed to control the energy management of the power system or microgrid in real time. Such an approach will significantly reduce computational costs, because a stochactic optimization problem is solved offline to find the optimal policy for all possible scenarios. In recent years, several successful studies have been published on the use of advanced RL methods for optimal control of microgrids based on deep Q-networks (DQN) [55,56], Monte-Carlo tree search (MCTS) [57], deep policy gradient [58], batch RL [59], multi-agent RL [60], etc. Part of the research is devoted to comparing the effectiveness of the RL methods (capable of giving quick, but approximate solutions) with traditional optimization methods, for example, mixed-integer linear programming (MILP) [61,62].
The aim of this work is to calculate and to optimize the assets of the operation of a hybrid microgrid based on renewable energy sources (solar energy and biomass gasification) and a traditional diesel power station. In order to achieve the formulated objectives, the following tasks were solved:
- The control problem of an isolated microgrid is formulated as an MDP. The modified open-source RL framework is employed for the modeling of an off-grid microgrid to investigate how state-of-the-art RL techniques can utilize the simulated data in order to learn an operation policy that minimizes the total system cost.
- The biomass gasification unit is employed to obtain producer gas. At the same time, the operation of the internal combustion engine (generator) is considered only in producer gas and dual-fuel mode (producer gas and diesel fuel). They operate as steerable generators of different configurations of a microgrid.
An optimization model based on MILP is used as a reference for comparing the effectiveness of RL models that gives a good approximation for the lower bound of the control problem.
2. Microgrid MDP-Based Environment Simulator
A separate feature of microgrids is the use of stochastic components: RES from the generation side and flexible active loads from the consumption side. In comparison with large power systems, microgrids are capable of independently generating and delivering electricity to consumers, but only do all this at a local level. To ensure reliable and optimal operation of the microgrid, such grids use an energy management system, which, in accordance with the developed policy (management strategy), are able to automatically switch between energy sources, exchange energy with an external network, and even make load shedding if necessary. At the same time, the possible activity of consumers and the presence of RES introduce a stochastic nature into the optimization problem, and the desire for off-grid operation makes it necessary to apply the principles of online optimization.
Online optimization is a stochastic optimization application that studies sequential decision making. One of the standard modeling approaches in this case is the MDP, which is a specification of the sequential decision-making problem for a fully observable environment with a Markov transition model and additional rewards. MDPs are useful for studying optimization problems solved based on dynamic programming and reinforcement learning. In recent years, MDP appears to be a promising mathematical formulation of the optimizing microgrid operation problem [63,64]. A number of studies clearly demonstrate the effectiveness of energy microgrids management using MDP-based methods: dynamic programming [65,66], deep RL [55,56,58,67], and Monte Carlo models [57,68].
This paper proposes an MDP-based environment that aims at simulating the techno-economic performance of a hybrid AC/DC microgrid, and in particular at quantifying the performance of an agent responsible for controlling the devices of the microgrids, as a function of the random processes governing all the variables that impact the microgrid operation, e.g., consumption, renewable generation, and market prices. Components of the microgrid include non-steerable (i.e., renewable PV or wind) and steerable (i.e., diesel, gasified biomass, or co-fired generators), as well as battery energy storage systems, and different type of loads. When the energy level from storages and from non-flexible production is not sufficient to ensure the loads are served, the steerable generators compensate for the remaining energy to be supplied.
2.1. Dynamics
The simulated system is composed of several consumption, storage, and generation devices. In this paper, intermittent generation and non-flexible consumption are represented by real data gathered from an off-grid microgrid.
2.1.1. Storage
Let us employ a linear model for the simulation of the battery since it is assumed that the simulation time-step size ∆t is large enough (1 h). The dynamics of a battery is modeled as
where denotes the state of charge at each time step; t, and correspond to the charging and discharging power, respectively; and , represent the charging and discharging efficiencies of the storage system, respectively. The charging () and discharging () power of the battery are assumed to be limited by a maximum charging and discharging rate respectively. For more sophisticated models of the storage systems readers may refer to [69] and the references therein.
2.1.2. Steerable Generator Model
Steerable generation allows any type of diesel or biomass-based generation that can be dispatched at any time-step t. The fuel curve can be used to determine the fuel amount that the steerable generator consumes to produce electricity. It is assumed that the fuel curve is a straight line and use the following equation gives the generator’s fuel consumption in units/h:
where is the fuel curve slope [units/h/kW], is the intercept coefficient [units/h/kW], is the rated capacity of the steerable generator [kW], and is the electrical output of the steerable generator [kW].
The generator fuel intercept coefficient gives the no-load fuel consumption of the generator divided by its rated capacity. The marginal fuel consumption of the generator is determined by the generator fuel curve slope, , and can be expressed in units of fuel per hour per kW of output, or equivalently, units of fuel per kWh.
The generator’s electrical efficiency can be defined as the relationship of the electrical energy coming out and the chemical energy of the fuel going in using the following equation:
where: is the mass flow rate of the fuel [kg/h], is the lower heating value of the fuel [MJ/kg]. If the fuel units are kilogram (i.e., gasified biomass unit) then and are equal. If the fuel units are L (i.e., diesel unit), the relationship between and involves the density .
A generator operates in dual-fuel mode (diesel fuel and producer gas). In each time step, the MDP-based environment simulator calculates the required output of the generator and the corresponding mass flow rates of diesel fuel and producer gas. The system in dual-fuel mode always attempts to maximize the use of producer gas and minimize the use of diesel fuel.
The fuel curve of a generator defines the fuel consumption of the generator in pure diesel mode. Therefore, the fuel consumption in pure diesel mode is given by the following equation
and
If actual value of the producer gas flow rate is known, at any time step, the diesel fuel flow rate can be calculated from Equation (5)
where is the diesel fraction, i.e., the ratio of diesel fuel used by the generator in dual-fuel mode to that required to produce the same output power in pure diesel mode.
2.2. Stochastic Optimization Formulation
Due to the stochastic nature of hybrid distributed generation, the dynamic dispatch of the microgrid is essentially a stochastic optimization problem. Usually, the goal is to minimize the operational cost. The optimization-based controller or agent serves as a baseline for comparison to our proposed methods. This controller receives as input all the parameters available and solves an optimization problem in receding horizon. The objective function to minimize aggregates curtailment, shedding, and fuel costs (the π parameters denote unit costs), are taken from [65]:
where is generation curtailment and the curtailment price, respectively; is load shedding and shedding price, respectively; and is the fuel price.
Due to constraints of the stochastic optimization model, the energy balance equation of the following form is suggested:
where are steerable and non-steerable generation, respectively; are charging and discharging power of battery b, respectively; and are shedding power and non-flexible demand, respectively.
In addition, the binary variables are added to the optimization model to specify the minimum operating point of the steerable generators, ∀t ∈ T:
The law of transition of the state of charge s of each battery b is modeled as presented in [57]. Thus, this mathematical problem in general is a MILP.
3. Reinforcement Learning for Energy Microgrids Management
3.1. Problem Statement
RL solves the problem of sequential optimal decision making [69]. The mathematical model of this problem is MDP. RL is a promising way of machine learning, which suggests that the agent learns by interacting with an environment, for example, a microgrid. In simple words, RL is trying to find a set of actions (policy) that would be the most beneficial for the agent.
Centralized microgrids’ control strategy can be separated into four following tasks: estimation of parameters of microgrid devices, forecasting consumption and generation from renewable energy sources, operational planning for predicting the impact of weather and human activities, and real-time control to adapt the planned solutions to the current control moment. RL methods use microgrid simulation data (or simulated data before the microgrid is actually involved) to study management strategies. Therefore, they actually combine the four steps described above. Theoretically, they can adapt to certain types of changes without the need for manual tuning.
This paper proposes the simulation framework, where the RL agent only has access to the current non-steerable generation and non-flexible consumption in the microgrid. It has also access to the state of charge of the different storages and it must decide how to use the storage systems. The steerable generation compensates to establish the equilibrium. In case there is an excess of non-steerable generation and no more room for storage, the non-steerable generation is “curtailed”, i.e., is lost. At each time-step t, the state variable contains all the relevant information for the optimization of the system. The control applied at each time-step t contains the charging/discharging decisions for the storage systems and the generation level of the steerable generator. At each time-step t, the system performs transitions based on the dynamics described above according to . Each transition generates a cost according to the cost function Figure 1 shows the main RL-based approach for energy microgrids optimal management.
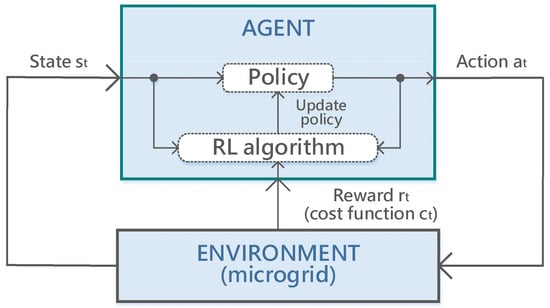
Figure 1.
The main reinforcement learning (RL)-based approach for the energy microgrids’ optimal management.
The total discounted cost for the microgrid associated to a policy is given by
An optimal policy is a policy that, for any initial state , yields the actions that minimize the total discounted cost such as:
Most of the RL algorithms include a quality function evaluation that says how “useful” or “valuable” the current state (V-function) or state–action pair (Q-function). Both functions return the mathematical expectation of the γ-discounted amount of rewards until the end of the simulation using a specific policy π. Additionally the state–action value function associated to an optimal policy is used to characterize the quality of taking action at state, and then acting optimally and is defined as:
where is the reward function, which define each transition and generates an operational revenue for each individual scenario of the network configuration.
The optimal action at each time-step t can be obtained using the optimal Q-value as:
3.2. Reinforcement Learning Agents
The key idea of this article was to study advanced RL models for optimal control of an off-grid PV-diesel-biomass microgrid. It was decided to consider RL algorithms that in recent years have shown so-called superhuman efficiency (i.e., they solved complex mathematical problems better than an expert in the subject field), namely DQN agents as the leader in Atari Games, and proximal policy optimization (PPO) agents who defeated the best players in Dota and Monte Carlo tree search (MCTS), which became the basis of the AlphaGO system. The results of optimizing the microgrid regime are compared with results of the reference, classical MILP algorithm.
The available information for RL agent at each time-step is composed of the consumption, the state of charge, the number of cycles and the capacity of each storage device, the renewable production, and its capacity. It is assumed that the RL agent has control of the storage devices. However, the original action space is continuous and of high-dimensionality. High-level actions are used in the decision-making process that are then mapped into the original action space. The instantaneous reward is defined as the negative total cost of operation of the microgrid according to Equation (7) and is composed of:
- fuel costs for the generation,
- curtailment cost for the excess of generation that had to be curtailed, and
- load shedding cost for the excess of load that had to be shed in order to maintain balance in the microgrid.
3.2.1. MILP-Based Optimizer
This optimizer solves a linear program that minimizes the cost to optimize its actions. The output actions are continuous actions showing the exact charge/discharge level of each storage and the exact generation from steerable generators. In the presented study, the authors used an optimization model based on MILP as a reference for comparing the effectiveness of RL models. MILP-based optimization formulations, however, suffer from important drawbacks. Most importantly, they are restricted in terms of the number of integer or binary variables that can be practically included and are difficult to efficiently parallelize. This limits possibilities for optimizing the planning and control of large-scale microgrids (e.g., larger than 30–100 buildings [62]) and power systems. Compared with MILP, RL generates near-optimal solutions on par with the research approaches of conventional operations; however, it makes it significantly faster (because an RL-agent has already found all the optimal policy offline). The statement of the MILP problem for optimizing microgrid management is described in detail above in Section 2.
3.2.2. Deep Q-Network Agent
The main idea is to employ the deep neural networks to represent the so-called DQN and train this network to predict the total reward [70,71]. The approach is based on the Q-learning algorithm, which implements an iterative approximation of the Q function through training on temporal differences, where the mean square error between the predictor and the goal is minimized at each step, see Equation (11). When the number of states is large, saving a lookup table with all possible values of action–state pairs is inappropriate. In [72], a general solution to this problem was proposed using the parameterized approximation function , so that . It was proposed to use a deep neural network as an approximator. The neural network parameters can be updated using stochastic gradient descent by sampling batches of transitions, a quadruple and the parameters are updated according to:
where is a scalar step size called the learning rate.
3.2.3. Monte-Carlo Tree Search Agent
MCTS is a policy-optimization algorithm for finite-horizon, finite-size MDP, based on random episode sampling structured by a decision tree, where each node in the tree represents a complete state of the domain and each link represents one possible valid action, leading to a child node representing the resulting state after taking an action. The statement of the problem in MCTS is based on game theory. It had a strong influence on programs for playing Go, although it finds its application in other games. Monte Carlo methods work by approximating future rewards that can be achieved through random samplings [73].
MCTS proceeds in four phases of selection, expansion, rollout, and back-propagation. The standard MCTS algorithm proceeds by repeatedly adding one node at a time to the current tree. Given that leaf nodes are likely to be far from terminal states, it uses random actions, to estimate state–action values. After the rollout phase, the total collected rewards during the episode is back-propagated through the tree branch, updating their empirical state–action values, and visit counts. Choosing which child node to expand (i.e., choosing an action) becomes an exploration/exploitation problem given the empirical estimates. Upper confidence bounds (UCB) is an optimization algorithm that is used for such settings with provable guarantees [74]. Each parent node chooses its child with the largest value according to the following formula
where is the visit count for the ith child; is the number of visit counts for the parent node. The parameter c ≥ 0 controls the tradeoff between choosing lucrative nodes (low c) and exploring nodes with low visit counts (high c). It is often set empirically.
High efficiency is determined by the fact that with the MCTS method the decision tree grows asymmetrically: more “interesting” nodes are visited more often, less “interesting” nodes less often, and it becomes possible to evaluate a single node without revealing the entire tree. If the task of managing a microgrid is formulated as a partially observable MDP, then a simulator of its operation (environment) can be developed in which all possible states can be formed in the form of a tree structure and passed using the MCTS agent.
3.2.4. Proximal Policy Optimization Agent
PPO agent trying to compute an update at each step that minimizes the cost function while ensuring the deviation from the previous policy is relatively small. PPO belongs to the family of policy gradient methods, which use several eras of random gradient rise to complete each policy update [75]. In this method [76], a parametrized stochastic policy function with parameters is directly optimized towards the objective defined in Equation (10). After the collection of N full trajectories a gradient step is performed for the update of the parameters as:
with clipped objective proposed in [72],
where denotes the empirical expectation over time steps, is the estimated advantage at time t, is probability ratio under the new and old policies respectively, is a hyperparameter, usually 0.1 or 0.2.
The optimal policy is derived by performing multiple steps of stochastic gradient descent on this objective. While standard policy gradient methods perform one gradient update per data sample, the PPO algorithm enables multiple epochs of minibatch updates resulting in better sample efficiency.
4. Results
The evaluation of the proposed methodology was performed using empirical data measured by the off-grid microgrid system composed of 10 kW of PV panels, 24 kWh of two battery storages, and a 10 kW generator. The microgrid configuration contained three loads (each one being 10 kW), a PV module, a steerable generator (biomass gasifier with an internal combustion engine operating in only producer gas and dual-fuel mode), as well as storage devices (Figure 2). Additionally, the costs for curtailment and load shedding were defined. Time-series from the two year historical parameter dataset (frequency of 1 h) are used to simulate the three loads and the PV module. The storage devices have slightly different characteristics, namely different charging/discharging efficiencies. The parameters used for this specific microgrid configuration are given in Table 1.
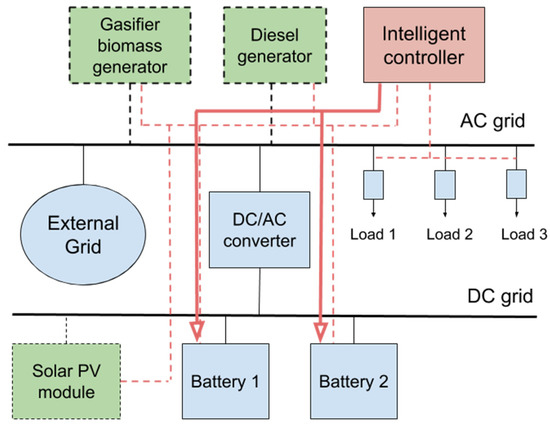
Figure 2.
General microgrid configuration.

Table 1.
Microgrid parameters.
The optimization agent system is intended to become multi-objective. It has to minimize the operation cost while ensuring the reliability by maximizing the service level or served demand. The case of an off-grid system is considered under the assumption that imports are equivalent to load shedding = 100 euro/kW) and exports are equivalent to production curtailment = 10.5 euro/kW).
The technical limits of the generator i.e., the maximum (capacity) and the minimum stable (percentage of the capacity) operating point are also specified. The operating points of the steerable generators from experimental studies are used to get their fuel curve. Two fuel curve inputs are the intercept coefficient and the slope according to Equation (2). For example, according to the practical studies [77], biomass consumption increased with an increase in load; however, specific biomass consumption decreased with an increase in load. The following operating points are selected: the biomass consumption 13.2 and 15 kg/h at 3.0 and 10.0 kW load, respectively.
4.1. Microgrid Simulator Description
To carry out the calculations, the open source simulator of the microgrid operation developed in Python [78] was used and modified by the authors. This simulator was implemented as a training environment for the optimization of RL agents such as DQN, MCTS, and PPO, for the implementation of which the TensorFlow and OpenAI gym libraries were used [79]. To implement the MILP model, the code from Gurobi Optimizer was used.
The optimization agent has control of the storage devices. The actions available at each decision step are the charging (C), discharging (D), and idling (I) of each storage device in the microgrid. The actions are then converted in implementable actions automatically following a rule-based strategy:
- If the total possible production (i.e., PV production, active steerable generators capacity, and the storages maximum discharge rate) is lower than the total consumption, a steerable generator is activated at its minimum stable generation. This instruction is repeated until the total load can be served or until all steerable generators are active. In a few words, the generators are activated one by one at their minimum stable generation until the total load can be served. Given the lower flexibility of the gasifier biomass generator compared to the diesel generator, it is assumed that the biomass generator does not turn off completely but continues to operate in idle mode. For the co-fired generator, the possibility of autonomous start-up on diesel fuel remains to ensure ignition of the gasifier biomass generator [80,81,82].
- Once all active steerable generators are known, the net generation can be calculated based on their minimum stable generation, the PV production, and the total consumption.
- If the net generation is positive, the storages (with charge instruction) charges the excess of energy until the net generation becomes zero. The storages with discharge or idle instructions do not do anything. The remaining excess of energy is curtailed.
- If the net generation is negative, the storages (with discharge instruction) discharges the deficit of energy until the net generation becomes zero. The storages with charge or idle instructions do not do anything. The remaining deficit of energy is then compensated by the active steerable generators which can be adjusted at a higher production level than their minimum stable power. If, in addition, steerable generators cannot handle the remaining deficit, this deficit is considered as lost load.
The following protocol was carried out for the training and the evaluation of the proposed RL-based algorithms and MILP. The policies were trained in the first three months (December–February) and were tested in one week of the fourth month (March). The performance of the algorithms was compared against the benchmarks of MILP described in Section 2. The following MILP-based optimization controller was considered for comparison purposes. A MILP optimization controller with perfect knowledge was considered with 12 periods of look-ahead and additional noise around the exact value of the stochastic variables. This gave a good approximation for the lower bound of the control problem.
4.2. Analysis of Different Microgrid Configuration Efficiency
In addition to evaluating the effectiveness of the state-of-the-art optimization models for the microgrid management, another and main goal of our paper was a comparative study of the use of various types of steerable generators on diesel fuel and wood biomass from the point of view of minimizing the operational costs of microgrid, according to Equation (7). The following microgrid configurations are examined:
- Configuration 1 (case 1)—PV (10 kW), diesel generator (10 kW), two storage devices (2 × 10 kWh), and three loads (3 × 10 kW).
- Configuration 2 (case 2)—PV (10 kW), gasifier biomass generator (10 kW), two storage devices (2 × 10 kWh), and three loads (3 × 10 kW).
- Configuration 3 (case 3)—PV (10 kW), co-fired generator (10 kW), two storage devices (2 × 10 kWh), and three loads (3 × 10 kW).
- Configuration 4 (case 3)—co-fired generator (20 kW), two storage devices (2 × 10 kWh), and three loads (3 × 10 kW).
Case 4 considers a realistic case for some regions of Siberia (Russia), where the installation of PV generation is not profitable in remote villages, and the use of generators using diesel fuel incurs increased costs (Figure 3). Therefore, the latter case included only a co-fired generator as the main energy source for the microgrid, operating in conjunction with two storage devices, where it becomes possible to accumulate electricity for cases of possible interruptions in the operation of the main generation (temporary lack of biofuel, possible generator breakdown, etc.). For case 4, it is assumed that the power of a co-fired generator is 20 kW. In all cases, a gasifier biomass generator and a co-fired generator used pellets as biofuel.
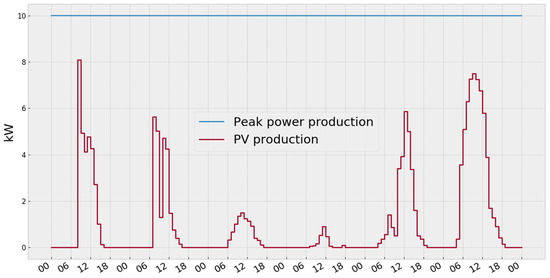
Figure 3.
Plot of the microgrid PV generation for the one-week testing period.
The results of the described protocol are presented in Table 2, which show the total cost of each strategy for each testing period, in order that a comparison can be drawn. As can be seen from the table, the closest to the MILP reference solution are policies of the MCTS algorithm for all considered cases of microgrid configuration.

Table 2.
Total cost of obtained optimal policies, for compared optimization agents.
It is clearly seen that the use of a gasifier biomass generator (Case 1) and a co-fired generator (Cases 3, 4) can reduce operational costs compared to using a diesel generator (Case 3) as a steerable generator in the microgrid. This is clearly shown in the graphs of Figure 4 and Figure 5, which show the total costs (including accumulated ones), as well as the dynamics of the components of generation and consumption for the microgrid for the one-week testing period. The best option was obtained for the configuration of a microgrid containing a solar station and a gasifier biomass generator (Case 2). It should also be noted that Case 4 provides slightly higher costs compared to Case 1, i.e., when there is no PV generation, due to the fact that the energy management system fails to fully realize the stored energy in the storage devices (Figure 5b). This is obvious, since it is more expedient to use storage devices if the microgrid contains any RES (sun or wind), and in this respect Case 4 as considered by us, may look somewhat artificial. However, for the configuration of a microgrid with only one generation source, the meaning of the optimal control problem is lost.
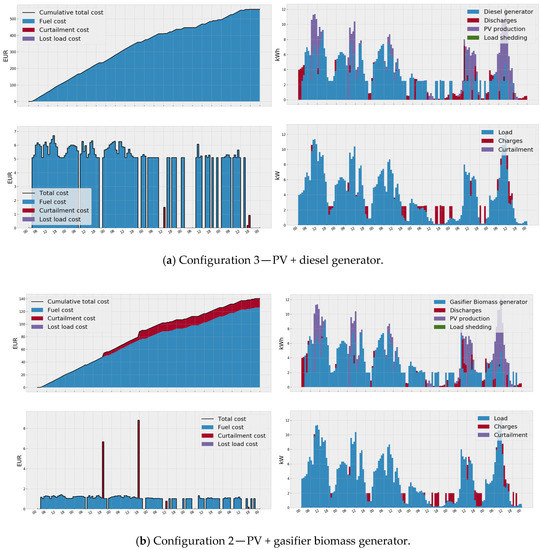
Figure 4.
Total costs (left) and generation/load mix – right (The load mix on the graph here does not mean the entire total load of the microgrid, but only an illustration of what components of the electricity consumption (load, battery, or curtailment) the generated power were used to ensure balance) of different microgrids’ configurations for optimal policies, obtained using the Monte-Carlo tree search (MCTS) for the one-week testing period.
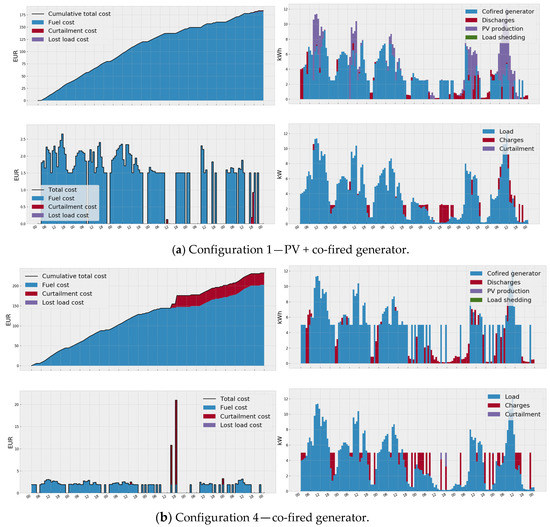
Figure 5.
Total costs (left) and generation/load mix (right) of different microgrids with co-fired generators for optimal policies, obtained using MCTS for the one-week testing period.
4.3. Comparative Study of RL-Based Models
It is observed that in all cases the MCTS policy performed very close to the MILP-based optimization controller (Table 2). Perhaps, this is due to the fact that the MCTS algorithm manages to anticipate periods of high energy curtailment or load shedding and manages to utilize the storage device accordingly. In addition, a fairly good policy, along with MCTS, is provided by the PPO algorithm (Figure 6). MCTS policy also gives good results for Case 4, when the optimization of energy storage is not always obvious, due to the lack of RES. It is clearly seen that the PPO and DQN algorithms actually fail to find adequate policies for this case and the high costs, in fact, are associated with large volumes of curtailment lost energy in the storage devices (Figure 7). It is important to note that the search for the optimal policy, in the training process, is much faster for PPO and DQN algorithms, when compared to that of the MCTS algorithm.
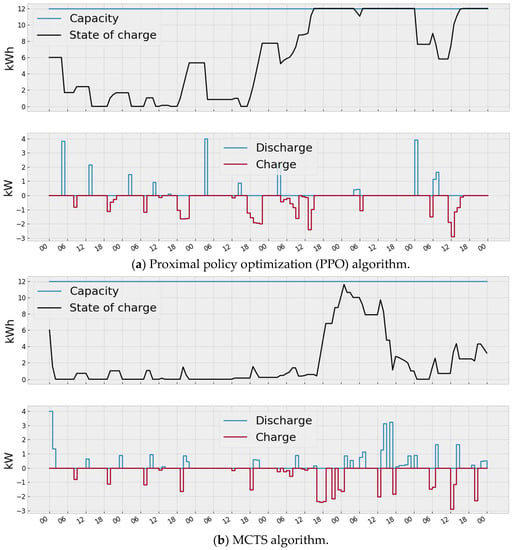
Figure 6.
Dynamics of the charge and discharge of batteries for Case 1 for optimal policies, obtained using PPO and MCTS algorithms for the one-week testing period.
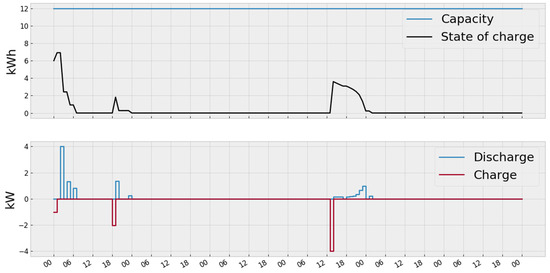
Figure 7.
Dynamics of the charge and discharge of batteries for Case 4 for optimal policies, obtained using PPO algorithm for the one-week testing period.
5. Discussion and Conclusions
This paper deals with the control and optimization problems for an isolated microgrid combining RES (solar energy and biomass gasification) with a diesel power plant. To attack this problem, the contemporary methods of stochastic online optimization based on reinforcement learning and linear programming were employed, when the microgrids control was based on the MDP. The main advanced reinforcement learning methods DQN, PPO, and MCTS were examined, and the results were compared with the reference solution of the MILP model. The closest results to the reference strategy were demonstrated by the MCTS algorithm for all cases of microgrid configuration.
The multi-objective optimization problem, which was minimizing the total cost of operating a microgrid, including the cost of fuel for controlled generators, electric power reduction, and load shedding, was addressed. As a result, the most economic microgrid configuration was found and it used the gasification of biomass with gasifier/internal combustion engine system operating both in single-fuel mode (producer gas) and in dual-fuel mode (diesel fuel and producer gas). Their use in the microgrid is cheaper when compared with diesel generators. This is obviously caused by the lower cost of biomass, which is pine pellets in our case. It is to be noted that fuel delivery was ignored in our case. It should also be outlined that the use of a conventional biomass-gasifier, which burned only the producer gas in an internal combustion engine, was somewhat more economical in comparison with that of the dual-fuel engine operation mode. However, the latter is more maneuverable due to the possibility of starting and flexible engine control by varying the share of diesel fuel use, which allows it to be used more efficiently (along with a conventional diesel generator) when the corresponding microgrid energy management system is operating.
Author Contributions
Conceptualization, A.N.K., N.V.T. and D.N.S.; Data curation, A.N.K.; Formal analysis, A.N.K., N.V.T., D.N.S. and E.E.S.L.; Funding acquisition, A.N.K.; Investigation, A.N.K.; Methodology, N.V.T.; Project administration, A.N.K.; Software, N.V.T.; Supervision, A.N.K.; Validation, N.V.T.; Visualization, A.N.K.; Writing—original draft, A.N.K., N.V.T. and D.N.S.; Writing—review & editing, D.N.S., E.E.S.L. and V.G.K. All authors have read and agreed to the published version of the manuscript.
Funding
The reported study was funded by the Russian Foundation for Basic Research (RFBR) №19-58-80016; the Department of Science and Technology of India (DST), №CRG/2018/004610, DST/TDT/TDP-011/2017; the Ministry of Science and Technology of the People’s Republic of China (MOST), №2018YFE0183600; the National Research Council of Brazil (CNPq), №402849/2019-1; and the National Research Foundation of South Africa (NRF), №BRIC190321424123. Studies were performed using equipment of the multi-access scientific center “High Temperature Circuit”.
Acknowledgments
Authors thank the anonymous reviewers for their careful reading of our manuscript and their many insightful comments and suggestions.
Conflicts of Interest
The authors declare that there is no conflict of interest.
References
- Siddaiah, R.; Saini, R.P. A review on planning, configurations, modeling and optimization techniques of hybrid renewable energy systems for off grid applications. Renew. Sustain. Energy Rev. 2016, 58, 376–396. [Google Scholar] [CrossRef]
- Chauhan, A.; Saini, R.P. A review on Integrated Renewable Energy System based power generation for stand-alone applications: Configurations, storage options, sizing methodologies and control. Renew. Sustain. Energy Rev. 2014, 38, 99–120. [Google Scholar] [CrossRef]
- Anvari, S.; Khalilarya, S.; Zare, V. Exergoeconomic and environmental analysis of a novel configuration of solar-biomass hybrid power generation system. Energy 2018, 165, 776–789. [Google Scholar] [CrossRef]
- Cuesta, M.A.; Castillo-Calzadilla, T.; Borges, C.E. A critical analysis on hybrid renewable energy modeling tools: An emerging opportunity to include social indicators to optimise systems in small communities. Renew. Sustain. Energy Rev. 2020, 122, 109691. [Google Scholar] [CrossRef]
- Rajbongshi, R.; Borgohain, D.; Mahapatra, S. Optimization of PV-biomass-diesel and grid base hybrid energy systems for rural electrification by using HOMER. Energy 2017, 126, 461–474. [Google Scholar] [CrossRef]
- Sawle, Y.; Gupta, S.C.; Bohre, A.K. Socio-techno-economic design of hybrid renewable energy system using optimization techniques. Renew. Energy 2018, 119, 459–472. [Google Scholar] [CrossRef]
- El-Emam, R.S.; Dincer, I. Assessment and Evolutionary Based Multi-Objective Optimization of a Novel Renewable-Based Polygeneration Energy System. J. Energy Res. Technol. 2017, 139. [Google Scholar] [CrossRef]
- Guo, S.; Liu, Q.; Sun, J.; Jin, H. A review on the utilization of hybrid renewable energy. Renew. Sustain. Energy Rev. 2018, 91, 1121–1147. [Google Scholar] [CrossRef]
- de Oliveira Vilela, A.; Lora, E.S.; Quintero, Q.R.; Vicintin, R.A.; Souza, T.P.D.S. A new technology for the combined production of charcoal and electricity through cogeneration. Biomass Bioenergy 2014, 69, 222–240. [Google Scholar] [CrossRef]
- Kohsri, S.; Meechai, A.; Prapainainar, C.; Narataruksa, P.; Hunpinyo, P.; Sin, G. Design and preliminary operation of a hybrid syngas/solar PV/battery power system for off-grid applications: A case study in Thailand. Chem. Eng. Res. Des. 2018, 131, 346–361. [Google Scholar] [CrossRef]
- Singh, A.; Baredar, P. Techno-economic assessment of a solar PV, fuel cell, and biomass gasifier hybrid energy system. Energy Rep. 2016, 2, 254–260. [Google Scholar] [CrossRef]
- Zhang, X.; Zeng, R.; Mu, K.; Liu, X.; Sun, X.; Li, H. Exergetic and exergoeconomic evaluation of co-firing biomass gas with natural gas in CCHP system integrated with ground source heat pump. Energy Convers. Manag. 2019, 180, 622–640. [Google Scholar] [CrossRef]
- González, A.; Riba, J.R.; Rius, A. Optimal sizing of a hybrid grid-connected photovoltaic–wind–biomass power system. Sustainability 2015, 7, 12787–12806. [Google Scholar] [CrossRef]
- Perez-Navarro, A.; Alfonso, D.; Álvarez, C.; Ibáñez, F.; Sanchez, C.; Segura, I. Hybrid biomass-wind power plant for reliable energy generation. Renew. Energy 2010, 35, 1436–1443. [Google Scholar] [CrossRef]
- Mago, P.J.; Chamra, L.M. Analysis and optimization of CCHP systems based on energy, economical, and environmental considerations. Energy Build. 2009, 41, 1099–1106. [Google Scholar] [CrossRef]
- Parihar, A.K.S.; Sethi, V.; Banerjee, R. Sizing of biomass based distributed hybrid power generation systems in India. Renew. Energy 2019, 134, 1400–1422. [Google Scholar] [CrossRef]
- Li, L.; Yao, Z.; You, S.; Wang, C.H.; Chong, C.; Wang, X. Optimal design of negative emission hybrid renewable energy systems with biochar production. Appl. Energy 2019, 243, 233–249. [Google Scholar] [CrossRef]
- Chauhan, A.; Dwivedi, V.K. Optimal sizing of a stand-alone PV/wind/MHP/biomass based hybrid energy system using PSO algorithm. In Proceedings of the 2017 6th International Conference on Computer Applications in Electrical Engineering-Recent Advances (CERA), Roorkee, India, 5 October 2017; pp. 7–12. [Google Scholar] [CrossRef]
- Munuswamy, S.; Nakamura, K.; Katta, A. Comparing the cost of electricity sourced from a fuel cell-based renewable energy system and the national grid to electrify a rural health centre in India: A case study. Renew. Energy 2011, 36, 2978–2983. [Google Scholar] [CrossRef]
- Banerjee, R. Comparison of options for distributed generation in India. Energy Policy 2006, 34, 101–111. [Google Scholar] [CrossRef]
- Mahapatra, S.; Dasappa, S. Rural electrification: Optimising the choice between decentralised renewable energy sources and grid extension. Energy Sustain. Dev. 2012, 16, 146–154. [Google Scholar] [CrossRef]
- Electric Microgrid on Mount Athos [Electronic Document]. Available online: https://energynet.ru/?p=articles&id=319 (accessed on 12 March 2020).
- Kartite, J.; Cherkaoui, M. Study of the different structures of hybrid systems in renewable energies: A review. Energy Procedia 2019, 157, 323–330. [Google Scholar] [CrossRef]
- Al Ghaithi, H.M.; Fotis, G.P.; Vita, V. Techno-economic assessment of hybrid energy off-grid system—A case study for Masirah island in Oman. Int. J. Power Energy Res. 2017, 1, 103–116. [Google Scholar] [CrossRef]
- Bhandari, B.; Lee, K.T.; Lee, G.Y.; Cho, Y.M.; Ahn, S.H. Optimization of hybrid renewable energy power systems: A review. Int. J. Pr. Eng. Man-Gt. 2015, 2, 99–112. [Google Scholar] [CrossRef]
- Kurbatsky, V.G.; Sidorov, D.N.; Spiryaev, V.A.; Tomin, N.V. The hybrid model based on Hilbert-Huang Transform and neural networks for forecasting of short-term operation conditions of power system. IEEE Trondheim Power Tech. 2011, 1–7. [Google Scholar] [CrossRef]
- Arun, P. Optimum Design of Biomass Gasifier Integrated Hybrid Energy Systems. Int. J. Energy Res. 2015, 5, 891–895. [Google Scholar]
- Sansaniwal, S.K.; Pal, K.; Rosen, M.A.; Tyagi, S.K. Recent advances in the development of biomass gasification technology: A comprehensive review. Renew. Sustain. Energy Rev. 2017, 72, 363–384. [Google Scholar] [CrossRef]
- García, R.; Pizarro, C.; Lavín, A.G.; Bueno, J.L. Biomass sources for thermal conversion. Techno-economical overview. Fuel 2017, 195, 182–189. [Google Scholar] [CrossRef]
- Molino, A.; Chianese, S.; Musmarra, D. Biomass gasification technology: The state of the art overview. J Energy Chem. 2016, 25, 10–25. [Google Scholar] [CrossRef]
- Castaldi, M.; Van Deventer, J.; Lavoie, J.M.; Legrand, J.; Nzihou, A.; Pontikes, Y.; Py, X.; Vandecasteele, C.; Vasudevan, P.T.; Verstraete, W. Progress and prospects in the field of biomass and waste to energy and added-value materials. Waste Biomass Valorization 2017, 8, 1875–1884. [Google Scholar] [CrossRef]
- Santanu, D.; Avinash, K.A.; Moholkar, V.S.; Thallada, B. Coal and Biomass Gasification. Recent Advances and Future; Springer: Singapore, 2018; Volume 524. [Google Scholar] [CrossRef]
- Heidenreich, S.; Foscolo, P.U. New concepts in biomass gasification. Prog. Energy Combust. Sci. 2015, 46, 72–95. [Google Scholar] [CrossRef]
- Hupa, M.; Karlstrom, O.; Vainio, E. Biomass combustion technology development—It is all about chemical details. Proc. Combust. Inst. 2017, 36, 113–134. [Google Scholar] [CrossRef]
- Kozlov, A.N.; Svishchev, D.A.; Khudiakova, G.I.; Ryzhkov, A.F. A kinetic analysis of the thermochemical conversion of solid fuels (A review). Solid Fuel Chem. 2017, 51, 205–213. [Google Scholar] [CrossRef]
- Ramos, A.; Monteiro, E.; Silva, V.; Rouboa, A. Co-gasification and recent developments on waste-to-energy conversion: A review. Renew. Sustain. Energy Rev. 2018, 81, 380–398. [Google Scholar] [CrossRef]
- Baroudi, D.; Ferrantelli, A.; Li, K.Y.; Hostikka, S. A thermomechanical explanation for the topology of crack patterns observed on the surface of charred wood and particle fibreboard. Combust. Flame 2017, 182, 206–215. [Google Scholar] [CrossRef]
- Costa, F.F.; Costa, M. Particle fragmentation of raw and torrefied biomass during combustion in a drop tube furnace. Fuel 2015, 159, 530–537. [Google Scholar] [CrossRef]
- Tolvanen, H.; Keipi, T.; Raiko, R. A study on raw, torrefied, and steam-exploded wood: Fine grinding, drop-tube reactor combustion tests in N2/O2 and CO2/O2 atmospheres, particle geometry analysis, and numerical kinetics modeling. Fuel 2016, 176, 153–164. [Google Scholar] [CrossRef]
- Kortelainen, M.; Jokiniemi, J.; Nuutinen, I.; Torvela, T.; Lamberg, H.; Karhunen, T.; Tissari, J.; Sippula, O. Ash behaviour and emission formation in a small-scale reciprocating-grate combustion reactor operated with wood chips, reed canary grass and barley straw. Fuel 2015, 143, 80–88. [Google Scholar] [CrossRef]
- Lanzerstorfer, C. Grate-Fired Biomass Combustion Plants Using Forest Residues as Fuel: Enrichment Factors for Components in the Fly Ash. Waste Biomass Valorization 2017, 8, 235–240. [Google Scholar] [CrossRef]
- Hirka, I.; Zivny, O.; Hrabovsky, M. Numerical Modelling of Wood Gasification in Thermal Plasma Reactor. Plasma Chem. Plasma Process. 2017, 37, 947–965. [Google Scholar] [CrossRef]
- Materazzi, M.; Lettieri, P.; Mazzei, L.; Taylor, R.; Chapman, C. Reforming of tars and organic sulphur compounds in a plasma-assisted process for waste gasification. Fuel Process. Technol. 2015, 137, 259–268. [Google Scholar] [CrossRef]
- Yakaboylu, O.; Harinck, J.; Smit, K.G.; De Jong, W. Testing the constrained equilibrium method for the modeling of supercritical water gasification of biomass. Fuel Process. Technol. 2015, 138, 74–85. [Google Scholar] [CrossRef]
- González, A.M.; Jaén, R.L.; Lora, E.E.S. Thermodynamic assessment of the integrated gasification-power plant operating in the sawmill industry: An energy and exergy analysis. Renew. Energy 2020, 147, 1151–1163. [Google Scholar] [CrossRef]
- Sutar, K.B.; Kohli, S.; Ravi, M.R. Design, development and testing of small downdraft gasifiers for domestic cookstoves. Energy 2017, 124, 447–460. [Google Scholar] [CrossRef]
- Susastriawan, A.A.P.; Saptoadi, H. Small-scale downdraft gasifiers for biomass gasification: A review. Renew. Sustain. Energy Rev. 2017, 76, 989–1003. [Google Scholar] [CrossRef]
- Elsner, W.; Wysocki, M.; Niegodajew, P.; Borecki, R. Experimental and economic study of small-scale CHP installation equipped with downdraft gasifier and internal combustion engine. Appl. Energy 2017, 202, 213–227. [Google Scholar] [CrossRef]
- Renzi, M.; Riolfi, C.; Baratieri, M. Influence of the syngas feed on the combustion process and performance of a micro gas turbine with steam injection. Energy Procedia 2017, 105, 1665–1670. [Google Scholar] [CrossRef]
- Obernberger, I.; Brunner, T.; Mandl, C.; Kerschbaum, M.; Svetlik, T. Strategies and technologies towards zero emission biomass combustion by primary measures. Energy Procedia 2017, 120, 681–688. [Google Scholar] [CrossRef]
- Wang, T.; Stiegel, G.J. Integrated gasification combined cycle (IGCC) technologies. Woodhead Publ. 2017, 929. [Google Scholar]
- Thattai, A.T.; Oldenbroek, V.; Schoenmakers, L.; Woudstra, T.; Aravind, P.V. Experimental model validation and thermodynamic assessment on high percentage (up to 70%) biomass co-gasification at the 253 MWe integrated gasification combined cycle power plant in Buggenum, The Netherlands. Appl. Energy 2016, 168, 381–393. [Google Scholar] [CrossRef]
- Cormos, A.-M.; Dinca, C.; Cormos, C.-C. Multi-fuel multi-product operation of IGCC power plants with carbon capture and storage (CCS). Appl. Therm. Eng. 2015, 74, 20–27. [Google Scholar] [CrossRef]
- Howaniec, N.; Smolinski, A.; Cempa-Balewicz, M. Experimental study on application of high temperature reactor excess heat in the process of coal and biomass co-gasification to hydrogen-rich gas. Energy 2015, 84, 455–461. [Google Scholar] [CrossRef]
- Francois-Lavet, V.; Tarella, D.; Ernst, D.; Forteneau, R. Deep Reinforcement Learning Solutions for Energy Microgrids Management. In European Workshop on Reinforcement Learning; 2016; Available online: http://hdl.handle.net/2268/203831 (accessed on 31 January 2020).
- Sidorov, D.; Panasetsky, D.; Tomin, N.; Karamov, D.; Zhukov, A.; Muftahov, I.; Dreglea, A.; Liu, F.; Li, Y. Toward Zero-Emission Hybrid AC/DC Power Systems with Renewable Energy Sources and Storages: A Case Study from Lake Baikal Region. Energies 2020, 13, 1226. [Google Scholar] [CrossRef]
- Shang, Y.; Wu, W.; Guo, J.; Lv, Z.; Ma, Z.; Sheng, W.; Chen, R. Stochastic Dispatch of Energy Storage in Microgrids: A Reinforcement Learning Approach Incorporated with MCTS. arXiv 2019, arXiv:1910.04541. [Google Scholar]
- Mocanu, E.; Mocanu, D.C.; Nguyen, P.H.; Liotta, A.; Webber, M.E.; Gibescu, M.; Slootweg, J.G. On-line building energy optimization using deep reinforcement learning. IEEE Trans. Smart Grid. 2018, 10, 3698–3708. [Google Scholar] [CrossRef]
- Mbuwir, B.V.; Ruelens, F.; Spiessens, F.; Deconinck, G. Battery Energy Management in a Microgrid Using Batch Reinforcement Learning. Energies 2017, 10, 1846. [Google Scholar] [CrossRef]
- Li, F.D.; Wu, M.; He, Y.; Chen, X. Optimal control in microgrid using multi-agent reinforcement learning. ISA Trans. 2012, 51, 743–751. [Google Scholar] [CrossRef]
- Sogabe, T.; Malla, D.B.; Takayama, S.; Shin, S.; Sakamoto, K.; Yamaguchi, K.; Okada, Y. Smart grid optimization by deep reinforcement learning over discrete and continuous action space. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), Waikoloa Village, HI, USA, 10–15 June 2018; pp. 3794–3796. [Google Scholar] [CrossRef]
- Bollinger, L.A.; Evins, R. Multi-Agent Reinforcement Learning for Optimizing Technology Deployment in Distributed Multi-Energy Systems; EG-ICE Workshop: Krakow, Poland, 2016. [Google Scholar]
- Duan, J.; Yi, Z.; Shi, D.; Lin, C.; Lu, X.; Wang, Z. Reinforcement-Learning-Based Optimal Control for Hybrid Energy Storage Systems in Hybrid AC/DC Microgrids. IEEE Trans. Ind. Inform. 2019. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, J.; Xu, J.; Fang, X.; Zhang, H. Real-Time Energy Management of a Microgrid Using Deep Reinforcement Learning. Energies 2019, 12, 2291. [Google Scholar] [CrossRef]
- Boukas, I.; El Mekki, S.; Cornélusse, B. Data-driven Parameterized Policies for Microgrid Control. Unpublished work. 2019. [Google Scholar]
- An, L.N.; Tuan, T.Q. Dynamic Programming for Optimal Energy Management of Hybrid Wind–PV–Diesel–Battery. Energies 2018, 11, 3039. [Google Scholar] [CrossRef]
- Zhuo, W. Microgrid Energy Management Strategy with Battery Energy Storage System and Approximate Dynamic Programming. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 7581–7587. [Google Scholar] [CrossRef]
- Jahangir, H.; Ahmadian, A.; Golkar, M.A. Optimal design of stand-alone microgrid resources based on proposed Monte-Carlo simulation. In Proceedings of the 2015 IEEE Innovative Smart Grid Technologies—Asia (ISGT ASIA), Bangkok, Thailand, 3–6 November 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Sidorov, D.N.; Muftahov, I.R.; Tomin, N.; Karamov, D.N.; Panasetsky, D.A.; Dreglea, A.; Liu, F.; Foley, A. A Dynamic Analysis of Energy Storage with Renewable and Diesel Generation using Volterra Equations. IEEE Trans. Ind. Inf. 2020, 3451–3459. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Introduction to Reinforcement Learning; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Watkins, C.J.C.H.; Dayan, P. Technical Note: Q-Learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Browne, C.B.; Powley, E.; Whitehouse, D.; Lucas, S.M.; Cowling, P.I.; Rohlfshagen, P.; Colton, S. A survey of Monte Carlo tree search methods. IEEE Trans. Comput. Intell. AI Games 2012, 4, 1–43. [Google Scholar] [CrossRef]
- Kartal, B.; Hernandez-Leal, P.; Taylor, M.E. Action Guidance with MCTS for Deep Reinforcement Learning. In Proceedings of the AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment, Atlanta, GA, USA, 8–12 October 2019; Volume 15, pp. 153–159. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Sutton, R.S.; McAllester, D.A.; Singh, S.P.; Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. In Advances in Neural Information Processing Systems; Massachusetts Institute of Technology Press: Cambridge, MA, USA, 2000; pp. 1057–1063. [Google Scholar]
- Kalbande, S.R.; Deshmukh, M.M.; Wakudkar, H.M.; Wasu, G. Evaluation of gasifier based power generation system using different woody biomass. ARPN J. Eng. Appl. Sci. 2010, 5, 82–88. [Google Scholar]
- Available online: https://github.com/bcornelusse/microgridRLsimulator (accessed on 12 March 2020).
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. Openai gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
- Zysin, L.V.; Koshkin, N.L.; Orlov, E.I.; Sergeev, V.V.; Steshenkov, L.P. A study of the joint operation of a diesel engine and a gas generator processing plant biomass. Therm. Eng. 2002, 49, 14–19. [Google Scholar]
- Martínez, J.D.; Mahkamov, K.; Andrade, R.V.; Lora, E.E.S. Syngas production in downdraft biomass gasifiers and its application using internal combustion engines. Renew. Energy 2012, 38, 1–9. [Google Scholar] [CrossRef]
- Sharma, M.; Kaushal, R. Performance and emission analysis of a dual fuel variable compression ratio (VCR) CI engine utilizing producer gas derived from walnut shells. Energy 2020, 192, 116725. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).