Decentralised Active Power Control Strategy for Real-Time Power Balance in an Isolated Microgrid with an Energy Storage System and Diesel Generators
Abstract
:1. Introduction
- Given extreme disturbances (such as a trip of the DGs), real-time power balance in an isolated microgrid is achieved without using communication systems.
- It has a simple structure and hence can be easily implemented in the outer control loop of the grid-forming BESS while ensuring the normal operations of inner control loops and, consequently, the device-level stability.
- Only the CVCF control is activated under normal operating conditions, minimising the fluctuation of microgrid frequency and active power of other DGs.
- Supplementing detailed explanations on the proposed control method and its simulation results, as well as the test bed with respect to load models and diesel generators
- Performing simulation case studies with consideration of practical microgrid components such as dead-bands and maximum/minimum limiters.
2. System Description
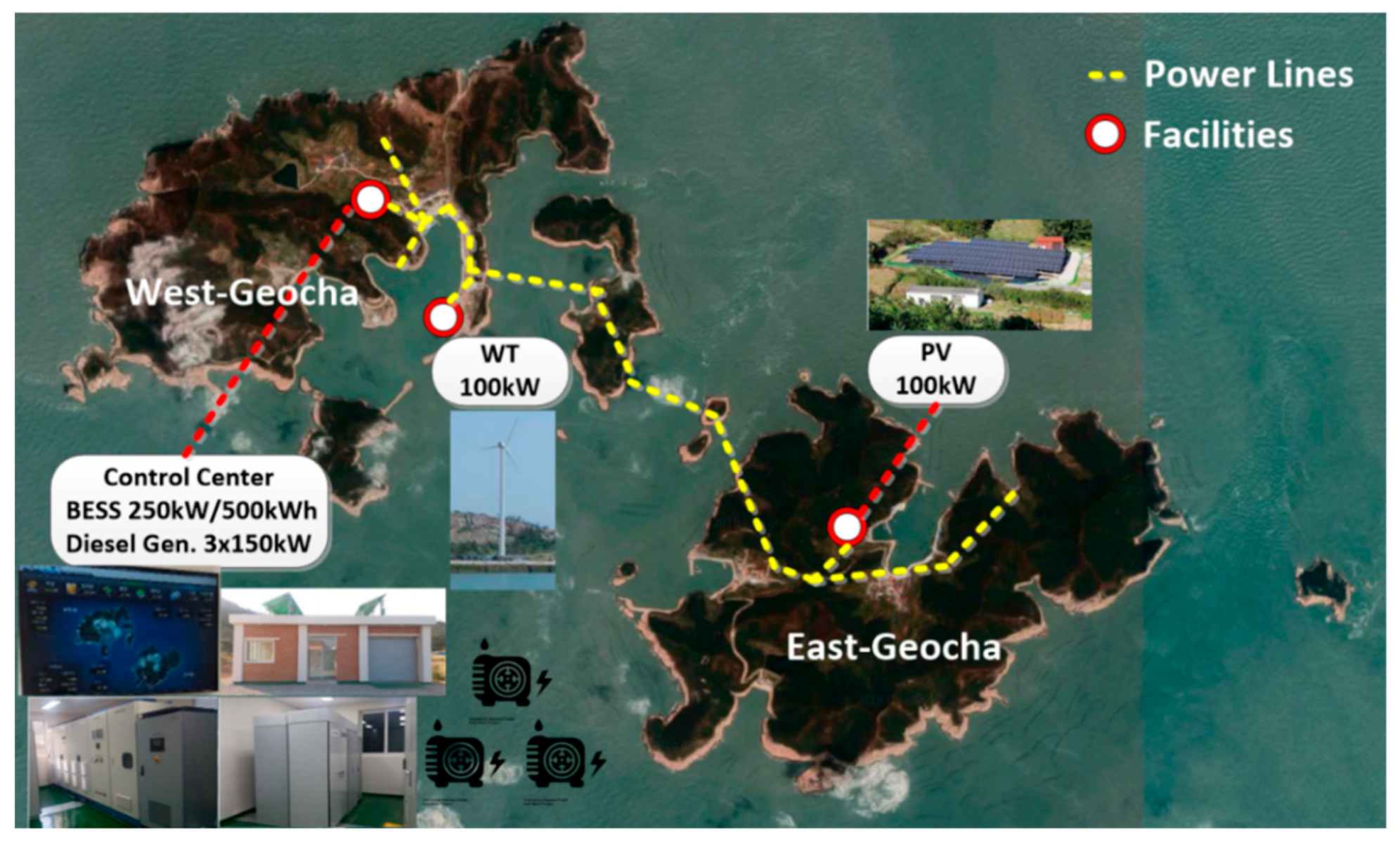
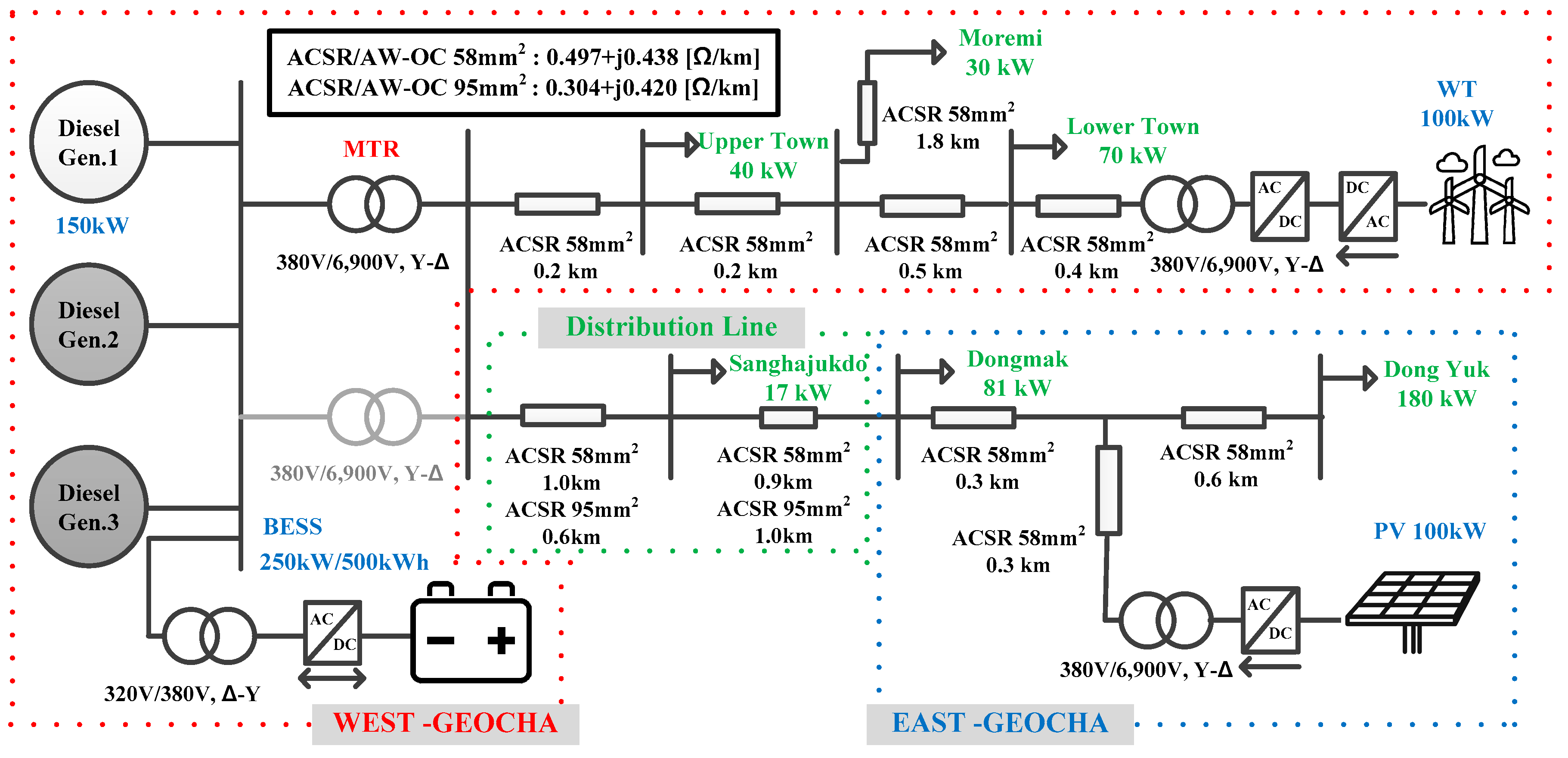
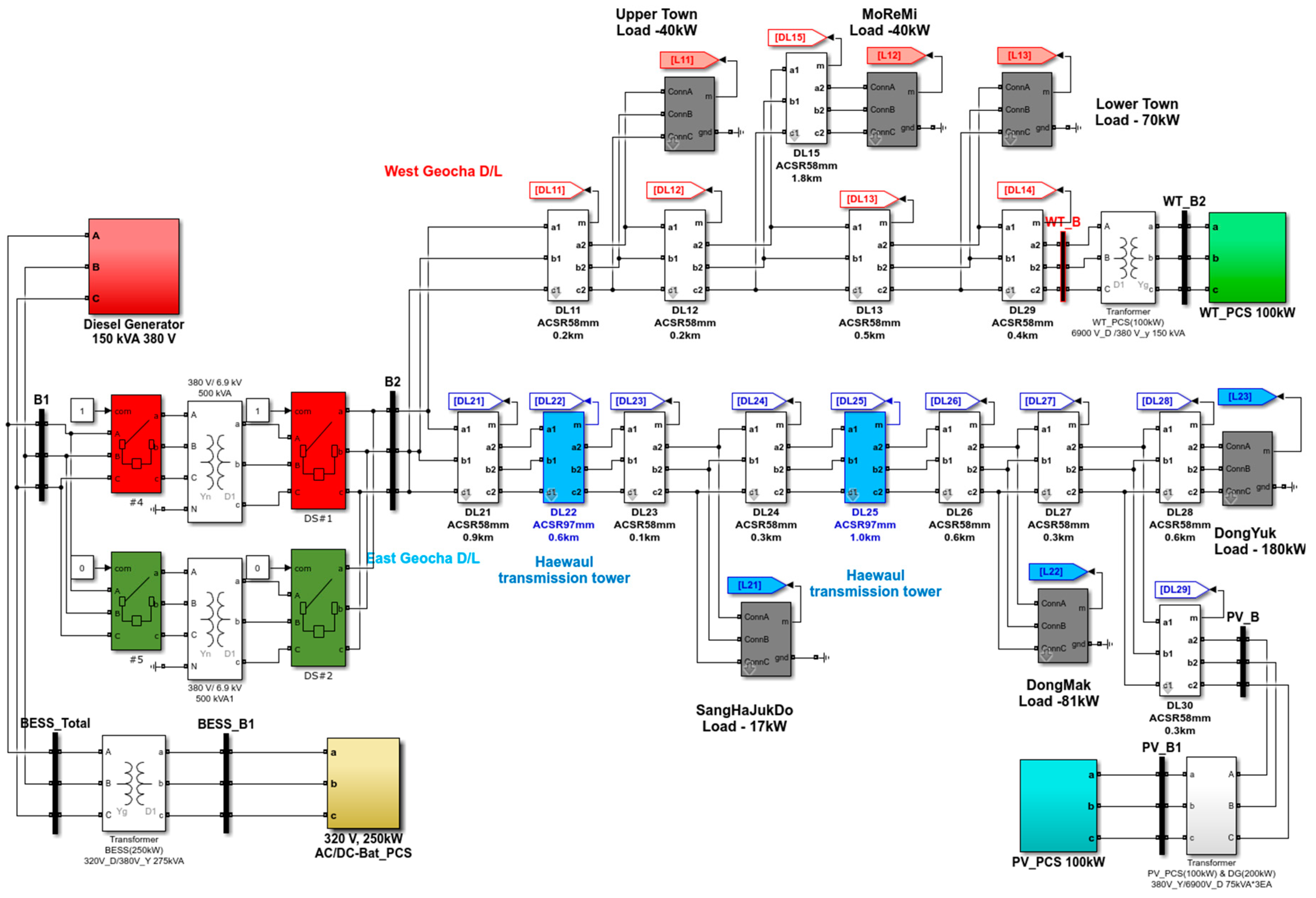
2.1. Geocha Island Microgrid
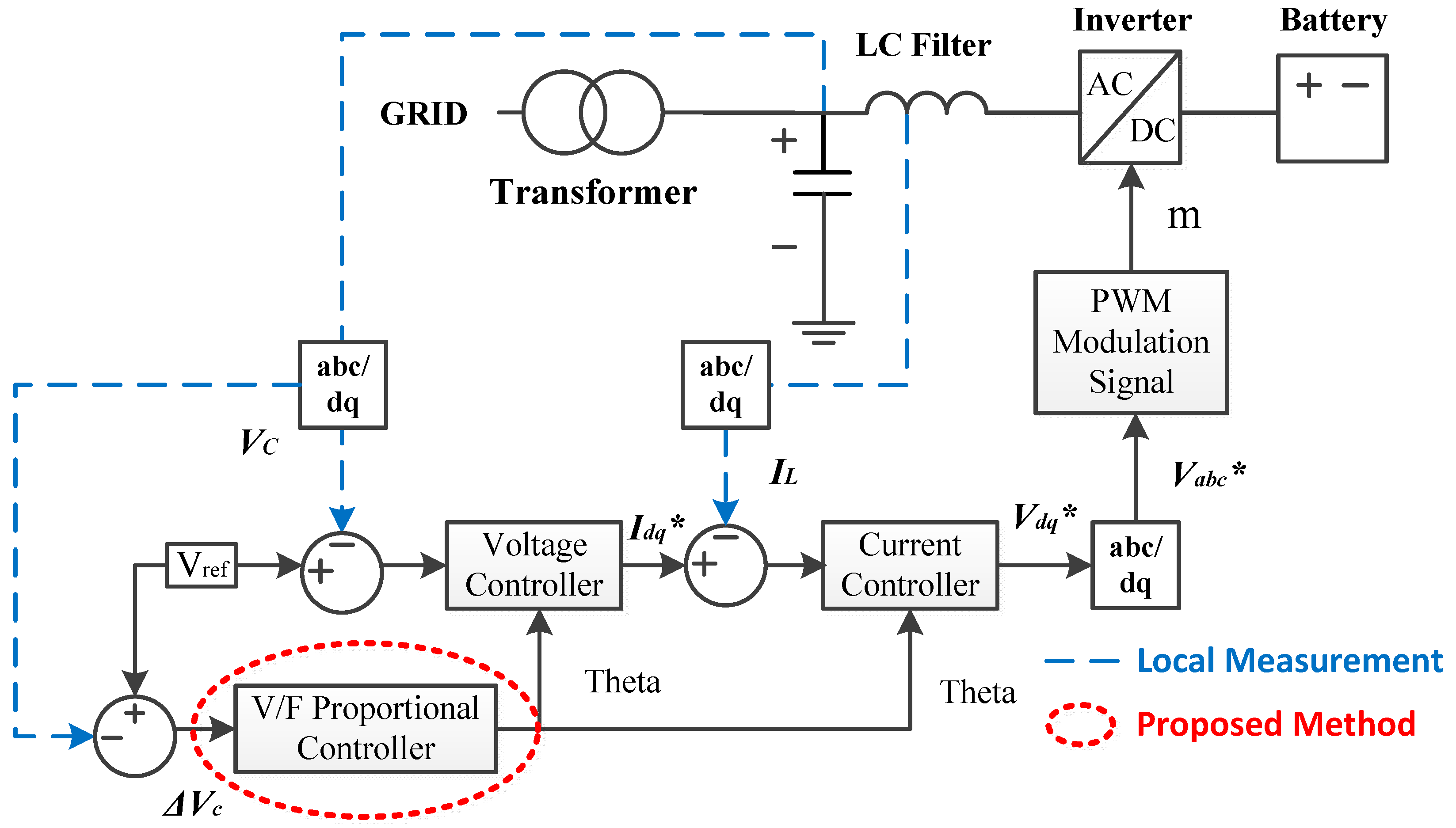
2.2. Grid-Forming BESS
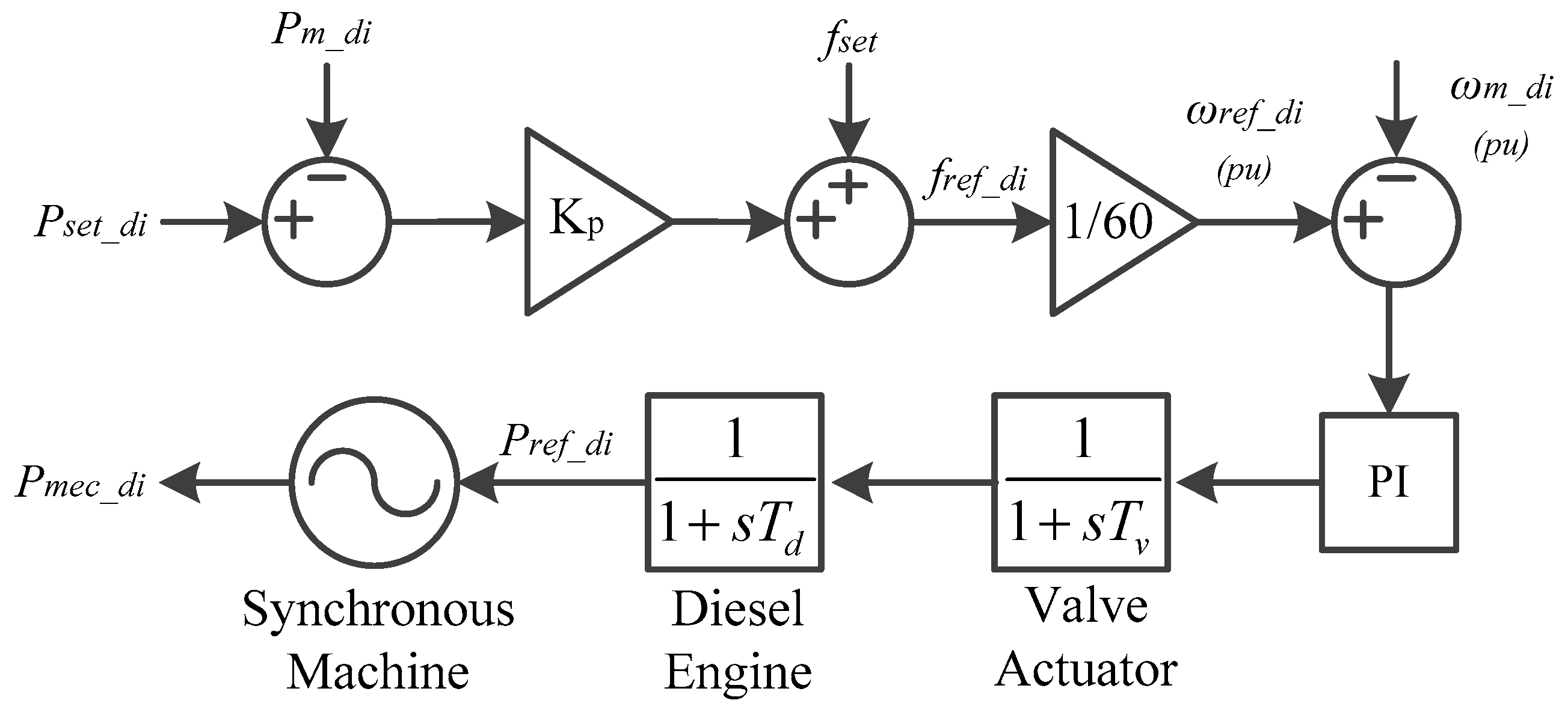
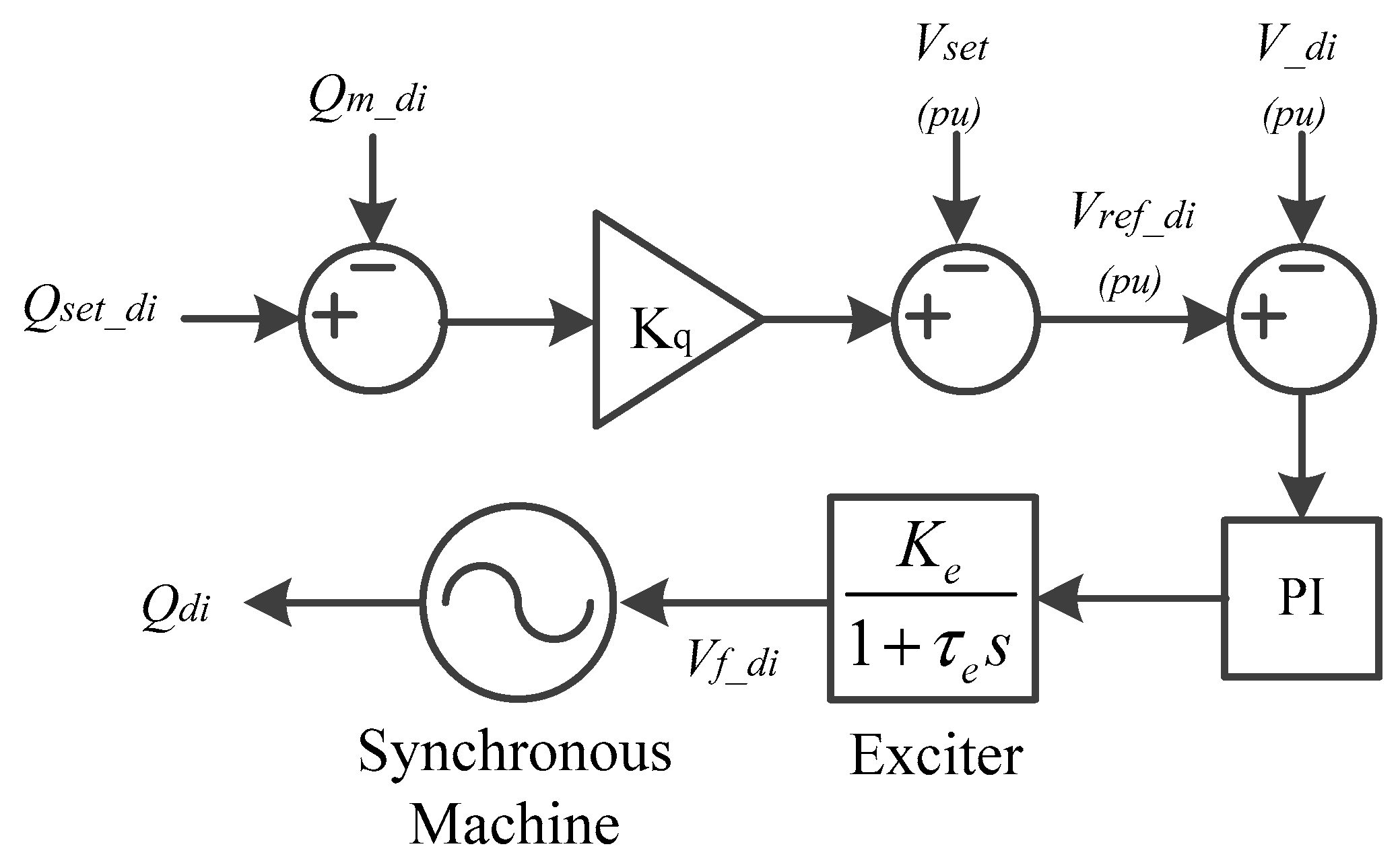
2.3. Diesel Generator
2.4. Basic Load Model
2.5. Active Power Balance Equation in an Isolated Microgrid with CVCF Control
3. Proposed Control Method
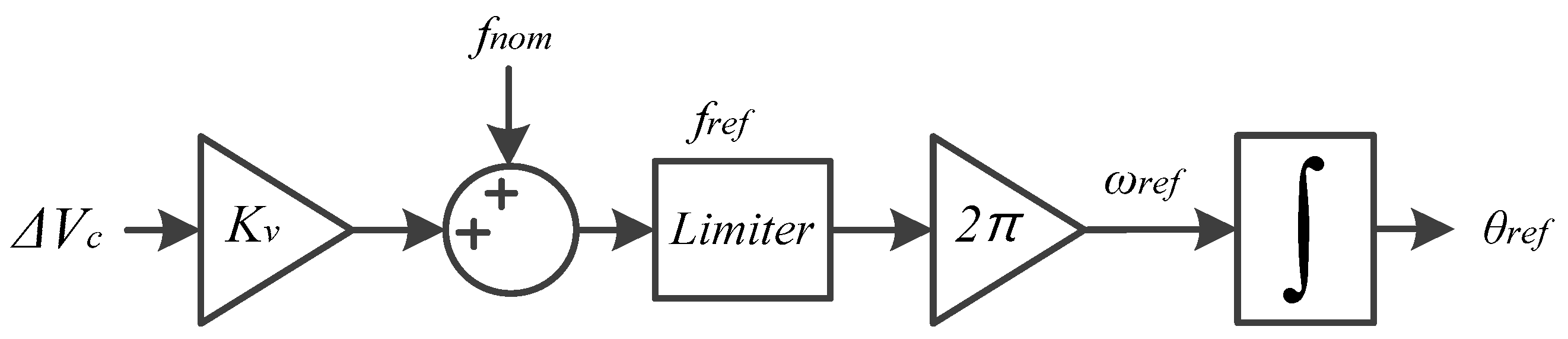
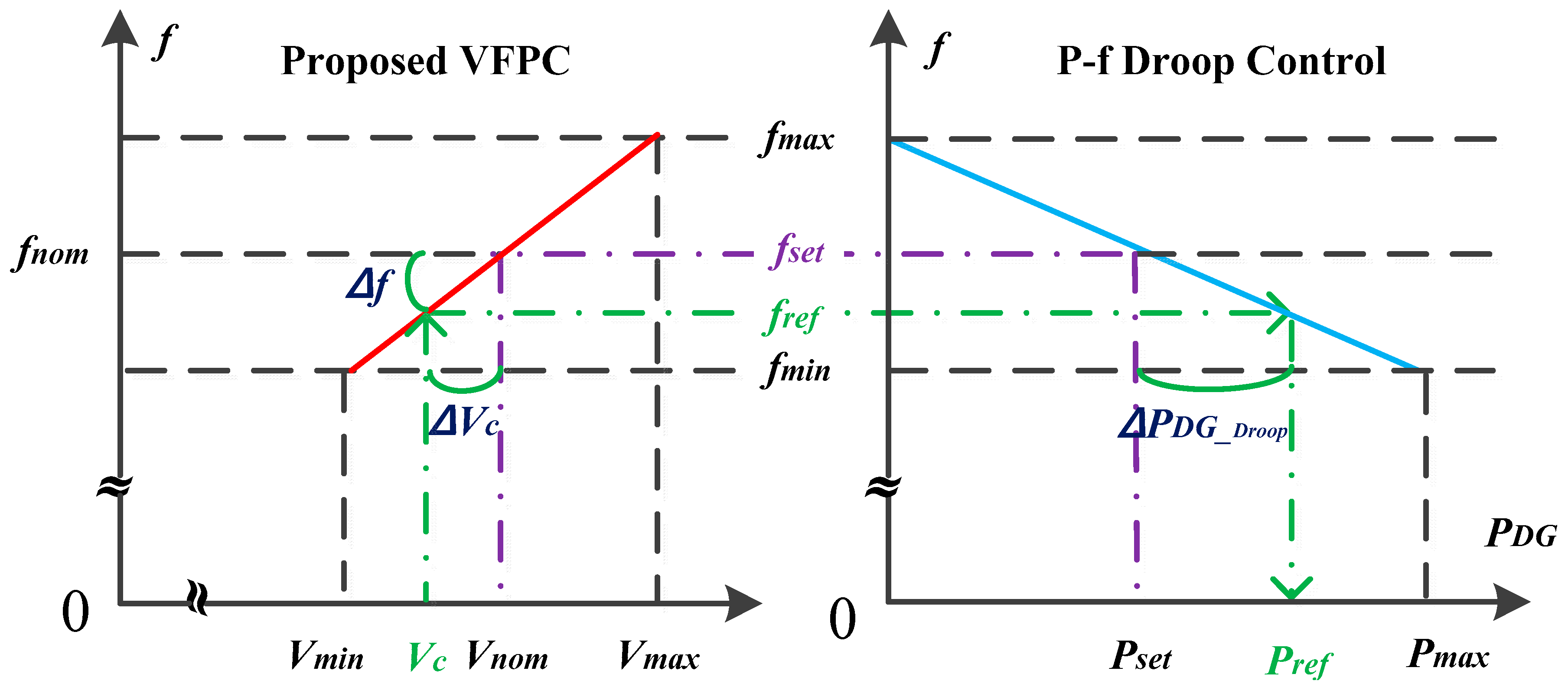
3.1. Frequency Control of BESS with VFPC
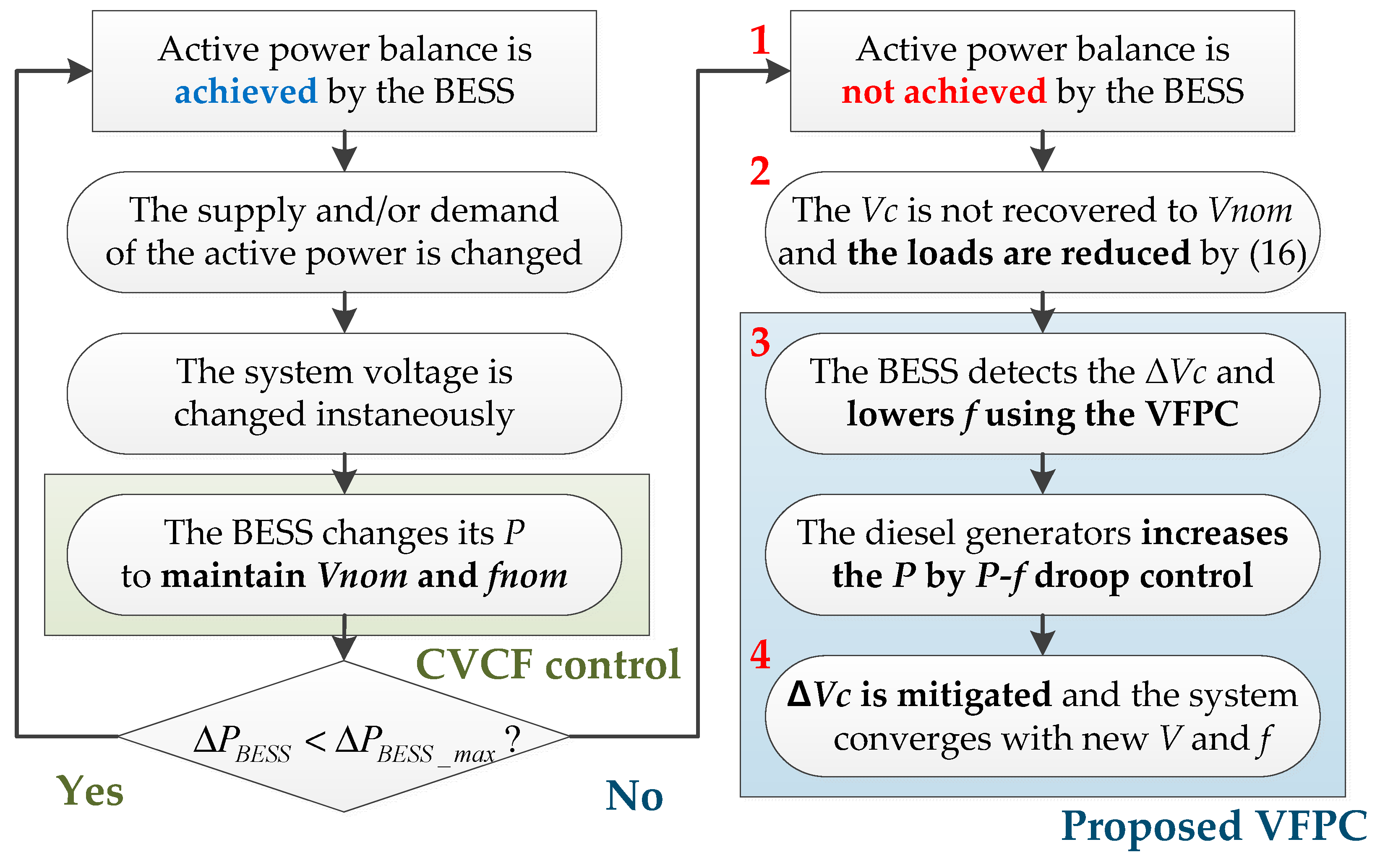
3.2. Proposed Autonomous Active Power Management
- The situation in which the remaining primary reserve of the BESS (ΔPBESS_max) is not enough to cover the active power balance occurs due to a rapid increase in the net demand (e.g., sudden disconnection of a DG).
- The overall bus voltage in the microgrid is reduced, inducing load reduction (ΔPload_VR). This leads to the reduction of variations in the maximum power output of the BESS (see Equations (12) and (13)).
- The BESS recognises the power shortage based on ΔVc and reduces fref (see Equation (15)) by the VFPC. The diesel generator increases its active power with the P-f droop controller (see Equation (1)).
- The participation of diesel generator, acting as a slave unit, enables the power shortage to be compensated for and consequently the microgrid voltages and load demand to be recovered. The reserve of the BESS is also procured and the microgrid starts operating with new levels of V and f (see Equation (20)).
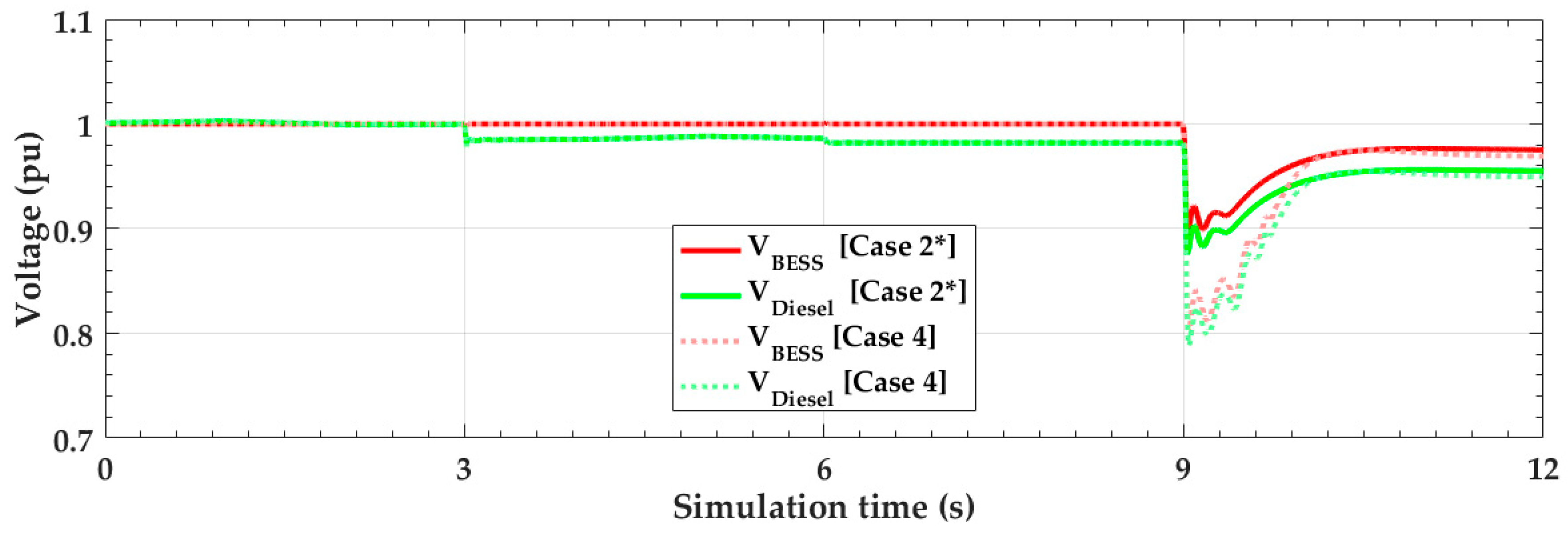
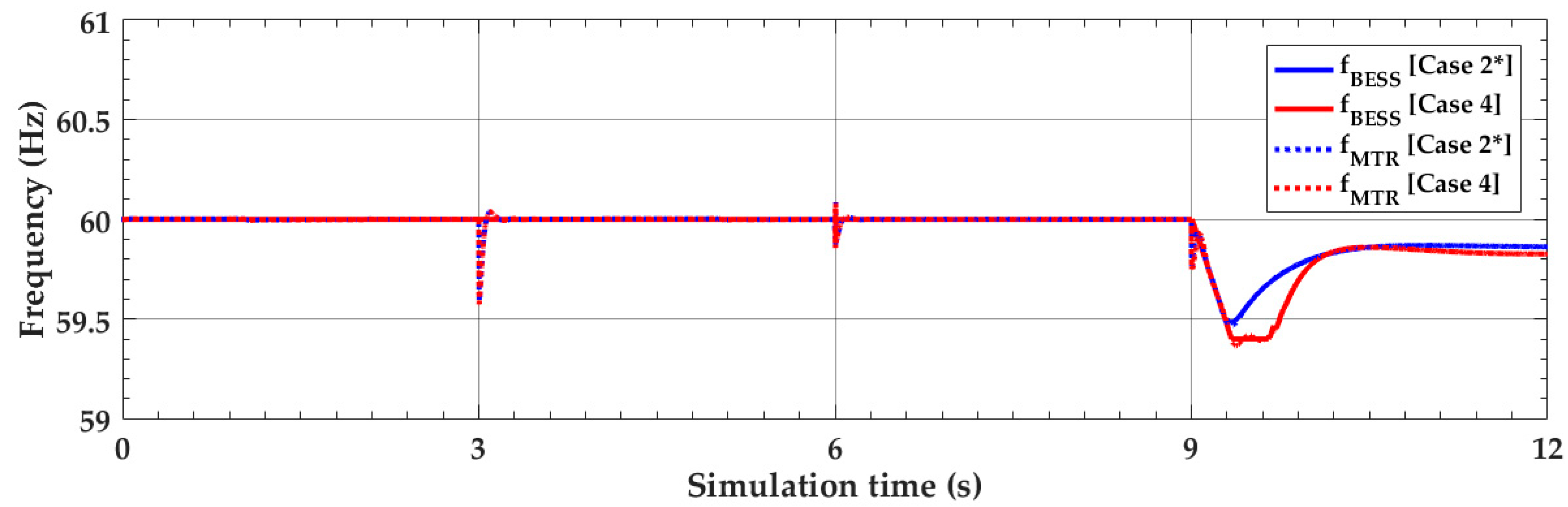
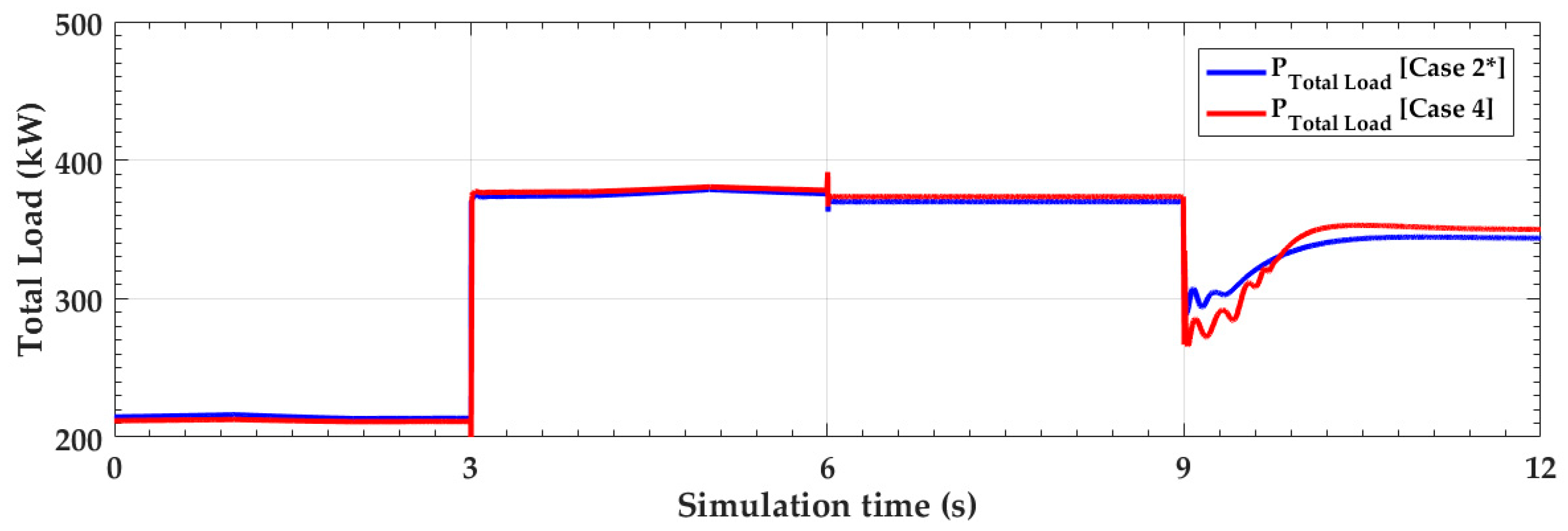
4. Case Studies and Simulation Results
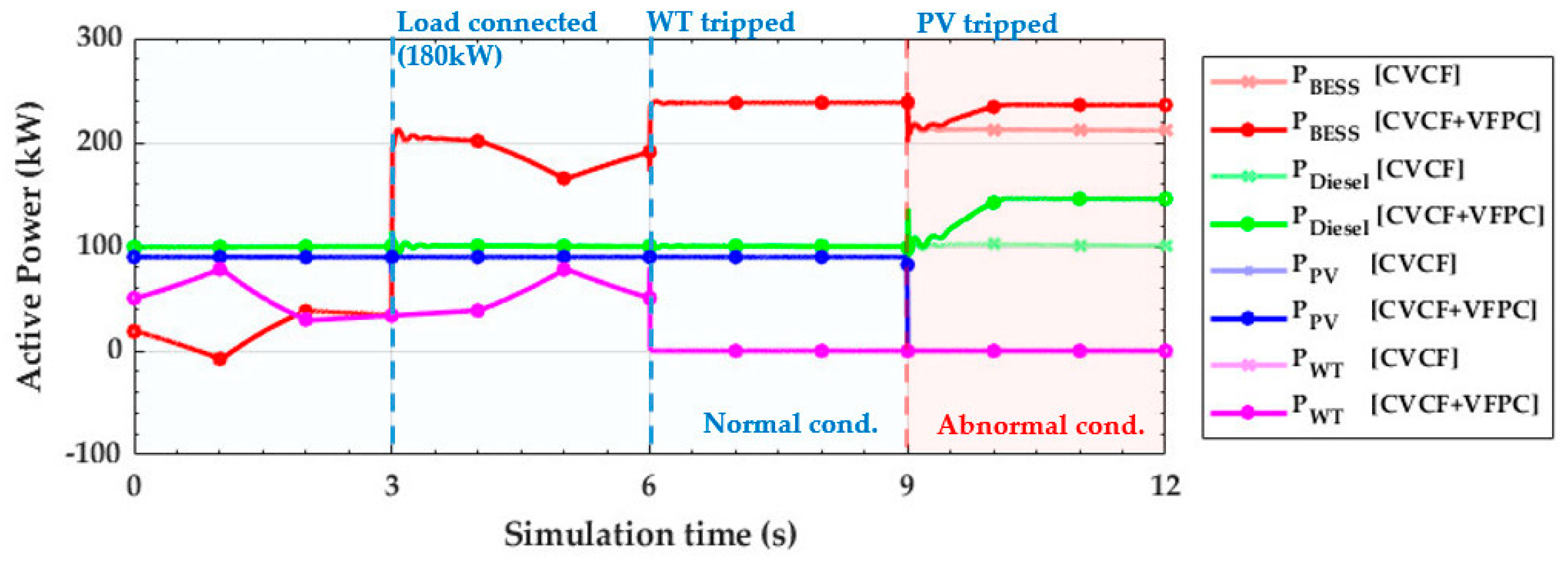
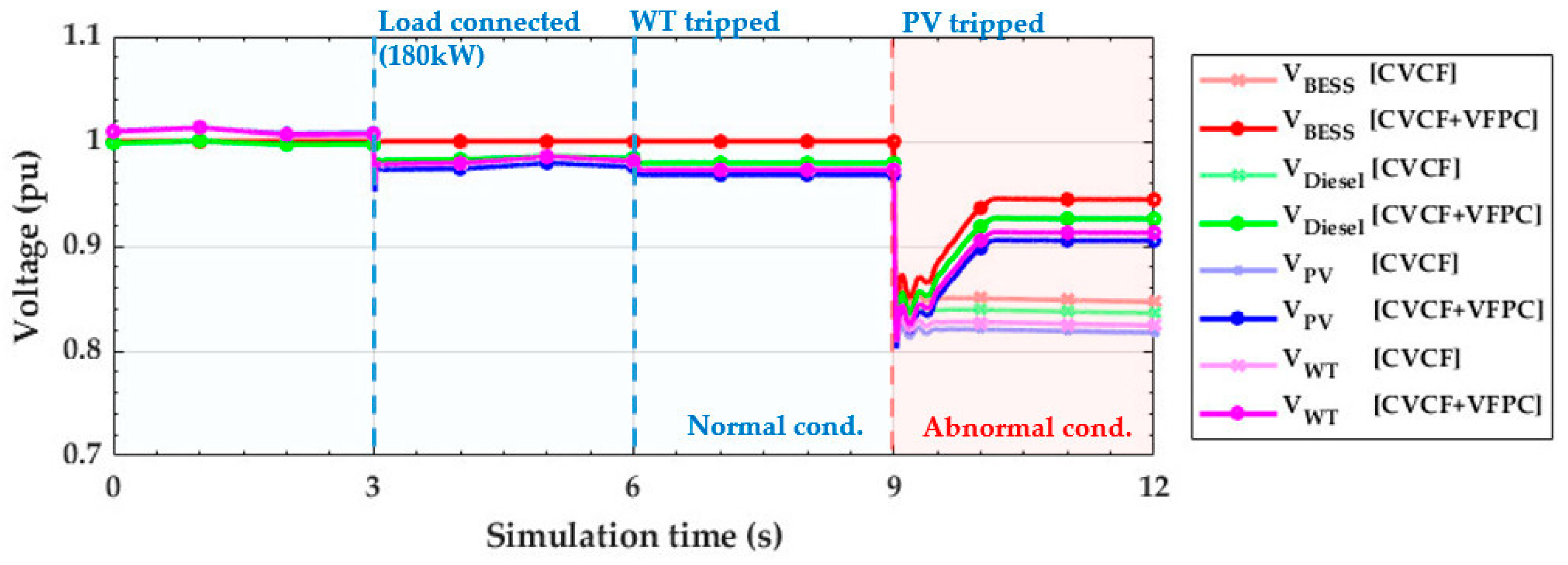
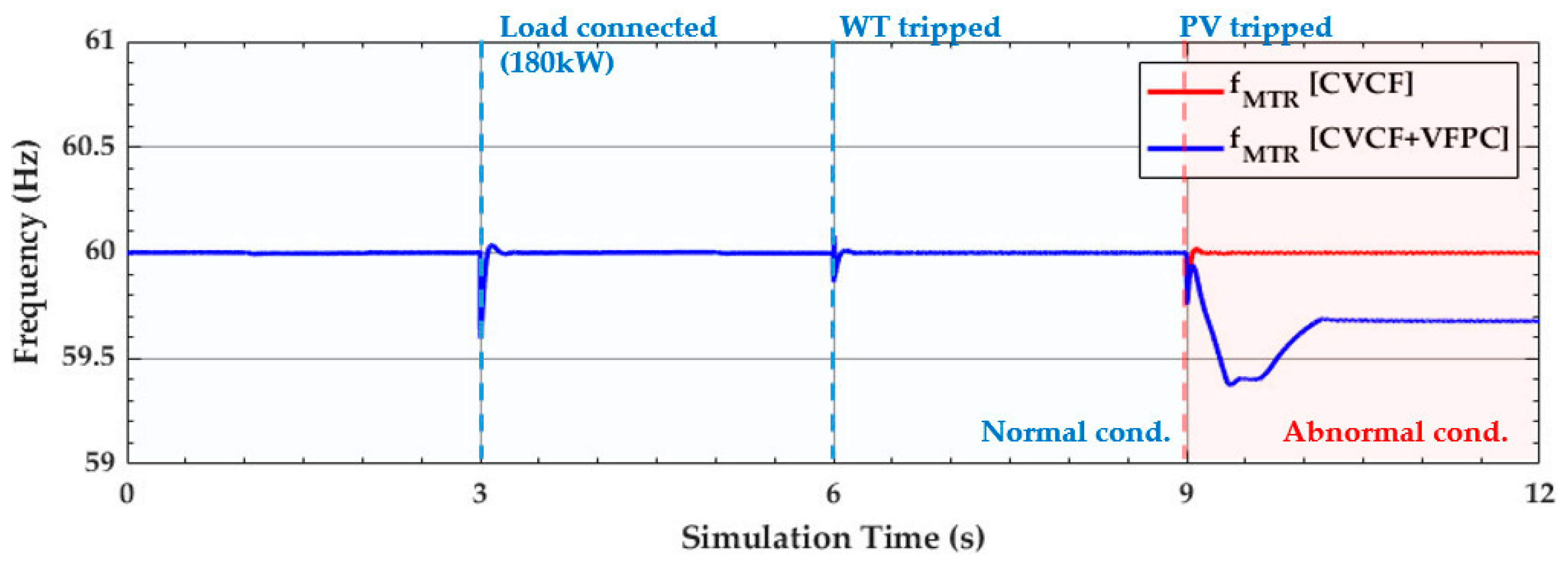
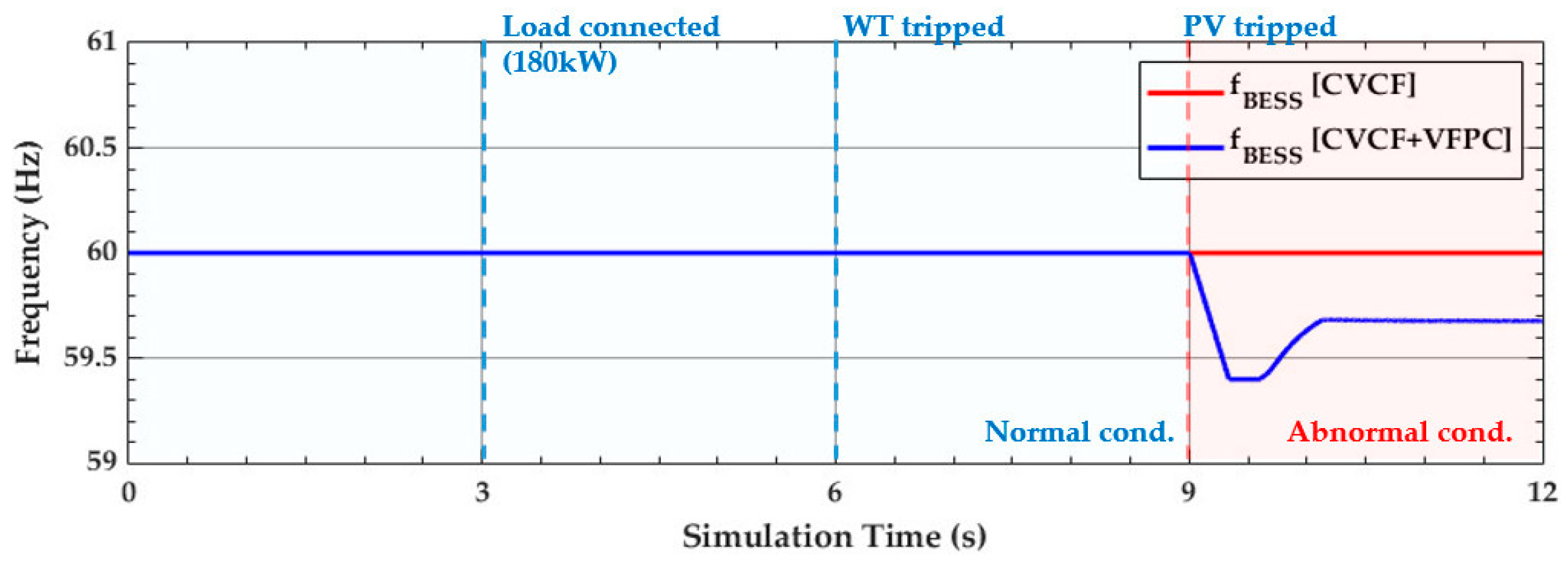
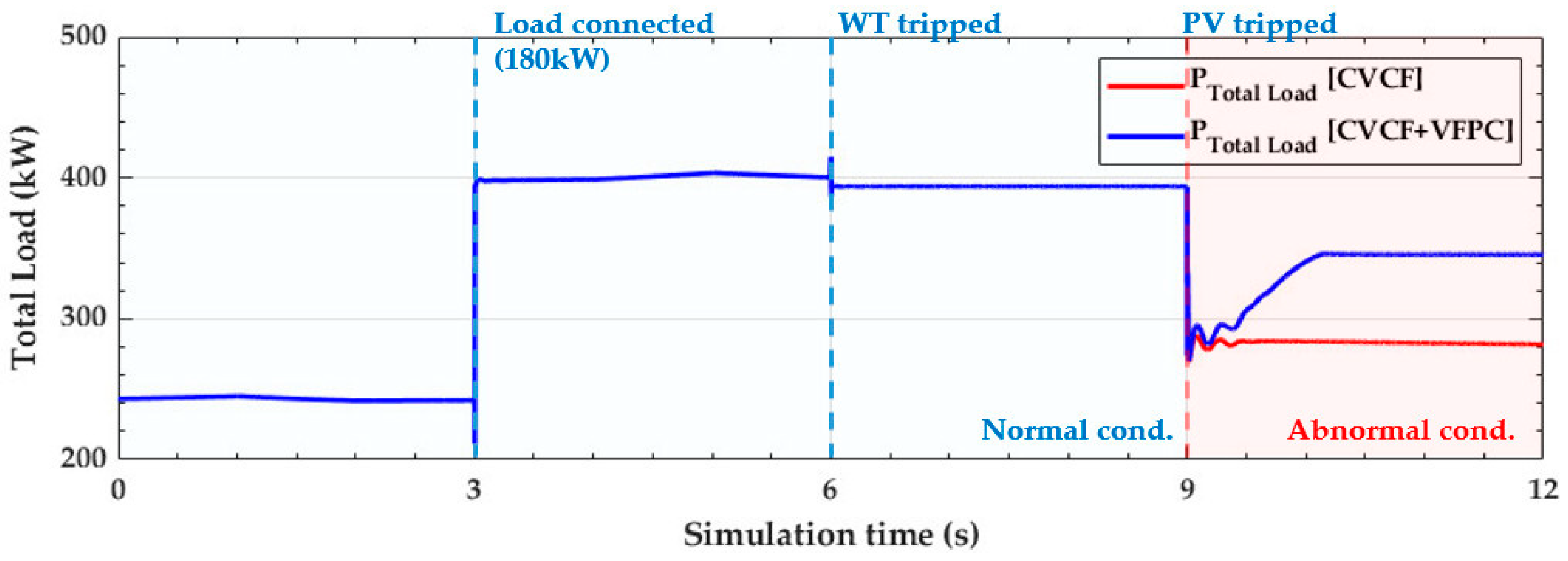
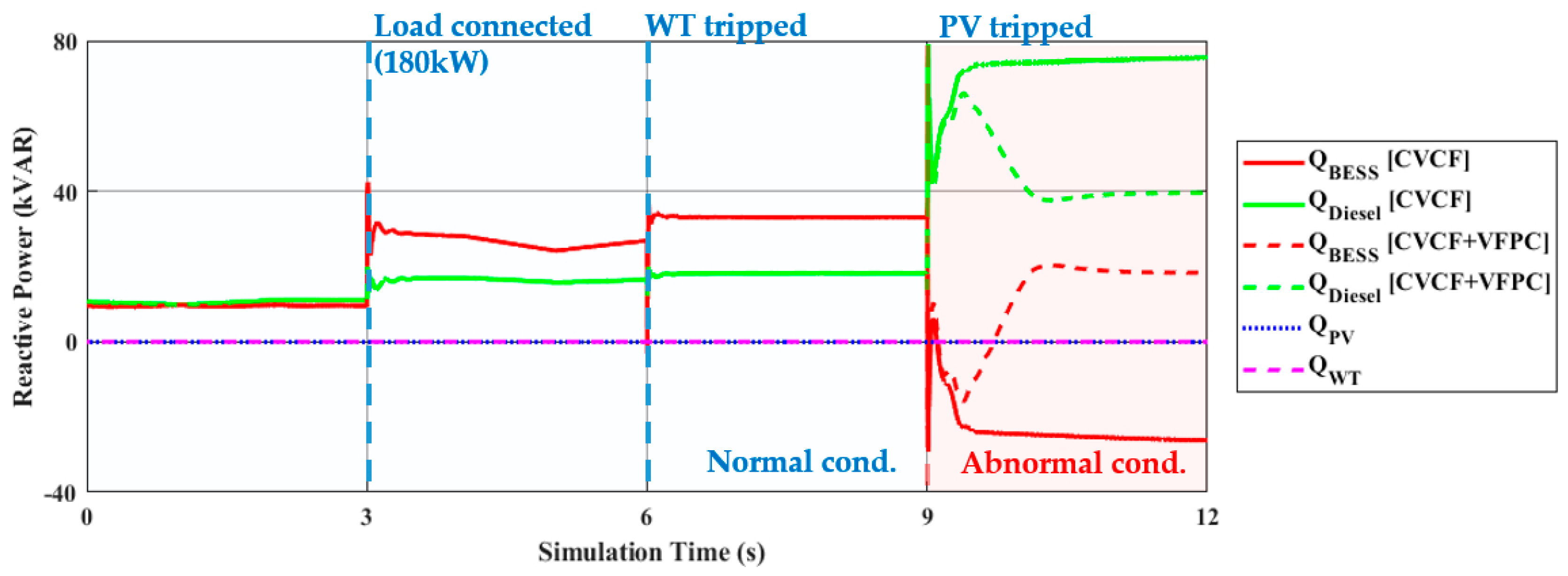
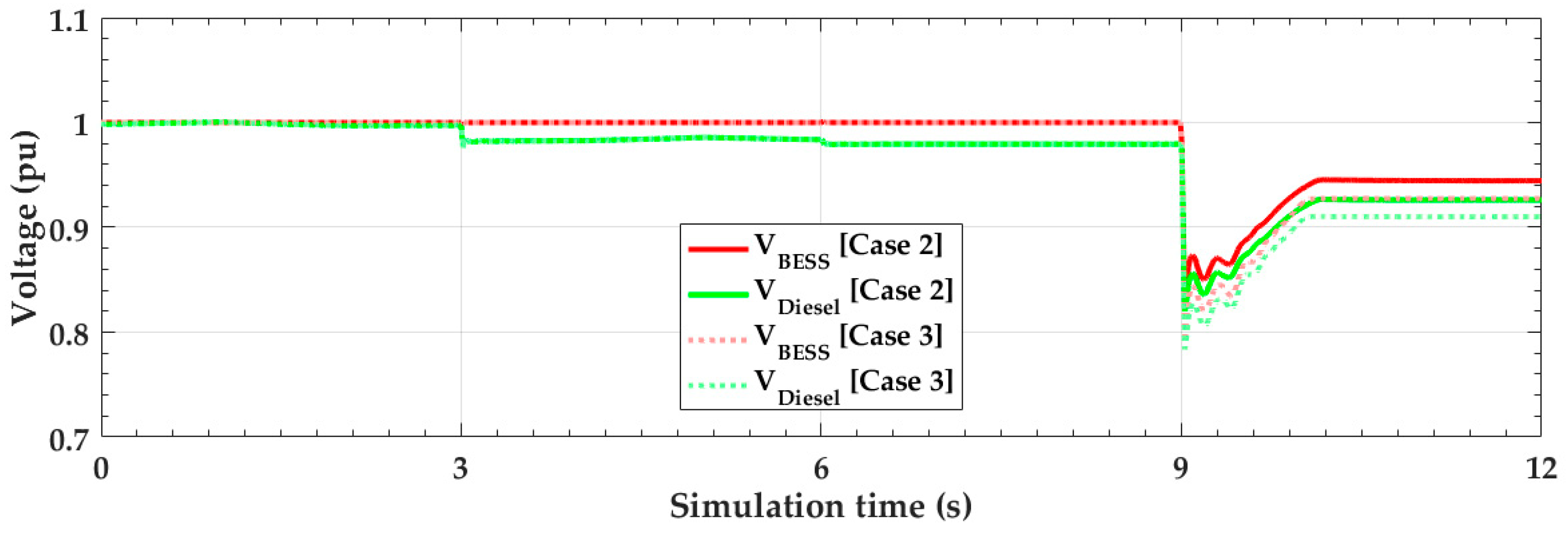
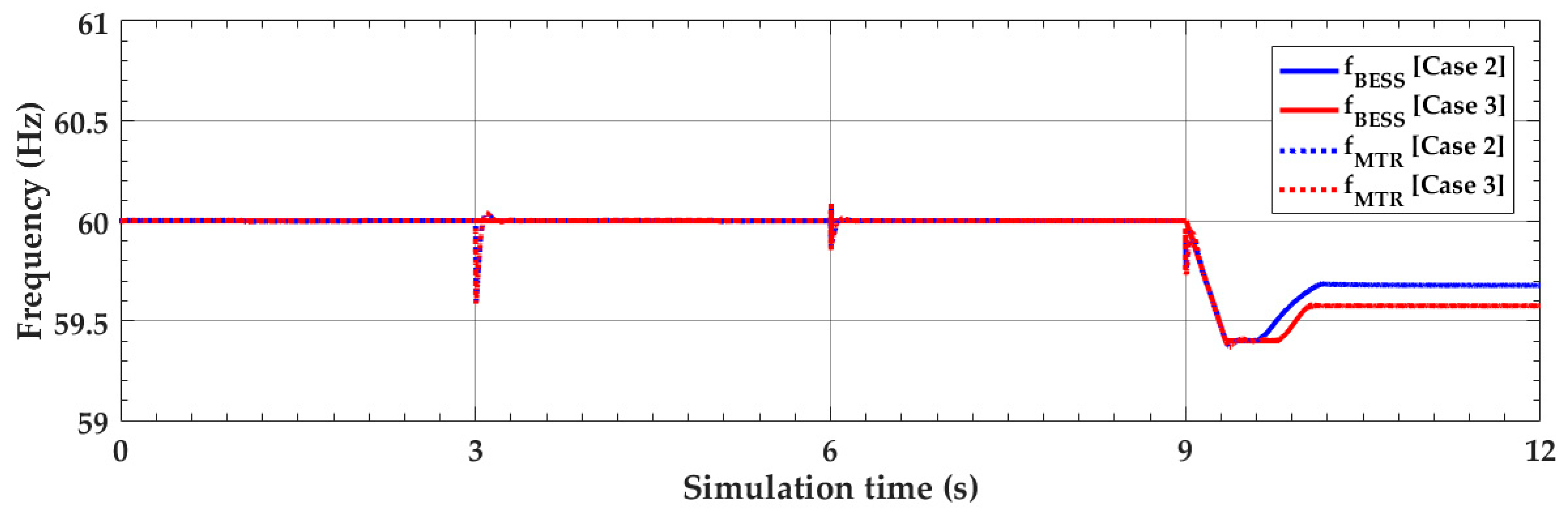
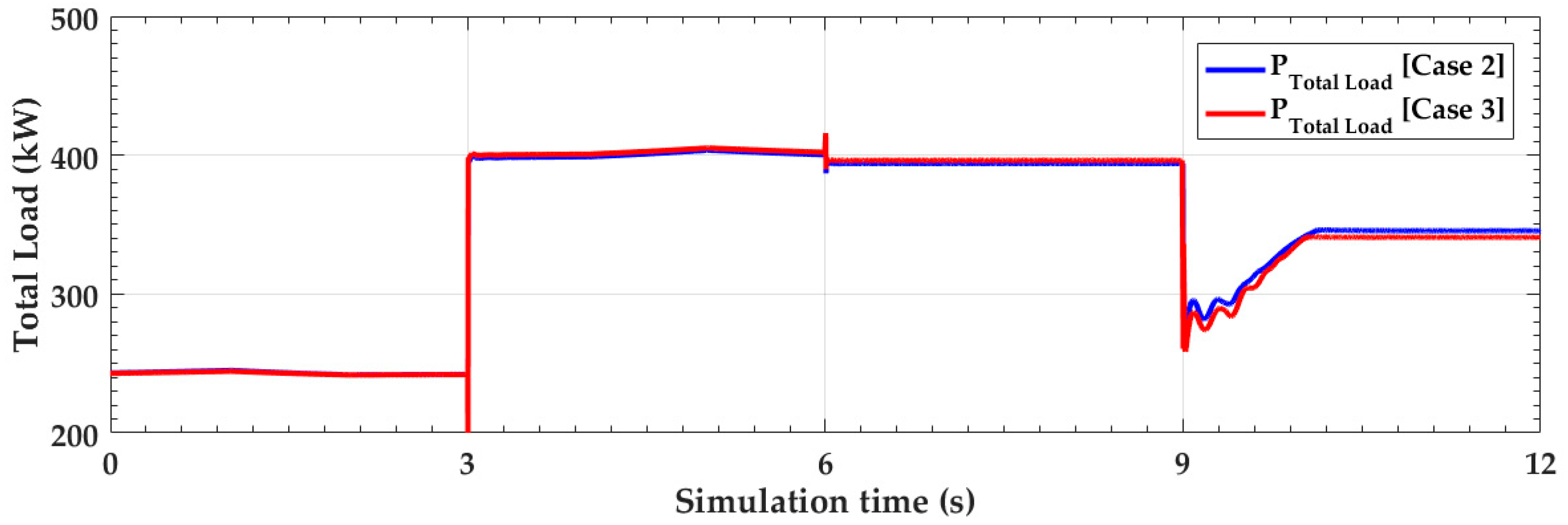
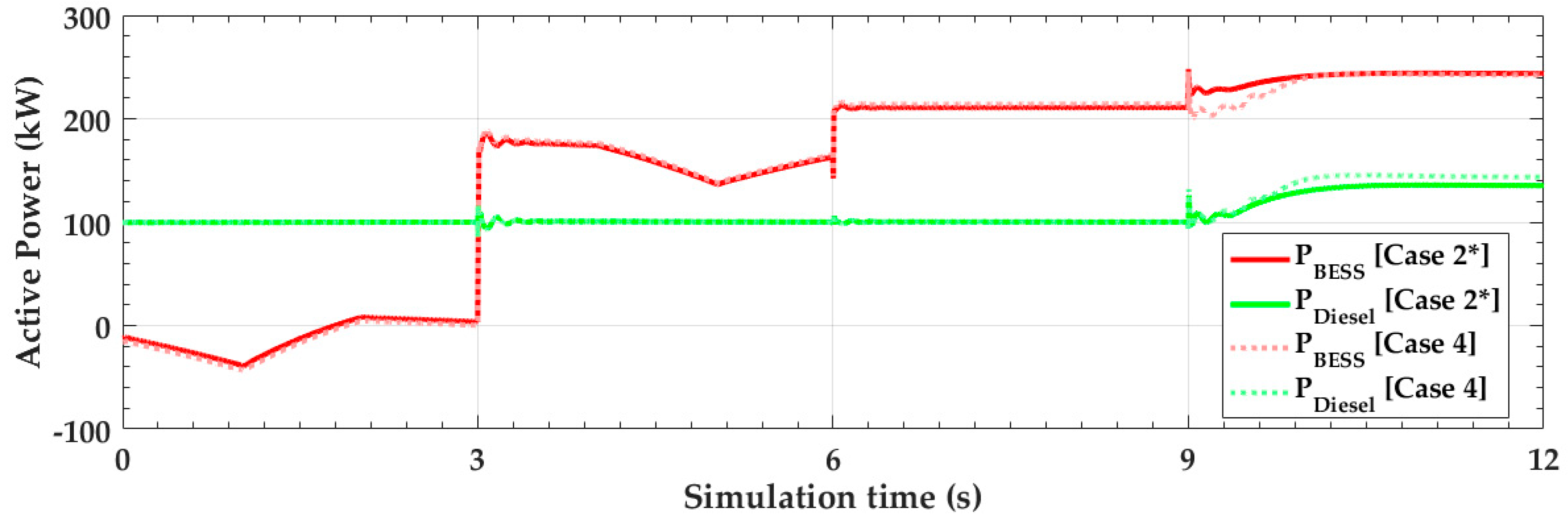
4.1. Simulation Results under the Normal Condition (t < 9 s)
4.2. Simulation Results under the Abnormal Conditions (t ≥ 9 s)
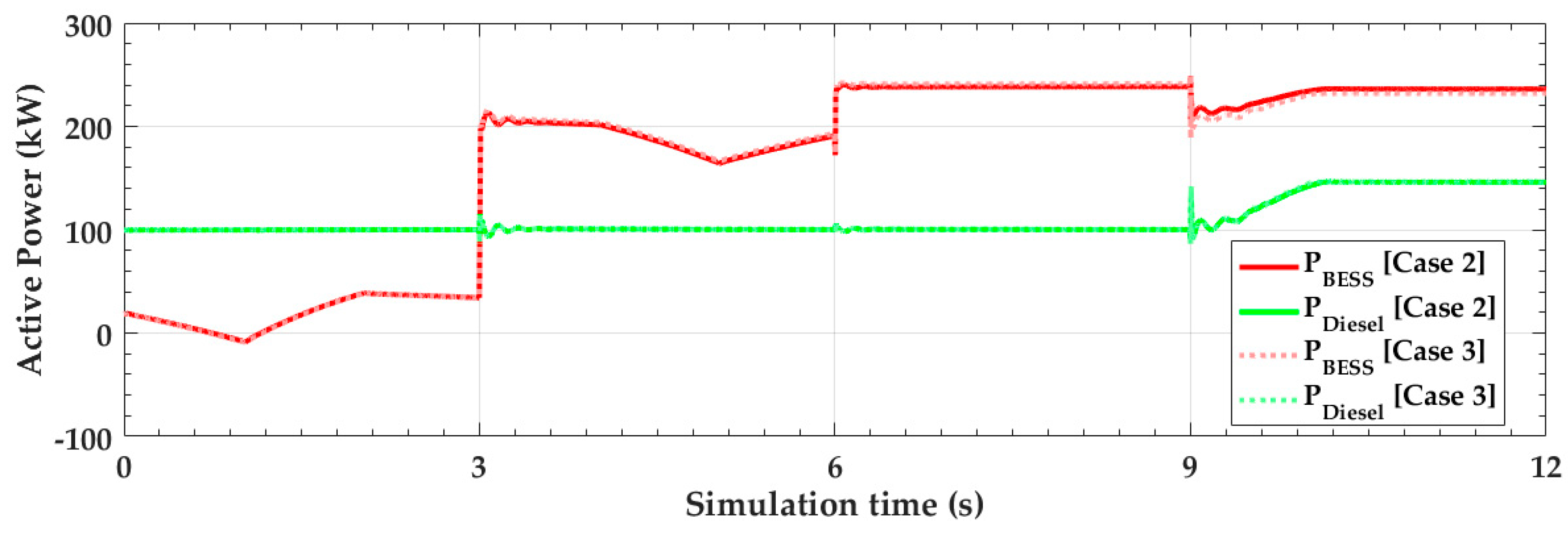
4.3. Simulation Results with Less Voltage-Dependent Loads
4.4. Discussion
5. Conclusions
- The proposed VFPC can be easily applied to the existing CVCF controller of the grid-forming BESS and enables the coordinated control with other DERs that operate with conventional P-f droop controllers.
- The proposed VFPC can be activated based on the local measurement of its bus voltage, not active power, even when sudden and severe imbalance of active power takes place in the microgrid.
- The proposed controller is activated only during the period of active power imbalance Unlike the conventional f-P droop method, the CVCF controller can still reduce the fluctuation of frequency and active power under the normal microgrid condition.
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| Parameters | Symbols | Values | Units |
| Inertia coefficient | J | 3.35 | kg·m2 |
| Friction factor | F | 0 | N·m·s |
| Pole pairs | p | 2 | - |
| Stator resistance per phase | Rs | 1.66 × 10−2 | Ω |
| Stator leakage inductance | Ll | 1.68 × 10−4 | H |
| d-axis magnetizing inductance viewed from stator | Lmd | 5.86 × 10−3 | H |
| q-axis magnetizing inductance viewed from stator | Lmq | 5.05 × 10−3 | H |
| Field resistance | Rf | 5.25 × 10−3 | Ω |
| Field leakage inductance | Llfd | 6.82 × 10−4 | H |
| d-axis resistance of Damper | Rkd | 1.53 × 10−1 | Ω |
| d-axis leakage inductance of Damper | Llkd | 3.40 × 10−3 | H |
| q-axis resistance of Damper | Rkq1 | 4.06 × 10−2 | H |
| q-axis leakage inductance of Damper | Llkq1 | 6.08 × 10−4 | H |
| P gain of PI controller for active power control | Kpp | 20 | - |
| I gain of PI controller for active power control | Kip | 60 | - |
| P gain of PI controller for reactive power control | Kpq | 5 | - |
| I gain of PI controller for reactive power control | Kiq | 13 | - |
| Parameters | Symbols | Values | Units |
| Time constant of diesel engine | Td | 0.5 | s |
| Time constant of valve actuator | Tv | 0.05 | s |
| P-f droop coefficients of the diesel generator | Kp | 4.0 × 10−6 | - |
| Amplification gain of the exciter | Ke | 70 | - |
| Time constant of the exciter | τe | 2.0 × 10−3 | - |
| Q-V droop coefficient of the diesel generator | Kq | 2.5 × 10−6 | - |
| P gain of PI controller for active power control | Kpp | 20 | - |
| I gain of PI controller for active power control | Kip | 60 | - |
| P gain of PI controller for reactive power control | Kpq | 5 | - |
| I gain of PI controller for reactive power control | Kiq | 13 | - |
References
- Teodorescu, R.; Liserre, M.; Rodriguez, P. Grid Converters for Photovoltaic and Wind Power Systems; John Wiley & Sons: West Sussex, UK, 2011; Volume 29. [Google Scholar]
- Jing, L.M.; Son, D.H.; Kang, S.H.; Nam, S.R. A Novel Protection Method for Single Line-to-Ground Faults in Ungrounded Low-Inertia Microgrids. Energies 2016, 9, 459. [Google Scholar] [CrossRef]
- Hatziargyriou, N. Microgrids Architectures and Control; Wiley, IEEE-Press: Chichester, UK, 2014; pp. XXI, 317. [Google Scholar] [CrossRef]
- Lu, X.N.; Wang, J.H. A Game Changer Electrifying remote communities by using isolated microgrids. IEEE Electrif. Mag. 2017, 5, 56–63. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, S.H.; Sul, S.K. Variable-Speed Engine Generator with Supercapacitor: Isolated Power Generation System and Fuel Efficiency. IEEE Trans. Ind. Appl. 2009, 45, 2130–2135. [Google Scholar] [CrossRef]
- Neto, M.R.B.; Carvalho, P.C.M.; Carioca, J.O.B.; Canafistula, F.J.F. Biogas/photovoltaic hybrid power system for decentralized energy supply of rural areas. Energy Policy 2010, 38, 4497–4506. [Google Scholar] [CrossRef]
- Arent, D.; Barnett, J.; Mosey, G.; Wise, A. The potential of renewable energy to reduce the dependence of the state of Hawaii on oil. In Proceedings of the 42nd HICSS’09Hawaii International Conference on System Sciences, Waikoloa, HI, USA, 5–8 January 2009; pp. 1–11. [Google Scholar]
- Tong, Z.M.; Zhang, K.M. The near-source impacts of diesel backup generators in urban environments. Atmos. Environ. 2015, 109, 262–271. [Google Scholar] [CrossRef]
- Uddin, M.N.; Rahman, M.A.; Sir, M. Reduce Generators Noise with Better Performance of a Diesel Generator Set using Modified Absorption Silencer. Glob. J. Res. Eng. 2016, XVI. Available online: https://globaljournals.org/GJRE_Volume16/5-Reduce-Generators-Noise.pdf (accessed on 6 February 2019).
- Prull, D.S. Design and Integration of an Isolated Microgrid with a High Penetration of Renewable Generation; University of California: Berkeley, CA, USA, 2008. [Google Scholar]
- Green, T.C.; Prodanovic, M. Control of inverter-based micro-grids. Electr. Power Syst. Res. 2007, 77, 1204–1213. [Google Scholar] [CrossRef]
- Katiraei, F.; Iravani, R.; Hatziargyriou, N.; Dimeas, A. Microgrids management. IEEE Power Energy Mag. 2008, 6, 54–65. [Google Scholar] [CrossRef]
- Wang, X.F.; Guerrero, J.M.; Blaabjerg, F.; Chen, Z. A Review of Power Electronics Based Microgrids. J. Power Electron. 2012, 12, 181–192. [Google Scholar] [CrossRef]
- de Matos, J.; Silva, F.; Ribeiro, L. Power Control in AC Isolated Microgrids with Renewable Energy Sources and Energy Storage Systems. IEEE Trans. Ind. Electron. 2014, 62. [Google Scholar] [CrossRef]
- Miao, Z.X.; Xu, L.; Disfani, V.R.; Fan, L.L. An SOC-Based Battery Management System for Microgrids. IEEE Trans. Smart Grid 2014, 5, 966–973. [Google Scholar] [CrossRef]
- Bevrani, H.; François, B.; Ise, T. Microgrid Dynamics and Control; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Kim, H.; Bae, J.; Baek, S.; Nam, D.; Cho, H.; Chang, H.J. Comparative Analysis between the Government Micro-Grid Plan and Computer Simulation Results Based on Real Data: The Practical Case for a South Korean Island. Sustainability 2017, 9, 197. [Google Scholar] [CrossRef]
- Kim, S.-Y.; Mathews, J.A. Korea’s Greening Strategy: The role of smart microgrids. Asia-Pac. J. 2016, 14, 6. [Google Scholar]
- Hwang, W.H.; Kim, S.K.; Lee, J.H.; Chae, W.K.; Lee, J.H.; Lee, H.J.; Kim, J.E. Autonomous Micro-grid Design for Supplying Electricity in Carbon-Free Island. J. Electr. Eng. Technol. 2014, 9, 1112–1118. [Google Scholar] [CrossRef]
- Chae, W.K.; Lee, H.J.; Won, J.N.; Park, J.S.; Kim, J.E. Design and Field Tests of an Inverted Based Remote MicroGrid on a Korean Island. Energies 2015, 8, 8193–8210. [Google Scholar] [CrossRef]
- Kim, S.-H.; Chung, I.-Y.; Lee, H.-J.; Chae, W.-K. Voltage and Frequency Control Method Using Battery Energy Storage System for a Stand-alone Microgrid. Trans. Korean Inst. Electr. Eng. 2015, 64, 1168–1179. [Google Scholar] [CrossRef]
- Chae, W.K.; Won, J.N.; Lee, H.J.; Kim, J.E.; Kim, J. Comparative Analysis of Voltage Control in Battery Power Converters for Inverter-Based AC Microgrids. Energies 2016, 9, 596. [Google Scholar] [CrossRef]
- Kim, Y.S.; Kim, E.S.; Moon, S.I. Frequency and Voltage Control Strategy of Standalone Microgrids with High Penetration of Intermittent Renewable Generation Systems. IEEE Trans. Power Syst. 2016, 31, 718–728. [Google Scholar] [CrossRef]
- Kim, H.; Baek, S.; Choi, K.H.; Kim, D.; Lee, S.; Kim, D.; Chang, H.J. Comparative Analysis of On- and Off-Grid Electrification: The Case of Two South Korean Islands. Sustainability-Basel 2016, 8, 350. [Google Scholar] [CrossRef]
- Moon, H.-J.; Chang, J.W.; Kim, E.-S.; Moon, S.-I. Frequency-based wireless control of distributed generators in an isolated microgrid: A case of Geocha Island in South Korea. In Proceedings of the 2017 52nd International Universities Power Engineering Conference (UPEC), Crete, Greece, 28–31 August 2017; pp. 1–6. [Google Scholar]
- Won, J.; Chae, W.; Lee, H.; Park, J.; Sim, J.; Shin, C. Demonstration of remote microgrid system in Korean island. CIRED-Open Access Proc. J. 2017, 2017, 2212–2214. [Google Scholar] [CrossRef]
- Belvedere, B.; Bianchi, M.; Borghetti, A.; Nucci, C.A.; Paolone, M.; Peretto, A. A Microcontroller-Based Power Management System for Standalone Microgrids with Hybrid Power Supply. IEEE Trans. Sustain. Energy 2012, 3, 422–431. [Google Scholar] [CrossRef]
- Tan, K.T.; So, P.L.; Chu, Y.C.; Chen, M.Z.Q. Coordinated Control and Energy Management of Distributed Generation Inverters in a Microgrid. IEEE Trans. Power Deliv. 2013, 28, 704–713. [Google Scholar] [CrossRef]
- Olivares, D.E.; Canizares, C.A.; Kazerani, M. A Centralized Energy Management System for Isolated Microgrids. IEEE Trans. Smart Grid 2014, 5, 1864–1875. [Google Scholar] [CrossRef]
- Kaur, A.; Kaushal, J.; Basak, P. A review on microgrid central controller. Renew. Sustain. Energy Rev. 2016, 55, 338–345. [Google Scholar] [CrossRef]
- Yazdanian, M.; Mehrizi-Sani, A. Distributed Control Techniques in Microgrids. IEEE Trans. Smart Grid 2014, 5, 2901–2918. [Google Scholar] [CrossRef]
- Abdelaziz, M.M.A.; Farag, H.E. An Enhanced Supervisory Control for Islanded Microgrid Systems. IEEE Trans. Smart Grid 2016, 7, 1941–1943. [Google Scholar] [CrossRef]
- Wu, D.; Tang, F.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M. A Control Architecture to Coordinate Renewable Energy Sources and Energy Storage Systems in Islanded Microgrids. IEEE Trans. Smart Grid 2015, 6, 1156–1166. [Google Scholar] [CrossRef]
- Mahmood, H.; Jiang, J. Decentralized Power Management of Multiple PV, Battery, and Droop Units in an Islanded Microgrid. IEEE Trans. Smart Grid 2017. [Google Scholar] [CrossRef]
- Solanki, A.; Nasiri, A.; Bhavaraju, V.; Familiant, Y.L.; Fu, Q. A New Framework for Microgrid Management: Virtual Droop Control. IEEE Trans. Smart Grid 2016, 7, 554–566. [Google Scholar] [CrossRef]
- Schonbergerschonberger, J.; Duke, R.; Round, S.D. DC-bus signaling: A distributed control strategy for a hybrid renewable nanogrid. IEEE Trans. Ind. Electron. 2006, 53, 1453–1460. [Google Scholar] [CrossRef]
- Wu, D.; Tang, F.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M. Autonomous Active Power Control for Islanded AC Microgrids with Photovoltaic Generation and Energy Storage System. IEEE Trans. Energy Conver. 2014, 29, 882–892. [Google Scholar] [CrossRef]
- Peyghami, S.; Mokhtari, H.; Blaabjerg, F. Autonomous Power Management in LVDC Microgrids Based on a Superimposed Frequency Droop. IEEE Trans. Power Electr. 2018, 33, 5341–5350. [Google Scholar] [CrossRef]
- Mastromauro, R.A. Voltage control of a grid-forming converter for an AC microgrid: A real case study. In Proceedings of the 3rd Renewable Power Generation Conference (RPG 2014), Naples, Italy, 24–25 September 2014; pp. 1–6. [Google Scholar]
- Moon, H.-J.; Chang, J.W.; Lee, S.-Y.; Moon, S.-I. Autonomous active power management in isolated microgrid based on proportional and droop control. Energy Procedia 2018, 153, 48–55. [Google Scholar] [CrossRef]
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994; Volume XXIII, p. 1176. [Google Scholar]
- Farrokhabadi, M.; Canizares, C.A.; Bhattacharya, K. Frequency Control in Isolated/Islanded Microgrids Through Voltage Regulation. IEEE Trans. Smart Grid 2017, 8, 1185–1194. [Google Scholar] [CrossRef]
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Optimization of perturb and observe maximum power point tracking method. IEEE Trans. Power Electr. 2005, 20, 963–973. [Google Scholar] [CrossRef]
- Abdullah, M.A.; Yatim, A.H.M.; Tan, C.W.A.; Saidur, R. A review of maximum power point tracking algorithms for wind energy systems. Renew. Sustain. Energy Rev. 2012, 16, 3220–3227. [Google Scholar] [CrossRef]
- IEEE Guide for Design, Operation, and Integration of Distributed Resource Island Systems with Electric Power Systems. IEEE Access 2011, 1–54. [CrossRef]
| Parameter Name | Symbol | Value | Units |
|---|---|---|---|
| Rated voltage of the system | Vnom | 1 | pu |
| System nominal frequency | fnom | 60 | Hz |
| Minimum reference frequency | fmin | 59.4 | Hz |
| Dead-band of the VFPC of the BESS | - | ±0.01 | |
| Rate limit of the reference frequency | - | 0.3 | Per s |
| V-f proportional gain | Kv | 6 | - |
| Maximum limit of d-axis current in the BESS | Id_max | 1 | pu |
| d-axis voltage reference of the BESS | Vd* | 1 | pu |
| q-axis voltage reference of the BESS | Vq* | 0 | pu |
| Sample time of the simulation | Ts | 5 × 10−5 | s |
| np | Pload_0 (kW) | VaBESS (pu) | VaDiesel (pu) | PBESS (kW) | PDiesel (kW) | Pload (kW) | fMTR (Hz) | |
|---|---|---|---|---|---|---|---|---|
| Case 2 | 2 | 418 | 0.944 | 0.926 | 236.1 | 145.9 | 345.6 | 59.68 |
| Case 3 | 1.81 | 418 | 0.927 | 0.910 | 231.8 | 145.9 | 340.8 | 59.58 |
| Case 2* | 2 | 388 | 0.975 | 0.955 | 243.8 | 135.4 | 343.7 | 59.86 |
| Case 4 | 1.56 | 388 | 0.969 | 0.949 | 242.3 | 143.7 | 350 | 59.83 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moon, H.-J.; Kim, Y.J.; Chang, J.W.; Moon, S.-I. Decentralised Active Power Control Strategy for Real-Time Power Balance in an Isolated Microgrid with an Energy Storage System and Diesel Generators. Energies 2019, 12, 511. https://doi.org/10.3390/en12030511
Moon H-J, Kim YJ, Chang JW, Moon S-I. Decentralised Active Power Control Strategy for Real-Time Power Balance in an Isolated Microgrid with an Energy Storage System and Diesel Generators. Energies. 2019; 12(3):511. https://doi.org/10.3390/en12030511
Chicago/Turabian StyleMoon, Hyeon-Jin, Young Jin Kim, Jae Won Chang, and Seung-Il Moon. 2019. "Decentralised Active Power Control Strategy for Real-Time Power Balance in an Isolated Microgrid with an Energy Storage System and Diesel Generators" Energies 12, no. 3: 511. https://doi.org/10.3390/en12030511
APA StyleMoon, H.-J., Kim, Y. J., Chang, J. W., & Moon, S.-I. (2019). Decentralised Active Power Control Strategy for Real-Time Power Balance in an Isolated Microgrid with an Energy Storage System and Diesel Generators. Energies, 12(3), 511. https://doi.org/10.3390/en12030511





