Object-Oriented Usability Indices for Multi-Objective Demand Side Management Using Teaching-Learning Based Optimization
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
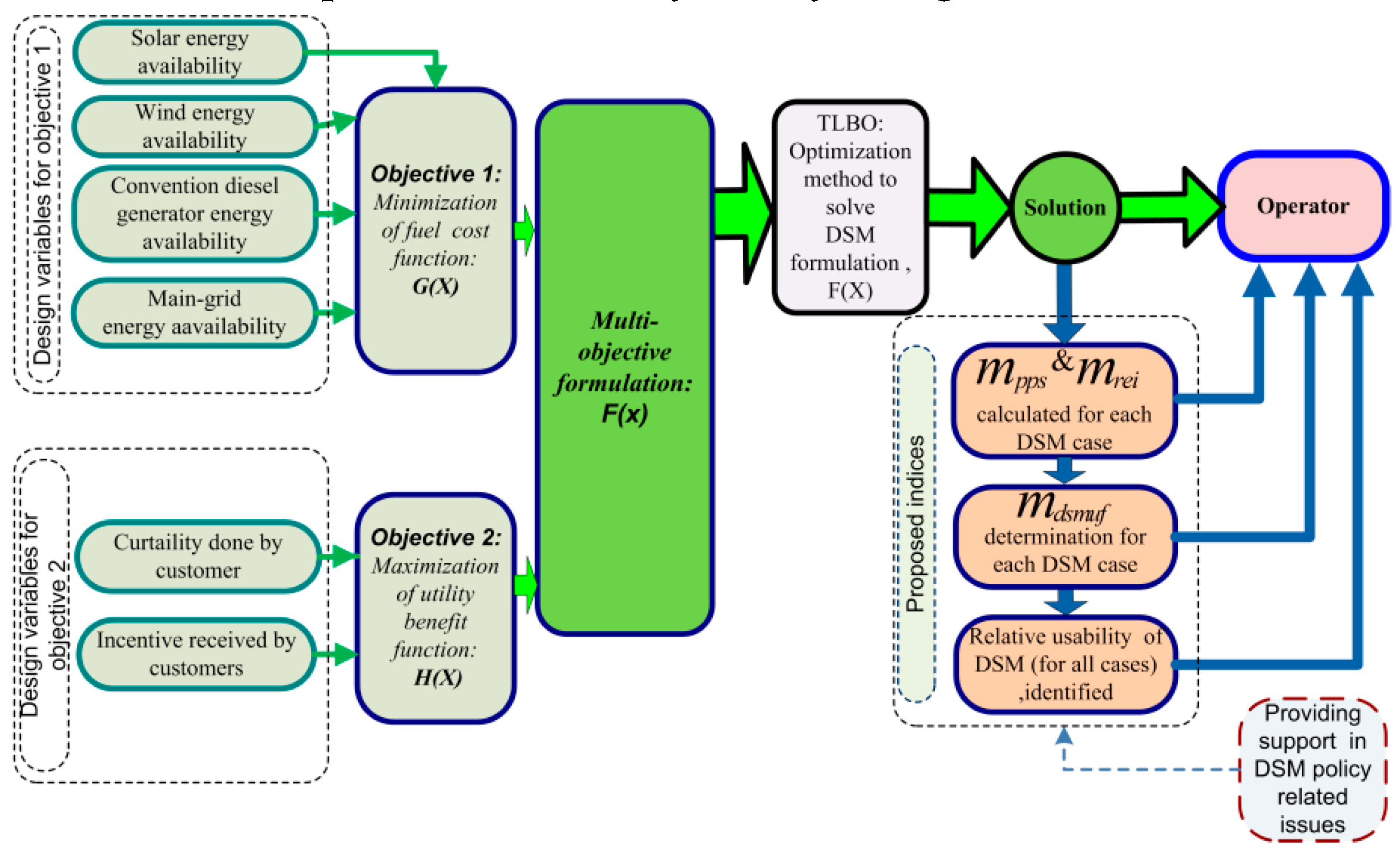
1.3. Contribution and Paper Organization
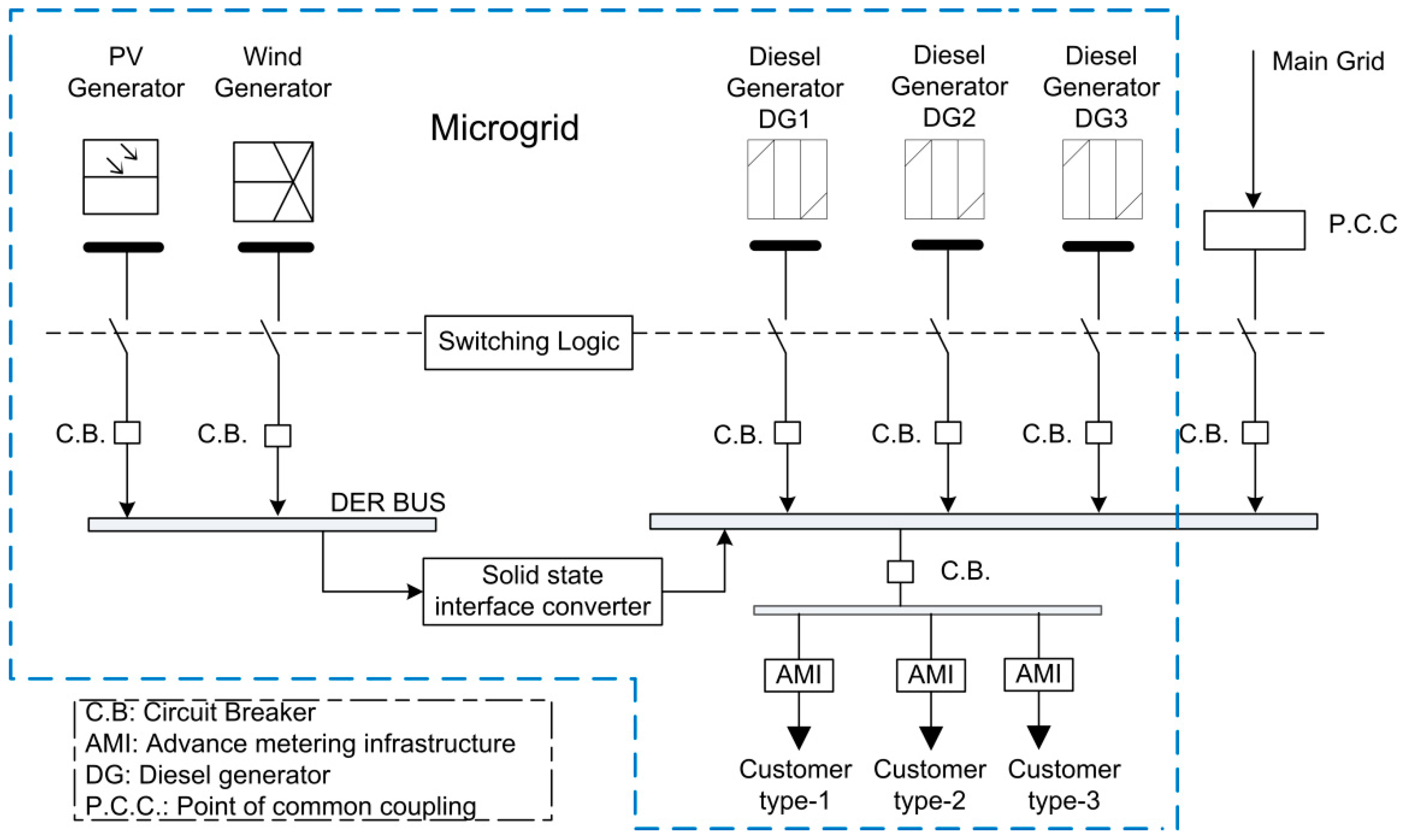
2. Microgrid Modeling
3. Microgrid DSM Problem Formulation
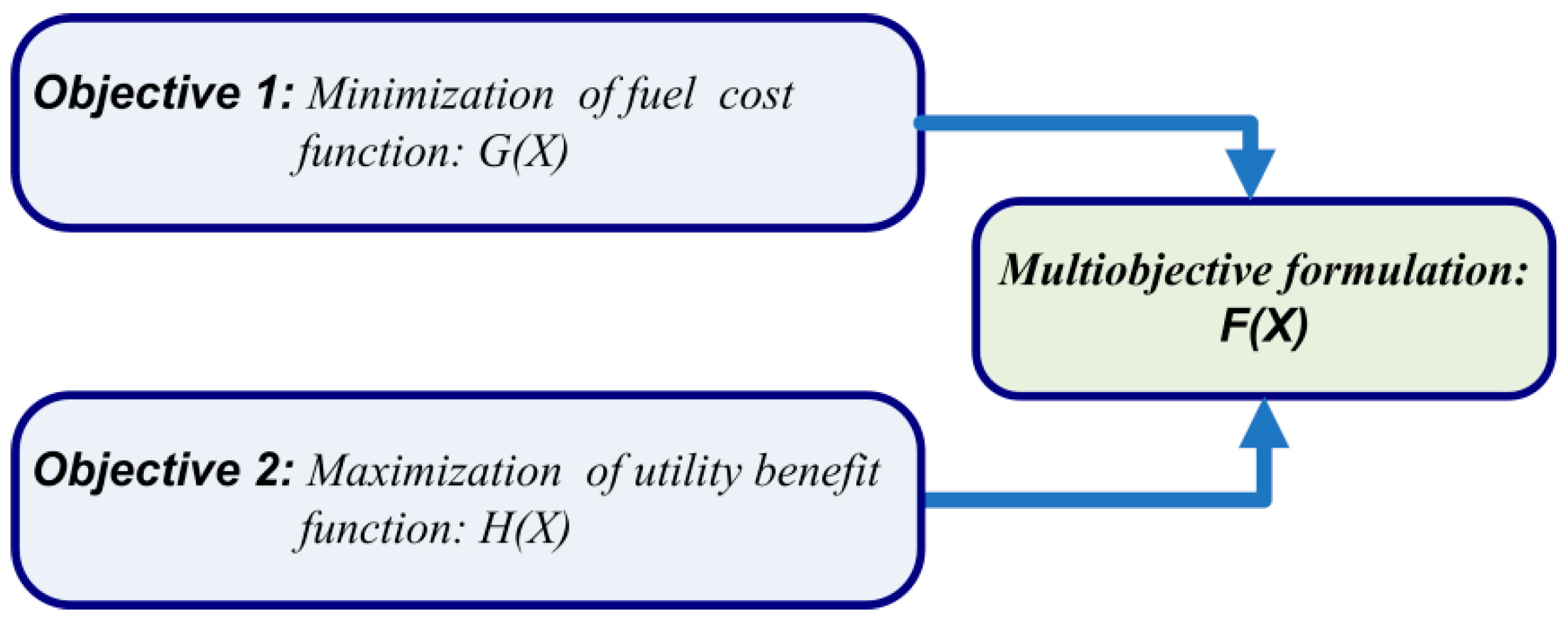
3.1. Objective1: Minimization of the Fuel Cost Function, G(X)
- : Variable to represent conventional generating units. Its value ranges from ;
- : Dispatch interval, in present work, is expanded over T = 24 time horizon.
- G(X): Operating cost function.
- : Total cost at time t to deliver power;
- : Conventional generator, number of units;
- : Fuel cost function for conventional generators.
- : Transferable power cost;
- : Transferable power;
- : Location marginal prices [33];
- : Total number of the conventional generating unit.
- i: Customer number;
- n: Total number of customers;
- : Curtailed power by customer number i, at tth time interval
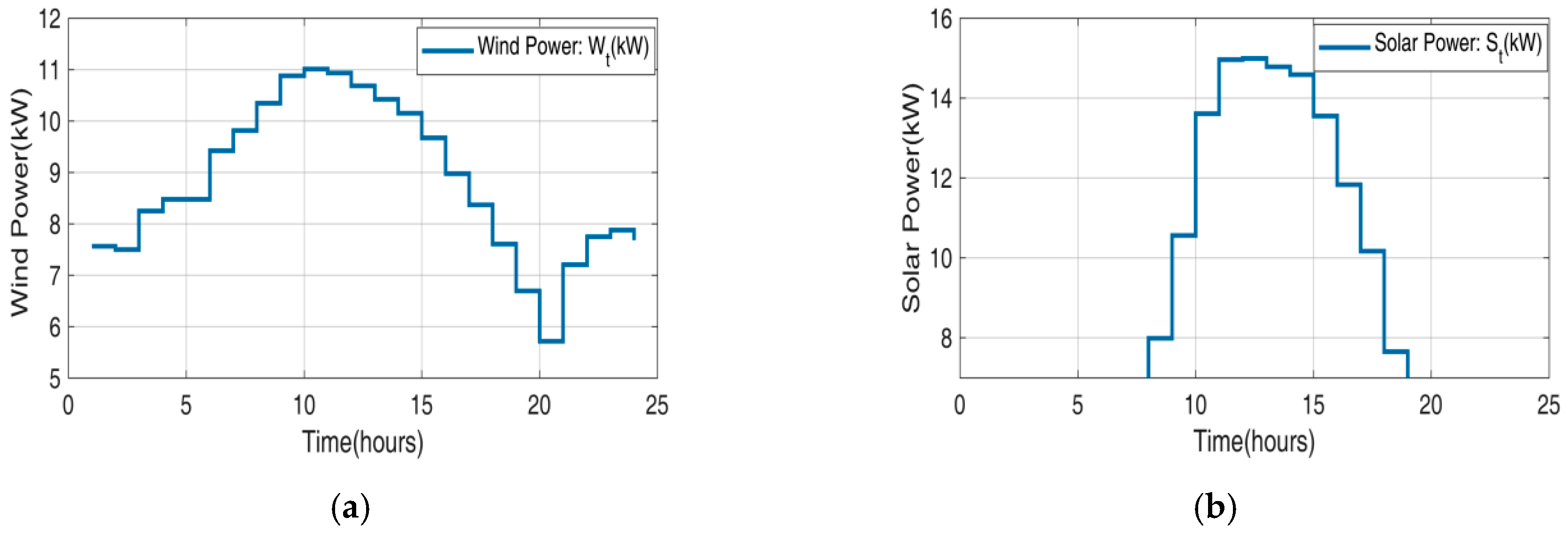
- : Forecast maximum wind power obtainable by available solar energy generators;
- : Forecast maximum solar power obtainable by available wind energy generators;
- : Wind generator power availability (during time t)
- : Solar generator power availability (during time t)
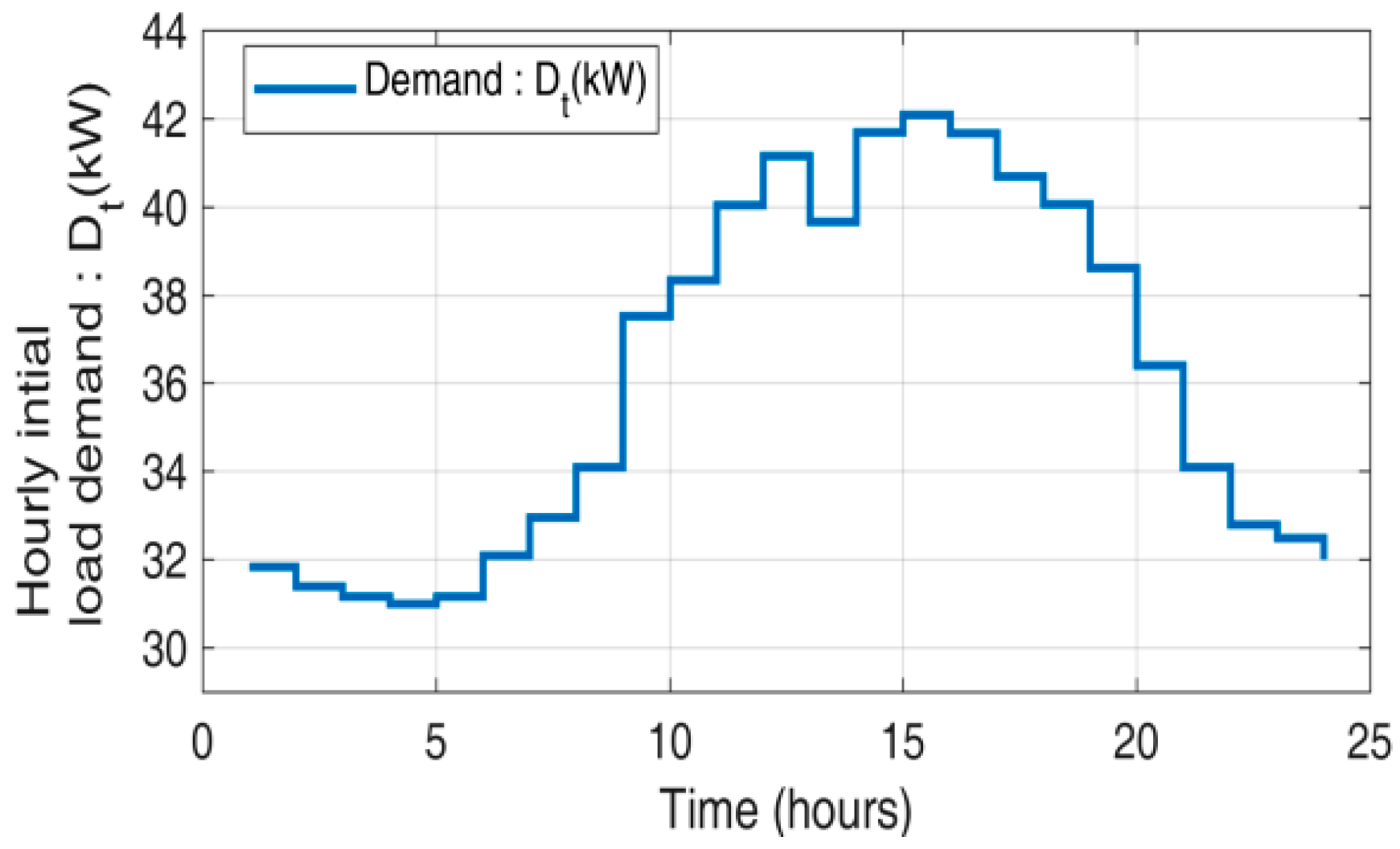
- : Load demand at time t;
- : Denotes maximum allowable exchange between grid and microgrid.
3.2. Objective2: Maximization of Utility Benefit Function, H(X), Using Demand Response
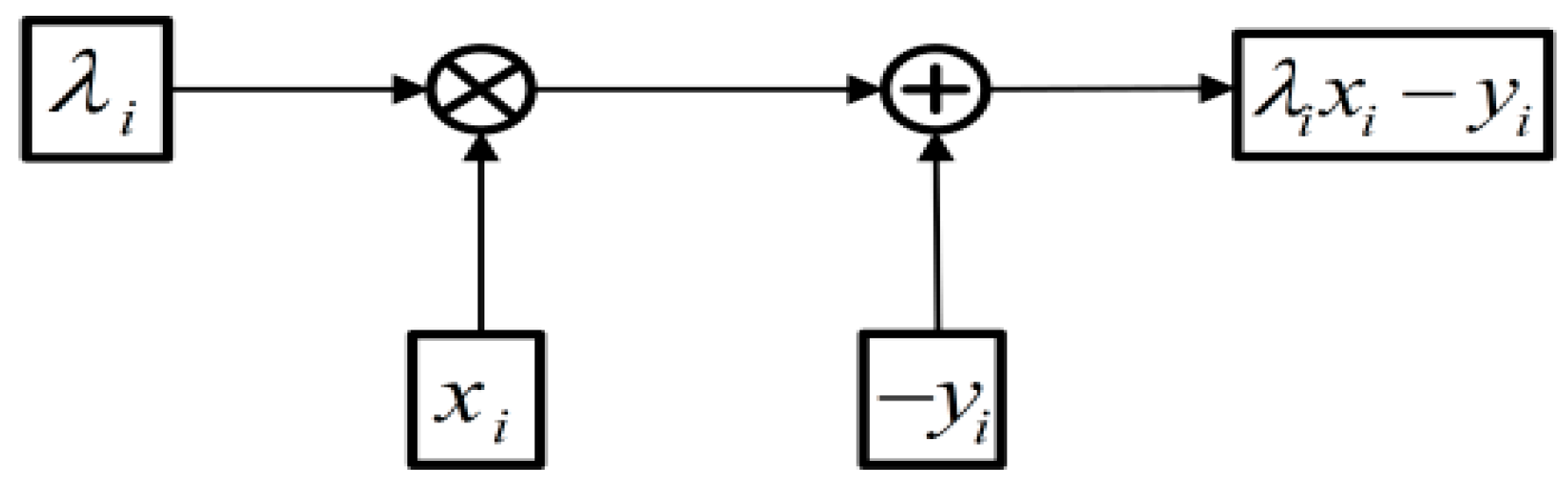
- : Customer benefit in . It must be 0 for user participation.
- : Utility benefit in .
- : Curtailed power by customer in kW;
- y: Monetary compensation the customer receives in $/kWh;
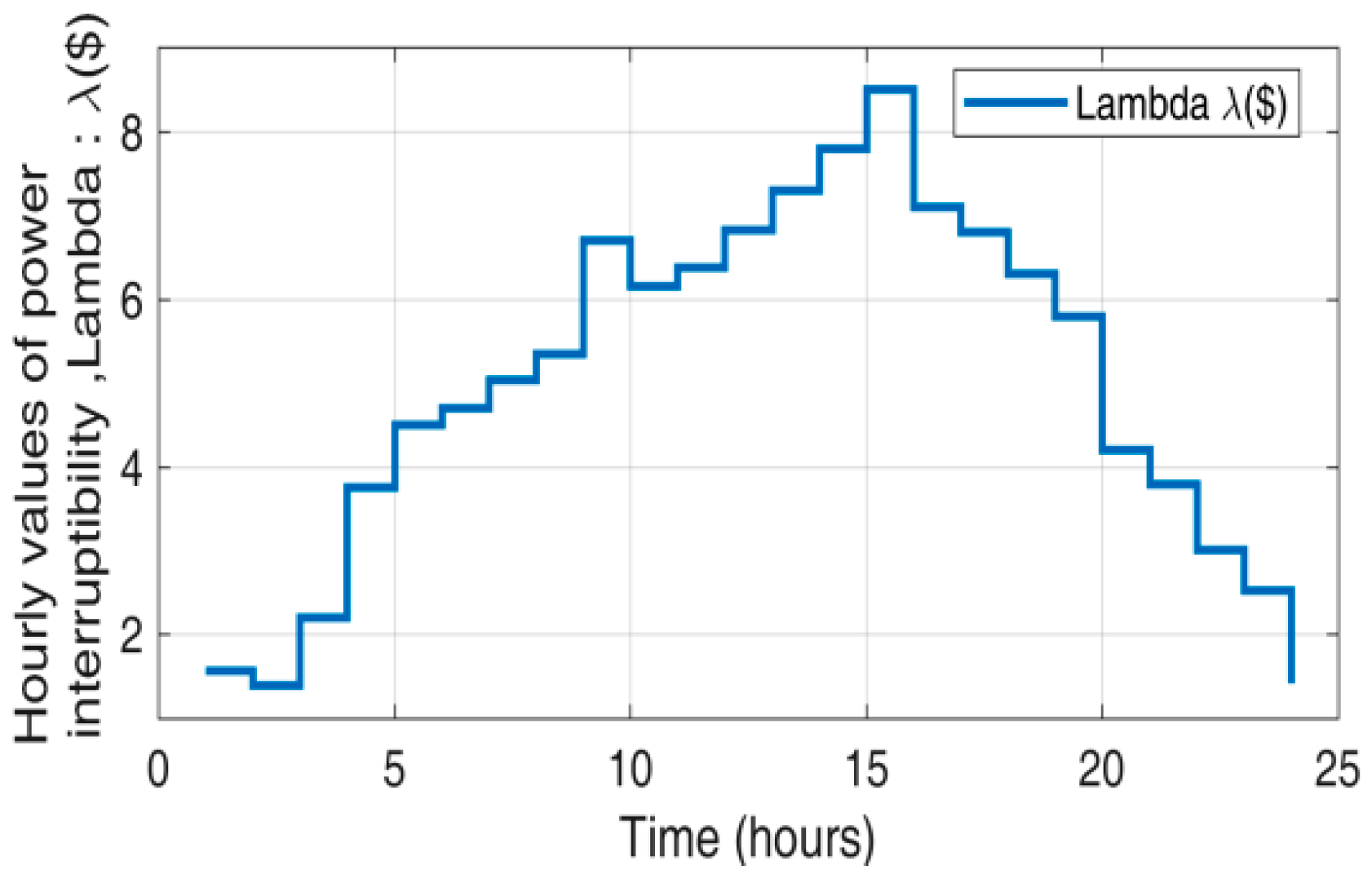
- λ: Cost of power.
3.3. Multi-Objective Formulation
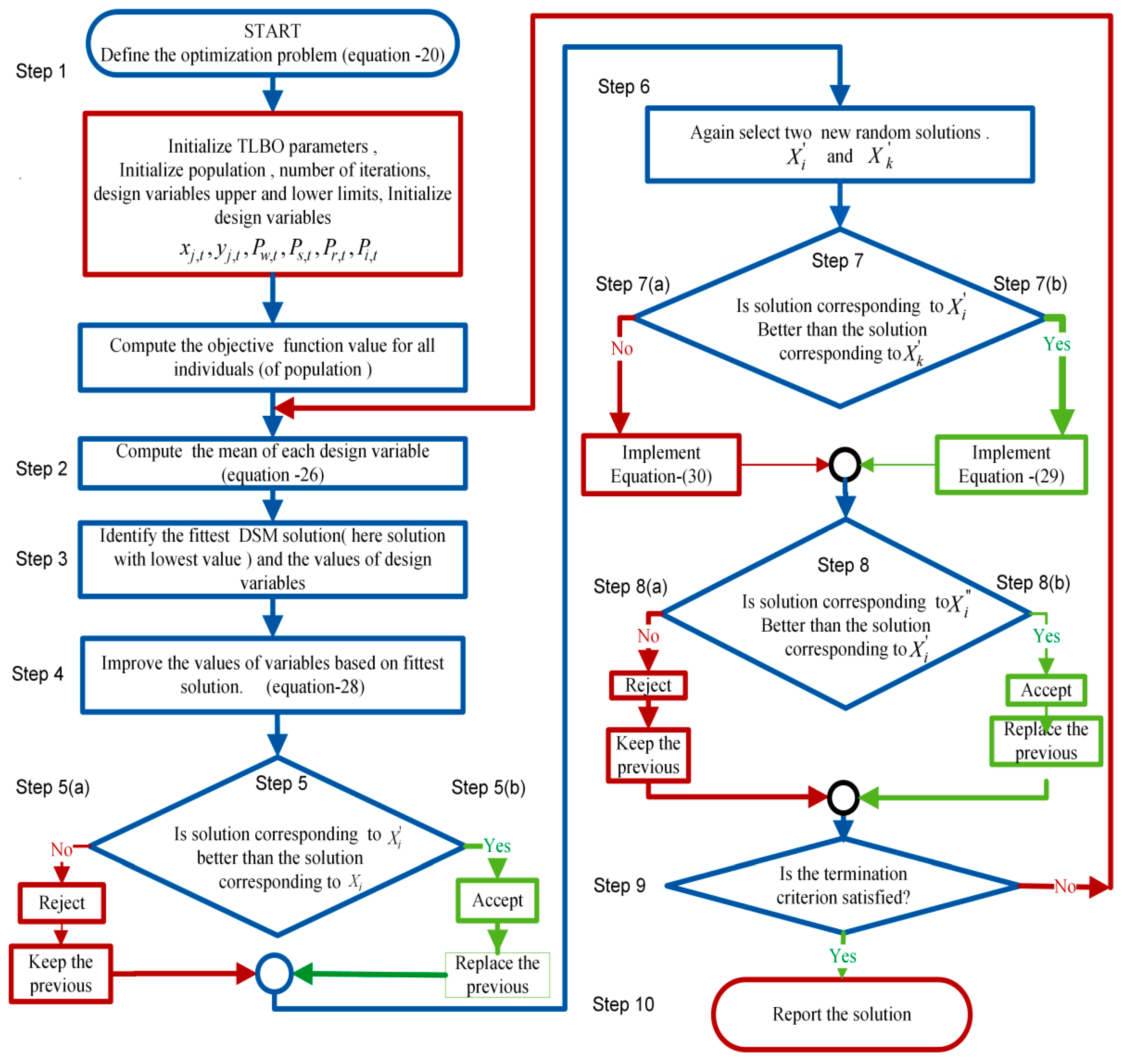
4. Teaching-Learing-Based Optimization (TLBO) Algorithm
- : Result of the best learner in subject j;
- : Random number in the range [0, 1]; and
- : Teaching factor. It decides the value of mean to be changed the value of is selected in random way with equal probability as:
- : A value in the solution,
- : Updated value of . Accept if it gives better value of the function
- : jth design variable. Denotes subject chosen by the learners. ;
- k: kth member of population. Denotes learner. ;
- i: ith iteration, ,
- : Denotes maximum iterations.
TLBO Steps Adopted to Optimize Multi-Objective DSM Function F(X)
5. Object-Oriented Usability Indices (OOUI)
Theoretical Analysis of the Proposed Indices
- t: dispatch interval.
- : load demand to utility when no DSM is applied.
- : maximum load over the time period T when no DSM is applied
- : load demand to utility when DSM is applied.
- : maximum load over the time period T when DSM is applied
- Peak power shaving index greater than one that is .
- Peak power shaving index less than one that is .
- Peak power shaving index equal one that is .
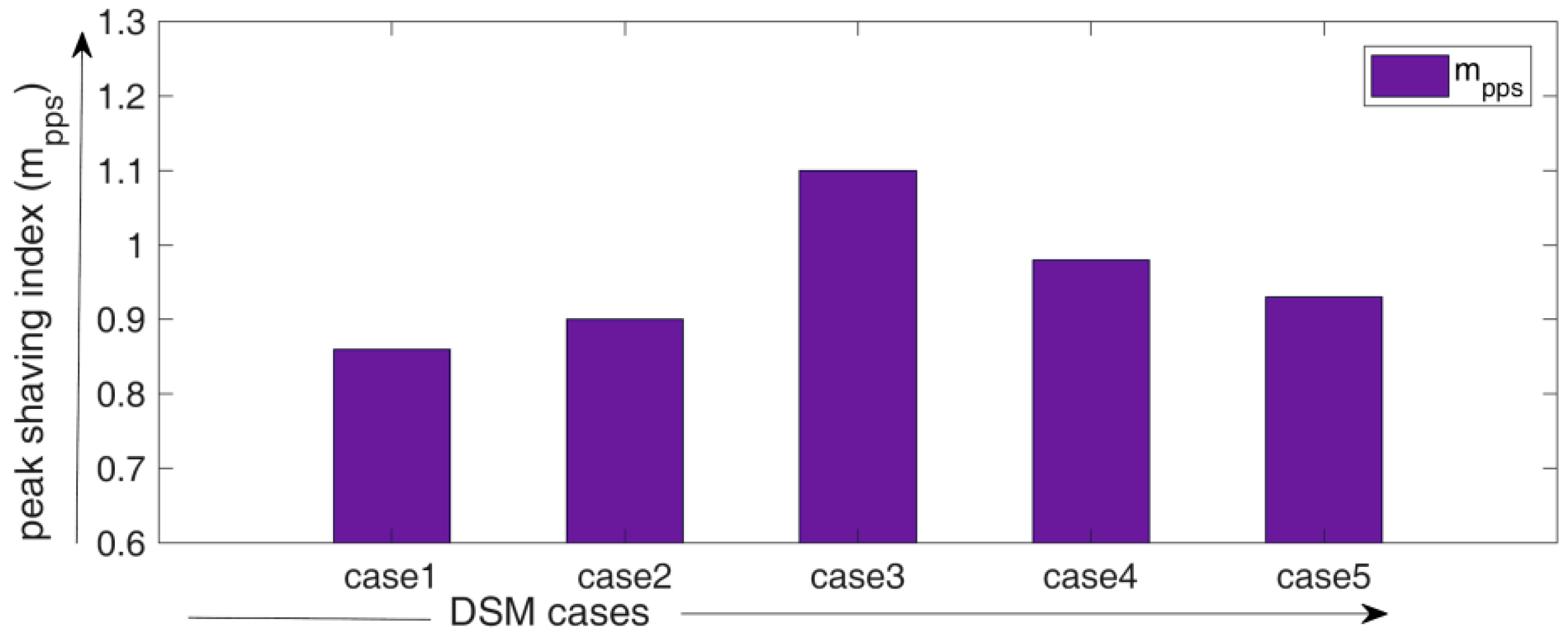
- Comparative result of peak power shaving index obtained for DSM solutions.
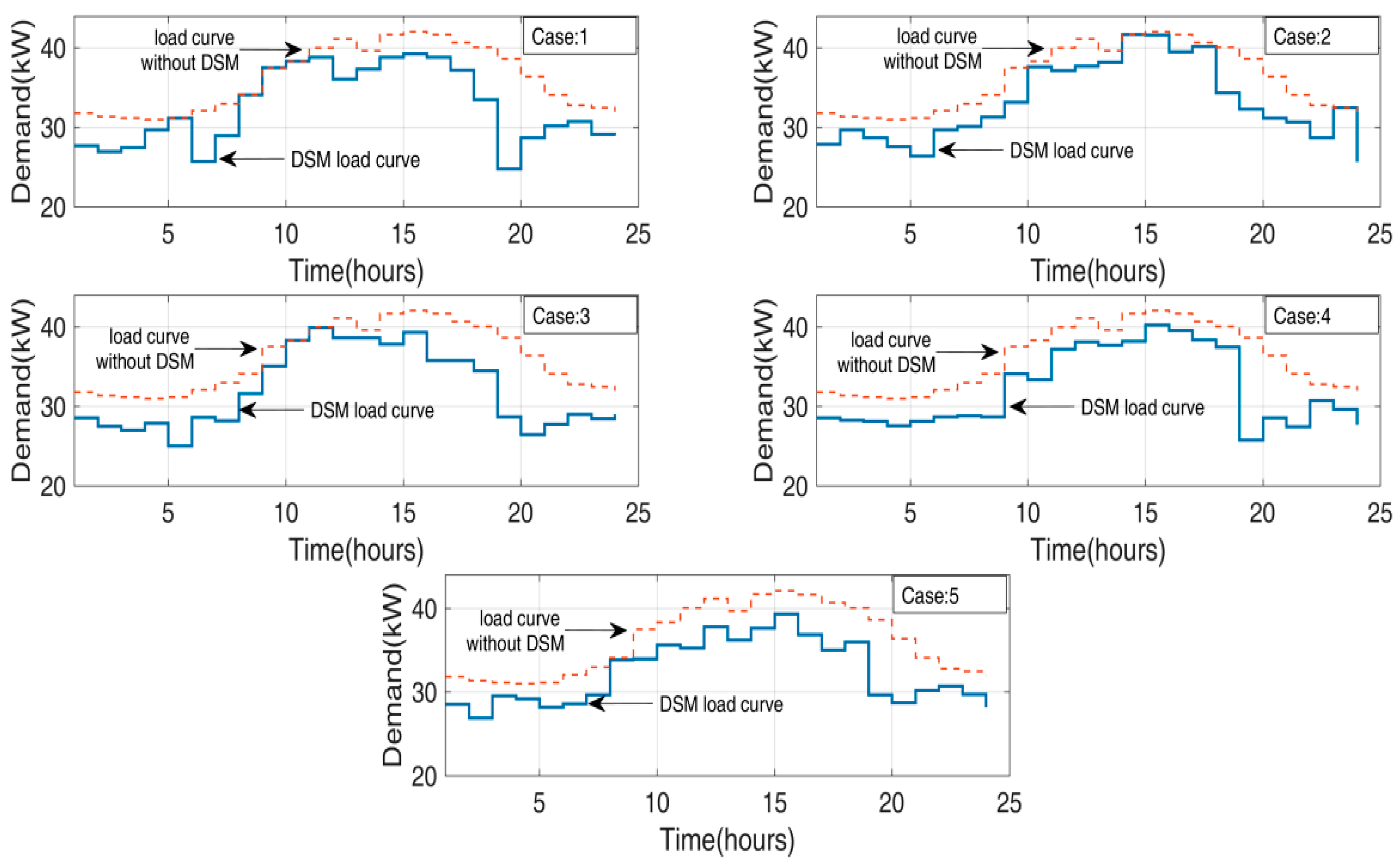
6. Case Studies, Simulation Results, and Discussion
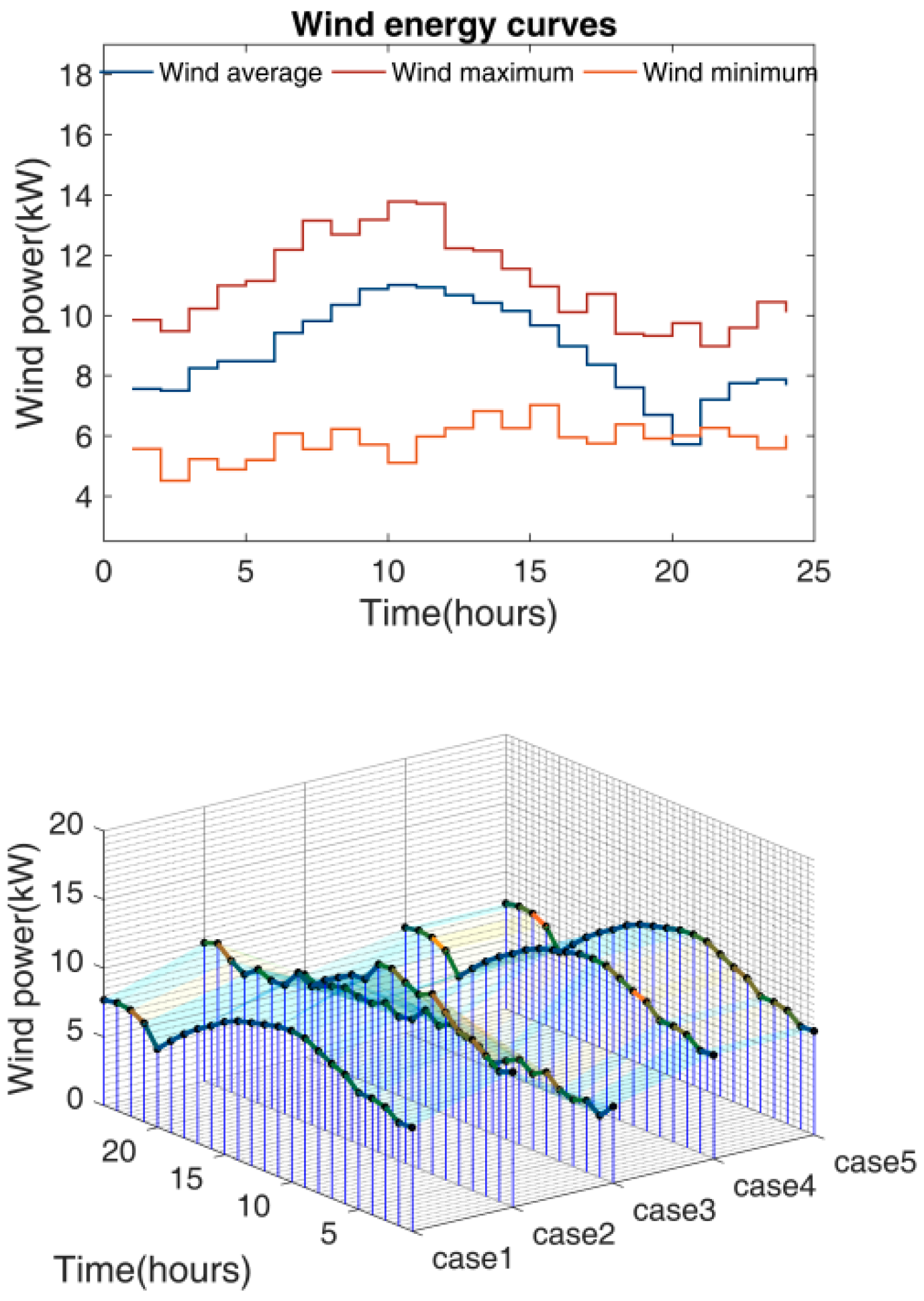
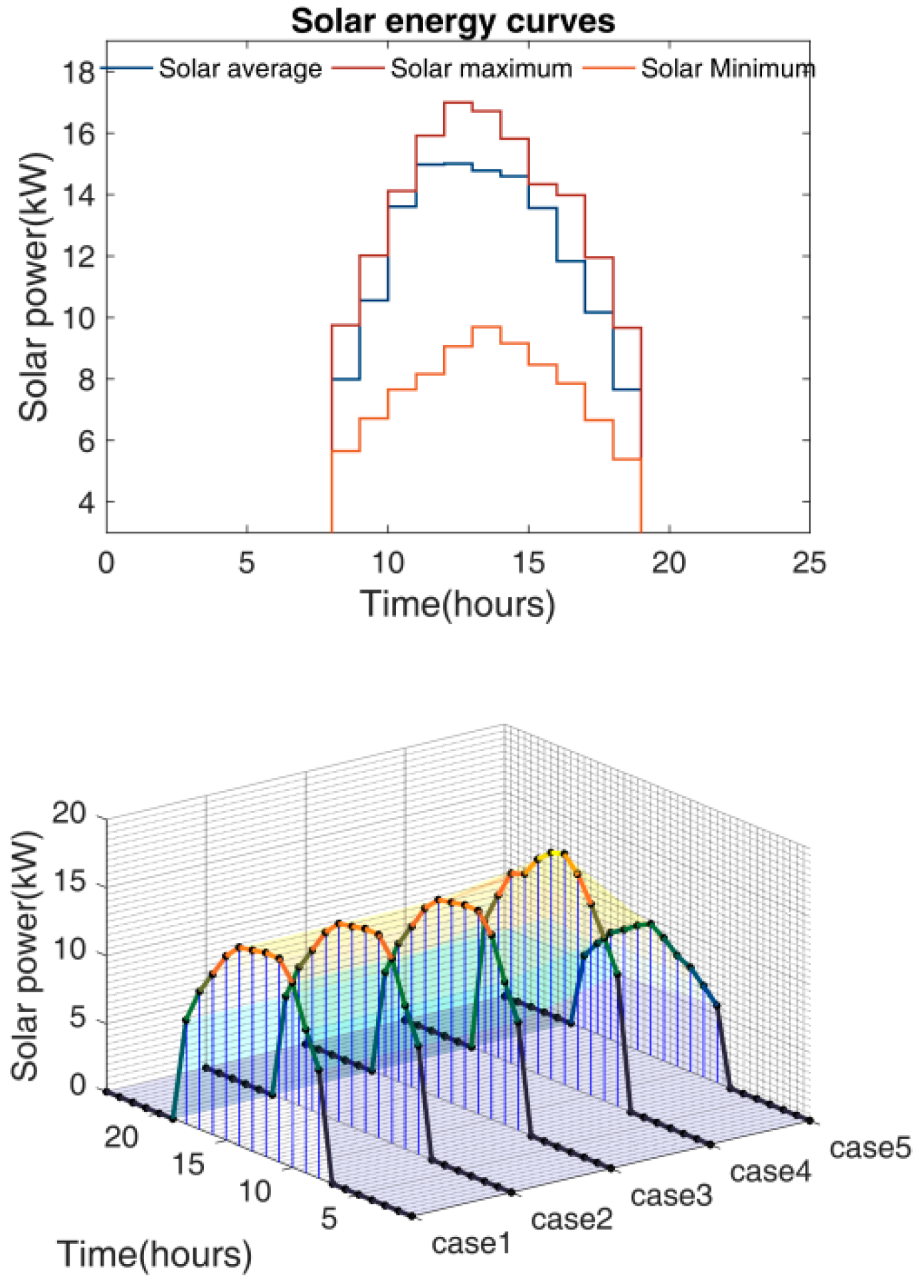
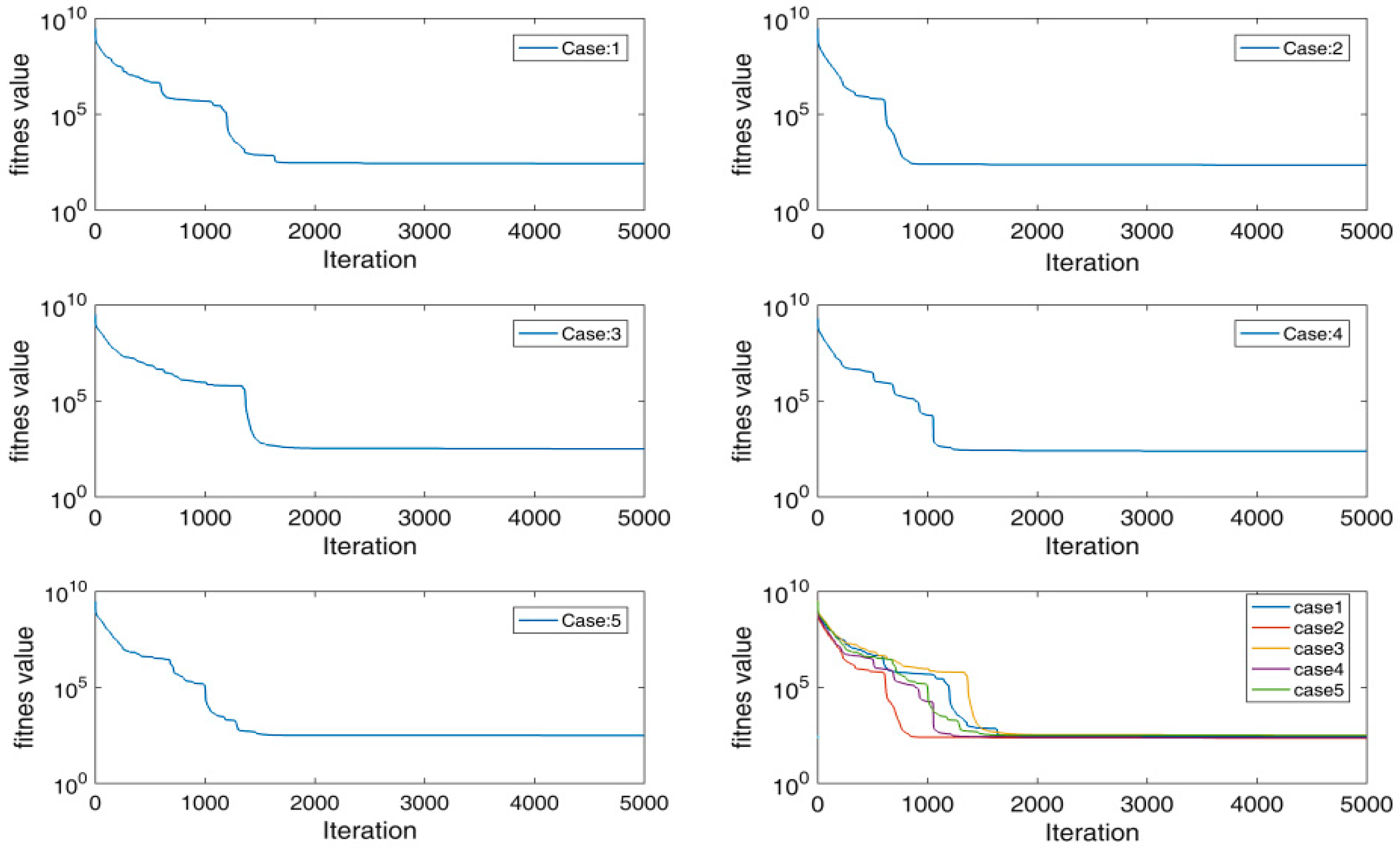
6.1. Case Studies, Simulation Results
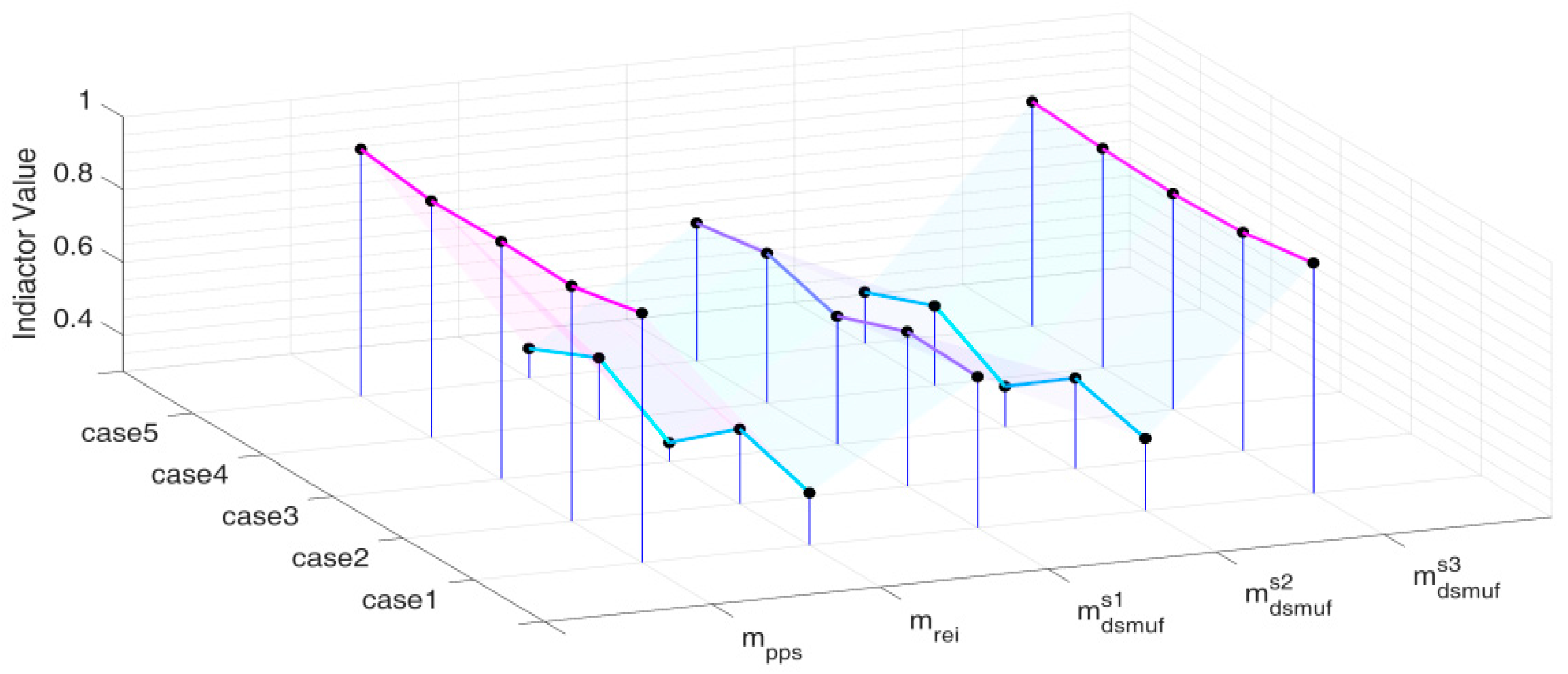
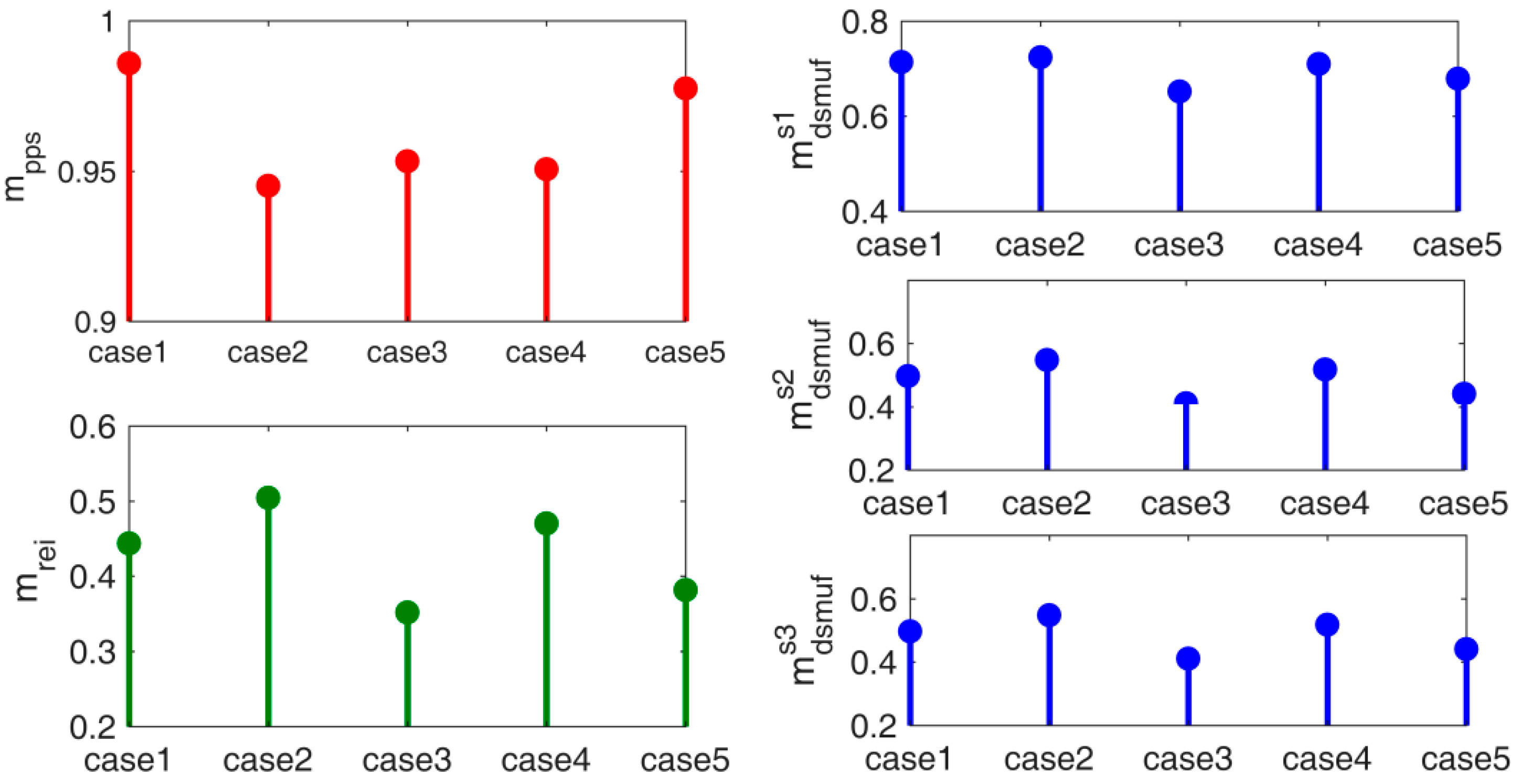
6.2. Calaulation of Proposed Indices
6.3. Discussion of the Results with Comparative Analysis
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jabir, H.J.; Teh, J.; Ishak, D.; Abunima, H. Impacts of Demand-Side Management on Electrical Power Systems: A Review. Energies 2018, 11, 1050. [Google Scholar] [CrossRef]
- Amoasi Acquah, M.; Kodaira, D.; Han, S. Real-Time Demand Side Management Algorithm Using Stochastic Optimization. Energies 2018, 11, 1166. [Google Scholar] [CrossRef]
- Naz, M.; Iqbal, Z.; Javaid, N.; Khan, Z.A.; Abdul, W.; Almogren, A.; Alamri, A. Efficient Power Scheduling in Smart Homes Using Hybrid Grey Wolf Differential Evolution Optimization Technique with Real Time and Critical Peak Pricing Schemes. Energies 2018, 11, 384. [Google Scholar] [CrossRef]
- Jabir, H.J.; Teh, J.; Ishak, D.; Abunima, H. Impact of Demand-Side Management on the Reliability of Generation Systems. Energies 2018, 11, 2155. [Google Scholar] [CrossRef]
- Nguyen, A.-D.; Bui, V.-H.; Hussain, A.; Nguyen, D.-H.; Kim, H.-M. Impact of Demand Response Programs on Optimal Operation of Multi-Microgrid System. Energies 2018, 11, 1452. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, W.; Qi, F.; Wang, L.; Zou, B.; Wen, F.; Xue, Y. Optimal Dispatch of a Virtual Power Plant Considering Demand Response and Carbon Trading. Energies 2018, 11, 1488. [Google Scholar] [CrossRef]
- Al-Alawi, A.; Islam, S.M. Demand side management for remote area power supply systems incorporating solar irradiance model. Renew. Energy 2004, 29, 2027–2036. [Google Scholar] [CrossRef]
- Alham, M.H.; Elshahed, M.; Ibrahim, D.K.; El Zahab, E.E. A dynamic economic emission dispatch considering wind power uncertainty incorporating energy storage system and demand side management. Renew. Energy 2016, 96, 800–811. [Google Scholar] [CrossRef]
- Kallel, R.; Boukettaya, G.; Krichen, L. Demand side management of household appliances in stand-alone hybrid photovoltaic system. Renew. Energy 2015, 81, 123–135. [Google Scholar] [CrossRef]
- Kotur, D.; Đurišić, Ž. Optimal spatial and temporal demand side management in a power system comprising renewable energy sources. Renew. Energy 2017, 108, 533–547. [Google Scholar] [CrossRef]
- Neves, D.; Brito, M.C.; Silva, C.A. Impact of solar and wind forecast uncertainties on demand response of isolated microgrids. Renew. Energy 2016, 87, 1003–1015. [Google Scholar] [CrossRef]
- Nwulu, N.I.; Xia, X. Optimal dispatch for a microgrid incorporating renewable and demand response. Renew. Energy 2017, 101, 16–28. [Google Scholar] [CrossRef]
- Rajanna, S.; Saini, R.P. Employing demand side management for selection of suitable scenario-wise isolated integrated renewal energy models in an Indian remote rural area. Renew. Energy 2016, 99, 1161–1180. [Google Scholar] [CrossRef]
- Fan, S.; Ai, Q.; Piao, L. Hierarchical Energy Management of Microgrids including Storage and Demand Response. Energies 2018, 11, 1111. [Google Scholar] [CrossRef]
- Khodaei, A.; Shahidehpour, M.; Choi, J. Optimal Hourly Scheduling of Community-Aggregated Electricity Consumption. J. Electr. Eng. Technol. 2013, 8. [Google Scholar] [CrossRef]
- Oprea, S.-V.; Bâra, A.; Reveiu, A. Informatics Solution for Energy Efficiency Improvement and Consumption Management of Householders. Energies 2018, 11, 138. [Google Scholar] [CrossRef]
- Cha, H.-J.; Won, D.-J.; Kim, S.-H.; Chung, I.-Y.; Han, B.-M. Multi-Agent System-Based Microgrid Operation Strategy for Demand Response. Energies 2015, 8, 14272–14286. [Google Scholar] [CrossRef]
- Oprea, S.V.; Bâra, A.; Ifrim, G. Flattening the electricity consumption peak and reducing the electricity payment for residential consumers in the context of smart grid by means of shifting optimization algorithm. Comput. Ind. Eng. 2018, 122. [Google Scholar] [CrossRef]
- Lizondo, D.; Rodriguez, S.; Will, A.; Jimenez, V.; Gotay, J. An Artificial Immune Network for Distributed Demand-Side Management in Smart Grids. Inf. Sci. 2018, 438, 32–45. [Google Scholar] [CrossRef]
- Di Santo, K.G.; Di Santo, S.G.; Monaro, R.M.; Saidel, M.A. Active demand side management for households in smart grids using optimization and artificial intelligence. Measurement 2018, 115, 152–161. [Google Scholar] [CrossRef]
- Mellouk, L.; Boulmalf, M.; Aaroud, A.; Zine-Dine, K.; Benhaddou, D. Genetic algorithm to Solve Demand Side Management and Economic Dispatch Problem. Procedia Comput. Sci. 2018, 130, 611–618. [Google Scholar] [CrossRef]
- Ng, K.-H.; Sheblé, G.B. Direct load control-A profit-based load management using linear programming. IEEE Trans. Power Syst. 1998, 13, 688–694. [Google Scholar] [CrossRef]
- Kurucz, C.N.; Brandt, D.; Sim, S. A linear programming model for reducing system peak through customer load control programs. IEEE Trans. Power Syst. 1996, 11, 1817–1824. [Google Scholar] [CrossRef]
- Hsu, Y.Y.; Su, C.C. Dispatch of direct load control using dynamic programming. IEEE Trans. Power Syst. 1991, 6, 1056–1061. [Google Scholar]
- Logenthiran, T.; Srinivasan, D.; Shun, T.Z. Demand Side Management in Smart Grid Using Heuristic Optimization. IEEE Trans. Smart Grid 2012, 3, 1244–1252. [Google Scholar] [CrossRef]
- Samuel, G.G.; Rajan, C.C. Hybrid: Particle Swarm Optimization–Genetic algorithm and Particle Swarm Optimization–Shuffled Frog Leaping Algorithm for long-term generator maintenance scheduling. Int. J. Electr. Power Energy Syst. 2015, 65, 432–442. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput.-Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-Learning-Based Optimization: An optimization method for continuous non-linear large scale problems. Inf. Sci. 2012, 183, 1–15. [Google Scholar] [CrossRef]
- Khan, B.; Singh, P. Selecting a Meta-Heuristic Technique for Smart Micro-Grid Optimization Problem: A Comprehensive Analysis. IEEE Access 2017, 5, 13951–13977. [Google Scholar] [CrossRef]
- Dharme, A.; Ghatol, A. Demand Side Management Quality Index for Assessment of DSM Programs. In Proceedings of the 2006 IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October–2 November 2006; pp. 1718–1721. [Google Scholar] [CrossRef]
- Tazvinga, H.; Zhu, B.; Xia, X. Energy dispatch strategy for a photovoltaic wind diesel battery hybrid power system. Sol. Energy 2014, 108, 412–420. [Google Scholar] [CrossRef]
- Moghaddam, A.A.; Seifi, A.; Niknam, T.; Pahlavani, M.R. Multi-objective operation management of a renewable MG (microgrid) with back-up micro-turbine/fuel cell/battery hybrid power source. Energy 2011, 36, 6490–6507. [Google Scholar] [CrossRef]
- Nwulu, N.I.; Fahrioglu, M. A soft computing approach to projecting Locational marginal price. Neural Comput. Appl. 2012, 22, 1115–1124. [Google Scholar] [CrossRef]
- Albadi, M.H.; El-Saadany, E.F. Demand Response in Electricity Markets: An Overview. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–5. [Google Scholar] [CrossRef]
- FERC. Staff Report. Assessment of Demand Response and Advanced Metering. Available online: www.FERC.gov (accessed on 7 August 2006).
- Fahrioglu, M.; Alvarado, F.L. Designing incentive compatible contracts for effective demand management. IEEE Trans. Power Syst. 2000, 15, 1255–1260. [Google Scholar] [CrossRef]
- Nwulu, N.I.; Fahrioglu, M. A neural network model for optimal demand management contract design. In Proceedings of the 2011 10th International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 8–11 May 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Nwulu, N.I.; Fahrioglu, M. Power system demand management contract design: A comparison between game theory and artificial neural networks. Int. Rev. Model. Simul. 2011, 4, 106–112. [Google Scholar]
- Fahrioglu, M.; Alvarado, F.L. Using utility information to calibrate customer demand management behavior models. IEEE Trans. Power Syst. 2001, 16, 317–322. [Google Scholar] [CrossRef]
- Deb, K. Optimization for Engineering Design: Algorithms and Examples; Prentice Hall of India: New Delhi, India, 2012; ISBN 81-203-0943-X. [Google Scholar]
- Rahman, S.; Rinaldy. An efficient load model for analyzing demand-side management impacts. IEEE Trans. Power Syst. 1993, 8, 1219–1226. [Google Scholar] [CrossRef]
- Khanh, B.Q. Analysis of DSM’s impacts on electric energy loss in distribution system using VPI model. In Proceedings of the Power and Energy Society General Meeting, Detroit, MI, USA, 24–29 July2011; pp. 1–8. [Google Scholar]
- Khelifa, R.F.; Jelassi, K. An energy monitoring and management system based on key performance indicators. In Proceedings of the 2016 IEEE 21st International Conference on Emerging Technologies and Factory Automation (ETFA), Berlin, Germany, 6–9 September 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Behrens, D.; Schoormann, T.; Bräuer, S.; Knackstedt, R. Empowering the selection of demand response methods in smart homes: Development of a decision support framework. Energy Inform. 2018, 1, 53. [Google Scholar] [CrossRef]
| Parameter | Abbreviations | |||
|---|---|---|---|---|
| First fuel cost coefficient | 0.06 | 0.03 | 0.04 | |
| Second fuel cost coefficient ($/kW) | 0.5 | 0.25 | 0.3 | |
| Minimum output power limit (kW) | 0 | 0 | 0 | |
| Maximum output power limit (kW) | 4 | 6 | 9 | |
| Ramp up rate(kW/hour) | 3 | 5 | 8 | |
| Ramp down rate(kW/hour) | 3 | 5 | 8 |
| Description | Abbr. | Customer Type1 | Customer Type2 | Customer Type3 |
|---|---|---|---|---|
| Customer type | 1 | 2 | 3 | |
| 1st coefficient related to customer cost function | 1.079 | 1.378 | 1.847 | |
| 2nd coefficient related to customer cost function | 1.32 | 1.63 | 1.64 | |
| User Type | 0 | 0.45 | 0.9 | |
| Curtail limit | 80 | 85 | 90 |
| Cases | Total Demand (kW) | Avg. Demand (kW) | Peak (kW) | Load Factor | Renewable Energy Availability | |
|---|---|---|---|---|---|---|
| (kW) | (%) | |||||
| case 1 | 780.236 | 32.50983 | 39.25754 | 0.828117 | 346.24 | 34.62 |
| case 2 | 793.9236 | 33.08015 | 41.66873 | 0.793884 | 400.45 | 40.04 |
| case 3 | 767.8551 | 31.99396 | 39.95539 | 0.800742 | 275.03 | 27.50 |
| case 4 | 771.3937 | 32.1414 | 40.25102 | 0.798524 | 362.76 | 36.27 |
| case 5 | 775.5615 | 32.31506 | 39.35548 | 0.821107 | 296.01 | 29.60 |
| Cases | |||||||
|---|---|---|---|---|---|---|---|
| Case 1 | Average | Average | 0.986 | 0.444 | 0.715 | 0.498 | 0.932 |
| Case 2 | Maximum | Average | 0.945 | 0.504 | 0.725 | 0.548 | 0.901 |
| Case 3 | Minimum | Average | 0.953 | 0.358 | 0.655 | 0.418 | 0.894 |
| Case 4 | Average | Maximum | 0.951 | 0.470 | 0.711 | 0.518 | 0.903 |
| Case 5 | Average | Minimum | 0.978 | 0.382 | 0.680 | 0.441 | 0.918 |
| Rank | Criteria for Ranking DSM | ||||
|---|---|---|---|---|---|
| 1 | Case 1 | Case 2 | Case 2 | Case 2 | Case 1 |
| 2 | Case 5 | Case 4 | Case 1 | Case 4 | Case 5 |
| 3 | Case 3 | Case 1 | Case 4 | Case 1 | Case 4 |
| 4 | Case 4 | Case 5 | Case 5 | Case 5 | Case 2 |
| 5 | Case 2 | Case 3 | Case 3 | Case 3 | Case 3 |
| S.N. | Point of Comparison | Proposed | Dharme et al. [30] Year: 2006 | Rahman et al. [41] Year: 1993 | Khanh et al. [42] Year: 2011 | Raihab et al. [43] Year: 2016 | Dennis et al. [44] Year: 2018 |
|---|---|---|---|---|---|---|---|
| 1 | Whether system under study is grid-tied microgrid | Yes | No | No | No | Yes | Yes |
| 2 | DSM Formulation | Multi-objective | Single objective | Single objective | Single objective | Single objective | Single objective |
| 3 | Optimization performed | Yes | No | Yes | No | No | Yes |
| 4 | Optimization method/solution strategies used | TLBO | No | Iterative | No | No | Greedy and multi-agent-system-based |
| 5 | Attributes for decision | OOUI | Index-based | VPI model-based | VPI model-based | Indicator-based | a decision support framework |
| 6 | Any proposed Indices | Yes | Yes | No | No | Yes | No |
| 7 | Any index for peak shaving | Yes | No | No | No | No | No |
| 8 | Any Index for renewable energy | Yes | No | No | No | No | No |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, M.; Jha, R.C. Object-Oriented Usability Indices for Multi-Objective Demand Side Management Using Teaching-Learning Based Optimization. Energies 2019, 12, 370. https://doi.org/10.3390/en12030370
Singh M, Jha RC. Object-Oriented Usability Indices for Multi-Objective Demand Side Management Using Teaching-Learning Based Optimization. Energies. 2019; 12(3):370. https://doi.org/10.3390/en12030370
Chicago/Turabian StyleSingh, Mayank, and Rakesh Chandra Jha. 2019. "Object-Oriented Usability Indices for Multi-Objective Demand Side Management Using Teaching-Learning Based Optimization" Energies 12, no. 3: 370. https://doi.org/10.3390/en12030370
APA StyleSingh, M., & Jha, R. C. (2019). Object-Oriented Usability Indices for Multi-Objective Demand Side Management Using Teaching-Learning Based Optimization. Energies, 12(3), 370. https://doi.org/10.3390/en12030370




