For a comparative analysis, six liquefaction processes were simulated with and without integration of cold storage under similar conditions. Results from energetic, exergetic, economic and exergoeconomic analyses were used to identify the most cost-effective liquefaction process for CES with cold storage.
2.1. Design and Simulation
Aspen Plus
® (Version 9, Aspen Technology Inc., Bedford, MA, USA) was chosen as a suitable software for process simulation. With the aid of the simulation software, all mass and energy balances are fulfilled and the specific enthalpy and entropy values of all streams and substances are calculated. The Peng-Robinson equation of state was employed and the simulation was performed under steady-state conditions. Fortran routines are integrated to calculate exergy values for the exergetic analysis. Six liquefaction processes were simulated: the simple Linde, the precooled Linde, the dual pressure Linde, the simple Claude, the Kapitza and the Heylandt process. At first, the liquefaction processes were manually optimized and later modified to accommodate the cold storage. The assumptions made in simulation are given in
Table 2.
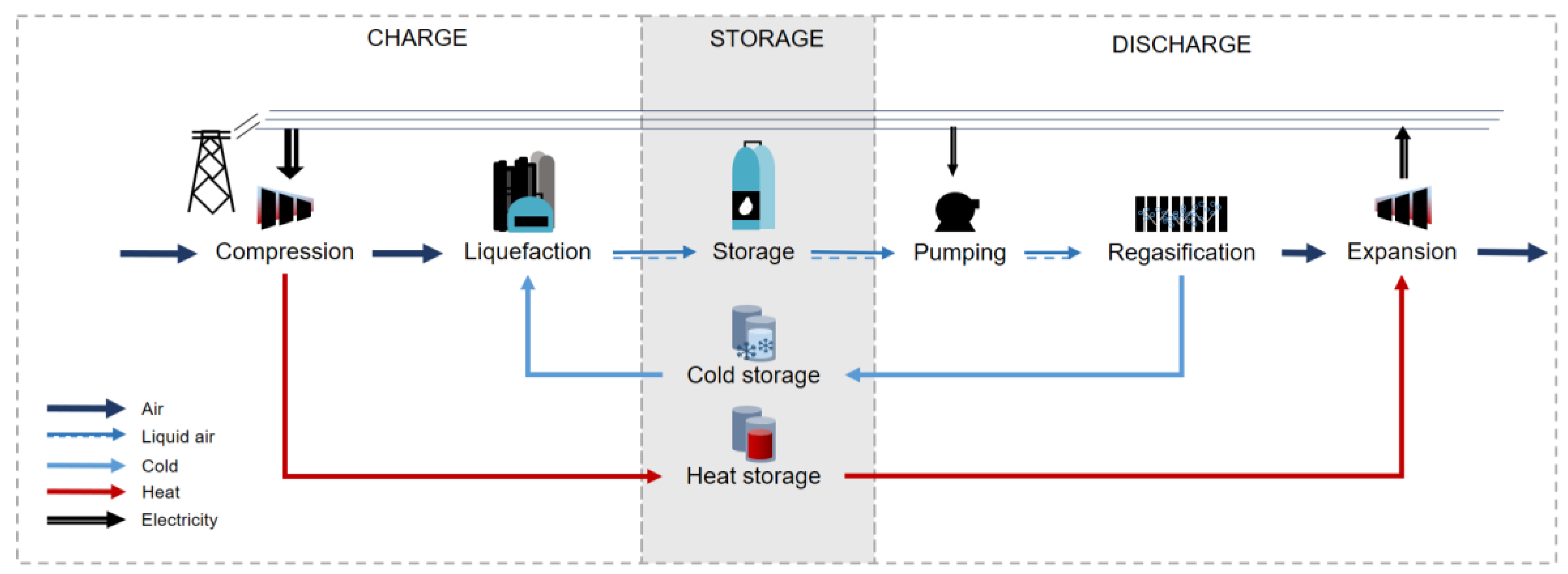
The overall system configuration is shown in
Figure 2. The pretreated air enters the analyzed system at 15 °C, 1.013 bar and a molar composition of 79% N
2 and 21% O
2 (a1). The compression block is the same for all systems. The air exits the last intercooler of the three-stage compression at a temperature of 25 °C and a pressure of
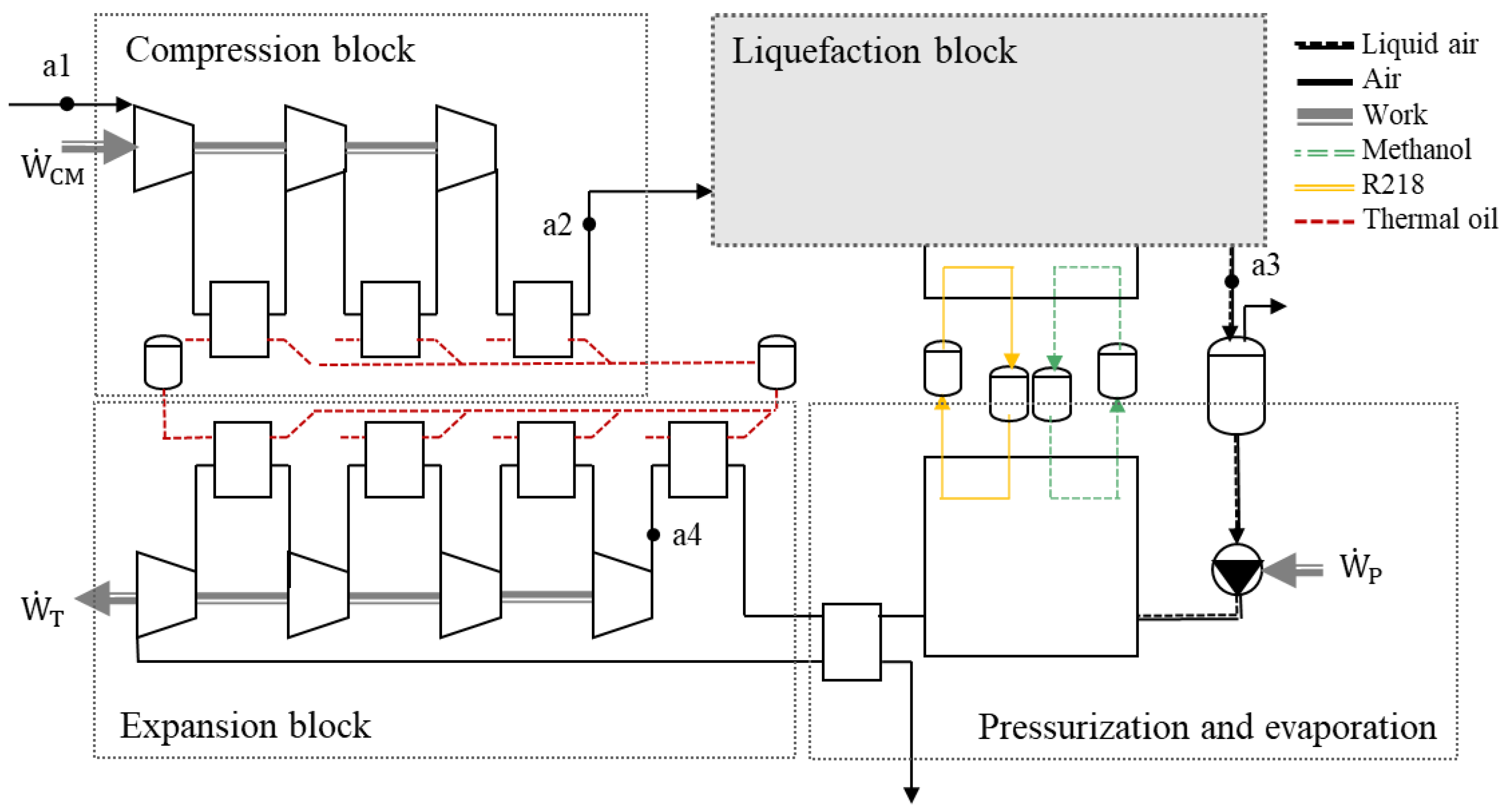
pmax,CM of 200 bar (a2). The largest part of the thermal energy increase during compression is recovered in a heat storage. The heat storage is realized with pressurized water tanks (5 bar, 205 °C). The design of the liquefaction block is different for each system. Two types of liquefaction processes can be distinguished: Linde-based (
Figure 3) and Claude-based (
Figure 4) liquefaction processes. The liquefied air exits the flasher and is stored at a temperature of −192 °C and slightly elevated pressure 1.3 bar. The liquid is stored in an insulated storage tank with boil-off losses of 0.2 %
Vol.
During discharge, the liquid air is pressurized to 150 bar, evaporated in heat exchange to the cold storage media, superheated ( = 195 °C) and fed to the four-stage expander with reheat. The specific power output of the discharge unit is constant for all systems ( = 470 kJ/kg of liquid air).
The assumed method of cold storage uses two fluid tanks and two circulating working fluids that recover the high-grade and low-grade cold rejected in the evaporation process. Reviewing a number of refrigerants,
R218 and
methanol are shown to be advantageous with respect to toxicity, flammability, boiling and freezing temperatures [
9]. The cold in the temperature interval −180 to −61 °C is recovered by
R218, while the cold at higher temperatures (−19 to −59 °C) is captured and stored using
methanol. The amount of cold recovered is determined by the amount of air liquefied in the liquefaction process. The mass flow rates of the cold storage media are therefore determined by a ratio of the mass flow rate of the liquefied air
:
The ratio is adjusted to the optimal heat transfer between the evaporating liquid air and the cold storage media. Thermal losses in the cold storage were accounted for and are equivalent to 4 K/cycle.
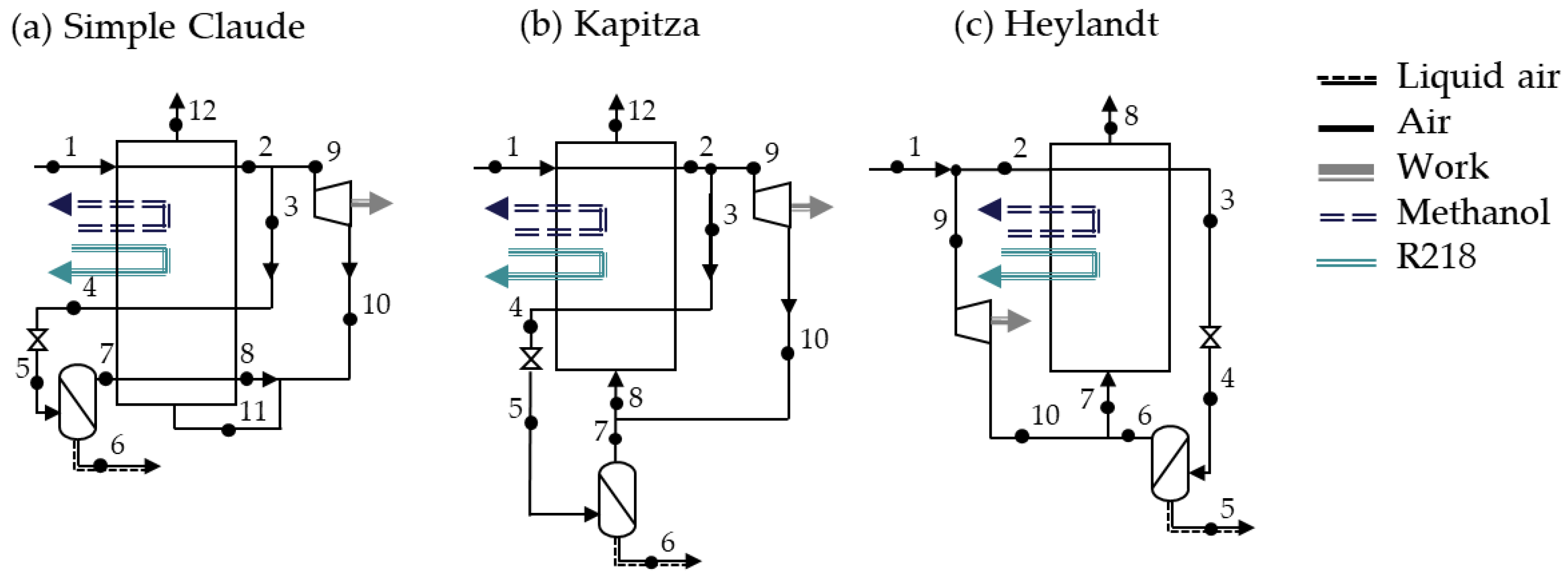
The liquefaction processes are shown in
Figure 3 and
Figure 4. A detailed description of the liquefaction processes and the fundamental concept can be found in fundamental publications e.g., [
23]. The stream values (mass flow
, temperature
T and pressure
p) can be found in
Table 3 and
Table 4.
The Linde-Hampson process,
Figure 3a, is the most straightforward of all liquefaction processes. The process consists of only four sets of components: the compressor(s), the main heat exchanger (MHE), the throttling valve and the flash tank. After compression, the temperature of the air is reduced (below −100 ℃) in the MHE. The low-temperature high-pressure air is throttled reducing the temperature close to the dew point resulting in partial condensation. In the flash tank, the liquid air is separated and stored. The gaseous air is supplied back to the MHE to precool the compressed air. The efficiency of the simple Linde-Hampson process strongly depends on the temperature of the high-pressure gas at the inlet of the MHE.
The precooled Linde-Hampson process, shown in
Figure 3b, intends to achieve a better performance and a higher liquid yield by lowering the temperature of the air with the addition of a compression refrigeration process. Working fluids such as ammonia, carbon dioxide or Freon compounds are commonly used for the secondary refrigeration cycle.
In the dual-pressure Linde process (
Figure 3c) the heat transfer in the MHE is improved by introducing a second pressure level. The air enters the liquefaction process at an intermediate-pressure (1). Together with the recycled stream, the pressure of the air is elevated further to the high-pressure level (3). The gas is cooled and throttled to the intermediate-pressure level (5). The gaseous and the liquid air are separated in the intermediate-pressure flash tank. The gaseous part is fed back to the MHE to precool the entering air stream (3) to (4) and is mixed to the entering intermediate-pressure air stream (1). The liquefied air is fed to the second pressure-stage. This modification reduces the specific work required to liquefy the air at the expense of the share of air liquefied.
The Claude process and its modifications are the most commonly employed process in commercial air liquefaction plants, as its efficiency is higher than that of the Linde process [
23]. In the Claude process the cooling of compressed air is provided by a cold recycle stream—a part of the pressurized air that underwent an isentropic expansion in cold expanders [
6]. The application of a cold expander avoids part of the exergy destruction in the throttling process and reduces the required power for liquefaction by the power output of the expander (
). The stream exiting the expander (
) is used to cool the air stream entering the MHE. The expander does not replace the throttling valve before the flash tank.
The Kapitza process is analogous to the Claude process but with the difference that the third partition of the MHE (or low-temperature heat exchanger) is eliminated. In other words, while using a multi-stream heat exchanger, stream 7 is not fed to the MHE before mixing. Streams 7 and 10 tend to have only a small temperature difference, which is why the difference in heat exchanger area and performance is little. The Heyland process is also adopted from the Claude process. Nevertheless, it can also be seen as a variation of the precooled Linde-Hampson process using air as a refrigerant. The precooling process—the splitting of the stream before entering the MHE—improves the heat transfer process in the MHE [
23].
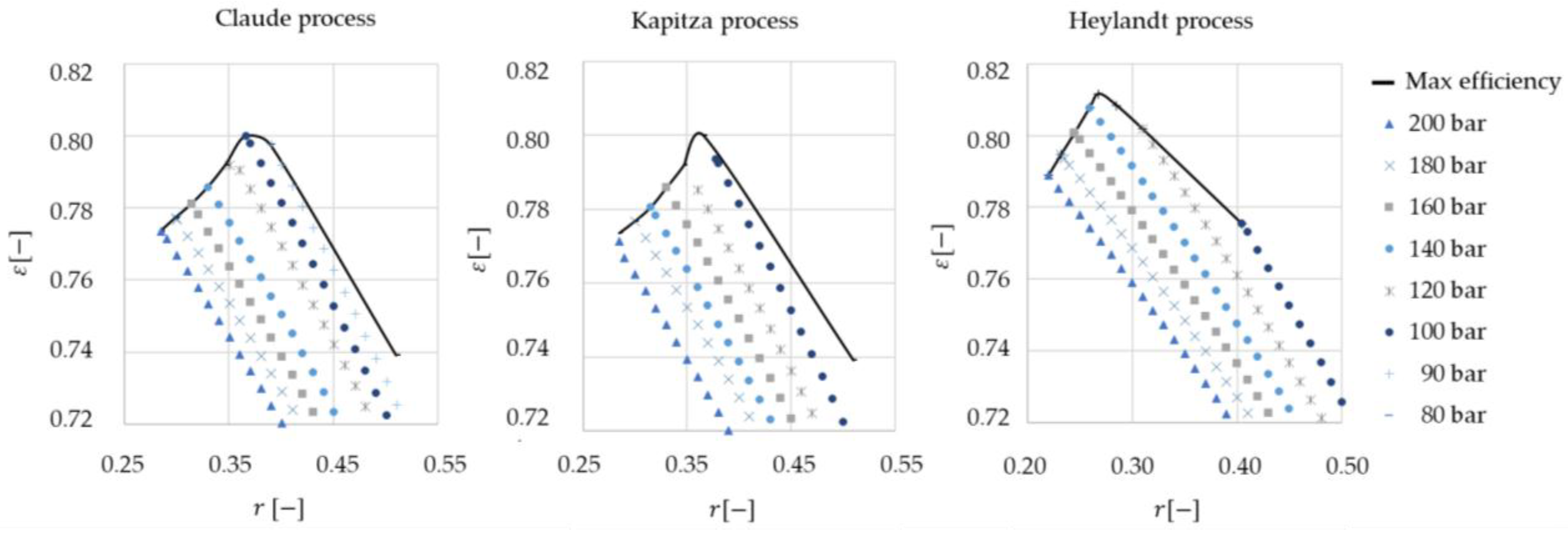
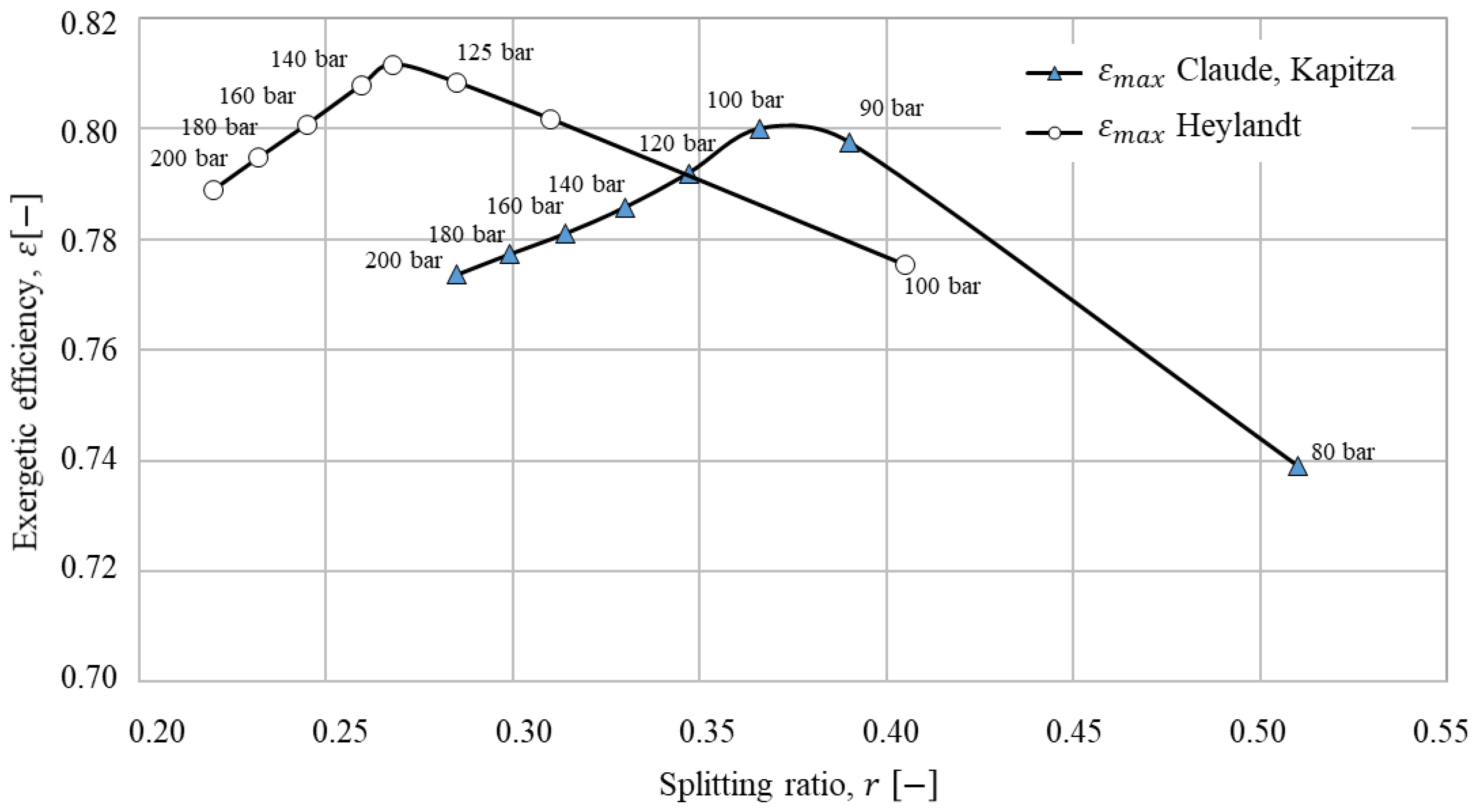
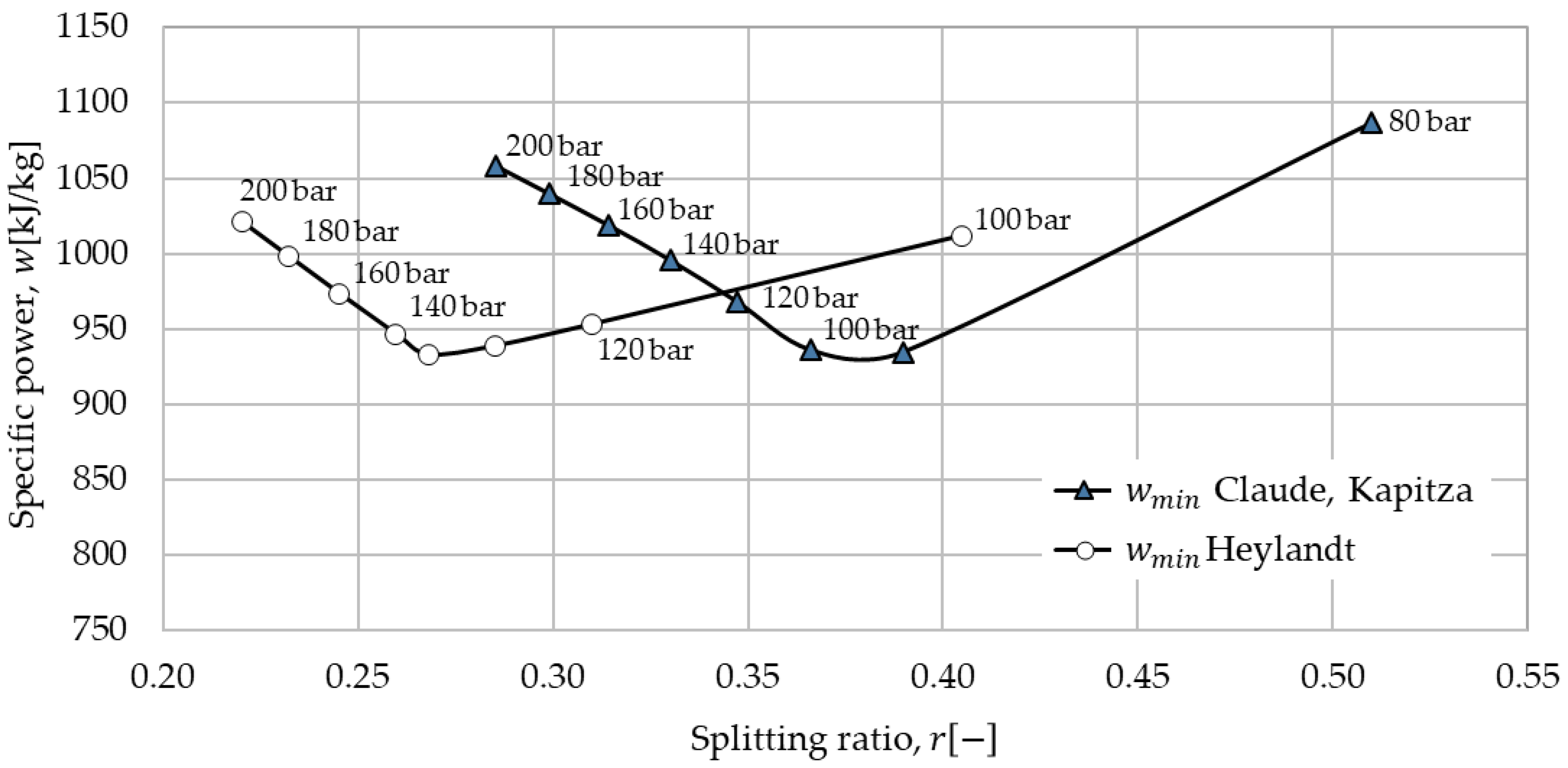
The performance of the Claude-based processes is dependent on the splitting ratio
. The splitting ratio is defined as the mass flow through the expander
over the mass flow through the last compression step
:
The Kapitza process dates back to 1939 when the inventor suggested the use of centrifugal expansion turbines in the Claude process [
10]. Most modern liquefiers utilize expansion turbines proposed by Kapitza [
10,
24] and most high-pressure air liquefaction plants operate with the Heylandt process. Highview Power Storage Ltd. base their charging unit on the Claude process relying on the maturity of the process and the trouble-free scale-up [
25]. The pilot plant operates with a Claude-based liquefaction process similar to the Kapitza configuration [
26]. The operation pressures for the different liquefaction processes differ [
23]. For a better comparison, the liquefaction pressure is kept to 200 bar [
23] first and later varied in sensitivity analysis.
2.2. Energetic and Exergetic Analyses
The six liquefaction processes were compared with and without cold storage in energetic and exergetic analyses at the system level. For the three most efficient processes, sensitivity analyses and exergetic analyses at the component level were further undertaken. The exergetic analysis is adopted from [
27]. The exergetic efficiency
, the liquid yield
and the specific power requirement
w of the systems were used as a basis for comparing the process’ performance with and without cold recovery. The parameters are defined below:
The general definition of the exergetic efficiency
is the ratio of the exergy of the product
and the exergy of the fuel
. The fuel supplied to the liquefaction system is the charging power
and the exergy of the low-temperature exergy supplied by the cold storage
:
(or
denote the thermodynamic mean temperatures at which the low-temperature energy (or the heat) is supplied. Both the exergy of the liquefied air
and the exergy of the heat supplied to the heat storage
are products of the liquefaction process:
The definitions of fuel and product for CES system components can be found in [
9]. As the systems partially operate below the ambient temperature, the physical exergy is split into its mechanical and thermal parts, according to [
28].
The liquefaction processes with the best performance with cold storage were identified (200 bar) and a sensitivity analysis was performed. In sensitivity analyses the splitting ratio and liquefaction pressure were varied. For the optimal liquefaction pressure and splitting ratio, the three systems were compared using economic and exergoeconomic analyses.
The round-trip efficiency (RTE) of the systems was calculated as base for comparison. The RTE is defined as the ratio between the electricity charged and the electricity discharged:
In contrast to evaluating the charging system only, for the overall system the charging duration and the discharge duration need to be accounted for. Reason for this is that the charge-to-discharge ratio () may be unequal to one. For calculation of the RTE an exergy density of approx. 445–465 kJ/kg and a charge-to-discharge ratio of two was accounted for.
2.3. Economic Analysis
The economic analysis was performed on the optimal system configuration (
) of the best performing processes. The processes were sized to 20 MW charging power
. The total revenue requirement (TRR) method was applied [
22]. The bare module costs (BMC) of the components were estimated with a number of methods. Cost estimating charts [
29,
30], cost estimating equations [
8] and past purchase orders [
27,
31,
32] were considered. Pressure and temperate ranges were also taken into account. The costs were adjusted to €2017 with the chemical engineering cost indexes of the reference years (CEPCI
2017 = 567.5 [
33]). The derived cost equations of the BMC for each type of component can be found in [
34].
The assumptions made in the economic analyses are summarized in
Table 5. The operation and maintenance costs (OMC) are assumed as a percentage of the fixed capital investment (FCI) which ranges from 1.5% to 3% of the plant purchase price per year [
35]. The system is assumed to operate at low electricity prices.
For better comparability the specific investment costs are determined. The total capital investment (TCI) of the charging unit is levelized to the charging capacity of the storage (€/kWchar).
For the exergoeconomic analysis, the levelized cost rate
of each component
needs to be determined. The component cost rate considers the costs associated with the capital investment
and the operation and maintenance costs
of the respective component. The component cost rate is calculated over the levelized carrying charges
, the levelized operation and maintenance costs
, the annual operation time of the component
and the share of the investment costs
associated with the
-th component in the total bare-module costs
of the overall system:
2.4. Exergoeconomic Analysis
The exergoeconomic analysis was applied to the best performing liquefaction processes. Aim is to identify the cost-effectiveness of the processes, the costs associated with the thermodynamic inefficiencies and the potential for cost reduction in the processes. This is achieved by “exergy costing” [
27], where the average cost per unit of exergy of each stream in the process is calculated with the aid of cost balances and auxiliary equations. The cost balance for the
-th component of the process is expressed by:
The cost balance needs to be fulfilled for each component in the system to determine the costs of the exiting streams. The sum of the costs associated with the n entering streams of matter
, the cost rate of the respective component
and the cost of heat supplied to the component
are equal to the sum of costs associated with the m exiting streams of matter
and the work done by the system. Each stream of matter, heat or work with associated exergy transfer rate has an average cost per unit of exergy
(€/GJ):
All costs associated with the streams entering the overall system need to be known. The specific cost of the incoming air is set to
= 0 €/MWh while the specific costs of the electricity is
= 17.5 €/MWh. The specific exergy costs of the entering cold storage media streams are assumed equal to the cost per unit of exergy of the liquid air:
If more than one stream exits the component, auxiliary equations based on the “fuel and product” approach are necessary [
24]. The cost balance at the component level can also be formulated as:
The cost associated with the thermodynamic inefficiencies—the exergy destruction—is calculated by the average cost per unit of exergy of the fuel to the component
and the exergy destruction
of the respective component:
The components which are of high importance to the system’s cost-effectiveness are determined by the sum of cost associated with the initial investment of the component
and the cost associated with the exergy destruction
. The exergoeconomic factor can be used to determine the type of changes required to improve the cost effectiveness of the respective component:
In the performed exergoeconomic analysis the major contributors to the overall costs are identified and their potential for cost reduction is compared. Moreover, the results facilitate a subsequent iterative optimization.