Evaluation of the Complexity, Controllability and Observability of Heat Exchanger Networks Based on Structural Analysis of Network Representations
Abstract
:1. Introduction
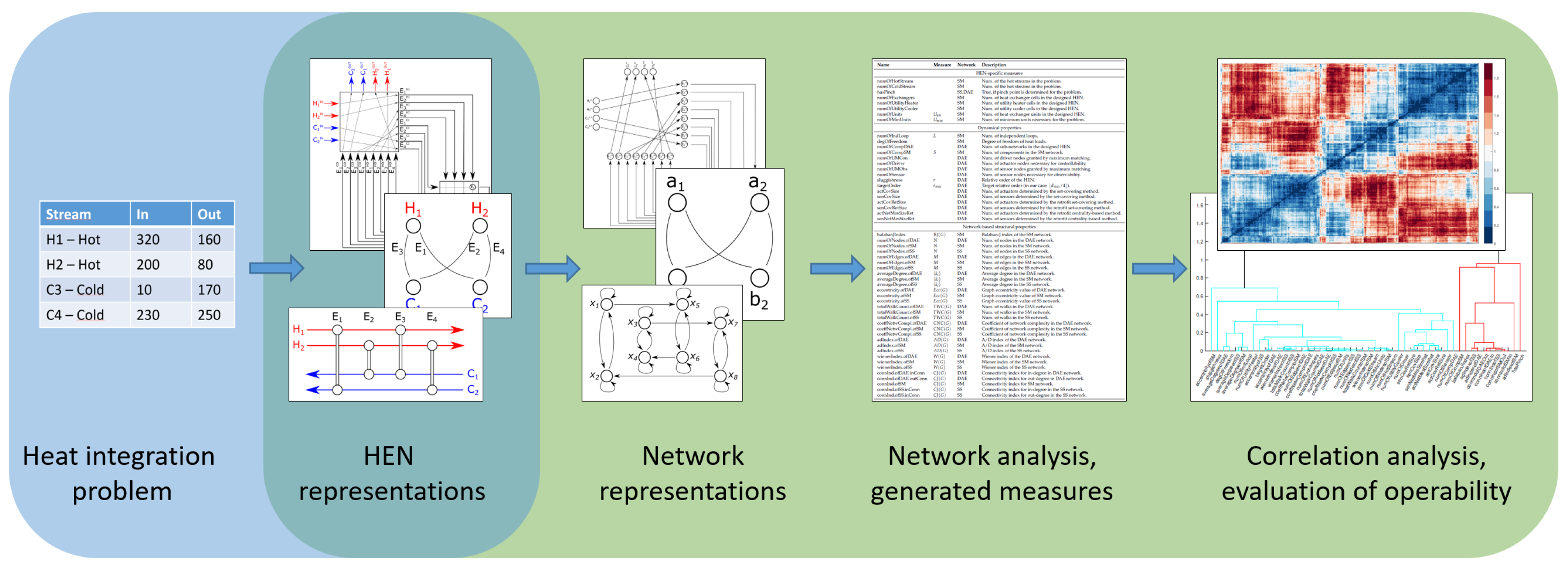
2. Network-Based Evaluation of the Complexity, Controllability and Observability of HENs
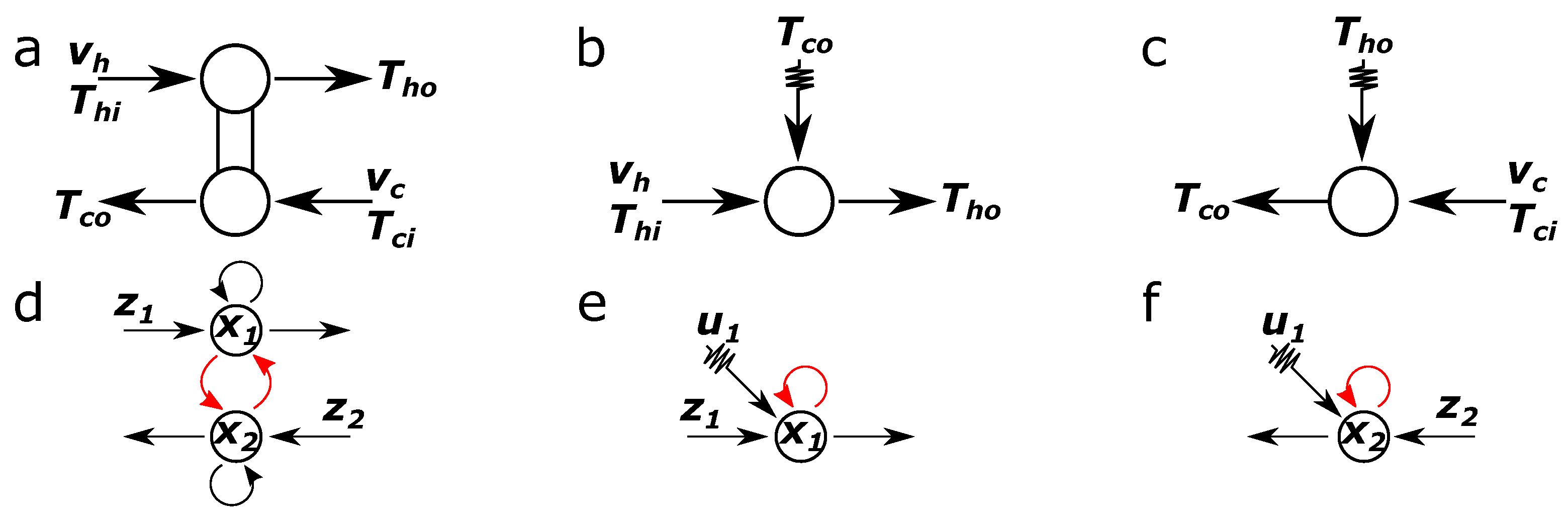
2.1. Network Representations of HENs
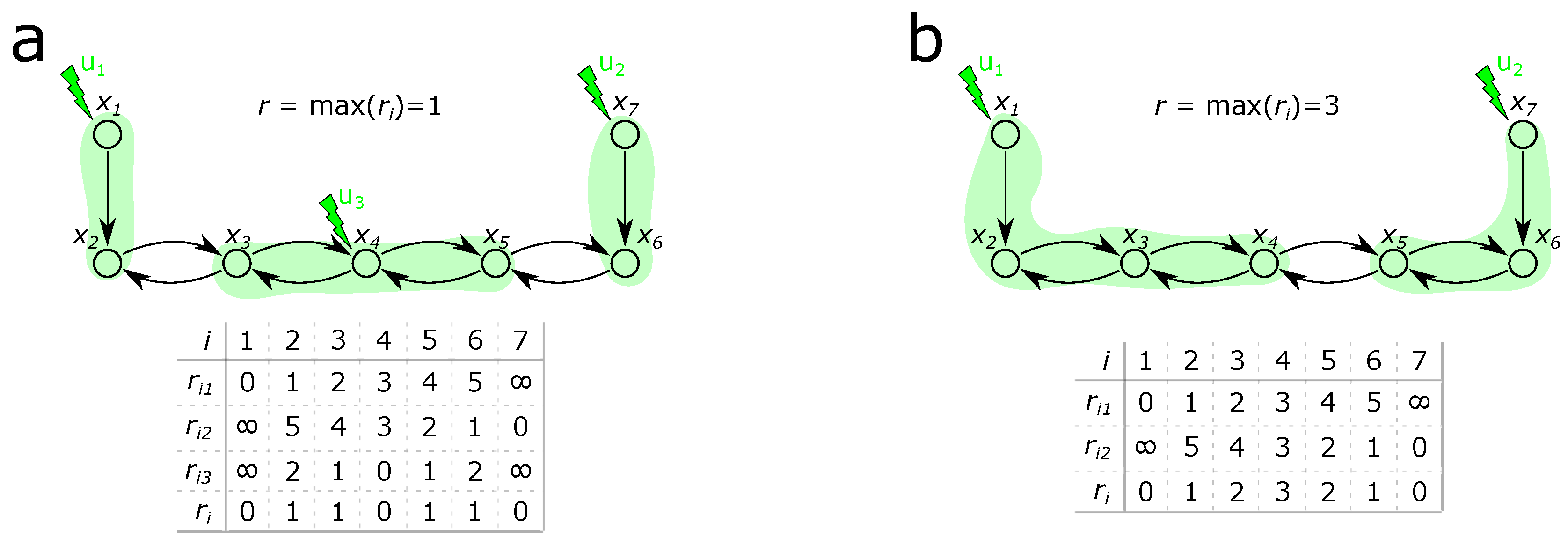
2.2. Operability-Focused Sensor and Controller Placement in HENs
3. Systematic Analysis of HENs
3.1. The Studied Benchmark Problems
3.2. Analysis of the 9sp-al1 Problem
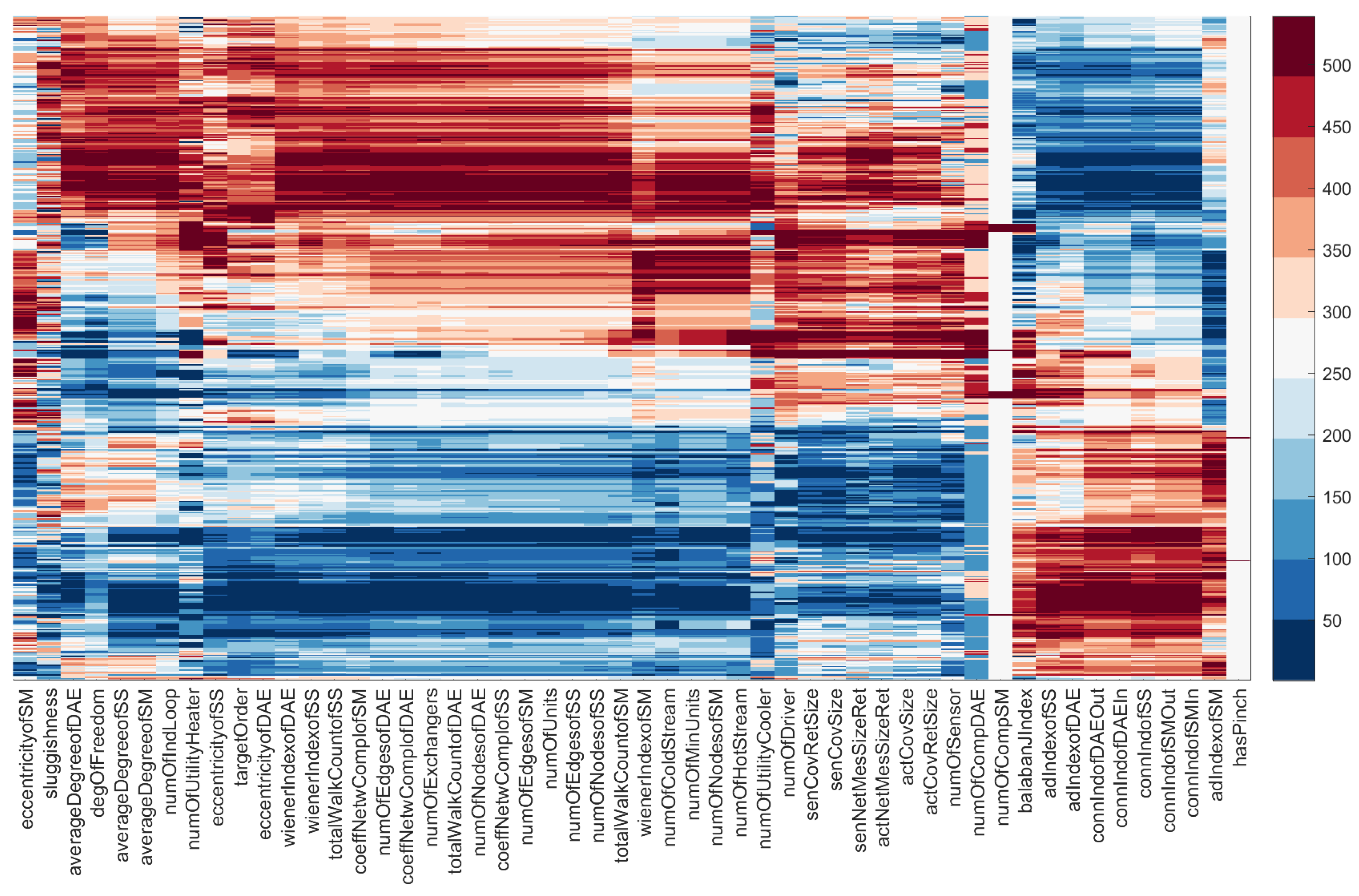
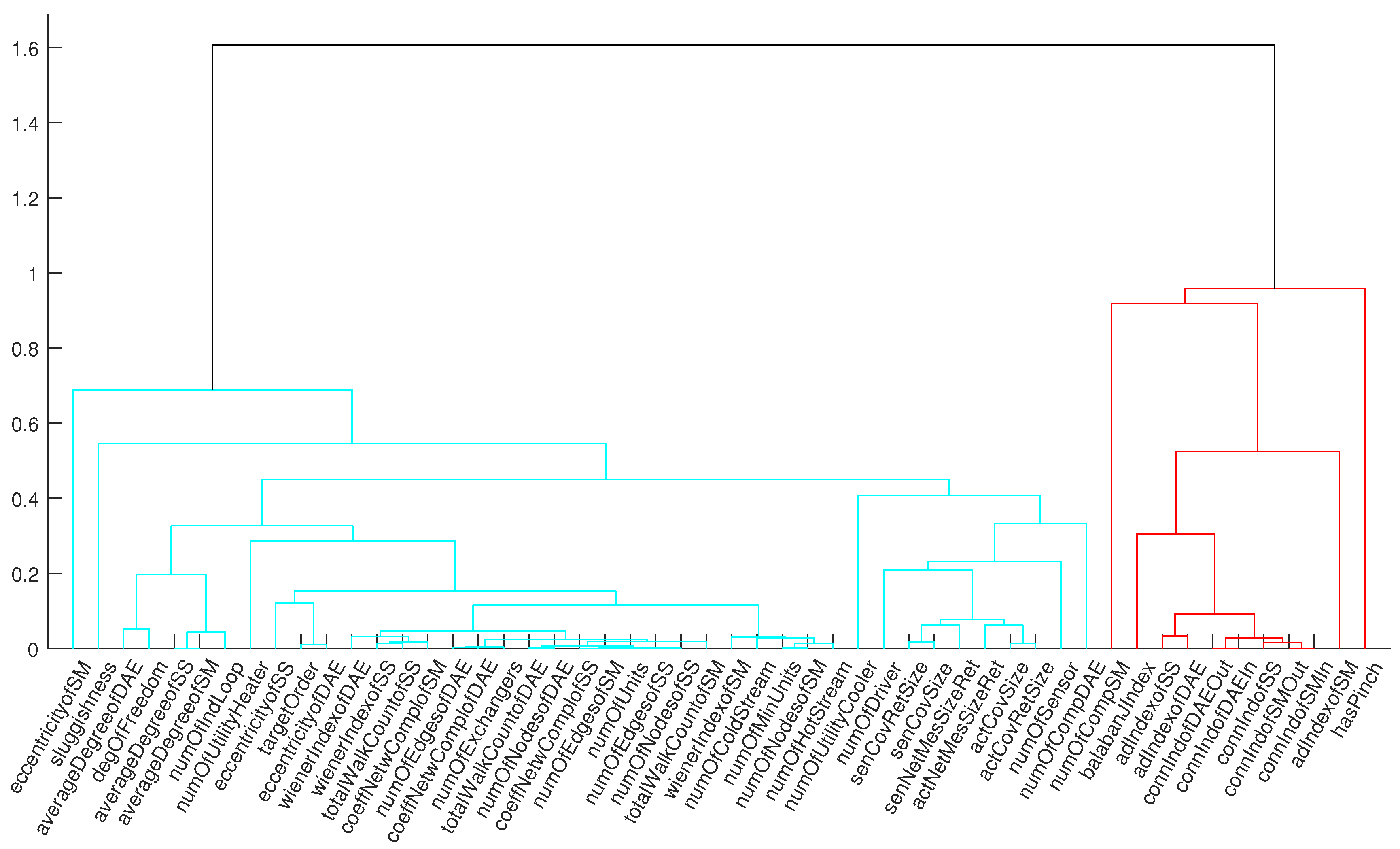
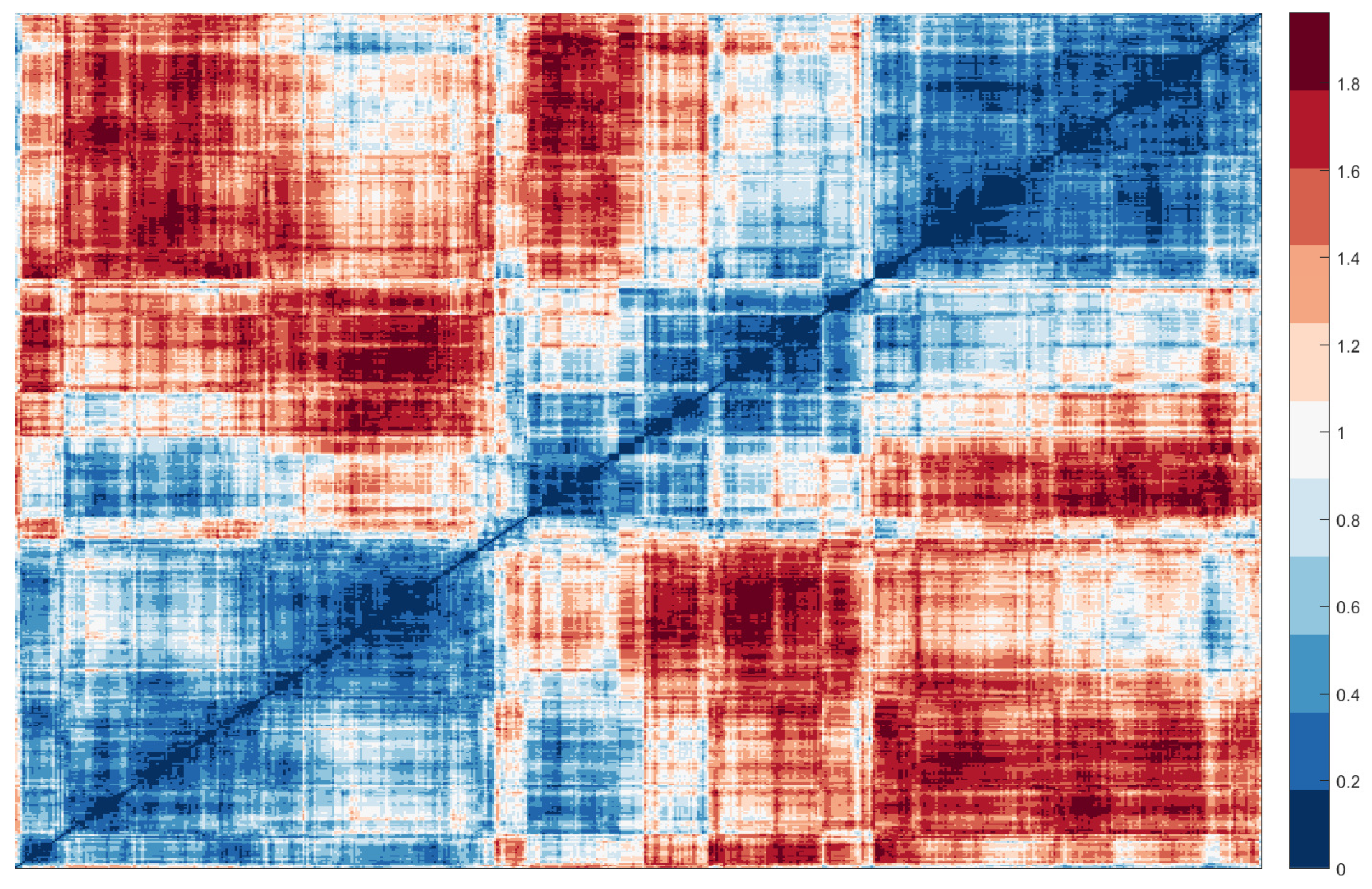
3.3. Results and Discussion of Systematic Correlation Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CNC | Coefficient of Network Complexity |
| DAE | Differential Algebraic Equations |
| DN | Distribution Network |
| GA | Genetic Algorithm |
| GD | Grid Diagram |
| HEN | Heat Exchanger Network |
| MER | Maximum Energy Recovery or Minimum Energy Requirement |
| PI | Process Integration |
| PFD | Process Flow Diagram |
| RI | Resilience Index |
| SA | Simulated Annealing |
| SCC | Strongly Connected Component |
| SM | Streams and Matches |
| SS | State Space |
| TAC | Total Annualised Cost |
| TWC | Total Walk Count |
Nomenclature
| SS-based graph | |
| Set of nodes of SS-based representation | |
| Set of edges of SS-based representation | |
| SM-based graph | |
| Set of nodes of SM-based representation | |
| Set of edges of SM-based representation | |
| Set of nodes of hot streams in SM-based representation | |
| Set of nodes of cold streams in SM-based representation | |
| Node of high pressure steam in SM-based representation | |
| Node of cold water in SM-based representation | |
| Set of edges of heat exchangers in SM-based representation | |
| Set of edges of utility heaters in SM-based representation | |
| Set of edges of utility coolers in SM-based representation | |
| DAE-based graph | |
| Set of nodes of DAE-based representation | |
| Set of edges of DAE-based representation | |
| Hot input temperature of a heat exchanger | |
| Cold input temperature of a heat exchanger | |
| Hot output temperature of a heat exchanger | |
| Cold output temperature of a heat exchanger | |
| t | Time |
| Flow rate of hot stream | |
| Flow rate of cold stream | |
| Volume of hot side of tank | |
| Volume of cold side of tank | |
| U | Heat transfer coefficient |
| A | Heat transfer area |
| Heat capacity of hot stream | |
| Heat capacity of cold stream | |
| Density of hot stream | |
| Density of cold stream | |
| Vector of state variables | |
| n | Number of state variables |
| Vector of inputs | |
| Vector of disturbances | |
| Vector of outputs | |
| State-transition matrix | |
| Input matrix | |
| Column j of matrix | |
| Disturbance matrix | |
| Output matrix | |
| Row j of matrix | |
| Feedthrough (or feedforward) matrix | |
| Controllability matrix | |
| Observability matrix | |
| Number of units | |
| Number of streams | |
| L | Number of independent loops |
| S | Number of separate components |
| H | Number of heat exchangers |
| Lie derivative | |
| Relative degree of input j and output i | |
| Relative degree of output i | |
| Relative degree of the system | |
| Upper bound for r | |
| Node i from node set V | |
| Edge i from edge set E | |
| Weight of node i | |
| Weight of edge i | |
| N | Number of nodes in the network |
| M | Number of edges in the network |
| Out-, in-, and simple degree of node i | |
| Average node degree | |
| Shortest path between nodes i and j | |
| D | Distance matrix |
| Total walk count measure of graph G | |
| Coefficient of network complexity of graph G | |
| Eccentricity of node i, or graph G | |
| Wiener index of graph G | |
| A/D index of graph G | |
| Balaban-J index of graph G | |
| Connectivity index of graph G | |
| Set of reachable nodes from node i in | |
| Set of all state variables | |
| C | Set of necessary driver nodes |
| O | Set of necessary sensor nodes |
| J | Set of driver/sensor nodes of the input/output configuration |
| P | Set of state variables covered by set J |
| Closeness centrality of node i | |
| Betweenness centrality of node i | |
| Number of shortest paths from node s to node t | |
| Number of shortest paths from node s to node t that intercept node i | |
| Diameter of the network |
References
- Chrissis, M.B.; Konrad, M.; Shrum, S. CMMI Guidlines for Process Integration and Product Improvement; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 2003. [Google Scholar]
- Varbanov, P.S.; Walmsley, T.G.; Klemes, J.J.; Wang, Y.; Jia, X.X. Footprint Reduction Strategy for Industrial Site Operation. Chem. Eng. Trans. 2018, 67, 607–612. [Google Scholar] [CrossRef]
- Klemes, J.J. Handbook of Process Integration (PI): Minimisation of Energy and Water Use, Waste and Emissions; Elsevier: Cambridge, UK, 2013. [Google Scholar]
- Klemeš, J.J.; Varbanov, P.S.; Walmsley, T.G.; Jia, X. New directions in the implementation of Pinch Methodology (PM). Renew. Sustain. Energy Rev. 2018, 98, 439–468. [Google Scholar] [CrossRef]
- Jamaluddin, K.; Wan Alwi, S.R.; Manan, Z.A.; Klemes, J.J. Pinch Analysis Methodology for Trigeneration with Energy Storage System Design. Chem. Eng. Trans. 2018, 70, 1885–1890. [Google Scholar] [CrossRef]
- Kemp, I.C. Pinch Analysis and Process Integration: A User Guide on Process Integration for the Efficient Use of Energy; Elsevier: Oxford, UK, 2011. [Google Scholar]
- Zafiriou, E. The Integration of Process Design and Control; Pergamon: Oxford, UK, 1994. [Google Scholar]
- Liu, Y.Y.; Slotine, J.J.; Barabási, A.L. Controllability of complex networks. Nature 2011, 473, 167. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.Y.; Slotine, J.J.; Barabási, A.L. Observability of complex systems. Proc. Natl. Acad. Sci. USA 2013, 110, 2460–2465. [Google Scholar] [CrossRef] [PubMed]
- Saboo, A.K.; Morari, M.; Woodcock, D.C. Design of resilient processing plants—VIII. A resilience index for heat exchanger networks. Chem. Eng. Sci. 1985, 40, 1553–1565. [Google Scholar] [CrossRef]
- Westphalen, D.L.; Young, B.R.; Svrcek, W.Y. A controllability index for heat exchanger networks. Ind. Eng. Chem. Res. 2003, 42, 4659–4667. [Google Scholar] [CrossRef]
- Düştegör, D.; Frisk, E.; Cocquempot, V.; Krysander, M.; Staroswiecki, M. Structural analysis of fault isolability in the DAMADICS benchmark. Control Eng. Pract. 2006, 14, 597–608. [Google Scholar] [CrossRef]
- Letsios, D.; Kouyialis, G.; Misener, R. Heuristics with performance guarantees for the minimum number of matches problem in heat recovery network design. Comput. Chem. Eng. 2018, 113, 57–85. [Google Scholar] [CrossRef]
- Linnhoff, B.; Ahmad, S. Supertargeting: Optimum synthesis of energy management systems. J. Energy Resour. Technol. 1989, 111, 121–130. [Google Scholar] [CrossRef]
- Ahmad, S.; Linnhoff, B. Supertargeting: Different process structures for different economics. J. Energy Resour. Technol. 1989, 111, 131–136. [Google Scholar] [CrossRef]
- Bagajewicz, M.J.; Pham, R.; Manousiouthakis, V. On the state space approach to mass/heat exchanger network design. Chem. Eng. Sci. 1998, 53, 2595–2621. [Google Scholar] [CrossRef]
- Mocsny, D.; Govind, R. Decomposition strategy for the synthesis of minimum-unit heat exchanger networks. AIChE J. 1984, 30, 853–856. [Google Scholar] [CrossRef]
- Ciric, A.; Floudas, C. A retrofit approach for heat exchanger networks. Comput. Chem. Eng. 1989, 13, 703–715. [Google Scholar] [CrossRef]
- Linnhoff, B.; Hindmarsh, E. The pinch design method for heat exchanger networks. Chem. Eng. Sci. 1983, 38, 745–763. [Google Scholar] [CrossRef]
- Trivedi, K.; O’Neill, B.; Roach, J. Synthesis of heat exchanger networks featuring multiple pinch points. Comput. Chem. Eng. 1989, 13, 291–294. [Google Scholar] [CrossRef]
- Wood, R.; Suaysompol, K.; O’Neill, B.; Roach, J.; Trivedi, K. A new option for heat exchanger network design. Chem. Eng. Prog. 1991, 87, 38–43. [Google Scholar]
- Pho, T.; Lapidus, L. Topics in computer-aided design: Part II. Synthesis of optimal heat exchanger networks by tree searching algorithms. AIChE J. 1973, 19, 1182–1189. [Google Scholar] [CrossRef]
- Yu, H.; Fang, H.; Yao, P.; Yuan, Y. A combined genetic algorithm/simulated annealing algorithm for large scale system energy integration. Comput. Chem. Eng. 2000, 24, 2023–2035. [Google Scholar] [CrossRef]
- Lee, K.F.; Masso, A.; Rudd, D. Branch and bound synthesis of integrated process designs. Ind. Eng. Chem. Fund. 1970, 9, 48–58. [Google Scholar] [CrossRef]
- Masso, A.; Rudd, D. The synthesis of system designs. II. Heuristic structuring. AIChE J. 1969, 15, 10–17. [Google Scholar] [CrossRef]
- Miranda, C.B.; Costa, C.B.B.C.; Andrade, C.M.G.; Ravagnani, M.A.S.S. Controllability and Resiliency Analysis in Heat Exchanger Networks. Chem. Eng. Trans. 2017, 61, 1609–1614. [Google Scholar]
- Svensson, E.; Eriksson, K.; Bengtsson, F.; Wik, T. Design of Heat Exchanger Networks with Good Controllability; Technical Report; CIT Industriell Energi AB: Göteborg, Sweden, 2018. [Google Scholar]
- Varga, E.; Hangos, K. The effect of the heat exchanger network topology on the network control properties. Control Eng. Pract. 1993, 1, 375–380. [Google Scholar] [CrossRef]
- Escobar, M.; Trierweiler, J.O.; Grossmann, I.E. Simultaneous synthesis of heat exchanger networks with operability considerations: Flexibility and controllability. Comput. Chem. Eng. 2013, 55, 158–180. [Google Scholar] [CrossRef]
- Calandranis, J.; Stephanopoulos, G. Structural operability analysis of heat exchanger networks. Chem. Eng. Res. Des. 1986, 64, 347–364. [Google Scholar]
- Zhelev, T.; Varbanov, P.; Seikova, I. HEN’s operability analysis for better process integrated retrofit. Hung. J. Ind. Chem. 1998, 26, 81–88. [Google Scholar]
- Leitold, D.; Vathy-Fogarassy, A.; Abonyi, J. Network Distance-Based Simulated Annealing and Fuzzy Clustering for Sensor Placement Ensuring Observability and Minimal Relative Degree. Sensors 2018, 18, 3096. [Google Scholar] [CrossRef]
- Linnhoff, B.; Mason, D.R.; Wardle, I. Understanding heat exchanger networks. Comput. Chem. Eng. 1979, 3, 295–302. [Google Scholar] [CrossRef]
- Bagajewicz, M.J.; Manousiouthakis, V. Mass/heat-exchange network representation of distillation networks. AIChE J. 1992, 38, 1769–1800. [Google Scholar] [CrossRef]
- Foggia, P.; Percannella, G.; Vento, M. Graph matching and learning in pattern recognition in the last 10 years. Int. J. Pattern Recognit. Artif. Intell. 2014, 28, 1450001. [Google Scholar] [CrossRef]
- Conte, D.; Foggia, P.; Sansone, C.; Vento, M. Thirty years of graph matching in pattern recognition. Int. J. Pattern Recognit. Artif. Intell. 2004, 18, 265–298. [Google Scholar] [CrossRef]
- Carletti, V.; Foggia, P.; Saggese, A.; Vento, M. Challenging the time complexity of exact subgraph isomorphism for huge and dense graphs with VF3. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 804–818. [Google Scholar] [CrossRef] [PubMed]
- Pósfai, M.; Liu, Y.Y.; Slotine, J.J.; Barabási, A.L. Effect of correlations on network controllability. Sci. Rep. 2013, 3, 1067. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Mo, Y.; Pequito, S.; Sinopoli, B.; Kar, S.; Aguiar, A.P. Minimum robust sensor placement for large scale linear time-invariant systems: A structured systems approach. IFAC Proc. Vol. 2013, 46, 417–424. [Google Scholar] [CrossRef]
- Yan, G.; Tsekenis, G.; Barzel, B.; Slotine, J.J.; Liu, Y.Y.; Barabási, A.L. Spectrum of controlling and observing complex networks. Nat. Phys. 2015, 11, 779–786. [Google Scholar] [CrossRef]
- Mangan, S.; Alon, U. Structure and function of the feed-forward loop network motif. Proc. Natl. Acad. Sci. USA 2003, 100, 11980–11985. [Google Scholar] [CrossRef] [PubMed]
- Vinayagam, A.; Gibson, T.E.; Lee, H.J.; Yilmazel, B.; Roesel, C.; Hu, Y.; Kwon, Y.; Sharma, A.; Liu, Y.Y.; Perrimon, N.; et al. Controllability analysis of the directed human protein interaction network identifies disease genes and drug targets. Proc. Natl. Acad. Sci. USA 2016, 113, 4976–4981. [Google Scholar] [CrossRef]
- Asgari, Y.; Salehzadeh-Yazdi, A.; Schreiber, F.; Masoudi-Nejad, A. Controllability in cancer metabolic networks according to drug targets as driver nodes. PLoS ONE 2013, 8, e79397. [Google Scholar] [CrossRef]
- Leitold, D.; Vathy-Fogarassy, Á.; Abonyi, J. Controllability and observability in complex networks–the effect of connection types. Sci. Rep. 2017, 7, 151. [Google Scholar] [CrossRef]
- Daoutidis, P.; Kravaris, C. Structural evaluation of control configurations for multivariable nonlinear processes. Chem. Eng. Sci. 1992, 47, 1091–1107. [Google Scholar] [CrossRef]
- Nishida, N.; Stephanopoulos, G.; Westerberg, A.W. A review of process synthesis. AIChE J. 1981, 27, 321–351. [Google Scholar] [CrossRef]
- Linnhoff, B.; Flower, J.R. Synthesis of heat exchanger networks: I. Systematic generation of energy optimal networks. AIChE J. 1978, 24, 633–642. [Google Scholar] [CrossRef]
- Varga, E.; Hangos, K.; Szigeti, F. Controllability and observability of heat exchanger networks in the time-varying parameter case. Control Eng. Pract. 1995, 3, 1409–1419. [Google Scholar] [CrossRef]
- Wood, R.; Wilcox, R.; Grossmann, I.E. A note on the minimum number of units for heat exchanger network synthesis. Chem. Eng. Commun. 1985, 39, 371–380. [Google Scholar] [CrossRef]
- Reinschke, K.J. Multivariable Control: A Graph Theoretic Approach; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Kalman, R.E. Mathematical description of linear dynamical systems. J. Soc. Ind. Appl. Math. Ser. A Control 1963, 1, 152–192. [Google Scholar] [CrossRef]
- Letellier, C.; Sendiña-Nadal, I.; Aguirre, L.A. A nonlinear graph-based theory for dynamical network observability. Phys. Rev. E 2018. [Google Scholar] [CrossRef] [PubMed]
- Volkmann, L. Estimations for the number of cycles in a graph. Periodica Math. Hung. 1996, 33, 153–161. [Google Scholar] [CrossRef]
- Bonchev, D.; Buck, G.A. Quantitative measures of network complexity. In Complexity in Chemistry, Biology, and Ecology; Springer: Richmond, VA, USA, 2005; pp. 191–235. [Google Scholar]
- Latva-Koivisto, A.M. Finding a Complexity Measure for Business Process Models; Helsinki University of Technology, Systems Analysis Laboratory: Helsinki, Finland, 2001. [Google Scholar]
- Dehmer, M.; Kraus, V.; Emmert-Streib, F.; Pickl, S. Quantitative Graph Theory; CRC Press: Danvers, MA, USA, 2014. [Google Scholar]
- Balaban, A.T. Highly discriminating distance-based topological index. Chem. Phys. Lett. 1982, 89, 399–404. [Google Scholar] [CrossRef]
- Leitold, D.; Vathy-Fogarassy, A.; Abonyi, J. Design-Oriented Structural Controllability and Observability Analysis of Heat Exchanger Networks. Chem. Eng. Trans. 2018, 70, 595–600. [Google Scholar]
- Gori, F.; Folino, G.; Jetten, M.S.; Marchiori, E. MTR: Taxonomic annotation of short metagenomic reads using clustering at multiple taxonomic ranks. Bioinformatics 2010, 27, 196–203. [Google Scholar] [CrossRef]
- Furman, K.C.; Sahinidis, N.V. Approximation algorithms for the minimum number of matches problem in heat exchanger network synthesis. Ind. Eng. Chem. Res. 2004, 43, 3554–3565. [Google Scholar] [CrossRef]
- Chen, Y.; Grossmann, I.E.; Miller, D.C. Computational strategies for large-scale MILP transshipment models for heat exchanger network synthesis. Comput. Chem. Eng. 2015, 82, 68–83. [Google Scholar] [CrossRef]
- Chen, Y.; Grossmann, I.E.; Miller, D.C. Large-Scale MILP Transshipment Models for Heat Exchanger Network Synthesis. 2015. A Collaboration of Carnegie Mellon University and IBM Research. Available online: https://www.minlp.org/library/problem/index.php?i=191&lib=MINLP (accessed on 4 February 2019).
- Grossmann, I.E. Personal Communication; Carnegie Mellon University: Pittsburgh, PA, USA, 2017. [Google Scholar]
- Gundersen, T.; Grossmann, I.E. Improved optimization strategies for automated heat exchanger network synthesis through physical insights. Comput. Chem. Eng. 1990, 14, 925–944. [Google Scholar] [CrossRef]
- Colberg, R.; Morari, M. Area and capital cost targets for heat exchanger network synthesis with constrained matches and unequal heat transfer coefficients. Comput. Chem. Eng. 1990, 14, 1–22. [Google Scholar] [CrossRef]
- Shenoy, U.V. Heat Exchanger Network Synthesis: Process Optimization by Energy and Resource Analysis; Gulf Professional Publishing: Houston, TX, USA, 1995. [Google Scholar]
- Trivedi, K.; O’Neill, B.; Roach, J.; Wood, R. Systematic energy relaxation in MER heat exchanger networks. Comput. Chem. Eng. 1990, 14, 601–611. [Google Scholar] [CrossRef]
- Dolan, W.; Cummings, P.; Le Van, M. Algorithmic efficiency of simulated annealing for heat exchanger network design. Comput. Chem. Eng. 1990, 14, 1039–1050. [Google Scholar] [CrossRef]
- Farhanieh, B.; Sunden, B. Analysis of an existing heat exchanger network and effects of heat pump installations. Heat Recov. Syst. CHP 1990, 10, 285–296. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Sargent, R. Optimum design of heat exchanger networks. Comput. Chem. Eng. 1978, 2, 1–7. [Google Scholar] [CrossRef]
- Hall, S.; Ahmad, S.; Smith, R. Capital cost targets for heat exchanger networks comprising mixed materials of construction, pressure ratings and exchanger types. Comput. Chem. Eng. 1990, 14, 319–335. [Google Scholar] [CrossRef]
- Tantimuratha, L.; Kokossis, A.; Müller, F. The heat exchanger network design as a paradigm of technology integration. Appl. Therm. Eng. 2000, 20, 1589–1605. [Google Scholar] [CrossRef]
- Polley, G.; Heggs, P. Don’t let the pinch pinch you. Chem. Eng. Prog. 1999, 95, 27–36. [Google Scholar]
- Ahmad, S.; Smith, R. Targets and design for minimum number of shells in heat exchanger networks. Chem. Eng. Res. Des. 1989, 67, 481–494. [Google Scholar]
- Arenas, A.; Fernandez, A.; Gomez, S. Analysis of the structure of complex networks at different resolution levels. New J. Phys. 2008, 10, 053039. [Google Scholar] [CrossRef]
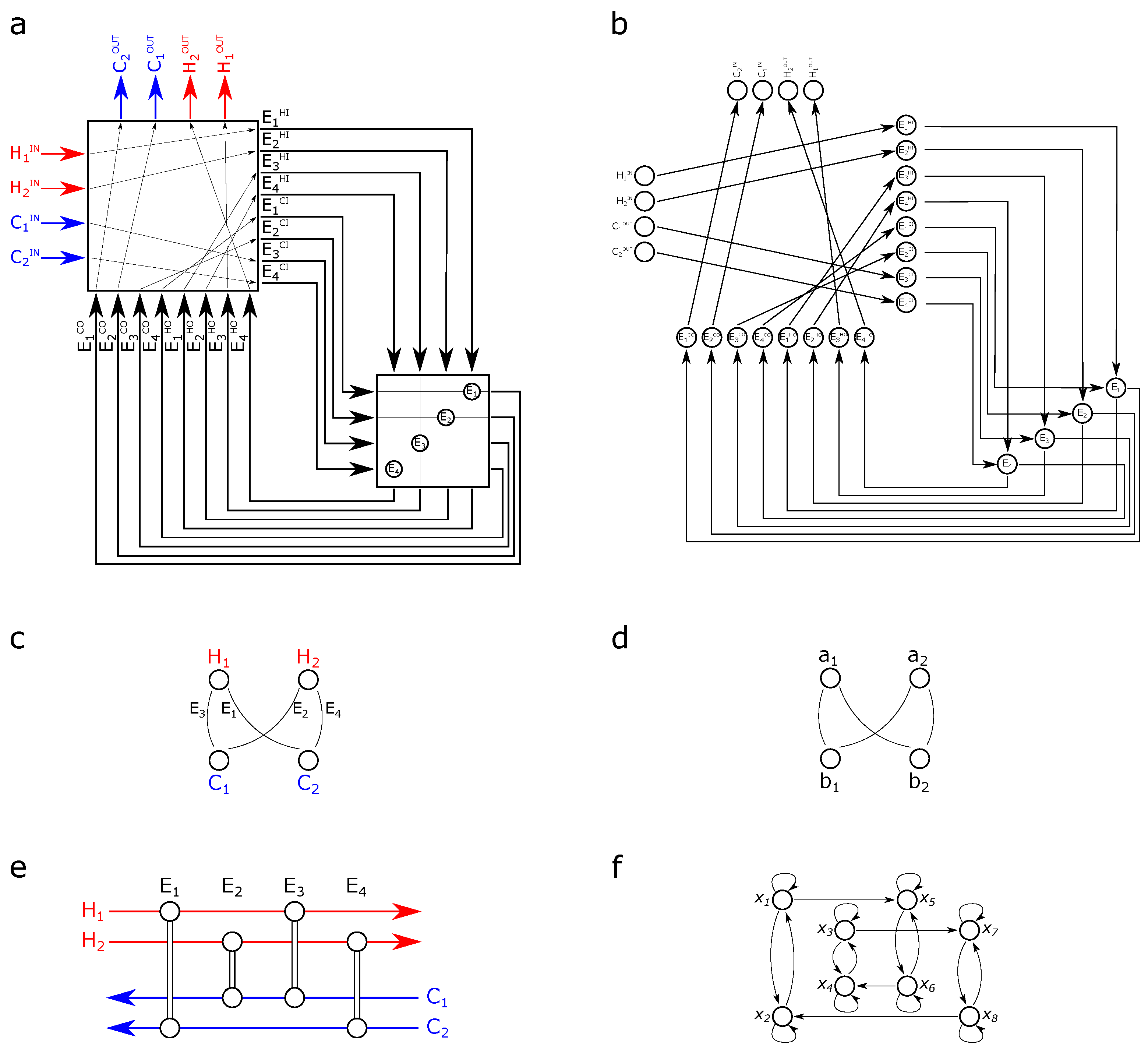
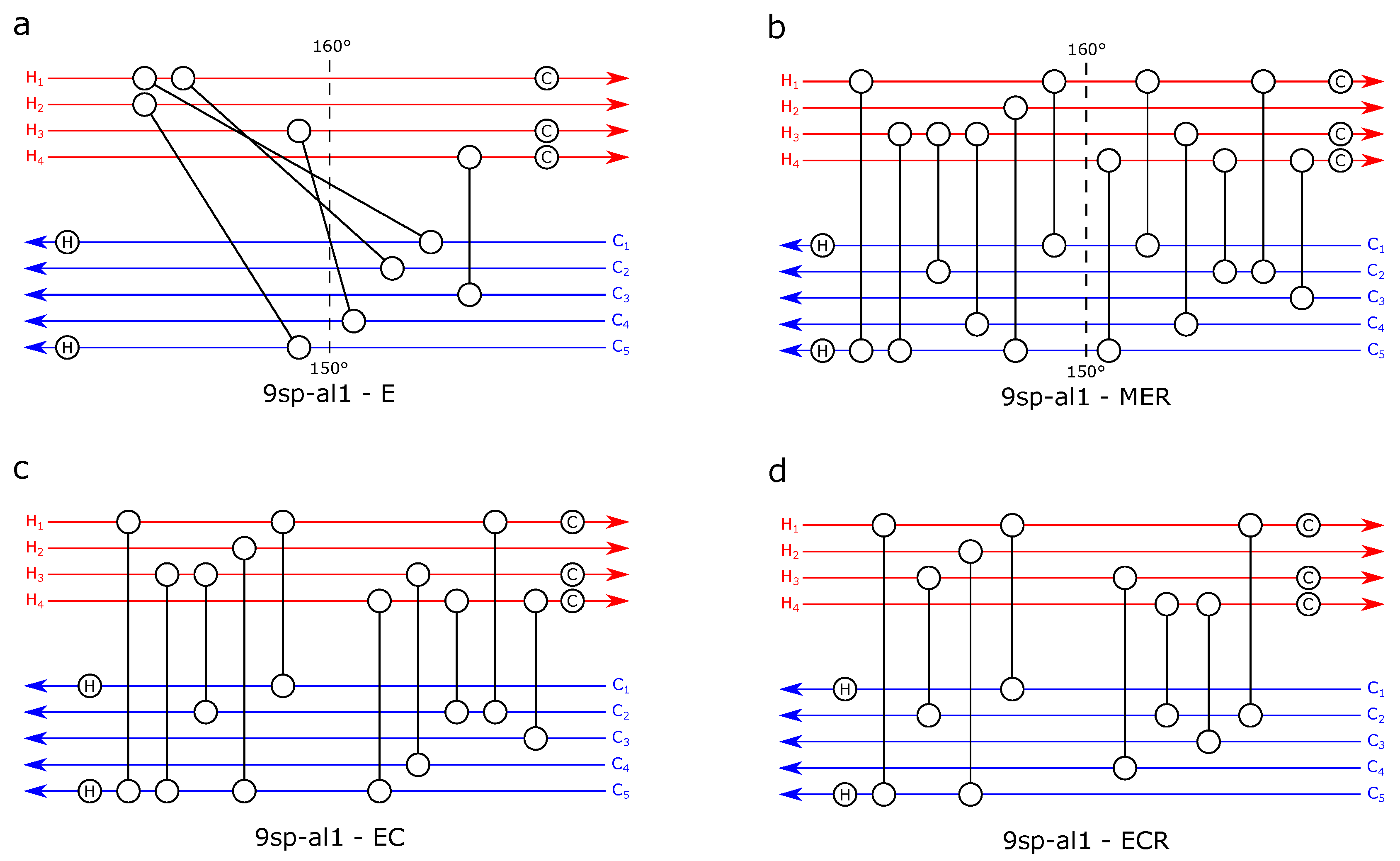
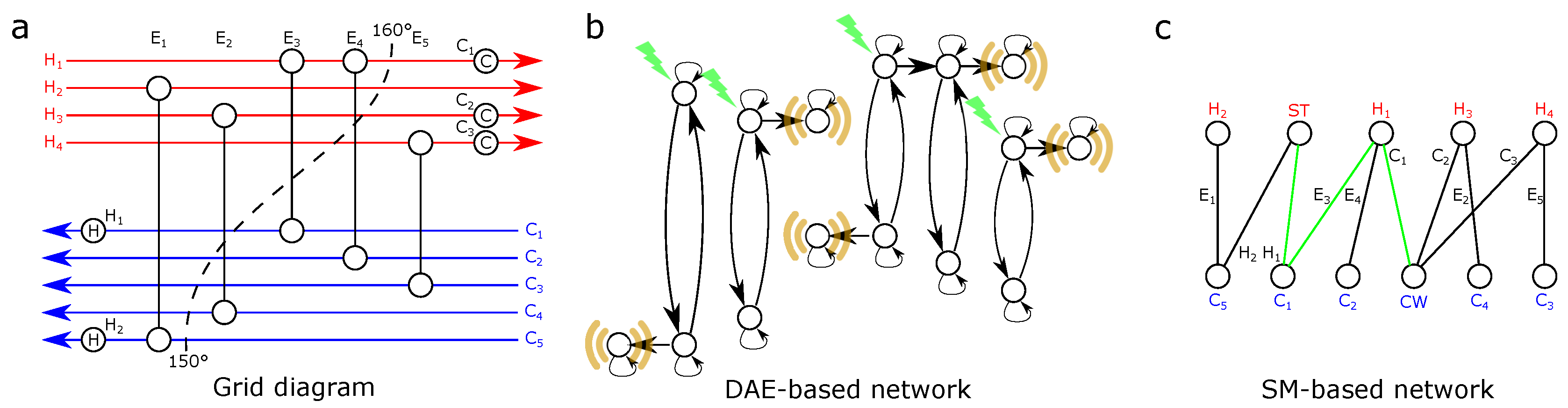
| Property | SS | SM | DAE |
|---|---|---|---|
| node () | Connection of streams. | Stream. | State variable. |
| edge () | Stream. | Match: a unit. | Dynamical effect between two state variables. |
| node weight () | The nodes are not weighted. | The heat load of the stream. | The output temperature of the exchanger. |
| edge weight () | Edges are not weighted. | Heat load exchanged between the streams. | Dynamical effect between state variables determined by the state-transition matrix. |
| direction | The network is directed, edge directions are based on the direction of the streams [34]. The network is more transparent when—similarly to Grid diagrams—the hot streams run from the left to the right and cold vice versa to follow the direction of Composite Curves. | The network is undirected. | The network is directed, the direction of edges is based on matrix [8] that reflects the direction of the streams and the heat transfer. |
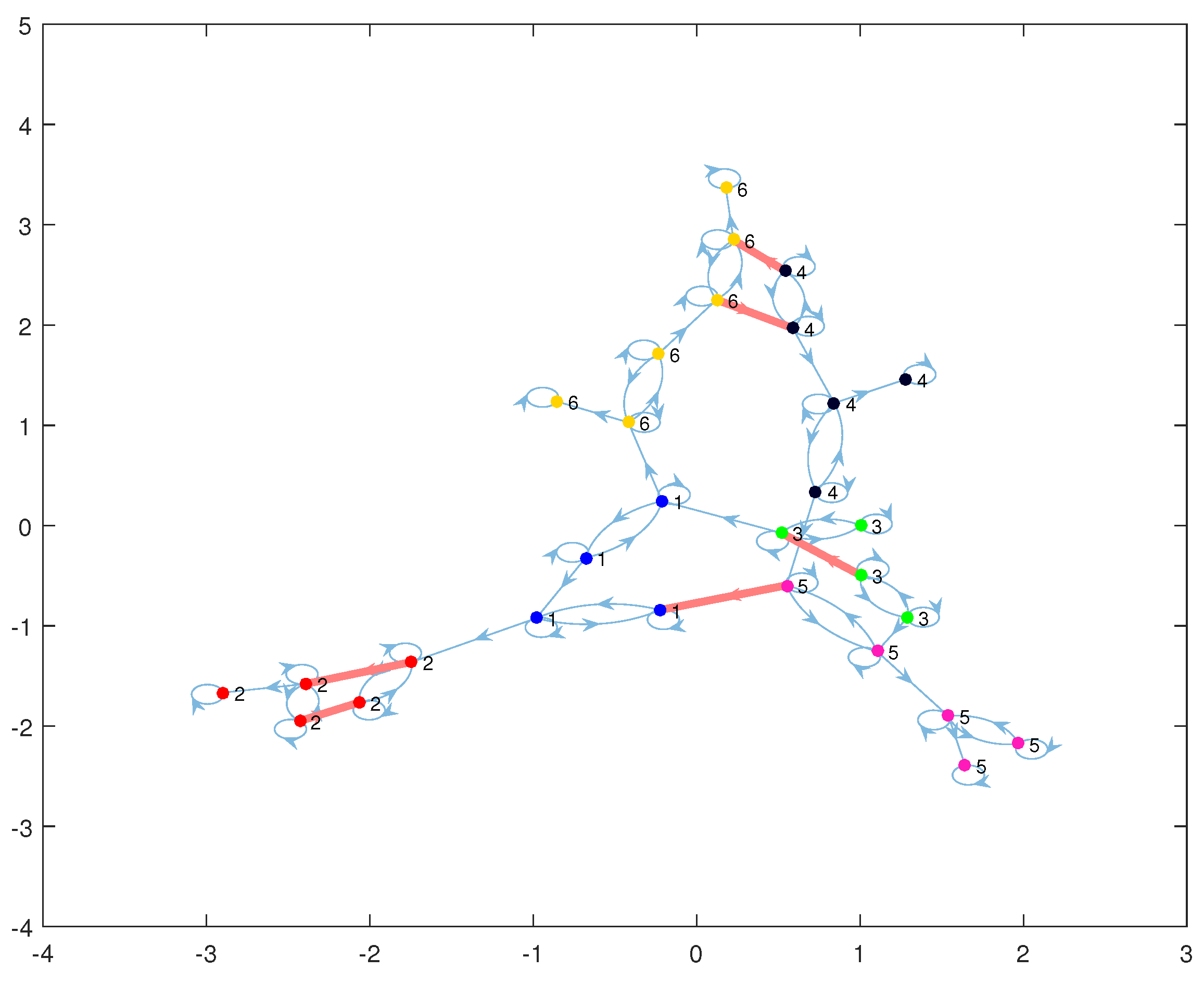
| loops | Loops can reflect superfluous units. | Loops appear when there are more units than necessary. | Loops create strongly connected components that can be controlled (or observed) by only one driver (or sensor) node. |
| maximum matching [8] | n/a | n/a | Unmatched nodes provide driver and sensor nodes. |
| relative order [45] | n/a | n/a | Difficulty in operation. |
| number of components (S) | Components are the disconnected sub-networks in the HEN. | ||
| Property | Calculation | SS | SM | DAE |
|---|---|---|---|---|
| number of nodes | Starting- and endpoints of the streams. | Number of streams (Process and utility). | Number of state variables necessary to describe the dynamics of HEN. | |
| number of edges | Number of stream intervals. | Number of units. | Nonzero elements of the state-transition matrix. | |
| degree | , , | Fixed for the nodes, for stream source and drains, for endpoints of stream intervals and for heat exchanger units. | is the number of units on stream. | Fixed for the nodes, moves from 2 to 4 in case of heat exchanger, and from 1 to 2 in case of utility units (loops are excluded). |
| shortest path | The minimum of length of paths from node i to node j. | |||
| distance matrix | D | The distance matrix contains the shortest distance between node i and . The distance of node j is . | ||
| cycle rank [53] | L | The number of independent loops in the network. | ||
| total walk count (TWC) [54] | The number of walks is proportional to the complexity, as the walks can represent the effect of an input signal in the system. More walks means more effect in the HEN. | |||
| coefficient of network complexity (CNC) [55] | Due to the fixed degree, the CNC is constrained. | The proportion of units to streams. | Due to the fixed degree, the CNC is constrained. | |
| eccentricity [54] | Maximum length of heat loads. | n/a. | The relative order of the system. | |
| Wiener index [56] | Reflects the size of the HEN, and the complexity as long paths increase . | In undirected case, should be divided by two. Since the network is undirected, approximates the size of the system. | Longer geodesic paths represent higher order dynamics. | |
| A/D index [54] | Since the degree is fixed, the index approximates the closeness of the units. | As the order of heat exchanger units is not given, the A/D index does not necessarily characterise heat loads or HEN. | Since degree is fixed, the index approximates the closeness of units. | |
| Balaban-J index [57] | Balaban-J index can only be calculated to undirected graphs. | It approximates the size of the HEN. | Balaban-J index can only be calculated to undirected graphs. | |
| connectivity index [56] | Since the degree is fixed, the index cannot characterise the HEN. | Shows how the streams are interconnected. | Since the degree is fixed, the index cannot characterise the HEN. | |
| Problem | Hot Streams | Cold Streams | Methods | Source |
|---|---|---|---|---|
| Furman and Sahinidis (2004) | ||||
| 4sp1 | 2 | 2 | HEU, BB | [24] |
| 6sp-cf1 | 3 | 3 | HEU, RET | [18] |
| 6sp-gg1 | 3 | 3 | HEU | [64] |
| 6sp1 | 3 | 3 | HEU, BB | [24] |
| 7sp-cm1 | 3 | 4 | HEU | [65] |
| 7sp-s1 | 6 | 1 | HEU | [66] |
| 7sp-torw1 | 4 | 3 | HEU | [67] |
| 7sp1 | 3 | 4 | HEU, SYN | [25] |
| 7sp2 | 3 | 3 | HEU, SYN | [25] |
| 7sp4 | 6 | 1 | HEU | [68] |
| 8sp-fs1 | 5 | 3 | HEU, E | [69] |
| 8sp1 | 4 | 4 | HEU | [70] |
| 9sp-al1 | 4 | 5 | HEU, E, MER, EC, ECR, ST | [15] |
| 9sp-has1 | 5 | 4 | HEU | [71] |
| 10sp-la1 | 4 | 5 | HEU | [14] |
| 10sp-ol1 | 4 | 6 | HEU | [66] |
| 10sp1 | 5 | 5 | HEU, BB | [22] |
| 12sp1 | 9 | 3 | HEU | [70] |
| 14sp1 | 7 | 7 | HEU | [70] |
| 15sp-tkm | 9 | 6 | HEU, E | [72] |
| 20sp1 | 10 | 10 | HEU | [70] |
| 22sp-ph | 11 | 11 | HEU | [73] |
| 22sp1 | 11 | 11 | HEU | [16] |
| 23sp1 | 11 | 12 | HEU, DS | [17] |
| 28sp-as1 | 16 | 12 | HEU | [74] |
| 37sp-yfyv | 21 | 16 | HEU, GASA | [23] |
| Chen et al. (2015a,b) | ||||
| balanced5 | 5 | 5 | HEU | [61,62] |
| balanced8 | 8 | 8 | HEU | [61,62] |
| balanced10 | 10 | 10 | HEU | [61,62] |
| balanced12 | 12 | 12 | HEU | [61,62] |
| balanced15 | 15 | 15 | HEU | [61,62] |
| unbalanced5 | 5 | 5 | HEU | [61,62] |
| unbalanced10 | 10 | 10 | HEU | [61,62] |
| unbalanced15 | 15 | 15 | HEU | [61,62] |
| unbalanced17 | 17 | 17 | HEU | [61,62] |
| unbalanced20 | 20 | 20 | HEU | [61,62] |
| Grossmann (2017) | ||||
| balanced12_random0 | 12 | 12 | HEU | [63] |
| balanced12_random1 | 12 | 12 | HEU | [63] |
| balanced12_random2 | 12 | 12 | HEU | [63] |
| balanced15_random0 | 15 | 15 | HEU | [63] |
| balanced15_random1 | 15 | 15 | HEU | [63] |
| balanced15_random2 | 15 | 15 | HEU | [63] |
| unbalanced17_random0 | 17 | 17 | HEU | [63] |
| unbalanced17_random1 | 17 | 17 | HEU | [63] |
| unbalanced17_random2 | 17 | 17 | HEU | [63] |
| unbalanced20_random0 | 20 | 20 | HEU | [63] |
| unbalanced20_random1 | 20 | 20 | HEU | [63] |
| unbalanced20_random2 | 20 | 20 | HEU | [63] |
| Name | Method | Objective Function | Source |
|---|---|---|---|
| BB | Branch and bound | Minimises the heat exchanger and utility costs. | [24] |
| CP | CPLEX-solved transportation model. | Minimum number of matches. | [13] |
| CRR | Covering Relaxation Rounding | Minimum number of matches. | [13] |
| CSH | CPLEX-solved transshipment model. | Minimum number of matches. | [13] |
| DS | Decomposition Strategy | Minimises the number of exchangers. | [17] |
| E | No method declared | Existing network, not optimised. | |
| EC | Pinch methodology | Energy-Capital cost minimisation. | [14,15] |
| ECR | Pinch methodology | Energy-Capital Retrofit cost minimisation. | [14,15] |
| FLPR | Fractional LP Rounding | Minimum number of matches. | [13] |
| GASA | Genetic Algorithm with Simulated Annealing | Minimises the annual cost. | [23] |
| GP | Gurobi-solved transportation model. | Minimum number of matches. | [13] |
| GSH | Gurobi-solved transshipment model. | Minimum number of matches. | [13] |
| LFM | Largest Fraction Match | Minimum number of matches. | [13] |
| LHM | Largest Heat Match Greedy | Minimum number of matches. | [13] |
| LHM-LP | Largest Heat Match LP-based | Minimum number of matches. | [13] |
| LRR | Lagrangian Relaxation Rounding | Minimum number of matches. | [13] |
| MER | Pinch methodology | Maximum Energy Recovery, Minimum Energy Requirement. | [14,15] |
| RET | Structural modifications by categories | Minimises the cost of new exchangers, exchanger areas and piping. | [18] |
| SS | Shortest Stream | Minimum number of matches. | [13] |
| ST | Pinch methodology | Supertargeting. | [14,15] |
| SYN | Heuristic stage-by-stage structuring synthesis | Minimises the annual cost. | [25] |
| WFG | Water Filling Greedy | Minimum number of matches. | [13] |
| WFM | Water Filling MILP | Minimum number of matches. | [13] |
| Name | Measure | Network | Description |
|---|---|---|---|
| HEN-specific measures | |||
| numOfHotStream | SM | Num. of the hot streams in the problem. | |
| numOfColdStream | SM | Num. of the hot streams in the problem. | |
| hasPinch | SS, DAE | True, if Pinch point is determined for the problem. | |
| numOfExchangers | SM | Num. of heat exchanger cells in the designed HEN. | |
| numOfUtilityHeater | SM | Num. of utility heater cells in the designed HEN. | |
| numOfUtilityCooler | SM | Num. of utility cooler cells in the designed HEN. | |
| numOfUnits | SM | Num. of heat exchanger units in the designed HEN. | |
| numOfMinUnits | SM | Num. of minimum units necessary for the problem. | |
| Dynamical properties | |||
| numOfIndLoop | L | SM | Num. of independent loops. |
| degOfFreedom | SM | Degree of freedom of heat loads. | |
| numOfCompDAE | DAE | Num. of sub-networks in the designed HEN. | |
| numOfCompSM | S | SM | Num. of components in the SM network. |
| numOfUMCon | DAE | Num. of driver nodes granted by maximum matching. | |
| numOfDriver | DAE | Num. of actuator nodes necessary for controllability. | |
| numOfUMObs | DAE | Num. of sensor nodes granted by maximum matching. | |
| numOfSensor | DAE | Num. of sensor nodes necessary for observability. | |
| sluggishness | r | DAE | Relative order of the HEN. |
| targetOrder | DAE | Target relative order (in our case: ). | |
| actCovSize | DAE | Num. of actuators determined by the set-covering method. | |
| senCovSize | DAE | Num. of sensors determined by the set-covering method. | |
| actCovRetSize | DAE | Num. of actuators determined by the retrofit set-covering method. | |
| senCovRetSize | DAE | Num. of sensors determined by the retrofit set-covering method. | |
| actNetMesSizeRet | DAE | Num. of actuators determined by the retrofit centrality-based method. | |
| senNetMesSizeRet | DAE | Num. of sensors determined by the retrofit centrality-based method. | |
| Network-based structural properties | |||
| balabanJIndex | SM | Balaban-J index of the SM network. | |
| numOfNodes.ofDAE | N | DAE | Num. of nodes in the DAE network. |
| numOfNodes.ofSM | N | SM | Num. of nodes in the SM network. |
| numOfNodes.ofSS | N | SS | Num. of nodes in the SS network. |
| numOfEdges.ofDAE | M | DAE | Num. of edges in the DAE network. |
| numOfEdges.ofSM | M | SM | Num. of edges in the SM network. |
| numOfEdges.ofSS | M | SS | Num. of edges in the SS network. |
| averageDegree.ofDAE | DAE | Average degree in the DAE network. | |
| averageDegree.ofSM | SM | Average degree in the SM network. | |
| averageDegree.ofSS | SS | Average degree in the SS network. | |
| eccentricity.ofDAE | DAE | Graph eccentricity value of DAE network. | |
| eccentricity.ofSM | SM | Graph eccentricity value of SM network. | |
| eccentricity.ofSS | SS | Graph eccentricity value of SS network. | |
| totalWalkCount.ofDAE | DAE | Num. of walks in the DAE network. | |
| totalWalkCount.ofSM | SM | Num. of walks in the SM network. | |
| totalWalkCount.ofSS | SS | Num. of walks in the SS network. | |
| coeffNetwCompl.ofDAE | DAE | Coefficient of network complexity in the DAE network. | |
| coeffNetwCompl.ofSM | SM | Coefficient of network complexity in the SM network. | |
| coeffNetwCompl.ofSS | SS | Coefficient of network complexity in the SS network. | |
| adIndex.ofDAE | DAE | A/D index of the DAE network. | |
| adIndex.ofSM | SM | A/D index of the SM network. | |
| adIndex.ofSS | SS | A/D index of the SS network. | |
| wienerIndex.ofDAE | DAE | Wiener index of the DAE network. | |
| wienerIndex.ofSM | SM | Wiener index of the SM network. | |
| wienerIndex.ofSS | SS | Wiener index of the SS network. | |
| connInd.ofDAE.inConn | DAE | Connectivity index for in-degree in DAE network. | |
| connInd.ofDAE.outConn | DAE | Connectivity index for out-degree in DAE network. | |
| connInd.ofSM | SM | Connectivity index for SM network. | |
| connInd.ofSS.inConn | SS | Connectivity index for in-degree in the SS network. | |
| connInd.ofSS.inConn | SS | Connectivity index for out-degree in the SS network. | |
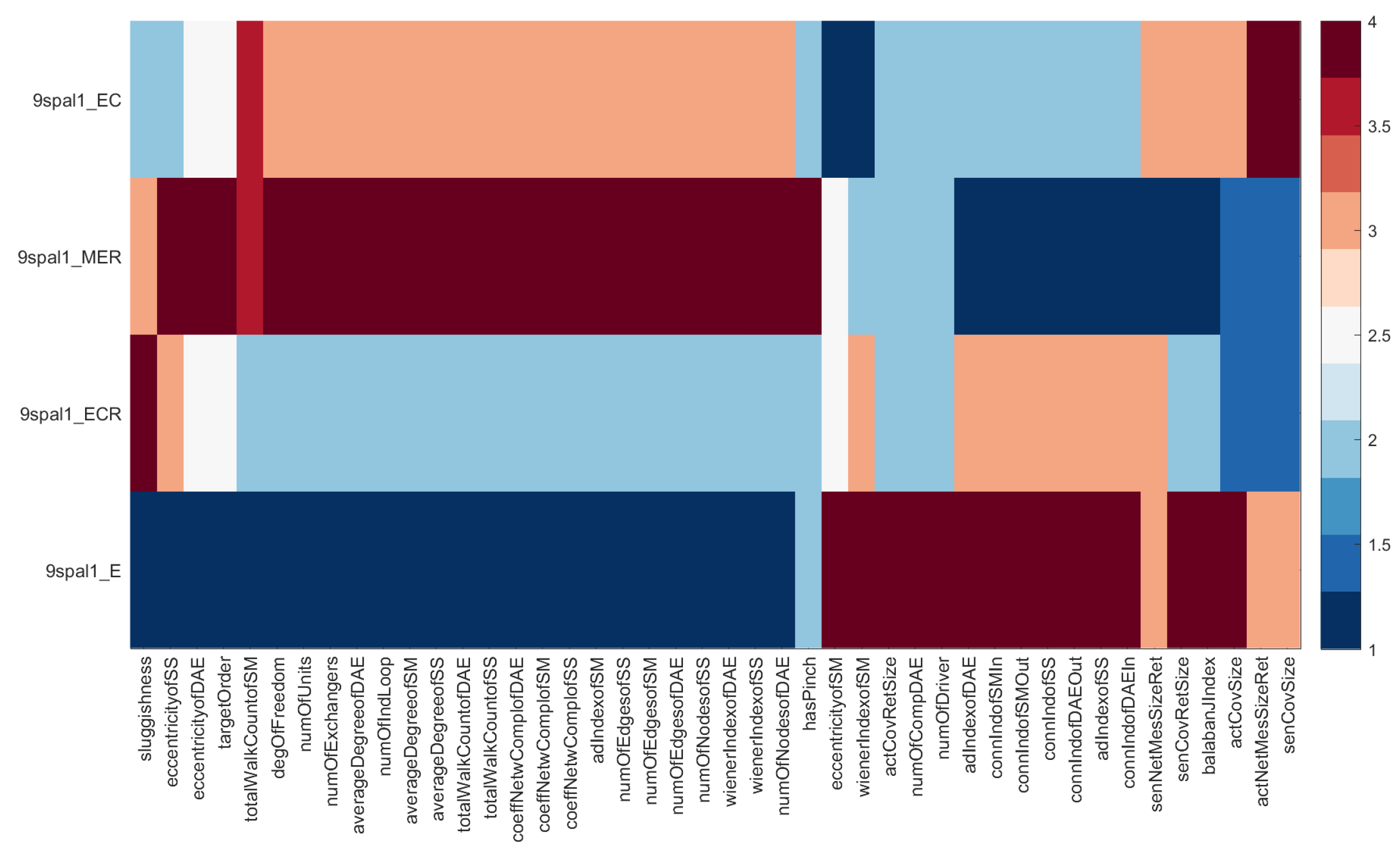
| Name | 9sp-al1 - E | 9sp-al1 - MER | 9sp-al1 - EC | 9sp-al1 - ECR |
|---|---|---|---|---|
| HEN-specific measures | ||||
| numOfHotStream | 4 | 4 | 4 | 4 |
| numOfColdStream | 5 | 5 | 5 | 5 |
| hasPinch | 0 | 1 | 0 | 0 |
| numOfExchangers | 5 | 12 | 10 | 8 |
| numOfUtilityHeater | 2 | 2 | 2 | 2 |
| numOfUtilityCooler | 3 | 3 | 3 | 3 |
| numOfUnits | 10 | 17 | 15 | 13 |
| numOfMinUnits | 10 | 10 | 10 | 10 |
| Dynamical properties | ||||
| numOfIndLoop | 0 | 7 | 5 | 3 |
| degOfFreedom | −5 | 2 | 0 | −2 |
| numOfCompDAE | 4 | 1 | 1 | 1 |
| numOfCompSM | 1 | 1 | 1 | 1 |
| numOfUMCon | 0 | 0 | 0 | 0 |
| numOfDriver | 4 | 1 | 1 | 1 |
| numOfUMObs | 0 | 0 | 0 | 0 |
| numOfSensor | 5 | 5 | 5 | 5 |
| sluggishness | 2 | 9 | 8 | 11 |
| targetOrder | 1 | 3 | 2 | 2 |
| actCovSize | 9 | 7 | 8 | 7 |
| senCovSize | 5 | 4 | 6 | 4 |
| actCovRetSize | 9 | 7 | 7 | 7 |
| senCovRetSize | 7 | 4 | 6 | 5 |
| actNetMesSizeRet | 9 | 8 | 10 | 8 |
| senNetMesSizeRet | 7 | 4 | 7 | 7 |
| Network-based structural properties | ||||
| balabanJIndex | 9.9212 | 4.3990 | 5.6234 | 5.2789 |
| numOfNodesofDAE | 15 | 29 | 25 | 21 |
| numOfNodesofSM | 11 | 11 | 11 | 11 |
| numOfNodesofSS | 72 | 107 | 97 | 87 |
| numOfEdgesofDAE | 31 | 73 | 61 | 49 |
| numOfEdgesofSM | 10 | 17 | 15 | 13 |
| numOfEdgesofSS | 71 | 113 | 101 | 89 |
| averageDegreeofDAE | 2.1333 | 3.0345 | 2.8800 | 2.6667 |
| averageDegreeofSM | 1.8182 | 3.0909 | 2.7273 | 2.3636 |
| averageDegreeofSS | 1.9722 | 2.1121 | 2.0825 | 2.0460 |
| eccentricityofDAE | 3 | 12 | 11 | 11 |
| eccentricityofSM | 7 | 5 | 4 | 5 |
| eccentricityofSS | 13 | 28 | 22 | 25 |
| totalWalkCountofDAE | 802,788 | 1.02127E+13 | 92,080,948,186 | 1,364,370,909 |
| totalWalkCountofSM | 34,258 | 2,114,490 | 2,114,490 | 410,032 |
| totalWalkCountofSS | 646 | 9138 | 3274 | 1977 |
| coeffNetwComplofDAE | 64.0667 | 183.7586 | 148.8400 | 114.3333 |
| coeffNetwComplofSM | 9.0909 | 26.2727 | 20.4545 | 15.3636 |
| coeffNetwComplofSS | 70.0139 | 119.3364 | 105.1649 | 91.0460 |
| adIndexofDAE | 0.8421 | 0.0522 | 0.0661 | 0.0787 |
| adIndexofSM | 0.1136 | 0.2636 | 0.2586 | 0.1857 |
| adIndexofSS | 0.0446 | 0.0067 | 0.0089 | 0.0107 |
| wienerIndexofDAE | 38 | 1687 | 1090 | 712 |
| wienerIndexofSM | 176 | 129 | 116 | 140 |
| wienerIndexofSS | 3,181 | 33,524 | 22,586 | 16,582 |
| connIndofDAEIn | 0.0154 | 0.0053 | 0.0065 | 0.0085 |
| connIndofDAEOut | 0.0147 | 0.0052 | 0.0063 | 0.0082 |
| connIndofSS | 0.0246 | 0.0082 | 0.0103 | 0.0143 |
| connIndofSMIn | 0.0131 | 0.0077 | 0.0087 | 0.0100 |
| connIndofSMOut | 0.0131 | 0.0077 | 0.0087 | 0.0100 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leitold, D.; Vathy-Fogarassy, A.; Abonyi, J. Evaluation of the Complexity, Controllability and Observability of Heat Exchanger Networks Based on Structural Analysis of Network Representations. Energies 2019, 12, 513. https://doi.org/10.3390/en12030513
Leitold D, Vathy-Fogarassy A, Abonyi J. Evaluation of the Complexity, Controllability and Observability of Heat Exchanger Networks Based on Structural Analysis of Network Representations. Energies. 2019; 12(3):513. https://doi.org/10.3390/en12030513
Chicago/Turabian StyleLeitold, Daniel, Agnes Vathy-Fogarassy, and Janos Abonyi. 2019. "Evaluation of the Complexity, Controllability and Observability of Heat Exchanger Networks Based on Structural Analysis of Network Representations" Energies 12, no. 3: 513. https://doi.org/10.3390/en12030513
APA StyleLeitold, D., Vathy-Fogarassy, A., & Abonyi, J. (2019). Evaluation of the Complexity, Controllability and Observability of Heat Exchanger Networks Based on Structural Analysis of Network Representations. Energies, 12(3), 513. https://doi.org/10.3390/en12030513







