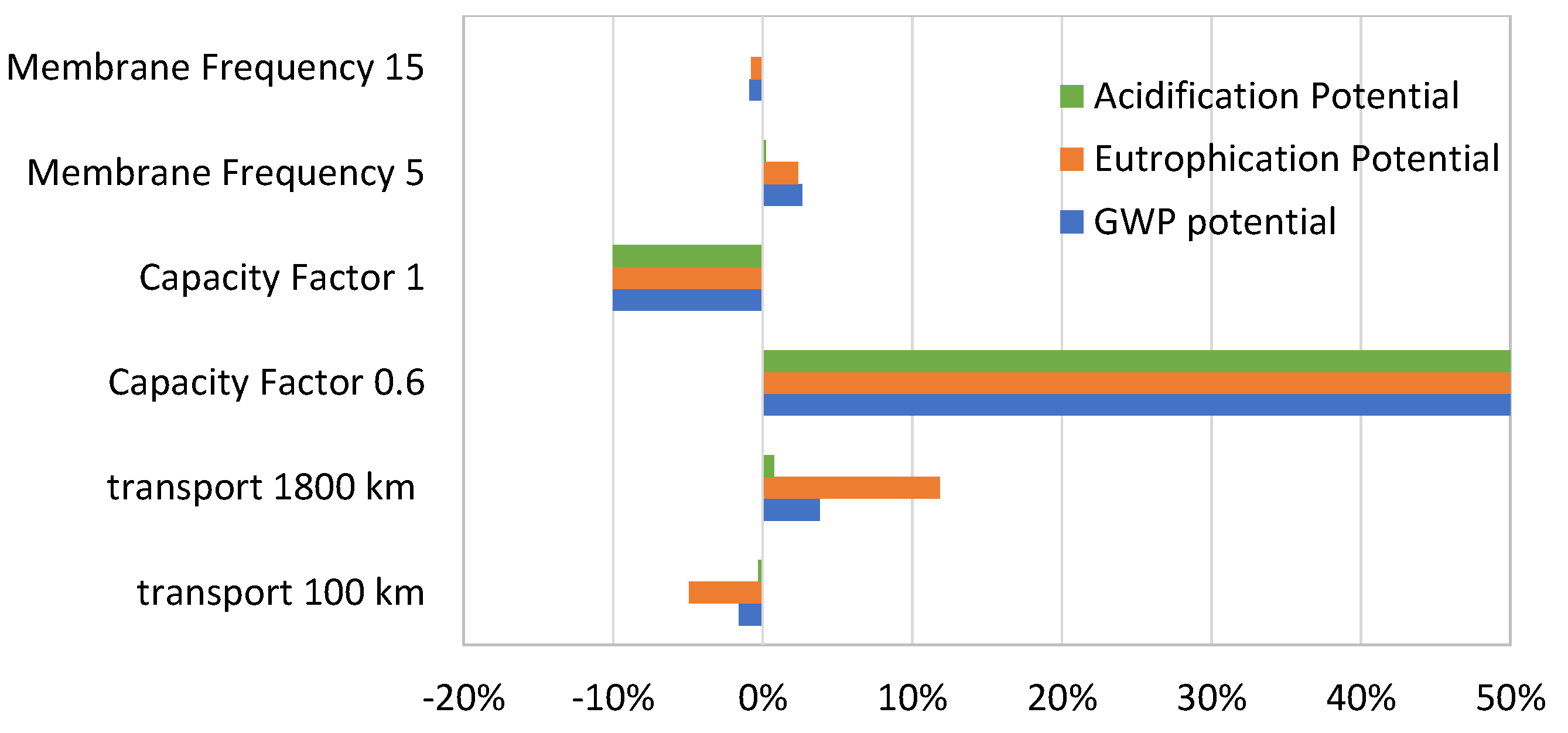1. Introduction
There are very large amounts of waste heat that remain unexploited all over the world. It is estimated that in the EU industries alone, the recoverable part of that heat is about 300 TWh/year [
1]. The main focus is on industrial waste heat that is mostly available at a temperature of over 100 °C and represents a significant fraction of the total. Various technologies are developed to exploit this heat and convert it into useful energy, with the main concepts dealing with the production of power/electricity [
2] or upgraded heat [
3]. Especially, the heat-to-power concept has attracted most of the attention [
4], with various heat engines developed that can exploit this low-temperature heat source and convert it into power [
5]. The most common one is a heat engine based on the organic Rankine cycle (ORC), which has reached commercial level and is applied in various industries and temperature ranges [
6]. Other heat engines have been also developed, attempting to offer improved performances or lower costs than the ORC one.
One alternative with increasing research interest is the salinity gradient power heat engine (SGP-HE) [
7]. This system consists of: (1) a power unit based on salinity gradient power, technology, in which the chemical energy associated to the mixing of two solutions at different salt concentrations is converted into electricity, and (2) a regeneration unit, where (waste) heat is used to restore the original concentration of the two solutions. Reverse electrodialysis (RED) is one of the main technologies for exploiting SGP and uses membranes that are selective towards the passage of ions, employed in a stack, which is composed of a series of anion and cation exchange membranes arranged in an alternate way. RED has been examined extensively in open-loop configuration, using natural streams (e.g., seawater and river water) [
8,
9] or streams deriving from human activity, such as brines [
9,
10]. In order to operate in a closed-loop with artificial solutions, the two solutions after passing the RED membrane stack need to be regenerated using a thermal separation system driven by waste heat to restore the initial salinity gradient [
11,
12].
The most suitable thermal separation technology, considering the heat supply of low-temperature heat at 100 °C, is multi-effect distillation (MED). MED is widely applied in desalination and other water treatment plants and is mostly applicable in cases with distilled flow rate over 5000 m
3/day, while small-scale designs have been also proposed [
13]. The use of a large number of effects improves the thermal efficiency but also drives up the heat exchanging surface and the capital cost. This issue has been examined in [
14], developing a detailed correlation to estimate the MED capital cost, including various parameters that are of use here. Except for MED, other separation technologies suitable for the RED heat engine are based on membrane distillation (MD) [
12] or distillation columns with thermolytic salts [
15], which show a lower potential due to their higher thermal energy consumption and specific capital cost [
16,
17].
Most of the works reported in the literature relevant to SGP-HE have focused on the use of sodium chloride salt-solutions [
16,
18,
19]. However, the adoption of alternative salts, such as lithium chloride or potassium and cesium acetate has the potential to increase the performance of the RED-MED thanks to their high solubility [
20]. Further performance improvements can also be obtained by operating the RED unit at temperatures higher than the ambient one [
21]. The impact of both improvements is considered in the present work by operating the RED unit at three different temperatures (i.e., 25 °C, 50 °C, and 80 °C) and by considering either sodium chloride (NaCl) or potassium acetate (KAc) as working solutions of the RED-MED.
The cost effectiveness of the open loop RED has been already examined [
9,
22], showing that further technological improvement is necessary before it can be cost-effective, related to the development of membranes with higher performance and lower cost. The closed-loop RED employing a regeneration stage is a more recent concept, with the studies conducted so far focusing on the solution specifications, temperature of the driving heat, cycle design, and the regeneration unit. An alternative regeneration unit is membrane distillation, which is especially suited for small-scale applications. The economics of the RED-MD system were examined in Ref. [
16] and it was shown that if high-performing ion exchange membranes (IEMs) were developed, the levelized cost of electricity (LCOE) would be around 0.40 €/kWh. This could be further reduced to values in the range of 0.10 to 0.25 €/kWh, assuming important reductions in membrane and MD costs in the future in the case of industrial-scale production.
The main purpose of the current work is to assess the capital and running costs of the RED-MED heat engine configuration and to calculate its levelized cost of electricity. A first indication has been provided in Ref. [
23] for a specific case and size with standard conditions (i.e., sodium chloride solutions and ambient temperature in the RED unit). Here, further details are examined, focusing on high-performing configurations, introducing the main parameters that affect the cost, such as the system scale, salt used, RED operating temperature, and the number of MED effects, with the aim to provide a more comprehensive approach in this field than existing relevant studies. Appropriate cost correlations are used for that purpose while examining the cost variation of the IEMs and of the MED. The case with the superior cost-effectiveness has been further examined in storage mode for calculating the LCOE for supplying peak power at times of high electricity prices.
Apart from the cost analysis, the life cycle assessment (LCA) methodology is used for assessing the environmental impacts of the different RED-MED system configurations. By accounting for the impacts throughout the system’s life cycle, the risk of missing any environmental trade-offs that could occur between the different life cycle phases is avoided [
24]. When looking at the conversion of low-temperature heat to electricity, most LCA studies are related to the ORC, focusing either on design aspects, such as in Ref. [
25], where the impacts of using different working fluids are compared, or on the application context, such as in Ref. [
26], where the impacts of using ORC to convert the waste heat from a biogas plant to electricity are explored.
The novelty of the current work is strengthened by the absence of similar studies on the environmental impacts of the RED heat engine. An overview of potential environmental concerns of RED and other SGP processes have been outlined in Ref. [
27], but the focus was mostly on open loop applications and the impacts from the use of natural streams to feed the process (e.g., river water with seawater). The only study that is related to the present one is the work on an osmotic heat engine [
28], where pressure-retarded osmosis (instead of RED) is used for power generation, operating in a closed loop and using MD powered by waste heat for the regeneration process. In that paper, the life-cycle impacts from converting waste heat to electricity are assessed, comparing the options of using an osmotic heat engine or an ORC for converting waste heat to electricity.
2. RED-MED Configurations and Performance Analysis
The initial performance calculations assume that the system uses commercially available IEMs. The permselectivity, electrical resistance, salt permeability, and water permeability of the specific membranes considered (reference values) have been presented as a function of the temperature in Ref. [
21]. In this initial calculation, a large number of MED effects is considered, since the aim was to maximize the thermal efficiency of the heat engine.
In order to examine different cases that affect the financial and environmental impacts, a variety of configurations have been considered, as follows:
The combination of these alternative options together with the initial reference case add up to a total of six RED-MED configurations considered in this work. An overview is provided in
Table 2, all supplied with waste heat at a temperature of 100 °C. Further details of the IEM types with their properties are provided in Ref. [
21].
For each of these configurations, the system performance has been calculated for a single RED stack, with 1000 cell pairs and a surface of 0.25 m
2 per membrane. The full technical analysis, description of the model used, and results are provided in Ref. [
21]. An overview of the system’s performance parameters with one stack for each configuration/case are provided in
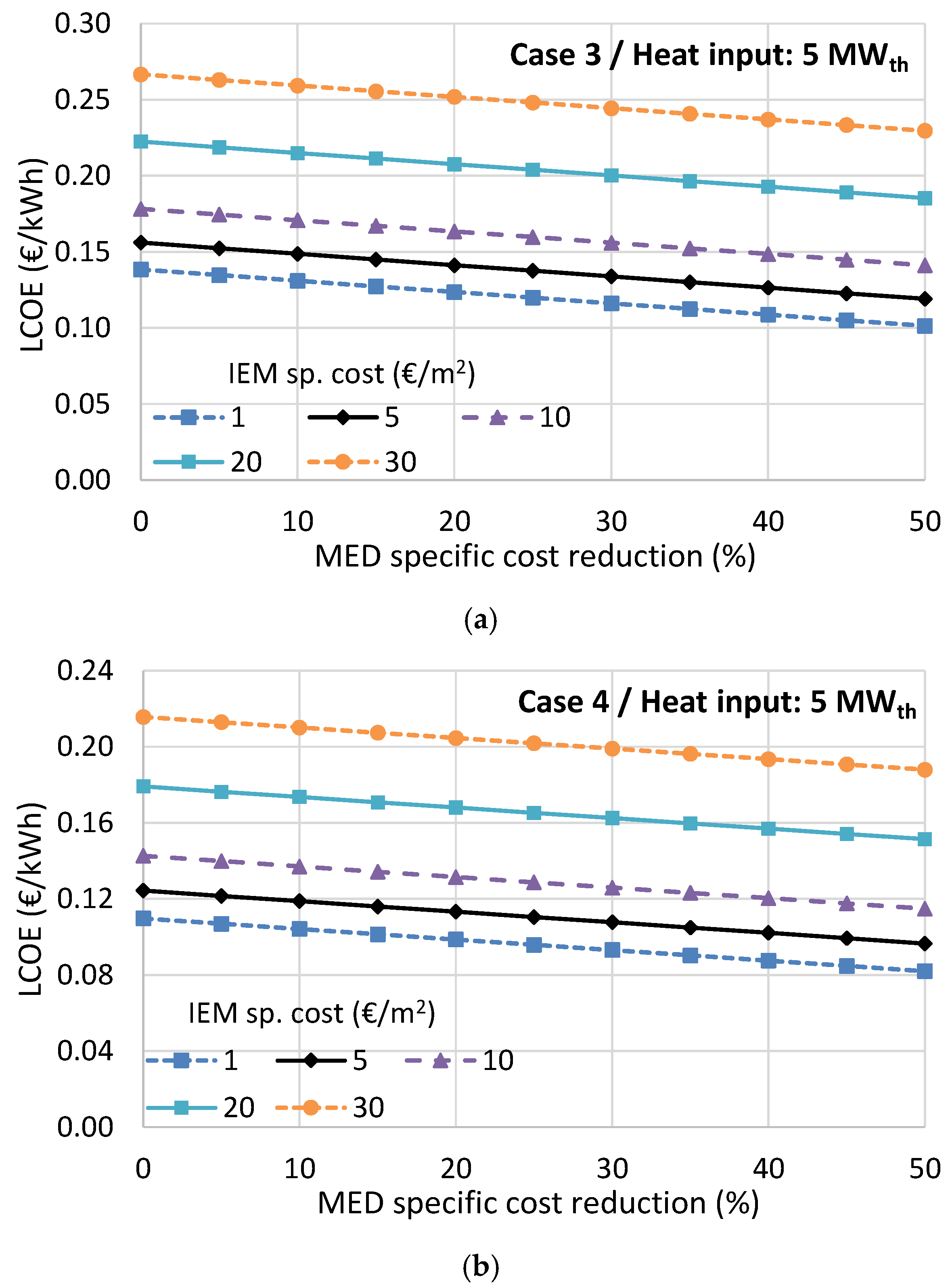
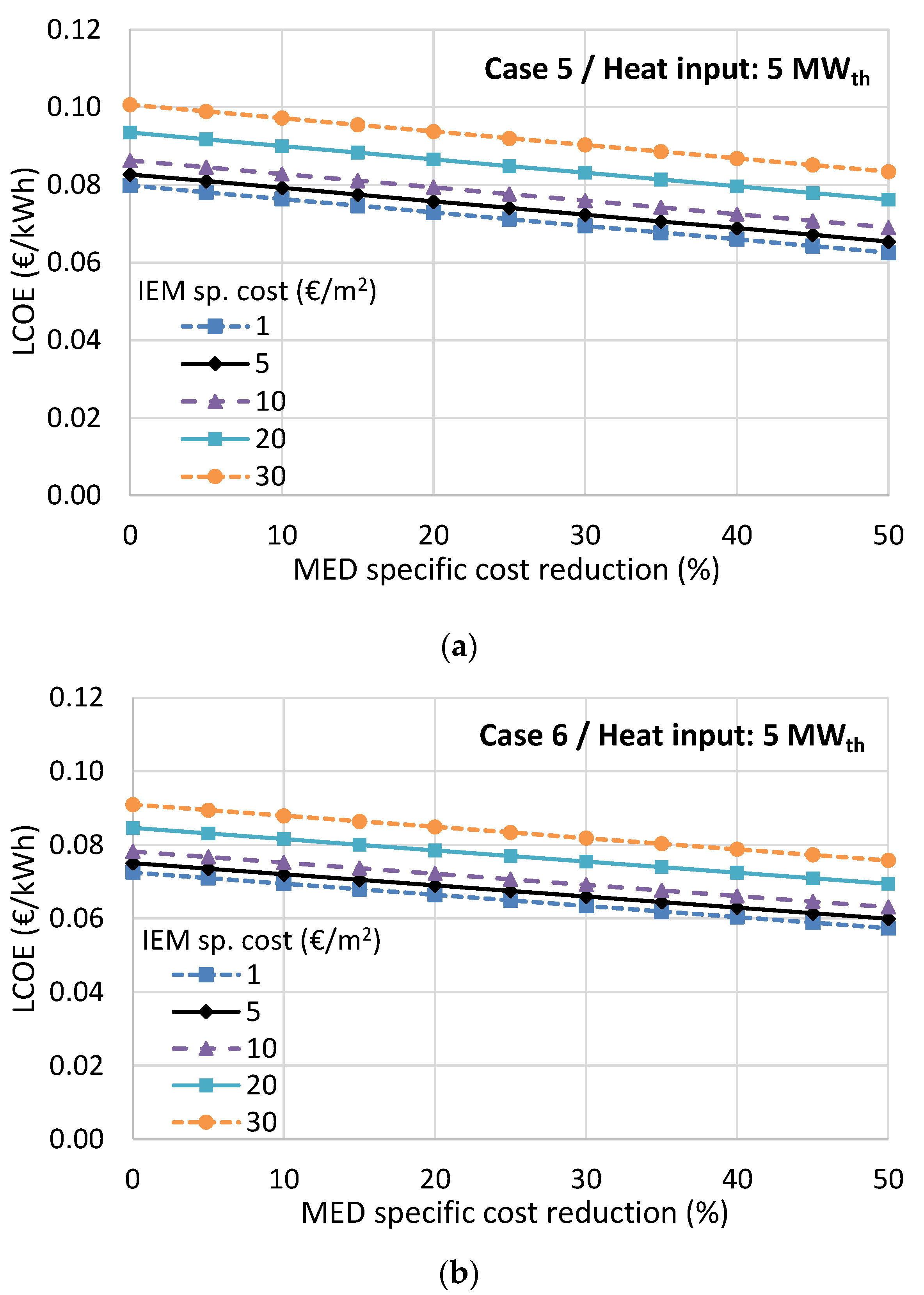
Table 3. These results are used as input in the cost analysis model to perform the LCOE calculations. The thermal efficiency is defined as the ratio of net power production to the heat input, including the heating of the solutions entering the stacks for cases 5 and 6.
The high-performing membranes bring more than a three-fold power production increase, and the use of KAc instead of NaCl accompanied by the reheating option greatly increases the thermal efficiency, reaching a value of 5.5%. This value is similar or even slightly higher compared to the ORC technology for the same heat source temperature of 100 °C [
29,
30,
31]. The thermal efficiency of the RED-MED system under cases 5 and 6 can be increased further, reaching values of about 10%, as presented in Ref. [
21], for a high number of MED effects. This high-efficiency option is examined further in
Section 5.4. For comparison, the Carnot efficiency for these temperatures is 20.1%.
For all configurations examined, a thorough cost analysis has been conducted based on the methodology presented in
Section 3. These results are presented in
Section 5 and are supported with an LCA described in
Section 4, in order to evaluate this technology from an environmental impact perspective.
6. Conclusions
The potential of different configurations of the RED-MED heat engine is presented by using a detailed economic analysis accompanied by a life-cycle environmental assessment. Various RED-MED configurations have been examined using both reference and high-performing membranes, introducing the system scale, and exploring a wide range of the main cost figures of the RED and MED parts.
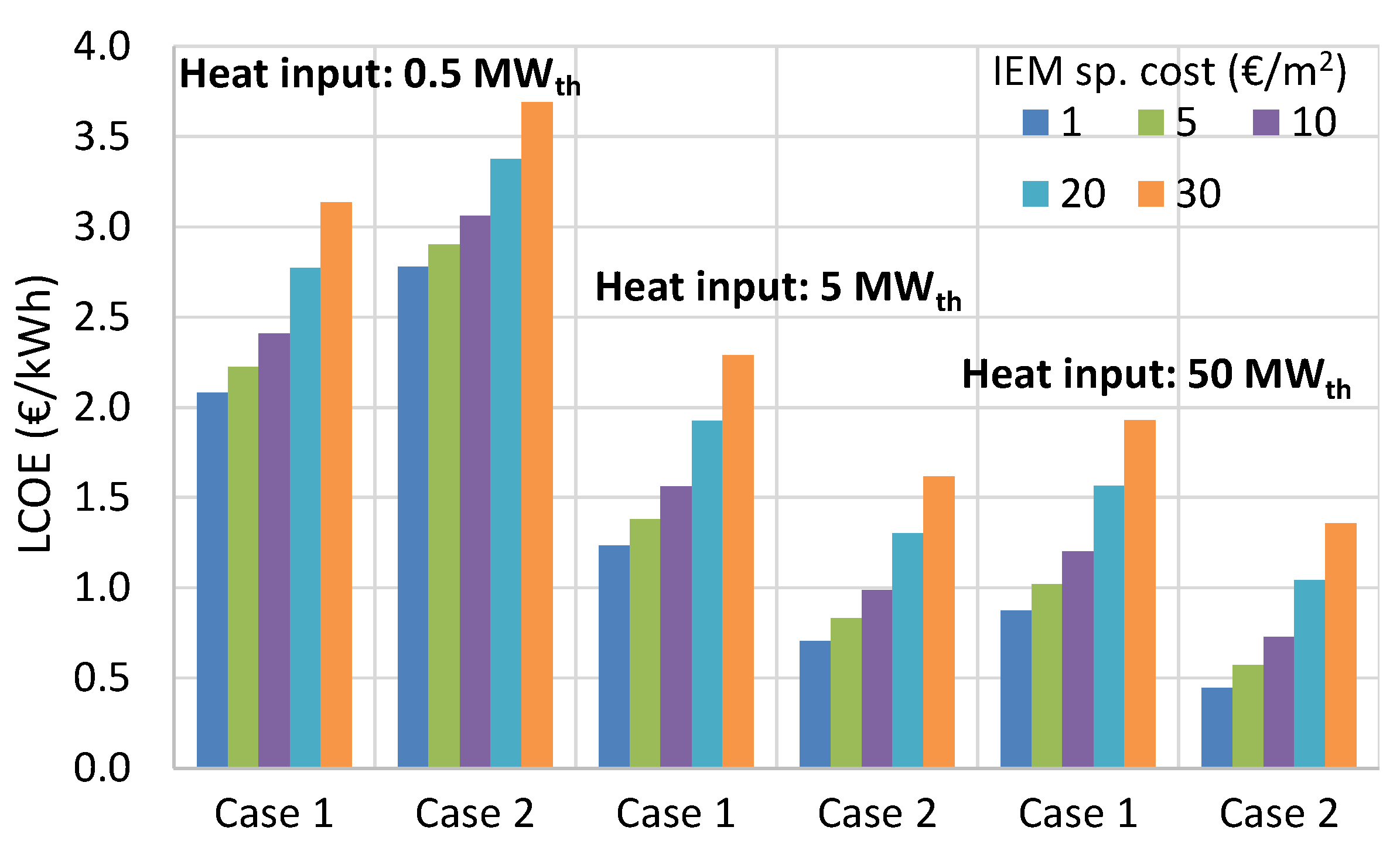
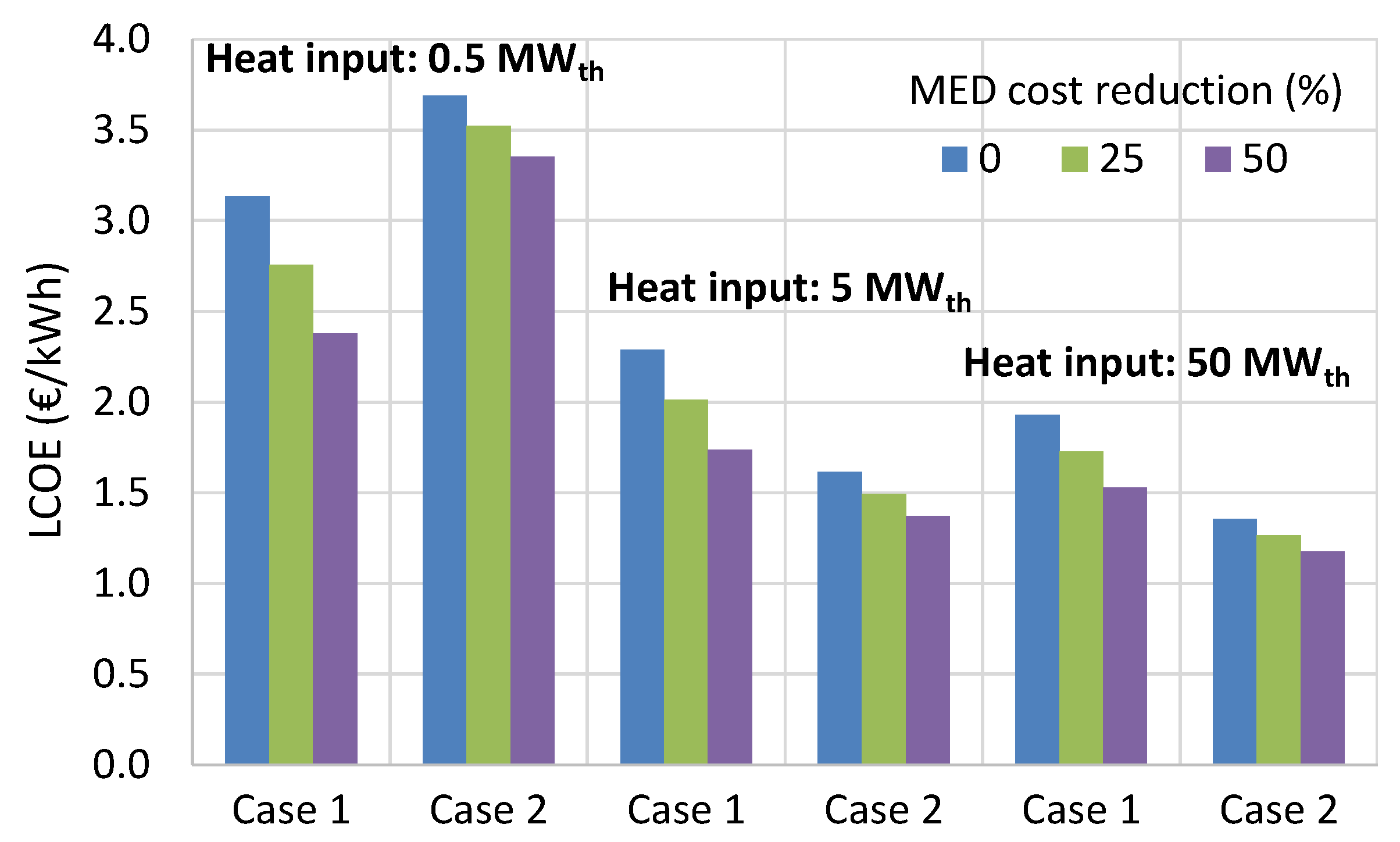
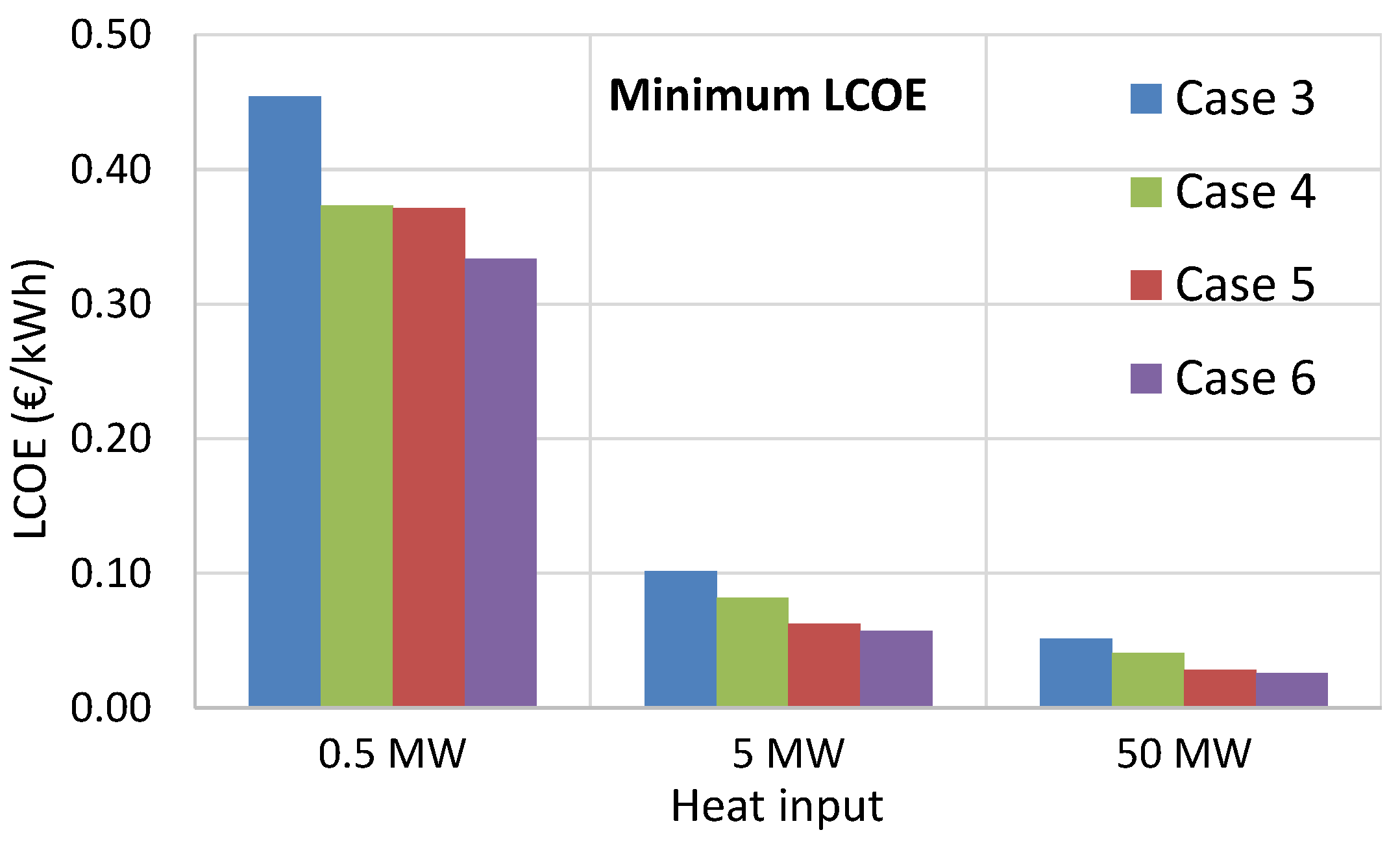
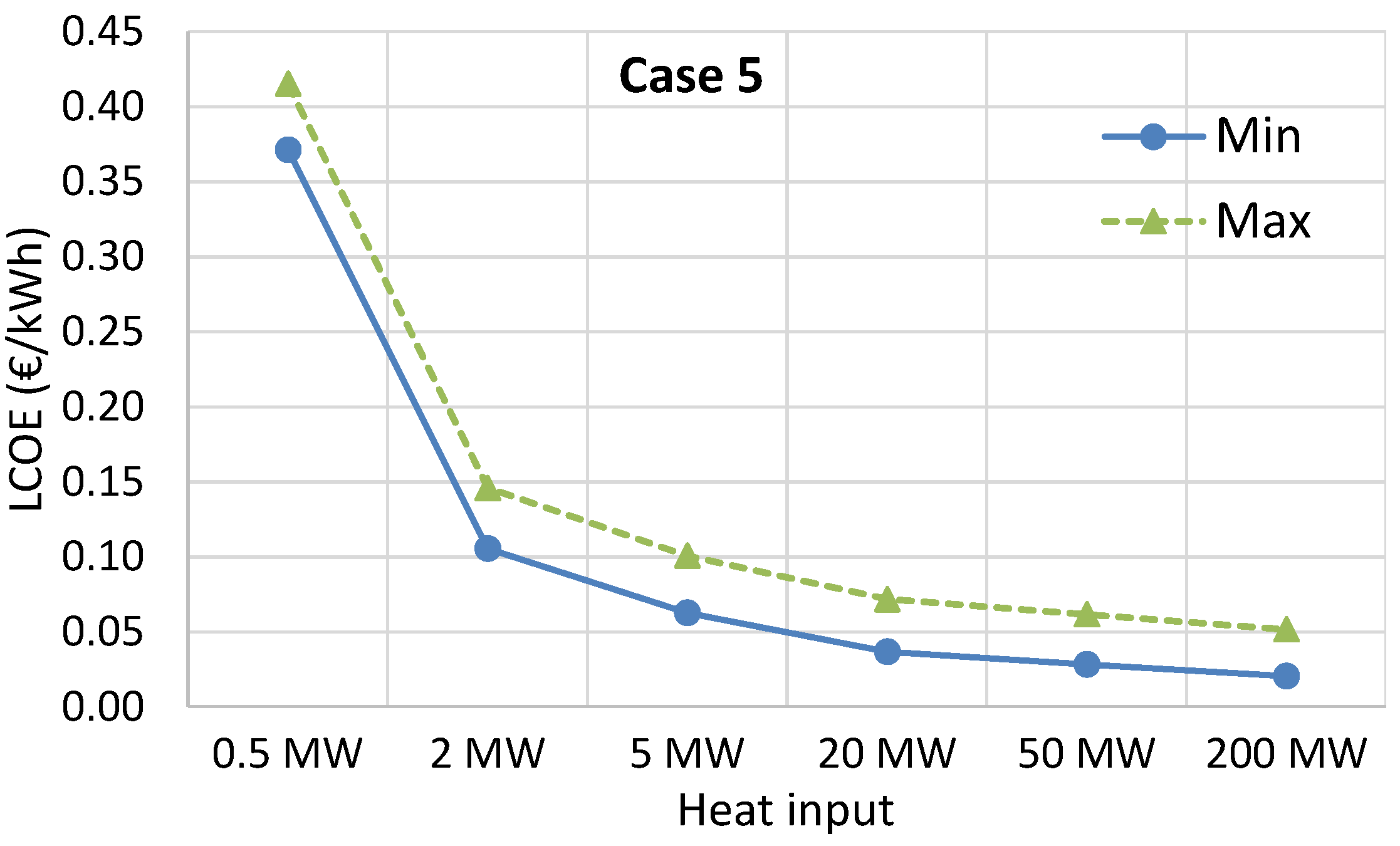
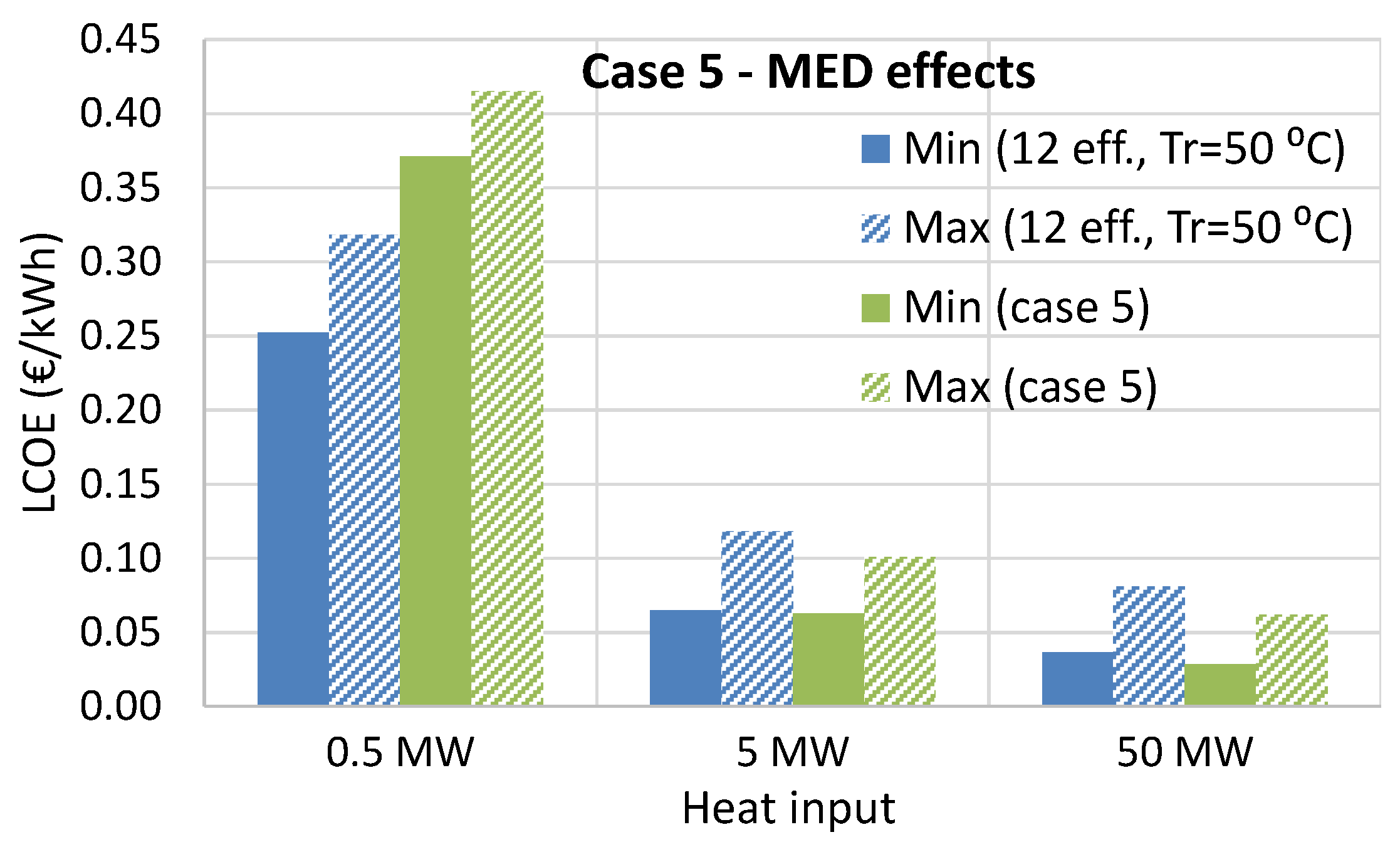
The economic analysis showed that the RED-MED system can become a promising and cost-competitive heat-to-power technology (reaching a LCOE of 0.06 €/kWh) for exploiting low-temperature waste heat when using high-performing IEMs, indicating that research in improving their performance should be a priority. When taking into account possible future reduction of the specific costs of the IEMs and MED equipment, while using preferably the KAc salt instead of NaCl, the resulting LCOE can be as low as 0.03 €/kWh for large-scale systems. However, there are many other cases that could offer very low LCOE values in the range of 0.04–0.10 €/kWh, even for medium-scale systems with a heat input of 5 MW, and without relying on drastic cost reductions of the RED and MED components. For small-scale systems with a heat input of 0.5 MW, the LCOE is much higher (the lowest possible value in the most optimistic scenario is 0.33 €/kWh), due to the high specific capital cost of the MED. The best performing case has been identified (case 5) that uses a low number of MED effects to reduce the specific cost of the regeneration process, while the use of KAc instead of NaCl has positive effects on both the performance and the cost. Finally, the reheating option to a reasonable temperature of 50 °C is necessary to improve the cost-effectiveness without imposing too much thermal stress on the membranes.
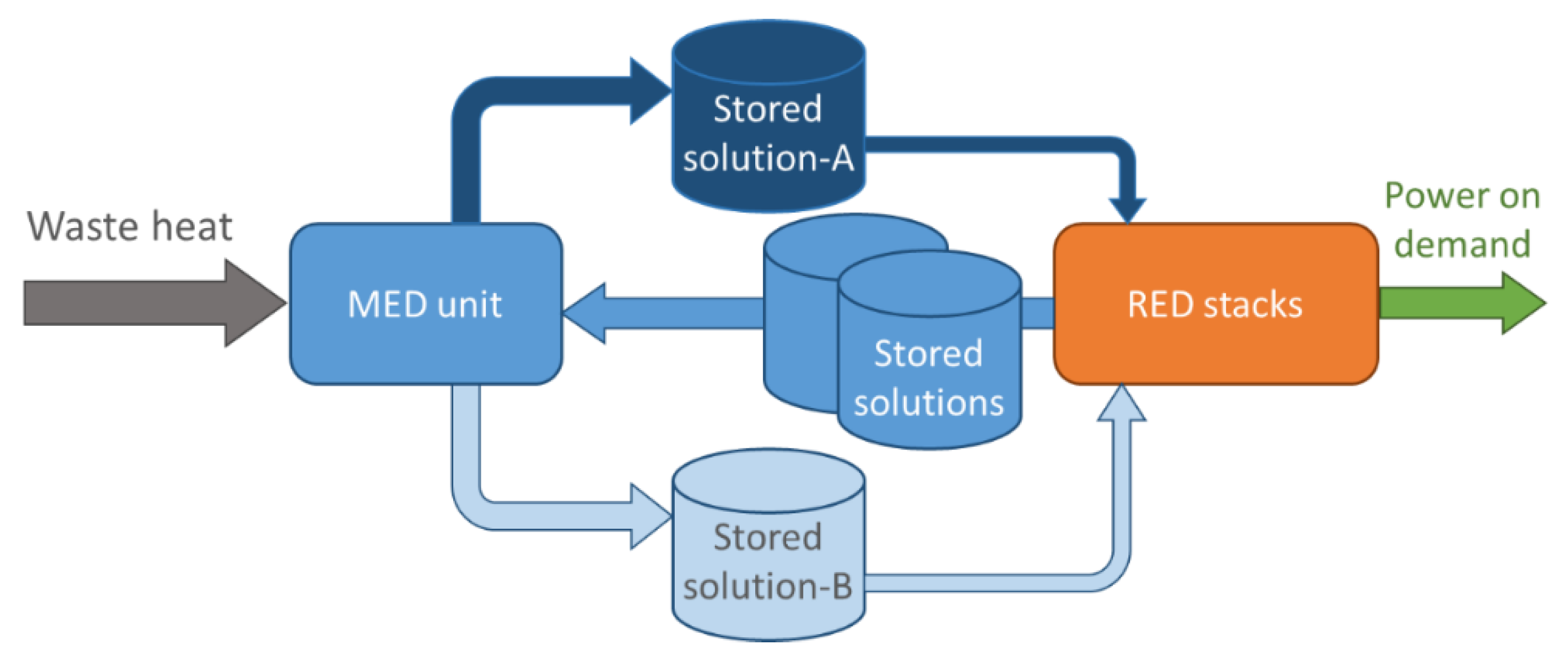
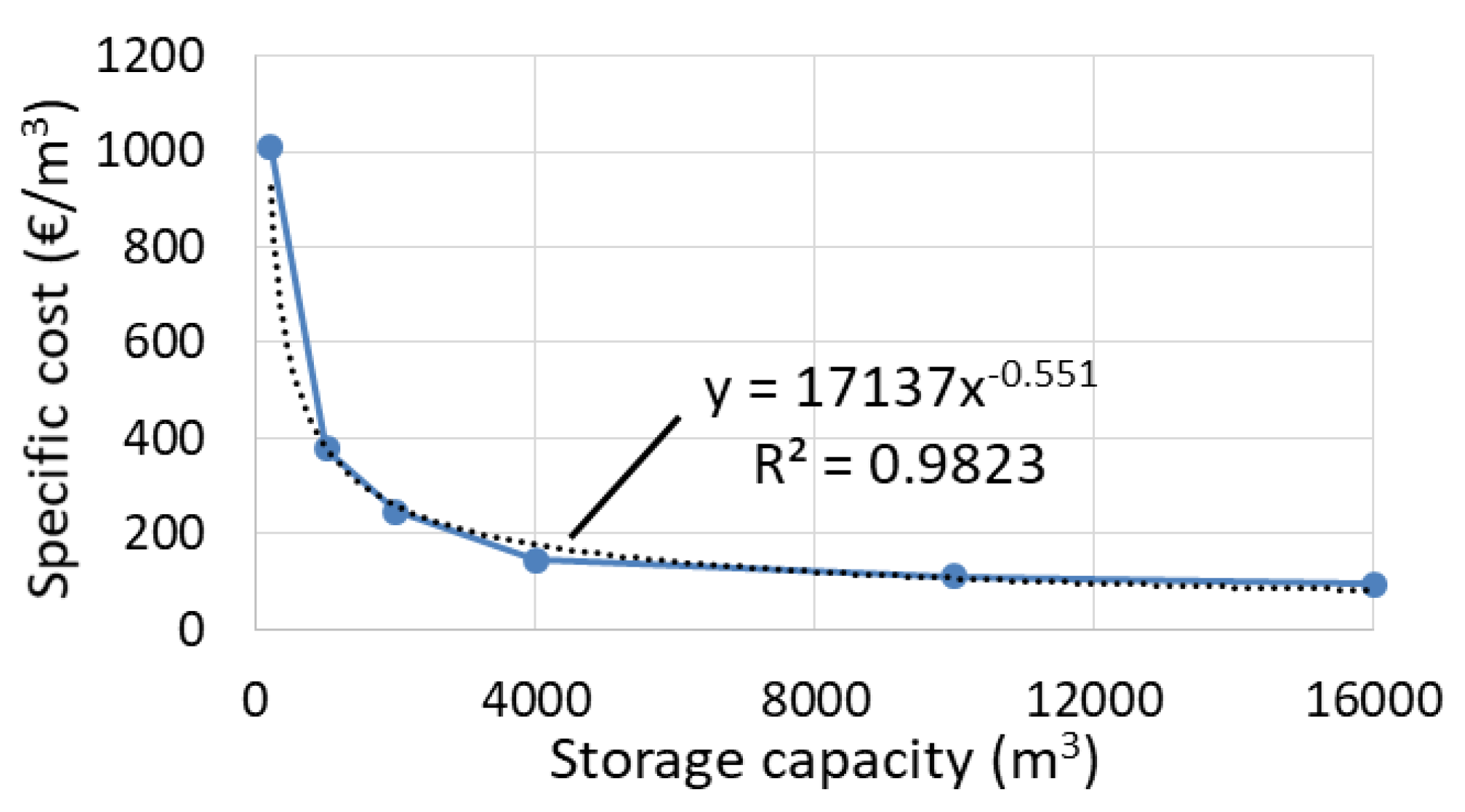
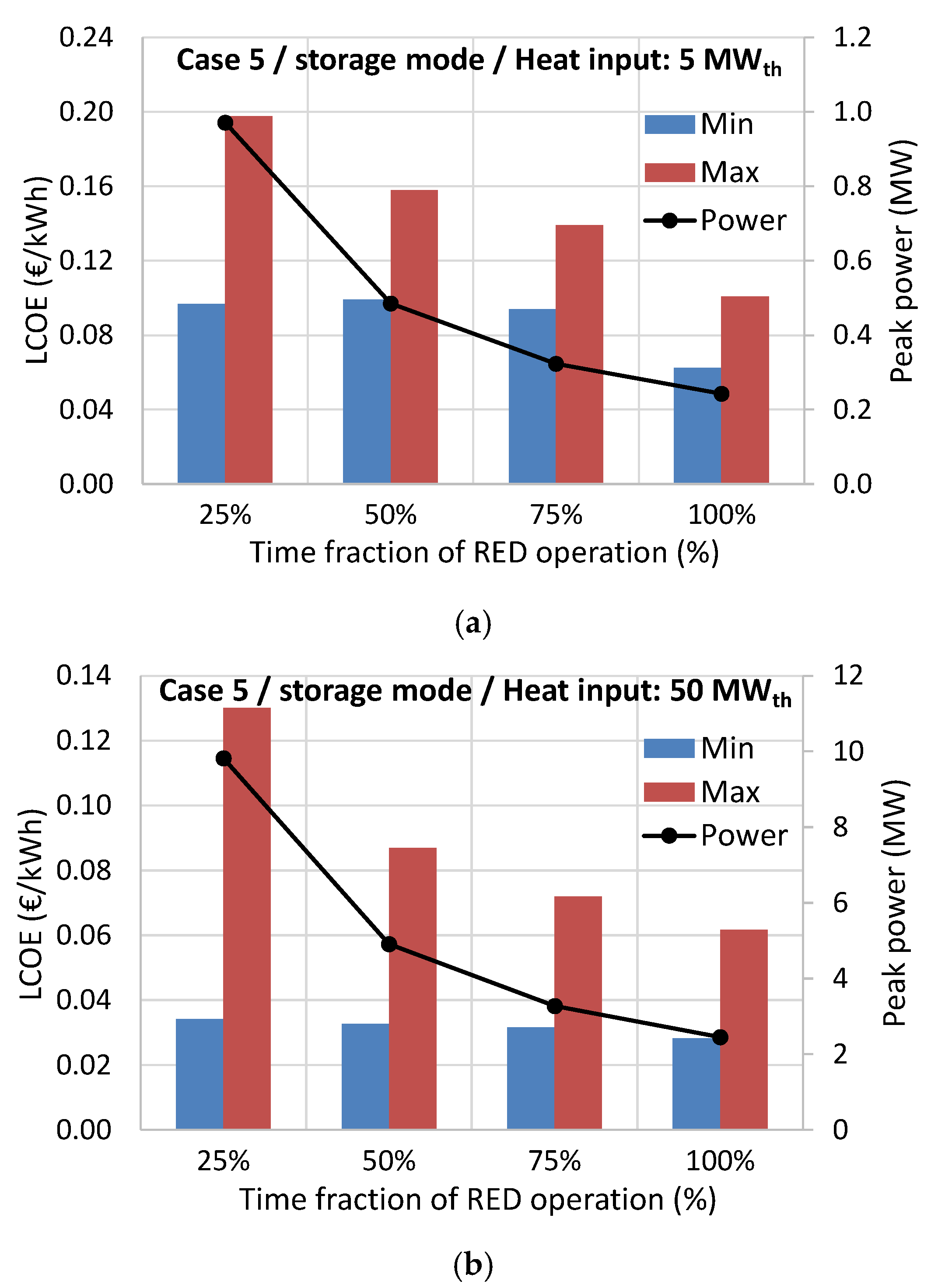
This best-performing case was then examined in storage mode, where the MED unit operates continuously to regenerate two solutions which are then stored in large reservoir tanks. A parameter that expresses the time fraction that the RED operates has been introduced, showing that the resulting LCOE increases for higher peak power production, but it can be kept below 0.10 €/kWh for large systems, even without relying on important future cost reductions of the RED and MED components, thus offering significant opportunities to industrial unit operators for peak power management and shifting.
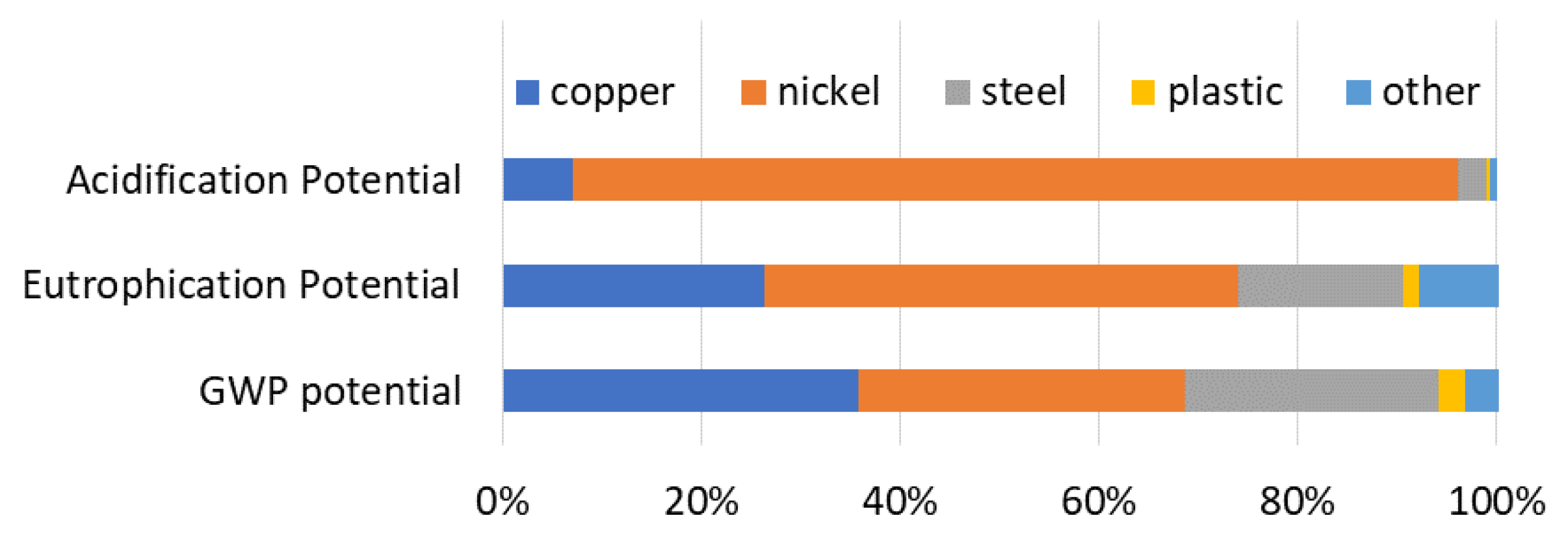
The conclusions of the life-cycle environmental analysis point to the same solution (case 5), since the lower number of MED effects reduces the amount of metals used in the construction, which are the materials responsible for most of the environmental impacts.
The overall conclusion of the RED-MED system in both continuous and storage modes is that it can be more cost-competitive than other membrane-based heat engines, as well as to standard ORC technology. Also, the environmental impacts of the RED-MED system are low; lower than most other sustainable energy technologies and similar to ORC systems. In order to exploit this potential and to bring the RED-MED system closer to the market, the membranes’ performance would need to approach the performance of the high-performing membranes, preferably accompanied by a cost reduction, which is a direct effect of the economy of scale and large-scale market uptake.