Abstract
HVDC cable systems connected to HVDC overhead lines are subject to fast front overvoltages emanating from the line when lightning strikes a shield wire (backflashover) or a pole conductor (shielding failure). Representative fast front overvoltage levels for HVDC cable systems are usually established without considering their statistical characteristics. A statistical method to determine overvoltages related to the acceptable mean time between failure (MTBF) for the cable system was developed previously. The method accounts for the statistical distribution of lightning current magnitudes as well as the attenuation of the overvoltage wave due to corona discharges on the line, since this effect dominates for system voltages up to about ±320 kV. To make the method suitable for higher system voltages as well, this article introduces an improved statistical method which also accounts for surge attenuation through resistive effects, soil ionization, and statistical treatment of overvoltages due to shielding failures. To illustrate the improved method, it is applied to a case study for a ±525 kV DC line.
1. Introduction
HVDC allows efficient transportation of large amounts of electric power over long distances. It is one of the enabling technologies in adapting the electric power system in the transition to a sustainable energy system, e.g., as part of a large-scale introduction of renewable energy sources. More and more HVDC systems take the form of mixed overhead line/cable systems, mainly due to environmental reasons. HVDC cable systems connected to HVDC overhead lines are subject to fast front overvoltages emanating from lightning strikes to the line [1,2]. Two causes of lightning overvoltages have to be considered: backflashovers across the line insulators that may occur when lightning strikes a shield wire, and shielding failures occurring when lightning bypasses the shield wire and terminates directly onto the pole conductor.
Representative fast front overvoltage levels for HVDC cable systems connected to overhead lines are usually established without considering the statistical characteristics of the overvoltages. This may lead to overly conservative dimensioning of the cable insulation. To determine representative fast front overvoltage levels for the cable system, a statistical method was developed focusing on type test requirements for ±320 kV DC cable systems [3]. The aim of the method was to minimize the number of simulations needed in order to determine overvoltage levels in the cables related to the acceptable mean time between failure (MTBF) for the cable system. The method is based on the statistical concept for overvoltage protection of substations described in references [4,5,6]. For substations, the steepness of the impinging overvoltage wave is of primary interest, considering the protective distances of surge arresters. For cable systems, on the other hand, the overvoltage magnitude is the main concern. Thus, the focus of the statistical method for cables is on the magnitude of overvoltage waves impinging on the cable at the line/cable transition station.
The original method [3] focuses on backflashovers and accounts for the statistical distribution of lightning current magnitudes as well as the attenuation of the overvoltage wave due to corona discharges on the line, since this effect dominates for system voltages up to about ±320 kV. To make the method suitable for higher system voltages as well, this article introduces an improved statistical method which also accounts for surge attenuation by resistive effects, the influence of soil ionization, and statistical treatment of overvoltages due to shielding failures. To illustrate the improved method, it is applied to a case study for a ±525 kV DC line.
2. Improved Statistical Method
The procedure for the improved statistical method is divided into three steps:
Step 1: Characterization of the line. The overhead line is characterized by its response to lightning strikes terminating at a shield wire or a pole conductor. At this stage, the cable is not considered. The response of the overhead line is determined through transient simulations and expressed as:
- the relationship between lightning current and surge voltage magnitude at the striking point,
- the shape of the overvoltage wave tail, and
- the attenuation of the overvoltage magnitude due to voltage drops in shield wires, conductors and tower grounds, primarily caused by resistive effects.
The simulations are performed without directly considering the effect of corona attenuation in order to minimize the complexity of the simulation model. Corona attenuation is instead considered in the statistical procedure described below.
Step 2: Statistical procedure. Corona discharges reduce the front steepness and, hence, the magnitude of the overvoltage wave as it travels down the line, as described in references [4,5,6]. The effect of corona attenuation can be considered in a simplified way by assuming that the overvoltage wave, after traveling some distance from the striking point, can be approximated by an impinging surge superimposed on the DC operating voltage of opposite polarity. The surge is characterized by a linearly rising front with the steepness S, a corresponding front time Tf, and an exponentially decaying tail with a time constant τ determined in Step 1, see Figure 1.
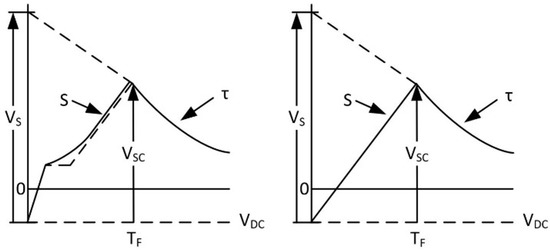
Figure 1.
Voltage surge from a backflashover after traveling some distance on the line (left), and the approximation as an impinging surge with a linear front (right).
By assuming that the voltage surge magnitude at the striking point is Vs, the surge magnitude Vsc at a distance d from the striking point can be calculated using the following expressions [5]:
where Kc is the corona damping coefficient (1700 km∙kV/µs for triple conductor bundles [4,5,6]).
When combining the corona attenuation with the attenuating effect of resistive voltage drops as the overvoltage wave travels down the line, the magnitude Vscr at a distance d is given by:
where the function r(d) is determined from the transient simulations by studying the overvoltage levels at various tower positions.
The expression for Vscr makes it possible to determine the overvoltage magnitude Vs that is required at the striking point to obtain a certain Vscr value at a certain point on the line. Furthermore, the relation between lightning current and surge voltage magnitudes at the striking point can be used to determine the required lightning current level and the associated probability of exceedance.
The procedure is simplified by assuming that all lightning strikes to a line terminate at a tower position. Hence, the expression for Vscr and the relationship between the lightning current and surge voltage magnitude can be used to determine the lightning current magnitude required at each tower position in order to obtain a certain Vscr value at the transition station.
In order to calculate the accumulated risk of exceeding a certain Vscr, it is required to consider lightning strikes at any tower along the line that produce the same Vscr at the transition station. In this way, a corresponding set of lightning current magnitudes is obtained for a given Vscr. Considering the statistical distribution of lightning current magnitudes [7], the associated probabilities can be accumulated in order to obtain the total risk of exceeding Vscr.
Further, by accounting for the annual number of lightning strikes to shield wires or pole conductors, the established set of lightning currents can be associated with a statistical return period, expressed as a mean time between surges (MTBS). Thus, by iterating the Vscr level until the MTBS equals the acceptable MTBF of the cable system, a resulting set of lightning currents is obtained which can be used to calculate representative lightning overvoltage levels in the cable system.
Step 3: Determination of representative lightning overvoltage levels in the cable system. Each lightning current in the set will produce the same Vscr at the transition station when injected at the respective tower. However, to minimize the effect of not considering corona attenuation in the simulation model, the lightning current is preferably injected at the first tower outside the transition station when calculating overvoltages in the cable system.
The improved statistical method described above may be applied to backflashovers as well as shielding failures. Special considerations for the two different applications are discussed below.
2.1. Backflashovers
Backflashovers on overhead lines are treated in detail in reference [8], therefore, only the special considerations regarding DC lines are discussed here.
When lightning strikes a shield wire on a DC line, the towers take on a negative or positive transient voltage depending on the polarity of the lightning flash. This may lead to high overvoltages across the line insulators, primarily at the stricken tower and especially across insulators for the pole conductor of opposite polarity. The risk of backflashover depends primarily on the ground flash density, the lightning stroke current magnitude, and the grounding resistance of the towers.
For backflashovers, the annual number of lightning strikes to a 100 km line may be estimated using the expression below [8]:
where Ng (flashes/km2/year) is the ground flash density, H (in meters) is the tower height and Sg (in meters) is the separation distance of the shield wires (Sg = 0 for a single shield wire).
2.2. Shielding Failures
Lightning strikes may bypass the shield wire and terminate directly onto the pole conductor, referred to as a shielding failure. The shielding properties of the line are analyzed by considering the presence and position of the shield wires with respect to the pole conductors. The important parameters are the critical current and the maximum penetration current: the critical current is the maximum lightning current that can be injected into the pole conductors without flashover of the line insulation, and the maximum penetrating current is the maximum current that can possibly terminate on the pole conductors. If the maximum penetrating current exceeds the critical current, then flashover of the line insulation can occur, thereby limiting the magnitude of the incoming surge to the cable system.
The critical current depends on the lightning overvoltage withstand strength of the line insulators and the surge impedance of the pole conductor. Near the transition station, the critical current is also affected by the presence of the cable system, which is characterized by its low surge impedance. Tower grounding has no effect on the critical current, since it is assumed that no flashover occurs.
The maximum penetrating current, on the other hand, depends on the lightning attachment properties of the shield wire(s) and pole conductors. Recent findings indicate that not only the positions of shield wires and pole conductors, but also the instantaneous value and the polarity of the operating voltage are important to the shielding properties [9,10].
In the present study, the lightning attachment properties are evaluated by means of the leader progression model (LPM) [9] as implemented in reference [11] and reference [12]. The simplified approach [12], originally developed for AC lines, is applied to the DC line in the present study by setting the instantaneous voltage of the pole conductors to be equal to the positive or negative DC operating voltage (±525 kV).
3. Case Study Description
The improved statistical method is demonstrated by calculations of lightning overvoltages in an exemplary ±525 kV HVDC cable system modeled in PSCAD (version 4.6.3, Manitoba Hydro International, Ltd., Winnipeg, MB, Canada). The cable system, which consists of two 100 km land cables, is connected to a long bipolar overhead line at one end and terminated in a converter station at the other end. An overview of the model is shown in Figure 2.
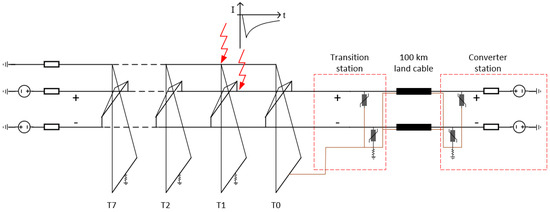
Figure 2.
Overview of model used for calculation of lightning overvoltages in the cable system.
3.1. Lightning Parameters
The annual ground flash density may vary from less than 0.1 to more than 10 flashes/km2/year depending on the location [7]; a moderate value of 2/km2/year is used for the case study. The magnitudes of (first) negative and positive lightning strokes may be approximated by log-normal distributions [7]. Most flashes are of negative polarity; positive polarity flashes account for less than 10% of the global lightning activity [7].
Backflashovers may be caused either by positive or negative lightning strokes. The combined statistical distribution of negative and positive first stroke current magnitudes [7] is used for backflashover calculations in this case study. The front time and maximum steepness of the lightning current waveform are determined as functions of the current magnitude as described in Section 3.2.1. The longer duration of positive flashes is further considered by choosing a conservative time to half value of the tail, 200 µs, which is exceeded by about 5% of negative first strokes and about 50% of positive strokes [7]. With a ground flash density of 2/km2/year and a tower height of 38 m, Equation (3) gives the annual number of lightning strokes to the line, NL, as 50 per 100 km. With a typical 400 m span length, this results in 0.2 strokes annually to each span on the line.
Shielding failures, on the other hand, are mainly associated with negative lightning strokes, thus, the distribution of negative first stroke current magnitudes [7] is used for shielding failure calculations. The maximum steepness and the front time are chosen as functions of the current magnitude as described in Section 3.2.1, and the time to half value for the tail is chosen as the mean value for negative first strokes, i.e., 75 µs. With a ground flash density of 2/km2/year and the average shield wire and pole conductor heights shown in Figure 3, the simplified LPM [12] yields a shielding failure rate of 0.064/100 km/year for the positive DC pole, and practically zero for the negative DC pole. Furthermore, the calculated maximum penetrating current is 25 kA for the positive DC pole [12].
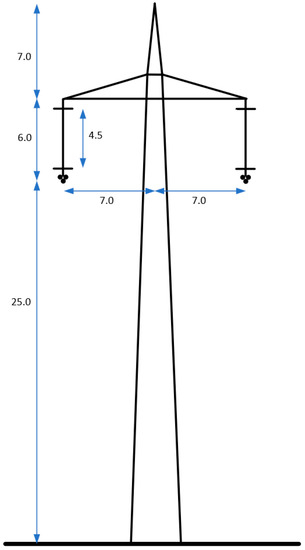
Figure 3.
Overhead line tower.
3.2. Modeling
3.2.1. Lightning Stroke Waveshape
The lightning stroke is modeled utilizing a wave shape based on the findings of [13]. The front of the wave is defined in terms of the front time, Tf, the maximum steepness, Sm, the peak amplitude, Ip, of the lightning current, while the tail is defined by the time to half value, Th. The relationships of these parameters are summarized in Table 1.

Table 1.
Lightning current waveshape parameters as functions of the current peak.
3.2.2. Underground Cable
The cable used for the study is a 525 kV, 2010 mm2 Al land cable. It is modeled in PSCAD using frequency dependent parameters.
3.2.3. Overhead Line
A model comprising seven towers is implemented in PSCAD to simulate the line section closest to the transition station. Each span has a length of 400 m and is modeled using frequency dependent parameters. Figure 3 shows the tower dimensions. The tower is modeled using a combination of inductances for shorter parts, e.g. cross-arms, and surge impedance for the tower leg based on a cylindrical tower shape [14]. The DC poles are equipped with triple conductor bundles with data according to Table 2. The conductors are terminated after the last tower by voltage sources behind surge impedances; the shield wire is terminated by a surge impedance. The LPM is used to simulate the flashover characteristics of the insulators when they are subject to lightning overvoltages [14].

Table 2.
Overhead line data.
Simulations are performed with and without considering the impact of soil ionization on the tower footing resistance. The ionization is considered in the model by a variable resistance Ri according to the following relation [14]:
where Ig is defined as
where E0 is the critical gradient required for soil ionization (chosen as 400 kV/m), ρ is the soil resistivity and R0 is the tower footing resistance at low currents.
3.2.4. Surge Arresters
Surge arresters are placed at the transition station and in the converter station. They are modeled as non-linear resistances based on their V-I characteristic, which is presented in Table 3. The inductive voltage drop due to the arrester height and connection leads is considered in the form of an additional series inductor (about 6 µH per arrester).

Table 3.
Surge arrester protective levels.
3.2.5. Converter Station
The converter station at the remote end of the cable system is modeled by ±525 kV DC voltage sources behind inductances of 20 mH per pole representing the smoothing reactor.
4. Results
4.1. Characterization of the Line
The response of the overhead line to lightning strikes is studied using a simulation model comprising 40 towers terminated by the surge impedance of each conductor. Currents are injected either into the shield wire or into the positive pole conductor at a tower at the midpoint of the line in order to determine:
- the relationship between lightning current and surge voltage magnitudes,
- the shape of the overvoltage wave tail, and
- the attenuation of the overvoltage magnitude due to voltage drops as function of the distance to the stricken tower.
4.1.1. Backflashover
Figure 4 and Figure 5 show the voltage in the positive pole at the stricken tower for different magnitudes of negative lightning current injected into the shield wire, with and without consideration for soil ionization. The surge is superimposed on the positive DC operating voltage (+525 kV). Observe that the results of the calculations in this section are solely used to characterize the response of the line, independently of the probability of actual occurrence of such high lightning current magnitudes. It should be noted that the overvoltage levels include large voltage drops between local tower grounds and remote earth due to comparatively high tower footing resistances, and that no flashover occurred for the negative pole conductor.
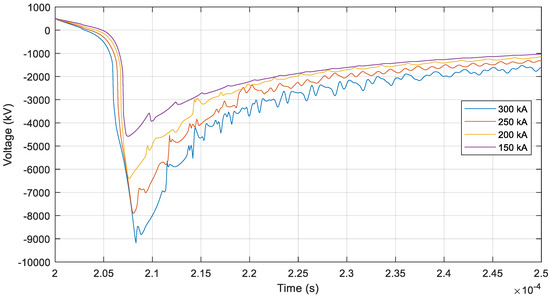
Figure 4.
Voltage on the positive pole conductor following a lightning strike to the shield wire for different lightning current magnitudes without considering soil ionization.
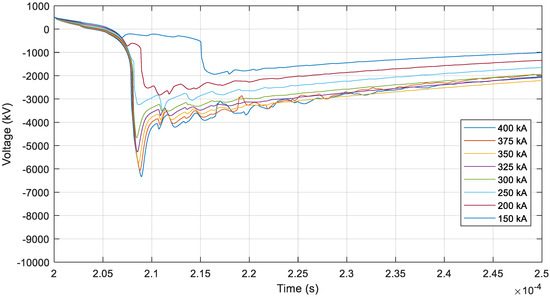
Figure 5.
Voltage on the positive pole conductor following a lightning strike to the shield wire for different lightning current magnitudes when considering soil ionization.
Based on the results above, Figure 6 shows the lightning current magnitudes as functions of the voltage Vs, with and without consideration for soil ionization. Despite the slightly non-linear characteristics, linear approximations are used to describe the relations between the lightning current and surge voltage magnitudes at the stricken tower.
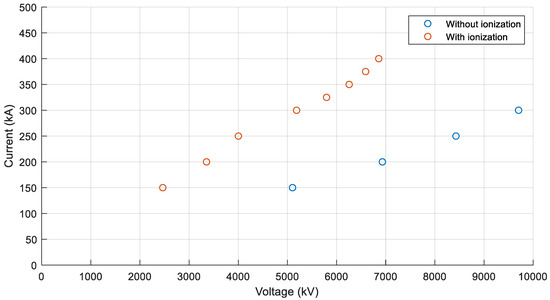
Figure 6.
Relation between lightning current and surge voltage magnitudes, with and without soil ionization.
When the tails of the overvoltage waves in Figure 4 and Figure 5 are approximated by exponentially decaying functions, the tail time constant τ is estimated at about 15 µs without considering soil ionization. When soil ionization is taken into account, the overvoltage waveshapes are modified, and the tail time constant τ increases to about 75 µs.
The attenuation due to voltage drops is determined by evaluating the surge magnitudes in the positive pole at several tower locations away from the stricken tower. Figure 7 and Figure 8 show the resulting overvoltages at different tower positions for a 250 kA lightning current stroke injected to the shield wire, with and without consideration for soil ionization. Based on the calculated overvoltages, curve-fitting is performed to find expressions describing the (mainly resistive) attenuation as a function of distance, r(d). The results of the curve-fitting are shown in Figure 9.
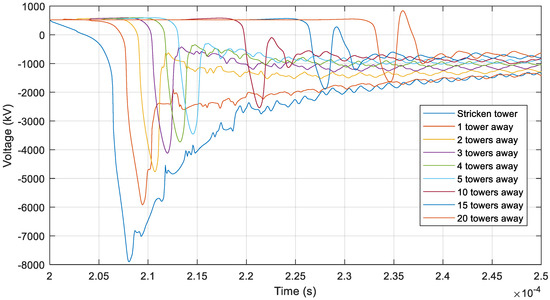
Figure 7.
Voltage on the positive pole conductor at different tower positions for a 250 kA lightning current stroke injected to the shield wire without considering soil ionization.
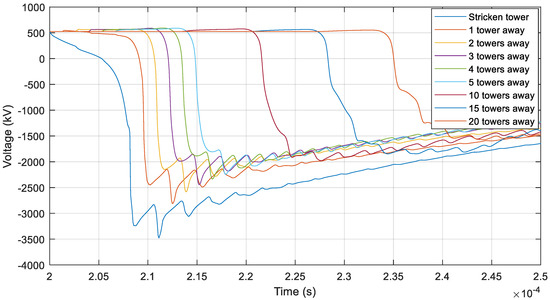
Figure 8.
Voltage on the positive pole conductor at different tower positions for a 250 kA lightning current stroke injected to the shield wire when considering soil ionization.
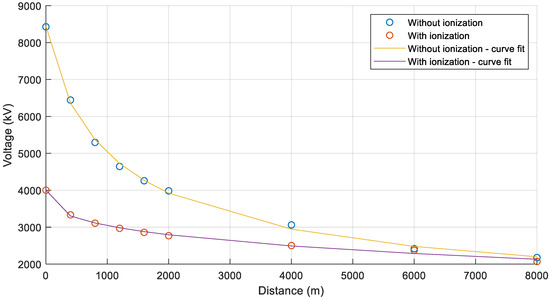
Figure 9.
Curve-fitting of the function r(d) for backflashovers.
4.1.2. Shielding Failure
Figure 10 shows the voltage on the positive pole at the stricken tower for different magnitudes of negative lightning current injected into the positive pole conductor. Since no flashover occurs, the overvoltage wave superimposed on the DC operating voltage has a shape similar to that of the lightning current, thus, the tail time constant τ is estimated to be 80 µs. As expected, the resulting relationship between the magnitudes of the lightning current and overvoltage Vs equals the inverse of the pole conductor surge impedance divided by two, see Figure 11 (the minor transients occurring at 2.6 × 10−4 s are caused by non-ideal terminations of the line model).
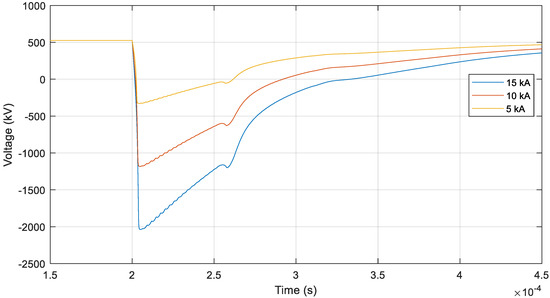
Figure 10.
Voltage on the positive pole conductor due to a lightning strike to the conductor for different lightning current magnitudes.
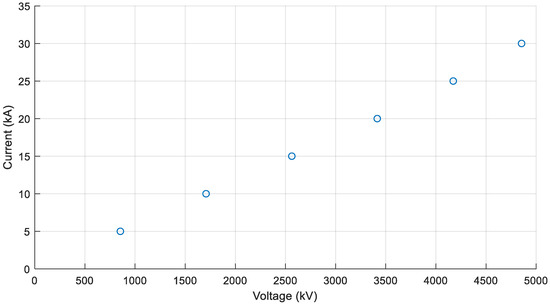
Figure 11.
Relation between lightning current and surge voltage magnitudes for shielding failure.
The attenuation due to voltage drops as a function of the distance to the striking point is determined by evaluating the surge magnitude on the positive pole at several towers. Figure 12 shows the resulting overvoltages at different tower positions for a 15 kA lightning current stroke injected to the positive pole conductor. Curve-fitting is performed in order to find an expression describing the (mainly resistive) attenuation of the overvoltage magnitude as a function of distance, r(d). The results of the curve-fitting are shown in Figure 13.
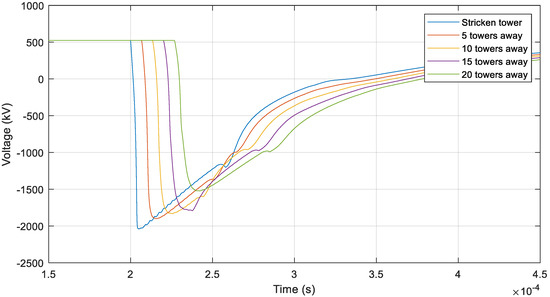
Figure 12.
Voltage at different tower positions for a 15 kA lightning current stroke injected to the positive pole conductor.
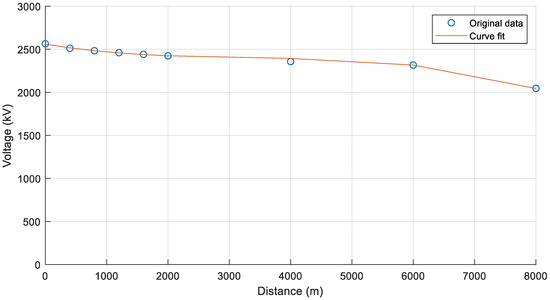
Figure 13.
Curve-fitting of the function r(d) for shielding failures.
4.2. Statistical Procedure
The results presented in Section 4.1 are used as input to the statistical method described in Section 2. The required MTBS is chosen as 300 years, corresponding to an accumulated annual risk of 0.00333. Both backflashovers and shielding failures contribute to the accumulated risk and should be treated separately since the stresses on the cable system may differ regarding overvoltage magnitude, duration, polarity change, etc.
4.2.1. Backflashovers
For the present study, due to the comparatively high tower footing resistances, it may be assumed that the major risk contributions emanate from backflashovers; thus, the MTBS requirement (300 years) is initially assigned solely to backflashovers.
Table 4 shows an excerpt from the statistical calculation for backflashovers without considering soil ionization. The table shows the lightning current I required at the respective towers to obtain equal impinging surge magnitudes Vscr at the transition station, with a return period equal to the desired MTBS. The annual risk per span of exceeding the respective current levels is calculated from the annual number of lightning strikes to each span. In this case, by setting Vscr to 4370 kV, the required MTBS of 300 years is attained by including risk contributions up to tower no. 8; more distant towers will give negligible contributions to the accumulated risk.

Table 4.
Statistical calculation for backflashover without considering soil ionization.
The statistical effect of soil ionization can be demonstrated by assuming the same overvoltage stress at the transition station while studying the influence on the MTBS. This is done by setting Vscr to the same value as before (4370 kV) while applying the calculated results for backflashovers with consideration for soil ionization presented in Section 4.1. As seen from Table 5, the slower decay of the overvoltage magnitude requires that significantly more towers be included in the risk accumulation. Hence, the lightning currents needed to obtain the same impinging surge as without soil ionization become significantly higher, and the corresponding MTBS increases from 300 to about 760 years.

Table 5.
Statistical calculation for backflashover with soil ionization considered.
4.2.2. Shielding Failures
Table 6 shows an excerpt from the statistical calculation when the MTBS requirement (300 years) is assigned solely to shielding failures. The table shows the lightning current I required at the respective towers to obtain equal impinging surge magnitudes Vscr at the transition station, with a return period equal to the desired MTBS. The annual risk per span of exceeding the respective current levels is calculated from the shielding failure rate for each span. Finally, the annual risk is accumulated for all towers where the required lightning current is below the maximum penetrating current, i.e., 25 kA. In the present case, the required MTBS of 300 years is attained by setting Vscr to 3160 kV and by including risk contributions up to tower no. 17.

Table 6.
Statistical calculation for shielding failure.
4.3. Simulation of Overvoltages in the Cable System
The calculated lightning current magnitudes shown in Table 4 and Table 6 are used as inputs to overvoltage calculations using a complete simulation model comprising both the overhead line and the cable system. As explained in Section 2, Step 3, the resulting overvoltages in the cable system for a backflashover (without considering soil ionization) or shielding failure are calculated by injecting negative lightning currents with a magnitude of 182 kA to the shield wire or 19 kA to the positive pole conductor, respectively, at the first tower outside of the transition station.
Figure 14 and Figure 15 show the resulting overvoltages across the cable insulation (i.e., between conductor and sheath) in the positive pole at different points along the cable: at the transition station, at 1, 3, 5, 20, and 50 km from the transition station, and at the remote end of the cable.
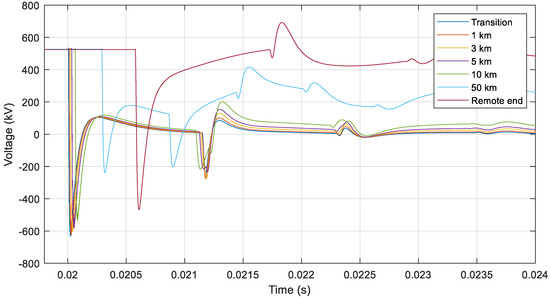
Figure 14.
Voltage on the positive pole at the transition station, at different points along the cable and at the remote end for a 182 kA lightning strike to the shield wire at the first tower outside of the transition station (without considering soil ionization).
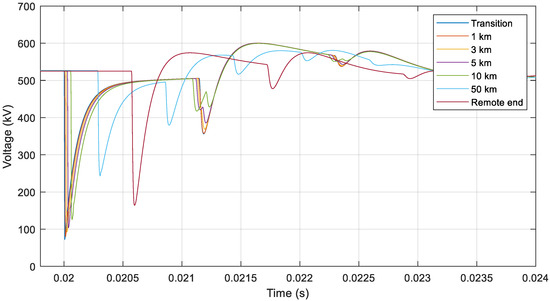
Figure 15.
Voltage on the positive pole at the transition station, at different points along the cable and at the remote end for a 19 kA lightning strike to the positive pole conductor at the first tower outside of the transition station.
5. Discussion
5.1. Backflashovers
The statistical calculation for backflashovers, without considering soil ionization, shows that overvoltages in the cable system, having an MTBS of 300 years, should be calculated for a current magnitude of 182 kA injected to the first tower outside the transition station. It can be noted that, although the current level depends on the ground flash density, grounding conditions and overhead line design chosen for the case study, the value is within the range of currents commonly used in deterministic studies, i.e., 150–250 kA.
As shown in Table 5, consideration of soil ionization results in an increased MTBS (from 300 to about 760 years) for the same overvoltage stress as without ionization. Thus, simulations without considering soil ionization will give conservative results in terms of MTBS.
Furthermore, the introduction of the resistive attenuation factor impacts the results in a significant way. Calculations have shown that by neglecting the resistive attenuation, the corresponding current to be injected into the first tower outside the transition station increases from 182 to 210 kA for the same MTBS. Thus, the calculated overvoltage levels in the cable system will be conservative if the resistive attenuation factor is not considered.
It is important to verify that the current used for the cable overvoltage calculations will cause a backflashover on the line. If the calculation results show that the current level for tower no. 1 is not high enough to cause backflashover when injected at the first tower outside the transition station, it indicates that the selected MTBS is exceeded, i.e., above 300 years in the present case. In such a case, to facilitate a comparison with overvoltages caused by shielding failures, it is suggested to repeat the calculations using a higher MTBS, until the current level for tower no. 1 is high enough to cause backflashover.
For the present case study, Figure 14 shows that 182 kA is a sufficiently large current to cause backflashover on the line. Furthermore, the results show that the maximum negative and positive overvoltage levels are −631 kV at the transition station and +692 kV at the remote end. However, it should be noted that the latter value will be affected by the response of the converter control system. No such response is being considered for this case study, while different actions by the control system are possible in practice.
5.2. Shielding Failures
The statistical calculation for shielding failures shows that overvoltages in the cable system, having the same MTBS as for backflashovers, i.e., 300 years in the present case, should be calculated for a current magnitude of 19 kA injected to the positive pole conductor at the first tower outside the transition station. Note that any changes in MTBS for backflashovers, as discussed in the previous section, must be reflected in the shielding failure calculations in order to achieve statistically comparable results.
Only towers for which the required lightning current is below the maximum penetrating current, i.e., 25 kA, should be included in the accumulated risk, in this case all towers up to no. 17. This is because shielding failures occurring beyond tower no. 17 will produce lower overvoltages at the transition station due to the combination of wave attenuation and the 25 kA current limitation.
It is important to verify that the current used for the cable overvoltage calculations will not cause flashover on the line, i.e., exceed the critical current, since this may limit the overvoltages in the cable system as discussed in Section 2.2. If the calculation results show that the current level is high enough to cause flashover, it is suggested to carry out calculations also for a current level just below the critical value. The highest overvoltages obtained from the two studies are then used for comparison with the results of the backflashover calculations.
For the present case study, Figure 15 shows that 19 kA is a sufficiently low current level not to cause flashover on the line. Furthermore, the results show that the maximum overvoltage level is +600 kV at the transition station.
5.3. Statistical Comparison
By introducing a similar statistical method for shielding failures as for backflashovers, it is possible to evaluate and compare the two phenomena with regard to the risk of insulation failure. The case study results show that overvoltages due to backflashovers for an MTBS of 300 years are higher than overvoltages due to shielding failures for the same MTBS. Furthermore, in the backflashover case, the cable is subject to a change of polarity. Hence, in this case, the representative overvoltage levels should be based on the backflashover results, as these are more severe for the cable insulation.
5.4. Comparison with Recommended Lightning Impulse Test Levels
Currently, CIGRE recommendations exist for testing HVDC cable systems only up to 500 kV [15]. The calculated lightning overvoltages as presented in this paper are in the range of 1.2–1.3 pu, which is comparatively lower than the test levels presented in reference [15]. However, it should be noted that the calculated values depend on project specific conditions such as lightning and grounding conditions or the length of the cable system. Nevertheless, the results of the case study indicate that the use of a statistical method may result in lower representative overvoltage levels compared to deterministic calculations.
6. Conclusions
Representative fast front overvoltage levels for HVDC cable systems connected to overhead lines are usually established without considering the statistical characteristics of overvoltages impinging on the cables from lightning strikes to the line. As discussed in reference [3], the statistical characteristics depend on parameters that are specific to each project, such as ground flash density, grounding conditions, and the design of the overhead line.
The original statistical method described in reference [3] focused on lightning overvoltages in ±320 kV DC cable systems. At this voltage level, lightning overvoltages on the line are often caused by backflashovers due to the comparatively low flashover voltage of the insulators. Furthermore, the attenuation of the overvoltage waves is dominated by corona discharges due to the comparatively small dimensions of the conductor bundles.
The improved statistical method overcomes the limitations of the original method by introducing overvoltage wave attenuation due to resistive effects, and by evaluating shielding failures in a similar way as backflashovers in order to facilitate a statistical comparison of the overvoltage levels. The improvements make the statistical method applicable for DC voltage levels above ±320 kV as well, as illustrated by the case study.
Author Contributions
Conceptualization, O.L., J.L. and C.E.; Data curation, O.L. and J.L.; Formal analysis, O.L. and J.L.; Funding acquisition, O.L. and M.H.J.B.; Investigation, O.L. and J.L.; Methodology, O.L., J.L. and C.E.; Project administration, O.L. and J.L.; Resources, O.L. and J.L.; Software, O.L., J.L. and C.E.; Supervision, J.L. and M.H.J.B.; Validation, O.L., J.L., C.E. and M.H.J.B.; Visualization, O.L. and J.L.; Writing—original draft, O.L. and J.L.; Writing—review & editing, O.L., J.L., C.E., T.K. and M.H.J.B.
Funding
This research was funded by the Swedish Energy Agency, Svenska kraftnät and Energiforsk.
Conflicts of Interest
The authors declare no conflict of interest.
References
- International Electrotechnical Commission. Insulation Co-Ordination—Part 1: Definitions, Principles and Rules, Edition 8.1; IEC 60071-1: 2011; International Electrotechnical Commission: Geneva, Switzerland, 2011. [Google Scholar]
- International Electrotechnical Commission. Insulation Co-Ordination—Part 2: Application Guide, Edition 3.0; IEC Standard 60071-2: 1996; International Electrotechnical Commission: Geneva, Switzerland, 1996. [Google Scholar]
- Lundquist, J.; Engelbrecht, C.; Thunberg, E.; Dubickas, V.; Jansson, H.; Worzyk, T. Lightning Impulse Test Levels for Extruded HVDC Cable Systems. In Proceedings of the CIGRE Session, Paris, France, 2014. [Google Scholar]
- IEEE. IEEE Guide for the Application of Insulation Coordination; IEEE Std.1313.2-1999; IEEE: Piscataway, NJ, USA, 1999. [Google Scholar]
- Hileman, A.R. Insulation Coordination for Power Systems, 1st ed.; Marcel Dekker: New York, NY, USA, 1999. [Google Scholar]
- IEEE WG on Lightning Performance of Lines. A Simplified Method for Estimating Lightning Performance of Transmission Lines. IEEE Trans. Power Appar. Syst. 1985, PAS-104, 918–932. [Google Scholar] [CrossRef]
- CIGRE Technical Brochure 549. Lightning Parameters for Engineering Applications; International Council on Large Electric Systems: Paris, France, 2013. [Google Scholar]
- CIGRE Technical Brochure 63. Guide to Procedures for Estimating the Lightning Performance of Transmission Lines; International Council on Large Electric Systems: Paris, France, 1991. [Google Scholar]
- CIGRE Technical Brochure 704. Evaluation of Lightning Shielding Analysis Methods for EHV and UHV DC and AC Transmission Lines; International Council on Large Electric Systems: Paris, France, 2017. [Google Scholar]
- Cuarán, J.; Becerra, M.; Roman, F. Lightning Attachment to UHV Power Transmission Lines: Effect of the Phase Voltage. IEEE Trans. Power Deliv. 2018, 34, 729–738. [Google Scholar] [CrossRef]
- Rizk, F. Modeling of UHV and double circuit EHV transmission line exposure to direct lightning strikes. IEEE Trans. Power Deliv. 2017, 32, 1739–1747. [Google Scholar] [CrossRef]
- Rizk, F. A Simplified Approach for Assessment of Exposure of EHV and UHV Lines to Direct Lightning. IEEE Trans. Power Deliv. 2018, 33, 2420–2427. [Google Scholar] [CrossRef]
- Takami, J.; Okabe, S. Observational Results of Lightning Current on Transmission Towers. IEEE Trans. Power Deliv. 2007, 22, 547–556. [Google Scholar] [CrossRef]
- Martinez-Velasco, J.; Ramirez, A.; Dávila, M. Overhead lines. In Power System Transients—Parameter Determination, 1st ed.; Martinez-Velasco, J., Ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- CIGRE Technical Brochure 496. Recommendations for Testing DC Extruded Cable Systems for Power Transmission at a Rated Voltage up to 500 kV; International Council on Large Electric Systems: Paris, France, 2012. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).