SOC and SOH Joint Estimation of the Power Batteries Based on Fuzzy Unscented Kalman Filtering Algorithm
Abstract
:1. Introduction
2. Model for the Lithium Battery
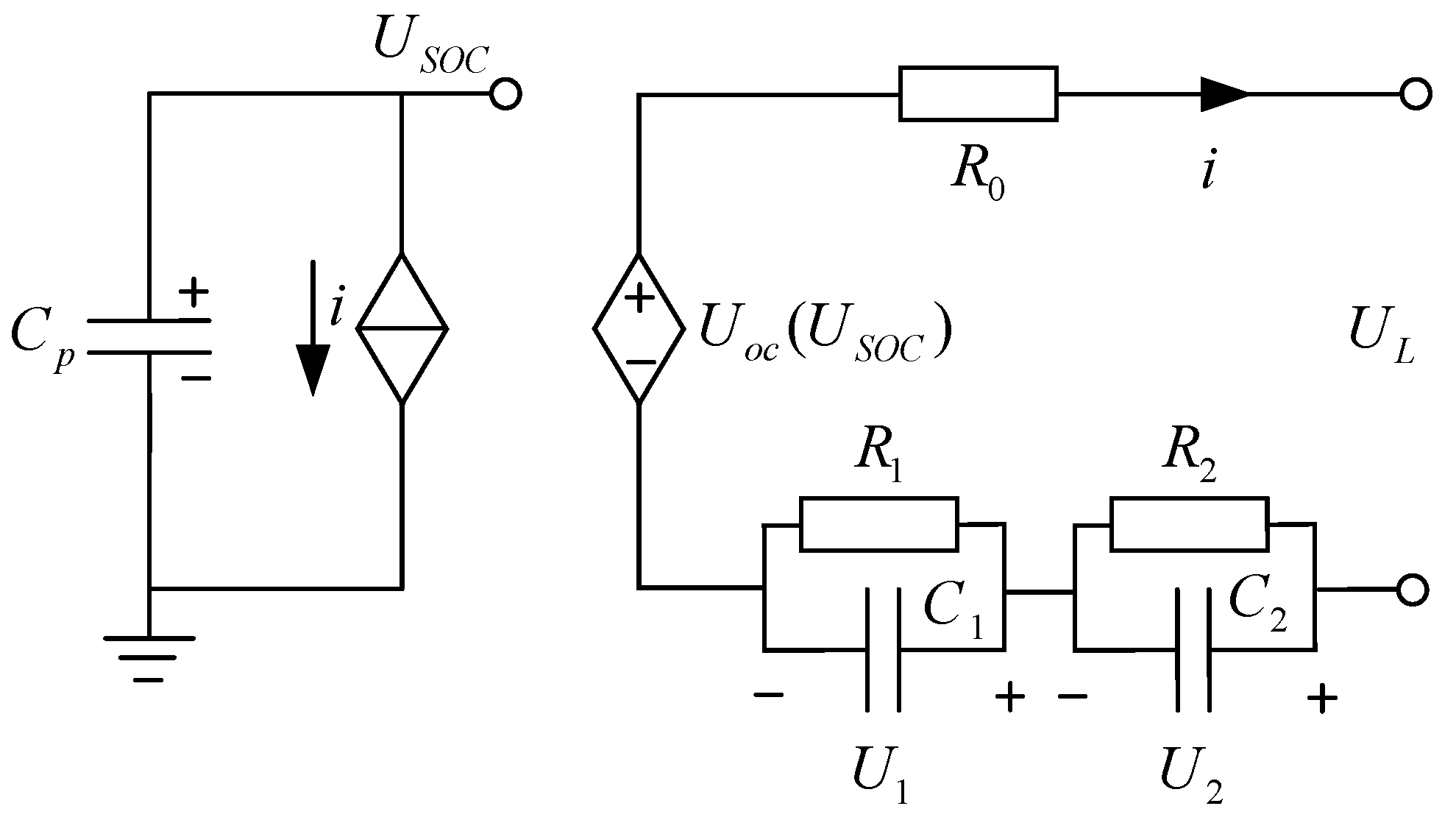
2.1. Setup of Equivalent Circuit Model for the Lithium Battery
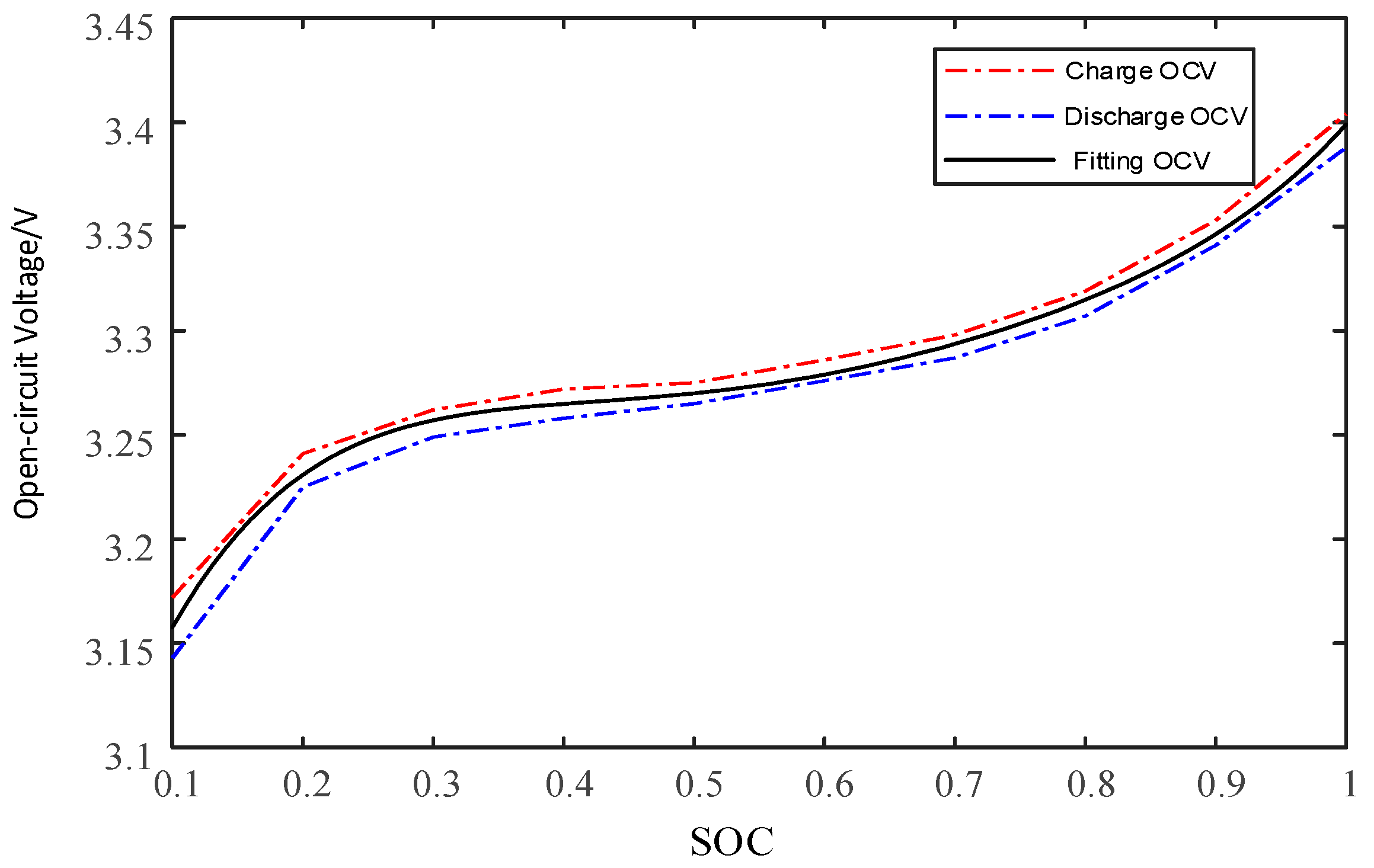
2.2. Open-Circuit Voltage and SOC Setting Experiments
2.3. Parameter Identification of the Lithium Battery Model
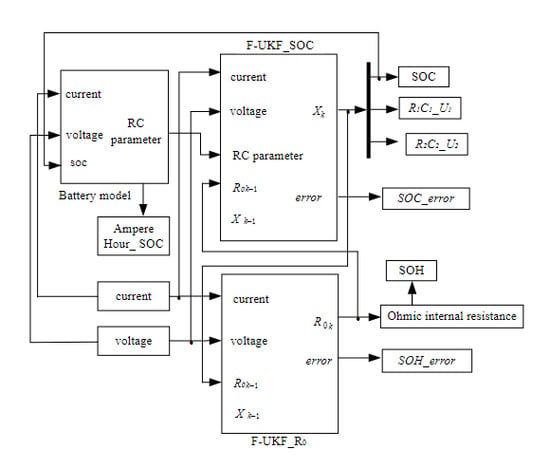
3. SOC and SOH Joint Estimation Based on F-UKF
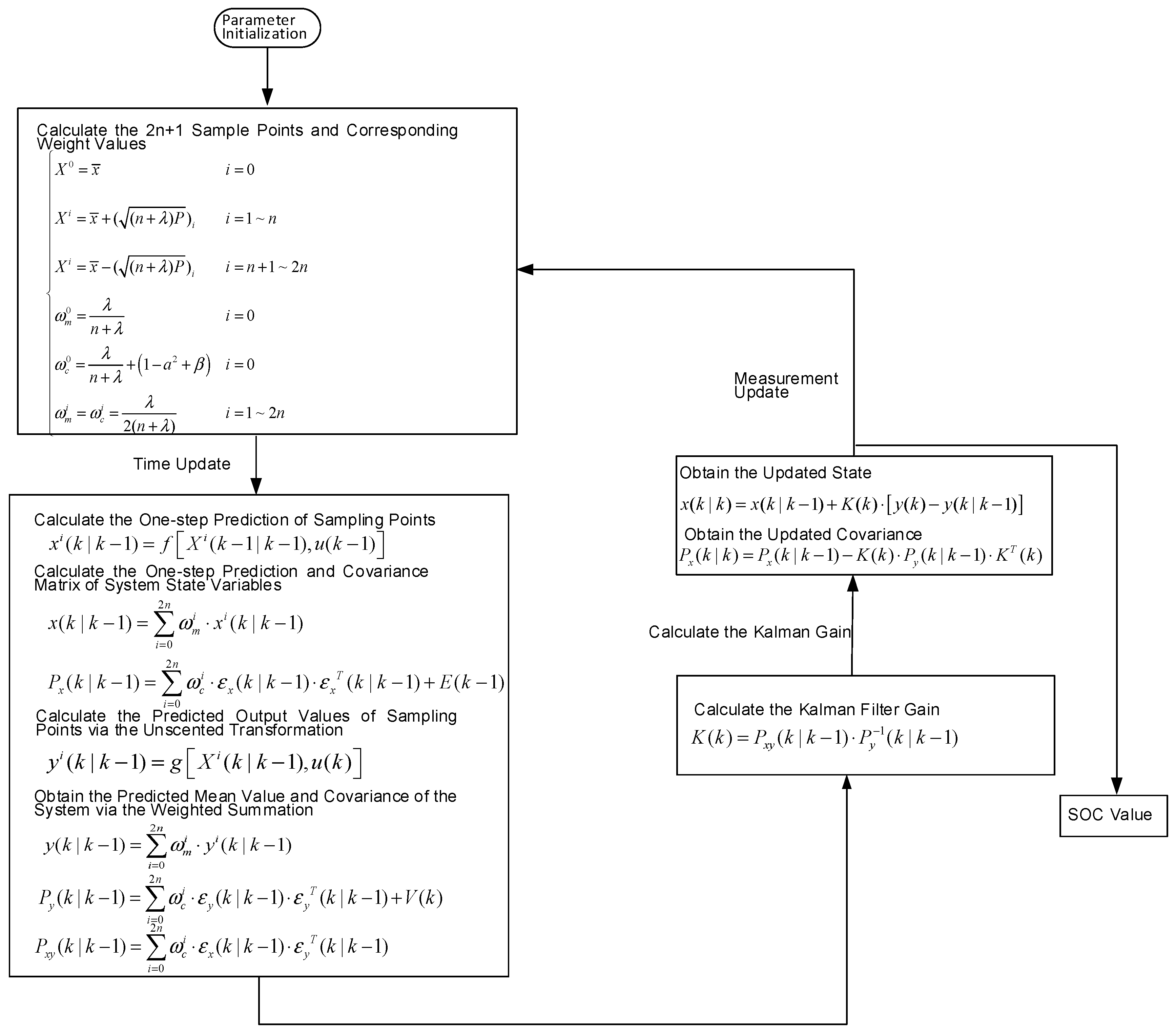
3.1. Unscented Kalman Filtering Algorithm
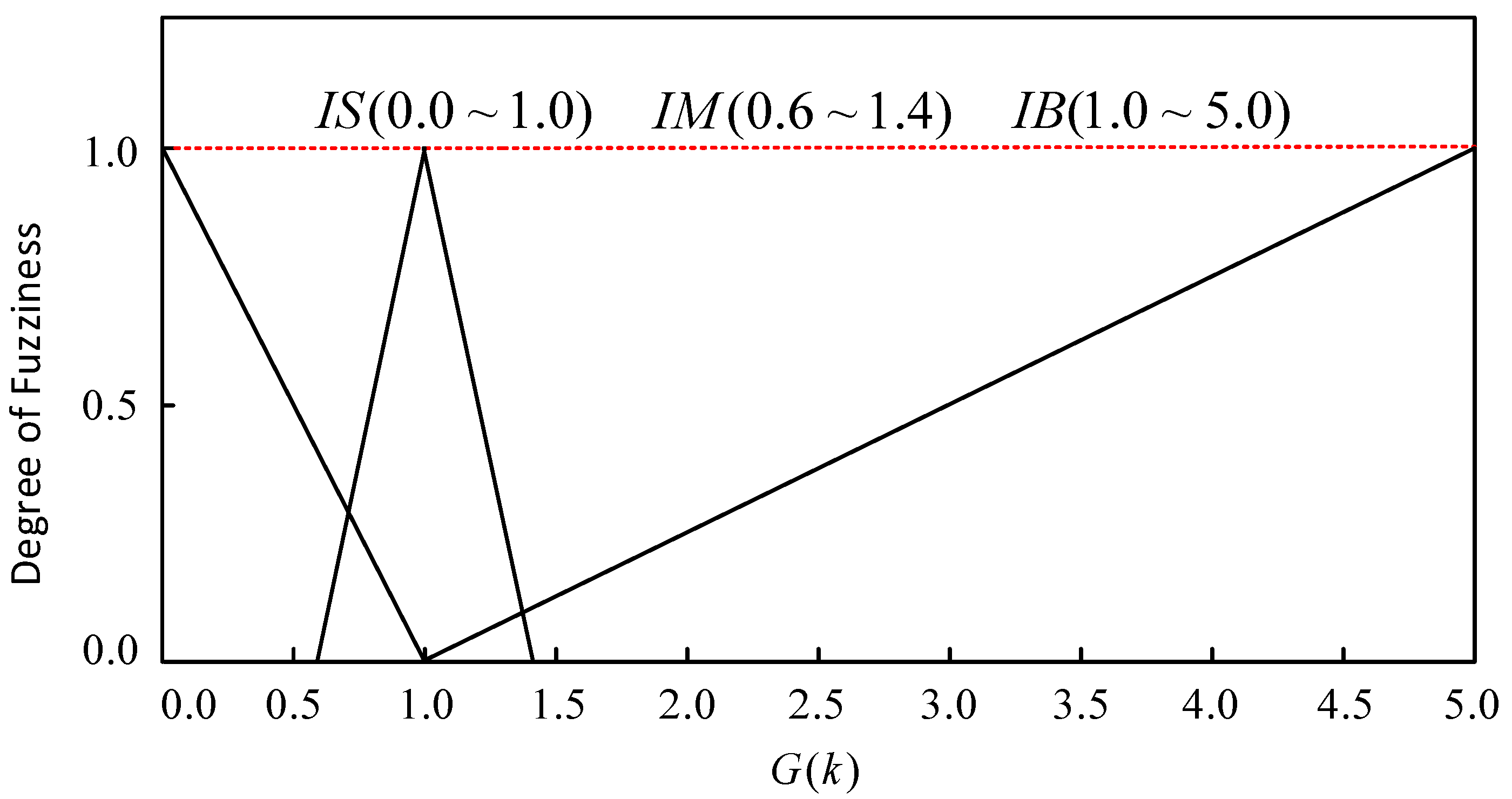
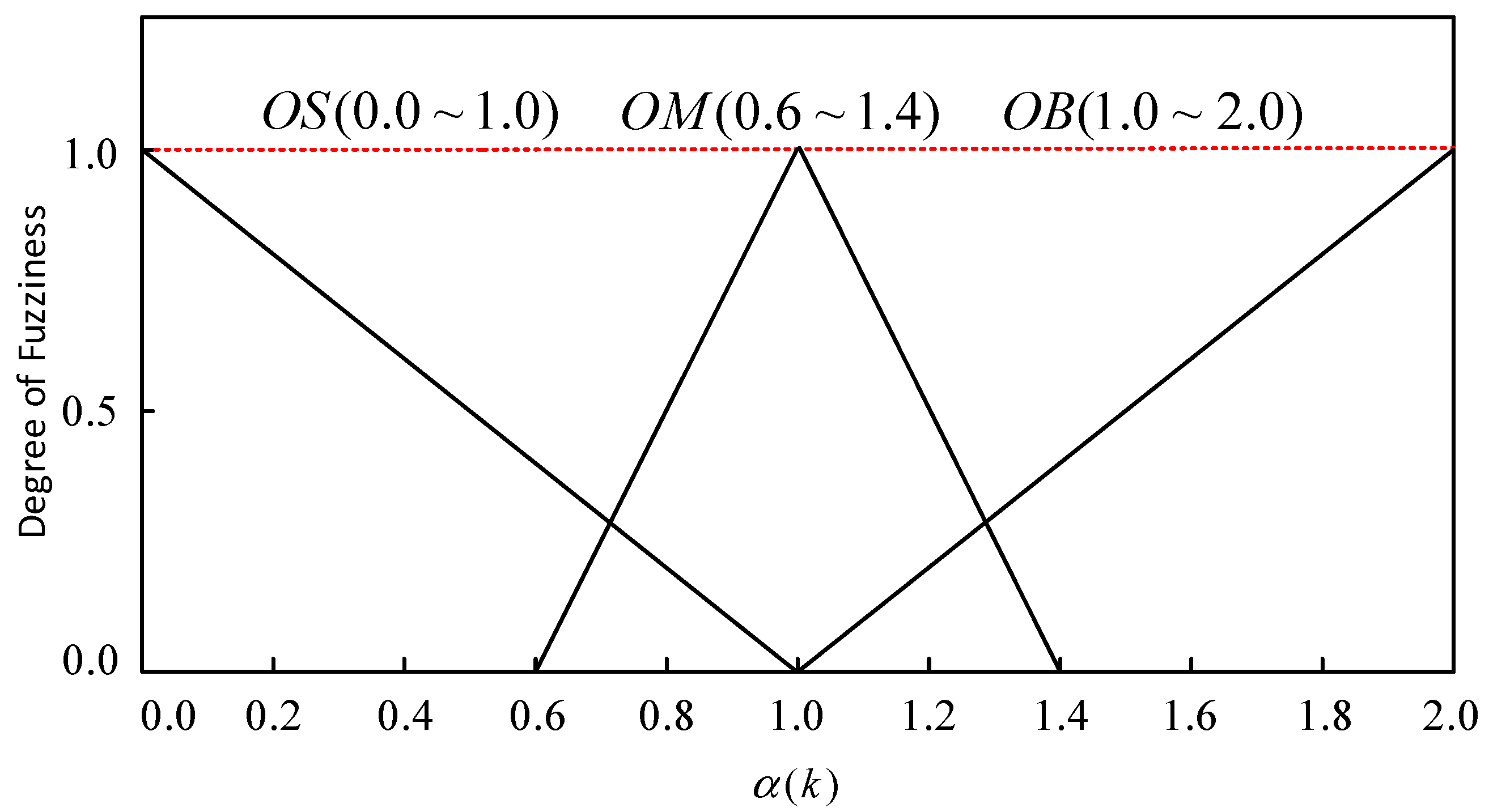
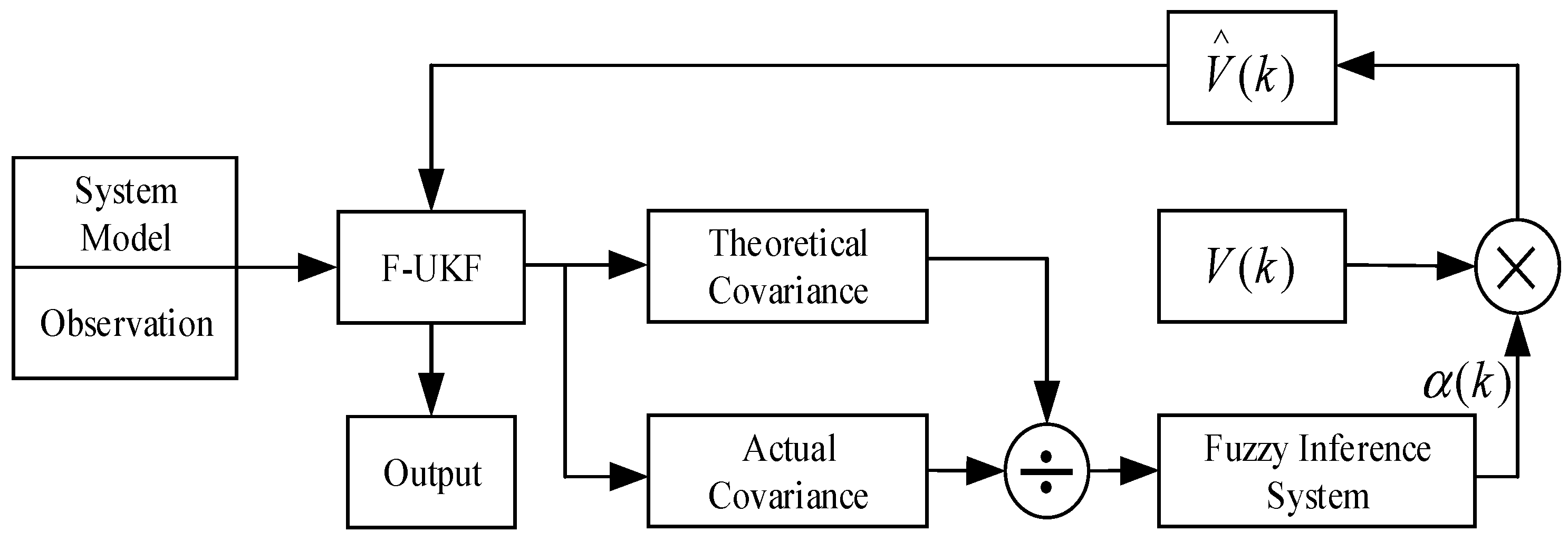
3.2. Fuzzy Unscented Kalman Filtering Algorithm
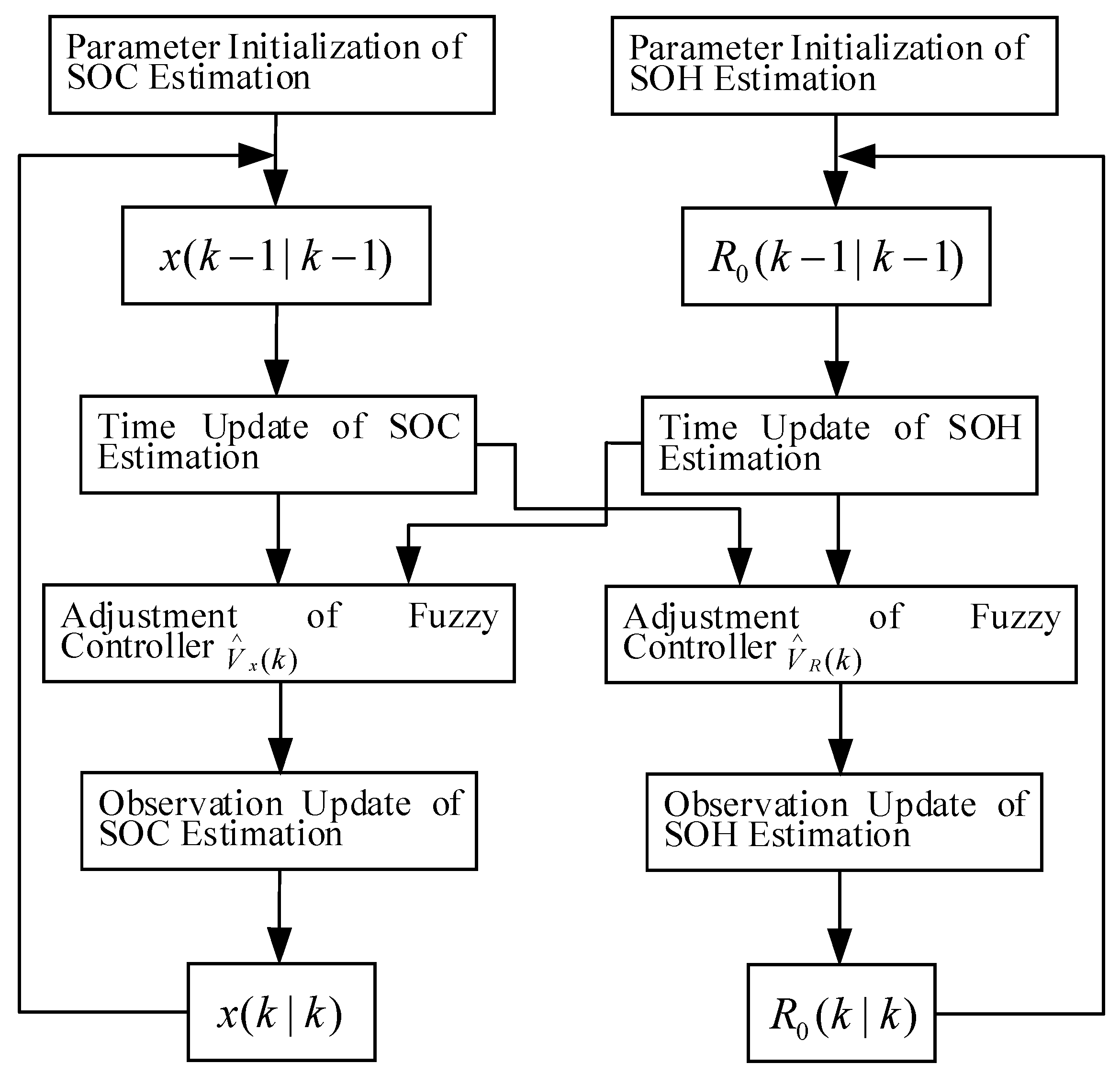
3.3. Design and Implementation of the SOC and SOH Joint Estimation Algorithm
- (1)
- Parameter initialization. First, initialize the corresponding parameters of the F-UKF algorithm for the battery SOC estimation; then, initialize the corresponding parameters of the F-UKF algorithm for the ohmic resistance estimation, and the ohmic resistance should be close to the actual value to ensure the fast convergence of the battery SOC.
- (2)
- Obtain the terminal voltage UL(k) and working current i(k) of the battery at the time k through the voltage-current acquisition module.
- (3)
- Obtain the estimated value of the battery SOC at the time k through the recursion formula using the F-UKF algorithm based on the above terminal voltage and working current at the time k.
- (4)
- Obtain the estimated value of ohmic resistance at the time k through the recursion formula using the F-UKF algorithm based on the estimated value of battery SOC and working current at the time k.
- (5)
- Take the value of SOC(k) obtained from step (3) into the nonlinear functions of open-circuit voltage and the battery SOC to obtain the open-circuit voltage UOC(k) at the time k; repeat the steps (2), (3), (4) and (5) for the real-time estimation of the battery SOC and ohmic resistance.
4. Experimental Verification and Result Analysis
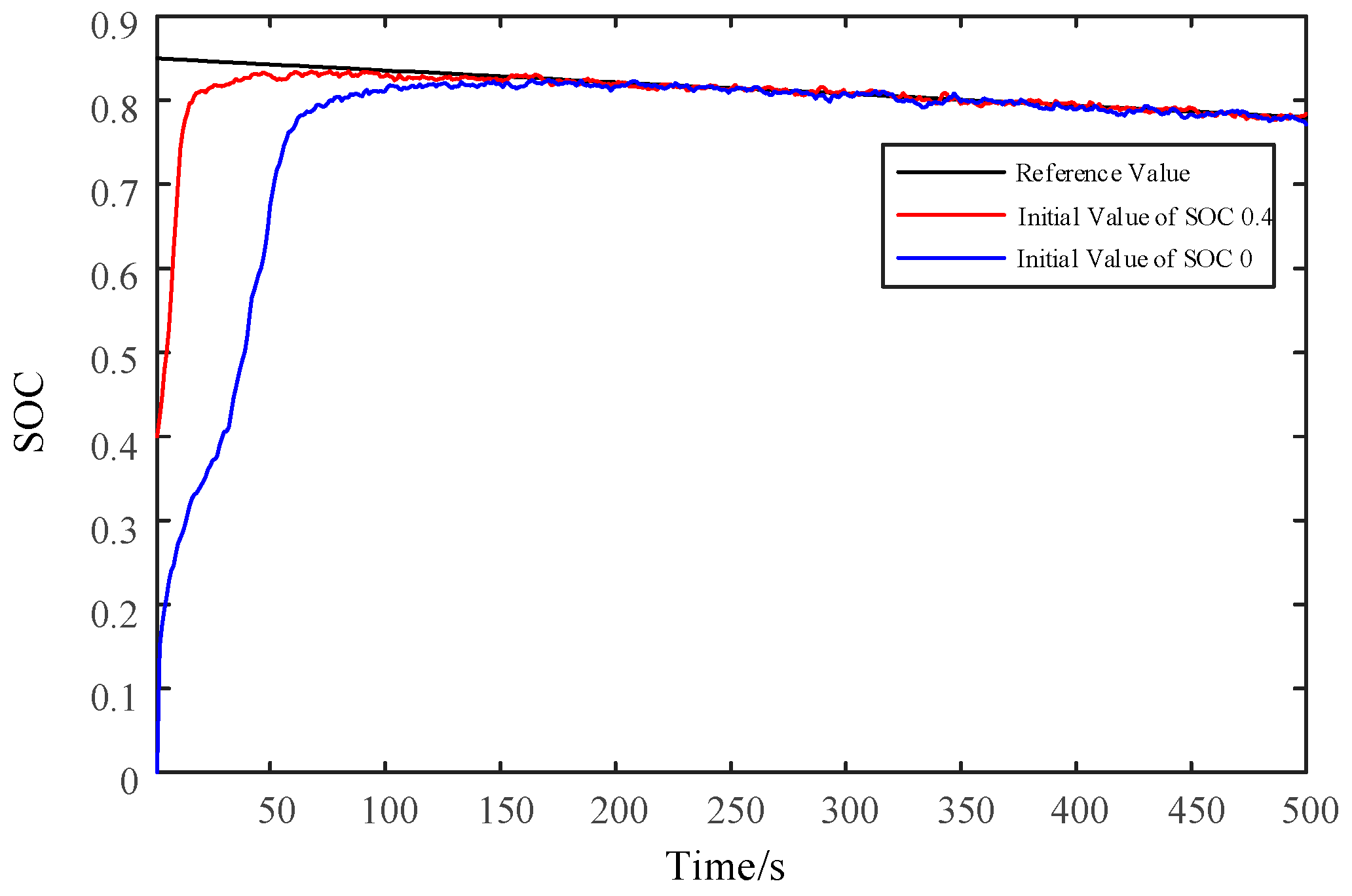
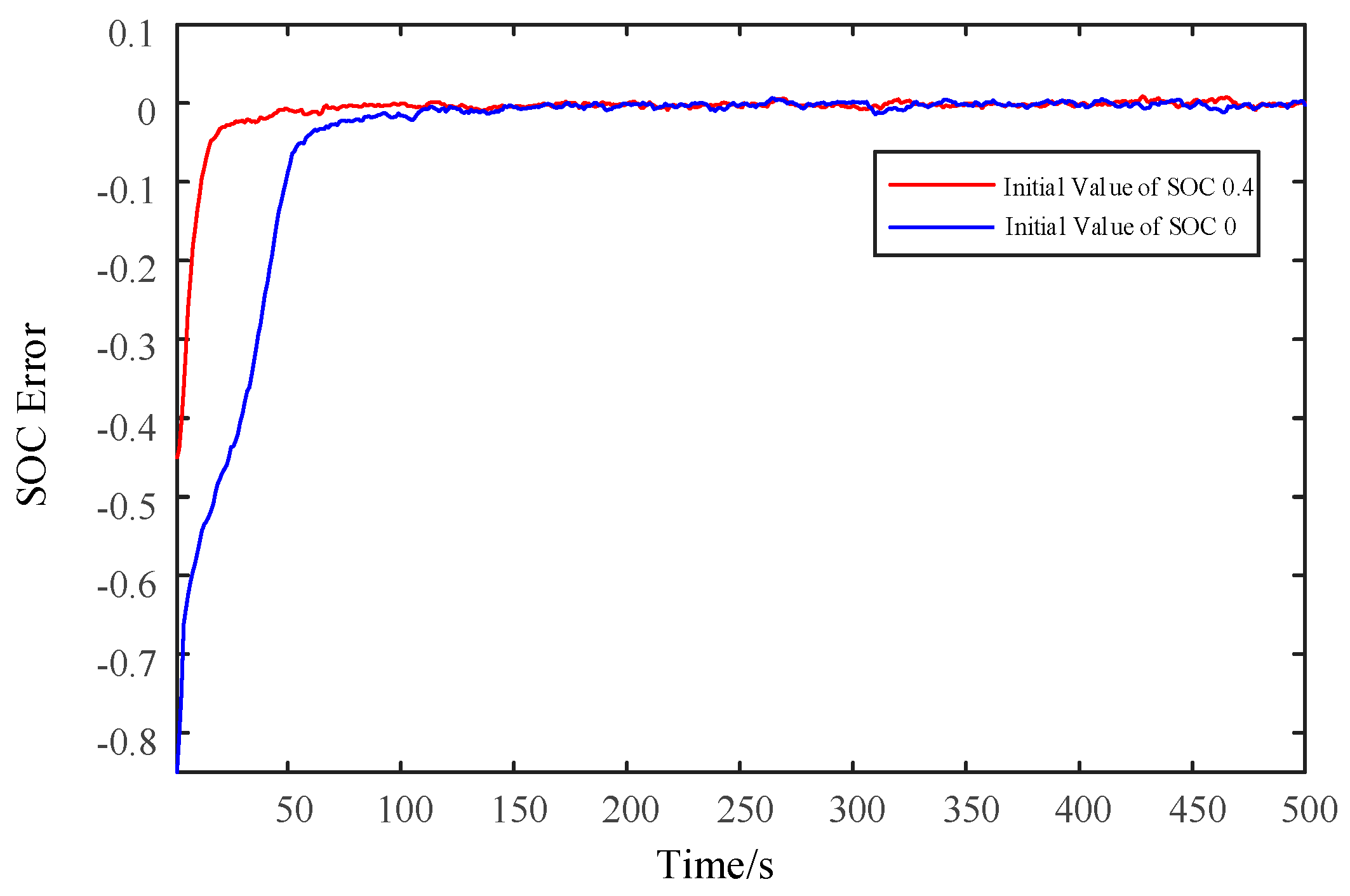
4.1. Sensitivity Verification of the F-UKF Algorithm against Initial Values
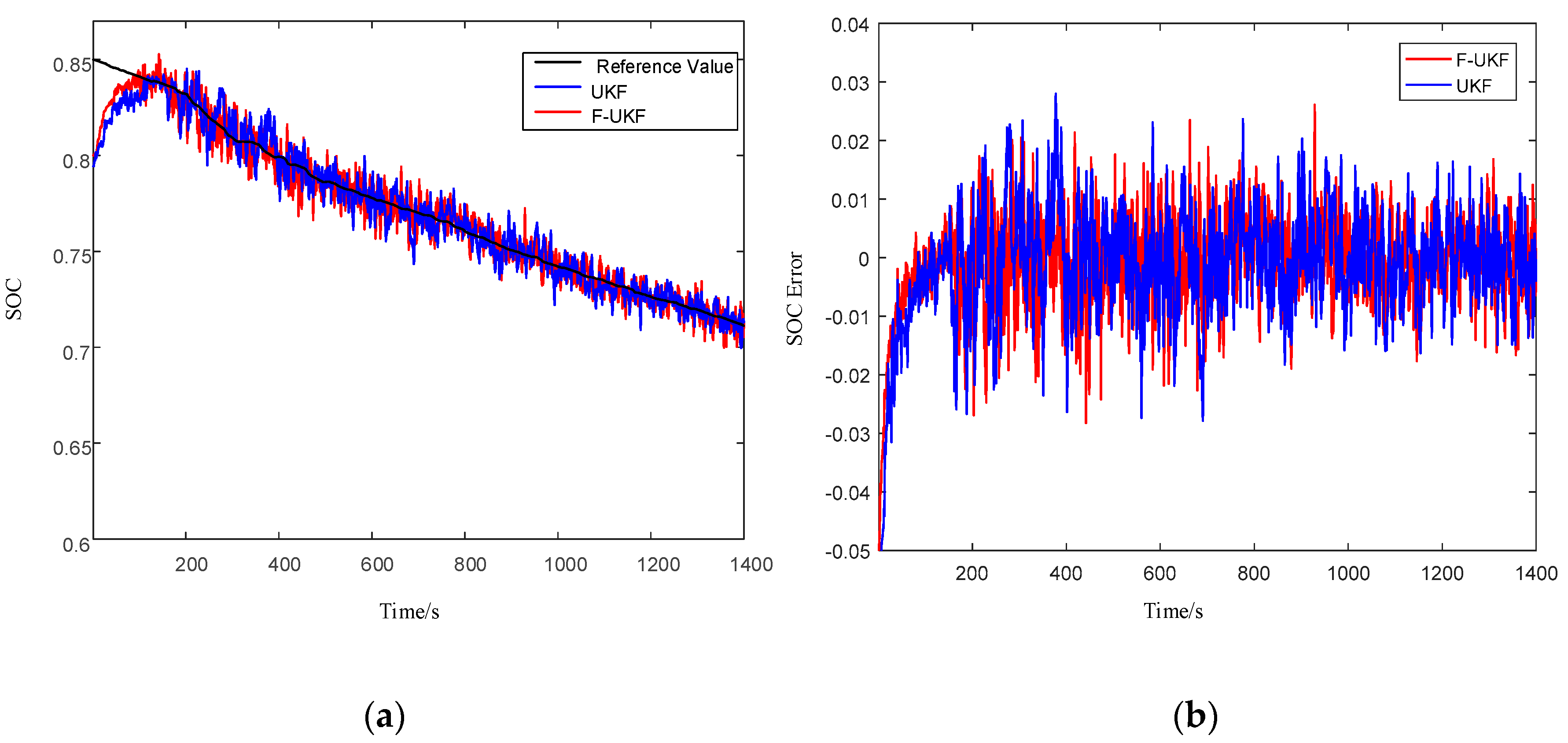
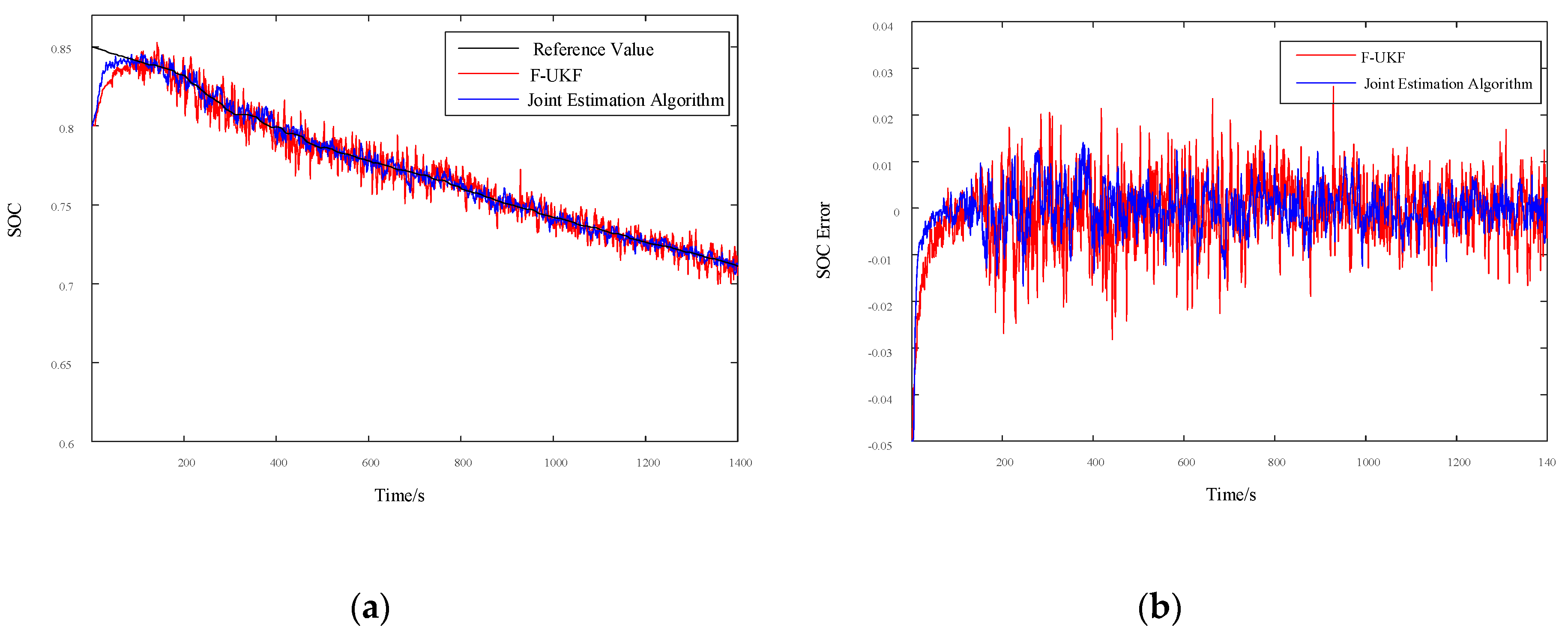
4.2. Joint Simulation Verification of UDDS Driving Cycles
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhu, X.; Fan, D.; Xiang, Z.; Quan, L.; Hua, W.; Cheng, M. Systematic multi-level optimization design and dynamic control of less-rare-earth hybrid permanent magnet motor for all-climatic electric vehicles. Appl. Energy 2019, 253, 113549. [Google Scholar] [CrossRef]
- Shen, P.; Ma, O.U.; Lu, L.G.; Li, J.Q.; Feng, X.N. The co-estimation of state of charge, state of health and state of function for lithium-ion batteries in electric vehicles. IEEE Trans. Veh. Technol. 2017, 67, 92–103. [Google Scholar] [CrossRef]
- Chen, Y.J.; Yang, G.; Liu, X.; He, Z.C. A time-efficient and accurate open circuit voltage estimation method for lithium-ion batteries. Energies 2019, 12, 1803. [Google Scholar] [CrossRef]
- Plett, G. Extended kalman filtering for battery management systems of lipb-based hev battery packs: Part 2. modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Cui, Y.Z.; Zuo, P.J.; Du, C.Y.; Gao, Y.D.; Yang, J.; Cheng, X.Q.; Ma, Y.L.; Yin, G.P. State of health diagnosis model for lithium ion batteries based on real-time impedance and open circuit voltage parameters identification method. Energy 2018, 144, 647–656. [Google Scholar] [CrossRef]
- Ramadan, H.S.; Becherif, M.; Claude, F. Extended kalman filter for accurate state of charge estimation of lithium-based batteries: a comparative analysis. Int. J. Hydrogen Energy 2017, 42, 29033–29046. [Google Scholar] [CrossRef]
- Meng, J.H.; Luo, G.Z.; Gao, F. Lithium polymer battery state-of-charge estimation based on adaptive unscented kalman filter and support vector machine. IEEE Trans. Power Electron. 2015, 31, 2226–2238. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Mierlo, V.; Bossche, V.D. Critical review of state of health estimation methods of li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2015, 56, 572–587. [Google Scholar] [CrossRef]
- Zhao, L.; Lin, M.Y.; Chen, Y. Least-squares based coulomb counting method and its application for state-of-charge (soc) estimation in electric vehicles. Int. J. Energy Res. 2016, 40, 1389–1399. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, H.; Zhang, J.R.; Ma, W.T. Adaptive unscented kalman filter with correntropy loss for robust state of charge estimation of lithium-ion battery. Energies 2018, 11, 3123. [Google Scholar] [CrossRef]
- Chen, Z.; Li, X.Y.; Shen, J.W.; Yan, W.S.; Xiao, R.X. A novel state of charge estimation algorithm for lithium-ion battery packs of electric vehicles. Energies 2016, 9, 710. [Google Scholar] [CrossRef]
- Li, J.; Adewuyi, K.; Lotfi, N.; Landers, R.G.; Park, J. A single particle model with chemical/mechanical degradation physics for lithium ion battery state of health (soh) estimation. Appl. Energy 2018, 212, 1178–1190. [Google Scholar] [CrossRef]
- Chen, L.; Lu, Z.Q.; Lin, W.L.; Li, J.Z.; Pan, H.H. A new state-of-health estimation method for lithium-ion batteries through the intrinsic relationship between ohmic internal resistance and capacity. Measurement 2018, 116, 586–595. [Google Scholar] [CrossRef]
- Zou, C.F.; Manzie, C.; Nešićb, D.; Kallapura, A.J. Multi-time-scale observer design for state-of-charge and state-of-health of a lithium-ion battery. J. Power Sources 2016, 335, 121–130. [Google Scholar] [CrossRef]
- Li, H.; Ravey, A.; N’Diaye, A.; Djerdir, A. Online adaptive equivalent consumption minimization strategy for fuel cell hybrid electric vehicle considering power sources degradation. Energy Convers. Manag. 2019, 192, 133–149. [Google Scholar] [CrossRef]
- Wei, Z.; Lim, T.M.; Skyllas-Kazacos, M.; Wai, N.; Tseng, K.J. Online state of charge and model parameter co-estimation based on a novel multi-timescale estimator for vanadium redox flow battery. Appl. Energy 2016, 172, 169–179. [Google Scholar] [CrossRef]
- Yang, J.F.; Xia, B.; Huang, W.X.; Fu, Y.H.; Mi, C. Online state-of-health estimation for lithium-ion batteries using constant-voltage charging current analysis. Appl. Energy 2018, 212, 1589–1600. [Google Scholar] [CrossRef]
- Zou, Y.; Hu, X.S.; Ma, H.M.; Li, S.E. Combined state of charge and state of health estimation over lithium-ion battery cell cycle lifespan for electric vehicles. J. Power Sources 2015, 273, 793–803. [Google Scholar] [CrossRef]
- Zheng, Y.; Ouyang, M.G.; Han, X.B.; Lu, L.G.; Li, J.Q. Investigating the error sources of the online state of charge estimation methods for lithium-ion batteries in electric vehicles. J. Power Sources 2018, 377, 161–188. [Google Scholar] [CrossRef]
- Yang, F.F.; Xing, Y.J.; Wang, D.; Tsui, K. A comparative study of three model-based algorithms for estimating state-of-charge of lithium-ion batteries under a new combined dynamic loading profile. Appl. Energy 2016, 164, 387–399. [Google Scholar] [CrossRef]
- Hua, Y.; Cordoba-Arenas, A.; Warner, N.; Rizzoni, G. A multi time-scale state-of-charge and state-of-health estimation framework using nonlinear predictive filter for lithium-ion battery pack with passive balance control. J. Power Sources 2015, 280, 293–312. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Song, W.J.; Lin, S.L.; Feng, Z.P. A novel model of the initial state of charge estimation for lifepo4 batteries. J. Power Sources 2014, 248, 1028–1033. [Google Scholar] [CrossRef]
- Deng, Y.W.; Ying, H.J.; Jiaqiang, E.; Zhu, H.; Wei, K.X.; Chen, J.W.; Zhang, F.; Liao, G.L. Feature parameter extraction and intelligent estimation of the state-of-health of lithium-ion batteries. Energy 2019, 176, 91–102. [Google Scholar] [CrossRef]
- Petricca, P.; Shin, D.; Bocca, A.; Macii, A.; Macii, A.; Poncino, M. Automated generation of battery aging models from datasheets. In Proceedings of the 2014 IEEE 32nd International Conference on Computer Design (ICCD), Seoul, South Korea, 19–22 October 2014; pp. 483–488. [Google Scholar]
- Bocca, A.; Sassone, A.; Shin, D.; Macii, A.; Macii, E.; Poncino, E. An equation-based battery cycle life model for various battery chemistries. In Proceedings of the 2015 IFIP/IEEE International Conference on Very Large Scale Integration (VLSI-SoC), Daejeon, South Korea, 5–7 October 2015; pp. 57–62. [Google Scholar]
- Yan, W.Z.; Zhang, B.; Zhao, G.Q.; Tang, S.J.; Niu, G.X.; Wang, X.F. A battery management system with lebesgue sampling-based extended kalman filter. IEEE Trans. Ind. Electron. 2019, 66, 3227–3236. [Google Scholar] [CrossRef]
- Wei, Z.B.; Zhao, J.Y.; Ji, D.X.; Tseng, K.J. A multi-timescale estimator for battery state of charge and capacity dual estimation based on an online identified model. Appl. Energy 2017, 204, 1264–1274. [Google Scholar] [CrossRef]
- Zhang, W.G.; Shi, W.; Ma, Z.Y. Adaptive unscented kalman filter based state of energy and power capability estimation approach for lithium-ion battery. J. Power Sources 2015, 289, 50–62. [Google Scholar] [CrossRef]
- Dong, G.Z.; Wei, J.W.; Chen, Z.H.; Sun, H.; Yu, X.W. Remaining dischargeable time prediction for lithium-ion batteries using unscented kalman filter. J. Power Sources 2017, 364, 316–327. [Google Scholar] [CrossRef]
- Li, Y.W.; Wang, C.; Gong, J.F. A wavelet transform-adaptive unscented kalman filter approach for state of charge estimation of lifepo4 battery. Int. J. Energy Res. 2018, 42, 586–600. [Google Scholar] [CrossRef]

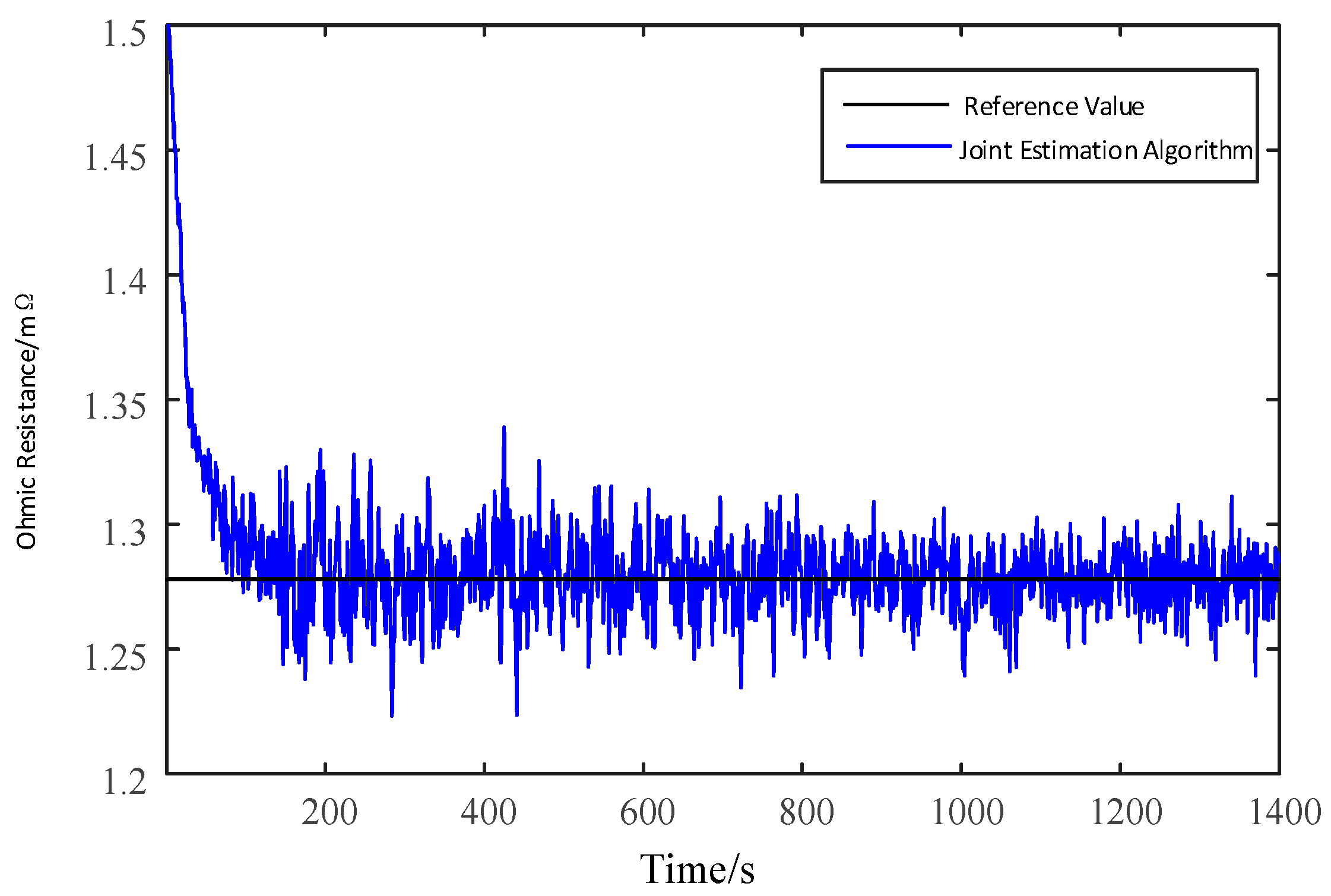
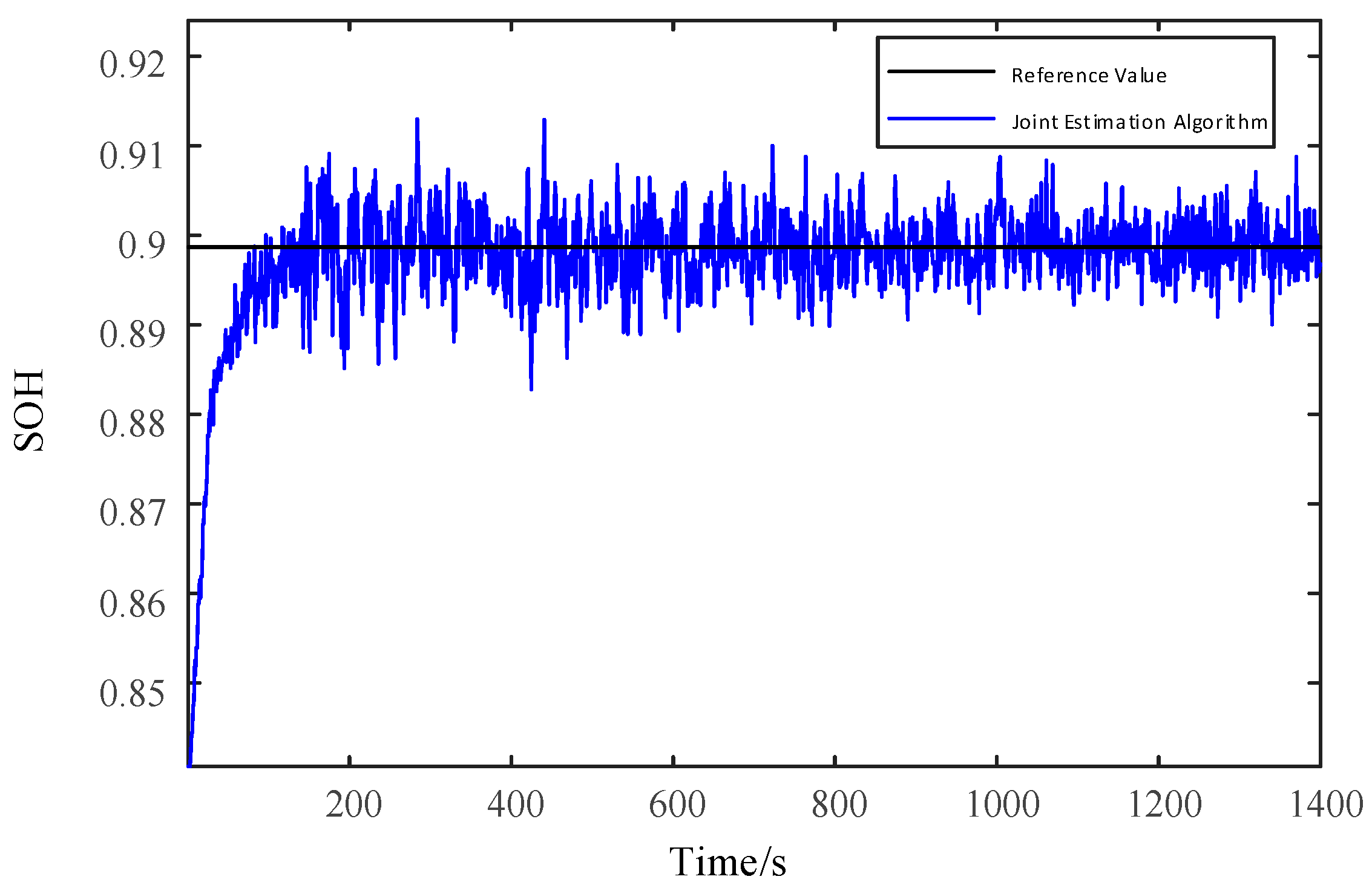
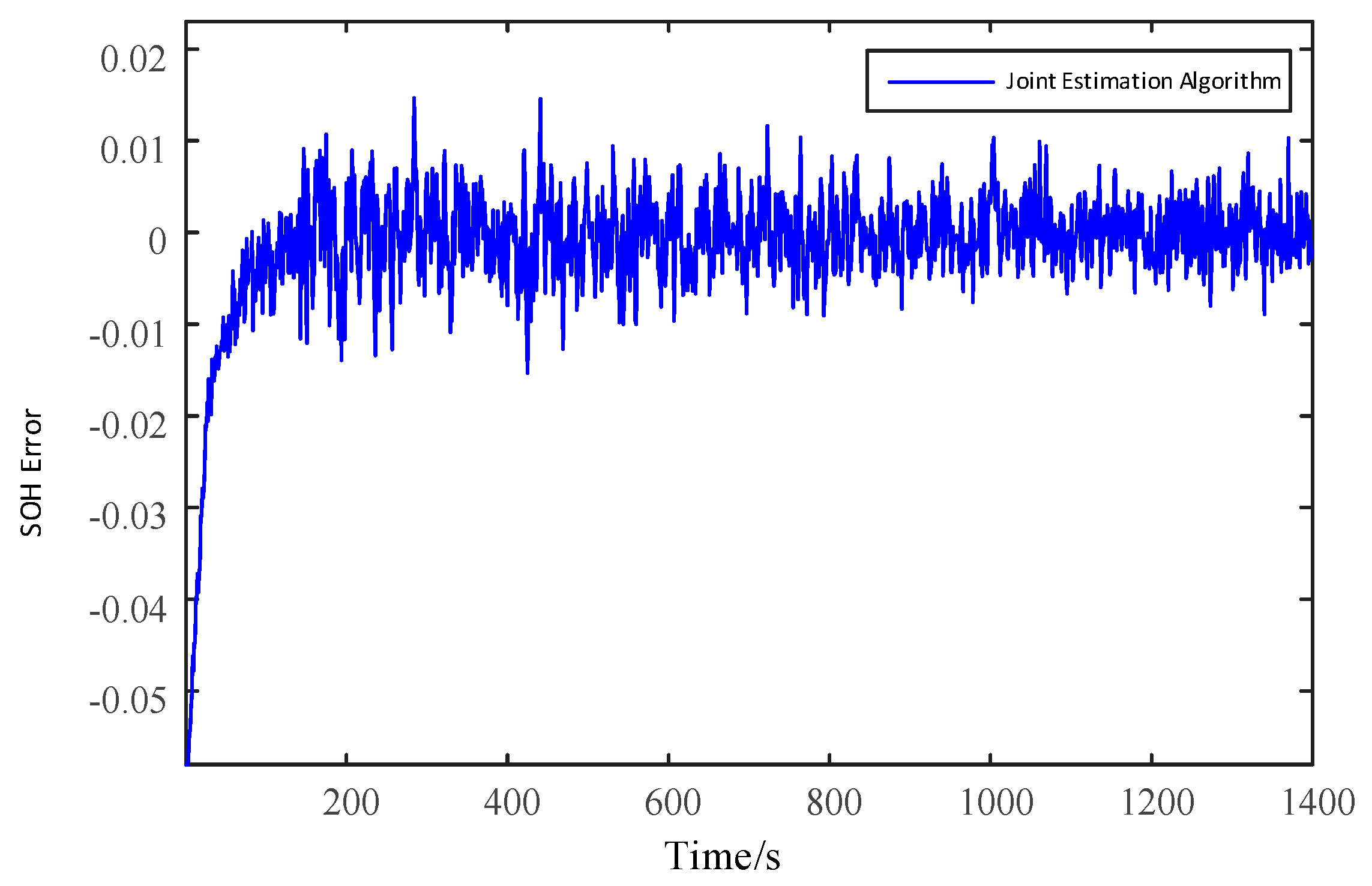
| Model Parameter | Maximum Value | Minimum Value | Average Value |
|---|---|---|---|
| Ohmic internal resistance R0 (mΩ) | 1.704 | 0.923 | 1.278 |
| Concentration polarization internal resistance R1 (mΩ) | 0.0603 | 0.1189 | 0.0927 |
| Concentration polarization capacitor C1 (KF) | 6.017 | 3.021 | 3.821 |
| Electrochemical polarization internal resistance R2 (mΩ) | 0.248 | 0.176 | 0.219 |
| Electrochemical polarization capacitance C2 (KF) | 3.281 | 2.683 | 2.746 |
| Input fuzziness | Input Small (IS) | Input Middle (IM) | Input Big (IB) |
| Output fuzziness | Output Small (OS) | Output Middle (OM) | Output Big (OB) |
| Nominal Capacity (Ah) | 40 | |
| Battery voltage (V) | Charge cutoff voltage | 3.6 |
| Discharge cutoff voltage | 2.0 | |
| Cycle life (times) | 80% DOD | ≥2000 |
| 70% DOD | ≥3000 | |
| Standard charge–discharge current (A) | 0.3C | |
| Maximum charge current (A) | 3C | |
| Maximum discharge current (A) | 4C | |
| Operating temperature (°C) | −25–55 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, M.; Zhang, P.; Yang, Y.; Xie, C.; Shi, Y. SOC and SOH Joint Estimation of the Power Batteries Based on Fuzzy Unscented Kalman Filtering Algorithm. Energies 2019, 12, 3122. https://doi.org/10.3390/en12163122
Zeng M, Zhang P, Yang Y, Xie C, Shi Y. SOC and SOH Joint Estimation of the Power Batteries Based on Fuzzy Unscented Kalman Filtering Algorithm. Energies. 2019; 12(16):3122. https://doi.org/10.3390/en12163122
Chicago/Turabian StyleZeng, Miaomiao, Peng Zhang, Yang Yang, Changjun Xie, and Ying Shi. 2019. "SOC and SOH Joint Estimation of the Power Batteries Based on Fuzzy Unscented Kalman Filtering Algorithm" Energies 12, no. 16: 3122. https://doi.org/10.3390/en12163122
APA StyleZeng, M., Zhang, P., Yang, Y., Xie, C., & Shi, Y. (2019). SOC and SOH Joint Estimation of the Power Batteries Based on Fuzzy Unscented Kalman Filtering Algorithm. Energies, 12(16), 3122. https://doi.org/10.3390/en12163122