Predictive-Fixed Switching Current Control Strategy Applied to Six-Phase Induction Machine
Abstract
:1. Introduction
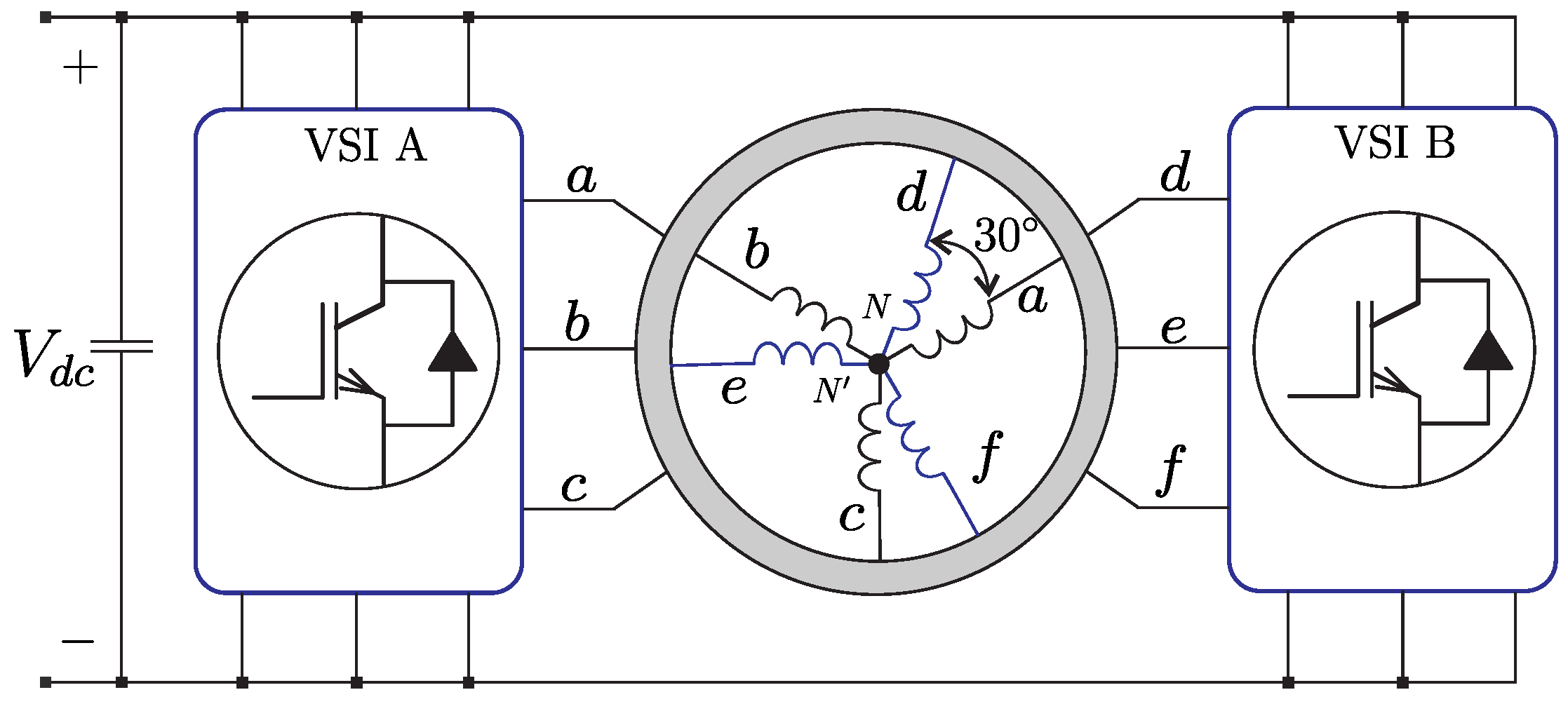
2. Six-Phase IM Drive Model
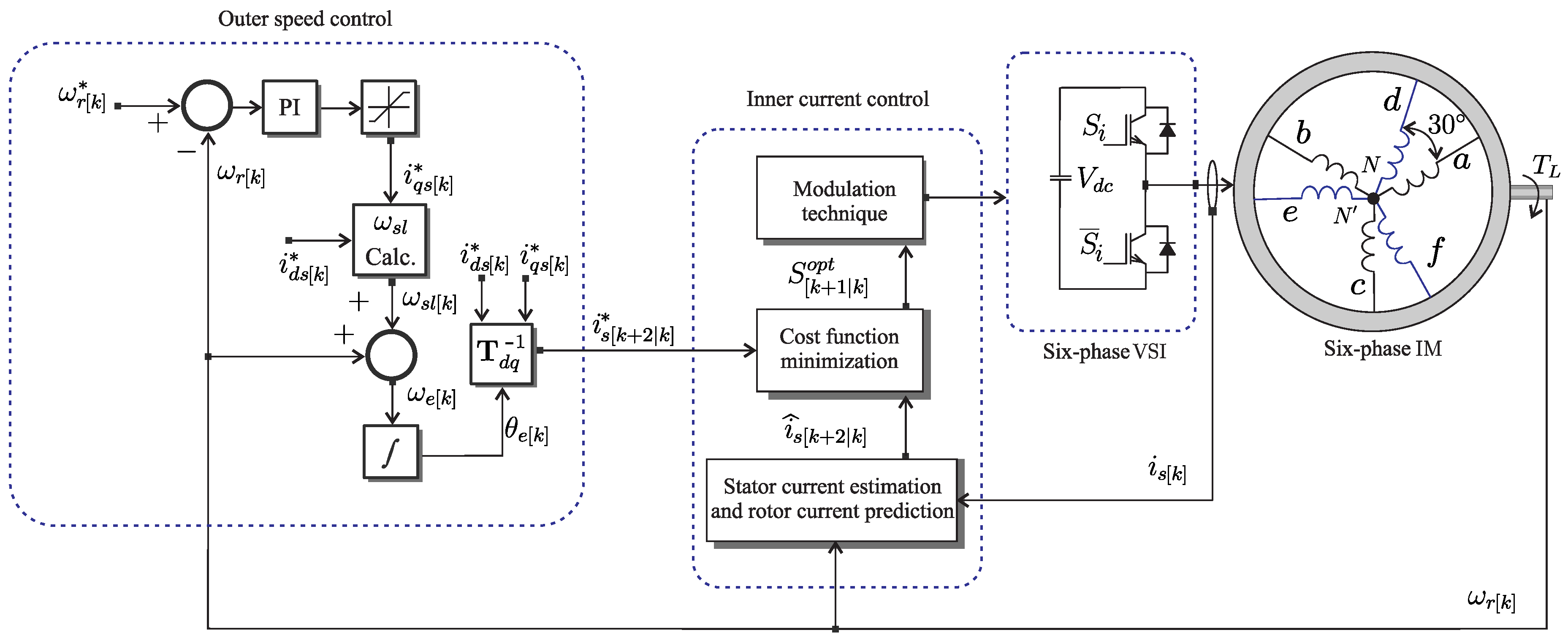
3. Drive Control
3.1. Speed Control
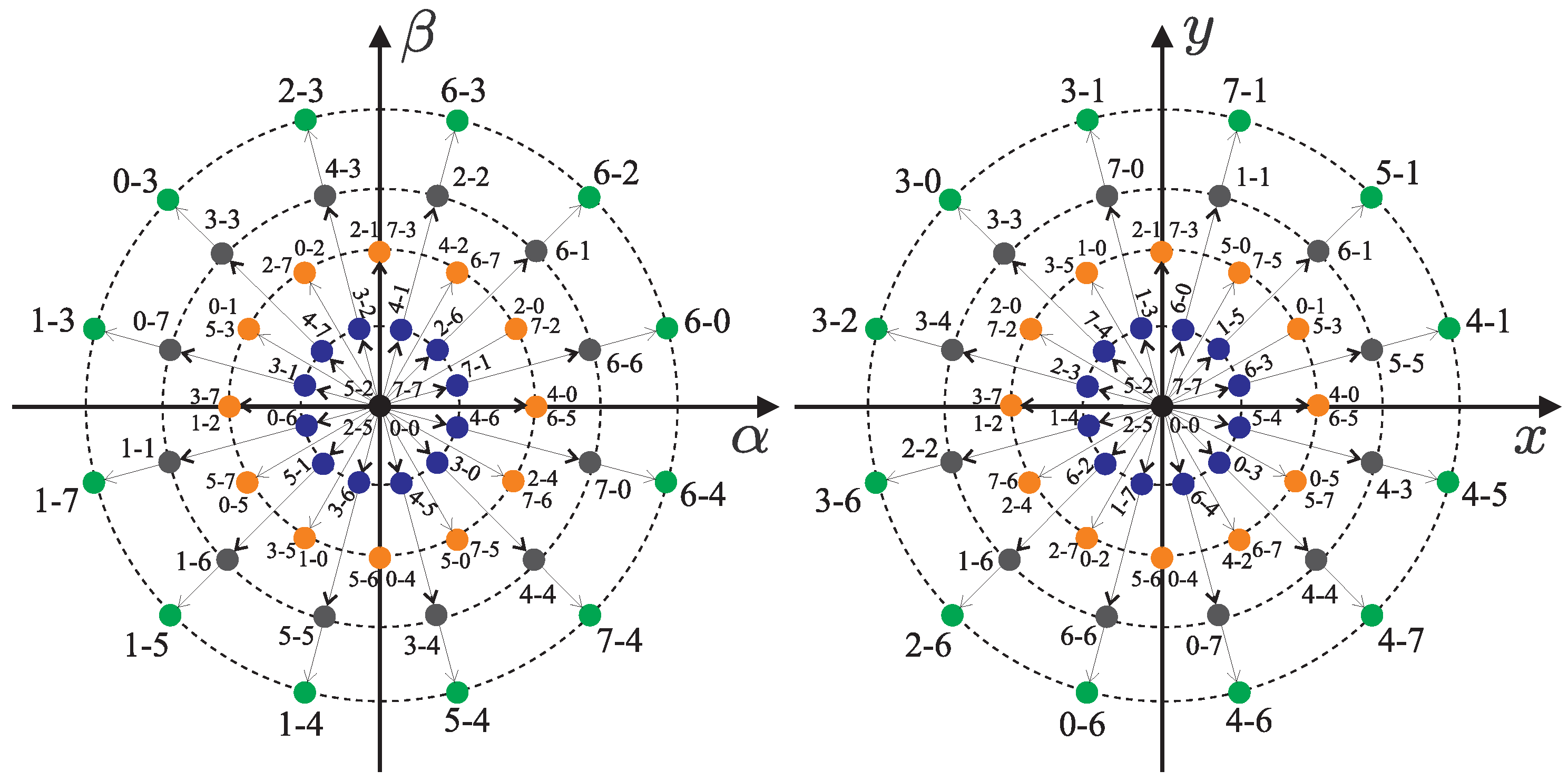
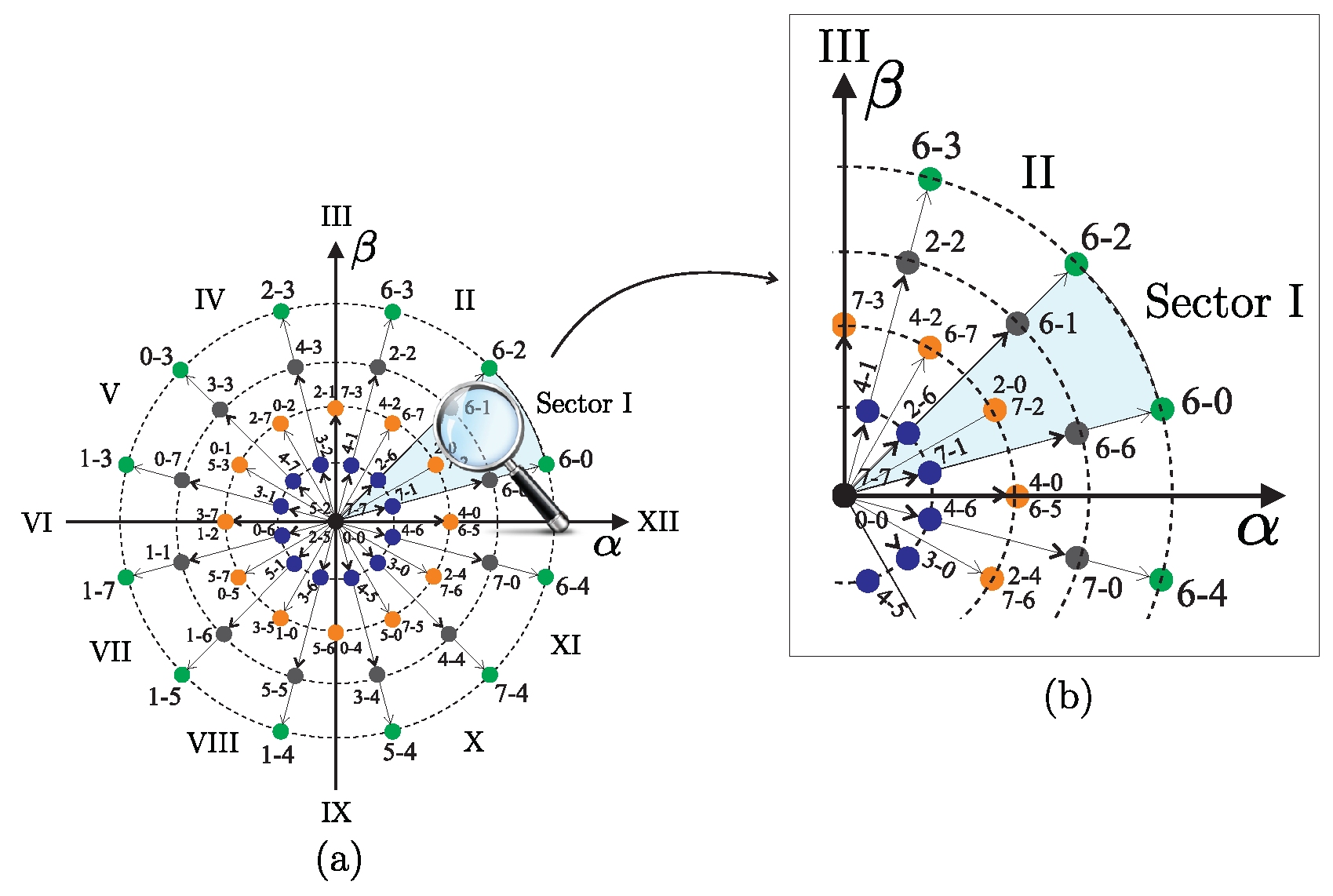
3.2. Classic MPC
Cost Function
3.3. Proposed Current Controller (Pfsccs)
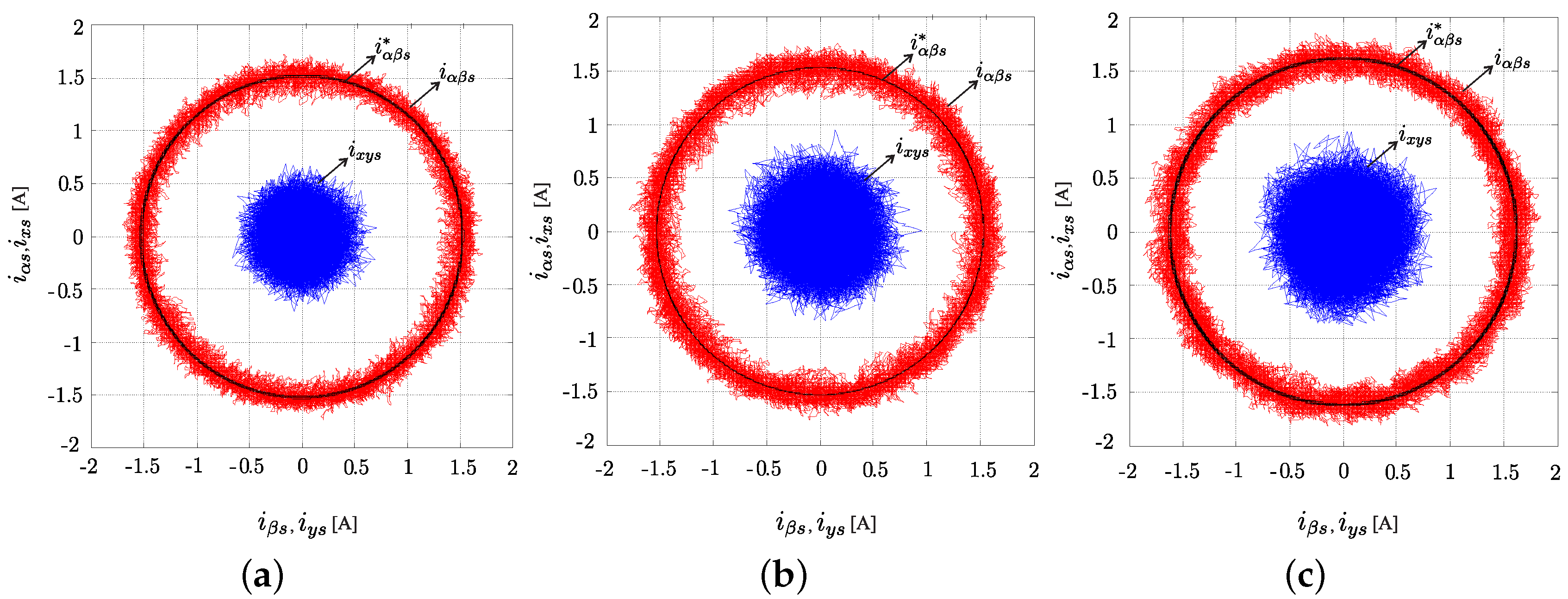
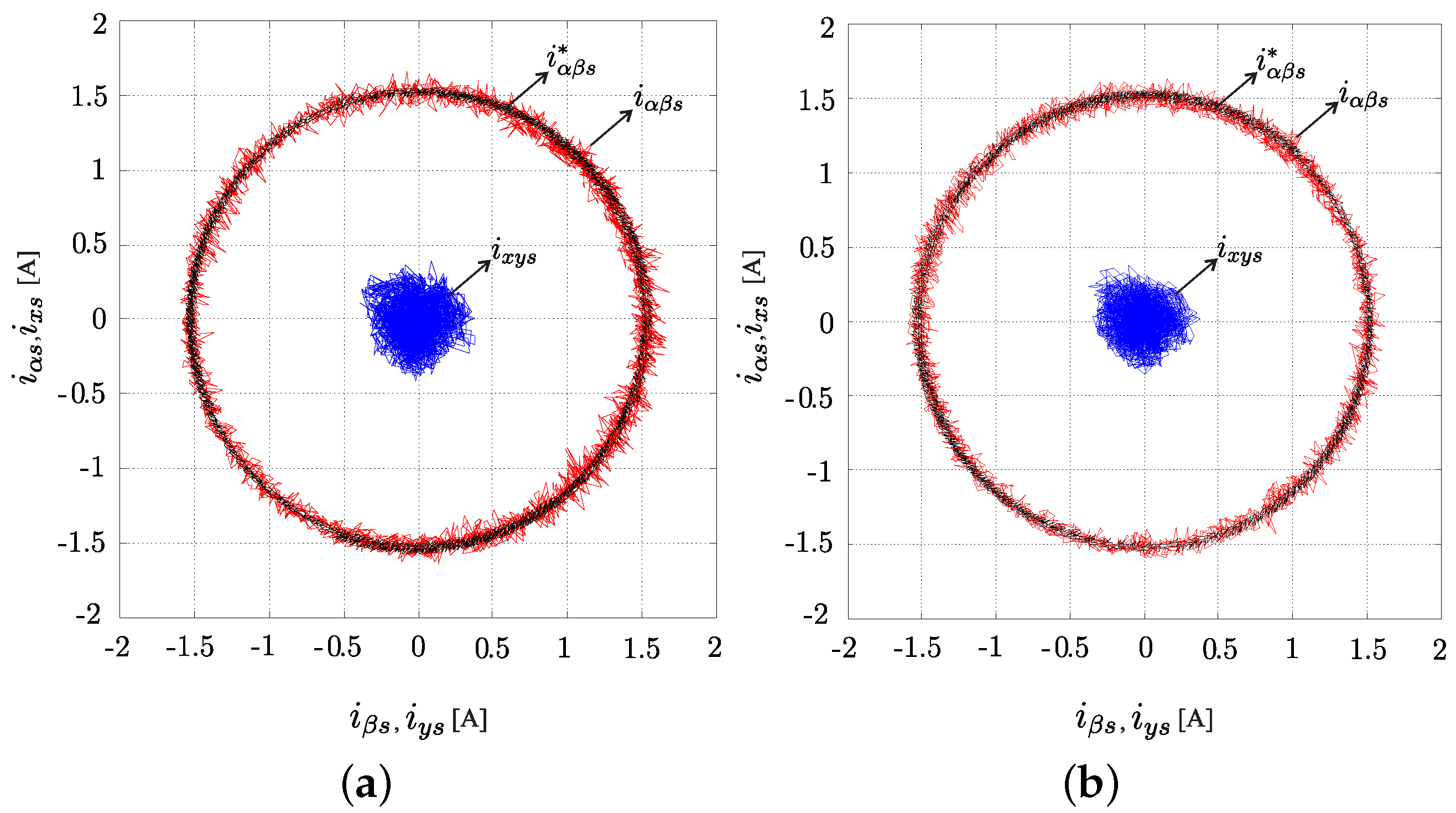
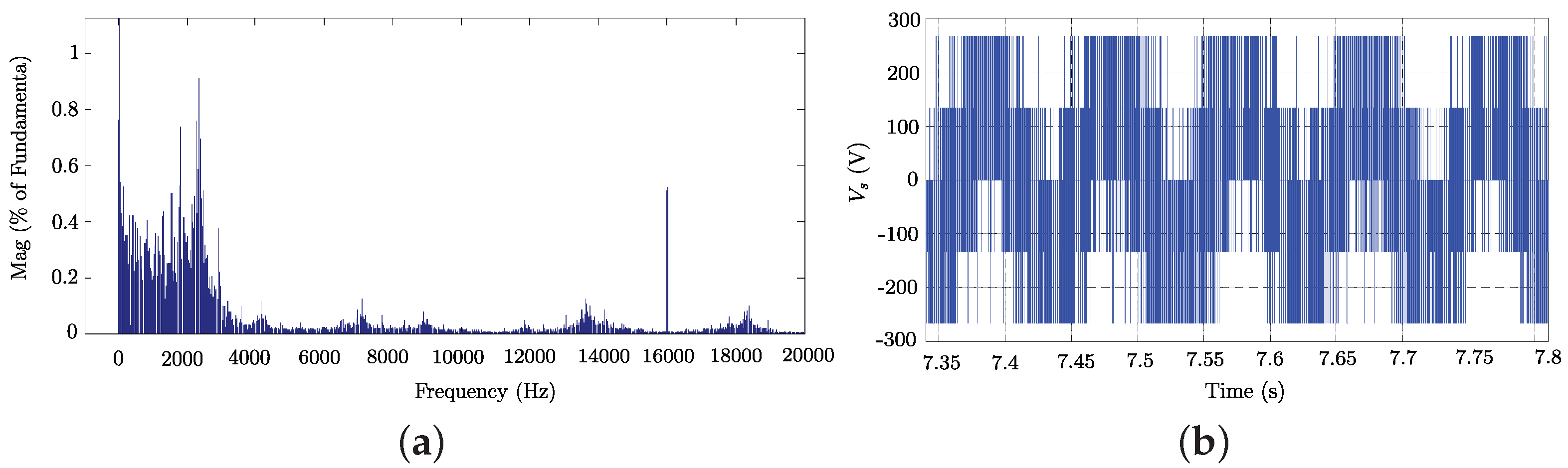
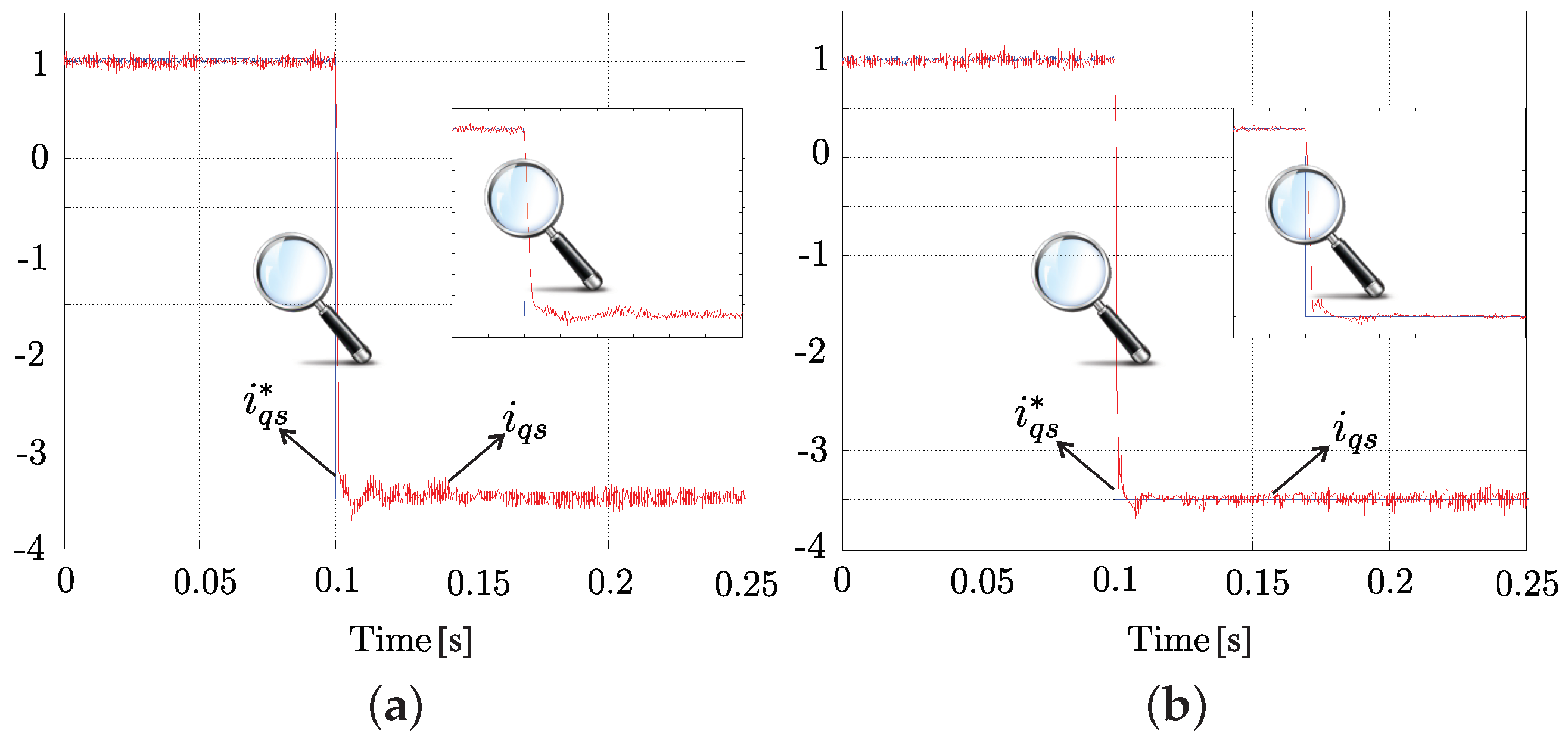
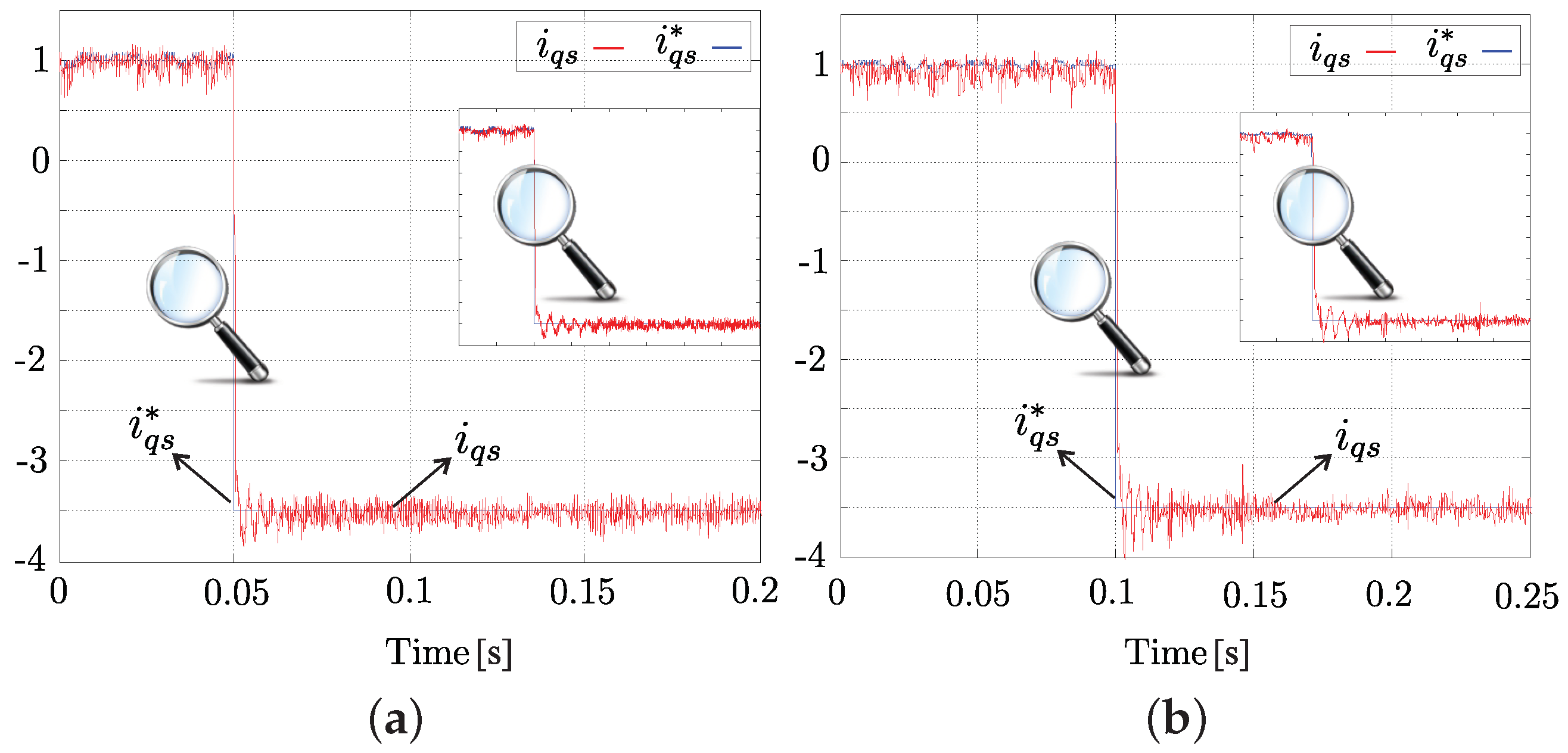
4. Simulation and Experimental Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FOC | Field Oriented Control |
| IM | Induction Machine |
| MPC | Model Predictive Control |
| PFSCCS | Predictive-Fixed Switching Current Control Strategy |
| MSE | Mean Squared Error |
| PI | Proportional-Integral |
| PWM | Pulse-Width Modulation |
| SVM | Space Vector Modulation |
| THD | Total Harmonic Distortion |
| VSI | Voltage Source Inverter |
| VSD | Vector Space Decomposition |
References
- Duran, M.J.; Levi, E.; Barrero, F. Multiphase Electric Drives: Introduction. In Wiley Encyclopedia of Electrical and Electronics Engineering; Available online: https://onlinelibrary.wiley.com/doi/abs/10.1002/047134608X.W8364 (accessed on 26 April 2019).
- Precup, R.E.; Kamal, T.; Hassan, S.Z. Advanced Control and Optimization Paradigms for Wind Energy Systems; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Subotic, I.; Bodo, N.; Levi, E. Integration of six-phase EV drivetrains into battery charging process with direct grid connection. IEEE Trans. Energy Conv. 2017, 32, 1012–1022. [Google Scholar] [CrossRef]
- Ayala, M.; Gonzalez, O.; Rodas, J.; Gregor, R.; Doval-Gandoy, J. A speed-sensorless predictive current control of multiphase induction machines using a Kalman filter for rotor current estimator. In Proceedings of the 2016 International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Toulouse, France, 2–4 November 2016; pp. 1–6. [Google Scholar]
- Munim, W.N.W.A.; Duran, M.J.; Che, H.S.; Bermúdez, M.; González-Prieto, I.; Rahim, N.A. A unified analysis of the fault tolerance capability in six-phase induction motor drives. IEEE Trans. Power Electron. 2017, 32, 7824–7836. [Google Scholar] [CrossRef]
- Jones, M.; Vukosavic, S.N.; Dujic, D.; Levi, E. A synchronous current control scheme for multiphase induction motor drives. IEEE Trans. Energy Conv. 2009, 24, 860–868. [Google Scholar] [CrossRef]
- Kali, Y.; Ayala, M.; Rodas, J.; Saad, M.; Doval-Gandoy, J.; Gregor, R.; Benjelloun, K. Current Control of a Six-Phase Induction Machine Drive based on Discrete-Time Sliding Mode with Time Delay Estimation. Energies 2019, 12, 170. [Google Scholar] [CrossRef]
- Che, H.S.; Duran, M.J.; Levi, E.; Jones, M.; Hew, W.P.; Rahim, N.A. Postfault operation of an asymmetrical six-phase induction machine with single and two isolated neutral points. IEEE Trans. Power Electron. 2014, 29, 5406–5416. [Google Scholar] [CrossRef]
- Mirzaeva, G.; Goodwin, G.C.; McGrath, B.P.; Teixeira, C.; Rivera, M. A generalized MPC framework for the design and comparison of VSI current controllers. IEEE Trans. Ind. Electron. 2016, 63, 5816–5826. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model Predictive Control for Power Converters and Drives: Advances and Trends. IEEE Trans. Ind. Electron. 2016, 64, 935–947. [Google Scholar] [CrossRef]
- Barrero, F.; Arahal, M.R.; Gregor, R.; Toral, S.; Durán, M.J. A proof of concept study of predictive current control for VSI-driven asymmetrical dual three-phase AC machines. IEEE Trans. Ind. Electron. 2009, 56, 1937–1954. [Google Scholar] [CrossRef]
- Barrero, F.; Prieto, J.; Levi, E.; Gregor, R.; Toral, S.; Durán, M.J.; Jones, M. An enhanced predictive current control method for asymmetrical six-phase motor drives. IEEE Trans. Ind. Electron. 2011, 58, 3242–3252. [Google Scholar] [CrossRef]
- Lim, C.S.; Levi, E.; Jones, M.; Rahim, N.A.; Hew, W.P. FCS-MPC-based current control of a five-phase induction motor and its comparison with PI-PWM control. IEEE Trans. Ind. Electron. 2013, 61, 149–163. [Google Scholar] [CrossRef]
- Vijayagopal, M.; Zanchetta, P.; Empringham, L.; De Lillo, L.; Tarisciotti, L.; Wheeler, P. Modulated model predictive current control for direct matrix converter with fixed switching frequency. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–10. [Google Scholar]
- Gregor, R.; Rodas, J.; Munoz, J.; Ayala, M.; Gonzalez, O.; Gregor, D. Predictive-Fixed Switching Frequency Technique for 5-Phase Induction Motor Drives. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Anacapri, Italy, 22–24 June 2016. [Google Scholar]
- Ayala, M.; Gonzalez, O.; Rodas, J.; Gregor, R.; Rivera, M. Predictive control at fixed switching frequency for a dual three-phase induction machine with Kalman filter-based rotor estimator. In Proceedings of the 2016 IEEE International Conference on Automatica (ICA-ACCA), Curico, Chile, 19–21 October 2016; pp. 1–6. [Google Scholar]
- Rivera, M.; Toledo, S.; Baier, C.; Tarisciotti, L.; Wheeler, P.; Verne, S. Indirect predictive control techniques for a matrix converter operating at fixed switching frequency. In Proceedings of the 2017 IEEE International Symposium on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Pucón, Chile, 18–20 October 2017; pp. 13–18. [Google Scholar]
- Comparatore, L.; Gregor, R.; Rodas, J.; Pacher, J.; Renault, A.; Rivera, M. Model based predictive current control for a three-phase cascade H-bridge multilevel STATCOM operating at fixed switching frequency. In Proceedings of the 2017 IEEE 8th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Florianopolis, Brazil, 17–20 April 2017; pp. 1–6. [Google Scholar]
- Harnefors, L.; Saarakkala, S.; Hinkkanen, M. Speed Control of Electrical Drives Using Classical Control Methods. IEEE Trans. Ind. Appl. 2013, 49, 889–898. [Google Scholar] [CrossRef]
- Zhao, Y.; Lipo, T. Space vector PWM control of dual three-phase induction machine using vector space decomposition. IEEE Trans. Ind. Electron. 1995, 31, 1100–1109. [Google Scholar]
- Ayala, M.; Rodas, J.; Gregor, R.; Doval-Gandoy, J.; Gonzalez, O.; Saad, M.; Rivera, M. Comparative Study of Predictive Control Strategies at Fixed Switching Frequency for an Asymmetrical Six-Phase Induction Motor Drive. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017; pp. 1–8. [Google Scholar]
- Rodas, J.; Barrero, F.; Arahal, M.R.; Martin, C.; Gregor, R. On-Line Estimation of Rotor Variables in Predictive Current Controllers: A Case Study Using Five-Phase Induction Machines. IEEE Trans. Ind. Electron. 2016, 63, 5348–5356. [Google Scholar] [CrossRef]
- Rodas, J.; Martin, C.; Arahal, M.R.; Barrero, F.; Gregor, R. Influence of Covariance-Based ALS Methods in the Performance of Predictive Controllers with Rotor Current Estimation. IEEE Trans. Ind. Electron. 2017, 64, 2602–2607. [Google Scholar] [CrossRef]
- Pandit, J.K.; Aware, M.V.; Nemade, R.V.; Levi, E. Direct torque control scheme for a six-phase induction motor with reduced torque ripple. IEEE Trans. Power Electron. 2017, 32, 7118–7129. [Google Scholar] [CrossRef]
- Gonzalez, O.; Ayala, M.; Rodas, J.; Gregor, R.; Rivas, G.; Doval-Gandoy, J. Variable-Speed Control of a Six-Phase Induction Machine using Predictive-Fixed Switching Frequency Current Control Techniques. In Proceedings of the 2018 9th IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Charlotte, NC, USA, 25–28 June 2018; pp. 1–6. [Google Scholar]
- Yepes, A.G.; Riveros, J.A.; Doval-Gandoy, J.; Barrero, F.; López, O.; Bogado, B.; Jones, M.; Levi, E. Parameter identification of multiphase induction machines with distributed windings Part 1: Sinusoidal excitation methods. IEEE Trans. Energy Conv. 2012, 27, 1056–1066. [Google Scholar] [CrossRef]
- Riveros, J.A.; Yepes, A.G.; Barrero, F.; Doval-Gandoy, J.; Bogado, B.; Lopez, O.; Jones, M.; Levi, E. Parameter identification of multiphase induction machines with distributed windings Part 2: Time-domain techniques. IEEE Trans. Energy Conv. 2012, 27, 1067–1077. [Google Scholar] [CrossRef]

| 6.9 | 654.4 mH | ||
| 12.8 mH | 626.8 mH | ||
| 5.3 mH | 2 kW | ||
| 6.7 | 0.07 kg.m | ||
| 614 mH | 0.0004 kg.m/s | ||
| P | 1 | 3000 rpm |
| = kHz | ||||||
|---|---|---|---|---|---|---|
| MSE | MSE | MSE | MSE | THD | THD | |
| 500 | 0.065 | 0.064 | 0.174 | 0.172 | 5.73 | 5.46 |
| 1000 | 0.076 | 0.075 | 0.211 | 0.203 | 5.43 | 5.34 |
| 1500 | 0.110 | 0.110 | 0.219 | 0.216 | 6.46 | 6.38 |
| = 8 kHz for Classic MPC | ||||||
| MSE | MSE | MSE | MSE | THD | THD | |
| 500 | 0.140 | 0.130 | 0.821 | 0.822 | 8.30 | 8.40 |
| 1000 | 0.147 | 0.138 | 0.953 | 0.934 | 7.40 | 7.30 |
| = 16 kHz for Classic MPC | ||||||
| MSE | MSE | MSE | MSE | THD | THD | |
| 500 | 0.073 | 0.072 | 0.491 | 0.483 | 8.40 | 8.30 |
| 1000 | 0.084 | 0.082 | 0.538 | 0.534 | 7.50 | 7.40 |
| = 8 kHz for PFSCCS | ||||||
| MSE | MSE | MSE | MSE | THD | THD | |
| 500 | 0.042 | 0.045 | 0.135 | 0.130 | 4.89 | 5.08 |
| 1000 | 0.069 | 0.068 | 0.197 | 0.204 | 4.69 | 4.78 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez, O.; Ayala, M.; Doval-Gandoy, J.; Rodas, J.; Gregor, R.; Rivera, M. Predictive-Fixed Switching Current Control Strategy Applied to Six-Phase Induction Machine. Energies 2019, 12, 2294. https://doi.org/10.3390/en12122294
Gonzalez O, Ayala M, Doval-Gandoy J, Rodas J, Gregor R, Rivera M. Predictive-Fixed Switching Current Control Strategy Applied to Six-Phase Induction Machine. Energies. 2019; 12(12):2294. https://doi.org/10.3390/en12122294
Chicago/Turabian StyleGonzalez, Osvaldo, Magno Ayala, Jesus Doval-Gandoy, Jorge Rodas, Raul Gregor, and Marco Rivera. 2019. "Predictive-Fixed Switching Current Control Strategy Applied to Six-Phase Induction Machine" Energies 12, no. 12: 2294. https://doi.org/10.3390/en12122294
APA StyleGonzalez, O., Ayala, M., Doval-Gandoy, J., Rodas, J., Gregor, R., & Rivera, M. (2019). Predictive-Fixed Switching Current Control Strategy Applied to Six-Phase Induction Machine. Energies, 12(12), 2294. https://doi.org/10.3390/en12122294










