Applications of Complex Network Analysis in Electric Power Systems
Abstract
:1. Introduction
2. Literature Survey
2.1. Examining the Electric Power System from an Abstract Perspective
- -
- The cumulative degree distribution of the North American grid follows an exponential function P(k > K)~e−0.5K, which agrees with that of the Western power grid that is categorized as a single-scale network.
- -
- The cumulative betweenness node distribution follows P(l > L)~(2500 + L)−0.7. The betweenness (l) of a node in a network is defined as the number of shortest paths that pass through it [26,27]. Assuming that the power is sent through the shortest route, the betweenness of a substation could be considered as an indication of how much energy passes through it. The calculated betweenness node distribution demonstrates that almost 40% of the substations are part of tens and hundreds of shortest paths, while 1% of the substations lie on a million or more shortest paths. These high betweenness substations, even though they may not be considered hubs, have a significant role in power transmission.
- -
- To ensure the reliability of the loads being continuously supplied, the transmission network of the electric power grid was designed in such a way that there is more than a single electrical line between any two substations. In an attempt to verify whether the North American grid topology has this characteristic of global redundancy or has vanished through the grid expansions, the authors presented a measure of the network redundancy called the “edge range”. This measure is defined as the distance between the ends of an edge if the edge linking them was removed [28]. It was found that around 900 TLs connecting generators and/or transmission substations are radial. These radial TLs represent a clear weakness, as their disconnection isolates their endpoints and subsequently creates islanded clusters in the electric power grid.
- -
- Degree-based and random disconnection of nodes was performed to examine the connectivity loss percentage, which quantifies the average reduction in the number of generators connected to a specific distribution substation. Through this experiment, it was found that the elimination of generating substations does not change the overall connectivity of the grid due to the high level of redundancy at the generating substation level. However, the situation can be radically different when the substations being disconnected were transmission substations. For accidental or random disconnection, the connectivity loss is considerably low and remains proportional to the number of nodes that got disconnected. On the other hand, the connectivity loss is significantly increased when high betweenness or high degree transmission hubs are disconnected. In their conclusion, the electric grid can endure only a few failures of this type before substantial parts of the grid become separated, leading to a significant connectivity loss at the distribution level. For example, the failure of 4% of the substations that have high betweenness might lead to a 60% loss of connectivity in the grid.
2.2. Scrutinizing the Electric Power System Utilizing Weighted Graphs
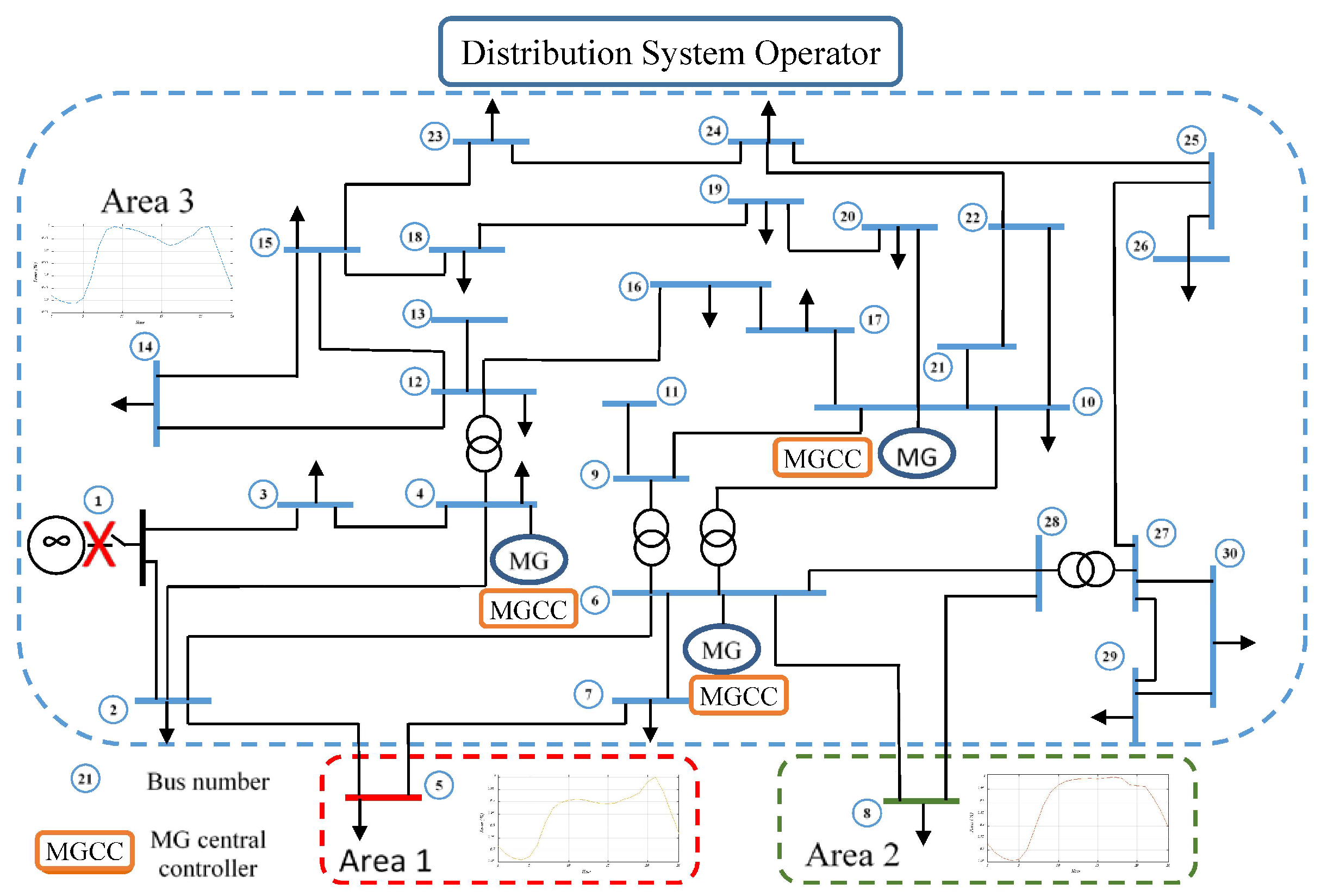
3. System Understudy
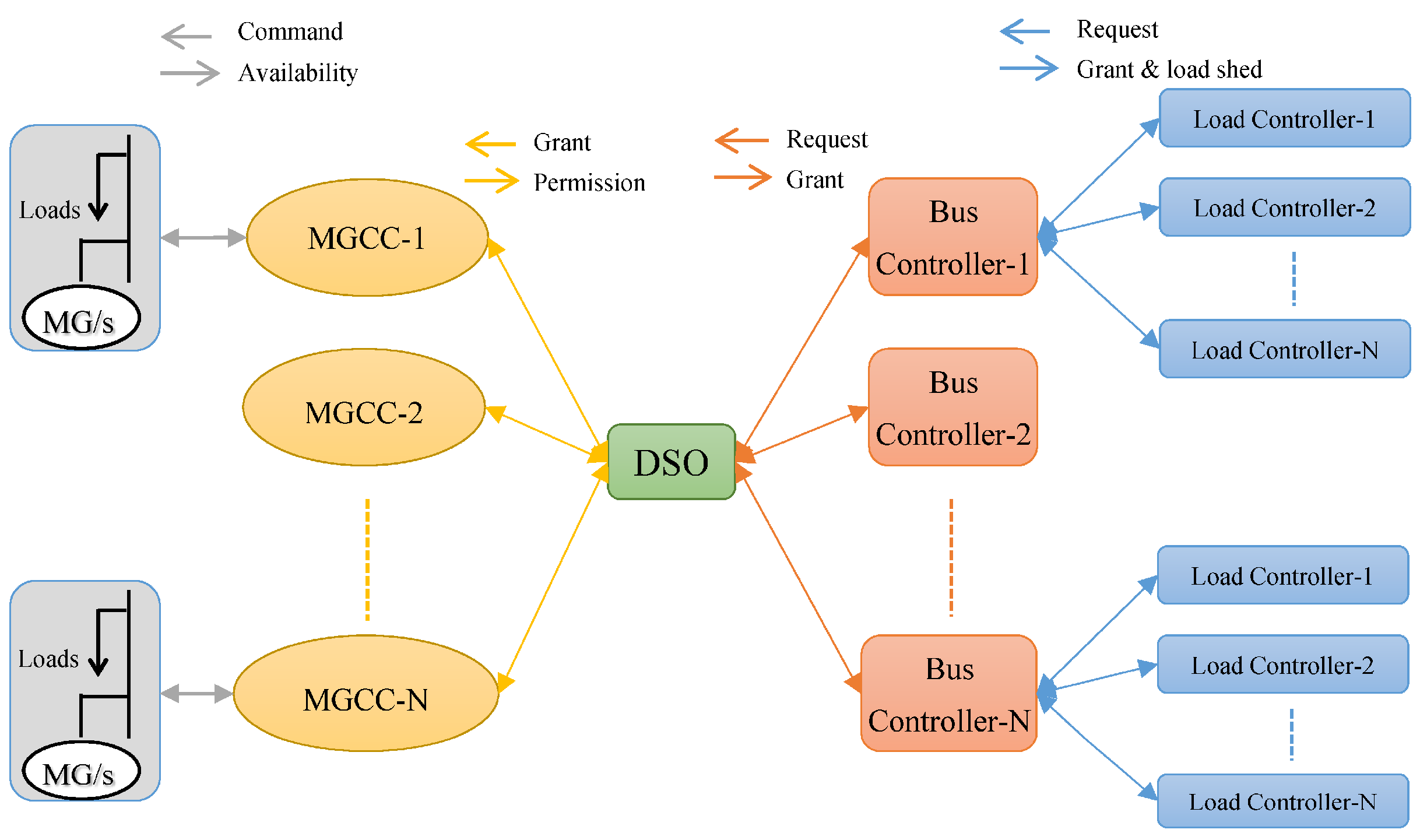
4. Complex Network Framework
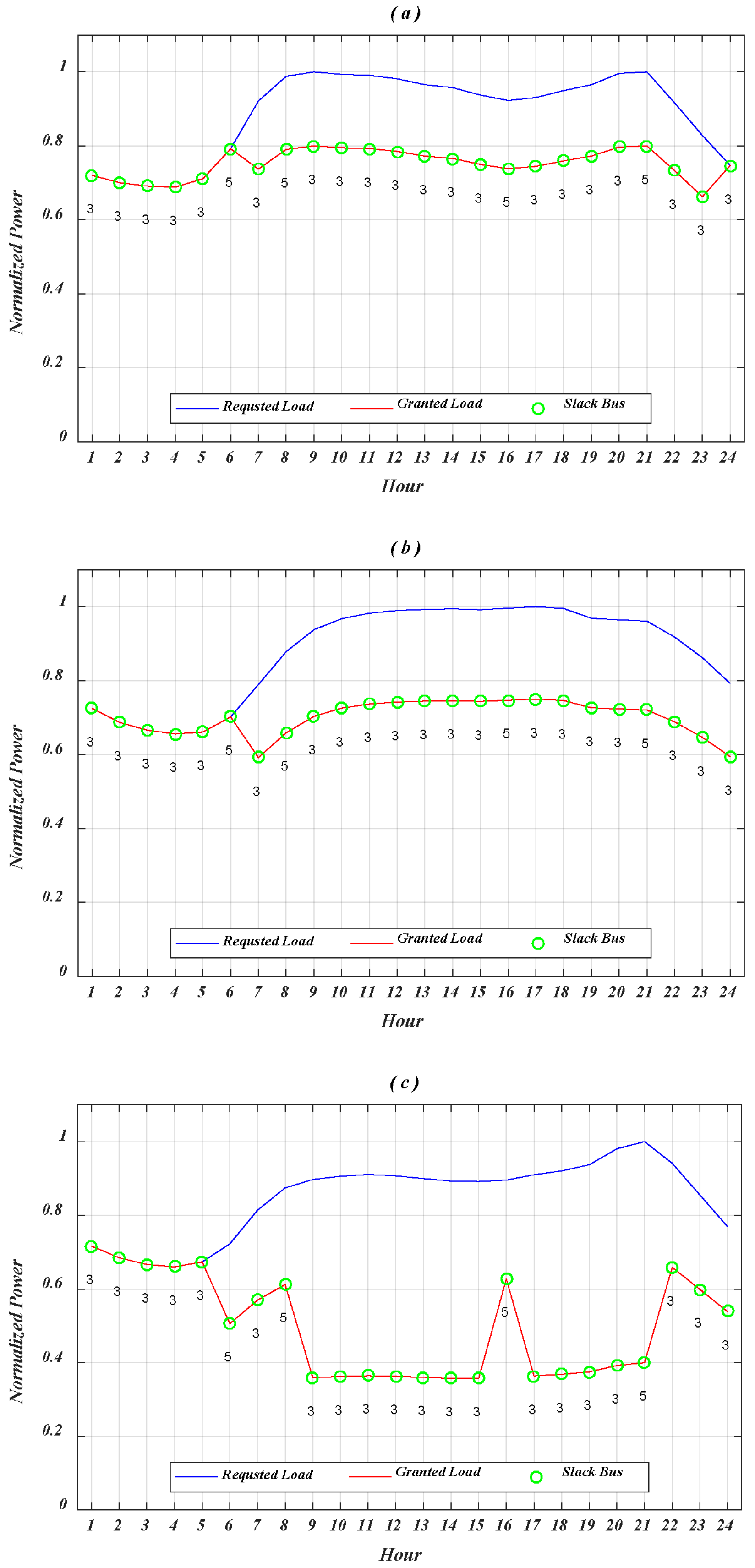
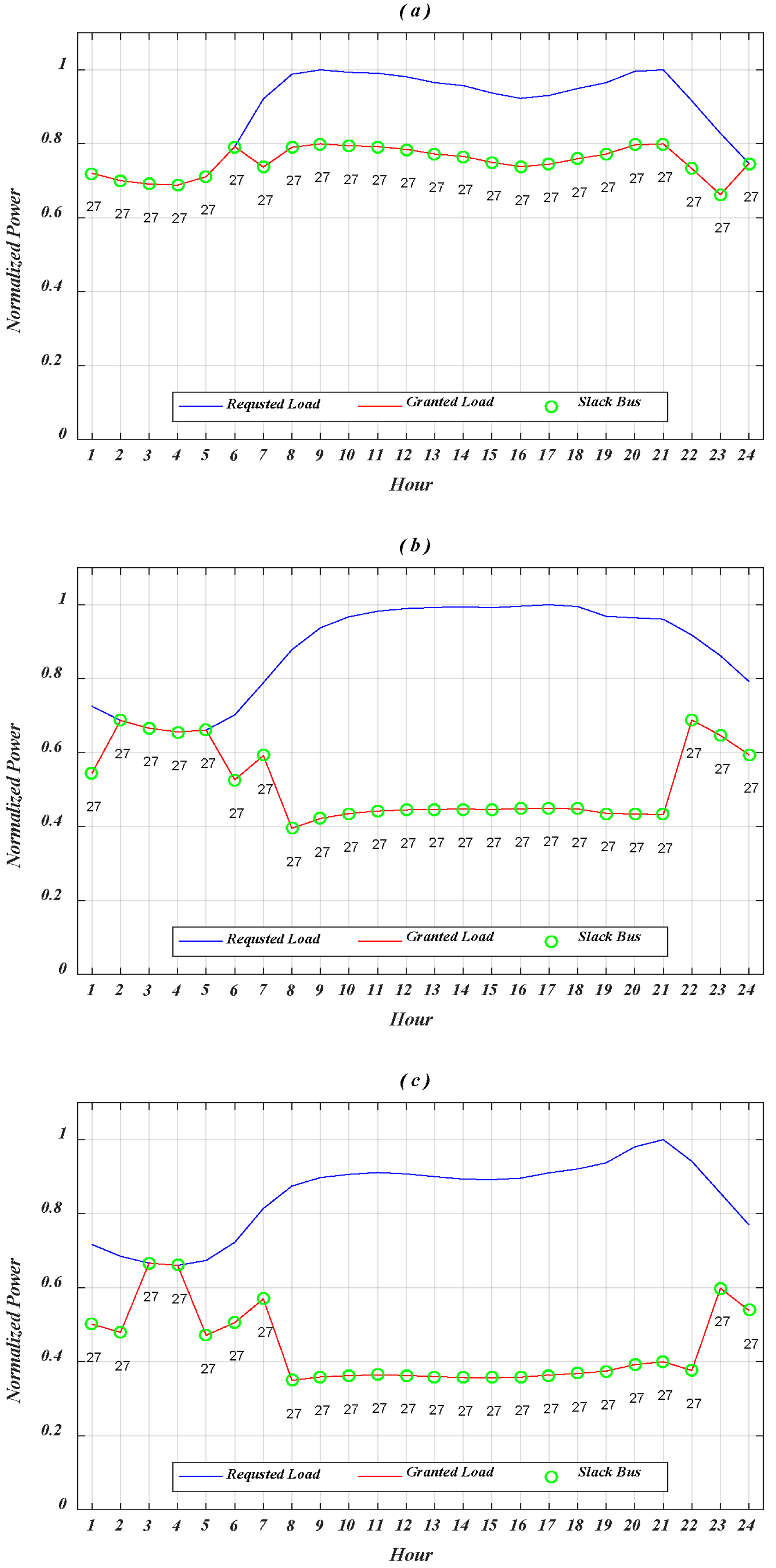
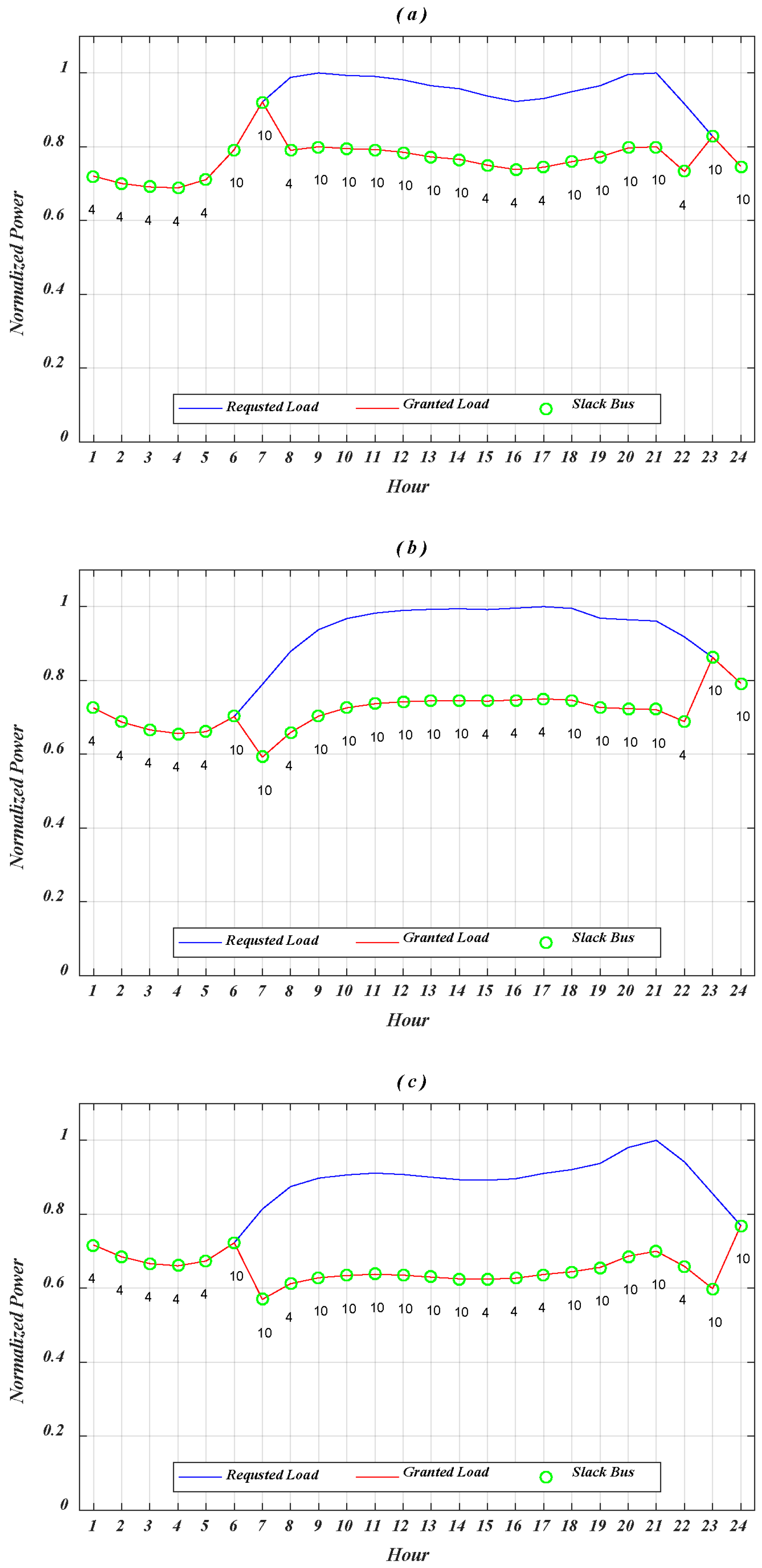
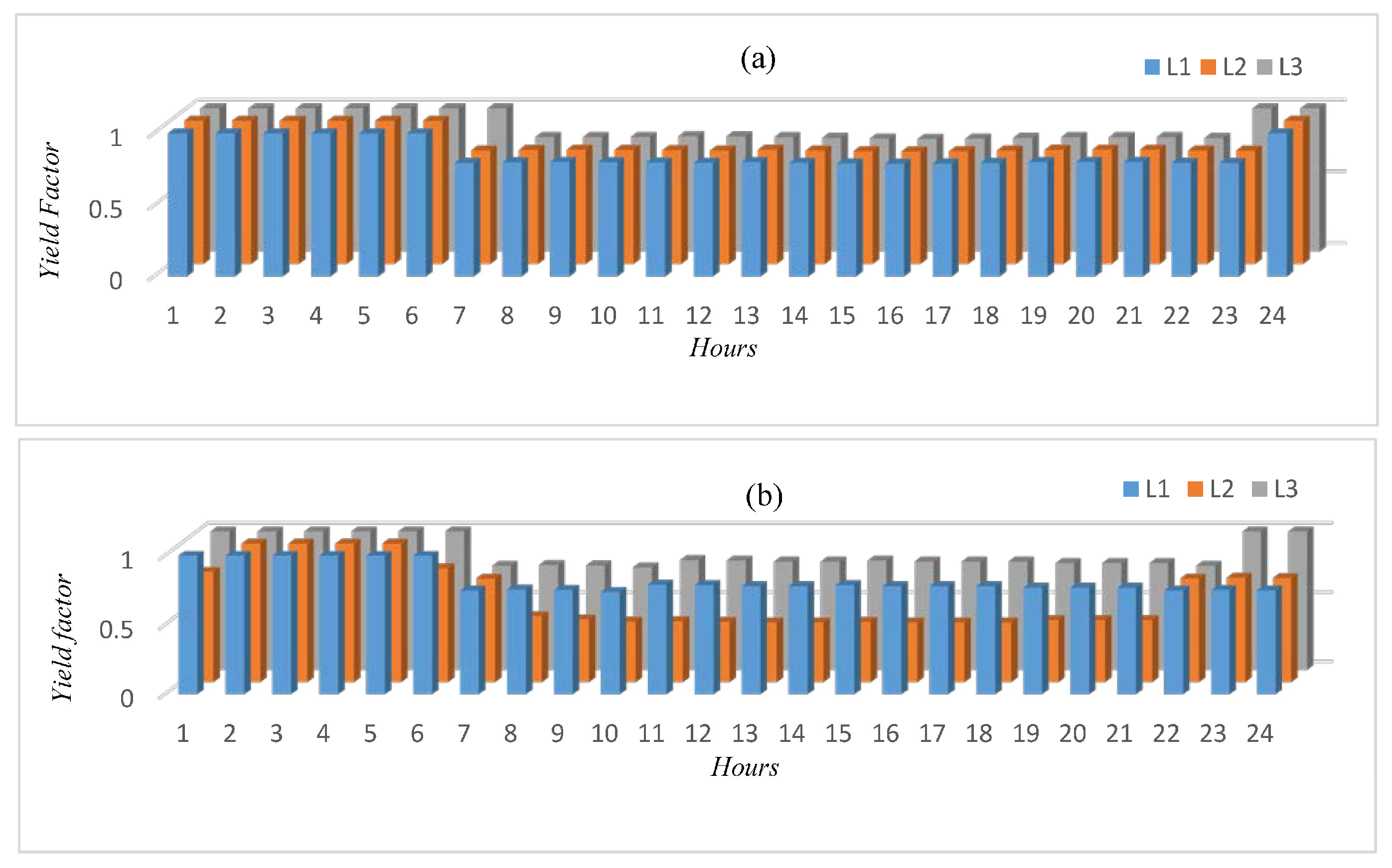
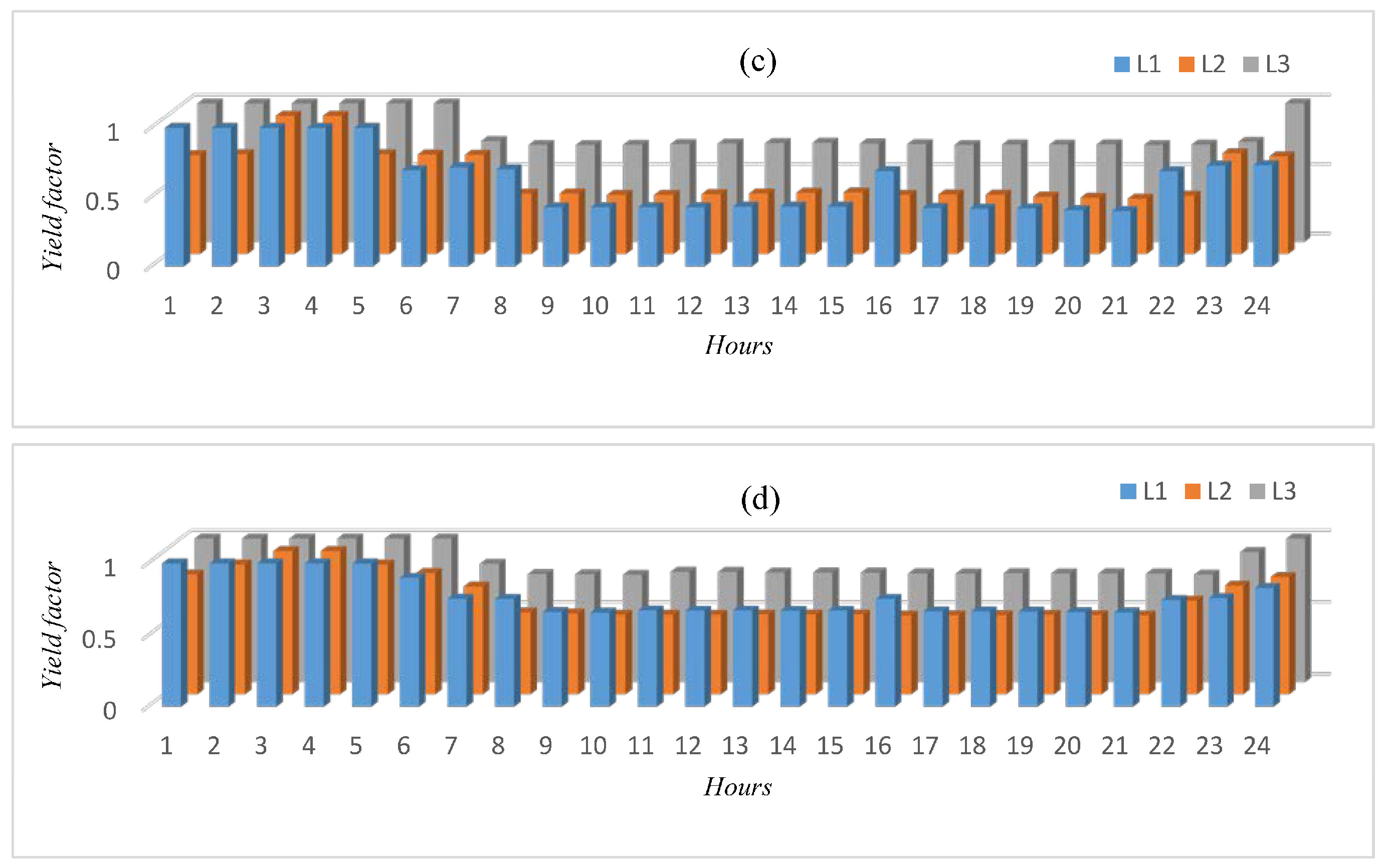
5. Results and Analysis
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Shields, R. Cultural Topology: The Seven Bridges of Königsburg, 1736. Theory Cult. Soc. 2012, 29, 43–57. [Google Scholar] [CrossRef]
- Complex Systems Tutorial. Available online: http://eldar.cz/cognition/complex/#Intuitive%20Definitions%20of%20Complexity.Steen,%20Maarten%20van.%20Graph%20Theory%20and%20Complex%20Networks:%20an%20Introduction.%20Maarten%20Van%20Steen,%202010 (accessed on 15 May 2018).
- Kim, J.; Wilhelm, T. What Is a Complex Graph? Phys. A Stat. Mech. Appl. 2008, 387, 2637–2652. [Google Scholar] [CrossRef]
- Nasiruzzaman, A.B.M.; Pota, H.R. Critical Node Identification of Smart Power System Using Complex Network Framework Based Centrality Approach. In Proceedings of the 2011 North American Power Symposium, Boston, MA, USA, 4–6 August 2011. [Google Scholar]
- Nasiruzzaman, A.B.M.; Pota, H.R. Transient Stability Assessment of Smart Power System Using Complex Networks Framework. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar]
- Gale, J. IEAGHG Information Paper: 2015-IP29; Emissions Performance Standards. Available online: http://www.ieaghg.org/docs/General_Docs/Publications/Information_Papers/2015-IP29.pdf (accessed on 16 May 2018).
- Digital Grid|ABB. Available online: http://new.abb.com/grid/stronger-smarter-greener/digital-grid (accessed on 16 May 2018).
- Fact Sheet: President Obama to Announce Historic Carbon Pollution Standards for Power Plants. Available online: https://obamawhitehouse.archives.gov/the-press-office/2015/08/03/fact-sheet-president-obama-announce-historic-carbon-pollution-standards (accessed on 3 August 2015).
- Modernizing Electric Power Delivery System. Available online: https://www.energy.gov/sites/prod/files/2014/10/f18/ModernizingElectricPowerDeliverySystem.pdf (accessed on 16 May 2018).
- Grid Modernization and the Smart Grid|Department of Energy. Available online: https://www.energy.gov/oe/activities/technology-development/grid-modernization-and-smart-grid (accessed on 16 May 2018).
- A Lucky Number: 13 Microgrids Proposed across New Jersey. Windpower Engineering & Development. Available online: https://www.windpowerengineering.com/slider/lucky-number-13-microgrids-proposed-across-new-jersey/ (accessed on 16 May 2018).
- Moradi, M.H.; Abedini, M. A Novel Method for Optimal DG Units Capacity and Location in Microgrids. Int. J. Electr. Power Energy Syst. 2016, 75, 236–244. [Google Scholar] [CrossRef]
- Cagnano, A.; de Tuglie, E. A Decentralized Voltage Controller Involving PV Generators Based on Lyapunov Theory. Renew. Energy 2016, 86, 664–674. [Google Scholar] [CrossRef]
- Ghiani, E.; Mocci, S.; Pilo, F. Optimal Reconfiguration of Distribution Networks According to the Microgrid Paradigm. In Proceedings of the 2005 International Conference on Future Power Systems, Amsterdam, The Netherlands, 16–18 November 2005. [Google Scholar]
- Rojas-Cessa, R.; Sahasrabudhe, V.; Miglio, E.; Balineni, D.; Kurylo, J.; Grebel, H. Testbed Evaluations of a Controlled-Delivery Power Grid. In Proceedings of the 2014 IEEE International Conference on Smart Grid Communications (SmartGridComm), Venice, Italy, 3–6 November 2014. [Google Scholar]
- Rojas-Cessa, R.; Xu, Y.; Grebel, H. Management of a Smart Grid with Controlled-Delivery of Discrete Power Levels. In Proceedings of the 2013 IEEE International Conference on Smart Grid Communications (SmartGridComm), Vancouver, BC, Canada, 21–24 October 2013. [Google Scholar]
- Saleh, M.; Esa, Y.; Mohamed, A.A.; Grebel, H.; Rojas-Cessa, R. Energy Management Algorithm for Resilient Controlled Delivery Grids. In Proceedings of the 2017 IEEE Industry Applications Society Annual Meeting, Cincinnati, OH, USA, 1–5 October 2017. [Google Scholar]
- Veolia. New Jersey Focuses on Resilience with State Microgrid Project. Text. Veolia North America. Available online: https://www.veolianorthamerica.com/en/media/newsroom/new-jersey-focuses-resilience-state-microgrid-project (accessed on 5 July 2017).
- Wang, K.; Ouyang, Z.; Krishnan, R.; Shu, L.; He, L. A Game Theory-Based Energy Management System Using Price Elasticity for Smart Grids. IEEE Trans. Ind. Inform. 2015, 11, 1607–1616. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, B.; Wang, J.; Chen, C. Networked Microgrids for Self-Healing Power Systems. IEEE Trans. Smart Grid 2016, 7, 310–319. [Google Scholar] [CrossRef]
- Albert, R.; Albert, I.; Nakarado, G.L. Structural Vulnerability of the North American Power Grid. Phys. Rev. E 2004, 69. [Google Scholar] [CrossRef] [PubMed]
- Albert, R.; Jeong, H.; Barabási, A.-L. Error and Attack Tolerance of Complex Networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef] [PubMed]
- Cohen, R.; Erez, K.; ben-Avraham, D.; Havlin, S. Resilience of the Internet to Random Breakdowns. Phys. Rev. Lett. 2000, 85, 4626–4628. [Google Scholar] [CrossRef] [PubMed]
- Callaway, D.S.; Newman, M.E.J.; Strogatz, S.H.; Watts, D.J. Network Robustness and Fragility: Percolation on Random Graphs. Phys. Rev. Lett. 2000, 85, 5468–5471. [Google Scholar] [CrossRef] [PubMed]
- World Electric Power Plants Database: Global Market Data and Price Assessments—Platts. Available online: https://www.platts.com/products/world-electric-power-plants-database (accessed on 16 May 2018).
- Goh, K.-I.; Kahng, B.; Kim, D. Universal Behavior of Load Distribution in Scale-Free Networks. Phys. Rev. Lett. 2001, 87. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. Scientific Collaboration Networks. II. Shortest Paths, Weighted Networks, and Centrality. Phys. Rev. E 2001, 64, 016132. [Google Scholar] [CrossRef] [PubMed]
- Motter, A.E.; Matias, M.A.; Kurths, J.; Ott, E. Dynamics on Complex Networks and Applications. Phys. D Nonlinear Phenom. 2006, 224, vii–viii. [Google Scholar] [CrossRef]
- Crucitti, P.; Latora, V.; Marchiori, M. A Topological Analysis of the Italian Electric Power Grid. Phys. A Stat. Mech. Appl. 2004, 338, 92–97. [Google Scholar] [CrossRef]
- Martí, R.-C.; Valverde, S.; Solé, R.V. Topological Vulnerability of the European Power Grid under Errors and Attacks. Int. J. Bifurc. Chaos 2007, 17, 2465–2475. [Google Scholar] [CrossRef]
- Solé, R.V.; Rosas-Casals, M.; Corominas-Murtra, B.; Valverde, S. Robustness of the European Power Grids under Intentional Attack. Phys. Rev. E 2008, 77. [Google Scholar] [CrossRef] [PubMed]
- Coelho, E.P.R.; Thomazelli, J.C.; Paiva, M.H.M.; Segatto, M.E.V. A Complex Network Analysis of the Brazilian Power Test System. In Proceedings of the 2015 IEEE PES Innovative Smart Grid Technologies Latin America (ISGT LATAM), Montevideo, Uruguay, 5–7 October 2015. [Google Scholar]
- Ding, M.; Han, P. Reliability Assessment to Large-Scale Power Grid Based on Small-World Topological Model. In Proceedings of the 2006 International Conference on Power System Technology, Chongqing, China, 22–26 October 2006. [Google Scholar]
- Lu, Z.; Meng, Z.; Zhou, S. Cascading Failure Analysis of Bulk Power System Using Small-World Network Model. In Proceedings of the 2004 International Conference on Probabilistic Methods Applied to Power Systems, Ames, IA, USA, 12–16 September 2004. [Google Scholar]
- Pagani, G.A.; Aiello, M. Towards Decentralization: A Topological Investigation of the Medium and Low Voltage Grids. IEEE Trans. Smart Grid 2011, 2, 538–547. [Google Scholar] [CrossRef]
- Mei, S.; Zhang, X.; Cao, M. Complex Small-World Power Grids. In Power Grid Complexity; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Hines, P.; Blumsack, S. A Centrality Measure for Electrical Networks. In Proceedings of the 41st Annual Hawaii International Conference on System Sciences (HICSS 2008), Big Island, HI, USA, 7–10 January 2008. [Google Scholar]
- Freeman, L.C. Centrality in Social Networks Conceptual Clarification. Soc. Netw. 1978, 1, 215–239. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community Structure in Social and Biological Networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. A Measure of Betweenness Centrality Based on Random Walks. Soc. Netw. 2005, 27, 39–54. [Google Scholar] [CrossRef]
- Rajasingh, I.; Rajan, B.; Florence, I.D. Betweeness-Centrality of Grid Networks. In Proceedings of the 2009 International Conference on Computer Technology and Development, Kota Kinabalu, Malaysia, 13–15 November 2009. [Google Scholar]
- Jawad, M.; Gou, B. Applications of Complex Network Theory on Power Grids. In Proceedings of the EIT 2013, IEEE International Conference on Electro-Information Technology, Lincoln, NE, USA, 14–17 May 2017. [Google Scholar]
- Dobson, I.; Carreras, B.A.; Lynch, V.E.; Newman, D.E. An Initial Model for Complex Dynamics in Electric Power System Blackouts. In Proceedings of the 34th Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 3–6 January 2001. [Google Scholar]
- Carreras, B.A.; Lynch, V.E.; Sachtjen, M.L.; Dobson, I.; Newman, D.E. Modeling Blackout Dynamics in Power Transmission Networks with Simple Structure. In Proceedings of the 34th Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 3–6 January 2001. [Google Scholar]
- Carreras, B.A.; Lynch, V.E.; Dobson, I.; Newman, D.E. Critical Points and Transitions in an Electric Power Transmission Model for Cascading Failure Blackouts. Chaos Interdiscip. J. Nonlinear Sci. 2002, 12, 985–994. [Google Scholar] [CrossRef] [PubMed]
- Carreras, B.A.; Lynch, V.E.; Newman, D.E.; Dobson, I. Blackout Mitigation Assessment in Power Transmission Systems. In Proceedings of the 36th Annual Hawaii International Conference on System Sciences, Big Island, HI, USA, 6–9 January 2003. [Google Scholar]
- Carreras, B.A.; Newman, D.E.; Dobson, I.; Poole, A.B. Evidence for Self-Organized Criticality in a Time Series of Electric Power System Blackouts. IEEE Trans. Circuits Syst. I Regul. Pap. 2004, 51, 1733–1740. [Google Scholar] [CrossRef]
- Dobson, I.; Carreras, B.A.; Lynch, V.E.; Newman, D.E. Complex Systems Analysis of Series of Blackouts: Cascading Failure, Critical Points, and Self-Organization. Chaos 2007, 17, 026103. [Google Scholar] [CrossRef] [PubMed]
- Dwivedi, A.; Yu, X.; Sokolowski, P. Analyzing Power Network Vulnerability with Maximum Flow Based Centrality Approach. In Proceedings of the 2010 8th IEEE International Conference on Industrial Informatics, Osaka, Japan, 13–16 July 2010. [Google Scholar]
- Dwivedi, A.; Yu, X. A Maximum-Flow-Based Complex Network Approach for Power System Vulnerability Analysis. IEEE Trans. Ind. Inform. 2013, 9, 81–88. [Google Scholar] [CrossRef]
- Nasiruzzaman, A.B.M.; Pota, H.R.; Mahmud, M.A. Application of Centrality Measures of Complex Network Framework in Power Grid. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, Australia, 7–10 November 2011. [Google Scholar]
- Chen, G.; Dong, Z.Y.; Hill, D.J.; Zhang, G.H. An Improved Model for Structural Vulnerability Analysis of Power Networks. Phys. A Stat. Mech. Appl. 2009, 388, 4259–4266. [Google Scholar] [CrossRef]
- Arianos, S.; Bompard, E.; Carbone, A.; Xue, F. Power Grid Vulnerability: A Complex Network Approach. Chaos 2009, 19, 013119. [Google Scholar] [CrossRef] [PubMed]
- Fang, X.; Yang, Q.; Yan, W. Modeling and Analysis of Cascading Failure in Directed Complex Networks. Saf. Sci. 2014, 65, 1–9. [Google Scholar] [CrossRef]
- Pg_tca30bus. Available online: https://www2.ee.washington.edu/research/pstca/pf30/pg_tca30bus.htm (accessed on 16 May 2018).
- Ieee_30_bus_technical_note.Pdf. Available online: https://hvdc.ca/uploads/knowledge_base/ieee_30_bus_technical_note.pdf?t=1460659229 (accessed on 16 May 2018).
- Examples of Microgrids|Building Microgrid. Available online: https://building-microgrid.lbl.gov/examples-microgrids (accessed on 16 May 2018).
- Freeman, L. A Set of Measures of Centrality Based on Betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Sabidussi, G. The Centrality Index of a Graph. Psychometrika 1966, 31, 581–603. [Google Scholar] [CrossRef] [PubMed]
- Salkind, N. Encyclopedia of Educational Psychology; SAGE: Thousand Oaks, CA, USA, 2008; Volume 2. [Google Scholar] [CrossRef]
- Saleh, M.; Esa, Y.; Mohamed, A.A. Communication Based Control for DC Microgrids. IEEE Trans. Smart Grid 2018, PP, 1. [Google Scholar] [CrossRef]
- Saleh, M.; Esa, Y.; Mohamed, A.A. Centralized Control for DC Microgrid Using Finite State Machine. In Proceedings of the IEEE Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 23–26 April 2017. [Google Scholar]
- Saleh, M.; Esa, Y.; Mohamed, A.A. Design and implementation of CCNY DC microgrid testbed. In Proceedings of the IEEE Industry Applications Society Annual Meeting, Portland, OR, USA, 2–6 October 2016. [Google Scholar]
- Saleh, M.; Althaibani, A.; Esa, Y.; Mhandi, Y.; Mohamed, A.A. Impact of clustering microgrids on their stability and resilience during blackouts. In Proceedings of the International Conference on Smart Grid and Clean Energy Technologies (ICSGCE), Offenburg, Germany, 20–23 October 2015; pp. 195–200. [Google Scholar] [CrossRef]
- Saleh, M.; Esa, Y.; Mohamed, A.A. Hardware Based Testing of Communication Based Control for DC Microgrid. In Proceedings of the International Conference on Renewable Energy Research and Applications (ICRERA), San Diego, CA, USA, 5–8 November 2017. [Google Scholar]
- Saleh, M.; Esa, Y.; Onuorah, N.; Mohamed, A.A. Optimal Microgrids Placement in Electric Distribution Systems Using Complex Network Framework. In Proceedings of the International Conference on Renewable Energy Research and Applications (ICRERA), San Diego, CA, USA, 5–8 November 2017. [Google Scholar]
- Saleh, M.; Esa, Y.; Mohamed, A.A. Impact of Communication Latency on the Bus Voltage of Centrally Controlled DC Microgrid during Islanding. IEEE Trans. Sustain. Energy 2017, in press. [Google Scholar]
- Saleh, M.; Esa, Y.; Mohamed, A.A. Effect of Wireless Communication Delay on Bus Voltage of Centralized Communication Based Control DC Microgrid. In Proceedings of the Energy Conversion Congress & Expo (ECCE) 2018 Conference, Portland, OR, USA, 23–27 September 2018. [Google Scholar]
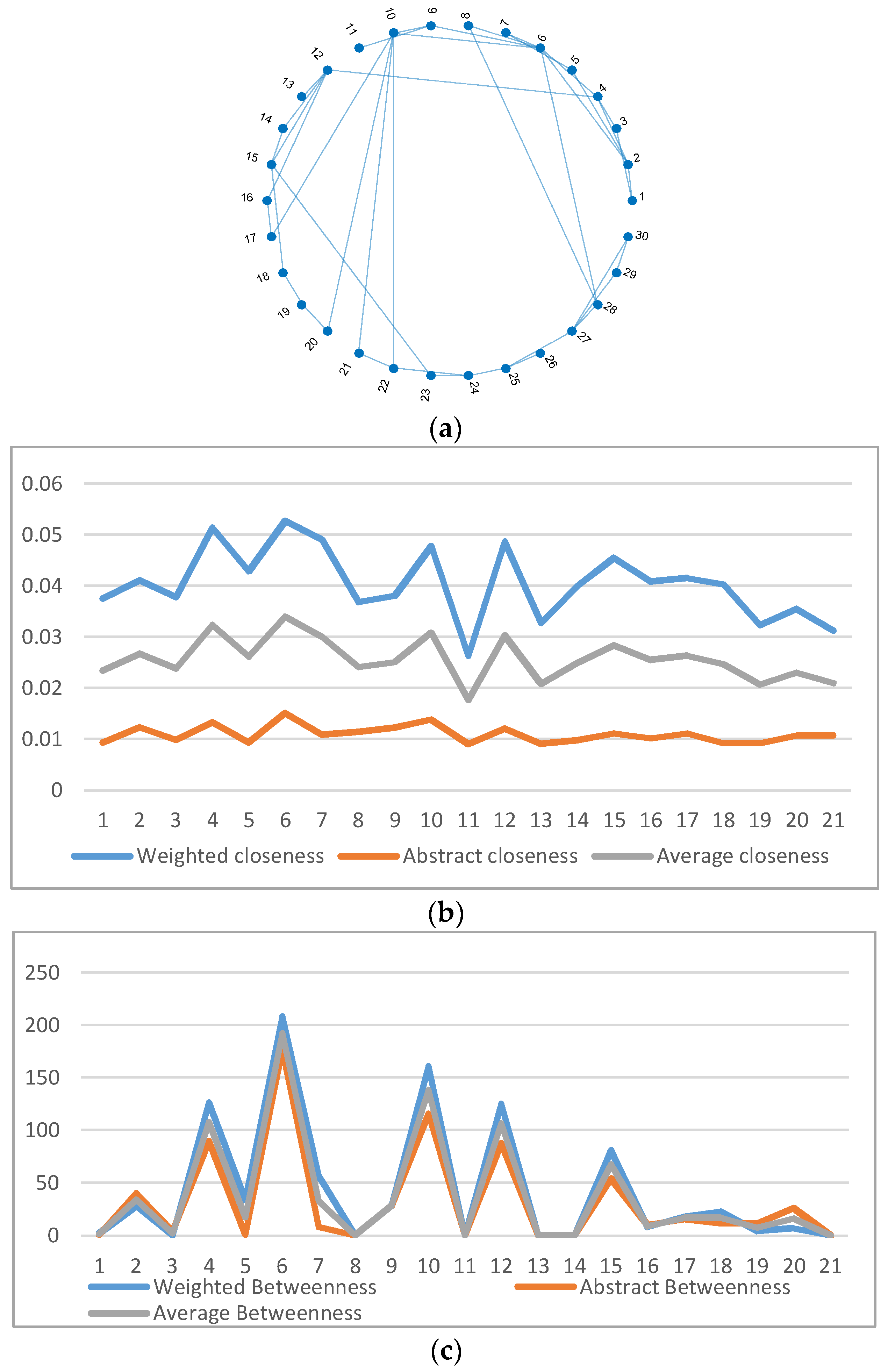
| Centrality Type | Closeness Centrality | Average Closeness | Betweenness | Average Betweenness | CC | |||
|---|---|---|---|---|---|---|---|---|
| Weights | |Z| | Abstract | - | 1/|Z| | Abstract | - | - | |
| Bus No. | ||||||||
| 1 | 0.03757 | 0.009346 | 0.023458 | 2 | 1 | 1.5 | 0 | |
| 2 | 0.04114 | 0.012346 | 0.026743 | 28 | 40.5 | 34.25 | 0.166667 | |
| 3 | 0.037896 | 0.009901 | 0.023898 | 0 | 4 | 2 | 0 | |
| 4 | 0.051342 | 0.013333 | 0.032338 | 126 | 89.75 | 107.875 | 0.166667 | |
| 5 | 0.04297 | 0.009346 | 0.026158 | 34 | 1 | 17.5 | 0 | |
| 6 | 0.052748 | 0.015152 | 0.03395 | 208 | 176.5833 | 192.2917 | 0.142857 | |
| 7 | 0.049101 | 0.01087 | 0.029985 | 57 | 8.5 | 32.75 | 0 | |
| 8 | 0.036862 | 0.011364 | 0.024113 | 0 | 0 | 0 | 1 | |
| 9 | 0.038094 | 0.012195 | 0.025145 | 28 | 28 | 28 | 0.333333 | |
| 10 | 0.047808 | 0.013889 | 0.030848 | 161 | 115.6667 | 138.3333 | 0.133333 | |
| 11 | 0.026385 | 0.009091 | 0.017738 | 0 | 0 | 0 | 0 | |
| 12 | 0.048605 | 0.012048 | 0.030326 | 125 | 87.5 | 106.25 | 0.1 | |
| 13 | 0.032721 | 0.009009 | 0.020865 | 0 | 0 | 0 | 0 | |
| 14 | 0.04005 | 0.009804 | 0.024927 | 0 | 0 | 0 | 1 | |
| 15 | 0.045568 | 0.011111 | 0.02834 | 81 | 54 | 67.5 | 0.166667 | |
| 16 | 0.040794 | 0.010101 | 0.025447 | 8 | 10.41667 | 9.208333 | 0 | |
| 17 | 0.041507 | 0.011111 | 0.026309 | 18 | 15.91667 | 16.95833 | 0 | |
| 18 | 0.040242 | 0.009174 | 0.024708 | 23 | 11.41667 | 17.20833 | 0 | |
| 19 | 0.03232 | 0.009174 | 0.020747 | 4 | 11.41667 | 7.708333 | 0 | |
| 20 | 0.035456 | 0.010753 | 0.023104 | 7 | 26.25 | 16.625 | 0 | |
| 21 | 0.031265 | 0.010638 | 0.020952 | 0 | 0 | 0 | 1 | |
| 22 | 0.037667 | 0.011765 | 0.024716 | 42 | 34.91667 | 38.45833 | 0.333333 | |
| 23 | 0.036848 | 0.010309 | 0.023579 | 24 | 31.25 | 27.625 | 0 | |
| 24 | 0.030453 | 0.011111 | 0.020782 | 54 | 56.41667 | 55.20833 | 0 | |
| 25 | 0.025163 | 0.010101 | 0.017632 | 37 | 48.83333 | 42.91667 | 0 | |
| 26 | 0.017861 | 0.007874 | 0.012868 | 0 | 0 | 0 | 0 | |
| 27 | 0.024411 | 0.010638 | 0.017525 | 54 | 76.83333 | 65.41667 | 0.166667 | |
| 28 | 0.044617 | 0.012346 | 0.028481 | 63 | 72.83333 | 67.91667 | 0.333333 | |
| 29 | 0.019412 | 0.008264 | 0.013838 | 0 | 0 | 0 | 1 | |
| 30 | 0.020425 | 0.008264 | 0.014345 | 28 | 0 | 14 | 1 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saleh, M.; Esa, Y.; Mohamed, A. Applications of Complex Network Analysis in Electric Power Systems. Energies 2018, 11, 1381. https://doi.org/10.3390/en11061381
Saleh M, Esa Y, Mohamed A. Applications of Complex Network Analysis in Electric Power Systems. Energies. 2018; 11(6):1381. https://doi.org/10.3390/en11061381
Chicago/Turabian StyleSaleh, Mahmoud, Yusef Esa, and Ahmed Mohamed. 2018. "Applications of Complex Network Analysis in Electric Power Systems" Energies 11, no. 6: 1381. https://doi.org/10.3390/en11061381
APA StyleSaleh, M., Esa, Y., & Mohamed, A. (2018). Applications of Complex Network Analysis in Electric Power Systems. Energies, 11(6), 1381. https://doi.org/10.3390/en11061381






