Hierarchical Energy Management of Microgrids including Storage and Demand Response
Abstract
:1. Introduction
- (1)
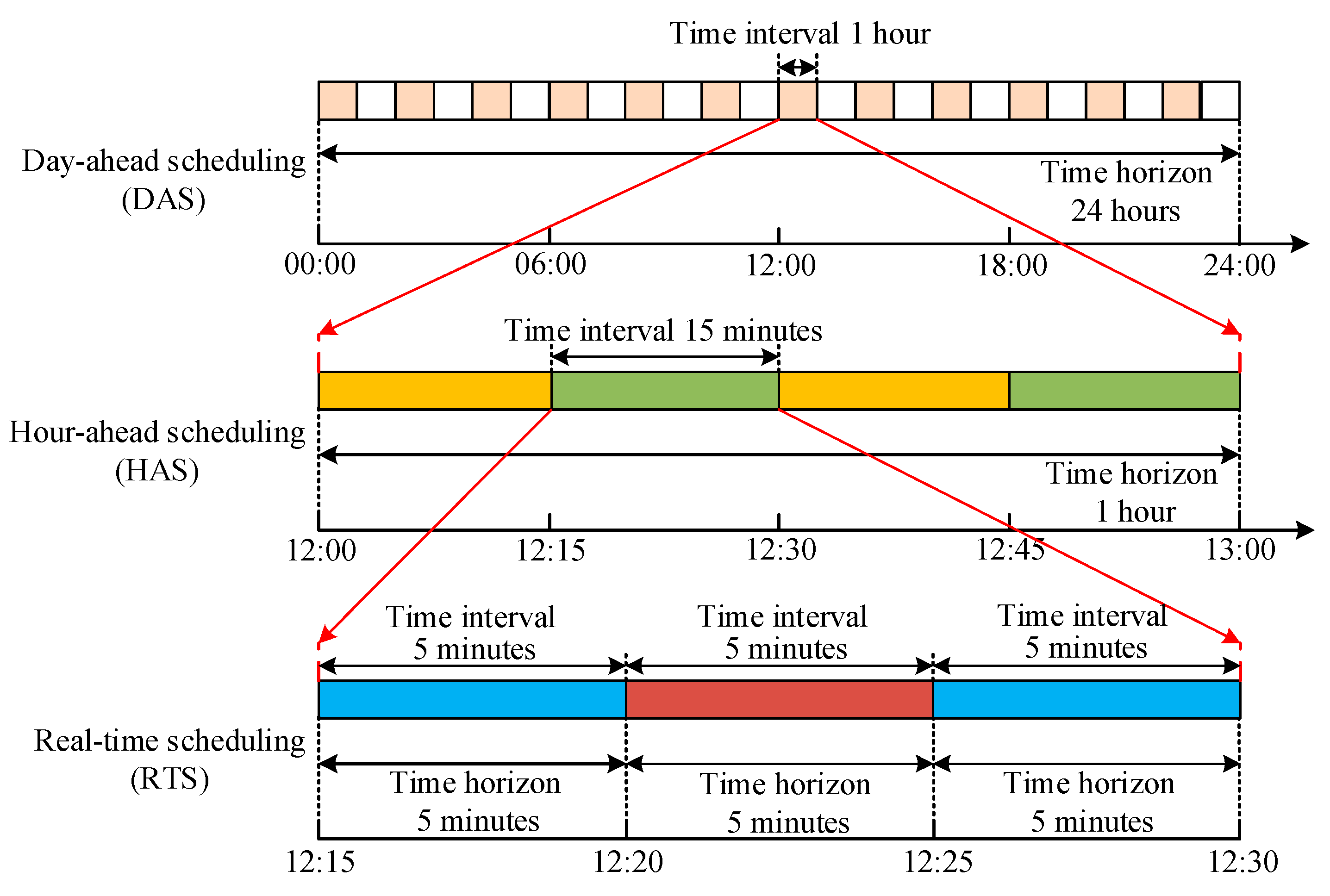
- A hierarchical energy management framework incorporating the multi-timescale characteristics of the BES and DR along with the security constraints is proposed for an MG in grid-connected mode, which consists of DAS, hour-ahead scheduling (HAS), as well as real-time scheduling (RTS).
- (2)
- A decomposition-based algorithm is adopted to effectively settle the optimization models in the DAS and HAS.
- (3)
- Impacts of the multi-timescale characteristics of the BES and DR on the energy management of MG are analyzed.
2. Architecture of the Hierarchical Energy Management
3. Model Formulation
3.1. Day-Ahead Scheduling
3.1.1. Objective Function
3.1.2. Decision Variables
3.1.3. Constraints
3.2. Hour-Ahead Scheduling
3.2.1. Objective Function
3.2.2. Decision Variables
3.2.3. Constraints
3.3. Real-Time Scheduling
3.3.1. Calculate the Initial Power References
3.3.2. Revise the Power References
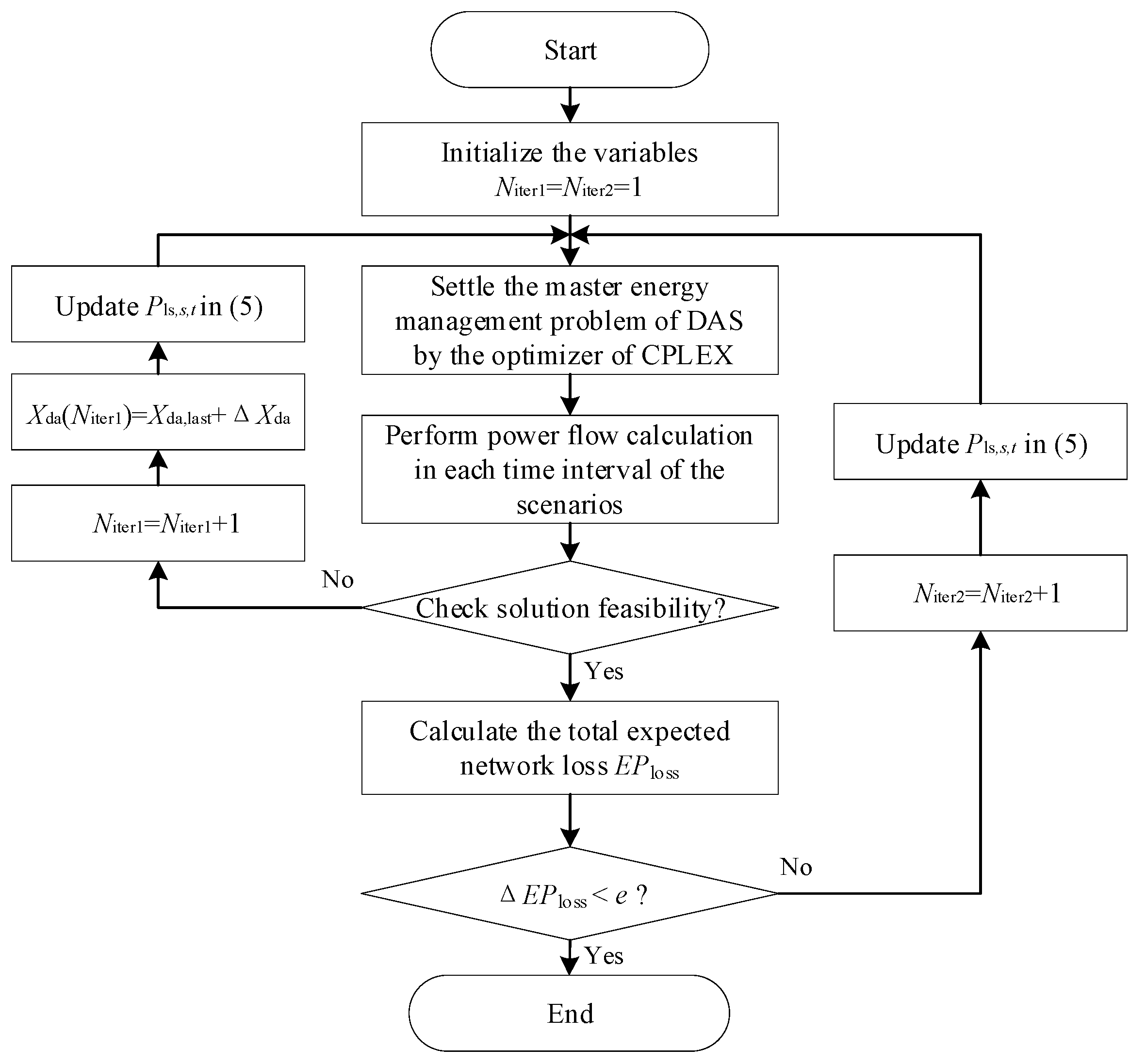
4. Solution Algorithm
- (1)
- The linearized master energy management problem is solved by the optimizer of CPLEX, and then the scheduling results Xda will be obtained.
- (2)
- The power flow calculation is implemented in each time interval of scenarios, and the security constraints would be checked to see whether they are met.
- (3)
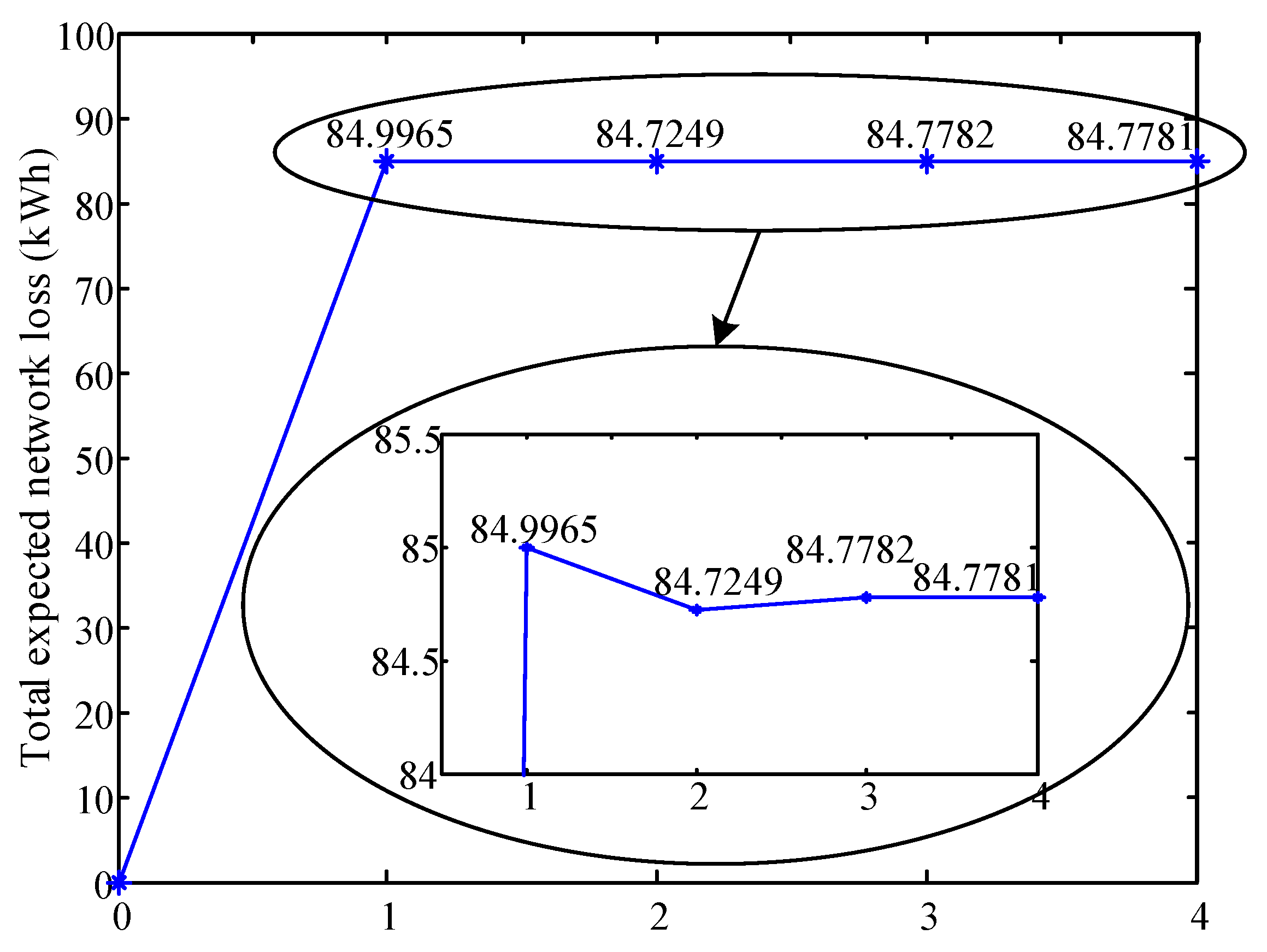
- When there exists a violation of security constraints, a tiny random vector ΔXda will be added to the last feasible solution Xda,last to calculate the power losses again. Then, the master problem will be rerun using the updated power balance constraints (5). [2]. If there is no violation of the constraints, the power loss will be calculated in each time interval of the scenarios, and the total expected network loss EPloss would be decided. The newly calculated power losses will be returned to the master problem for updating the power balance constraints (5), until the variation of the total expected network loss ΔEPloss is less than the tolerance limit e.
- (4)
- After finite iterations, a new steady-state condition can be determined.
5. Case Study
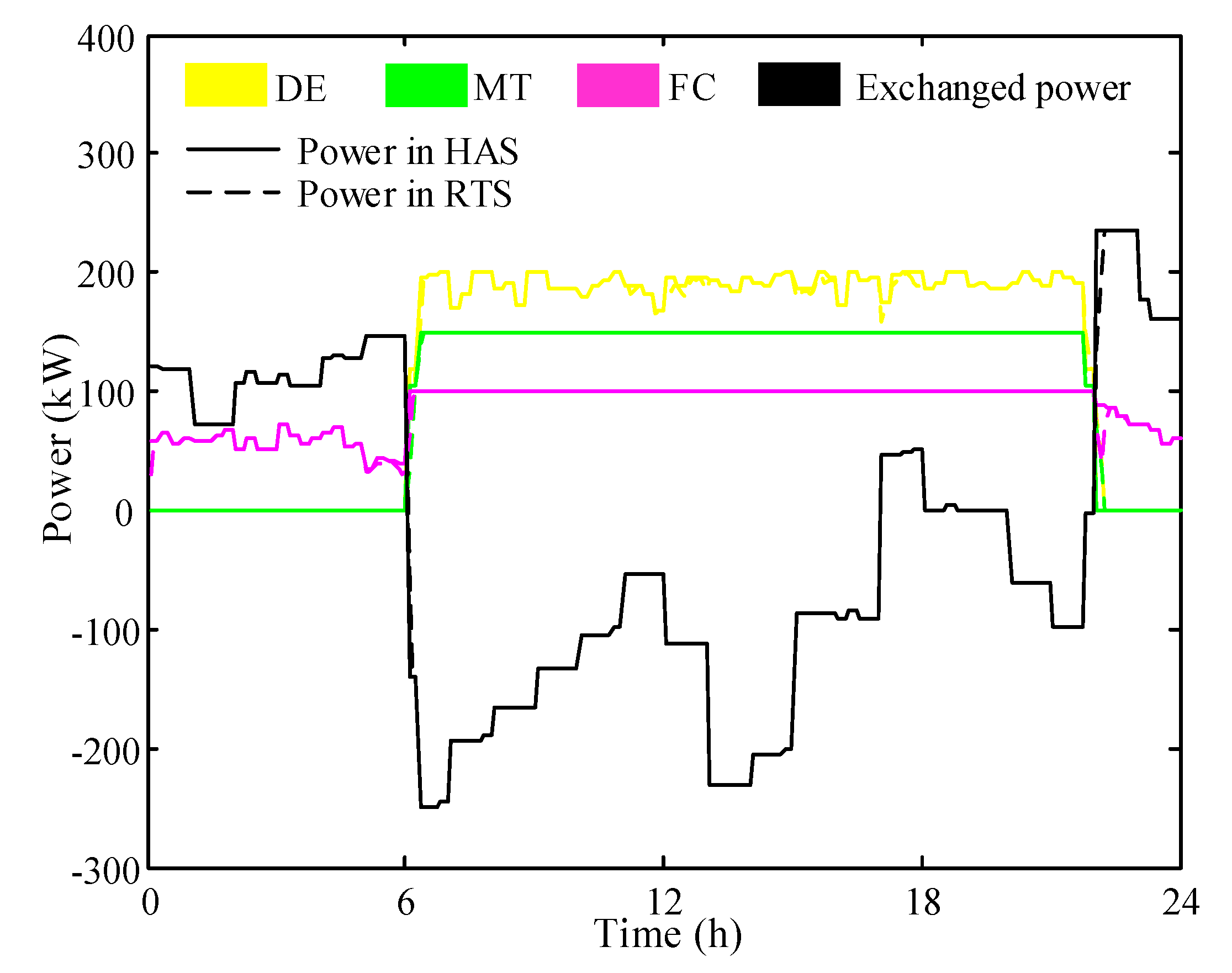
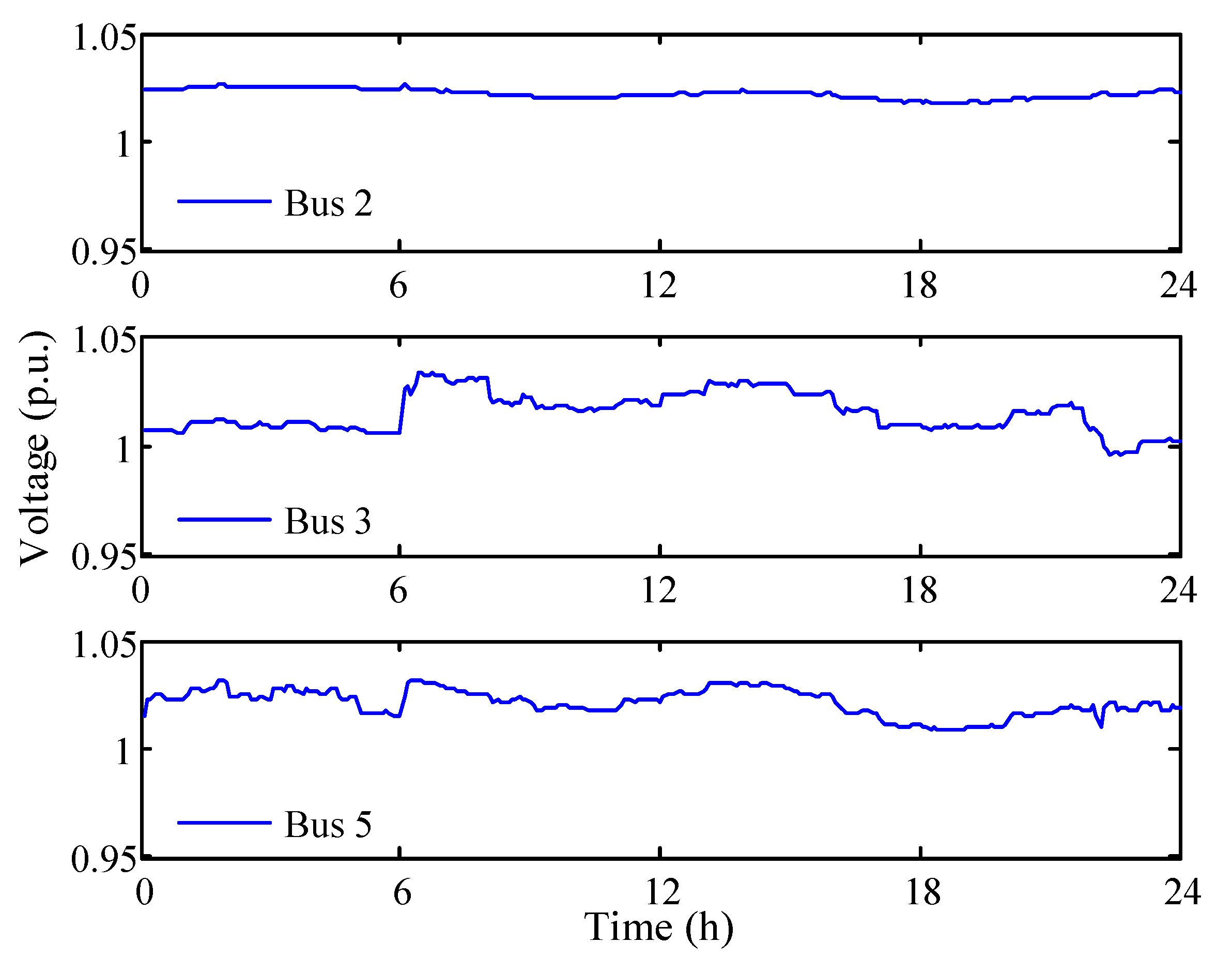
5.1. Simulation of the Hierarchichal Energy Management
5.2. Impacts of the Multi-Timescale Characteristics of the BES and DR on the Energy Management of MG
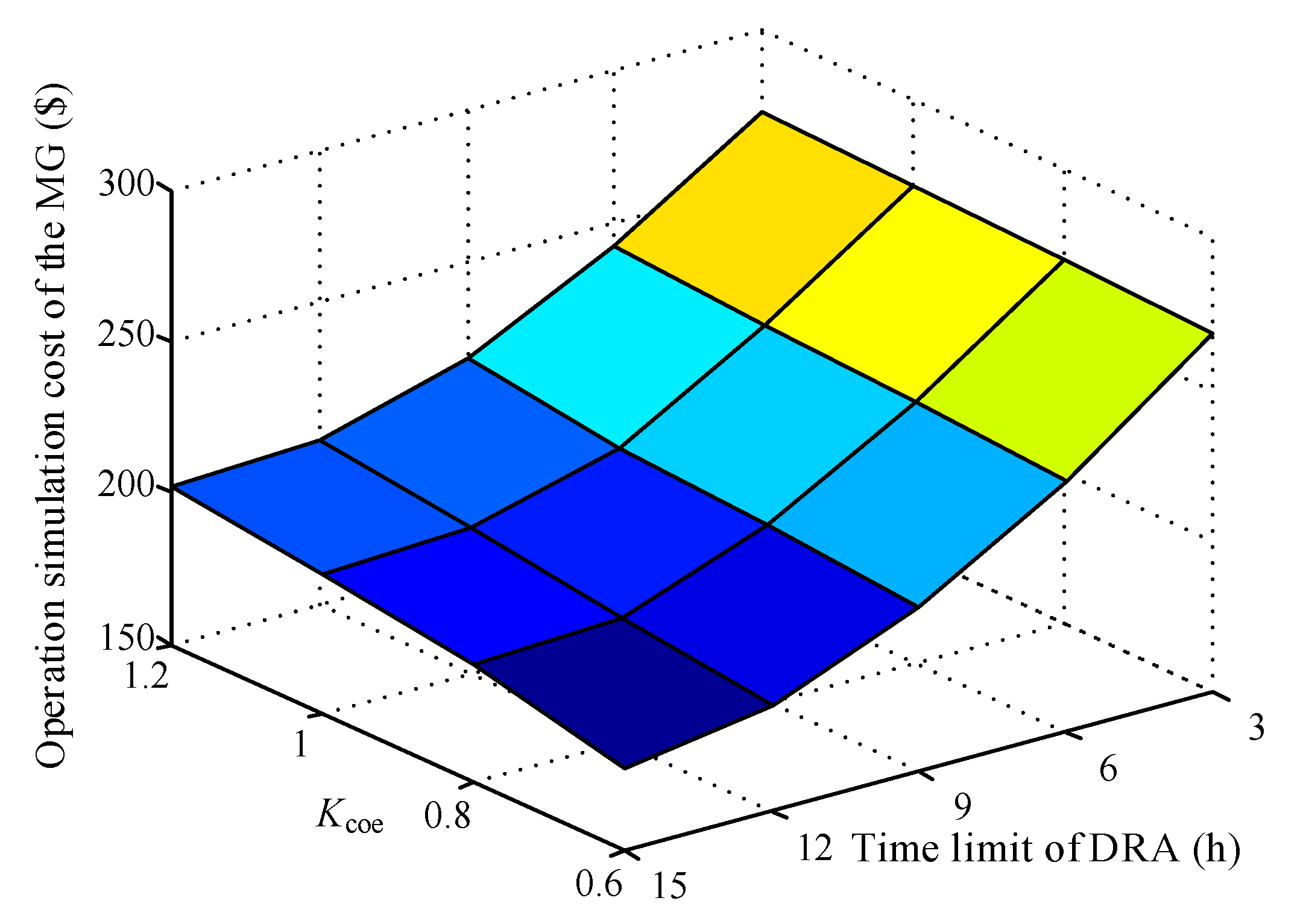
5.3. Impacts of the Cost and the Time Limit of DRA on the Energy Management of MG
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Notations for the Model Formulation
| Acronyms | |
| MG | Microgrid |
| WD | Wind power |
| BES | Battery energy storage |
| DRA | Demand response aggregator |
| CDG | Controllable distributed generators |
| SOC | State of charging |
| Parameters | |
| Number of CDG, BES, and DRA | |
| Number of buses and branches | |
| Number of hours in a day | |
| Number of scenarios | |
| Probability of scenario s | |
| Unit OMC of CDG i, BES j, and WD | |
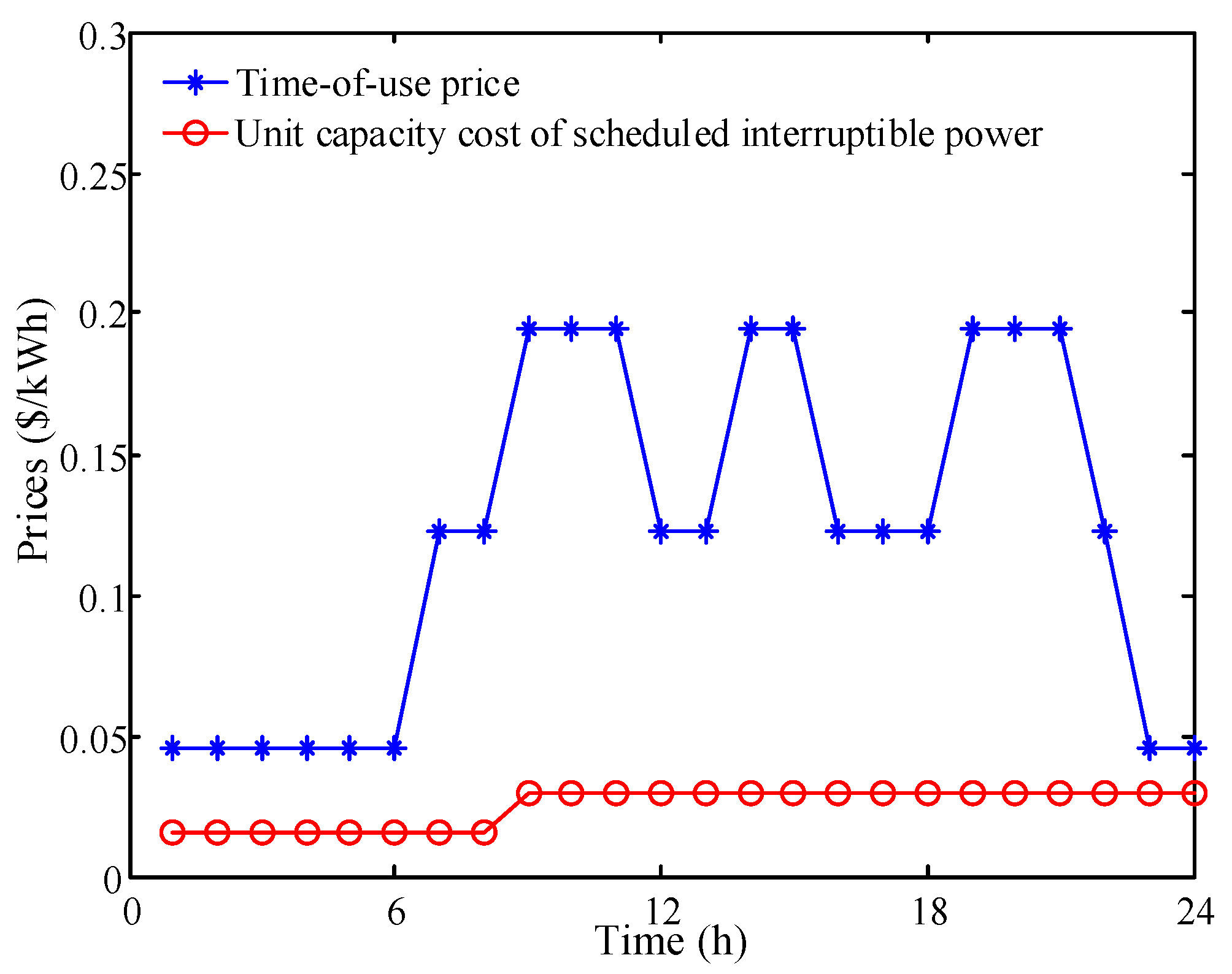
| Time-of-use price at hour t | |
| Penalty price at hour t | |
| Required spinning reserve | |
| Maximum thermal limit of branch x | |
| Maximum and minimum bounds of the voltage of bus y | |
| Startup and shutdown costs | |
| Coefficients of the quadratic cost function of CDG i | |
| Maximum and minimum operation limits of CDG i | |
| Ramp up and ramp down rates of CDG i | |
| Minimum on and off time of CDG i | |
| Required on and off time at the start time of the day of CDG i | |
| Response time of the spinning reserve (e.g., 10 min) | |
| Maximum power and capacity of BES j | |
| Charging and discharging efficiency factors of BES j | |
| Maximum and minimum permissible SOC of BES j | |
| SOC limit at the end of the day of BES j | |
| Unit capacity cost of the scheduled interruptible power of DRA k at hour t | |
| Unit energy cost of the interruptible power deployed in DAS, HAS, and RTS of DRA k at hour t | |
| Maximum and minimum bounds of the scheduled interruptible power of DRA k at hour t | |
| Response time limit of DRA k | |
| Allowable time set of the scheduling interruptible power of DRA k | |
| Transmission capacity limit of the exchanged power | |
| Variables | |
| Operation status, startup status, and shutdown status of CDG i at hour t | |
| Power and spinning reserve of CDG i at hour t in scenario s | |
| Discharging and charging statuses of BES j at hour t | |
| Discharging and charging power of BES j at hour t | |
| Spinning reserve of BES j at hour t in scenario s | |
| Operation status of DRA k at hour t | |
| Scheduled interruptible power of DRA k at hour t | |
| Interruptible power deployed in DAS of DRA k at hour t | |
| Exchanged power with the main grid at hour t | |
| Load flow of branch x and voltage of bus y at hour t in scenario s | |
| Load and network loss at hour t in scenario s | |
| Power of WD at hour t in scenario s | |
| (t, m) | The m-th 15-min time interval at hour t |
| Power and spinning reserve of CDG i | |
| Discharging and charging statuses of BES j | |
| Discharging and charging power of BES j | |
| Spinning reserve of BES j | |
| Interruptible power deployed in HAS of DRA k | |
| Exchanged power with the main grid | |
| Load and network loss | |
| (t, m, n) | The n-th 5-min time interval in the m-th 15-min time interval at hour t |
| Imbalanced power of MG at real time | |
| Initial power reference of CDG i | |
| Initial and final power references of DRA k | |
| Initial and final power references of BES j | |
| Upward and downward regulation capacities of BES j | |
| Upward and downward total regulation capacities of BES j | |
| Initial and final power references of the exchanged power | |
References
- Fathima, A.H.; Palanisamy, K. Optimization in microgrids with hybrid energy systems—A review. Renew. Sustain. Energy Rev. 2015, 45, 431–446. [Google Scholar] [CrossRef]
- Su, W.; Wang, J.; Roh, J. Stochastic energy scheduling in microgrids with intermittent renewable energy resources. IEEE Trans. Smart Grid 2014, 5, 1876–1883. [Google Scholar] [CrossRef]
- Li, P.; Xu, D.; Zhou, Z.; Lee, W. Stochastic optimal operation of microgrid based on chaotic binary particle swarm optimization. IEEE Trans. Smart Grid 2016, 7, 66–73. [Google Scholar] [CrossRef]
- Ding, Z.; Lee, W. A stochastic microgrid operation scheme to balance between system reliability and greenhouse gas emission. IEEE Trans. Ind. Appl. 2016, 52, 1157–1166. [Google Scholar]
- Tavakoli, M.; Shokridehaki, F.; Akorede, M.F.; Marzband, M.; Vechiu, I.; Pouresmaeil, E. CVaR-based energy management scheme for optimal resilience and operational cost in commercial building microgrids. Int. J. Electr. Power Energy Syst. 2018, 100, 1–9. [Google Scholar] [CrossRef]
- Xiong, H.; Xiang, T.; Chen, H.; Lin, F.; Su, J. Research of fuzzy chance constrained unit commitment containing large-scale intermittent power. Proc. CSEE 2013, 33, 36–44. [Google Scholar]
- Xiang, Y.; Liu, J.; Liu, Y. Robust energy management of microgrid with uncertain renewable generation and load. IEEE Trans. Smart Grid 2016, 7, 1034–1043. [Google Scholar] [CrossRef]
- Wang, S.; Wang, D.; Han, L. Interval linear programming method for day-ahead optimal economic dispatching of microgrid considering uncertainty. Autom. Electr. Power Syst. 2014, 38, 5–11. [Google Scholar]
- Wu, X.; Wang, X.; Qu, C. A hierarchical framework for generation scheduling of microgrids. IEEE Trans. Power Deliv. 2014, 29, 2448–2457. [Google Scholar] [CrossRef]
- Bao, Z.; Zhou, Q.; Yang, Z.; Yang, Q.; Xu, L.; Wu, T. A multi time-scale and multi energy-type coordinated microgrid scheduling solution-Part I: Model and methodology. IEEE Trans. Power Syst. 2015, 30, 2257–2266. [Google Scholar] [CrossRef]
- Xu, X.; Jia, H.; Wang, D.; Yu, D.C.; Chiang, H. Hierarchical energy management system for multi-source multi-product microgrids. Renew. Energy 2015, 78, 621–630. [Google Scholar] [CrossRef]
- Xu, G.; Shang, C.; Fan, S.; Hu, X.; Cheng, H. A hierarchical energy scheduling framework of microgrids with hybrid energy storage systems. IEEE Access 2017, 6, 2472–2483. [Google Scholar] [CrossRef]
- Nolan, S.; O’Malley, M. Challenges and barriers to demand response deployment and evaluation. Appl. Energy 2015, 152, 1–10. [Google Scholar] [CrossRef]
- Sahin, C.; Shahidehpour, M.; Erkmen, I. Allocation of hourly reserve versus demand response for security-constrained scheduling of stochastic wind energy. IEEE Trans. Sustain. Energy 2013, 4, 219–228. [Google Scholar] [CrossRef]
- Talari, S.; Yazdaninejad, M.; Haghifam, M. Stochastic-based scheduling of the microgrid operation including wind turbines, photovoltaic cells, energy storages and responsive loads. IET Gener. Transm. Distrib. 2015, 9, 1498–1509. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Le, L.B. Risk-constrained profit maximization for microgrid aggregators with demand response. IEEE Trans. Smart Grid 2015, 6, 135–146. [Google Scholar] [CrossRef]
- Nunna, H.S.; Doolla, S. Energy management in microgrids using demand response and distributed storage—A multiagent approach. IEEE Trans. Power Deliv. 2013, 28, 939–947. [Google Scholar] [CrossRef]
- Mehdizadeh, A.; Taghizadegan, N.; Salehi, J. Risk-based energy management of renewable-based microgrid using information gap decision theory in the presence of peak load management. Appl. Energy 2018, 211, 617–630. [Google Scholar] [CrossRef]
- Bui, V.; Hussain, A.; Kim, H. A multiagent-based hierarchical energy management strategy for multi-microgirds considering adjustable power and demand response. IEEE Trans. Smart Grid 2018, 9, 1323–1333. [Google Scholar] [CrossRef]
- Marzband, M.; Fouladfar, M.H.; Akorede, M.F.; Lightbody, G.; Pouresmaeil, E. Framework for smart transactive energy in home-microgrids considering coalition formation and demand side management. Sustain. Cities Soc. 2018, 40, 136–154. [Google Scholar] [CrossRef]
- Marzband, M.; Azarinejadian, F.; Savaghebi, M.; Pouresmaeil, E.; Guerrero, J.M.; Lightbody, G. Smart transactive energy framework in grid-connected multiple home microgrids under independent and coalition operations. Renew. Energy 2018, 126, 95–106. [Google Scholar] [CrossRef]
- Mohsenian-Rad, A.; Wong, V.; Jatskevich, J.; Schober, R.; Leon-Garcia, A. Autonomous demand-side management based on game-theoretic energy consumption scheduling for the future smart grid. IEEE Trans. Smart Grid 2010, 1, 320–331. [Google Scholar] [CrossRef]
- Maharjan, S.; Zhu, Q.; Zhang, Y.; Gjessing, S.; Basar, T. Demand response management in the smart grid in a large population regime. IEEE Trans. Smart Grid 2016, 7, 189–199. [Google Scholar] [CrossRef]
- Pourmousavi, S.A.; Nehrir, M.H.; Sharma, R.K. Multi-timescale power management for islanded microgrids including storage and demand response. IEEE Trans. Smart Grid 2015, 6, 1185–1195. [Google Scholar] [CrossRef]
- Wang, B.; Tang, N.; Fang, X.; Yang, S.; Ji, W. A multi time scales reserve rolling revision model of power system with large scale wind power. Proc. CSEE 2017, 37, 1645–1656. [Google Scholar]
- Bao, Z.; Qiu, W.; Wu, L.; Zhai, F.; Xu, W.; Li, B.; Li, Z. Optimal multi-timescale demand side scheduling considering dynamic scenarios of electricity demand. IEEE Trans. Smart Grid 2018, 1–12. [Google Scholar] [CrossRef]
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
- Department of Energy. Benefits of Demand Response in Electricity Markets and Recommendations for Achieving Them: A Report to the United States Congress Pursuant to Section 1252 of the Energy Policy Act of 2005; Department of Energy: Washington, DC, USA, 2006.
- Henriquez, R.; Wenzel, G.; Olivares, D.E.; Negrete-Pincetic, M. Participation of demand response aggregators in electricity markets: Optimal portfolio management. IEEE Trans. Smart Grid 2017, 1–11. [Google Scholar] [CrossRef]
- Wang, B.; Liu, X.; Zhu, F.; Hu, X.; Ji, W.; Yang, S.; Wang, K.; Feng, S. Unit commitment model considering flexible scheduling of demand response for high wind integration. Energies 2015, 8, 13688–13709. [Google Scholar] [CrossRef]
- Suazo-Martinez, C.; Pereira-Bonvallet, E.; Palma-Behnke, R.; Zhang, X. Impacts of energy storage on short term operation planning under centralized spot markets. IEEE Trans. Smart Grid 2014, 5, 1110–1118. [Google Scholar] [CrossRef]
- Jiang, Q.; Gong, Y.; Wang, H. A battery energy storage system dual-layer strategy for mitigating wind farm fluctuations. IEEE Trans. Power Syst. 2013, 28, 3263–3273. [Google Scholar] [CrossRef]
- Wu, X.; Wang, X.; Bie, Z.; Zeng, P. Real-time energy management strategies for microgrids. In Proceedings of the IEEE PES General Meeting Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014. [Google Scholar]
- Carrion, M.; Arroyo, J.M. A computationally efficient mix-integer linear formulation for the thermal unit commitment problem. IEEE Trans. Power Syst. 2006, 21, 1371–1378. [Google Scholar] [CrossRef]
- Guan, X.; Xu, Z.; Jia, Q. Energy-efficient buildings facilitated by microgrid. IEEE Trans. Smart Grid 2010, 1, 243–252. [Google Scholar] [CrossRef]
- Carrion, M.; Philpott, A.B.; Conejo, A.J.; Arroyo, J.M. A stochastic programming approach to electric energy procurement for large consumers. IEEE Trans. Power Syst. 2007, 22, 744–754. [Google Scholar] [CrossRef]
- Yang, Z.; Song, Y.; Cao, R.; Sun, W.; Wu, J. Application of ultra-short term load forecasting in power market. Autom. Electr. Power Syst. 2000, 1, 14–17. [Google Scholar]
- Teleke, S.; Baran, M.E.; Bhattacharya, S.; Huang, A.Q. Rule-based control of battery energy storage for dispatching intermittent renewable sources. IEEE Trans. Sustain. Energy 2010, 1, 117–124. [Google Scholar] [CrossRef]





| Types | DE | MT | FC | WD |
|---|---|---|---|---|
| Upper limit (kW) | 200 | 150 | 100 | 100 |
| Lower limit (kW) | 20 | 15 | 10 | - |
| Ramp-up/ramp-down limit (kW/min) | 8 | 7 | 6 | - |
| Quadratic coefficient ($/(kW)2 h) | 0.00004 | 0.00002 | 0.00003 | - |
| Monomial coefficient ($/kWh) | 0.004 | 0.006 | 0.006 | - |
| Constant coefficient ($/h) | 6.908 | 4.922 | 2.590 | - |
| Minimum up/down time (h) | 2 | 2 | 2 | - |
| Required up/down time at the start time of the day (h) | 0 | 0 | 0 | - |
| Startup/shutdown cost ($) | 0.317 | 0.476 | 0.317 | - |
| Unit OMC ($/kWh) | 0.006 | 0.006 | 0.005 | 0.011 |
| Case Number | Multi-Timescale Characteristic of BES | Multi-Timescale Characteristic of DR |
|---|---|---|
| 1 | √ | √ |
| 2 | √ | × |
| 3 | × | √ |
| 4 | × | × |
| Case Number | CDG | Exchanged Power | ||
|---|---|---|---|---|
| FPAR | AAPR (kW) | FPAR | AAPR (kW) | |
| 1 | 51 | 315.76 | 3 | 210.90 |
| 2 | 51 | 315.76 | 5 | 319.72 |
| 3 | 282 | 1707.61 | 11 | 310.57 |
| 4 | 282 | 1707.61 | 20 | 588.95 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, S.; Ai, Q.; Piao, L. Hierarchical Energy Management of Microgrids including Storage and Demand Response. Energies 2018, 11, 1111. https://doi.org/10.3390/en11051111
Fan S, Ai Q, Piao L. Hierarchical Energy Management of Microgrids including Storage and Demand Response. Energies. 2018; 11(5):1111. https://doi.org/10.3390/en11051111
Chicago/Turabian StyleFan, Songli, Qian Ai, and Longjian Piao. 2018. "Hierarchical Energy Management of Microgrids including Storage and Demand Response" Energies 11, no. 5: 1111. https://doi.org/10.3390/en11051111
APA StyleFan, S., Ai, Q., & Piao, L. (2018). Hierarchical Energy Management of Microgrids including Storage and Demand Response. Energies, 11(5), 1111. https://doi.org/10.3390/en11051111




