An Enhanced Hybrid Switching-Frequency Modulation Strategy for Fuel Cell Vehicle Three-Level DC-DC Converters with Quasi-Z Source
Abstract
:1. Introduction
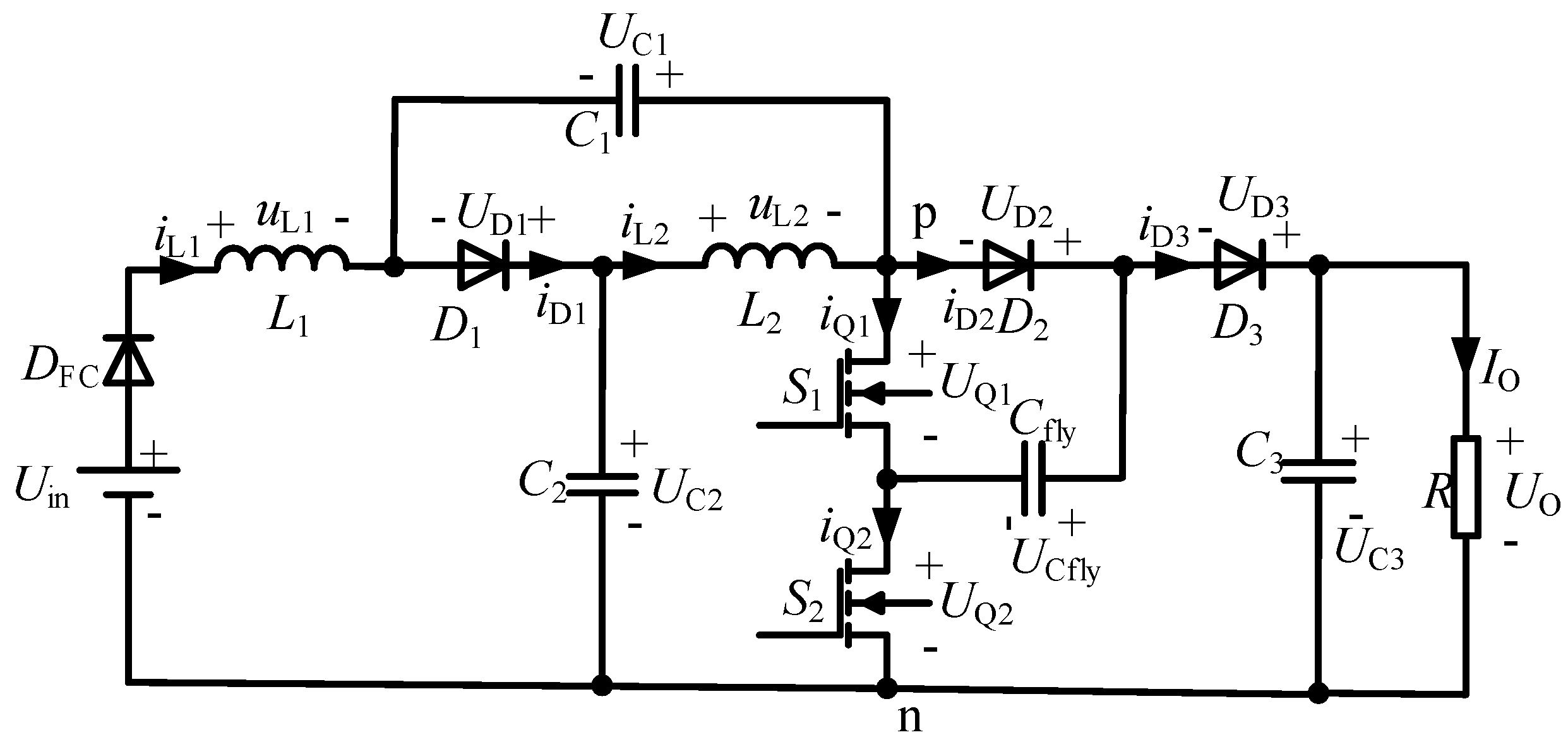
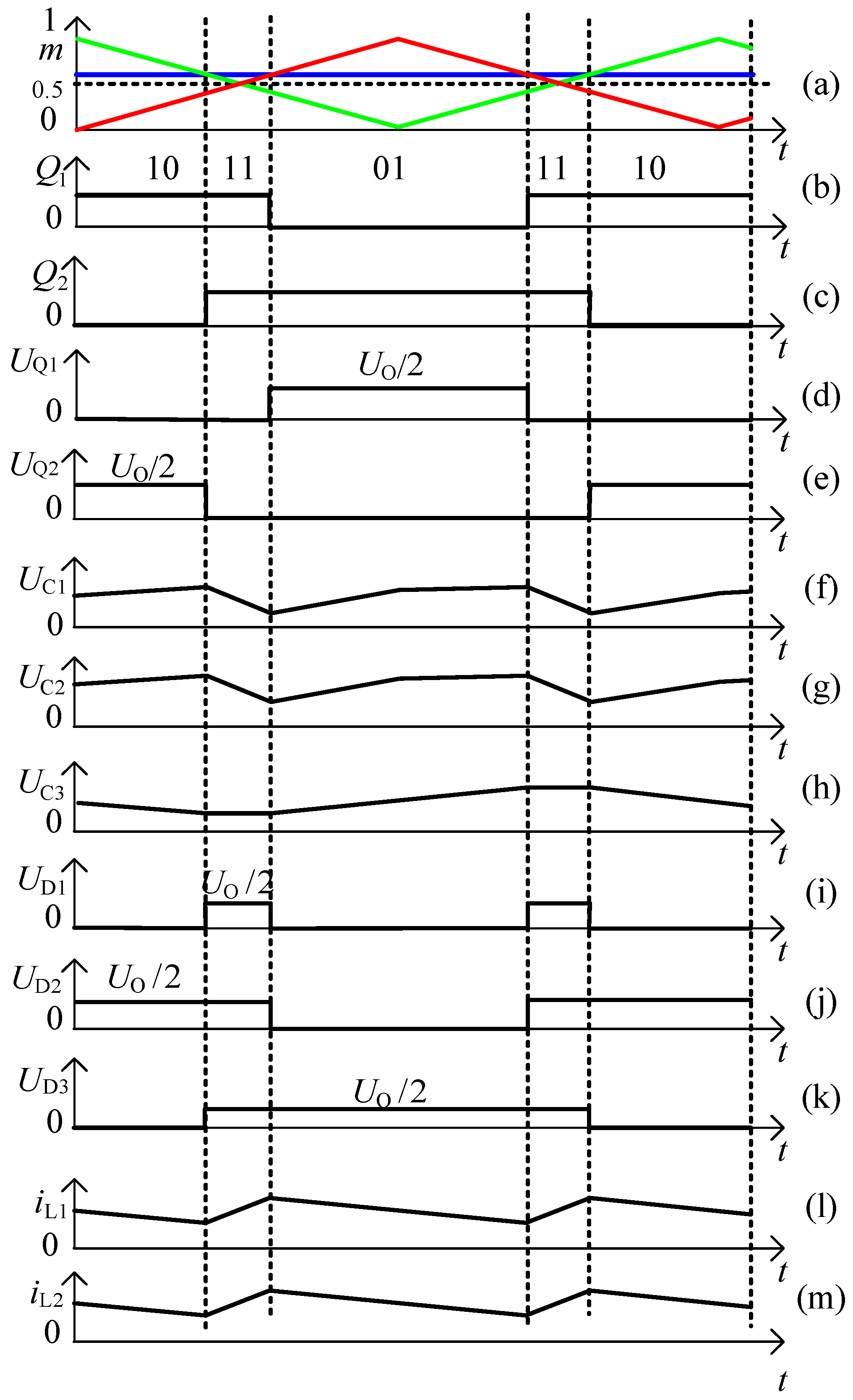
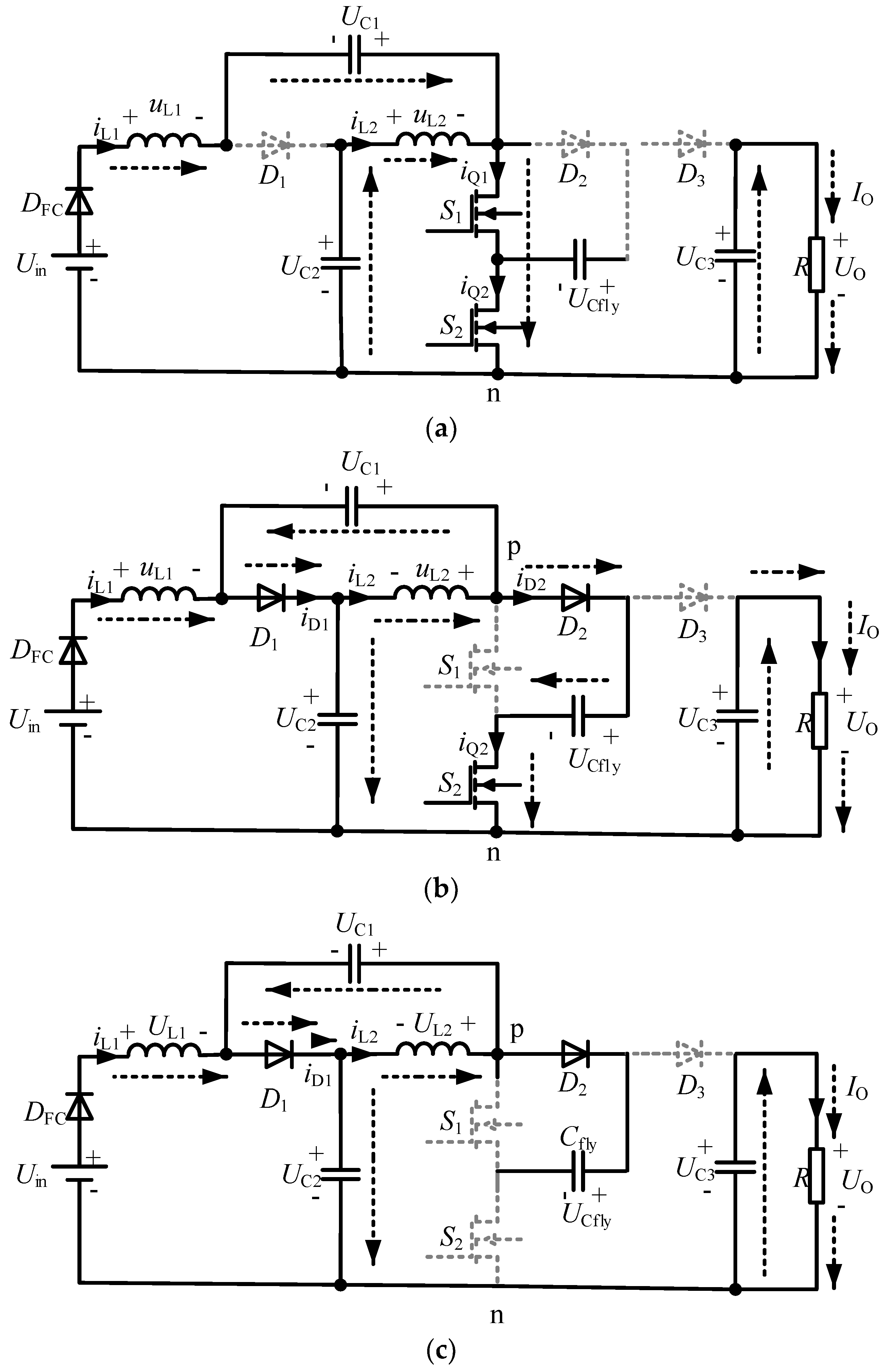
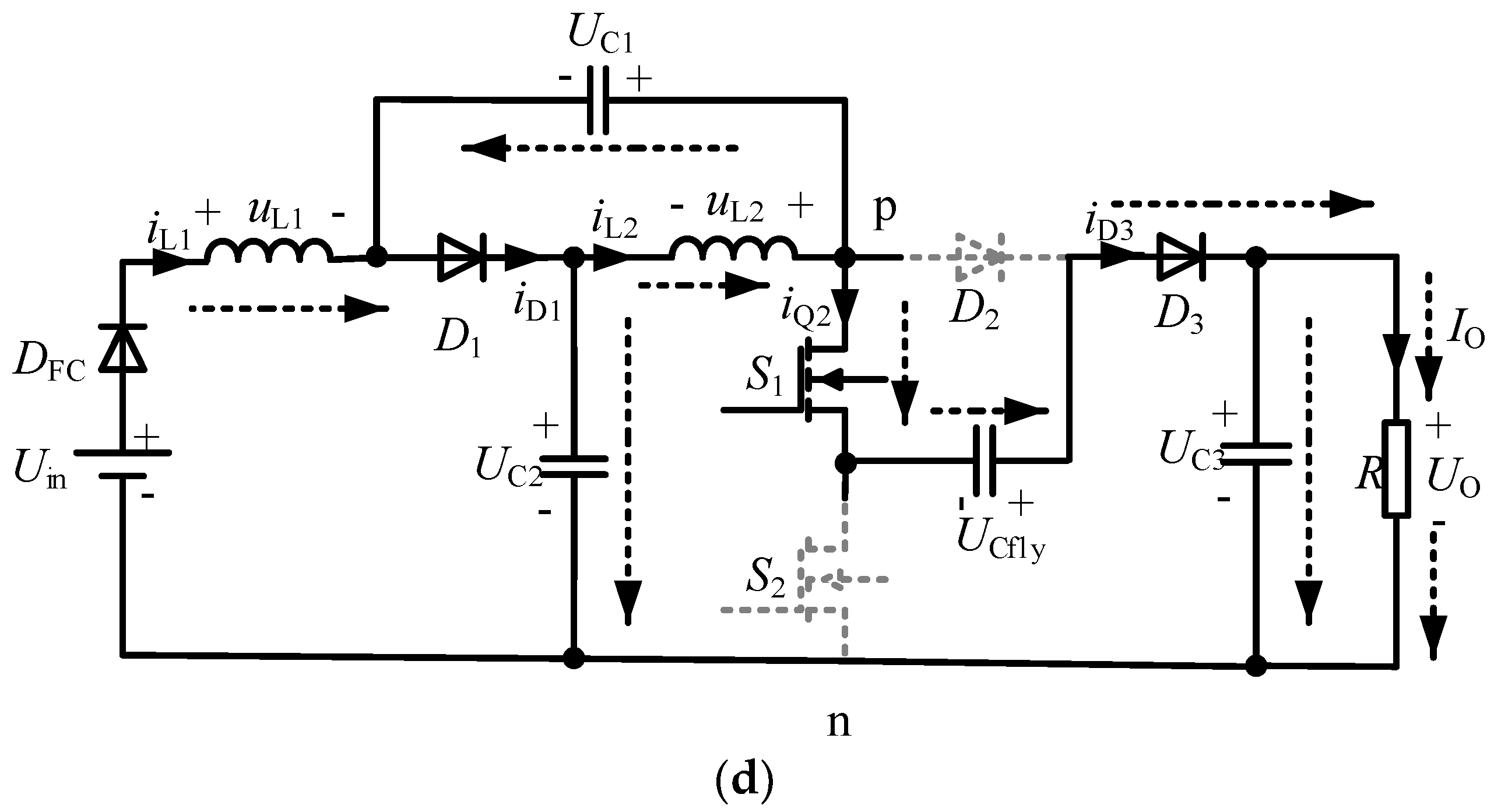
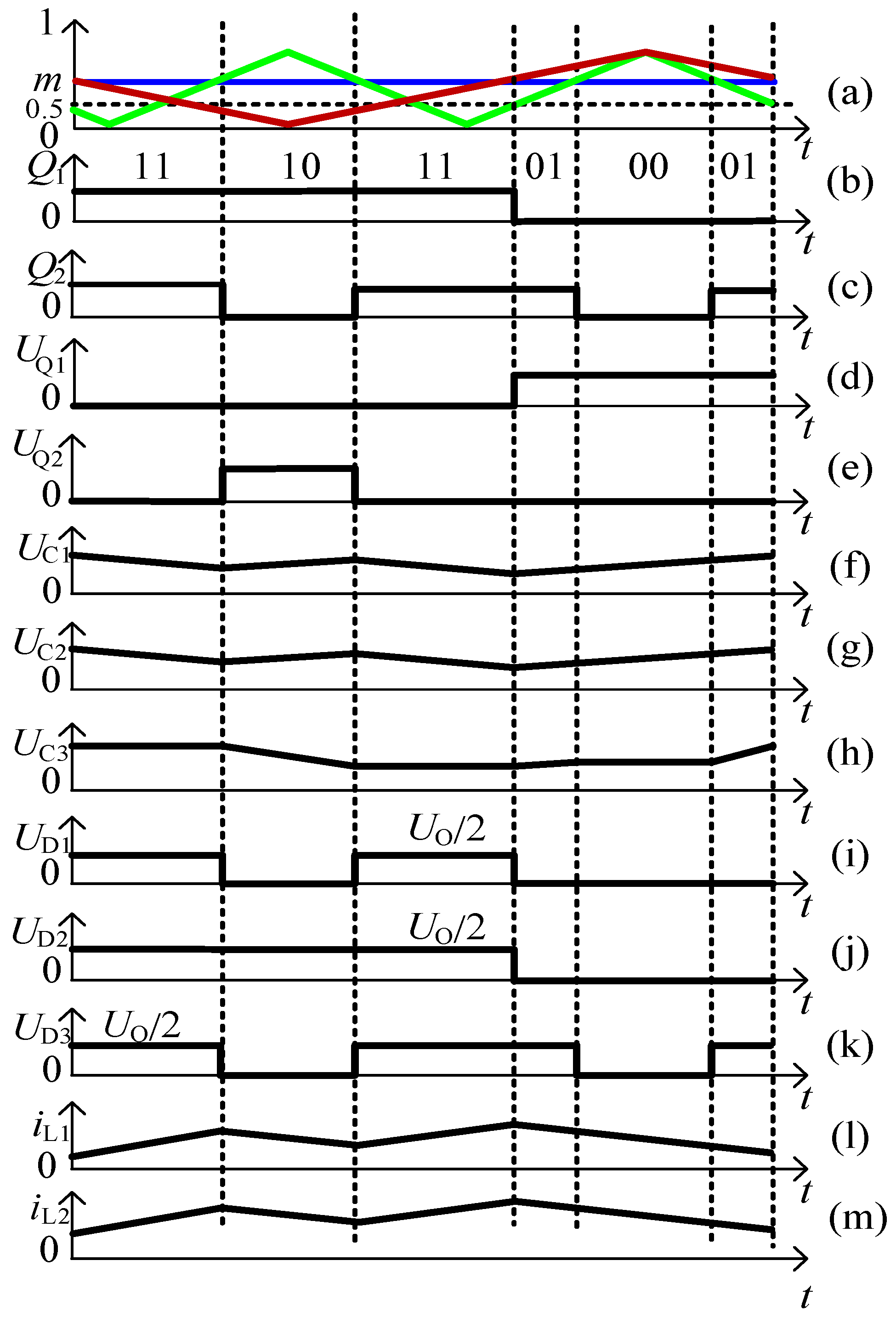
2. Operating Principle of the Hybrid Switching-Frequency Modulation Strategy
2.1. Analysis of Operating States
2.2. Voltage-Gain
- (1)
- The capacitance of the capacitors in Figure 1 is infinite, as well as the inductance of the inductors. Therefore, capacitors are regarded as constant voltage sources, and inductors can be considered as constant current sources.
- (2)
- All the power semiconductors and energy storage components are in the ideal conditions, namely the on-state resistances of the power semiconductors, the forward voltage drops of the diodes, and the equivalent series resistances (ESRs) of the inductors and capacitors are ignored.
3. Comparisons between Proposed and Original Modulation Strategies
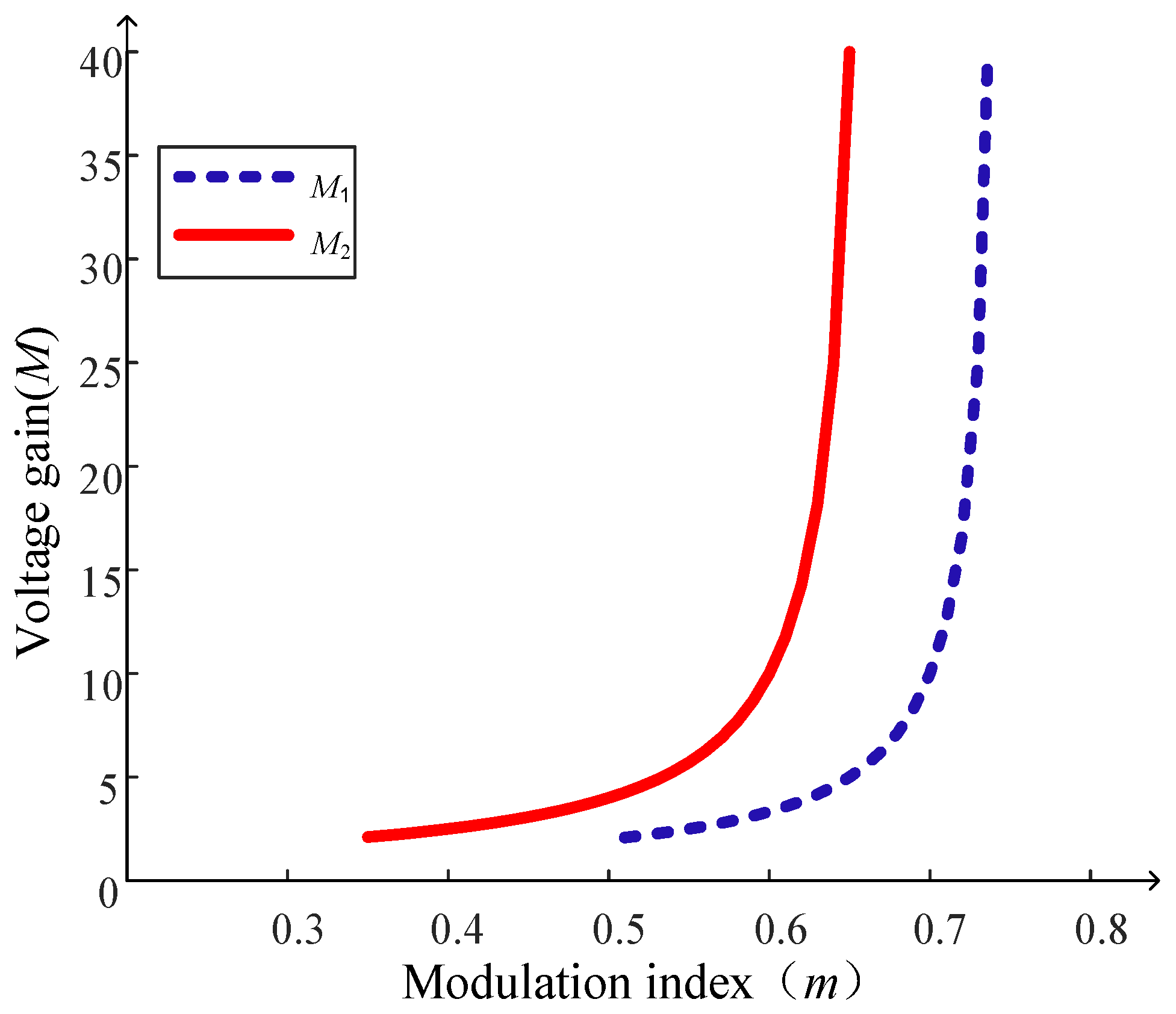
3.1. Comparisons of Voltage Gain
3.2. Comparisons of Voltage and Current Stresses
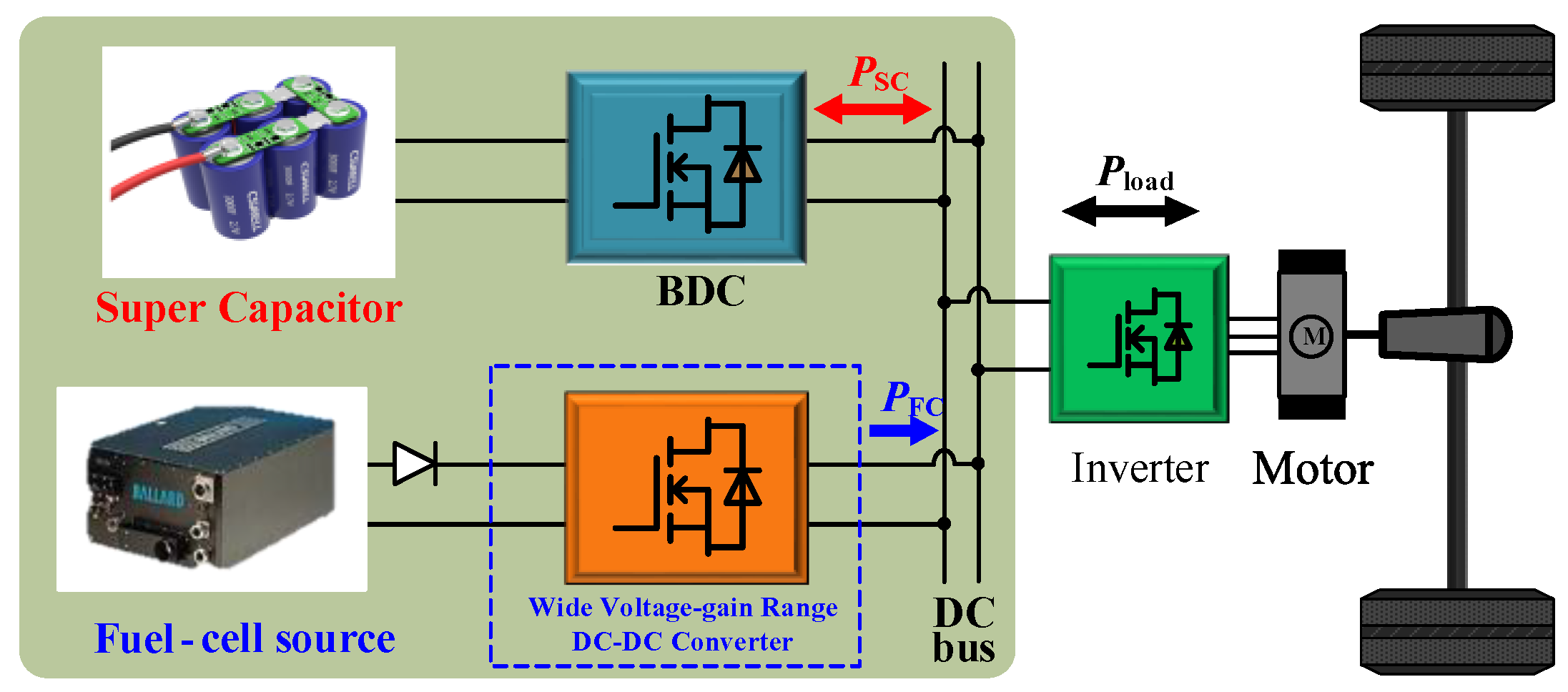
4. Application of the Converter for Fuel Cell Vehicles
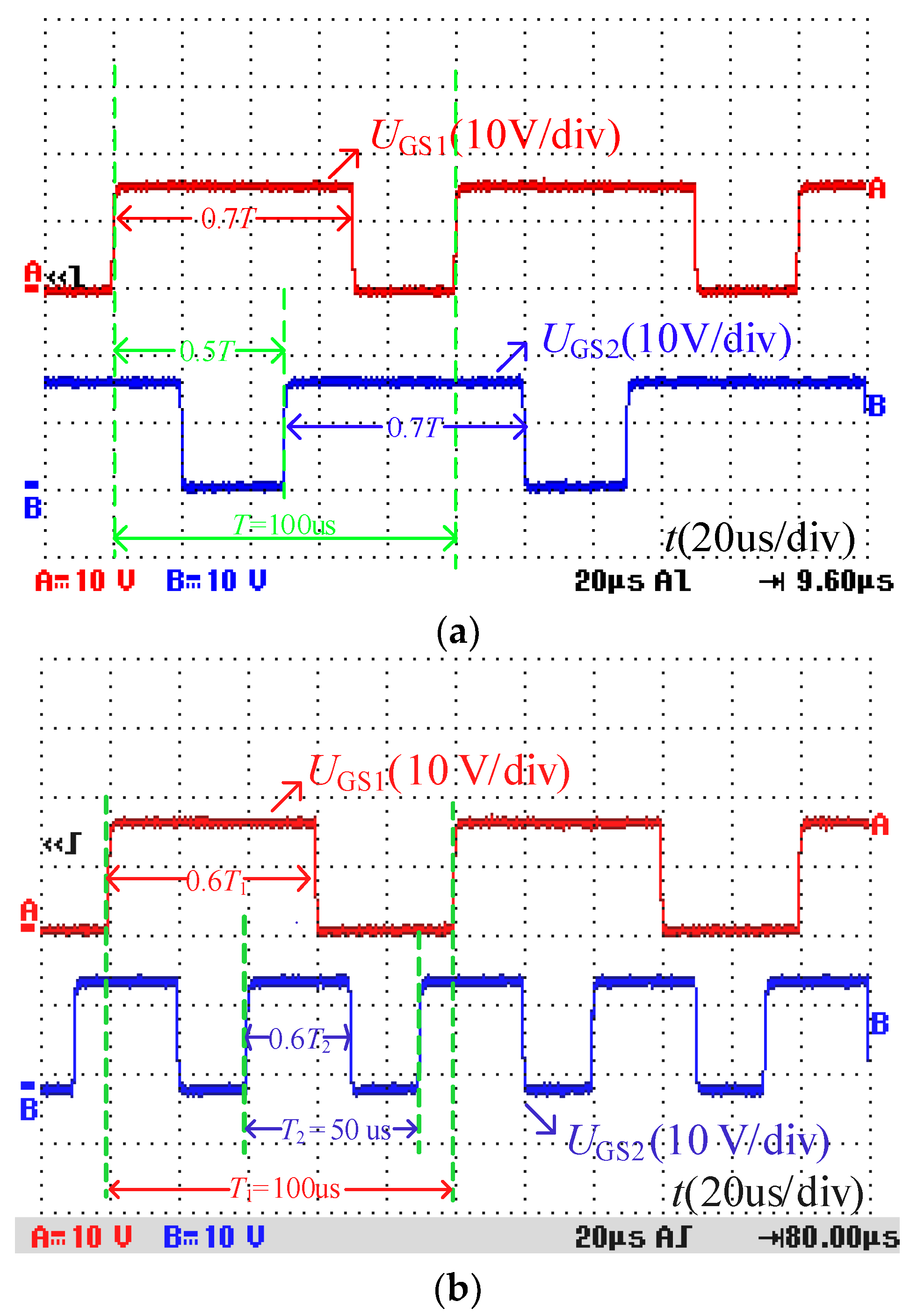
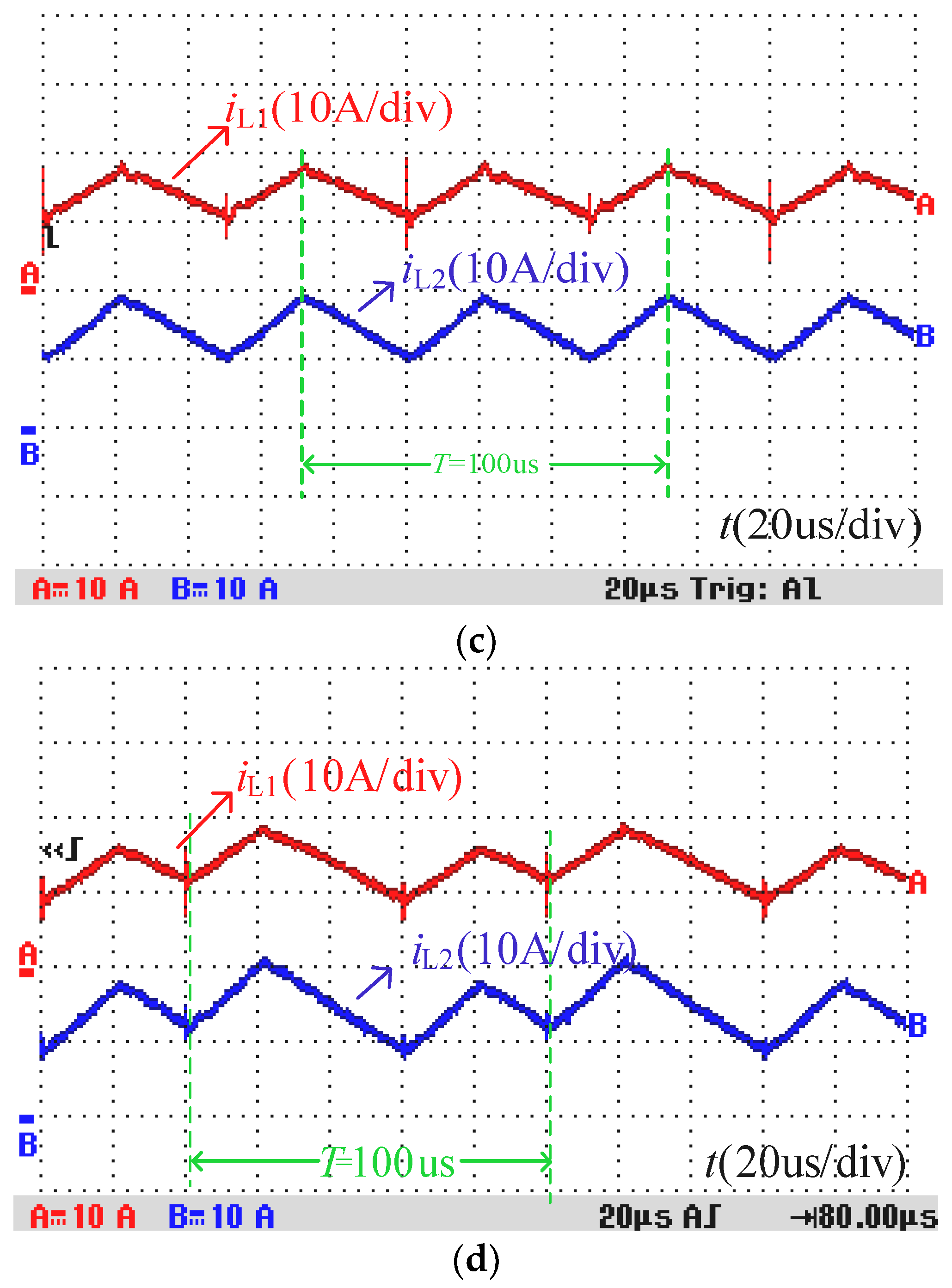
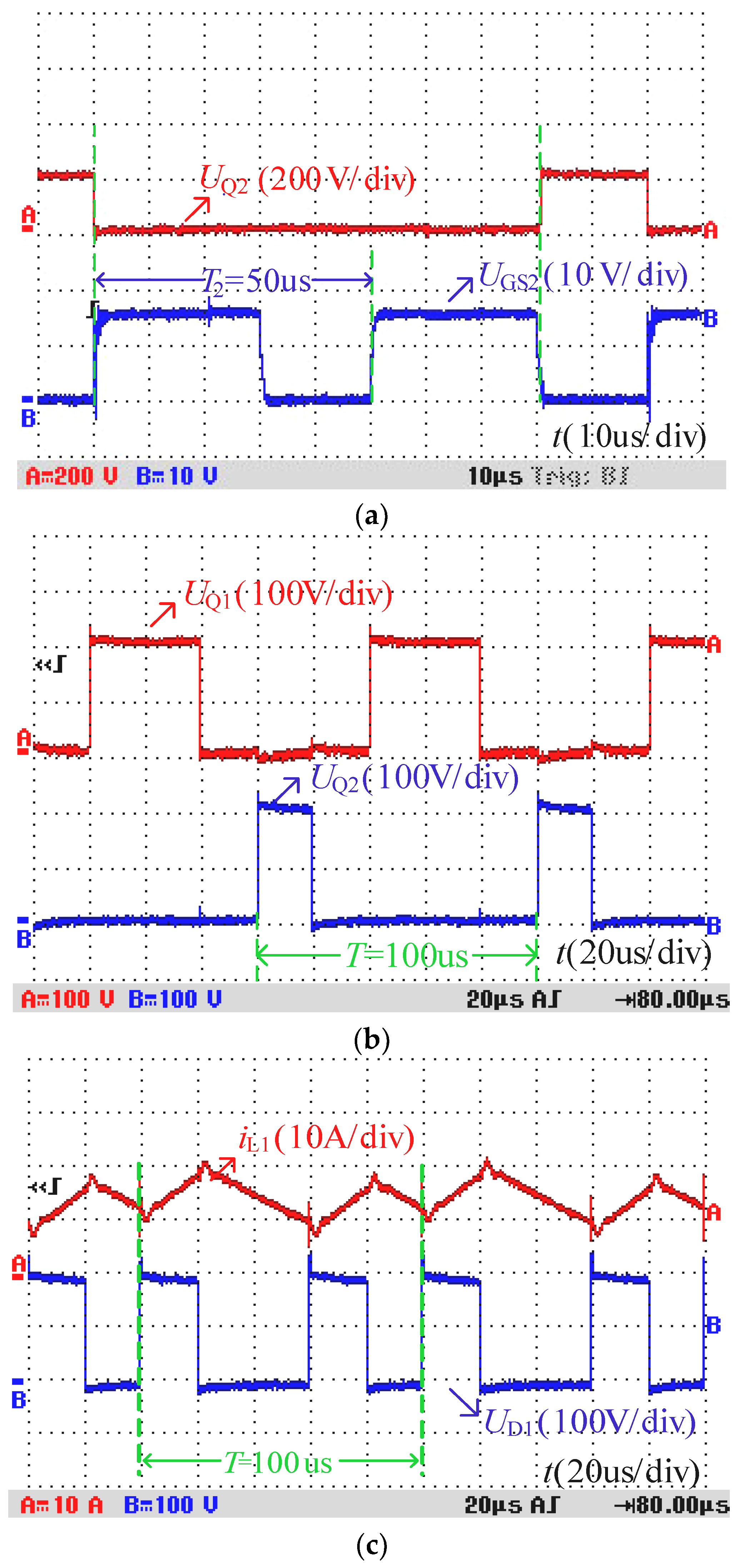
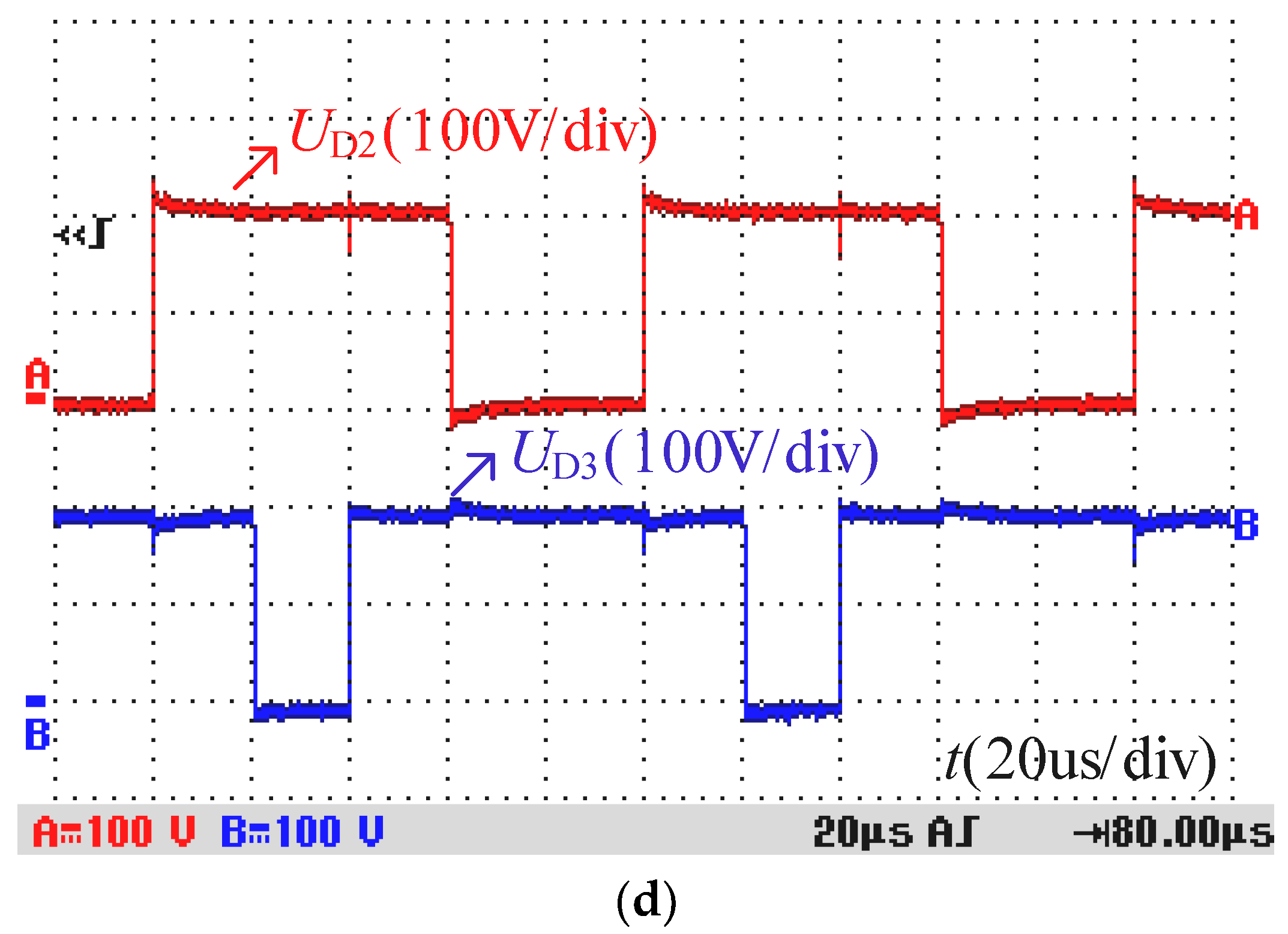
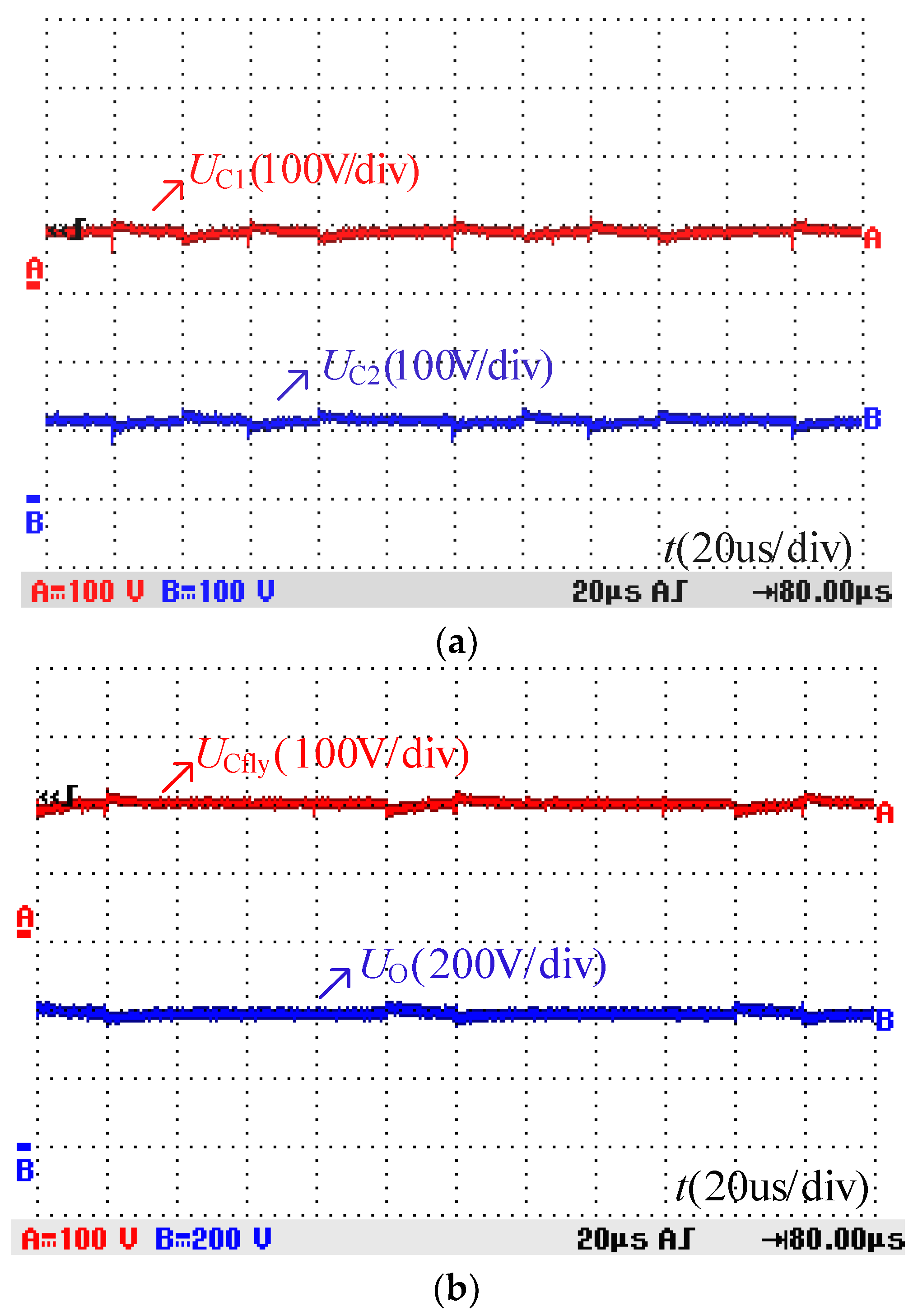
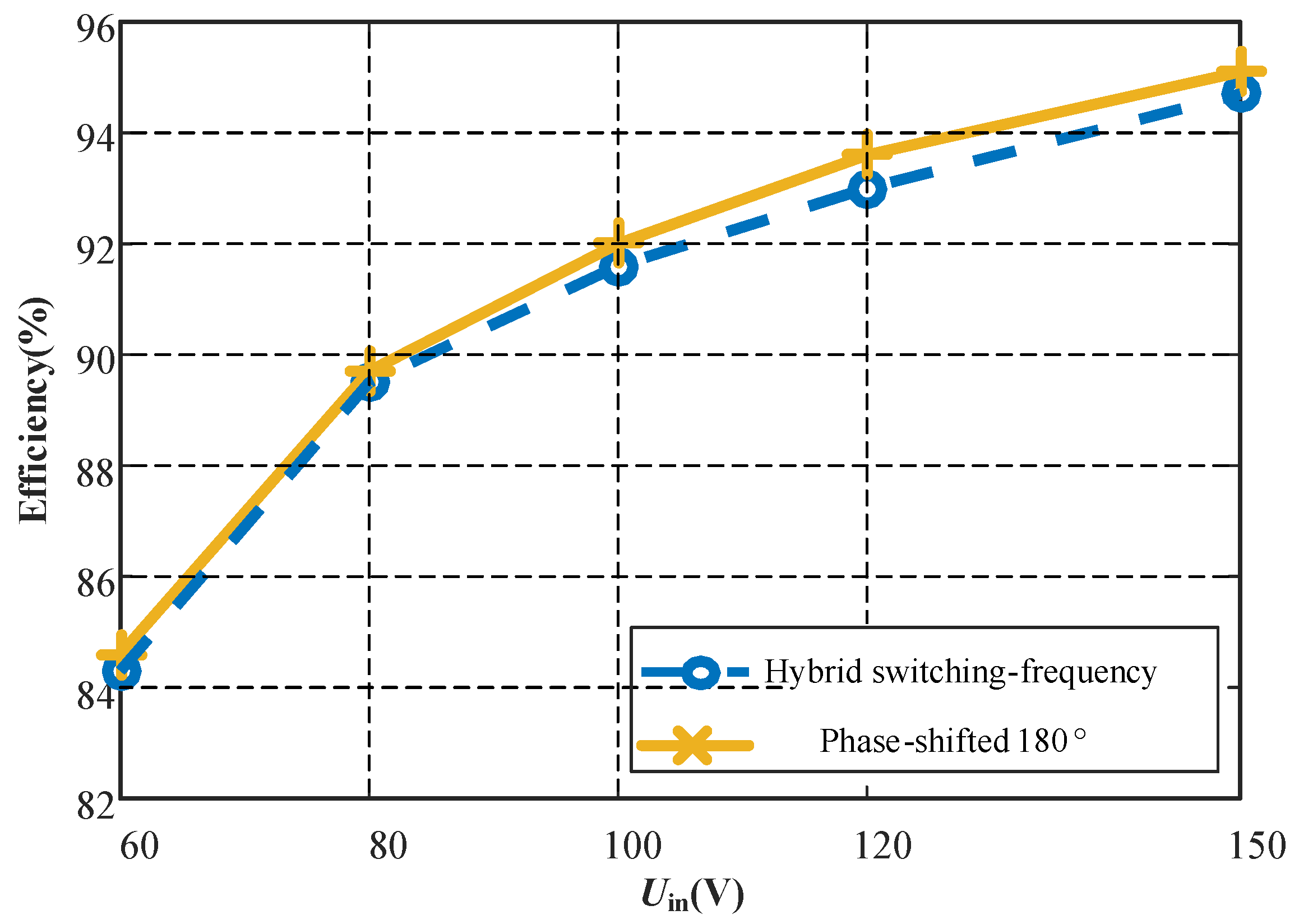
5. Experimental Results and Analysis
6. Conclusions
Author Contributions
Conflicts of Interest
Nomenclature
| L1, L2 | Inductances of the inductors in the quasi-Z source. |
| C1, C2, C3, Cfly | Capacitances of the capacitors in the quasi-Z source, the output capacitor and the flying capacitor. |
| P | The rated power of the converter. |
| R | The load resistance. |
| M1, M2 | The step-up voltage-gains of the BTL-Qz DC-DC converter with the 180-degree modulation phase-shifted strategy and the enhanced hybrid switching-frequency modulation strategy. |
| m | The modulation index of power switches Q1 and Q2. |
| UCfly | The voltage across the flying capacitor in the converter. |
| UC1, UC2 | The voltages across the capacitors in the quasi-Z source. |
| UQ1, UQ2 | The voltage stresses across power switches Q1 and Q2. |
| UD1, UD2, UD3 | The voltage stresses across diodes D1, D2 and D3. |
| t1-t4 | The durations of the corresponding switching states. |
| f | The carrier frequency of the gate signal Q1. |
| Uin, UO | The input and output voltages of the converter. |
| UGS1, UGS2 | The gate signals of power switches Q1 and Q2. |
| iL1, iL2 | The inductor currents of L1 and L2. |
References
- Migliardini, F.; Capasso, C.; Corbo, P. Optimization of hydrogen feeding procedure in PEM fuel cell systems for transportation. Int. J. Hydrogen Energy 2014, 39, 21746–21752. [Google Scholar] [CrossRef]
- Veneria, O.; Capassoa, C.; Patalano, S. Experimental investigation into the effectiveness of a super-capacitor based hybrid energy storage system for urban commercial vehicles. Appl. Energy 2017. [CrossRef]
- Omar, N.; Daowd, M.; Hegazy, O.; Bossche, P.; Coosemans, T.; Mierlo, J. Electrical double-layer capacitors in hybrid topologies—Assessment and evaluation of their performance. Energies 2012, 5, 4533–4568. [Google Scholar] [CrossRef]
- Gopinath, R.; Kim, S.; Hahn, J.H.; Enjeti, P.N.; Yeary, M.B.; Howze, J.W. Development of a low cost fuel cell inverter system with DSP control. IEEE Trans. Power Electron. 2004, 19, 1256–1262. [Google Scholar] [CrossRef]
- Palma, L.; Enjeti, P.N. A modular fuel cell, modular DC–DC converter concept for high performance and enhanced reliability. IEEE Trans. Power Electron. 2009, 24, 1437–1443. [Google Scholar] [CrossRef]
- Pagano, M.; Piegari, L. Electrical networks fed by fuel-cells for uninterruptible electrical supply. In Proceedings of the IEEE International Symposium on Industrial Electronics-ISIE, L’Ayuila, Ttaly, 8–11 July 2002; pp. 953–958. [Google Scholar]
- Tekin, M.; Hissel, D.; Pera, M.C.; Kauffmann, J.M. Energy-management strategy for embedded fuel-cell systems using fuzzy logic. IEEE Trans. Ind. Electron. 2007, 54, 595–603. [Google Scholar] [CrossRef]
- Jia, J.; Wang, G.; Cham, Y.T.; Wang, Y.; Han, M. Electrical characteristic study of a hybrid PEMFC and ultracapacitor system. IEEE Trans. Ind. Electron. 2010, 57, 1945–1953. [Google Scholar]
- Prasanna, U.R.; Rathore, A.K. Dual three-pulse modulation-based high-frequency pulsating DC link two-stage three-phase inverter for electric/hybrid/fuel cell vehicles applications. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 477–486. [Google Scholar] [CrossRef]
- Su, G.; Tang, L. A reduced-part, triple-voltage DC–DC converter for EV/HEV power management. IEEE Trans. Power Electron. 2009, 24, 2406–2410. [Google Scholar]
- Pera, M.C.; Candusso, D.; Hissel, D.; Kauffmann, J.M. Power Generation by Fuel Cells. IEEE Ind. Electron. Mag. 2007, 1, 28–37. [Google Scholar] [CrossRef]
- Shen, M.; Joseph, A.; Wang, J.; Peng, F.Z.; Adams, D.J. Comparison of Traditional Inverters and Z-Source Inverter for Fuel Cell Vehicles. IEEE Trans. Power Electron. 2007, 22, 1453–1463. [Google Scholar] [CrossRef]
- Fontes, G.; Turpin, C.; Astier, S. A Large-Signal and Dynamic Circuit Model of a H2/O2 PEM Fuel Cell: Description, Parameter Identification, and Exploitation. IEEE Trans. Ind. Electron. 2010, 57, 1874–1881. [Google Scholar] [CrossRef]
- Martins, G.M.; Pomilio, J.A.; Buso, S.; Spiazzi, G. Three-phase low frequency commutation inverter for renewable energy systems. IEEE Trans. Ind. Electron. 2006, 53, 1522–1528. [Google Scholar] [CrossRef]
- Wai, R.J.; Lin, C.Y.; Duan, R.Y.; Chang, Y.R. High-efficiency DC–DC converter with high voltage gain and reduced switch stress. IEEE Trans. Ind. Electron. 2007, 54, 354–364. [Google Scholar] [CrossRef]
- Todorovic, M.H.; Palma, L.; Enjeti, P.N. Design of a Wide Input Range DC–DC Converter with a Robust Power Control Scheme Suitable for Fuel Cell Power Conversion. IEEE Trans. Ind. Electron. 2008, 55, 1247–1255. [Google Scholar] [CrossRef]
- Shahin, A.; Hinaje, M.; Martin, J.; Pierfederici, S.; Raël, S.; Davat, B. High Voltage Ratio DC–DC Converter for Fuel-Cell Applications. IEEE Trans. Ind. Electron. 2010, 57, 3944–3955. [Google Scholar] [CrossRef]
- Zhang, M.T.; Jiang, Y.; Lee, F.C.; Jovanovic, M.M. Single-phase three-level boost power correction converter. Proc. APEC 1995, 1, 434–439. [Google Scholar]
- Fontes, G.; Turpin, C.; Astier, S.; Meynard, T. Interactions between fuel cell and power converters: Influence of current harmonics on a fuel cell stack. IEEE Trans. Power Electron. 2007, 22, 670–678. [Google Scholar] [CrossRef]
- Kwon, J.M.; Kim, E.H.; Kwon, B.H.; Nam, K.H. High-efficiency fuel cell power conditioning system with input current ripple reduction. IEEE Trans. Ind. Electron. 2009, 56, 826–834. [Google Scholar] [CrossRef]
- Tseng, K.C.; Liang, T.J. Novel high-efficiency step-up converter. Proc. Inst. Electr. Eng. Electr. Power Appl. 2004, 151, 182–190. [Google Scholar] [CrossRef]
- Prudente, M.; Pfitscher, L.L.; Emmendoerfer, G.; Romaneli, E.F.; Gules, R. Voltage Multiplier Cells Applied to Non-Isolated DC–DC Converters. IEEE Trans. Power Electron. 2008, 23, 871–887. [Google Scholar] [CrossRef]
- Zhao, Q.; Lee, F.C. High-efficiency, high step-up DC–DC converters. IEEE Trans. Power Electron. 2003, 18, 65–73. [Google Scholar] [CrossRef]
- Graditi, G.; Adinolfi, G.; Tina, G.M. Photovoltaic optimizer boost converters: Temperature influence and electro-thermal design. Appl. Energy 2014, 115, 140–150. [Google Scholar] [CrossRef]
- Peng, F.Z.; Li, H.; Su, G.; Lawler, J.S. A new ZVS bidirectional DC–DC converter for fuel cell and battery application. IEEE Trans. Power Electron. 2004, 19, 54–65. [Google Scholar] [CrossRef]
- Amodeo, S.J.; Chiacchiarini, H.G.; Oliva, A.R. High-performance control of a DC–DC Z-source converter used for an excitation field river. IEEE Trans. Power Electron. 2012, 27, 2947–2957. [Google Scholar] [CrossRef]
- Anderson, J.; Peng, F.Z. A class of quasi-Z-source inverters. In Proceedings of the IEEE Industry Applications Society Annual Meeting, Edmonton, AB, Canada, 5–9 October 2008; pp. 1–7. [Google Scholar]
- Yang, S.; Peng, F.Z.; Lei, Q.; Inoshita, R.; Qian, Z. Current-fed quasi-Z-source inverter with voltage Buck–Boost and regeneration capability. IEEE Trans. Ind. Appl. 2011, 47, 882–892. [Google Scholar] [CrossRef]
- Ellabban, O.; Abu-Rub, H.; Ge, B. A quasi-Z-source direct matrix converter feeding a vector controlled induction motor drive. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 1063–1072. [Google Scholar] [CrossRef]
- Patidar, K.; Umarikar, A.C. High step-up pulse-width modulation DC–DC converter based on quasi-Z-source topology. IET Power Electron. 2015, 8, 477–488. [Google Scholar] [CrossRef]
- Ruan, X.; Li, B.; Chen, Q.; Tan, S.; Tse, C.K. Fundamental considerations of three-level DC–DC converters: Topologies, analyses, and control. IEEE Trans. Circuits Syst. I Reg. Papers 2008, 55, 3733–3743. [Google Scholar] [CrossRef]
- Chen, H.; Liao, J. Design and implementation of sensorless capacitor voltage balancing control for three-level Boosting PFC. IEEE Trans. Power Electron. 2014, 29, 3808–3817. [Google Scholar] [CrossRef]
- Dusmez, S.; Hasanzadeh, A.; Khaligh, A. Comparative analysis of bidirectional three-level DC–DC converter for automotive applications. IEEE Trans. Ind. Electron. 2015, 62, 1063–1072. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, J.; Zhou, L.; Li, J.; Sumner, M.; Wang, P.; Xia, C. Wide Input-Voltage Range Boost Three-Level DC-DC Converter with Quasi-Z Source for Fuel Cell Vehicles. IEEE Trans. Power Electron. 2017, 32, 6728–6738. [Google Scholar] [CrossRef]

| Modulation Strategy | C1 | C2 | Cfly | Q1 | Q2 | D1 | D2 | D3 |
|---|---|---|---|---|---|---|---|---|
| Phase shifted 180-degree | UO/2 | UO/2 | UO/2 | UO/2 | UO/2 | UO/2 | ||
| hybrid switching-frequency | UO/2 | UO/2 | UO/2 | UO/2 | UO/2 | UO/2 |
| Modulation Strategy | Q1 | Q2 | D1 | D2 | D3 |
|---|---|---|---|---|---|
| Phase-shifted 180-degree | 2MIO | 2MIO | |||
| hybrid switching-frequency | 2MIO | 2MIO | 2MIO |
| Parameters and Components | Values (units) |
|---|---|
| Input voltage Uin | 40~150 V |
| Output voltage UO | 400 V |
| Inductor L1 | 228 μH |
| Inductor L2 | 225 μH |
| Capacitors C1, C2 and Cfly | 450 V/660 μF |
| Capacitor C3 | 450 V/440 μF |
| Rated power P | 400 W |
| Load R | 400 Ω |
| MOSFETs Q1 and Q2 | IXTK102N30P |
| Diodes DFC, D1, D2 and D3 | DSEC60-03A |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Shi, J.; Fu, C.; Zhang, W.; Wang, P.; Li, J.; Sumner, M. An Enhanced Hybrid Switching-Frequency Modulation Strategy for Fuel Cell Vehicle Three-Level DC-DC Converters with Quasi-Z Source. Energies 2018, 11, 1026. https://doi.org/10.3390/en11051026
Zhang Y, Shi J, Fu C, Zhang W, Wang P, Li J, Sumner M. An Enhanced Hybrid Switching-Frequency Modulation Strategy for Fuel Cell Vehicle Three-Level DC-DC Converters with Quasi-Z Source. Energies. 2018; 11(5):1026. https://doi.org/10.3390/en11051026
Chicago/Turabian StyleZhang, Yun, Jilong Shi, Chuanzhi Fu, Wei Zhang, Ping Wang, Jing Li, and Mark Sumner. 2018. "An Enhanced Hybrid Switching-Frequency Modulation Strategy for Fuel Cell Vehicle Three-Level DC-DC Converters with Quasi-Z Source" Energies 11, no. 5: 1026. https://doi.org/10.3390/en11051026
APA StyleZhang, Y., Shi, J., Fu, C., Zhang, W., Wang, P., Li, J., & Sumner, M. (2018). An Enhanced Hybrid Switching-Frequency Modulation Strategy for Fuel Cell Vehicle Three-Level DC-DC Converters with Quasi-Z Source. Energies, 11(5), 1026. https://doi.org/10.3390/en11051026






