Eigen-Analysis Considering Time-Delay and Data-Loss of WAMS and ITS Application to WADC Design Based on Damping Torque Analysis
Abstract
:1. Introduction
- A unified mathematical model of WAMS signal is proposed according to the mathematical expectation of sampling data and transformed to the frequency domain based on the Pade rational polynomial approximation.
- By applying the model to the linearized equations, the eigenvalue calculation model containing time-delay and data-loss is derived. This model can analyze the impact of data corruption on system dynamic performance and calculate the system stability time-delay margin.
- On the basis of DTA theory, the damping torque index considering data corruption is obtained. The DTI can reflect the sensitivity of eigenvalues impacted by the WADC transfer function and thus, can be applied to execute wide-area signals selection and parameter tuning.
2. Eigen-Analysis Model Considering Time-Delay and Data-Loss
2.1. Closed-Loop Linearized Model with WAMS
2.2. Unified Mathematical Model of Time-Delay and Data-Loss
2.3. Pade Approximation
2.4. Linearized Model of Controller with Wide-Area Signals
3. Wide-Area Damping Controller Design Based on the Damping Torque Index
3.1. Damping Torque Index Considering Time-Delay and Data-Loss
3.2. Wide-Area Damping Controller Design
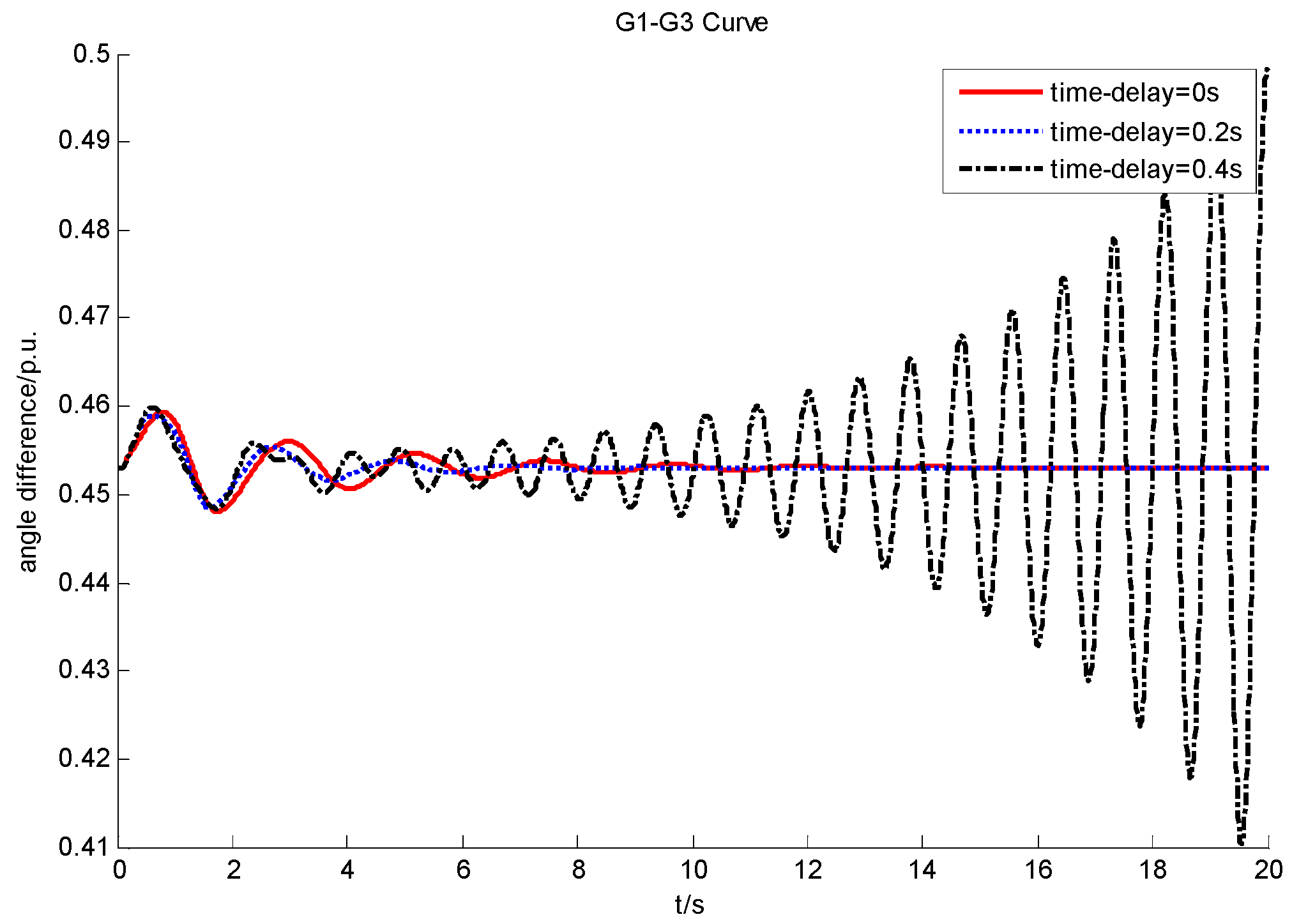
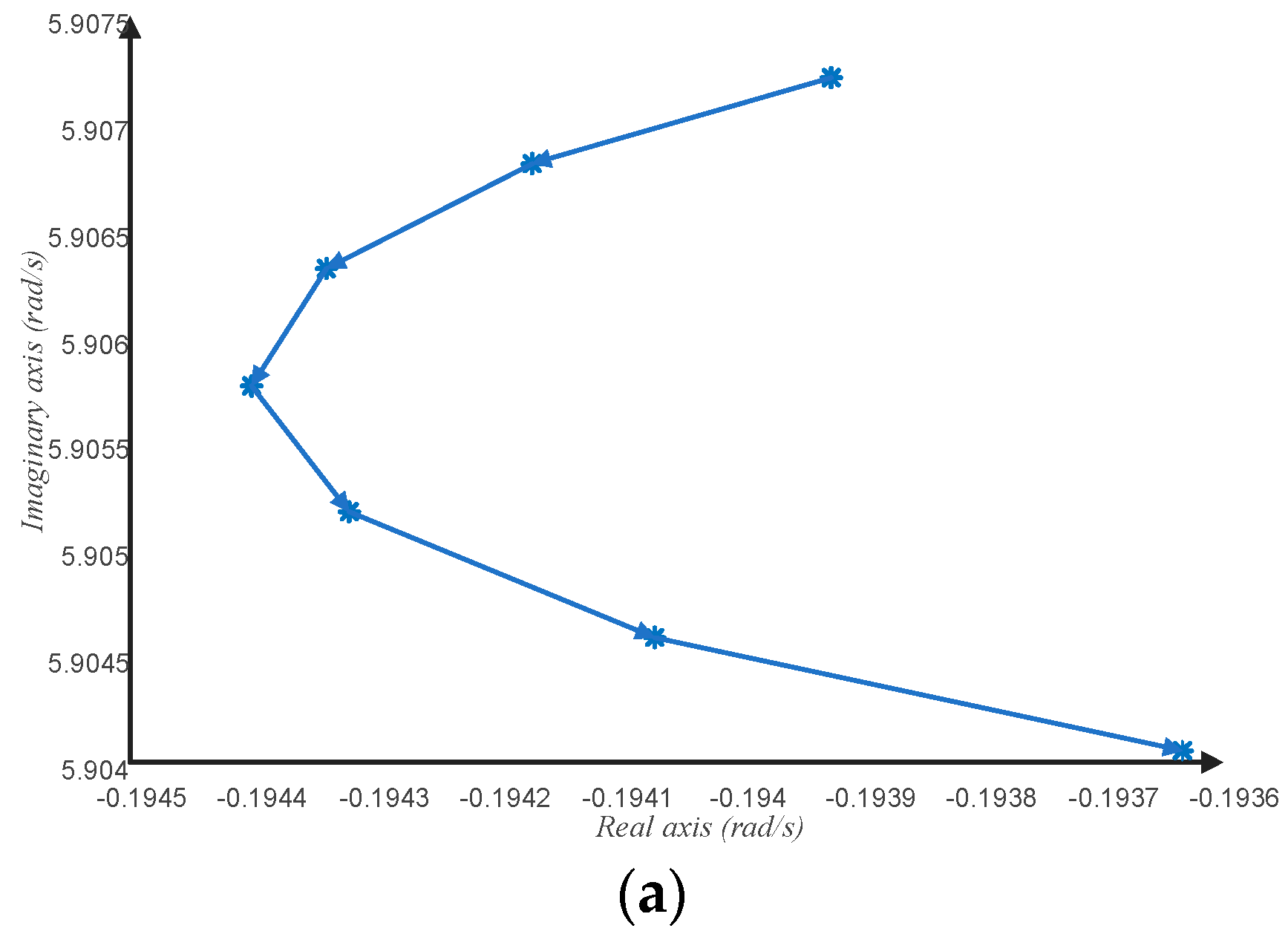
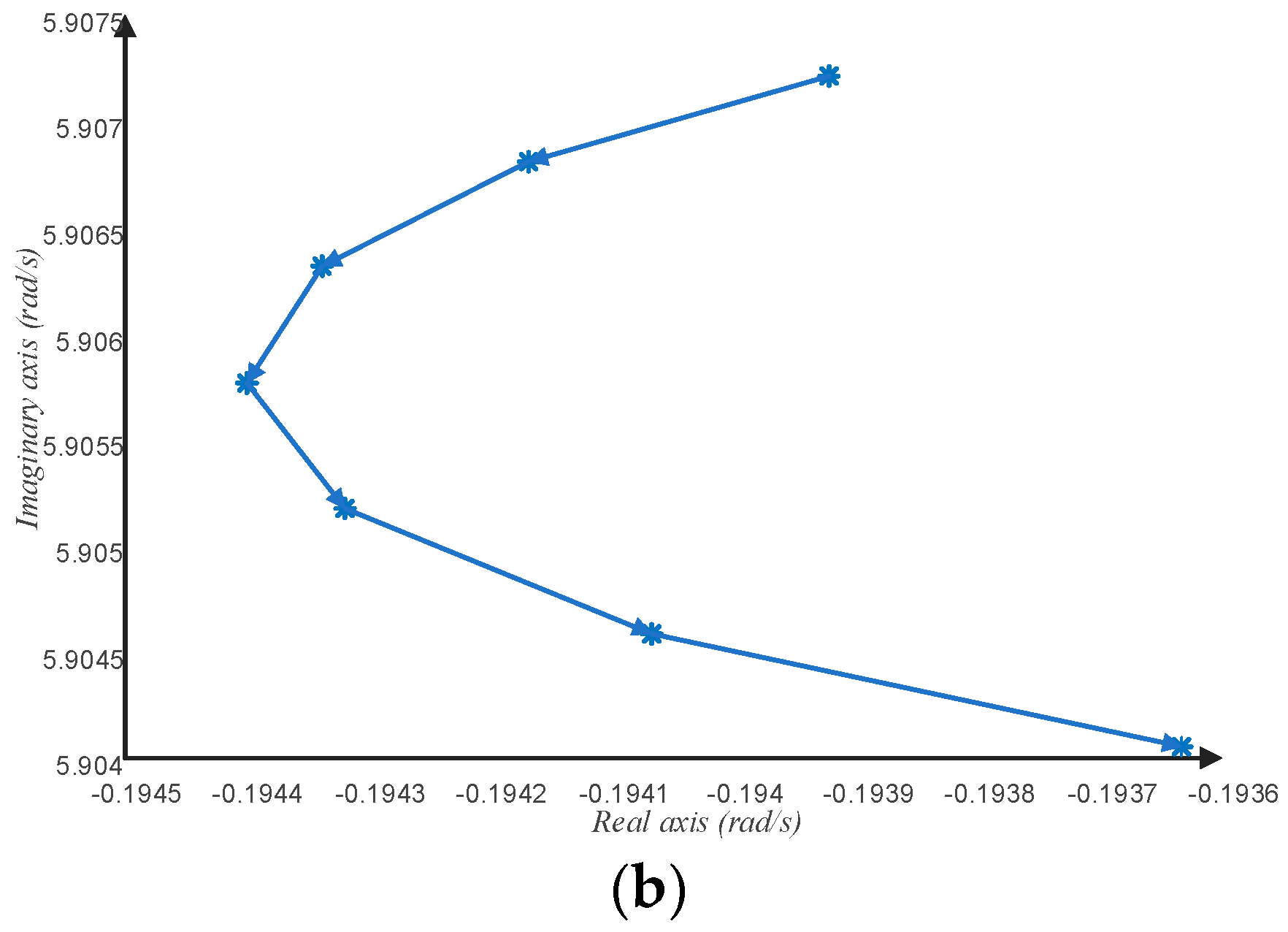
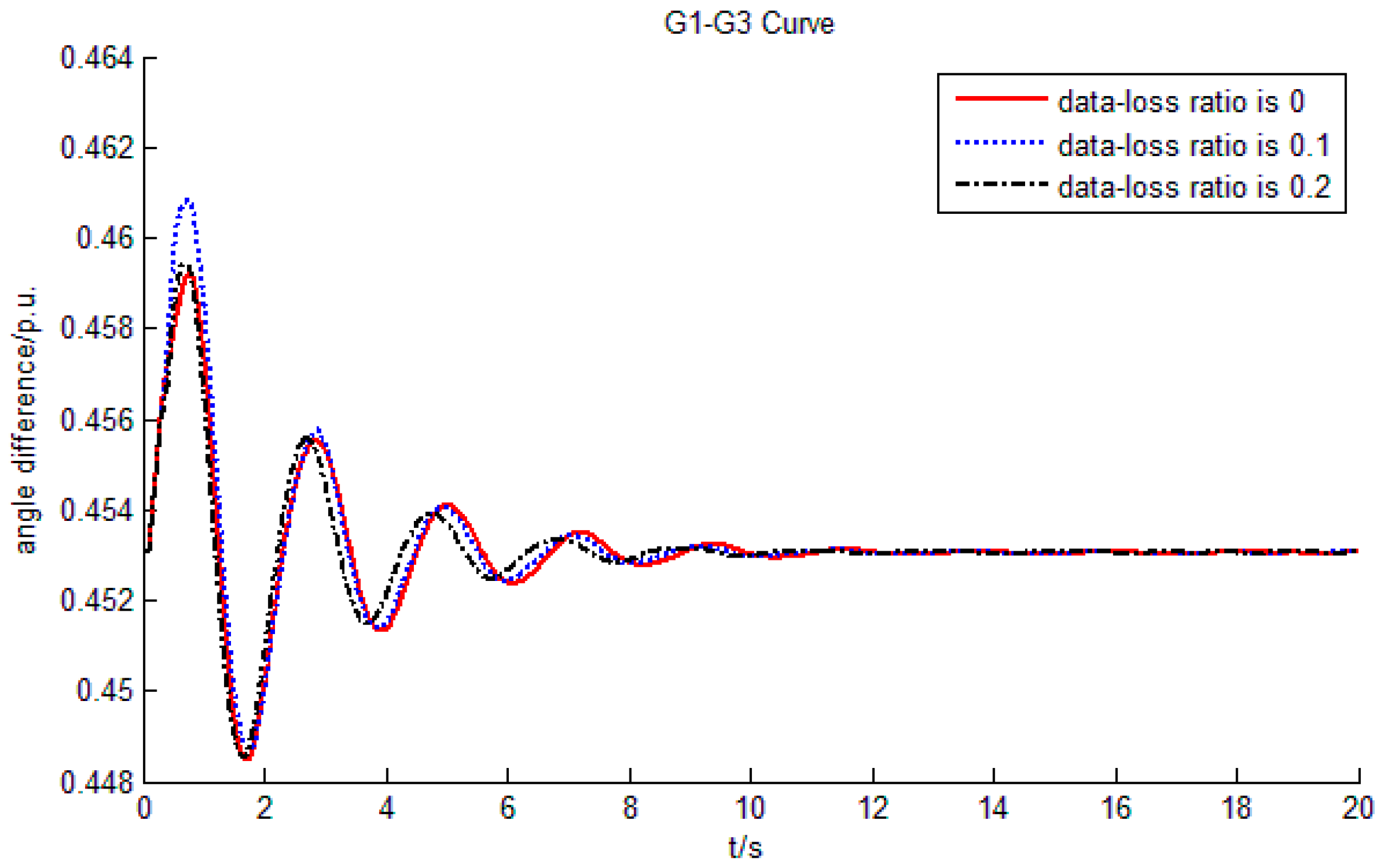
4. Case Study
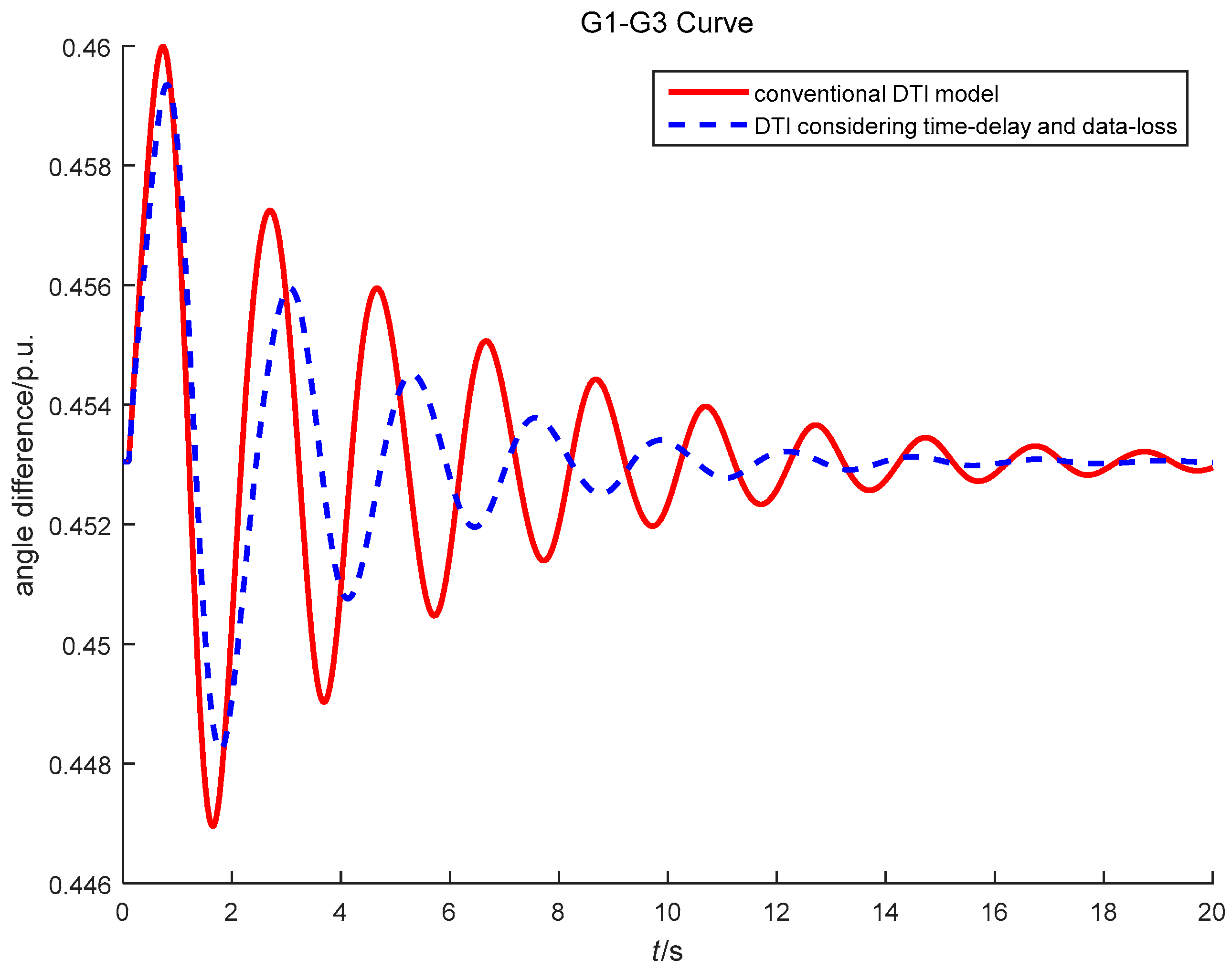
4.1. Simulations of Different Models of Data-Loss
4.2. Impact Mechanism
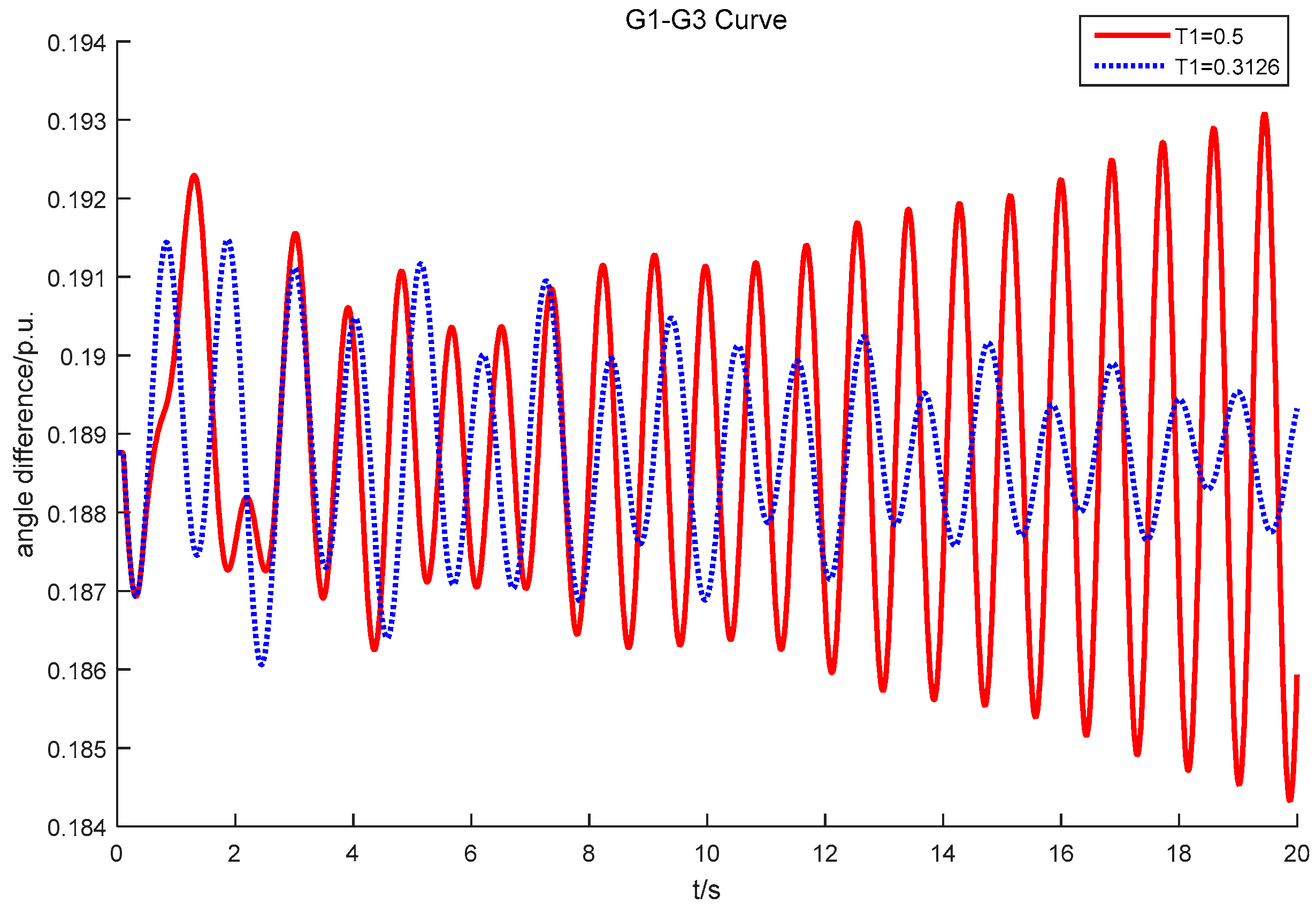
4.3. Controller Signal Selection and Parameter Tuning
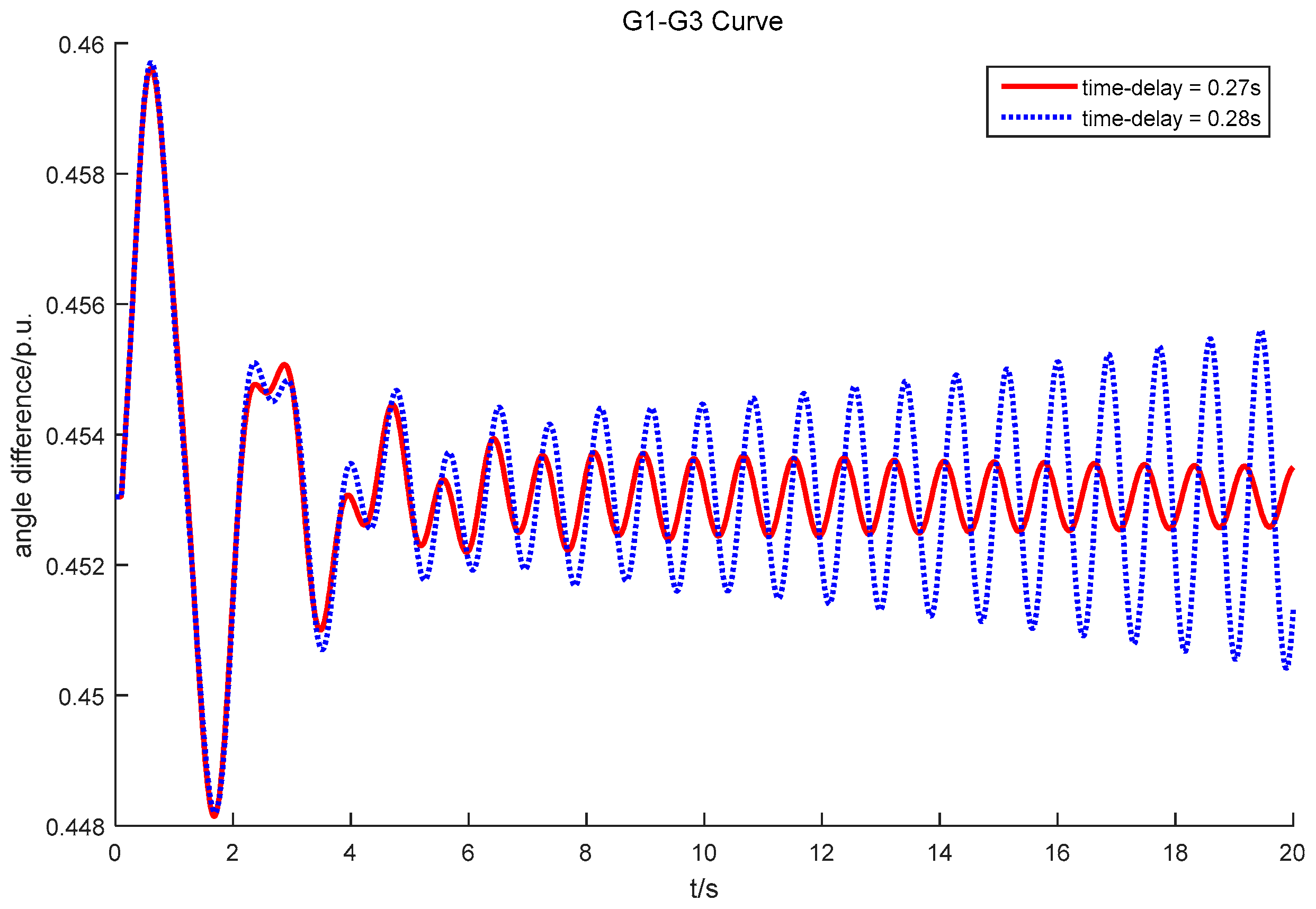
4.4. System Stability Time-Delay Margin Calculation
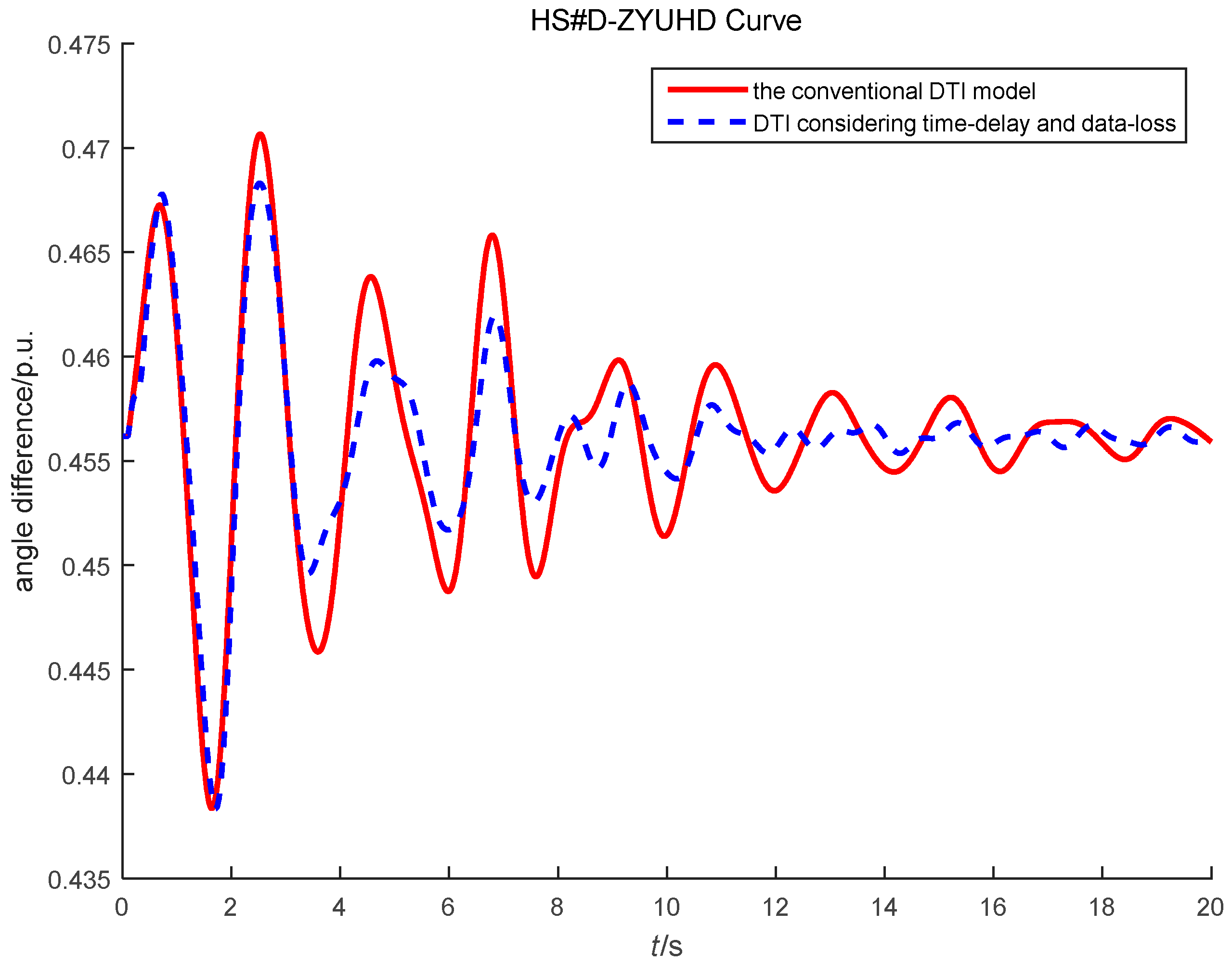
4.5. WADC Parameter Tuning in ECPG
5. Conclusions
- (1)
- The impact mechanism of the time-delay on small-signal dynamics is complicated. An increase in the time-delay may increase the damping of one oscillation mode when it is relatively small. However, when the time-delay is over the stability margin, system stability will get worse rapidly.
- (2)
- Data-loss can reduce the delay margin and system stability. However, the impact is relatively small as it generates an equivalent time-delay of . Therefore, in practical applications, more attention should be paid to the negative impact brought about by time-delay than data-loss.
- (3)
- The system delay margin can be derived by using the proposed eigenvalue calculation model. It is an important parameter of the power system and is helpful for wide-area device improvement and signal selection. The parameter tuning method of WADC based on DTI can extend the system’s time-delay margin and thus enhance system dynamic performance.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wu, X.; Dorfler, F.; Jovanovic, M.R. Input-Output Analysis and Decentralized Optimal Control of Inter-Area Oscillations in Power Systems. IEEE Trans. Power Syst. 2016, 31, 2434–2444. [Google Scholar] [CrossRef]
- Nezam Sarmadi, S.A.; Venkatasubramanian, V.; Salazar, A. Analysis of November 29, 2005 Western American Oscillation Event. IEEE Trans. Power Syst. 2016, 31, 5210–5211. [Google Scholar] [CrossRef]
- Che, Y.; Xu, J.; Shi, K.; Liu, H.; Chen, W.; Yu, D. Stability analysis of aircraft power systems based on a unified large signal model. Energies 2017, 10, 1–15. [Google Scholar] [CrossRef]
- Salimian, M.R.; Aghamohammadi, M.R. Intelligent out of Step Predictor for Inter Area Oscillations Using Speed-Acceleration Criterion as a Time Matching for Controlled Islanding. IEEE Trans. Smart Grid 2018, 9, 2488–2497. [Google Scholar] [CrossRef]
- Khandeparkar, K.V.; Soman, S.A.; Gajjar, G. Detection and Correction of Systematic Errors in Instrument Transformers Along with Line Parameter Estimation Using PMU Data. IEEE Trans. Power Syst. 2017, 32, 3089–3098. [Google Scholar] [CrossRef]
- Liao, K.; Wang, Y. A comparison between voltage and reactive power feedback schemes of DFIGs for inter-Area oscillation damping control. Energies 2017, 10, 1206. [Google Scholar] [CrossRef]
- Preece, R.; Milanović, J.V.; Almutairi, A.M.; Marjanovic, O. Damping of inter-area oscillations in mixed AC/DC networks using WAMS based supplementary controller. IEEE Trans. Power Syst. 2013, 28, 1160–1169. [Google Scholar] [CrossRef]
- Yao, W.; Jiang, L.; Wen, J.; Wu, Q.H.; Cheng, S. Wide-area damping controller of Facts devices for inter-area oscillations considering communication time delays. IEEE Trans. Power Syst. 2014, 29, 318–329. [Google Scholar] [CrossRef]
- Zhu, K.; Chenine, M.; Nordström, L. ICT Architecture Impact on Wide Area Monitoring and Control Systems’ Reliability. IEEE Trans. Power Deliv. 2011, 26, 2801–2808. [Google Scholar] [CrossRef]
- Huang, D.; Chen, Q.; Ma, S.; Zhang, Y.; Chen, S. Wide-Area Measurement—Based Model-Free Approach for Online Power System Transient Stability Assessment. Energies 2018, 11, 958. [Google Scholar] [CrossRef]
- Yang, B.; Sun, Y. A novel approach to calculate damping factor based delay margin for wide area damping control. IEEE Trans. Power Syst. 2014, 29, 3116–3117. [Google Scholar] [CrossRef]
- Cai, G.; Yang, D.; Liu, C. Adaptive wide-area damping control scheme for smart grids with consideration of signal time delay. Energies 2013, 6, 4841–4858. [Google Scholar] [CrossRef]
- Li, J.; Chen, Z.; Cai, D.; Zhen, W.; Huang, Q. Delay-Dependent Stability Control for Power System with Multiple Time-Delays. IEEE Trans. Power Syst. 2016, 31, 2316–2326. [Google Scholar] [CrossRef]
- Jungers, R.M.; Kundu, A.; Heemels, W.P.M.H. Observability and Controllability Analysis of Linear Systems Subject to Data Losses. IEEE Trans. Automat. Contr. 2017, 63, 3361–3376. [Google Scholar] [CrossRef]
- Li, C.; Li, G.; Wang, C.; Du, Z. Eigenvalue Sensitivity and Eigenvalue Tracing of Power Systems with Inclusion of Time Delays. IEEE Trans. Power Syst. 2018, 33, 3711–3719. [Google Scholar] [CrossRef]
- Wang, X.; Song, Y.; Irying, M. Modern Power Systems Analysis; Springer: Berlin, Germany, 2011. [Google Scholar]
- Li, Y.; Geng, G.; Jiang, Q. An Efficient Parallel Krylov-Schur Method for Eigen-Analysis of Large-Scale Power Systems. IEEE Trans. Power Syst. 2016, 31, 920–930. [Google Scholar] [CrossRef]
- Sinha, N.K.; Bereznai, G.T. Optimum approximation of high-order systems by low-order models. Int. J. Control 1971, 14, 951–959. [Google Scholar] [CrossRef]
- Nie, Y.; Zhang, P.; Ma, Y.; Zhang, Y.; Fang, B.; Lv, D. Time delay trajectory analysis of modes in wide-area power system based on Pade approximation. Dianli Xitong Zidonghua Autom. Electr. Power Syst. 2018, 42, 87–92. (In Chinese) [Google Scholar] [CrossRef]
- Hwang, C.; Lee, Y.C. Multifrequency Pade approximation via Jordan continued-fraction expansion. IEEE Trans. Autom. Contr. 1989, 34, 444–446. [Google Scholar] [CrossRef]
- Gurrala, G.; Sen, I. Synchronizing and damping torques analysis of nonlinear voltage regulators. IEEE Trans. Power Syst. 2011, 26, 1175–1185. [Google Scholar] [CrossRef]
- Zhou, T.; Chen, Z.; Guo, R.X. Power System Stabilizer Parameter Tuning Based on Closed-loop Damping Torque Analysis Method. Autom. Electr. Power Syst. 2016, 40, 56–60. (In Chinese) [Google Scholar] [CrossRef]
- Li, H.F.; Du, W.; Wang, H.F.; Xiao, L.Y. Damping torque analysis of energy storage system control in a multi-machine power system. IEEE PES Innov. Smart Grid Technol. Conf. Eur. 2011, 1–8. [Google Scholar] [CrossRef]
- Du, W.; Bi, J.; Lv, C.; Littler, T. Damping torque analysis of power systems with DFIGs for wind power generation. IET Renew. Power Gener. 2017, 11, 10–19. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Chung, C.Y.; Han, Y. A novel modal decomposition control and its application to PSS design for damping interarea oscillations in power systems. IEEE Trans. Power Syst. 2012, 27, 2015–2025. [Google Scholar] [CrossRef]
- Klein, M.; Rogers, G.J.; Kundur, P. A fundamental study of inter-area oscillations in power systems. IEEE Trans. Power Syst. 1991, 6, 914–921. [Google Scholar] [CrossRef]
- Wang, C.; Li, J.; Li, L.; Sun, W.; Ni, Q.; Zhang, J. Low frequency oscillation characteristics of east china power grid after commissioning of huainan-shanghai uhv project. Dianli Xitong Zidonghua Autom. Electr. Power Syst. 2013, 37, 120–125. (In Chinese) [Google Scholar] [CrossRef]


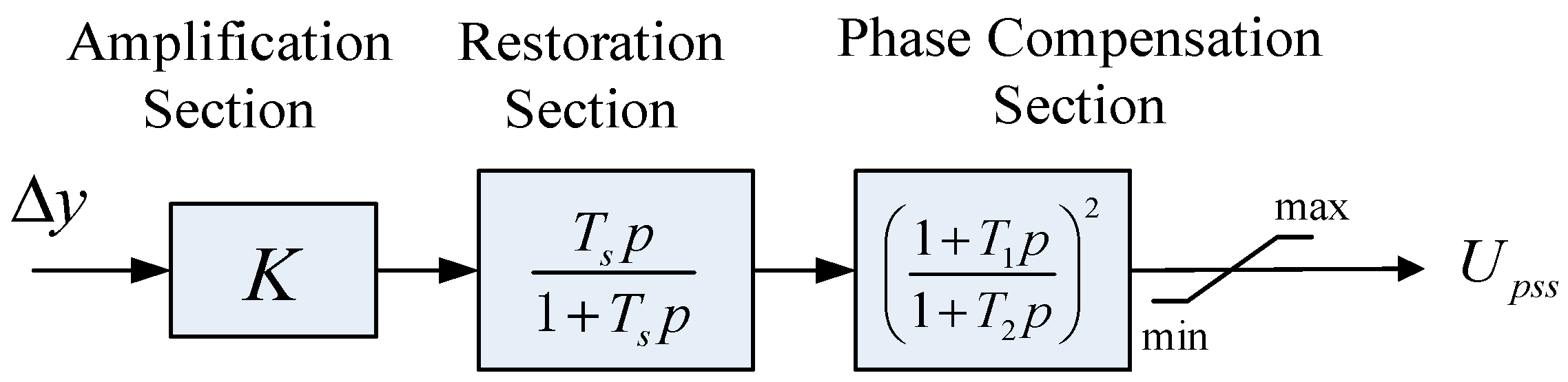
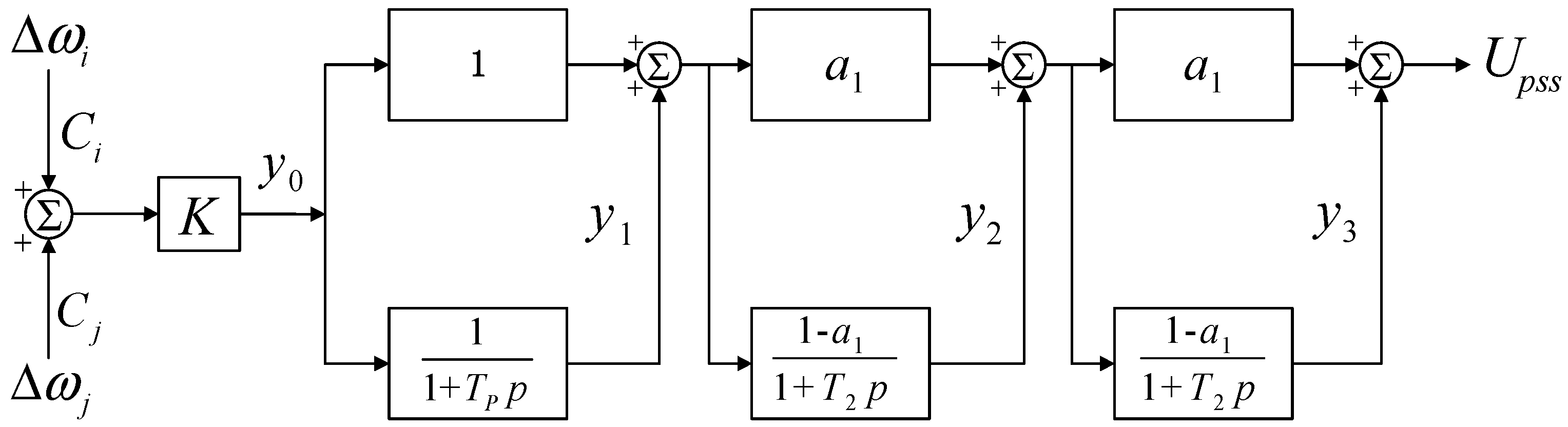
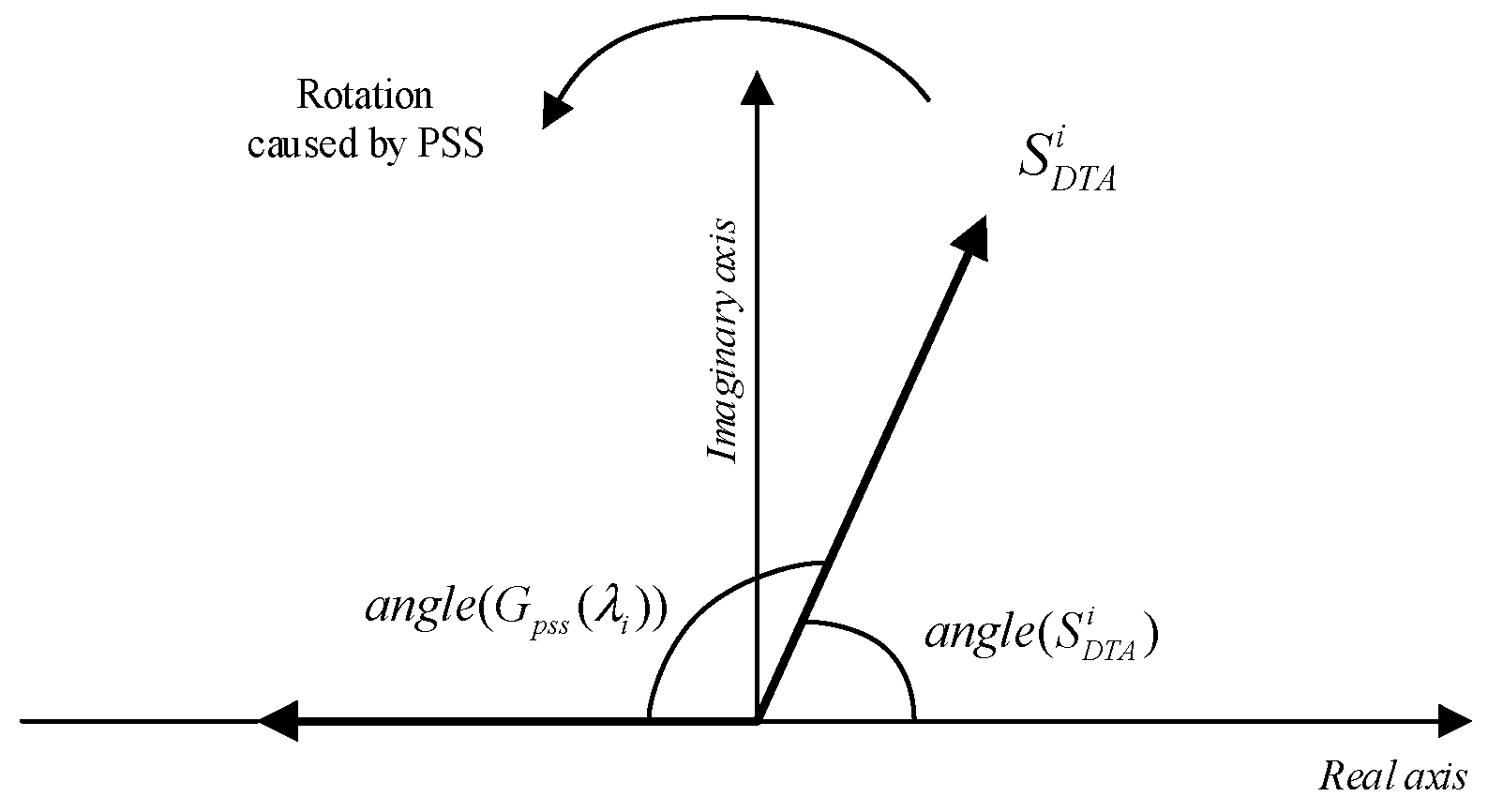
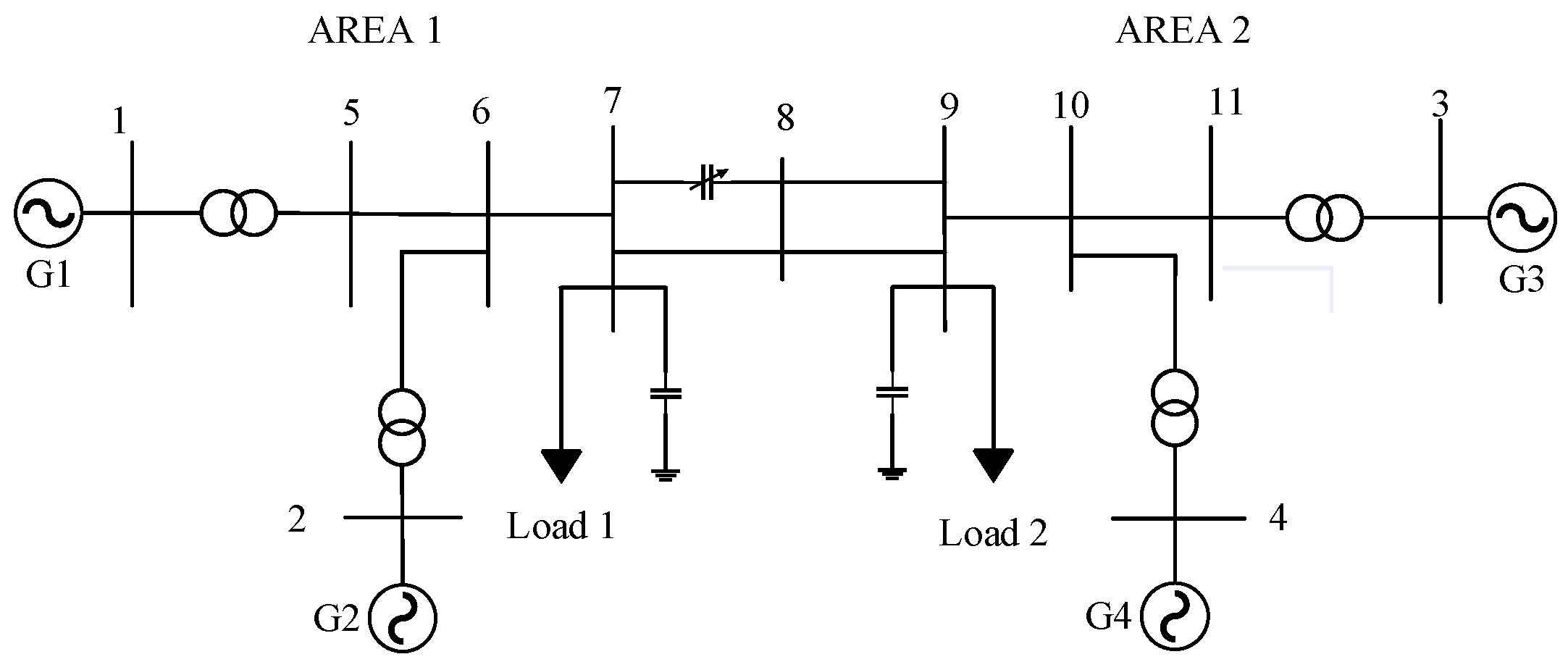


| Feedback Signal | Time-Delay/s | Data-Loss Ratio | Time-Delay/s | Data-Loss Ratio | Abs (DTI)/p.u. | Angle (DTI)/° |
|---|---|---|---|---|---|---|
| 0.08 () | 0.1 () | 0.08 () | 0.1 () | 0.0006 | −62.35 | |
| 0.08 () | 0.1 () | 0.08 () | 0.1 () | 0.0042 | −157.54 | |
| 0.08 () | 0.1 () | 0.08 () | 0.1 () | 0.1856 | −145.32 | |
| 0.06 () | 0.1 () | 0.06 () | 0.1 () | 0.1058 | −150.97 |
| Model | Real Part/Rad/s | Imaginary Part/Rad/s | Frequency/Hz | Damping Ratio |
|---|---|---|---|---|
| The conventional model | −0.19421 | 5.9067 | 0.9401 | 0.03278 |
| The proposed model | −0.34402 | 2.8285 | 0.4502 | 0.1193 |
| Mode | Real Part/Rad/s | Imaginary Part/Rad/s | Frequency/Hz | Damping Ratio |
|---|---|---|---|---|
| The conventional model | −0.18688 | 4.4643 | 0.7105 | 0.04183 |
| The proposed model | −0.25484 | 4.8136 | 0.7661 | 0.05287 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, T.; Chen, Z.; Bu, S.; Tang, H.; Liu, Y. Eigen-Analysis Considering Time-Delay and Data-Loss of WAMS and ITS Application to WADC Design Based on Damping Torque Analysis. Energies 2018, 11, 3186. https://doi.org/10.3390/en11113186
Zhou T, Chen Z, Bu S, Tang H, Liu Y. Eigen-Analysis Considering Time-Delay and Data-Loss of WAMS and ITS Application to WADC Design Based on Damping Torque Analysis. Energies. 2018; 11(11):3186. https://doi.org/10.3390/en11113186
Chicago/Turabian StyleZhou, Tao, Zhong Chen, Siqi Bu, Haoran Tang, and Yi Liu. 2018. "Eigen-Analysis Considering Time-Delay and Data-Loss of WAMS and ITS Application to WADC Design Based on Damping Torque Analysis" Energies 11, no. 11: 3186. https://doi.org/10.3390/en11113186
APA StyleZhou, T., Chen, Z., Bu, S., Tang, H., & Liu, Y. (2018). Eigen-Analysis Considering Time-Delay and Data-Loss of WAMS and ITS Application to WADC Design Based on Damping Torque Analysis. Energies, 11(11), 3186. https://doi.org/10.3390/en11113186






