Real-Time Implementation of Robust Control Strategies Based on Sliding Mode Control for Standalone Microgrids Supplying Non-Linear Loads

Abstract

In this paper enhanced control strategies for standalone microgrids based on solar photovoltaic systems (SVPAs) and diesel engine driven fixed speed synchronous generators, are presented. Single-phase d-q theory-based sliding mode controller for voltage source converter voltage source converter (VSC) is employed to mitigate harmonics, balance diesel generator (DG) current, and to inject the generated power by SVPA into local grid. To achieve fast dynamic response with zero steady-state error during transition, sliding mode controller for inner control loop is employed. To achieve maximum power point tracking (MPPT) from SVPA without using any MPPT method, a DC-DC buck boost converter supported by battery storage system is controlled using a new control strategy based on sliding mode control with boundary layer. In addition, modeling and detailed stability analysis are performed. The performance of the developed control strategies, are validate by simulation using MATLAB/Simulink and in real-time using hardware prototype.

1. Introduction

Most of remote areas in the world are not connected to the main grid. Generally, conventional diesel generators (DGs) are employed as the energy source to provide electricity to the connected loads in these areas [1,2,3]. Considering the transport and fuel costs, electricity in these isolated areas is costly. In addition, the performance of a DG is reduced when it is operated at light load, as well as, when connected to balanced and unbalanced nonlinear loads [4]. Many solutions are proposed in the literature to solve these issues and to reduce CO₂ emissions [5,6,7,8]. In [9], a hybrid wind-diesel system-based solution is proposed, and in [10,11] solar-wind-diesel hybrid systems are suggested. These solutions are effective from the point of view of fuel consumption but hard to implement in practice. Recently, in [12], many technical solutions with reduced number of power converters, are suggested to reduce the complexity of hybrid standalone system and achieve high performance from the available energy sources (ESs) in isolated localities.

Solar is the most abundant renewable energy source (RES) in the world. This RES is stochastic, not available at night, and it cannot dispatch power directly to the load. To ensure uninterruptible power supply to connected isolated loads, DG and storage elements, such as batteries, are required as reliable ESs. In a standalone system configuration proposed in [13], a solar photovoltaic system (SPVA) is connected to the DC bus through a DC-DC boost converter and a battery is connected directly to the DC bus without using any power converter. However, in [14], SPVA and batteries are connected to the DC bus through power converters. This configuration is costly and hard to implement in a real situation. In addition, operating many power converters, which are connected to the same DC bus using different switching frequency is challenging and can damage the batteries, and affect the system stability. In [13,14], the DC-DC boost converter and the DC-DC buck boost converter, are controlled using simple control algorithms based on a linear proportional integral (PI) controller, which is not robust and cannot perform well under large variations of the system parameters or loading conditions. To overcome these problems and achieve high performance without saturation issues, sliding mode control is proposed in [15]. The obtained simulation results showed satisfactory performance. Unfortunately, in [15] the chattering issue is not considered. To overcome this issue, terminal sliding mode control (SMC), and high-order SMC, are proposed in [16,17]. The obtained experimentally results show satisfactory performance without any chattering issues. Compared to the classical SMC proposed in [15], terminal and high-order SMCs are robust but complex and require more compilation time, which is hard to implement using simple microprocessors.

Generally, in the conventional grid, power quality issues at the point of common coupling (PCC), such as voltage sag and swell, harmonics, etc. can be solved using filters [18]. This solution is also adopted in standalone microgrid to improve the power quality at the point of common coupling (PCC).

In standalone microgrids based on SPVA and DG, the interfacing power electronic converter is mostly controlled to achieve various tasks, such as regulation of the voltage and frequency, as well as improve the power quality at PCC [19,20]. Regarding the harmonics mitigation and to balance the source current at PCC, many control strategies are proposed in the literature such as the synchronous reference frame (SRF) control strategy applied in [21], or the instantaneous p-q theory developed first by Akagi and applied to improve the power quality in standalone microgrid in [18]. In [18], direct and indirect controls are suggested. In the control strategies proposed in [18,21], the authors have used a conventional proportional integral (PI) controller to track the errors in outer and inner loops. This controller is simple but requires tuning to achieve optimal regulation, which is hard to achieve, especially if the proposed control strategy requires more than one PI controller. Furthermore, PI controllers can saturate during transition and when input signals are polluted. To solve this issue, a proportional integral based artificial neural network fuzzy interference system (PI-ANFIS) controller is proposed in [22], and in [23] an adaptive controller is suggested. These controllers are robust compared to simple PI controllers but require more computation time, which is hard to implement in real time using simple microprocessor chips. To overcome the issue of the linear PI controller, a fuzzy sliding mode controller is proposed in [24], in [25] a neural global SMC using a fuzzy approximator is employed, and in [26], an adaptive fractional fuzzy SMC, is suggested. The solutions proposed in [24,25,26], are effective but complex to implement, especially if the inner and outer loop control requires more than one controller. Sliding mode (SM)-based control is proposed in [27] for the inner loop control in order instead of the conventional PI controller to ensure a fast-time and optimal tracking control. The obtained experimental and simulation results show satisfactory performance. Unfortunately, the proposed concept is dedicated to controlling an interfacing voltage source converter, which is connected to the grid, where the frequency and voltage regulation are not achieved by the control system, and synchronization between the interfacing converter and the grid is not a big challenge. In addition, DC link voltage regulation is ensured by a PI controller, where saturation issues are not considered.

To solve these issues, which are related to the cost of energy in isolated areas, power quality and stable operation of standalone microgrids based on SPVA and DG, the following solutions are proposed:

(1)

Standalone microgrid -microgrid configurations with less power converters where SPVA and battery energy storage system are controlled using only one DC-DC buck-boost converter to connect and control the lead acid battery pack.

(2)

Using only one PI controller with anti-windup for the outer control loop for DC-link voltage regulation.

(3)

Replacing the PI controller by a SMC with boundary layer in the inner control loop for single-phase d-q control strategy, which is proposed for power quality improvement.

(4)

Developing a new control strategy based on sliding mode control for DC-DC buck boost converter where the system parameters are taken on consideration in equivalent control.

(5)

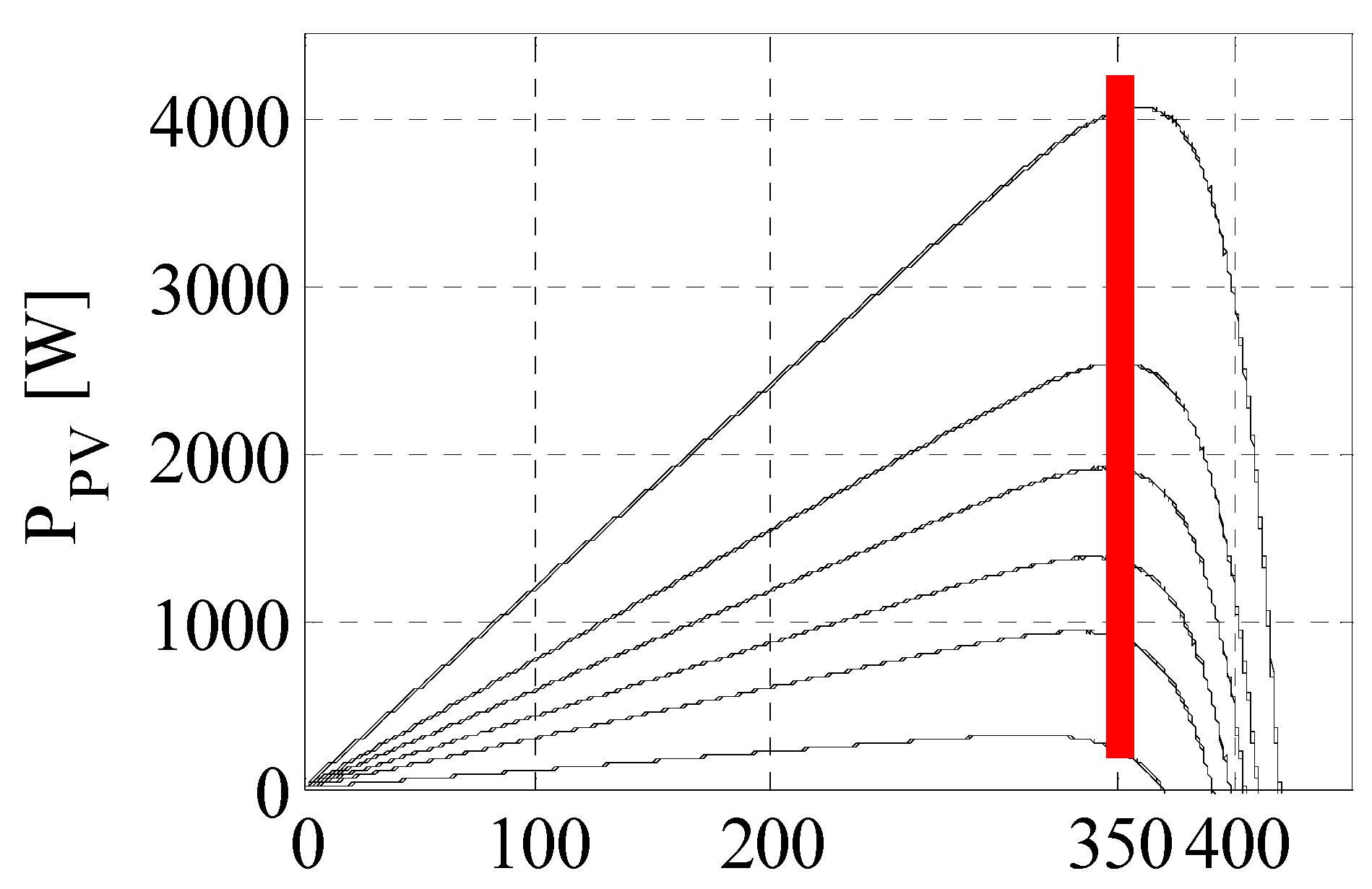
Achieving maximum power point tracking (MPPT) from SPVA by controlling only the DC link voltage.

(6)

Employing the boundary layer in SMC to reduce the chattering phenomena.

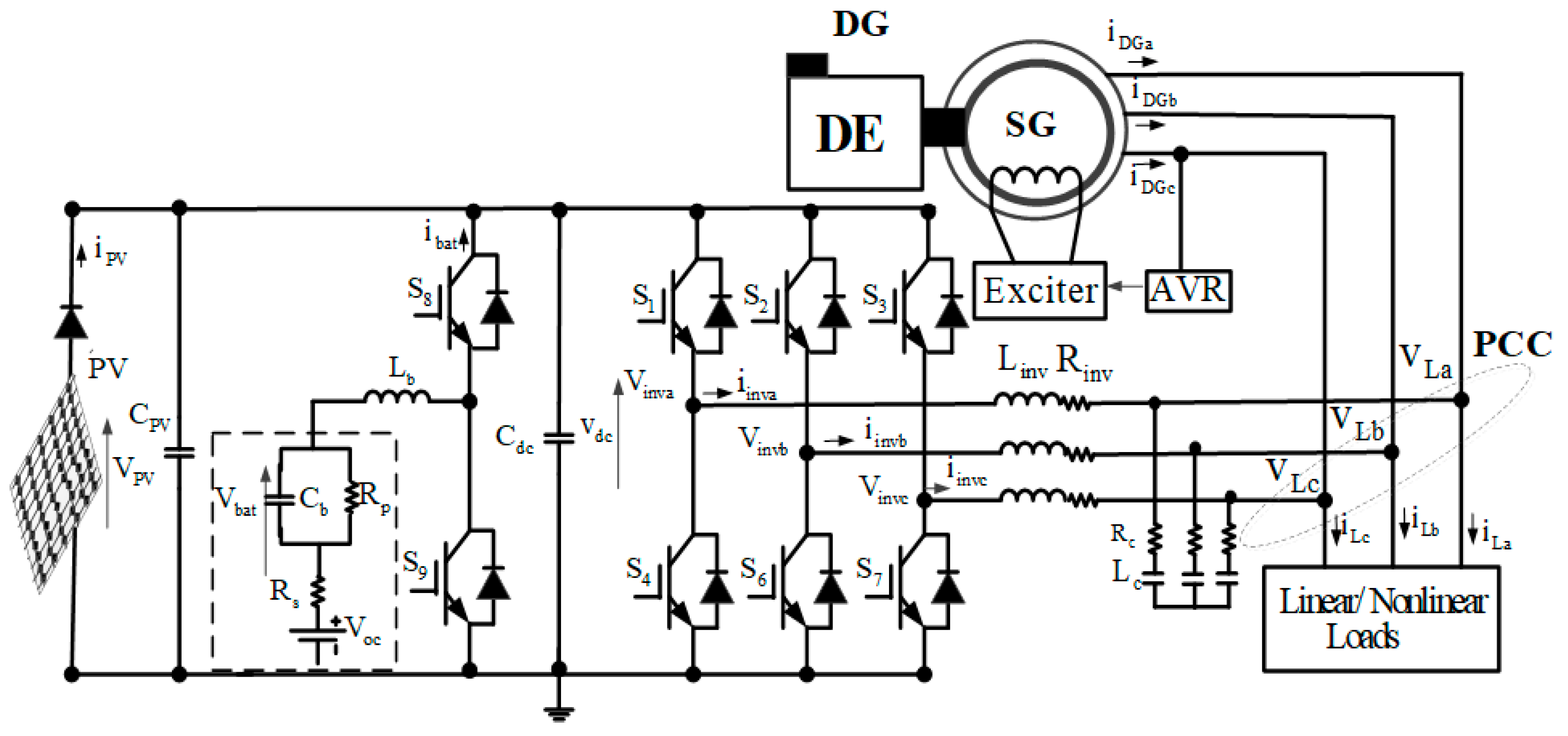
2. System Description and Operation Mode

Figure 1 shows a standalone microgrid-based configuration for remote areas. It consists of two energy sources: (1) a fixed speed diesel engine driven synchronous generator, and (2) a SPVA. The DG is connected directly to the PCC and the SPVA is connected directly to the common DC bus and to the PCC through a three-phase voltage source converter (VSC). A lead acid battery pack is connected to the common DC bus through a controller DC-DC buck boost converter. For the proposed configuration, the AC voltage and system frequency are regulated by the governor and automatic voltage regulator (AVR) of the DG. For power quality improvement at the PCC and injection of the generated power from SPVA, the VSC is controlled using a single-phase d-q theory based-sliding mode control strategy. Regarding the power balance in the system and for achieving MPPT from SPVA, an enhanced control strategy based on sliding mode control is used to control the DC-DC buck boost converter. To reduce the ripple voltage due to high switching frequency of VSC, a resistance-inductor-capacitor (RLC) passive filter is employed.

3. Control System

In this section, the developed control strategies for the DC-DC buck boost converter and for three-phase voltage source converter (VSC), are detailed.

3.1. Control of the DC-DC Buck-Boost Converter

As shown in Figure 1 the lead acid battery is connected to the common DC-link through a controlled DC-DC buck-boost converter, which consists of two continuous systems. To balance the power in the system and achieve MPPT from SPVA, sliding mode control (SMC) with boundary layer is used.

3.1.1. Modeling of the DC-DC Buck-Boost Converter

The DC-DC buck-boost converter shown in Figure 1 consists of battery voltage (V_bat) controlled switches (S₈ and S₉), inductor (L_b), output voltage (V_dc) and a capacitor (C_dc). Depending on the state of the switches, the state-space equations of the DC-DC buck boost converter when the switch is ON are written as:

$$\{\begin{array}{c}\frac{d{i}_{bat}}{dt}=\frac{V_{bat}}{L_b}\\ \frac{d{V}_{dc}}{dt}=-\frac{V_{dc}}{R{C}_{dc}}\end{array}$$

(1)

where R is load resistance, and when the switch is OFF the state-space equations are expressed as:

$$\{\begin{array}{c}\frac{d{i}_{bat}}{dt}=\frac{V_{dc}}{L_b}\\ \frac{d{V}_{dc}}{dt}=-\frac{i_{bat}}{C_{dc}}-\frac{V_{dc}}{R{C}_{dc}}\end{array}$$

(2)

Replacing, x₁ by i_bat, and x₂ by V_dc, then; $\dot{x_1}=\frac{d{i}_{bat}}{dt}$, $\dot{x_2}=\frac{d{V}_{dc}}{dt}$. The state-space equations, which are expressed in (1) and (2) are written as:

$$\{\begin{array}{l}\dot{x_1}=A_{1}x+B_{1}u\\ V_{dc}=C_{1}x\end{array}$$

(3)

where $A_1=\left[\begin{array}{cc}0& 0\\ 0& -\frac{1}{R{C}_{dc}}\end{array}\right],B_1=\left[\begin{array}{c}\frac{1}{L_b}\\ 0\end{array}\right],C_1=\left[\begin{array}{cc}0& 1\end{array}\right]$ and $u=v_{bat}$

$$\{\begin{array}{l}\dot{x_2}=A_{2}x+B_{2}u\\ V_{dc}=C_{2}x\end{array}$$

(4)

where $A_2=\left[\begin{array}{cc}0& \frac{1}{L_b}\\ -\frac{1}{C_{dc}}& -\frac{1}{R{C}_{dc}}\end{array}\right],B_1=\left[\begin{array}{c}0\\ 0\end{array}\right],C_1=\left[\begin{array}{cc}0& 1\end{array}\right]$ and $u=v_{bat}$

The average state-space equation of the DC-DC buck-boost converter is obtained using (3) and (4) as,

$$\{\begin{array}{c}\dot{x\left(t\right)}=Ax\left(t\right)+Bu\left(t\right)\\ V_{dc}=Cx\left(t\right)\end{array}$$

(5)

where $A=\left[\begin{array}{cc}0& \frac{1-d}{L_b}\\ -\frac{1-d}{C_{dc}}& -\frac{1}{R{C}_{dc}}\end{array}\right],\mathrm{B}=\left[\begin{array}{c}\frac{d}{L_b}\\ 0\end{array}\right]v_{bat},\mathrm{and}C=\left[\begin{array}{cc}0& 1\end{array}\right]$.

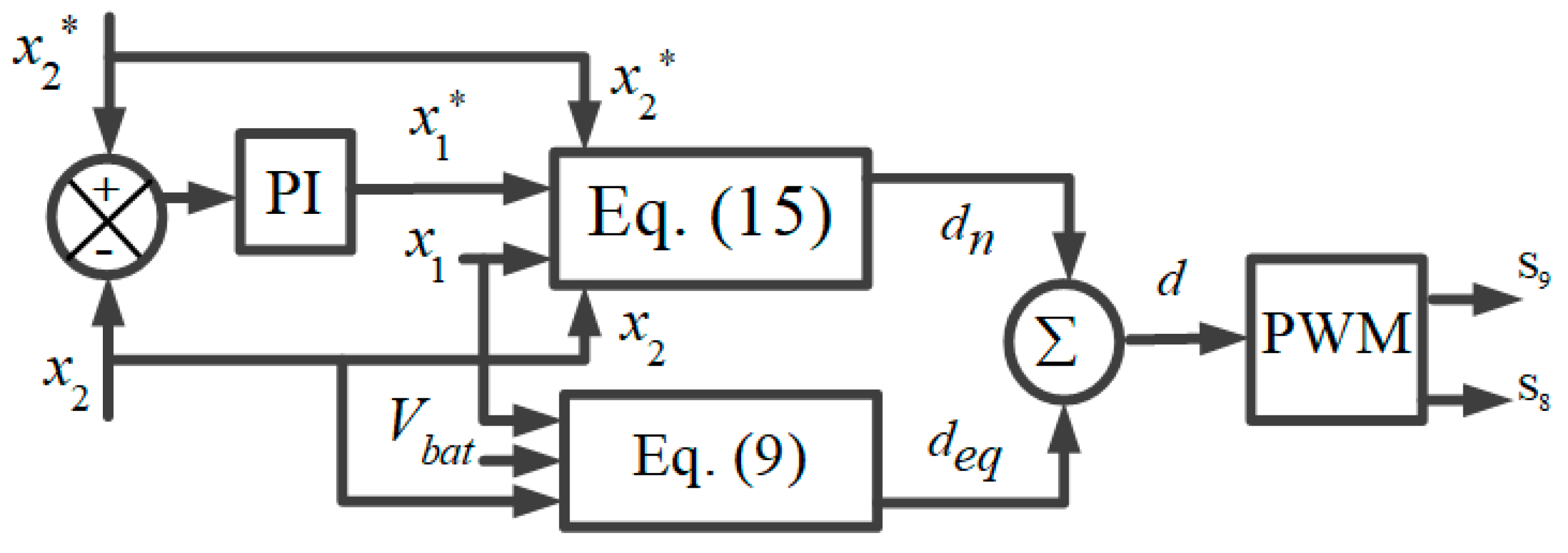
3.1.2. Sliding Mode Control for the DC-DC Buck-Boost Converter

Figure 2 shows the block diagram of the developed control strategy for the DC-DC buck boost converter. Based on (6), the model of the DC-DC buck-boost converter is nonlinear. However, for achieving high dynamic performance during transition with optimal accuracy regulation and robust trajectory tracking in presence of uncertain parameters, the SMC approach is employed. The control design of the general control (d) for the DC-DC buck boost converter is obtained using the following steps:

3.1.3. Selection of the Sliding Surface

The sliding surface (σ) as expressed in (6) is selected to ensure reaching the surface with desiring dynamics of the corresponding sliding motion [28,29,30]:

$$\sigma ={\beta }_1\left(x_1-x_1^{*}\right)+{\beta }_2\left(x_2-x_2^{*}\right)$$

(6)

where β₁ and β₂ represent the sliding gains and they should be positive.

The $x_1^{*}$ and $x_2^{*}$ denote the battery current and DC-link voltage references, respectively. The value of the DC-link voltage reference is equal to output PV voltage (V_PV), which is selected equal to 350 V. As presented in Figure 3, V_PV corresponds to the maximum extracted power from the SPVA for different solar irradiations. Therefore, by controlling the DC-link voltage, one can easily extract the maximum of power without using any MPPT method.

3.1.4. Equivalent Control

The structure of the desired control (d) is obtained as:

$$d=d_{eq}+d_n$$

(7)

where $d_n$ represents the nonlinear control and $d_{eq}$ is the equivalent control, which is obtained using (5), (6) and by setting the derivative of (6) to zero as:

$$\dot{\sigma }=0$$

(8)

By replacing $\dot{x_1}$ and $\dot{x_2}$ by their equality, one obtains the following expression as:

$$d_{eq}=\frac{x_2\left({\beta }_{1}R{C}_{dc}-{\beta }_2{L}_b\right)-{\beta }_{2}R{L}_b{x}_1}{{\beta }_{2}R{L}_b{x}_1+{\beta }_{1}R{C}_{dc}\left(x_2-V_{bat}\right)}$$

(9)

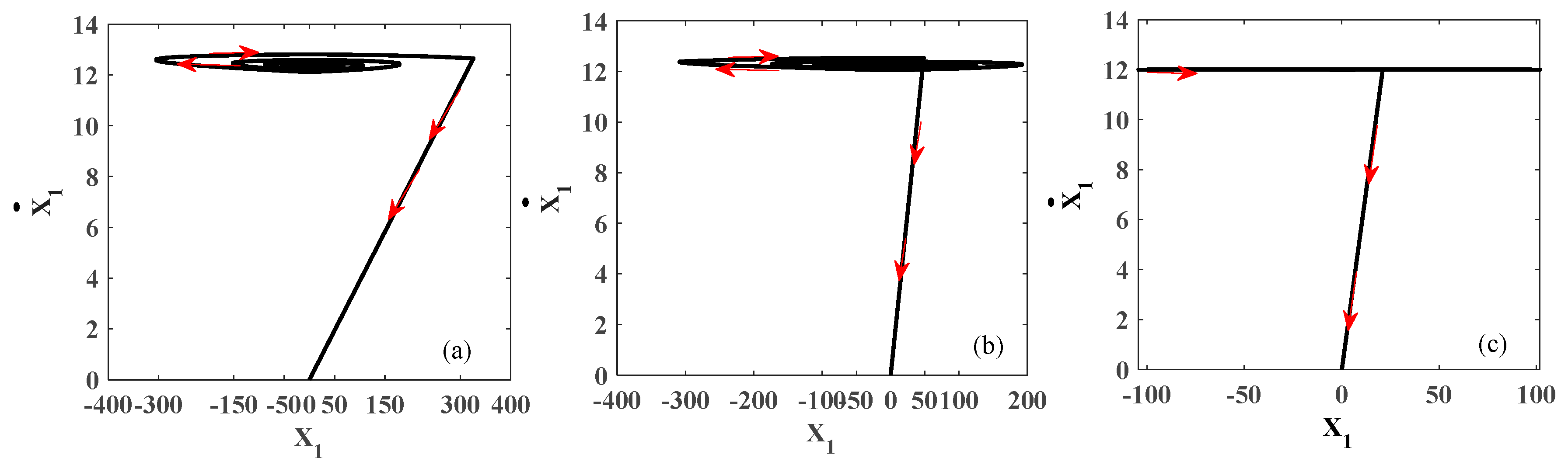
3.1.5. Stability Analysis

The objective of the approach using SMC is to ensure the convergence of the operating points to define the sliding boundary. Therefore, for assuring the stability of the control, Lyapunov stability function. According to Lyapunov theorem, a non-linear time variant system is globally and uniformly stable if satisfies the following conditions as [31,32]:

$$\{\begin{array}{c}V\left(0\right)=0\\ V\left(X\right)>0\\ \dot{V\left(X\right)}<0\\ ThenX=0isasymptoticallystable\end{array}$$

(10)

For the DC-DC buck-boost converter Lyapunov function is defined as [33,34] as:

$$V=\frac{1}{2}{\sigma }^2$$

(11)

The system is considered asymptotically stable as detailed in (10), the derivative of (11) should be negative:

$$\dot{V}=\sigma \dot{\sigma }<0$$

(12)

Replacing (6) and (8) in (12), one gets:

$$\dot{V}=\sigma \dot{\sigma }=\left({\beta }_1\left(x_1-x_1^{*}\right)+{\beta }_2\left(x_2-x_2^{*}\right)\right)\left({\beta }_1\dot{x_1}+{\beta }_2\dot{x_2}\right)<0$$

(13)

where the $x_1^{*}$ and $x_2^{*}$ denote the references of the battery current, which represents the output of the PI controller with anti-windup DC link voltage regulator, and DC-link voltage, which is equal to the 350 V, respectively

Substituting terms $\dot{x_1}$, $\dot{x_2}$, $x_1$, $x_2$, and $d$ by their equivalences in (12) gives the following expression:

$$\begin{array}{l}\dot{V}=\sigma \dot{\sigma }=-\left[\stackrel{Term1}{\overbrace{\begin{array}{c}\left(\frac{V_{dc}^2{\beta }_2^2}{R{C}_{dc}}\right)+\left(\frac{i_{bat}^2{V}_{bat}{\beta }_2{\beta }_1}{V_{dc}}\right)+\left(\frac{V_{bat}^2{\beta }_2{\beta }_1}{L_b}\right)+\left(\frac{V_{bat}{\beta }_2{\beta }_1}{L_b}{x}_2^{*}\right)\\ +\left(\frac{V_{dc}{i}_{bat}{\beta }_2{\beta }_1}{R{C}_{dc}}\right)+\left(V_{dc}{i}_{bat}{\beta }_2^2{x}_1^{*}\right)\end{array}}}\right]\\ +\left[\stackrel{Term2}{\overbrace{\begin{array}{c}\left(\frac{V_{dc}^2{\beta }_1}{L_b}\right)+\left(V_{bat}{\beta }_1^2{i}_{bat}\right)+\left(\frac{V_{dc}{\beta }_2}{R{C}_{dc}}\right)+\left(\frac{V_{dc}{\beta }_2{\beta }_1}{R{C}_{dc}}{x}_1^{*}\right)+\left(\frac{V_{bat}{V}_{dc}{\beta }_2{\beta }_1}{L_b}\right)\\ +\left(\frac{V_{bat}{\beta }_1^2{i}_{bat}}{L_b}\right)+\left(\frac{V_{bat}{\beta }_1^2{i}_{bat}}{C_{dc}{V}_{dc}}{x}_2^{*}\right)+\left(\frac{i_{bat}{V}_{bat}{\beta }_2{\beta }_1}{C_{dc}{V}_{dc}}{x}_1^{*}\right)\end{array}}}\right]<0\end{array}$$

(14)

Replacing the parameters $L_b$, $C_{dc}$, $V_{bat}$, $V_{dc}$, as well as the optimal gains of the SMC ${\beta }_1$ and ${\beta }_2$ by their value given in

Table 1. System parameters.

Parameters	Value	Parameters	Value
$v_{DG}$	208 V	$k_1$, $k_{i1}$,	0.1, 25
$f_r$	60 Hz	$F_{sw}$ VSC	10 kHz
$V_{dc}^{*}$	350 V	$C_{dc}$	1000 µF
$C_{PV}$	100 µF	$L_{inv}$	5 mH
$L_b$	1.5 mH	$R_{inv}$	0.01 Ω
$F_{sw}$ DC-DC Converter	10 kHz	$R_c$	5 Ω
${\beta }_1,{\beta }_2 \mathrm{and} {\beta }_3$	0.001, 0.8 and 5	$C_c$	10 µF

, the first term with negative sign in (14) is larger than the second term. This leads that condition given in (13) is satisfied, which confirms that the system is asymptotically stable.

To ensure the robustness, the second of the desired control $d_n$, which represents the discontinuous control is written as [35,36,37]:

$$d_n={\beta }_{3}sat\left(\sigma ,\varnothing \right)$$

(15)

where ${\beta }_3$ is positive control gain.

To reduce the chattering of the control signal, saturation function with boundary conditions is defined as:

$$sat\left(\sigma ,\varnothing \right)\{\begin{array}{cc}1& \sigma >\varnothing \\ \frac{\sigma }{\varnothing }& \left|\sigma \right|\le \varnothing \\ -1& \sigma <-\varnothing \end{array}$$

(16)

where $\varnothing$ denotes the sliding layer, which is selected between 0.5 and −0.5 [11].

The optimal gains (${\beta }_1,{\beta }_2\mathrm{and}{\beta }_3$) of the SMC, are selected equal to ${\beta }_1=0.001, {\beta }_2=0.8$, and ${\beta }_3=5$, respectively. One observes in Figure 4c, that based on the optimal values of ${\beta }_1,{\beta }_2\mathrm{and}{\beta }_3$ the signal reaches the origin rapidly.

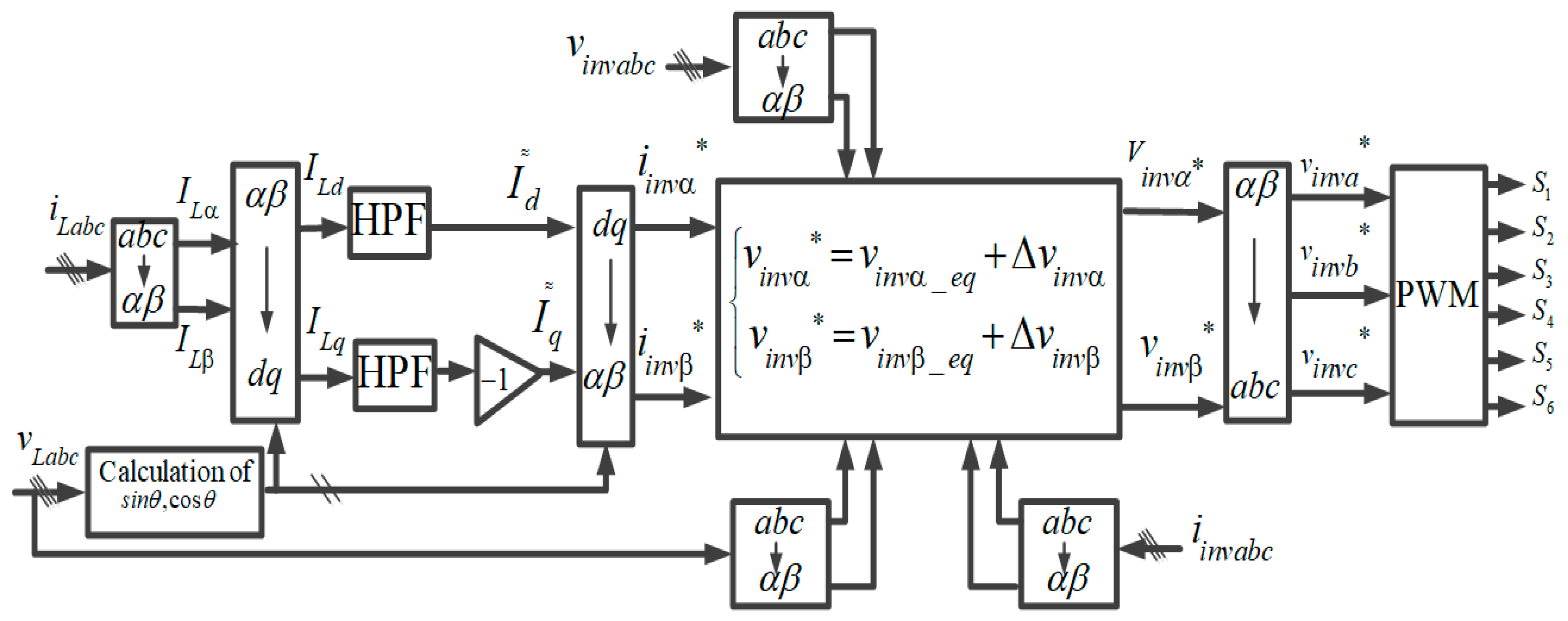
3.2. Control of Three-Phase Voltage Source Converter

In Figure 5 the single-phase d-q theory-based sliding mode controller for VSC to improve the power quality and inject the generated power from the solar photovoltaic system into PCC, is presented. Regarding the DC link voltage regulation, is ensured by controlling the DC-DC buck boost converter. Inverter voltage ($v_{invabc}$) and current ($i_{invabc}$), load current ($i_{Labc}$) and voltage$(v_{Labc}),$ are used to determine the inverter voltage references ($v_{invabc}^{*}$). The d-q rotating frame and (α-β) stationary frame are employed to transform all time-varying signals to DC quantities with time-invariant.

The rotating angle of d-q frame is calculated using the in-phase and quadrature united vectors as in [18]. The amplitude of the PCC voltage (V_p) is calculated as:

$$V_p=\sqrt{\frac{2}{3}\left(\left(v_{La}^2+v_{Lb}^2+v_{Lc}^2\right)\right)}$$

(17)

The in-phase unit templates of the PCC voltage, are calaculted as follows:

$$u_{pa}=\frac{v_{La}}{V_p},u_{pb}=\frac{v_{Lb}}{V_p},u_{pc}=\frac{v_{Lc}}{V_p}$$

(18)

and the quadrature unit templates of the PCC voltages are expreesed as:

$$u_{qa}=-\frac{u_{pa}}{\sqrt{3}}+\frac{u_{pc}}{\sqrt{3}},u_{qb}=\sqrt{3}\frac{u_{pa}}{2}+\frac{\left(u_{pb-}{u}_{pc}\right)}{2\sqrt{3}},u_{qc}=-\sqrt{3}\frac{u_{pa}}{2}+\frac{\left(u_{pb-}{u}_{pc}\right)}{2\sqrt{3}}$$

(19)

The cosθ and sinθ, are defined as:

$$\{\begin{array}{c}sin\theta =u_{pa}\\ cos\theta =u_{qa}\end{array}$$

(20)

The obtained dq-axis load current consist of the fundamentals ($\overline{I_d},\overline{I_q}$) and harmonics components ($\widetilde{I_q},\widetilde{I_d}$):

$$\{\begin{array}{c}{I}_{Ld}=\overline{I_d}+\widetilde{I_d}\\ I_{Lq}=\overline{I_q}+\widetilde{I_q}\end{array}$$

(21)

Regarding the harmonics ($\widetilde{I_q},\widetilde{I_d}$), which are extracted using high pass filter (HPF) represent the output inverter currents, they are transformed into the (α-β) stationary frame., and are used after to determine the reference inverter voltages.

3.2.1. Sliding Mode Current Controller

A sliding mode current controller (SMCC) is proposed for the inner current control loop to achieve high performance during transition with a fast-dynamic response. To design the controller, the following steps are used.

3.2.2. Selecting the Switching Surface

Switching surface for SMCC ${\sigma }_1={\left[\begin{array}{cc}{\sigma }_{\alpha }& {\sigma }_{\beta }\end{array}\right]}^T$ is selected to ensure fast dynamic response during transition with zero steady-state [38]:

$$\{\begin{array}{c}{\sigma }_{\alpha }=k_1{e}_{\alpha }\left(t\right)+k_{i1}\underset{0}{\overset{t}{{\displaystyle \int }}}{e}_{\alpha }\left(i_{inv\alpha }\right)dt\\ {\sigma }_{\beta }=k_1{e}_{\beta }\left(t\right)+k_{i1}\underset{0}{\overset{t}{{\displaystyle \int }}}{e}_{\beta }\left(i_{inv\beta }\right)dt\end{array}$$

(22)

where $k_1$, and $k_{i1}$ are positive gains. The $e_{\alpha }$, $e_{\beta }$ represent the obtained errors between measured and reference output VSC currents, which are defined as:

$$\{\begin{array}{c}{e}_{\alpha }=\left(i_{inv\alpha }^{*}-i_{inv\alpha }\right)\\ e_{\beta }=\left(i_{inv\beta }^{*}-i_{inv\beta }\right)\end{array}$$

(23)

Applying the Kirchhoff current and voltage law at the output of the VSC, one obtains the following expression in stationary (α-β) frame:

$$\{\begin{array}{c}\dot{i_{inv\alpha }}=\frac{1}{L_{inv}}\left(v_{inv\alpha }-v_{L\alpha }\right)-\frac{R_{inv}}{L_{inv}}{i}_{inv\alpha }\\ \dot{i_{inv\beta }}=\frac{1}{L_{inv}}\left(v_{inv\beta }-v_{L\beta }\right)-\frac{R_{inv}}{L_{inv}}{i}_{inv\beta }\end{array}$$

(24)

where $L_{inv}$ and $R_{inv}$ denote the inductor and resistor of the output filter of VSC.

Using (24), (22) and (23) and its derivative, one obtains the following expression:

$$\{\begin{array}{c}\dot{{\sigma }_{\alpha }}=k_1\left(\dot{i_{inv\alpha }^{*}}-\left(\frac{1}{L_{inv}}\left(v_{inv\alpha }-v_{L\alpha }\right)-\frac{R_{inv}}{L_{inv}}{i}_{inv\alpha }\right)\right)+k_{i1}{e}_{\alpha }\\ \dot{{\sigma }_{\beta }}=k_1\left(\dot{i_{inv\beta }^{*}}-\left(\frac{1}{L_{inv}}\left(v_{inv\beta }-v_{L\beta }\right)-\frac{R_{inv}}{L_{inv}}{i}_{inv\beta }\right)\right)+k_{i1}{e}_{\beta }\end{array}$$

(25)

The structure of the desired control ($v_{inv\alpha }^{*}$, and $v_{inv\beta }^{*}$), are expressed as:

$$\{\begin{array}{c}{v}_{inv\alpha }^{*}=v_{inv\alpha \_eq}+\Delta v_{inv\alpha }\\ v_{inv\beta }^{*}=v_{inv\beta \_eq}+\Delta v_{inv\beta }\end{array}$$

(26)

where $v_{inv\alpha \_eq}$, $v_{inv\beta \_eq}$, $\Delta v_{inv\alpha }$, and $\Delta v_{inv\beta }$ represent the equivalent controls and nonlinear control in the stationary (α-β) frame.

Regarding, the equivalent controls are obtained by set the sliding switching $\dot{{\sigma }_1}={\left[\begin{array}{cc}\dot{{\sigma }_{\alpha }}& \dot{{\sigma }_{\beta }}\end{array}\right]}^T$ equal to zero:

$$\{\begin{array}{c}\dot{{\sigma }_{\alpha }}=k_1\left(\dot{i_{inv\alpha }^{*}}-\left(\frac{1}{L_{inv}}\left(v_{inv\alpha \_eq}-v_{L\alpha }\right)-\frac{R_{inv}}{L_{inv}}{i}_{inv\alpha }\right)\right)+k_{i1}{e}_{\alpha }=0\\ \dot{{\sigma }_{\beta }}=k_1\left(\dot{i_{inv\beta }^{*}}-\left(\frac{1}{L_{inv}}\left(v_{inv\beta \_eq}-v_{L\beta }\right)-\frac{R_{inv}}{L_{inv}}{i}_{inv\beta }\right)\right)+k_{i1}{e}_{\beta }=0\end{array}$$

(27)

From (25), one obtains the equivalent controls stationary (α-β) frame:

$$\{\begin{array}{c}{v}_{inv\alpha \_eq}=\frac{k_{i1}}{k_1}{L}_{inv}{e}_{\alpha }+v_{L\alpha }+R_{inv}{i}_{inv\alpha }+L_{inv}\dot{i_{inv\alpha }^{*}}\\ v_{inv\beta \_eq}=\frac{k_{i1}}{k_1}{L}_{inv}{e}_{\beta }+v_{L\alpha }+R_{inv}{i}_{inv\beta }+L_{inv}\dot{i_{inv\beta }^{*}}\end{array}$$

(28)

The nonlinear control is selected equal to:

$$\{\begin{array}{c}\Delta v_{inv\alpha }=K_{2}Sat\left({\sigma }_{\alpha }\right)\\ \Delta v_{inv\beta }=K_{2}Sat\left({\sigma }_{\beta }\right)\end{array}$$

(29)

where $K_2$ represents the controller gain and is positive.

3.2.3. Stability Analysis

The system is considered globally stable only if the derivative of (10) is negative. Using (26) and (22), one gets the following expression:

$$\{\begin{array}{c}\dot{{\sigma }_{\alpha }{\sigma }_{\alpha }}=\left(k_1\left(\dot{i_{inv\alpha }^{*}}-\left(\frac{1}{L_{inv}}\left(v_{inv\alpha }-v_{L\alpha }\right)-\frac{R_{inv}}{L_{inv}}{i}_{inv\alpha }\right)\right)+k_{i1}{e}_{\alpha }\right)\left(k_1{e}_{\alpha }\left(t\right)+k_{i1}\underset{0}{\overset{t}{{\displaystyle \int }}}{e}_{\alpha }\left(i_{inv\alpha }\right)dt\right)<0\\ {\sigma }_{\beta }\dot{{\sigma }_{\beta }}=\left(k_1\left(\dot{i_{inv\beta }^{*}}-\left(\frac{1}{L_{inv}}\left(v_{inv\beta }-v_{L\beta }\right)-\frac{R_{inv}}{L_{inv}}{i}_{inv\beta }\right)\right)+k_{i1}{e}_{\beta }\right)\left(k_1{e}_{\beta }\left(t\right)+k_{i1}\underset{0}{\overset{t}{{\displaystyle \int }}}{e}_{\beta }\left(i_{inv\beta }\right)dt\right) <0\end{array}$$

(30)

Equation (28) can be written as:

$$\{\begin{array}{c}\dot{{\sigma }_{\alpha }{\sigma }_{\alpha }}=\left(\left(\stackrel{term1}{\overbrace{\dot{k_1{i}_{inv\alpha }^{*}}}}\stackrel{term2}{\overbrace{-\frac{k_1{v}_{inv\alpha }}{L_{inv}}+\frac{k_1{v}_{L\alpha }}{L_{inv}}}}+\stackrel{Term3}{\overbrace{k_{i1}{i}_{inv\alpha }^{*}}}\stackrel{term4}{\overbrace{-\frac{R_{inv}}{L_{inv}}{i}_{inv\alpha }-k_{i1}{i}_{inv\alpha }}}\right)\right)\left(\stackrel{term5}{\overbrace{k_1{e}_{\alpha }\left(t\right)}}+\stackrel{term6}{\overbrace{k_{i1}\underset{0}{\overset{t}{{\displaystyle \int }}}{e}_{\alpha }\left(i_{inv\alpha }\right)dt}}\right)<0\\ \dot{{\sigma }_{\beta }{\sigma }_{\beta }}=\left(\left(\stackrel{term1}{\overbrace{\dot{k_1{i}_{inv\beta }^{*}}}}\stackrel{term2}{\overbrace{-\frac{k_1{v}_{inv\beta }}{L_{inv}}+\frac{k_1{v}_{L\beta }}{L_{inv}}}}+\stackrel{Term3}{\overbrace{k_{i1}{i}_{inv\beta }^{*}}}\stackrel{term4}{\overbrace{-\frac{R_{inv}}{L_{inv}}{i}_{inv\beta }-k_{i1}{i}_{inv\beta }}}\right)\right)\left(\stackrel{term5}{\overbrace{k_1{e}_{\beta }\left(t\right)}}+\stackrel{term6}{\overbrace{k_{i1}\underset{0}{\overset{t}{{\displaystyle \int }}}{e}_{\beta }\left(i_{inv\beta }\right)dt}}\right)<0\end{array}$$

(31)

To determine the sign of (31), one determines first the sign of each term independently. Considering the first term ($k_1\dot{i_{inv\alpha }^{*}}$), which represents the derivative of the reference inverter current, is equal to zero and regarding, that DG ensures the regulation of the voltage at PCC, one assumes that the PCC voltage and the voltage at the output of the VSC are equal, which leads that the second term ($-\frac{k_1{v}_{inv\alpha }}{L_{inv}}+\frac{k_1{v}_{L\alpha }}{L_{inv}}$) being equal to zero, and $k_{i1}{i}_{inv\alpha }^{*}\ll -\frac{R_{inv}}{L_{inv}}{i}_{inv\alpha }-k_{i1}{i}_{inv\alpha }$. As known the integral is always positive, so the sign of the sixth term ($k_{i1}{{\displaystyle \int }}_0^t{e}_{\alpha }\left(i_{inv\alpha }\right)dt$) is positive. The error between the inverter current and its reference is smaller, so, the fifth term ($k_1{e}_{\alpha }\left(t\right)$) is smaller than the sixth term. Based on this analysis, one concludes that the sign of $\dot{{\sigma }_{\alpha }{\sigma }_{\alpha }}$ is always negative, which implies that the system is asymptotically stable.

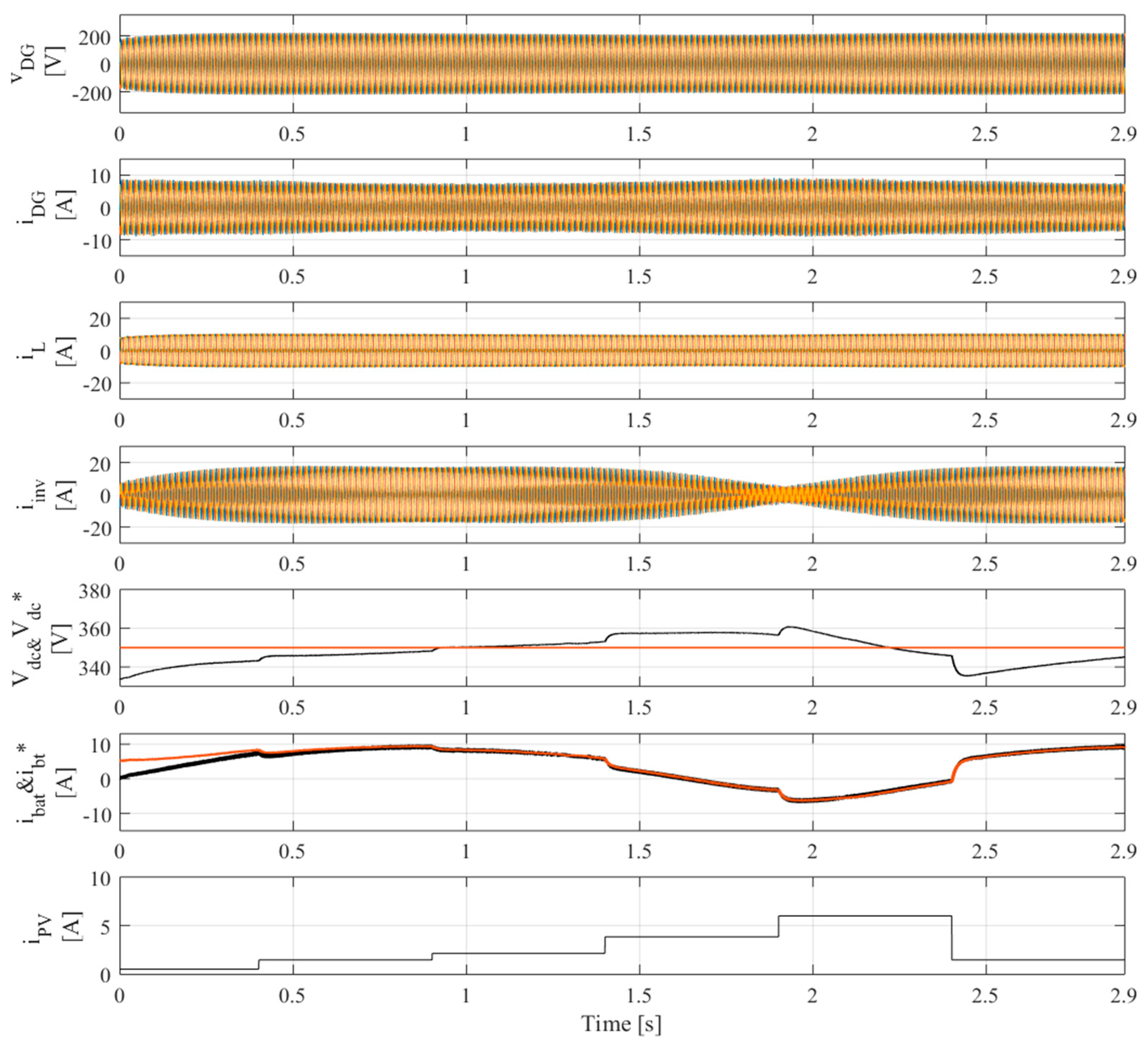
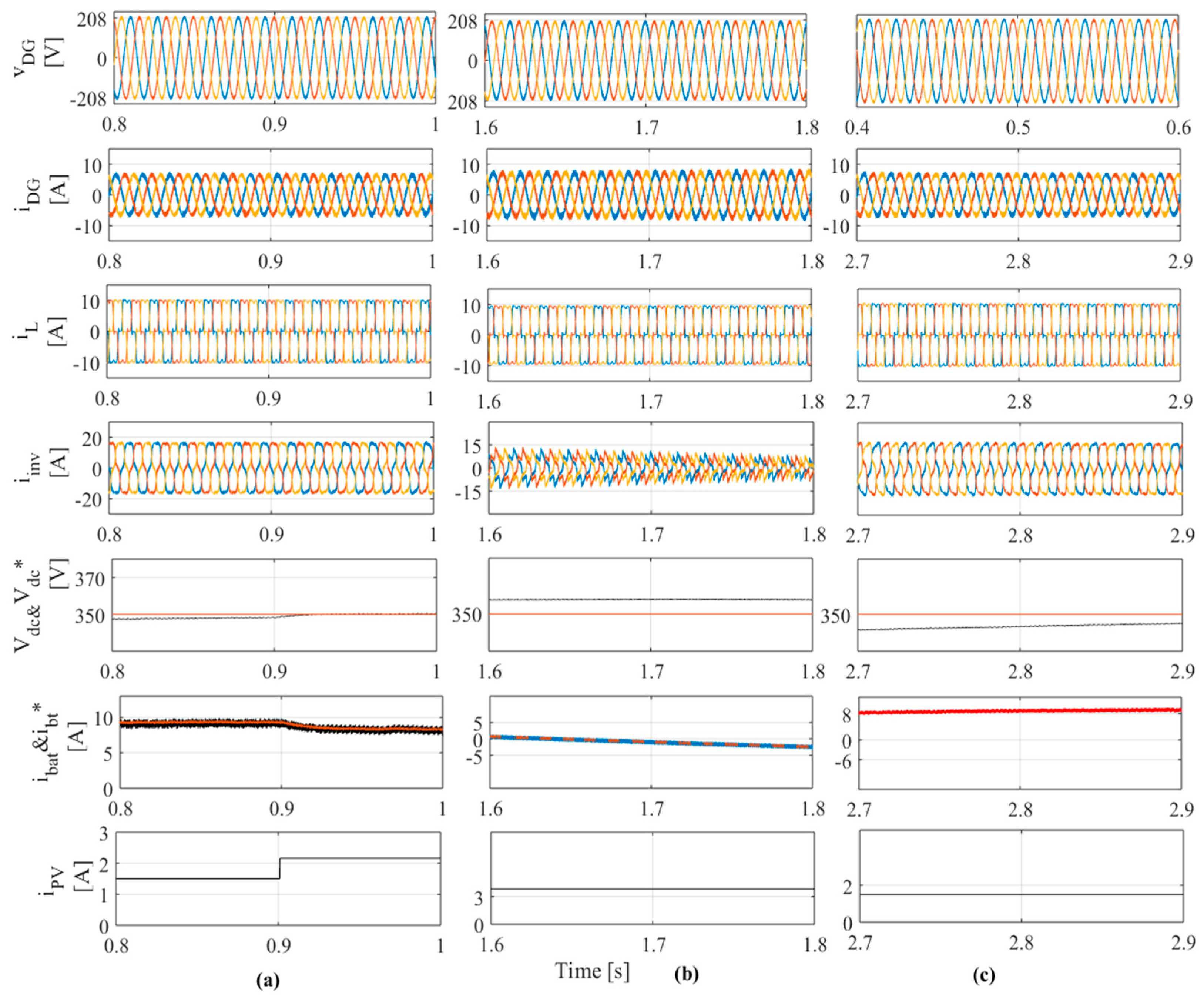
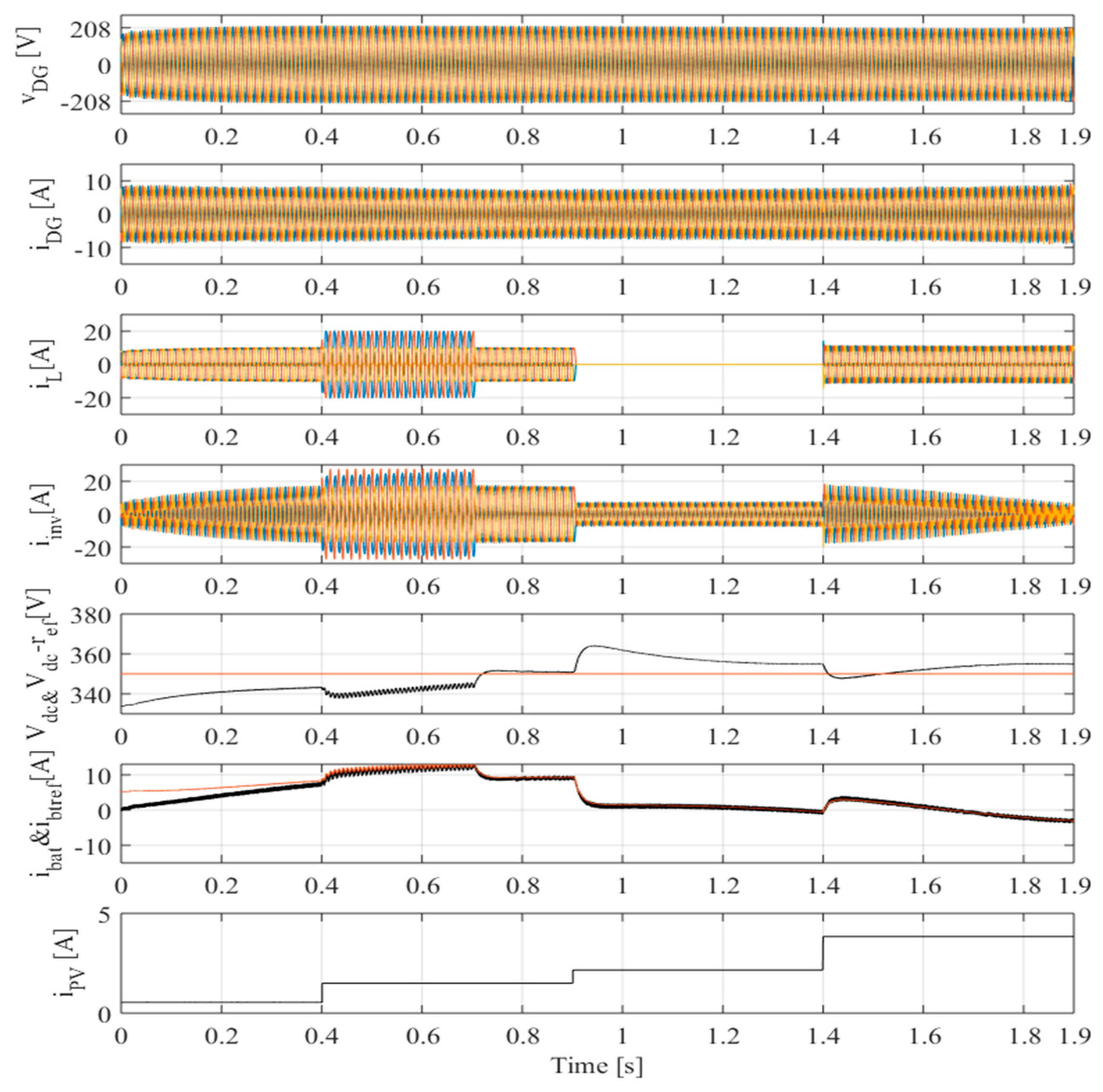
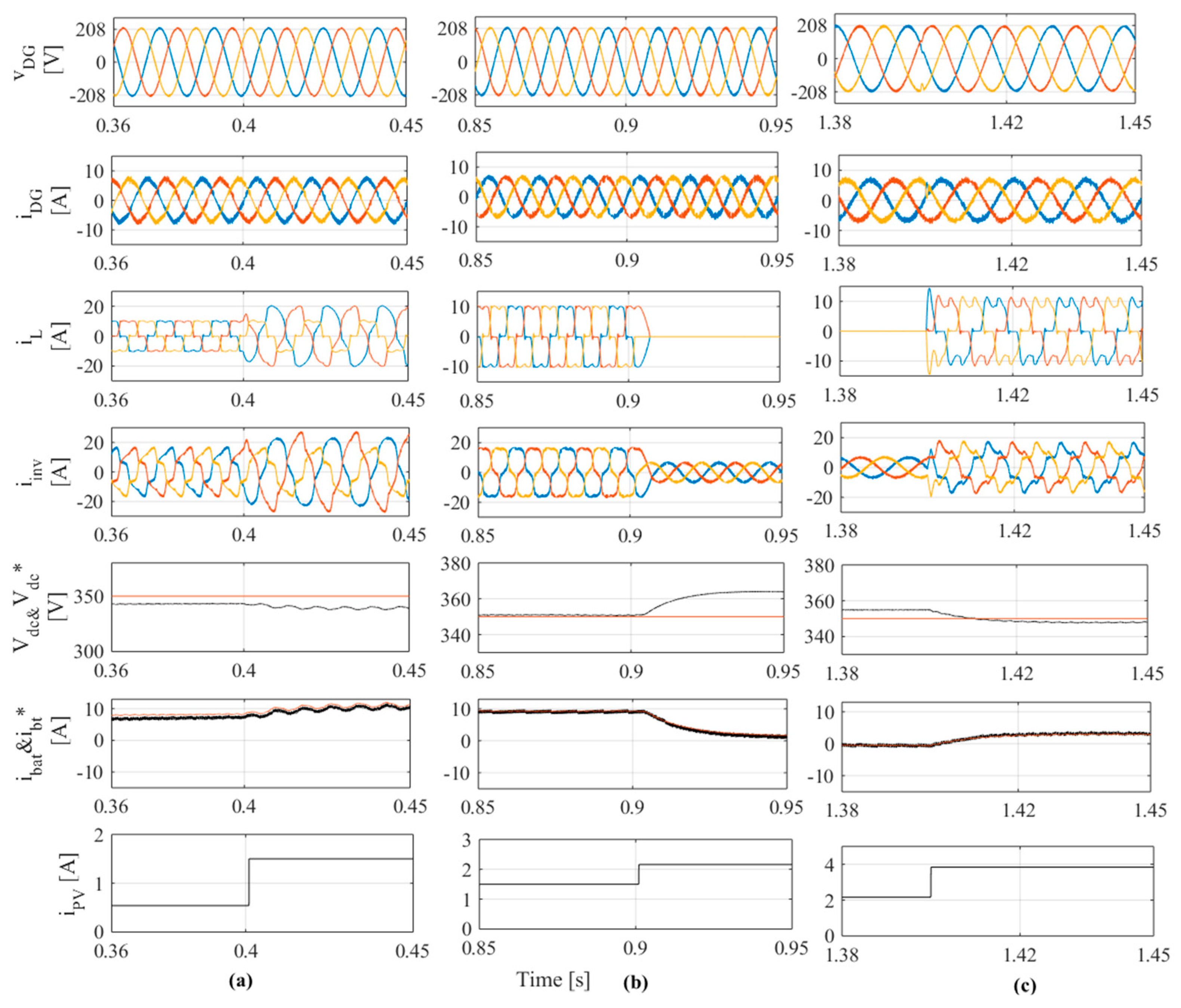
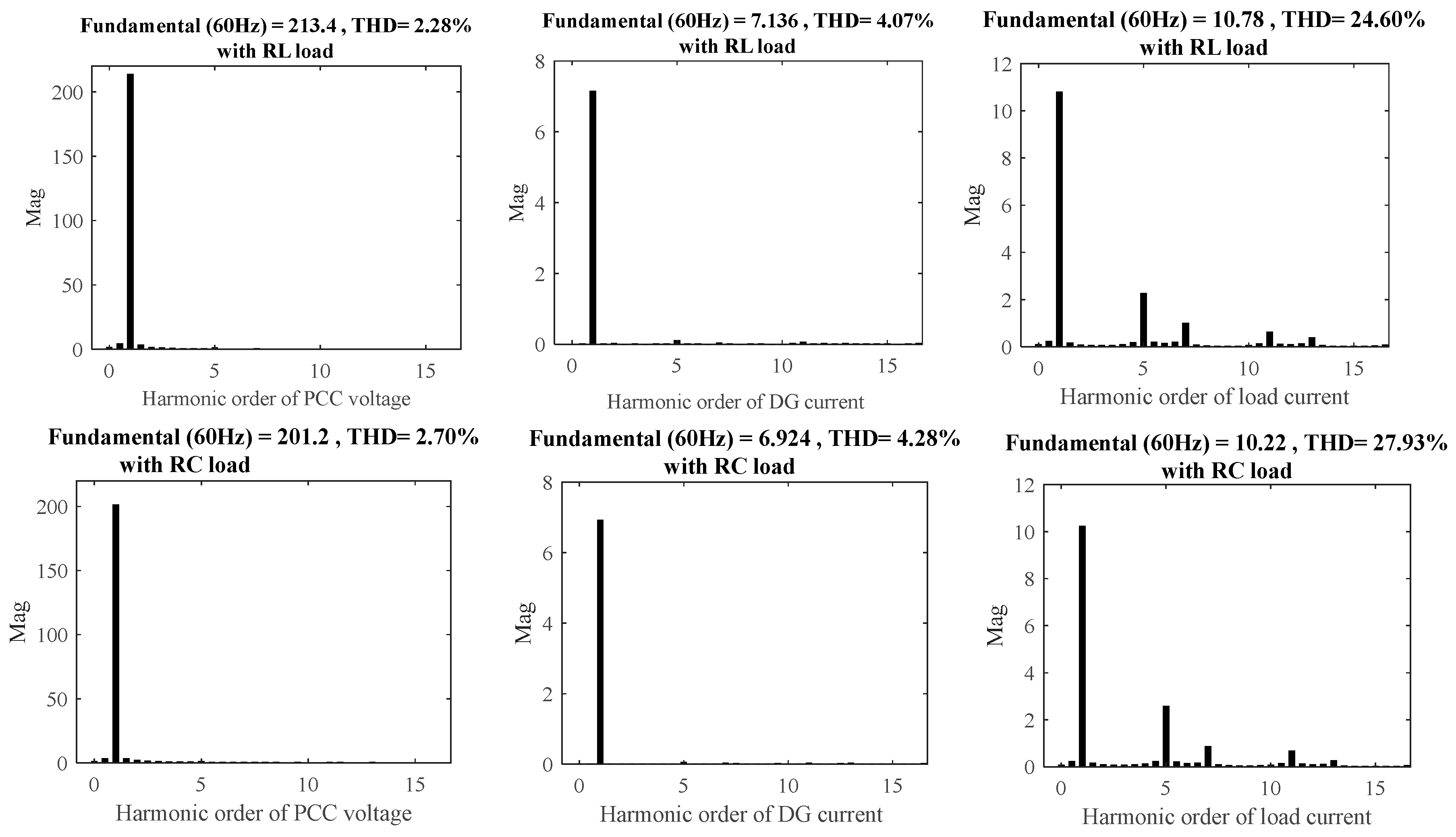
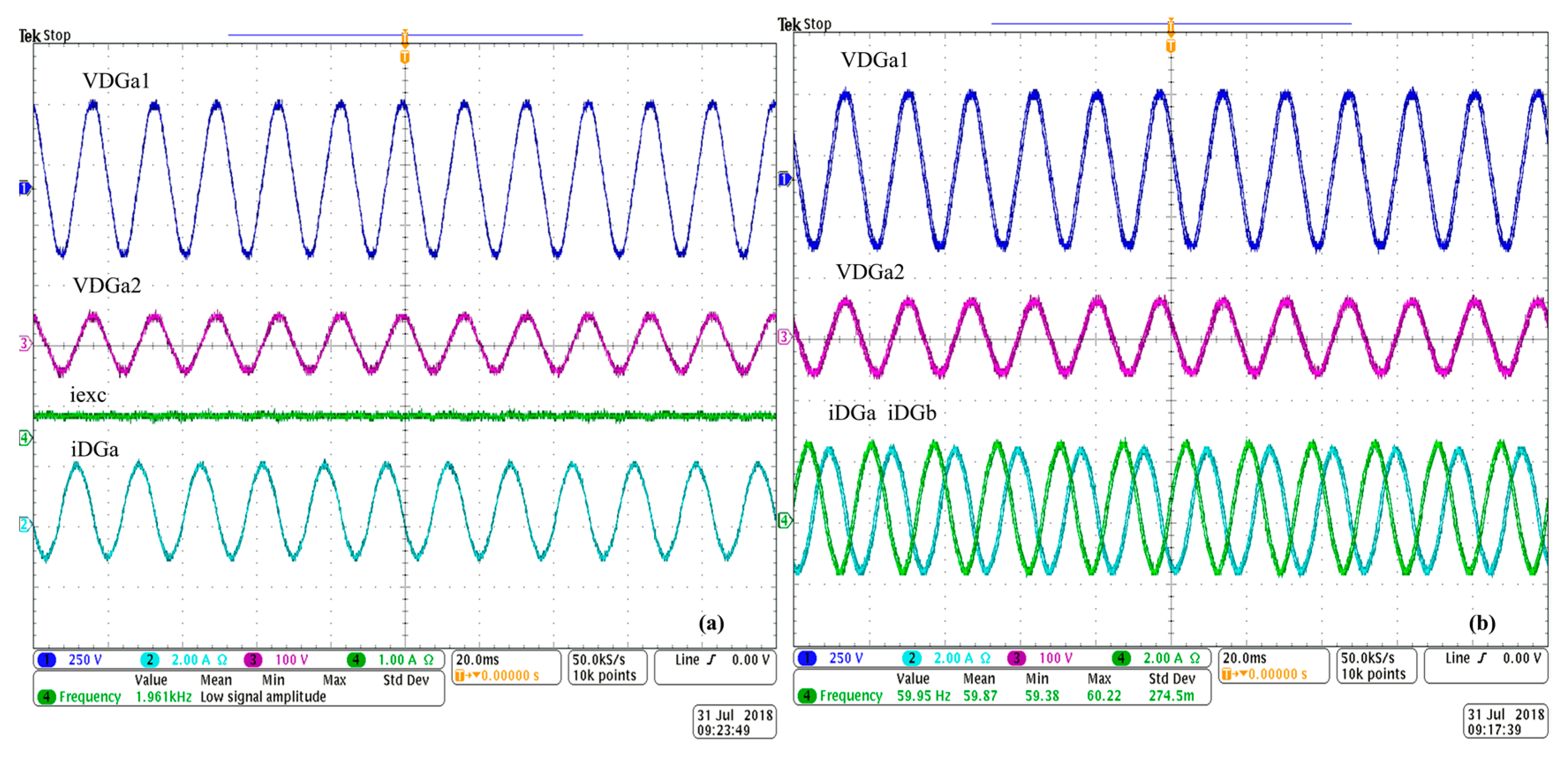
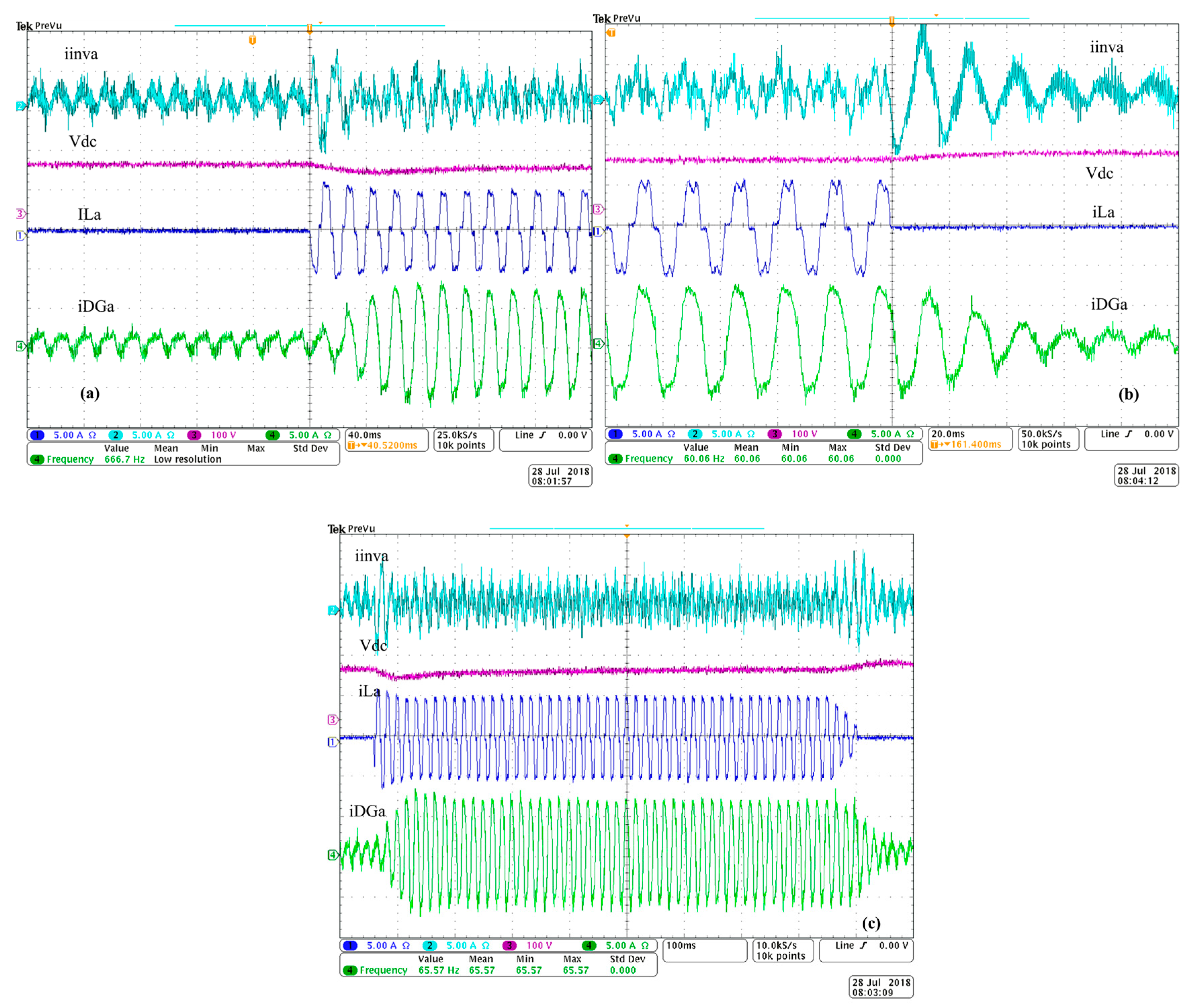
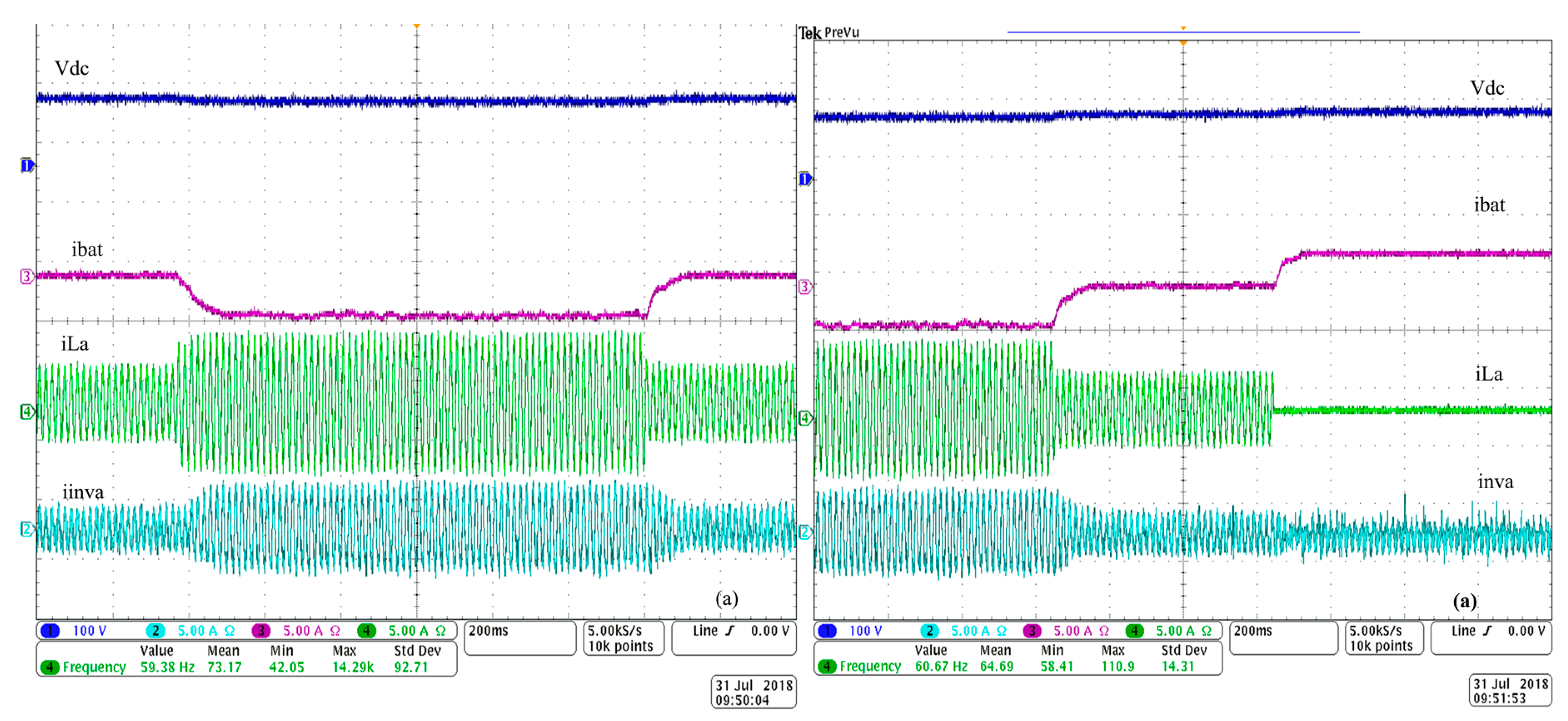
4. Results and Discussion

The performance of the developed control strategies for the VSC and DC-DC buck-boost converter, was tested through a simulation using MATLAB/Simulink and in real-time using a hardware prototype. In Figure 6 the hardware prototype of a standalone microgrid is presented. It consists of: (1) ABB drive, (2) synchronizer of DG, (3) induction motor, (4) synchronous generator, (5) SPVA simulator, (6) loads, (7) Protections cards, dSPACE and SEMIKRON power converter, (8) sensors, (9) step down transformer, (10) RC passive filter, and (11) lead acid battery pack.

In Figure 7 the dynamic performances of the terminal voltage ($v_{DG}$) and current $i_{DG}$ of synchronous generator, load current $i_L$, inverter current ($i_{inv}$), DC-link voltage ($V_{dc}$) and its reference ($v_{dc}^{*}$), battery current ($v_{DG}$) and its reference ($v_{DG}$), and output SPVA current ($I_{PV}$) are shown. The zoomed waveforms presented in Figure 6 are shown in Figure 8. It is observed that the AC voltage at the PCC and the frequency are regulated at their rated values, which confirms that the governor and the automatic voltage regulator of the DG are working well. One can see clearly in the zoomed waveforms presented in Figure 8a–c, that the DG currents are balanced and sinusoidal, which confirms that the single-phase d-q control-based sliding mode controller performs well in the presence of balanced nonlinear loads. One observes that the DC-link voltage and battery current follow their references during solar irradiation changes, which confirms the robustness of the developed control strategy-based sliding mode control with boundary layer. One observes from the obtained results shown in Figure 8a–c that during transitions when solar irradiation changes the battery current follows its reference, which represents the output of the DC-link voltage regulator without saturation and with zero steady state error. The output SPVA current, which represents the maximum of SPVA current and DC-link voltage varies with variation of solar irradiation as shown in Figure 3, which confirms that it is possible to achieve MPPT without using any MPPT method.

In Figure 9 and Figure 10, the waveforms and the zoomed of terminal voltage ($v_{DG}$) and current $i_{DG}$ of synchronous generator, load current $i_L$, inverter current ($i_{inv}$), DC-link voltage ($V_{dc}$) and its reference ($v_{dc}^{*}$), battery current ($v_{DG}$) and its reference ($v_{DG}$), and output SPVA current ($I_{PV}$), are presented. To test the performance of the developed control strategies, the system is subjected to severe conditions, such as the presence of balanced and unbalanced nonlinear RL and RC load types as well as during solar irradiation changes. It is observed that in the presence of different loads, the DG current is balanced and sinusoidal.

In addition, DC-DC buck boost can extract the maximum of power from the SPVA and balance the power in the system by charging and discharging the battery, which confirms the robustness of the proposed control strategies based on sliding mode control for the standalone microgrid system. In Figure 11 the harmonics spectrum of the PCC voltage, DG current, and load currents when RL and RC nonlinear load, are presented. It is observed that in the both cases the total harmonic distortion (THD) of the load current is high (THD = 24% with RL nonlinear and 27% with RC nonlinear load), and the THD of the source current, which represents in the standalone microgrid shown in Figure 1, the output current of the DG is less than 5% (THD = 4.07% with RL nonlinear and 4.28% with RC nonlinear load). This respects the norms of IEEE standard 519-1992. One sees clearly that the THD of the PCC voltage is less than to 5% in the presence of the both nonlinear loads, which confirms the robustness of the proposed Single-phased d-q theory-based on SMC for power quality improvement.

In Figure 12a,b, the steady-state performance of the DG is presented. One observes that the terminal voltage before step down transformer ($v_{DGa1}$) and at the secondary of transformer $v_{DGa2}$ are regulated constant and sinusoidal. Seeing that DG operates at fixed speed, excitation current ($i_{exc}$) is constant, one can observe that the system frequency is constant, and the stator current are sinusoidal.

To test the performance of the developed control strategies-based sliding mode control, the system is subjected to load variations as presented in Figure 13a–c. It is observed in Figure 13a that at t = 0.2 ms the system is subjected to a sudden variation of nonlinear load type RL. One observes that VSC operates as a shunt active filter, and it compensates the harmonics and balances the DG current. One observes that the DC-link voltage is well regulated. In Figure 13b, the system is subjected to sudden switching off the nonlinear load type RC at t = 0.2 ms. It is observed that the VSC acts as a shunt filter and compensates the harmonics as well as balances the DG current. One sees that DC-link voltage is increased when the load is switched off, because the battery starts charging. In Figure 13c, the system is subjected to sudden switching on and off at t = 0.1 ms and at t = 1 s, and one observes that the DC-link voltage is well regulated and the VSC acts as a shunt active filter and injects the power into the PCC. One sees clearly in Figure 13a–c, that the both developed control strategies perform well in the presence of severe conditions.

The performance of DC-link voltage ($V_{dc}$), battery current ($i_{bat}$), load current ($i_{La}$) and inverter current ($i_{inva}$), are presented in Figure 14a,b. It is observed that the DC-link voltage is regulated at their rated value when the system is subjected to load variations at t = 0.4 s and t = 0.8 s in Figure 14a, and at t = 0.3 s, and t = 0.8 s in Figure 14b. One observes that the battery current varies with load variation, balancing the power in the system. This leads that the system performing well during all conditions, which confirms the robustness of the developed control strategy-based sliding mode control.

5. Conclusions

In this paper, a real-time implementation of robust control strategies based on sliding mode control for a standalone microgrid has been presented. Single-phase d-q theory based on sliding mode controller for fast inner control loop for three-phase voltage source converter was studied and analyzed. Furthermore, modeling and stability analyses are given in detail. Sliding mode control with boundary layer is developed for DC-DC buck boost. It has been proven that the developed control strategies perform well during severe conditions, such as load variation and solar irradiation changes. The obtained simulation, as well as, experimental results show satisfactory performance.