Decision Support for Negotiations among Microgrids Using a Multiagent Architecture †
Abstract
1. Introduction
1.1. Objectives
1.2. Related Work
1.3. Contributions
- The definition of a local market setting for internal microgrids management. This local market model is extended from the preliminary work initially presented in [22]. The extension from the model of [22] includes the improvement of the optimal power flow formulation and the detail of the market model formulation;
- The introduction of a negotiation portfolio optimization model for decision support in negotiations in local and wholesale markets;
- The modeling of the integrated microgrids in the market environment using a MAS approach.
2. Operation of Interconnected Microgrids
2.1. Microgrids’ Internal (Local) Market
2.2. Negotiation among MGCCs
2.3. Wholesale Electricity Market
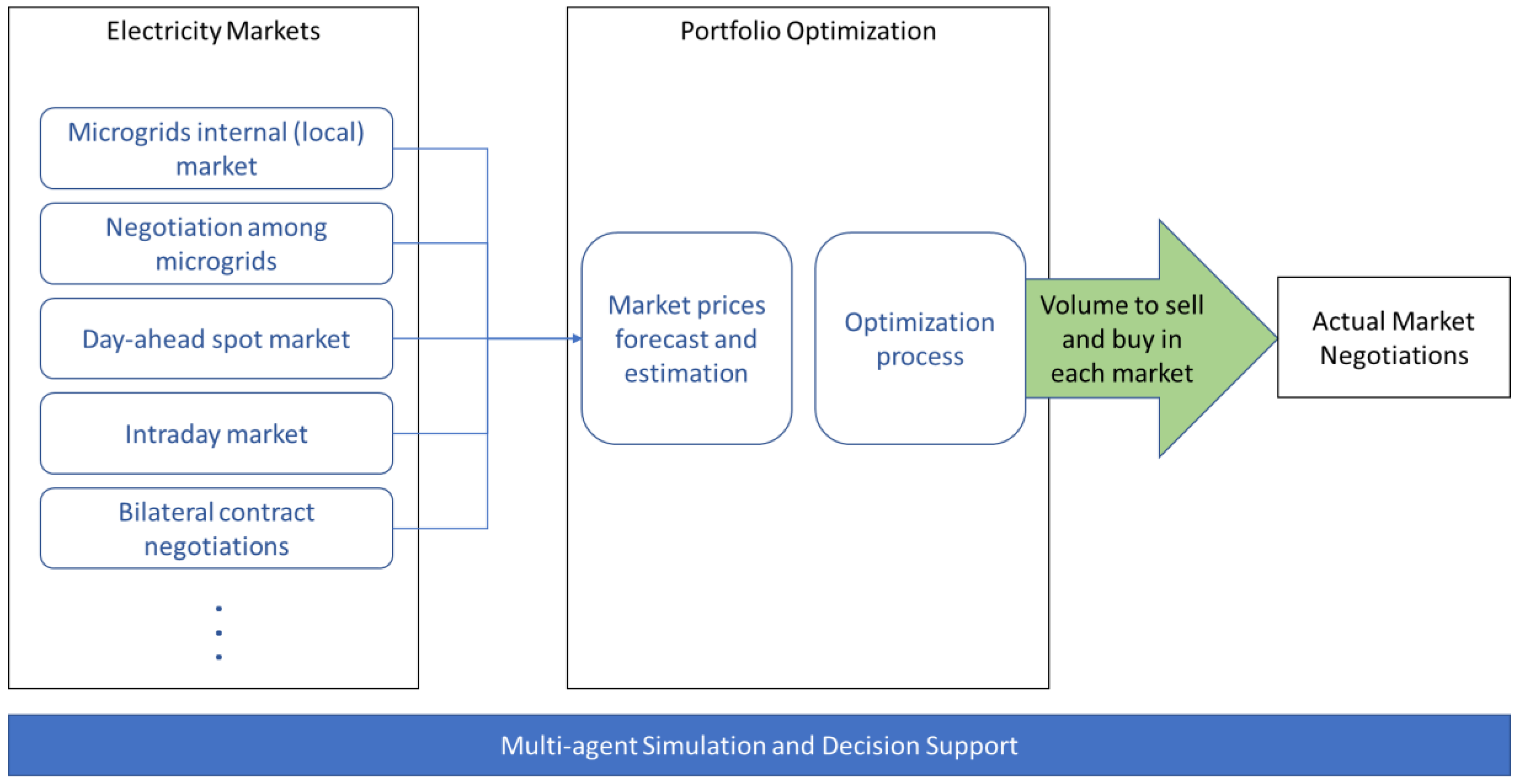
3. Proposed Negotiation Portfolio Optimization Model
3.1. Mathematical Formulation
- the weekday, referred as d in Equation (6);
- the number of days, Nday;
- the negotiation period, referred as p;
- the number of periods, Nper;
- a boolean variable for each distinct market or negotiation platform, indicating if this player can enter it to sell: ;
- a boolean variable for each session of the balancing market, indicating if this player is allowed to buy in each of them: ;
- M1, M2, …, NumM are the considered markets;
- S1, S2, …, NumS are the considered balancing market sessions;
- representing the amount of power to sell in each market;
- representing the amount of power to buy in each session of the balancing market;
- Play with the possibility of negotiating in different market opportunities depending on the expected prices at each moment, considering the negotiation amount;
- Play with the possibility of negotiating with neighbor players in search for advantageous deals, thus avoiding the need to negotiate solely in regional or wholesale markets;
- Play with the possibility to negotiate with different players in the bilateral contracts, and so having the chance to get higher or lower prices, depending on the circumstances;
- Play with the chance to wait for the later sessions of the balancing market to provide higher amounts of energy, if it is expected for the price to go up;
- Play with the possibility for sellers to buy and buyers to sell in the balancing market, to get good business opportunities: using arbitrage opportunities, buying extra energy when the prices are expected to be lower, and then selling it later when the prices go up; or if the prices show the opposite tendency, offer more energy than the player actually expects to produce, to get greater profit, and then buy that difference in the expected lower prices opportunities.
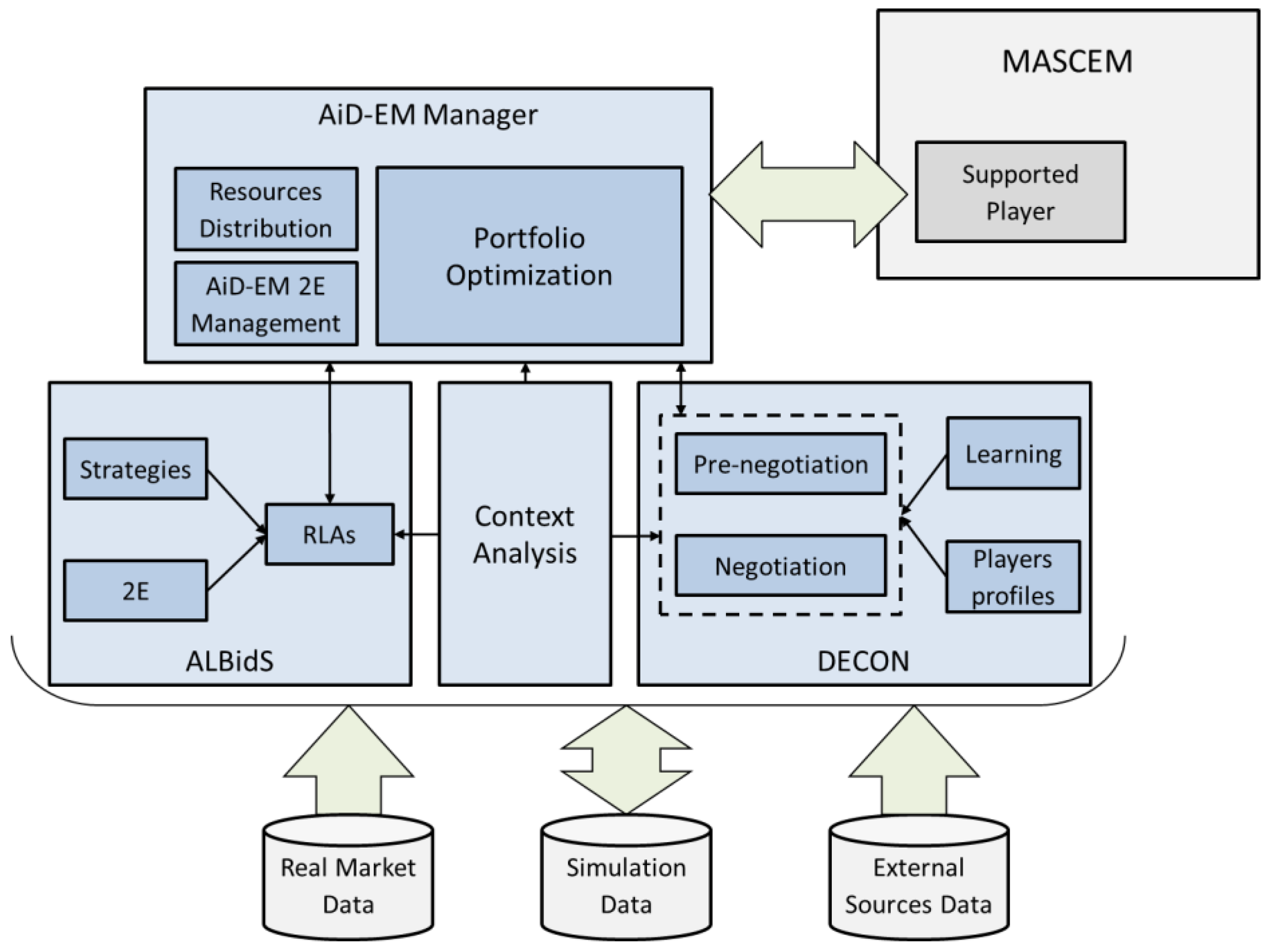
3.2. Multi-Agent Architecture
3.2.1. AiD-EM
3.2.2. MASCEM
3.2.3. MASGriP
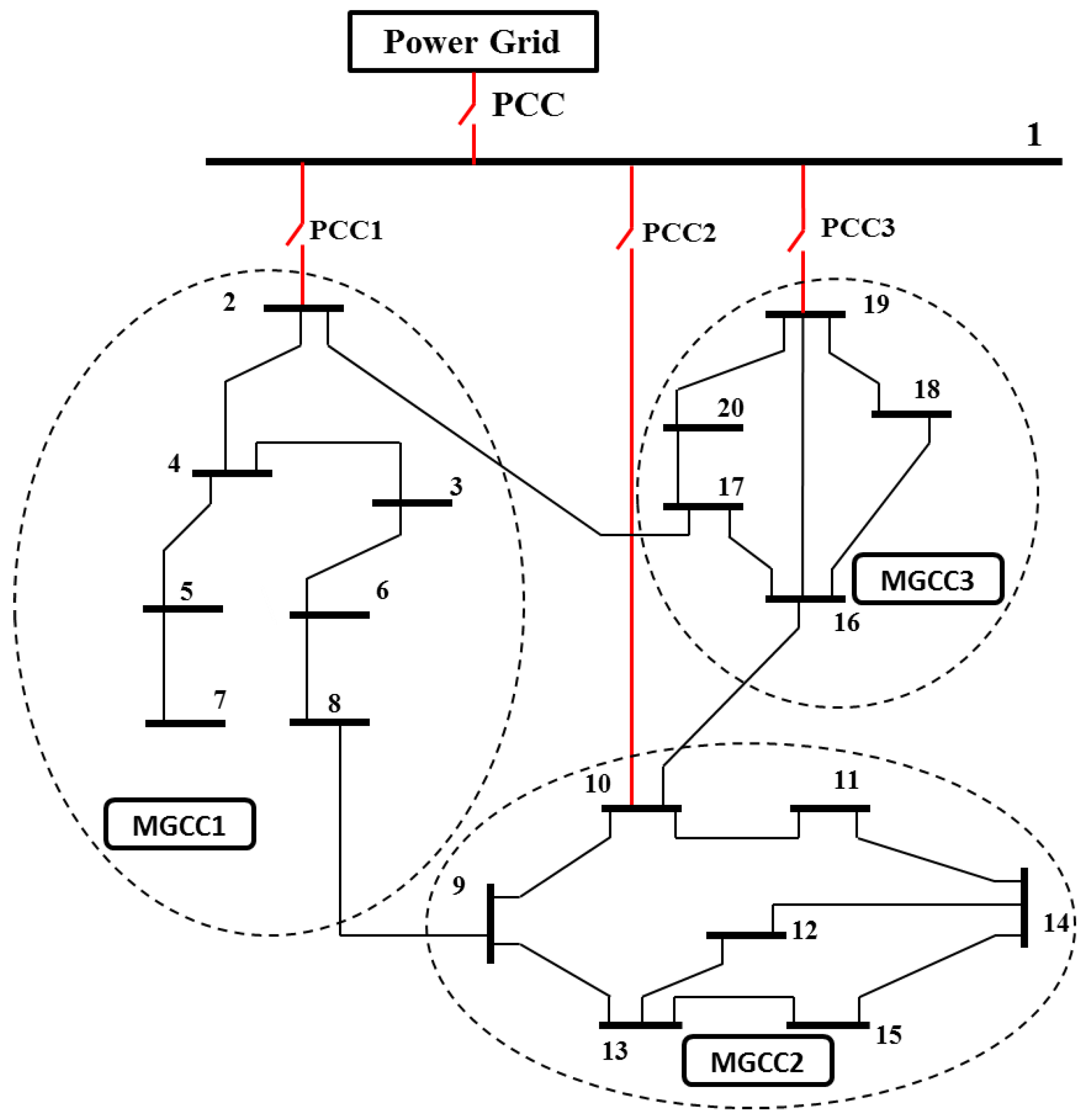
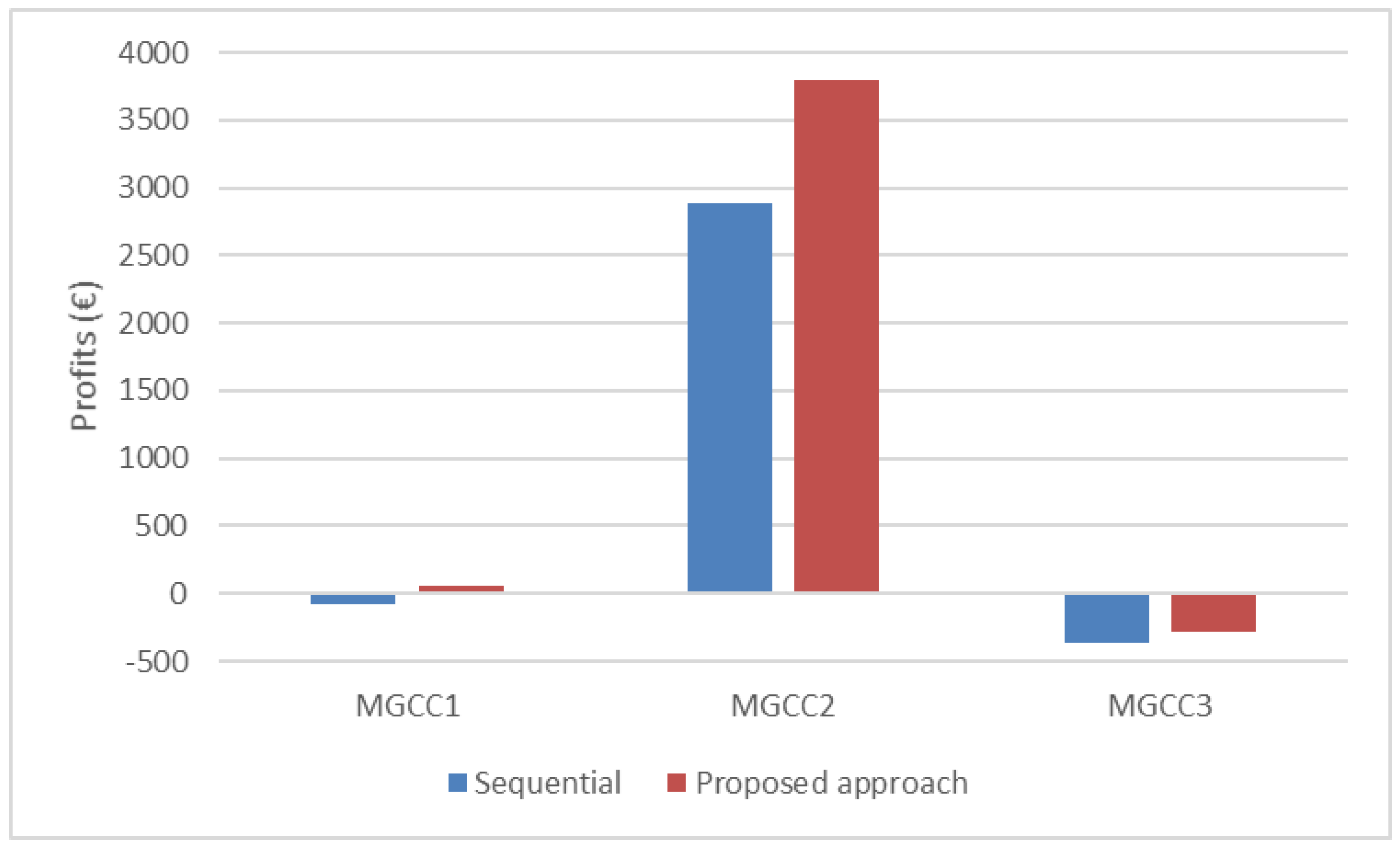
4. Case Studies
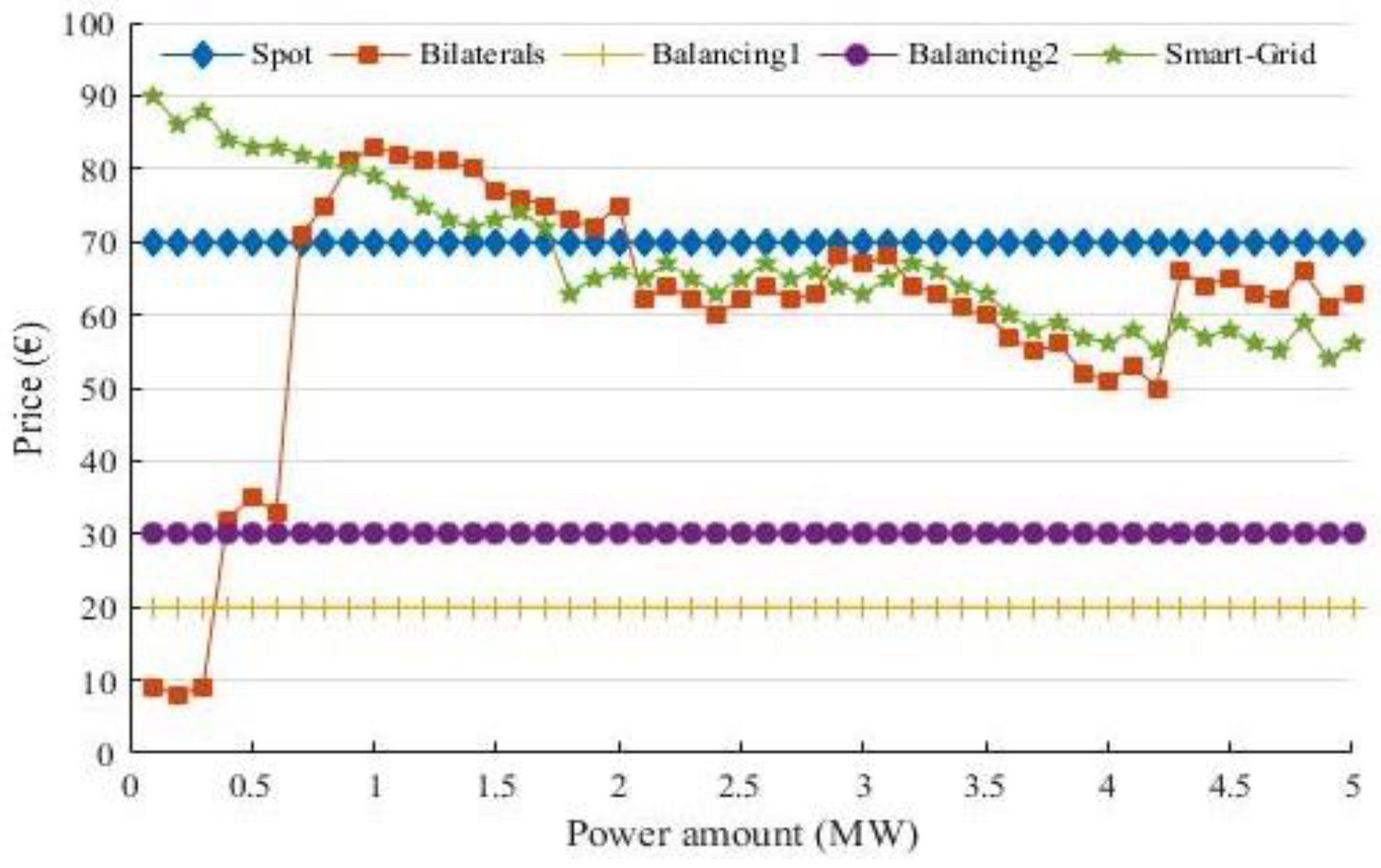
4.1. Case Study 1
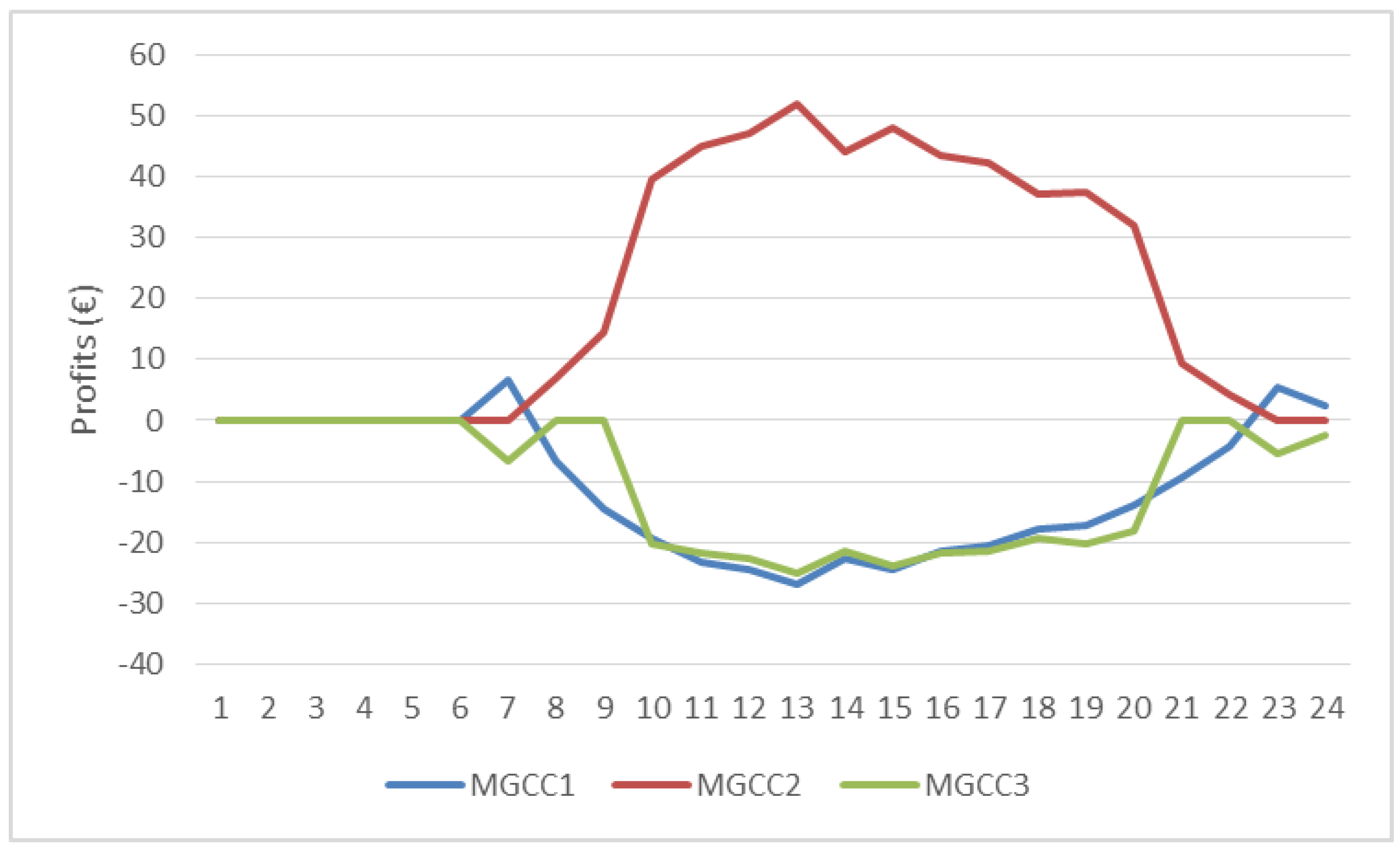
4.2. Case Study 2
- MGCC 1: Has power to sell in hours 1 to 7, 23 and 24;
- MGCC 2: Has extra generation in all hours of the day;
- MGCC 3: Sells from hours 1 to 7, and needs to buys on the remaining hours of the simulated day.
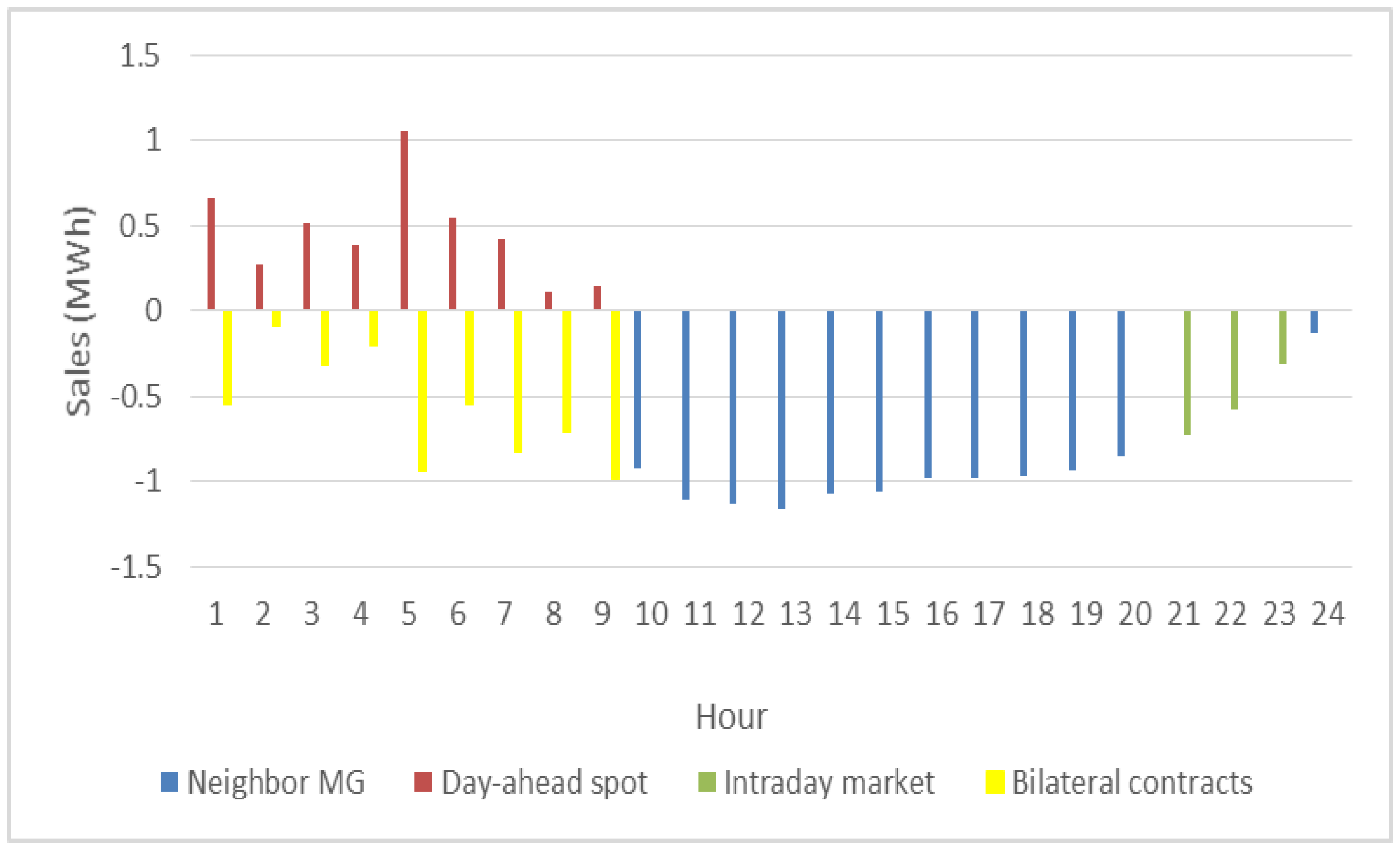
- Day-ahead spot market;
- Intraday (or balancing) market;
- Negotiation of bilateral contracts.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Indices | |
| Time periods. | |
| Buses. | |
| d | Days. |
| Loads. | |
| M | Markets. |
| Nday | Number of days. |
| Nper | Number of periods. |
| Asell | Allowed to sell |
| Abuy | Allowed to buy |
| p | Periods. |
| Distributed generation (DG) units. | |
| Microgrids. | |
| S | Sessions. |
| Parameters | |
| Minimum/maximum power generation of DG g (kW). | |
| Minimum/maximum power consumption of load l (kW). | |
| Series inductive reactance of the line connected between buses c-b. | |
| Minimum/maximum bus voltage. | |
| Variables | |
| Active power generation of DG g (kW). | |
| Active power consumption of load l (kW). | |
| Bus voltage angle. | |
| Spow | Power to sell. |
| Bpow | Power to buy. |
| Sets | |
| Set of time periods in the scheduling horizon. | |
| Set of buses in microgrid i. | |
| Set of DGs connected to bus b. | |
| Set of loads connected to bus b. | |
References
- Logenthiran, T. Multi-Agent System for Control and Management of Distributed Power Systems. Ph.D. Thesis, National University of Singapore, Singapore, 2012. [Google Scholar]
- Dimeas, A.L.; Hatziargyriou, N.D. Operation of a Multiagent System for Microgrid Control. IEEE Trans. Power Syst. 2005, 20, 1447–1455. [Google Scholar] [CrossRef]
- Melton, R. Gridwise Transactive Energy Framework (Draft Version). Available online: https://www.osti.gov/biblio/1123244 (accessed on 10 July 2018).
- The GridWise Architecture Council GridWise Transactive Energy Framework Version 1.0. Available online: https://www.gridwiseac.org/pdfs/te_framework_report_pnnl-22946.pdf (accessed on 10 July 2018).
- Khodayar, M.E.; Manshadi, S.D.; Vafamehr, A. The short-term operation of microgrids in a transactive energy architecture. Electr. J. 2016, 29, 41–48. [Google Scholar] [CrossRef]
- Covig, C.F.; Ardelean, M.; Vasiljevska, J.; Mengolini, A.; Fulli, G.; Amoiralis, E.; Covrig, C.F.; Ardelean, M.; Vasiljevska, J.; Mengolini, A.; et al. Smart grid projects outlook 2014. Jt. Res. Cent. Eur. Comm. Petten Neth. 2014, 1–157. [Google Scholar] [CrossRef]
- Conejo, A.J.; Carrion, M.; Morales, J.M. Decision Making Under Uncertainty in Electricity Markets; Springer: New York, NY, USA, 2010; ISBN 9781441974204. [Google Scholar]
- Gao, T.; Huang, M.; Wang, Q.; Yin, M.; Ching, W.K.; Lee, L.H.; Wang, X. A systematic model of stable multilateral automated negotiation in e-market environment. Eng. Appl. Artif. Intell. 2018, 74, 134–145. [Google Scholar] [CrossRef]
- Renna, P. Negotiation policies and coalition tools in e-marketplace environment. Comput. Ind. Eng. 2010, 59, 619–629. [Google Scholar] [CrossRef]
- Lee, C.-C. Development and evaluation of the many-to-many supplier negotiation strategy. Comput. Ind. Eng. 2014, 70, 90–97. [Google Scholar] [CrossRef]
- Hsu, C.-Y.; Kao, B.-R.; Ho, V.L.; Li, L.; Lai, K.R. An agent-based fuzzy constraint-directed negotiation model for solving supply chain planning and scheduling problems. Appl. Soft Comput. 2016, 48, 703–715. [Google Scholar] [CrossRef]
- Logenthiran, T.; Srinivasan, D. Multi-agent system for the operation of an integrated microgrid. J. Renew. Sustain. Energy 2012, 4, 13116. [Google Scholar] [CrossRef]
- Wooldridge, M. An Introduction to Multiagent Systems; John Wiley & Sons, Inc.: New York, NY, USA, 2008; ISBN 047149691X. [Google Scholar]
- Zhao, B.; Zhang, X.; Chen, J.; Bo, Z.; Xuesong, Z.; Jian, C.; Zhao, B.; Zhang, X.; Chen, J. Integrated microgrid laboratory system. IEEE Trans. Power Syst. 2012, 27, 2175–2185. [Google Scholar] [CrossRef]
- Fotouhi Ghazvini, M.A.; Morais, H.; Vale, Z. Coordination between mid-term maintenance outage decisions and short-term security-constrained scheduling in smart distribution systems. Appl. Energy 2012, 96, 281–291. [Google Scholar] [CrossRef]
- Duy Thanh, N.; Michael, N.; Martin de, G.; Nguyen, D.T.; Negnevitsky, M.; De Groot, M. Walrasian Market Clearing for Demand Response Exchange. IEEE Trans. Power Syst. 2012, 27, 535–544. [Google Scholar] [CrossRef]
- Baldi, S.; Karagevrekis, A.; Michailidis, I.T.; Kosmatopoulos, E.B. Joint energy demand and thermal comfort optimization in photovoltaic-equipped interconnected microgrids. Energy Convers. Manag. 2015, 101, 352–363. [Google Scholar] [CrossRef]
- Bui, V.H.; Hussain, A.; Kim, H.M. Demand bidding and real-time pricing-based optimal operation of multi-microgrids. Int. J. Smart Home 2016, 10, 193–208. [Google Scholar] [CrossRef]
- Pratt, A.; Krishnamurthy, D.; Ruth, M.; Wu, H.; Lunacek, M.; Vaynshenk, P. Transactive Home Energy Management Systems: The Impact of Their Proliferation on the Electric Grid. IEEE Electrif. Mag. 2016, 4, 8–14. [Google Scholar] [CrossRef]
- Rahimi, F.; Ipakchi, A. Using a Transactive Energy Framework: Providing Grid Services from Smart Buildings. IEEE Electrif. Mag. 2016, 4, 23–29. [Google Scholar] [CrossRef]
- Chakraborty, S.; Nakamura, S.; Okabe, T. Real-time energy exchange strategy of optimally cooperative microgrids for scale-flexible distribution system. Expert Syst. Appl. 2015, 42, 4643–4652. [Google Scholar] [CrossRef]
- Ghazvini, M.A.F.; Abedini, R.; Pinto, T.; Vale, Z. Multiagent system architecture for short-term operation of integrated microgrids. IFAC Proc. Vol. 2014, 47, 6355–6360. [Google Scholar] [CrossRef]
- Pinto, T.; Morais, H.; Sousa, T.M.; Sousa, T.; Vale, Z.; Praça, I.; Faia, R.; Pires, E.J.S. Adaptive Portfolio Optimization for Multiple Electricity Markets Participation. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1720–1733. [Google Scholar] [CrossRef] [PubMed]
- Ambrosio, R. Transactive Energy Systems [Viewpoint]. IEEE Electrif. Mag. 2016, 4, 4–7. [Google Scholar] [CrossRef]
- Sotkiewicz, P.M.; Vignolo, J.M. Nodal pricing for distribution networks: Efficient pricing for efficiency enhancing DG. IEEE Trans. Power Syst. 2006, 21, 1013–1014. [Google Scholar] [CrossRef]
- Pinto, T.; Vale, Z.; Sousa, T.M.; Praça, I.; Santos, G.; Morais, H. Adaptive Learning in Agents Behaviour: A Framework for Electricity Markets Simulation. Integr. Comput. Eng. 2014, 21, 399–415. [Google Scholar] [CrossRef]
- Vale, Z.; Pinto, T.; Praca, I.; Morais, H. MASCEM: Electricity Markets Simulation with Strategic Agents. Intell. Syst. IEEE 2011, 26, 9–17. [Google Scholar] [CrossRef]
- Oliveira, P.; Pinto, T.; Morais, H.; Vale, Z. MASGriP—A Multi-Agent Smart Grid Simulation Platform. In Proceedings of the Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Salam, A.A.; Mohamed, A.; Hannan, M.A. Technical challenges on microgrids. ARPN J. Eng. Appl. Sci. 2008, 3, 64–69. [Google Scholar]
- Bollen, M.; Zhong, J.; Samuelsson, O.; Bjornstedt, J. Performance indicators for microgrids during grid-connected and island operation. In Proceedings of the PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–6. [Google Scholar]
- Rasheduzzaman, M.; Bhaskara, S.N.; Chowdhury, B.H.; Bhaskar, S.N.; Chowdhury, B.H. Implementation of a microgrid central controller in a laboratory microgrid network. In Proceedings of the North American Power Symposium (NAPS), Champaign, IL, USA, 9–11 September 2012. [Google Scholar] [CrossRef]
- Singh, K.; Yadav, V.K.; Padhy, N.P.; Sharma, J. Congestion Management Considering Optimal Placement of Distributed Generator in Deregulated Power System Networks. Electr. Power Compon. Syst. 2014, 42, 13–22. [Google Scholar] [CrossRef]
- Liu, H.; Tesfatsion, L.; Chowdhury, A.A. Locational marginal pricing basics for restructured wholesale power markets. In Proceedings of the Power and Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009. [Google Scholar]
- Eddy, Y.S.F.; Gooi, H.B.; Chen, S.X. Multi-Agent System for Distributed Management of Microgrids. IEEE Trans. Power Syst. 2014, 30, 1–11. [Google Scholar]
- Chanana, S. LMP Based Zone Formation in Electricity Markets. In Proceedings of the 8th WSEAS International Conference on Power Systems, Santander, Cantabria, Spain, 23–25 September 2008. [Google Scholar]
- Yang, Z.; Bose, A.; Zhong, H.; Zhang, N.; Lin, J.; Xia, Q.; Kang, C. LMP Revisited: A Linear Model for the Loss-Embedded LMP. IEEE Trans. Power Syst. 2017, 32, 4080–4090. [Google Scholar] [CrossRef]
- Sioshansi, F.P. Evolution of Global Electricity Markets: New Paradigms, New Challenges, New Approaches; Academic Press: Cambridge, MA, USA, 2013; ISBN 0123979064. [Google Scholar]
- Biggar, D.R.; Hesamzadeh, M.R. The Economics of Electricity Markets; John Wiley & Sons: New York, NY, USA, 2014. [Google Scholar]
- Pinto, T.; Sousa, T.M.; Vale, Z. Dynamic artificial neural network for electricity market prices forecast. In Proceedings of the Intelligent Engineering Systems (INES), Lisbon, Portugal, 13–15 June 2012. [Google Scholar]
- Faia, R.; Pinto, T.; Vale, Z. Dynamic Fuzzy Clustering Method for Decision Support in Electricity Markets Negotiation. ADCAIJ Adv. Distrib. Comput. Artif. Intell. J. 2016, 5, 23. [Google Scholar] [CrossRef]
- Pinto, T.; Vale, Z.; Praça, I.; Pires, J.E.; Lopes, F. Decision Support for Energy Contracts Negotiation with Game Theory and Adaptive Learning. Energies 2015, 8, 9817–9842. [Google Scholar] [CrossRef]
- Praça, I.; Ramos, C.; Vale, Z.; Cordeiro, M. MASCEM: A multiagent system that simulates competitive electricity markets. IEEE Intell. Syst. 2003, 18, 54–60. [Google Scholar] [CrossRef]
- Silva, F.; Teixeira, B.; Pinto, T.; Santos, G.; Vale, Z.; Praça, I. Generation of realistic scenarios for multi-agent simulation of electricity markets. Energy 2016, 116, 128–139. [Google Scholar] [CrossRef]
- Gomes, L.; Faria, P.; Morais, H.; Vale, Z.; Ramos, C. Distributed, agent-based intelligent system for demand response program simulation in smart grids. IEEE Intell. Syst. 2014, 29, 56–65. [Google Scholar] [CrossRef]
- Pinto, T.; Morais, H.; Oliveira, P.; Vale, Z.; Praça, I.; Ramos, C. A new approach for multi-agent coalition formation and management in the scope of electricity markets. Energy 2011, 36, 5004–5015. [Google Scholar] [CrossRef]
- Moran, D.; Suzuki, J. Curtailment Service Providers: They Bring the Horse to Water… Do We Care if It Drinks? In Proceedings of the 16th Biennial ACEEE Summer Study on Energy Efficiency in Buildings, Pacific Grove, CA, USA, 15–20 August 2010. [Google Scholar]
- OMIE Market Results. Available online: http://m.omie.es/reports/?m=yes&lang=en (accessed on 10 July 2018).




| Spot Market | Bilateral | Balancing 1 | Balancing 2 | Local Market | |
|---|---|---|---|---|---|
| Sales (MWh) | 1.478 | 1.150 | 0 | 0 | 0.846 |
| Purchases (MWh) | 0 | 0.475 | 1.000 | 1.000 | 0 |
| Generators | Min Real Power Output (PU) | Max Real Power Output (PU) | Bus | MGCC |
|---|---|---|---|---|
| gen1 | 0.00 | 0.20 | 1 | 1 |
| gen2 | 0.01 | 0.23 | 4 | 1 |
| gen3 | 0.00 | 0.24 | 6 | 1 |
| gen4 | 0.06 | 0.15 | 7 | 1 |
| gen5 | 0.01 | 0.29 | 8 | 1 |
| gen6 | 0.00 | 0.20 | 9 | 2 |
| gen7 | 0.01 | 0.23 | 10 | 2 |
| gen8 | 0.00 | 0.24 | 11 | 2 |
| gen9 | 0.06 | 0.15 | 12 | 2 |
| gen10 | 0.01 | 0.29 | 13 | 2 |
| gen11 | 0.00 | 0.30 | 14 | 2 |
| gen12 | 0.00 | 0.40 | 15 | 2 |
| gen13 | 0.00 | 0.15 | 16 | 3 |
| gen14 | 0.01 | 0.20 | 17 | 3 |
| gen15 | 0.00 | 0.10 | 18 | 3 |
| gen16 | 0.06 | 0.12 | 19 | 3 |
| gen17 | 0.01 | 0.14 | 20 | 3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinto, T.; Fotouhi Ghazvini, M.A.; Soares, J.; Faia, R.; Corchado, J.M.; Castro, R.; Vale, Z. Decision Support for Negotiations among Microgrids Using a Multiagent Architecture. Energies 2018, 11, 2526. https://doi.org/10.3390/en11102526
Pinto T, Fotouhi Ghazvini MA, Soares J, Faia R, Corchado JM, Castro R, Vale Z. Decision Support for Negotiations among Microgrids Using a Multiagent Architecture. Energies. 2018; 11(10):2526. https://doi.org/10.3390/en11102526
Chicago/Turabian StylePinto, Tiago, Mohammad Ali Fotouhi Ghazvini, Joao Soares, Ricardo Faia, Juan Manuel Corchado, Rui Castro, and Zita Vale. 2018. "Decision Support for Negotiations among Microgrids Using a Multiagent Architecture" Energies 11, no. 10: 2526. https://doi.org/10.3390/en11102526
APA StylePinto, T., Fotouhi Ghazvini, M. A., Soares, J., Faia, R., Corchado, J. M., Castro, R., & Vale, Z. (2018). Decision Support for Negotiations among Microgrids Using a Multiagent Architecture. Energies, 11(10), 2526. https://doi.org/10.3390/en11102526











