State-Space Approximation of Convolution Term in Time Domain Analysis of a Raft-Type Wave Energy Converter
Abstract
1. Introduction
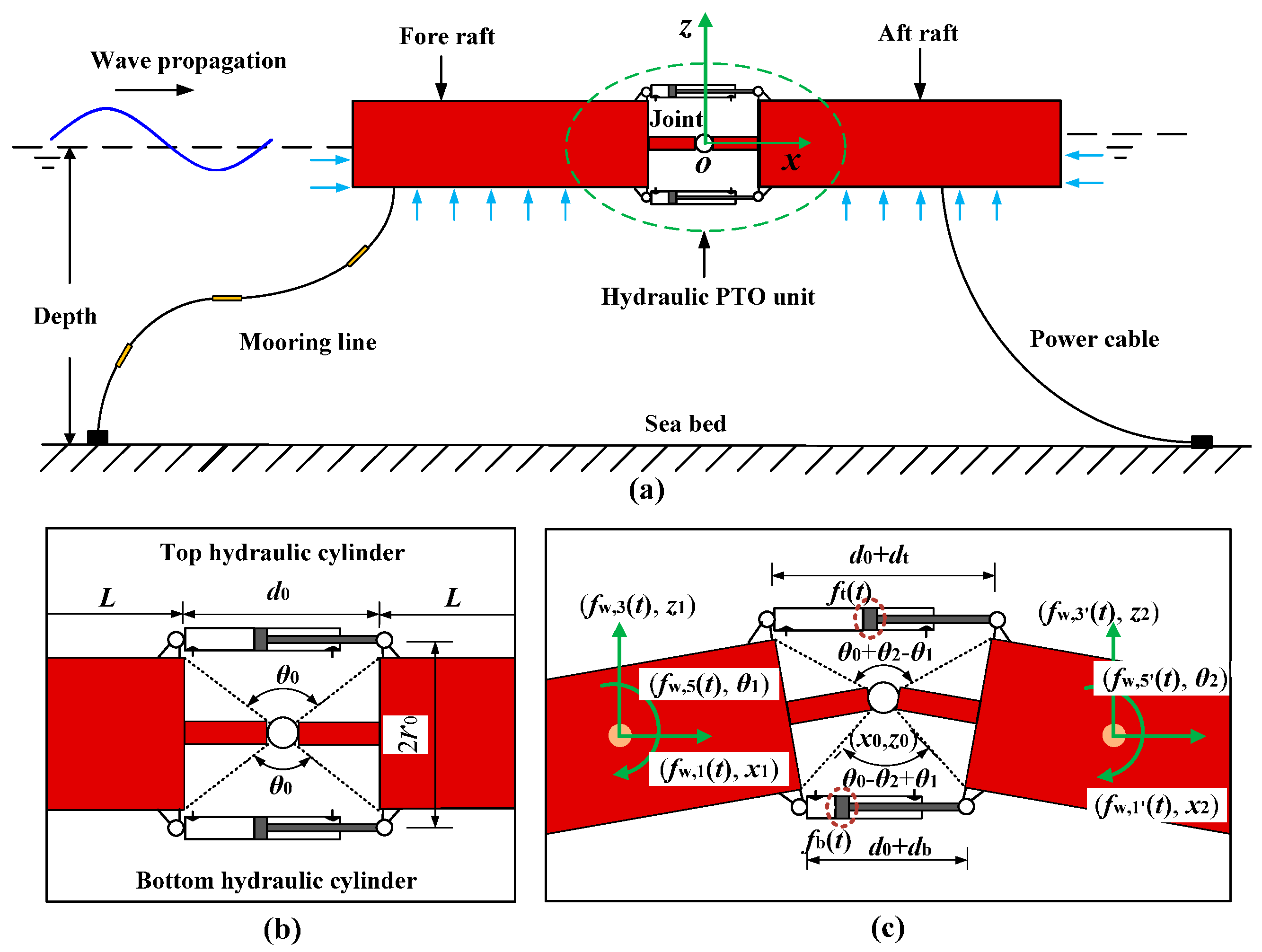
2. Description of the Device
3. Frequency Domain Analysis
3.1. Frequency Response Function
3.2. Power Capture Ability
4. Time Domain Analysis
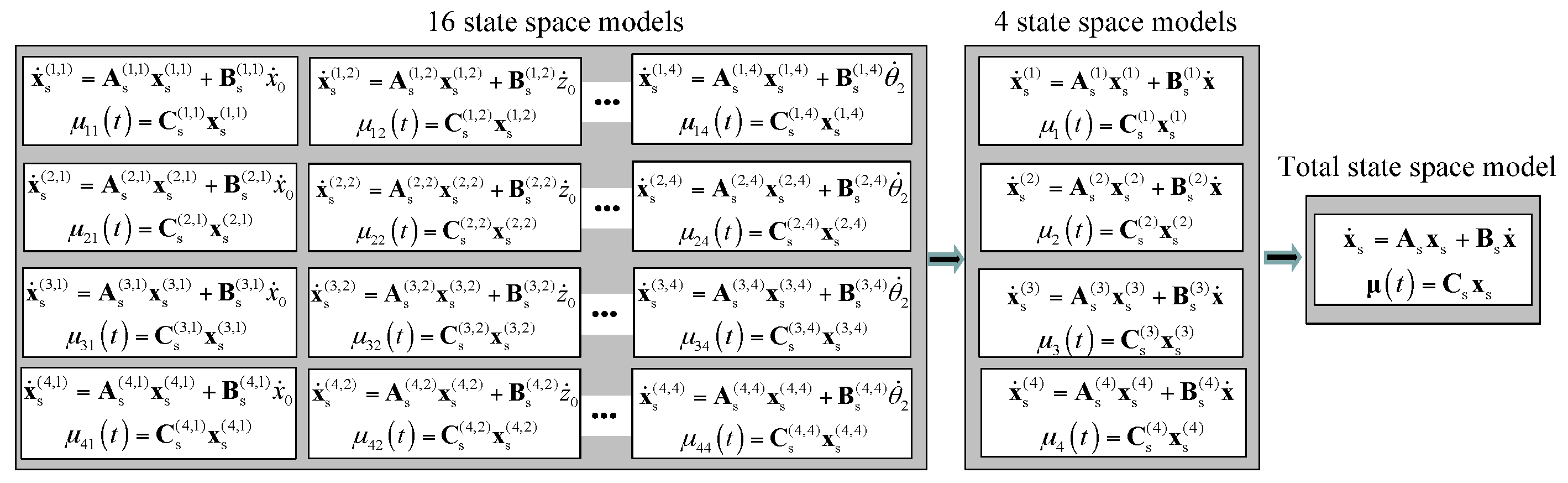
4.1. State-Space Model of Convolution Term
4.2. Transfer Function Estimation Using Regression in Frequency Domain
4.3. Power Capture Ability
5. Numerical Results and Discussion
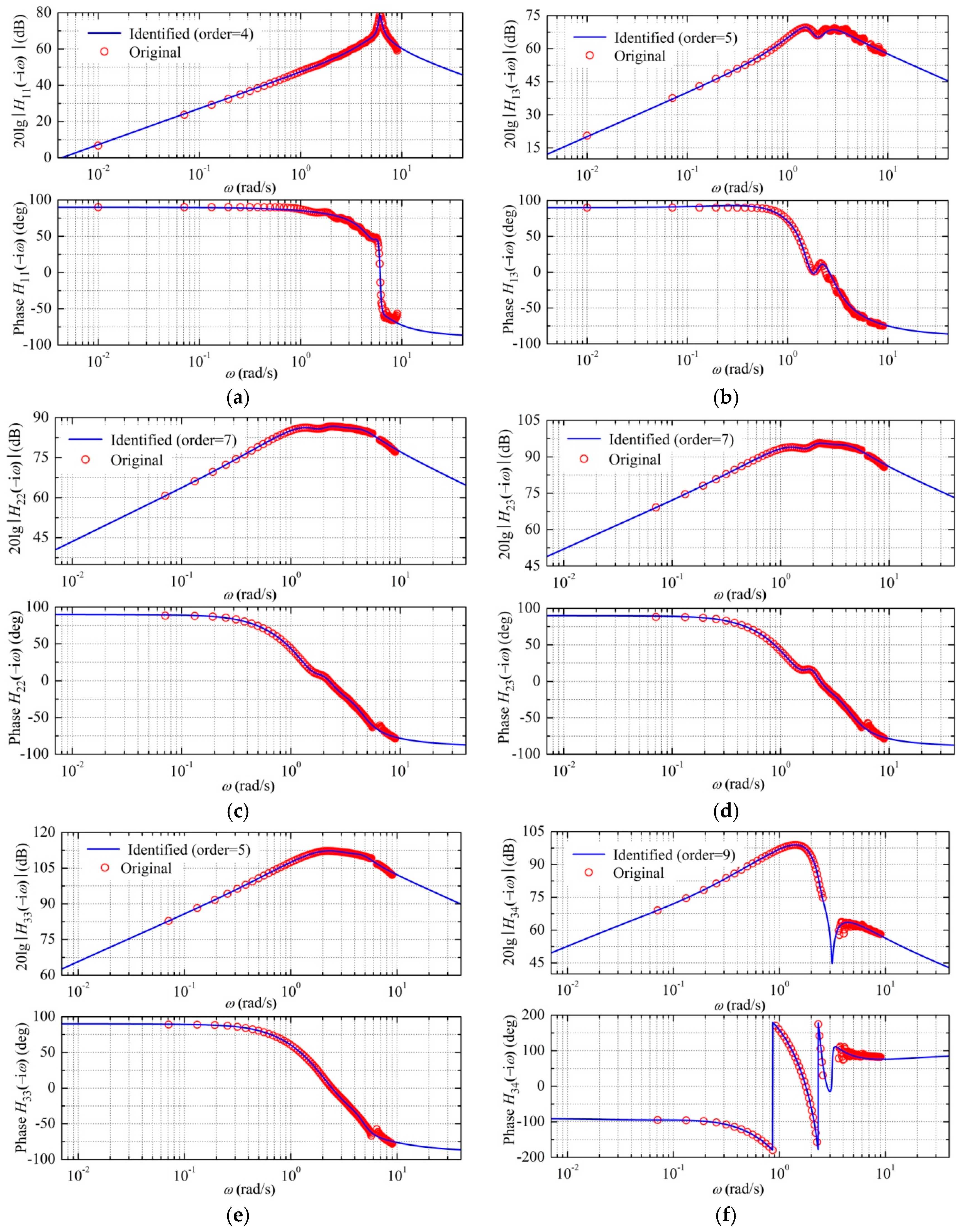
5.1. Identification of State-Space Model
5.2. Validation of Time Domain Analysis
5.3. Numerical Results in Regular Waves
5.3.1. Influence of Wave Frequency
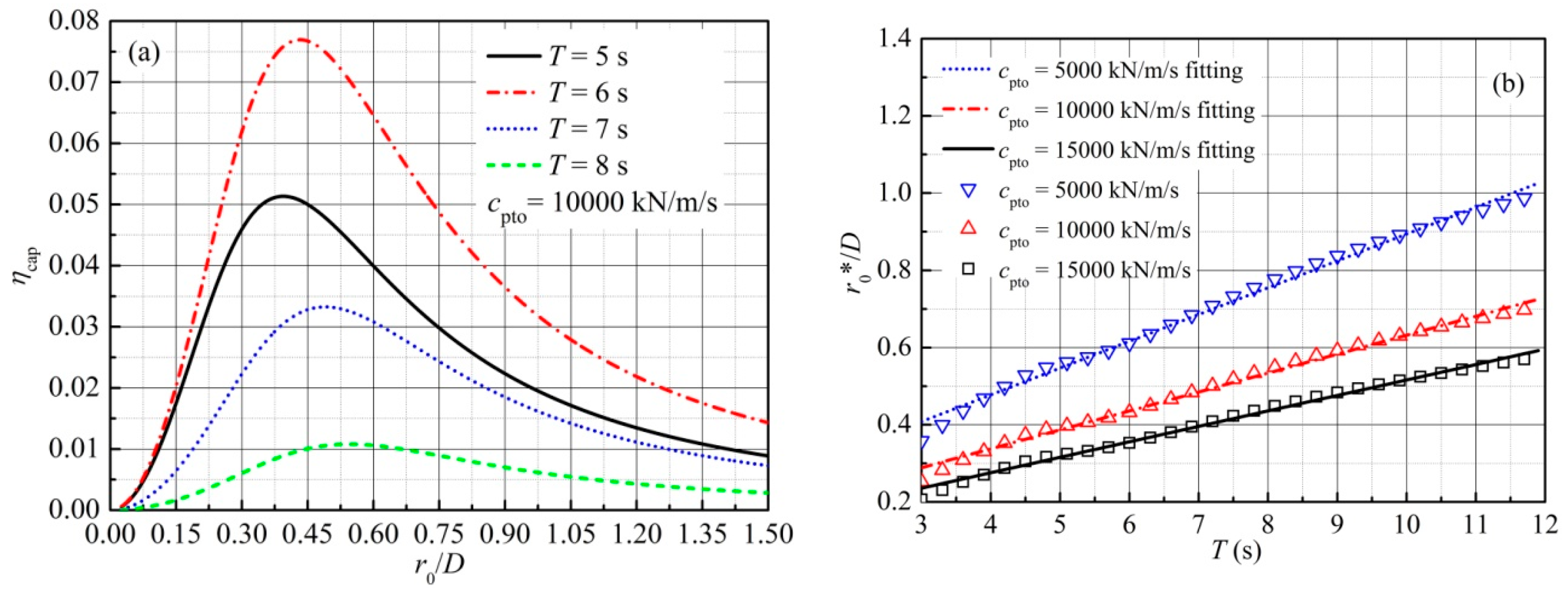
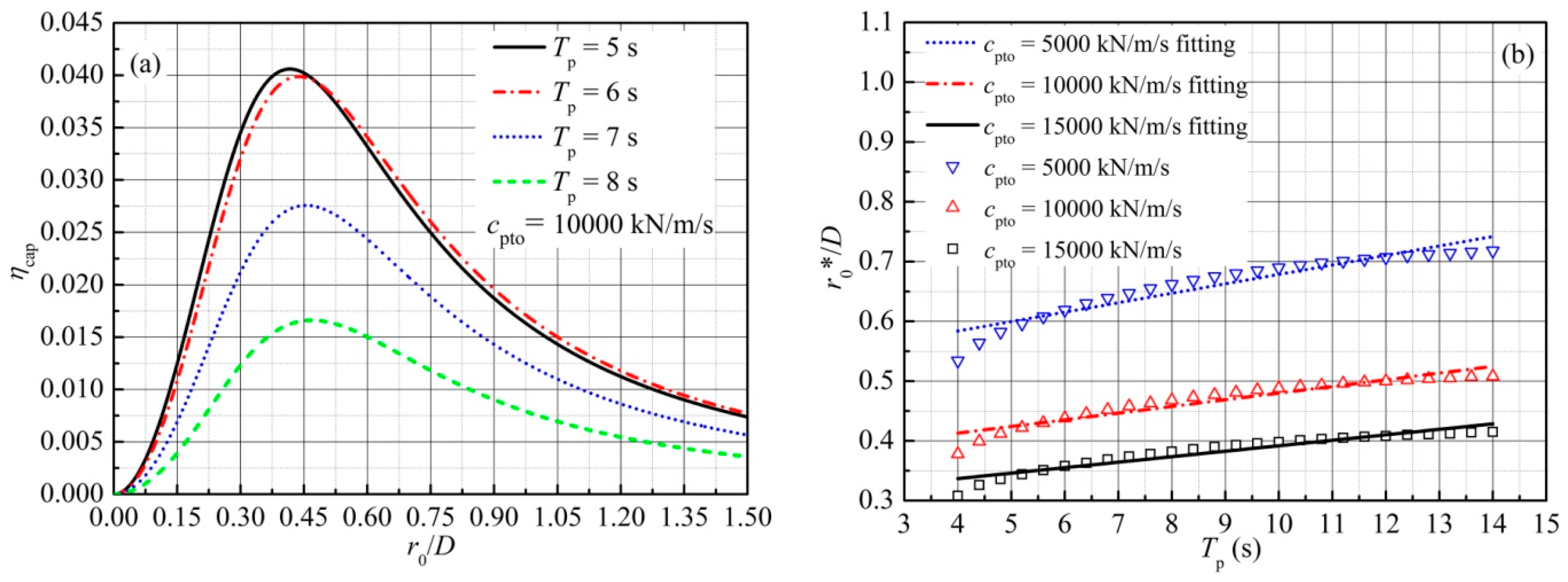
5.3.2. Influence of Mounting Position r0
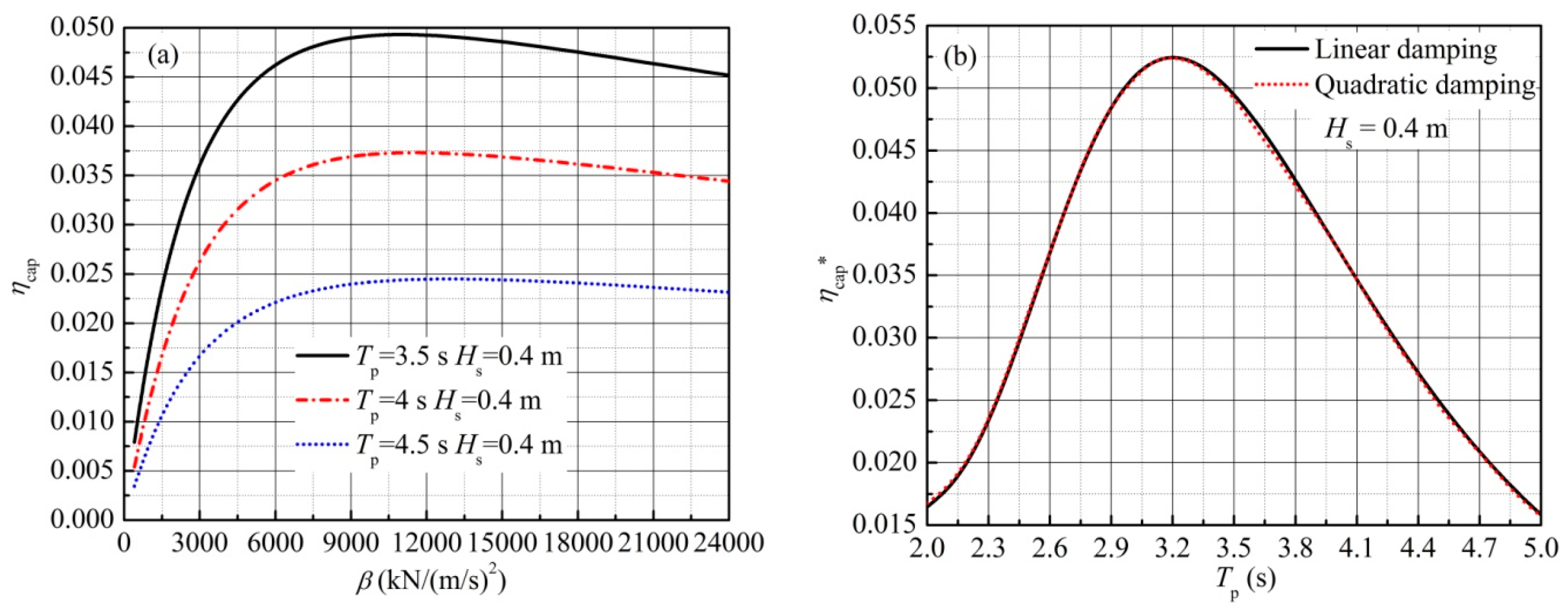
5.3.3. Influence of Damping Coefficient cpto and Stiffness kpto
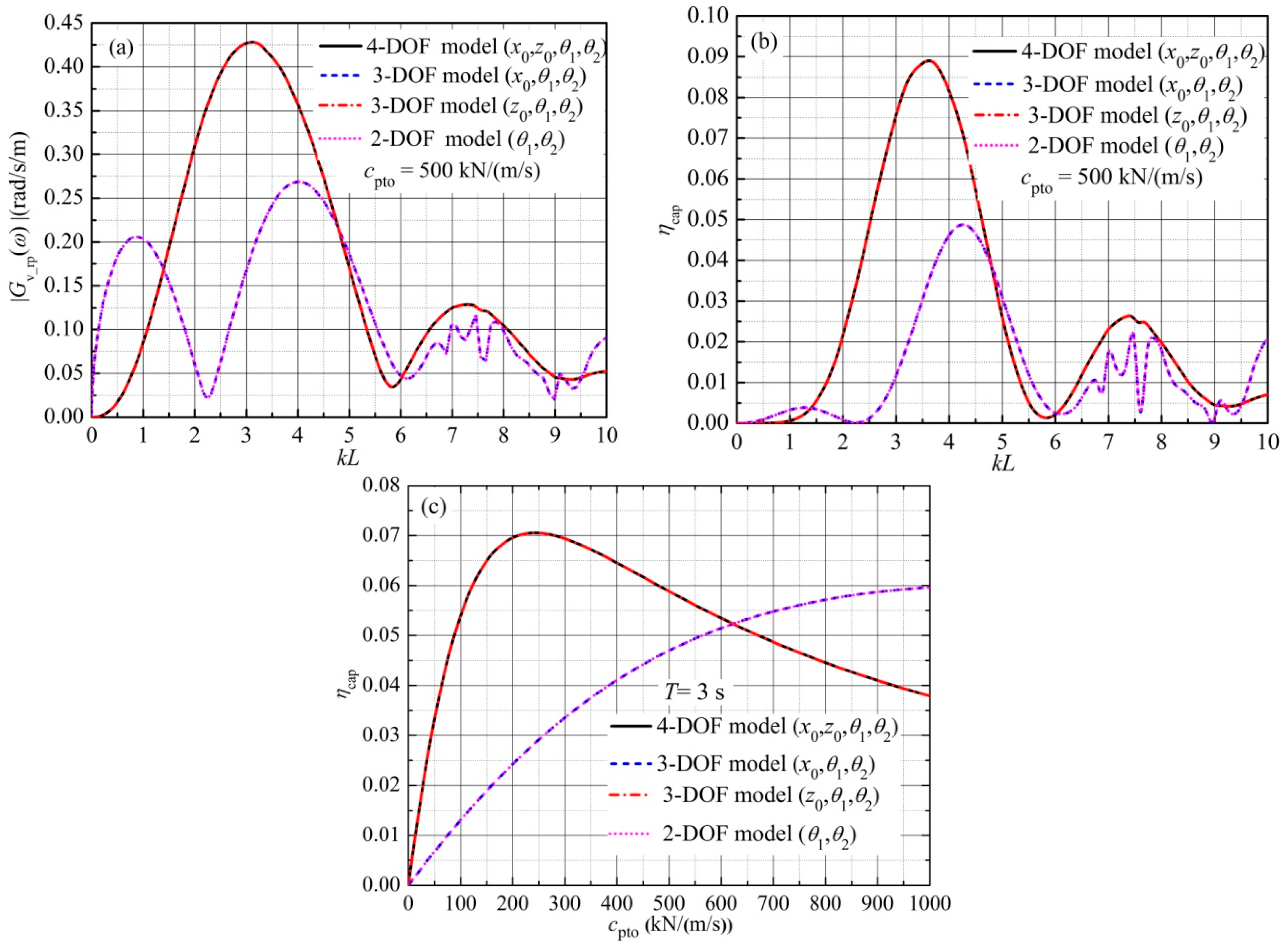
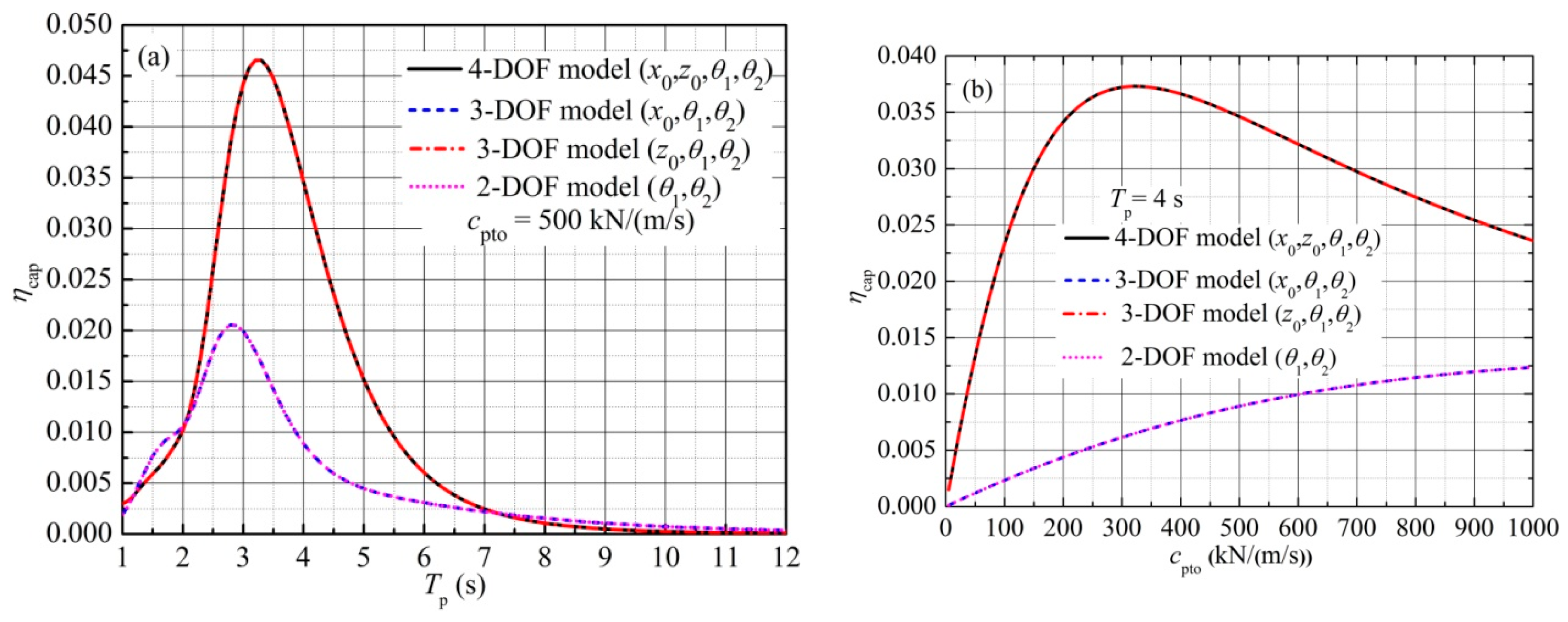
5.3.4. Influence of Surge and Heave Motions of Joint
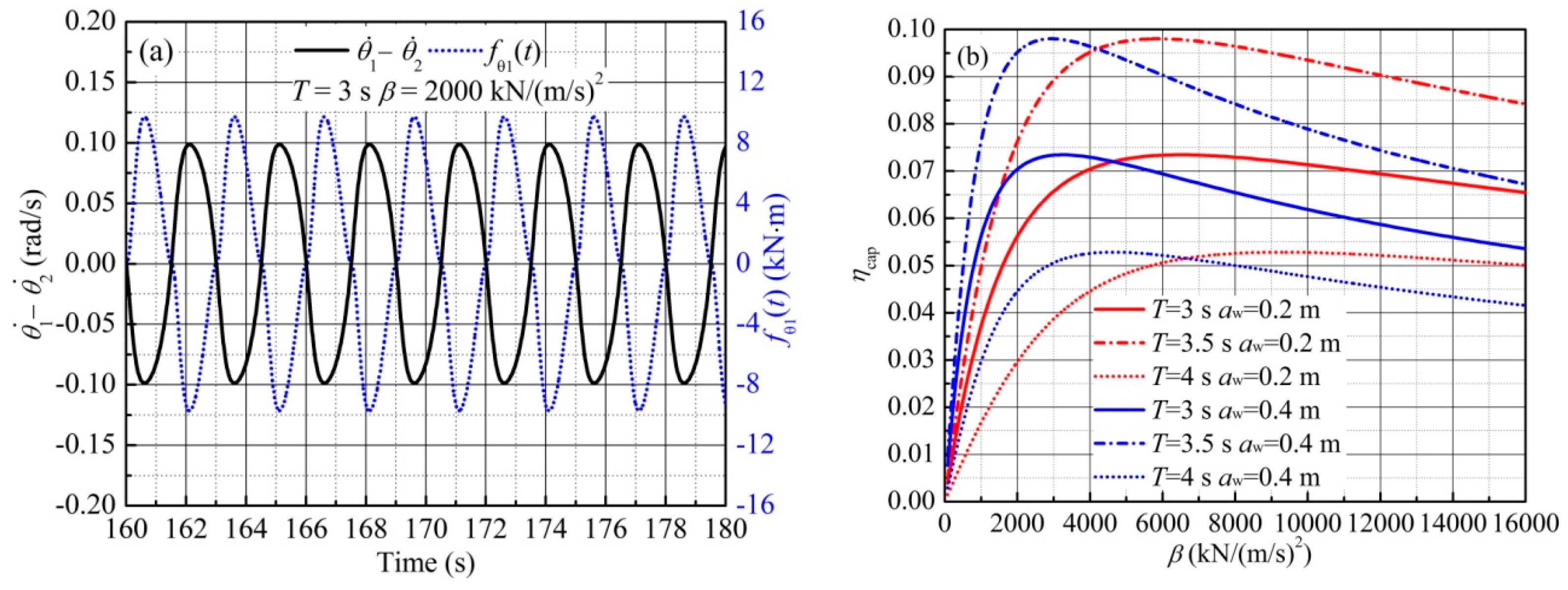
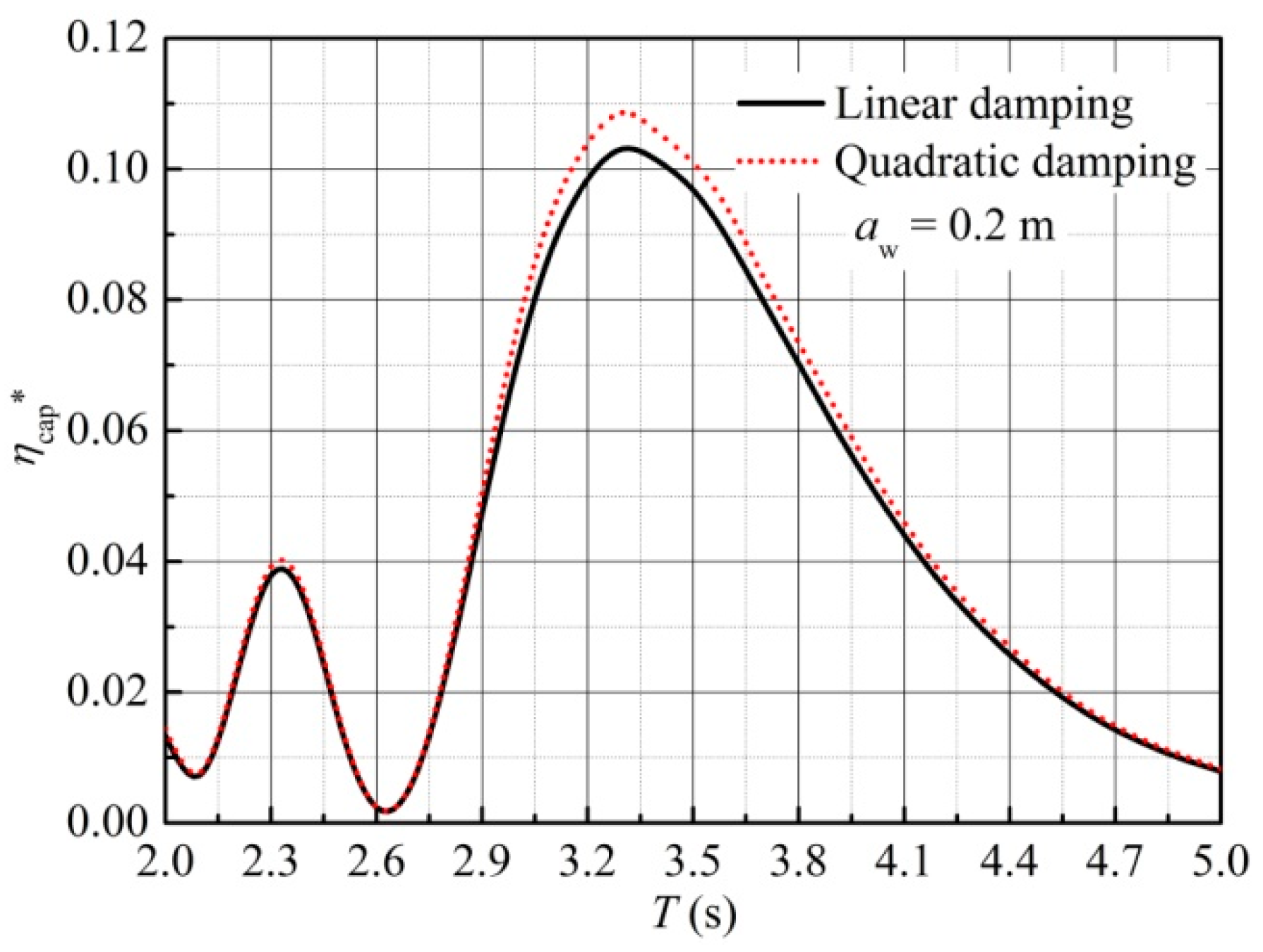
5.3.5. Influence of Quadratic Damping PTO
5.4. Numerical Results in Irregular Waves
5.4.1. Influence of Mounting Position R0
5.4.2. Influence of Damping Coefficient cpto and Stiffness kpto
5.4.3. Influence of Surge and Heave Motions of Joint
5.4.4. Influence of Quadratic Damping PTO
6. Conclusions
- (1)
- State-space approximation of the convolution term through regression in the frequency domain has sufficient accuracy. The time domain analysis with the convolution term approximated by a state-space model could be used to investigate the performance of the device.
- (2)
- To obtain a relatively large capture width ratio, the resonant frequency of the designed device should be as close to the considered wave frequency as possible. When there is no control included in the PTO unit, the arrival of resonance is usually at the cost of a relatively large raft size.
- (3)
- For a certain wave period (or peak wave period), there exists an optimal mounting position r0*, corresponding to a peak capture width ratio ηcap*. In regular waves, the relationship between the optimal normalized mounting position r0*/D and the wave period is approximately linear, and a smaller damping coefficient cpto gives a larger gradient of the approximately linear relationship; however, this relationship presents nonlinear characteristics in irregular waves.
- (4)
- In regular waves, the optimal stiffness kpto* only depends on wave period, and the optimal damping coefficient cpto* relies on wave period and stiffness kpto, and is symmetric to the optimal stiffness kpto*. However, in irregular waves, the optimal stiffness kpto* depends on not only the wave period, but also the damping coefficient cpto, and the optimal damping coefficient cpto* is not symmetric to the optimal stiffness kpto*. The optimal damping coefficient cpto* in the optimal combination increases with increasing wave period (or peak wave period), and then decreases after reaching a peak value, whereas the optimal stiffness kpto* in the optimal combination is usually negative and decreases monotonously.
- (5)
- The surge motion of the joint could be neglected. The motion equation of the device can be reduced to a three-DOF model only with the consideration of heave motion of the joint and two pitch motions of the two rafts.
- (6)
- In regular waves, the peak capture width ratio ηcap* obtained by using quadratic damping is slightly larger than that obtained by using linear damping; however, this advantage vanishes in irregular waves.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- McCormick, M.E. Ocean Wave Energy Conversion; Dover Publications: Mineola, NY, USA, 2007; Volume 45, ISBN 9780486462455. [Google Scholar]
- Cruz, J. Ocean Wave Energy-Current Status and Future Prespectives; Springer Science & Business Media: Berlin, Germany, 2008; ISBN 978-3-540-74894-6. [Google Scholar]
- Drew, B.; Plummer, A.R.; Sahinkaya, M.N. A review of wave energy converter technology. Proc. Inst. Mech. Eng. Part A J. Power Energy 2009, 223, 887–902. [Google Scholar] [CrossRef]
- López, I.; Andreu, J.; Ceballos, S.; de Alegría, I.M.; Kortabarria, I. Review of wave energy technologies and the necessary power-equipment. Renew. Sustain. Energy Rev. 2013, 27, 413–434. [Google Scholar] [CrossRef]
- Haren, P. Optimal Design of Hagen-Cockerell Raft. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1979. [Google Scholar]
- Haren, P.; Mei, C.C. Head-sea diffraction by a slender raft with application to wave-power absorption. J. Fluid Mech. 1981, 104, 505–526. [Google Scholar] [CrossRef]
- Haren, P.; Mei, C.C. An array of Hagen-Cockerell wave power absorbers in head seas. Appl. Ocean Res. 1982, 4, 51–56. [Google Scholar] [CrossRef]
- Haren, P.; Mei, C.C. Wave power extraction by a train of rafts: Hydro-dynamic theory and optimum design. Appl. Ocean Res. 1979, 1, 147–157. [Google Scholar] [CrossRef]
- Farley, F.J.M. Wave energy conversion by flexible resonant rafts. Appl. Ocean Res. 1982, 4, 57–63. [Google Scholar] [CrossRef]
- Kraemer, D.R.B. The Motions of Hinged-Barge Systems in Regular Seas. Ph.D. Thesis, Johns Hopkins University, Baltimore, MD, USA, 2001. [Google Scholar]
- Nolan, G.; Catháin, M.; Murtagh, J.; Ringwood, J. Modelling and Simulation of the Power Take-Off System for a Hinge-Barge Wave-Energy Converter. In Proceedings of the Fifth European Wave Energy Conference, University College Cork, Ireland, 17–20 September 2003; pp. 1–8. [Google Scholar]
- Paparella, F.; Bacelli, G.; Paulmeno, A.; Mouring, S.E.; Ringwood, J.V. Multibody Modelling of Wave Energy Converters Using Pseudo-Spectral Methods with Application to a Three-Body Hinge-Barge Device. IEEE Trans. Sustain. Energy 2016, 7, 966–974. [Google Scholar] [CrossRef]
- Retzler, C. Measurements of the slow drift dynamics of a model Pelamis wave energy converter. Renew. Energy 2006, 31, 257–269. [Google Scholar] [CrossRef]
- Yemm, R.; Pizer, D.; Retzler, C.; Henderson, R. Pelamis: Experience from concept to connection. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 365–380. [Google Scholar] [CrossRef] [PubMed]
- Henderson, R. Design, simulation, and testing of a novel hydraulic power take-off system for the Pelamis wave energy converter. Renew. Energy 2006, 31, 271–283. [Google Scholar] [CrossRef]
- Thiam, A.G.; Pierce, A.D. Segmented and continuous beam models for the capture of ocean wave energy by Pelamis-like devices. Proc. Meet. Acoust. 2012, 11, 65001. [Google Scholar] [CrossRef]
- Thiam, A.G.; Pierce, A.D. Radiation loss in Pelamis-like ocean wave energy conversion devices. Proc. Meet. Acoust. 2013, 12, 65003. [Google Scholar] [CrossRef]
- Thiam, A.G.; Pierce, A.D. Damping mechanism concepts in ocean wave energy conversion: A simplified model of the Pelamis converter. J. Acoust. Soc. Am. 2010, 127, 65002. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, Y.; Sheng, W. Maximum theoretical power absorption of connected floating bodies under motion constraints. Appl. Ocean Res. 2016, 58, 95–103. [Google Scholar] [CrossRef]
- Zheng, S.-M.; Zhang, Y.-H.; Zhang, Y.-L.; Sheng, W.-A. Numerical study on the dynamics of a two-raft wave energy conversion device. J. Fluids Struct. 2015, 58, 271–290. [Google Scholar] [CrossRef]
- Sun, L.; Taylor, R.E.; Choo, Y.S. Responses of interconnected floating bodies. IES J. Part A Civ. Struct. Eng. 2011, 4, 143–156. [Google Scholar] [CrossRef]
- Sun, L.; Stansby, P.; Zang, J.; Moreno, E.C.; Taylor, P.H. Linear diffraction analysis for optimisation of the three-float multi-mode wave energy converter M4 in regular waves including small arrays. J. Ocean Eng. Mar. Energy 2016, 2, 429–438. [Google Scholar] [CrossRef]
- Sun, L.; Zang, J.; Stansby, P.; Moreno, E.C.; Taylor, P.H.; Taylor, R.E. Linear diffraction analysis of the three-float multi-mode wave energy converter M4 for power capture and structural analysis in irregular waves with experimental validation. J. Ocean Eng. Mar. Energy 2017, 3, 51–68. [Google Scholar] [CrossRef]
- Stansby, P.; Moreno, E.C.; Stallard, T. Large capacity multi-float configurations for the wave energy converter M4 using a time-domain linear diffraction model. Appl. Ocean Res. 2017, 68, 53–64. [Google Scholar] [CrossRef]
- Taghipour, R.; Perez, T.; Moan, T. Hybrid frequency-time domain models for dynamic response analysis of marine structures. Ocean Eng. 2008, 35, 685–705. [Google Scholar] [CrossRef]
- Kristiansen, E.; Hjulstad, Å.; Egeland, O. State-space representation of radiation forces in time-domain vessel models. Model. Identif. Control 2006, 27, 23–41. [Google Scholar] [CrossRef]
- Liu, C.; Yang, Q.; Bao, G. Performance investigation of a two-raft-type wave energy converter with hydraulic power take-off unit. Appl. Ocean Res. 2017, 62, 139–155. [Google Scholar] [CrossRef]
- Falnes, J. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2002; Volume 56, ISBN 0521017491. [Google Scholar]
- Newman, J.N. Absorption of wave energy by elongated bodies. Appl. Ocean Res. 1979, 1, 189–196. [Google Scholar] [CrossRef]
- Taghipour, R.; Perez, T.; Moan, T. Time-Domain Hydroelastic Analysis of a Flexible Marine Structure Using State-Space Models. J. Offshore Mech. Arct. Eng. 2008, 131, 11603. [Google Scholar] [CrossRef]
- Perez, T.; Fossen, T.I. Practical aspects of frequency-domain identification of dynamic models of marine structures from hydrodynamic data. Ocean Eng. 2011, 38, 426–435. [Google Scholar] [CrossRef]
- Duarte, T.; Sarmento, A.; Alves, M.; Jonkman, J. State-Space Realization of the Wave-Radiation Force within FAST. In Proceedings of the ASME 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013; pp. 1–12. [Google Scholar] [CrossRef]
- Sanathanan, C.; Koerner, J. Transfer function synthesis as a ratio of two complex polynomials. IEEE Trans. Automat. Contr. 1963, 8, 56–58. [Google Scholar] [CrossRef]
- ANSYS AQWA. Available online: http://www.ansys.com/fr-fr/products/structures/ansys-aqwa (accessed on June 2015).
- Wang, D.; Qiu, S.; Ye, J. An experimental study on a trapezoidal pendulum wave energy converter in regular waves. China Ocean Eng. 2015, 29, 623–632. [Google Scholar] [CrossRef]
- Faltinsen, O.M. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1990; Volume 1, ISBN 0-521-45870-6. [Google Scholar]
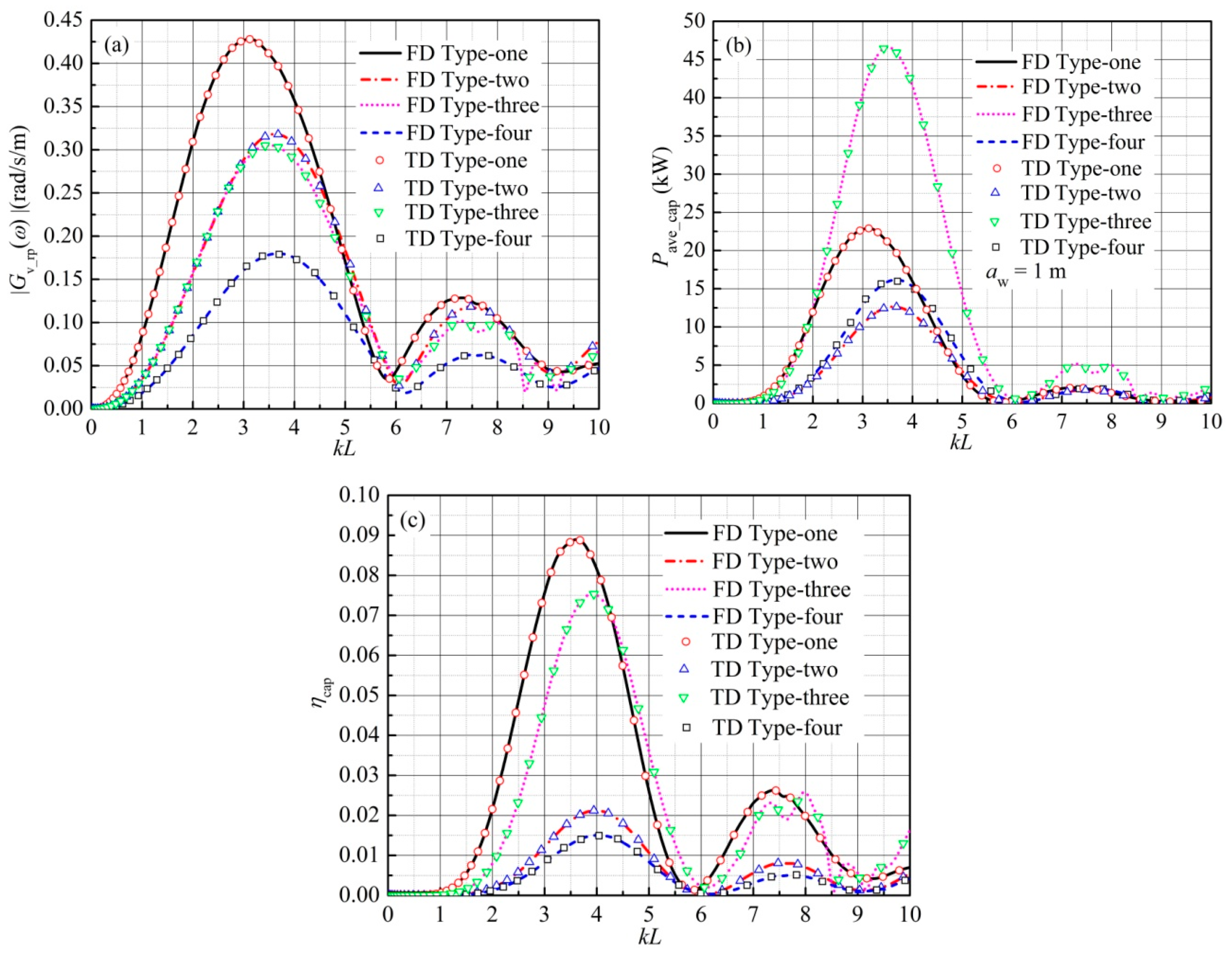
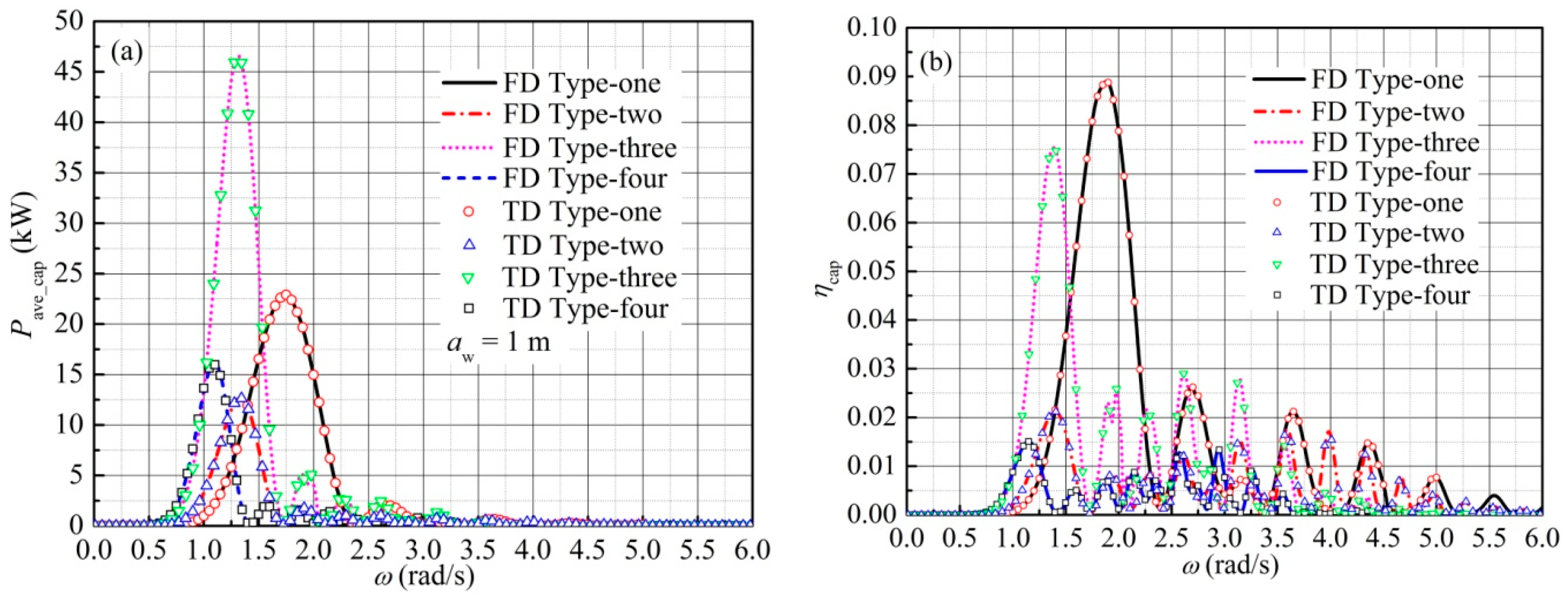


| Parameter | Type-One | Type-Two | Type-Three | Type-Four |
|---|---|---|---|---|
| Raft length L (m) | 10 | 20 | 20 | 30 |
| Raft diameter D (m) | 1 | 1 | 2 | 2 |
| Raft space d0 (m) | 1 | 1 | 1 | 1 |
| Raft density ρ0 (kg/m3) | 512.5 | 512.5 | 512.5 | 512.5 |
| Raft volume V/m3 | 7.8540 | 15.7080 | 62.8319 | 94.2478 |
| Damping coefficient cpto (kN/m/s) | 500 | 500 | 500 | 500 |
| Mounting position r0 (m) | 0.5 | 0.5 | 1 | 1 |
| Optimal ratio kL | 3.1163 | 3.6184 | 3.4987 | 3.6715 |
| Optimal ratio of raft length to wavelength | 0.4960 | 0.5759 | 0.5568 | 0.5843 |
| Resonant frequency of relative pitch velocity ωrp (rad/s) | 1.7485 | 1.3322 | 1.3100 | 1.0957 |
| Resonant frequency of heave velocity ωh (rad/s) | 1.4078 | 1.2354 | 1.2100 | 1.0179 |
| Resonant frequency of surge velocity ωs (rad/s) | 1.0144 | 0.7370 | 0.7322 | 0.6021 |
| Amplitude of FRF of wave amplitude to relative pitch velocity at ωrp (rad/s/m) | 0.4281 | 0.3181 | 0.3054 | 0.1799 |
| Amplitude of FRF of wave amplitude to heave velocity at ωh (m/s/m) | 1.2623 | 1.5099 | 1.4735 | 1.2589 |
| Amplitude of FRF of wave amplitude to surge velocity at ωs (m/s/m) | 0.7881 | 0.5624 | 0.5655 | 0.4674 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Yang, Q.; Bao, G. State-Space Approximation of Convolution Term in Time Domain Analysis of a Raft-Type Wave Energy Converter. Energies 2018, 11, 169. https://doi.org/10.3390/en11010169
Liu C, Yang Q, Bao G. State-Space Approximation of Convolution Term in Time Domain Analysis of a Raft-Type Wave Energy Converter. Energies. 2018; 11(1):169. https://doi.org/10.3390/en11010169
Chicago/Turabian StyleLiu, Changhai, Qingjun Yang, and Gang Bao. 2018. "State-Space Approximation of Convolution Term in Time Domain Analysis of a Raft-Type Wave Energy Converter" Energies 11, no. 1: 169. https://doi.org/10.3390/en11010169
APA StyleLiu, C., Yang, Q., & Bao, G. (2018). State-Space Approximation of Convolution Term in Time Domain Analysis of a Raft-Type Wave Energy Converter. Energies, 11(1), 169. https://doi.org/10.3390/en11010169





