Laboratory Investigation of Flow Paths in 3D Self-Affine Fractures with Lattice Boltzmann Simulations

Abstract

In this study, laboratory experiments and simulations have been conducted to investigate single water phase flow through self-affine rough fractures. It is the first time that 3D printing technology is proposed for the application of generating self-affine rough fractures. The experimental setup was designed to measure the water volume by dividing the discharging surface into five sections with equal distances under constant injection flow rates. Water flow through self-affine rough fractures was simulated numerically by using the Lattice Boltzmann method (LBM). An agreement between the experimental data and the numerical simulation results was achieved. The fractal dimension is positively correlated to fracture surface roughness and the fracture inclination represents the gravity force acting on the water flow. The influences of fracture inclinations, fractal dimensions, and mismatch wavelengths were studied and analyzed, with an emphasis on flow paths through a self-affine rough fracture. Different values of fractal dimensions, fracture inclinations, and mismatch wavelengths result in small changes of flow rates from five sections of discharging surface. However, the section of discharging surface with the largest flow rate remains constant. In addition, it is found that the gravity force can affect flow paths. Combined with the experimental data, the simulation results are used to explain the preferential flow paths through fracture rough surfaces from a new perspective. The results may enhance our understanding of fluid flow through fractures and provide a solid background for further research in the areas of energy exploration and production.

1. Introduction

Fluid flow in fracture networks that are constituted by individual fractures in reservoir rocks is encountered in different areas, such as enhanced oil and gas recovery, geothermal reservoir exploitation, geological sequestration of carbon dioxide, and water resources exploitation [1,2,3,4]. Therefore, the understanding of fluid flow in a fracture is of crucial importance for modeling flow in more complex fracture networks.

For fully saturated, single phase flow in a single fracture, the parallel plate model is the most widely used conceptual model because it is very convenient for quantitative analysis [5,6]. In a parallel plate model, the derivation of the cubic law is given as the solution to the Navier-Stokes equations for incompressible, steady state flow through a single fracture [7]. However, it ignores the complex roughness of actual fracture surfaces. The roughness of fracture surfaces is of great importance in qualifying the flow and transport processes through fractures. Although the roughness of fractures is really complex, many experimental approaches and modeling methods have been proposed to investigate fracture roughness and its impact on flow. Among different experimental approaches, X-ray computed tomography and 3D laser scanning techniques have been proved as effective experimental approaches to characterize fracture surfaces with variable apertures [8,9,10]. Experimental studies show that fracture roughness determines fracture aperture density distribution and affects fluid flow through fractures [11,12,13,14,15].

In order to represent fluid flow through fractures, the Reynolds Lubrication Equation was introduced, describing laminar flow between slightly nonparallel surfaces, a more computationally intensive solution of the Navier-Stokes equations [16]. A new model considering the spatial variability of fracture apertures was developed by solving the Reynolds equation [17], which is well known as the classical Local Cubic Law. On the basis of solving the Reynolds Equation, many researchers evaluated and applied this approximation for estimating the hydraulic behaviors of rough-walled fractures [18,19,20,21]. Modeling a rough-walled fracture required three main parameters: the fractal dimension, the roughness at a reference length scale, and a length scale describing the degree of mismatch between two fracture surfaces [22]. The use of various simplifications of the Navier-Stokes equation including the lubrication equations was discussed, showing that at low Reynolds numbers (Re < 1), the effective cubic law aperture was lower than the actual aperture by a factor related to the ratio of the mean aperture to the aperture standard deviation [23,24]. Flow in synthetic self-affine fractures was simulated [25] and an applied range of the Reynolds Equation for flow in a fracture was analyzed by Yeo and Ge [26]. A modified Local Cubic Law that takes into account local tortuosity and roughness and works across a low range of local Reynolds Numbers was developed by Wang et al. [27].

In recent decades, the Lattice Boltzmann method (LBM), an extension of Lattice Gas Automata, has been applied to solve problems with geometrically complex boundaries [28,29,30,31,32]. Fluid flow in the fractures with rough surfaces was modeled and simulated using the Lattice Gas Automata [33,34]. LBM was applied for the permeability prediction of rough-walled fractures through various simulation confining pressure conditions appropriate to mid-crustal depths [35]. The scaling behaviors of transport properties in rough self-affine fractures was studied through the Lattice Boltzmann simulations, showing that anisotropy of the fracture has more influence on the fracture permeability than the fractal dimension and the mean fracture aperture [36]. Dou et al. [37] used the LBM to investigate the influence of wettability in a 3D self-affine rough fracture, finding that the wettability has a significant effect on the evolution of effective interfacial areas. With the application of the LBM, the influence of surface roughness on nonlinear flow behaviors in 3D self-affine rough fractures was simulated by considering the secondary roughness [38]. Briggs et al. [39] also investigated the effects of roughness on flow in fractures, showing that increasing fracture roughness led to greater eddy volumes and lower effective hydraulic conductivities for the same Re values.

2. Mathematical Methods

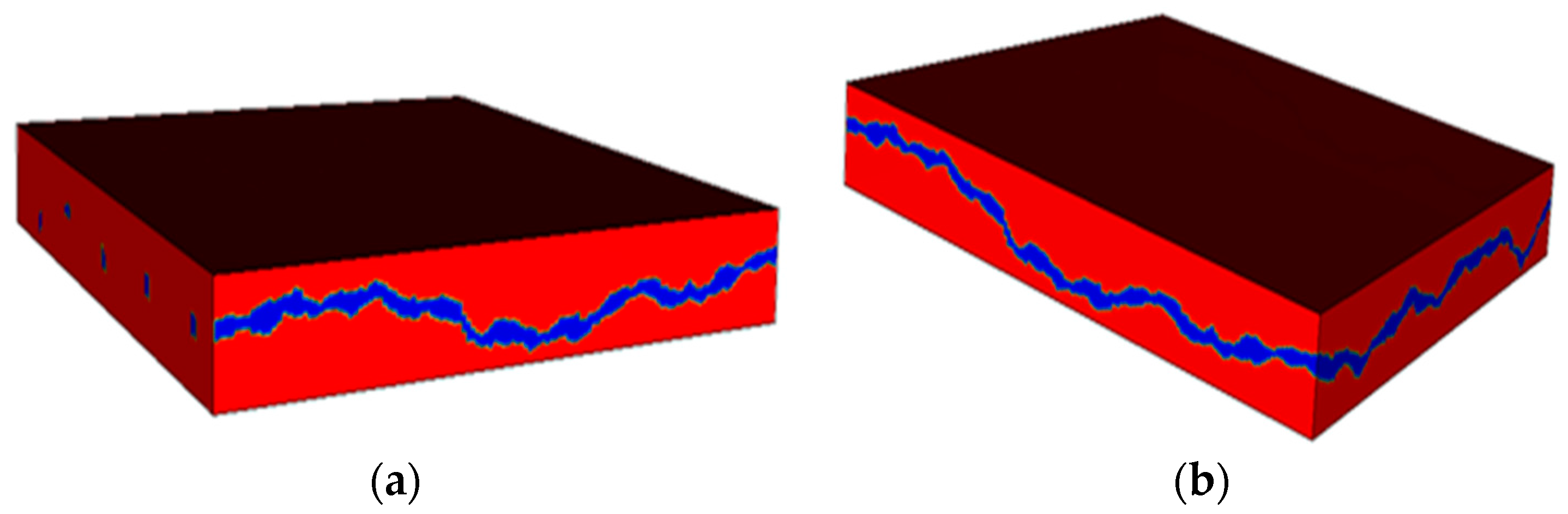
2.1. Generation of Fracture Rough Surfaces

The term self-affine fractal was used to describe fractal shapes that occur as natural surfaces, and are scaled by different amounts in all directions to produce statistical equivalence with self-similar fractals [40,41,42,43,44,45,46]. Mandelbrot [40] introduced the fractional Brownian motions (fBm) concept as a generalization of random function. The rough surfaces of natural fractures are generated synthetically by following a self-affine fractal distribution and the self-affinity is usually tested by fBm [34,47,48,49].

The statistical self-affine property can be expressed with the following mean and a variance of increments [50]:

$${\sigma }^2\left(r\right)={\sigma }^2\left(1\right)r^{2H}$$

(1)

where ${\sigma }^2$ is the variance defined as a function of r, r is a constant, and H is the Hurst exponent.

The range of the Hurst exponent varies from 0 to 1, noting that the value of the Hurst exponent has been proved to mainly distribute between 0.45 and 0.85 [49,51]. The self-affine distribution is produced with the fractal dimension D = 3 − H. For example, a Hurst exponent of 0.8 means that the fractal dimension is equal to 2.2.

In addition, the variation between two real fracture surfaces should be taken into consideration [22,52]. Based on a previous study, Ogilvie et al. [53] proposed a parameter PSD ratio with the following form:

$$\mathrm{PSDR}=\frac{\mathrm{PSD}\left(\mathrm{aperture}\right)}{\mathrm{PSD}\left(\mathrm{upper} \mathrm{surface}\right)+\mathrm{PSD}\left(\mathrm{lower} \mathrm{surface}\right)}$$

(2)

The PSDR calculates the ratio of the PSDs from the aperture with the sum of the PSDs of the two surfaces composing the fracture.

Based on the theories proposed above, the software SynFrac [53] has been used to produce 128 × 128 data sets for generating self-affine rough fracture surfaces with controlled fracture surface properties. In addition to the fractal dimension, capturing the fracture properties at all wavelengths is an important consideration when generating synthetic fractures. An example of input parameters used to generate self-affine rough fracture surfaces synthetically is shown in the following section.

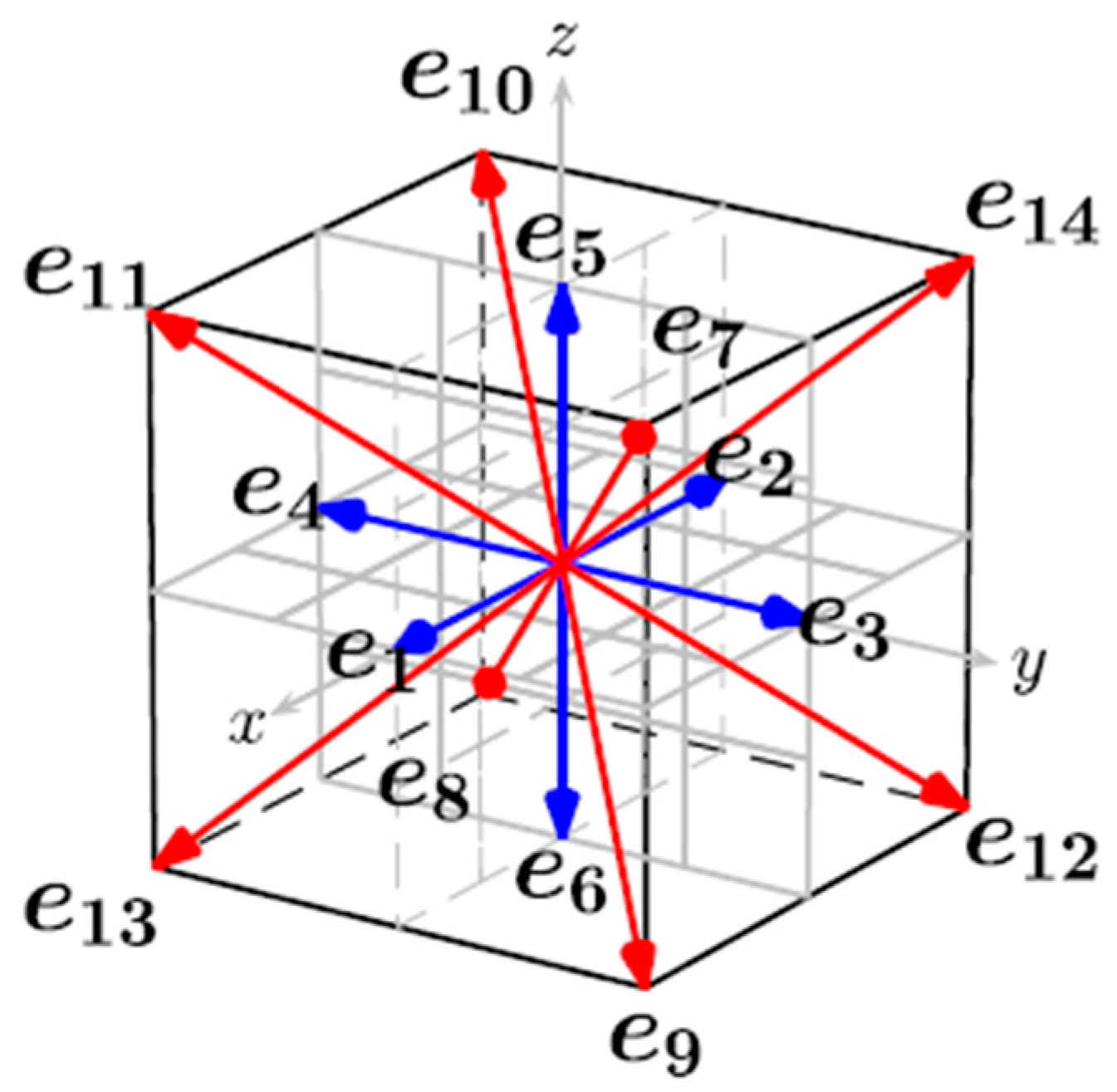
2.2. Lattice Boltzmann Method

LBM provides an effective numerical method for the computational modeling of single and multiphase flow systems with complex geometries. LBM has solved the Boltzmann equation on a discrete lattice and proved that Navier-Stokes equations can be recovered at a macroscopic scale [32,54]. This method has been successfully applied to the simulation of various cases, such as flow in porous media, colloidal suspensions, and thermal flows [55,56,57].

In this study, a three-dimensional D3Q15 lattice model was used for the simulation of water phase flow through a single self-affine rough fracture [58,59]. The space of the D3Q15 model is divided into a cubic domain that has fifteen discrete velocities in Figure 1 [59]. The velocity vectors ${\overrightarrow{e}}_i$ are given by:

$${\overrightarrow{e}}_i=\{\begin{array}{c}0,\\ \left(\pm 1,0,0\right),\left(0,\pm 1,0\right),\left(0,0,\pm 1\right),\\ \left(\pm 1,\pm 1,\pm 1\right),\end{array}\begin{array}{c}i=0,\\ i=1–6,\\ i=7–14.\end{array}$$

(3)

Based on the Chapman-Enskog expansion of the Boltzmann equation [60], the distribution function satisfying the evolution rule is shown as follows:

$$f_i\left(\overrightarrow{x}+{\overrightarrow{e}}_i{\delta }_t,t+{\delta }_t\right)=f_i\left(\overrightarrow{x},t\right)+{\mathsf{\Omega }}_{col}$$

(4)

where $f_i\left(\overrightarrow{x},t\right)$ is the fluid particle distribution function with velocity ${\overrightarrow{e}}_i$ (the mesoscopic velocity in the i-th direction) at position $\overrightarrow{x}$ and time t, ${\delta }_t$ is the length of time step, and ${\mathsf{\Omega }}_{col}$ is the collision operator representing the relaxation process due to the collision of the fluid particles.

The Bhatnagar-Gross-Krook model for the collision operator is used [54]:

$${\mathsf{\Omega }}_{col}=\frac{{\delta }_t}{\tau }\left(f_i^{eq}-f_i\right)$$

(5)

where τ is the relaxation time and $f_i^{eq}$ is the equilibrium distribution.

In lattice units, the relaxation time τ governs the rate at which the fluid tends towards equilibrium with the following expression:

$$\tau =\frac{3\upsilon {\delta }_t}{{\delta }_x^2}+0.5$$

(6)

where ν is the kinematic viscosity of the fluid.

The definition of $f_i^{eq}$ is given by:

$$f_i^{eq}={\omega }_i\rho \left(1+3\frac{{\overrightarrow{e}}_i\cdot \overrightarrow{u}}{C^2}+\frac{9{\left({\overrightarrow{e}}_i\cdot \overrightarrow{u}\right)}^2}{C^4}-\frac{3u^2}{2C^2}\right)$$

(7)

with C = δ_x/δ_k defined as a characteristic lattice velocity in a cell size δ_x.

The bounce-back boundary condition [57,58,61,62] is used here because the fluid is assumed to be reflected by the solid boundaries. In the bounce-back condition, after the collision step, the distribution functions are swapped symmetrically as follows:

$$f_{-i}=f_i$$

where the subscript −i refers to the opposite direction to the i-th velocity.

The density $\rho$ and the velocity $\overrightarrow{u}$ at a cell position $\overrightarrow{x}$ can be calculated as:

$$\rho \left(\overrightarrow{x}\right)={\displaystyle {\sum }_{i=0}^{14}{f}_i}\left(\overrightarrow{x}\right)$$

(8)

$$\overrightarrow{u}\left(\overrightarrow{x}\right)=\frac{{\displaystyle {\sum }_{i=0}^{14}{f}_i\left(\overrightarrow{x}\right){\overrightarrow{e}}_i}}{\rho \left(\overrightarrow{x}\right)}$$

(9)

And the weight factors for the D3Q15 model are:

$${\omega }_i=\{\begin{array}{c}2/9,\\ 1/9,\\ 1/72,\end{array}\begin{array}{c}i=0,\\ i=1\sim 6,\\ i=7\sim 14.\end{array}$$

(10)

With the purpose of modeling any additional forces, a net force $\overrightarrow{F}$ that modifies the velocity used for the calculation of the equilibrium function is introduced as follows [63]:

$${\overrightarrow{u}}^{eq}=\overrightarrow{u}+\frac{{\delta }_t\overrightarrow{F}}{\rho }$$

(11)

For this study, the gravity force should be taken into consideration. The additional force is $\overrightarrow{F}=\rho \overrightarrow{g}$, where $\overrightarrow{g}$ is the gravitational acceleration [64].

3. Experimental Design and Setup

In recent years, 3D printing has been proved to be an efficient technology that can be applied in the areas of manufacturing, medical, and industry [65,66,67,68]. In this experiment, 3D printing technology was used in order to reflect rough surfaces of fractures accurately based on the data generated by the numerical method mentioned above. Figure 2 shows an example of top and bottom surfaces for a facture model used in the 3D builder. Self-affine rough fractures with square shapes were printed by using brightly colored filaments with 204.8 mm each side (Figure 3). In order to handle fractures easily during the experiment process, the 3D printed fractures were put into the formwork mould and concrete was poured on the outer surface of the 3D printed fractures (Figure 4). Three sets of self-affine rough fractures are printed and moulded with different fractal dimensions that correspond to 2.2, 2.3, and 2.4, respectively. In Figure 5, a 30 L water drum was installed and filled with water with a green color that was easily identified. Five micro drippers were used for water injection into self-affine rough fractures. In order to maintain a constant injection flow rate, water should be added into the water drum to maintain a constant hydraulic head during the experimental process. Based on the constant hydraulic head, flow rates for five drippers can be calculated, which is 0.0728 mL/s. The fracture sample was put on the top of a container that was divided into five equal sections and there was another same container located below the upper container for measuring the volume of water discharging from each section. With the application of software called Time-lapse Video, a laptop was placed in front of the experimental apparatus to record the volume of water discharging from each section of the fracture sample every 20 s.

During the experiments, water volume discharging from the fracture sample in the containers was measured and recorded. The record would stop when one of the containers was full of water. In order to identify this more easily, the water volume in each container was marked as Outlet 1, 2, 3, 4, and 5.

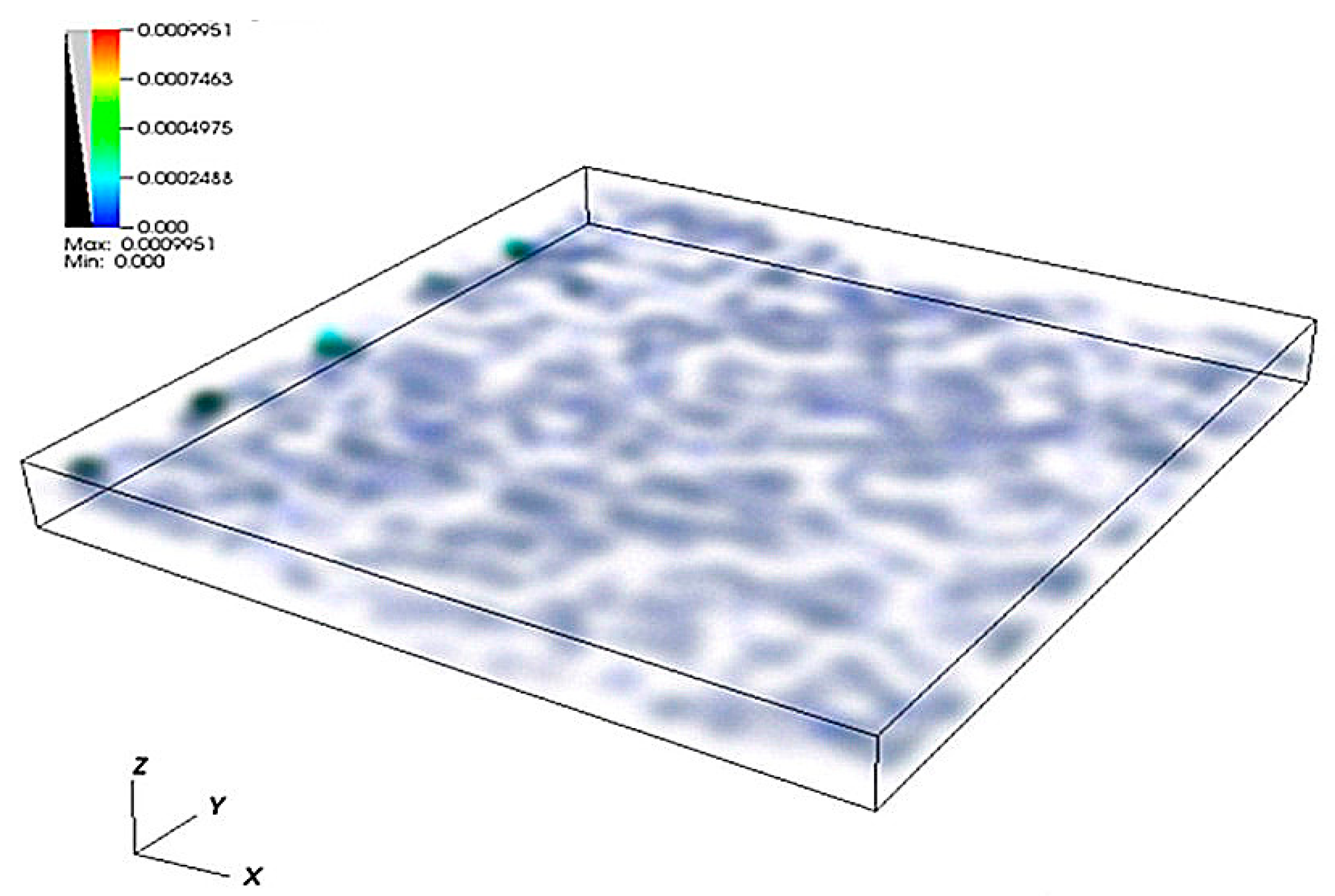
4. Results and Discussion

The length and width of self-affine rough fracture samples for the experiments is 204.8 mm. The value of height is 20.8 mm because it is larger than apertures from 128 × 128 data sets used for generating fracture samples and it can save computational costs. The sample is divided into 512 × 512 × 52 cells and the length, width, and height of each cell is 0.4 mm. The real physical units can be transformed into lattice units based on non-dimensional parameters and relevant correlations.

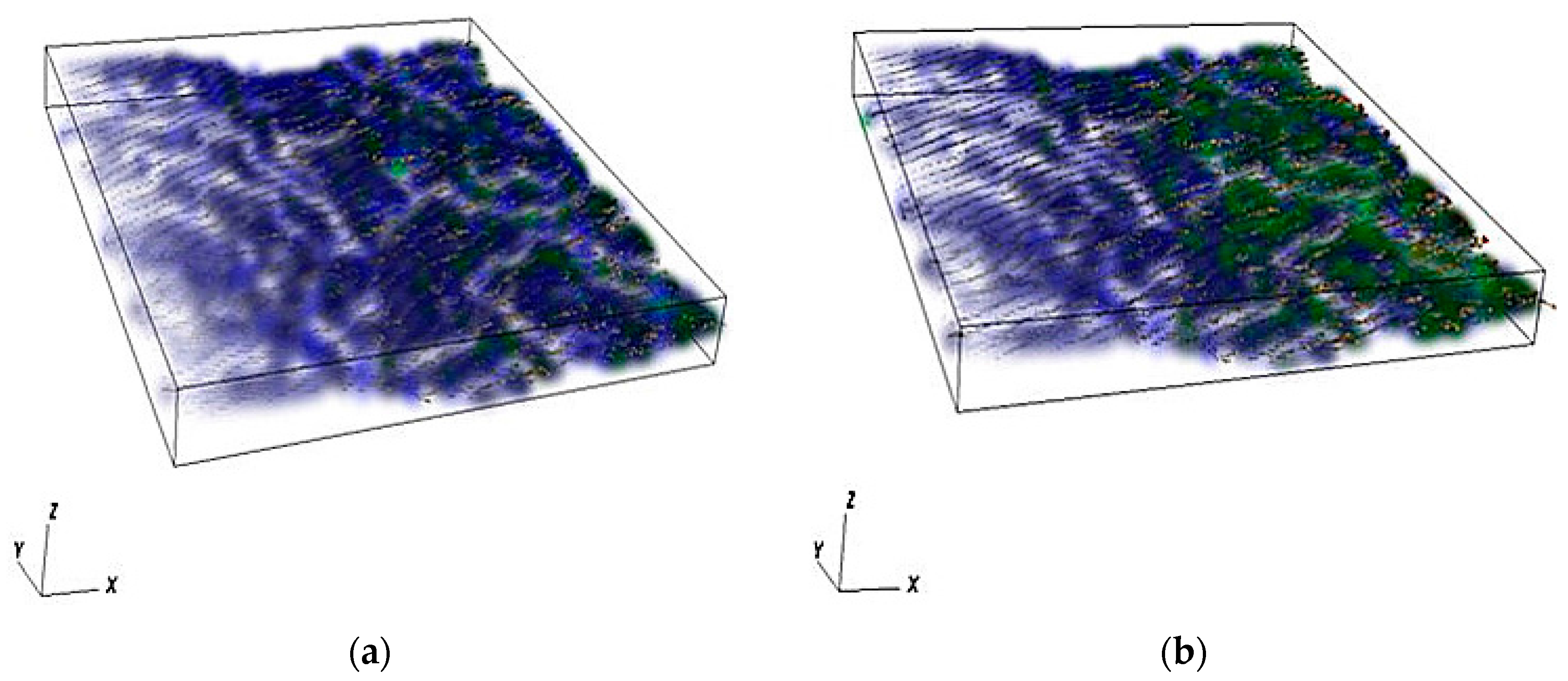
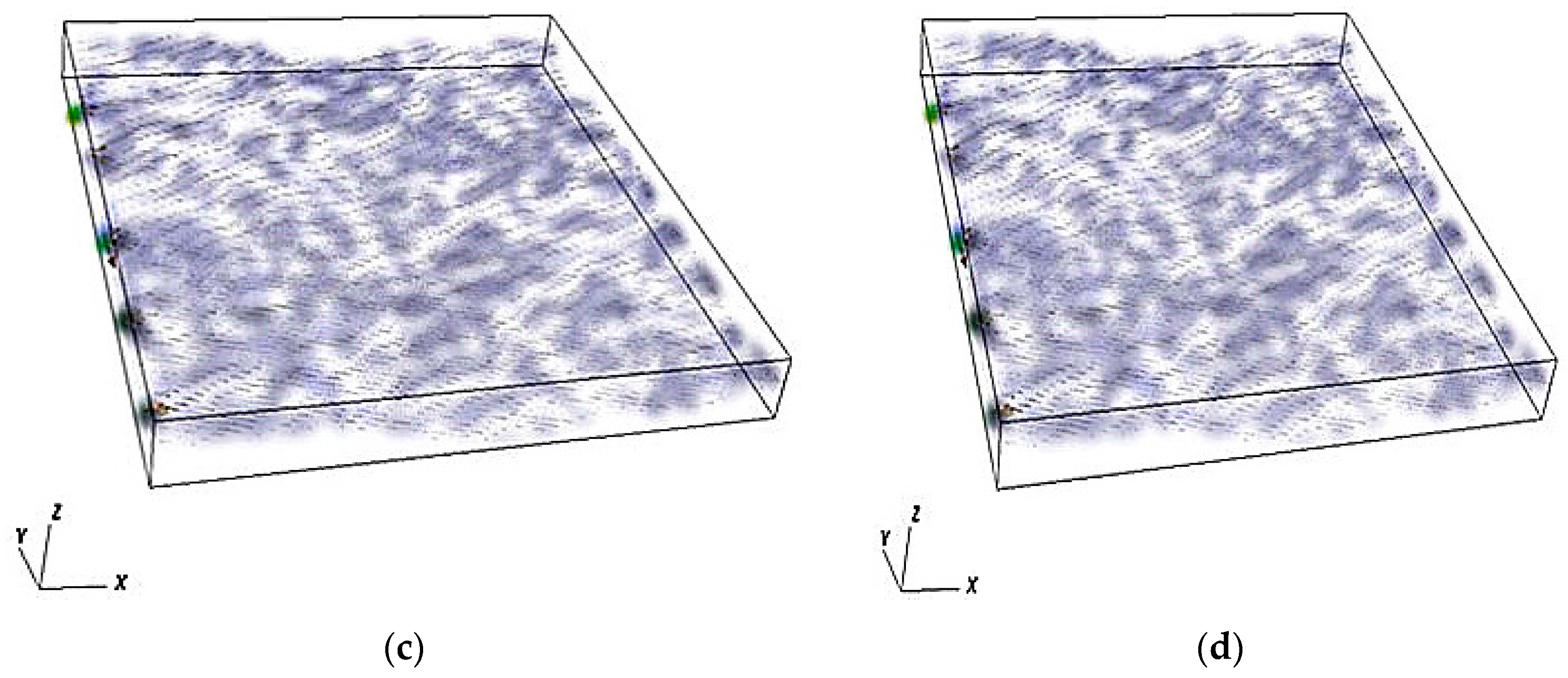
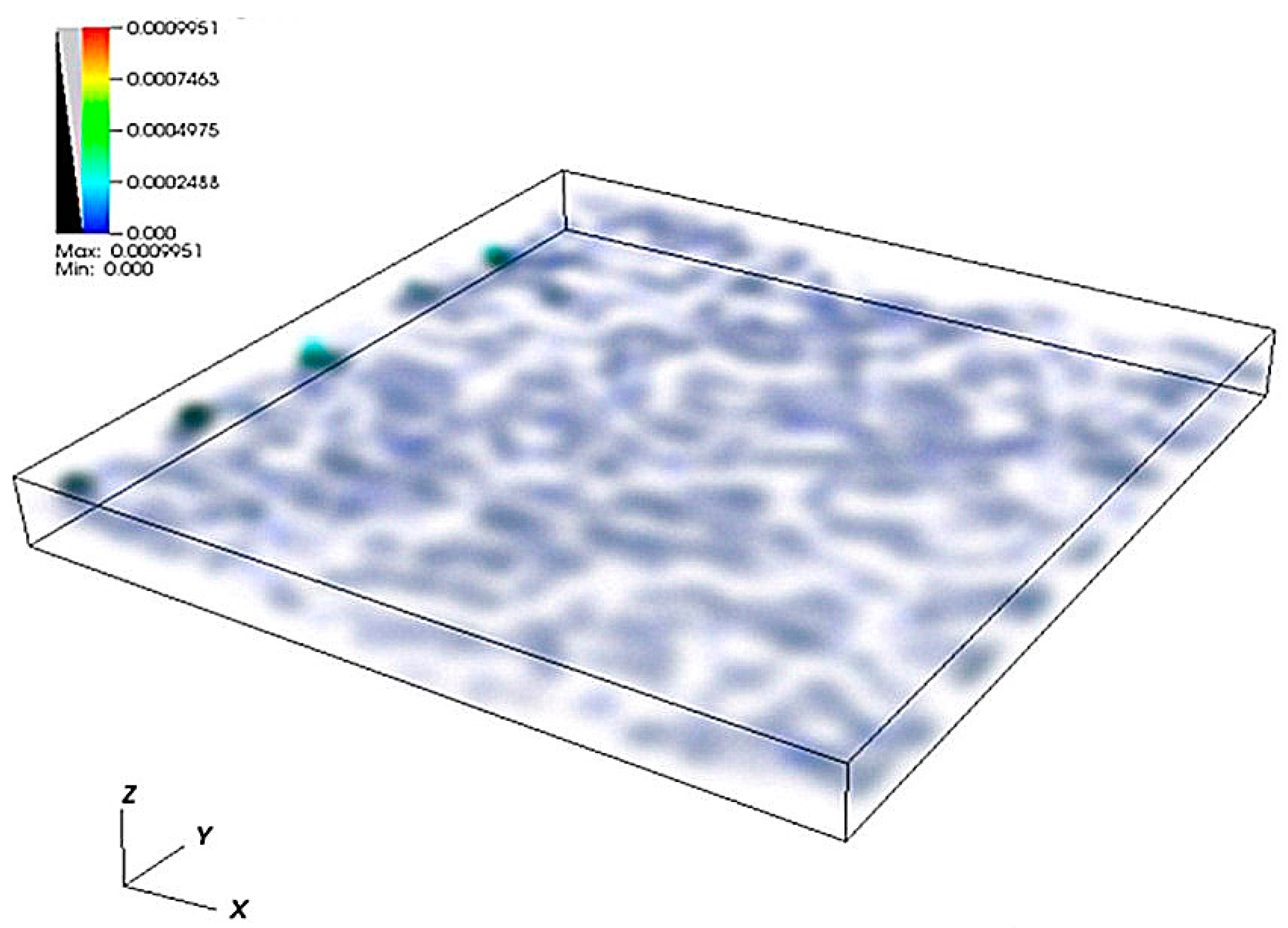
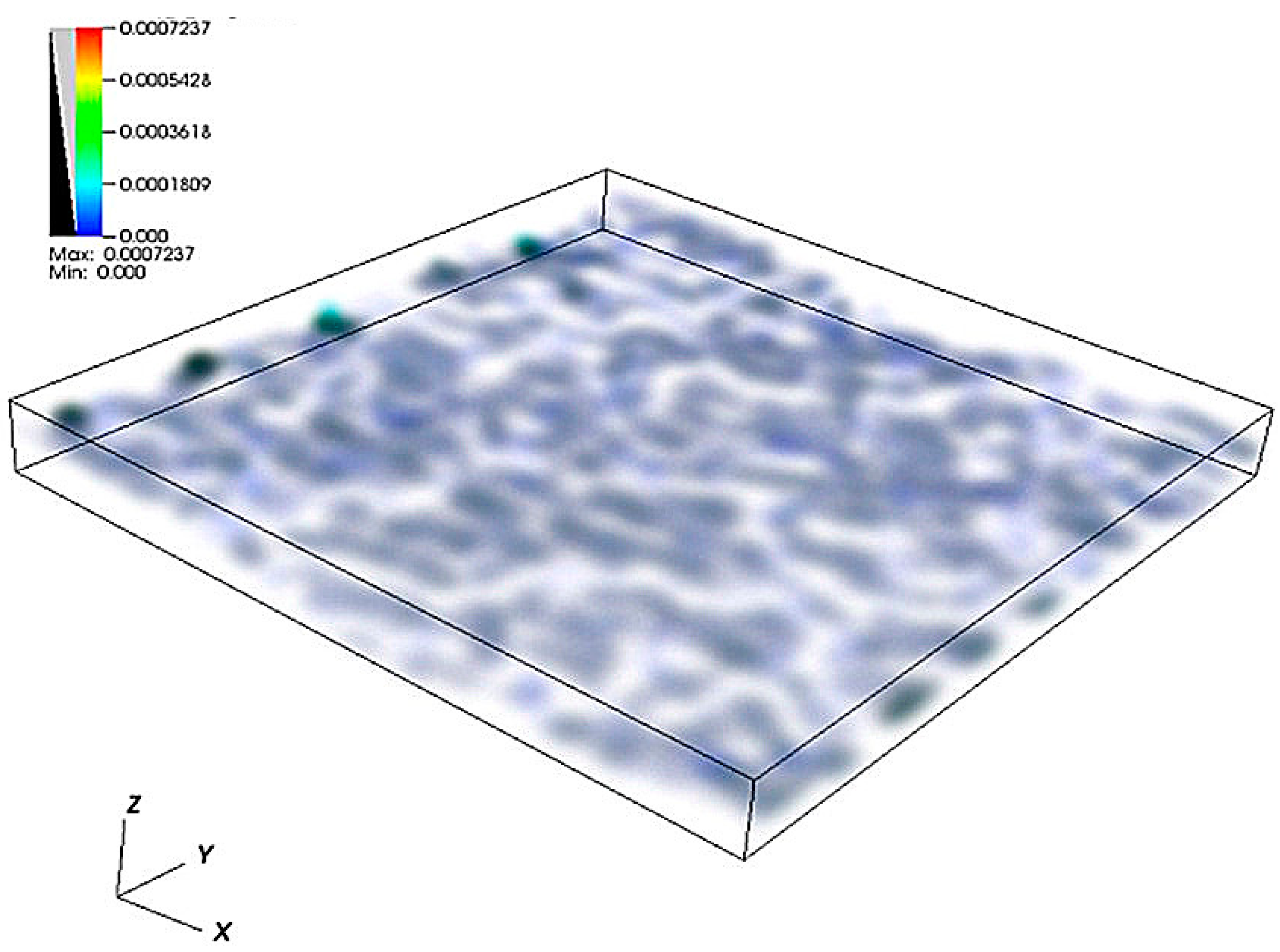
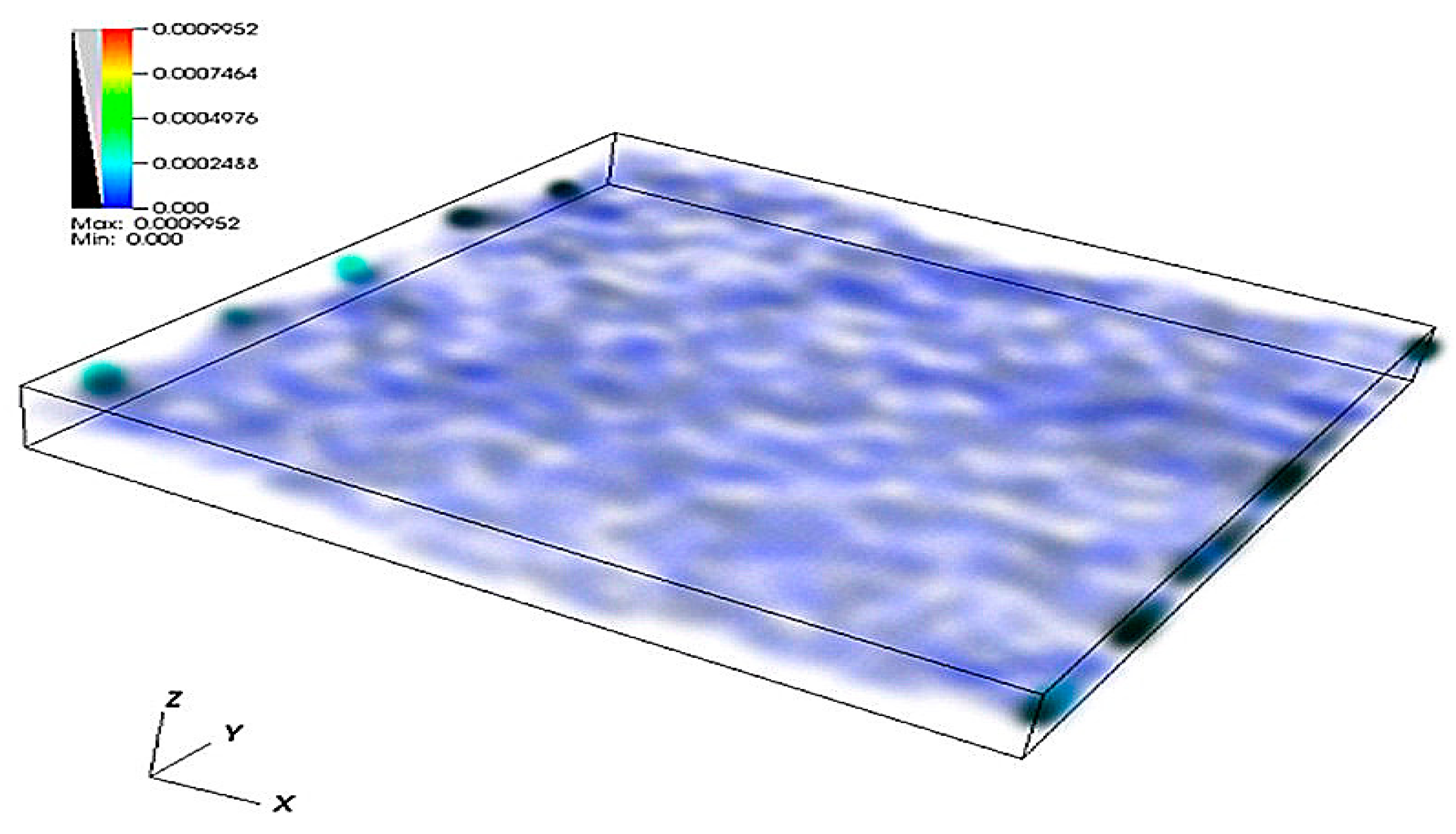
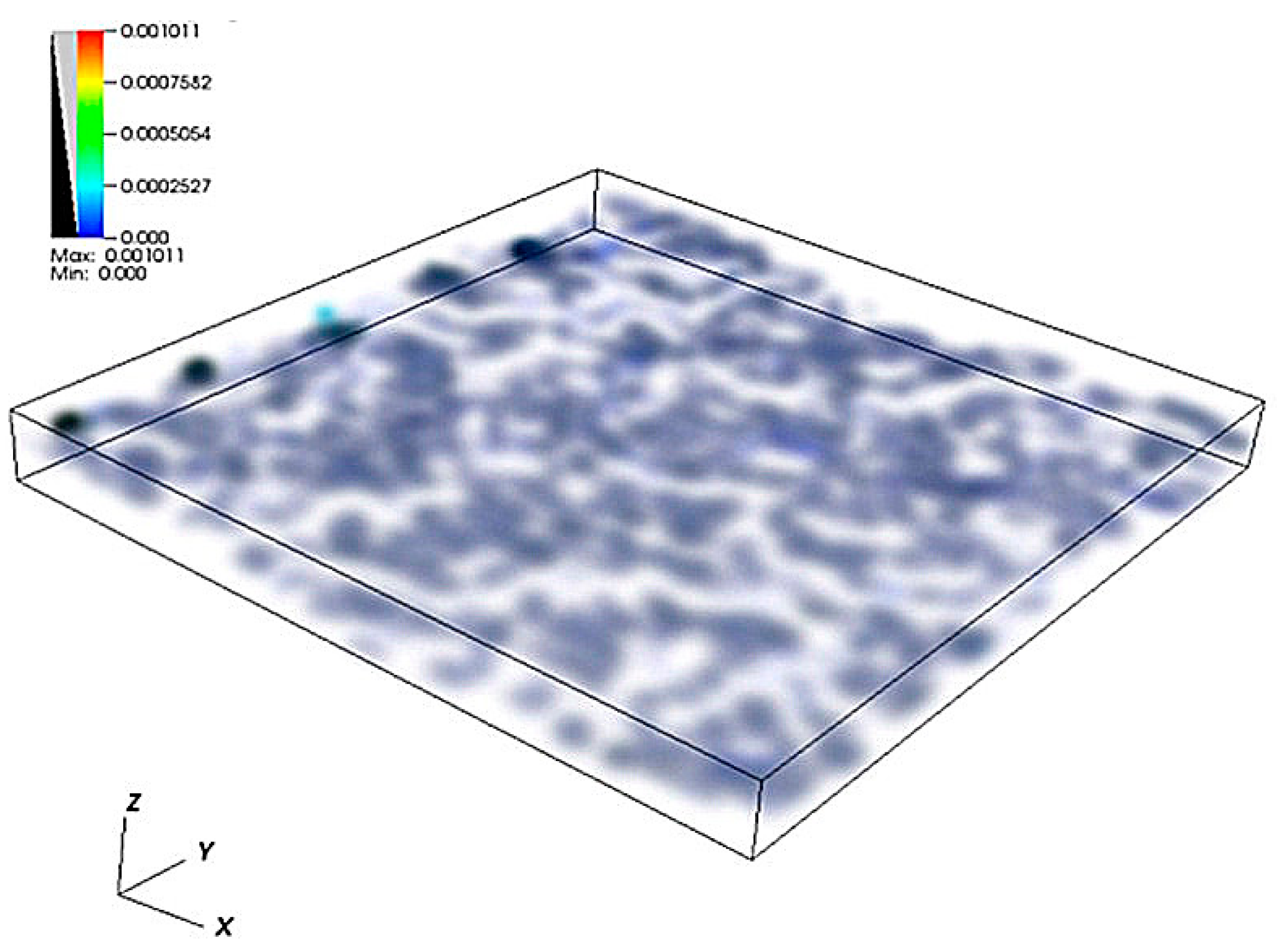
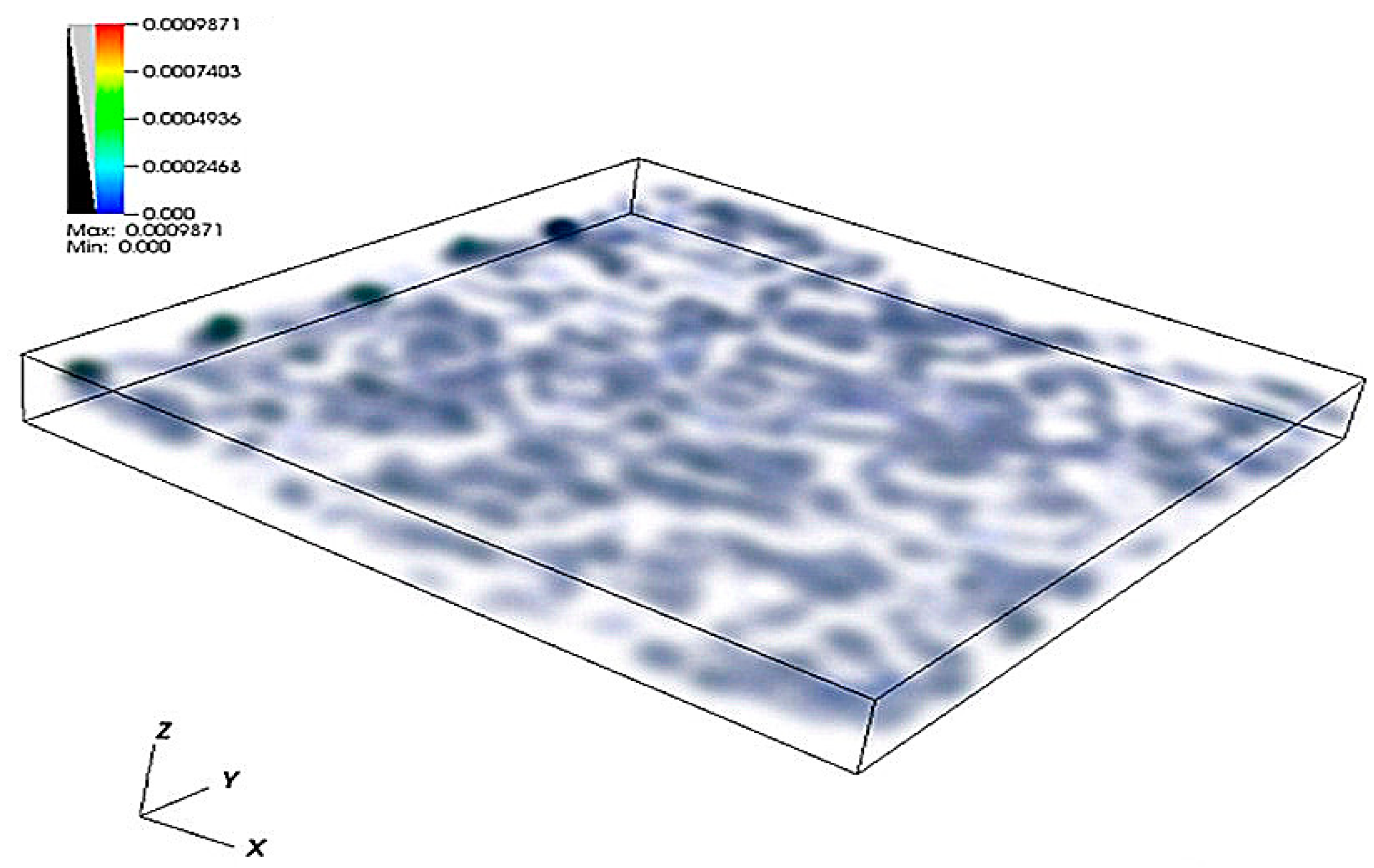
4.1. Simulation of Water Flow through the Self-Affine Rough Fracture

The self-affine rough fracture model with fractal dimension 2.2 is shown in Figure 6. Five injection holes on the surface of the fracture model are shown to reflect the fact that five micro drippers were used in the experiment. In addition, the areas of the injection holes are the same to guarantee the same injection rates. The velocity distributions of water flow through the fracture with fractal dimension 2.2 and inclination 65° at different times are shown in Figure 7. It is obvious that the flow paths can be identified on the basis of the velocity distributions. Unlike the parallel plate model, the flow paths in this study are irregular and based on a smaller scale distribution of fracture roughness. The values of velocity and velocity distributions are variable at the time t_a = 5000, 10,000, and 60,000 ts, respectively. This is because the water flow through the fracture is at an unsteady state. Based on the simulation results, the maximum velocity and velocity distributions between the time t_a = 60,000 and 70,000 ts are the same. It can be concluded that the water flow has reached a steady state at the time t_a = 60,000 ts in Figure 7. The values of velocities at the steady state are used to calculate flow rates of five sections from the discharging surface and the results are compared with experimental data in the following sections.

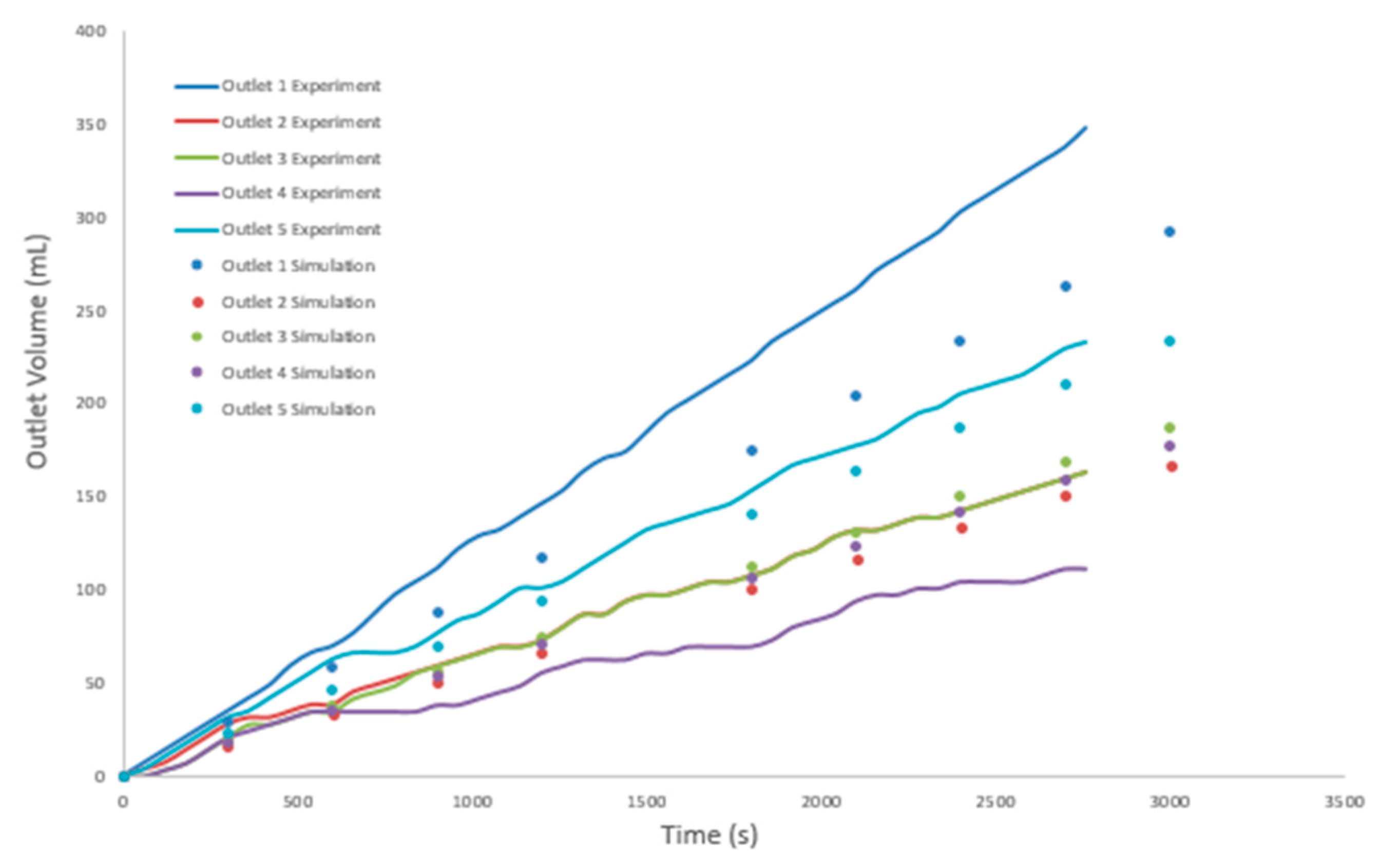
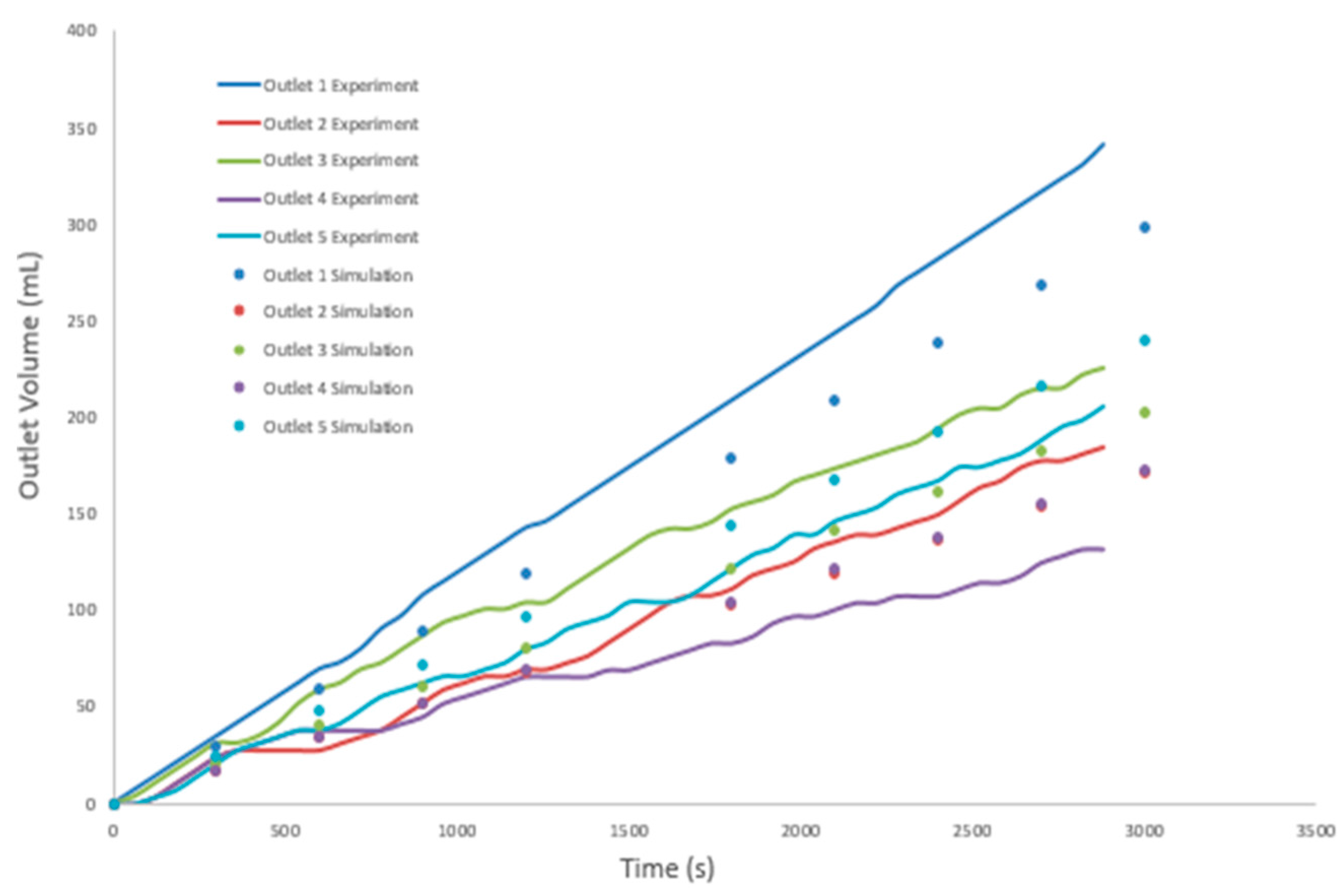
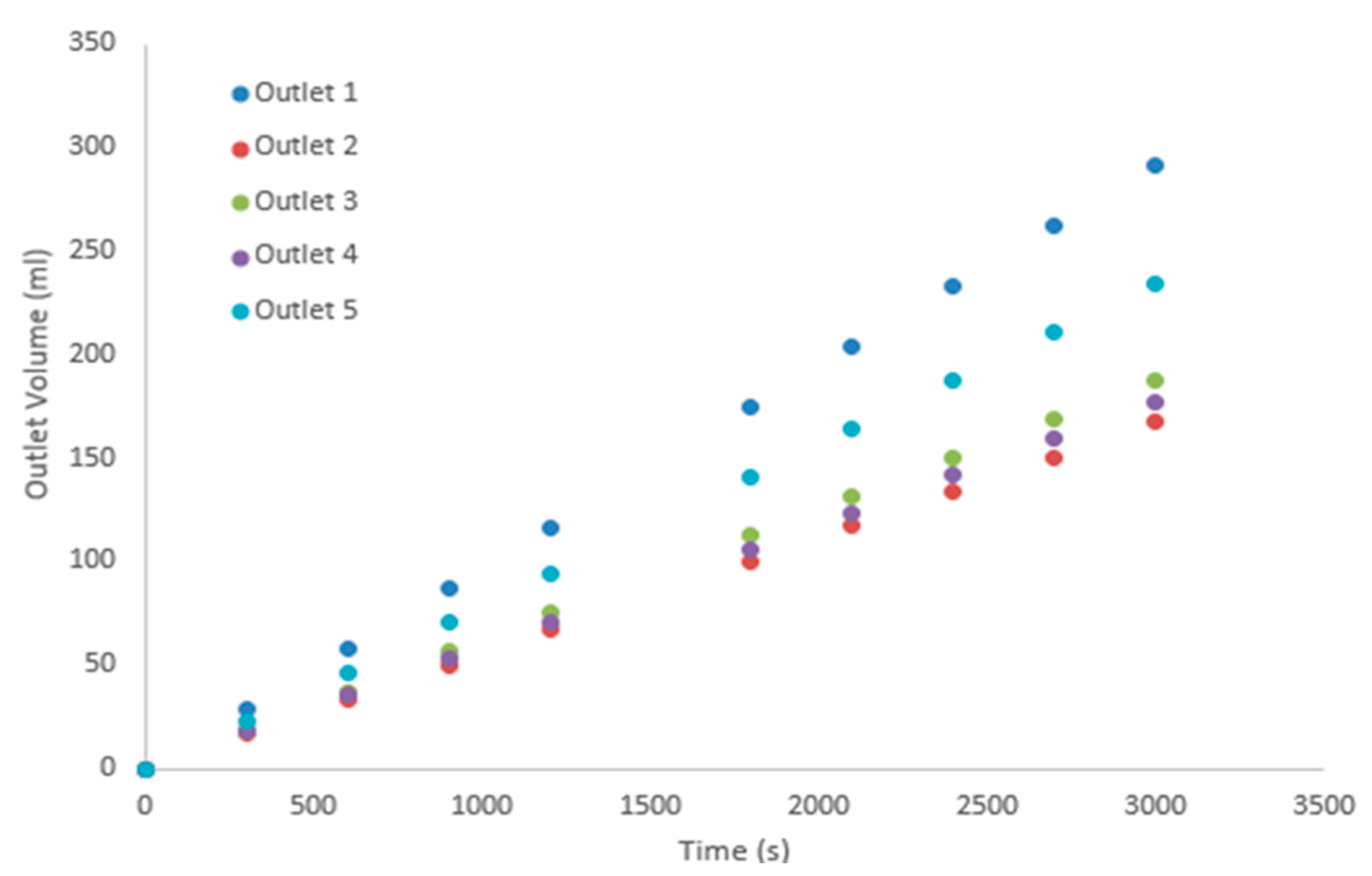
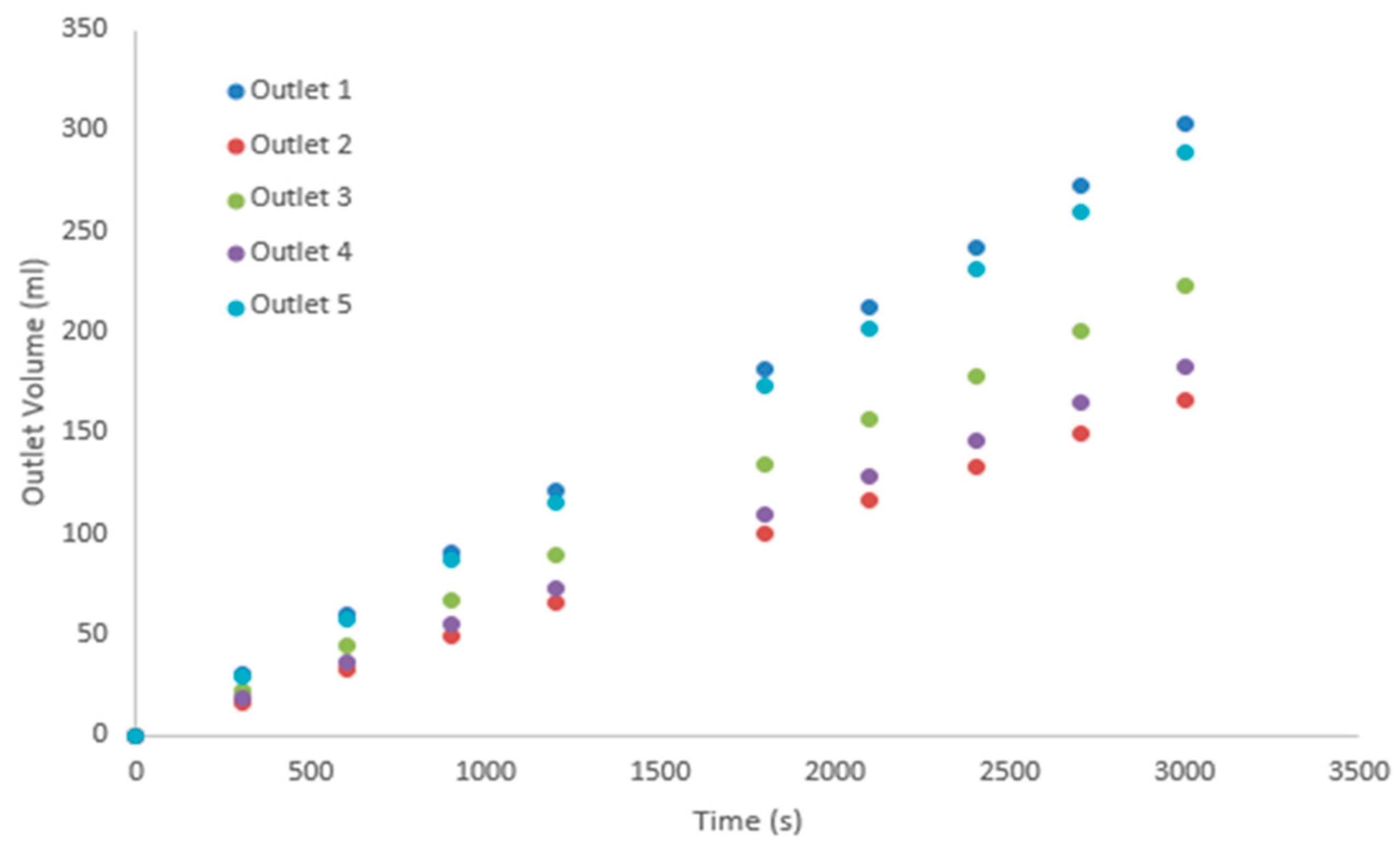
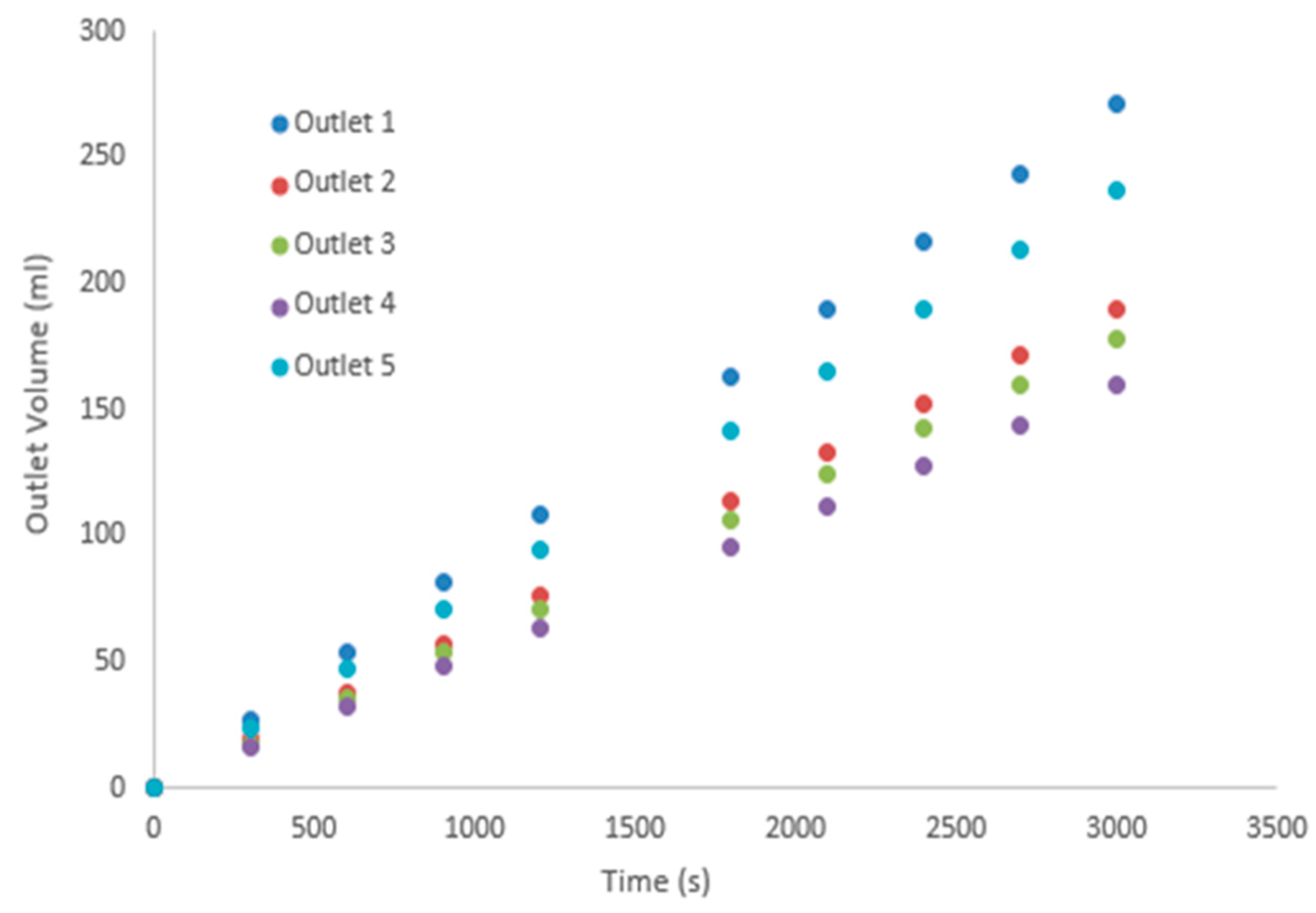
4.2. Model Validation

In this section, the data set includes: the fractal dimension is equal to 2.2 and the fracture inclinations are 65° and 75°. The simulation results from the LBM model are presented in Figure 8 and Figure 9 to allow comparisons with the experimental data. The data for Figure 8 and Figure 9 are shown in in the

Table A1. Experimental data for Figure 8.

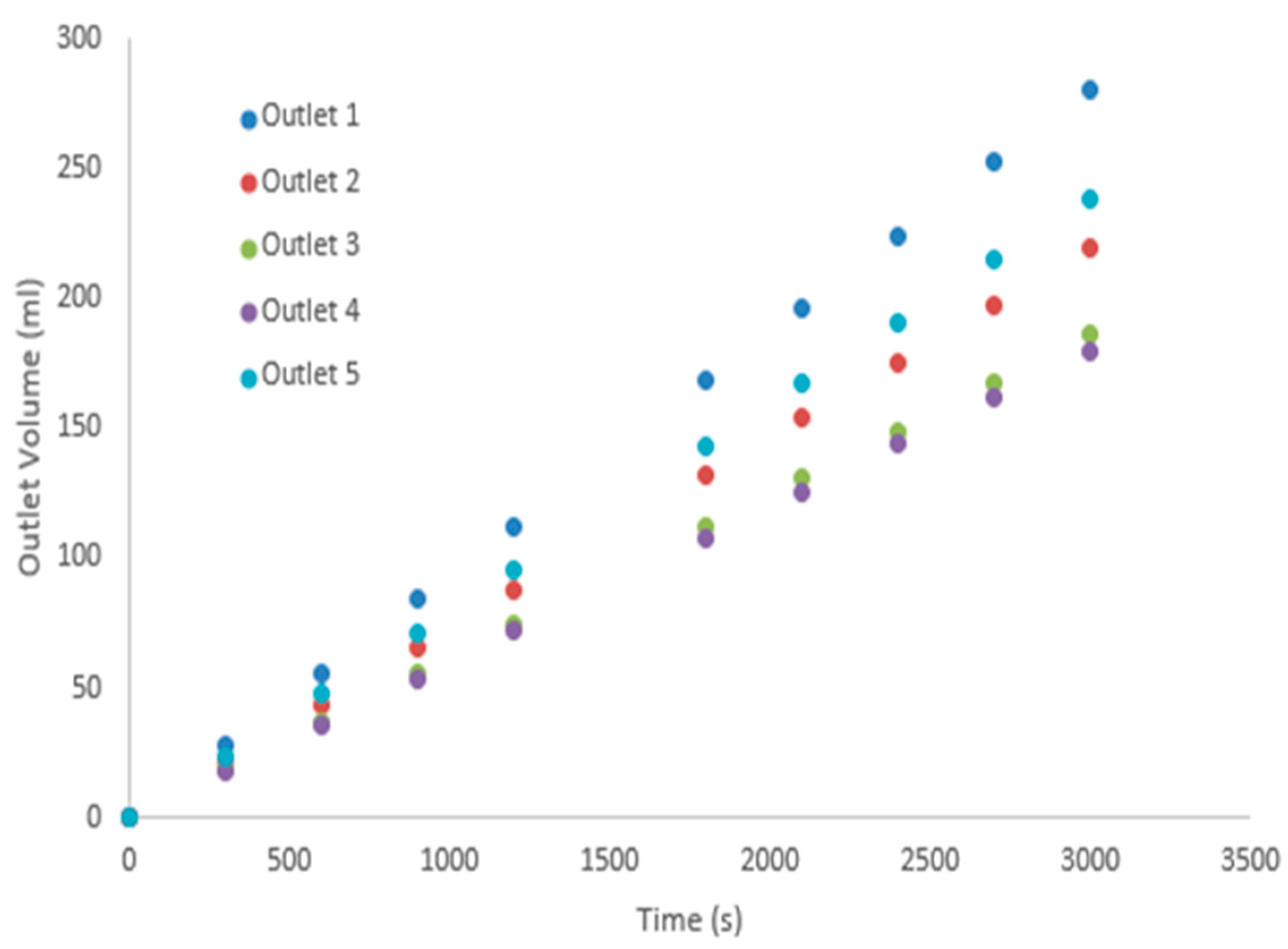
Time (s)	Outlet 1 (mL)	Outlet 2 (mL)	Outlet 3 (mL)	Outlet 4 (mL)	Outlet 5 (mL)
0	0	0	0	0	0
60	0	0	0	0	0
120	6.956	3.478	0	0	3.478
180	13.912	6.956	3.478	3.478	10.434
240	20.868	13.912	6.956	6.956	17.39
300	27.824	20.868	13.912	13.912	24.346
360	34.78	27.824	20.868	20.868	31.302
420	41.736	31.302	27.824	24.346	34.78
480	48.692	31.302	27.824	27.824	41.736
540	59.126	34.78	31.302	31.302	48.692
600	66.082	38.258	34.78	34.78	55.648
660	69.56	38.258	34.78	34.78	62.604
720	76.516	45.214	41.736	34.78	66.082
780	86.95	48.692	45.214	34.78	66.082
840	97.384	52.17	48.692	34.78	66.082
900	104.34	55.648	55.648	34.78	69.56
960	111.296	59.126	59.126	38.258	76.516
1020	121.73	62.604	62.604	38.258	83.472
1080	128.686	66.082	66.082	41.736	86.95
1140	132.164	69.56	69.56	45.214	93.906
1200	139.12	69.56	69.56	48.692	100.862
1260	146.076	73.038	73.038	55.648	100.862
1320	153.032	79.994	79.994	59.126	104.34
1380	163.466	86.95	86.95	62.604	111.296
1440	170.422	86.95	86.95	62.604	118.252
1500	173.9	93.906	93.906	62.604	125.208
1560	184.334	97.384	97.384	66.082	132.164
1620	194.768	97.384	97.384	66.082	135.642
1680	201.724	100.862	100.862	69.56	139.12
1740	208.68	104.34	104.34	69.56	142.598
1800	215.636	104.34	104.34	69.56	146.076
1860	222.592	107.818	107.818	69.56	153.032
1920	233.026	111.296	111.296	73.038	159.988
1980	239.982	118.252	118.252	79.994	166.944
2040	246.938	121.73	121.73	83.472	170.422
2100	253.894	128.686	128.686	86.95	173.9
2160	260.85	132.164	132.164	93.906	177.378
2220	271.284	132.164	132.164	97.384	180.856
2280	278.24	135.642	135.642	97.384	187.812
2340	285.196	139.12	139.12	100.862	194.768
2400	292.152	139.12	139.12	100.862	198.246
2460	302.586	142.598	142.598	104.34	205.202
2520	309.542	146.076	146.076	104.34	208.68
2580	316.498	149.554	149.554	104.34	212.158
2640	323.454	153.032	153.032	104.34	215.636
2700	330.41	156.51	156.51	107.818	222.592
2760	337.366	159.988	159.988	111.296	229.548
2820	347.8	163.466	163.466	111.296	233.026

,

Table A2. Simulation data for Figure 8.

Time (s)	Outlet 1 (mL)	Outlet 2 (mL)	Outlet 3 (mL)	Outlet 4 (mL)	Outlet 5 (mL)
0	0	0	0	0	0
300	29.184	16.728	18.723	17.679	23.382
600	58.368	33.456	37.446	35.358	46.764
900	87.552	50.184	56.169	53.037	70.146
1200	116.736	66.912	74.892	70.716	93.528
1800	175.104	100.368	112.338	106.074	140.292
2100	204.288	117.096	131.061	123.753	163.674
2400	233.472	133.824	149.784	141.432	187.056
2700	262.656	150.552	168.507	159.111	210.438
3000	291.84	167.28	187.23	176.79	233.82

,

Table A3. Experimental data for Figure 9.

Time (s)	Outlet 1 (mL)	Outlet 2 (mL)	Outlet 3 (mL)	Outlet 4 (mL)	Outlet 5 (mL)
0	0	0	0	0	0
60	6.956	0	3.478	0	0
120	13.912	3.478	10.434	3.478	3.478
180	20.868	10.434	17.39	10.434	6.956
240	27.824	17.39	24.346	17.39	13.912
300	34.78	24.346	31.302	24.346	20.868
360	41.736	27.824	31.302	27.824	27.824
420	48.692	27.824	34.78	31.302	31.302
480	55.648	27.824	41.736	34.78	34.78
540	62.604	27.824	52.17	38.258	38.258
600	69.56	27.824	59.126	38.258	38.258
660	73.038	31.302	62.604	38.258	41.736
720	79.994	34.78	69.56	38.258	48.692
780	90.428	38.258	73.038	38.258	55.648
840	97.384	45.214	79.994	41.736	59.126
900	107.818	52.17	86.95	45.214	62.604
960	114.774	59.126	93.906	52.17	66.082
1020	121.73	62.604	97.384	55.648	66.082
1080	128.686	66.082	100.862	59.126	69.56
1140	135.642	66.082	100.862	62.604	73.038
1200	142.598	69.56	104.34	66.082	79.994
1260	146.076	69.56	104.34	66.082	83.472
1320	153.032	73.038	111.296	66.082	90.428
1380	159.988	76.516	118.252	66.082	93.906
1440	166.944	83.472	125.208	69.56	97.384
1500	173.9	90.428	132.164	69.56	104.34
1560	180.856	97.384	139.12	73.038	104.34
1620	187.812	104.34	142.598	76.516	104.34
1680	194.768	107.818	142.598	79.994	107.818
1740	201.724	107.818	146.076	83.472	114.774
1800	208.68	111.296	153.032	83.472	121.73
1860	215.636	118.252	156.51	86.95	128.686
1920	222.592	121.73	159.988	93.906	132.164
1980	229.548	125.208	166.944	97.384	139.12
2040	236.504	132.164	170.422	97.384	139.12
2100	243.46	135.642	173.9	100.862	146.076
2160	250.416	139.12	177.378	104.34	149.554
2220	257.372	139.12	180.856	104.34	153.032
2280	267.806	142.598	184.334	107.818	159.988
2340	274.762	146.076	187.812	107.818	163.466
2400	281.718	149.554	194.768	107.818	166.944
2460	288.674	156.51	201.724	111.296	173.9
2520	295.63	163.466	205.202	114.774	173.9
2580	302.586	166.944	205.202	114.774	177.378
2640	309.542	173.9	212.158	118.252	180.856
2700	316.498	177.378	215.636	125.208	187.812
2760	323.454	177.378	215.636	128.686	194.768
2820	330.41	180.856	222.592	132.164	198.246
2880	340.844	184.334	226.07	132.164	205.202

and

Table A4. Simulation data for Figure 9.

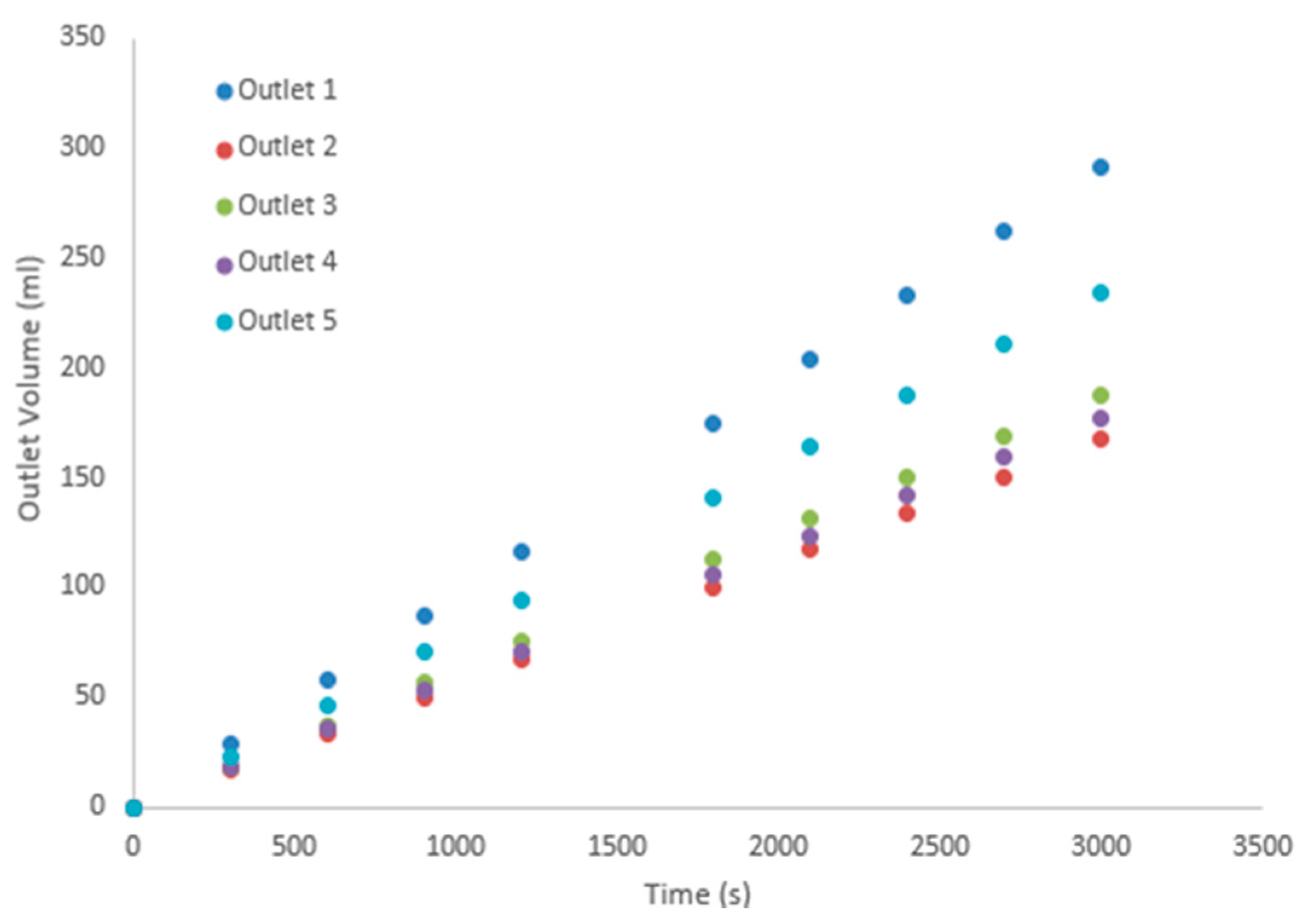
Time (s)	Outlet 1 (mL)	Outlet 2 (mL)	Outlet 3 (mL)	Outlet 4 (mL)	Outlet 5 (mL)
0	0	0	0	0	0
300	29.844	17.109	20.244	17.298	24.048
600	59.688	34.218	40.488	34.596	48.096
900	89.532	51.327	60.732	51.894	72.144
1200	119.376	68.436	80.976	69.192	96.192
1800	179.064	102.654	121.464	103.788	144.288
2100	208.908	119.763	141.708	121.086	168.336
2400	238.752	136.872	161.952	138.384	192.384
2700	268.596	153.981	182.196	155.682	216.432
3000	298.44	171.09	202.44	172.98	240.48

in the Appendix A respectively. It can be seen that the simulation results are in good agreement with the experimental data, though small differences exist. As is shown in Figure 8, Outlet 1 has the largest flow rate and Outlet 5 has the second largest flow rate in both simulation and experimental data. However, the flow rates of Outlet 2 and 3 are almost same and Outlet 4 has the smallest flow rate. The simulation results show that the flow rates of Outlet 2, 3, and 4 are similar. In Figure 9, the flow rate of Outlet 1 is also the largest flow rate in both simulation and experimental data. Moreover, Outlet 2 has a smaller flow rate than that of Outlet 1 and larger than those of other outlets from simulation results. The flow rates of Outlet 2, 3, and 4 are similar, while Outlet 3 has a larger flow rate in the experimental data. As for velocity distributions from simulation results, a deeper color means a higher velocity. The differences in flow rates among every outlet are caused by the velocity distributions and the number of cells to calculate the flow rates in the area of the outlets. In Figure 10 and Figure 11, the areas on the discharging surface corresponding to Outlet 1 and 5 have more concentrated velocity distributions. This gives an explanation that Outlet 1 and 5 have larger flow rates than Outlet 2, 3, and 4. It is also shown that there are three concentrated velocity distributions with higher values of velocity on the discharging surface corresponding to Outlet 2, 3, and 4. However, there are three velocity distributions: one belongs to Outlet 2, one belongs to Outlet 2 and 3, and one belongs to Outlet 3 and 4. Though there are three concentrated velocity distributions with higher values in the areas of Outlet 2, 3, and 4, it cannot be ignored that the existence of blank areas occupying large proportions of areas of Outlet 2, 3, and 4 means much lower values of velocity. The velocity distributions in the areas of Outlet 2, 3, and 4 result in the smaller flow rates. It should be noted that the maximum velocity shown in the Figure 10 and Figure 11 only represents the velocity for certain numbers of cells in Lattice Boltzmann Domain. In addition, in Section 4.3 and Section 4.4, the cells on discharging surfaces are different for each case. The analysis above gives a detailed explanation of different flow rates corresponding to different outlets.

On the basis of the above statements, the fracture inclination affects the flow paths to a certain extent, meaning that the gravity force has an effect on the flow paths. It has shown that the main trends of simulation results are in good agreement with those of experimental data, despite the differences that exist among them.

4.3. Influence of Fractal Dimension

With the inclination being 65°, the fractal dimension is set as 2.2, 2.3, and 2.4 and the other input parameters remain constant. The simulation results from the LBM model are presented in Figure 10, Figure 11 and Figure 12, corresponding to the fractal dimension of 2.2, 2.3, and 2.4, respectively. In Figure 12, Outlet 1 has the largest volume at the same time, meaning that the flow rate of Outlet 1 is the maximum. Additionally, the flow rate of Outlet 5 is smaller than that of Outlet 1, but larger than those of the other outlets. The flow rates of Outlet 2, 3, and 4 are similar. According to Figure 13, the flow rate of Outlet 1 is also the maximum, but Outlet 5 has a smaller flow rate. In addition, Outlet 3 and 4 have similar flow rates while the flow rate of Outlet 2 is the minimum. Figure 14 shows that Outlet 1 has the largest flow rate and Outlet 2 has the second largest flow rate. The flow rates of Outlet 3, 4, and 5 are almost the same and a half of the flow rate of Outlet 1. Based on Figure 12, Figure 13 and Figure 14, the same phenomenon is exhibited in that Outlet 1 has the largest flow rate and Outlet 5 has the second largest flow rate, which can be identified from flow rates of other outlets easily. However, there are small differences in the distributions of flow rates for Outlet 2, 3, and 4. With the increase of the fractal dimension, the differences of flow rates between Outlet 1 and 5 become smaller and the flow rates of Outlet 3 are larger than those of Outlet 2 and 4. It proves that the changes of the fractal dimension lead to the changes of roughness on fracture surfaces, resulting in different flow rates of the outlets.

As is shown in Figure 15, Figure 16 and Figure 17, it is obvious that preferential flow paths exist on the fracture rough surfaces based on the velocity distribution, where a deeper color means a higher velocity. The areas on the discharging surface corresponding to Outlet 1 and 5 have more concentrated velocity distributions, which explains the flow rates of Outlet 1 and 5 are larger than those of other flow rates. In addition, the areas on the discharging surface corresponding to Outlet 2, 3 and 4 have three concentrated velocity distributions with higher values of velocity. However, three velocity distributions: one belongs to Outlet 2, one belongs to Outlet 2 and 3, and one belongs to Outlet 3 and 4. Though there are three concentrated velocity distributions with higher values in the areas of Outlet 2, 3, and 4, there are still blank areas meaning much lower values of velocity, which occupy large proportions of areas of Outlet 2, 3, and 4. The velocity distributions in the areas of Outlet 2, 3, and 4 lead to the smaller flow rates of Outlet 2, 3, and 4 compared with those of Outlet 1 and 5. The analysis above gives a detailed explanation of different flow rates corresponding to different outlets.

4.4. Influence of Mismatch Wavelength

The inclination is set as 65° and the fractal dimension is equal to 2.2. The mismatch wavelengths are 20 mm, 25 mm, and 30 mm, respectively. As is shown in Figure 18, Outlet 1 exhibits the largest volume at the same time, which means that Outlet 1 has the largest flow rate among the five outlets. Additionally, the flow rate of Outlet 5 is a little smaller than that of Outlet 1, but larger than those of the other outlets. The flow rates of Outlet 2 and 3 are similar and the flow rate of Outlet 4 is the minimum. According to Figure 19, the flow rate of Outlet 1 is also the maximum, but Outlet 5 has a smaller flow rate. In addition, Outlet 3 and 4 have similar flow rates, while the flow rate of Outlet 2 is larger than those of Outlet 3 and 4 and close to the flow rate of Outlet 5. Figure 20 illustrates that Outlet 1 has the largest flow rate and Outlet 2 has the second largest flow rate. The flow rates of Outlet 3, 4, and 5 are almost the same. Unlike Figure 18 and Figure 19, the flow rate of Outlet 2 is the minimum, which is smaller than those of Outlet 3 and 4. Based on Figure 18, Figure 19 and Figure 20, it is clear that Outlet 1 has the largest flow rate and Outlet 5 has the second largest flow rate, which can be identified from flow rates of other outlets easily. With the increase of the fractal dimension, the flow rate of Outlet 2 decreases from third to the minimum. It can be concluded that the changes of mismatch wavelength result in different flow rates of the outlets.

In Figure 21, Figure 22 and Figure 23, it can also be seen that there are preferential flow paths on the fracture rough surfaces according to the velocity distribution. In these cases, a deeper color means a higher velocity. The areas on the discharging surface corresponding to Outlet 1 and 5 have concentrated velocity distributions covering the whole area of Outlet 1 and 5. This explains why the flow rates of Outlet 1 and 5 are larger than those of other flow rates. Three concentrated velocity distributions with higher values of velocity exist in the areas of the discharging surface corresponding to Outlet 2, 3, and 4. Moreover, three velocity concentrations are distributed as: one locates in Outlet 2, one is shared by Outlet 2 and 3, and one is shared by Outlet 3 and 4. Though three concentrated velocity distributions exist with higher values, there are still large proportions of blank areas, meaning much lower values of velocity in the areas of Outlet 2, 3, and 4. The velocity distributions in the areas of Outlet 2, 3, and 4 result in the smaller flow rates of Outlet 2, 3, and 4 compared with those of Outlet 1 and 5.

5. Conclusions

A novel experimental method with the application of 3D printing technology was proposed to study the water flow through a self-affine rough fracture. Compared with experimental methods that apply tensile forces for the generation of fractures, 3D printing technology can reduce the uncertainty of fracture surfaces and reflect fracture surfaces accurately. The LBM was adopted and a D3Q15 LBM code was programmed to simulate water flow in the single fracture. The agreement between the experimental data and the LBM simulation results implies that the LBM can be used to simulate flows through a self-affine rough fracture with reasonable accuracy. Additionally, the results from LBM simulations provide a detailed analysis for the preferential flow paths through the fracture rough surfaces. In the above cases, the flow rate of Outlet 1 is obviously larger than those of other outlets and Outlet 5 has the second largest flow rates. The flow rates of Outlet 2, 3, and 4 are variable in different cases, which reflects the effects of different fracture inclinations, fractal dimensions, and mismatch wavelengths. It should be noted that the influence of the fracture inclination (gravity force) on the flow paths cannot be ignored, though it is small in this study. For applications in reservoir systems (oil/gas, geothermal, shale gas), further research will focus on the scale and wettability effects of two-phase flow with different boundary conditions.