Abstract
Around the world wind energy is starting to become a major energy provider in electricity markets, as well as participating in ancillary services markets to help maintain grid stability. The reliability of system operations and smooth integration of wind energy into electricity markets has been strongly supported by years of improvement in weather and wind power forecasting systems. Deterministic forecasts are still predominant in utility practice although truly optimal decisions and risk hedging are only possible with the adoption of uncertainty forecasts. One of the main barriers for the industrial adoption of uncertainty forecasts is the lack of understanding of its information content (e.g., its physical and statistical modeling) and standardization of uncertainty forecast products, which frequently leads to mistrust towards uncertainty forecasts and their applicability in practice. This paper aims at improving this understanding by establishing a common terminology and reviewing the methods to determine, estimate, and communicate the uncertainty in weather and wind power forecasts. This conceptual analysis of the state of the art highlights that: (i) end-users should start to look at the forecast’s properties in order to map different uncertainty representations to specific wind energy-related user requirements; (ii) a multidisciplinary team is required to foster the integration of stochastic methods in the industry sector. A set of recommendations for standardization and improved training of operators are provided along with examples of best practices.
Keywords:
wind energy; uncertainty; decision-making; quantiles; ensembles; forecast; statistics; weather 1. Introduction
Wind power has been one of the fastest growing electric generation technologies worldwide over the past decade. In contrast to traditional thermal generation units, wind power output is both variable and uncertain, because it depends on local meteorological conditions. Wind power forecasting has thus been utilized to reduce and forecast the uncertainty associated with wind power output. Traditionally, this has been in form of a single point forecast; however, advanced forecasting techniques can provide more information, often in form of uncertainty forecasts. Presently, these uncertainty forecasts have not gained widespread usage in power system operations or electricity market bidding, but there are significant opportunities to improve economic applications [1] as well as reliability applications [2] in the power industry by utilizing such additional forecast information in novel ways.
Uncertainty information is routinely conveyed in public weather forecasts to provide some indication of the probability of an event’s occurrence. Everybody has experienced the morning weather forecast claiming that “there is an 80% chance of rain this afternoon” and thereafter grabbed an umbrella on the way out of the door. Due to this inherent possibility for an end-user of forecasts to take action, when forecasts lack precision, it is important to understand how wind power forecasts are currently being utilized by the electric power industry and analyze the gaps that prevent more prevalent usage of such uncertainty information in wind power applications [3,4].
The most common usage of wind power forecasts in power system operations is in Unit Commitment (UC), Economic Dispatch (ED) [5] processes and in allocating required reserve [6]. These are the scheduling processes by which power system generators are assigned an on/off status and output level for future time periods. For UC, this is typically performed in the day-ahead, and thus deterministic wind power forecasts used in this process typically range from 12–48 h ahead of the operating hour. Deterministic forecasts of load and renewable generation are critical in this process as it is currently designed due to the search of a single “optimal” solution. For reserve requirements, deterministic rules (e.g., covering a certain percentage of the historical load or wind point forecast errors) are generally used by system operators.
There is a very extended literature on stochastic approaches for the various power system functions like congestion management, energy trading, UC, ED, reserves estimation, power flow and optimal power flow, storage placement and sizing, etc. [3]. The consensus today is that there is a mismatch between the proposed methods in the literature and their adoption by the industry, and we do not speak about the uncertainty forecasts but the decision making tools that use these forecasts. Nevertheless, there are exceptions. For example, the probabilistic-dynamic rule of the Electric Reliability Council of Texas (ERCOT) for non-spinning reserve (updated on a daily basis based on historical data, the solar forecast, and the power system state forecast) [7], the probabilistic method for allocating the maximum import net transfer capacity between Portugal and Spain [8] or the probabilistic method from Red Eléctrica de España (REE) for allocating replacement reserve [6].
Another application for uncertainty forecasts in the electric power industry is to provide graphical tools to enhance the “situational awareness” of critical events in the grid operation that enhances the confidence and efficiency with which grid operators may change dispatch schedules in real-time to maintain system reliability in critical situations according to updated forecast information [7,9,10]. This is one area in which uncertainty information has made more of an impact, especially for system operators that receive some sort of probability information. This is often in the form of a value that tells about the probability of exceedance of a given parameter, e.g., the 20th percentile, which need to have a 80% probability of exceedance in a well-calibrated forecast. While useful, this simplified representation does not provide all of the information available from the forecasts and can thus lead to sub-optimal decisions due to a lack of information.
Despite uncertainty forecasts being widely available, in general, for electricity market optimal bidding (i.e., minimum imbalance costs), mostly point forecasts are being used to derive wind power bids for a given wind farm or pool of wind farms to the day-ahead, intra-day, or real-time markets [11,12]. According to [13], common practice consists of scaling point forecasts and schedule backup capacity during periods of high uncertainty, which helps to avoid over-promising generation and increases reliability, but leads to decreased economic potential.
The change of paradigm to the stochastic one in the business practices of end-users is very slow for various reasons. For example, a critical step towards a better utilization of forecast uncertainty information is understanding the source of uncertainty in the forecast chain. In the guideline of the World Meteorological Organization on communicating uncertainty in forecasts [14], the main sources of uncertainty in weather forecasts are identified as:
- Atmospheric unpredictability,
- Uncertainty of (observational) data interpretation,
- Uncertainty when composing the forecast, and
- Forecast interpretation.
Furthermore, industry questionnaires conducted in the framework of IEA Task 36 [15] showed that: (i) there is very little knowledge of the tools and applications available to deal with uncertainty; (ii) all market players are to some extent aware of the risks associated with weather variability and uncertainty, but awareness alone is not strong enough to start including uncertainty information in operational practices [4]. In this context and considering the aforementioned barriers, the present paper aims to contribute to a better understanding of these sources of uncertainty, which are perceived as potential barriers for the integration of uncertainty forecasts into energy-related decision-making problems.
The following structure has been chosen in order to shed light into topics and to encourage the use of uncertainty forecasts in the power industry decision-making problems: (i) review of the weather products and statistical tools for wind and wind power uncertainty (Section 2, Section 3 and Section 4); (ii) a discussion of existing and required methods to better communicate uncertainty information (Section 5); (iii) establishing a relationship between the properties of the uncertainty products (and communication tools) and several decision-making problems (Section 6 and Section 7); Furthermore, we will provide recommendations for wind power forecast end-users to identify their non-functional requirements (Section 8). Finally, it is important to underline that most of the findings and recommendations are equally applicable to solar power forecasting.
2. Definition of Forecast Uncertainty
Before discussing the technical aspects of the generation and use of wind power forecast uncertainty information, it is important to establish a standard terminology for uncertainty forecasts and uncertainty representation. The first definition, and important distinction, is between forecast error and forecast uncertainty. Forecast error is the actual deviation between a forecast value and a measured value at one point in time (in the past or present), while forecast uncertainty refers to a possible range of forecasting errors (or true values) in the future. Forecast error could also refer to an average error provided by an error metric, e.g., mean absolute error (MAE) or root mean square error (RMSE). The most widely adopted representation for forecast uncertainty is a forecast interval [16]. Since for a specific lead-time with the forecast horizon k the forecast interval only comprises information from a marginal distribution, it can also be named marginal forecast interval. Mathematically, it is defined as:
where and are the quantile nominal proportions of the interval limits L and H, the coverage rate that corresponds to the probability of having the observed value inside the forecast interval at hour . An individual quantile, , is the quantity that will be exceeded with probability . Quantiles of a given random variable are linked to the cumulative distribution function of that variable. When constructing prediction intervals, it is a standard convention that the interval is centered on the median, in terms of probability.
In some situations, the concept of confidence interval [17] may be confused with the forecast interval, which can lead to a misunderstanding of forecast uncertainty [18]. The confidence interval is applied to situations, where the purpose is to compute a statistical metric (e.g., mean, standard deviation) by taking a random sample from a population. It defines how well the sample statistic estimates the underlying population value, or in other words, provides an interval of values that is likely to contain the population parameter of interest. On the other hand, forecast intervals indicate a range of values, and the respective probability, that is likely to contain the real value (which is yet to be observed) of the target variable.
Forecast intervals can be derived from parametric (e.g., Gaussian distribution) or non-parametric (e.g., empirical distribution function, kernel density estimation) representations of uncertainty [18]. Moreover, from the probability density function (PDF) it is possible to extract quantiles to form a marginal distribution function or higher-order statistics such as skewness and kurtosis. In meteorology, forecast intervals are typically formed from a larger number of Numerical Weather Predictions (NWP) forecasts in an ensemble forecasting system [19,20]. In both cases however, it is important to emphasize the following aspects:
- Uncertainty estimation should be conditional to a set of explanatory variables, like forecasted wind speed, wind direction, expected value of the generation level, etc. Meteorologists call this flow dependent uncertainty (e.g., [21,22]). The collection of historical forecast errors and construction of the empirical distribution should not be named the forecast intervals or identified as the forecast uncertainty.
- In some cases, wind power forecast uncertainty is wrongly assumed to follow a Gaussian distribution for the forecast errors, which, as shown in [23,24], may lead to a poor representation of the uncertainty and impact the respective decision-making quality negatively.
None of the aforementioned statistical uncertainty representations capture the temporal and spatial dependency of forecast errors. This additional information, essential for multi-period optimization (problem formulation with time coupled constraints, e.g. battery state of charge, ramp constraints of power plants) and/or spatial optimization (problem formulation with decision or state variables that are geographically distributed, e.g., multiple renewable power plants, electrical grid variables), is only captured by sets of alternative temporal and spatio-temporal scenarios that represent various possible realizations of a pre-defined value, such as wind power generation over a specific time horizon. This representation has different names in different disciplines: random vectors (statistics); path forecasts (econometrics) [25]; numerical weather prediction (NWP) ensembles (meteorology). Although the output of these methods may be of the same quality, it is important to emphasize that the methods employed to generate these types of uncertainty forecasts are very different across these disciplines. For instance, NWP ensembles are configured to represent the physical uncertainty of the weather ahead of time rather than uncertainty as a function of past experience as in pure statistical learning methods. For the sake of simplicity, in the remainder of this paper this uncertainty representation will be called ensembles, which can be generated by physical (Section 3 and Section 4.2.1 or statistical (Section 4.1.2) methods.
Mathematically, a set of temporal ensembles for a time horizon of length T can be defined as follows:
where each row of contains an individual ensemble member. Collectively, the ensemble should exhibit the correct auto- and cross-correlation structure in well-calibrated forecasts (see Section 3 for more details).
The concept of simultaneous or multi-period quantiles can also be found in the statistical literature [26]. Simultaneous forecast intervals differ from marginal forecast intervals since they take into account the temporal dependency of forecast errors. These intervals are mathematically defined as:
where T is the time horizon, and quantile trajectories between 1 and T, and the observed wind power trajectory. Equation (3) means that the observed wind power is completely contained inside the simultaneous forecast intervals during all hours of the time horizon T.
3. Review of Weather Uncertainty Forecasting Approaches and Methods
In meteorology, the practical implementation of a stochastic–dynamic (SD) approach that couples probability with determinism was already known as ensemble prediction in the late 1950s [19]. Its roots start in work from 1949 by Eric Eady ([27]) and was later developed by Philip Thomson and Edward Lorenz who discovered the uncertainty of numerical results by using more or less digits in the main variables in the initial states [19]. Epstein, a statistical meteorologist interested in Monte-Carlo simulations discovered in 1968 that “variables must no longer be regarded as deterministic variables, but rather as random variables with associated probabilistic, that is, stochastic properties” [19]. Lewis [19] describes Epstein in his review of ensemble prediction as the one who carried out much of the fundamental work on ensemble simulations in 1969. His main finding was that there is an inherent uncertainty in the model’s initial state of the atmosphere due to the impossibility of observing the atmosphere either in sufficient detail or with sufficient accuracy. From this, he developed equations that solved the SD-problem in an analytic way with an ensemble error matrix. The matrix contained a small number of equations resembling the initial errors of the atmospheric state, in contrast to the many random perturbations that the Monte Carlo method required to simulate the uncertainty of the initial conditions. He showed that the same problem could be solved with 9 error terms, where the Monte Carlo method required 1000 runs [28]. The method can be considered the predecessor of the Ensemble Kalman Filter (EnKF) method introduced by Evensen in 1994 [29].
Even though Lorenz and Thomson came to the conclusion that Epstein’s SD method was the most promising, they were heavily restricted by limited computing resources until the start of the 1990s, when parallel computing made it possible to further develop these methods ([30]). The so-called singular vector (SV) and breeding approaches were the first to be implemented into operational forecasting between 1993 and 1996 with Palmer and Molteni (ECMWF—European Centre for Medium-Range Weather Forecasts) [31,32], Toth, Kalnay [33], Tracton (NCEP—National Centers for Environmental Prediction) [34] and Mitchell and Houtekamer [35,36] (CMC—Canadian Meteorological Center) as the lead scientists for the implementations in Europe, USA and Canada. Even though Lorenz and Thomson came to the conclusion that Epstein’s SD method was the most promising [19], they were heavily restricted by limited computing resources until the start of the 1990s, when parallel computing made it possible to further develop these methods . The so-called singular vector (SV) and breeding approaches were the first to be implemented into operational forecasting between 1993 and 1996 with Palmer and Molteni (ECMWF—European Centre for Medium-Range Weather Forecasts) [31,32], Toth, Kalnay [33], Tracton (NCEP—National Centers for Environmental Prediction) [34] and Mitchell and Houtekamer [35,36] (CMC—Canadian Meteorological Center) as the lead scientists for the implementations in Europe, USA and Canada. These first implementations of ensemble prediction systems have been improved over the past 20 years in a number of ways, especially in resolution and area size. Nevertheless, these operational systems are mostly medium-range (3–10 days) ensemble systems. In the short-range (day-ahead), the perturbations in the initial conditions, as done for example by ECMWF with singular vectors or NCEP with breeding, are insufficient [20]. Palmer concluded in 2002 that on the meso-scale there are a number of assumptions in the model equations that are a major source of forecast uncertainty. These assumptions need to be taken into account when creating ensemble forecasts. He showed that with the SV method, correlation is only visible after day 4 of the forecast, which proves that perturbations of the initial conditions with singular vectors are only feasible for the medium range. Also, this approach only addresses effects of uncertain initial conditions on the forecast and assumes a perfect physical model. However, model physics representations are also imperfect, in particular physical parameterizations for unresolved sub-grid scale processes, which add a significant source of uncertainty to the resulting forecast.
To summarize, reliable and sharp ensemble forecasts that give satisfactory estimates for the forecast uncertainty on all temporal horizons of interest require that all sources of uncertainties in an ensemble forecasting system are addressed:
- Initial condition uncertainties.
- Physical approximation uncertainties.
- Boundary condition uncertainties (at the surface and, for limited area models, at the lateral boundaries from the driving models).
3.1. NWP Ensemble Generation
In order to quantify these different sources of uncertainty, the following methodologies are being developed that aim to match the forecast uncertainty with observed variability, by introducing targeted perturbations within the model system.
- Quantification of initial conditions uncertainties:
- Singular vector methodsSingular Vectors (SV) identify the directions of initial uncertainty that are responsible for the largest forecast uncertainty of a model state at a given time in the future. In their review, Diaconescu and Laprise [37] describe SVs to provide optimal information about the probability density function of model states at a future time. The fact that SVs capture the dynamically most unstable perturbations means that they identify the directions of initial uncertainty that are responsible for the largest forecast uncertainty. This property made the SV a good candidate in producing uncertainty from the initial conditions with reasonable dispersion and very suitable for medium range ensemble forecasting. In recent developments, SV are used to detect regions of large sensitivity to small perturbations in order to generate adaptive observations. Such adaptive observations have a large influence on enhancing weather forecasts and producing a better representation of uncertainty [38].
- Breeding methodsThe bred-vectors can be understood as difference fields between two non-linear fields. In order to obtain a realistic development of growing errors in the analysis cycle, the difference between the current analysis fields and the previous ensemble member fields are applied. The bred vectors are constructed as superpositions of leading local time-dependent Lyapunov vectors (named after Aleksandr Lyapunov, describe characteristic expanding and contracting directions of a dynamical system, and are being used in predictability analysis and as initial perturbations for ensemble forecasting in NWP.) of the atmosphere. When implemented back in 1994, it was important that the structure of the leading Lyapunov vectors assumed a transient period, which for large-scale atmospheric processes are 3 days, fitting the target time frame for the uncertainties in the medium range forecasting [39]. Bred vectors grow slower than singular vectors and therefore have been shown in comparisons to the singular vectors to lack spread in the first 3–6 days , but then approach the SV results [40].
- Ensemble Kalman Filter techniquesEnKF techniques are today mostly used to provide initial conditions for Ensemble prediction systems (EPS). In that sense, the EnKF is a variant of the initial conditions perturbations. The EnKF was first introduced in 1994 by [29] and has, according to Evensen gained popularity, because of its conceptual formulation and relative ease of implementation. The work in [41] states that it requires no derivation of a tangent linear operator or adjoint equations, and no integrations backward in time, such that the computational requirements are affordable and comparable with other popular sophisticated assimilation methods. The most known methods applied in the generation of initial conditions perturbations are:
- –
- Stochastic and Deterministic Ensemble Kalman Filter (EnKF)The assumption in the stochastic EnKF is that in order to generate a consistent analysis field, the observations need to be treated as random variables with stochastic features. To keep the filter computationally reasonable, a Gaussian error distribution of the observation matrix is assumed [42].The deterministic EnKF does not treat the observations as random, because it is assumed that the small, but spurious correlations between the ensembles of backgrounds and observations could lead to a degradation of analysis quality. The disadvantage of the deterministic EnKF is that the ensemble often becomes under-dispersive and needs covariance inflation or relaxation procedures to compensate for the missing spread [42]. Variants of the deterministic EnKF are:
- (a)
- Ensemble square root filter (EnSRF)
- (b)
- Ensemble adjustment Kalman filter (EAKF)
- (c)
- Ensemble transform Kalman filter (ETKF)
All these variants follow in large the same principles. - –
- Sequential and Local Ensemble Kalman Transform Filter (EnKTF)The sequential EnKF is a data assimilation method that applies an ensemble of model states to represent the error statistics of the model estimate, it applies ensemble integrations to predict the error statistics forward in time, and it uses an analysis scheme which operates directly on the ensemble of model states when observations are assimilated (EnKF: The ensemble Kalman filter home page: enkf.nersc.no).In the Local EnKF (LETKF) the computational heavy part is moved to a smaller, local scale. This practice has the advantage that more observations can be handled with parallel computing techniques and thereby exponential increase in required computational resources is avoided. The EnKF takes the analysis resulting from the data assimilation to lie in the same subspace as the expected forecast error. The LETKF makes use of the hypothesis that the dimension of the subspace corresponding to local regions is low and therefore allows operations only on relatively low-dimensional matrices in a local space. In this way all local matrices are used to compute the global states for advancement to the next forecast time [43]. The main difference between the algorithms are that the sequential algorithm assimilates observations in a sequence of small batches, while in the local algorithm the spatial domain is split into a number of local areas, where the analysis is solved independently ([42]).
Newest developments also use the EnKF method for data assimilation and perturbations in order to overcome the spacial scales issues in the global models [44]. Hybrids of EnKF, LETKF and Physical parameterization schemes, multi-models or other physics perturbations are applied in a number of meteorological centers in order to capture both initial condition and model uncertainties, even though many issues remain and no optimal solution has been found as yet [42].
- Quantification of uncertainties due to physical approximations:
- Stochastic physics (perturbations of tendencies in the physics)The principle of stochastic physics is to represent uncertainty in the model physics, or in other words the uncertainty arising from assumptions made to solve the physical equations of motion is used to perturb physical tendencies such as wind components, temperature and humidity. The first stochastic physics perturbation scheme was introduced by [45] in order to make ensemble forecasts using only perturbations in the initial conditions more reliable. In fact, it had been found that uncertainties in the model and the model’s parameterization schemes to solve sub-grid scale problems have an equally large effect on the uncertainty of weather predictions as uncertainties in the initial conditions. The first versions of the stochastic physics contained multiplicative noise perturbations on the net parametrized physics tendencies of the wind components, temperature and humidity.Since then, other, more refined or complementary methods have been developed. One of them is the so-called Stochastically Perturbed Parameterization Tendencies (SPPT) method that uses perturbations collinear to the unperturbed tendencies [46]. The main difference is that the multivariate distribution of the original scheme is replaced by an univariate distribution in order to achieve perturbations that are more consistent with the model physics. The so-called Backscatter scheme is a complementary scheme and describes aspects of structural uncertainty in the dynamic parametrization that is missing in conventional parameterization schemes [47].In summary, these types of perturbations try to simulate the uncertainty related to the assumptions taken in the NWP models physical and dynamical equations due to non-solvable sub-grid scale processes.
- Multi-Scheme approach (application of different physics schemes)The multi-scheme approach is characterized by using one NWP model, where entire parameterization schemes are exchanged in order to form new members. In that way, perturbations can be added effectively in the dynamics and physics of the model, e.g., convection, cloud and micro physics, horizontal and vertical diffusion, radiation and surface roughness. This approach, even though computationally relatively expensive, has the advantage over a multi-model approach that it is computationally easier to handle, due to the common model kernel. Additionally, the differences of the individual model results are well-defined. The main advantage of the multi-scheme approach is that the uncertainty has no time-dependence and is valid in every time step of a forecast. This means, if the amount of members is large enough and the chosen parameterization schemes reflect the uncertainty of the variables of interest, there is no post-processing or calibration required. The use of multiple physical parameterizations also permits the sampling of different possible closure assumptions in deep convection and in boundary layer processes [42], which are the main driver of uncertainty in the context of renewable energy forecasting. Here, the ideal multi-scheme ensemble is one, where the schemes are targeted to the fast physical processes in the boundary layer since these processes at the surface are the driver for uncertainty. If the uncertainties are covered by the EPS member’s parameterization schemes, the uncertainty will be well described by the ensemble in every time step of the forecast. An example of such a dedicated system for the power industry is the Multi-Scheme Ensemble Prediction System (MSEPS) run by weather ensemble service provider WEPROG (Weather & Energy PROGnoses) [48,49].
- Quantification of surface boundary condition uncertainties:
- Perturbation of surface parametersAlthough given a lower weight compared to the impact of initial conditions perturbations and model perturbations on the forecast uncertainty in the literature so far ([50]), several centers apply perturbations on surface boundary conditions. The main objective here is to account for the effects of uncertainties in the surface energy budget and the surface roughness which significantly determine latent and sensible heat fluxes and turbulences in the planetary boundary layer. Parameters that are most commonly varied include roughness length, soil moisture, snow cover, surface albedo, vegetation properties, sea surface temperature. The variations are introduced e.g., by time constant perturbation fields [50], variations relative to the climatological analysis fields ([51]), or additive, multiplicative and correlated stochastic perturbations [52]. Their impact have been shown to be significant on the quality of forecasts in particular near the surface [52,53].
- Methods that implicitly combine several sources of uncertainties:
- Multi-model approachProbably the easiest way to create an ensemble is simply to combine forecasts from several NWP models [42,54]. The underlying assumption is that the combination of different model systems is a good representation of model error. Depending on the nature of the combined models (deterministic and/or including initial condition perturbations), the resulting ensemble may also include effects of uncertain initial conditions. The interpretation of the outcome again depends on the characteristics of the ensemble. The members can be taken as random, equally likely draws from a probability distribution or as scenarios with assigned probability of occurrence [55]. Based on these assumptions, probabilistic products can be derived. This approach is particularly attractive for (energy-) meteorological services without running an own operational NWP model system. However, the sources of the resulting variability in the forecast are not necessarily transparent and therefore the statistical assumptions on the resulting distributions are error-prone. In addition, optimization of the forecast distribution can only be done statistically as a post-processing step (see later) rather than by optimizing the ensemble properties themselves. Forming a multi-model EPS with deterministic NWP models are often prone to being under-dispersive, because deterministic models usually suppress extremes, which are desired in an EPS for reliability purposes.
Today, almost 20 years after the first EPS have gone operational, many meteorological centers, research institutions and some private organizations run ensemble forecasting systems of one of these types or combinations of different approaches. The most important difference of medium-range EPS versus short-range EPS is in their characteristics of the target time horizon. While the medium range EPS mostly use initial conditions perturbations (1) their representation of uncertainty is targeted to a specific time, e.g., 96 h and is often under-dispersive in the short-range. The short-range EPS or combinations of initial conditions perturbations with methods that apply perturbations inside the model’s code of computing physical properties (2) provide a realistic uncertainty representation in every time step in the short-range.
Most real-time EPS today use combinations that take hand upon both major uncertainty terms (the initial conditions and model uncertainty) with different variants. Nevertheless, not every approach is capable of solving any type of problem [20]. Therefore, we reviewed the methods and approaches used mostly in today’s ensemble prediction systems in order to provide a reference to the aspects of uncertainty solved in the forecasting process of the various methods.
Applications in the power industry, where the target horizon is usually every time step of the forecast, need to be aware of the limitations of medium-range ensemble techniques that usually use some type of initial condition perturbations. Due to their non-representative uncertainty in the first 3–4 days, these approaches are unsuitable for applications such as trading of wind/solar power, unit commitment, reserve predictions, etc. Approaches that have target horizons in the medium range require that the raw model output is being calibrated for the target application to be applicable. For the choice of an approach, it is therefore important to distinguish the applicability at the various time horizons and ensure that the underlying weather input can solve the end-user’s problem at hand.
3.2. Reliable Weather Forecast Products through Statistical Post-Processing
Although the skill of ensemble weather prediction systems is improving as a result of a steady research and operationalization process, statistical post-processing of NWP output is still one important step towards reliable and calibrated probabilistic forecast products. The main objective here is to correct for (local) model biases and mismatches between observed and modeled distributions. For this, most approaches use past forecasts and matching observations of the variable of interest and some statistical model for the estimation of the historical error distribution assuming that the error properties are preserved in the current forecast. Obviously, the best calibration is achieved with long and comprehensive samples of the error distribution. Also, forecasts from the same NWP model version are desired in order to assume stationary forecast error properties. Several studies demonstrated the impressive improvements of the quality of weather forecasts using such ensemble re-forecast datasets ([56,57,58]). Acknowledging this added value, some meteorological centers maintain an ensemble re-forecast dataset despite the significant computational effort ([59]).
Not only past forecast data but, in particular for wind energy applications, the availability of past and on-line observational data of variables that are not part of the standard meteorological measurement network can limit the applicability of statistical post-processing. Although NWP model analysis fields can be used as a surrogate, near surface variables exhibit significant error, especially if they are only sparsely used in the assimilation cycle (e.g., for wind from radio soundings). To get best results in the power industry, wind speed and direction at hub height needs to be made available by e.g., wind energy plant owners, quality controlled and integrated into the data infrastructure of meteorological services.
Once the database is available, there is a variety of statistical post-processing techniques presented in the literature to choose from [57]. Rather than providing a comprehensive overview of the different methods, the remainder of this section focuses on the interests of end-users who are planning to implement probabilistic weather forecast products in their energy forecast models and decision making tools. Specific aspects of statistical post-processing will be discussed in detail.
3.2.1. Deterministic or Probabilistic Weather Input
Since the 1970s, so-called model output statistics (MOS) techniques [60] have been widely and successfully used and extended in meteorological NWP post-processing. In its original form, the forecast error of a deterministic NWP model is statistically formulated as a multiple linear regression model. The coefficients of this model are estimated minimizing the sum of squared residuals resulting in a new, bias-free deterministic forecast for the variable of interest. If a logistic regression model is used instead, probabilities of exceeding a specific threshold can be derived [61]. The work in [62] extends the logistic regression model by the thresholds being additional predictors of the regression equation themselves. With this model, full probability distributions rather than probabilities exceeding single thresholds can be estimated. Thus, this rather simple technique can transform output of a deterministic NWP model into probabilistic forecast products.
A rather different approach to post-processing deterministic weather forecasts is the analog ensemble technique proposed by Delle Monache [63]. The analog ensemble (AnEn) approach to uncertainty quantification also leverages the concept that when models have errors, they are similar in magnitude and direction for analogous conditions. The AnEn technique searches the historical forecast data for situations when the forecast was most similar (or analogous) to the current forecast. For each of those analogous forecasts, the corresponding observation is collected. These collected observations form an ensemble which may be used to calculate an empirical PDF or a parametric PDF. The mean of this observation ensemble becomes a correction to the deterministic forecast, while the spread represents the uncertainty [63]. One of the deficiencies with the AnEn is that it has no capability on a spatial or temporal scale to provide forecast uncertainty, as it is derived from single past events and cannot combine the uncertainty at different locations. There is research ongoing to solve the spatial scales issues by combining the AnEn approach with an NWP ensemble to form a hybrid ensemble with the computational benefits of the AnEn and the capabilities of NWP models [64].
The temporal scale issues are inherent to all statistical models introduced so far and can only be solved by the use of NWP ensemble forecasts as an underlying database for statistical models as they provide physical coherence along with estimates of flow dependent uncertaintyİn order to use this valuable information in MOS techniques and to derive calibrated full probability density forecasts, [65] proposes a non-homogeneous Gaussian regression analysis that allows the variance of the regression residuals to be variable as a function of the ensemble spread. If the ensemble members are distinguishable (e.g., as in multi-model or multi-scheme ensembles), the ensemble MOS (EMOS) method can be used by choosing each member as an own predictor [65]. Otherwise the ensemble mean of the target variable (and optionally additional suited variables) can serve as predictors [58]. In [66], Bayesian Model Averaging (BMA) that combines forecasted distributions from different sources (or models) is adapted to post-process ensembles. The output probability density function of the BMA is a weighted average of PDFs centered on the individual bias-corrected forecasts, and the weights, which are equal to posterior probabilities of the models generating the forecasts, can be used to select ensemble members.
For some wind energy applications, both, wind speed and wind direction forecasts might be of interest. Schuhen’s [67] work extends the EMOS technique by a bivariate model formulation estimating the zonal (west-east) and meridional (north-south) wind vectors simultaneously. In this way the correlation between the two variables is also determined, resulting in more physically coherent wind speed and direction forecasts.
Despite significant differences in the proposed statistical modeling approaches, several comparative studies conclude that the underlying training database determines the improvement over the raw ensemble weather forecast rather than the choice of the post-processing technique [57,68]. Therefore, it is the specific application’s objective that determines the required type of weather forecast product and respective suitable statistical post-processing method.
3.2.2. Application-Specific Weather Forecast Products
Depending on the size of the problem at hand, the weather forecasts used in wind power applications for e.g., power forecast at a single wind turbine or a small wind park use point forecasts. If it comes to forecasting the power of large wind parks or of entire transmission networks, wind forecasts on a grid might be required. The work in [69] add a geostatistical step to a non-homogeneous Gaussian regression analysis in order to deliver calibrated wind forecasts at any desired location.
The output of such statistical post-processing can take several forms: probabilities for specific thresholds (as from logistic regression analyses), full PDFs (as from extended logistic regression analyses, BMA or AnEn) or as individual scenarios (ensembles). This latter product unifies several desired aspects of weather forecasts: calibrated information and a temporal dependence between consecutive lead-times in each scenario such that the resulting new ensemble preserves the physical dynamics and the flow dependent uncertainty. Schefzik [70] and Wilks [71] propose to use ensemble (or empirical) copula coupling to recreate scenarios after calibration. With this, the ensemble member rank structure from the original ensemble is translated to the random draws from the estimated probability densities in the calibration step. In order to also re-establish the temporal dependency in each scenario, Ben Bouallegue [72] adds autocorrelation of the forecast error over consecutive forecast lead times with a dual-ensemble copula-coupling approach and reports promising results.
In summary, NWP models can provide a variety of input data for wind power models ranging from probabilistic forecast on a specific location to calibrated ensemble forecasts on a grid and from probabilities for specific thresholds to full probability density functions or separate scenarios. Weather service providers and the power industry therefore need to work hand in hand in order to ensure that the weather input is suitable to the respective power forecast modeling approach and fulfills the end-users needs (see Section 6 for more details).
3.3. Overview of NWP Ensemble Methods and Their Applicability in the Power Industry
Table 1 provides an overview and a summary of the different ensemble prediction approaches and their applicability at different time horizons as well as the so-called target time horizon. These characteristics are important parameters when selecting an EPS system’s output for a specific application. The target horizon is an important parameter to look at in cases, where the uncertainty is not required at a specific time horizon, e.g., 96 h, but over a time window. In that case, EPS techniques that have a specific target time need to be post-processed and calibrated as described in the previous Section 3.2, otherwise the output cannot be expected to represent a correct atmospheric picture of the expected uncertainty. The same is true for the type of perturbations and their respective application. If an EPS is not targeted to represent the uncertainty of the variables that an end-user is concerned about, then such an EPS will not satisfy the end-users needs [20] and in most cases be highly under- or over-dispersive.

Table 1.
Summary of Numerical Weather Predictions (NWP) ensemble prediction methods.
4. From Weather to Wind Power Uncertainty
In a deterministic context, wind power can be derived from weather variables by physical or statistical methods. Uncertainty forecasts may be produced using similar approaches as for the deterministic problem in the case of a methodology that uses weather ensemble input. In the case of uncertainty forecasts with statistical methods, these can be derived from deterministic NWP input and do not require NWP ensembles. For this reason, we can make the following distinction:
- Statistical methods based on deterministic NWP forecastsUncertainty is determined by a statistical approach using deterministic NWP input
- Methods based on NWP ensemble forecastsUncertainty is derived by applying a weather-to-power conversion method on each NWP ensemble member or by considering input derived by a reduction method applied on the ensembles
Statistical methods based on deterministic NWP forecasts have one very clear advantage: costs. The computational costs of these methods are much less than for the NWP ensemble based approaches. On the other hand, statistical approaches always depend on the historical data at hand and therefore always will have inherit its sampling limitations. Not all statistical methods provide the type of uncertainty estimates that a specific application may require, such as real-time uncertainty estimates. The same applies to NWP ensemble based methods as described in Section 3, and in particular in the Section 3.1 and Section 3.2, where it is shown that the generation of a NWP ensemble can be done with various methods and that not all methods are appropriate to use in any type of wind power application.
To conclude, all methodologies have a number of pitfalls for the end-user when evaluating the applicability of a given methodology to the end-user’s problem. Therefore, it is imperative to have some basic understanding of these methodologies in a selection process due to the large cost differences. We will discuss in the following two sections these two methodologies in detail and focus on their applicability in the power industry.
4.1. Statistical Methods Based on Deterministic NWP Forecasts
It is best practice to employ a statistical model of the wind turbine’s (or farm’s) power curve in order to capture the effects of wake losses, complex terrain, turbine degradation, and other factors. The typical wind turbine power curve, such as that supplied by turbine manufacturers, is idealized and a poor representation of reality in the majority of situations. Furthermore, statistical models of the weather forecast-to-power process simultaneously account for systematic bias in weather forecasts, akin to common post-processing techniques [60]. These models only implicitly use a power curve to transform weather input variables into power output. The two methodologies of implicitly transforming weather input into power and generating representative power curves in a probabilistic manner will be discussed in the following section to provide an overview of the differences between methods.
4.1.1. Parametric and Non-Parametric Probabilistic Forecasts
As discussed above, uncertainty forecasts for single points in space and time may take the form of a parametric distribution, such as the normal or beta distribution, in which case the parameters of that distribution must be predicted [23]. In the case of the Normal distribution, the maximum-likelihood estimate of the mean of the predictive distribution is identical to the ordinary least squares estimator which enables computationally efficient parameter estimation; however, the normal distribution is not appropriate unless the underlying data is suitably transformed, as in generalized linear modeling. For example, in order to model the non-linear power curve, a power curve data transformation is proposed in [73]. Wind power production is bounded by zero and the rated power, unlike the Gaussian distribution which is unbounded, so care must also be taken in this regard. The beta distribution is by its definition bounded by 0 and 1 and may be scaled according to the rated capacity of the wind power plant of interest as in [23]. In [73] censored normal distributions are employed, while in [74] a mixture of a censored distribution and probability masses on the upper and lower boundaries is proposed.
It should be noted that the properties of forecast errors may vary over time depending on meteorological conditions. This non-stationarity may be captured in parametric power forecast models by conditioning higher order moments (variance, skewness and kurtosis, or shape parameters) on available NWP input. This process is sometimes called distributional regression [75,76]. The advantage of distributional regression is that, given an appropriate choice of parametric distributions, density forecasts are naturally bounded between zero power and nominal power. A conditional heteroscedastic framework is proposed in [77] in which the error variance is conditional on multiple explanatory variables, while [78] used an adaptive variance model to track the dynamics of very-short-term wind power forecast errors. These methods provide the ability to efficiently model a wide range of error distributions. However, greater flexibility is available from non-parametric methods, which do not restrict density forecasts to an analytic probability distribution, but on the other hand tend to be more computationally and data intensive.
A non-parametric predictive distribution may be constructed from a discrete set of quantile forecasts. Quantile regression is the process by which models for predictive quantiles are estimated, similar to linear regression; however, in contrast to ordinary least-squares, the quantile loss function is asymmetric and its second derivative is zero, meaning that there is no closed form solution to perform parameter estimation. A variety of numerical methods exist to solve quantile regression problems [79]. Quantile regression-based methods have received much attention due to their ability to produce well-calibrated forecasts. While there are many statistical learning techniques capable of performing quantile regression, those based on decision-trees have enjoyed notable success. The top two finishers in the 2014 Global Energy Forecasting Competition wind power track employed tree-based methods and a large number of input parameters from deterministic NWP models [80,81]. The choice of inputs, or feature selection, in machine learning is critical for the successful implementation of statistical learning. Features should be selected via a rigorous cross-validation procedure, and others may be “engineered” based on domain knowledge [82,83]. When considering the tails of the predictive distribution, threshold predictors implemented with logistic regression can offer better convergence for extreme quantiles than with quantile regression [75]. Another alternative is to use conditional extreme value theory or exponential tails with conditional parameters [8].
The AnEn method introduced in Section 3 may be applied directly to wind power forecasting in order to produce parametric or non-parametric predictive distributions. In this case, the wind power observations corresponding to historical situations with weather forecasts similar to the current weather situation are collected and form a sample set which may then be used to calculate an empirical or parametric distribution. This approach is computationally efficient but relies on the existence of a large historic dataset to represent uncertainty.
Recently, different variations of vector autoregression models are being proposed to generate point and probabilistic forecasts using geographically distributed time series data and with significant accuracy improvements in the first six hours time horizon [84,85]. Finally, the AnEn method was extended in [86] to a two-dimensional grid, where each grid point is treated independently, using meteorological analysis instead of observations. This method is suitable for use cases requiring gridded probabilistic products.
4.1.2. Statistically-Based Ensembles
Probability density forecasts can be used to generate statistical ensembles as shown in [87,88] where the dependency of forecast errors in space and/or time is modeled. First the marginal distributions are used to transform the forecast errors to a normal distributed random variable from which the interdependence structure can be represented by a covariance matrix which defines a multi-dimensional distribution. Ensembles are then generated by sampling from this multi-dimensional normal distribution followed by a subsequent back transformation to the original distribution. This approach is equivalent to modeling the full multi-variate predictive distribution via a Gaussian copula, and provides a link to other copula models, which are a focus of current research in wind power forecasting.
An alternative approach has been proposed by [89], which estimated a stochastic differential equation from the forecast errors. This differential equation describes the evolution of the forecast error around the deterministic forecast and can be integrated separately for each ensemble member. Here, a Markovian assumption is used, i.e., the next time step depends only on the previous time step. A recent work explores epi-spline basis functions that allow users to control the degree to which extreme errors are captured [90].
In addition, the Schaake Shuffle [91] may be employed to reconstruct space-time structures from analog ensembles. In this method, the analog ensemble members are ranked and re-ordered to match the ordering of historic observations, and by doing so the spatial and/or temporal structure is recovered.
The main advantages of statistical methods to generate ensembles are: (i) it is a “cheap” method to generate thousands of scenarios; (ii) there is a possibility to include complex dependence structures such as lead-time-dependent conditional precisions and direction-dependent cross-correlations [92]. The main disadvantages are: (i) it requires a large historic dataset of forecast errors; (ii) the quality of distribution tails significantly affects the quality of the ensembles; (iii) in contrast to the ensembles from the next Section 4.2, there is no physical dependency since it is based on past climatology.
4.2. Methods Based on NWP Ensembles
Since weather is chaotic and wind is the main driver of wind power production, the two main sources of uncertainty in the prediction of wind power forecasting stems from the weather uncertainty and the uncertainty that comes from the non-linear relationship between wind and power production. Uncertainty forecasts in the power space based on NWP ensembles can be computed with a physical or a statistical methodology as described in Section 3.1 and applied on every ensemble member. In that way, both weather and power uncertainty is accounted for in the resulting prediction.
4.2.1. Physical Methods
In Section 3 and in particular in the Section 3.1 and Section 3.2 we have shown that the generation of a weather ensemble can be completed with various methods and that not all methods are appropriate to use in any type of wind power application. Therefore there are a number of pitfalls for the end-user when evaluating the applicability of a given methodology to the end-user problem.
When applying physical methods, the task is a non-trivial mathematical challenge due to the non-linear structure of the power curve. To the authors knowledge there has not been a methodology published that has solved the power curve mathematically over-holding the physical laws associated with the conversion from wind to power. To overcome this problem, the most straight forward method to convert wind to power is to use a power curve look-up table. The very simplest way would be to take a power curve from a turbine manufacturer and apply this to the forecasted wind speed and the density. However, such an approach does not consider factors like the locations of the turbines, the surrounding orography, the characteristic of the turbines, etc. Therefore, the physical conversion from weather variables to power requires that at least terrain and direction dependencies that cause shadowing and wake effects are taken into consideration.
A common methodology and industry standard today is to use measured time series of the power production of a turbine or a wind farm and generate a matrix of power curves for different directions and typical weather systems, including the effective heights of the wind that arrives at the turbines, reflecting the physical properties at the wind park. In that way, power curves have different shapes, dependent on the weather conditions. For example, power curves become flatter for wind directions where there are obstacles in the wind flow direction and steeper where there are accelerating topographical conditions. If wind speeds are available at different heights, a wind profile can best be simulated by finding the level that is the effective height of the wind driving the turbine’s production at a given wind direction.
Examples are statistical power curves (e.g., [93,94]), physical models (e.g., [48,49]) or artificial neuronal networks (e.g., [95]). The resulting scenarios represent the uncertainty and the time dependency modeled by the ensemble.
When using such physical methodologies applied for each ensemble member of an EPS that contains a representative weather uncertainty, then there is no more calibration required.
What that means is that, if the NWP ensemble is designed in a way so the output variables contain a representative spread (uncertainty), the conversion from weather data to power can directly be applied to generate uncertainty forecasts in power and used in nearly any application and be communicated as percentiles, quantiles, probabilities or other relevant output forms such as graphics. The calibration step on the weather ensemble data is only necessary, if the output after the conversion to power shows under- or over-dispersiveness. Sometimes, this is however also due to a lack of available variables or time resolution from the NWP ensemble (see also Section 4.2.2). The disadvantage of the physical methodologies usually is the higher computational costs of the approach in comparison to statistical methods.
4.2.2. Statistical Methods
We have seen in the previous section that NWP ensemble forecasts can be used straightforwardly to obtain wind power uncertainty. The EPS usually contains a good representation of the uncertainties and a realistic space-time dependency. If this is the case, probability density forecasts can be derived from the converted wind power scenarios with kernel dressing [87]. The results are non-parametric density forecasts, which are based on the physical properties of the ensembles.
Nevertheless, not every EPS system can deliver the required representativeness for the desired variable, which usually is shown in a lack of spread, that does not cover the observations. As described in Section 3.1, in a well-designed EPS, the observation should not be different to any one possible outcome or scenario of the ensemble members. Especially in power applications, where the wind speed and the wind profile are main driving factors this is often not the case. There are various reasons for this: (1) while in meteorology parameters like the 500 hPa, 850 hPa temperatures, 10 m wind or precipitation may be the focal points in the design of the EPS, wind power applications look at the spread of winds between 35 and 150 m; (2) not all EPS providers are willing to deliver wind speed forecasts for all ensemble members in different heights to obtain a representative wind profile; (3) the EPS are often run in coarser resolution due to computational constraints and data is sometimes only delivered in a low-temporal resolution of 3 h.
Figure 1 shows an example of an apparently under-dispersive ensemble in power space for a wind farm in Spain. In this case, the wind speed at 10 m from 75 members of a MSEPS from weather ensemble service provider WEPROG, has been converted into power load factor. In Figure 2, 300 wind speeds at 10 m, 40 m, 100 m and 150 m from the same EPS has been converted into power load factor. In that case, the spread of the ensemble is sufficient and not under-dispersive. When analyzing the case, it can be seen in Figure 3 that the 75 wind speeds from the 35 m wind speed would have been sufficient to cover the observations. However, this is only a single case and may be very different with just the next extreme or in a different weather situation. The example therefore is a good illustration of the importance to understand that when working with weather prediction models, whether deterministic or from an ensemble, the uncertainty of the resulting forecast is a mixture of uncertainty in the initial conditions and boundary conditions and model insufficiencies due to the requirement of parameterization. This has been discussed lengthly in Section 3. Nevertheless, it is when evaluating the end products, e.g., power production forecasts, and the limitations that come from the weather uncertainties, the applicability of these data in the further processing needs to be understood.
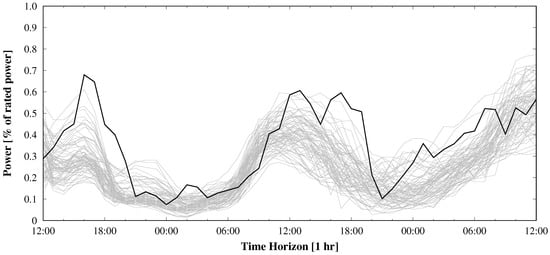
Figure 1.
Example spaghetti plot of 75 normalized wind power forecasts converted from wind speed forecasts at 10 m from a multi-scheme ensemble prediction system (MSEPS) from weather ensemble service provider WEPROG at a near-coastal wind farm in the North of Spain.
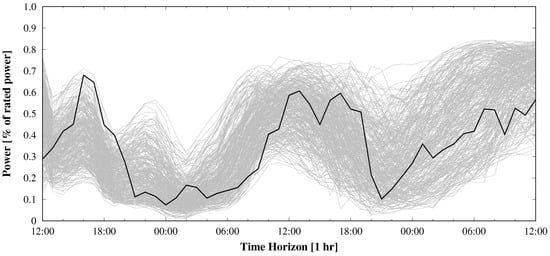
Figure 2.
Same plot as Figure 1, in this case with 300 normalized wind power from wind speeds at 10 m, 40 m, 100 m and 150 m, illustrating that an entire wind profile may be required to capture the uncertainty of the power generation.
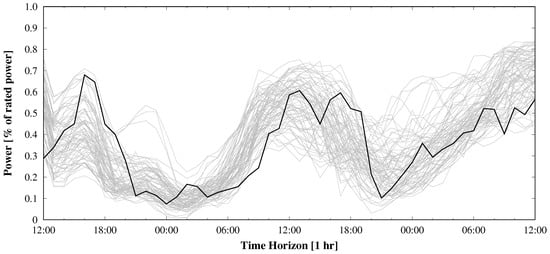
Figure 3.
Same as Figure 1, in this case with 75 normalized wind power from wind speeds 40 m, illustrating that in this specific case the effective wind speed at the turbines, where the MSEPS captured the entire uncertainty was at that model level.
In those cases, where it is not possible to work with the extend of forecasts that would cover the uncertainty of the focal parameter, or the EPS is in too coarse resolution to resolve the local weather conditions, a calibration of the raw output from the EPS needs to be performed [95,96]. Such a calibration step can correct for a weather ensemble that lacks spread for the focal variable. Often the first step is to derive quantiles from such an ensemble and then add a calibration to the quantiles [94,97]. The quantiles can be calculated form the ensemble forecasts by ranking the members for every time step. If is the rank of the i-th scenario and M is the number of ensembles, then gives the quantiles [98].
For the calibration a so-called Ensemble Copula Coupling (ECC) can be used to calibrate the distribution of the ensemble while preserving the time evolution of the original ensemble data [70]. When applied to power, the calibration has to include the non-linearity of the power conversion. In that case the quantiles have to be calibrated, i.e., adjusted in such a way that the probabilities are in accordance with observations [94,97]. It has been found that the time evolution and the spatial correlations of the calibrated ensemble often deviate from the observations. A way to combine the observed temporal or spatial correlations with ECC is by using dual Ensemble Copula Coupling (d-ECC), which was presented by [72] for meteorological ensembles, but has been proven to be applicable in the same way to wind power ensembles. The results are well calibrated ensembles with realistic spatial-temporal correlations.
To summarize, well calibrated ensembles or other probabilistic wind power forecast representations are produced, if the NWP ensemble is well calibrated, the power transformation is appropriately chosen and the results are calibrated with respect to the observed power. Under certain conditions, steps of this procedure can be omitted or be performed in one step. For example the calibration of the meteorological variables can be omitted, if the final power is calibrated, or if the raw ensemble contains an appropriate representation of the uncertainty of the driving variables for the wind power conversion as described in Section 3.
An alternative approach that consists in extracting statistical variables from the NWP ensemble and use these engineered variables as input to a statistical method is discussed in [99]. The following inputs were tested by the authors that used quantile regression forests as statistical model: (a) mean and variance; and (b) median and median absolute deviation. The results show that the use of ensemble information can improve the forecasting skill. However, it is important to highlight that the temporal dependency of forecast uncertainty is “removed” with this feature engineering approach. In [98], it is suggested to sort the wind speed NWP ensemble members and then use the ensemble member that corresponds to the quantile of interest as predictor in a statistical model.
In Figure 4 we provide a summary and the links between input data methodologies and forecast types. In some cases, it is possible to construct one forecast type from another with relative ease. Interval forecasts are constructed from pairs of quantiles, as discussed in Section 2. Deterministic forecasts may be taken as the mean or median of a PDF forecast, or the 50% quantile. Quantile forecasts can be calculated directly from PDF forecasts. PDF forecasts may be calculated by interpolating or smoothing between forecast quantiles, or estimated from ensembles. Simultaneous interval forecasts are derived from ensembles. The mean of ensemble NWP may be treated like a deterministic NWP.
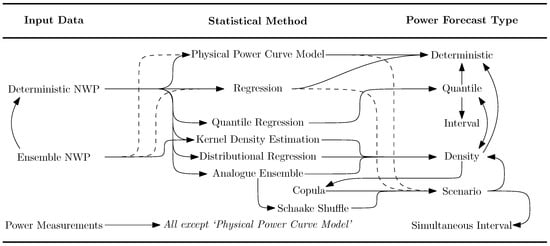
Figure 4.
Illustration of links between input data statistical methodologies and forecast types. Dashed lines indicate that methods relate to individual members of ensemble NWP which require calibration.
4.3. Regional Aggregation
Until now, we have only been considering the general conversion from wind to power, but not, how the requirements for the uncertainty forecasts change, if we scale our problem up from one wind farm or one turbine to an entire region or country or into power pools. As the wind power industry matures, there are very few applications, where it is not required to aggregate over areas, regions, countries or power pools. Three distinct cases can be considered: (a) when there is a full observability of the wind farms as is the case of virtual power plant (VPP); (b) when not all wind farms are observable or their number is too high to deal with them individually, and then some upscaling technique is required to forecast the total production from a sample of wind farms; (c) when the aggregation contains not only wind farms but other sources like photovoltaic plants, load etc., which can be the case in a VPP or nodal forecasting. In the case of deterministic forecasting the first problem is resolved by adding the point forecasts of all involved wind farms, while in the second case there are well established upscaling techniques in the literature and in daily use by end-users [100,101]. The third case is challenging since the dynamics of the process are highly variable and complex. It is a subject under research in some projects like the EU project REstable, where among others the power of a combined VPP is forecasted to provide ancillary services [102].
However, when it comes to probabilistic forecasting, the task is more cumbersome. This is mainly because simple addition of probabilistic forecasts is not mathematically correct. Secondly, the aggregated power is in fact a different stochastic process, because it is characterized by lower variability due to the smoothing effect obtained from the geographical dispersion of the wind farms. Moreover, a number of additional issues make the forecasting task more challenging:
- The capacity of the aggregation may change as new wind farms can be installed or old ones decommissioned.
- Historical data of the new wind farms are not necessarily available to retrain the forecast models on the new configuration.
- Maintenance operations and down-regulation of the wind farms production due to grid issues corrupt the measured production time series and impact the forecast performance.
Several operational systems consider today the aggregated power as a stand-alone stochastic process and make probabilistic forecasts directly for that. The main challenge, especially in the case of wind farms spread over a wide area, is to select representative points of the NWP grid to be used as input to the model. This approach is successfully applied today in systems like the one of Australia (AWEFS/ANEMOS forecasting system) where the adapted re-sampling method proposed in [103] has been applied to provide quantile forecasts for aggregations. Such model has acceptable performance when new wind farms are added in the system, thanks to its auto-adaptivity. Performance in transitory periods of new wind farm additions can be enhanced through pre-training of the model based on synthetic wind power series derived from pre-existing wind speed measurements. Lower performance of the probabilistic forecasts during such transitory periods can be thought as of less importance than the impact of scheduled maintenance or wind farm down-regulation may have, if that information is not considered to correct the forecasts. To keep operational implementation of the models simple, empiric simple corrections are applied for scheduled maintenance and down-regulation.
However, in some applications statistical or physical ensembles may be requested for the aggregation rather than quantile forecasts. In the case of statistically-based ensembles (Section 4.1.2) it is important to generate them taking into account spatial-temporal correlations. For the case of physically-based ensembles the most straightforward approach is the summing up of forecasts from a NWP ensemble (Section 3.1), where no specific calibrations are required or where the power conversion step is performed implicitly. In the latter case, it however has to be an approach that contains the spatial and temporal dependencies to be applicable for this type of area aggregation. In fact, it requires that the individual ensemble members or scenarios have been converted to wind power, contain a representative uncertainty and are then summed up per member to an area aggregation. Only then, the resulting ensemble of aggregated members also contains a representative uncertainty (spread) for the area (e.g., [49] p. 84). Moreover, physically-based ensembles can provide better information about extreme events.
To conclude, in order to provide probabilistic forecasts of aggregated capacity a number of aspects have to be taken into consideration, especially the correct mathematical sampling of the uncertainty forecasts is crucial for representativeness of the resulting aggregated uncertainty. In any case it is important for end-users to describe the requirements of their applications thoroughly and to understand, which methods may be used or may contain limitations that can by definition not solve the problem at hand.
5. Communication of Uncertainty
Although uncertainty terms are part of our day-to-day communication and language, communication and application of uncertainty in weather forecasting and the power industry’s decision making processes is still in its infancy on many levels. Research in psychology and cognitive decision-making has proven over the past decade that uncertainty information not only helps decision making, but also reduces the distrust in forecasts when they do fail significantly [104]. In order to unlock the full potential of uncertainty information for better decision making, it has to be communicated effectively [105]. On the receiver’s side, end-users have to acquire a sufficient understanding of both weather uncertainty and how that translates into their particular application.
In this section we focus on means of communicating both weather uncertainty and wind power uncertainty for different power system applications.
5.1. Communication of Weather Uncertainty
Communicating weather uncertainty is about conveying information regarding expected forecast skill to the end-user. There are several reasons why communicating the weather forecast uncertainty is useful, both for the forecast providers and for the end-users. In the WMO guidelines on communicating forecast uncertainty [14], the main reasons identified are to:
- Promote enhanced decision making;
- Manage user expectations;
- Promote user confidence;
- Reflect the state of the science.
For a specific decision-making problem, a cost function can be estimated that describes the costs of taking different decisions, given the actual outcome of the weather. End-users can then use this information together with probabilistic forecasts in order to react appropriately to the situation at hand (for instance by determining an optimal threshold for taking preventive action). Indeed, it has been found in several studies that end-users receiving information on uncertainty make significantly better decisions than end-users without uncertainty information. This important result has been found to be valid for both expert and non-expert users [106,107]. For example, lab experiments showed that end-users with deterministic forecasts make more risk-averse than risk-seeking errors. When given a deterministic forecast, end-users are forced to estimate forecast uncertainty on their own, leading to a risk-aversion bias [108]. Including an estimate of the uncertainty narrows the range of expectations and neutralizes the bias. This allows decision makers to take more risk when forecasts are estimated to be more certain [109]. Another effect of using uncertainty information is that decisions from several individuals tend to converge, meaning lower variability of test results [110]. This implies that uncertainty information can allow for more systematic decision-making, especially among multiple individuals. Furthermore, end-users who understand that forecasts are inherently uncertain are much more likely to retain confidence even in situations where the models fail. In fact, for end-users faced with deterministic forecasts, large model errors has been seen to lead to a reluctance to take any decision at a later point in time [14,111]. This fact suggests that the user’s confidence in the forecast has been reduced. Lastly, probabilistic forecasts can be motivated scientifically. A deterministic forecast only represent one possible outcome of a given situation. Therefore, in order to communicate weather forecasts in a manner that represents the full range of possible outcomes, uncertainty information is required.
Weather forecast uncertainty can be communicated in several ways: through charts, graphs, tables, images, and written or oral narratives. Visual representations have enormous potential to convey the weather uncertainty information in an easy to understand manner. These representations are especially suitable for web-based display and can be accompanied with additional explanatory information. Interactive charts permit the user to explore the data and extract information relevant to their specific application. Furthermore, the use of colors has shown to have a stronger impact on memory than abstract information [112]. However, visualizations can be misinterpreted and there are situations in which they may lead the end-user to false conclusions [113]. Care must be taken so that colors (and color scales) are chosen to send the right message to the end-user [14,112]. For instance, in experiments performed in [113], no advantages were found for visualizations over text only formats, demonstrating that visualizations may not always improve comprehension.
There is not a single correct way to communicate weather forecast uncertainty. On the contrary, depending on the weather-related decision problem and end-users intention, many different ways of expressing uncertainty estimates may be appropriate [105]. An example of this are the inconclusive results that have been found for whether frequency or probability representation or uncertainty is the preferred way of receiving such information [109,114]. In addition, different users, using the same application have their own preferences for visualization, as well as specific criteria and thresholds for decision making [115]. Even though communication should be dependent on context, one general guideline when designing systems to communicate weather uncertainty can be stated. By reducing the mental load on the end-users (e.g., number of cognitive steps) increased performance is generally achieved [112]. An observation in this respect was the improved performance of participants in experiments, where all possible weather outcomes (not only the most probable outcome) were indicated. This eased the burden on the end-user from having to perform supplementary in-head calculations by themselves [14,114].
5.2. Communication of Wind Power Uncertainty
Wind power uncertainty can be communicated to the end-user through several different representations. The main representations are [116]:
- Probabilistic forecasting;
- Scenario or ensemble forecasting;
- Skill forecast;
- Ramp forecasting.
In the probabilistic forecasting representation, the wind power output is regarded as a stochastic variable. Its properties can for example be represented by quantiles, moments of the probability distribution (e.g., mean and variance) or the full PDF, from which quantiles and moments can be derived. A commonly used visualization is the “fan” chart, which is a set of forecast intervals aggregated in one plot. However, charts similar to the one in Figure 5 may give misleading information to a decision-maker. For instance, the decision-maker may interpret each one of the quantiles as a possible temporal evolution in time. If the chart is built by a statistical model, this would be incorrect. In fact, the marginal intervals can only be interpreted individually for each lead-time. For instance, in hour 12:00 of the first day there is a probability of around (limited by quantiles 95% and 5%) that the observed value is within approximately and .
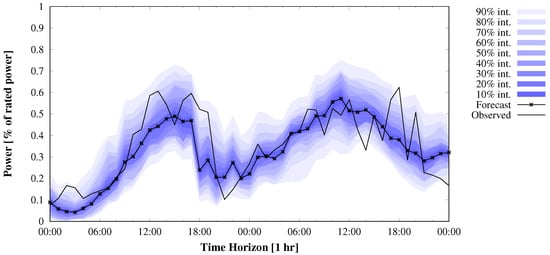
Figure 5.
“Fan” chart with wind power marginal forecast intervals.
The “fan” chart from Figure 5 was generated with the statistical method described in [82]. Figure 6 depicts a second plot for the same wind farm (in North of Spain) and day, but built from a NWP based ensemble. The physically-based quantiles show a wider spread explained by the ability of NWP ensembles to produce outliers and also catch extremes. This is a clear distinction from statistical methods, because even long time-series of historic data often contain too few extreme events to have impact in the learning algorithms. It is therefore imperative to know the background data from which such a chart is generated.
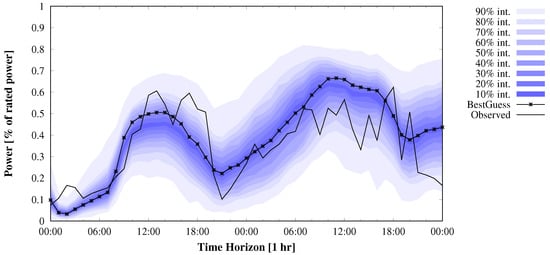
Figure 6.
“Fan” chart with wind power forecasts from a NWP ensemble approach.
An alternative representation with the temporal dependency is a “fan” chart with simultaneous forecast intervals [117], as depicted in Figure 7. These intervals were constructed with the methodology described in [117] and from the NWP ensembles of Figure 6. For example, the darkest blue area represents a 10% probability of having the observed wind power trajectory completely inside the interval defined by quantiles 45% and 55%. Comparing Figure 6 and Figure 7 shows the following differences: (a) the simultaneous forecast intervals with lower coverage are wider than the marginal intervals; (b) the shape of the quantile curves from the marginal forecast intervals are similar to the point forecast. The estimation of simultaneous forecast intervals results in quantile trajectories that represent a certain probability of having an observed wind power lower or equal to that trajectory.
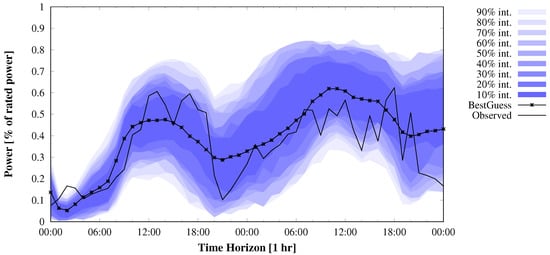
Figure 7.
“Fan” chart with wind power simultaneous forecast intervals.
However, the most common representation of uncertainty in stochastic multi-period optimization problems is through scenarios [118]. The temporal ensembles represented in Figure 8 are alternative representations for the uncertainty that includes temporal dependency of forecast errors and represent short-term scenarios. Figure 8 is wind power converted from a 75 member NWP multi-scheme ensemble and is a subset of the forecast data shown in Figure 6, this time as 75 individual scenarios from wind speeds at 100 m height.
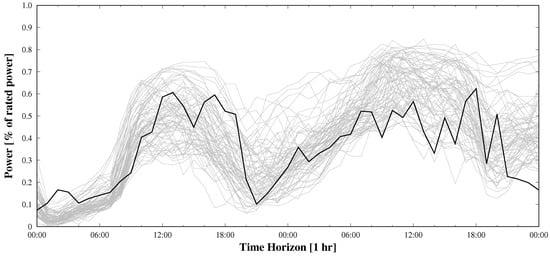
Figure 8.
Seventy-five wind power forecasts from 75 ensemble members at 4 different model levels at 100 m for a 48 h-ahead time horizon.
The number of ensemble members can vary, where a larger number of ensembles might have a higher probability to represent the actual uncertainty. However, if the spread becomes too large such a representation might not provide clear information any more to the end-user and can increase cognitive load [119]. The ensemble’s dimension should therefore ideally be reduced to the end-users needs or a realistic spread of the focal variable.
Both methodologies, the physically and statistically-based ensembles can be used to represent interdependence of forecast uncertainty across multiple wind power plants or electrical system network nodes, where cross-dependency is conditioned by the prevailing weather situation (e.g., characterized by wind speed and direction) [49,92]. The difference between the methodologies has been discussed in Section 4.
Recently, it was proposed in [120] a different representation of forecast uncertainty through multivariate “ellipsoidal prediction regions”, which was specifically developed for time-coupled chance-constrained or robust stochastic optimization problems.
Another way of communicating forecast uncertainty is through “risk” indices that provide information on the expected level of forecast skill, encompassing qualitative information about the predictability of the atmospheric condition. Such an index can, for example, be expressed as color codes or as integer or continuous values. Higher risk values indicate a less reliable forecast. Two metrics have been proposed in the literature: (i) the Meteo-Risk Index (MRI), which reflects atmospheric predictability through the spread of the available NWP ensemble at any given lead-time [96]; (ii) the Normalized Prediction Risk Index (NPRI) reflects the spread of an ensemble of wind power forecasts for a single lead-time or over a time period [121]. NWP ensembles are obtained by considering multiple forecasts through the perturbation of the initial conditions of the NWP model, different NWP models, different parametrization schemes or lagged forecasts obtained from different initial conditions, and can be used as input for these metrics. An example for the use of these metrics is given in [121]. The authors compute the weighted standard deviation of the ensemble members, where each weight is interpreted as each ensemble member’s ability to provide information on predictability. Then, a relationship is established between five equally populated classes of NPRI values and the distributions of forecast errors.
For an end-user, this information is a qualitative measure that provides an a priori warning on the expected level of forecast error. Compared to forecasting intervals and ensembles, these skill indices may be more easily understood by operators and forecast users and provide timely information about the potential magnitude of forecast errors. However, the use of the word “risk” might be misleading since technically risk entails two components, uncertainty and exposure, and can be defined as “exposure to a proposition of which one is uncertain” [122]. These indices provide information about uncertainty, but not about exposure (i.e., the possible consequences). The term skill forecasts is more accurate [121]. Moreover, risk indices only provide a single numerical value that informs about the spread of the wind power forecasts at a given period, thus only providing information on the confidence of the point forecasts. A potential use would be to adjust the size of the forecast intervals. For instance, if the MRI is low, narrow forecast intervals are expected. This information was included in a quantile regression model, but the results showed that skill forecasts seem to have a very minor influence on the 25% and 75% quantiles [123].
Finally, information about wind power uncertainty can also be communicated as ramp forecasts. In wind power, a ramp is characterized by the following parameters [124]:
- Magnitude : wind power variation observed during the event;
- Duration : time period associated to the large variation event;
- Ramp rate: ramp intensity, which is the ratio between magnitude and duration ;
- Timing : time instant related with the ramp occurrence, which can be the start or central time instant of the event;
- Direction: increase or decrease in wind power.
Different definitions have been proposed to identify ramp events (a detailed discussion can be found in [124]) where threshold values are defined for the pair and . The uncertainty of ramp events is often represented by probability distributions for amplitude, timing, and duration. The European Project SafeWind (2008–2012) recommended that it may be better to display the probability of particular extreme events (e.g., ramps, cut-offs and potential curtailment) in a classification output format, e.g., four color-coded risk levels (green, yellow, amber and red) [125]. The project has adapted the color and risk levels currently employed by the Met Office for describing extreme weather events in a early warning system, which requires the cooperation between the end-users and the forecasters. Moreover, the project also suggested to communicate EPS forecasts on a geographic map that enables end-users to detect areas with high forecast uncertainties immediately [125]. This approach was demonstrated for the 50 Hertz Transmission control area, which is in the Eastern part of Germany with 17 GW and 10 GW of installed wind and solar capacity, respectively. An interesting development from ERCOT is the application of extreme value theory for examining the tail characteristics of hourly wind power ramp data, followed by a risk assessment (e.g., value-at-risk based metrics) for wind power up ramps and down ramps separately [126].
6. Mapping Uncertainty Representations and End-User Requirements
In this section we will discuss five typical decision-making problems in the electric power industry and the respective end-user requirements in terms of uncertainty representation and forecast quality. At the end of the Section 6.6 we provide a summary table of these items.
6.1. Reserve Requirements and Unit Commitment
Setting the operating reserve requirements is the responsibility of system operators and the use of probabilistic wind power forecasts for this purpose is becoming a standard practice in several countries [6]. The decision problem is applied independently to each time interval (in general, this corresponds to the time resolution of the electricity market). Even in control areas where UC/ED processes are in place, the reserve requirements are included as a constraint in the UC/ED process and are a result of a dynamic probabilistic rule [5,127]. In this case, the uncertainty product can be a conditional quantile included in a probabilistic dynamic rule (see [5]), a conditional PDF to convolve with other PDFs (see [2]) or the relationship between spread and the skill of a forecast by using a NWP multi-scheme ensemble (see [49] p. 127).
Qualitative information from skill forecasts can also be used in combination with empirical rules for reserve allocation. Traditionally, and before the deployment of wind power technologies, system operators were used to apply empirical rules like a percentage of the forecasted load plus the large generation unit in the system. Similar rules can be derived to include a percentage of the forecasted wind power that varies with the level of predictability. This establishes a link with the well-being framework that is used in power system reliability analysis to classify the system states into healthy, marginal and at risk according to a predefined deterministic criterion [128]. In other words, skill forecasts can be used to combine deterministic perception (or empirical rules) with probabilistic information about the predictability level of wind power forecasts.
For system operators, the regulatory framework imposes very low levels of risk (e.g., loss of load probability, probability of RES curtailment), while requiring minimum operating cost. This creates a cost-risk trade-off that should be assessed and included in the decision making process [2]. It also defines an important requirement for uncertainty forecasts.
For example, in electric systems with large amounts of wind power (and solar power) the core input for the risk evaluation is the ramp rate uncertainty of this aggregated non-scheduled generation. When aggregated, the ramp rate uncertainty can for example be computed from the time derivative of each ensemble member of a NWP ensemble approach. In a well functioning market, it can then be assumed that the prices are likely to peak when the standard deviation of this vector approaches the level of secondary reserve [49].
Another requirement may be the calibration of distribution tails (i.e., below 1%) and sharpness, which is critical to derive “good” decisions. For instance, consider a scenario where the 1% quantile of the national aggregated power is 60% of the total rated power and the system operator is interested in having a loss of load probability (LOLP) below or equal to 0.1% (which corresponds to 87.6 h per year). The key information is in the tail between the 1% quantile with 60% of rated power and zero generation and its forecast quality has a significant impact in the following decision quality parameters [129]: (i) match between the predefined risk threshold value and the observed number of insufficient reserve situations (i.e., mobilized reserve greater than suggested reserve); (ii) the amount of suggested reserve and the ability to provide different reserve levels for different conditions of the power system operation.
On the other hand, in Hydro Quebec, the system operator of Quebec in Canada, gamma-like distributions with time-varying parameters are estimated from real data to approximate the wind generation forecast errors and from that the required balancing reserve for the wind driven part. They developed a dynamic balancing reserve model for the 1-48h horizon with a clear risk criterion and have demonstrated that this improved modeling significantly reduces the required balancing reserves and associated risk [130].
As previously mentioned, the wind power uncertainty can also be included in the UC/ED problems as external information resulting from a probabilistic dynamic rule [6]. The alternative is a two-stage stochastic programming with recourse, where wind power uncertainty is represented by a set of temporal ensembles [127]. This alternative becomes relevant in the presence of multi-period constraints, such as inter-temporal operation of conventional power plants (e.g., minimum operating time, ramps) and state of charge of energy storage.
In this multi-period optimization framework, two types of requirements are relevant: (i) information about the temporal evolution of forecast errors, which is captured by the simultaneous forecast intervals and temporal ensembles; (ii) ability to forecast critical events for the power system (e.g., large ramps, long periods with high/low generation), where aspects such as phase errors are critical for the decision quality. Sari et al. [131] conjectured that for this problem, calibration (measured with multivariate rank histogram) of ensembles is more important than their sharpness since it might lead to operating conditions with over-commitment or under-commitment of generators (i.e., higher cost); a similar conjecture was also stated in [132] for imbalance-biased wind power point forecasts. The recommendation in [131] is to use the mass transportation distance (MTD) rank histogram metric to select the ensemble-generation method with best calibration, in contrast to the traditional energy score [133] that has low discrimination ability and can give misleading information (e.g., can indicate high quality of sharp ensembles that are not perfectly calibrated. Metrics like the p-variogram score [134] also allow a better identification of misspecified dependence structures when compared to the energy score (see [135] for a numerical example).
Event-based evaluation frameworks like the one proposed in [136] can quantify the forecasting skill of ensembles for specific critical events for the power system. For instance, the comparison in [136] between ensembles generated with the Gaussian copula and from calibrated NWP ensembles showed that physically-based ensembles can better detect events characterized by rapid changes in power generation (e.g., ramp-up and ramp-down). However, the economic impact of this improved detection requires UC simulations, like the ones presented in [137]. Moreover, it is important to highlight that physically-based ensembles already capture the spatial-temporal uncertainty dependency structure, while statistical methods require complex techniques and further research for an operational deployment [92].
Finally, accurate forecast of large ramps is particularly relevant for the transition periods between market intervals, where interconnection line usage might change from export to import or vice-versa and power plants ramp up or down trying to adjust to the next market period [10]. In situations with large wind power ramps, the system operator might need to call fast-reserve units in advance to accommodate these variations in combination with the market hour transitions. On the other hand, there is also a growing interest to hedge reserve prices for short, but large forecast errors or ramps.
Möhrlen and Jørgensen [138] showed an example about how to solve such situations with a NWP multi-scheme ensemble for a system operator that wanted to allocate parts of the reserve requirements a few days ahead. One of the first hurdles they found was that in a real-time environment, there are often non-weather related processes that suddenly need to be considered that are in demonstration phases ignored or dealt with through simple assumptions.
In their study they had to deal with a cross-border exchange that generated reserve requirements that could not be ignored. The overall recommendation for a control area with non-specific requirements or as a starting point to gain experience is therefore to use the hourly mean reserve forecast (P50) together with a spread band of MIN/MAX width. These MIN/MAX bands are then used to set the requirements for the ramping capabilities of the additional reserve and should be understood as the uncertainty of the hourly mean collective ramp rate of load and wind (and possibly photovoltaic generation).
6.2. Participation in Electricity Markets
The wind power market bidding problem has two fundamental objectives: (a) optimize forecasts/bids to minimize imbalance costs; (b) boost ability to participate as price maker in the electrical energy market to maximize income.
Different decision-aid paradigms can be used to derive the optimal bid. Botterud et al. tested three different paradigms: expected value; risk-expected value trade-off; utility theory (risk averse or risk prone) [139]. All of these paradigms are based on conditional quantiles that can be forecasted by statistical algorithms or calibrated NWP ensembles.
A well-known analytical result is the following [98]: the maximum expected profit is obtained when the wind power bid is the quantile of the forecasted marginal distribution. This makes perfect calibration a very important requirement, with direct impact on market revenue. Sharpness is only critical for risk-expected profit decision paradigms, since low sharpness means high risk for similar values of expected profit.
Presently, an interesting challenge for the market bidding problem is the impact of wind power forecast errors on market prices. For instance, REE in Spain showed a day in which the forecast error is −1.5 GW (overestimation) and the price is under 10 €/MWh (valley period) and 3 GW (underestimation) around the peak period [140]. This illustrates that in power systems where the wind power plants participate directly in the electricity market, the dependency between the price and wind power forecast errors can be non-marginal, which increases the complexity of uncertainty modeling. In [141] wind power is also reported to be a “price driver” in the UK, where wind forecasts affect the market-clearing price.
The same applies in Denmark and even more so in Germany in the Nord Pool and EPEX markets, respectively. In both countries wind and solar power are handled by independent balancing responsible parties that also carry the balancing costs for their forecast error. In both markets wind power, in Germany also solar power, are driving the market prices at times even below their own marginal costs. This has started to become a problem in both markets, more though in Denmark, where a lot of the rather old turbines have to be dismantled once they fall out of their support scheme, as the market prices can no longer recover maintenance and service costs of the turbines.
This is due to a number of factors. One main factor is the market coupling to the central European market that maximizes the value of renewable energy, but only as far as the transmission and load allows. While the expansion of renewables is unbreakable prices do not follow the possible flow of energy. The results are low prices that pushes fossil plants out of the market, which is a good development on the one hand, but also makes the system more and more rely on non-scheduled generation [4]. If the increased renewable generation implies increased curtailment, this can reduce the advantages of the renewable energy production, reducing transparency and thereby enhancing speculations in the market that will lead to increased balancing costs. In other words, if the prices no longer reflect the production capacity’s costs, the market will implode. The solar power expansion in Germany with more than 40GW installed capacity at the end of 2016, have lowered even the prices in the market that have traditionally been high. Möhrlen et al. [4] concluded that the current situation suggests that owners or operators of renewable power plants have to become price makers in order to not destroy the market structures. With current volatility of weather and load pattern at different time scales that cause continuously changes in the flow of energy and spot market prices, uncertainty forecasts play a major role in solving this problem.
Such situations in fact establish new end-user requirements to adequately model the dependency between wind power and price forecast errors. Another requirement is to built VPP that include some storage capacity in order to diminish possible speculations in the market against wind power in windy periods, when the price is below the marginal cost and the competitiveness of wind power as well as the incentives to investments in wind power become inefficient and unattractive [142]. Some works in literature already propose analytical models for defining optimal market bidding strategies based on uncertainty forecasts including cases where the real-time prices and real-time generation are not independent [142,143,144] (author’s English version is available online: http://download.weprog.com/WEPROG_Trading_strategies_EEG2012_ZEFE_71-2012-01_en.pdf).
Support schemes such as feed-in tariffs are ending in many regions and wind power plants are forced to enter into ancillary service markets to increase their revenues. Some examples are the Elia pilot in Belgium [145] for downward automatic frequency restoration reserve (aFRR) and Kombikraftwerk 2 in Germany [146] for tertiary control reserve. The provision of frequency control services requires a methodology that gives a reliable forecast of the available reserve capacity. Both pilots concluded that the best scheme was the available active power (AAP) mechanism [147]:
- Uses wind speed measurements, power curves of the wind turbines and/or physical models of the turbines to estimate in real-time the reference power (i.e., called AAP);
- Delivered amount of reserve power is calculated in real-time as the difference between the reference and the actual feed-in of the wind farm.
In this scheme and in order to define a reserve capacity offer in advance (e.g., day-ahead), conditional quantiles are used to determine reserve offers with a certain level of reliability (see [146] for more details about the bidding method). It is important to underline that system operators usually define some reserve quality standards, e.g., Elia defined “in >99% of the cases it is forecasted that the wind farm will be able to deliver a certain amount (MW) of aFRR capacity”; a reliability of 99.994% was assumed in the Kombikraftwerk 2 project. Therefore, the end-user (market agent) requirements are: (i) perfect calibration since it impacts the reliability of offered reserve; (ii) high sharpness since it influences the amount of available reserve capacity (forecast intervals with high amplitude mean lower downward reserve capacity band). If multiple wind power plants are aggregated in a portfolio for market bidding, the spatial dependence structure must be included in the decision model and therefore spatial ensembles are a key requirement.
In this use case, multi-temporal information of uncertainty is not required if the wind power plant is not participating in combination with a storage unit. If storage is available to form a VPP [148], temporal or spatial-temporal ensembles (in case of spatially distributed resources) are required. For instance, the analytical work of Haessig et al. [149] showed that discarding autocorrelation of day-ahead forecast errors can lead to underestimation of storage capacity.
The work of Pahlow et al. [142] had already paved the path in 2008 to the findings of Castronuovo [148] and Haessig et al. [149] including the use of uncertainty forecasts. They showed the benefits of optimization of VPPs by applying a NWP multi-scheme ensemble prediction system. Especially due to the asymmetry of reserve prices for up- and down-regulation, but also the increasing complexity and the changing structures of weather and load patterns, they suggested that an optimization model has to be kept small to achieve fast convergence of the objective decision process. This in turn means that the “intelligence” needs to lie in the input data to the optimization model.
If this is the case, Pahlow et al. [142] showed that the possibility for the trained user to redefine boundary conditions and test the solution’s sensitivity to various likely and less likely events is greatly enhanced with the availability and use of uncertainty forecasts. They in fact concluded that “... the net result is then that the market can no longer force the intermittent generator to bid in with low prices. The intermittent generator thereby gains freedom with the dynamically changing cocktail of pooled energy and weather uncertainty ...”. Such trading strategies, whether in the spot market or the reserve market should be enough incentive to ensure that wind power does not destroy it’s own market by staying price taker, underbidding even the marginal costs of RES, which is in the long run counter productive for the market as well as the entire electric system.
6.3. Predictive Grid Management
System operators of transmission and distribution systems are exploring the predictive grid management paradigm [150] that is divided in two phases: (a) detect technical problems such as congestion and voltage limits violation in the electrical grid in advance; (b) procure available flexibility in the electrical grid to solve the detected technical problems.
A tool that comprises these two phases is the multi-period optimal power flow [151], which can include wind power uncertainty in the form of spatial-temporal ensembles [152]. A framework to test uncertainty forecast for grid security as been proposed in [153]. It comprises scenario forecasts, load flow calculations for each scenario, the identification of the statistics of critical system states and an optimal power flow for re-dispatch.
The uncertainty representation should fully capture the spatial-temporal dependence structure, where the temporal dimension is indispensable, if storage units or temporal constraints are included in the optimization problem. The main requirements in terms of quality are: (a) perfect calibration to avoid false positive and false negative alarms; (b) high sharpness to avoid excessive operating costs due to a continuous use of flexible resources as a result of high uncertainty bands; (c) accurate spatial correlations to get the right power flows; (d) accurate temporal correlations for storage planning.
In [129] an evaluation framework is proposed, inspired by receiver operating characteristic curves (ROC) from data mining problems, to evaluate the detection quality of grid technical constraints violation. The basic idea was to find a trade-off between percentage of false alarms and percentage of overlooked violations when setting the probability threshold value for an alarm generation.
The main challenge in this use case is to have a computational running time acceptable for an operational deployment of stochastic optimization methods. The representation of uncertainty with a discrete set of ensemble members might result in prohibitive computational times. Therefore, further research is needed in two directions: (a) find uncertainty representations (e.g., spatial-temporal simultaneous forecast intervals or quantiles, analytical joint density functions) that contribute to decrease computational time of mixed integer non-linear optimization problems; (b) explore decomposition techniques to parallelize the optimization problem. For challenge (a), the ellipsoidal prediction regions can be integrated as additional constraints in stochastic optimization problems [120], and contribute to decrease the computational demand.
6.4. Maintenance Scheduling of Wind Power Plants
Renewable energy companies, with the advent of Internet of Things technology, are hiring data scientists to develop new predictive maintenance and conditioning monitoring data-driven methods for their assets. For example, the high cost of offshore wind power plants maintenance demands new monitoring and maintenance planning methods [154].
Since maintenance operations involve multiple periods, the temporal dependency of forecast errors is an important requirement for the uncertainty forecast. The interest is in periods with wind speed and wave height below particular safety thresholds e.g., for using a crane or transferring technicians to an offshore turbine. These thresholds vary depending on the requirements for the maintenance operation, such as accessing the turbine roof, and the capability of specialist equipment, particularly in the case of offshore access vessels. In this case the forecast representation can be discrete, e.g., probability of having wind speed below 4 m/s during an X hours window. The economic cost for deterministic forecast errors is therefore dependent on whether the forecasts and realizations fall on the same side of the threshold or not which makes forecast evaluation challenging [155] and is a strong argument for taking a probabilistic approach.
Short-term probabilistic forecast of access windows can be derived from deterministic weather forecasts and integrated in decision-making problems under risk (cost-loss model) for offshore wind power plants maintenance [78]. Ensemble forecasts may also be employed as an input to stochastic optimization to generate maintenance schedules [156]. The simultaneous forecast intervals cover all these requirements and their use is recommended. Perfect calibration is desired for an accurate estimation of the financial risk associated to the maintenance task.
In contrast to power system operation, where forecasts are required continuously for operational decision-making, for maintenance applications weather conditions are only one of many constraints including the availability of spare parts, technicians with appropriate certification and specialist equipment. Nevertheless, the importance of uncertainty forecasts to efficient decision making and planning is still underestimated in many areas.
6.5. Long-Term Portfolio Planning
In contrast to short-term planning, mid and long-term planning (i.e., monthly, seasonal, and over decades) analysis depend on climatology and climate oscillations for the specific analysis region. Even though the long-term planning of wind power generation resources is investigated by various institutions and universities, the business practices of this field still needs to mature in particular going beyond using only climatological information from deterministic model output. A limited number of seasonal (or climate) forecasts applications are used in energy industry, as an input for their decision-making processes for investment and portfolio optimization.
The benefits for multiple end-users are [157]:
- Policy makers and regulatory authorities: Annual and decadal forecasts can be utilized to investigate the associated future risks of wind resource volatility for a specific region and country. Annual to decadal forecasts help the policy makers to understand the changes in energy mix.
- Energy investors and wind power operators: Seasonal forecasts can be used to plan operation and trading of portfolios with mixed wind power and other generation capacity.
- Power transmission and distribution system operators: Weekly, monthly, seasonal, and annual wind power forecasts can be used to plan energy balance, UC/ED, and future power grid capacity expansion / reinforcement purposes for the target power system. Generation cost models simulate the UC and ED operations of the specific power system in the short to long term forecast horizon (one week to a year) with 5 min to hourly resolution.
It is important to mention that a forecasting product might have more value when the seasonality and inter-annual variability of wind resources is high [158].
The seasonal forecasts are generally represented by the 10 m height wind speed PDF, assuming a Gaussian distribution for the wind speed uncertainty. Probabilistic multi-category events are also an alternative representation and can be constructed from the quintiles (five categories) or terciles (three categories) [159]. The temporal resolution are usually in a monthly or yearly scale.
Presently, little understanding exists about the impact of seasonal forecast properties, like calibration and sharpness, in the aforementioned use cases. However, in [159] it is highlighted that the main limitation of seasonal forecasts is the systematic error (bias), which requires bias correction and calibration methods for successful integration of this product in the industry practices. Also according to [159], the utilization of advanced post-processing methods in long-term forecasts has potential to reduce the uncertainty and generate valuable climate information, which was identified as a primary requirement by the wind energy industry. The Gaussian assumption for the wind speed forecast uncertainty is a subject for further work since it requires non-Gaussian post-processing methods.
The current quality verification measures are mainly: ranked probability skill scores for continuous and categorical forecasts; calibration/rank and sharpness diagrams [159].
Finally, uncertainty forecasts can assist in simulating power system requirements for the future, even if the length of the hindcast is not as long as climatology model reanalysis data may be available. The major advantage of using uncertainty hindcasts e.g., from an NWP ensemble is that the weather pattern of the past few years inclusive extremes and recent climate developments are taken into account. In this way, a 5 year period with an NWP ensemble of 50 members has a higher value for grid simulations of the future requirements than a single climate forecast over the past 20 years due to it’s ability to provide worst case scenarios. Some system operators have started to use such data for their future planning (e.g., the system operator in Alberta, Canada), although the advantages are still widely unrecognized.
6.6. Summary of Links between Uncertainty Representations and End-User Requirements
In Table 2 we provide a summary of the main conclusions from the discussions and literature review presented in Section 6.1, Section 6.2, Section 6.3, Section 6.4 and Section 6.5. It is important to underline that the column “end-user requirements” should be perceived as a set of general guidelines or recommendations that forecast users can follow when analyzing a set of uncertainty products from a service provider, and in a context of a specific decision-making problem.

Table 2.
Mapping between uncertainty representations and end-user requirements.
7. Pitfalls in Decision-Aid Methods
7.1. Uncertainty Modeling and Integration in the Decision-Making Phase
In many cases the wind power uncertainty is wrongly assumed to follow a Gaussian distribution. Typically, the classical central limit theorem (CTL) is used to support the assumption of Gaussian wind power forecast errors at the regional/national level. However, the classical CTL assumes the i.i.d. real valued random variables have a common distribution function [160], which is not valid for wind forecast errors since their distribution’s shape changes from site to site. Even at the wind power plant level, the probability distribution of the wind farm’s aggregated power cannot be characterized using the classical CLT. In summary, the wrong choice of a parametric function to represent uncertainty might result in decision situations with over- and under-estimation of the risk [2].
Another approach that is still widely used in the power industry, but often misunderstood as a probabilistic approach is the so-called “multiple-supplier” approach. Here a number of different forecast vendors are used to supply forecasts for the same target. In most cases, this approach is rather a smoothing method, usually able to reduce mean forecast error scores, but cannot be considered probabilistic. This is because deterministic models by default suppress outliers and extremes and therefore the “members” of such an approach do not represent an atmospheric uncertainty, but rather a random difference. Such a “multi-supplier” approach only becomes probabilistic, if the number of models is large enough to contain a realistic spread of the weather development and the underlying models are sufficiently different.
Another approach that is still misused in industry application as probabilistic approach to uncertainty forecasting is if a perturbation is added to the wind speed and translated into wind power through the non-linear power curve. For example, if a standard deviation of the mean wind speed is added and subtracted to a predicted wind speed and translated into power, an uncertainty band around the power can be built that varies with the dependency of the wind to power conversion. At the steep part of a wind turbine’s power curve, the wind power increases with a power of 3 to the wind speed, i.e., small variations in wind speed can appear as a strong spread (uncertainty) in power space. Therefore, one need to be careful in decision-making when using such approaches, as this methodology does not provide any realistic representation of uncertainty, but rather a climatological deviation from the mean. This deficiency becomes most apparent when looking at extreme events that generate high errors and costs.
In general, it can be stated that in a decision-making problem composed by multiple random variables, it is important to assess the dependency between random variables. Frequently, this dependency is neglected by the decision modeler when constructing the probabilistic model, which may result in errors during the probabilistic assessment, e.g., calculation of risk metrics [161]. The copula theory to construct joint distributions and pairwise correlations to incorporate dependence among the random variables is one possible method [162]. Examples of random variables that might exhibit non-marginal dependency are wind and solar power forecasts, wind power and electricity price forecasts, as well as load forecasts and solar power in a smart grid context. Finally, a typical pitfall is to mix dependency between time series (e.g., wind power and load time series) and dependency between forecast uncertainty (e.g., probabilistic forecasts of wind power and load; wind power and load forecast errors). In some cases, autocorrelation of the time series is also confused with the forecast uncertainty temporal dependence structure.
7.2. Decision Quality Evaluation
As discussed in Section 6, an important challenge is to develop problem-specific metrics that establish a link between forecast quality and value. An important phase in decision-making, but often neglected in literature, is the evaluation of the decision quality, which has a direct connection with the forecast value and should integrate the decision-maker risk profile (e.g., risk averse, prone or neutral). For instance, in market bidding problems the typical evaluation of alternative forecasts and decision rules is to calculate the total profit over a test period. However, for a risk averse decision-maker a forecast/decision-rule A that results in a lower total profit is more appealing than a forecast/decision-rule B, where the decision-maker is less exposed to large financial losses in case of extreme forecast errors and imbalance prices; see [139,142] for detailed evaluation of decision-quality under uncertainty in market bidding problems and how to define cost functions by using ensemble forecasts together with optimization models.
It is important to underline that several scoring rules used for quantile assessment can be directly used to assess the forecast value in use cases like market bidding with convex loss functions [163] and [142], but only when the expected-value paradigm (risk neutral decision-maker) is being applied. Pahlow et al. [142] showed that the correlation of the produced wind power diminishes and the predictability of wind power increases as the wind generation capacity grows. It is at that level, where it becomes beneficial to optimize a system by defining and applying cost functions rather than optimizing forecasts on the mean absolute error or the root mean square error.
The evaluation of the decision quality should therefore consider the decision-maker trade-off value, defined as “how much must be gained in the achievement of one objective to compensate for a lesser achievement on a different objective”, which should be determined by value judgments [164]. This requires a full understanding of the decision context, which means to know what the decision is, what is intended to accomplish and what the available alternatives are. Moreover, it is indispensable to quantify (or measure) the consequences of each alternative [164]. For instance, the decision-maker should be able to quantify the impact (e.g., technical, economic) of not having sufficient reserve capacity available in a specific hour.
With increasing renewable energy penetration and coupling of markets the complexity of the problem easily increases over the level a human can handle in a deterministic sense. Uncertainty forecasts can in these cases reduce the level of complexity and ease the decision finding [142].
Finally, in decision paradigms, like utility or prospect theory [165], where utility functions are applied directly to the probability distributions of the attributes, it is important to guarantee that the evaluation of the decision quality includes an assessment of the probabilities’ calibration or forecast uncertainty calibration.
7.3. The Role of Short-Term Forecasting Uncertainty in Longer Term Decisions
As mentioned above, in Section 6.2, the bidding problem aims primarily at optimizing forecasts to minimize imbalance costs that aim to reduced revenue for a wind farm. When the revenue of a wind farm is generated from the participation in the market rather than a support scheme (i.e., feed-in tariffs), it is important for wind farm developers to analyze the impact that short-term wind power predictability may have on the investment performance of a projected wind farm. This analysis is often referred to as “predictability assessment” [166], as opposed to the “resource assessment”, which is the standard process to decide on the location of a wind farm based on the wind potential of a site. Predictability assessment is first of all the assessment of the expected energy yield and associated income related to the return on investment of a wind farm. It is also often followed by the analysis of hedging options to deal with weather uncertainties, e.g., the dimensioning of storage devices to couple with a wind farm. So far, it is mainly based on deterministic forecasts.
However, by applying probabilistic forecasts, it is possible to capture weather uncertainties in the assessments and the economic calculations and thereby be prepared for deviations from the mean yields.
In the state of the art, a site’s predictability is denoted by the average level of forecast errors that can be obtained for that site and is seldom characterized with respect to properties of probabilistic forecasts. Previous studies, like the benchmark exercise in the ANEMOS project [167], have shown that predictability is location-dependent and can be, for example, related to terrain complexity; it is higher for wind farms located at flat terrain and lower for wind farms at complex terrain. This means that a site at complex terrain would be subject to higher penalties due to forecast errors. In contrast, a wind farm at a complex terrain has often higher energy yield potential. It was shown also in [18] that predictability tends to decrease when wind speeds increase. It will be thus worth the while in the future to study in a similar way as done for deterministic forecasts, how the properties of probabilistic forecasts are influenced by factors like the site characteristics.
The authors in [168] have studied the impact that the predictability of a site may have on the investment phase of a wind farm. They examined, if a compromise can be of interest when choosing between two sites to install a wind farm, one with higher potential but lower predictability (i.e., complex terrain site) and an alternative with lower potential but higher predictability (i.e., flat terrain site). Then, such a compromise might lead to choosing the site with lower potential, if the loss in revenue can be compensated by lower penalties when participating in the market. Their main conclusion was that within the current market schemes, the amount of penalties applied for imbalances represents a low share compared to the revenue generated by the day-ahead market. Under these conditions the role of predictability was found to be limited in the investment phase and the most dominant factor that determines the revenue remains the energy yield which depends on the wind resource of a site.
However, the fundamental issue in the above questions is the possibility to simulate long time series (i.e., for a typical year or multi-annual) not only of the power production output, but also of a realistic probabilistic representation. Such series can then be used as input in decision making processes such as the return of investment of a wind farm, the composition of a VPP portfolio or even the spatial planning of wind farm developments in a region. Usually, this simulation is done by using roughly the same tools as in the operational forecasting environments, but applied in hindcast mode to virtual time series of wind power production that have been generated with resource-assessment models or from measurements taken at the wind farm, if it is already running. The form of the probabilistic forecasts (i.e., quantiles, scenarios, ensembles) may vary as a function of the stochastic optimization process involved or the way the decision making process shall consider the forecasting uncertainty. By applying probabilistic approaches it will be possible to better simulate e.g., system adequacy of future wind integration scenarios or to generate more accurate economic estimates of the future income from the production due to the possibility to work with maximum and minimum likelihoods and variations in yield over time due to weather extremes or changes in weather pattern.
Depending on the application, this does not necessary translate to lower costs than the deterministic approach, since the consideration of uncertainties in the decision making process may lead to “hedging” against a higher number of critical events (i.e., allocation of larger amounts of reserves) and this can be translated to higher costs, but also higher system security compared to the deterministic approach. On the other hand, a cost optimization with the help of probabilistic forecasts may lead to lower security, nonetheless knowing the risk of that security loss.
To conclude, probabilistic methods provide more information to the decision making process. The results however largely dependent on the formulation of the problem at hand.
8. Recommendations and Best Practices
The preceding sections provided the forecast end-user with: (i) an overview on the various sources of wind power forecast uncertainty; (ii) a better understanding of how wind power forecast uncertainty is quantified, represented, and visualized; (iii) guidelines for defining probabilistic forecast requirements for specific applications. This section will present recommendations to promote the more widespread and better utilization of forecast uncertainty in practice, as well as examples of best practices in integrating forecast uncertainty into decision making processes.
There are a number of aspects of wind power forecasting where standardization would aid its industrial adoption. At the most basic level, different forecasting nomenclature is often used to describe the same concepts depending on, if the practitioner has a meteorological or power system background. A standard set of concepts described by a widely accepted set of terms will greatly facilitate the communication of the complex information wind forecasts along with uncertainty encompasses. This includes common (and intuitive) metrics for describing the degree of forecasting skill in a way so that forecasting performance may be more comparable. There is also a need for the community to define standard rules for data cleaning that are easy to implement and that will reduce the burden of forecast validation and comparisons. Inclusion of a forecast uncertainty class in the Common Information Model (CIM) adopted by the International Electrotechnical Commission (IEC), which aims to facilitate the exchange of power system network and market data, would provide a standard format for sharing uncertainty information. As an example, IEC 62325 (Part 301: CIM extensions for markets) currently only has a LoadForecast class that comprises point forecasts per grid node/control zone. The standard could however be a stepping stone to include RES forecast uncertainty as it can be considered as negative load in most areas.
Finally, standard procedures capturing functional and non-functional requirements available to the forecast end-user would help in conveying the necessary requirements of forecasts for different applications. A good practice from the smart grid area was the creation of standardization processes and collaborative tools to enable stakeholder interactions, including requirements based on gap analysis [169]. One example is the IEC 62559 IntelliGrid methodology for use case management, widely used to identify business and system requirements considering a particular system under design described from a technology-neutral viewpoint. Similar procedures can be applied to identify how the end-user wants to receive and communicate forecast uncertainty, or identify the required properties (e.g., event detection, spatial-temporal dependency) of the forecasting products.
Today, there is a basic lack of understanding about probabilistic forecasts, and how to best make use of them, by potential industrial end-users, as shown in the industry surveys conducted in IEA Task 36 [4]. This lack of understanding very often leads to mistrust in uncertainty forecasts, which echoes the mistrust in deterministic wind power forecasts in the industry 5–15 years ago. Several research groups designed experiments to study the behavior and decision quality of decision-makers using forecast uncertainty information (see Section 5.1 for further details). Experiments such as those in hydrological forecasting and flood protection [110] can be borrowed by system operators and market players to increase the awareness of their technical staff on the added value of forecast uncertainty information, and train them to gauge confidence in using this information. An example of good practice is the “Ensemble Prediction System (EPS) Training” (http://collaboration.cmc.ec.gc.ca/cmc/ensemble/Formation-Training/Read-me.html) course created by the Meteorological Service of Canada. This course has three objectives: (i) introduce participants to ensemble forecasting; (ii) provide basic training on EPS for operational forecasters; (iii) move away from the deterministic paradigm towards a probabilistic paradigm. It is important to emphasize that this training should be conducted both on the users side and on the forecasters’ side to create a better mutual understanding of forecast providers and users. However, the task of understanding forecasting quality and uncertainty information by the end-user is not only the end-user’s business. Forecast providers also need to improve the communication of forecasting quality to the end-user and use a common language. The typical industry criteria to choose a forecast service vendor is currently mostly oriented around point forecast quality (e.g., normalized mean absolute error). Concepts like sharpness, calibration or forecasting skill scores are more difficult to interpret by non-statisticians and are today barriers at the end-users to pursue this road. One way to overcome this situation is the design of games that help end-users to understand e.g., the impact of a poorly calibrated forecast or too wide forecast intervals. Moreover, the forecast evaluation might also focus on critical events identified by the end-user (e.g., ramps, phase errors) and, in this case, event-oriented evaluation metrics [136] might provide a more intuitive interpretation and evaluation possibility of uncertainty forecast skill for the end-user. In the same vein, forecasting providers must work to improve their visual representations of uncertainty so that the information becomes more intuitive to the end-user. Work in this field should consider multiple topical fields, such as: statistics, human-computer interaction, meteorology, and psychology. The challenge here is not to improve the communication of uncertainty information to the general public. Instead, it is to design a intuitive interface for experts in the control or trading room. The current practices in system operators control rooms show that simplicity in the visualization tools and flexibility to adjust the forecast visualization for different situations are key requirements for operators [10]. Warnings about large ramps and respective probability of occurrence are already operational in some control rooms, e.g., ERCOT’s Large Ramp Alert System [7], and will be a pre-requisite to manage large amounts of RES in the future.
As renewable energy penetration rates rise, the energy industry should consider the creation of internal departments and groups specifically focused on forecasting uncertainty and its impact on system operations. The purpose of these groups is to embed forecasting domain knowledge into the process of analyzing forecast uncertainty and potentially making manual corrections of forecasts and related products. This requires the creation of a multi-disciplinary team composed by people with backgrounds in meteorology or atmospheric science, as well as power systems. Three examples of recent implementations in industrial practice are:
- ERCOT added a “Reliability Risk Desk” in January 2017 into its control room for RES forecasting and extreme weather monitoring. This desk makes forecast adjustments during icing and other extreme weather events and monitors the adequacy of scheduled resources to cover forecast errors and net-load ramps [170].
- The Compagnie Nationale du Rhône (CNR) included meteorological feedback in the wind power forecasting system by exploring expert charts (maps) from different NWPs available over France. This information is then used to examine spatial-temporal trajectories when forecast uncertainty is high, and to use expert knowledge to provide different weightings to different NWP models [171].
- The Hawaiian Electric Company (HECO), system operator in Hawaii, is in the process of implementing uncertainty forecasts, a ramp warning system, Automatic Generation Control, reserve monitoring and unit commitment into the control room. The implementation is part of the Distributed Resource Energy Analysis and Management System) project (DREAMS)[172] that supports the development of the next generation, integrated energy management infrastructure able to incorporate advance visualization of behind-the-meter distributed technology performance information and probabilistic renewable energy generation forecasts to inform operational decisions [9].
It is important for the forecasting community to demonstrate the value of incorporating forecasting uncertainty information into system operations, as this is a critical step in gaining broader user acceptance and better situational awareness of the higher volatility RES are subject to. Here, technology demonstration business cases for decision-making problems that require forecast uncertainty as input are crucial in development projects. Examples of good practices are the FP6 European Project ANEMOS.plus (2008–2011) [173] , German Projects EWeLiNE (2012–2017) [174] and gridcast (2017–2021), Horizon 2020 European Project InteGrid (2017–2020) [175], the Wind Forecasting Improvement Projects I [176] and II [177], the Solar Forecasting Improvement projects [178] funded by the U.S. Department of Energy from 2012–2018 and the DREAMS project (2014–2016) [172] funded under the SunShot program of the US Department of Energy [179].
These projects with “private/public relationships” combine applied research and demonstration activities in order to conduct a cost-benefit analysis of forecasting integration into business practices of different end-users. However, it should be underlined that the forecasting value needs to be considered in the context of the specific power system and specific application. Variables such as the generation mix of the power system and the utility’s operating procedures greatly influence the forecast value [180]. For instance, an electrical utility with multiple generation technologies in its portfolio might see lower value in uncertainty information in comparison with a utility with wind power only. Moreover, the wind power forecast value might also be affected by other forecasts, such as solar power forecasts or price forecasts for electrical energy and ancillary service markets.
In general, stochastic methods require a considerable computational effort and end-users need fast decision processes. Therefore, a decision to incorporate the uncertainty paradigm may require to make use of synergies with the high-performance computing community, which can improve the performance of EPS generation or support the integration of uncertainty forecasts (e.g., spatially distributed ensembles) in stochastic optimization methods like optimal power flow or unit commitment. One example is the European Project Energy oriented Centre of Excellence in computing applications EoCoE (2015–2018) [181], that is improving the predictability of wind power and solar power with a focus on low-probability extreme-error events by ultra-large meteorological ensemble forecasts with particle filtering. Finally, seasonal probabilistic forecasts of wind power (with acceptable accuracy) is a gap in the current forecasting services market. This problem requires the identification of interesting business cases. Some potential candidates for probabilistic forecast application are: long-term portfolio and capacity management, mid-term electricity price forecasting and security of supply assessment studies for capacity markets. European Projects like SPECS (2012–2017) [182] and EUPORIAS (2012–2017) [183] recommended to increase the interaction between the monthly-to-seasonal forecasting research community and the wind energy industry in order to understand how long range forecasts can be useful in this field [184].
One recent business case on long-term adequacy planning has been carried out at the Alberta Electric System Operator (AESO) to study future RES integration for the Alberta Climate Leadership Program 2030, where all coal based production shall be phased out. Past real-time uncertainty forecasts from an 75 member NWP ensemble has been used to study system impact with various future scenarios of utility-scale wind power and solar power implementations. By providing 75 hindcasts over 5 years resulting in 375 model years, the trend of the currently predominant weather was well captured. Additionally, an Ensemble Kalman Filter was used to distribute measurement influence to future sites and thereby provide very realistic scenarios for the future, inclusive extreme events and minimum/maximum generation patterns. The study is being extended to the load pattern, as the probabilistic hindcasts enable the AESO to study combined uncertainty intervals for all non-scheduled generation and load as well as extreme events for their system adequacy report and strategic planning.
This business case shows how probabilistic information can be used in more advanced development of long-term strategic planning at system operators in order to incorporate renewable energy policies, as they provide the possibility to study extreme events and minimum/maximum requirements for secure system operation with much shorter hindcast data series than when using deterministic climatology or reanalysis data. Especially the combinations of different non-scheduled generation sources and load pattern provide a very realistic picture of the system load. The business case can also be extended to study and plan the resilience of the electrical power system under extreme weather conditions and climate change [185].
Acknowledgments
This work is a result of the international collaboration IEA Wind Task 36 Forecasting for Wind Power. The authors would like also to thank Gregor Giebel, Gianni Goretti, Morgane Barthod and Sue Ellen Haupt for their valuable comments during the writing of the paper. The work of Ricardo J. Bessa was performed in the frame of project SmartGP/0001/2015 supported by the ERDF—European Regional Development Fund through the Operational Programme for Competitiveness and Internationalisation—COMPETE 2020 Programme, and by National Funds through the FCT—Fundação para a Ciência e a Tecnologia (Portuguese Foundation for Science and Technology). Corinna Möhrlen was supported by the Danish EUDP project Wind Task 36 Forecasting Danish Consortium under the contract no. 2015-II-499149. Bri-Mathias Hodge was supported by the National Renewable Energy Laboratory under the U.S. Department of Energy Prime Contract No. DE-AC36-08GO28308. The work of George Kariniotakis was performed in the frame of the European project REstable supported by the ERA-Net Smart Grids Plus program and ADEME.
Author Contributions
Ricardo J. Bessa coordinated this joint work and contributed to Section 1, Section 2, Section 5, Section 6, Section 7 and Section 8; Corinna Möhrlen contributed to Section 1, Section 3, Section 4, Section 5, Section 6 and Section 8; Vanessa Fundel contributed to Section 3; Malte Siefert contributed to Section 4 and Section 6; Jethro Browell contributed to Section 2, Section 4 and Section 6; Sebastian Haglund El Gaidi contributed to Section 2 and Section 5; Bri-Mathias Hodge contributed to Section 1, Section 4, Section 5 and Section 6; Umit Cali contributed to Section 6; George Kariniotakis contributed to Section 4 and Section 7.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AAP | Available Active Power |
| aFRR | Automatic Frequency Restoration Reserve |
| AnEn | Analog Ensemble |
| BMA | Bayesian Model Averaging |
| CIM | Common Information Model |
| CLT | Central Limit Theorem |
| CMC | Canadian Meteorological Center |
| CRPS | Continuous Ranked Probability Score |
| EAKF | Ensemble Adjustment Kalman Filter |
| ECC | Ensemble Copula Coupling |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| ED | Economic Dispatch |
| EMOS | Ensemble Model Output Statistics |
| EnKF | Ensemble Kalman Filter |
| EnSRF | Ensemble Square Root Filter |
| EPS | Ensemble Prediction Systems |
| ERCOT | Electric Reliability Council of Texas |
| ETKF | Ensemble Transform Kalman Filter |
| IEA | International Energy Agency |
| IEC | International Electrotechnical Commission |
| LETKF | Local Ensemble Kalman Filter |
| MAE | Mean Absolute Error |
| MOS | Model Output Statistics |
| MTD | Mass Transportation Distance |
| MSEPS | Multi-Scheme Ensemble Prediction System |
| NCEP | National Centers for Environmental Prediction |
| NWP | Numerical Weather Predictions |
| Probability Density Function | |
| RMSE | Root Mean Square Error |
| RTO | Regional Transmission Operators |
| SD | Stochastic–Dynamic |
| SPPT | Stochastically Perturbed Parameterization Tendencies |
| SV | Singular Vector |
| UC | Unit Commitment |
| VPP | Virtual Power Plant |
References
- Pinson, P.; Chevallier, C.; Kariniotakis, G. Trading wind generation from short-term probabilistic forecasts of wind power. IEEE Trans. Power Syst. 2007, 22, 1148–1156. [Google Scholar] [CrossRef]
- Matos, M.A.; Bessa, R. Setting the operating reserve using probabilistic wind power forecasts. IEEE Trans. Power Syst. 2011, 26, 594–603. [Google Scholar] [CrossRef]
- Bessa, R.; Moreira, C.; Silva, B.; Matos, M. Handling renewable energy variability and uncertainty in power systems operation. Wiley Interdiscip. Rev. Energy Environ. 2014, 3, 156–178. [Google Scholar] [CrossRef]
- Möhrlen, C.; Bessa, R.J.; Barthod, M.; Goretti, G.; Siefert, M. Use of forecast uncertainties in the power sector: State-of-the-art of business practices. In Proceedings of the 15th International Workshop on Large-Scale Integration of Wind Power into Power Systems as well as on Transmission Networks for Offshore Wind Power Plants, Energynautics, Vienna, Austria, 15–17 November 2016. [Google Scholar]
- Sioshansi, R.; Hurlbut, D. Market protocols in ERCOT and their effect on wind generation. Energy Policy 2010, 38, 3192–3197. [Google Scholar] [CrossRef]
- Holttinen, H.; Milligan, M.; Ela, E.; Menemenlis, N.; Dobschinski, J.; Rawn, B.; Bessa, R.; Flynn, D.; Lazaro, E.; Detlefsen, N. Methodologies to determine operating reserves due to increased wind power. IEEE Trans. Sustain. Energy 2012, 3, 713–723. [Google Scholar] [CrossRef]
- Steffan, N.; Du, P.; Mago, N.; Sharma, S. Integrating probabilistic forecasts into the energy management system (EMS) and market management system (MMS) software. In Proceedings of the UVIG Forecasting Workshop, Atlanta, GA, USA, 20–22 June 2017. [Google Scholar]
- Matos, M.; Bessa, R.J.; Gonçalves, C.; Cavalcante, L.; Miranda, V.; Machado, N.; Marques, P.; Matos, F. Setting the maximum import net transfer capacity under extreme RES integration scenarios. In Proceedings of the 2016 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Beijing, China, 16–20 October 2016. [Google Scholar]
- Nakafuji, D.; Gouveia, L.; Oshiro, S. Distributed Resource Energy Analysis and Management System (DREAMS) Development for Real-Time Grid Operations; Technical Report DOE-EE0006331-FTR1; Hawaiian Electric Company: Honolulu, HI, USA, 2016. [Google Scholar]
- Miettinen, J.; Holttinen, H.; Ammälä, J.; Piironen, M. Wind power forecasting at Transmission System Operator’s control room. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015. [Google Scholar]
- Storck, P.; Grimit, E.; Holger, T. Determining the value of more accurate wind power forecasting in global electricity markets. In Proceedings of the EWEA Technical Workshop on Wind Power Forecasting, Leuven, Belgium, 1–2 October 2015. [Google Scholar]
- Koblitz, T. What’s next for wind energy forecasting systems? In Proceedings of the EWEA Technical Workshop on Wind Power Forecasting, Leuven, Belgium, 1–2 October 2015. [Google Scholar]
- Grimit, E. Providing uncertainty information to end users in the electric sector. In Proceedings of the UVIG Forecasting Workshop, Tutorial on Integration of Uncertainty Forecasts into Power System Operations, Atlanta, GA, USA, 20–22 June 2017. [Google Scholar]
- Gill, J.; Rubiera, J.; Martin, C.; Cacic, I.; Mylne, K.; Dehui, C.; Jiafeng, G.; Xu, T.; Yamaguchi, M.; Foamouhoue, A.K.; et al. Guidelines on Communicating Forecast Uncertainty; Technical Report WMO/TD No. 4122; World Meteorological Organization: Geneve, Switzerland, 2008. [Google Scholar]
- IEA Wind Task 36 Wind Energy Forecasting Project (2016–2018). Available online: http://www.ieawindforecasting.dk (accessed on 17 August 2017).
- Stine, R.A. Bootstrap prediction intervals for regression. J. Am. Stat. Assoc. 1985, 80, 1026–1031. [Google Scholar] [CrossRef]
- Smithson, M. Confidence Intervals, 1st ed.; Quantitative Applications in the Social Sciences; SAGE Publications Inc.: Thousand Oaks, CA, USA, 2002. [Google Scholar]
- Pinson, P. Estimation of the Uncertainty in Wind Power Forecasting. Ph.D. Thesis, PSL Research University, Ecole des Mines de Paris, Center for Energy and Processes, Sophia Antipolis, France, 2006. [Google Scholar]
- Lewis, J.M. Roots of ensemble forecasting. Mon. Weather Rev. 2005, 133, 1865–1885. [Google Scholar] [CrossRef]
- Palmer, T.N. The economic value of ensemble forecasts as a tool for risk assessment: From days to decades. Q. J. R. Meteorol. Soc. 2002, 128, 747–774. [Google Scholar] [CrossRef]
- Frame, T.H.A.; Methven, J.; Gray, S.L.; Ambaum, M.H.P. Flow-dependent predictability of the North Atlantic jet. Geophys. Res. Lett. 2013, 40, 2411–2416. [Google Scholar] [CrossRef]
- Engström, A.; Magnusson, L. Estimating trajectory uncertainties due to flow dependent errors in the atmospheric analysis. Atmos. Chem. Phys. 2009, 9, 8857–8867. [Google Scholar] [CrossRef]
- Bludszuweit, H.; Dominguez-Navarro, J.; Llombart, A. Statistical analysis of wind power forecast error. IEEE Trans. Power Syst. 2008, 23, 983–991. [Google Scholar] [CrossRef]
- Hodge, B.M.; Ela, E.; Milligan, M. The distribution of wind power forecasting errors from operational systems. In Proceedings of the 10th International Workshop on Large-Scale Integration of Wind Power into Power Systems, Energynautics, Aarhus, Denmark, 25–26 October 2011. [Google Scholar]
- Jordá, O.; Marcellino, M. Path forecast evaluation. J. Appl. Econom. 2010, 25, 635–662. [Google Scholar] [CrossRef]
- Chew, V. Simultaneous prediction intervals. Technometrics 1968, 10, 323–330. [Google Scholar] [CrossRef]
- Eady, E. Long waves and cyclone waves. Tellus 1949, 1, 33–52. [Google Scholar] [CrossRef]
- Epstein, E.S. Stochastic dynamic prediction. Tellus 1969, 21, 739–759. [Google Scholar] [CrossRef]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. Oceans 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Thompson, P.; Lorenz, E. Dialogue between Phil Thompson and Ed Lorenz on 31 July 1986. Am. Meteor Soc. Tape Rec. Interview 1986, 1, 19–53. [Google Scholar]
- Palmer, T.N. Extended-range atmospheric prediction and the Lorenz model. Bull. Am. Meteorol. Soc. 1993, 74, 49–65. [Google Scholar] [CrossRef]
- Molteni, F.; Buizza, R.; Palmer, T.N.; Petroliagis, T. The ECMWF Ensemble Prediction System: Methodology and validation. Q. J. R. Meteorol. Soc. 1996, 122, 73–119. [Google Scholar] [CrossRef]
- Toth, Z.; Kalnay, E. Ensemble forecasting at NMC: The generation of perturbations. Bull. Am. Meteorol. Soc. 1993, 74, 2317–2330. [Google Scholar] [CrossRef]
- Tracton, M.S.; Kalnay, E. Operational ensemble prediction at the National Meteorological Center: Practical aspects. Weather Forecast. 1993, 8, 379–398. [Google Scholar] [CrossRef]
- Mitchell, H.L.; Houtekamer, P.L. An adaptive ensemble Kalman filter. Mon. Weather Rev. 2000, 128, 416–433. [Google Scholar] [CrossRef]
- Houtekamer, P.L.; Mitchell, H.L. A sequential ensemble Kalman filter for atmospheric data assimilation. Mon. Weather Rev. 2001, 129, 123–137. [Google Scholar] [CrossRef]
- Diaconescu, E.P.; Laprise, R. Singular vectors in atmospheric sciences: A review. Earth-Sci. Rev. 2012, 113, 161–175. [Google Scholar] [CrossRef]
- Kim, H.M.; Jung, B.J. Singular vector structure and evolution of a recurving tropical cyclone. Mon. Weather Rev. 2009, 137, 505–524. [Google Scholar] [CrossRef]
- Toth, Z.; Kalnay, E. Ensemble forecasting at NCEP and the breeding method. Mon. Weather Rev. 1997, 125, 3297–3319. [Google Scholar] [CrossRef]
- Magnusson, L.; Leutbecher, M.; Källén, E. Comparison between singular vectors and breeding vectors as initial perturbations for the ECMWF ensemble prediction system. Mon. Weather Rev. 2008, 136, 4092–4104. [Google Scholar] [CrossRef]
- Evensen, G. The ensemble Kalman filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Houtekamer, P.L.; Zhang, F. Review of the ensemble Kalman filter for atmospheric data assimilation. Mon. Weather Rev. 2016, 144, 4489–4532. [Google Scholar] [CrossRef]
- Ott, E.; Hunt, B.; Szunyogh, I.; Zimin, A.; Kostelich, E.; Corazza, M.; Kalnay, E.; Patil, D.; Yorke, J. A local ensemble Kalman filter for atmospheric data assimilation. Tellus A 2004, 56, 415–428. [Google Scholar] [CrossRef]
- Meng, Z.; Zhang, F. Limited-area ensemble-based data assimilation. Mon. Weather Rev. 2011, 139, 2025–2045. [Google Scholar] [CrossRef]
- Buizza, R.; Miller, M.; Palmer, T.N. Stochastic representation of model uncertainties in the ECMWF ensemble prediction system. Q. J. R. Meteorol. Soc. 1999, 125, 2887–2908. [Google Scholar] [CrossRef]
- Palmer, T.; Buizza, R.; Doblas-Reyes, F.; Jung, T.; Leutbecher, M.; Shutts, G.; Steinheimer, M.; Weisheimer, A. Stochastic Parametrization and Model Uncertainty; Technical Report 598, ECMWF Technical Memoranda; ECMWF: Reading, UK, 2009. [Google Scholar]
- Shutts, G. A kinetic energy backscatter algorithm for use in ensemble prediction systems. Q. J. R. Meteorol. Soc. 2005, 131, 3079–3102. [Google Scholar] [CrossRef]
- Möhrlen, C. Uncertainty in Wind Energy Forecasting. Ph.D. Thesis, National University of Ireland, Cork, Ireland, 2004. [Google Scholar]
- Möhrlen, C.; Jørgensen, J. chapter The role of ensemble forecasting in integrating renewables into power systems: From theory to real-time applications. In Integration of Large-Scale Renewable Energy into Bulk Power Systems. From Planning to Operation; Springer Nature; Springer International Publishing AG: Cham, Switzerland, 2008; pp. 79–134. [Google Scholar]
- Buizza, R.; Houtekamer, P.L.; Pellerin, G.; Toth, Z.; Zhu, Y.; Wei, M. A comparison of the ECMWF, MSC, and NCEP Global Ensemble Prediction Systems. Mon. Weather Rev. 2005, 133, 1076–1097. [Google Scholar] [CrossRef]
- Stensrud, D.J.; Bao, J.W.; Warner, T.T. Using initial condition and model physics perturbations in short-range ensemble simulations of mesoscale convective systems. Mon. Weather Rev. 2000, 128, 2077–2107. [Google Scholar] [CrossRef]
- Lavaysse, C.; Carrera, M.; Bélair, S.; Gagnon, N.; Frenette, R.; Charron, M.; Yau, M.K. Impact of surface parameter uncertainties within the Canadian regional ensemble prediction system. Mon. Weather Rev. 2013, 141, 1506–1526. [Google Scholar] [CrossRef]
- Deng, G.; Zhu, Y.; Gong, J.; Chen, D.; Wobus, R.; Zhang, Z. The effects of land surface process perturbations in a global ensemble forecast system. Adv. Atmos. Sci. 2016, 33, 1199–1208. [Google Scholar] [CrossRef]
- Emmrich, P.B.K. A gratis two-model-ensemble versus EPS. In Fifth Workshop on Meteorological Operational Systems; ECMWF: Reading, UK, 1995. [Google Scholar]
- Krishnamurti, T.; Kishtawal, C.; Zhan, Z.; Larow, T.; Bachiochi, D.; Williford, E.; Gadgill, S.; Surendran, S. Multimodel ensemble forecasts for weather and seasonal climate. J. Clim. 2000, 13, 4196–4216. [Google Scholar] [CrossRef]
- Hamill, T.M.; Whitaker, J.S.; Wei, X. Ensemble reforecasting: Improving medium-range forecast skill using retrospective forecasts. Mon. Weather Rev. 2004, 132, 1434–1447. [Google Scholar] [CrossRef]
- Wilks, D.S.; Hamill, T.M. Comparison of ensemble-MOS methods using GFS reforecasts. Mon. Weather Rev. 2007, 135, 2379–2390. [Google Scholar] [CrossRef]
- Hagedorn, R.; Hamill, T.M.; Whitaker, J.S. Probabilistic forecast calibration using ECMWF and GFS ensemble reforecasts. Part I: Two-meter temperatures. Mon. Weather Rev. 2008, 136, 2608–2619. [Google Scholar] [CrossRef]
- Hamill, T.M.; Bates, G.T.; Whitaker, J.S.; Murray, D.R.; Fiorino, M.; Galarneau, T.J., Jr.; Zhu, Y.; Lapenta, W. NOAA’s second-generation global medium-range ensemble reforecast dataset. Bull. Am. Meteorol. Soc. 2013, 94, 1553–1565. [Google Scholar] [CrossRef]
- Glahn, H.R.; Lowry, D.A. The use of model output statistics (MOS) in objective weather forecasting. J. Appl. Meteorol. 1972, 11, 1203–1211. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences: An Introduction, 1st ed.; International Geophysics; Academic Press: Cambridge, MA, USA, 1995; Volume 59. [Google Scholar]
- Wilks, D.S. Extending logistic regression to provide full-probability-distribution MOS forecasts. Meteorol. Appl. 2009, 16, 361–368. [Google Scholar] [CrossRef]
- Monache, L.D.; Nipen, T.; Liu, Y.; Roux, G.; Stull, R. Kalman Filter and Analog Schemes to Postprocess Numerical Weather Predictions. Mon. Weather Rev. 2011, 139, 3554–3570. [Google Scholar] [CrossRef]
- Eckel, F.A.; Monache, L.D. A hybrid NWP-analog ensemble. Mon. Weather Rev. 2016, 144, 897–911. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E.; Westveld, A.H., III; Goldman, T. Calibrated probabilistic forecasting using ensemble model output statistics and minimum CRPS estimation. Mon. Weather Rev. 2005, 133, 1098–1118. [Google Scholar] [CrossRef]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using bayesian model averaging to calibrate forecast ensembles. Mon. Weather Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef]
- Schuhen, N.; Thorarinsdottir, T.L.; Gneiting, T. Ensemble model output statistics for wind vectors. Mon. Weather Rev. 2012, 140, 3204–3219. [Google Scholar] [CrossRef]
- Schmeits, M.J.; Kok, K.J. A Comparison between Raw Ensemble Output, (Modified) Bayesian Model Averaging, and Extended Logistic Regression Using ECMWF Ensemble Precipitation Reforecasts. Mon. Weather Rev. 2010, 138, 4199–4211. [Google Scholar] [CrossRef]
- Scheuerer, M.; MMöller, D. Probabilistic wind speed forecasting on a grid based on ensemble model output statistics. Ann. Appl. Stat. 2015, 9, 1328–1349. [Google Scholar] [CrossRef]
- Schefzik, R.; Thorarinsdottir, T.L.; Gneiting, T. Uncertainty quantification in complex simulation models using ensemble copula coupling. Stat. Sci. 2013, 28, 616–640. [Google Scholar] [CrossRef]
- Wilks, D.S. Multivariate ensemble Model Output Statistics using empirical copulas. Q. J. R. Meteorol. Soc. 2015, 141, 945–952. [Google Scholar] [CrossRef]
- Ben Bouallègue, Z.; Heppelmann, T.; Theis, S.E.; Pinson, P. Generation of scenarios from calibrated ensemble forecasts with a dual-ensemble copula-coupling approach. Mon. Weather Rev. 2016, 144, 4737–4750. [Google Scholar] [CrossRef]
- Messner, J.W.; Zeileis, A.; Broecker, J.; Mayr, G.J. Probabilistic wind power forecasts with an inverse power curve transformation and censored regression. Wind Energy 2013, 17, 1753–1766. [Google Scholar] [CrossRef]
- Pinson, P. Very short-term probabilistic forecasting of wind power with generalized logit-Normal distributions. J. R. Stat. Soc. Ser. C 2012, 61, 555–576. [Google Scholar] [CrossRef]
- Koenker, R.; Leorato, S.; Peracchi, F. Distributional vs. Quantile Regression; CEIS Working Paper No. 300; CEIS: Glasgow, UK, 2013. [Google Scholar]
- Foresi, S.; Peracchi, F. The conditional distribution of excess returns: An empirical analysis. J. Am. Stat. Assoc. 1995, 90, 451–466. [Google Scholar] [CrossRef]
- Ziel, F.; Croonenbroeck, C.; Ambach, D. Forecasting wind power—Modeling periodic and non-linear effects under conditional heteroscedasticity. Appl. Energy 2016, 177, 285–297. [Google Scholar] [CrossRef]
- Dowell, J.; Dinwoodie, I.; McMillan, D. Forecasting for offshore maintenance scheduling under uncertainty. In Proceedings of the European Safety and Reliability Conference, ESRA, Glasgow, UK, 25–29 September 2016. [Google Scholar]
- Koenker, R. Encyclopedia of Environmetrics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014; chapter Quantile regression. [Google Scholar]
- Landry, M.; Erlinger, T.P.; Patschke, D.; Varrichio, C. Probabilistic gradient boosting machines for GEFCom2014 wind forecasting. Int. J. Forecast. 2016, 32, 1061–1066. [Google Scholar] [CrossRef]
- Hong, T.; Pinson, P.; Fan, S.; Zareipour, H.; Troccoli, A.; Hyndman, R.J. Probabilistic energy forecasting: Global Energy Forecasting Competition 2014 and beyond. Int. J. Forecast. 2016, in press. [Google Scholar] [CrossRef]
- Andrade, J.; Bessa, R. Improving renewable energy forecasting with a grid of numerical weather predictions. IEEE Trans. Sustain. Energy 2017, in press. [Google Scholar] [CrossRef]
- Anastasiades, G.; McSharry, P. Quantile forecasting of wind power using variability indices. Energies 2013, 6, 662–695. [Google Scholar] [CrossRef]
- Cavalcante, L.; Bessa, R.J.; Reis, M.; Dowell, J. LASSO vector autoregression structures for very short-term wind power forecasting. Wind Energy 2017, 20, 657–675. [Google Scholar] [CrossRef]
- Dowell, J.; Pinson, P. Very-short-term probabilistic wind power forecasts by sparse vector autoregression. IEEE Trans. Smart Grid 2016, 7, 763–770. [Google Scholar] [CrossRef]
- Sperati, S.; Alessandrini, S.; Monache, L.D. Gridded probabilistic weather forecasts with an analog ensemble. Q. J. R. Meteorol. Soc. 2017, in press. [Google Scholar] [CrossRef]
- Pinson, P.; Madsen, H. Ensemble-based probabilistic forecasting at Horns Rev. Wind Energy 2009, 12, 137–155. [Google Scholar] [CrossRef]
- Papaefthymiou, G.; Pinson, P. Modeling of spatial dependence in wind power forecast uncertainty. In Proceedings of the 10th International Conference on Probabilistic Methods Applied to Power Systems (PMAPS 2008), Rincón, Puerto Rico, 25–29 May 2008; pp. 1–9. [Google Scholar]
- Møller, J.K.; Zugno, M.; Madsen, H. Probabilistic forecasts of wind power generation by stochastic differential equation models. J. Forecast. 2016, 35, 189–205. [Google Scholar] [CrossRef]
- Staid, A.; Watson, J.P.; Wets, R.J.B.; Woodruff, D.L. Generating short-term probabilistic wind power scenarios via nonparametric forecast error density estimators. Wind Energy 2017, in press. [Google Scholar] [CrossRef]
- Clark, M.; Gangopadhyay, S.; Hay, L.; Rajagopalan, B.; Wilby, R. The Schaake shuffle: A method for reconstructing space-time variability in forecasted precipitation and temperature fields. J. Hydrometeorol. 2004, 5, 243–262. [Google Scholar] [CrossRef]
- Tastu, J.; Pinson, P.; Madsen, H. Modeling and Stochastic Learning for Forecasting in High Dimensions. In Lecture Notes in Statistics; Chapter Space-Time Trajectories of Wind Power Generation: Parameterized Precision Matrices Under a Gaussian Copula Approach; Springer: Berlin, Germany, 2015; Volume 217, pp. 267–296. [Google Scholar]
- McLean, J. Equivalent Wind Power Curves; Technical Report, Deliverable 2.4 of the TradeWind Project; Garrad Hassan and Partners Ltd.: Glasgow, UK, 2008. [Google Scholar]
- Nielsen, H.A.; Madsen, H.; Nielsen, T.S.; Badger, J.; Giebel, G.; Landberg, L.; Sattler, K.; Feddersen, H. Wind power ensemble forecasting. In Proceedings of the 2004 Global Windpower Conference and Exhibition, London, UK, 22–25 November 2004. [Google Scholar]
- Junk, C.; von Bremen, L.; Heinemann, D. Assessment of probabilistic wind power forecasts for wind farms in Northern Ireland. In Proceedings of the EWEA 2012 Annual Event, Copenhagen, Denmark, 16–19 April 2012. [Google Scholar]
- Pinson, P.; Kariniotakis, G. On-line assessment of prediction risk for wind power production forecasts. Wind Energy 2004, 7, 119–132. [Google Scholar] [CrossRef]
- Giebel, G.; Badger, J.; Landberg, L.; Nielsen, H.A.; Nielsen, T.S.; Madsen, H.; Sattler, K.; Feddersen, H.; Vedel, H.; Tøfting, J.; et al. Wind Power Prediction Using Ensembles; Technical Report Risø-R-1527, Risø; RisÃ: Foothill Ranch, CA, USA, 2005. [Google Scholar]
- Bremnes, J.B. Probabilistic wind power forecasts using local quantile regression. Wind Energy 2004, 7, 47–54. [Google Scholar] [CrossRef]
- Juban, J.; Fugon, L.; Kariniotakis, G. Uncertainty estimation of wind power forecasts. In Proceedings of the European Wind Energy Conference (EWEC 2008), Brussels, Belgium, 31 March–3 April 2008. [Google Scholar]
- Nielsen, T.; Landberg, L.; Giebel, G. Prediction of regional wind power. In Proceedings of the 2002 Global Wind Power Conference, EWEA, Paris, France, 10–12 March 2002. [Google Scholar]
- Siebert, N. Development of Methods for Regional Wind Power Forecasting. Ph.D. Thesis, PSL Research University, Centre for Process Energies and Energy Systems (PERSEE), Sophia Antipolis, France, 2008. [Google Scholar]
- Camal, S.; Michiorri, A.; Kariniotakis, G.; Liebelt, A. Short-term forecast of automatic frequency restoration reserve from a renewable energy based virtual power plant. In Proceedings of the 2017 IEEE PES ISGT Europe Conference, Torino, Italy, 26–29 September 2017. [Google Scholar]
- Pinson, P.; Kariniotakis, G. Conditional prediction intervals of wind power generation. IEEE Trans. Power Syst. 2010, 25, 1845–1856. [Google Scholar] [CrossRef]
- Joslyn, S.L.; LeClerc, J.E. Uncertainty forecasts improve weather-related decisions and attenuate the effects of forecast error. J. Exp. Psychol. Appl. 2012, 18, 126–140. [Google Scholar] [CrossRef] [PubMed]
- Council, N.R. Completing the Forecast: Characterizing and Communicating Uncertainty for Better Decisions Using Weather and Climate Forecasts; The National Academies Press: Washington, DC, USA, 2006. [Google Scholar]
- Nadav-Greenberg, L.; Joslyn, S.L.; Taing, M.U. Uncertainty forecasts improve decision making among nonexperts. J. Cogn. Eng. Decis. Mak. 2009, 3, 209–227. [Google Scholar] [CrossRef]
- Joslyn, S.; LeClerc, J. The cry wolf effect and weather-related decision making. Risk Anal. 2015, 35, 385–395. [Google Scholar]
- Joslyn, S.; Savelli, S. Communicating forecast uncertainty: public perception of weather forecast uncertainty. Meteorol. Appl. 2010, 17, 180–195. [Google Scholar] [CrossRef]
- LeClerc, J. Communicating Weather and Climate Uncertainty: Exploratory Research in Cognitive Psychology. Ph.D. Thesis, University of Washington, Seattle, WA, USA, 2014. [Google Scholar]
- Ramos, M.H.; van Andel, S.J.; Pappenberger, F. Do probabilistic forecasts lead to better decisions? Hydrol. Earth Syst. Sci. 2013, 17, 2219–2232. [Google Scholar] [CrossRef]
- Joslyn, S.; Pak, K.; Jones, D.; Pyles, J.; Hunt, E. The effect of probabilistic information on threshold forecasts. Weather Forecast. 2006, 22, 804–812. [Google Scholar] [CrossRef]
- Nadav-Greenberg, L.; Joslyn, S.L.; Taing, M.U. The effect of uncertainty visualizations on decision making in weather forecasting. J. Cogn. Eng. Decis. Mak. 2008, 2, 24–47. [Google Scholar] [CrossRef]
- Joslyn, S.; Savelli, S. The advantages of predictive interval forecasts for non-expert users and the impact of visualizations. Appl. Cogn. Psychol. 2013, 27, 527–541. [Google Scholar]
- Joslyn, S.L.; Nichols, R.M. Probability or frequency? Expressing forecast uncertainty in public weather forecasts. Meteorol. Appl. 2009, 16, 309–314. [Google Scholar] [CrossRef]
- Morss, R.E.; Lazo, J.K.; Demuth, J.L. Examining the use of weather forecasts in decision scenarios: results from a US survey with implications for uncertainty communication. Meteorol. Appl. 2010, 17, 149–162. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Wang, X. Review on probabilistic forecasting of wind power generation. Renew. Sustain. Energy Rev. 2014, 32, 255–270. [Google Scholar] [CrossRef]
- Bessa, R.J. From marginal to simultaneous prediction intervals of wind power. In Proceedings of the 18th Intelligent Systems Applications to Power Systems Conference and Debate (ISAP 2015), Porto, Portugal, 14–16 September 2015. [Google Scholar]
- Rockafellar, R.T.; Wets, R.J.B. Scenarios and policy aggregation in optimization under uncertainty. Math. Oper. Res. 1991, 6, 119–147. [Google Scholar] [CrossRef]
- Raftery, A.E. Use and communication of probabilistic forecasts. Stat. Anal. Data Min. ASA Data Sci. J. 2016, 9, 397–410. [Google Scholar] [CrossRef] [PubMed]
- Golestaneh, F.; Pinson, P.; Azizipanah-Abarghooee, R.; Gooi, H.B. Ellipsoidal prediction regions for multivariate uncertainty characterization. arXiv 2017, arXiv:1708.02703. [Google Scholar]
- Pinson, P.; Nielsen, H.; Madsen, H.; Kariniotakis, G. Skill forecasting from ensemble predictions of wind power. Appl. Energy 2009, 86, 1326–1334. [Google Scholar] [CrossRef]
- Holton, G.A. Defining risk. Financ. Anal. J. 2004, 60, 6. [Google Scholar] [CrossRef]
- Nielsen, H.A.; Madsen, H.; Nielsen, T.S. Using quantile regression to extend an existing wind power forecasting system with probabilistic forecasts. Wind Energy 2006, 9, 95–108. [Google Scholar] [CrossRef]
- Gallego-Castillo, C.; Cuerva-Tejero, A.; Lopez-Garcia, O. A review on the recent history of wind power ramp forecasting. Renew. Sustain. Energy Rev. 2015, 52, 1148–1157. [Google Scholar] [CrossRef]
- McSharry, P.; von Bremen, L.; Holmgren, E.; Siebert, N.; Kariniotakis, G.; Girard, R. Predictability Measure and Communication of Information on Uncertainty to Forecast Users; Technical Report, EU Project SafeWind, Deliverable DP-6.6; European Union: Brussels, Belgium, 2012. [Google Scholar]
- Zhao, J.; Abedi, S.; He, M.; Du, P.; Sharma, S.; Blevins, B. Quantifying risk of wind power ramps in ERCOT. IEEE Trans. Power Syst. 2017, in press. [Google Scholar] [CrossRef]
- Wang, J.; Botterud, A.; Bessa, R.; Keko, H.; Miranda, V.; Akilimali, J.; Carvalho, L.; Issicaba, D. Wind power forecasting uncertainty and unit commitment. Appl. Energy 2011, 88, 4014–4023. [Google Scholar] [CrossRef]
- Da Silva, A.; de Resende, L.; da Fonseca Manso, L.; Billinton, R. Well-being analysis for composite generation and transmission systems. IEEE Trans. Power Syst. 2004, 19, 1763–1770. [Google Scholar] [CrossRef]
- Bessa, R.J.; Matos, M.A.; Costa, I.C.; Bremermann, L.; Franchin, I.G.; Pestana, R.; Machado, N.; Waldl, H.P.; Wichmann, C. Reserve setting and steady-state security assessment using wind power uncertainty forecast: A case study. IEEE Trans. Sustain. Energy 2012, 3, 827–836. [Google Scholar] [CrossRef]
- Menemenlis, N.; Huneault, M.; Robitaille, A. Computation of Dynamic Operating Balancing Reserve for Wind Power Integration for the Time-Horizon 1–48 Hours. IEEE Trans. Sustain. Energy 2012, 3, 692–702. [Google Scholar] [CrossRef]
- Sari, D.; Lee, Y.; Ryan, S.; Woodruff, D. Statistical metrics for assessing the quality of wind power scenarios for stochastic unit commitment. Wind Energy 2015, 19, 873–893. [Google Scholar] [CrossRef]
- Bessa, R.; Miranda, V.; Botterud, A.; Wang, J. Good or bad wind power forecasts: a relative concept. Wind Energy 2011, 14, 625–636. [Google Scholar] [CrossRef]
- Gneiting, T.; Stanberry, L.; Grimit, E.; Held, L.; Johnson, N. Assessing probabilistic forecasts of multivariate quantities, with an application to ensemble predictions of surface winds. TEST 2008, 17, 211–235. [Google Scholar] [CrossRef]
- Scheuerer, M.; Hamill, T.M. Variogram-based proper scoring rules for probabilistic forecasts of multivariate quantities. Mon. Weather Rev. 2015, 143, 1321–1334. [Google Scholar] [CrossRef]
- Bessa, R. On the quality of the gaussian copula for multi-temporal decision-making problems. In Proceedings of the 19th Power Systems Computation Conference (PSCC 2016), Genoa, Italy, 20–24 June 2016. [Google Scholar]
- Pinson, P.; Girard, R. Evaluating the quality of scenarios of short-term wind power generation. Appl. Energy 2012, 96, 12–20. [Google Scholar] [CrossRef]
- Botterud, A.; Wang, J.; Valenzuela, J.; Bessa, R.; Keko, H.; Miranda, V.; Akilimali, J. Unit commitment and operating reserves with probabilistic wind power forecasts. In Proceedings of the IEEE PowerTech Conference, Trondheim, Norway, 19–23 June 2011. [Google Scholar]
- Möhrlen, C.; Jorgensen, J.U. Reserve forecasting for enhanced renewable energy management. In Proceedings of the 12th International Workshop on Large-Scale Integration of Wind Power into Power Systems as well as on Transmission Networks for Offshore Wind Farms, Energynautics, Berlin, Germany, 11–13 November 2014. [Google Scholar]
- Botterud, A.; Wang, J.; Zhou, Z.; Bessa, R.; Keko, H.; Akilimali, J.; Miranda, V. Wind power trading under uncertainty in LMP markets. IEEE Trans. Power Syst. 2012, 27, 894–903. [Google Scholar] [CrossRef]
- Rodriguez, A. Wind generation forecasting at REE. In Proceedings of the Workshop on Experiences in using Wind Power Predictions and Gaps in Forecasting Research, Barcelona, Spain, 6 June 2016. [Google Scholar]
- Gogolou, E. Significance of the forecast in the short term power trading. In Proceedings of the Workshop on Experiences in using Wind Power Predictions and Gaps in Forecasting Research, Barcelona, Spain, 6 June 2016. [Google Scholar]
- Pahlow, M.; Möhrlen, C.; Jørgensen, J. Chapter Application of cost functions for large-scale integration of wind power using a multi-scheme ensemble prediction technique. In Optimization Advances in Electric Power Systems; Nova Science Publishers: Hauppauge, NY, USA, 2009; pp. 151–180. [Google Scholar]
- Dent, C.J.; Bialek, J.W.; Hobbs, B.F. Opportunity cost bidding by wind generators in forward markets: Analytical results. IEEE Trans. Power Syst. 2011, 26, 1600–1608. [Google Scholar] [CrossRef]
- Möhrlen, C.; Pahlow, M.; Jørgensen, J.U. Untersuchung verschiedener Handelsstrategien für Wind- und Solarenergie unter Berücksichtigung der EEG 2012 Novellierung. Z. Energiewirtschaft 2012, 36, 9–25. [Google Scholar] [CrossRef]
- Elia, Windvision, Enercon, and Eneco Delivery of Downward aFRR by Wind Farms (2014–2015). Available online: http://www.elia.be/~/media/files/Elia/users-group/task-force-balancing/Downward_aFRR_windfarms_EN_2015.pdf (accessed 17 August 2017).
- Knorr, K.; Zimmermann, B.; Kirchner, D.; Steinke, F.; Wolfrum, P.; Leveringhaus, T.; Lager, T.; Filzek, D.; Kusserow, B.; Nicklaus, L.; Ritter, P. Kombikraftwerk 2. Final Report. Technical Report, Kombikraftwerk 2 Consortium. 2014. Available online: http://www.kombikraftwerk.de/fileadmin/Kombikraftwerk_2/English/Kombikraftwerk2_FinalReport.pdf (accessed 17 August 2017).
- Jansen, M.; Speckmann, M. Wind turbine participation on control reserve markets. In Proceedings of the European Wind Energy Conference and Exhibition (EWEC 2013), Vienna, Austria, 4–7 February 2013; pp. 1432–1439. [Google Scholar]
- Castronuovo, E.; Usaola, J.; Bessa, R.; Matos, M.; Costa, I.; Bremermann, L.; Lugaro, J.; Kariniotakis, G. An integrated approach for optimal coordination between wind power and hydro pumping storage. Wind Energy 2014, 17, 829–852. [Google Scholar] [CrossRef]
- Haessig, P.; Multon, B.; Ahmed, H.B.; Lascaud, S.; Bondon, P. Energy storage sizing for wind power: Impact of the autocorrelation of day-ahead forecast errors. Wind Energy 2015, 18, 43–57. [Google Scholar] [CrossRef]
- Hayes, B.P.; Prodanovic, M. State forecasting and operational planning for distribution network energy management systems. IEEE Trans. Smart Grid 2016, 7, 1002–1011. [Google Scholar] [CrossRef]
- Capitanescu, F. Critical review of recent advances and further developments needed in AC optimal power flow. Electr. Power Syst. Res. 2016, 136, 57–68. [Google Scholar] [CrossRef]
- Soares, T.; Bessa, R.; Pinson, P.; Morais, H. Active distribution grid management based on robust AC optimal power flow. IEEE Trans. Smart Grid 2017, in press. [Google Scholar] [CrossRef]
- European Union. Report on Uncertainty Modeling; Technical Report, EU Project UMBRELLA, Deliverable D2.1; European Union: Brussels, Belgium, 2013. [Google Scholar]
- Antoniadou, I.; Dervilis, N.; Maguire, E.P.A.; Worden, K. Aspects of structural health and condition monitoring of offshore wind turbines. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2015, 373, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Catterson, V.M.; McMillan, D.; Dinwoodie, I.; Revie, M.; Dowell, J.; Quigley, J.; Wilson, K. An economic impact metric for evaluating wave height forecasters for offshore wind maintenance access. Wind Energy 2016, 19, 199–212. [Google Scholar] [CrossRef]
- Besnard, F.; Patriksson, M.; Stromberg, A.; Wojciechowski, A.; Fischer, K.; Bertling, L. A stochastic model for opportunistic maintenance planning of offshore wind farms. In Proceedings of the 2011 IEEE Trondheim PowerTech, Trondheim, Norway, 19–23 June 2011. [Google Scholar]
- MacLeod, D.; Davis, M.; Doblas-Reyes, P. Modelling Wind Energy Generation Potential on Seasonal Timescales With Impact Surfaces; Technical Report, SPECS Technical Note 3; SPECS: Berlin, Germany, 2014. [Google Scholar]
- Schmidt, J.; Cancella, R.; Junior, A.O.P. Combing Windpower and Hydropower to Decrease Seasonal and Inter-Annual Availability of Renewable Energy Sources in Brazil; Universität für Bodenkultur Wien: Wien, Austria, 2014. [Google Scholar]
- Torralba, V.; Doblas-Reyes, F.J.; MacLeod, D.; Christel, I.; Davis, M. Seasonal climate prediction: A new source of information for the management of wind energy resources. J. Appl. Meteorol. Climatol. 2017, 56, 1231–1247. [Google Scholar] [CrossRef]
- Sen, P.; Singer, J. Large Sample Methods in Statistics: An Introduction with Applications; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Pircalabu, A.; Hvolby, T.; Jung, J.; Høg, E. Joint price and volumetric risk in wind power trading: A copula approach. Energy Econ. 2017, 62, 139–154. [Google Scholar] [CrossRef]
- Clemen, R.T.; Reilly, T. Correlations and copulas for decision and risk analysis. Manag. Sci. 1999, 45, 208–224. [Google Scholar] [CrossRef]
- Jose, V.R.R.; Winkler, R.L. Evaluating quantile assessments. Oper. Res. 2009, 57, 1287–1297. [Google Scholar] [CrossRef]
- Keeney, R.L. Common mistakes in making value trade-offs. Oper. Res. 2002, 50, 935–945. [Google Scholar] [CrossRef]
- Weber, E.U.; Johnson, E.J. Chapter Decisions Under Uncertainty: Psychological, Economic, and Neuroeconomic Explanations of Risk Preference. In Neuroeconomics: Decision Making and the Brain; Academic Press: London, UK, 2008; pp. 127–144. [Google Scholar]
- Rodrigo, J.S.; Paredes, L.F.; Stoffels, N.; von Bremen, L. Wind power predictability assessment from large to local scale. In Proceedings of the European Wind Energy Conference (EWEA 2013), Wien, Austria, 4–7 February 2013. [Google Scholar]
- Kariniotakis, G.; Marti, I.; Casas, D.; Pinson, P. What performance can be expected by short-term wind power prediction models depending on site characteristics? In Proceedings of the European Wind Energy Conference (EWEC 2004) EWEA, London, UK, 22–25 November 2004. [Google Scholar]
- Laquaine, K.; Girard, R.; Kariniotakis, G. Assessment of wind power predictability as a decision factor in the investment phase of wind farms. Appl. Energy 2012, 101, 609–617. [Google Scholar]
- Uslar, M.; Specht, M.; Dänekas, C.; Trefke, J.; Rohjans, S.; González, J.M.; Rosinger, C.; Bleiker, R. Standardization in Smart Grids. Introduction to IT-Related Methodologies, Architectures and Standards; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Steffan, N.; Du, P.; Mago, N.; Sharma, S. Recent ERCOT developments in applications of uncertainty forecasts to system operations. In Proceedings of the 2017 UVIG Forecasting Workshop, Tutorial on Integration of Uncertainty Forecasts into Power System Operations, Atlanta, GA, USA, 20–22 June 2017. [Google Scholar]
- Siblot, S.; Bendaoud, A. Wind power forecasting in a French context. Meteorological feedback. In Proceedings of the IEA Wind Task 36 Forecasting: Workshop on Experiences and Research Gaps, Barcelona, Spain, 9 June 2016. [Google Scholar]
- DREAMS: Distributed Resource Energy Analysis and Management System Project (2014–2016). Available online: https://energy.gov/eere/sunshot/distributed-resource-energy-analysis-and-management-system-dreams-development-real-time (accessed on 17 August 2017).
- ANEMOS.plus: Advanced Tools for the Management of Electricity Grids with Large-Scale Wind Generation Project (2018–2011). Available online: https://www.anemos-plus.eu (accessed on 17 August 2017).
- EWeLiNE: Development of Innovative Weather and Power Forecast Models for the Grid Integration of Weather Dependent Energy Sources Project (2012–2017). Available online: http://www.projekt-eweline.de (accessed on 17 August 2017).
- InteGrid Project (2017–2020). Available online: http://integrid-h2020.eu (accessed on 17 August 2017).
- Wind Forecasting Improvement Project I (2011–2013). Available online: https://www.energy.gov/eere/wind/downloads/wind-forecast-improvement-project-wfip-publicprivate-partnership-improving-short (accessed on 17 August 2017).
- Wind Forecasting Improvement Project II (2015–2017). Available online: http://www.esrl.noaa.gov/gsd/renewable/wfip2.html (accessed on 17 August 2017).
- Solar Forecasting Improvement Projects (2012–2018). Available online: https://energy.gov/eere/sunshot/solar-forecast-improvement-project (accessed on 17 August 2017).
- US Department of Energy SunShot Initiative (2011–2020). Available online: https://energy.gov/eere/sunshot/about-sunshot-initiative (accessed on 17 August 2017).
- Kariniotakis, G.; Matos, M.; Miranda, V. Assessment of the benefits from advanced load & wind power forecasting in autonomous power systems. In Proceedings of the 1999 European Wind Energy Conference, Wind Energy for the Next Millennium, Nice, France, 1–5 March 1999; Petersen, E., Ed.; pp. 391–394. [Google Scholar]
- EoCoE: Energy Oriented Centre of Excellence in Computing Applications Project (2015–2018). Available online: http://www.eocoe.eu (accessed on 17 August 2017).
- SPECS: Seasonal to Decadal Climate Prediction for the Improvement of European Climate Services Project SPECS (2012–2017). Available online: http://www.specs-fp7.eu (accessed on 17 August 2017).
- EUPORIAS: European Provision of Regional Impacts Assessments on Seasonal and Decadal Timescales project EUPORIAS (2012–2017). Available online: http://www.euporias.eu (accessed on 17 August 2017).
- MacLeod, D.; Torralba, V.; Davis, M.; Doblas-Reyes, F. Transforming climate model output to forecasts of wind power production: How much resolution is enough? Meteorol. Appl. 2017, in press. [Google Scholar] [CrossRef]
- Pantel, M.; Mancarella, P. Influence of extreme weather and climate change on the resilience of power systems: Impacts and possible mitigation strategies. Electr. Power Syst. Res. 2015, 127, 259–270. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).