Grid-Connected Control Strategy of Five-level Inverter Based on Passive E-L Model
Abstract
:1. Introduction
2. Topology and Mathematical Mode
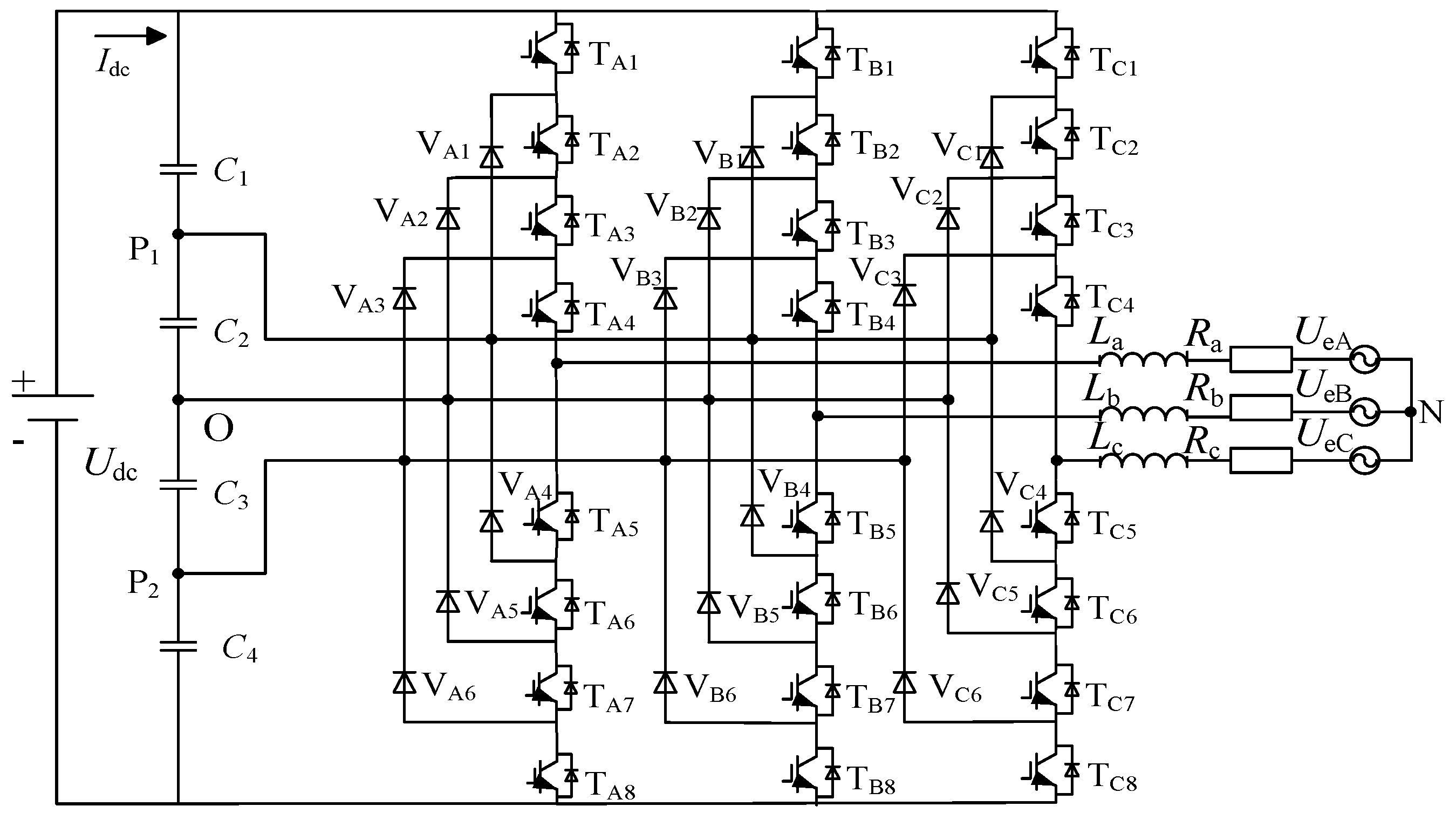
2.1. Topology
2.2. Working Principle
- (1)
- TA1, TA2, TA3, and TA4 shut down at the same time; TA5, TA6, TA7, and TA8 switch on at the same time; and then the output phase voltage of the inverter is +Udc/2 and SA = +2.
- (2)
- TA2, TA3, TA4, and TA5 shut down at the same time; TA1, TA6, TA7, and TA8 switch on at the same time; and then the output phase voltage of the inverter is +Udc/4 and SA = +1.
- (3)
- TA3, TA4, TA5, and TA6 shut down at the same time, and TA1, TA2, TA7, and TA8 switch on at the same time. O point and N point have the same potential at the same moment, so the output phase voltage of the inverter is 0. Meanwhile, SA = 0.
- (4)
- TA4, TA5, TA6, and TA7 shutdown at the same time; TA1, TA2, TA3, and TA8 switch on at the same time; and the output phase voltage of the inverter is −Udc/4 and SA = −1.
- (5)
- TA5, TA6, TA7, and TA8 shut down at the same time; TA1, TA2, TA3, and TA4 switch on at the same time; and the output phase voltage of the inverter is −Udc/2 and SA = −2.
2.3. Mathematical Model
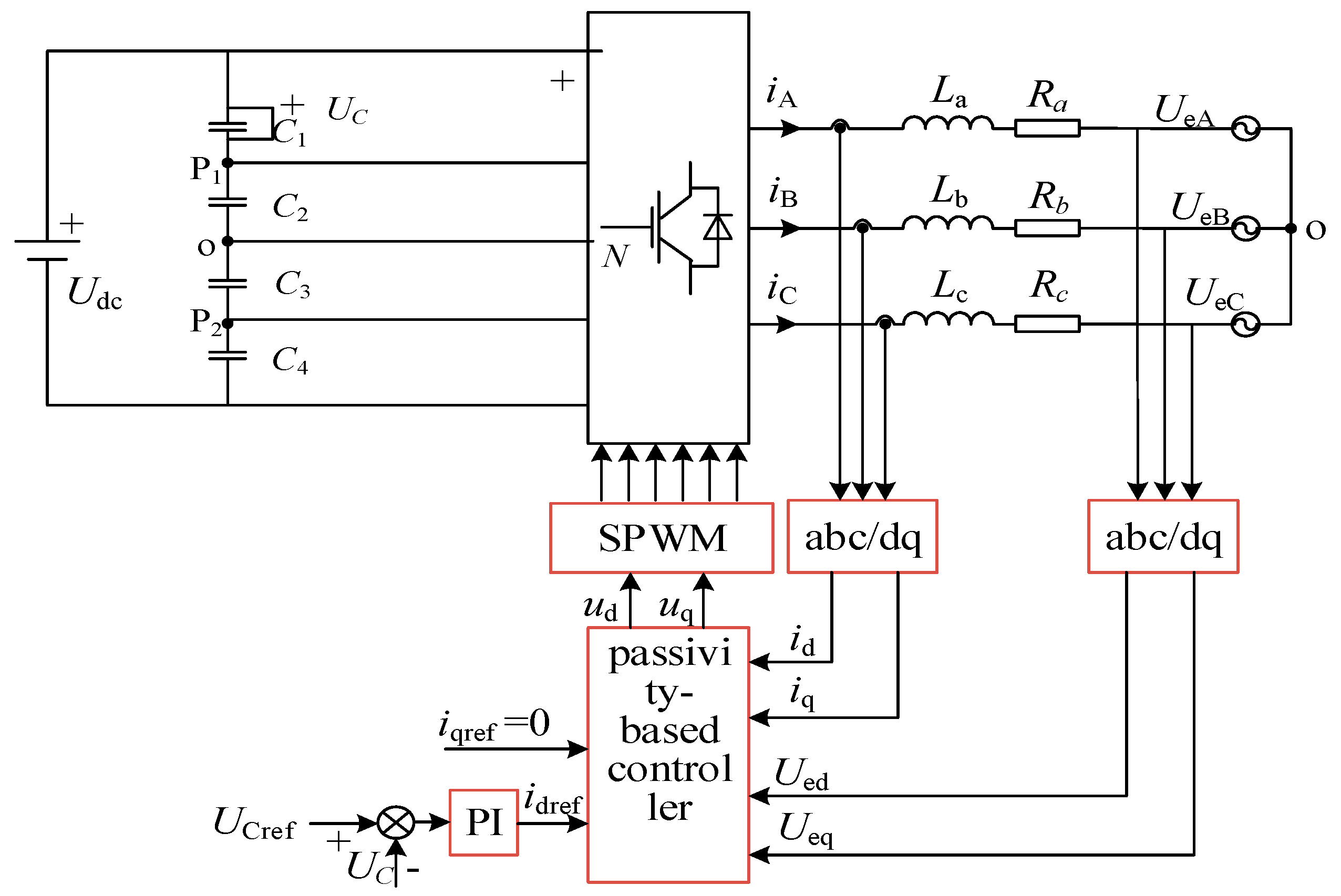
3. SPWM Modulation Strategy
4. Design of Passive Controller
4.1. Passive E-L Model of the Five-Level Inverter
4.2. Design of Passive E-L Model Controller
5. Software Simulation
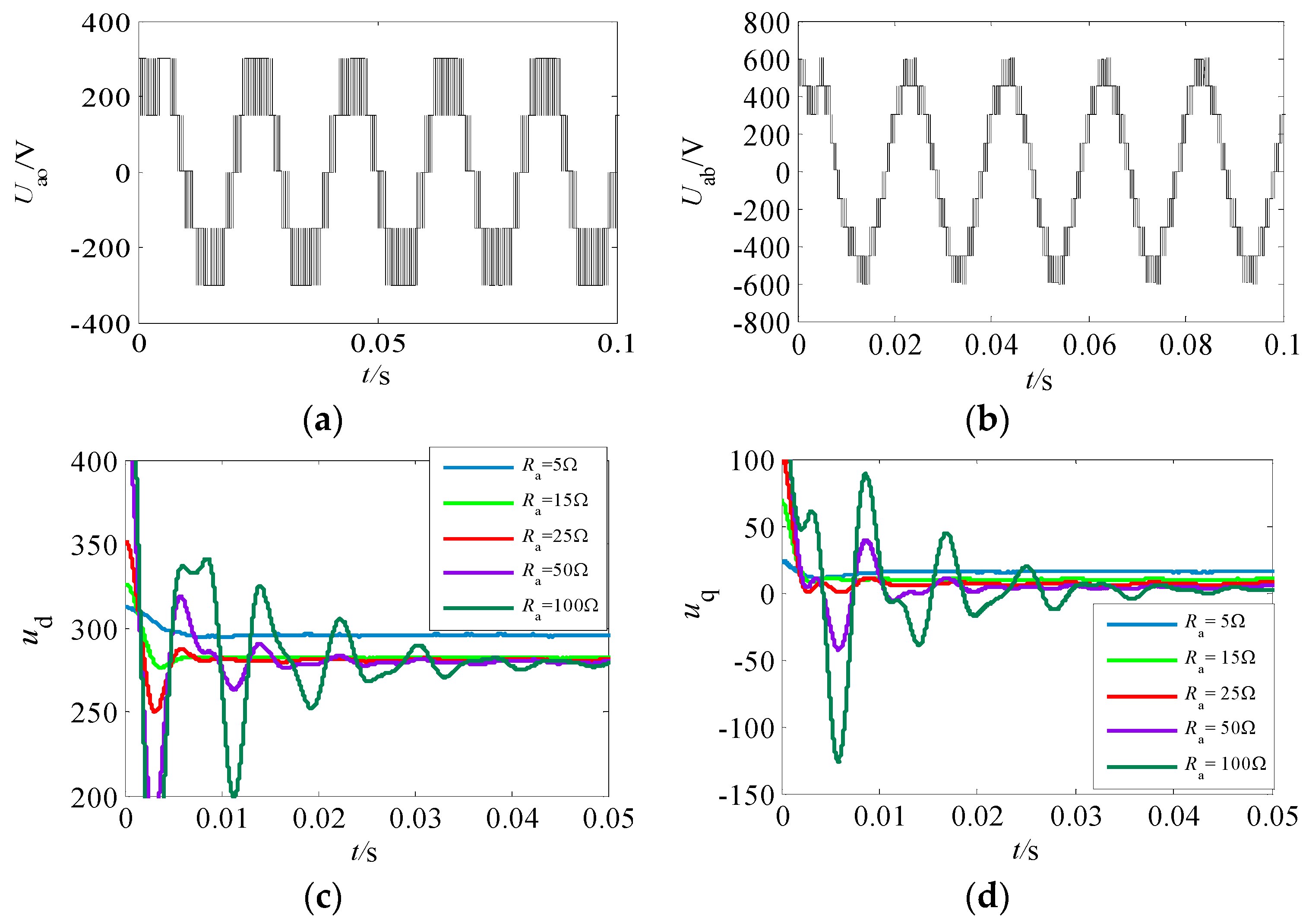
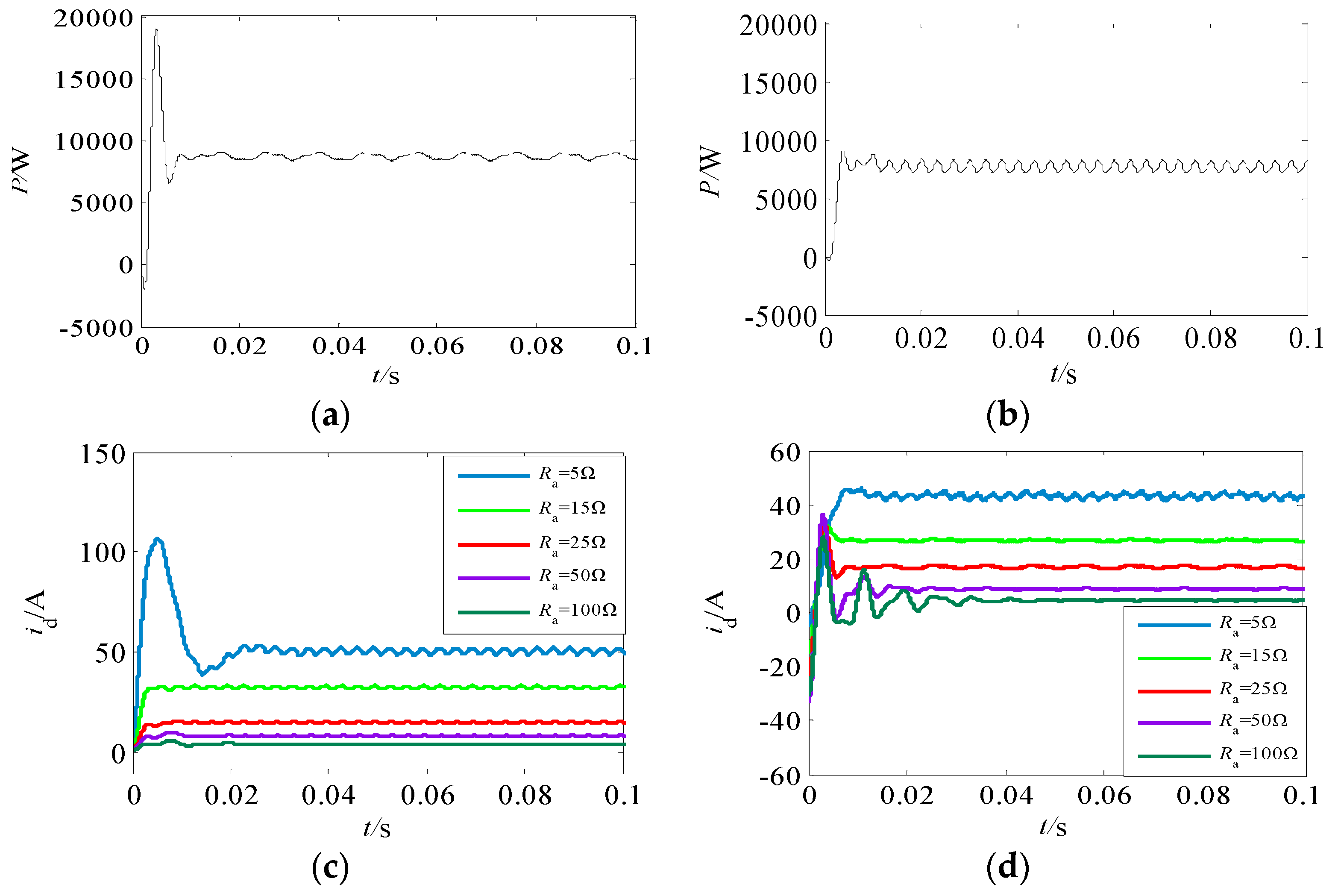
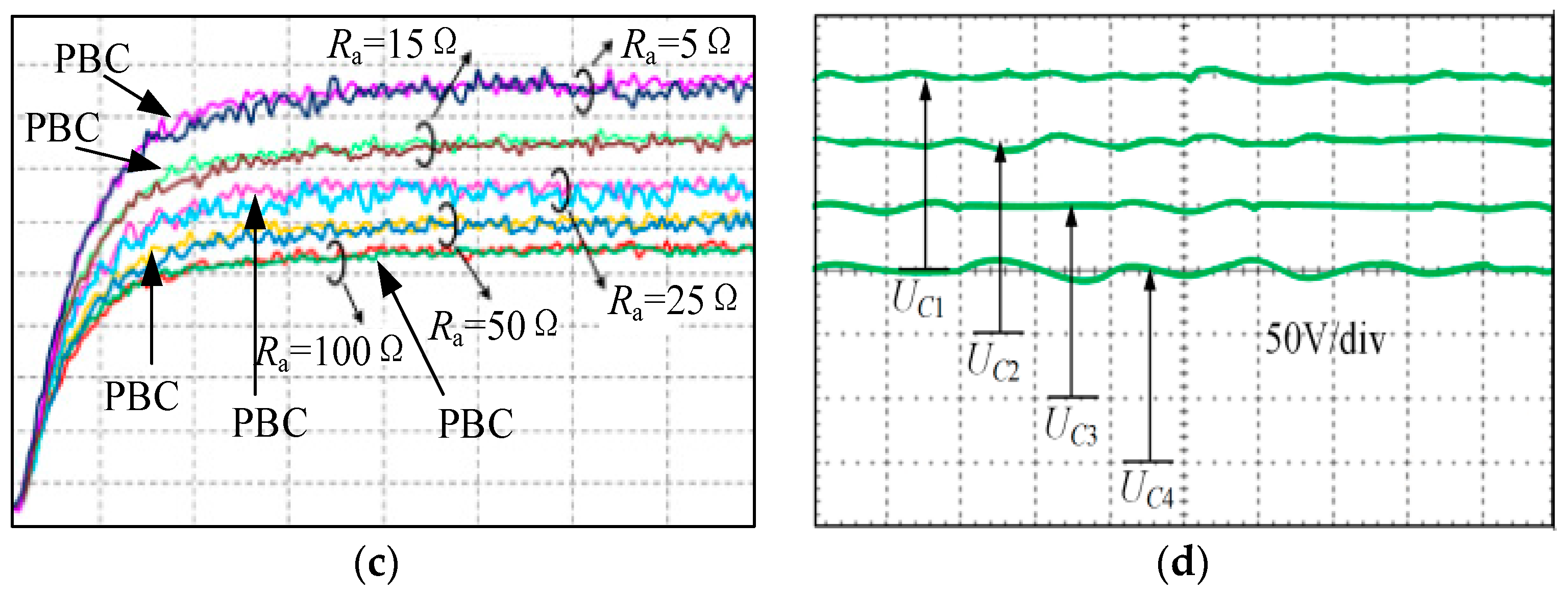
5.1. Simulation of Passivity Control Mentioned in This Paper
5.2. The Passivity-Based Control of This Paper Is Compared with the Traditional PI Control
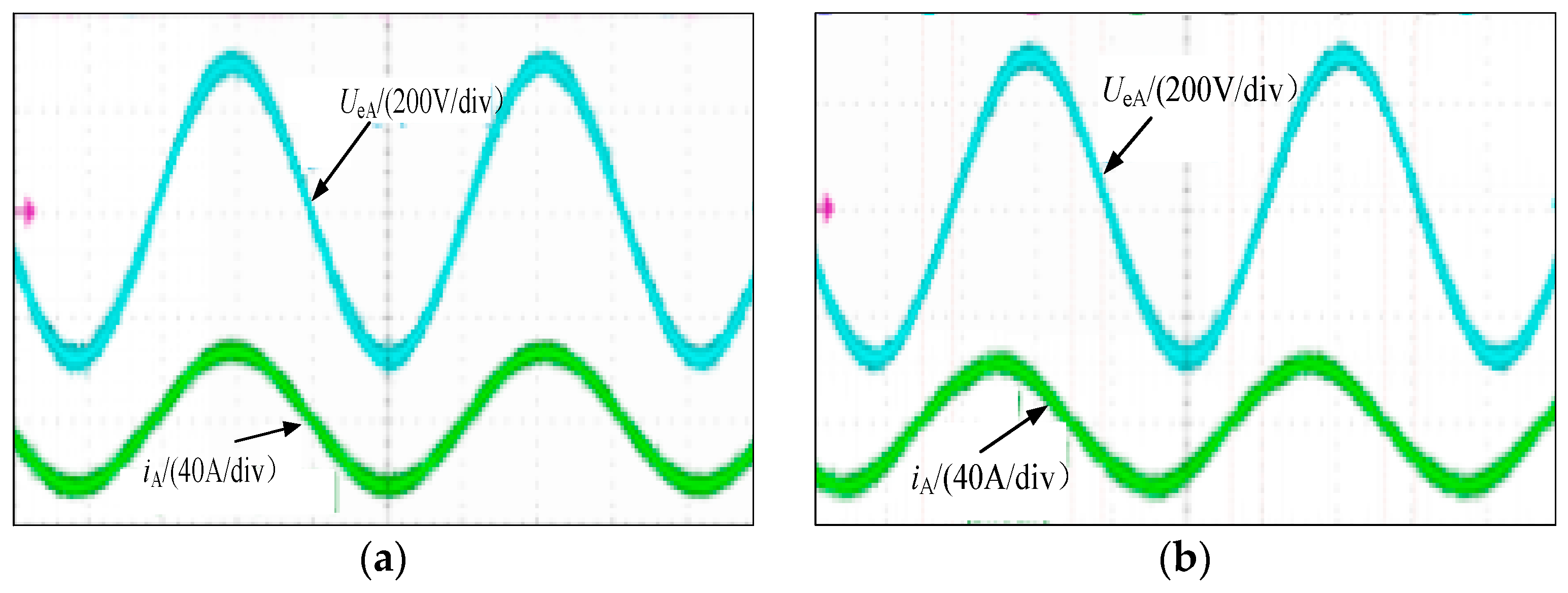
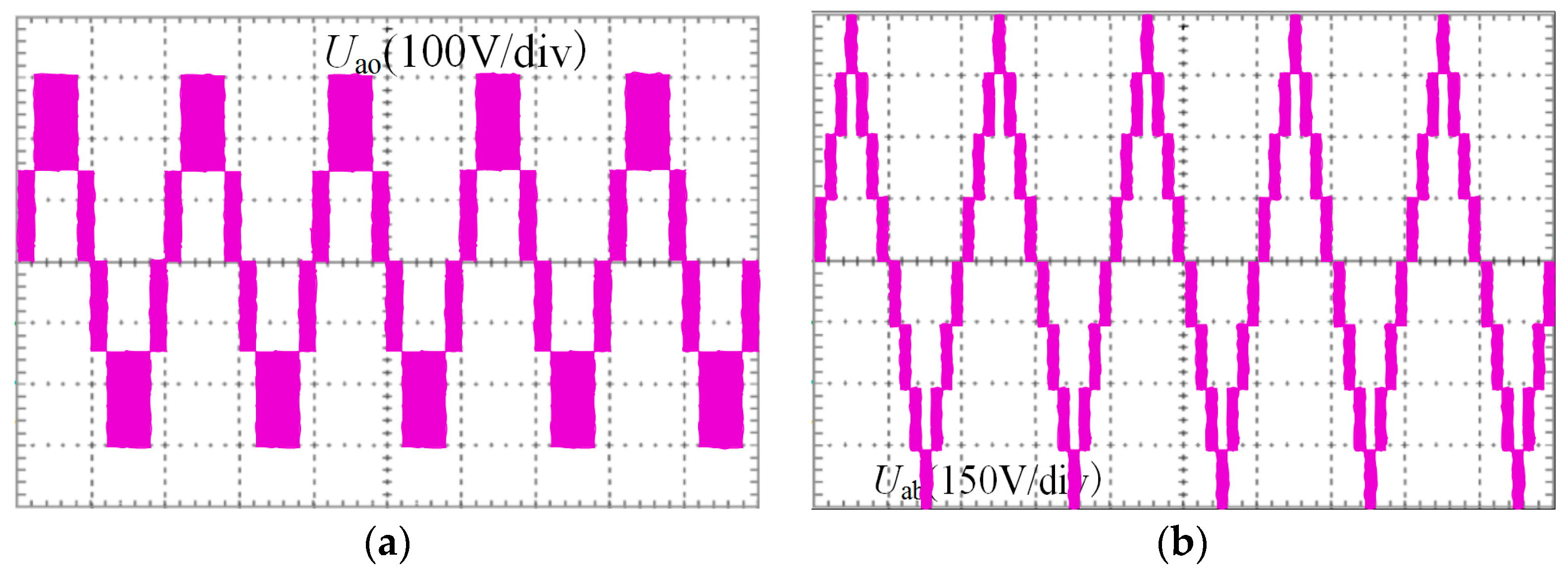
6. Prototype Experiment
7. Conclusions
- (1)
- The optimum stability of the system can be achieved by selecting the appropriate energy function and injection damping.
- (2)
- Compared with the traditional PI control method, the passivity-based control strategy has better static and dynamic stability and makes the system achieve a higher power factor.
- (3)
- In terms of economy, the harmonic loss very small under passivity-based control.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mokhtar, A.; Ahmed, E.M.; Masahito, S. Thermal Stresses Relief Carrier-Based PWM Strategy for Single-Phase Multilevel Inverters. IEEE Trans. Power Electron. 2017, 32, 9376–9388. [Google Scholar]
- Wang, H.; Liu, Y.; Sen, P.C. A neutral point clamped multilevel topology flow graph and space NPC multilevel topology. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 3615–3621. [Google Scholar]
- Ahmed, M.; Zainal, S.; Amjad, A.M. Harmonics elimination PWM based direct control for 23-level multilevel distribution STATCOM using differential evolution algorithm. Electr. Power Syst. Res. 2017, 152, 48–60. [Google Scholar]
- Georgios, K.; Josep, P.; Daniel, P. A Hybrid Modular Multilevel Converter with Partial Embedded Energy Storage. Energies 2016, 9, 12. [Google Scholar]
- Lee, K.S.; Oh, G.; Chu, D.; Pak, S.W.; Kim, E.K. High power conversion efficiency of intermediate band photovoltaic solar cell based on Cr-doped ZnTe. Sol. Energy Mater. Sol. Cells 2017, 170, 27–32. [Google Scholar] [CrossRef]
- Genevieve, S.; Julian, C. Subsidies for residential solar photovoltaic energy systems in Western Australia: Distributional, procedural and outcome justice. Renew. Sustain. Energy Rev. 2016, 65, 262–273. [Google Scholar]
- Gupta, K.K.; Ranjan, A.; Bhatnagar, P.; Sahu, L.; Jain, S. Multilevel inverter topologies with reduced device count: A review. IEEE Trans. Power Electron. 2016, 31, 135–151. [Google Scholar] [CrossRef]
- Hu, C.; Yu, X.; Holmes, D.G.; Shen, W.; Wang, Q.; Luo, F.; Liu, N. An Improved Virtual Space Vector Modulation Scheme for Three-Level Active Neutral-Point-Clamped Inverter. IEEE Trans. Power Electron. 2017, 32, 7419–7434. [Google Scholar] [CrossRef]
- Xia, C.; Zhang, G.; Yan, Y.; Gu, X.; Shi, T.; He, X. Discontinuous Space Vector PWM Strategy of Neutral-Point-Clamped Three-Level Inverters for Output Current Ripple Reduction. IEEE Trans. Power Electron. 2017, 32, 5109–5121. [Google Scholar] [CrossRef]
- Song, K.; Georgios, K.; Li, J.; Wu, M.; Vassilios, G.A. High performance control strategy for single-phase three-level neutral-point-clamped traction four-quadrant converters. IET Power Electron. 2017, 10, 884–893. [Google Scholar]
- Lei, Y.; Barth, C.; Qin, S.; Liu, W.-C.; Moon, I.; Stillwell, A.; Chou, D.; Foulkes, T.; Ye, Z.; Liao, Z.; et al. A 2-kW Single-Phase Seven-Level Flying Capacitor Multilevel Inverter with an Active Energy Buffer. IEEE Trans. Power Electron. 2017, 32, 8570–8581. [Google Scholar] [CrossRef]
- Dekka, A.; Wu, B.; Zargari, N.R. Start-Up Operation of a Modular Multilevel Converter with Flying Capacitor Submodules. IEEE Trans. Power Electron. 2017, 32, 5873–5877. [Google Scholar] [CrossRef]
- Liangzong, H.; Chen, C. A Flying-Capacitor-Clamped Five-Level Inverter Based on Bridge Modular Switched-Capacitor Topology. IEEE Trans. Ind. Electron. 2016, 63, 7814–7822. [Google Scholar]
- Youngjong, K.; Markus, A.; Giampaolo, B. Power Routing for Cascaded H-Bridge Converters. IEEE Trans. Power Electron. 2017, 32, 9435–9446. [Google Scholar]
- Saeed, O.; Reza, Z.M.; Masih, K. Improvement of Post-Fault Performance of a Cascaded H-bridge Multilevel Inverter. IEEE Trans. Ind. Electron. 2017, 64, 2779–2788. [Google Scholar]
- Sheng, X.; Zhendong, J. A Study of the SPWM High-Frequency Harmonic Circulating Currents in Modular Inverters. J. Power Electron. 2016, 16, 2119–2128. [Google Scholar]
- Liu, Z.; Zheng, Z.; Sudhoff, S.D.; Gu, C.; Li, Y. Reduction of Common-Mode Voltage in Multiphase Two-Level Inverters Using SPWM with Phase-Shifted Carriers. IEEE Trans. Power Electron. 2015, 31, 6631–6645. [Google Scholar] [CrossRef]
- Jacob, L.; Behrooz, M. An Adaptive SPWM Technique for Cascaded Multilevel Converters with Time-Variant DC Sources. IEEE Trans. Ind. Appl. 2016, 52, 4146–4155. [Google Scholar]
- Dong, X.; Yu, X.; Yuan, Z.; Xia, Y.; Li, Y. An Improved SPWM Strategy to Reduce Switching in Cascaded Multilevel Inverters. J. Power Electron. 2016, 16, 490–497. [Google Scholar] [CrossRef]
- Niu, L.; Xu, D.; Yang, M.; Gui, X.; Liu, Z. On-line inertia identification algorithm for pi parameters optimization in speed loop. IEEE Trans. Power Electron. 2015, 30, 849–859. [Google Scholar] [CrossRef]
- Li, B.; Zhang, M.; Huang, L.; Hang, L.; Tolbert, L.M. A robust multi-resonant PR regulator for three-phase grid-connected VSI using direct pole placement design strategy. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013; pp. 960–966. [Google Scholar]
- Zhang, X.; Sun, L.; Zhao, K.; Sun, L. Nonlinear speed control for PMSM system using sliding-mode control and disturbance compensation techniques. IEEE Trans. Power Electron. 2013, 28, 1358–1365. [Google Scholar] [CrossRef]
- Pichan, M.; Rastegar, H.; Monfared, M. Deadbeat control of the stand-alone four-leg inverter considering the effect of the neutral line inductor. IEEE Trans. Ind. Electron. 2017, 64, 2592–2601. [Google Scholar] [CrossRef]
- Mahmood, H.; Michaelson, D.; Jiang, J. Accurate reactive power sharing in an islanded microgrid using adaptive virtual impedances. IEEE Trans. Power Electron. 2015, 30, 1605–1617. [Google Scholar] [CrossRef]
- Abrishamifar, A.; Ahmad, A.A.; Mohamadian, M. Fixed switching frequency sliding mode control for single-phase unipolar inverters. IEEE Trans. Power Electron. 2012, 27, 2507–2514. [Google Scholar] [CrossRef]
- Harnefors, L.; Wang, X.; Yepes, A.G.; Blaabjerg, F. Passivity-based stability assessment of grid-connected VSCs—An overview. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 116–125. [Google Scholar] [CrossRef]
- Harnefors, L.; Yepes, A.G.; Vidal, A.; Doval-Gandoy, J. Passivity-based controller design of grid-connected VSCs for prevention of electrical resonance instability. IEEE Trans. Ind. Electron. 2015, 62, 702–710. [Google Scholar] [CrossRef]
- Santos, G.V.; Cupertino, A.F.; Mendes, V.F.; Seleme, S.I. Interconnection and damping assignment passivity-based control of a PMSG based wind turbine for maximum power tracking. In Proceedings of the 2015 IEEE 24th International Symposium on Industrial Electronics (ISIE), Rio de Janeiro, Brazil, 3–5 June 2015; pp. 306–311. [Google Scholar]
- Hou, R.S.; Hui, H.; Nguyen, T.T. Robustness improvement of superconducting magnetic energy storage system in microgrids using an energy shaping passivity-based control strategy. Energies 2017, 10, 5. [Google Scholar] [CrossRef]
- Liu, X.B.; Li, C.B.; Sun, K. Voltage support for industrial distribution network by using positive/negative sequence passivity-based control. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 June 2016; pp. 674–679. [Google Scholar]
- Ramrez-Leyva, F.H.; Peralta-Sanchez, E.; Vasquez-Sanjuan, J.J.; Trujillo-Romero, F. Passivity–Based Speed Control for Permanent Magnet Motors. Procedia Technol. 2013, 7, 215–222. [Google Scholar] [CrossRef]
- Baile, Z.; Jiuhe, W.; Fengjiao, Z. The PCHD model and control of TNPC PV grid-connected inverter. Proc. CSEE 2014, 34, 204–210. [Google Scholar]
- Zhang, Z.; Liu, X.; Wang, C.; Kang, L.; Liu, H. A Passivity-based Power Control for a Three-Phase Three-level NPC Rectifier. In Proceedings of the International Conference on Electrical Machines and Systems (ICEMS), Pattaya, Thailand, 25–28 October 2015; pp. 383–386. [Google Scholar]
- Cao, Y.J.; Xu, Y.; Li, Y.; Yu, J.Q. A Lyapunov Stability Theory-Based Control Strategy for Three-Level Shunt Active Power Filter. Energies 2017, 10, 112. [Google Scholar] [CrossRef]
- Lozano-Hernandez, B.; Vasquez-Sanjuan, J.J.; Rangel-Magdaleno, J.J.; Olivos Pérez, L.I. Simulink/PSim/Active-HDL Co-Simulation of Passivity–Based Speed Control of PMSM. In Proceedings of the International Conference on Power Electronics, Inst Tecnologico Super Irapuato, Guanajuato, Mexico, 20–23 June 2016; pp. 7–11. [Google Scholar]
- Flota, M.; Ali, B.; Villanueva, C. Passivity-Based Control for a Photovoltaic Inverter with Power Factor Correction and Night Operation. IEEE Lat. Am. Trans. 2016, 14, 3569–3574. [Google Scholar] [CrossRef]



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Udc | 600 V | Lf | 1 mH |
| C1 (C2 C3 C4) | 220 μF | R | 1 Ω |
| C | 50 μF | UeA UeB UeC | 311 V |
| L | 500 mH | frequency (f) | 50 HZ |
| Injection Damping | Stability Time of ud | Stability Time of uq |
|---|---|---|
| Ra = 5 Ω | 0.006 s | 0.005 s |
| Ra = 15 Ω | 0.005 s | 0.005 s |
| Ra = 25 Ω | 0.005 s | 0.006 s |
| Ra = 50 Ω | 0.02 s | 0.02 s |
| Ra = 100 Ω | 0.04 s | 0.045 s |
| Parameter | PBC | Traditional PI | ||
|---|---|---|---|---|
| Stability Time | Amplitude of Fluctation | Stability Time | Amplitude of Fluctation | |
| p | 0.01 s | smaller | 0.01 s | larger |
| Ra = 5 Ω | 0.02 s | smaller | 0.01 s | larger |
| Ra = 15 Ω | 0.003 s | smaller | 0.01 s | larger |
| Ra = 25 Ω | 0.003 s | smaller | 0.01 s | larger |
| Ra = 50 Ω | 0.004 s | smaller | 0.02 s | smaller |
| Ra = 100 Ω | 0.004 s | smaller | 0.04 s | smaller |
| THD (%) | 0.26 | 3.39 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Cheng, Q.; Sun, W.; Chen, L. Grid-Connected Control Strategy of Five-level Inverter Based on Passive E-L Model. Energies 2017, 10, 1657. https://doi.org/10.3390/en10101657
Li T, Cheng Q, Sun W, Chen L. Grid-Connected Control Strategy of Five-level Inverter Based on Passive E-L Model. Energies. 2017; 10(10):1657. https://doi.org/10.3390/en10101657
Chicago/Turabian StyleLi, Tao, Qiming Cheng, Weisha Sun, and Lu Chen. 2017. "Grid-Connected Control Strategy of Five-level Inverter Based on Passive E-L Model" Energies 10, no. 10: 1657. https://doi.org/10.3390/en10101657
APA StyleLi, T., Cheng, Q., Sun, W., & Chen, L. (2017). Grid-Connected Control Strategy of Five-level Inverter Based on Passive E-L Model. Energies, 10(10), 1657. https://doi.org/10.3390/en10101657






