A Novel Probabilistic Optimal Power Flow Method to Handle Large Fluctuations of Stochastic Variables
Abstract
:1. Introduction
2. Traditional CM for P-OPF
- Take the mean values of wind power outputs and loads, and solve the aforementioned deterministic OPF model using LBIPM.
- Obtain the KKT first-order conditions, when the optimization is converged:where is the set of equations defining the KKT first-order conditions. is a vector consisting of magnitude and angle of voltage at each bus, active and reactive generation of each conventional generator, slack variables and Lagrange multipliers.
- Treat loads and wind power outputs as random input variables, and formulate new KKT first-order conditions:where and are the vectors of load and wind power output at each bus, respectively.
- Take the full derivative of (5), and find a linear relationship between input variables and output variables:where is the Hessian of the Lagrangian function with respect to when the optimization is completed. , and are vectors of the changes in , and . and are obtained by taking the partial derivatives of (5) with respect to and , respectively. Equation (6) can be reformed as the following equation:where is the inverse of the obtained Hessian, , and .From Equation (7), an unknown variable can be formulated as a linear combination of known input variables (loads and wind power outputs):where is the value of evaluated by the deterministic OPF in step 1. is the change of . and are the values at the i-th row and j-th column of and , respectively. and are the j-th variables in and , respectively. and are the mean values of and , respectively. is the number of load variables, and is the number of wind power variables. .
- If the known input variables (loads and wind power outputs) are independent of each other, the cumulants of unknown output variables can be computed by a linear combination of cumulants of known input variables based on the property of cumulants (see Appendix A):where is the v-th order cumulant of . and are the v-th order cumulants of and , respectively.
3. The Proposed Method for P-OPF
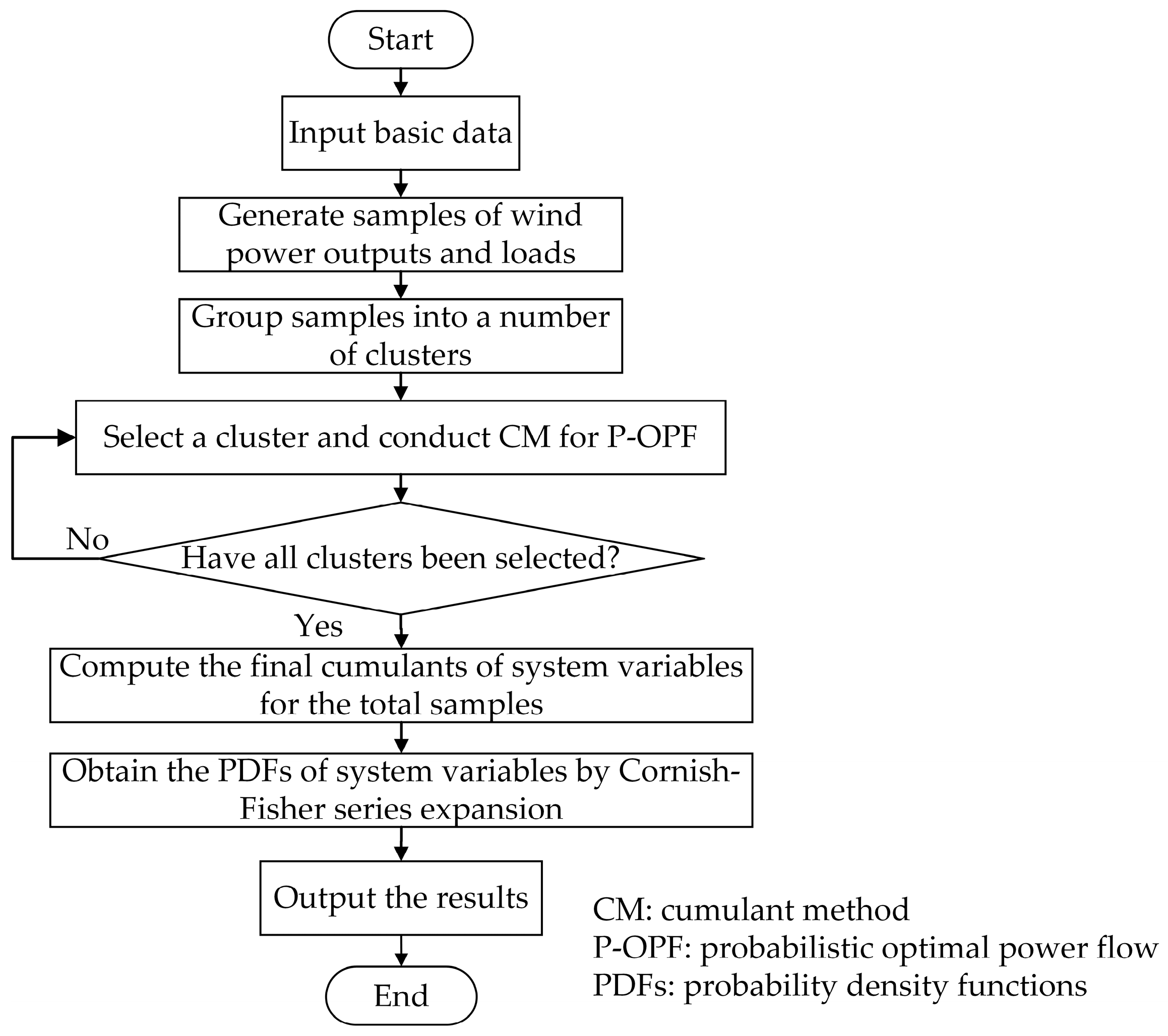
3.1. The Overall Procedure of the Proposed Method
- Input the basic data, including network data, the distribution functions of wind speeds and loads, and the correlation matrix.
- Group the samples of wind power outputs and loads into a number of clusters using the K-means algorithm.
- In each cluster, the CM for P-OPF considering correlations among input variables is applied. Firstly, the samples for each cluster are converted to uncorrelated samples. Then, the cumulants of uncorrelated input variables are calculated based on uncorrelated samples [33]. Finally, the CM for P-OPF is applied to compute the cumulants of system variables for each cluster.
- Compute the final cumulants of system variables for the total samples.
- PDFs of system variables are produced by Cornish–Fisher series expansion [42].
- Output the cumulants and PDFs of system variables.
3.2. Generating Samples of Correlated Wind Power Outputs and Loads
3.3. Application of the K-Means Algorithm to Group Samples into Clusters
- (1).
- Pick initial mean values of all clusters, which are defined as the following equations:where is a multi-dimensional vector comprised of initial mean values of all clusters, is the pre-set number of clusters, is the mean value vector of cluster , and is the picked initial mean value of the variable in cluster .
- (2).
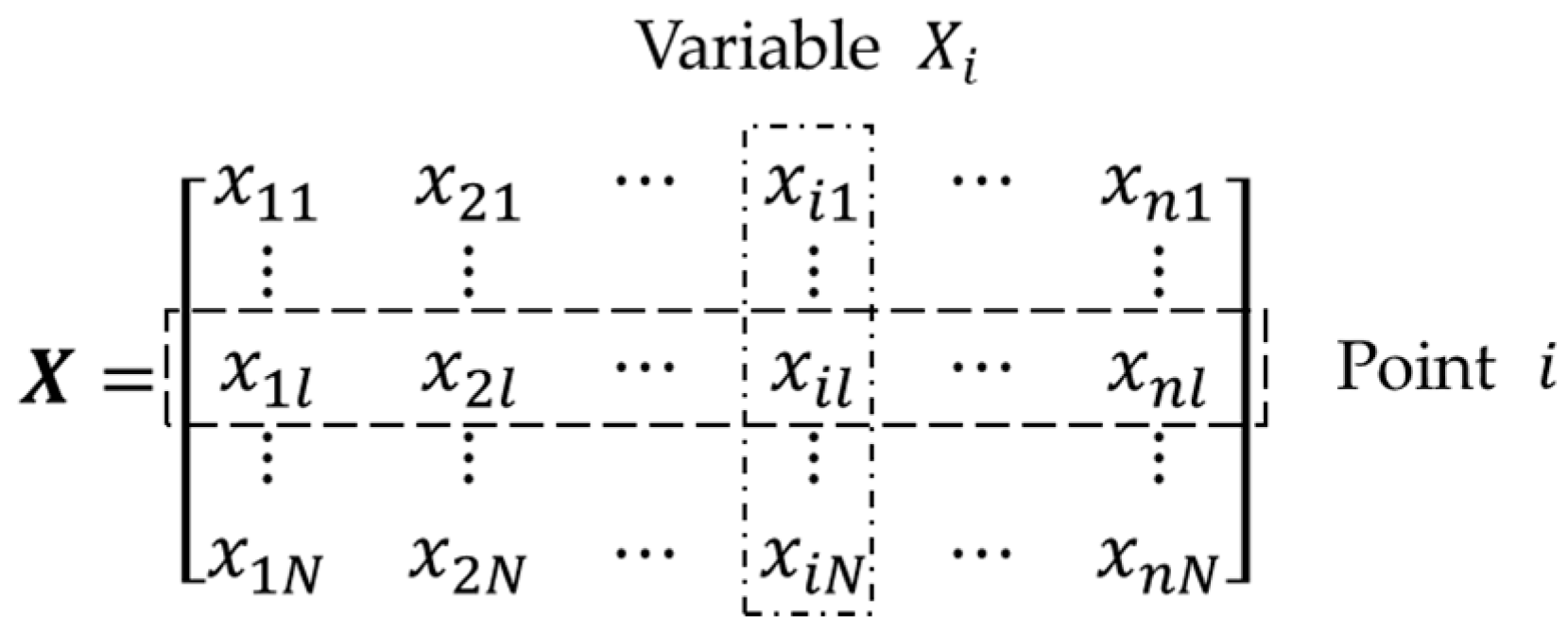
- Calculate Euclidean distances from each point to each cluster mean according to the following equation:where is the Euclidean distance from point to the mean of clusters , point is expressed as , and is the l-th element of .
- (3).
- Assign every point to the nearest cluster according to the Euclidean distances, and update the mean values of all clusters.
- (4).
- Repeat steps 2 and 3 until points in each cluster are no longer changed.
3.4. The Method of Handling Correlations among Input Variables
3.5. Computation of the Cumulants of System Variables
- (1).
- In each cluster, cumulants of a system variable for each cluster can be obtained based on the algorithms introduced in Section 3.2, Section 3.3 and Section 3.4. The moments of the system variable for each cluster are computed using the following equation:where is the v-th order moment of a variable for cluster , is the v-th order cumulant of a variable for cluster , and is a combination of elements from v − 1 different elements.
- (2).
- The property that moments meet the total probability formula is applied to combine the moments of the system variable for all clusters. The moments of the system variable for the total samples are calculated using the following equation:where is the v-th order moment of a system variable for the total samples, k is the number of clusters, and is the proportion of the number of elements in cluster to the total samples.
- (3).
- The final cumulants of the system variable for the total samples are obtained using the following equation:where is the v-th order cumulant of a system variable for the total samples.
3.6. Computation of PDFs of System Variables
4. Case Studies
4.1. The Modified IEEE 9-Bus Test System
4.1.1. Application of the K-Means Algorithm to Group Samples into Clusters
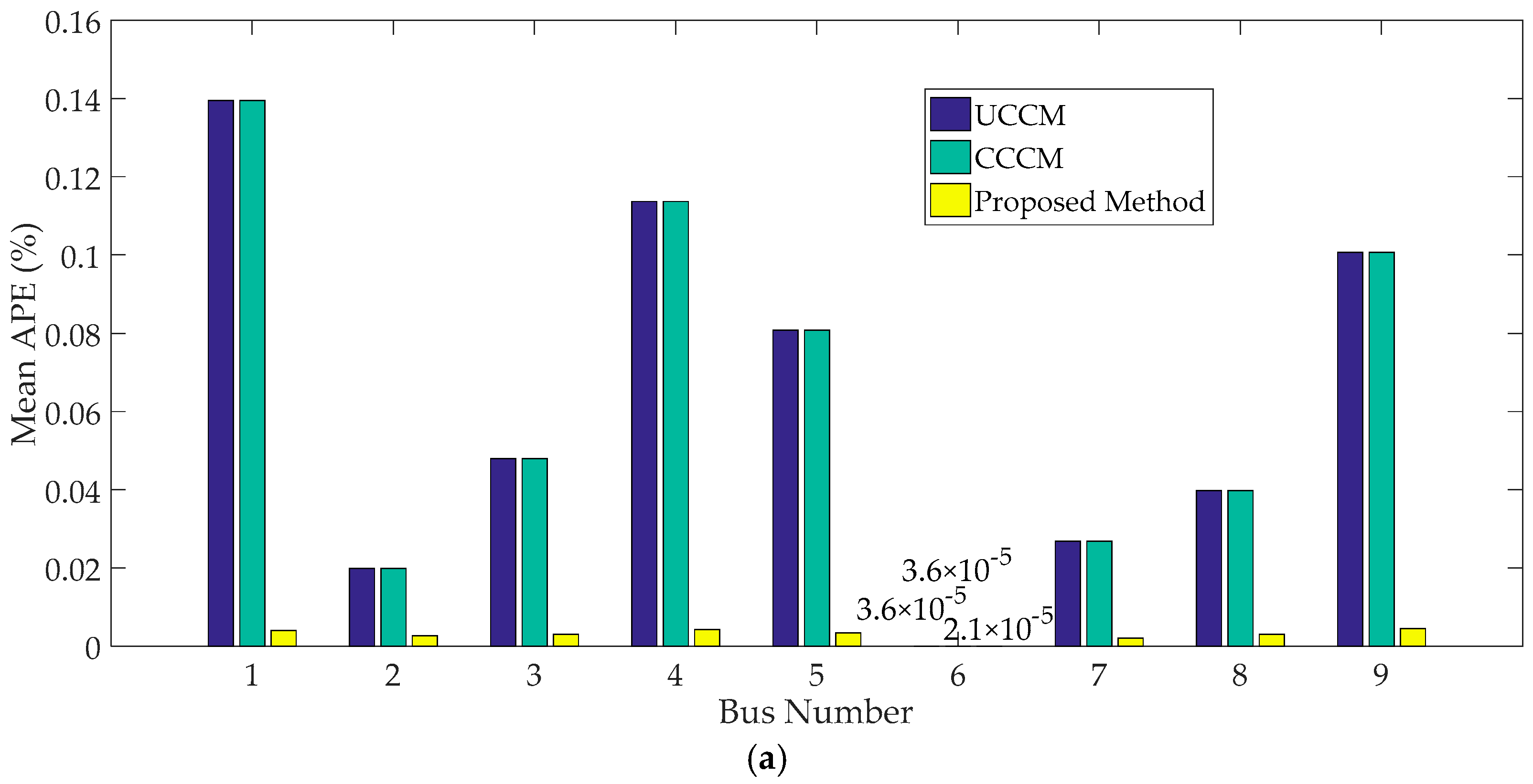
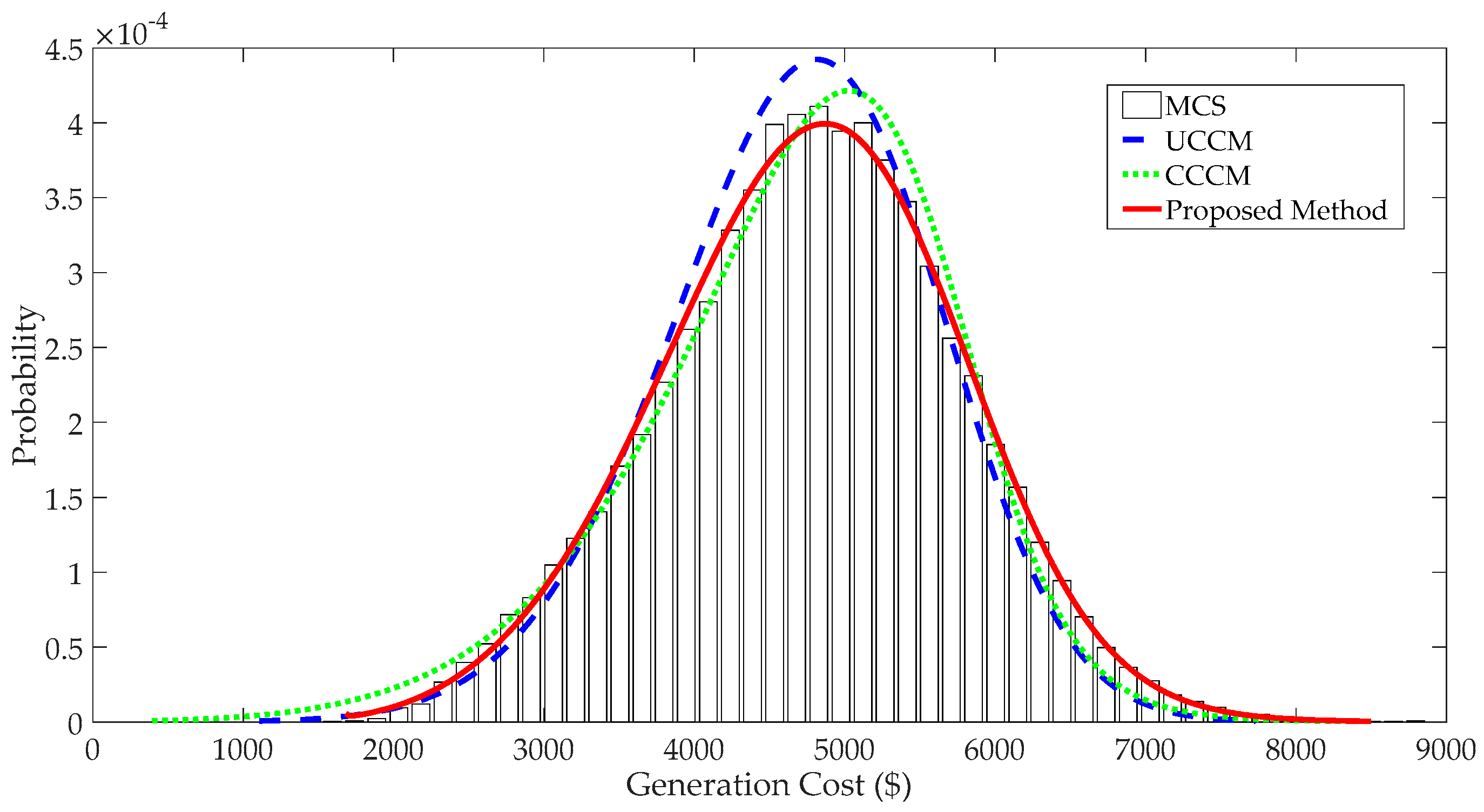
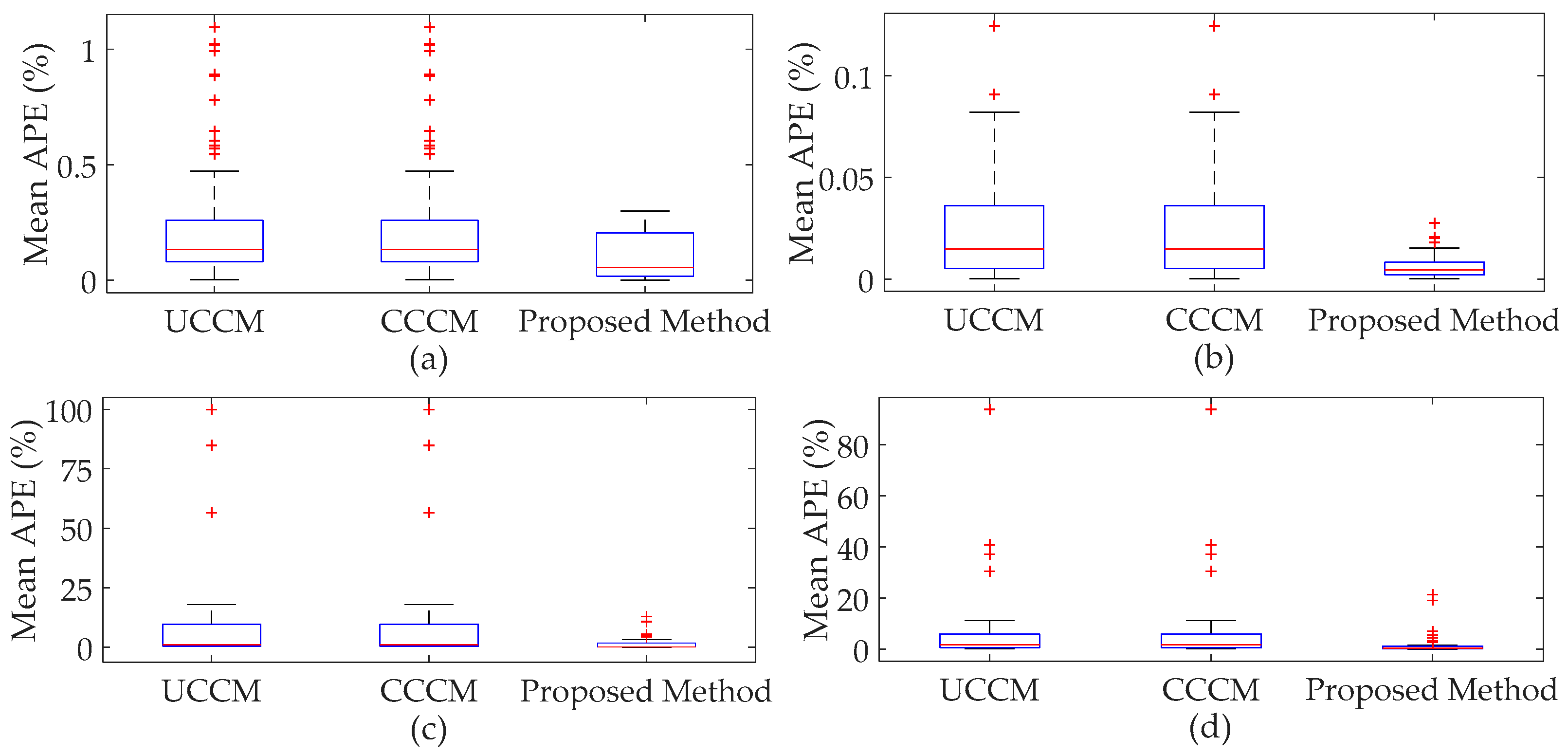
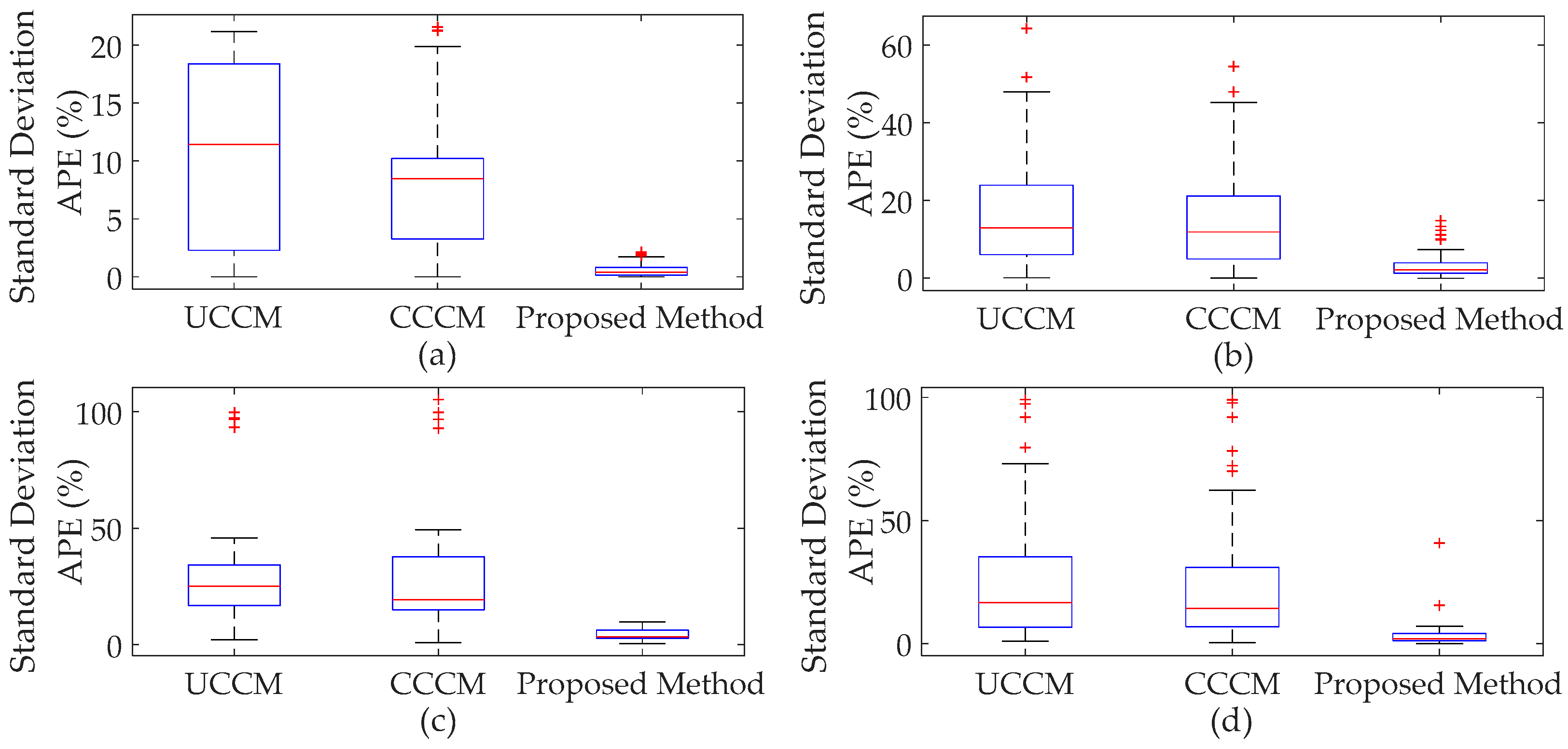
4.1.2. Cumulants of System Variables and Comparison
4.1.3. PDFs of System Variables and Comparison
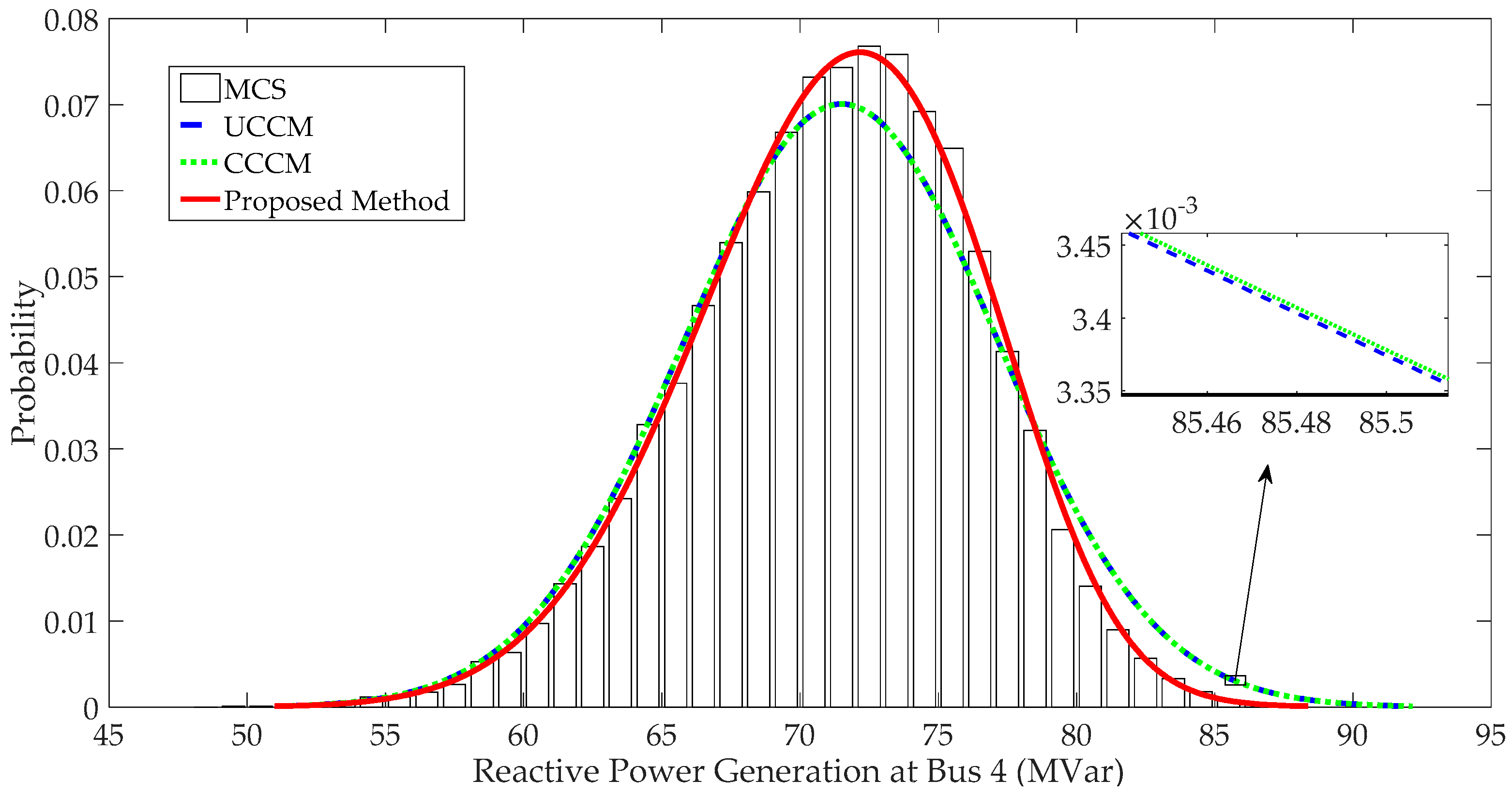
4.2. The Modified IEEE 118-Bus Test System
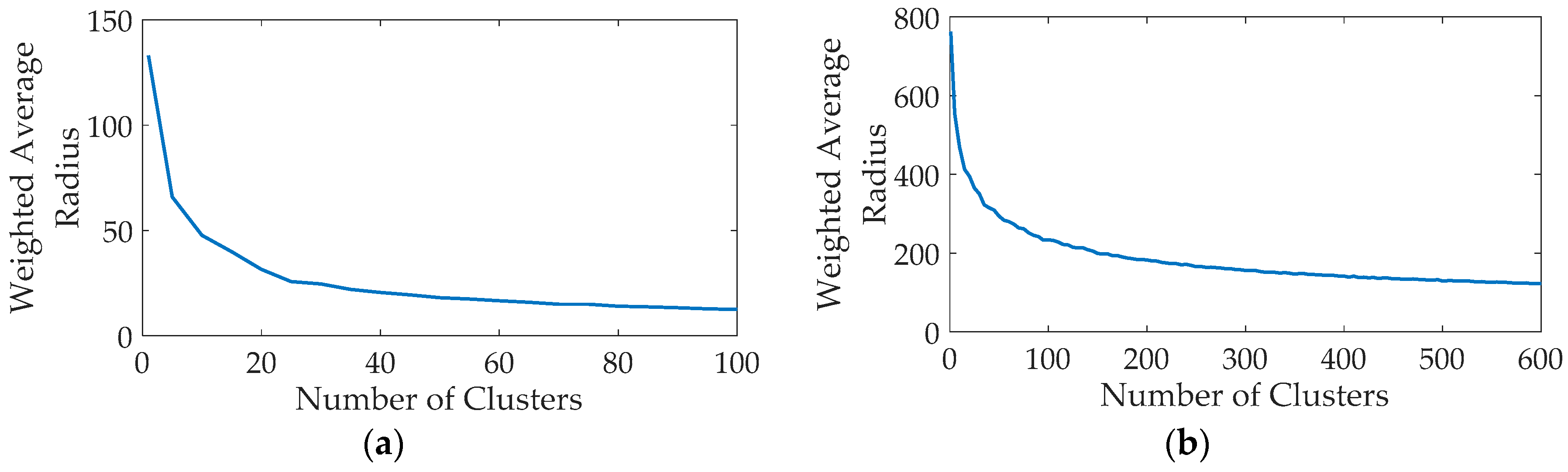
4.3. Discussions about Number of Clusters
5. Conclusions
- When input variables have large fluctuations, P-OPF results obtained using the traditional CM have large APE values and significant errors at the tails of PDFs, which indicates that the traditional CM is not suitable to solve P-OPF problems with large fluctuations of stochastic variables.
- The proposed method can handle correlations and large fluctuations of input variables. Case studies indicate that the proposed method has more accurate results than traditional CM and is more efficient than MCS.
- The performance of the proposed method is influenced by the number of clusters. Generally, the proposed method with more clusters has more accurate results, but will require more computation time. The appropriate number of clusters can be determined by the weighted average radius.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| CM | cumulant method |
| OPF | optimal power flow |
| PLF | probabilistic load flow |
| P-OPF | probabilistic optimal power flow |
| KKT | Karush–Kuhn–Tucker |
| CDFs | cumulative distribution functions |
| PDFs | probability density functions |
| IS | importance sampling |
| LHS | Latin hypercube sampling |
| LSS | Latin supercube sampling |
| NPNT | ninth-order polynomial normal transformation |
| PEM | point estimation method |
| UTM | unscented transformation method |
| LT | Laplace transform |
| FFT | fast Fourier transform |
| FOSMM | First-Order Second-Moment Method |
| GMM | Gaussian mixture model |
| LBIPM | Logarithmic Barrier Interior Point Method |
| APE | absolute percent error |
| , | the active and reactive power generation of conventional generator at bus |
| , , | cost coefficients of generator at bus |
| the active power output of wind farm at bus | |
| the reactive power injected by compensation device at bus | |
| , | the active and reactive loads at bus |
| the magnitude of voltage at bus | |
| the phase angle difference between bus and | |
| , | the real and imaginary parts of the element in bus admittance matrix |
| the complex power flow of branch | |
| , | the lower and upper bounds of |
| , | the lower and upper bounds of |
| , | the lower and upper bounds of |
| the line rating of branch | |
| the number of buses | |
| the number of branches | |
| the set of equations defining the KKT first-order conditions | |
| a vector consisting of magnitude and angle of voltage at each bus, active and reactive generation of each conventional generator, slack variables and Lagrange multipliers | |
| the vector of load at each bus | |
| the vector of wind power output at each bus | |
| the Hessian of the Lagrangian function with respect to when the optimization is completed | |
| , , | vectors of the changes in , and |
| , | matrixes obtained by taking the partial derivatives with respect to and |
| an unknown variable | |
| the value of evaluated by the deterministic OPF | |
| the change of | |
| , | the values at row and column of and |
| , | the j-th variables in and |
| , | the mean values of and |
| , | the number of load variables and wind power variables |
| the v-th order cumulant of | |
| , | the v-th order cumulants of and |
| the wind speed of wind farm at bus | |
| the rated power of a wind farm | |
| the cut-in speed of a wind farm | |
| the rated speed of a wind farm | |
| the cut-out speed of a wind farm | |
| , , | coefficients of wind power output model |
| a multi-dimensional vector comprised of initial mean values of all clusters | |
| the pre-set number of clusters | |
| the mean value vector of cluster | |
| the mean value of variable in cluster | |
| the Euclidean distance from point to the mean of clusters | |
| a variable in | |
| the standardized vector corresponding to | |
| the standardized variable corresponding to | |
| the mean of | |
| the standard deviation of | |
| the correlation matrix of | |
| D | a diagonal matrix |
| a lower triangular matrix | |
| an uncorrelated vector | |
| the v-th order moment of a variable for cluster | |
| the v-th order cumulant of a variable for cluster | |
| a combination of elements from v − 1 different elements | |
| the v-th order moment of a system variable for the total samples | |
| the proportion of the number of elements in cluster to the total samples | |
| the v-th order cumulant of a system variable for the total samples | |
| the weighted average radius | |
| the radius of cluster | |
| a random variable | |
| the probability density function of | |
| the moment generating function of | |
| the cumulant generating function of | |
| the v-th order cumulant of | |
| a linear combination of independent variables | |
| the v-th order cumulant of |
Appendix A
References
- Momoh, J.A.; Koessler, R.J.; Bond, M.S.; Stott, B.; Sun, D.; Papalexopoulos, A.; Ristanovic, P. Challenges to optimal power flow. IEEE Trans. Power Syst. 1997, 12, 444–455. [Google Scholar] [CrossRef]
- Huneault, M.; Galiana, F.D. A survey of the optimal power flow literature. IEEE Trans. Power Syst. 1991, 6, 762–770. [Google Scholar] [CrossRef]
- Huang, C.M.; Kuo, C.J.; Huang, Y.C. Short-term wind power forecasting and uncertainty analysis using a hybrid intelligent method. IET Renew. Power Gener. 2017, 11, 678–687. [Google Scholar] [CrossRef]
- Ellis, A.; Schoenwald, D.; Hawkins, J.; Willard, S.; Arellano, B. PV output smoothing with energy storage. In Proceedings of the 2012 38th IEEE Photovoltaic Specialists Conference, Austin, TX, USA, 3–8 June 2012. [Google Scholar]
- Aien, M.; Rashidinejad, M.; Firuz-Abad, M.F. Probabilistic optimal power flow in correlated hybrid wind-PV power systems: A review and a new approach. Renew. Sustain. Energy Rev. 2015, 41, 1437–1446. [Google Scholar] [CrossRef]
- Prusty, B.R.; Jena, D. A critical review on probabilistic load flow studies in uncertainty constrained power systems with photovoltaic generation and a new approach. Renew. Sustain. Energy Rev. 2017, 69, 1286–1302. [Google Scholar] [CrossRef]
- Zhang, H.; Li, P. Probabilistic analysis for optimal power flow under uncertainty. IET Gener. Transm. Distrib. 2010, 4, 553–561. [Google Scholar] [CrossRef]
- Cao, J.; Yan, Z. Probabilistic optimal power flow considering dependences of wind speed among wind farms by pair-copula method. Int. J. Electr. Power 2017, 84, 296–307. [Google Scholar] [CrossRef]
- Rubinstein, R.Y.; Kroese, D.P. Simulation and the Monte Carlo Method, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Gentle, J.E. Random Number Generation and Monte Carlo Methods, 2nd ed.; Springer: New York, NY, USA, 2003. [Google Scholar]
- Huang, J.; Xue, Y.; Dong, Z.Y.; Wong, K.P. An adaptive importance sampling method for probabilistic optimal power flow. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–29 July 2011; pp. 1–6. [Google Scholar]
- Gang, L.; Jinfu, C.; Defu, C.; Dongyuan, S.; Xianzhong, D. Probabilistic assessment of available transfer capability considering spatial correlation in wind power integrated system. IET Gener. Transm. Distrib. 2013, 7, 1527–1535. [Google Scholar] [CrossRef]
- Yu, H.; Chung, C.Y.; Wong, K.P.; Lee, H.W.; Zhang, J.H. Probabilistic Load Flow Evaluation with Hybrid Latin Hypercube Sampling and Cholesky Decomposition. IEEE Trans. Power Syst. 2009, 24, 661–667. [Google Scholar] [CrossRef]
- Hajian, M.; Rosehart, W.D.; Zareipour, H. Probabilistic Power Flow by Monte Carlo Simulation with Latin Supercube Sampling. IEEE Trans. Power Syst. 2013, 28, 1550–1559. [Google Scholar] [CrossRef]
- Xie, Z.Q.; Ji, T.Y.; Li, M.S.; Wu, Q.H. Quasi-Monte Carlo Based Probabilistic Optimal Power Flow Considering the Correlation of Wind Speeds Using Copula Function. IEEE Trans. Power Syst. 2017, 1. [Google Scholar] [CrossRef]
- Zou, B.; Xiao, Q. Solving Probabilistic Optimal Power Flow Problem Using Quasi Monte Carlo Method and Ninth-Order Polynomial Normal Transformation. IEEE Trans. Power Syst. 2014, 29, 300–306. [Google Scholar] [CrossRef]
- Prasad, C.B.; Chintham, V. Probabilistic Optimal Power Flow with wind energy penetration and integration of storage system. In Proceedings of the 2015 Annual IEEE India Conference (INDICON), New Delhi, India, 17–20 December 2015; pp. 1–6. [Google Scholar]
- Verbic, G.; Canizares, C.A. Probabilistic Optimal Power Flow in Electricity Markets Based on a Two-Point Estimate Method. IEEE Trans. Power Syst. 2006, 21, 1883–1893. [Google Scholar] [CrossRef]
- Arabali, A.; Ghofrani, M.; Etezadi-Amoli, M. Cost analysis of a power system using probabilistic optimal power flow with energy storage integration and wind generation. Int. J. Electr. Power 2013, 53, 832–841. [Google Scholar] [CrossRef]
- Morales, J.M.; Perez-Ruiz, J. Point Estimate Schemes to Solve the Probabilistic Power Flow. IEEE Trans. Power Syst. 2007, 22, 1594–1601. [Google Scholar] [CrossRef]
- Sebastián, G.-C.J.; Alexander, C.-L.J.; Mauricio, G.-E. Stochastic AC Optimal Power Flow Considering the Probabilistic Behavior of the Wind, Loads and Line Parameters. Ing. Investig. Tecnol. 2014, 15, 529–538. [Google Scholar] [CrossRef]
- Li, X.; Cao, J.; Du, D. Probabilistic optimal power flow for power systems considering wind uncertainty and load correlation. Neurocomputing 2015, 148, 240–247. [Google Scholar] [CrossRef]
- Morales, J.M.; Baringo, L.; Conejo, A.J.; Minguez, R. Probabilistic power flow with correlated wind sources. IET Gener. Transm. Distrib. 2010, 4, 641–651. [Google Scholar] [CrossRef]
- Wang, X.; Gong, Y.; Jiang, C. Regional Carbon Emission Management Based on Probabilistic Power Flow with Correlated Stochastic Variables. IEEE Trans. Power Syst. 2015, 30, 1094–1103. [Google Scholar] [CrossRef]
- Li, Y.; Li, W.; Yan, W.; Yu, J.; Zhao, X. Probabilistic Optimal Power Flow Considering Correlations of Wind Speeds Following Different Distributions. IEEE Trans. Power Syst. 2014, 29, 1847–1854. [Google Scholar] [CrossRef]
- Shargh, S.; Khorshid ghazani, B.; Mohammadi-ivatloo, B.; Seyedi, H.; Abapour, M. Probabilistic multi-objective optimal power flow considering correlated wind power and load uncertainties. Renew. Energy 2016, 94, 10–21. [Google Scholar] [CrossRef]
- Xia, S.; Luo, X.; Chan, K.W.; Zhou, M.; Li, G. Probabilistic Transient Stability Constrained Optimal Power Flow for Power Systems with Multiple Correlated Uncertain Wind Generations. IEEE Trans. Sustain. Energy 2016, 7, 1133–1144. [Google Scholar] [CrossRef]
- Aien, M.; Fotuhi-Firuzabad, M.; Aminifar, F. Probabilistic Load Flow in Correlated Uncertain Environment Using Unscented Transformation. IEEE Trans. Power Syst. 2012, 27, 2233–2241. [Google Scholar] [CrossRef]
- Valverde, G.; Saric, A.T.; Terzija, V. Probabilistic load flow with non-gaussian correlated random variables using gaussian mixture models. IET Gener. Transm. Distrib. 2012, 6, 701–709. [Google Scholar] [CrossRef]
- Pei, Z.; Lee, S.T. Probabilistic load flow computation using the method of combined cumulants and Gram-Charlier expansion. IEEE Trans. Power Syst. 2004, 19, 676–682. [Google Scholar]
- Fan, M.; Vittal, V.; Heydt, G.T.; Ayyanar, R. Probabilistic Power Flow Studies for Transmission Systems with Photovoltaic Generation Using Cumulants. IEEE Trans. Power Syst. 2012, 27, 2251–2261. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhou, J.; Ju, P.; Feuchtwang, J. Probabilistic load flow computation of a power system containing wind farms using the method of combined cumulants and Gram-Charlier expansion. IET Renew. Power Gener. 2011, 5, 448–454. [Google Scholar] [CrossRef]
- Cai, D.; Chen, J.; Shi, D.; Duan, X.; Li, H.; Yao, M. Enhancements to the Cumulant Method for probabilistic load flow studies. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- Ran, X.; Miao, S. Three-phase probabilistic load flow for power system with correlated wind, photovoltaic and load. IET Gener. Transm. Distrib. 2016, 10, 3093–3101. [Google Scholar] [CrossRef]
- Prusty, B.R.; Jena, D. Combined cumulant and Gaussian mixture approximation for correlated probabilistic load flow studies: A new approach. CSEE J. Power Energy Syst. 2016, 2, 71–78. [Google Scholar] [CrossRef]
- Schellenberg, A.; Rosehart, W.; Aguado, J. Cumulant-based probabilistic optimal power flow (P-OPF) with Gaussian and gamma distributions. IEEE Trans. Power Syst. 2005, 20, 773–781. [Google Scholar] [CrossRef]
- Tamtum, A.; Schellenberg, A.; Rosehart, W.D. Enhancements to the Cumulant Method for Probabilistic Optimal Power Flow Studies. IEEE Trans. Power Syst. 2009, 24, 1739–1746. [Google Scholar] [CrossRef]
- Allan, R.N.; Silva, A.M.L.D.; Burchett, R.C. Evaluation Methods and Accuracy in Probabilistic Load Flow Solutions. IEEE Trans. Power Appl. Syst. 1981, PAS-100, 2539–2546. [Google Scholar] [CrossRef]
- Torres, G.L.; Quintana, V.H. Optimal power flow via interior point methods: An educational tool in Matlab. In Proceedings of the 1996 Canadian Conference on Electrical and Computer Engineering, Calgary, AB, Canada, 26–29 May 1996; Volume 2, pp. 996–999. [Google Scholar]
- Giorsetto, P.; Utsurogi, K.F. Development of a New Procedure for Reliability Modeling of Wind Turbine Generators. IEEE Trans. Power Appl. Syst. 1983, PAS-102, 134–143. [Google Scholar] [CrossRef]
- Qin, Z.; Li, W.; Xiong, X. Generation System Reliability Evaluation Incorporating Correlations of Wind Speeds with Different Distributions. IEEE Trans. Power Syst. 2013, 28, 551–558. [Google Scholar] [CrossRef]
- Usaola, J. Probabilistic load flow in systems with wind generation. IET Gener. Transm. Distrib. 2009, 3, 1031–1041. [Google Scholar] [CrossRef] [Green Version]
- Rajaraman, A.; Leskovec, J.; Ullman, J.D. Mining of Massive Datasets; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Liu, J.; Hao, X.; Cheng, P.; Fang, W.; Niu, S. A Parallel Probabilistic Load Flow Method Considering Nodal Correlations. Energies 2016, 9, 1041. [Google Scholar] [CrossRef]
- Papoulis, A.; Pillai, S.U. Probability, Random Variables, and Stochastic Processes, 4th ed.; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- MATPOWER. Available online: http://www.pserc.cornell.edu/matpower/ (accessed on 7 January 2017).
- Aien, M.; Fotuhi-Firuzabad, M.; Rashidinejad, M. Probabilistic Optimal Power Flow in Correlated Hybrid Wind-Photovoltaic Power Systems. IEEE Trans. Smart Grid 2014, 5, 130–138. [Google Scholar] [CrossRef]
- Masseran, N.; Razali, A.M.; Ibrahim, K. An analysis of wind power density derived from several wind speed density functions: The regional assessment on wind power in Malaysia. Renew. Sustain. Energy Rev. 2012, 16, 6476–6487. [Google Scholar] [CrossRef]

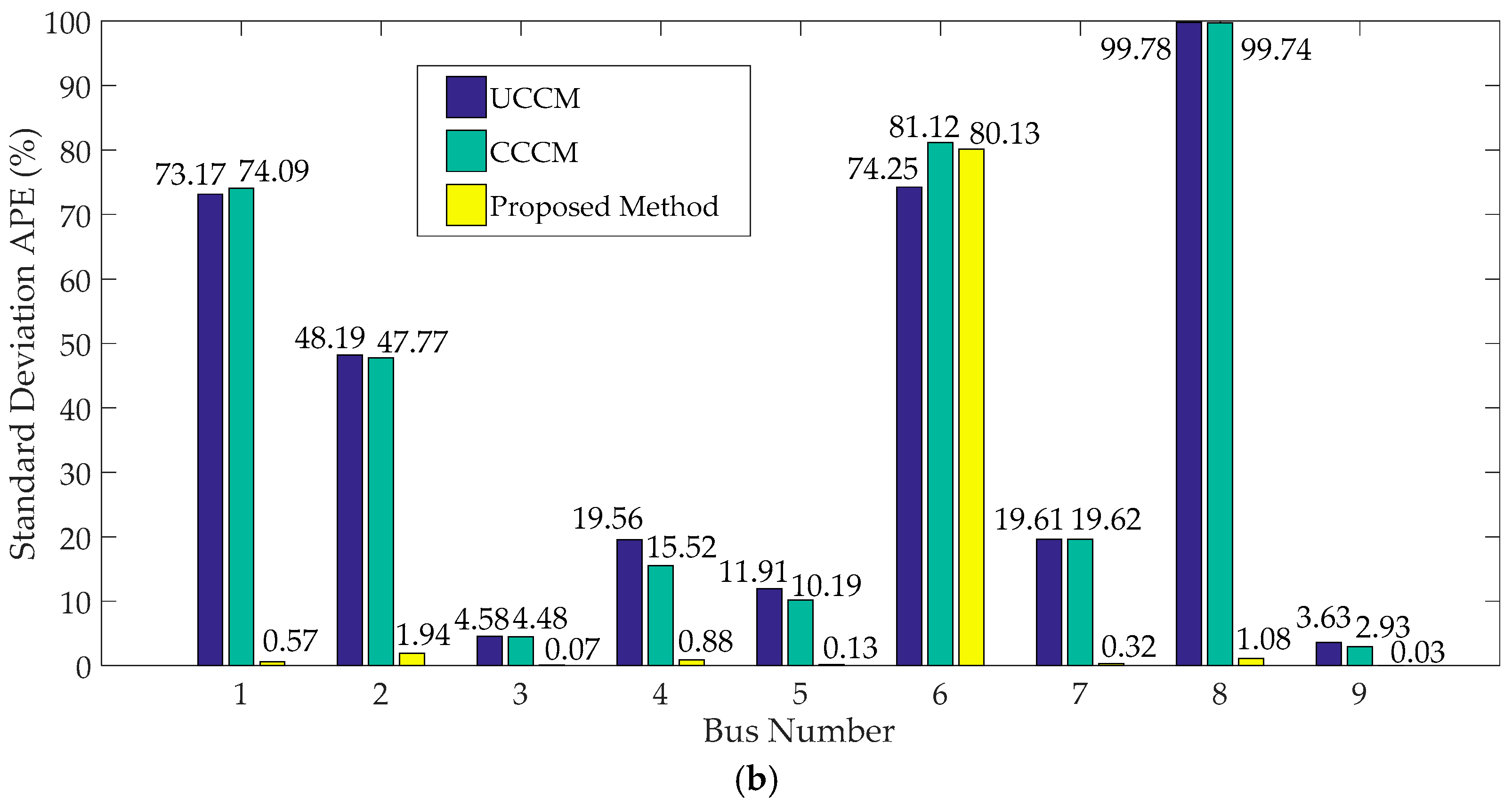


| Systems | Buses Connected with Wind Farms | Rated Capacities (MW) |
|---|---|---|
| IEEE 9-Bus Test System | 1, 3 | 60 |
| IEEE 118-Bus Test System | 59, 80, 90 | 250 |
| Wind Speed Distribution | Shape Parameter | Scale Parameter |
|---|---|---|
| W1 (Connected to Bus 1) | 1.732 | 6.611 |
| W2 (Connected to Bus 3) | 2.036 | 7.933 |
| Input Variable | |||
|---|---|---|---|
| Wind Power 1 (Connected to Bus 1) | 7.0850 | 10.9982 | 2.8596 |
| Wind Power 2 (Connected to Bus 3) | 7.2758 | 11.6619 | 3.6242 |
| Total System Load | 8.1510 | 14.3702 | 3.4837 |
| Algorithm | Mean | Mean APE | Standard Deviation | Standard Deviation APE |
|---|---|---|---|---|
| MCS | 4769.75 | \ | 992.97 | \ |
| UCCM | 4697.13 | 1.52% | 910.72 | 8.28% |
| CCCM | 4697.13 | 1.52% | 1022.13 | 2.94% |
| Proposed Method | 4765.08 | 0.10% | 994.90 | 0.19% |
| Algorithm | Time (s) |
|---|---|
| MCS | 1912.72 |
| UCCM | 4.21 |
| CCCM | 4.58 |
| Proposed Method | 6.27 |
| Wind Speed Distribution | Shape Parameter | Scale Parameter |
|---|---|---|
| W1 (Connected to Bus 59) | 1.732 | 6.611 |
| W2 (Connected to Bus 80) | 2.036 | 7.933 |
| W3 (Connected to Bus 90) | 1.350 | 5.774 |
| W1 | W2 | W3 | |
|---|---|---|---|
| W1 | 1.00 | 0.76 | 0.64 |
| W2 | 0.76 | 1.00 | 0.36 |
| W3 | 0.64 | 0.36 | 1.00 |
| Area | Bus Number |
|---|---|
| Area 1 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 113, 114, 115, 117 |
| Area 2 | 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 116 |
| Area 3 | 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 118 |
| Algorithm | Mean | Mean APE | Standard Deviation | Standard Deviation APE |
|---|---|---|---|---|
| MCS | 124,281.33 | \ | 11,864.39 | \ |
| UCCM | 124,093.19 | 0.15% | 10,969.98 | 7.54% |
| CCCM | 124,093.19 | 0.15% | 11,961.51 | 0.82% |
| Proposed Method | 124,244.89 | 0.03% | 11,884.53 | 0.17% |
| Algorithm | Time (s) |
|---|---|
| MCS | 6195.28 |
| UCCM | 13.24 |
| CCCM | 13.46 |
| Proposed Method | 171.48 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, X.; He, J.; Zhang, P. A Novel Probabilistic Optimal Power Flow Method to Handle Large Fluctuations of Stochastic Variables. Energies 2017, 10, 1623. https://doi.org/10.3390/en10101623
Deng X, He J, Zhang P. A Novel Probabilistic Optimal Power Flow Method to Handle Large Fluctuations of Stochastic Variables. Energies. 2017; 10(10):1623. https://doi.org/10.3390/en10101623
Chicago/Turabian StyleDeng, Xiaoyang, Jinghan He, and Pei Zhang. 2017. "A Novel Probabilistic Optimal Power Flow Method to Handle Large Fluctuations of Stochastic Variables" Energies 10, no. 10: 1623. https://doi.org/10.3390/en10101623





