Global Gust Climate Evaluation and Its Influence on Wind Turbines
Abstract
:1. Introduction
2. Material and Methods
2.1. Overview
2.2. Data
2.3. Distribution Fitting
2.4. Goodness-of-Fit Evaluation
2.5. Wakeby Distribution
2.6. Determination of Gust Characteristics
2.7. Calculation of Wind Turbine Gust Index
2.8. Determination of the Meteorological and Geographical Wind Energy Potential
3. Results and Discussion
3.1. Goodness-of-Fit Evaluation of Gust Speed Distributions
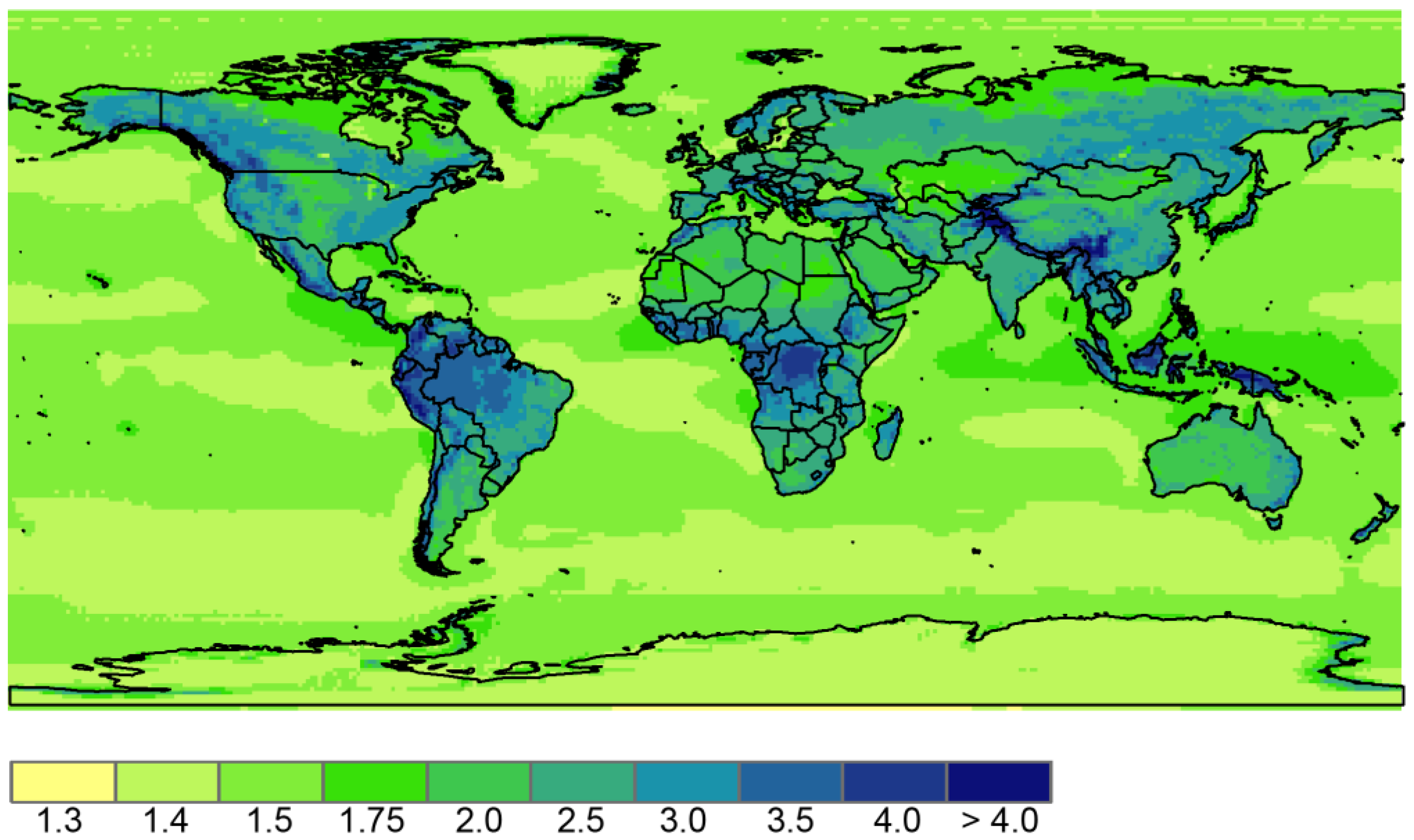
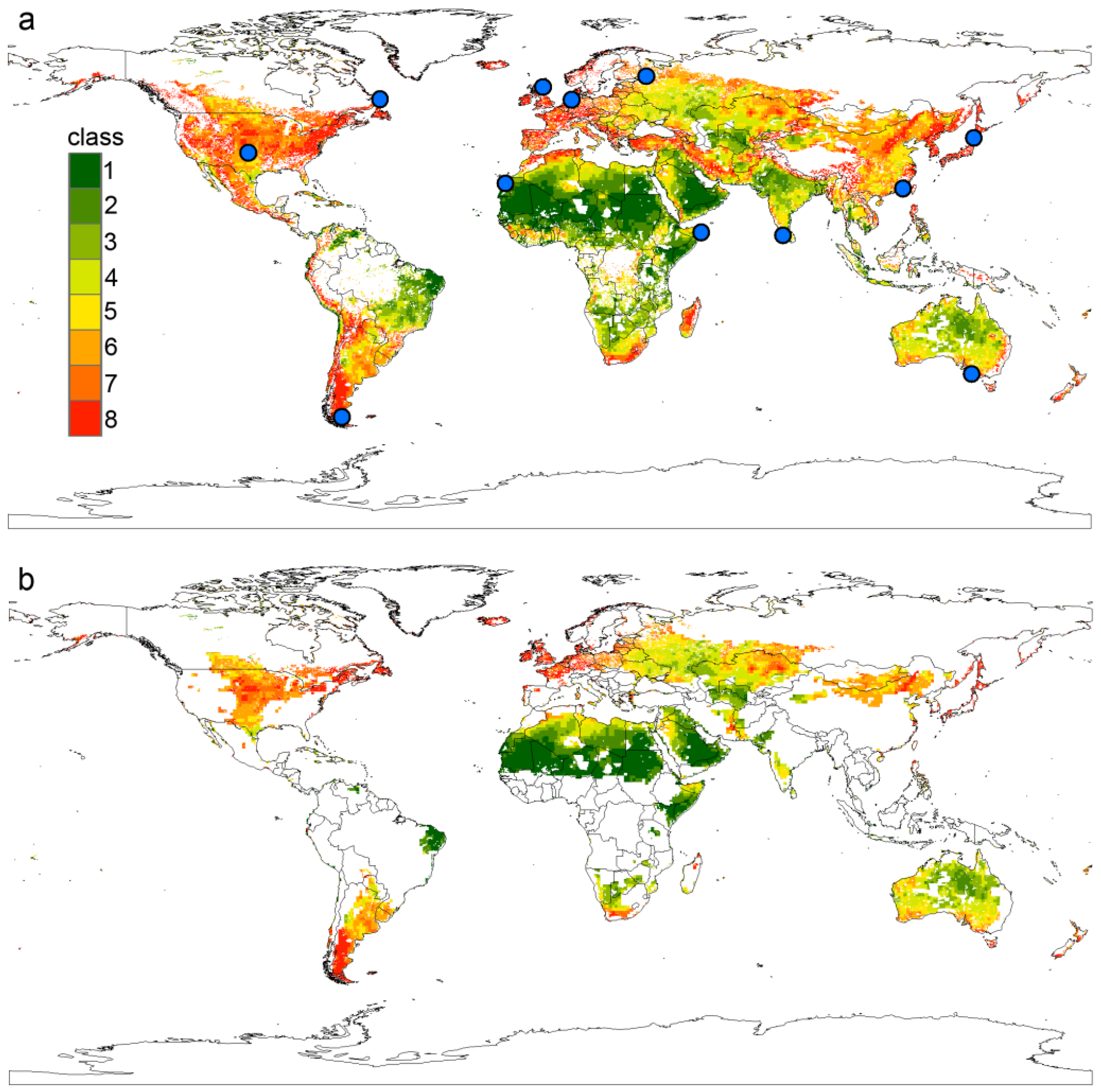
3.2. Gust Characteristics around the World
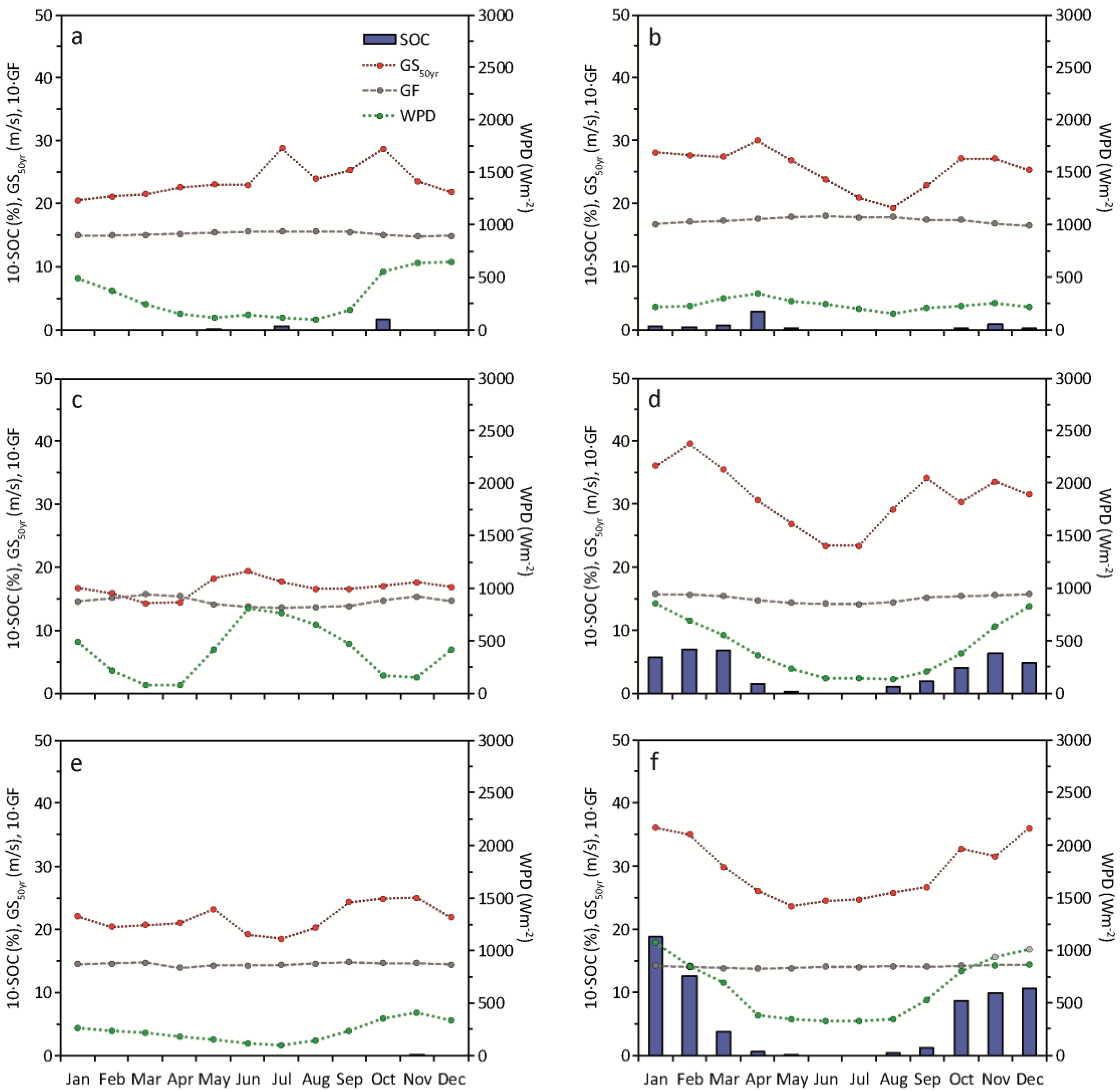
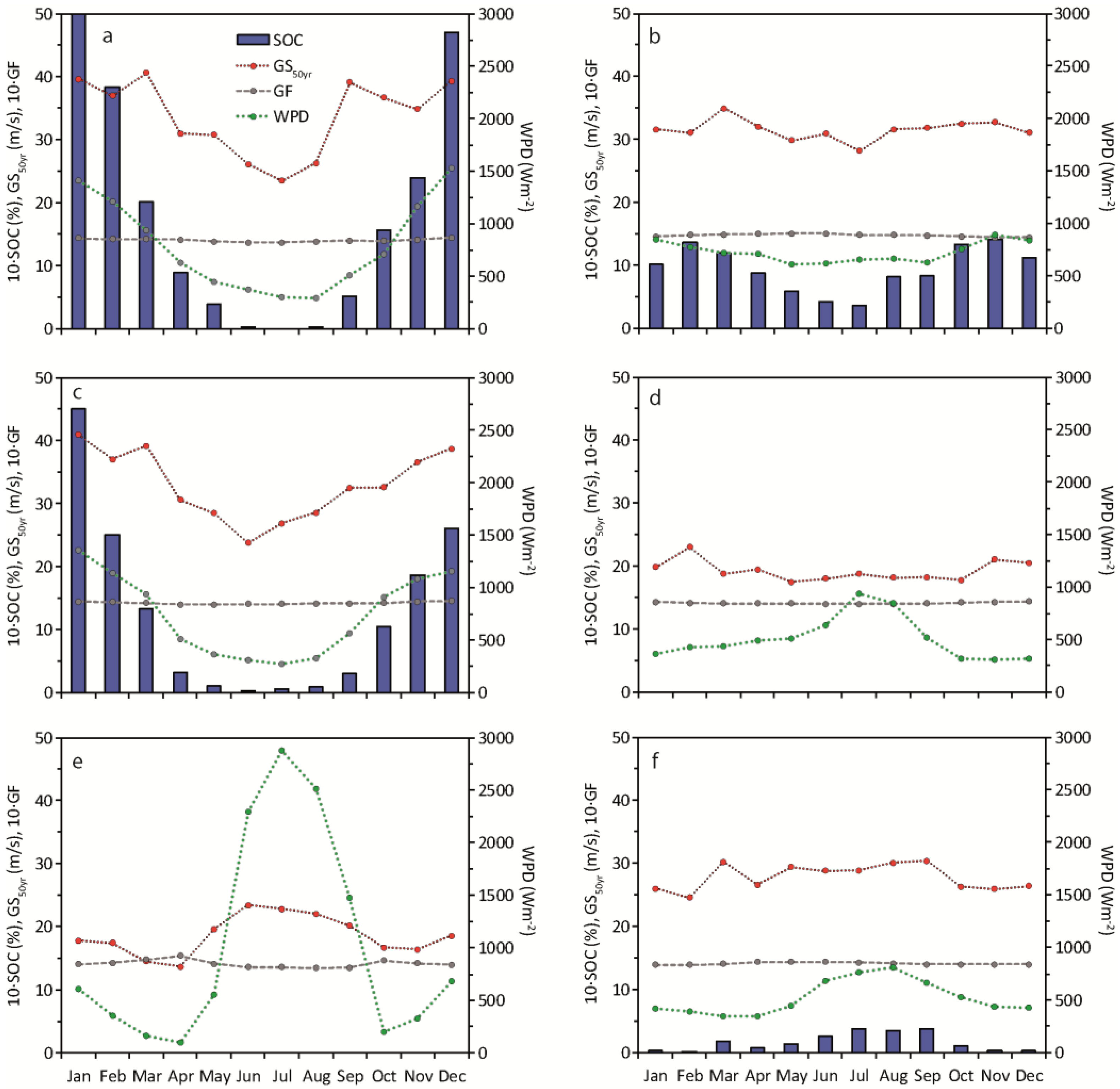
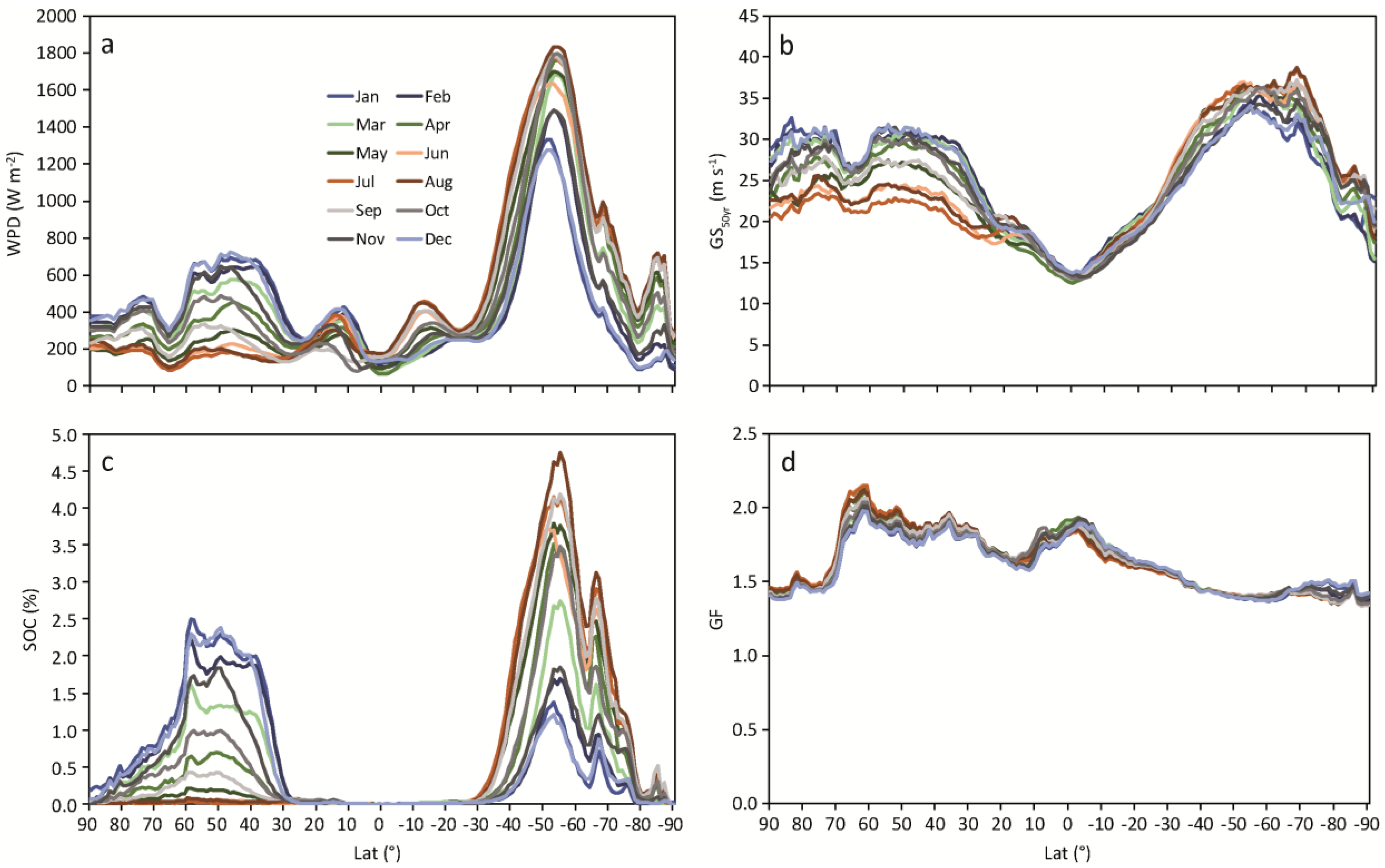
3.3. Monthly Gust Characteristics
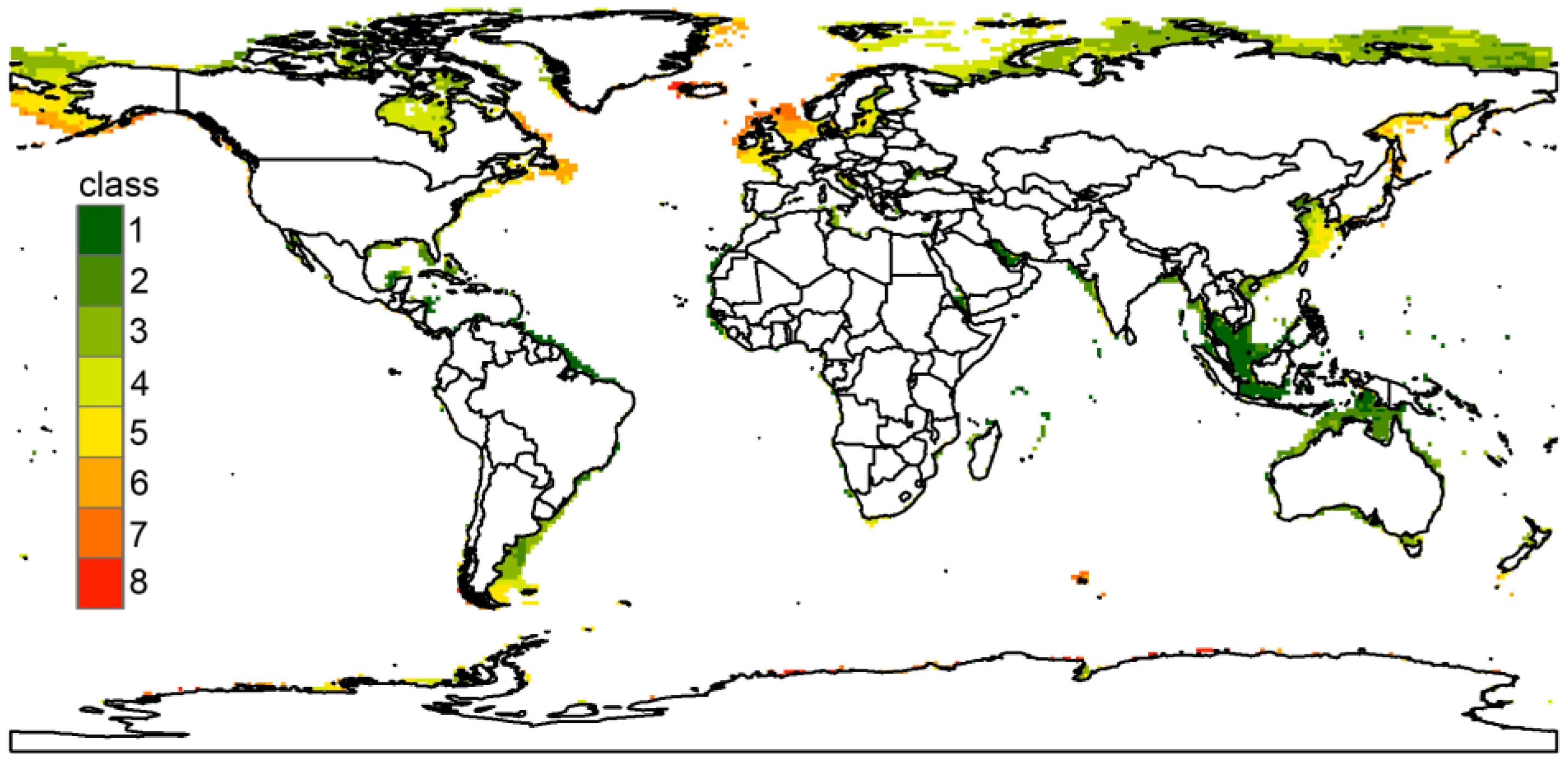
3.4. Wind Turbine Gust Index
4. Conclusions
Author Contributions
Conflicts of Interest
Nomenclature
| Acronyms | |
| cdf | cumulative distribution function |
| ecdf | empirical cumulative distribution function |
| epdf | empirical probability density function |
| G | two-parameter Gamma distribution |
| GEV | three-parameter Generalized Extreme Value distribution |
| GL | three-parameter Generalized Logistic distribution |
| GN | three-parameter Generalized Normal distribution |
| GoF | goodness-of-fit |
| GP | three-parameter Generalized Pareto distribution |
| Gu | two-parameter Gumbel distribution |
| K | four-parameter Kappa distribution |
| L | two-parameter Lognormal distribution |
| L3 | three-parameter Lognormal distribution |
| LM | L-moment method |
| M | Moment method |
| ML | Maximum Likelihood estimation |
| P3 | three-parameter Pearson 3 distribution |
| PEM | parameter estimation method |
| S | abbreviation |
| Wak | five-parameter Wakeby distribution |
| Wei | two-parameter Weibull distribution |
| Symbols | |
| estimated cumulative distribution function | |
| median gust factor | |
| mean wind power density | |
| AD | Anderson–Darling statistic |
| APR | atmospheric pressure |
| F | cumulative distribution function |
| F−1 | quantile function |
| GC | gust characteristic |
| GC′ | normalized gust characteristic |
| GF | gust factor |
| GS | gust speed |
| KS | Kolmogorov–Smirnov statistic |
| Lat | latitude |
| Lon | longitude |
| n | sample size |
| NP | number of parameters |
| R | atmospheric gas constant |
| RP | return period |
| SOC | percentage number of exceedances of cut-out speed |
| TA | air temperature |
| T | return period |
| u | zonal wind vector component |
| v | meridional wind vector component |
| WPD | wind power density |
| WTGI | wind turbine gust index |
| x | wind speed |
| α | first scale parameter |
| β | first shape parameter |
| γ | second scale parameter |
| δ | second shape parameter |
| ε | location parameters |
| air density | |
| Subscripts | |
| 100yr | 100-year return period |
| 30yr | 30-year return period |
| 50yr | 50-year return period |
| max | maximum |
| min | minimum |
| i | ith value of data sample |
| WAK | Wakeby distribution |
References
- Payne, J.E. A survey of the electricity consumption-growth literature. Appl. Energy 2010, 87, 723–731. [Google Scholar] [CrossRef]
- Panteli, M.; Mancarella, P. Influence of extreme weather and climate change on the resilience of power systems: Impacts and possible mitigation strategies. Electr. Power Syst. Res. 2015, 127, 259–270. [Google Scholar] [CrossRef]
- Campbell, R.J. Weather-Related Power Outages and Electric System Resiliency; Congressional Research Service: Washington, DC, USA, 2012.
- Cadini, F.; Agliardi, G.L.; Zio, E. A modeling and simulation framework for the reliability/availability assessment of a power transmission grid subject to cascading failures under extreme weather conditions. Appl. Energy 2017, 185, 267–279. [Google Scholar] [CrossRef]
- He, W.; Ge, S.S. Vibration control of a nonuniform wind turbine tower via disturbance observer. IEEE ASME Trans. Mechatron. 2015, 20, 237–244. [Google Scholar] [CrossRef]
- Durst, C.S. Wind speeds over short periods of time. Meteorol. Mag. 1960, 89, 181–186. [Google Scholar]
- Jung, C.; Schindler, D.; Albrecht, A.; Buchholz, A. The role of highly-resolved gust speed in simulations of storm damage in forests at the landscape scale: A case study from southwest Germany. Atmosphere 2016, 7, 7. [Google Scholar] [CrossRef]
- Wang, J.; Qin, S.; Jin, S.; Wu, J. Estimation methods review and analysis of offshore extreme wind speeds and wind energy resources. Renew. Sustain. Energy Rev. 2015, 42, 26–42. [Google Scholar] [CrossRef]
- Quaschning, V. Regenerative Energiesysteme. Technologie—Berechnung—Simulation, 9th ed.; Carl Hanser Verlag GmbH & Co.: München, Germany, 2011; ISBN 978-3-446-44267-2. [Google Scholar]
- Morgan, E.C.; Lackner, M.; Vogel, R.M.; Baise, L.G. Probability distributions for offshore wind speeds. Energy Convers. Manag. 2011, 52, 15–26. [Google Scholar] [CrossRef]
- Lydia, M.; Kumar, S.S.; Selvakumar, A.I.; Prem Kumar, G.E. A comprehensive review on wind turbine power curve modeling techniques. Renew. Sustain. Energy Rev. 2014, 30, 452–460. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application, 2nd ed.; John Wiley & Sons: Chichester, UK, 2009; ISBN 978-0470015001. [Google Scholar]
- Jung, C.; Schindler, D. Modelling monthly near-surface maximum daily gust speed distributions in Southwest Germany. Int. J. Climatol. 2016, 36, 4058–4070. [Google Scholar] [CrossRef]
- Haanpää, S.; Lehtonen, S.; Peltonen, L.; Talockaite, E. Impacts of Winter Storm Gudrun of 7th–9th January 2005 and Measures Taken in Baltic Sea Region. Available online: http://www.astra-project.org/06_winterstorm_study.html (accessed on 27 August 2017).
- Lee, B.-H.; Ahn, D.-J.; Kim, H.-G.; Ha, Y.-C. An estimation of the extreme wind speed using the Korea wind map. Renew. Energy 2012, 42, 4–10. [Google Scholar] [CrossRef]
- Chang, P.-C.; Yang, R.-Y.; Lai, C.-M. Potential of Offshore Wind Energy and Extreme Wind Speed Forecasting on the West Coast of Taiwan. Energies 2015, 8, 1685–1700. [Google Scholar] [CrossRef]
- Kang, D.; Ko, K.; Huh, J. Determination of extreme wind values using the Gumbel distribution. Energy 2015, 86, 51–58. [Google Scholar] [CrossRef]
- Pes, M.P.; Pereira, E.B.; Marengo, J.A.; Martins, F.R.; Heinemann, D.; Schmidt, M. Climate trends on the extreme winds in Brazil. Renew. Energy 2017, 109, 110–120. [Google Scholar] [CrossRef]
- Gong, K.; Ding, J.; Chen, X. Estimation of long-term extreme response of operational and parked wind turbines: Validation and some new insights. Eng. Struct. 2014, 81, 135–147. [Google Scholar] [CrossRef]
- Chiodo, E.; De Falco, P. Inverse Burr distribution for extreme wind speed prediction: Genesis, identification and estimation. Electr. Power Syst. Res. 2016, 141, 549–561. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- WMO Guide to Meteorological Instruments and Methods of Observations. Available online: https://library.wmo.int/opac/doc_num.php?explnum_id=3177 (accessed on 27 August 2017).
- Hellman, G. Über die Bewegung der Luft in den untersten Schichten der Atmosphäre. Meteorol. Z. 1915, 32, 1–16. (In German) [Google Scholar]
- Deacon, E.L. Gust variation with height up to 150 m. Q. J. R. Meteorol. Soc. 1955, 81, 562–573. [Google Scholar] [CrossRef]
- Grau, L.; Jung, C.; Schindler, D. On the annual cycle of meteorological and geographical potential of wind energy: A case study from Southwest Germany. Sustainability 2017, 9, 1169. [Google Scholar]
- Kim, J.-Y.; Kim, H.-G.; Kang, Y.-H. Offshore wind speed forecasting: The correlation between satellite-observed monthly sea surface temperature and wind speed over the seas around the Korean peninsula. Energies 2017, 10, 994. [Google Scholar]
- Cehak, K. Der Jahresgang der monatlichen höchsten Windgeschwindigkeiten in der Darstellung durch Fisher-Tippett III-Verteilungen. Arch. Meteorol. Geophys. Bioklimatol. 1971, 19, 165–182. (In German) [Google Scholar] [CrossRef]
- Friederichs, P.; Göber, M.; Bentzien, S.; Lenz, A.; Krampitz, R. A probabilistic analysis of wind gusts using extreme value statistics. Meteorol. Z. 2009, 18, 615–629. [Google Scholar] [CrossRef] [PubMed]
- Jung, C.; Schindler, D. Global comparison of the goodness-of-fit of wind speed distributions. Energy Convers. Manag. 2017, 133, 216–234. [Google Scholar] [CrossRef]
- Massey, F.J. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Anderson, T.W.; Darling, D.A. A test of goodness of fit. J. Am. Stat. Assoc. 1954, 49, 765–769. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D.; Laible, J.; Buchholz, A. Introducing a system of wind speed distributions for modeling properties of wind speed regimes around the world. Energy Convers. Manag. 2017, 144, 181–192. [Google Scholar] [CrossRef]
- Houghton, J.C. Birth of a parent: The Wakeby distribution for modeling flood flows. Water Resour. Res. 1978, 14, 1105–1109. [Google Scholar] [CrossRef]
- Jung, C. High spatial resolution simulation of annual wind energy yield using near-surface wind speed time series. Energies 2016, 9, 344. [Google Scholar] [CrossRef]
- Rahman, A.; Zaman, M.A.; Haddad, K.; El Adlouni, S.; Zhang, C. Applicability of Wakeby distribution in flood frequency analysis: a case study for eastern Australia. Hydrol. Process. 2015, 29, 602–614. [Google Scholar] [CrossRef]
- Hosking, J.; Wallis, J. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Schindler, D.; Jung, C.; Buchholz, A. Using highly resolved maximum gust speed as predictor for forest storm damage caused by the high-impact winter storm Lothar in Southwest Germany. Atmos. Sci. Lett. 2016, 17, 462–469. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D. Development of a statistical bivariate wind speed-wind shear model (WSWS) to quantify the height-dependent wind resource. Energy Convers. Manag. 2017, 149, 303–317. [Google Scholar] [CrossRef]
- Loveland, T.R.; Reed, B.C.; Brown, J.F.; Ohlen, D.O.; Zhu, Z.; Yang, L.; Merchant, J.W. Development of a global land cover characteristics database and IGBP DISCover from 1 km AVHRR data. Int. J. Remote Sens. 2000, 21, 1303–1330. [Google Scholar] [CrossRef]
- The World Database on Protected Areas (WDPA). Available online: https://www.iucn.org/theme/protected-areas/our-work/world-database-protected-areas (accessed on 3 August 2017).
- Danielson, J.J.; Gesch, D.B. Global Multi-Resolution Terrain Elevation Data 2010 (GMTED2010); Open-File Report 2011-1073; U.S. Geological Survey: Reston, VA, USA, 2011.
- Mentis, D.; Hermann, S.; Howells, M.; Welsch, M.; Siyal, S.H. Assessing the technical wind energy potential in Africa a GIS-based approach. Renew. Energy 2015, 83, 110–125. [Google Scholar] [CrossRef]
- Gruber, S. Derivation and analysis of a high-resolution estimate of global permafrost zonation. Cryosphere 2012, 6, 221–233. [Google Scholar] [CrossRef] [Green Version]
- Global Permafrost Zonation Index Map. Available online: http://www.geo.uzh.ch/microsite/cryodata/pf_global/ (accessed on 3 August 2017).
- Lu, X.; McElroy, M.B.; Kiviluoma, J. Global potential for wind-generated electricity. Proc. Natl. Acad. Sci. USA 2009, 106, 10933–10938. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wieringa, J. Roughness-dependent geographical interpolation of surface wind speed averages. Q. J. R. Met. Soc. 1986, 112, 867–889. [Google Scholar] [CrossRef]
- Global Carbon Atlas. Available online: http://www.globalcarbonatlas.org/en/CO2-emissions (accessed on 3 August 2017).

| Distribution | S | NP | PEM |
|---|---|---|---|
| Gamma | G | 2 | ML, LM |
| Gumbel | Gu | 2 | ML, LM |
| Lognormal | L | 2 | ML, M |
| Weibull | Wei | 2 | ML, M, LM |
| Gen. Extreme Value | GEV | 3 | ML, LM |
| Generalized Logistic | GL | 3 | LM |
| Gen. Normal | GN | 3 | LM |
| Gen. Pareto | GP | 3 | LM |
| Pearson 3 | P3 | 3 | LM |
| Lognormal | L3 | 3 | LM |
| Kappa | K | 4 | LM |
| Wakeby | Wak | 5 | LM |
| S | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Wak-LM | 66/42 | 66/42 | 66/43 | 67/43 | 67/44 | 66/43 | 67/44 | 67/44 | 66/43 | 66/43 | 67/44 | 67/43 |
| GL-LM | 30/11 | 32/11 | 33/11 | 32/11 | 33/12 | 31/11 | 34/12 | 33/11 | 33/11 | 32/12 | 34/12 | 34/11 |
| K-LM | 29/9 | 28/9 | 28/9 | 28/9 | 27/8 | 29/9 | 27/9 | 27/9 | 27/8 | 28/9 | 27/9 | 28/9 |
| GEV-LM | 24/4 | 24/4 | 26/5 | 25/4 | 24/4 | 25/5 | 24/4 | 25/4 | 24/4 | 25/4 | 26/4 | 25/4 |
| Wei-LM | 22/6 | 21/6 | 21/6 | 22/6 | 21/6 | 22/6 | 21/6 | 21/6 | 22/6 | 21/6 | 21/6 | 21/6 |
| GN-LM | 14/1 | 17/2 | 17/2 | 17/2 | 17/2 | 18/2 | 18/2 | 17/2 | 18/2 | 17/2 | 17/2 | 17/2 |
| GP-LM | 15/5 | 13/4 | 13/4 | 14/4 | 13/4 | 14/4 | 13/4 | 13/4 | 13/4 | 13/4 | 12/4 | 13/4 |
| L3-LM | 15/2 | 13/1 | 13/1 | 12/1 | 13/1 | 13/1 | 13/1 | 13/1 | 13/1 | 13/1 | 12/1 | 12/1 |
| L-ML | 12/2 | 12/2 | 11/2 | 13/2 | 12/2 | 12/2 | 12/2 | 12/2 | 12/2 | 13/2 | 12/2 | 12/2 |
| GEV-ML | 12/3 | 12/3 | 12/3 | 11/3 | 12/3 | 11/3 | 12/3 | 12/3 | 12/3 | 12/3 | 12/3 | 12/3 |
| Gu-ML | 12/4 | 11/3 | 11/3 | 11/3 | 11/3 | 10/3 | 10/3 | 11/3 | 11/3 | 10/3 | 11/3 | 11/3 |
| P3-LM | 10/2 | 11/2 | 11/2 | 10/2 | 10/2 | 10/2 | 10/2 | 10/2 | 11/3 | 10/2 | 10/2 | 10/2 |
| L-M | 10/2 | 10/3 | 9/2 | 10/2 | 10/2 | 10/2 | 10/2 | 10/2 | 10/2 | 10/2 | 10/2 | 10/2 |
| G-LM | 9/2 | 9/2 | 9/2 | 10/2 | 10/2 | 9/2 | 9/2 | 9/2 | 9/2 | 10/2 | 10/2 | 9/2 |
| Gu-LM | 10/2 | 10/3 | 10/2 | 9/2 | 9/2 | 8/2 | 9/2 | 9/2 | 9/2 | 8/2 | 9/2 | 9/2 |
| G-ML | 7/1 | 7/1 | 6/1 | 7/1 | 7/1 | 7/1 | 7/1 | 7/1 | 7/1 | 7/1 | 8/1 | 7/1 |
| Wei-M | 2/0 | 2/0 | 1/0 | 2/0 | 2/0 | 2/0 | 2/0 | 2/0 | 2/0 | 2/1 | 2/0 | 2/0 |
| Wei-ML | 2/0 | 2/0 | 1/0 | 1/0 | 2/0 | 2/0 | 2/0 | 2/0 | 2/0 | 1/0 | 2/0 | 2/0 |
| S | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Wak-LM | 61/49 | 62/50 | 62/50 | 62/38 | 64/52 | 62/50 | 62/51 | 62/50 | 62/51 | 63/50 | 62/51 | 63/50 |
| GL-LM | 38/12 | 40/12 | 42/13 | 39/7 | 40/12 | 39/12 | 42/13 | 42/13 | 41/13 | 40/13 | 43/14 | 42/13 |
| GEV-LM | 34/6 | 36/6 | 35/6 | 33/5 | 34/5 | 36/6 | 34/6 | 35/6 | 36/6 | 34/5 | 34/5 | 35/5 |
| K-LM | 32/13 | 31/14 | 31/13 | 55/37 | 30/13 | 32/14 | 30/13 | 30/13 | 29/12 | 31/13 | 30/12 | 31/13 |
| Wei-LM | 32/8 | 30/8 | 29/7 | 31/8 | 31/8 | 33/8 | 31/8 | 30/8 | 30/7 | 31/8 | 30/7 | 30/8 |
| GN-LM | 33/3 | 31/3 | 30/3 | 23/1 | 31/3 | 31/3 | 32/3 | 30/3 | 31/3 | 31/3 | 31/3 | 30/3 |
| L3-LM | 19/2 | 20/2 | 21/2 | 16/1 | 20/2 | 20/2 | 20/2 | 21/2 | 20/2 | 21/2 | 20/2 | 20/2 |
| P3-LM | 18/3 | 17/2 | 16/3 | 15/2 | 16/2 | 16/2 | 16/2 | 16/2 | 16/2 | 17/3 | 15/2 | 16/2 |
| GEV-ML | 10/1 | 10/1 | 11/1 | 7/0 | 9/1 | 9/1 | 9/1 | 10/1 | 10/1 | 9/1 | 10/1 | 11/1 |
| Gu-ML | 5/1 | 4/1 | 5/1 | 4/1 | 4/1 | 4/1 | 4/1 | 5/1 | 4/1 | 4/1 | 4/1 | 5/1 |
| Gu-LM | 4/0 | 4/0 | 5/0 | 4/0 | 4/0 | 4/0 | 4/0 | 5/0 | 5/0 | 4/0 | 4/0 | 4/0 |
| L-ML | 4/0 | 4/0 | 4/0 | 4/0 | 4/0 | 4/0 | 4/0 | 4/0 | 2/0 | 4/0 | 4/0 | 4/0 |
| G-LM | 3/0 | 3/0 | 3/0 | 3/0 | 4/0 | 3/0 | 3/0 | 3/0 | 3/0 | 3/0 | 3/0 | 3/0 |
| G-ML | 2/0 | 2/0 | 2/0 | 2/0 | 4/0 | 2/0 | 2/0 | 2/0 | 2/0 | 2/0 | 2/0 | 2/0 |
| L-M | 2/0 | 2/0 | 2/0 | 1/0 | 4/0 | 2/0 | 2/0 | 2/0 | 2/0 | 2/0 | 2/0 | 2/0 |
| GP-LM | 2/1 | 2/1 | 2/0 | 2/1 | 2/1 | 2/1 | 2/1 | 2/1 | 2/1 | 2/1 | 2/1 | 2/1 |
| Wei-ML | 1/0 | 1/0 | 1/0 | 1/0 | 1/0 | 1/0 | 1/0 | 1/0 | 1/0 | 1/0 | 1/0 | 1/0 |
| Wei-M | 1/0 | 1/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 1/0 | 1/0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, C.; Schindler, D.; Buchholz, A.; Laible, J. Global Gust Climate Evaluation and Its Influence on Wind Turbines. Energies 2017, 10, 1474. https://doi.org/10.3390/en10101474
Jung C, Schindler D, Buchholz A, Laible J. Global Gust Climate Evaluation and Its Influence on Wind Turbines. Energies. 2017; 10(10):1474. https://doi.org/10.3390/en10101474
Chicago/Turabian StyleJung, Christopher, Dirk Schindler, Alexander Buchholz, and Jessica Laible. 2017. "Global Gust Climate Evaluation and Its Influence on Wind Turbines" Energies 10, no. 10: 1474. https://doi.org/10.3390/en10101474
APA StyleJung, C., Schindler, D., Buchholz, A., & Laible, J. (2017). Global Gust Climate Evaluation and Its Influence on Wind Turbines. Energies, 10(10), 1474. https://doi.org/10.3390/en10101474





