EyeMMV Toolbox: An Eye Movement Post-Analysis Tool Based on a Two-Step Spatial Dispersion Threshold for Fixation Identification
Abstract
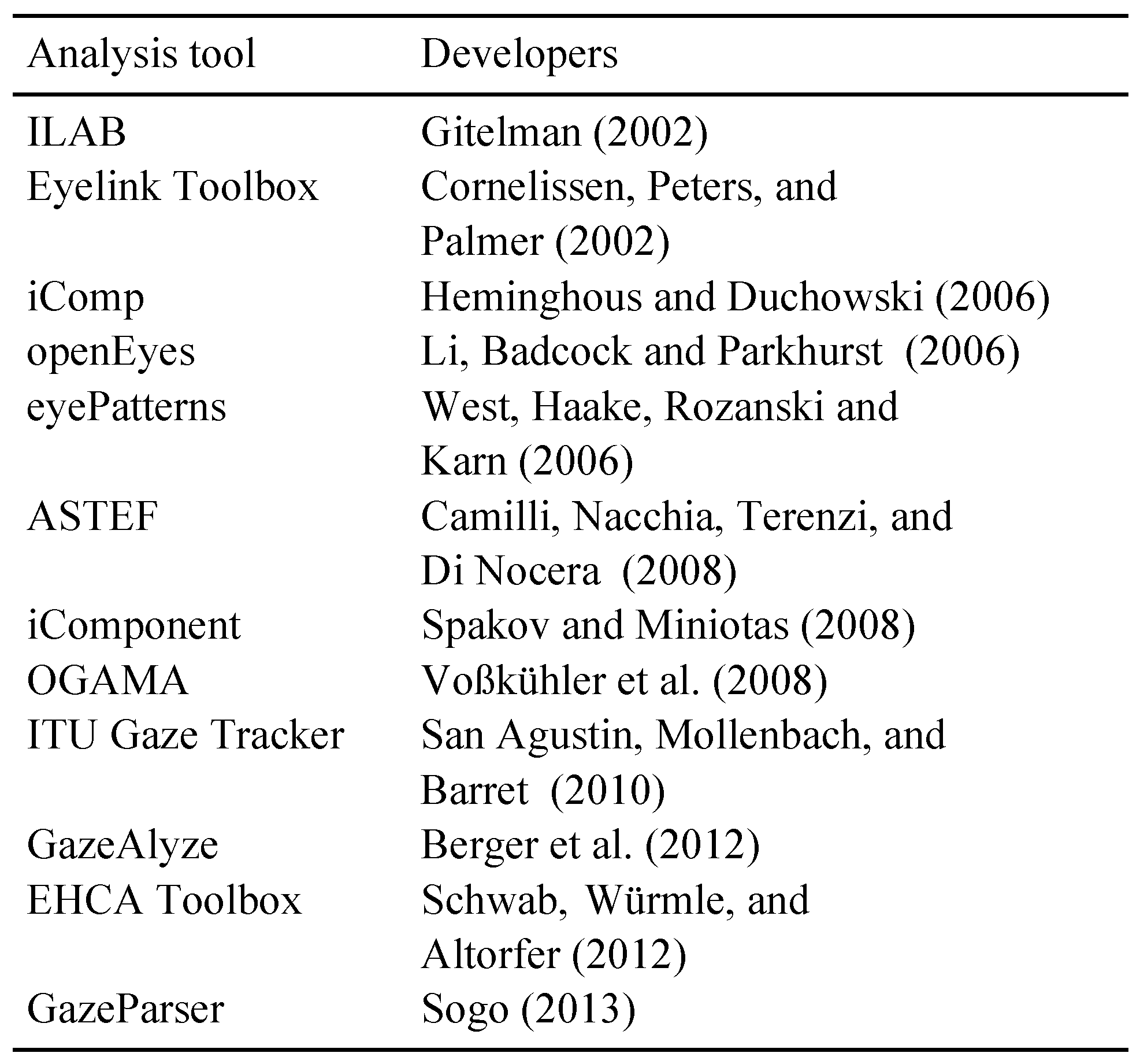
:Introduction
Methods
Fixation Identification Algorithm
Metrics analysis and Visualizations
Toolbox Execution
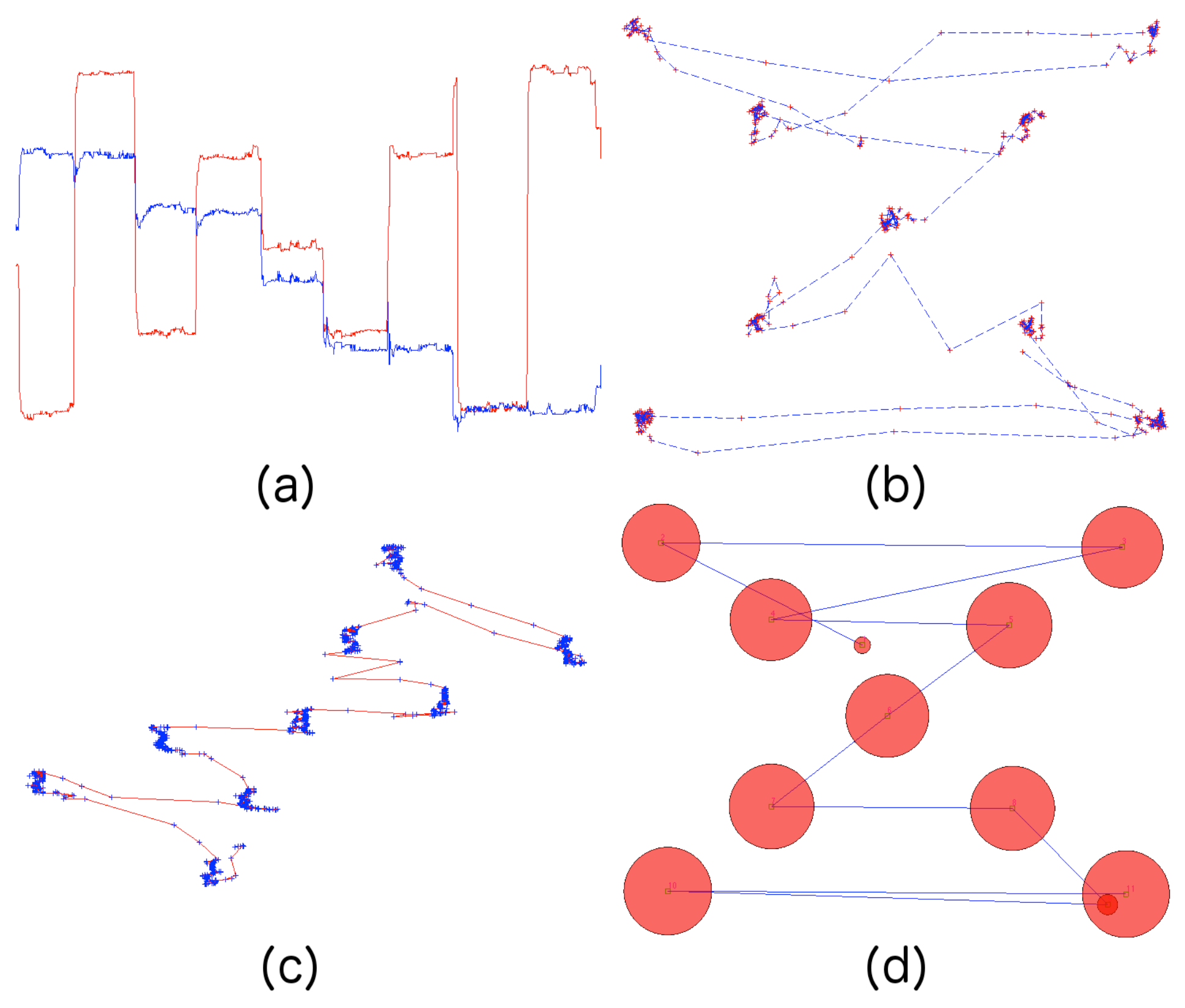
Case Study
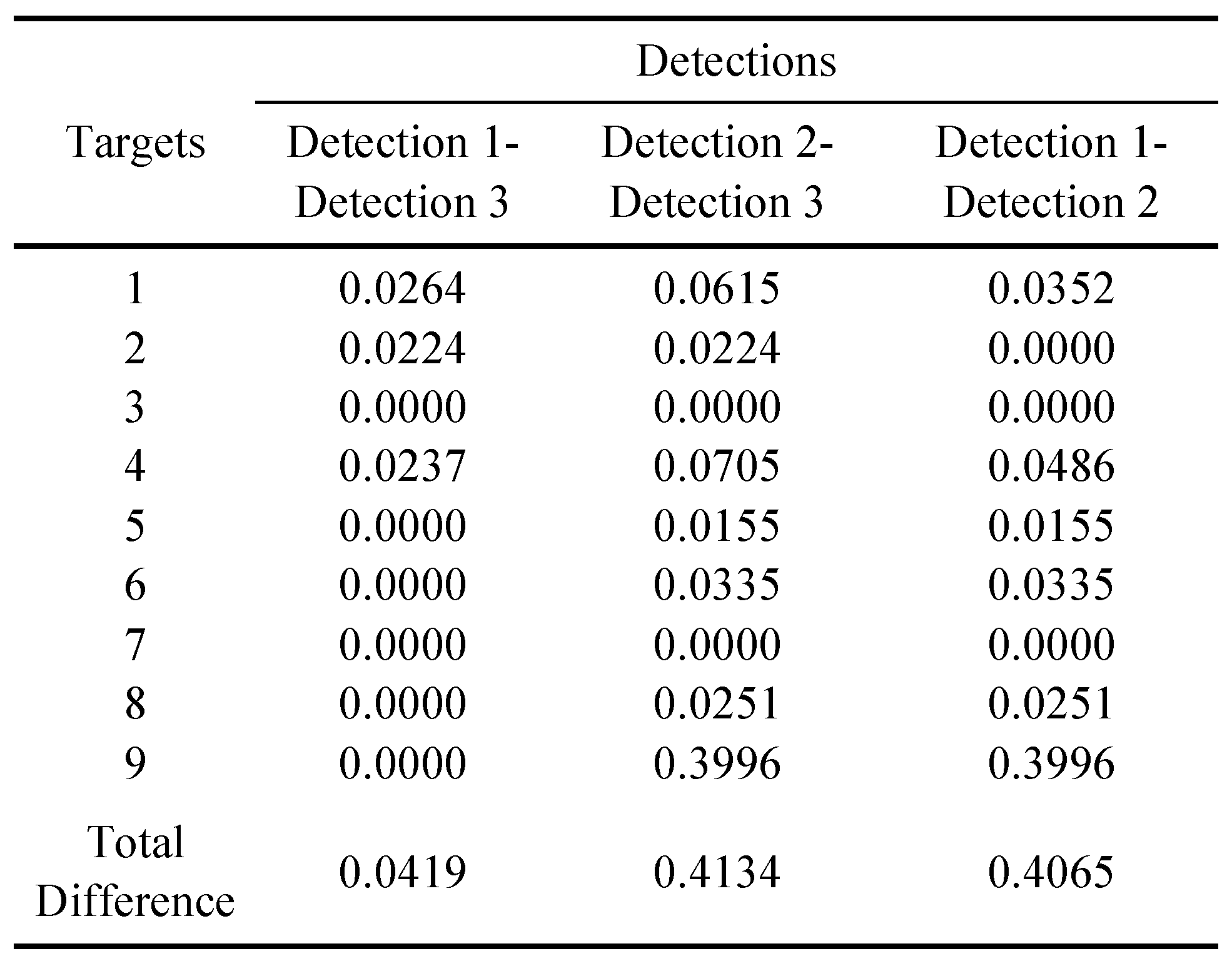
Results
Discussion
Conclusion
Appendix A
 |
References
- Andersson, R., M. Nyström, and K. Holmqvist. 2010. Sampling frequency and eye-tracking measures: how speed affects durations, latencies, and more. Journal of Eye Movement Research 3, 3 6. : 1–12. [Google Scholar] [CrossRef]
- Blignaut, P. 2009. Fixation identification: The optimum threshold for dispersion algorithm. Attention, Perception, & Psychophysics 71, 4: 881–895. [Google Scholar]
- Berger, C., M. Winkels, A. Lischke, and J. Hoppner. 2012. GazeAlyze: a MATLAB toolbox for the analysis of eye movement data. Behavior Research Methods 44: 404–419. [Google Scholar] [CrossRef] [PubMed]
- Bojko, A. 2009. Edited by J.A. Jacko. Informative or Misleading? Heatmaps Deconstruction. In Human-Computer Interaction. Berlin: Springer-Verlag, pp. 30–39. [Google Scholar]
- Camilli, M., R. Nacchia, M. Terenzi, and F. Di Nocera. 2008. ASTEF: A simple tool for examining fixations. Behavior Researcher Methods 40, 2: 373–382. [Google Scholar] [CrossRef] [PubMed]
- Cornelissen, F. W., E. M. Peters, and J. Palmer. 2002. The Eyelink Toolbox: Eye tracking with MATLAB and the Psychophysics Toolbox. Behavior Research Methods, Instruments, & Computers 34, 4: 613–617. [Google Scholar]
- Duchowski, A. T. 2002. A breath-first survey of eye-tracking applications. Behavior Research Methods, Instruments & Computers 34, 4: 455–470. [Google Scholar]
- Duchowski, A.T. 2007. Eye Tracking Methodology: Theory & Practice, 2nd ed. London: Springer-Verlag. [Google Scholar]
- Gitelman, D. R. 2002. ILAB: A program for postexperimental eye movement analysis. Behavior Research Methods, Instruments, & Computers 34, 4: 605–612. [Google Scholar]
- Goldberg, J. H., and X. P. Kotval. 1999. Computer interface evaluation using eye movements: methods and constructs. International Journal of Industrial Ergonomics 24: 631–645. [Google Scholar] [CrossRef]
- Heminghous, J., and A.T. Duchowski. 2006. iComp: A tool for scanpath visualization and comparison. In Proceedings of the 3rd Symposium on Applied Perception in Graphics and Visualization; pp. 152–152. [Google Scholar]
- Holmqvist, K., M. Nyström, R. Andersson, R. Dewhurst, H. Jarodzka, and J. Van de Weijer. 2011. Eye tracking: A comprehensive guide to methods and measures. Oxford: Oxford University Press. [Google Scholar]
- Jacob, R. J. K., and K. S. Karn. 2003. Edited by Radach Hyona and Deubel. Eye Tracking in Human-Computer Interaction and Usability Research: Ready to Deliver the Promises. In The Mind’s Eyes: Cognitive and Applied Aspects of Eye Movements. Oxford: Elsevier Science, pp. 573–605. [Google Scholar]
- Krassanakis, V., V. Filippakopoulou, and B. Nakos. 2011. An Application of Eye Tracking Methodology in Cartographic Research. In Proceedings of the Eye-TrackBehavior2011(Tobii). [Google Scholar]
- Lankford, C. 2000. GazeTrackerTM: Software designed to facilitate eye movement analysis. In Proceedings of the 2000 symposium on Eye Tracking research & applications; pp. 51–55. [Google Scholar]
- Li, D., J. Badcock, and D. J. Parkhurst. 2006. openEyes: a low-cost head-mounted eye-tracking solution. In Proceedings of the 2006 symposium on Eye Tracking research & applications; pp. 95–100. [Google Scholar]
- Li, X., A. Çöltiken, and M. J. Kraak. 2010. Edited by Fabrik and et al. Visual exploration of eye movement data using the Space-Time-Cube. In Geographic Information Science. Berlin: Spinger-Verlag: pp. 295–309. [Google Scholar]
- Martinez-Conde, S., S. L. Macknik, and D. H. Hubel. 2004. The role of fixational eye movements in visual perception. Nature Reviews Neuroscience 5, 3: 229–240. [Google Scholar] [CrossRef] [PubMed]
- Nyström, M., and K. Holmqvist. 2010. An adaptive algorithm for fixation, saccade, and glissade detection in eyetracking data. Behavior Research Methods 42, 1: 188–204. [Google Scholar] [CrossRef] [PubMed]
- Poole, A., and L. J. Ball. 2005. Edited by C. Ghaoui. Eye Tracking in Human-Computer Interaction and Usability Research: Current Status and Future Prospects. In Encyclopedia of human computer interaction. Pennsylvania: Idea Group, pp. 211–219. [Google Scholar]
- Richardson, D. C. 2004. Edited by G. Wnek and G. Bowlin. Eye tracking: Research areas and applications. In Encyclopedia of biomaterials and biomedical engineering. New York: Marcel Dekker, pp. 573–582. [Google Scholar]
- Salvucci, D. D. 2000. An interactive model-based environment for eye-movement protocol analysis and visualization. In Proceedings of the Symposium on Eye Tracking Research and Applications; pp. 57–63. [Google Scholar]
- Salvucci, D. D., and J. H. Goldberg. 2000. Identifying Fixations and Saccades in Eye-Tracking Protocols. In Proceedings of the Symposium on Eye Tracking Research and Applications; pp. 71–78. [Google Scholar]
- San Agustin, J., E. Mollenbach, and M. Barret. 2010. Evaluation of a Low-Cost Open-source Gaze Tracker. In Proceedings of the 2010 symposium on Eye Tracking research & applications; pp. 77–80. [Google Scholar]
- Schwab, S., O. Würmle, and A. Altorfer. 2012. Analysis of eye and head coordination in a visual peripheral recognition task. Journal of Eye Movement Research 5, 2 3. : 1–9. [Google Scholar] [CrossRef]
- Sogo, H. 2013. GazeParser: an open-source and multi platform library for low-cost eye tracking and analsysis. Behavior Research Methods 45, 3: 684–695. [Google Scholar] [CrossRef] [PubMed]
- Spakov, O., and D. Miniotas. 2008. iComponent: software with flexible architecture for developing plug-in modules for eye trackers. Information Technology and Control 37, 1: 26–32. [Google Scholar]
- Shic, F., B. Scassellati, and K. Chawarska. 2008. The Incomplete Fixation Measure. In Proceedings of the Symposium on Eye Tracking Research and Applications; pp. 111–114. [Google Scholar]
- Tsang, H. Y., M. Tory, and C. Swindells. 2010. eSeeTrack-Visualizing Sequential Fixation Patters. IEEE Transactions on Visualization and Computer Graphics 16, 6: 953–962. [Google Scholar] [CrossRef] [PubMed]
- Voßkühler, A., V. Nordmeier, L. Kuchinke, and A. M. Jacobs. 2008. OGAMA (Open Gaze and Mouse Analyzer): Open-source software designed to analyze eye and mouse movements in slideshow study designs. Behavior Researcher Methods 40, 4: 1150–1162. [Google Scholar] [CrossRef] [PubMed]
- West, J. M., A. R. Haake, P. Rozanski, and K. S. Karn. 2006. eyePatterns: Software for Identifying Patterns and Similarities Across Fixation Sequences. In Proceedings of the 2006 symposium on Eye Tracking research & applications; pp. 149–154. [Google Scholar]




 |
 |
Copyright © 2014. This article is licensed under a Creative Commons Attribution 4.0 International License.
Share and Cite
Krassanakis, V.; Filippakopoulou, V.; Nakos, B. EyeMMV Toolbox: An Eye Movement Post-Analysis Tool Based on a Two-Step Spatial Dispersion Threshold for Fixation Identification. J. Eye Mov. Res. 2014, 7, 1-10. https://doi.org/10.16910/jemr.7.1.1
Krassanakis V, Filippakopoulou V, Nakos B. EyeMMV Toolbox: An Eye Movement Post-Analysis Tool Based on a Two-Step Spatial Dispersion Threshold for Fixation Identification. Journal of Eye Movement Research. 2014; 7(1):1-10. https://doi.org/10.16910/jemr.7.1.1
Chicago/Turabian StyleKrassanakis, Vassilios, Vassiliki Filippakopoulou, and Byron Nakos. 2014. "EyeMMV Toolbox: An Eye Movement Post-Analysis Tool Based on a Two-Step Spatial Dispersion Threshold for Fixation Identification" Journal of Eye Movement Research 7, no. 1: 1-10. https://doi.org/10.16910/jemr.7.1.1
APA StyleKrassanakis, V., Filippakopoulou, V., & Nakos, B. (2014). EyeMMV Toolbox: An Eye Movement Post-Analysis Tool Based on a Two-Step Spatial Dispersion Threshold for Fixation Identification. Journal of Eye Movement Research, 7(1), 1-10. https://doi.org/10.16910/jemr.7.1.1



