Evidence Supporting Open-Loop Control During Early Vergence

Abstract

Disparity vergence eye movements were analyzed to determine if the early component of this response operates under open-loop, or preprogrammed, control. The analysis compares ratios of peak velocity to response amplitude (i.e., main sequence ratios) for the isolated early component and for the entire disparity vergence response. The stimuli were limited a 4 deg step changes in vergence so that any differences in movement dynamics (i.e., peak velocities) were due only to internal noise. Nine binocularly normal subjects were studied. A significant correlation between peak velocity and amplitude was observed during the early portion of the movement (p < 0.002), but not for the overall vergence response. Results support the widely held, but unproven assumption that the early component of symmetrical vergence is guided by open-loop, or preprogrammed, control processes while the overall response is influenced by external and/or internal feedback

Introduction

Eye movement neural control processes are faced with two major challenges: the need for a quick response despite substantial processing delays, and the need to attain accurate positioning despite errors inherent in the neural and muscular apparatus. Unfortunately, these two challenges are best met with different control strategies: feedback can produce extremely accurate responses, but for stability, response velocity must be reduced when delays are present in the feedback loop. Conversely, open-loop (i.e., preprogrammed) control can generate rapid responses, even in systems with long delays, but these responses provide limited accuracy. Both version and vergence control systems achieve speed and accuracy by combining the two strategies. In version, the two control strategies manifest as separate movements: preprogrammed saccades and feedback controlled pursuit movements. In vergence, the two control components are less obvious as they merge into a single coordinated response. Nonetheless, considerable evidence supports a “dual mode” control strategy (Semmlow et al., 1986; Hung et al., 1986) that consists of: a sustained component that is driven by visual and internal feedback to slowly bring the response to the final position, and an open-loop pulse-like component that enhances early movement dynamics. (We favor the term “dual-mode” to describe this general configuration rather than “pulsestep” to emphasize the difference in control strategies: open-loop versus feedback.)

The neural structures behind these eye movement control components were originally inferred from behavioral data (Jones, 1980; Semmlow et al., 1986; Semmlow et al., 1993; Semmlow et al., 1994; Horng et al, 1998; Alvarez et al. 1998; Lee et al. 2008), but have also been identified in neurophysiological studies (Mays, 1984; Mays et al., 1986). For example, patients with cerebellar stroke especially with lesions localized to the cerebellar vermis can respond to symmetrical vergence step stimuli but cannot fuse slowly moving vergence ramp or sinusoidal stimuli (Sander, et al. 2009). Conversely, patients with lesions to the pontine region show preservation of responses to symmetrical vergence ramps and sinusoids, but impaired initiation of symmetrical vergence step responses (Rambold et al. 2005) ) These clinical findings support dual control of vergence suggesting different neural substrates are responsible to program step (preprogrammed) and smoothly tracking (feedback controlled) movements. 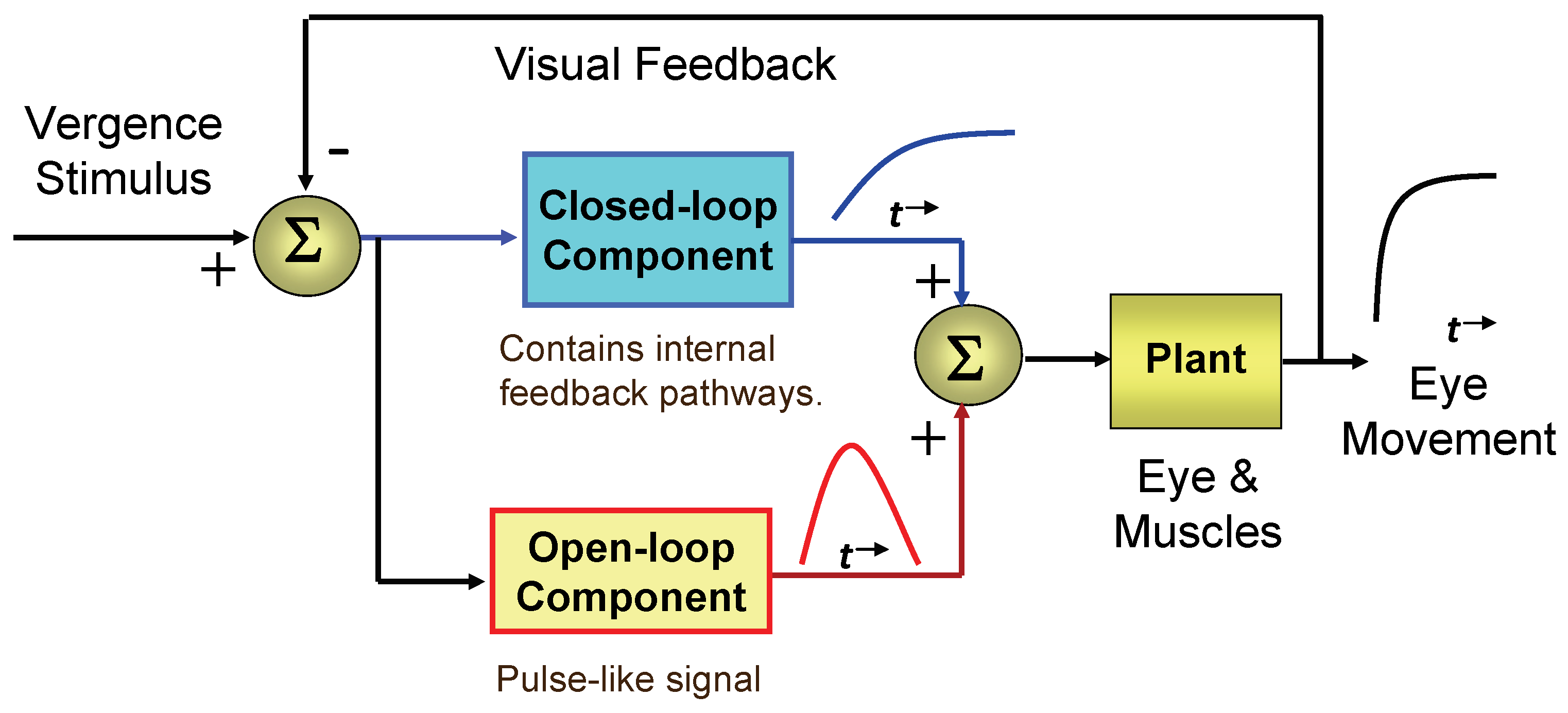A schematic representation of vergence control is summarized in Figure 1.

A number of sophisticated models have been developed that expand on the simple structure illustrated in Figure 1 (Zee and Levi, 1989; Zee, et al., 1992; Maxwell, Tong, and Schor, 2010; Erkelens, 2011). Most of these models include an open-loop component in the form of a pulse signal (this signal is also called the phasic, pulse, or velocity signal). A recent model by Erkelens (2011) features a pulse signal, but this component can be altered by feedback and therefore is not truly open-loop. All of these models include additional internal feedback signals usually driven by efference copy. This additional control signal may be essential to achieve the speed and stability of the vergence response (Erkelens, 2011). The Erkelens model has demonstrated appropriate simulations to both step and sinusoidal stimuli, while the model of Maxwell, Tong, and Schor, (2010) has accurately simulated behavioral characteristics of both the static and dynamic disparity vergence as well as accommodative vergence.

The assumption that the sustained component is under external (i.e., visual) feedback control is strongly supported by empirical data: sustained vergence achieves binocular position errors of only a few minutes of arc. It is impossible to achieve such accuracy from a noisy and variable neurological control system without the use of visual feedback. The case for an internal feedback pathway has been justified based on stability considerations. However support for a preprogrammed early component is not as strong and is based on an analogy with version control features and the relatively fast dynamics attained during early vergence (although not nearly as fast as saccades). Here we provide strong behavioral evidence that the early component of a vergence eye movement is mediated by open-loop control signals.

The relationship between maximum velocity and response amplitude is frequently used as a descriptor of the first-order dynamic properties of a movement: this ratio completely describes the dynamics of a first-order system. If the system is open-loop, this ratio is a constant over all response amplitudes. This is true even if internal noise modifies the response amplitude. This feature was exploited by Stark to develop the “main sequence” description of saccadic dynamics (Bahill, Clark and Stark, 1975; Stark et al., 1975; Stark et al., 1980; Zangemeister et al., 1981). For saccades, a plot of peak velocity (in deg/sec) versus movement amplitude (in deg) follows an approximate straight line over a wide range of amplitudes.

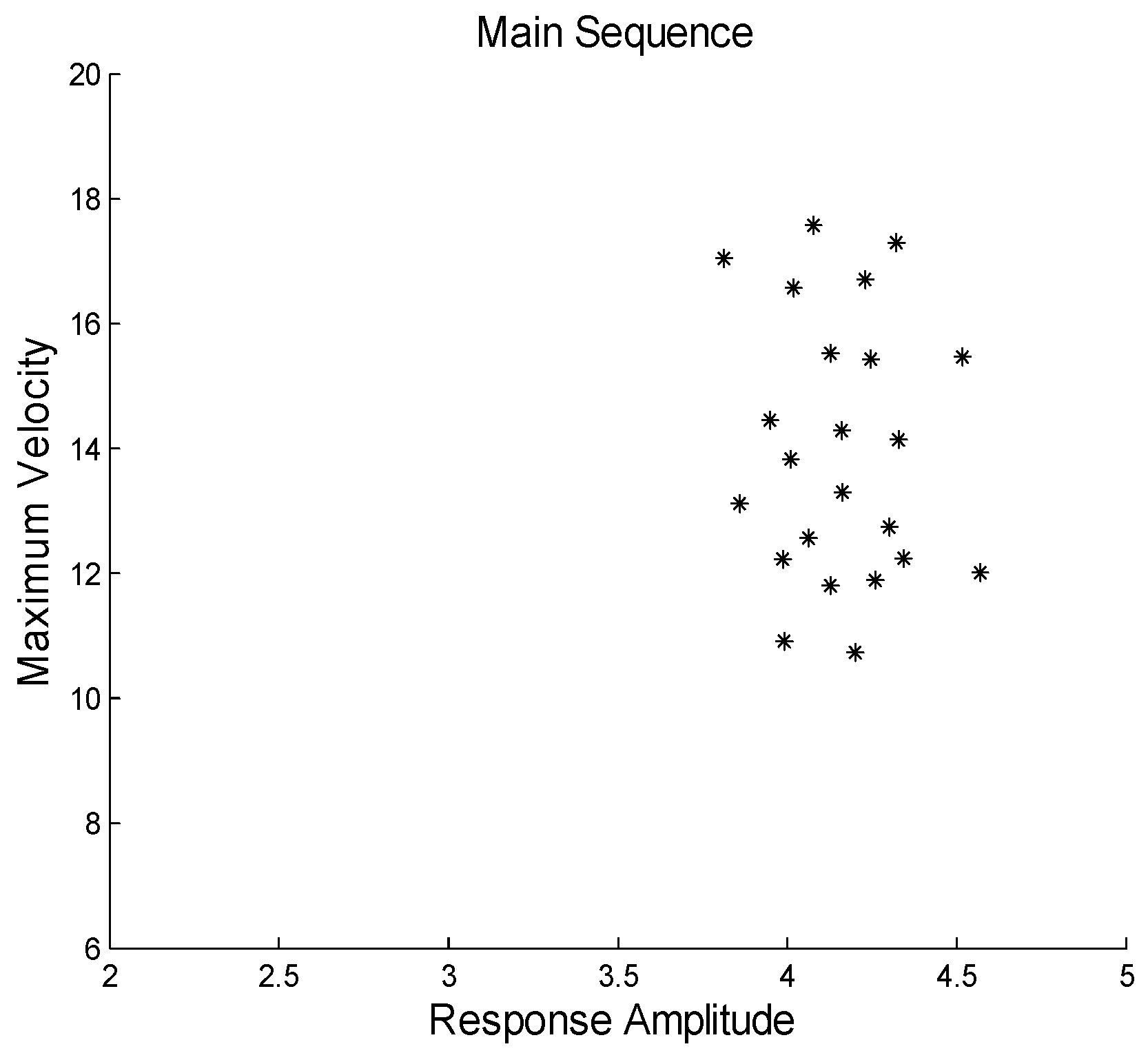
A linear dependency between peak velocity and amplitude can also be found in feedback controlled systems, but only if there is no noise or variability in the controlling processes. Feedback control systems which contain internal noise exhibit variable dynamics; for example, a range of peak velocities to the same stimulus amplitude, but such responses will no longer show a linearly dependent relationship between peak velocity and amplitude. Consider the response of a feedback control system with a variable internal element, for example a gain element which undergoes movement-to-movement changes in gain. When responding to a series of step stimuli, the variation in internal gain gives rise to responses with differing peak velocities, but the feedback will guide all these responses to the same amplitude. Peak velocities will vary while amplitudes stay the same eliminating the functional relationship between velocity and amplitude. The relationship will now be essentially random.

Vergence eye movements have been shown to follow the main sequence paradigm with a linear relationship between peak velocity and response amplitude (Hsu, Bahill et al. 1976, Hung et al., 1994, Maxwell, Tong and Schor, 2010). Measurements of peak velocity and response amplitude show a linear (Erkelens, 2011; Hung et al., 1994) or close to linear (Maxwell, Tong and Schor, 2010) relationship: larger movements are generally faster. A linear relationship means the ratio of peak velocity to response amplitude, the main sequence ratio, will be constant. However, as shown here, this is not true if the range of peak velocities is highly restricted; for example, the range of peak velocities observed in response to a single stimulus amplitude. 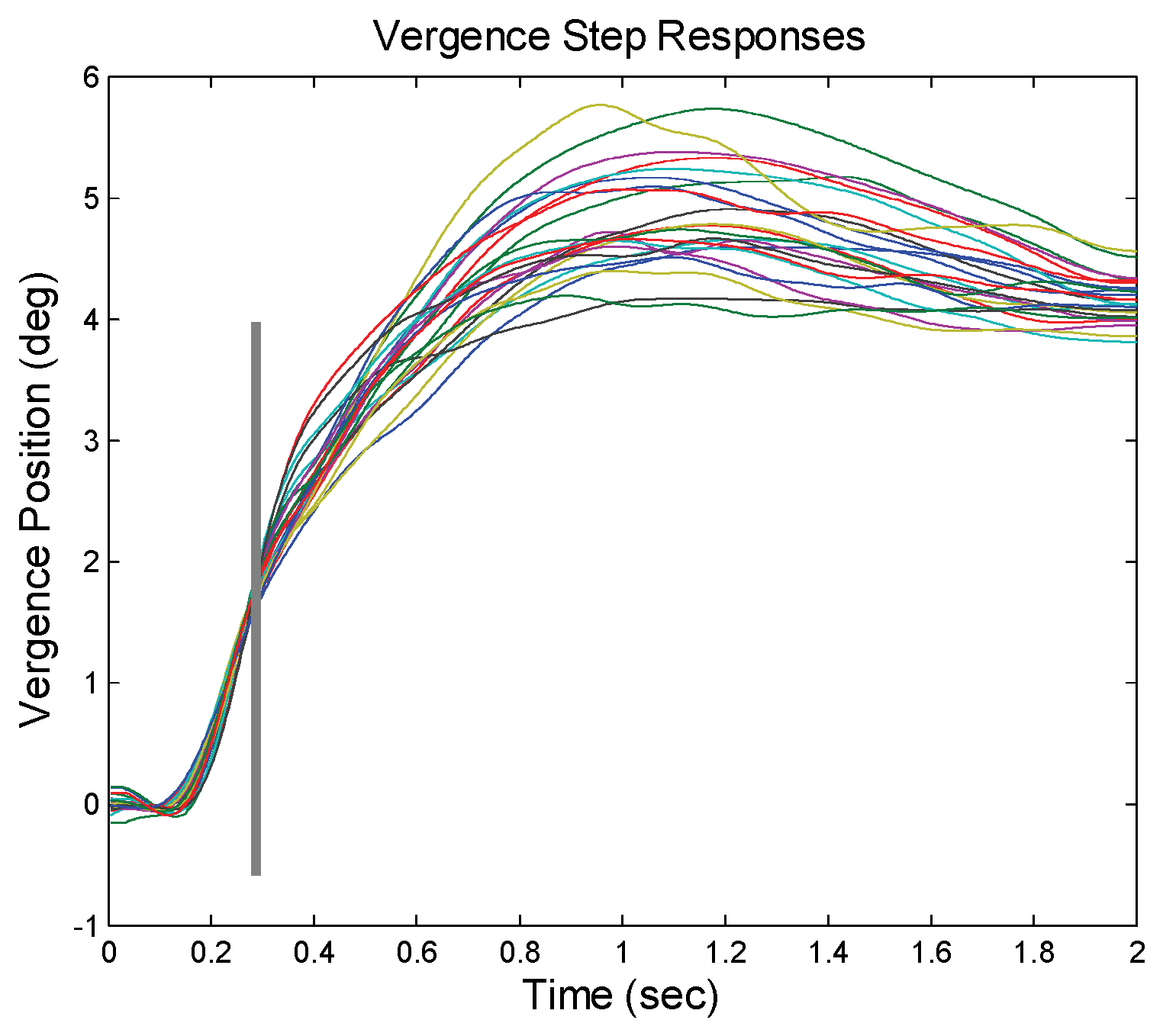Figure 2 shows an ensemble of responses to a 4 deg convergent step change in vergence stimulus. The variation in velocity is evident, but the final values are fairly consistent. If velocity varies, but the amplitude remains the same, the main sequence ratio cannot be constant.

Figure 3 shows the main sequence that results from this response ensemble. There is no linearly dependent relationship between peak velocity and amplitude. Rather, a variation in peak velocities is seen along with a variation in response amplitudes, but there is no apparent relationship between the two: the ratio between these two dynamic descriptors is random.

If the early component of vergence is open-loop then a linear main sequence relationship would be expected, at least for the initial movement. Here, we compare the main sequence relationships of the early portion of a vergence response, where the open-loop component is expected to be dominant, with that of the overall movement. We show that while the overall movement may not demonstrate a linear main sequence, the initial segment does. This provides strong evidence that the early vergence response is mediated primarily by an open-loop control process.

Methods

Recording

Left and right-eye movements were recorded using an infrared video-based ISCAN (Burlington, MA) eye tracker with a reported accuracy of 0.3° over a ±20° horizontal and vertical range. Symmetrical convergence vergence step stimuli of from 2.0 to 6.0 deg (i.e., 4.0 step amplitude) were produced using two computer screens placed 40 cm from the subject arranged as a haploscope using a custom software package (Guo et al. 2011). The stimulus was calibrated using real-world targets at known distances and the eye movement monitor was calibrated throughout the experiment using controlled stimuli. Stimulus and data recording were under computer control and eye movements were sampled at 500 Hz using a 12-bit ADC. Approximately 8 to 20 artifact-free recordings were obtained from each subject. Calibration data was taken before and after each movement.

Subjects:

Nine presbyopic binocularly normal subjects (5 females) between 46 and 72 years of age (57 ±11.2 years) participated in this study. The average near point of conference was 9.8 ± 1.9 cm measured from the bridge of the nose while viewing a high acuity target as described in our previous publication.(Alvarez, Vicci et al. 2010) The near (40cm) dissociated phoria measured using a flashed Maddox was 5±2.5 exophoria (range of 1 exo to 8 exo) as well as our eye movement monitor.(Han, Guo et al. 2010) All subjects had a normal stereopsis of <70 seconds are arc assessed using the Randot Stereopsis Test. All subjects signed written informed consent approved by the New Jersey Institute of Technology Institution Review Board.

Analysis:

Vergence responses were computed as the difference between separately calibrated left and right eye movements using the calibration data taken before and after each response. A typical ensemble of vergence movements was shown in Figure 2. Velocity was determined using the classic two-point central-difference algorithm. The velocity curve was used to quantify peak velocity and, in conjunction with the position curve, was used to plot the main sequence of the responses.

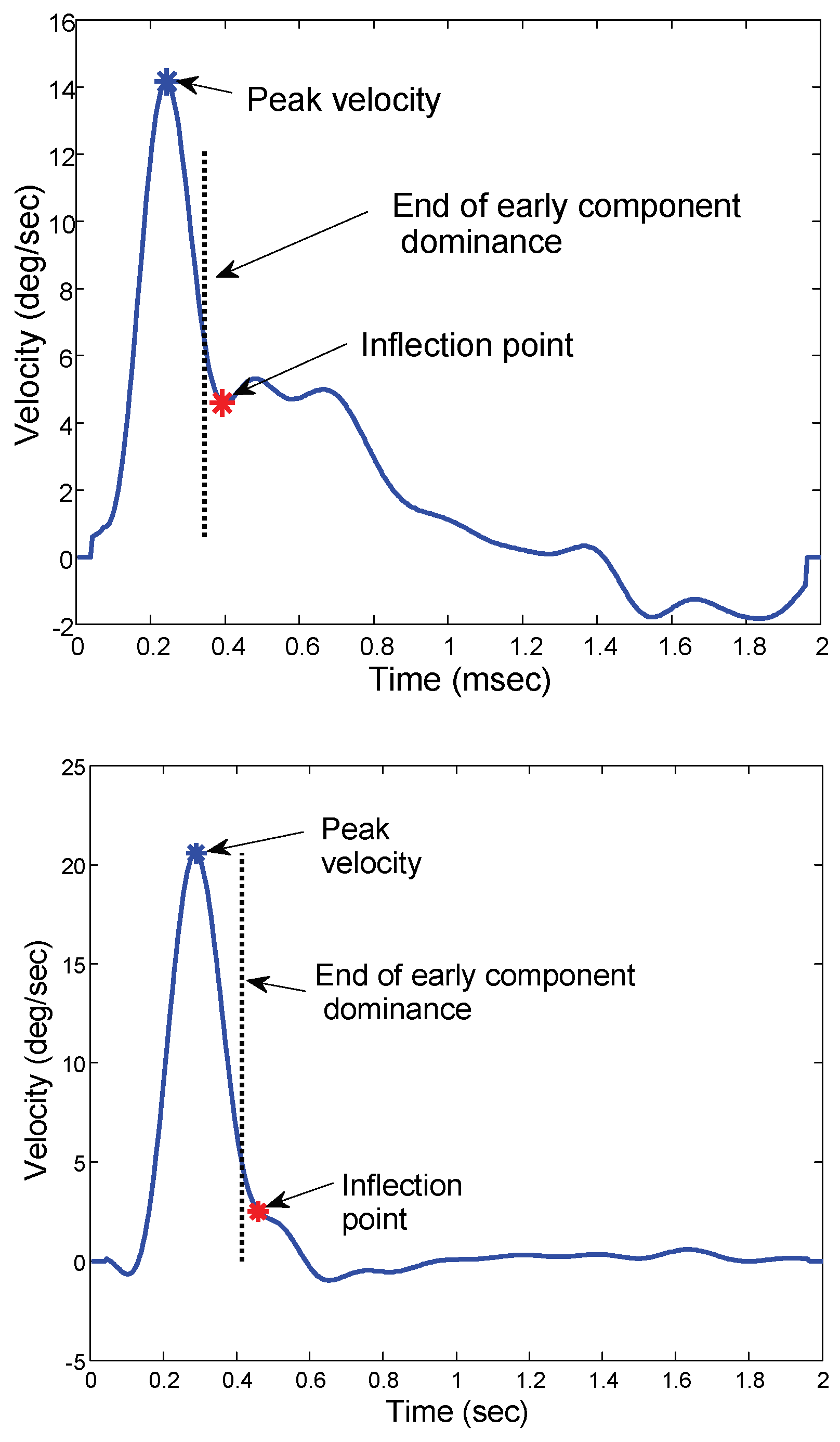
Isolating the early component from the total vergence response is the most challenging aspect of this study. While methods have been developed using independent component analysis to separate the initial and sustained components, they operate on a group, or ensemble of movements and identify component averages across the group (Semmlow and Yuan 2002; Semmlow and Yuan 2002; Semmlow et al. 2007). Here we need to identify the segment dominated by the early response in individual eye movements. Fortunately, the identification of this segment need only be approximate; slight variations will have little effect on the result. As independent component analysis has shown that the early component is much faster than the sustained component (Semmlow and Yuan 2002; Semmlow and Yuan 2002; Castillo et al. 2006; Alvarez et al. 2007; Semmlow et al. 2007), we can safely assume that the early component dominates the vergence step response up through and beyond the time of peak velocity (Alvarez et al. 1999). We also assume that when the sustained component becomes significant, it will alter the velocity profile of the overall response due to the influences of visual and internal feedback. Therefore, to isolate the early component, we examine the velocity trace and search for an inflection which marks the onset of a substantial additional component.

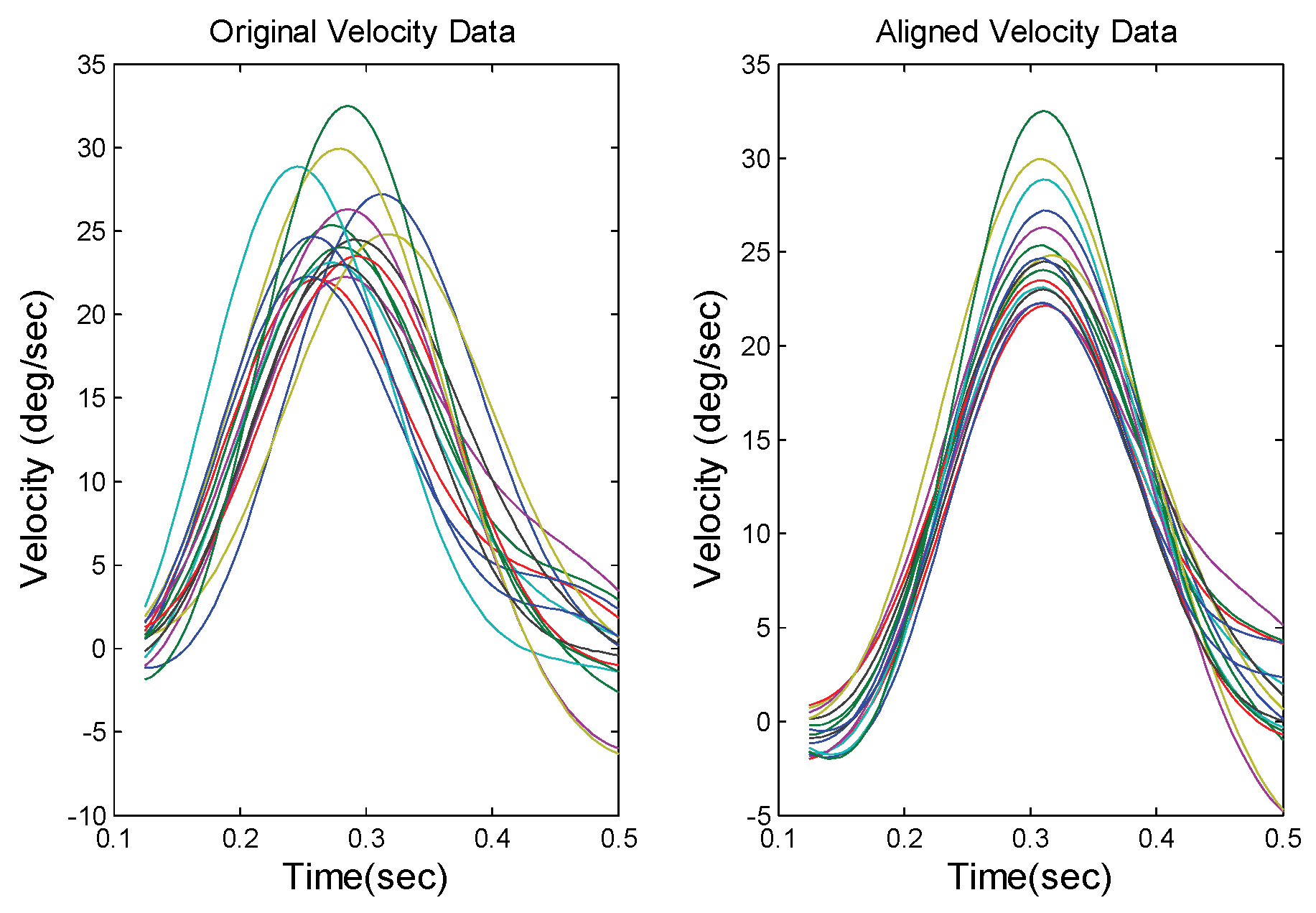
To isolate the early response, it is easiest and most accurate to use the ensemble average of individual velocity traces. To eliminate the influences of variable response latencies we first align the responses based on the time of peak velocity, Figure 4. Next, we display the ensemble average of the velocity trace and identify the first inflection point following the velocity peak. This is the point where the smooth downward curve of the velocity trace either reverses or changes slope, Figure 5. Since this is the point where the sustained component becomes dynamically significant, we use the time point 50 msec prior to this inflection as the period of early component dominance. Hence, the vergence position at that time point is taken as the position variable for determining the early component main sequence. This time point is not critical so long as the isolated segment contains a substantial portion of the early component and very little of the sustained movement.

Two main sequence plots are then developed. The peak velocity versus overall movement amplitude is constructed and represents the traditional disparity vergence main sequence. The peak velocity versus early component amplitude (found as described in the preceding paragraph) is taken as the early component main sequence. The points for both are plotted for all the responses from a given subject. To determine if the collection of points result in a linear main sequence, the points are fitted using linear regression and the R² and p values determined. Because there is little change in the position values for the overall movement (the responses were all to the same stimulus amplitude), velocity was taken as the independent variable and position as the dependent variable. However, in the main sequence plots, position was plotted along the horizontal axis as is traditional for these plots.

Results

As argued above, if a response is open-loop, the main sequence, the plot of peak velocity versus amplitude, will show a linear dependency. This has been shown in the saccadic response which is known to be preprogrammed or open-loop. It is possible for a feedback system to produce a constant main sequence, but only if the system is noise-free. Fortunately for our analysis, there exists some movement-to-movement variability in the vergence response to step stimuli (for example, see Figure 2 and Figure 4). The vergence system does have an approximately linear relationship between maximum velocity and amplitude (Maxwell, Tong and Schor, 2010; Erkelens, 2011; Hung et al., 1994), but only if evaluated over a larger range of amplitudes. For a fixed stimulus level, variation peak velocity is limited and it is not dependent on response amplitude, Figure 2.

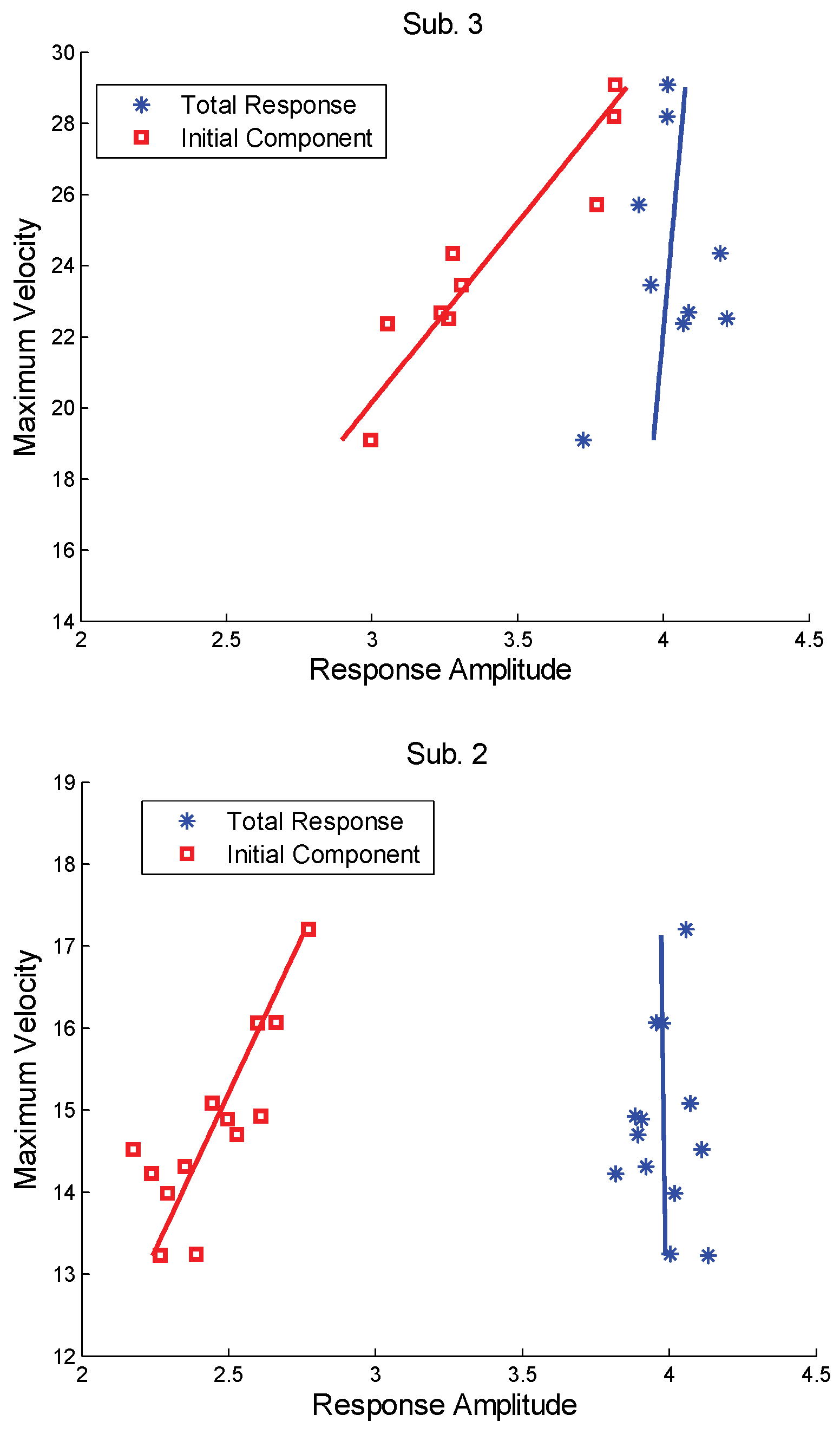
The main sequence relationship of the early component (isolated as described above) is shown for two subjects in Figure 6 (square points). A linearly dependent relationship is seen between peak velocity and amplitude in both subjects, even though the response amplitude is limited. As argued above, this indicates that the early response is under the guidance of an open-loop process. However, the main sequence for the overall response is a near vertical line (Figure 6, dashed line) showing no significant relationship between the two measures. Again, this is the behavior expected from a feedback control system if internal noise is present.

The linear dependency, or lack thereof, can be quantified using standard regression. The regression lines shown in Figure 6 were determined using velocity as the dependent variable (Either variable could be used as the dependent variable and would lead to the same interpretation with regard to linear dependencies. However, since the main sequence of the overall response is usually near vertical, taking velocity as the dependent variable produces a vertical regression line that is more visually informative.). The main sequence linear dependency can be quantified by the regression coefficient of determination (R²) and the statistical significance determined from this coefficient.

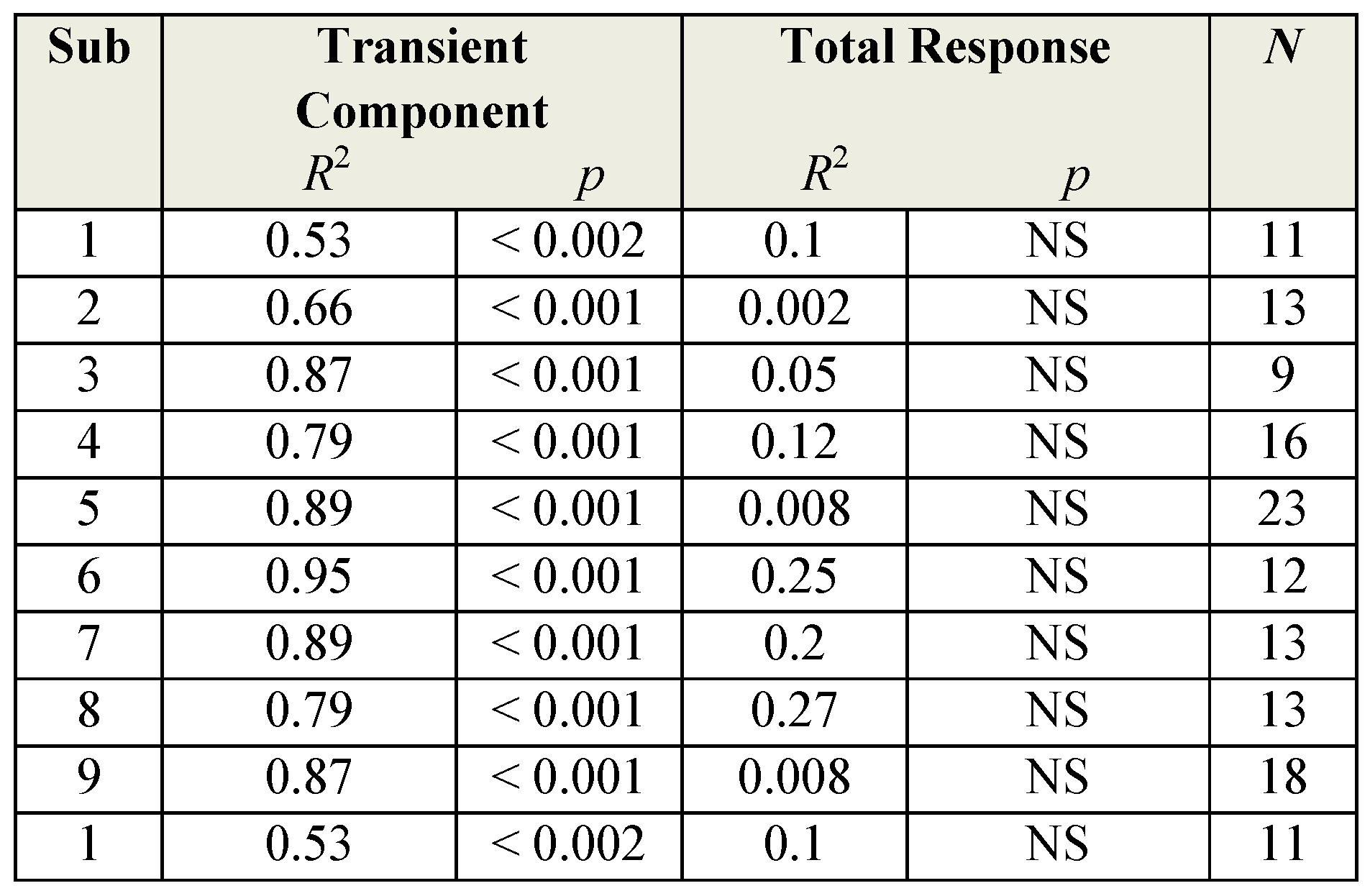
Table 1. Main Sequence Regression Analysis. 

summarized the findings for all 9 subjects. For the overall vergence response, none of the values are significant (p > 0.05), while for the isolated initial transient components, all of the values are significant (p < 0.002).

A dynamic analysis of 4 deg. disparity vergence step responses shows a linearly dependent relationship between maximum velocity and amplitude (i.e., the main sequence) for isolated initial fast components, but not for the overall responses. This result provides strong support for the notion that the fast component of vergence is preprogramed or open-loop. This behavior is similar to the control strategy used for saccadic eye movements. The variation in the ratio of maximum velocity and amplitude for the overall movement further indicates that the vergence system contains a compensatory feedback component that is active in the latter portion of the response

Discussion

A number of studies have found that the peak velocity of disparity vergence eye movements is dependent on response amplitudes. An approximately linear relationship has been shown for a variety of stimulus conditions (Hung et al., 1994; Maxwell, Tong and Schor, 2010) and over a range of stimulus amplitudes (Erkelens et al. 1989). However, these and other studies examined the peak velocity/amplitude ratio over a wide range of amplitudes and associated velocities. When the range of amplitudes and velocities is restricted by using only one stimulus amplitude, the dependence of velocity on amplitude is no longer found in disparity vergence responses. This could be predicted intuitively since we know the final vergence position closely matches the final stimulus position while movement-to-movement velocities tend to vary. This produces a disconnect between peak velocity and amplitude so the quasi-linear relationship between them no longer exists. Yet for the same responses, an approximately linear relationship between peak velocity and response amplitude is found for the isolated early component. Together these findings argue the while the overall movement is influenced by feedback, the early response is open-loop.

The decoupling of peak velocity from response amplitude is due to feedback. Feedback, be it internal or external, acts to decrease the sustained component(s) when velocity is excessive and increase this signal when velocity is low. In theory, both internal and/or external feedback could alter movement dynamics to decouple peak velocity from response amplitude. Unfortunately, current results provide no indication of the contributions of the two feedback components. An intriguing challenge to eye movement experimentalists is to design an experiment which would shed some light on the relative roles of the two feedback pathways.

These results support a number of models of disparity vergence that include an open-loop, pulse-like component (Zee and Levi, 1989; Zee, et al., 1992; Maxwell, Tong, and Schor, 2010). Although these pulse components are driven by signals within the feedback path, their pulselike behavior makes the component, and hence the signal, open-loop. This would lead to the stereotyped early response behavior seen here. In a recent model by Erkelens (2011), the pulse component is under continuous influence from both internal and external feedback, so the pulse component is not open-loop. A pulse component that was modified by the ongoing response would be in conflict with our findings; however, given the delays in the model, it is unclear if feedback signals could affect the pulse component within the time frame of the early response (i.e., the first 300 to 400 msec.), or if such modifications would be large enough to be detected in the movement. Further simulations of the Erkelens model (2011) could address this question.

Conclusion

Multiple disparity vergence responses to the same stimulus exhibit small differences in dynamics as quantified by the ratio of peak velocity to response amplitude (the main sequence ratio). These small changes in dynamics do not follow the main sequence; they do not show a linearly dependent relationship between peak velocity and response amplitude. This deviation is due to the influence of some type of feedback on the motor signal, either internal, or external (visual) feedback, or likely both. However, if only the early portion of the response is analyzed, a linear dependent relationship is found, indicating that this portion of the disparity vergence response is driven by an open-loop, or preprogrammed signal. This finding supports the models of the disparity vergence control system that include an open-loop, pulselike component.