On the Structure of Measurement Noise in Eye-Tracking

Abstract

Past research has discovered fractal structure in eye movement variability and interpreted this result as having theoretical ramifications. No research has, however, investigated how properties of the eye-tracking instrument might affect the structure of measurement variability. The current experiment employed fractal and multifractal methods to investigate whether an eye-tracker produced intrinsic random variation and how features of the data recording procedure affected the structure measurement variability. The results of this experiment revealed that the structure of variation from a fake eye was indeed random and uncorrelated in contrast to the fractal structure from a fixated, real human eye. Moreover, the results demonstrated that data-averaging generally changes the structure of variation, introducing spurious structure into eye movement variability.

Introduction

The folk expression that ‘the eyes are the window to the soul’ is a telling example of the common supposition that observable behaviors reveal underlying processes of mind. Specifically in reference to eye movements, we might feel we can distinguish a casual glance from a lustful once-over, or a penetrating stare from a vacant gaze. Even if framed in far less poetic terms, the behavioral sciences seem to be in tacit agreement with the folk belief that mind can be inferred from behavior.

Although some accounts eye movement behaviors have stressed the importance of properties of the stimulus (e.g., Findlay & Walker, 1999; Itti, Koch, & Niebur, 1998; Koch & Ullman, 1985; Lamy, Leber, & Egeth, 2004; Parkhurst, Law, & Niebur, 2002), much of the past research supports the conclusion that such behavior cannot be driven exclusively by bottom-up, saliency-based processes (Land & Hayhoe, 2001; Oliva, Torralba, Castelhano, Henderson, 2003; Rothkopf, Ballard, & Hayhoe, 2007; Underwood & Foulsham, 2006). Proponents of the latter claim contend that natural visual behaviors, both eye movements and fixations, must also be constrained by top-down, cognitive processes (e.g., working memory) to allow for the collection of behaviorally-relevant, task-specific information (Brandt & Stark, 1997; Hayhoe & Ballard, 2005; Henderson, 2003; Laeng & Teodorescu, 2002; Land, 2006, 2009; Liversedge & Findlay, 2000; Spivey & Geng, 2001). In a classical example, Yarbus (1967) found that providing participants with different observational tasks, requiring the acquisition of different sets of information, yielded characteristically different patterns of eye movements and fixations, despite being directed at the same stimulus (i.e., Repin’s “The Unexpected Vistor”).

Most attempts to explicate how these processes bear a causal relationship to eye movement behavior have relied on traditional statistical techniques that assume an independence of observations and uncorrelated error variance (Aks, 2005). For instance, a researcher might collapse a span of measured eye movements into summary variables that represent an important quality of the eye movement behavior (e.g., fixation times), and examine these variables using traditional linear statistics (e.g., t-tests, correlations). Recent developments in statistical methods, however, have provided an alternative framework to investigate and explain the organization of eye movement behaviors (e.g., Aks, Zelinsky, & Sprott, 2002; Stephen & Mirman, 2010). Specifically, this alternative approach is made possible by fractal statistics (see Brown & Liebovitch, 2010; West & Deering, 1995).

In contrast to datasets that are characterized well by the arithmetic average and standard deviation and obey the assumption of uncorrelated error variance, recent research has demonstrated that many standard tasks of repeated human performances yield distributions or autocorrelations in time-series that display fractal structure (e.g., Ferrer-i-Cancho & Elvevag, 2010; Kiefer, Riley, Shockley, Villard, & Van Orden, 2009; Eke, Herman, Kocsis, & Kozak, 2002; Eke, Herman, Bassingthwaighte, Raymond, Percival, Cannon, Balla, Ikrenyi, 2000; Gilden, 2001; Holden, Van Orden, Turvey, 2009; Kuznetsov & Wallot, 2011; Phillipe, 2000; Rhodes & Turvey, 2007; Wallot & Van Orden, 2011a, b; Warren, Carciun, & Anderson-Butcher, 2005). Conceptually similar to geometric fractal patterns (Mandelbrot, 1982), fractal scaling relations in experimental data are nested patterns found in the variability across repeatedly measured behaviors. Unlike normally, Gaussian distributed data, these datasets possess self-similar properties and are scale-invariant, such that small variations in the data have essentially the same structure as large variations (Brown & Liebovitch, 2010; West & Deering, 1995). As in geometrical fractal patterns, if one were to “zoom in” (i.e., examine a smaller scale) on the measurement timeseries, one would discover essentially the same pattern of fluctuations evident at the larger scale (Holden, 2005). Accordingly, fractal statistical methods do not rely on partitioning the variability in measurement into different components, but rather assess the structure of the time-evolving behavior for these fractal properties.

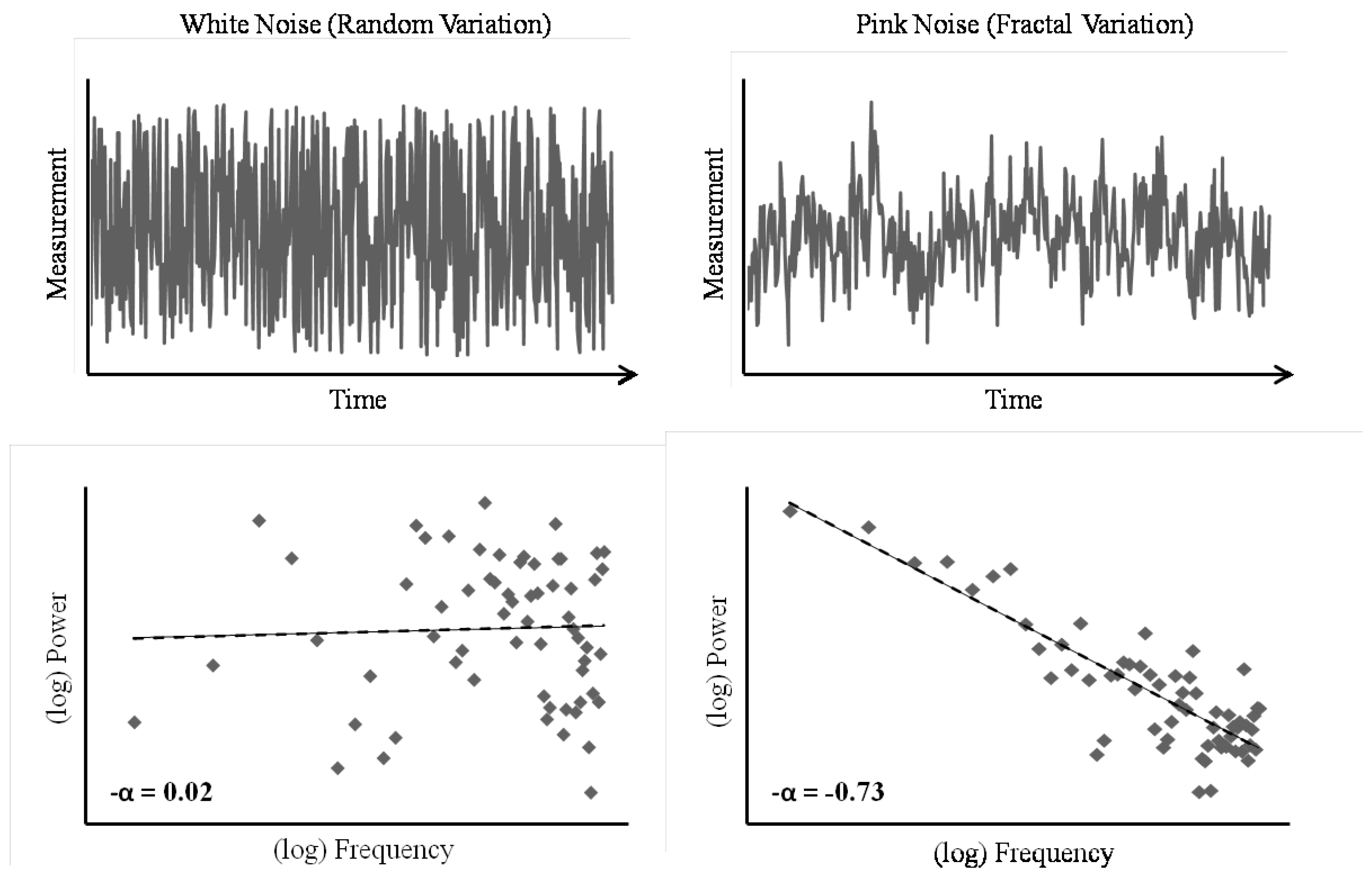
More technically, fractal patterns are reflected in an inversely proportional relationship between the power (P) and frequency (f) of observed variation in a time-series of measurements. That is, in a fractal time-series, there exists a proportional relationship between the size of a change and how frequently changes of that size occur, and this relationship is stable across changes in scale. In this sense, the pattern of variability in the behavior is self-similar and scale-invariant; large-scale changes occur with the same relative frequency as small-scale changes. The degree to which a dataset approximates this ideal relationship between power and frequency, P = 1/f^α, can be summarized in the scaling exponent, α. The fractal structure inherent in such power-law distributed datasets can be depicted as a linear scaling relation between the power and frequency of fluctuations in measurements by plotting one against the other on double-logarithmic axes. On such a “spectral plot”, -α is equivalent to the slope of the line that best fits the data (see Figure 1). Hence, α captures the relationship between size and frequency of fluctuations in the measurement time-series. Random fluctuations (i.e., white noise) produce a flat line on the spectral plot, and thus a scaling exponent near α = 0, which indicates that changes of all different sizes occur with approximately the same frequency in the time-series. Alternatively, fractal structure (i.e., pink or 1/f noise) produces a line with a slope of -1, and thus an exponent near α = 1, which indicates the self-similarity and scale-invariance of fractal patterns.

Time-series can contain even more complex patterns of fluctuation than (mono)fractal structure. Independently of monofractal structure, time-series might also display multifractal structure wherein a single scaling exponent does not adequately characterize the pattern of variability in the data (Mandelbrot, 1997). Multifractal structure can result in a time-series for a number of different reasons. Kantelhardt, Zschiegner, Koscielny-Bunde, Havlin, Bunde, and Stanley (2002) propose that multifractality might be evident in a time-series either due to intermittent periods of high variability interspersed with periods of low variability, or a probability density distribution with a heavy tail (e.g., inverse power-law distribution). In the former case, a relatively greater number of fluctuations at a particular scale might create differences in the slope of the scaling relation between high-amplitude, low-frequency fluctuations and low-amplitude, high-frequency fluctuations. In this case, different regions of the spectral plot of the power-frequency relation are characterized by different values of α. In the latter case, the scaling relation between power and frequency of fluctuation changes inevitably over the course of measurement, as extreme values (i.e., very large scale changes that only happen very rarely) impact the scaling relationship. Recent research has found such multifractal patterns in a number of human physiological and behavioral datasets (Ivanov, Amaral, Goldberger, Havlin, Rosenblum, Struzik, & Stanley, 1999; Stosic & Stosic, 2005; Humeau, Buard, Chapeau-Blondeau, Rousseau, Mahe, & Abraham, 2009; West & Scafetta, 2002; Morales & Kolaczyk, 2001; Ihlen & Vereijken, 2010; Kuznetsov & Wallot, 2011).

Fractal structure has been observed in visual behavior tasks as well (Aks & Sprott, 2003; Aks, Zelinsky, & Sprott, 2002; Stephen & Mirman, 2010; Stephen, Mirman, Magnuson, & Dixon, 2009). The discovery of these statistical properties has theoretical ramifications concerning the organization of the system that gave rise to the observed behaviors (Van Orden, Holden, & Turvey, 2003; Van Orden, Kloos, & Wallot, 2011). Fractal and multifractal structure reflect qualitatively different patterns of variation in behavior than those that give rise to normally, Gaussian distributed datasets. Fractal datasets are indicative of interaction-dominant dynamics (Kello, Beltz, Holden, & Van Orden, 2007; Van Orden, et al., 2003). In a system governed by component-dominant dynamics, the processes responsible for causing variation in observed behavior are independent of one another, and interact with one another linearly, in an additive fashion. In other words, when behavior is a product of component-dominant system it can be understood as the sum total of independent contributions from its various components. In reference to eye movements, one might claim that the gaze trajectories obtained during measurement are the result of all bottom-up, stimulus-driven processes in addition to all top-down, participant-driven processes. Contrarily, in a system governed by interaction-dominant dynamics the processes giving rise to the observed behavior are interdependent, and interact with one another in a non-linear fashion. The contribution of any one process to the behavior is dependent on the states of the other processes. It is this interdependence between components that gives rise to datasets with power-law distribution and fractal properties. Thus, finding fractal structure in eye movements suggests that these behaviors are not the end result of independent contributions from “top-down” and “bottom-up” processes, but rather are the result of inherently interwoven processes.

These conclusions of course require empirical support from careful investigation of how these statistical properties get into the data. The simplest consideration is the measurement device recording the data. The presence of structured (i.e., non-random) variability in the measurement noise of the requisite eye-tracking system would eliminate the ability to attribute structured variability in the results of the eye movement task to the participant. Moreover, eye-tracking systems offer a number of features as to how the data are recorded. For instance, eyetracking software might offer data-averaging, which records the data as a running average of eye position at a specified number of data points, as opposed to recording the raw, non-averaged data. Again, drawing conclusions as to the importance of these findings requires knowledge of how such treatments affect the data. With these concerns in mind, we designed an experiment to investigate the fractal structure of a simple fixation task using both monofractal and multifractal methods.

Method

Participants

Seven graduate students and one undergraduate research assistant from the University of Cincinnati volunteered to participate. All were over 18 years of age and had normal vision.

Apparatus

The desk-mounted eye-tracker (D6, Applied Science Laboratories), placed on top of a desk, was 79cm from the floor. Directly above the eye-tracker was a computer screen (1280 x 1024) used for displaying the target stimulus. A chair with a seat 46cm from the floor was used to seat participants in front of the eye-tracker. The eye-tracker was set to record at 60Hz.

Procedure and Design

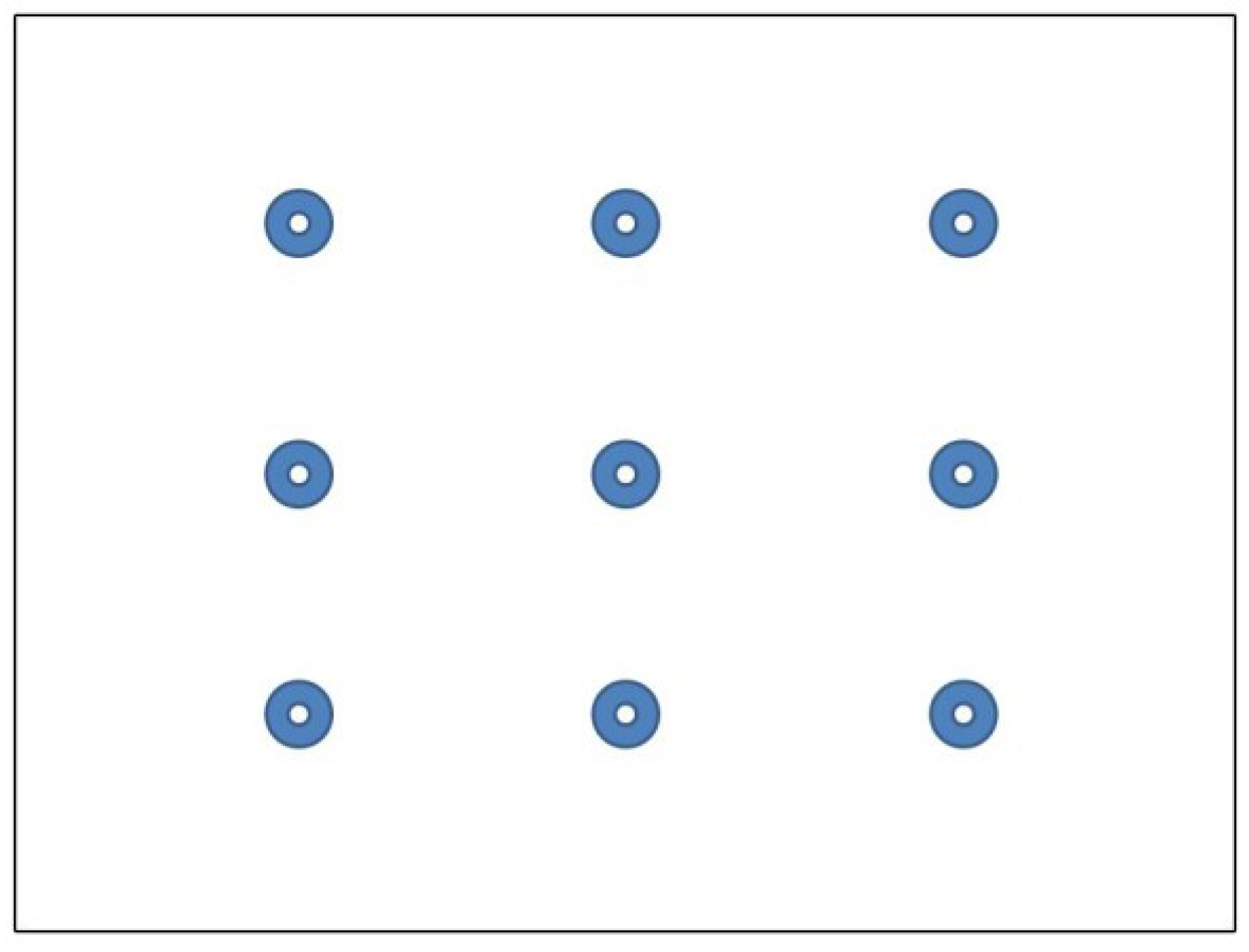
Following consent and instructions, participants were seated such that their eyes were approximately 65cm away from the eye-tracker. On each trial, participants were instructed to fixate their eyes on a central target in a stimulus display of nine dots (see Figure 2) with each trial lasting 30 seconds.

We also took recordings of a fake eye (Applied Science Laboratories) with 30 seconds per trial. The fake eye was positioned 65cm away from the eyetracker and 115cm above the floor. The fake eye was oriented toward the eye-tracker such that it produced a fixation point on the stimulus display. For real eye trials, we calibrated the eye-tracker to each participant and recorded eye movement positions either with a four-sample running average (factory settings of the eye-tracker) or without averaging. Every participant underwent three trials in each condition. Similarly, for fake eye trials, we first calibrated the eye-tracker to a participant and then recorded three trials under each data-averaging condition.

Data Analysis

The eye-tracker recorded the position and orientation of both the head and eye, via separate camera systems, and integrated this information to calculate the point-of-gaze (POG) on the stimulus display. The software recording the POG split the data from each trial into a horizontal position and a vertical position time-series. These time-series were integrated into a single two-dimensional gaze-interval time-series. Before subjecting the time-series data to analysis, artifacts were removed (i.e., blinks, periods in the time-series where the eye-tracker lost the eye). As outliers and linear trends in a time-series can adversely affect an assessment of the monofractal structure in behavior (see Eke et al., 2000), fluctuations greater than three standard deviations were removed, and a linear bridge detrending was applied to the time-series prior to the monofractal analyses. As these properties of the data do not adversely affect an assessment of multifractal structure, the raw time-series were used in the multifractal analyses.

Power-Spectral Density analysis (PSD) and Detrended Fluctuation Analysis (DFA) were used to estimate monofractal characteristics of the gazeinterval time-series. Comprehensive descriptions of these methods are beyond the scope of this article, and have been provided elsewhere (e.g., Delignieres, Ramdani, Lemoine, Torre, Fortes, & Ninot, 2006; Holden, 2005; Marmelat & Delignieres, 2011), but a brief description of the techniques employed here is necessary for an accessible interpretation of the results.

As discussed above, PSD estimates the scaling exponent α that characterizes monofractal fluctuations. First, the time-series is submitted to a Fourier transformation, which decomposes the observed measurements into a series of sinusoids with a range of different amplitudes and frequencies. The logarithm of the power (i.e., amplitude squared) and the logarithm of the frequency for this series of sinusoids are plotted against one another on a spectral plot. The slope (S) of the regression line that best fits the data on the log-log spectral plot estimates the scaling exponent alpha (α), where α = -S (Holden, 2005).

The outcome of DFA is in principle the same to PSD, but we used both analyses to corroborate the results, as each technique breaks up the time-series in different ways. In DFA, the time-series is broken down into bins of different sizes. The smallest size used here was 4 data points, so a whole time-series was broken down into adjacent bins of 4 data points. Then, a leastsquare regression line was fitted to and subtracted from each bin, and the variance of the residuals was calculated. This is done in order to avoid spurious results due only to simple, local trends in the time-series. This procedure is repeated for increasingly larger bin sizes up to one quarter of the length of the whole time-series. Similarly to PSD, the logarithm of the resulting bin sizes is then plotted against the logarithm of the resulting variances, and a straight line was fitted to the plot. The slope of that line estimates the Hurst Exponent (H), which is equivalent to the scaling exponent with α = (H – 0.5) * 2 (Peng, Havlin, Stanley, & Goldberger, 1995).

We similarly used two multifractal analysis techniques to ensure the robustness of the results: Multifractal Continuous Wavelet Analysis (MFCWT) and Multifractal Detrended Fluctuations Analysis (MFDFA). Again, a full, technical description of these techniques can be found elsewhere (e.g., Ihlen, 2012; Ihlen & Vereijken, 2010; Kantelhardt et al., 2002; Percival & Walden, 2000). In brief, however, both techniques allow for an assessment of how well the timeseries can be characterized by a single scaling relation. MFCWT is a wavelet-based extension of PSD, and uses the continuous wavelet transform (CWT) to analyze variability in a time-series over different scales of fluctuation (Percival & Walden, 2000). Similarly, MFDFA functions like a regular DFA analysis, but changes in variability with bin size can be assessed for higher statistical moments than the variance, tapping into different scales of fluctuation (Kantelhardt et al., 2002). Ultimately, both analyses assess “multifractal spectrum width”. That is, the magnitude of multifractality in a data-series can be assessed by calculating the difference between the scaling exponent which characterizes the highest scale (h max) as compared to the exponent of the lowest scale (h min), h max – h min. The greater the multifractal spectrum width, the larger the difference between the scaling characteristics of small and large fluctuations in a timeseries, and the less well the time series is described by a single scaling exponent. To conduct the analyses, we followed the recommendations of Ihlen and Vereijken (2010) on estimating multifractal structure from relatively short time-series (less than 10,000 data points, Kantelhardt et al., 2002).

For both monofractal and multifractal techniques, analyses were performed on the time-series of measurements in sequential order and on the same timeseries with the values randomly shuffled. This comparison was conducted to test the validity of any monoor multifractal structure detected and likewise any effect of the experimental manipulations on the structure of variation. Finding that shuffling the time-series does not affect the structure of variation would suggest that the processes that gave rise to the observed structure in the original time-series were not time-dependent processes and that the observed structure was due to other properties of the data (Kantelhardt et al., 2002).

Results

Monofractal Analyses

A 2 (eye type) x 2 (averaging) repeated-measures ANOVA on scaling exponents from the PSD analysis revealed significant main effects of eye type [F (1, 7) = 15.03, p = .006, η ² = .682] and averaging [F (1, 7) = 24.97, p = .002, η ² = .781], but no significant interaction. As depicted in Figure 3a, the real eye produced scaling exponents more towards the pink noise region (α = 1) than the fake eye. Similarly, data-averaging produced scaling exponents more towards pink noise than the non-averaged data. This pattern of results did not hold in an analysis of the randomly shuffled timeseries. There were no significant effects of either eye type or data-averaging, and the scaling exponent estimates for every condition were in the white noise, random fluctuation region (i.e., near α = 0).

This overall pattern of effects was supported in the 2 (eye type) x 2 (averaging) repeated-measures ANOVA on the scaling exponents as estimated from DFA. As in the PSD analysis, there were significant effects of both eye type [F (1, 7) = 14.27, p = .007, η ² = .671] and data-averaging [F (1, 7) = 15.91, p = .005, η ² = .694], but no significant interaction. Again, the real eye produced scaling exponents more toward pink noise than the fake eye, and averaged data produced exponents toward pink noise than did non-averaged data (see Figure 3b). Unlike the PSD analysis, the DFA on the shuffled time-series did reveal significant effects of eye type, data-averaging, and a significant interaction. However, like the PSD analysis, all the means were in the white noise scaling region (i.e., near α = 0). Thus, the latter DFA shuffled time-series results are somewhat trivial and do not invalidate the DFA results found for the non-shuffled data.

Multifractal Analyses

A 2 (eye type) x 2 (averaging) repeated-measures ANOVA conducted on multifractal spectrum widths obtained from the MFCWT analysis revealed only a significant main effect of eye type [F (1, 7) = 22.47, p = .002, η ² = .762] in which the real eye produced multifractal spectrum widths greater than those for the fake eye (see Figure 4a). The analysis of the shuffled time-series, however, revealed a similar main effect for eye type [F (1, 7) = 25.98, p = .001, η ² = .788], suggesting that the multifractal spectrum widths observed for the non-shuffled (raw) time-series may be due to time-independent aspects of the data. There were no other significant effects (see Figure 4b).

The same overall pattern of results was found for MFDFA. That is, an ANOVA on the multifractal spectrum widths of the raw time-series revealed only a significant effect of eye type [F (1, 7) = 9.37, p = .018, η² = .572], with greater spectrum widths observed for the real eye. As in the MFCWT analysis, the MFDFA on the shuffled time-series also revealed a significant effect of eye type [F (1, 7) = 14.65, p = .006, η ² = .677]. There were no other significant effects.

Discussion

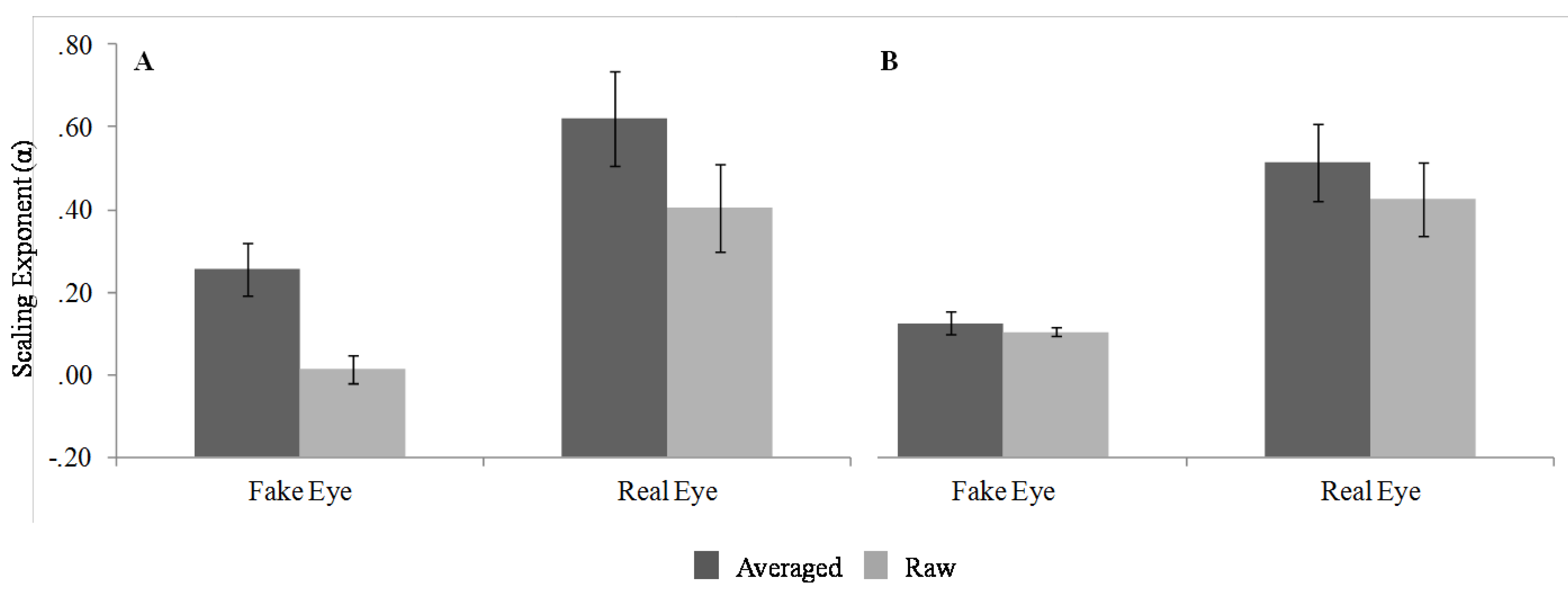
Several conclusions can be drawn from this pattern of results. First, the effects of eye type were generally as expected. With regard to the monofractal analyses, the fake eye indeed does generally produce random fluctuations (i.e., white noise), whereas the real human eye reliably produces fractal scaling relations (i.e., pink noise). This result partially resolves the concern over the structure of measurement noise in the eye-tracking system in that the eye-tracking measurement device indeed only inserts random variation. The current results provide evidence that the monofractal structured variability in the eye-movement data is likely due to time-dependent processes of participant behavior and not an artifact of the data recording device.

It is important to note, however, that the effects of data averaging do change the structure of the variability even for the fake eye, and impact the estimation of scaling in the data. Data-averaging might be an advantageous step in data-processing for some eye movement research because applying a running average to the raw data smoothes the time-series of eye positions. For instance, working with a smooth, relatively cleaner eye movement trajectory could be helpful in research primarily interested in salience properties or areas of interest in particular stimuli. Applying this treatment to the data does, however, inject spurious correlated structure into a time-series by spreading the effects of fluctuations out across several data-points. As such, data-averaging affects both data from the fake eye and the real eye alike. As portrayed in the spectral plots, data-averaging dampens frequencies in the spectrum from 7 to 30Hz (see Figure 5). This is plausible, since the averaging effectively removes variability on scales faster than 66ms, corresponding to a reduction of the effective sampling rate to 15Hz (as far as moment-to-moment fluctuations are concerned). Overall, these results suggest that future research concerned with the fractal structure of eye movement should avoid data-averaging procedures.

In regard to the results of the multifractal analyses, only the eye type seemed to have an effect on the multifractal spectrum width. For the analysis of the raw data, the results obtained for both MFCWT and MFDFA suggested that the real, human eye produced a slightly multifractal signal, while the fake eye produced something close to a monofractal signal.

Unlike the monofractal analyses, data-averaging did not seem to have any effect on mutlifractal spectrum width. More importantly, the analyses of the shuffled surrogates still resulted in a significant difference in multifractal spectrum width for the real eye compared to the fake eye. It is important to appreciate that this latter result does not invalidate the multifractal structure evident in the raw time-series, but rather provides some insight as to what properties of the real eye fluctuations gave rise to this structure. As mentioned previously, Kantelhardt and colleagues (2002) suggest that multifractal structure can result from either a time-dependent process (i.e., intermittent periods of relatively high and low fluctuations), or from timeindependent aspects of the data (i.e., a distribution with a broad probability function). For instance, Kantelhardt and colleagues demonstrate that a time-series with a power-law distribution can result in multifractality although it lacks any sequential dependence or long-term correlations between successive values. The fact that the shuffled time-series did not eliminate the multifractality associated with fluctuations from the real eye would therefore suggest that this structure is the result of a power-law distribution. This finding adds to the existing literature on the specific processes give rise to the structure of eye movement variability. For instance, Stephan and Mirman (2010) found evidence in eye movement behavior consistent with interdependence between component processes, but of a different specific variety (i.e., log-normal distribution).

Overall, these results suggest that the fluctuations in eye position (POG) that occur during simple fixation tasks show both monofractal and multifractal structure. This structure can safely be attributed to the participant when the eye-tracker produces random intrinsic measurement noise and the analyses are performed on non-averaged POG data. More interestingly, finding these properties in the current experiment suggests that even the simplest of visual behaviors (i.e., fixation) are the result of interaction-dominant dynamics. As discussed above, in an interaction-dominant dynamics imply that the component processes contributing to behavior are interdependent with one another. This suggests that eye movement behaviors are in fact an emergent result of non-linear interactions between “bottom-up” and “top-down” processes, and thus that these processes are inherently interwoven. Perhaps most importantly, these findings demonstrate that the framework of fractal statistics offers promising new windows into understanding the organization and control of eye movement.