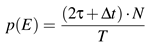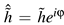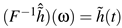Introduction
The act of visual fixation is the basis for perception of a stationary target objects. In the beginning eyemovement research, miniature eye movements have been discovered during fixation of the eyes. Furthermore, under suppressed eye movements, perception is disturbed. In the 1950s it was demonstrated in a laboratory experiment that stationary objects rapidly fade from perception when our eyes are artificially stabilized
Ditchburn and Ginsborg (
1952);
Pritchard (
1961); Riggs, Ratliff, Cornsweet, and Cornsweet (1953)). This perceptual fading is caused by the adaptation of retinal receptor systems to constant input and can occur rapidly (
Coppola & Purves, 1996). Thus, while our eyes fixate a stimulus for the visual analysis of fine details, ironically, miniature eye movements must be produced to counteract perceptual fading. Consequently, the term
fixational eye movements (FEM) was introduced to capture this seemingly paradoxical behavior. Perceptual performance as a function of self-generated noise is an unimodal function which lends support to underlying nonlinear mechanisms (
Starzynski & Engbert, 2009).
Fixational eye movement is classified as tremor, drift and microsaccades (e.g.,
Ciuffreda & Tannen, 1995). The largest component of fixational eye movements is produced by microsaccades which are high-velocity movements with small amplitudes. Recent findings demonstrated various neural, perceptual and behavioral functions of microsaccades (Martinez-Conde, Macknik, & Hubel, 2004; Martinez-Conde, Macknik, Troncoso, & Hubel, 2009;
Rolfs, 2009). The relevance of microsaccades to diverse neural and cognitive systems offers a possible explanation for the difficulties in identifying a specific function for microsaccades (for recent overviews see
Martinez-Conde et al., 2004). Here, the following section gives a very simple and brief overview of recent findings about functions of microsaccades:
Oculomotor control of fixation. Microsaccades enhance retinal image slip (to counteract retinal fatigue) on a short time scale and control fixational errors on a long time scale (
Engbert & Kliegl, 2004). Moreover, recent evidence suggests that microsaccades are triggered on perceptual demand based on estimation of retinal image slip (
Engbert & Mergenthaler, 2006).
Perception. Microsaccades are important for peripheral and parafoveal vision. During the perception of bistable visual scenes, microsaccades induce transitions to visibility and counteract transitions to perceptual fading (Engbert, 2006; Martinez-Conde, Macknik, Troncoso, & Dyar, 2006; Rucci, Iovin, Poletti, & Santini, 2007). Moreover, fixational eye movements and microsaccades represent noise sources that enhance perception (
Starzynski & Engbert, 2009). Furthermore during fixation, microsaccades play a part in supporting second-order visibility (Troncoso, Macknik, & Martinez-Conde, 2008).
Attention. Microsaccades can be suppressed voluntarily with focused attention (
Bridgeman & Palca, 1980; Gowen, Abadi, & Poliakoff, 2005). They are also modulated by crossmodal attention with a pronounced signature in both rate and orientation (e.g.,
Engbert & Kliegl, 2003; Galfano, Betta, & Turatto, 2004;
Hafed & Clark, 2002; R. Laubrock, Engbert, & Kliegl, 2005; Rolfs, Engbert, & Kliegl, 2005). The hypothesis that microsaccades represent an index of covert attention has been criticized by Horowitz, Fine, Fencsik, Yurgenson, and Wolfe (2007) (but see Horowitz, Fencsik, Fine, Yurgenson, & Wolfe, 2007; J. Laubrock, Engbert, Rolfs, & Kliegl, 2007), however new work by J. Laubrock, Kliegl, Rolfs, and Engbert (2010) lends support to the coupling between attention and microsaccades.
Saccadic latency. Microsaccades interact with upcoming saccadic responses which can result in prolonged as well as shortened latencies for saccadic reactions (Rolfs, Laubrock, & Kliegl, 2006). Recently,
Sinn and Engbert (
2009) demonstrated that this effect contributes to the saccadic facilitation effect in nature background.
Individual differences. The pattern of successive microsaccades (called saccadic intrusion in this study) has been proposed as a stable characteristic between persons (
Abadi & Gowen, 2004). In general, there is much overlap but also a few differences tied to the distinction between microsaccades and saccadic intrusions (Gowen, Abadi, Poliakoff, Hansen, & Miall, 2007).
The list of results demonstrates that microsaccades are associated with a wide range of research areas in behavior, cognition and neural functioning. For the detection of microsaccades in trajectories of fixational eye movements, methods were developed by
Boyce (
1967),
Martinez-Conde et al. (
2000) and
Engbert and Kliegl (
2004) that used the microsaccade property of their high velocity, i.e. they used their amplitude. The idea underlying their methods is to describe microsaccades as high velocity events of certain length. It was
Mergenthaler and Engbert (
2007) who reported that fixational eye movements can be modelled as fractional Brownian motion with persistent and anti-persistant behavior on a short and long time scale, respectively. They also investigated the influence of microsaccades on the scaling exponent which determines the characteristics of the underlying structure. Our working hypothesis is the definition of microsaccades as events that compared to the general structure in fixational eye movement trajectories have low regularities. We propose a scale-free detection method for microsaccades using the continuous wavelet transform (
Holschneider, 1995;
Mallat, 1998). It uses structural properties of the trajectory and the unlikeliness of microsaccadic events in the underlying drift movements, to detect microsaccades.
Using the results obtained by a detection method that uses structure properties of fixational eye movements, we continue with an analysis of the shapes obtained. We show, how to arrive at a data-driven microsaccade shape characterization by the use of principal component analysis (
Jolliffe, 2002). We will see that already two components are enough to describe the microsaccade shape within an appropriate range.
Methods
Microsaccades are rapid small-amplitude events with typical durations between 6 to 30 ms and amplitudes below 1
◦ (for an overview see (Engbert, 2006)). In this paper however we propose to not use their higher velocity as in (
Engbert & Kliegl, 2003) or (
Engbert & Mergenthaler, 2006), but rather use their local singularity structure. Wavelet analysis is a well suited toll to detect and characterize singularities within a more regular background.
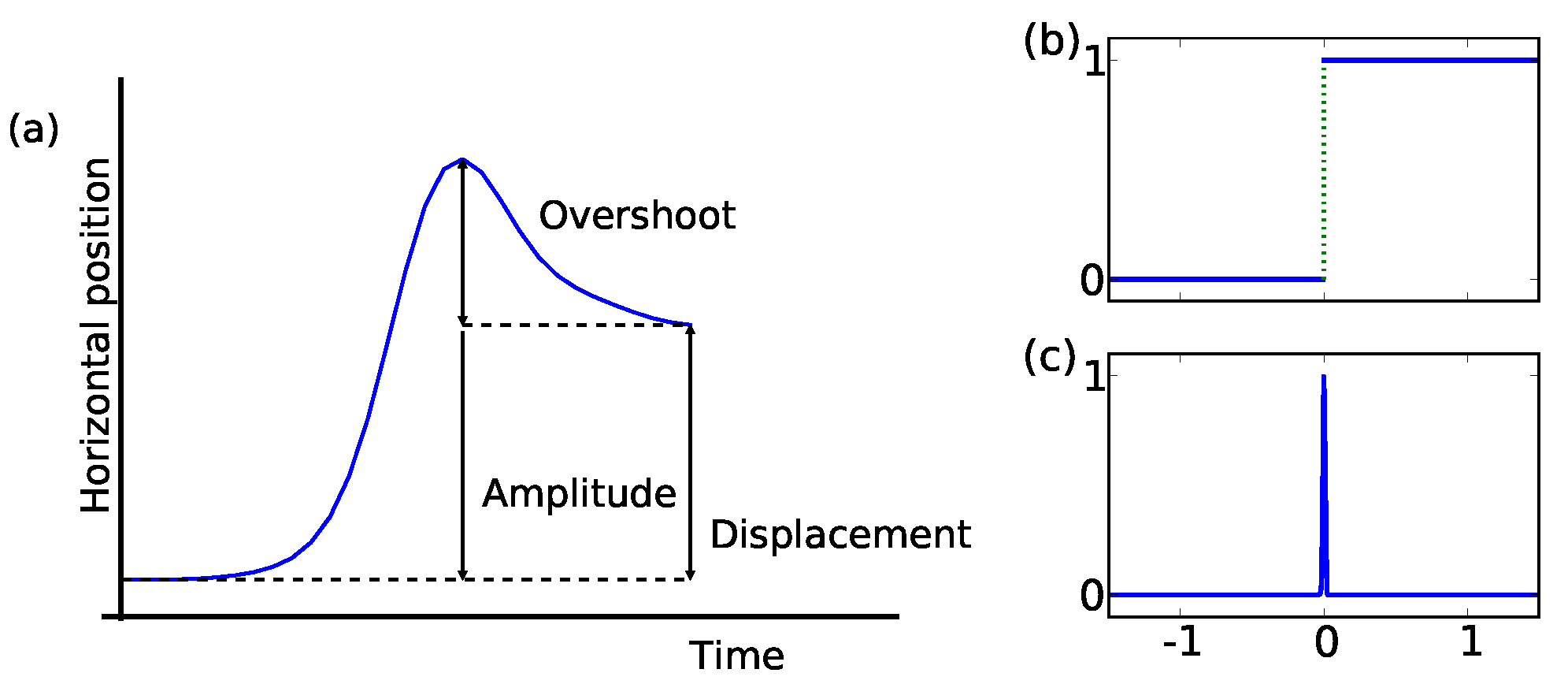
Singularities and local regularityOne first might ask how the mathematically motivated term singularity applies to the description of a microsaccade. Following Zuber, Stark, and Cook (1965), we sketch a prototypical microsaccade shape in
Figure 1. The y-axis is the horizontal eye movement plotted over time (x-axis). Thus, in this example, after an initial period of rest, the eye moves quickly towards the right and returns partially towards the left before arriving at the new horizontal position. The illustration depicts three important characteristics of microsaccade topology: amplitude, displacement, and overshoot. We refer to the maximum excursion as the amplitude and amplitude minus overshoot as the effective displacement (see
Figure 1a). Thus, the distinction between amplitude and displacement is due to variations in the overshoot component and is relevant to kinematic as well as functional aspects of microsaccades.
Figure 1.
Microsaccades can mathematically be defined as superposition of two functions with singular points. (a) We have labeled several attributes which allow a further description of the eye’s displacement. The eye’s trajectory is drawn on the Y-axis against time on the X-axis. Smoothing the (a) Heavyside and (b) Dirac delta function and superpose them, will return a microsaccade shape.
Figure 1.
Microsaccades can mathematically be defined as superposition of two functions with singular points. (a) We have labeled several attributes which allow a further description of the eye’s displacement. The eye’s trajectory is drawn on the Y-axis against time on the X-axis. Smoothing the (a) Heavyside and (b) Dirac delta function and superpose them, will return a microsaccade shape.
This schematic representation of a microsaccade shape can mathematically be described by a superposition of smoothed versions of the singularities depict in
Figure 1b and 1c. These two schematically show shapes of functions that have scale invariant singularities: the Heavyside and Dirac delta function. Both functions are singular at zero. In fixational eye movement trajectories, the drift and tremor movement describe the baseline of position-time displacements. Microsaccades do not share the same property of self-similarity at this baseline (compare
Mergenthaler & Engbert, 2007), influence the latter and appear as singular events in the more regular drift movement.
Singularity detection
For the analysis of microsaccades, we exploit the idea that microsaccades are more irregular than some background movement. In real data however perfect singularities cannot be observed. Perfect singularities are physiologically impossible because they would require infinite accelerations. We rather expect to have smoothed singularity. This is a shape which at large scale looks singular, whereas at small scale the physiologal limitations enforce a more regular behavior.
A pure singularity will give rise to a conelike structure of strong wavelet coefficients with the top at the time-point, where the singularity occures. A smoothed singularity will behave the same at all scales, which are large compared to the smoothing scale. In
Figure 3, such small cones that cross the whole frequency range can be identified by eye.
Numerically singularity detection with wavelets is usually done using the so called method of
maximum modulus lines (see
Marr & Hildreth, 1980;
Witkin, 1983). A maximum modulus line is a line in the time-scale plane on which the modulus of the wavelet transform has a local maximum with respect to small variation in
b0 such that
![Jemr 03 00022 i003 Jemr 03 00022 i003]() | (3) |
Connecting such points will give the maximum modulus lines. It can be shown that if a signal has a singularity at point then there is a maximum modulus line which at small scale converges towards the location of the singularity (e.g., (
Mallat & Hwang, 1992)). In smoothed singularities the maximumum modulus line may end at a scale which is about the smoothing scale of the singularity. For this reason we consider those maximum modulus lines, which go from a fixed highest frequency / smallest scale to a smallest frequency / largest scale. The estimated position of the singularity is simply the small-scale end of the corresponding maximum modulus line.
Figure 3b shows a typical example of a wavelet transform for the horizontal component of fixational eye movements. The maximum modulus in the (
a,b)plane, here highlighted in red.
Taking previous works into consideration (
Ditchburn & Ginsborg, 1952; Krauskopf, Cornsweet, & Riggs, 1960), microsaccades are generally binocular, conjugated eye movements and we consider only binocular singularities. This means, positions of a singularity in one eye are not allowed to differ more than τ from the positions of a singularity in the other eye, i.e., microsaccades in one eye have their simultaneous appearing microsaccades in the other eye in a time window (
t0−τ
,t0+τ). We will refer to this criterion as
binocularity criterion.
In this study, we restrict the analysis to the horizontal component of fixational eye movements. Previous work suggested that microsaccades show a preference for horizontal orientation (
Engbert & Kliegl, 2003; Engbert & Kliegl, 2003).
Microsaccade characterization
In the previous section we have shown how the analysis of the continuous wavelet transform helps us to detect singularities in fixational eye movement trajectories. We use this information to extract an area around these singularities to investigate the characteristics of the eye’s position as e.g., the shape of a microsaccade. For each of the binocular singularities detected with the method described in the previous section, we extract
K data samples corresponding to an epoch of the time series around the location of a singularity. We call this segment a signal snippet. To investigate if typical shapes for microsaccades exist in fixational eye movement data, we made use of the
principal component analysis (PCA, see
Jolliffe, 2002;
Smith, 2002, for a short tutorial) to systematically describe the large variability of all possible microsaccadic shapes. The principal component analysis is a way to represent a given data set in a reference frame whose dimensions, the principal components, are such that: the first accounts for as much of the variance in the data as possible, the second for as much as possible of the remaining variance and so on. All
pci together represent an empirical orthonormal system. In addition to the principal components
pci, we obtain a measure of the importance of each dimension in relation to the others, given by the singular values
s. Now, one rewrites the shape of a microsaccade (
ms) with a linear combination of these principal shapes:
where
pci is the
ith principal component,
ci is the coefficient that explains the contribution of this
ith shape, and
K is the length of a signal snippet. Due to the interpretation of the obtained principal components for fixational eye movements, we will use
principal shapes and
principal components as synonyms.
Before the analysis of our data for their
pci, we need to preprocess the input data. First, we remove the constant signal offset by subtracting the mean value from each signal snippet, i.e.
![Jemr 03 00022 i005 Jemr 03 00022 i005]() | (5) |
with
l indicating one individual signal snippet. Then we compose a matrix
M of dimension
Nx
K with
N given by the total number of detected singularities and
K the length of each snippet. We subtract the ensemble mean from
M, i.e.,
![Jemr 03 00022 i006 Jemr 03 00022 i006]() | (6) |
with
mij being the elements of the matrix
M. Using
singular value decomposition (SVD, see
Venegas, 2001) we write
as a product of three matrices
![Jemr 03 00022 i007 Jemr 03 00022 i007]() | (7) |
where
U is an orthogonal
Kx
K matrix which contains as columns the orthonormal vectors that represent the orthonormal system for all row vectors of
. The matrix
V is an orthonormal
Nx
N matrix whose columns represent the orthonormal system for all column vectors of
and
S is a rectangular, diagonal
Kx
N matrix containing the
K singular values in its diagonal. After SVD, the columns of
U contain the principal components
pci,
i =0
,...,K−1 which best describe the collection of the singularities along the
K dimensions. The diagonal entries of
S, namely
s0,0,...,sk−1,k−1 give us a measurement for the importance of each
pci. Therefore we evaluate
![Jemr 03 00022 i008 Jemr 03 00022 i008]() | (8) |
with
hh =(0
,0)
,...,(
k−1
,k−1). Having this measure we are able to reduce the dimensions of the obtained orthonormal system to a lower complexity but still containing sufficient information to describe the variability of inlying functions to a high level.
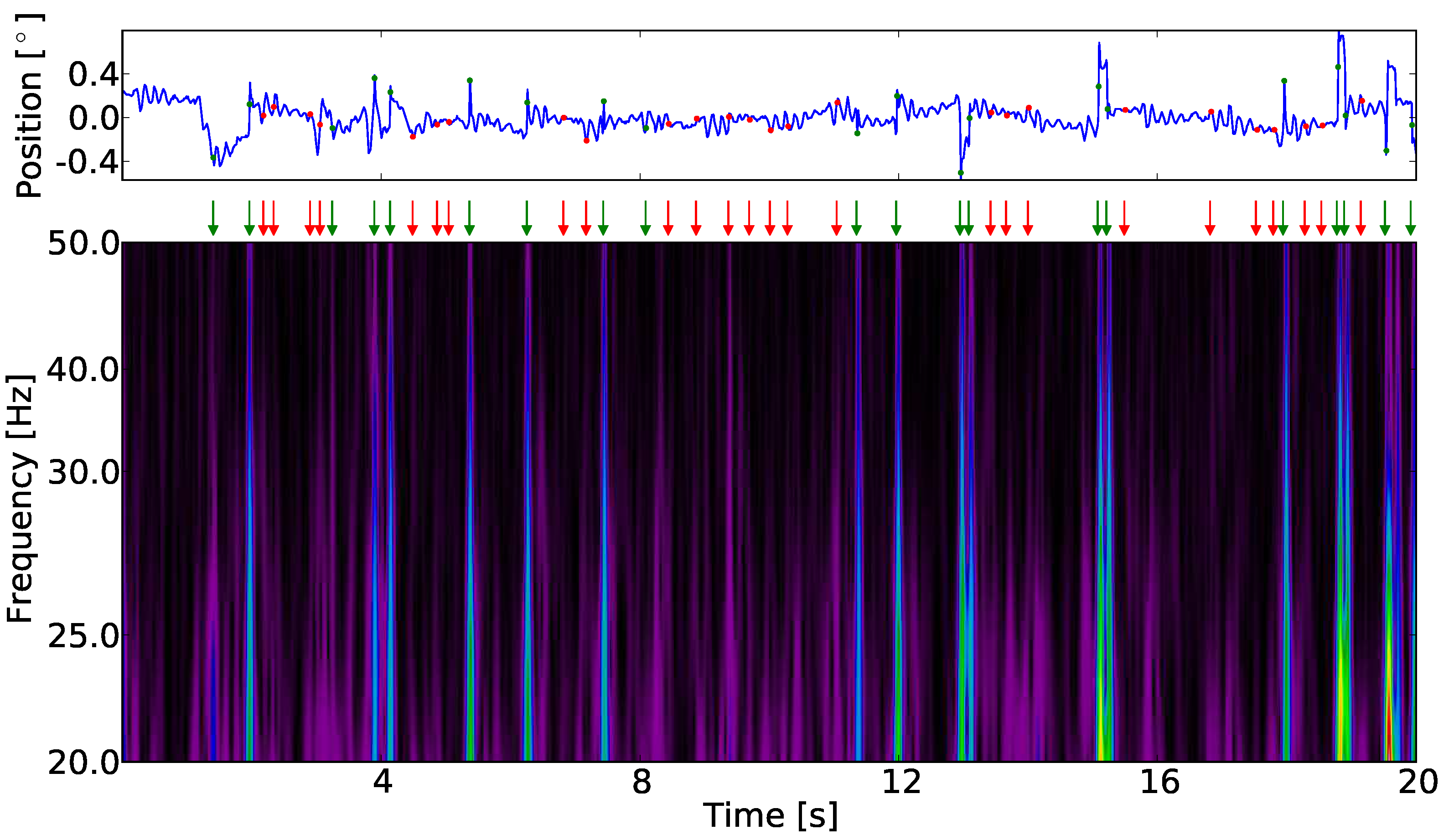
Figure 3.
One horizontal fixational eye movement trajectory in position-time and time-frequency representation. The marker indicate the positions of singularities (red dots and arrows) and binocular (green dots and arrows) singularities. The modulus of the wavelet transform allows the identification of maximum modulus lines. The time point at which a singularity occurs is taken at the highest frequency. The positions of maximum modulus lines match candidates in the time-position trajectory which e.g., by visual inspection would be identified as microsaccades.
Figure 3.
One horizontal fixational eye movement trajectory in position-time and time-frequency representation. The marker indicate the positions of singularities (red dots and arrows) and binocular (green dots and arrows) singularities. The modulus of the wavelet transform allows the identification of maximum modulus lines. The time point at which a singularity occurs is taken at the highest frequency. The positions of maximum modulus lines match candidates in the time-position trajectory which e.g., by visual inspection would be identified as microsaccades.
In the process of this work we reconstruct the shape of binocular singularities with the principal components. We will see how these representations vary between subjects.
In summary, we identify binocular singularities that give us candidates for binocular microsaccades in our fixational eye movemement study. The representation of a signal snippet with principal components gives possibilities for further discussion about the importance of each component contributing to the variability of microsaccadic eye movement. This will be discussed in the result section below.
Results
The method of singularity detection identified segments of fixational eye movements that represent candidates for microsaccades.
Figure 3 displays the wavelet transform of a time series of one single trial of fixational eye movement. All local maximum modulus lines which passed without interruption between 20 Hz to 50 Hz and met the condition in Equation (3) with at maximum ε=5 ms at 20 Hz are included in the analyses. We have chosen this frequency range because the left and right eye are well correlated over this range. Additionally we want to work above a threshold of 20 Hz as the wavelet transform maximum modulus lines will get influenced by modulus maxima of the other structures present in our data at lower frequency. A binocular singularity is defined by the time point a singularity is detected in left and right eye. The time point is allowed to differ of most by 30 ms. In
Figure 3a we have marked the positions of singularities detected in the wavelet plane. In
Table 1 we summarize the number of detected monocular singularities as well as the binocular singularities per participant in left and right eye, respectively.
In the total number of 682 trials, we detected 35531 and 35066 singularities in left and right eyes, respectively. The difference in the number of detections between eyes is lower than 1.3%, yielding good agreement for the microsaccadic processes in both eyes. After application of the binocularity criterion as described in section , we retain a total number of 16947 binocular singularities. The mean rate of binocular singularities is 1.2 per second with a standard deviation of 0.5. In this study, seven participants contributed less than one binocular singularity per second in their fixational eye movement. As the number of detected singularities in their eye movement trials is in agreement with those of other participants, their results are suggestive of monocular events.
Figure 5.
Representation of a time series snippet around the location of a singularity with its principal shapes processed by the principal component analysis. The left side of this equationlike representation is the horizontal position in a 60 ms time window around an identified singularity. Here, it is defined by the linear combination of principal shapes. We identified that already two shapes are sufficient to represent roughly 95% of the variances contained in each individual shape. The coefficients c0,c1,... are individual for each binocular singularity and explain the contribution of the corresponding shape to the individual shape.
Figure 5.
Representation of a time series snippet around the location of a singularity with its principal shapes processed by the principal component analysis. The left side of this equationlike representation is the horizontal position in a 60 ms time window around an identified singularity. Here, it is defined by the linear combination of principal shapes. We identified that already two shapes are sufficient to represent roughly 95% of the variances contained in each individual shape. The coefficients c0,c1,... are individual for each binocular singularity and explain the contribution of the corresponding shape to the individual shape.
Next, we investigate the signal snippets around the detected binocular singularities for common features. Equation (4) enables us to rewrite each shape as a linear combination of reliably measured basic shapes. The variance contribution of each is measured in the individual coefficients for the shape. We have taken snippets of the fixational eye movement trajectory with the length
K = 31 around a binocular singularity position. We are interested in the 30 ms before and after the time point we detected. We preprocess the data as described in section
Microsaccade characterization and obtain a representation as shown in
Figure 5 which is a visual representation of the components in Equation (4).
The PCA of the detected snippets reveals that the first two principal components pc0 and pc1 account for roughly 95% of the variability of microsaccadic shapes (compare Equation (8) which measures the importance of each single pci or combination of the same). At this, each component separately accounts (in average of both eyes) for 82.7 and 81.2% as well as 12.2 and 13.4% for pc0 and pc1 in left and right eye, respectively. We restrict therefore our analysis to these first two principal shapes. We decompose each single microsaccade ms(l) into the following five terms:
a linear combination of pc0 and pc1
a vector ρ, representing the mean of the whole ensemble for each eye (see Equation (6))
a scalar κ(l), representing the mean of each snippet (see Equation (5))
a small residual vector r capturing numerical errors
Table 1.
Rates of detected singularities in the horizonal eye movement in our fixation task experiment. The number of binocular singularities is a subset of all detected. The total rates are given as mean ± standard deviation.
Table 1.
Rates of detected singularities in the horizonal eye movement in our fixation task experiment. The number of binocular singularities is a subset of all detected. The total rates are given as mean ± standard deviation.
| Participant | Number of trials | | |
| left | right |
| 1 | 30 | 2.6 | 2.7 | 1.5 |
| 2 | 29 | 3.3 | 3.3 | 2.4 |
| 3 | 30 | 2.7 | 2.8 | 1.4 |
| 4 | 30 | 2.2 | 2.1 | 0.3 |
| 5 | 22 | 2.3 | 2.3 | 0.6 |
| 6 | 30 | 2.8 | 2.9 | 1.8 |
| 7 | 30 | 2.8 | 2.8 | 1.7 |
| 8 | 30 | 2.9 | 2.8 | 1.7 |
| 9 | 30 | 2.1 | 2.0 | 0.5 |
| 10 | 17 | 2.6 | 2.5 | 1.0 |
| 11 | 28 | 2.5 | 2.4 | 1.0 |
| 12 | 30 | 2.4 | 2.4 | 0.8 |
| 13 | 29 | 2.3 | 2.3 | 0.6 |
| 14 | 30 | 2.6 | 2.5 | 1.2 |
| 15 | 29 | 3.1 | 2.9 | 1.8 |
| 16 | 30 | 2.7 | 2.5 | 1.2 |
| 17 | 29 | 2.4 | 2.4 | 0.8 |
| 18 | 23 | 2.6 | 2.5 | 1.4 |
| 20 | 29 | 2.8 | 2.7 | 1.7 |
| 21 | 29 | 2.9 | 2.9 | 1.9 |
| 22 | 30 | 2.1 | 2.1 | 0.3 |
| 23 | 29 | 2.6 | 2.5 | 1.2 |
| 24 | 30 | 2.8 | 2.7 | 1.7 |
| 25 | 29 | 2.5 | 2.5 | 1.2 |
| Total | 682 | 2.6±0.3 | 2.6±0.3 | 1.2±0.5 |
Except for the residual vector, all these components are directly computed from the data. Now, we write our model for a typical microsaccade by the linear combination
![Jemr 03 00022 i009 Jemr 03 00022 i009]() | (9) |
while
l denotes the index of each individual microsaccade. The shapes of
pc0 and
pc1 are shown in
Figure 6a and 6b, respectively.
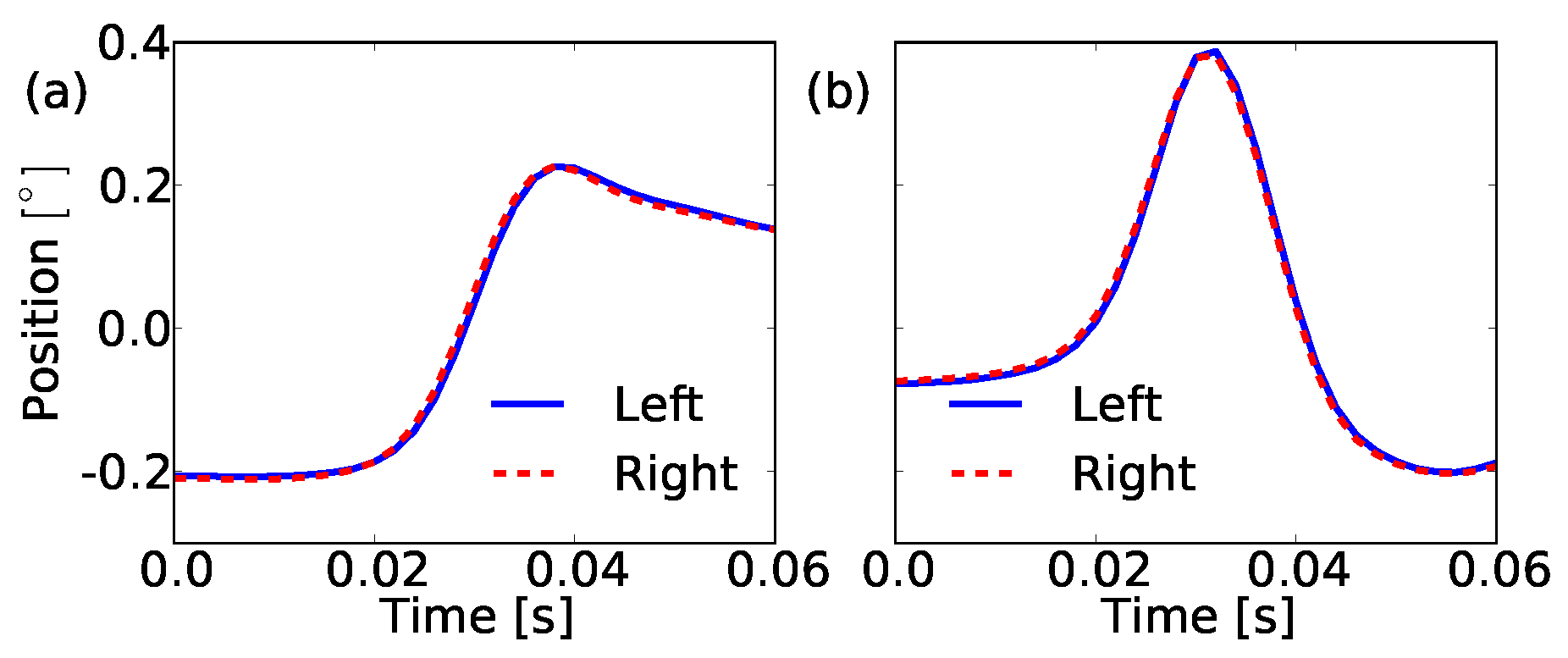
The first principal shape pc0 represents a movement of the eye with a short linearly increasing part and more importantly, it exhibits an overshoot. This returns the significance of this shape property and creates a prominent marker for microsaccadic movements. The second component pc1 is a bump whose contribution to the microsaccade shape seems to regulate the height of the overshoot.
Figure 6.
Graph of the shapes of the first two principal components which go into our model for a microsaccade. (a) We have for pc0 a steplike shape which has the tendency to return after it reached the maximum amplitude. This overshoot, typical for microsaccades, dominates together with the almost linear increasing shoot part this shape. (b) The shape of the second component pc1 is bumplike. It identifies how much overshoot each microsaccade has. The left (blue solid line) and right (red dashed line) eye agree in the shape of the first two principal components.
Figure 6.
Graph of the shapes of the first two principal components which go into our model for a microsaccade. (a) We have for pc0 a steplike shape which has the tendency to return after it reached the maximum amplitude. This overshoot, typical for microsaccades, dominates together with the almost linear increasing shoot part this shape. (b) The shape of the second component pc1 is bumplike. It identifies how much overshoot each microsaccade has. The left (blue solid line) and right (red dashed line) eye agree in the shape of the first two principal components.
For an investigation of individual microsaccade shapes, we need to measure how much each principal component contributes to the individual microsaccade shape. We quantify this by computing the projection of each microsaccade
ms(l) on
pc0 and
pc1 as follows
![Jemr 03 00022 i010 Jemr 03 00022 i010]() | (10) |
with |
ms(l)| = 1 and <
a,b> =
aTb denoting a column vector scalar product. Next, we represent the coefficient pairs (
c0,c1) in a coordinate system. The axes are given by the first and second principal shape which means that each microsaccade shape is plotted according to its reconstruction by the principal shapes. One representation is shown in
Figure 7.
Figure 7.
Representation of each microsaccade candidate in the pc0-pc1-coordinate system. Each dot is given by (c0,c1). The contribution of both of our model components is explained in this coordinate system. We take binocular singularities as binocular microsaccades whose variability is described to more or equal than 80% by our model (red dots between inner blue dashed and outer green solid circle).
Figure 7.
Representation of each microsaccade candidate in the pc0-pc1-coordinate system. Each dot is given by (c0,c1). The contribution of both of our model components is explained in this coordinate system. We take binocular singularities as binocular microsaccades whose variability is described to more or equal than 80% by our model (red dots between inner blue dashed and outer green solid circle).
With respect to these coefficient pairs we define microsaccades as those binocular shapes whose variability is described by more than 80% of the first two principal components. Expressed in an equation we write
![Jemr 03 00022 i011 Jemr 03 00022 i011]() | (11) |
A geometrical interpretation of this condition is shown in
Figure 7. Every point - marking one single binocular shape - between inner and outer ring is modeled as binocular microsaccade. To investigate the probabilities for a certain shape to occur in our trials, we sample the two-dimensional coefficient distribution to an one-dimensional distribution by taking the angle between the
c0-axis and the vector which points to our (
c0,c1) pairs, and obtain α
(l) by
![Jemr 03 00022 i012 Jemr 03 00022 i012]() | (12) |
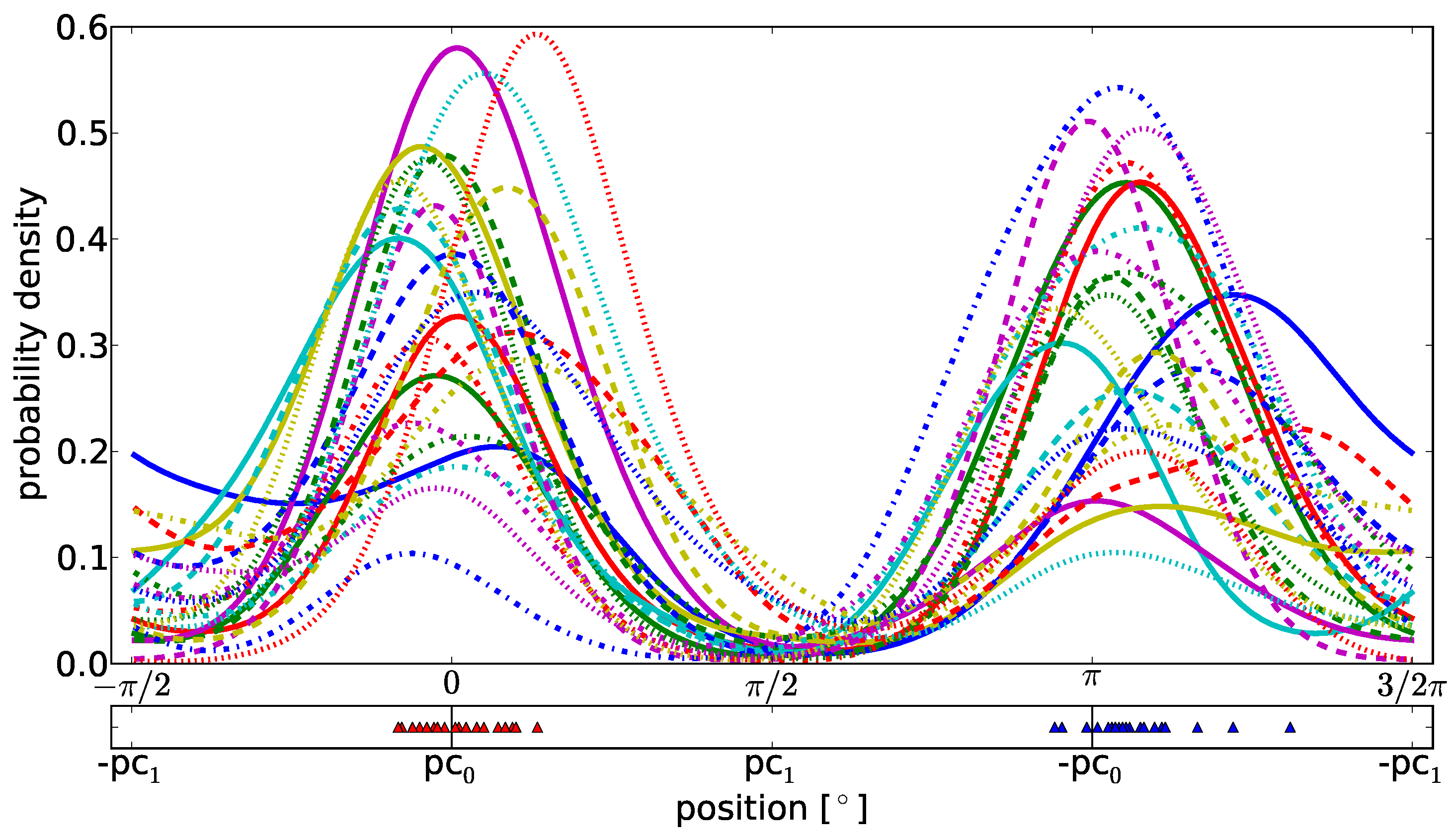
With the Gaussian kernel density estimation as shown in
Figure 8, we discover that the dominating shape of a microsaccade is given by
pc0, a steplike shape including an overshoot
. This result is true for all participants. The different widths of the peaks define how much the second component
pc1 varies the overshoot height between participants.
In the bottom of
Figure 8 we have selected the most probable shapes for each participant in the one and the contraverse direction. The individual contribution of
pc0 and
pc1 to these shapes is marked with a marker for each participant. Apparently, interindividual differences between humans are not based on the shapes of microsaccades but on their variation in overshoots and therefore, in the precision of the microsaccadic eye movement.
To sum up the results, we see that given all binocular singularities, two principal components explain the variance of roughly 95% of the microsaccade shape and define our microsaccade model with these two shapes. The steplike shape with an overshoot represents the dominant shape of microsaccadic eye movement. Additionally, we see that the second component is a measure parameter for the overshoot and furthermore a criterion which admits a comparison of microsaccades between different participants. The second component does not yield an absolute measurement of the microsaccade and overshoot length but is a relative parameter between microsaccade amplitude and overshoot. Our model is capable of describing microsaccadic eye movements and lets us quantify characteristic statistics between individual participants.
Singularity detection and characterization in amplitude-adjusted surrogate data
In this section, we validate the applicability of our detection and characterization methods. First, we check the reliability of singularities detected with the continuous wavelet transform by comparison of original data and time series which mimic properties of the original fixational eye movement data. Second we want to support that the identified shapes of the first principal components are typical for microsaccadic eye movements.
Figure 8.
(Upper graph) Gaussian kernel density estimation for binocular microsaccades which fit to our model and (lower graph) representation of the most probable shape combination of pc0 and pc1 for each individual participant. Each microsaccade coefficient pair (c0,c1) is transformed to the one dimensional α(l) with l being the index of a microsaccade. The density estimation reveals the dominance of the first principal shape pc0 (localization around 0 and π) above pc1. The lower graph shows the distribution of the most probable shapes in left and right direction and supports the former statement. This result holds for all participants. The contribution of the second component pc1 to the microsaccade shape differs between them which we see in the different widths of the peaks.
Figure 8.
(Upper graph) Gaussian kernel density estimation for binocular microsaccades which fit to our model and (lower graph) representation of the most probable shape combination of pc0 and pc1 for each individual participant. Each microsaccade coefficient pair (c0,c1) is transformed to the one dimensional α(l) with l being the index of a microsaccade. The density estimation reveals the dominance of the first principal shape pc0 (localization around 0 and π) above pc1. The lower graph shows the distribution of the most probable shapes in left and right direction and supports the former statement. This result holds for all participants. The contribution of the second component pc1 to the microsaccade shape differs between them which we see in the different widths of the peaks.
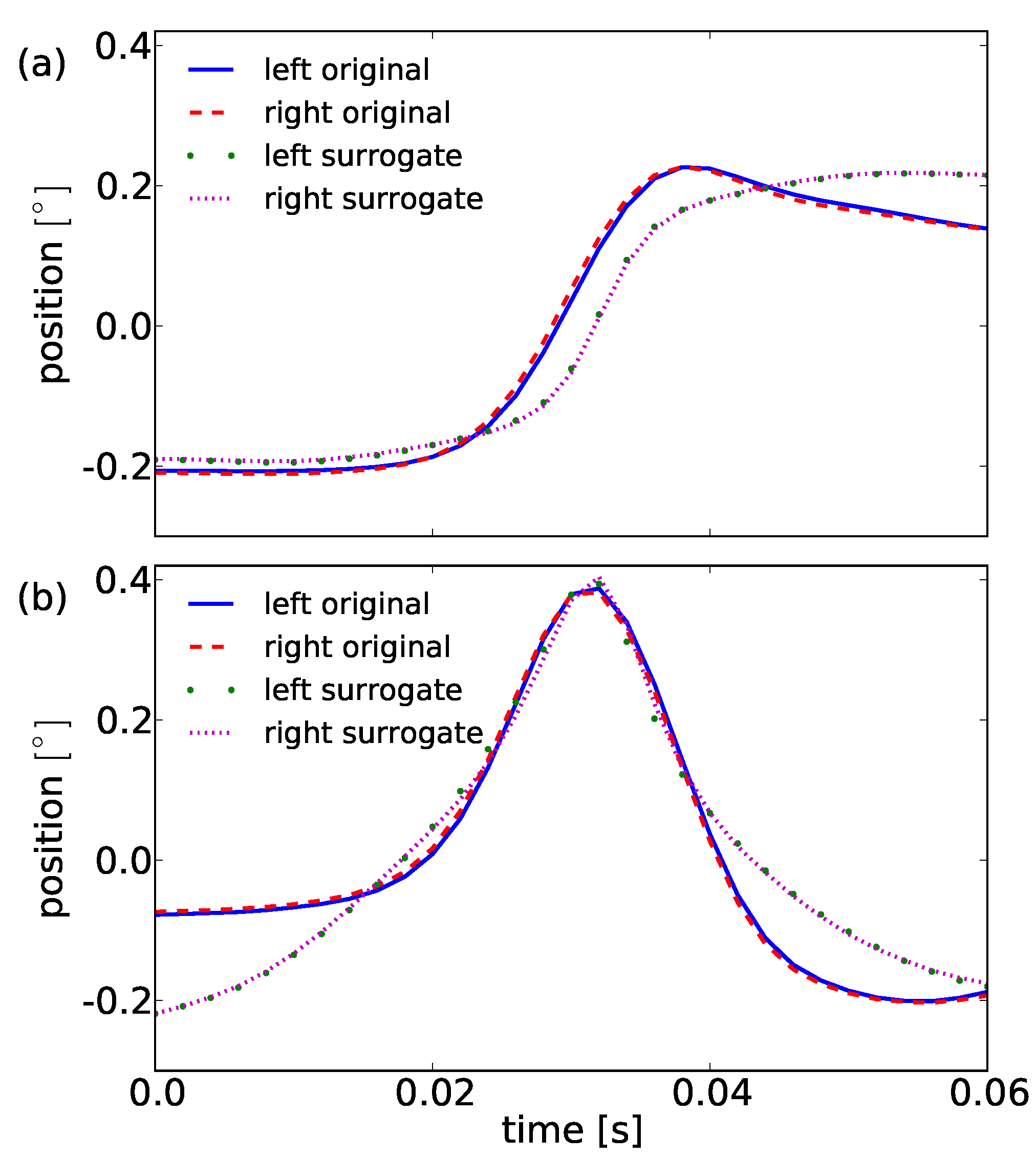
We generate a time series which mimic properties of fixational eye movements while destroying microsaccades, by applying an appropriate surrogate data generation method. In fixational eye movements studies we observe a persistent behavior on a short time scale (
Engbert & Kliegl, 2004;
Engbert & Mergenthaler, 2006) which is reflected in a positive autocorrelation function of the velocities for small lags. We need to reject the null hypothesis that positively autocorrelated samples in the drift are the reason for the observation of high-velocity epochs in fixational eye movements detected as singularities. A surrogate data type allowing to test the null hypothesis is amplitude-adjusted phase-randomized surrogate data (Theiler, Galdrikian, Longtin, Eubank, & Farmer, 1992) which maintains the velocity distribution and approximate the autocorrelation function. The velocity of our fixational eye movements is obtained as in Engbert and Kliegl (2003) via
![Jemr 03 00022 i013 Jemr 03 00022 i013]() | (13) |
where
s(
t) is the signal at position
t and ∆
t =0.002s. The generation of amplitude-adjusted surrogates is split into the following steps:
Sort v and obtain a rank series r of v
Generate a series g of Gaussian distributed random numbers with the same length as v, sort it and rearrange it according to the rank series r. In this way, we generate a time series h that is a rescaled time series of v with the property that the amplitudes of the samples belong to a normal distribution
Transform h to the Fourier space and obtain
- 4.
Randomize the phase:
![Jemr 03 00022 i015 Jemr 03 00022 i015]()
. φ is a series containing equally distributed random numbers between −π and π with identical values for positive and negative frequency
- 5.
Calculate the inverse of the Fourier transform:
![Jemr 03 00022 i016 Jemr 03 00022 i016]()
- 6.
Obtain a rank series of
![Jemr 03 00022 i017 Jemr 03 00022 i017]()
and rearrange
v in accordance with the new rank series
To return to a position-time series one sums the velocities divided by the sampling frequency cumulatively. In the following we refer to the latter as the surrogates or surrogate data of fixational eye movement time series. We take all 682 trials of surrogates and perform the same analysis as performed for the original data. The results for the detected singularities are shown in
Table 2.
We explain the higher number of singularities detected in the surrogate data by the conservation of each original velocity sample during surrogate data generation. Nevertheless, epochs of high velocities in fixational eye movement data, corresponding to microsaccades, can be split into two or more singularities in the surrogates. But this is only true for monocular singularities. However, we also observe a high number of binocular singularities, on average 10 per trial. The high number of binocular events results from the probability of randomly co-occuring extended events of length 2τ. Co-occuring means: A singularity in one eye happens within the window of τ milliseconds before or after a singularity in the other eye. Estimating the probability of this co-occurrence, we take a monocular time series of length T and a number of monocular singularities N.
As each singularity is in the center of a 2τ window and at least on sample ∆
t apart, a significant number of data samples belong to those which are possible candidates for a co-occurrence. Thus, the probability to observe a binocular event
E by chance is given by
![Jemr 03 00022 i018 Jemr 03 00022 i018]() | (14) |
which is the ratio of time, belonging to points of possible co-occurrence candidates in the full trajectory. For the presented data the values are: τ = 30 ms, ∆
t = 2 ms,
T = 20000 ms, and
N = 57, which is the average number of detected monocular singularities in our surrogate data. Inserting these values one gets
p(
E)·
N ≈ 10 binocular events simply by chance in our surrogate data. This result is in very good agreement with the numbers of observed binocular events in the surrogate data: On average 10 binocular events. Now, we argue that the obtained number of binocular events in surrogates mainly depends on the probabilitiy
p(
E) of random co-occurence, which is set by our time frame to define an event as binocular.
These randomly occurring binocular singularities, which also can happen in the original data, cannot be explained by the first principal components
pc0 and
pc1 by more than 80%. Thus, applying Equation (11) one filters out random binocular singularities in the analysis of original data. Further processing of the binocular singularities with the principal component analysis (see section
Microsaccade characterization) results in the principal components shown in
Figure 9. In this case, the first two components explain even more than 95% of the variance in our data and we choose
pc0s and
pc1s to reduce our 31 dimensional system of shapes to this two dimensions. Both components look similar but differ strongly in their shapes, compared to the principal components obtained for the original data. This becomes obvious by consideration of combinations of the two components. For surrogates the principal component
pc0s is a smoothed step and does not show any overshoot. The second component
pc1s is a very smooth peak-like bump. Both
pc0s and
pc1s are smoothed version of singularities, i.e. a step and a single peak as illustrated in
Figure 1.
Figure 9.
Representation of the first principal components’ shapes for the original data and surrogate data. Compare (a) pc0 and pc0s, the typical overshoot behavior in the smooth step is not present. Left (blue solid line) and right (red dashed line) eye again show approximately the same principal component in original as well as in surrogate data (green dotted and magenta dash-dotted line). (b) The second component for the original pc1 is a bump whether pc1s is a smooth peak shape.
Figure 9.
Representation of the first principal components’ shapes for the original data and surrogate data. Compare (a) pc0 and pc0s, the typical overshoot behavior in the smooth step is not present. Left (blue solid line) and right (red dashed line) eye again show approximately the same principal component in original as well as in surrogate data (green dotted and magenta dash-dotted line). (b) The second component for the original pc1 is a bump whether pc1s is a smooth peak shape.
Importantly, the
pc0 and
pc1 of the original data show a directionality in time: They cannot be reversed. The principal components
pc0s and
pc1s for the surrogate data can be reversed. Both fulfill the condition of symmetry, i.e.
f(−
t) = −
f(
t) and do not show any directionality. On the basis of the described differences in
pc0 and
pc1, we reject the described null hypothesis and conclude that the observed binocular singularities in fixational eye movement time series result from high-velocity epochs in fixations with a distinct shape given by a linear combination as explained in our model equation (9) with the components
pc0 and
pc1 of the original data, shown in
Figure 6.
Table 2.
Rates for the detected monocular and binocular singularities in the surrogates of horizontal fixational eye movement data sets. The total rates are given as mean± standard deviation.
Table 2.
Rates for the detected monocular and binocular singularities in the surrogates of horizontal fixational eye movement data sets. The total rates are given as mean± standard deviation.
| Participant | Number of trials | | |
| L | R |
| 1 | 30 | 2.5 | 2.6 | 0.4 |
| 2 | 29 | 3.1 | 3.1 | 0.6 |
| 3 | 30 | 2.8 | 2.7 | 0.4 |
| 4 | 30 | 2.4 | 2.2 | 0.4 |
| 5 | 22 | 2.7 | 2.5 | 0.5 |
| 6 | 30 | 2.9 | 2.9 | 0.5 |
| 7 | 30 | 3.1 | 3.0 | 0.6 |
| 8 | 30 | 3.2 | 3.2 | 0.7 |
| 9 | 30 | 2.5 | 2.5 | 0.4 |
| 10 | 17 | 2.7 | 2.6 | 0.4 |
| 11 | 28 | 3.1 | 3.0 | 0.6 |
| 12 | 30 | 3.0 | 3.2 | 0.6 |
| 13 | 29 | 2.3 | 2.3 | 0.3 |
| 14 | 30 | 2.8 | 2.4 | 0.5 |
| 15 | 29 | 3.1 | 3.0 | 0.6 |
| 16 | 30 | 2.7 | 2.5 | 0.4 |
| 17 | 29 | 2.4 | 2.3 | 0.4 |
| 18 | 23 | 3.3 | 3.3 | 0.7 |
| 20 | 29 | 3.2 | 3.2 | 0.7 |
| 21 | 29 | 3.4 | 3.3 | 0.7 |
| 22 | 30 | 2.5 | 2.4 | 0.4 |
| 23 | 29 | 3.3 | 3.3 | 0.7 |
| 24 | 30 | 2.8 | 2.7 | 0.4 |
| 25 | 29 | 3.4 | 3.3 | 0.7 |
| Total | 682 | 2.9±0.3 | 2.8±0.4 | 0.5±0.1 |
Discussion
We investigated the hypothesis that microsaccades can be modelled as events of lower regularity and see that the continuous wavelet transform successfully distinguishes microsaccades of fixational eye movement from background activity (i.e., drift). Our methods are based on a pre-defined minimal set of parameters (related to maximum modulus lines, binocularity, and the fit to the model). A validation that uses amplitude-adjusted surrogate data verifies that almost simultaneously appearing structures of low regularity in fixational eye-movement trajectories cannot be explained by randomly co-occuring autocorrelated samples in both eyes’ drift movements.
In comparison to current methods which use amplitudes (or its derivatives) for the detection of microsaccades, our alternative approach can identify large scale saccades and microsaccades within one detection procedure, e.g., in eye movements recorded during scene viewing or reading. Methods that use velocities require predefined thresholds such that an analysis either uses two detection runs to first separate saccades and then microsaccades (i.e., one uses a threshold related to the variance in the trajectory for saccade detection and subsequently another threshold related to the remaining variance), or instead uses a threshold defined by the variance obtained in co-recorded fixation-task experiments. Using the shared property of lower regularity (between microsaccades and saccades) allows the identification of both within the same detection process.
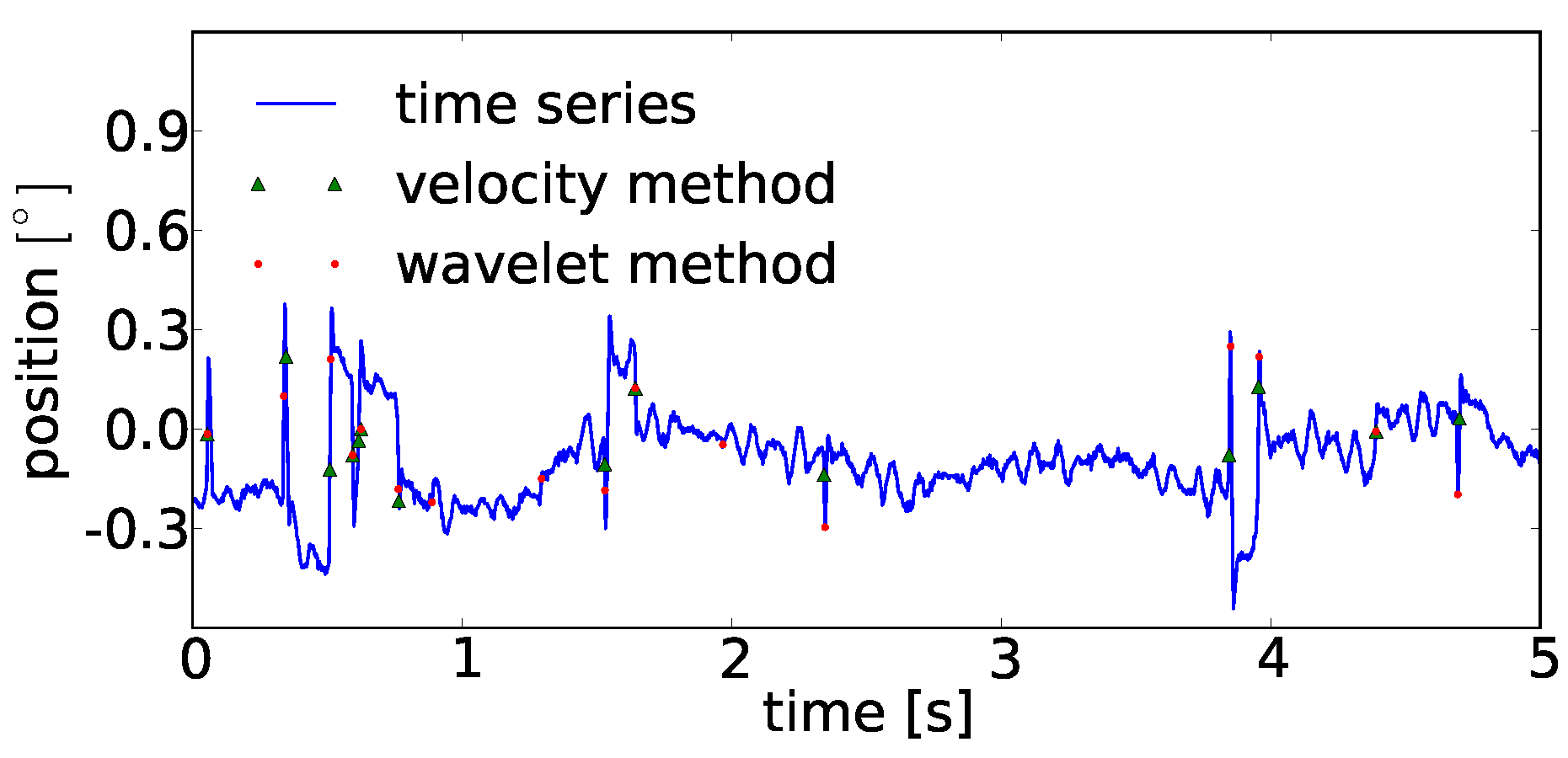
A very brief analysis between performances of the velocity threshold and continuous wavelet transform method on eye movement trajectories in a fixation task can be found in the
Appendix A. Seemingly, the detected microsaccade positions in fixational eye movements look quite similar.
We continued our analysis with a comparison of detected microsaccades between participants and performed a principal components analysis, yielding two main components whose linear combination describes the shapes of microsaccades. These two shapes cover over 94% of the present variance in the shapes of binocular microsaccades. The established simple linear model for a typical microsaccade shape convincingly agrees with the microsaccadic shape reported in studies of
Zuber et al. (
1965) which likewise reported an overshoot as typical property of a microsaccade (for more recent results that show microsaccades with overshoot in eye position traces recorded with electromagnetic induction technique, see Hafed, Goffart, & Krauzlis, 2009). The first principal component is a steplike shape with an overshoot and the second principal component characterizes the overshoot height. Combining both, we can represent microsaccades with all possible overshoot heights. This also includes rare microsaccades which do not share the overshoot shape. A two-dimensional coefficient pair and a measure for the amplitude returns the most simple property set for microsaccades.
In
Abadi and Gowen (
2004), four types of saccadic intrusions were reported for studies about characteristics of saccadic intrusions. Two microsaccadic shapes with a
Single Saccadic Pulse (
SSP), and
Double Saccadic Pulse (
DSP) were introduced by the authors. Additionally, two sequences of microsaccades were investigated which took two and three subsequent microsaccadic movements into account, the
Monophasic Square Wave Intrusion (
MSWI) and
Biphasic Square Wave Intrusion (
BSWI). Our microsaccade model is able to separate SSP and DSP simply by investigation of the more dominant principal shape, i.e., if the first prinicipal shape
pc0 is dominant, we count a SSP whereas if the second principal shape
pc1 is leading, we see a DSP.
In perspective, an analysis of sequences of microsaccadic shapes allows studies on short- and long-term dependencies as well as investigations with co-registered EEG data which profits from a better understanding of microsaccades and the induced potentials (Dimigen, Sommer, Hohlfeld, Jacobs, & Kliegl, under revision).
Future work will consider a stronger comparison of the two methods and the possibility to extend the detection method to horizontal and vertical (2D) eye movements and analyze their interplay in the context of microsaccadic movements. A subsequent classification of microsaccade shapes seems promising to investigate the spatiotemporal dynamics of microsaccades and may lead to a new model for the dynamics of fixational eye movements. An understanding of the latter under the well-defined conditions in fixation-task experiments allows the modeling of eye movements at its baseline. Establishing a model at this point will provide a foundation to study trajectories and reactions to attractions of the eye in more complex experimental setups.
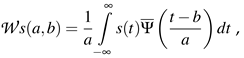


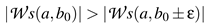
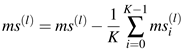
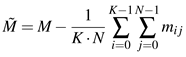
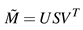
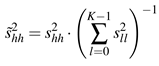


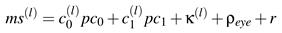


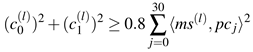
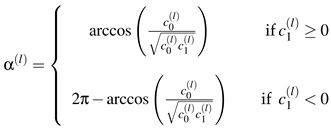
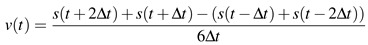
. φ is a series containing equally distributed random numbers between −π and π with identical values for positive and negative frequency
and rearrange v in accordance with the new rank series