Time Course and Hazard Function: A Distributional Analysis of Fixation Duration in Reading
Abstract
:Introduction
Fixations, Processes, and Popcorn
A Distributional Model of the Time Course of Reading Eye Movements
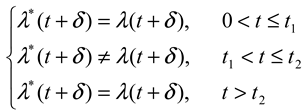
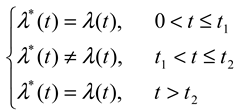
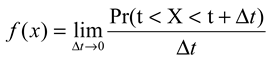
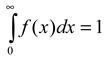 . This turns out to be a serious limitation for the present application: it implies that if X increases the saccadic pdf prior to t2, the pdf thereafter must be lower, just like the more efficient popcorn maker eventually makes less noise because most corn is already popped. Unfortunately, this violates the third condition in (2), where λ(t) = λ*(t) for t > t2; in other words, we cannot estimate the offset of the process X from the pdf. Another problem stems from the same constraint: because the pdf approaches zero for very long fixations, comparing the right tails of distributions becomes difficult (see Chechile, 2003; Luce, 1986; Van Zandt, 2000; Van Zandt & Ratcliff, 1995). For these reasons the pdf does not have the properties we sought in (2).
. This turns out to be a serious limitation for the present application: it implies that if X increases the saccadic pdf prior to t2, the pdf thereafter must be lower, just like the more efficient popcorn maker eventually makes less noise because most corn is already popped. Unfortunately, this violates the third condition in (2), where λ(t) = λ*(t) for t > t2; in other words, we cannot estimate the offset of the process X from the pdf. Another problem stems from the same constraint: because the pdf approaches zero for very long fixations, comparing the right tails of distributions becomes difficult (see Chechile, 2003; Luce, 1986; Van Zandt, 2000; Van Zandt & Ratcliff, 1995). For these reasons the pdf does not have the properties we sought in (2).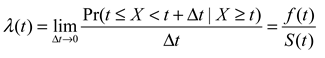
 is the survival function of X. The hazard rate λ(t) can be seen as f(t) with its right tail magnified by a factor of 1/S(t). The two functions are closely connected:
is the survival function of X. The hazard rate λ(t) can be seen as f(t) with its right tail magnified by a factor of 1/S(t). The two functions are closely connected: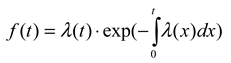
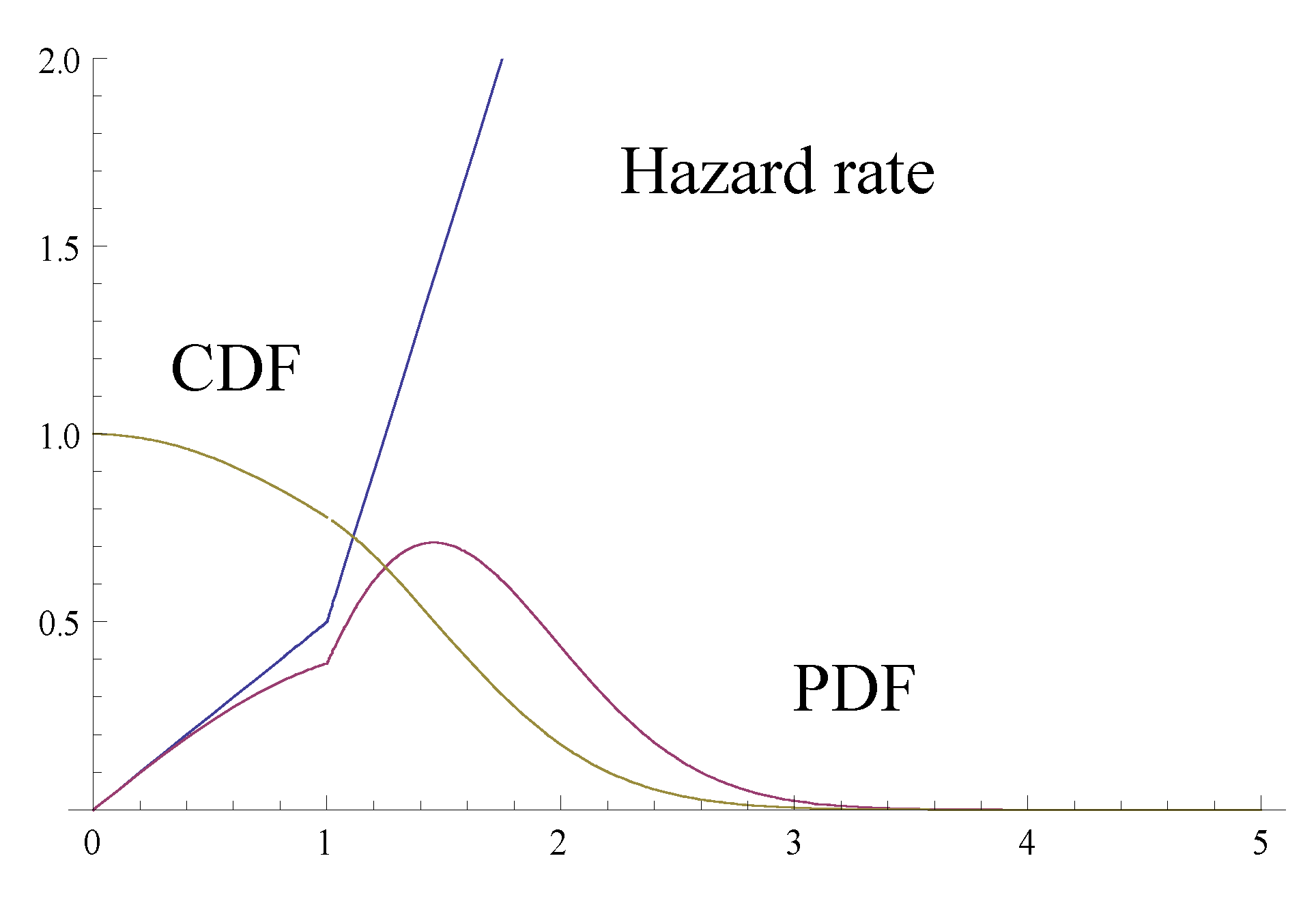
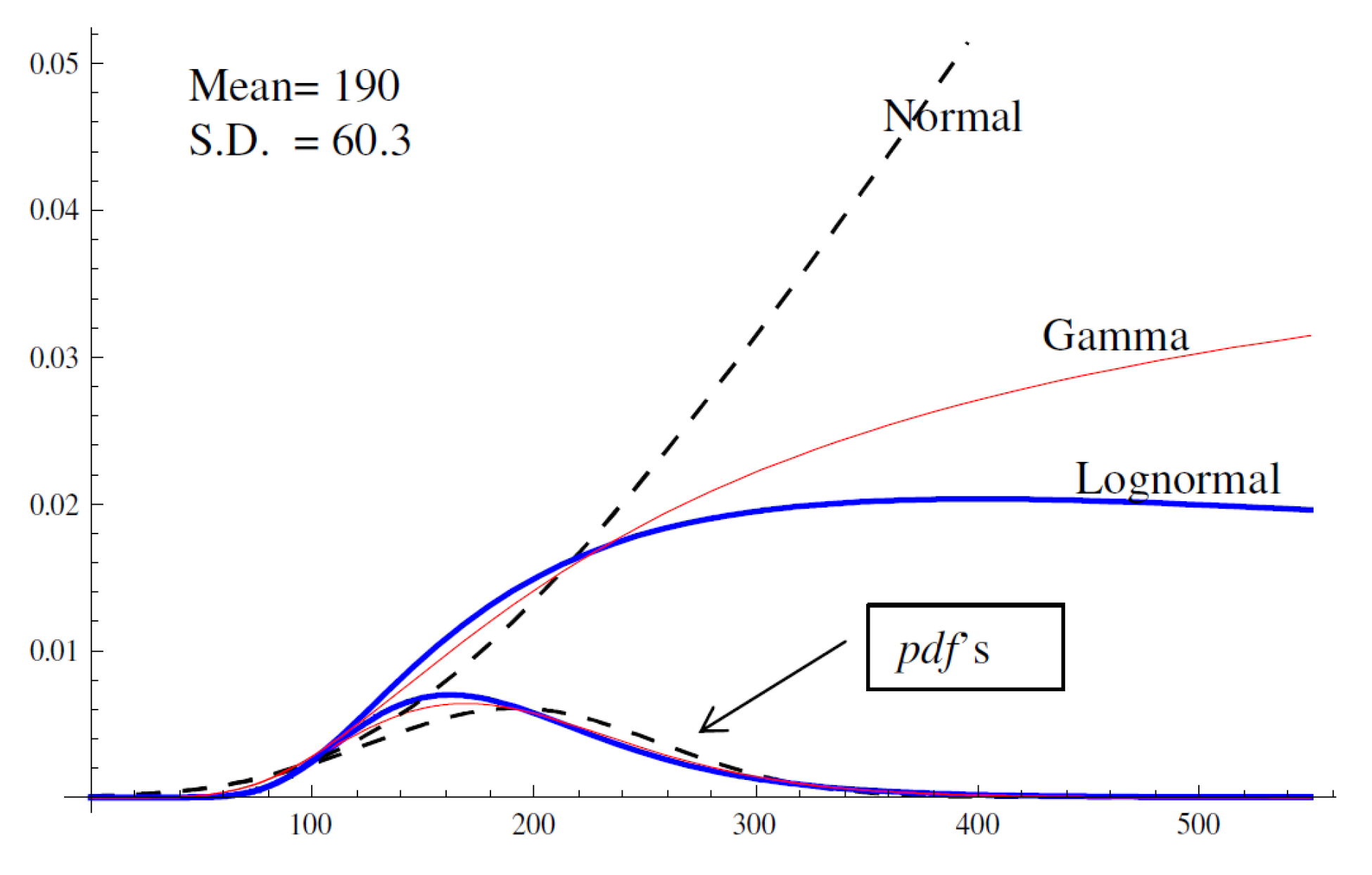
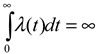 (i.e., the “lifetime” risk of saccade is infinity, to avoid “eternal fixations”). Figure 1 shows the pdf’s and hazard functions of three familiar distributions– the normal distribution, gamma distribution, and lognormal distribution – with the same means and standard deviations. All three distributions have been used as models of reading fixation duration (Feng, 2006; Reichle, Pollatsek, Fisher, & Rayner, 1998; Reilly & O’Regan, 1998). Despite similar shapes of the pdf’s, the hazard functions show distinct trajectories, especially at the right tail.
(i.e., the “lifetime” risk of saccade is infinity, to avoid “eternal fixations”). Figure 1 shows the pdf’s and hazard functions of three familiar distributions– the normal distribution, gamma distribution, and lognormal distribution – with the same means and standard deviations. All three distributions have been used as models of reading fixation duration (Feng, 2006; Reichle, Pollatsek, Fisher, & Rayner, 1998; Reilly & O’Regan, 1998). Despite similar shapes of the pdf’s, the hazard functions show distinct trajectories, especially at the right tail. , because some probability mass is discarded. To ensure a proper pdf, one must re-norm the function, which will elevate the entire function (shown as the green line in Figure 2). In contrast, the hazard function is not subject to the same constraint. The piecewise linear regression in Figure 2 is estimated with artifacts simply removed. The less jagged black line is a smoothed version (using the 3RS3R algorithm; see Tukey, 1977) of the cleaned-up hazard rate, demonstrating the fit of the linear function.
, because some probability mass is discarded. To ensure a proper pdf, one must re-norm the function, which will elevate the entire function (shown as the green line in Figure 2). In contrast, the hazard function is not subject to the same constraint. The piecewise linear regression in Figure 2 is estimated with artifacts simply removed. The less jagged black line is a smoothed version (using the 3RS3R algorithm; see Tukey, 1977) of the cleaned-up hazard rate, demonstrating the fit of the linear function.Relation with Other Distributional Models
The Empirical Study
Methods
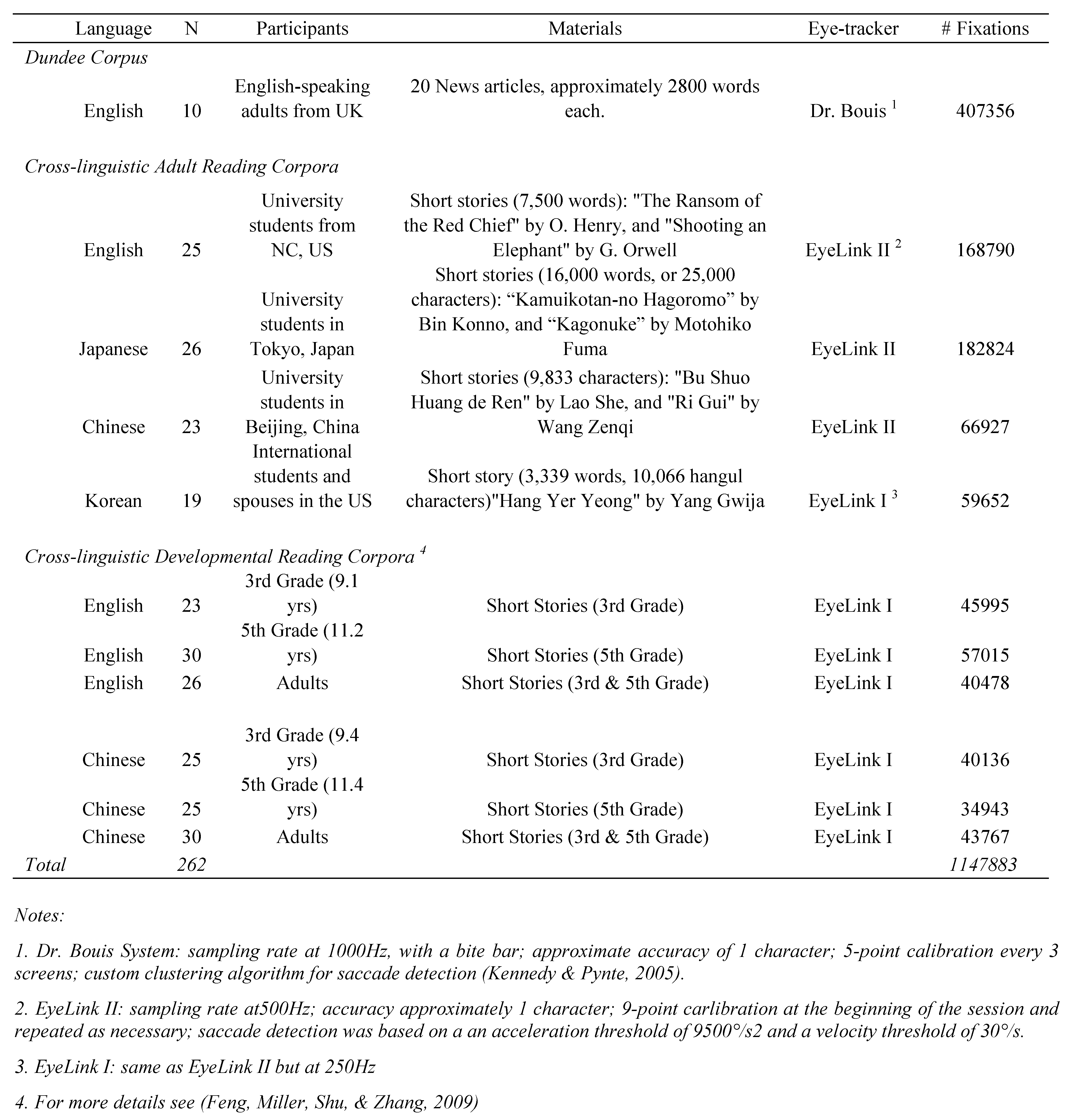
Corpora of Reading Eye Movements
Data Analysis
Results
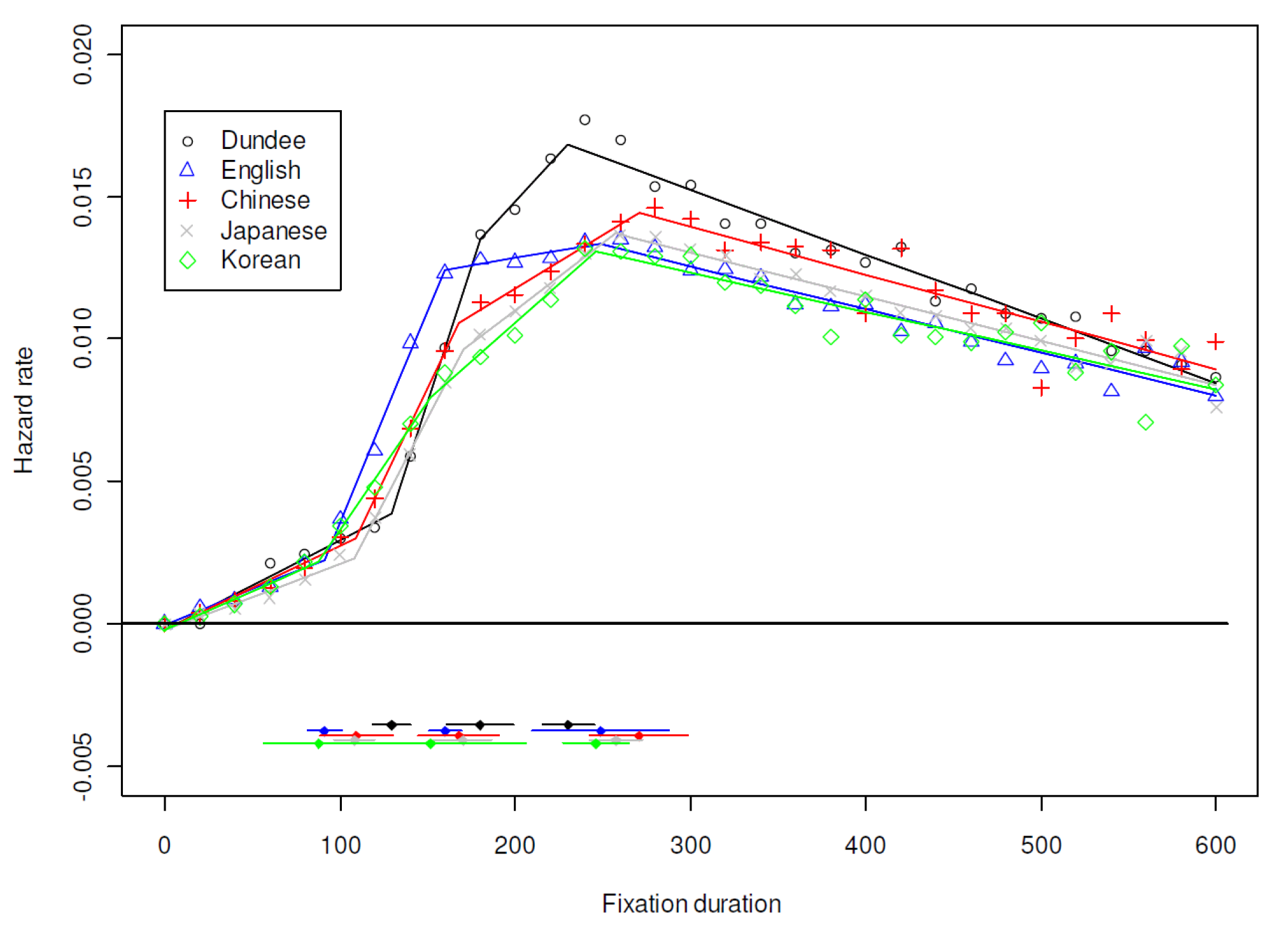
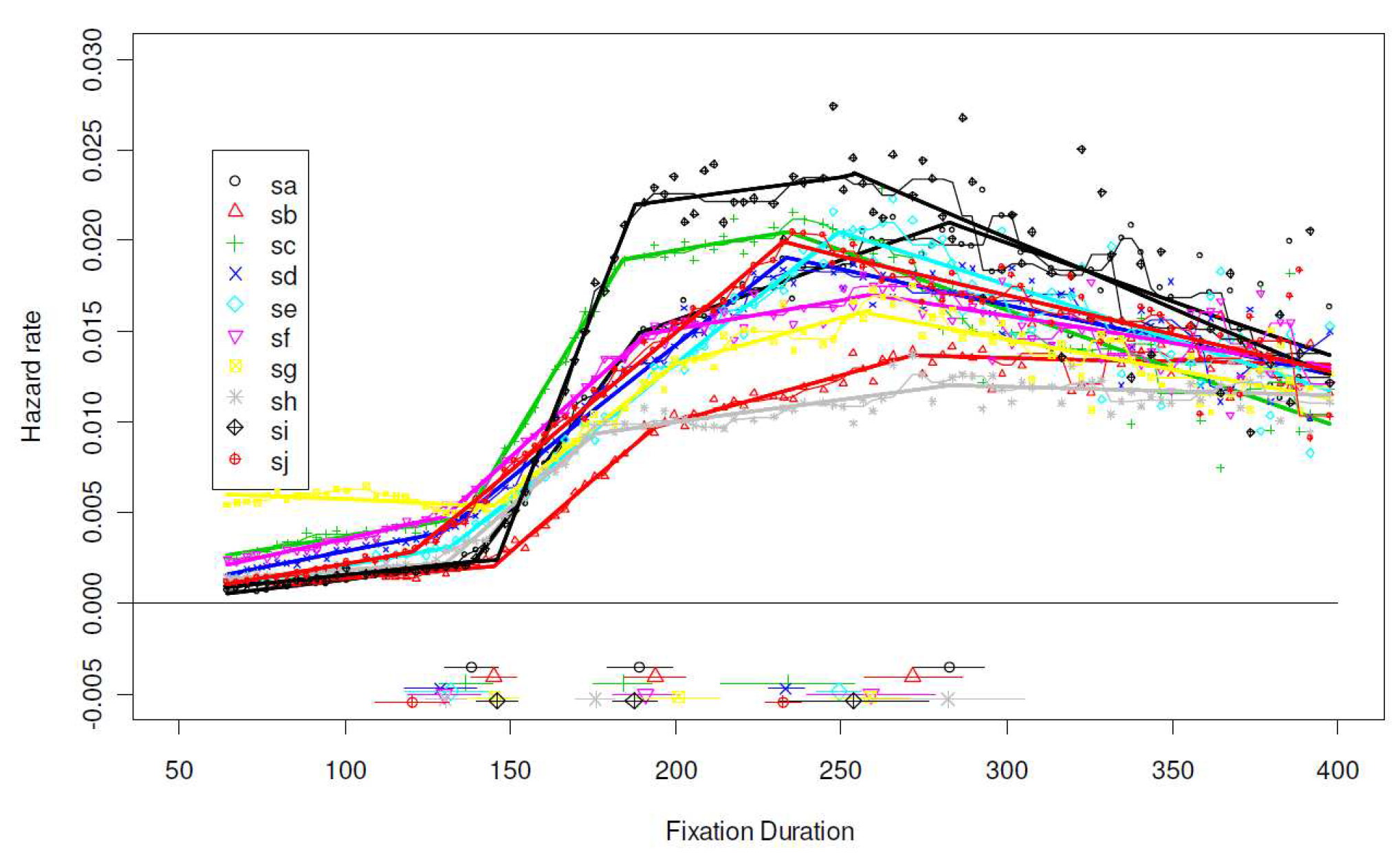
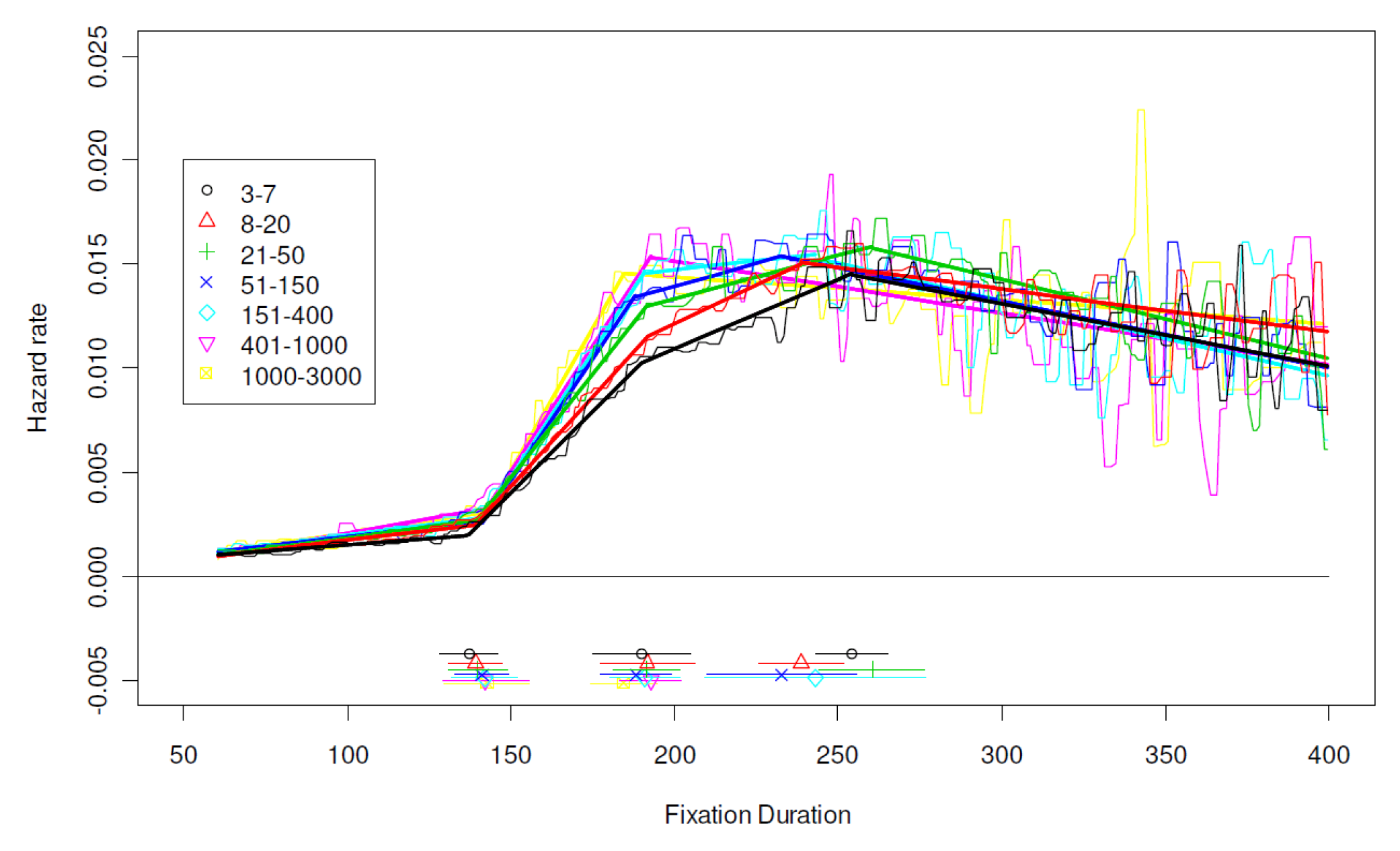
Language, Age, and Individual Differences
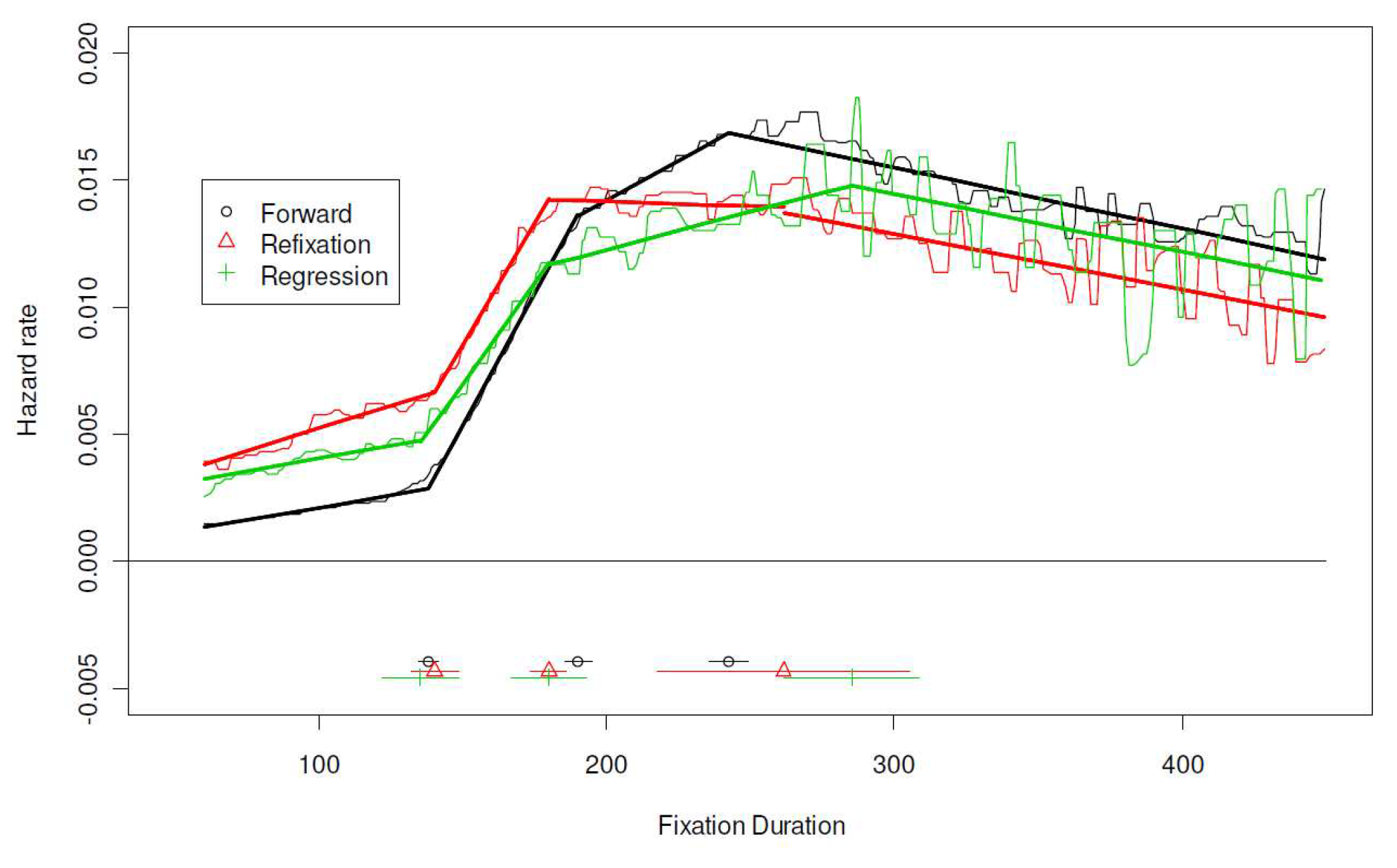
Modulation of Hazard Function by Processing Variables
Pooled Hazard Functions
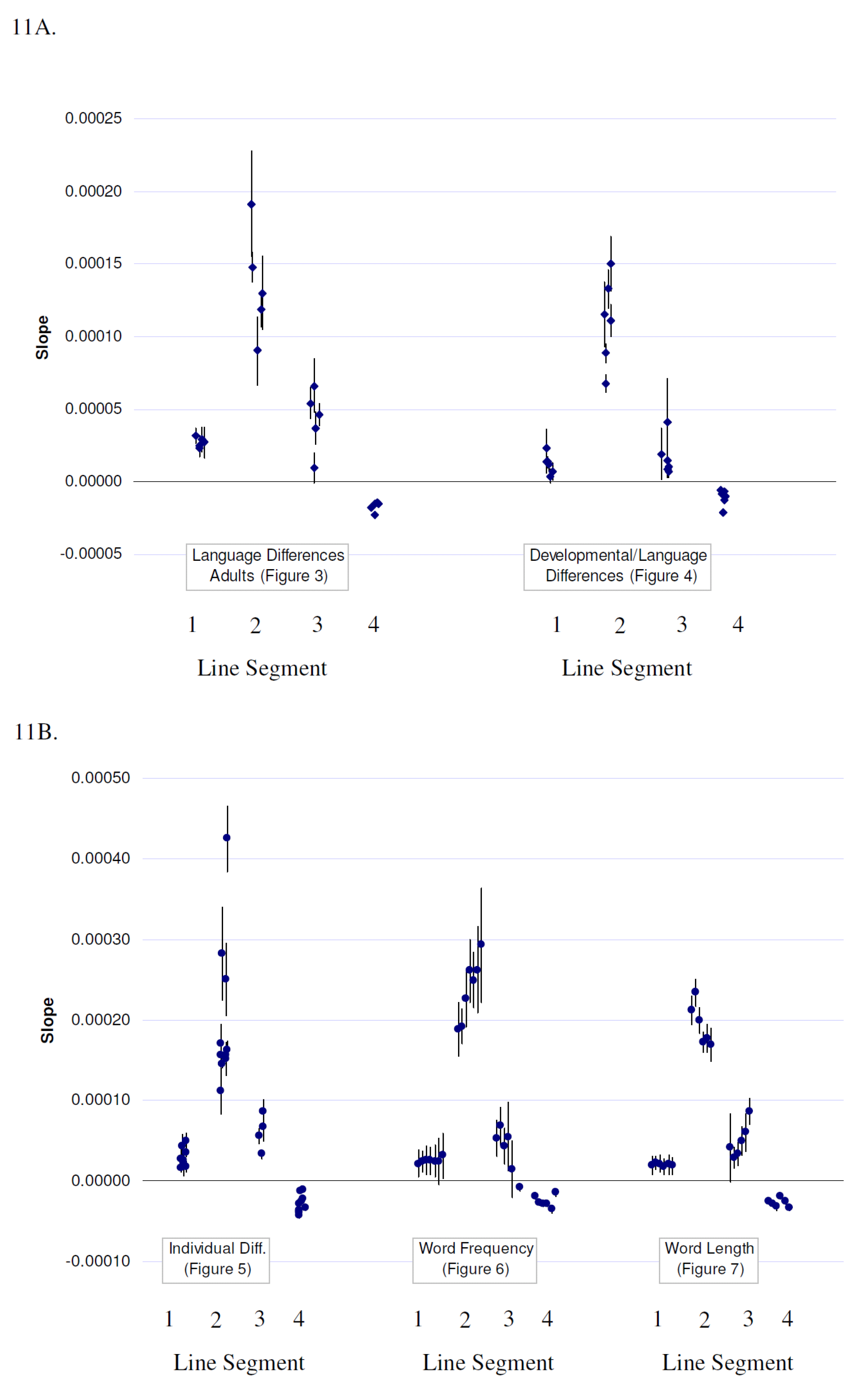
Summary of Changepoints and Regression Slopes
Discussion
Linking Distributions to Processes: The Instantaneity Assumption
Toward a Model of Reading Eye Movement Control


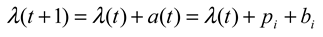
Funding
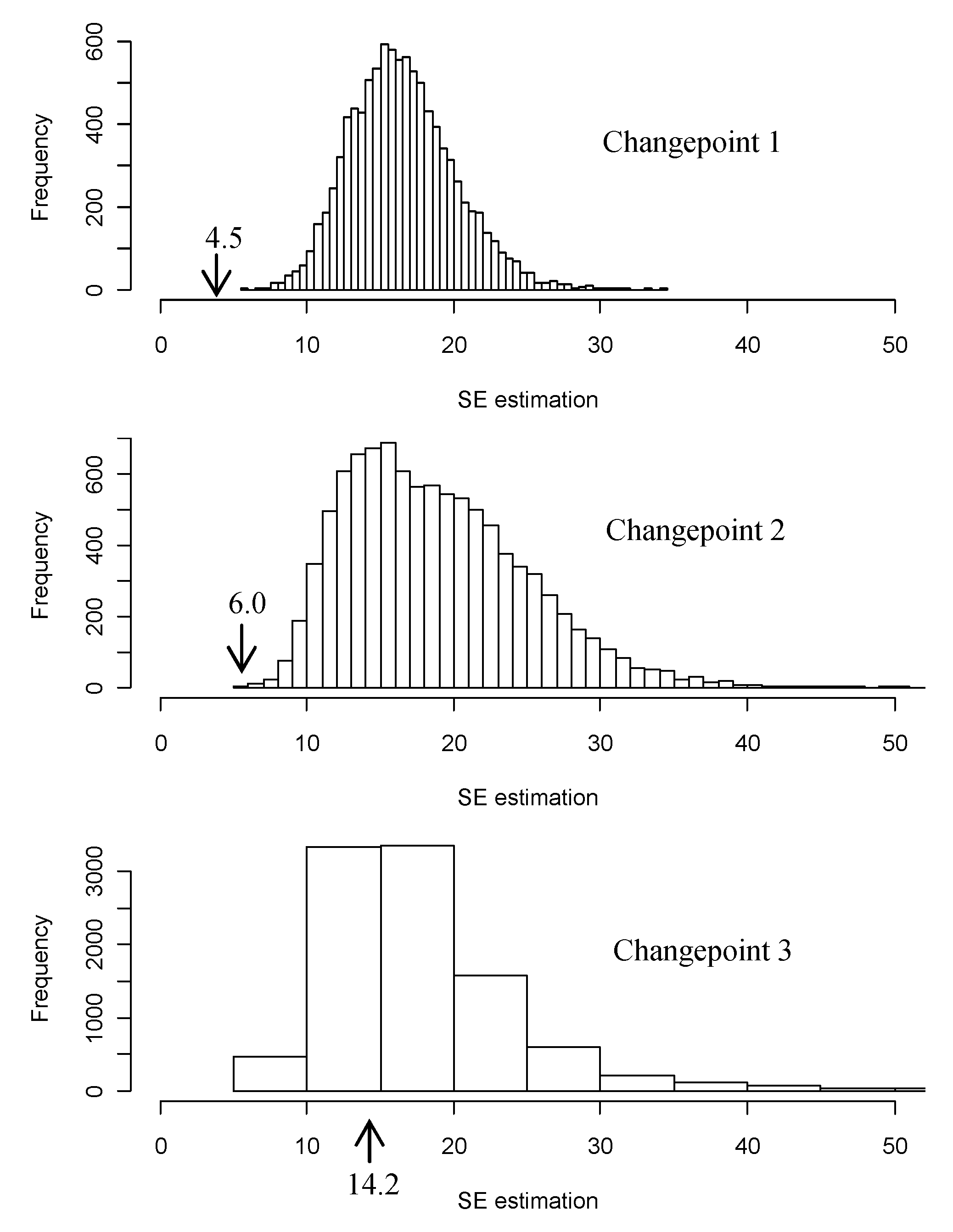
Appendix A. A Monte Carlo Study of Potential Biases of the Segmented Algorithm

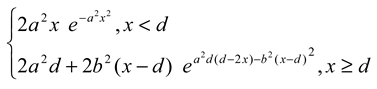

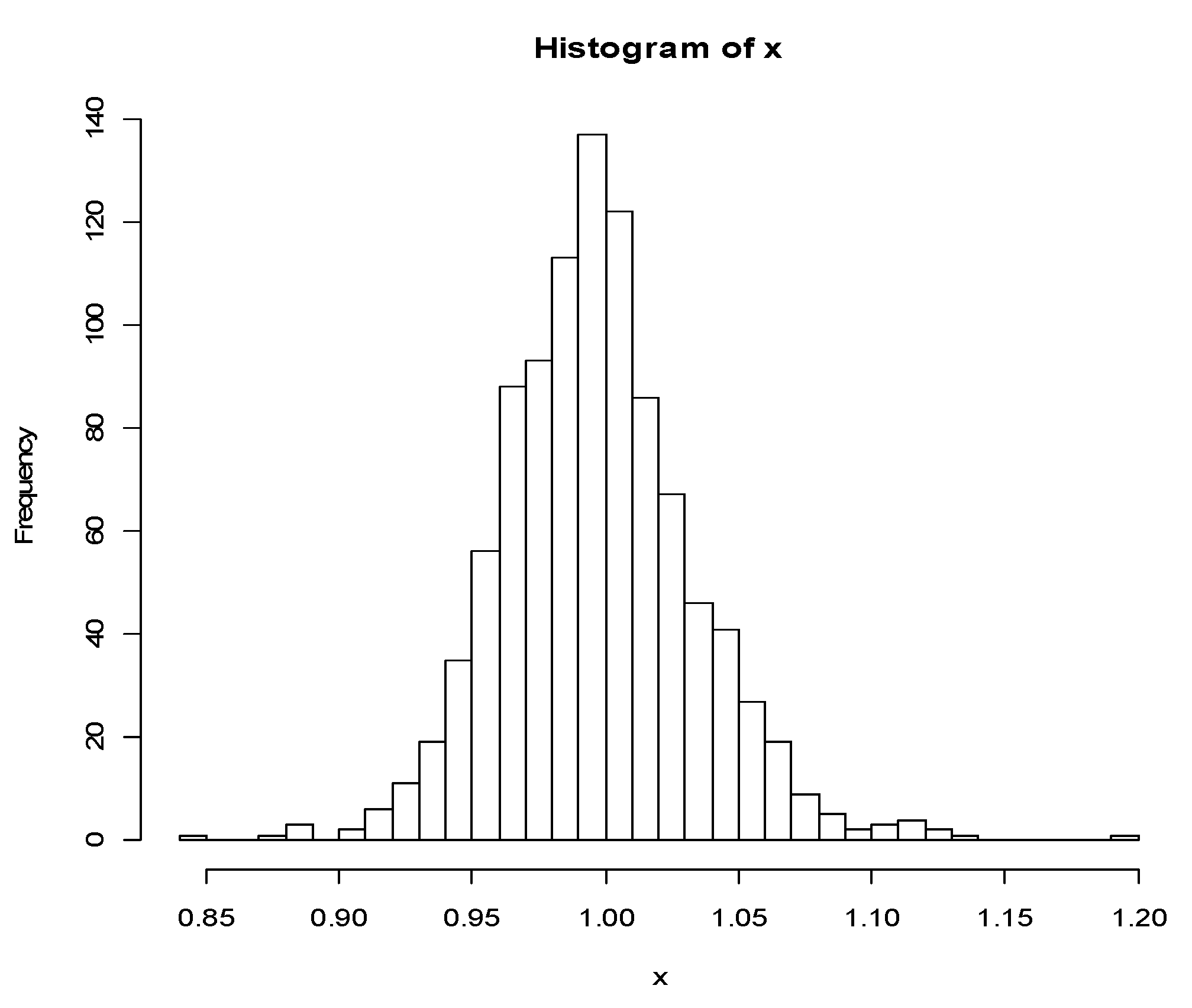
Appendix B. A Bootstrap Study of Potential Biases of the Reported SE
References
- Aalen, O. O. 1989. A linear regression model for the analysis of life times. Statistics in Medicine 8: 907–925. [Google Scholar] [PubMed]
- Aalen, O. O. 1993. Further results on the non-parametric linear regression model in survival analysis. Statistics in Medicine 12: 1569–1588. [Google Scholar]
- Barlow, R. E., A. W. Marshall, and F. Proschan. 1963. Properties of Probability Distributions with Monotone Hazard Rate. The Annals of Mathematical Statistics 34: 375–389. [Google Scholar]
- Carpenter, R. H., and M. L. Williams. 1995. Neural computation of log likelihood in control of saccadic eye movements. Nature 377: 59–62. [Google Scholar] [CrossRef] [PubMed]
- Carpenter, R. H. S. 1988. Movements of the eyes, 2nd rev. & enlarged ed. Pion Limited. [Google Scholar]
- Carpenter, R. H. S. 1999. A neural mechanism that randomises behaviour. Journal of Consciousness Studies 6: 13–22. [Google Scholar]
- Carpenter, R. H. S. 2000. The neural control of looking. Current Biology 10: R291–R293. [Google Scholar]
- Carpenter, R. H. S., and S. McDonald. 2007. LATER predicts saccade latency distributions in reading. Experimental Brain Research 177: 176–183. [Google Scholar]
- Chechile, R. 2003. Mathematical tools for hazard function analysis. Journal of Mathematical Psychology 47: 478–494. [Google Scholar]
- Clifton, C., A. Staub, and K. Rayner. 2007. Eye movements in reading words and sentences. In Eye movements: A window on mind and brain. Edited by R. v. Gompel. Elsevier: pp. 341–372. [Google Scholar]
- Cox, D. R. 1972. Regression Models and Life Tables. Journal of the Royal Statistical Society. Series B 34: 187–220. [Google Scholar]
- Cutsuridis, V., N. Smyrnis, I. Evdokimidis, and S. Perantonis. 2007. A neural model of decision-making by the superior colicullus in an antisaccade task. Neural Networks 20: 690–704. [Google Scholar]
- Dambacher, M., and R. Kliegl. 2007. Synchronizing timelines: Relations between fixation durations and N400 amplitudes during sentence reading. Brain Research 1155: 147–162. [Google Scholar] [PubMed]
- Duchowski, A. T. 2003. Eye Tracking Methodology: Theory and Practice. Springer. [Google Scholar]
- Engbert, R., and R. Kliegl. 2001. Mathematical models of eye movements in reading: a possible role for autonomous saccades. Biological Cybernetics 85: 77–87. [Google Scholar]
- Engbert, R., and R. Kliegl. 2003. Microsaccades uncover the orientation of covert attention. Vision Research 43: 1035–1045. [Google Scholar]
- Engbert, R., A. Nuthmann, E. Richter, and R. Kliegl. 2005. SWIFT: A dynamical model of saccade generation during reading. Psychological Review 112: 777–813. [Google Scholar]
- Feng, G. 2003. From eye movement to cognition: Toward ageneral framework of inference. Comment on Liechty et al., 2003. Psychometrika 68: 551–556. [Google Scholar]
- Feng, G. 2006. Eye movements as time-series random variables: A stochastic model of eye movement control in reading. Cognitive Systems Research 7: 70–95. [Google Scholar]
- Feng, G. 2009. Mixed Responses: Why Readers Spend Less Time at Unfavorable Landing Positions. Journal of Eye Movement Research 3, 2: 1–26. [Google Scholar]
- Feng, G., K. F. Miller, H. Shu, and H. Zhang. 2009. Orthography and the Development of Reading Processes: An Eye Movement Study of Chinese and English. Child Development 80: 720–735. [Google Scholar]
- Findlay, J. M., and R. Walker. 1999. A model of saccade generation based on parallel processing and competitive inhibition. Behavioral & Brain Sciences 22: 661–721. [Google Scholar]
- Harris, C. M., L. Hainline, I. Abramov, E. Lemerise, and C. Camenzuli. 1988. The distribution of fixation durations in infants and naive adults. Vision Research 28: 419–432. [Google Scholar]
- Hess, K., and R. Gentleman. 2008. Muhaz: Hazard function estimation in survival analysis. Available online: http://cran.r-project.org/web/packages/muhaz/index.html.
- Hosmer, D. W., and S. Lemeshow. 1999. Applied survival analysis: regression modeling of time to event data. Wiley. [Google Scholar]
- Huey, E. B. 1908. The psychology and pedagogy of reading; with a review of the history of reading and writing and of methods, texts, and hygiene in reading. M.I.T. Press. [Google Scholar]
- Inhoff, A. W., and R. Radach. 1998. Definition and computation of oculomotor measures in the study of cognitive processes. In Eye guidance in reading and scene perception. Edited by G. Underwood. Anonima Romana: pp. 29–53. [Google Scholar]
- Johnson, N. L., S. Kotz, and N. Balakrishnan. 1994. Continuous univariate distributions, 2nd ed. Wiley & Sons. [Google Scholar]
- Kennedy, A., and J. Pynte. 2005. Parafoveal-on-foveal effects in normal reading. Vision Research 45: 153–168. [Google Scholar] [PubMed]
- Lawless, J. F. 1982. Statistical models and methods for lifetime data. Wiley. [Google Scholar]
- Le, C. T. 1997. Applied survival analysis. Wiley. [Google Scholar]
- Luce, R. D. 1986. Response times: their role in inferring elementary mental organization. Oxford University Press. [Google Scholar]
- Marshall, A. W., and I. Olkin. 2007. Life distributions: structure of nonparametric, semiparametric, and parametric families. Springer. [Google Scholar]
- Martinussen, T., and T. Scheike. 2006. Dynamic Regression Models for Survival Data (Statistics for Biology and Health). Springer. [Google Scholar]
- Matin, E. 1974. Saccadic suppression: a review and an analysis. Psychological bulletin 81: 899–917. [Google Scholar] [PubMed]
- McConkie, G. W. 1981. Evaluating and reporting data quality in eye movement research. Behavior Research Methods & Instrumentation 13: 97–106. [Google Scholar]
- McConkie, G. W., and B. P. Dyre. 2000. Eye fixation durations in reading: Models of frequency distributions. In Reading as a perceptual process. Edited by A. Kennedy, R. Radach, D. Heller and J. Pynte. Elsevier Science Ltd. [Google Scholar]
- McConkie, G. W., P. W. Kerr, and B. P. Dyre. 1994. What are "normal "eye movements during reading: Toward a mathematical description. In Eye movements in reading. Edited by J. Ygge and G. Lennerstrand. Pergamon: pp. 315–327. [Google Scholar]
- McConkie, G. W., D. Zola, J. Grimes, P. W. Kerr, N. R. Bryant, and P. M. Wolff. 1991. Children’s eye movements during reading. In Vision and visual dyslexia. Edited by J. F. Stein. Macmillan Press: pp. 251–262. [Google Scholar]
- McDonald, S. A., R. H. S. Carpenter, and R. C. Shillcock. 2005. An anatomically constrained, stochastic model of eye movement control in reading. Psychological review 112: 814–840. [Google Scholar]
- Morrison, R. E. 1984. Manipulation of stimulus onset delay in reading: Evidence for parallel programming of saccades. Journal of Experimental Psychology: Human Perception & Performance 10: 667–682. [Google Scholar]
- Moscoso Del Prado Martin, F. submitted. A Theory of Reaction Time Distributions. Behavior and Brain Sciences.
- Muggeo, V. M. R. 2008. segmented: An R package to fit regression models with broken-line relationships. R News 8: 20–25. [Google Scholar]
- Munoz, D. 2002. Saccadic eye movements: overview of neural circuitry. In The Brain’s eye: Neurobiological and clinical aspects of oculomotor research. Edited by J. Hyona, D. P. Munoz, W. Heide and R. Radach. Elsevier: pp. 89–96. [Google Scholar]
- Nakahara, H., K. Nakamura, and O. Hikosaka. 2006. Extended LATER model can account for trial-by-trial variability of both pre-and post-processes. Neural Networks 19: 1027–1046. [Google Scholar]
- Pynte, J., and A. Kennedy. 2006. An influence over eye movements in reading exerted from beyond the level of the word: Evidence from reading English and French. Vision Research 46: 3786–3801. [Google Scholar]
- R Development Core Team. 2008. R: A language and environment for statistical computing. R Foundation. [Google Scholar]
- Ratcliff, R. 1979. Group reaction time distributions and an analysis of distribution statistics. Psychological Bulletin 86: 446–461. [Google Scholar]
- Rayner, K. 1986. Eye movements and the perceptual span in beginning and skilled readers. Journal of Experimental Child Psychology 41: 211–236. [Google Scholar]
- Rayner, K. 1998. Eye movements in reading and information processing: 20 years of research. Psychological Bulletin 124: 372–422. [Google Scholar] [CrossRef] [PubMed]
- Rayner, K. 2009. Eye movements and attention in reading, scene perception, and visual search. The Quarterly Journal of Experimental Psychology. [Google Scholar] [CrossRef] [PubMed]
- Reddi, B. A., K. N. Asrress, and R. H. Carpenter. 2003. Accuracy, information, and response time in a saccadic decision task. J Neurophysiol 90: 3538–3546. [Google Scholar] [CrossRef] [PubMed]
- Reichle, E. D., A. Pollatsek, D. L. Fisher, and K. Rayner. 1998. Toward a model of eye movement control in reading. Psychological Review 105: 125–157. [Google Scholar] [CrossRef]
- Reichle, E. D., A. Pollatsek, and K. Rayner. 2006. E-Z reader: A cognitive-control, serial-attention model of eye-movement behavior during reading. Cognitive Systems Research 7: 4–22. [Google Scholar] [CrossRef]
- Reichle, E. D., K. Rayner, and A. Pollatsek. 1999. Eye movement control in reading: accounting for initial fixation locations and refixations within the E-Z Reader model. Vision Research 39: 4403–4411. [Google Scholar] [CrossRef]
- Reichle, E. D., K. Rayner, and A. Pollatsek. 2003. The E-Z Reader model of eye-movement control in reading: Comparisons to other models. [Google Scholar]
- Reichle, E. D., T. Warren, and K. McConnell. 2009. Using E-Z Reader to model the effects of higer-level language processing on eye movements during reading. Behavioral and Brain Sciences Psychonomic Bulletin & Review 16: 1–21. [Google Scholar]
- Reilly, R. G., and J. K. O’Regan. 1998. Eye movement control during reading: A simulation of some word-targeting strategies. Vision Research 38: 303–317. [Google Scholar]
- Richter, E. M., R. Engbert, and R. Kliegl. 2006. Current advances in SWIFT. Cognitive Systems Research 7: 23–33. [Google Scholar]
- Robert, C. 1991. Generalized inverse normal distributions. Statistics & Probability Letters 11: 37–41. [Google Scholar]
- Sereno, S. C., and K. Rayner. 2003. Measuring word recognition in reading: eye movements and event-related potentials. Trends in Cognitive Sciences 7: 489–493. [Google Scholar] [PubMed]
- Suppes, P. 1990. Eye-movement models for arithmetic and reading performance. In Eye movements and their role in visual and cognitive processes. Edited by E. Kowler. Elsevier: Vol. 4, pp. 455–477. [Google Scholar]
- Suppes, P. 1994. Stochastic models of reading. In Eye movements in reading. Edited by J. Ygge and G. Lennerstrand. Pergamon Press: pp. 349–4364. [Google Scholar]
- Suppes, P. M., Laddaga Cohen R., J. Anliker, and R. Floyd. 1983. A procedural theory of eye movements in doing arithmetic. Journal of Mathematical Psychology 27: 341–369. [Google Scholar]
- Tukey, J. W. 1977. Exploratory Data Analysis. Addison-Wesley. [Google Scholar]
- Van Zandt, T. 2000. How to fit a response time distribution. Psychonomic bulletin & review 7: 424–465. [Google Scholar]
- Van Zandt, T., and R. Ratcliff. 1995. Statistical mimicking of reaction time data: Single-process models, parameter variability, and mixtures. Psychonomic Bulletin & Review 2: 20–54. [Google Scholar]
- Wolverton, G. S., and D. Zola. 1983. The temporal characteristics of visual information extraction during reading. In Eye movements in reading: Perceptual and language processes. Edited by K. Rayner. Academic Press: pp. 41–52. [Google Scholar]
- Yang, S.-n. 2006. An oculomotor-based model of eye movements in reading: The competition/Interaction model. Cognitive Systems Research 7: 56–69. [Google Scholar]
- Yang, S.-N., and G. W. McConkie. 2001. Eye movements during reading: a theory of saccade initiation times. Vision Research 41: 3567–3585. [Google Scholar]





Copyright © 2009. This article is licensed under a Creative Commons Attribution 4.0 International license.
Share and Cite
Feng, G. Time Course and Hazard Function: A Distributional Analysis of Fixation Duration in Reading. J. Eye Mov. Res. 2009, 3, 1-23. https://doi.org/10.16910/jemr.3.2.3
Feng G. Time Course and Hazard Function: A Distributional Analysis of Fixation Duration in Reading. Journal of Eye Movement Research. 2009; 3(2):1-23. https://doi.org/10.16910/jemr.3.2.3
Chicago/Turabian StyleFeng, Gary. 2009. "Time Course and Hazard Function: A Distributional Analysis of Fixation Duration in Reading" Journal of Eye Movement Research 3, no. 2: 1-23. https://doi.org/10.16910/jemr.3.2.3
APA StyleFeng, G. (2009). Time Course and Hazard Function: A Distributional Analysis of Fixation Duration in Reading. Journal of Eye Movement Research, 3(2), 1-23. https://doi.org/10.16910/jemr.3.2.3



