GMM-HMM-Based Eye Movement Classification for Efficient and Intuitive Dynamic Human–Computer Interaction Systems
Abstract
1. Introduction
- An Advanced Gaussian Mixture Model–Hidden Markov Model (GMM-HMM)-Based Algorithm for Ternary Eye Movement Classification: A novel algorithm is proposed, integrating a sum of squared error (SSE) metric for improved feature extraction and hierarchical training. This algorithm demonstrates higher accuracy compared to current mainstream methods and is well-suited for use with commercial-grade eye trackers, enabling robust and adaptable ternary eye movement classification.
- Integration of GMM-HMM with a Robotic Arm for Gaze-Guided Interaction: The proposed algorithm is seamlessly integrated with a robotic arm system, enabling gaze trajectories to directly guide robotic motion. This approach eliminates dependence on graphical user interfaces or static target selection, providing a dynamic and intuitive solution to human–computer interaction. Compared to traditional gaze-based target selection combined with path-planning methods, the proposed algorithm demonstrates a significant advantage in real-time performance. Experimental results validate the robotic arm’s motion trajectories, confirming the feasibility of key performance indicators such as trajectory curvature variation, angular deviation, and path jitter in handling complex tasks. This integration bridges the gap between gaze behavior recognition and practical interaction, offering a robust and efficient framework for dynamic scenarios.
2. Related Work
2.1. Eye Movement Classification
2.2. Eye Tracking and HCI
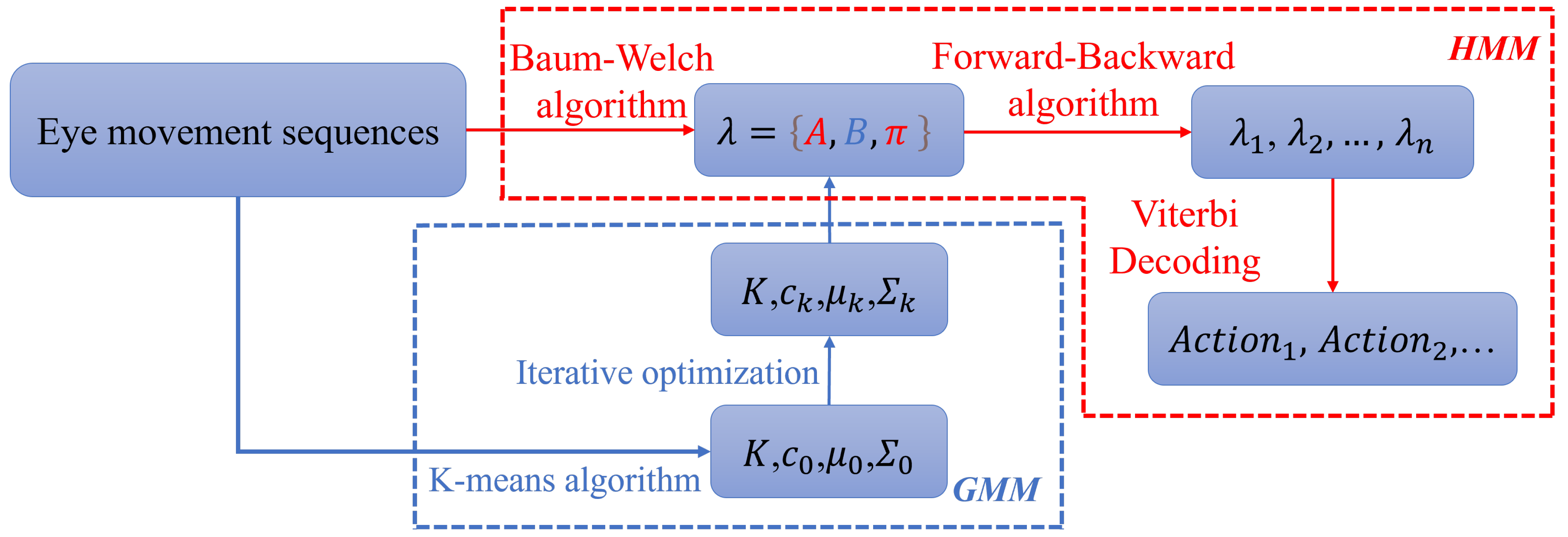
3. GMM-HMM for Eye Movement Classification
3.1. GMM-HMM Model Framework for Gaze Extraction
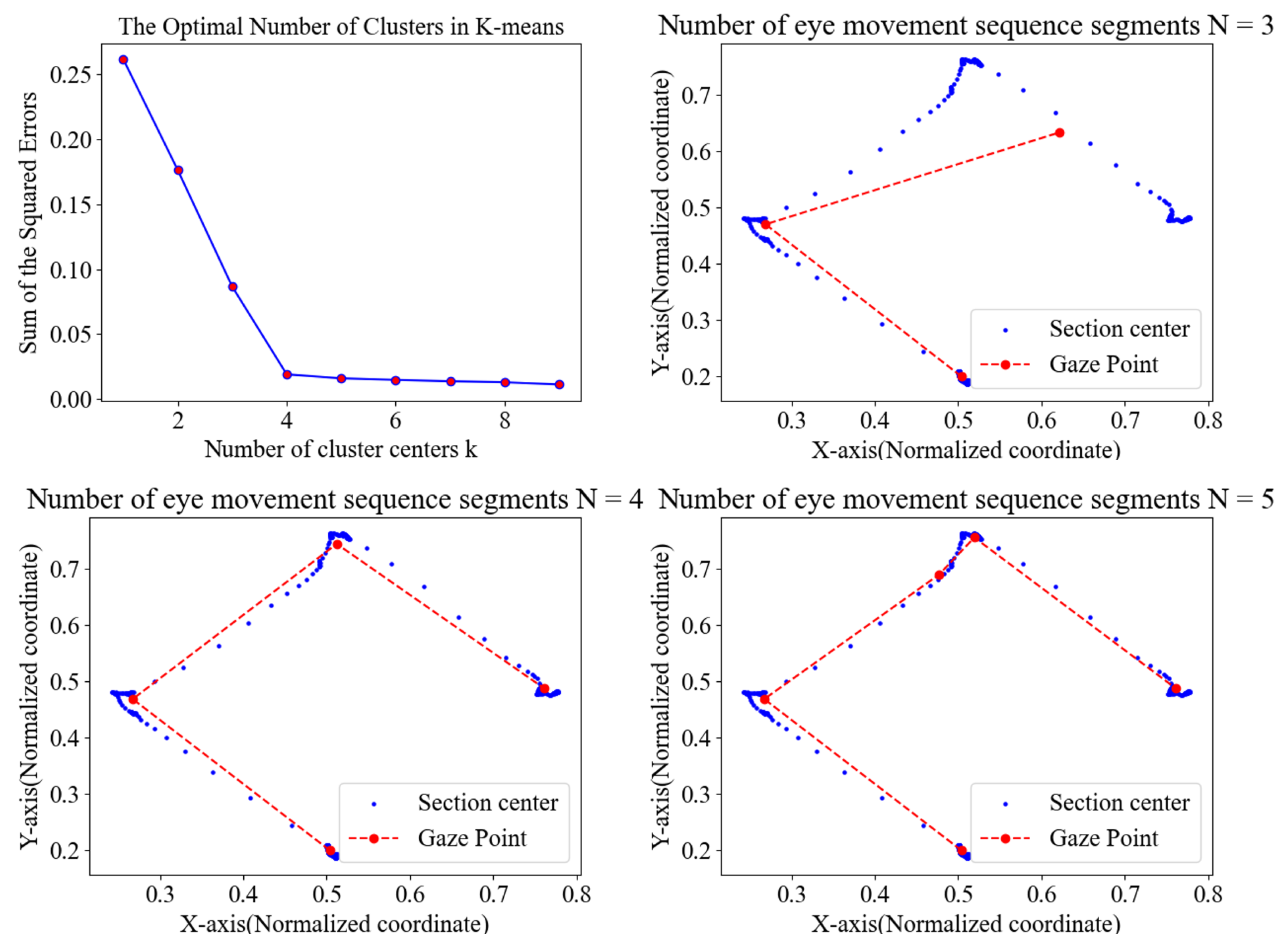
3.2. Eye Movement Path Segmentation
| Algorithm 1 Kmeans-SSE |
|
3.3. Hierarchical GMM-HMM Algorithm Implementation
| Algorithm 2 Hierarchical GMM-HMM based on SSE |
|
4. Experimental Setup and Comparative Analysis
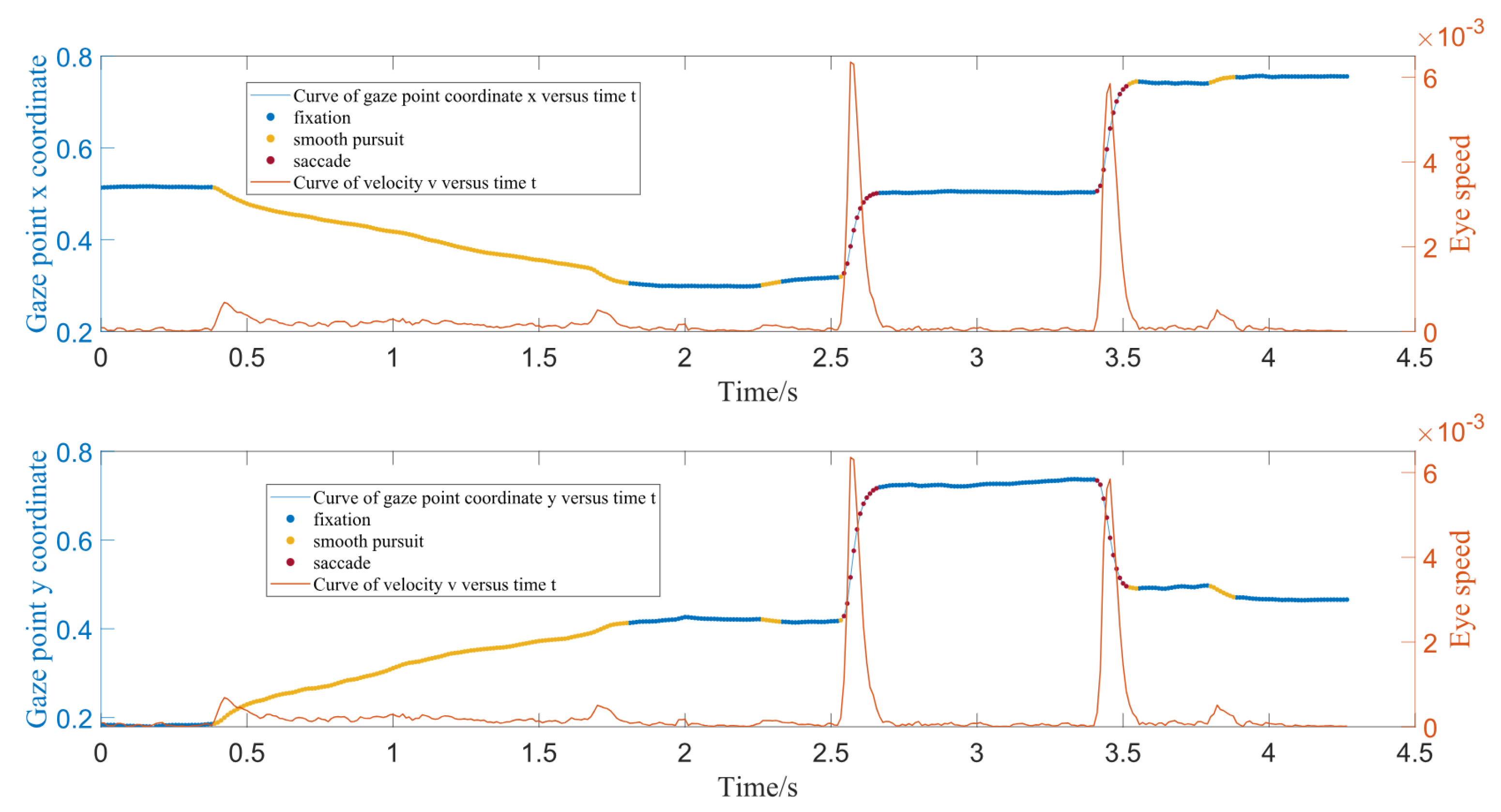
4.1. Data Collection Methods
4.2. Comparison of Classification Algorithms
5. Implementation in Robotic Arm Interaction
5.1. System Architecture and Calibration
5.2. Gaze-Guided Grasping Strategy and Experimental Design
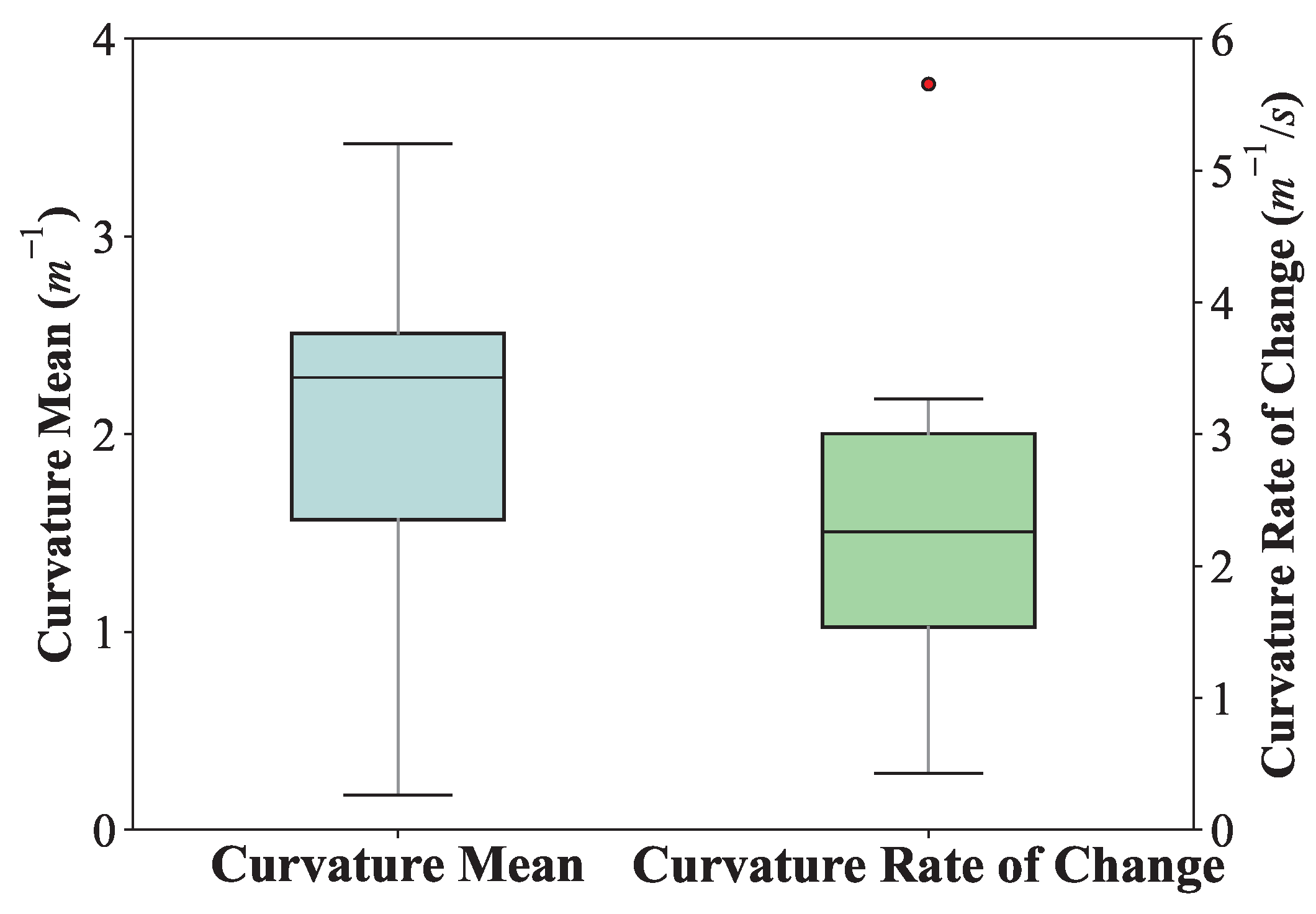
5.3. Results and Comparative Analysis
6. Limitations and Future Work
- Improving System Robustness: Efforts will be directed toward enhancing the robustness of the system. This includes applying filtering and compensation techniques to the camera’s point cloud data, as well as employing Kalman filtering and other advanced methods, such as Unscented Kalman Filtering, to filter eye-tracking data. These techniques will help eliminate errors introduced by gaze drift, improving the system’s overall robustness and accuracy.
- Enhancing Model Capabilities with HMM: The second direction involves leveraging Hidden Markov Models (HMMs) to address evaluation challenges. Specifically, different models will be trained for various eye-tracking trajectories, enabling the system to perform different tasks based on the classified gaze behaviors. While the current approach relies primarily on the decoding capabilities of HMM for classifying eye movements in trajectories, future work will explore combining the two capabilities—trajectory filtering and gaze intent recognition—toward expanding the range of possible applications for this system.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Majaranta, P.; Bulling, A. Eye tracking and eye-based human–computer interaction. In Advances in Physiological Computing; Springer: Berlin/Heidelberg, Germany, 2014; pp. 39–65. [Google Scholar]
- Klaib, A.F.; Alsrehin, N.O.; Melhem, W.Y.; Bashtawi, H.O.; Magableh, A.A. Eye tracking algorithms, techniques, tools, and applications with an emphasis on machine learning and Internet of Things technologies. Expert Syst. Appl. 2021, 166, 114037. [Google Scholar]
- Khan, W.; Topham, L.; Alsmadi, H.; Al Kafri, A.; Kolivand, H. Deep face profiler (DeFaP): Towards explicit, non-restrained, non-invasive, facial and gaze comprehension. Expert Syst. Appl. 2024, 254, 124425. [Google Scholar]
- Isomoto, T.; Yamanaka, S.; Shizuki, B. Interaction Design of Dwell Selection Toward Gaze-Based AR/VR Interaction. In Proceedings of the 2022 Symposium on Eye Tracking Research and Applications (ETRA ’22), Seattle, WA, USA, 8–11 June 2022; Association for Computing Machinery: New York, NY, USA, 2022. Article 39. pp. 1–2. [Google Scholar] [CrossRef]
- Carter, B.T.; Luke, S.G. Best practices in eye tracking research. Int. J. Psychophysiol. 2020, 155, 49–62. [Google Scholar] [PubMed]
- Cio, Y.S.L.K.; Raison, M.; Menard, C.L.; Achiche, S. Proof of concept of an assistive robotic arm control using artificial stereovision and eye-tracking. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 2344–2352. [Google Scholar]
- Perez Reynoso, F.D.; Niño Suarez, P.A.; Aviles Sanchez, O.F.; Calva Yañez, M.B.; Vega Alvarado, E.; Portilla Flores, E.A. A custom EOG-based HMI using neural network modeling to real-time for the trajectory tracking of a manipulator robot. Front. Neurorobotics 2020, 14, 578834. [Google Scholar]
- Meena, Y.K.; Cecotti, H.; Wong-Lin, K.; Prasad, G. A multimodal interface to resolve the Midas-Touch problem in gaze controlled wheelchair. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju, Republic of Korea, 11–15 July 2017; pp. 905–908. [Google Scholar]
- Andersson, R.; Larsson, L.; Holmqvist, K.; Stridh, M.; Nyström, M. One algorithm to rule them all? An evaluation and discussion of ten eye movement event-detection algorithms. Behav. Res. Methods 2017, 49, 616–637. [Google Scholar]
- Komogortsev, O.V.; Gobert, D.V.; Jayarathna, S.; Koh, D.H.; Gowda, S.M. Standardization of automated analyses of oculomotor fixation and saccadic behaviors. IEEE Trans. Biomed. Eng. 2010, 57, 2635–2645. [Google Scholar]
- Prabha, A.J.; Bhargavi, R. Predictive model for dyslexia from fixations and saccadic eye movement events. Comput. Methods Programs Biomed. 2020, 195, 105538. [Google Scholar] [CrossRef]
- Komogortsev, O.V.; Karpov, A. Automated classification and scoring of smooth pursuit eye movements in the presence of fixations and saccades. Behav. Res. Methods 2013, 45, 203–215. [Google Scholar]
- Wolfe, J.M.; Horowitz, T.S. Five factors that guide attention in visual search. Nat. Hum. Behav. 2017, 1, 0058. [Google Scholar] [CrossRef]
- Zhu, Y.; Yan, Y.; Komogortsev, O. Hierarchical HMM for eye movement classification. In Proceedings of the Computer Vision–ECCV 2020 Workshops, Glasgow, UK, 23–28 August 2020; Proceedings, Part I 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 544–554. [Google Scholar]
- Santini, T.; Fuhl, W.; Kübler, T.; Kasneci, E. Bayesian identification of fixations, saccades, and smooth pursuits. In Proceedings of the Ninth Biennial ACM Symposium on Eye Tracking Research and Applications, New York, NY, USA, 14–17 March 2016; pp. 163–170. [Google Scholar]
- Startsev, M.; Agtzidis, I.; Dorr, M. 1D CNN with BLSTM for automated classification of fixations, saccades, and smooth pursuits. Behav. Res. Methods 2019, 51, 556–572. [Google Scholar] [PubMed]
- Goltz, J.; Grossberg, M.; Etemadpour, R. Exploring simple neural network architectures for eye movement classification. In Proceedings of the 11th ACM Symposium on Eye Tracking Research & Applications, New York, NY, USA, 25–28 June 2019; pp. 1–5. [Google Scholar]
- Majaranta, P.; Räihä, K.J.; Hyrskykari, A.; Špakov, O. Eye Movements and Human-Computer Interaction. In Eye Movement Research: An Introduction to Its Scientific Foundations and Applications; Klein, C., Ettinger, U., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 971–1015. [Google Scholar] [CrossRef]
- Dar, A.H.; Wagner, A.S.; Hanke, M. REMoDNaV: Robust eye-movement classification for dynamic stimulation. Behav. Res. Methods 2021, 53, 399–414. [Google Scholar] [PubMed]
- Fischer-Janzen, A.; Wendt, T.M.; Van Laerhoven, K. A scoping review of gaze and eye tracking-based control methods for assistive robotic arms. Front. Robot. 2024, 11, 1326670. [Google Scholar]
- Stalljann, S.; Wöhle, L.; Schäfer, J.; Gebhard, M. Performance analysis of a head and eye motion-based control interface for assistive robots. Sensors 2020, 20, 7162. [Google Scholar] [CrossRef]
- Sunny, M.S.H.; Zarif, M.I.I.; Rulik, I.; Sanjuan, J.; Rahman, M.H.; Ahamed, S.I.; Wang, I.; Schultz, K.; Brahmi, B. Eye-gaze control of a wheelchair mounted 6DOF assistive robot for activities of daily living. J. Neuroeng. Rehabil. 2021, 18, 1–12. [Google Scholar]
- Cojocaru, D.; Manta, L.F.; Pană, C.F.; Dragomir, A.; Mariniuc, A.M.; Vladu, I.C. The design of an intelligent robotic wheelchair supporting people with special needs, including for their visual system. Healthcare 2021, 10, 13. [Google Scholar] [CrossRef]
- Krishna Sharma, V.; Saluja, K.; Mollyn, V.; Biswas, P. Eye Gaze Controlled Robotic Arm for Persons with Severe Speech and Motor Impairment. In Proceedings of the ACM Symposium on Eye Tracking Research and Applications (ETRA ’20 Full Papers), Stuttgart, Germany, 2–5 June 2020; Association for Computing Machinery: New York, NY, USA, 2020. Article 12. pp. 1–9. [Google Scholar] [CrossRef]
- Li, S.; Zhang, X.; Webb, J.D. 3-D-gaze-based robotic grasping through mimicking human visuomotor function for people with motion impairments. IEEE Trans. Biomed. Eng. 2017, 64, 2824–2835. [Google Scholar]
- Yang, B.; Huang, J.; Sun, M.; Huo, J.; Li, X.; Xiong, C. Head-free, human gaze-driven assistive robotic system for reaching and grasping. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 4138–4143. [Google Scholar]
- Wang, Y.; Xu, G.; Song, A.; Xu, B.; Li, H.; Hu, C.; Zeng, H. Continuous shared control for robotic arm reaching driven by a hybrid gaze-brain machine interface. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4462–4467. [Google Scholar] [CrossRef]
- Tostado, P.M.; Abbott, W.W.; Faisal, A.A. 3D gaze cursor: Continuous calibration and end-point grasp control of robotic actuators. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 3295–3300. [Google Scholar] [CrossRef]
- Gwak, S.; Park, K. Designing Effective Visual Feedback for Facial Rehabilitation Exercises: Investigating the Role of Shape, Transparency, and Age on User Experience. Healthcare 2023, 11, 1835. [Google Scholar] [CrossRef]
- Wöhle, L.; Gebhard, M. Towards robust robot control in cartesian space using an infrastructureless head-and eye-gaze interface. Sensors 2021, 21, 1798. [Google Scholar]
- Velichkovsky, B.; Sprenger, A.; Unema, P. Towards gaze-mediated interaction: Collecting solutions of the “Midas touch problem”. In Proceedings of the Human-Computer Interaction INTERACT’97: IFIP TC13 International Conference on Human-Computer Interaction, Sydney, Australia, 14–18 July 1997; pp. 509–516. [Google Scholar] [CrossRef]
- Swietojanski, P.; Ghoshal, A.; Renals, S. Revisiting hybrid and GMM-HMM system combination techniques. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6744–6748. [Google Scholar] [CrossRef]
- Xuan, G.; Zhang, W.; Chai, P. EM algorithms of Gaussian mixture model and hidden Markov model. In Proceedings of the 2001 International Conference on Image Processing (Cat. No. 01CH37205), Thessaloniki, Greece, 7–10 October 2001; Volume 1, pp. 145–148. [Google Scholar] [CrossRef]
- Rabiner, L.; Juang, B. An introduction to hidden Markov models. IEEE Assp Mag. 1986, 3, 4–16. [Google Scholar] [CrossRef]
- Nainggolan, R.; Perangin-angin, R.; Simarmata, E.; Tarigan, A.F. Improved the performance of the K-means cluster using the sum of squared error (SSE) optimized by using the Elbow method. J. Physics Conf. Ser. 2019, 1361, 012015. [Google Scholar] [CrossRef]
- Golluccio, G.; Gillini, G.; Marino, A.; Antonelli, G. Robot dynamics identification: A reproducible comparison with experiments on the Kinova Jaco. IEEE Robot. Autom. Mag. 2020, 28, 128–140. [Google Scholar] [CrossRef]
- Tsai, R.Y.; Lenz, R.K. A new technique for fully autonomous and efficient 3 d robotics hand/eye calibration. IEEE Trans. Robot. Autom. 1989, 5, 345–358. [Google Scholar] [CrossRef]
- He, P.F.; Fan, P.F.; Wu, S.E.; Zhang, Y. Research on Path Planning Based on Bidirectional A* Algorithm. IEEE Access 2024, 12, 109625–109633. [Google Scholar] [CrossRef]
- Fusic, S.J.; Ramkumar, P.; Hariharan, K. Path planning of robot using modified dijkstra Algorithm. In Proceedings of the 2018 National Power Engineering Conference (NPEC), Madurai, India, 9–10 March 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Nowakiewicz, M. MST-Based method for 6DOF rigid body motion planning in narrow passages. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 5380–5385. [Google Scholar] [CrossRef]
- Liu, X.; Nie, H.; Li, D.; He, Y.; Ang, M.H. High-Fidelity and Curvature-Continuous Path Smoothing with Quadratic Bézier Curve. IEEE Trans. Intell. Veh. 2024, 9, 3796–3810. [Google Scholar] [CrossRef]
- Kano, H.; Fujioka, H. B-spline trajectory planning with curvature constraint. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 1963–1968. [Google Scholar] [CrossRef]
- Miao, X.; Fu, H.; Song, X. Research on motion trajectory planning of the robotic arm of a robot. Artif. Life Robot. 2022, 27, 561–567. [Google Scholar] [CrossRef]
- Wei, H.; Lu, W.; Zhu, P.; Huang, G.; Leonard, J.; Ferrari, S. Optimized visibility motion planning for target tracking and localization. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 76–82. [Google Scholar] [CrossRef]
- Yang, B.; Huang, J.; Chen, X.; Li, X.; Hasegawa, Y. Natural grasp intention recognition based on gaze in human–robot interaction. IEEE J. Biomed. Health Inform. 2023, 27, 2059–2070. [Google Scholar]


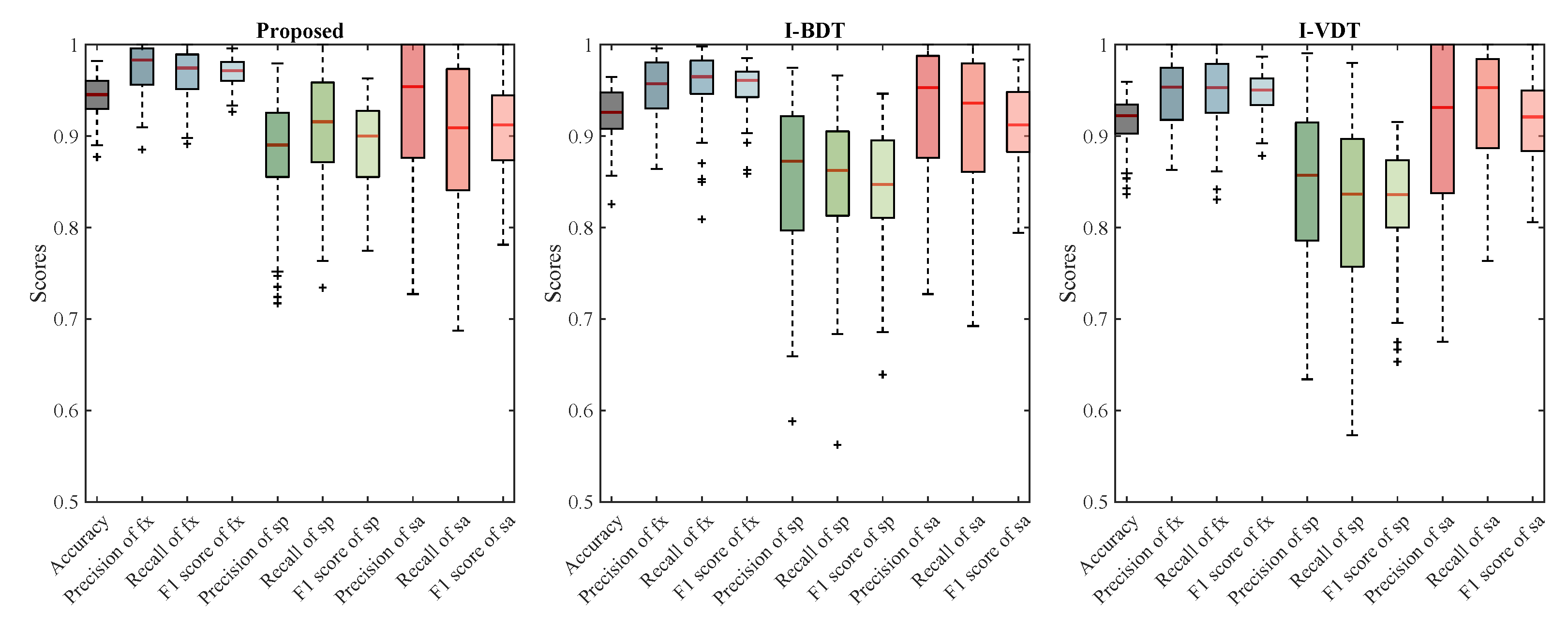


| Algorithm | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|
| Proposed | , | , | , | , |
| I-BDT | , | , | , | , |
| I-VDT | , | , | , | , |
| Fixation | Precision | Recall | F1 Score |
|---|---|---|---|
| Proposed | 0.9743 | 0.9665 | 0.9699 |
| I-BDT | 0.9514 | 0.9553 | 0.9527 |
| I-VDT | 0.9447 | 0.9487 | 0.9457 |
| Smooth Pursuit | Precision | Recall | F1 Score |
|---|---|---|---|
| Proposed | 0.8784 | 0.9076 | 0.8893 |
| I-BDT | 0.8530 | 0.8473 | 0.8445 |
| I-VDT | 0.8439 | 0.8226 | 0.8271 |
| Saccade | Precision | Recall | F1 Score |
|---|---|---|---|
| Proposed | 0.9301 | 0.8967 | 0.9077 |
| I-BDT | 0.9208 | 0.9135 | 0.9116 |
| I-VDT | 0.9094 | 0.9335 | 0.9162 |
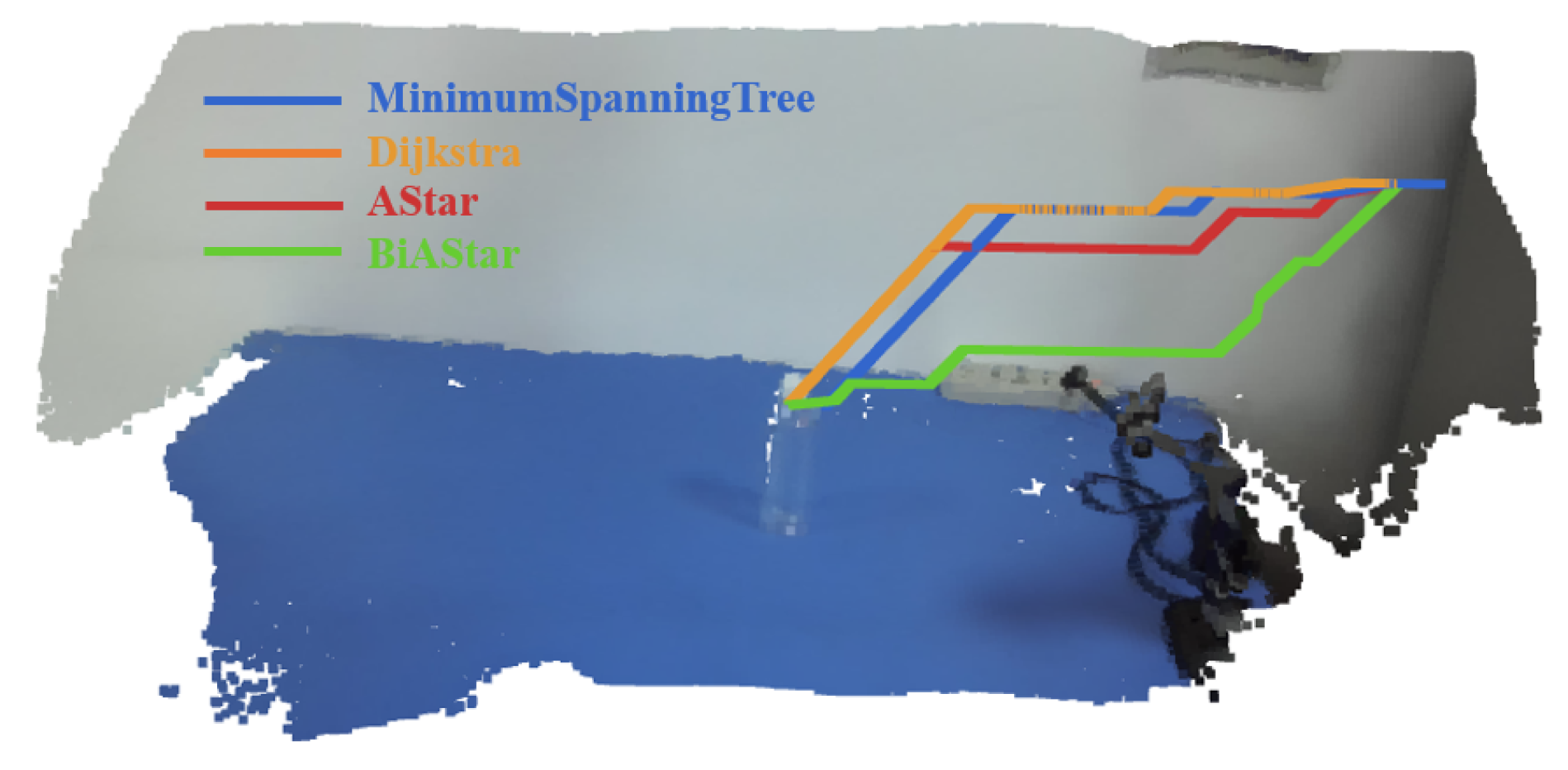
| Planning Methods | Mean (ms) | Std Dev (ms) | CoV (%) | Median (ms) | Success Rate (%) |
|---|---|---|---|---|---|
| Proposed | 2.97 | 0.83 | 27.81 | 3.00 | 91.00 |
| A* [6] | 11.88 | 5.17 | 43.52 | 11.15 | 92.00 |
| BiA* [38] | 7.55 | 3.57 | 47.28 | 6.80 | 90.00 |
| Dijkstra [39] | 2829.50 | 749.38 | 26.48 | 2876.90 | 92.00 |
| MST [40] | 2869.37 | 1044.00 | 36.39 | 3465.80 | 92.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, J.; Chen, R.; Liu, Z.; Zhou, J.; Hou, J.; Zhou, Z. GMM-HMM-Based Eye Movement Classification for Efficient and Intuitive Dynamic Human–Computer Interaction Systems. J. Eye Mov. Res. 2025, 18, 28. https://doi.org/10.3390/jemr18040028
Xie J, Chen R, Liu Z, Zhou J, Hou J, Zhou Z. GMM-HMM-Based Eye Movement Classification for Efficient and Intuitive Dynamic Human–Computer Interaction Systems. Journal of Eye Movement Research. 2025; 18(4):28. https://doi.org/10.3390/jemr18040028
Chicago/Turabian StyleXie, Jiacheng, Rongfeng Chen, Ziming Liu, Jiahao Zhou, Juan Hou, and Zengxiang Zhou. 2025. "GMM-HMM-Based Eye Movement Classification for Efficient and Intuitive Dynamic Human–Computer Interaction Systems" Journal of Eye Movement Research 18, no. 4: 28. https://doi.org/10.3390/jemr18040028
APA StyleXie, J., Chen, R., Liu, Z., Zhou, J., Hou, J., & Zhou, Z. (2025). GMM-HMM-Based Eye Movement Classification for Efficient and Intuitive Dynamic Human–Computer Interaction Systems. Journal of Eye Movement Research, 18(4), 28. https://doi.org/10.3390/jemr18040028






