Dynamics of Eye Movements Under Time Varying Stimuli
Abstract
Introduction



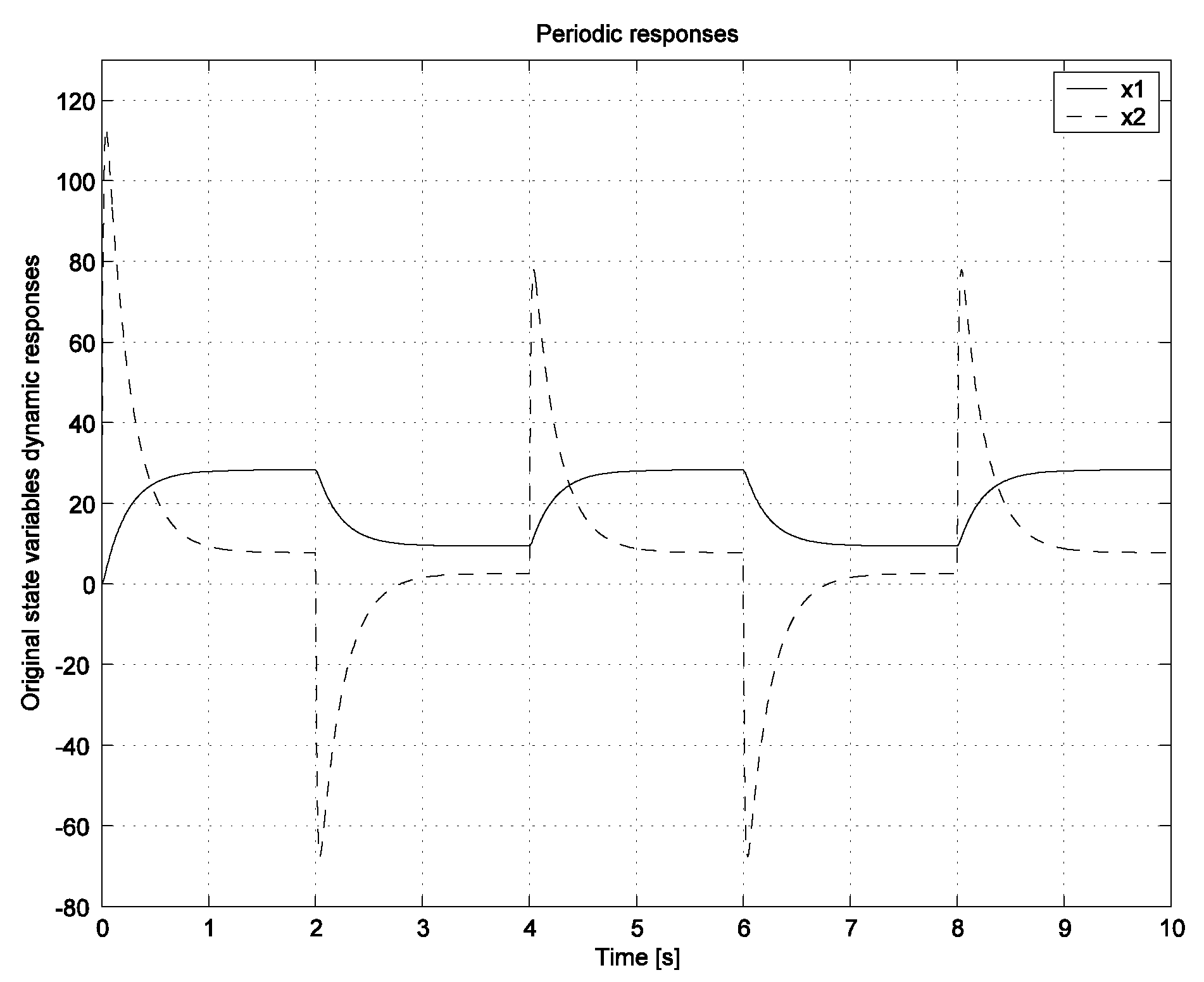
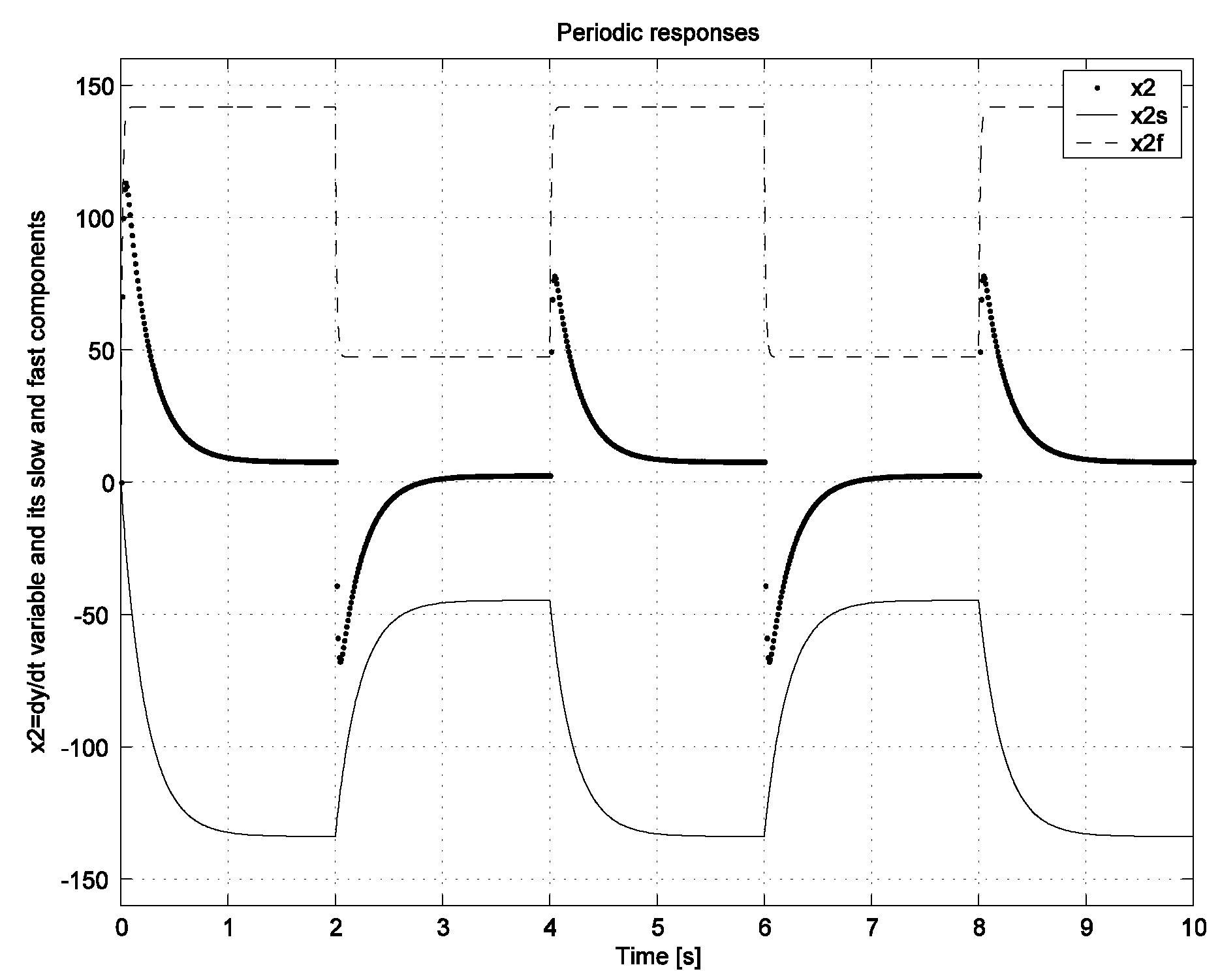
Discussion of the Obtained Simulation Results
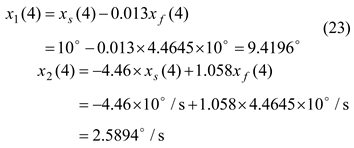
Conclusions
Ethics and Conflict of Interest
References
- Alvarez, T. L. 2015. A pilot study of disparity vergence and near dissociated phoria in convergence insufficiency patients before vs. after vergence therapy. Front Hum Neurosci 9: 419. [Google Scholar] [CrossRef][Green Version]
- Alvarez, T. L., M. Bhavsar, J. L. Semmlow, M. T. Bergen, and C. Pedrono. 2005. Short-term predictive changes in the dynamics of disparity vergence eye movements. Journal of Vision 5, 7: 4–4. [Google Scholar] [CrossRef]
- Alvarez, T. L., R. Jaswal, S. Gohel, and B. B. Biswal. 2014. Functional activity within the frontal eye fields, posterior parietal cortex, and cerebellar vermis significantly correlates to symmetrical vergence peak velocity: An ROI-based, fMRI study of vergence training. Frontiers in Integrative Neuroscience 8: 50. [Google Scholar] [CrossRef]
- Alvarez, T. L., J. L. Semmlow, and C. Pedrono. 2005. Divergence eye movements are dependent on initial stimulus position. Vision Res 45, 14: 1847–1855. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, T. L., J. L. Semmlow, and W. Yuan. 1998. Closely Spaced, Fast Dynamic Movements in Disparity Vergence. Journal of Neurophysiology 79, 1: 37–44. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, T. L., J. L. Semmlow, W. Yuan, and P. Munoz. 1999. Dynamic details of disparity convergence eye movements. Ann Biomed Eng 27, 3: 380–390. [Google Scholar] [CrossRef] [PubMed]
- Chang, K. W. 1972. Singular Perturbations of a General Boundary Value Problem. SIAM Journal on Mathematical Analysis 3, 3: 520–526. [Google Scholar] [CrossRef]
- Gajic, Z. 2003. Linear Dynamic Systems and Signals. Prentice Hall/Pearson Education. [Google Scholar]
- Horng, J. L., J. L. Semmlow, G. K. Hung, and K. J. Ciuffreda. 1998. Initial component control in disparity vergence: A model-based study. IEEE Trans Biomed Eng 45, 2: 249–257. [Google Scholar] [CrossRef] [PubMed]
- Hung, G. K. 1998. Dynamic model of the vergence eye movement system: Simulations using MATLAB/SIMULINK. Comput Methods Programs Biomed 55, 1: 59–68. [Google Scholar] [PubMed]
- Hung, G. K., J. L. Semmlow, and K. J. Ciufferda. 1986. A Dual-Mode Dynamic Model of the Vergence Eye Movement System. IEEE Transactions on Biomedical Engineering BME-33, 11: 1021–1028. [Google Scholar] [CrossRef]
- Jiang, B.-c., G. K. Hung, and K. J. Ciuffreda. 2002. Models of Vergence and AccommodationVergence Interactions. In Models of the Visual System. Edited by G. K. Hung and K. J. Ciuffreda. Boston, MA: Springer US, pp. 341–384. [Google Scholar]
- Kennard, C., and R. J. Leigh. 2008. Using Eye Movement as an Experimental Probe of Brain Function. Vol. 171. [Google Scholar]
- Khosroyani, M., and G. K. Hung. 2002. A dual-mode dynamic model of the human accommodation system. Bull Math Biol 64, 2: 285–299. [Google Scholar] [CrossRef] [PubMed]
- Kim, E. H., V. R. Vicci, B. Granger-Donetti, and T. L. Alvarez. 2011. Short-term adaptations of the dynamic disparity vergence and phoria systems. Exp Brain Res 212, 2: 267–278. [Google Scholar] [CrossRef] [PubMed]
- Kokotović, P., H. K. Khali, and J. O’Reilly. 1986. Singular Perturbation Methods in Control: Analysis and Design. Society for Industrial and Applied Mathematics. [Google Scholar]
- Lee, Y. Y., J. L. Semmlow, and T. L. Alvarez. 2012. Assessment of Dual-Mode and SwitchedChannel Models with Experimental Vergence Responses. 5, 2. [Google Scholar] [CrossRef]
- Leigh, R. J., and D. S. Zee. 2006. The Neurology of Eye Movements. Oxford University Press. [Google Scholar]
- Radisavljevic-Gajic, V. 2006. Slow-fast decoupling of the disparity convergence eye movements dynamics. Ann Biomed Eng 34, 2: 310–314. [Google Scholar] [CrossRef] [PubMed]


Copyright © 2018. This article is licensed under a Creative Commons Attribution 4.0 International License.
Share and Cite
Radisavljevic-Gajic, V. Dynamics of Eye Movements Under Time Varying Stimuli. J. Eye Mov. Res. 2018, 11, 1-7. https://doi.org/10.16910/jemr.11.1.6
Radisavljevic-Gajic V. Dynamics of Eye Movements Under Time Varying Stimuli. Journal of Eye Movement Research. 2018; 11(1):1-7. https://doi.org/10.16910/jemr.11.1.6
Chicago/Turabian StyleRadisavljevic-Gajic, Verica. 2018. "Dynamics of Eye Movements Under Time Varying Stimuli" Journal of Eye Movement Research 11, no. 1: 1-7. https://doi.org/10.16910/jemr.11.1.6
APA StyleRadisavljevic-Gajic, V. (2018). Dynamics of Eye Movements Under Time Varying Stimuli. Journal of Eye Movement Research, 11(1), 1-7. https://doi.org/10.16910/jemr.11.1.6


